Entropy generation effect of a buoyancy force on hydromagnetic heat generating couple stress fluid through a porous medium with isothermal boundaries

Abstract

This investigation addresses the influence of a buoyancy force on the flow of a couple stress hydromagnetic heat generating fluid across a porous channel with isothermal boundaries. The analytical formulations for the momentum and energy equations are derived to seek the solutions for the rate of fluid momentum, heat transfer and the rate of entropy generation with the use of a well known and efficient series solution of Adomian decomposition method (ADM). The findings are compared with earlier acquired findings for validation and hereby showed the speedy convergence of the series solution. The results showed the substantial influence of inward warmth inside the stream and buoyancy force on the motion and thermal energy of the flow system. Also, the activities of entropy generation generally occur maximally at the centreline of the flow stream with significant reduction with respect to buoyancy force and magnetic field strength.

Applied mathematics; Computational mathematics; Mathematics; Mechanical engineering; Thermodynamics; Computational fluid dynamics; Computational heat transfer; Couple stress fluid; Porous medium; Entropy generation; Internal heat generation; Buoyancy force; Adomian decomposition method

1. Introduction

Several studies exist in the literature that investigated buoyancy driven flow in which the interest is justified by its many applications in [1] which include gas turbine, nuclear plants, thermal energy storage, etc. The likely occurrence of buoyancy forces in a boundary layer flow over isothermal boundaries which affect a longitudinal pressure gradient and, by this, the velocity and heat transfer characteristics of the basic forced - convection flow may be remodeled. To buttress the significant attribute of buoyancy force on fluid flow include [2] that presents an investigation on the combined effects of buoyancy force and fluid injection/suction on heat and mass transfer by a steady hydromagnetic limited layer stream of a governing incompressible liquid that is homogeneously chemically reactive over a penetrable surface accompanied by the heat source and sink. Also, recently, [3] examined the lightness driven progression of a warmth reactive hydromagnetic fluid through a permeable channel.

Meanwhile, various analyses on couple stress fluids attract the attention of researchers due to copious industrial applications with many procedures. For example, an extrusion of polymer liquids, the refreshing of metallic plates in a shower, to reference a few as described in [4]. Other examples to show the significant account of couple stress fluid include [5] where the examination researched the effects of temperature - dependent fluid density on the reactive couple pressure liquid which is active in a vertical stream within permeable substances and of recent, [6] investigated the survey on the entropy generation of a reactive hydromagnetic couple stress fluid flow over a soaked permeable stream. Other literatures on couple stress fluid include [7], [8], [9], [10].

Still, there is need to lay more emphasis on the significant rate of entropy generation which according to [10], is a measure of the account of irreversibility associated with the real process or as measure of disorderliness in a system with respect to preserve the quality of energy in a fluid flow process in order to reduce the entropy generation. To show the significance of entropy generation as mentioned earlier, [6] recently investigated the entropy generation analysis of a reactive hydromagnetic flow of couple stress fluid flowing through a permeable substance.

However, from designing and modern applications, the impact of heat transfer on a liquid stream within parallel plates cannot be completely overlooked as the estimation of heat transfer relies on the temperature which raises the interaction of moving liquid and consequently leads to internal energy on the stream framework as referenced in [11], [12], [13], [14]. Additionally, the influence of other multiple physical properties on fluid flow has been investigated by researchers. In order to show these, few researchers are mentioned in this investigation such as in magnetic field strength studied in [6], [15], [16], porous permeability materials as described in [16], [17], [18], [19], viscosity mentioned in [20], [21], [22], thermal radiation in [23], [24], buoyancy force in [1], [3], [5], [25] and other thermophysical properties which affect fluid flow and heat transfer in different aspects.

Meanwhile, the circumstances upon which the buoyancy impacts are substantial are thus of ultimate interest, and it was to analyze the consolidated impacts of buoyancy force and the internal warmth on a couple stress fluid through a porous medium with isothermal boundaries subject to these combined effects, that is, buoyancy force and internal heat source which were not accounted for in the previous studies. Therefore, this study is to extend the investigations done in [6], [10] where both effects were not accounted for. The analytical computations for the momentum and energy equations are derived to determine the rate of fluid motion, heat transfer and the pace of entropy generation with the utilization of notable proficient series solution called Adomian decomposition method (ADM). The preference for this approach is to accelerate the rapid convergence and does not demand any linearization, discretization, use of guess or perturbation and drastically reduce the number of iterations as mentioned in [26]. The abundance of knowledge on the series solution (ADM) from literature [27], [28], [29], [30], [31], [32] has been proved to be efficient, reliable, and as an alternative powerful tool in providing solution to differential and integral equations and hence, reduce computational volume. The estimation on the quality of being genuine of the ordered solution and its convergence were ascertained in tables, shown in the discussion section, concerning the already accomplished discoveries in [6], [10] where perturbation method was utilized and examined justifiably with other thermophysical parameters existing in the flow system. More importantly, our results shall be of interest to industries in improving the efficiency and effectiveness of hydromagnetic lubricants used in engineering systems.

2. Flow analysis

Consider the consistent free flow of a couple stress fluid actuated by a steady pressure gradient regarding impact of buoyancy force and attractive magnetic field strength $B_0$ running across a permeable medium with isothermal channels fixed at $y=0$ and $y=h$ with constant temperature as depicted in Fig. 1.

Figure 1.

The physical geometry of the flow regime.

The internal heat generation is communicated as a direct articulation of temperature. Following [6], [10], [11], [33], the equations directing the fluid momentum and energy are given in non-dimensional form as:

$$0=-\frac{\mathrm{d}p}{\mathrm{d}x}+\mu \frac{{\mathrm{d}}^2\bar{u}}{\mathrm{d}{\bar{y}}^2}-\frac{\mu }{K}\bar{u}-\eta \frac{{\mathrm{d}}^4\bar{u}}{\mathrm{d}{\bar{y}}^4}-\sigma B_0^2\bar{u}+\rho g\alpha (\bar{T}-T_0)$$ (1)

$$0=k\frac{{\mathrm{d}}^2\bar{T}}{\mathrm{d}{\bar{y}}^2}+\frac{\mu }{K}{\bar{u}}^2+\mu {\left(\frac{\mathrm{d}\bar{u}}{\mathrm{d}\bar{y}}\right)}^2+\eta {\left(\frac{{\mathrm{d}}^2\bar{u}}{\mathrm{d}{\bar{y}}^2}\right)}^2+\sigma B_0^2{\bar{u}}^2+Q_0(\bar{T}-T_0)$$ (2)

together with undermentioned boundary conditions

$$\bar{u}(0)={\bar{u}}^{″}(0)={\bar{u}}^{″}(h)=\bar{u}(h)=0\text{and}\bar{T}(0)=\bar{T}(h)=0$$ (3)

The last terms in equations (1) and (2) respectively show the remarkable attribute of buoyancy force on the fluid motion as done in [3], [5] and the influence of internal heat generation as mentioned in [3], [11], [18], [26], [34]. Additionally, the expression for the degree of disturbance of the couple stress liquid under the domination of the attractive magnetic strength in dimensional rate denoted $E_G$ can be composed as recorded in [10]

$$E_G=\frac{k}{T_0^2}{\left(\frac{\mathrm{d}\bar{T}}{\mathrm{d}\bar{y}}\right)}^2+\frac{\mu }{T_0}{\left(\frac{\mathrm{d}\bar{u}}{\mathrm{d}\bar{y}}\right)}^2+\frac{\mu }{T_{0}K}{\bar{u}}^2+\frac{\eta }{T_0}{\left(\frac{{\mathrm{d}}^2\bar{u}}{\mathrm{d}{\bar{y}}^2}\right)}^2+\frac{\sigma B_0^2}{T_0}{\bar{u}}^2$$ (4)

In equations (1)–(4), $\bar{u}$ and $\bar{T}$ respectively stand for dimensional axial velocity and fluid temperature, η is the coefficient for couple stress, μ is the fluid viscosity and p stands for pressure. The constant for porous medium permeability is represented with K, the fluid density evaluated at the mean temperature is ρ and σ stands for electrical conductivity while k denotes thermal conductivity. Also, α denotes coefficient of thermal expansion, $Q_0$ is the dimensional heat generation coefficient, h and $T_0$ respectively represent the channel width and temperature. It is absolutely necessary to mention that the first expression in equation (4) denotes the heat transfer rate while the other four terms respectively represent the domestic entropy for viscous dissipation, effect of porosity, couple stress and magnetic field strength.

Developing the subsequent dimensionless parameters and variables in equations (1)–(4):

$$y=\frac{\bar{y}}{h},u=\frac{\bar{u}}{UM},\theta =\frac{E(\bar{T}-T_0)}{R{T}_0^2},M=-\frac{h^2}{\mu U}\frac{\mathrm{d}p}{\mathrm{d}x},ϵ=\frac{R{T}_0}{E},H^2=\frac{\sigma B_0^2{h}^2}{\rho },l=\sqrt{\frac{\eta }{\mu }},\beta =\sqrt{\frac{1}{Da}},\gamma =\frac{h}{l},Da=\frac{K}{h^2},\delta =\frac{Q_0{h}^2}{k},Gr=\frac{\rho g\alpha h^{2}R{T}_0^2}{\mu MUE},Br=\frac{E\mu U^2{M}^2}{kR{T}_0^2},\mathrm{\Omega }=\frac{R{T}_0}{E}\text{and}{N}_s=\frac{h^2{E}^2{E}_G}{k{R}^2{T}_0^2}$$ (5)

accordingly, we obtain the following boundary valued problems as:

$$1+\frac{{\mathrm{d}}^{\mathrm{2}}u}{\mathrm{d}{y}^2}-({\beta }^2+H^2)u-\frac{1}{\gamma }\frac{{\mathrm{d}}^{\mathrm{4}}u}{\mathrm{d}{y}^4}+Gr\theta =0$$ (6)

$$\frac{{\mathrm{d}}^{\mathrm{2}}\theta }{\mathrm{d}{y}^2}+Br({\left(\frac{\mathrm{d}u}{\mathrm{d}y}\right)}^2+({\beta }^2+H^2)u^2+\frac{1}{\gamma }{\left(\frac{{\mathrm{d}}^{\mathrm{2}}u}{\mathrm{d}{y}^2}\right)}^2+\delta \theta )=0$$ (7)

together with the boundary conditions

$$u(0)=u^{″}(0)=u^{″}(1)=u(1)=0\text{and}\theta (0)=\theta (1)=0.$$ (8)

Also, the entropy generation rate in dimensionless form is:

$$N_s={\left(\frac{\mathrm{d}\theta }{\mathrm{d}y}\right)}^2+\frac{Br}{\mathrm{\Omega }}({\left(\frac{\mathrm{d}u}{\mathrm{d}y}\right)}^2+\frac{1}{\gamma }{\left(\frac{{\mathrm{d}}^{2}u}{\mathrm{d}{y}^2}\right)}^2+({\beta }^2+H^2)u^2)$$ (9)

here u and θ respectively represent the fluid velocity and temperature, U represents the fluid characteristic velocity, E for activation energy, R for universal gas constant and l is a relation normally used for the fluid molecular dimension. Moreover, δ, γ, β, Br and Ω are respectively parameters for internal heat generation, inverse of couple stress, porous medium permeability, viscous heating named after Brinkman and wall temperature. Additionally, Da stands for the Darcy number, H is the number for magnetic field strength parameter named after Hartmann, Gr is the Grashof number for buoyancy force and $N_s$ is the dimensionless entropy generation rate. In addition, considering present investigation under scrutiny, solutions of equations (6)–(9) shall be pertinent and appropriate if and only if $\gamma \ne 0$.

3. Mathematical solution

The coupled conditions in (6) and (7) are fathomed at the same time with suitable limit conditions utilizing the general technique of Adomian decomposition method (ADM)). In this manner, we along these lines change the differential equations (6) and (7) into integral structures by integrating four and two times respectively to acquire the followings:

$$u(y)=b_{0}y+\frac{a_0}{6}{y}^3+\frac{\gamma }{24}{y}^4+\gamma \underset{0}{\overset{y}{\int }}\underset{0}{\overset{y}{\int }}\underset{0}{\overset{y}{\int }}\underset{0}{\overset{y}{\int }}[\frac{{\mathrm{d}}^{2}u}{\mathrm{d}{y}^2}-({\beta }^2+H^2)u(y)+Gr\theta (y)]\mathrm{d}Y\mathrm{d}Y\mathrm{d}Y\mathrm{d}Y$$ (10)

$$\theta (y)=c_{0}y-Br\underset{0}{\overset{y}{\int }}\underset{0}{\overset{y}{\int }}[{\left(\frac{\mathrm{d}u}{\mathrm{d}y}\right)}^2+\frac{1}{\gamma }{\left(\frac{{\mathrm{d}}^{2}u}{\mathrm{d}{y}^2}\right)}^2+({\beta }^2+H^2){(u(y))}^2+\delta \theta (y)]\mathrm{d}Y\mathrm{d}Y$$ (11)

where $a_0=u^{‴}(0)$, $b_0=u^{\prime }(0)$ and $c_0={\theta }^{\prime }(0)$ which are to be determined by using the other boundary conditions stated in (8).

Moreover, to obtain the solutions of the coupled equations in (10) and (11), we adopt the infinite series form of solutions as

$$u(y)=\sum _{n=0}^{\infty }{u}_n(y)\text{and}\theta (y)=\sum _{n=0}^{\infty }{\theta }_n(y)$$ (12)

such that when (12) is assigned in equations (10) and (11), we obtain,

$$\begin{gathered} u(y)=b_{0}y+\frac{a_0}{6}{y}^3+\frac{\gamma }{24}{y}^4+\gamma \underset{0}{\overset{y}{\int }}\underset{0}{\overset{y}{\int }}\underset{0}{\overset{y}{\int }}\underset{0}{\overset{y}{\int }}\left[\frac{{\mathrm{d}}^2({\sum }_{n=0}^{\infty }{u}_n(y))}{\mathrm{d}{y}^2}\right]\mathrm{d}Y\mathrm{d}Y\mathrm{d}Y\mathrm{d}Y \\ -\gamma ({\beta }^2+H^2)\underset{0}{\overset{y}{\int }}\underset{0}{\overset{y}{\int }}\underset{0}{\overset{y}{\int }}\underset{0}{\overset{y}{\int }}(\sum _{n=0}^{\infty }{u}_n(y))\mathrm{d}Y\mathrm{d}Y\mathrm{d}Y\mathrm{d}Y \\ +\gamma Gr\underset{0}{\overset{y}{\int }}\underset{0}{\overset{y}{\int }}\underset{0}{\overset{y}{\int }}\underset{0}{\overset{y}{\int }}(\sum _{n=0}^{\infty }{\theta }_n(y))\mathrm{d}Y\mathrm{d}Y\mathrm{d}Y\mathrm{d}Y \end{gathered}$$ (13)

$$\begin{gathered} \theta (y)=c_{0}y-Br\underset{0}{\overset{y}{\int }}\underset{0}{\overset{y}{\int }}{\left(\frac{\mathrm{d}({\sum }_{n=0}^{\infty }{u}_n(y))}{\mathrm{d}y}\right)}^2+({\beta }^2+H^2){(\sum _{n=0}^{\infty }{u}_n(y))}^2\mathrm{d}Y\mathrm{d}Y \\ -Br\underset{0}{\overset{y}{\int }}\underset{0}{\overset{y}{\int }}\frac{1}{\gamma }{\left(\frac{{\mathrm{d}}^2({\sum }_{n=0}^{\infty }{u}_n(y))}{\mathrm{d}{y}^2}\right)}^2+\delta (\sum _{n=0}^{\infty }{\theta }_n(y))\mathrm{d}Y\mathrm{d}Y \end{gathered}$$ (14)

However, sequel to the use of the series solution, the non - linear terms in equations (13) and (14) are presented as:

$$\begin{gathered} \sum _{n=0}^{\infty }{A}_n(y)=\frac{{\mathrm{d}}^2({\sum }_{n=0}^{\infty }{u}_n(y))}{\mathrm{d}{y}^2},\sum _{n=0}^{\infty }{B}_n(y)={\left(\frac{\mathrm{d}({\sum }_{n=0}^{\infty }{u}_n(y))}{\mathrm{d}y}\right)}^2,\sum _{n=0}^{\infty }{C}_n(y)={(\sum _{n=0}^{\infty }{u}_n(y))}^2 \\ \text{and}\sum _{n=0}^{\infty }{D}_n(y)={\left(\frac{{\mathrm{d}}^2({\sum }_{n=0}^{\infty }{u}_n(y))}{\mathrm{d}{y}^2}\right)}^2 \end{gathered}$$ (15)

where the particular segments of $A_0$, $A_1$, $A_2$, ..., $B_0$, $B_1$, $B_2$, ..., $C_0$, $C_1$, $C_2$, ..., and $D_0$, $D_1$, $D_2$, ... are called Adomian polynomials. Then (15) is thereby expanded such that:

$$\begin{gathered} A_0=u_0^{″}(y),A_1=u_1^{″}(y),A_2=u_2^{″}(y),...B_0=u_0^{\prime }(y){}^2,B_1=2u_0^{\prime }(y)u_1^{\prime }(y),B_2=u_1^{\prime }(y){}^2+2u_0^{\prime }(y)u_2^{\prime }(y),...C_0=u_0{(y)}^2,C_1=2u_0(y)u_1(y),C_2=u_1{(y)}^2+2u_0(y)u_2(y),...\text{and} \\ {D}_0=u_0^{″}{(y)}^2,D_1=2u_0^{″}(y)u_1^{″}(y),D_2=u_1^{″}{(y)}^2+2u_0^{″}(y)u_2^{″}(y),... \end{gathered}$$ (16)

With (16), the coupled equations for momentum and energy respectively reduce to:

$$\begin{gathered} u(y)=b_{0}y+\frac{a_0}{6}{y}^3+\frac{\gamma }{24}{y}^4+\gamma \underset{0}{\overset{y}{\int }}\underset{0}{\overset{y}{\int }}\underset{0}{\overset{y}{\int }}\underset{0}{\overset{y}{\int }}(\sum _{n=0}^{\infty }{A}_n(y))\mathrm{d}Y\mathrm{d}Y\mathrm{d}Y\mathrm{d}Y \\ -\gamma [\underset{0}{\overset{y}{\int }}\underset{0}{\overset{y}{\int }}\underset{0}{\overset{y}{\int }}\underset{0}{\overset{y}{\int }}(({\beta }^2+H^2)\sum _{n=0}^{\infty }{u}_n(y))-Gr(\sum _{n=0}^{\infty }{\theta }_n(y))]\mathrm{d}Y\mathrm{d}Y\mathrm{d}Y\mathrm{d}Y \end{gathered}$$ (17)

$$\begin{gathered} \theta (y)=c_{0}y-Br[\underset{0}{\overset{y}{\int }}\underset{0}{\overset{y}{\int }}(\sum _{n=0}^{\infty }{B}_n(y))+({\beta }^2+H^2)(\sum _{n=0}^{\infty }{C}_n(y))]\mathrm{d}Y\mathrm{d}Y \\ -Br[\underset{0}{\overset{y}{\int }}\underset{0}{\overset{y}{\int }}\frac{1}{\gamma }(\sum _{n=0}^{\infty }{D}_n(y))+\delta (\sum _{n=0}^{\infty }{\theta }_n(y))]\mathrm{d}Y\mathrm{d}Y \end{gathered}$$ (18)

A that point, following recursive condition with the zeroth part as already mentioned in [27], [31], [32], [35] are obtained as follows:

$$u_0(y)=b_{0}y+\frac{a_0}{6}{y}^3+\frac{\gamma }{24}{y}^4$$ (19)

$${\theta }_0(y)=C_{0}y$$ (20)

$$u_1(y)=\gamma \underset{0}{\overset{y}{\int }}\underset{0}{\overset{y}{\int }}\underset{0}{\overset{y}{\int }}\underset{0}{\overset{y}{\int }}[A_0(y)-({\beta }^2+H^2)u_0[y]+Gr\left({\theta }_0\right)]\mathrm{d}Y\mathrm{d}Y\mathrm{d}Y\mathrm{d}Y$$ (21)

$${\theta }_1(y)=-Br\underset{0}{\overset{y}{\int }}\underset{0}{\overset{y}{\int }}[B_0+({\beta }^2+H^2)C_0+\frac{1}{\gamma }{D}_0+\delta {\theta }_0]\mathrm{d}Y\mathrm{d}Y$$ (22)

$$u_{n+1}(y)=\gamma \underset{0}{\overset{y}{\int }}\underset{0}{\overset{y}{\int }}\underset{0}{\overset{y}{\int }}\underset{0}{\overset{y}{\int }}[(A_n(y))+({\beta }^2+H^2)+Gr{\theta }_n(y)]\mathrm{d}Y\mathrm{d}Y\mathrm{d}Y\mathrm{d}Y$$ (23)

$${\theta }_{n+1}=-Br\underset{0}{\overset{y}{\int }}\underset{0}{\overset{y}{\int }}[B_n+({\beta }^2+H^2)C_n+\frac{1}{\gamma }{D}_n+\delta {\theta }_n]\mathrm{d}Y\mathrm{d}Y$$ (24)

Accordingly, equations (19)–(24) are correspondingly arranged to secure approximate series solutions in the next equations for fluid momentum, energy transfer and the rate of entropy generation as

$$u(y)=\sum _{n=0}^k{u}_n(y)\text{and}\theta (y)=\sum _{n=0}^k\theta (y)$$ (25)

Furthermore, to analyze the pace of entropy generation inside the liquid substances over the channel with the use of expressions acquired in (25). For easy estimation, we divided $N_s$ in (9) into two sections as follows:

$$N_1={\left(\frac{\mathrm{d}\theta }{\mathrm{d}y}\right)}^2\text{and}{N}_2=\frac{Br}{\mathrm{\Omega }}[{\left(\frac{\mathrm{d}u}{\mathrm{d}y}\right)}^2+\frac{1}{\gamma }{\left(\frac{{\mathrm{d}}^{2}u}{\mathrm{d}{y}^2}\right)}^2+({\beta }^2+H^2)u^2]$$ (26)

where $N_1$ points out the irreversibilty expected from heat transfer and $N_2$ denotes the domestic entropy generation required to show the outcome of viscous dissipation, couple stress, porous permeability and magnetic strength of the flow scheme.

Furthermore, the irreversibility formation is illustrated as (ϕ) and is expressed as:

$$\varphi =\frac{N_2}{N_1}$$ (27)

which signify the control of heat transfer when $0\le \varphi <1$ such that the fluid friction controls when $\varphi >1$. This is utilized to govern the significant addition of heat transfer in a great number of engineering structures. As a supplementary to the irreversibility formation parameter, the Bejan number (Be) is expressed as

$$Be=\frac{N_1}{N_s}=\frac{1}{1+\varphi },\text{such that}0\le Be\le 1$$ (28)

4. Results and discussion

This part presents the outcomes showing the significance of a buoyancy force on the motion of a couple stress heat producing hydromagnetic liquid flowing across a saturated porous channel with isothermal boundaries where the heat source is assumed to be a linear expression of temperature. The existing outcome shall be similar to [6] where the effects of buoyancy force and heat source parameters are both zero and to substantiate the results attained as disclosed in Table 2. Table 1 reveals the speedy convergence of the series solution with fewer iterations for $a_0$, $b_0$ and $c_0$ as earlier mentioned in equations (10) and (11). However, Table 2 revealed the comparison of investigational outcome of velocity profile from earlier acquired results in [6], [10] and the series solutions of ADM without the impact of buoyancy force and magnetic field strength. The positive error of an average order is ${10}^{-4}$ which bring forth the proficiency of ADM as another modified technique for getting comparable outcomes to differential equations.

Table 2.

Comparison of analytic result of velocity profile.

$n=5,\gamma =1,\beta =0.1,Gr=Br=H=0$
u(y)	Exact Solutions	ADM	Absolute error
0.0	0	0	0
0.1	0.00371505	0.0037458665	3.0814 × 10−5
0.2	0.00702528	0.0070847385	5.9454 × 10−5
0.3	0.00961357	0.0096973058	8.3739 × 10−5
0.4	0.01125560	0.0113571328	1.0151 × 10−4
0.5	0.01181780	0.0119285135	1.1074 × 10−4
0.6	0.01125560	0.0113653273	1.0971 × 10−4
0.7	0.00961357	0.0097108958	9.7329 × 10−5
0.8	0.00702528	0.0070988406	7.3557 × 10−5
0.9	0.00371505	0.0037549423	3.9890 × 10−5
1.0	0	−8.8905−18	8.8905−18

Table 1.

Rapid convergence of the series solution for a₀, b₀ and c₀.

$\gamma =\beta =H=Br=1,\delta =Gr=0.1$
n	a0	b0	c0
0	−0.500000	0.0416667	0
1	−0.457765	0.0375443	0.00335940
2	−0.455467	0.0372138	0.00369165
3	−0.455406	0.0372040	0.00375007
4	−0.455405	0.0372038	0.00375372
5	−0.455405	0.0372038	0.00375386
6	−0.455405	0.0372038	0.00375386

The velocity profiles of the flow distribution in terms of parameters for porosity (β), magnetic field strength (H), buoyancy force $(Gr)$ and internal heat generation (δ) are respectively displayed in Figs. 2 to 5. Generally, the effect of each parameter is strongest at the centre of the plate and diminishes towards the upper and lower plates. The minimum speed is noticed as the porosity parameter (β) in Fig. 2 and magnetic field strength (H) in Fig. 3 increase in values. The reduction noticed is caused by the presence of obstacles in the saturated porous channel and the electromagnetic force resisting the fluid motion. Meanwhile, the increase in the estimations of the buoyancy force parameter called Grashof number $(Gr)$ in Fig. 4 and internal heat source parameter (δ) in Fig. 5 bring about the maximum velocity in the liquid stream. This is valid in all actuality as both parameters will increase the fluid speed due to the presence of buoyancy force and increase in the fluid temperature.

Figure 2.

Effects of β on u(y).

Figure 5.

Effects of δ on u(y).

Figure 3.

Effects of H on u(y).

Figure 4.

Effects of Gr on u(y).

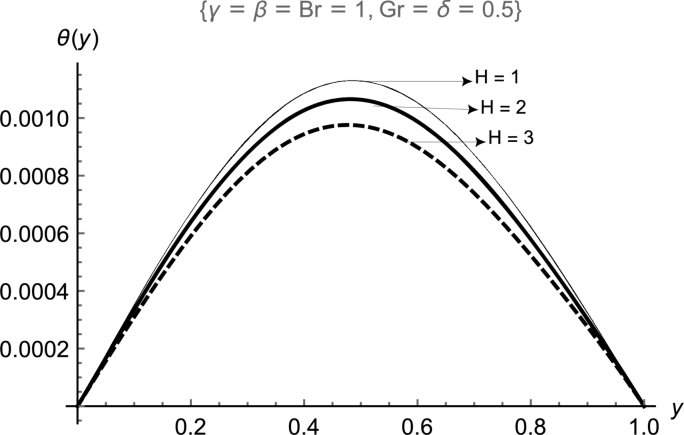
The temperature profiles of the flow system are respectively displayed in Figure 6, Figure 7, Figure 8, Figure 9 showing the variations in the influence of porosity (β) in Fig. 6, magnetic field strength (H) in Fig. 7, buoyancy force $(Gr)$ in Fig. 8 and internal heat generation (δ) in Fig. 9. The presence and further increment of porous materials in the fluid particles and electromagnetic forces in the flow system justify the reduction in the fluid temperature in the process of heat transfer. However, the reverse is the case when there are increase in the buoyancy force and internal heat generation across the flow channel, hence a progressive increase in the fluid temperature as shown in Fig. 8 with buoyancy force parameter $(Gr)$ and in Fig. 9 with the variations in the internal heat generation within the flow system. This is because of inner interaction of the stream system due to thick warning and thereby increases the fluid temperature.

Figure 6.

Effects of β on θ(y).

Figure 7.

Effects of H on θ(y).

Figure 8.

Effects of Gr on θ(y).

Figure 9.

Effects of δ on θ(y).

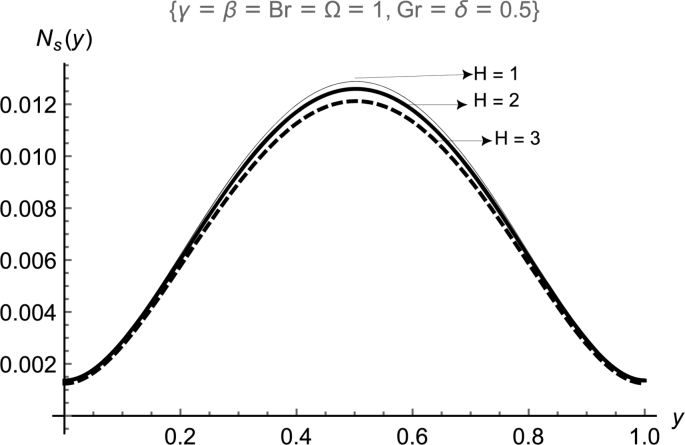
The entropy generation analysis of the flow system with variations in parameters representing the impact of magnetic field strength (H) in Fig. 10, the wall temperature (Ω) in Fig. 11, buoyancy force $(Gr)$ in Fig. 12 and viscous heating $(Br)$ in Fig. 13. On a general note, the maximum activity occurs at the centreline of the flow regime for all the parameters. The rate of entropy generation decreases with increment in the values of magnetic field strength (H) in Fig. 10 and the wall temperature (Ω) in Fig. 11 while the reverse is observed in Fig. 12 and Fig. 13 for buoyancy force $(Gr)$ and viscous heating $(Br)$.

Figure 10.

Effects of H on N_s.

Figure 11.

Effects of Omega on N_s.

Figure 12.

Effects of Gr on N_s.

Figure 13.

Effects of Br on N_s.

Furthermore, the display in Figs. 14 to 18 respectively represents the Bejan number for variations in the parameters of porosity (β) in Fig. 14, magnetic field strength (H) in Fig. 15, buoyancy force $(Gr)$ in Fig. 16, viscous heating $(Br)$ in Fig. 17 and wall temperature (Ω) in Fig. 18. The fluid friction irreversibility increasingly dominates around the core region and heat transfer irreversibility dominates around the channel walls with increasing values of parameters of porosity (β) in Fig. 14 and magnetic field strength (H) in Fig. 15 while the reverse is noticed with the expanding estimations of parameters of buoyancy force $(Gr)$ in Fig. 16, viscous heating $(Br)$ in Fig. 17 and wall temperature (Ω) in Fig. 18.

Figure 14.

Effects of β on Be.

Figure 18.

Effects of Ω on Be.

Figure 15.

Effects of H on Be.

Figure 16.

Effects of Gr on Be.

Figure 17.

Effects of Br on Be.

5. Conclusion

This investigation is conducted on the impact of a buoyancy force on the flow of an hydromagnetic heat generating couple stress liquid across the permeable substances with isothermal limits. The analytical expressions for the momentum and energy equations are obtained to determine the rate of fluid motion, heat transfer and the rate of entropy generation, utilizing a well-known and efficient series solution of Adomian decomposition method (ADM). The results compared with the recently got outcomes signified a good correlation. The results obtained to show the significant impact of buoyancy force $(Gr)$ with respect to internal heat generation (δ) and magnetic field strength (H) can be listed as follows:

• •the fluid speed reduces as parameters for porosity (β) and magnetic field strength (H) increases due to obstacles in the saturated substances and electromagnetic force respectively resisting the fluid flow.
• •the fluid speed remarkably increases with respect to increment in the parameters of buoyancy force $(Gr)$ and that of internal heat generation (δ) due to the significant impact on the fluid flow.
• •the fluid temperature progressively increases with the significant increment in the parameters of buoyancy force $(Gr)$ and internal heat generation (δ) while the reverse is observed with the porosity permeability (β) and magnetic field strength (H) parameters.
• •the least rate of entropy generation occur around the significance zone and increases to the uttermost around the plate surfaces with respect to the wall temperature parameter (Ω) and otherwise with buoyancy force $(Gr)$ and viscous heating $(Br)$ parameters.
• •the fluid fiction irreversibility increasingly dominates around the core region and heat transfer irreversibility dominates around the channel walls with increasing values of parameters of porosity (β) and magnetic field strength (H), but the opposite is noticed with increments in the values of buoyancy force $(Gr)$, viscous heating $(Br)$ and wall temperature (Ω).

However, the results showed the significant impact of buoyancy force $(Gr)$ under the influence of inward warmth inside the stream and other thermophysical parameters on the fluid movement and heat transfer.

Declarations

Author contribution statement

Anthony R Hassan & Olugbenga J Fenuga: Conceived and designed the analysis; Analyzed and interpreted the data; Wrote the paper.

Akeem B. Disu: Analyzed and interpreted the data; Contributed analysis tools or data; Wrote the paper.

Funding statement

This research did not receive any specific grant from funding agencies in the public, commercial, or not-for-profit sectors.

Competing interest statement

The authors declare no conflict of interest.

Additional information

No additional information is available for this paper.