Quantification of model and data uncertainty in a network analysis of cardiac myocyte mechanosignalling

Abstract

Cardiac myocytes transduce changes in mechanical loading into cellular responses via interacting cell signalling pathways. We previously reported a logic-based ordinary differential equation model of the myocyte mechanosignalling network that correctly predicts 78% of independent experimental results not used to formulate the original model. Here, we use Monte Carlo and polynomial chaos expansion simulations to examine the effects of uncertainty in parameter values, model logic and experimental validation data on the assessed accuracy of that model. The prediction accuracy of the model was robust to parameter changes over a wide range being least sensitive to uncertainty in time constants and most affected by uncertainty in reaction weights. Quantifying epistemic uncertainty in the reaction logic of the model showed that while replacing ‘OR’ with ‘AND’ reactions greatly reduced model accuracy, replacing ‘AND’ with ‘OR’ reactions was more likely to maintain or even improve accuracy. Finally, data uncertainty had a modest effect on assessment of model accuracy.

This article is part of the theme issue ‘Uncertainty quantification in cardiac and cardiovascular modelling and simulation’.

1. Introduction

Increased haemodynamic loads acting on the heart can result in ventricular hypertrophy and remodeling. In response to altered mechanical loading, a variety of mechanotransduction mechanisms and mechanosensitive cell signalling pathways are activated in cardiomyocytes [1]. A mechanosignalling network model that our groups developed earlier [2] successfully predicted 134 qualitative results of 172 input–output (9/9), input-intermediate (43/43) and inhibitor (82/120) experiments that had been reported in 55 published papers not used for the initial model formulation. The model was represented as a Boolean network and implemented as a system of logic-based ordinary differential equations in which 94 normalized state variables represent upstream stimuli and ligands, cell surface receptors, signalling molecules, transcriptional regulators and cardiomyocyte marker genes and phenotypes. The parameters of the 125 activating and inhibitory reactions linking the species of the network included the Hill coefficient n (set to a constant of 1.4) and half-maximal effective concentration EC₅₀ (set everywhere to 0.5). Each state variable had an initial activation of 0, maximal activation of 1 and a time constant τ of 1.

While our original report did investigate the robustness of the model accuracy to parameter uncertainty [2], here we extend the analysis by exploring which network modules and outputs are most sensitive to parameter uncertainty and which parameters propagate the most error. We also use uncertainty quantification (UQ) to investigate the consequences of epistemic uncertainty in the model logic, and finally we quantify how data uncertainty in the experimental results used to validate the model affects the estimated accuracy of the model. Of particular interest regarding this type of data uncertainty is the greater likelihood of type II than type I errors in cell biological experiments, which are almost invariably under-powered.

For deterministic systems of ordinary differential equations with known initial conditions, parameter values are usually chosen based on reported models or experiments, or they are optimized to fit observations. However, these parameters are typically uncertain owing to limitations in the availability, reproducibility or accuracy of experimental measurements [3]. UQ has been widely used to identify statistical estimates of model outputs where parameters, such as the reaction weights and Hill coefficients in our network model, are approximations or a consensus of differing estimates [4]. A variety of UQ methods have been used including Monte Carlo (MC) methods [5] and polynomial chaos expansions (PCEs) [6], which can be more computationally efficient. Here, we used both approaches to quantify the effects of uncertainty in model parameters, model logic and validation data on estimated model accuracy. We used these findings to identify specific model parameters, subnetworks and data limitations that should be the focus of further experimental investigation for model improvement.

2. Methods

We performed UQ analysis of the mathematical model of the cardiac myocyte mechanosignalling network described by us earlier [2] to assess the effects of uncertainty in model parameters, model logic and the experimental validation data on assessments of model prediction accuracy.

(a). Model formulation

The interactions between species within the cardiac myocyte mechanosignalling network were modelled using Hill-type equations based on logical operators [2]. The activity of each species in the network is represented by a state variable normalized to vary between 0 and 1, and reactions are represented by logic-based differential equations developed for modelling biochemical networks [7] in which the activation of each species varies according to a sigmoidal Hill function. The state variable y_i for species i in the network regulated by species j is governed by

$$\frac{\text{d}{y}_i}{\text{d}t}=\frac{1}{{\tau }_{ji}}[{\omega }_{ji}{f}_j{y}_{i,\max }-y_i],$$ 2.1

where τ_ji is the reaction time constant determining the rate of change of species i, ω_ji is the general reaction weight that can vary between 0 and 1, and $y_{i,\max }$ is defined as the maximal activation of species i in the network. Typically, ω_ji is 1 or close to one unless the node is being pharmacologically or genetically inhibited or knocked down. The Hill function f_ji, can be activating (act) or inhibitory (in)

$$f_{ji}=\{\begin{array}{cc}{f}_{act}(y_j)=\frac{B{y}_j^n}{K^n+y_j^n}& \mathrm{if}\hspace{0.17em}\mathrm{activating}\\ f_{in}(y_j)=1-\frac{B{y}_j^n}{K^n+y_j^n}& \mathrm{if}\hspace{0.17em}\mathrm{inhibitory},\end{array}$$

where B is a function of the the Hill coefficient n and the half-maximal activation EC₅₀ [7]:

$$B=\frac{{\text{EC}}_{50}^n-1}{2{\text{EC}}_{50}^n-1}$$

and

$$K={(B-1)}^{1/n}.$$

Continuous representations of logic gates are used to represent signalling interactions between two converging upstream nodes. When either input node is sufficient but not necessary for activation (for example, when two kinases can phosphoregulate a target protein), the ‘OR’ interaction between reactions is used. When both inputs are necessary (for example, when two co-factors must bind to the promoter region to activate or repress transcription), the ‘AND’ logic interaction between reactions is used. The detailed mathematical representation of these interactions and other common interactions in the network model are given in Morris et al. [8].

The model [2] has 125 reactions and 94 species derived from published experimental reports. The default parameter values were ω = 0.9, n = 1.4, EC₅₀ = 0.5, τ = 1 min, and y_i,max = 1 for all species and reactions. Applying a stretch input of 0.7 to the system stimulates output responses similar to those observed in response to an in vitro strain of ≈20%. The constant input and parameter values of stretch (0.7), weights (0.9), Hill coefficient (1.4), EC₅₀ (0.5) and time constant (1 min) selected in the original model study [2] were used here as default values with no formal attempt at parameter optimization. The default input stretch and weight values were chosen manually in the original study to achieve steady-state activation of between 50% and 95% of network nodes [2]. The default Hill coefficient and EC₅₀ were chosen in the original paper based on typical values commonly reported in biochemical literature [2,7]. The resulting system of ordinary differential equations that describe the regulatory network dynamics is integrated numerically using the LSODA algorithm for stiff ODEs that automatically switches between the Adams’ method and the backward differentiation formulae (BDF) method. Our numerical implementation of this network has been customized and released as a Jupyter notebook available to the public (Refer to the example folder in the Github repository for simulated data).¹

(b). Model validation

To validate the predictions of the mathematical model in the original study, experimental data were set aside from 55 papers that had not been used during the initial model formulation [2]. These studies contained 172 experimental results collected from in vitro experiments comprising 52 input–output or input-intermediate experiments and 120 inhibition experiments. Using the reported statistical threshold, the result of each published experiment was classified as the output node being increased, decreased or unchanged. For comparison, a change in the magnitude of the model-computed output of greater than or equal to a threshold of 0.05 was classified as an increase or decrease, while responses of less than 0.05 were classified as unchanged. A mathematical definition of this metric for model accuracy is summarized in electronic supplementary material, S1. Applying these criteria to the model with default parameters, the model correctly predicted 100% of input–output and input-intermediate observations and 68% of the 120 inhibition results. In this study, we examined the effects of parameter, structural and data uncertainties on these validation metrics (figure 1).

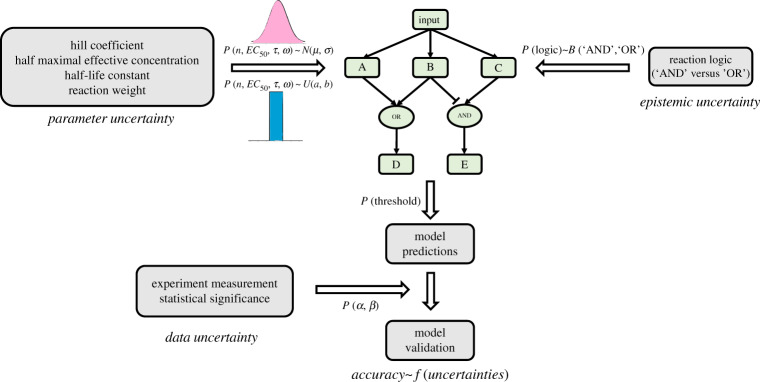
Figure 1.

Sources of uncertainty in validating the accuracy of logic-based network models of cell signalling. An example network with five nodes that includes examples of ‘NOT’, ‘AND’ and ‘OR’ reaction logic. Uncertainty in model-predicted results arises from parameter uncertainty and epistemic uncertainty in model structure and logic. Validation requires comparison of model results with experimental data that are subject to statistical uncertainty. (Online version in colour.)

(c). Sources of uncertainty

We investigate the effects of parameter uncertainty in model reaction coefficients, epistemic uncertainty in pathway logic, and data uncertainty in validation measurements on estimates of overall model prediction accuracy. In the original analysis, the parameters n, ω, EC₅₀ and τ were set to be constant for every reaction, but here we allow every parameter to be assigned to a different random value for every ODE. Moreover, while the molecules and basic structure of the signalling network are in general clearly reported in the experimental literature, the choice of reaction logic that best reflects the literature is more often subject to interpretation. Finally, there is statistical uncertainty in the conclusions from the experimental studies. While all of the input–output and input-intermediate validation results were based on statistically significantly increased or decreased measurements that were subject to type I error, the inhibition experiments also included findings that were not significantly changed. They are subject to a greater likelihood of type II errors in cell biological experiments, which are typically under-powered. Hence, data uncertainty represent a potential source of bias in model validation.

(i). Parameter uncertainty

We quantified the effects of uncertainty in the magnitudes of the model reaction parameters (ω, n, EC₅₀, τ) on the assessment of model accuracy. We repeated the model validation by randomly sampling each of these parameters for each ODE from uniform distributions with mean values that were not necessarily the same as the constant values used in the original validation analysis. Since K and B in the model are nonlinear functions of EC₅₀ and n, it was necessary during the sampling process of these two particular parameters to ensure that B > 1 so that K is represented by a real number that satisfies the following inequality:

$$\frac{{\text{EC}}_{50}^n-1}{2{\text{EC}}_{50}^n-1}>1,$$

which leads to the following restrictions on these two parameters:

$$n>\frac{\ln \frac{1}{2}}{\ln {\text{EC}}_{50}}$$

and

$${\text{EC}}_{50}<2^{-(1/n)}.$$

Using these constraints, the default Hill coefficient of n = 1.4 requires EC₅₀ < 0.61, and the default half-maximal activation of EC₅₀ = 0.5 requires n > 1.0.

Similarly, the values of both ω and τ were sampled from uniform distributions in the ranges [0.2, 1] and [0.5, 10], respectively. To allow for comparison between uniform and Gaussian distributions, we calculated the mean and standard deviations of the Gaussian distribution such that ±2 s.d. spanned 95% of the range in the uniform distribution.

As in the original report, a threshold change of 0.05 in a network intermediate or output variable was used when comparing between model predictions and experimental results. Parameter perturbations, particularly in ω, that affected the overall input–output gain of the system predictably affected validation accuracy reciprocally with a change in threshold. Therefore, we also analysed the effects of simultaneously sampling the stretch input and the threshold from uniform random distributions ranging from 0.1 to 0.9 and 0.01 to 0.09, respectively. For each calculation, the analysis of the input stimulus and reaction weight ω were drawn from the same uniform random distributions used above with ranges of [0.4, 1] and [0.2, 1], respectively.

(ii). Epistemic uncertainty

Epistemic uncertainty is the uncertainty caused by incomplete knowledge of the system. Compared with the network components and structure, which are readily appreciated from the experimental literature, the choice of logic that best represents reactions with multiple inputs is more prone to errors of interpretation and the limitations on the ability of a logic-based formulation to properly represent biochemical processes. In this study, 52 of 94 signalling components were regulated by multiple upstream nodes, and these interactions were approximated in the mathematical model using 19 ‘AND’ and 33 ‘OR’ logic gates. To explore the effects of epistemic uncertainty in the model logic, we performed three UQ analyses: First, each ‘AND’ reaction was randomly changed to ‘OR’ with a probability of 0.5; similarly each ‘OR’ reaction was randomly changed to ‘OR’ with a probability of 0.5; and lastly, we randomly switched the logic sampling from a binomial distribution with a mean probability of 0.5.

(iii). Data uncertainty

Finally, we also analysed the effects of the data uncertainty inherent in all biological experiments on the validation accuracy obtained by comparing the model with the subset of 120 inhibition experiments used for validation. Cell biology studies invariably rely on the conventional statistical threshold (p-value) of p < 0.05, which corresponds to the risk of making a type I error. But these studies rarely have large enough sample sizes to achieve a comparably low risk β of making a type II error. We reviewed the papers from which the 120 inhibition validation experiments were drawn; they included 106 significantly downregulated, 10 unchanged and 4 upregulated responses. Statistical power was rarely reported, so we made use of webplotdigitizer [9,10] and recalculated power from the published inhibition experiments that reported no significant change. Power was in the range of 0.6–0.8 so we chose a value for β of 0.4. UQ was used to measure the effects of statistical uncertainty on model validation accuracy by testing how the model accuracy changed when the published experimental conclusions were randomly overturned. For each of the 110 experiments that showed significantly changed stretch response to an inhibitor, we randomly reassigned each result with a 5% probability of overturning the significant change. We randomly resampled the remaining 10 experiments reporting no significant change, with a 40% probability of reclassifying them to be significantly up- or downregulated. Since the ratio of decrease versus increase in the experiments was 106:4, the conditional probabilities of the overturned non-significant experiments being classified as upregulated was set to $\frac{4}{110}$ and downregulated was set to $\frac{106}{110}$.

(d). Uncertainty quantification methods

For UQ analysis, we used MC [5] or PCE [6] simulations. PCE is an approximate method that makes use of polynomial expansions to reduce calculation time significantly over MC simulations provided the number of parameters is not too large [11]. Therefore, here we performed preliminary analyses comparing computed accuracy distributions and computational performance of PCE with MC simulations to determine when PCE could be reliably used to save on computation time without significantly affecting the resulting distribution. We also tested the Markov Chain Monte Carlo (MCMC) method, an exact MC method that samples the distribution via a stochastic process, to test whether MCMC sampling had any effect on computational cost. While MC simulations typically require a large sample size to account adequately for all possibilities, PCE methods are an efficient and mathematically rigorous strategy for UQ and sensitivity analysis [12] that are typically faster than MC methods when the number of sampled parameters is fewer than 20 and the output has smooth behaviour with respect to the input parameters [11].

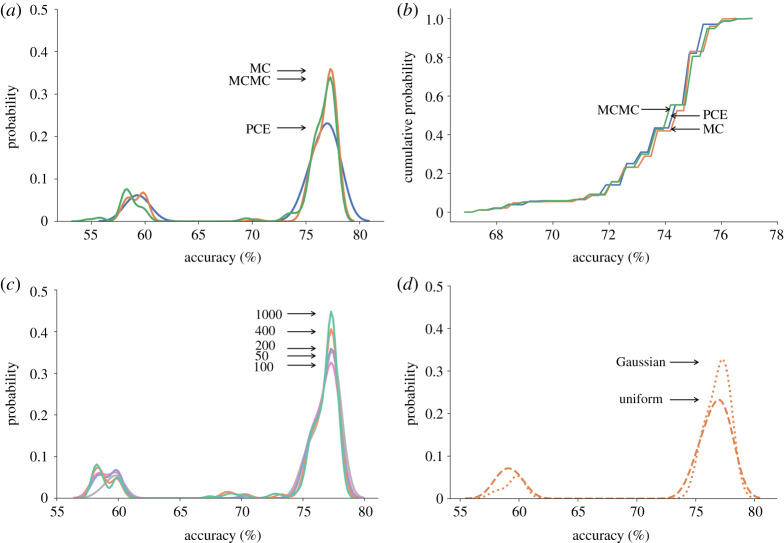
Previous studies have reported that PCE simulations achieve comparable accuracy to MC simulations and are significantly faster when the number of parameters is fewer than 20 [11,13,14]. We, therefore, compared the distributions of simulated model accuracy distributions using PCE, MC and Markov Chain MC simulations to quantify the effects of parameter uncertainty for different numbers of parameters. Randomly sampling the stretch input variable with all three methods achieved very similar distributions of model accuracy (figure 2a) that were not significantly different by Kolmogorov–Smirnov (K-S) test (p > 0.99 for PCE versus MC and PCE versus MCMC). Simulations varying 15 weight parameters also produced distributions of accuracy that were not significantly different by K-S test (p > 0.99) between order 3 PCE simulation and MC simulations with sample sizes of 3000 and similar computation times for each method (figure 2b). Simulation using order 2 PCE also resulted in distributions that were not significantly different from those with 3000 MC samples (p > 0.95) but with run times that were 1/5th as long on average. For more than 20 parameters, PCE simulations took an average of over three times as long to compute as comparably accurate MC simulations. K-S tests comparing the accuracy distributions obtained using MCMC simulations showed no significant differences with the results of PCE (p > 0.99) or MC (p > 0.30) simulations, though the required number of MCMC model evaluations was slightly lower than for the standard MC approach yet still more than the PCE method required to achieve comparable accuracy. Thus, for all the parameter UQ simulations reported here, we used order 2–4 PCE simulations when the uncertain component size was fewer than 20, otherwise we used MC simulations. We conducted initial simulations sampling from both uniform and Gaussian distributions (figure 2d). Since there were no statistically significant differences between the predicted accuracy distributions (p > 0.65 by K-S test), we used a uniform distribution as the default statistical sampling distribution for all the UQ simulations reported here, except where specified otherwise (figure 2).

Figure 2.

(a) Model predictive accuracy distributions computed for univariate sampling of the input stretch using MC (150 samples, in orange), MCMC (150 samples, in green) and PCE (order = 4, in blue) (arrows from top to bottom). (b) Cumulative accuracy distribution due to uncertainty in 20 weight parameters using different UQ methods and a comparable number of model evaluations (green: MCMC with 3000; blue: order 3 PCE; orange: MC with 3000 samples; arrows from top to bottom). (c) Model prediction accuracy distributions computed by MC sampling the input stretch with different sample sizes (sea green: 1000; orange: 400; steel blue: 200; grey: 50; pink: 100; arrows from top to bottom). (d) Model prediction accuracy distributions computed by MC sampling of the input stretch from different random distributions (dotted line: Gaussian distribution; dashed line: uniform distribution; arrows from top to bottom) with a sample size of 40. (Online version in colour.)

For reaction parameters n, EC₅₀, w and τ of all 125 reactions, we used MC simulations to sample from uniform random distributions in the following ranges:

$$\begin{array}{rl}& n\sim U(1,3),\\ & {\text{EC}}_{50}\sim U(0.4,0.6),\\ & \omega \sim U(0.2,1),\omega \sim U(0.8,1)\\ \text{and}& \tau \sim U(0.5,10).\end{array}$$

The ranges of n, EC₅₀ and τ sampled for parameter UQ were determined based on values commonly reported in the biochemical literature [2,7] together with mathematical constraints imposed by the model equations to prevent negative function values. Ordinarily, the reaction weights ω would be set at or close to 1 (the original default value was 0.9) unless the effects of an inhibitor, knockout or knockdown were being simulated. Therefore, we sampled ω from U(0.8, 1). Recognizing that this is a narrow range, we repeated the analysis for ω in the range U(0.2, 1). As expected, sampling from a wider range of ω that included lower node weights decreased average model accuracy when maintaining the same threshold. We, therefore, investigated the extent to which this effect was dependent on the chosen threshold. MC sampling was also used for analysing uncertainty in the validation data and the model threshold in the range (0.01, 0.09). We used MC sampling to quantify the epistemic uncertainty due to the choice of interaction logic by switching AND and OR logic with a random probability of 0.5.

To test whether sufficient parameter combinations were sampled, we increased the sample size in the UQ analysis of ω from 2500 samples to 100 000. The resulting distributions of model accuracy were not significantly different (p > 0.05 using Student’s t-test).

3. Results

(a). Parameter uncertainty

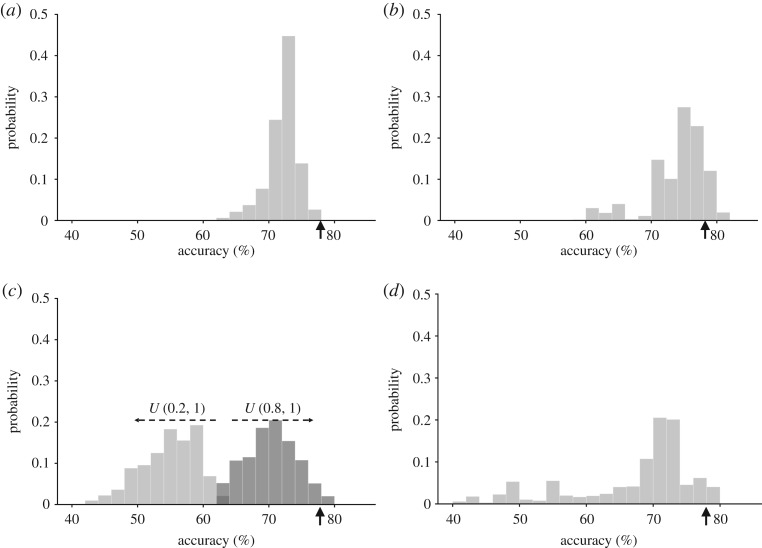
The effects of uncertainty in the parameters of all 125 reactions on computed model validation accuracy were quantified separately for ω, n, EC₅₀ and τ as shown in figure 3. Accuracy was generally robust to parameter variation, but most sensitive to uncertainty in ω (figure 3c) and insensitive to uncertainty in τ (not shown). Most perturbations decreased model accuracy but some increased it marginally suggesting some potential for model improvement. Uncertainty in the Hill coefficient n and half activation parameter EC₅₀ had similar effects on the distribution of model accuracy. These two parameters of the activation function are coupled numerically and only affect the speed at which signalling molecules reach steady state. Perturbations in τ were not large enough relative to the four-hour time-course of the simulation to affect the steady-state results. A global UQ analysis of all the model parameters led to a flatter accuracy distribution than that of the distributions obtained by sampling individual parameters. This distribution was similar to the sum of the individual parameter distributions suggesting that the impact of uncertainty in each individual parameter may be a good indicator of its contribution to the impact of parameter uncertainty in all parameters (figure 3d).

Figure 3.

Parameter uncertainty quantification. Model predictive accuracy distributions computed for univariate random sampling of uncertainty in reaction parameters: Hill coefficient n (a), half-activation EC₅₀ (b), reaction weight ω (c) and all model parameters combined (d). Vertical arrows indicate original default model accuracy. See text for details.

In assessing the effects of uncertainty in n, EC₅₀ and ω, we found that the loss of accuracy was mainly due to changes in the ability of the model to correctly predict the results of inhibition experiments rather than input–output experiments. In the analysis of parameter uncertainty in EC₅₀, the average accuracy of the input–output and input-intermediate validation decreased from 100% to 92% while the average accuracy of inhibitor experiment validations fell from 68% to 33%. For ω sampled in U(0.8,1), mean input–output accuracy only fell to 98% whereas mean inhibition experiment prediction accuracy fell to 29%. This conclusion was also consistent in the global UQ analysis on all parameters where the corresponding decreases were 100% to 60% and 68% to 15%, respectively. It is not surprising that inhibition experiments represent a more stringent test of model accuracy than input–output experiments, but they are also more likely to be subject to experimental error and more sensitive to model perturbations.

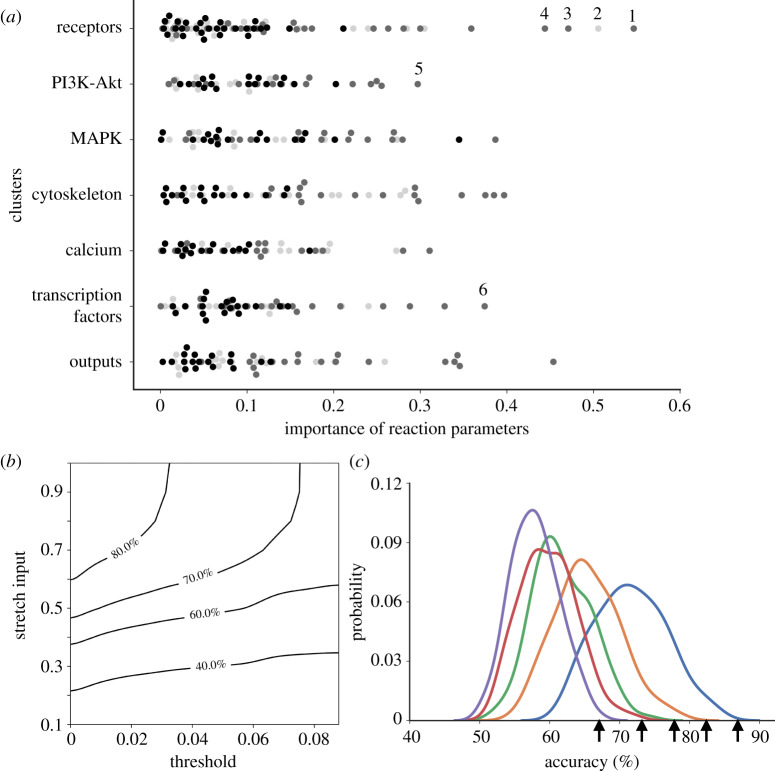
Taken together, the importance of the effects of perturbations in the reaction parameters on accuracy (figure 4a) as estimated by Pearson correlation analysis was not significantly different between the seven major modules of the network: cell surface receptors; the phosphoinositide 3-kinase/protein kinase B (PI3K/Akt) pathway; the mitogen-activated protein kinase (MAPK) pathway; cytoskeletal signalling; calcium signalling; transcription factors; and outputs. For this purpose, reactions were assigned to modules based on the module containing the target of the reaction, not the inputs.

Figure 4.

Analysis of parameter importance and the effects of model threshold. (a) Importance analysis of reaction parameters ω (light grey), EC₅₀ (dark grey) and n (black) by network module calculated using Pearson correlation of parameter variations with accuracy. Outlying reactions with the highest importance tended to be input or output reactions and included the reactions that activate endothelin-1 (1) and the endothelin-1 receptor (2), integrins (3), angiotensin II (4), phosphoinositide 3-kinase (5) and the skeletal α-actin gene (6). (b) Relationship between the effects of input and weight uncertainty and threshold uncertainty on accuracy contours. (c) Effects of varying model prediction threshold (between 0.09 purple, 0.07 red, 0.05 green, 0.03 orange and 0.01 blue, arrows from left to right) on accuracy distributions due to uncertainty in input and reaction weights. Vertical arrow indicates original default model accuracy. (Online version in colour.)

Lower inputs or reaction weights may have reduced validation accuracy by reducing overall system gain causing more responses to fall below the fixed threshold. To test this, we allowed the input to vary randomly from 0.1 to 0.9 and simultaneously allowed the threshold to vary randomly from 0.01 to 0.09. The contours of constant accuracy on the input-versus-threshold plane (figure 4b) show that decreases in model accuracy due to decreased input stretch could be partially offset by decreasing the threshold for categorizing an output of the model as significantly changed. Consequently, lowering the threshold increased mean accuracy (figure 4c).

(b). Model logic uncertainty

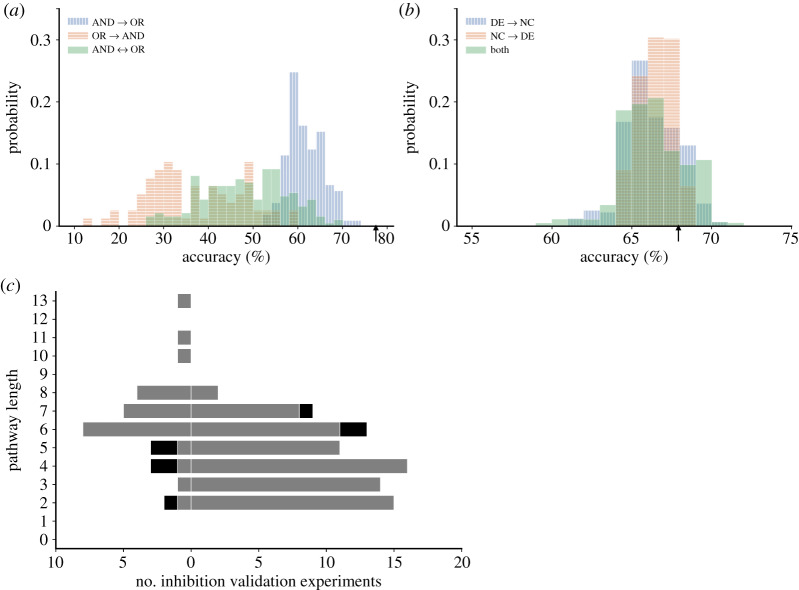
We examined the individual impact of model logic uncertainty for the 19 reaction combinations with ‘AND’ logic and 33 interactions with ‘OR’ logic on validation accuracy. As seen in figure 5a, switching model logic could greatly reduce accuracy, with changing ‘OR’ to ‘AND’ interactions causing much larger reductions than switching ‘AND’ reactions to ‘OR’ logic.

Figure 5.

Analysis of uncertainty in reaction logic and validation data. (a) Effects on model validation accuracy of randomly changing ‘AND’ logic to ‘OR’ logic (blue —), ‘OR’ reactions to ‘AND’ logic (orange -) or both (green), all with a probability of 0.5. (b) Effects of data uncertainty on model validation accuracy assessed only using reported inhibition experiments [2], for which the original accuracy was 67%. Effects on accuracy of changing significantly changed (SC) validation measurements to no change (NC) with a probability α of 0.05 (blue —). Effects of changing NC to SC with a probability β of 0.4 (orange -). Combined effects of both random changes (green). (Vertical arrows indicate original default model accuracy). (c) Effects on model accuracy of the length of the pathway between the inhibited node and the measured response node in the inhibition validation experiment [2]. Values to the left represent incorrect model predictions and values to the right represent correct predictions. Light grey represents model predictions of no change and black represents model predictions of significant change. (Online version in colour.)

A stepwise regression analysis of all the ‘AND’ logic interactions and a statistical analysis correcting for multiple comparisons (Benjamin–Hochberg false discovery rate) showed that predictive accuracy was significantly affected (p < 0.05) by the logic choice of 12 of the 19 ‘AND’ interactions (table 1). Switching all 12 interactions from ‘AND’ to ‘OR’ would decrease model accuracy from 77.9% to 56.4%. Eight interactions were highly significant (p < 0.01); they are all either output nodes of the system such as B-type natriuretic peptide (BNP), cell area, β-MHC, connexin 43 (Cx43) or particularly well-known regulators of mechanotransduction signalling such as focal adhesion kinase (FAK), protein kinase C (PKC), extracellular-regulated kinases (ERK1/2) and calcineurin (CaN). The ‘AND’ interaction between the reactions activating the muscle LIM-domain protein (MLP) was the only one to have a negative coefficient in the regression analysis suggesting that switching this ‘AND’ logic to ‘OR’ resulted in a slight improvement in accuracy. Reformulating the network by changing the interaction logic of the reactions activating MLP increased model accuracy by 1%. For the inhibition validation experiments, the original model predicted that MEF2 gene expression was only reduced by 8% when PKC was inhibited compared with a reduction of 100% block in published experiments [15,16]. Changing the logic by which PKC and calcium-calmodulin kinase (CaMK) regulate histone deacetylase 4 (HDAC4) from ‘AND’ to ‘OR’ increased the inhibitory effect of PKC blockade on MEF2 to greater than 20% and significantly improved model accuracy by more than 5%.

Table 1.

Regression analysis on perturbation of reaction interaction logic.

output node	estimate	s.e	Pr(>|t|)
BNP	0.095	0.025	0.0003
β-MHC	0.093	0.025	0.0004
CaN	0.093	0.027	0.0008
Cx43	0.085	0.025	0.0012
CellArea	0.086	0.027	0.0017
FAK	0.084	0.026	0.0018
PKC	0.080	0.026	0.003
ERK12	0.075	0.026	0.005
HDAC	0.067	0.025	0.010
PrSynth	0.062	0.026	0.019
CREB	0.060	0.025	0.019
sACT	0.059	0.025	0.022
ANP	0.049	0.025	0.054
SRF	0.052	0.027	0.056
IP3	0.045	0.028	0.107
Ao	0.039	0.025	0.127
FHL2	0.040	0.027	0.131
MuRF	0.016	0.026	0.538
MLP	−0.002	0.028	0.932

(c). Data uncertainty

The final source of uncertainty we investigated was statistical uncertainty in the experimental results of the inhibitor studies used to validate the model. In particular, while 110/120 of the published validation experiments reported a significant change in intermediate or output due to inhibitor treatment, 10/120 reported no change. However, the uncertainty inherent in the unchanged responses was four to eight times higher than the uncertainty in significantly changed responses because the conventional choice of α (p < 0.05) is much lower than β in the cell biological experiments, which are invariably under-powered owing to small sample sizes. Overall, data uncertainty had a limited impact on model accuracy; the original baseline inhibition accuracy was 68% and accuracy in almost all the UQ simulations was between 60% and 70% (figure 5b). The number of validation comparisons that would have been reversed by switching validation results from significant to unchanged was approximately the same as if the validation finding had been switched from unchanged to significant. Overall though, switching unchanged findings to changed led to a higher mean accuracy. This suggests that better powered experimental studies may be justified for experiments designed to test significant model-predicted responses to inhibitors that had no observed statistical effect in published experimental studies.

The accuracy with which the model correctly predicted the results of inhibitor experiments depended on the length of the pathway between the inhibited node and the readout node. For pathway lengths exceeding five, prediction accuracy decreased markedly (figure 5c).

Pathway analysis of the 120 inhibition experiment node pairs revealed 11 node pairs that were not connected in the network with the result that only 2 of these 11 experiments, ET1R/STAT and PI3K/JNK, could possibly have been correctly predicted by our model. For the other nine node pairs, we examined the original experimental studies and found there was either a lack of corroborating data [17–20], evidence of pathway crosstalk (e.g. between PI3K and Ras or Src and FAK) that was not represented in the original model [21–23] or contradictory data in subsequent publications.² In the other 109 node pairs, pathway analysis suggested that the longer the pathway (above six steps) between inhibited node and readout node, the higher the probability that the model would predict no change. This difference was mainly caused by the accumulated loss of activity values and a consequent decrease in likelihood that the model would reach the threshold for significant change with a consequent decrease in model accuracy.

4. Discussion

In this study, we explored the effects of uncertainty in parameters, model logic and experimental validation data on estimates of prediction accuracy by a published network model of mechanosignalling pathways in ventricular myocytes [2]. Model prediction accuracy was fairly robust to moderate uncertainty in network reaction parameters, but large decreases in model reaction weight did significantly impair accuracy. However, this was largely attributable to a reduction in overall system gain that could be compensated by a corresponding decrease in the threshold used to classify a particular model output as changed or unchanged for the purposes of comparison with experimental observations.

In contrast to parameter uncertainty, epistemic uncertainty analysis showed that model accuracy is more vulnerable to uncertainty in the choice of reaction logic. Randomly replacing ‘AND’ logic reactions with ‘OR’ logic had modest effects on accuracy, but the converse greatly reduced it. In the original publication, it was concluded that changing all logic to ‘OR’ type lowered the model performance if effects of varying stretch input and reaction weights were kept unchanged as studied in the original paper. Thus, there may be opportunities to improve model predictive accuracy and reliability by performing new experiments that can more confidently identify the most appropriate reaction logic. For example, we found that changing the interaction logic by which PKC and CaMK regulate HDAC4 from ‘AND’ to ‘OR’ increased the inhibitory effect of PKC blockade on MEF2 and significantly improved model accuracy. However, neither choice resulted in close quantitative agreement with experiments. The mechanisms by which different kinases and phosphatases regulate nuclear translocation of HDACs where they alter chromatin structure and gene expression are complex. They involve the successive phosphorylation of multiple residues that are targets of multiple kinases and phosphatases and could be cooperative [24]. A more complete investigation of uncertainty in the network structure could have been achieved by also completely removing reactions or adding new ones. However, determining which new reactions to be added to the model requires developing an improved model with more reactions. The effects of removing nodes was approximated when we sampled from a wider range of reaction weights since lower weights had the effect of rendering reactions ineffective at changing downstream node values enough to exceed the threshold for classifying them as significantly changed. Hence, it is not surprising that the resulting biochemical interactions may not be accurately approximated by a single logic gate. Therefore, improving quantitative model predictive accuracy and reliability may require a combination of reaction parameter and logic or the inclusion of additional types of reaction equations that more accurately approximate biochemical mechanisms.

Most combinations of parameter, data or logic perturbations tended to decrease the prediction accuracy compared with the default model accuracy. This is not unexpected given that the data and logic choices by default in the original model were based on published experimental literature that we expect to be correct substantially more often than not. Similarly, while the original default model parameters were not optimized, they were based on prior published knowledge and hand-tuned to give expected levels of network activity. Given this, a more rigorous approach to determining the distributions in §2 could be to compute posteriors for the parameters and the model in a Bayesian setting, and use those posteriors in place of the distributions described. Perturbations to parameters and reaction logic more often caused decreases than increases in output values. This difference was mainly due to the accumulated loss of activity values and thus a decrease in likelihood that the model would reach the threshold for significant change leading to a decrease in model accuracy. Particularly for ω, large variations could cause large decreases in accuracy. However, these parameters are normally set to 1 or close to 1 (0.9 by default) unless the reaction is being pharmacologically or genetically inhibited. Moreover, some of this loss of accuracy could be offset by a corresponding adjustment of the threshold for categorizing a model output as changed or unchanged. For realistic ranges of ω and all other model parameters the accuracy of model predictions was generally robust.

Finally, data uncertainty due to the risk of type I and type II errors in experimental data did not significantly affect estimated model accuracy. Interestingly, the higher uncertainty due to low power in the small fraction of inhibitor experiments with no significant change was less likely to decrease model accuracy than the much lower uncertainty associated with the larger number of experiments resulting in a statistically significant change. False positive model predictions could be worth investigating further by repeating previously reported experiments with larger sample sizes and statistical power.

In this study, we use two different UQ sampling methods: MC simulations and PCE. The latter method produced equivalent distributions of accuracy with less computational cost than the former when fewer than 20 parameters were being sampled, and was over ten times faster for ten or fewer parameters. We also found that sampling reaction parameters from uniform distributions yielded very similar findings to those obtained when the uncertainty was Gaussian. In our analysis, we found a numerical error rate of up to approximately 10% because some extreme combinations of parameters could force the system to its limits and increase the stiffness of the system of ODEs.

5. Conclusion

Quantification of the effects of uncertainty in model parameters, logic and validation data on the estimated accuracy of an ODE network model of the ventricular myocyte mechano-signalling network showed that the model was robust to parameter and data uncertainty but more vulnerable to errors in the choice of logic used to represent biochemical interactions between interacting biochemical species. In particular, incorrect interpretation of experimental data to represent ‘AND’ reaction logic can significantly decrease prediction accuracy. The findings of this UQ analysis point to opportunities for model parameter refinement and extension of model pathway structure and logic, and for new experimental measurements that improve the power of statistical conclusions.

Data accessibility

This article does not contain any additional data.

Authors' contributions

S.C. implemented the Python code and methodology for uncertainty quantification analysis and also edited the manuscript. Y.A. conceived of applying UQ to the network model and edited the manuscript. A.W. edited the manuscript and tested the code. J.J.S. provided the original model and edited the manuscript. D.V.J. edited the mathematics and manuscript. J.H.O. organized the manuscript structure and edited the manuscript. A.D.M. conceived of the project idea, acquired funding, administered and supervised the project, and edited the manuscript. All authors read and approved the manuscript.

Competing interests

A.D.M. and J.H.O. are co-founders of and have equity interests in Insilicomed. A.D.M. has an equity interest in Vektor Medical. He serves on the scientific advisory board of Insilicomed and as scientific advisor to both companies. Some of his research grants, including those acknowledged here, have been identified for conflict of interest management based on the overall scope of the project and its potential benefit to these companies.

Funding

This work was also supported in part by National Institutes of Healthawards (HL105242, HL137100, HL122199, HL126273) and the National Biomedical Computation Resource (P41 GM103426 to A.D.M.).