Quantification of uncertainty in a new network model of pulmonary arterial adventitial fibroblast pro-fibrotic signalling

Abstract

Here, we present a novel network model of the pulmonary arterial adventitial fibroblast (PAAF) that represents seven signalling pathways, confirmed to be important in pulmonary arterial fibrosis, as 92 reactions and 64 state variables. Without optimizing parameters, the model correctly predicted 80% of 39 results of input–output and inhibition experiments reported in 20 independent papers not used to formulate the original network. Parameter uncertainty quantification (UQ) showed that this measure of model accuracy is robust to changes in input weights and half-maximal activation levels (EC₅₀), but is more affected by uncertainty in the Hill coefficient (n), which governs the biochemical cooperativity or steepness of the sigmoidal activation function of each state variable. Epistemic uncertainty in model structure, due to the reliance of some network components and interactions on experiments using non-PAAF cell types, suggested that this source of uncertainty had a smaller impact on model accuracy than the alternative of reducing the network to only those interactions reported in PAAFs. UQ highlighted model parameters that can be optimized to improve prediction accuracy and network modules where there is the greatest need for new experiments.

This article is part of the theme issue ‘Uncertainty quantification in cardiac and cardiovascular modelling and simulation’.

1. Introduction

Cell signalling networks are cascades of biochemical reactions that regulate cellular responses to external cues, and their dysregulation is important in the progression of disease. Pulmonary arterial hypertension (PAH) involves pathological remodelling of the vascular wall mediated in part by pulmonary arterial adventitial fibroblasts (PAAFs) in response to pathological strain and stresses such as mechanical overload and hypoxia. PAAFs residing in the adventitial layer of the arterial wall regulate vascular extracellular matrix (ECM) and mechanical properties [1]. Studying the interplay between the effects of signalling cytokines, hypoxia and the mechanical stimuli that are activated in PAH will help to elucidate signalling pathway interactions and may aid in developing novel therapies to reverse vascular fibrosis and disease progression.

Mathematical modelling of cell signalling networks is a useful tool for synthesizing available experimental data and investigating interactions between pathways that are difficult to study experimentally. Here, we introduce a new logic-based ordinary differential equation model [2] of the major biochemical networks known to regulate pro-fibrotic cell responses such as ECM expression, proliferation and myofibroblast transformation in PAAFs [3]. The network model was derived from published cell biological experiments and transcriptional measurements in primary PAAFs supplemented, where necessary, with information on canonical pathway structure from better studied fibroblast types, mainly cardiac fibroblasts (CFBs). Inputs to the PAAF signalling network model were based on reported stimuli upregulated in PAH [1].

While the signalling pathways included in this model have been identified in PAAFs, their interplay is not well understood, and there is a paucity of experimental data in the literature specific to these fibroblast cells. Therefore, after constructing a PAAF signalling network model, we carried out a sensitivity analysis to identify the important nodes in the network.

Creating a cell signalling model inherently introduces parameter uncertainty, since experimental studies rarely report quantitative biochemical reaction properties. There are also epistemic uncertainties in the structure and logic of the network, which depend on published experiments from a variety of cell types and conditions that are occasionally inconsistent or ambiguous [4]. Therefore, to analyse the robustness of the developed model and identify how small perturbations in the parameters leads to changes in model predictions, we have carried out uncertainty quantification (UQ) analysis of the model parameters. Using a separate set of data not used in the model formulation, we determined the prediction capabilities of the model and its qualitative accuracy. We also used this method to determine if adding pathways from other fibroblast cell types impacts model accuracy.

Here, we have not attempted to optimize model parameters, so we cannot expect close quantitative agreement between model predictions and experimental data. Rather, objective qualitative comparison criteria were used, and we used UQ to assess the robustness of model prediction accuracy and to identify the modules and parameters that are most affected by incomplete or noisy data [5]. Analysis of parameter and structural uncertainty showed that the PAAF model is robust to most parameter uncertainty and identified the new experiments that are needed the most to improve model confidence and accuracy.

2. Methods

(a). Computational model of pro-fibrotic pulmonary arterial adventitial fibroblast cell signalling

The PAAF signalling model was manually constructed with the same default parameters and model file structures as the one developed by Zeigler et al. for CFBs [6]. Out of the 92 reactions in our model, 52 reactions are unique to PAAFs. The model construction was based on results reported in 52 published papers describing experimental studies in PAAFs or other fibroblast types [7–58] when necessary to complete 18 intermediate reactions not described in the comparatively sparse literature on PAAF signalling. In addition, 20 independent papers documenting in vitro or in vivo experiments in rat or human PAAFs and not used in the original model formulation were set aside to measure the predictive capability of the model.

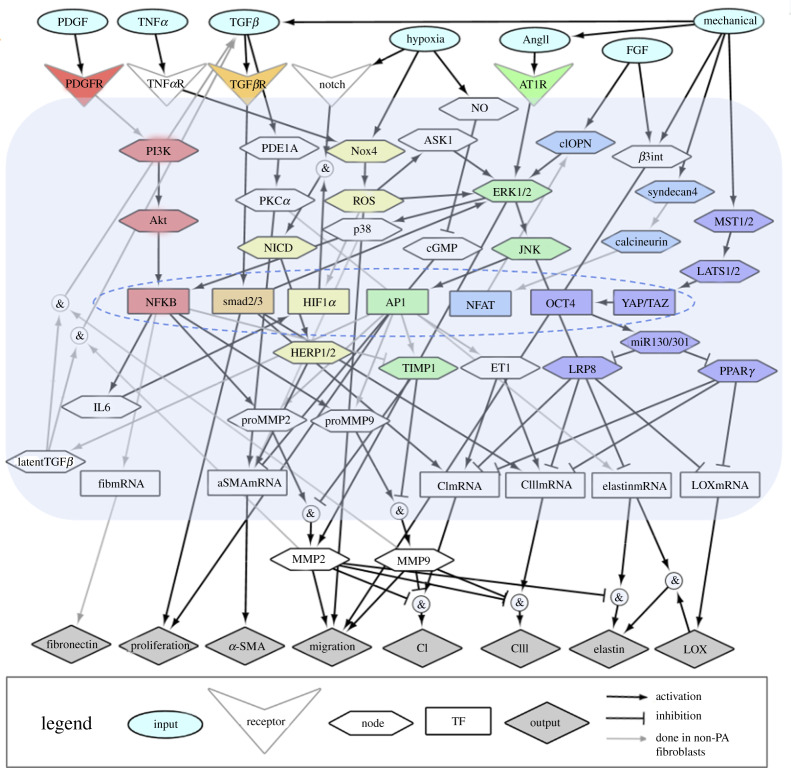
The resulting PAAF signalling network (figure 1) integrates seven input stimuli that are implicated in PAH pathogenesis including mechanical loading, transforming growth factor-β (TGFβ), tumour necrosis factor-α (TNFα), platelet-derived growth factor (PDGF), angiotensin II (AngII), fibroblast growth factor (FGF) and hypoxia. These activate seven receptors and signalling modules, namely the phosphoinositide 3-kinase (PI3K), TGFβ, Notch, reactive oxygen species (ROS), mitogen-activated protein kinase (MAPK), calcineurin and Hippo pathways. Downstream transcription factors regulate the expression of eight outputs important in the pro-fibrotic cell phenotype and ECM remodelling [59]. Overall, there are 64 nodes that represent physical stimuli, ligands, receptors, signalling molecules, transcription factors, messenger RNA (mRNA), proteins and cell phenotypes interconnected via 92 reactions. The publications used to justify each individual reaction and interaction are cited in electronic supplementary material, S1.

Figure 1.

A schematic of a pro-fibrotic PAAF cell signalling network comprised of 64 nodes with input stimuli (blue ovals), receptors (triangles), signalling molecules (hexagons), transcription factors (coloured rectangles), messenger RNA (rectangles) and phenotypic outputs (grey diamonds). The colours represent the recognized signalling modules including phosphoinositide 3-kinase (PI3K) (red), TGFβ (orange), Notch, reactive oxygen species (ROS, yellow), mitogen-activated protein kinase (MAPK, green), calcineurin (blue) and Hippo (purple). The arrows indicate the 92 activation or inhibition reactions, with the grey arrows denoting reactions based only on experiments in non-PA fibroblasts. Converging reactions denoted by & indicate ‘AND’ gate logic, while other combinations imply ‘OR’ gate logic. (Online version in colour.)

Using previously described methods [6,60], the PAAF signalling network model was implemented as a system of logic-based ordinary differential equations that were integrated numerically using the explicit second- and third-order Runge–Kutta method. Each state variable is normalized to a value between 0 and 1 and follows a Hill-type activation function [2]. This approach allows a Boolean system to be translated into a continuous time system with parameters that are representative of biochemical reactions [2]. Logical operators are used to represent signalling interactions with ‘NOT’ representing inhibition, ‘OR’ a reaction in which the node can be activated by multiple inputs, and ‘AND’ representing where the activation requires the activity of more than one upstream node.

The system of differential equations is formulated for each node y_i in the network, i = 1…64

$$\frac{\text{d}{y}_i}{\text{d}t}=\frac{1}{{\tau }_{y_i}}[{\omega }_{y_i}{f}_j{y}_i^{\text{max}}-y_i],$$ 2.1

with a general reaction weight ω and Hill function f_j, where j can be an activation (act) or inhibition (inhib) reaction

$$f_{\text{act}}(y_i)=\frac{B{y}_i^n}{K^n+y_i^n}$$

and

$$f_{\text{inhib}}(y_i)=1-\frac{B{y}_i^n}{K^n+y_i^n},$$

where B is a function of the half-maximal activation EC₅₀ and the Hill coefficient n, which is a measure of nonlinear cooperative activation [2].

$$B=\frac{{\text{EC}}_{50}^n-1}{2{\text{EC}}_{50}^n-1}$$

and

$$K={(B-1)}^{1/n}.$$

In the case where y_i is an input, f_j = 1 and the input reaction weight is denoted w.

To represent ‘OR’ logic interactions, equation (2.1) is modified to represent the sum of the reactions with respective weights for each node and subtracting the intersection of f_j(y_k) and f_j(y_l)

$$\frac{\text{d}{y}_i}{\text{d}t}=\frac{1}{{\tau }_{y_i}}[({\omega }_{y_k}{f}_j(y_k)+{\omega }_{y_l}{f}_j(y_l)-{\omega }_{y_k}{f}_j(y_k){\omega }_{y_l}{f}_j(y_l))y_i^{\text{max}}-y_i],$$

where y_k and y_l are upstream nodes that activate or inhibit y_i.

For ‘AND’ logic interactions, equation (2.1) is modified to be the product of the general reaction weight ω, f_j(y_k) and f_j(y_l)

$$\frac{\text{d}{y}_i}{\text{d}t}=\frac{1}{{\tau }_{y_i}}[{\omega }_{y_k}{f}_j(y_k)f_j(y_l)y_i^{\text{max}}-y_i].$$

The baseline model solution was obtained using a default Hill coefficient of n = 1.4 and EC₅₀ of 0.6 for every node. The time constants τ for each different reaction type in the network followed those used previously [6]: 0.1 h for signalling reactions; 1 h for transcription; and 10 h for translation. Timepoints chosen were run at steady state. Input weights (w) were initialized to 0.25 to represent baseline activity. Reaction weights for the rest of the system (ω) were set to a default value of 1. The system of ODEs was generated from a tabular representation of the network using custom software available on Github.¹

(b). Model validation

To validate the model, 39 input–output experiments in rat or human PAAF cells (reported in 20 papers [61–80]) were classified as observing a significant increase or decrease, or no significant change in activity of an output quantity that is a node in the model in response to a stimulus, that was also an input to the model. The threshold for considering a response in the model to represent a significant change in output activity was chosen to be 0.05. In vivo data were used when there were no in vitro data reported in the literature on PAAFs. The time-course of the model for each comparison was matched to that of the corresponding experimental measurement. Citations to the publications used for each model comparison experiment are given in electronic supplementary material, S2.

(c). Sensitivity analysis

A model baseline was calculated by setting all input weights to 0.25 and the initial values of all state variables to 0. They were then integrated until a steady state was achieved for all nodes at 200 min. One hundred per cent knockdown of each node was simulated by reducing y_max from 1 to 0, and the subsequent effect at every node was calculated as knockdown activity minus baseline activity. Sensitivity analysis was performed under baseline conditions and under conditions of high mechanical stretch (mechanical input weight set to 0.9) to represent the effects of mechanical overload and matrix stiffening associated with PAH.

(d). Uncertainty quantification

The model system of ordinary differential equations (equation (2.1)) can be represented as $\dot{\mathbf{y}}=f(\mathbf{y},\mathit{\theta }),\mathbf{y}\in {\mathbb{R}}^i,$ where $\dot{\mathbf{y}}$ is a vector representing the time rate of the change of the nodal network states y. The index i represents the problem dimension, which in this case is equal to the number of nodes in the network shown in figure 1. The vector θ contains the parameters that can be represented as $\mathit{\theta }\in {\mathbb{R}}^k$, where k is the number of uncertain model parameters that we intend to investigate.

To propagate parameter uncertainties in the network, we followed the approach described by Marino et al. [81], in which each parameter in θ is assumed to be a uniform random variable from the uniform distribution ∼U(min, max). Herein, we propagate three uncertain independent parameters: n, EC₅₀, and w (θ = {n, EC₅₀, w}). These parameters were sampled randomly from uniform distributions. The ranges chosen for the model parameters vary roughly 30% around their mean when carrying out UQ analysis. For example, n was chosen to be a uniform random variable such that n ∼ U(1.36, 2.36). It should be noted that the range of n was set from 1.36 to 2.36 as guided by the equation by Kraeutler et al. [2]: $B=({\text{EC}}_{50}^n-1)/(2{\text{EC}}_{50}^n-1)$, since a default value of EC₅₀ = 0.6 gives a minimum of n to be 1.36 or else B would be negative and thus K = (B − 1)^1/n would not produce a viable value. When n is set to 1.4, the EC₅₀ can only vary slightly around the default value of 0.6, so the UQ analysis was run with n set to 2, in order to perturb a wider range of EC₅₀ from 0.4 to 0.7, EC₅₀ ∼ U(0.4, 0.7). Similarly, the input weight w was also run with n set to 2 to keep the results consistent, and was set to vary from 0.1 to 0.4, around the default value (0.25), w ∼ U(0.1, 0.4).

The UQ simulations were performed using the package Uncertainpy 1.2.1 in Python [82]. The package was run in order to quantify the change in model accuracy compared to validation data when varying the aforementioned three parameters: n, EC₅₀ and w. Since there are only seven locations in the network that depend on the input weight w, we used the polynomial chaos expansion approach with fourth-order approximation to non-intrusively propagate uncertainty. This is generally less computationally expensive than Monte Carlo simulations; however, for systems with over 20 uncertain parameters, the required number of model evaluation scales worse than the Monte Carlo method [82]. Because of this, the (quasi-)Monte Carlo method was used with 5000 model evaluations for UQ analysis of n and EC₅₀ due to there being 99 reactions each with individual n and EC₅₀ values being perturbed in the network. The ranges of parameter values that are noted in the UQ results are identified by examining the output file and sorting by accuracy, then analysing the combinations of parameters that led to notable changes in accuracy.

Moreover, to compare the baseline model results with a model derived only from experiments in PAAFs or CFBs, we ran UQ analysis using the (quasi-)Monte Carlo approach varying all three parameters where n ∼ U(2, 2.4), EC₅₀ ∼ U(0.4, 0.6) and w ∼ U(0.1, 0.4), and with 10 000 model evaluations. The effects on model accuracy of changing parameters and the network structure were evaluated by classifying input–output model results as increased, decreased or unchanged using a threshold change of 0.05 and determining the percentage of model results in agreement with the published experimental findings.

3. Results and discussion

(a). Model validation

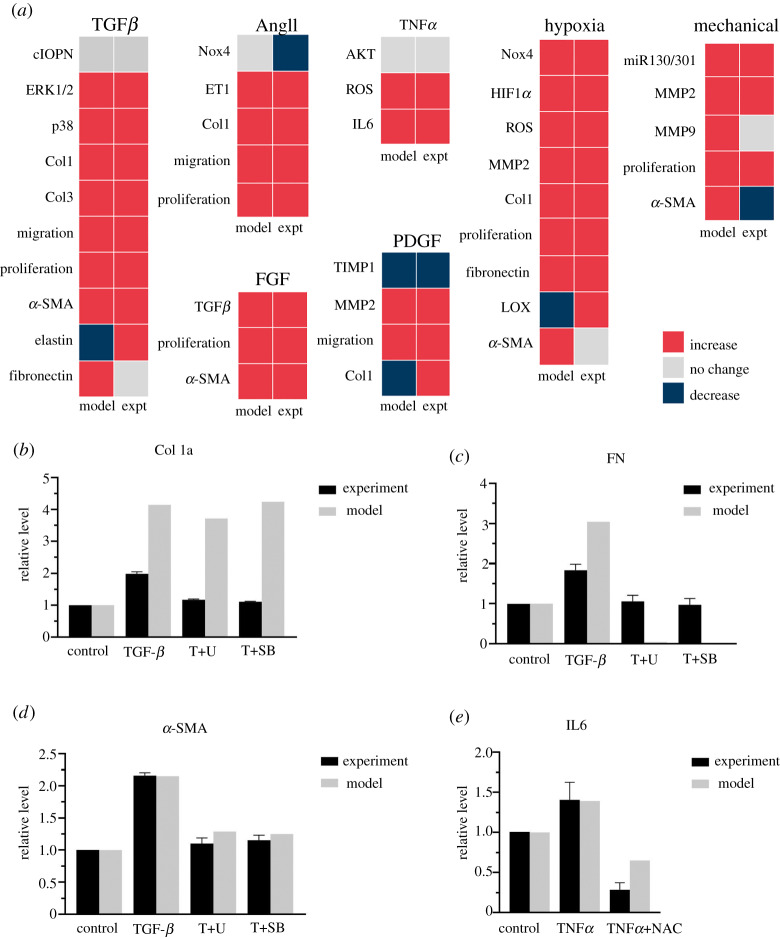
The model accurately predicted 31 out of 39 (80%) of the qualitative experimental validation results, including 4 out of 5 of the in vivo (bolded) and 27/34 of the in vitro experimental findings (figure 2a). Model accuracy went down to 35% when not using PAAF-specific pathways and using only reactions from the CFB model by Zeigler et al. [6] (data not shown).

Figure 2.

Model prediction of qualitative input–output experiments (a) and inhibition results (b–e). (a) Input–output validation: model predictions agreed with published experimental observations for 31 out of 39 (80%) of the input–output responses measured in rat or human PAAFs. Intermediate and phenotypic output results are organized by input stimulus, where the bolded node names indicate experimental results that were measured in vivo. (b–e) Inhibition validation: results of the PAAF model are compared with the results of inhibition experiments in cultured rat PAAFs reported by Zhang et al. (b–d) [76] and He et al. (e) [77]. Each model prediction was normalized to the baseline condition obtained when all inputs were 0.25. Stimulation with TGFβ and TNFα were simulated by increasing these inputs to 0.475 and 0.375, respectively, to be consistent with the experimental protocol. The effects of the ERK inhibitor (T+U), p38 inhibitor (T+SB) and ROS scavenger (NAC) were simulated by decreasing y_max for those nodes from 1.0 to 0.3, 0.05 and 0, respectively, consistent with the published reports [83,84]. (Online version in colour.)

The model was also able to predict results from in vitro experiments in rat PAAFs in which TGFβ, TNFα or ROS were inhibited pharmacologically [76,77]. Each node in the model was first initialized with a default baseline value of 0.25, and the control activity of collagen I, alpha-smooth muscle actin (α-SMA), fibronectin and interleukin 6 (IL6) were computed. Next, stimulation with TGFβ and TNFα was simulated by increasing the input weights corresponding to those nodes to 0.475 and 0.375, respectively. These two values were chosen to best match the increase in relative level of α-SMA as reported by Zhang et al. [76] and IL6 as reported by He et al. [77]. Experiments using 10 μM ERK inhibitor U0126 (T+U) reduced its activity to 30% [83]. Similarly, 10 μM p38 inhibitor SB203580 (T+SB) reduced p38 activity to 5% [84]; the ROS scavenger N-acetyl-L-cysteine (NAC) completely blocked ROS activity [77]. Hence, after stimulation of the baseline model with TGFβ, the effects inhibiting the ERK1/2 and p38 nodes were simulated in the model by reducing y_max from 1.0 to 0.3 and 0.05, respectively (figure 2b–d). Similarly, the effects of NAC on TNFα were simulated by reducing the ROS node from 1.0 to 0.0 (figure 2e). Simulations ran for 24 h [76] and 8 h [77] to match the time-course of the corresponding experimental measurements, as depicted in figure 2b–e.

Per cent errors between model-predicted and experimental results for collagen I expression stimulated by TGFβ and with TGFβ in the presence of the ERK1/2 and p38 inhibitors were 109%, 218% and 283%, respectively [76]. Although these errors were high, the model did qualitatively predict the observed increase in collagen I stimulated by TGFβ but not the observed inhibitory effects of either inhibitor. This may be because of incomplete or inaccurate interaction logic in the module of the network regulating collagen I expression. On the other hand, the model did correctly predict observed trends for fibronectin with % errors of 66%, −95% and −99%, though predicted inhibition was greater than observed, perhaps because only MAPK signalling regulates fibronectin in the model. Because the model simulation was matched to the α-SMA experimental results, the error for TGFβ stimulation was only −0.4%, and there was a good match with the inhibition results with % errors of 16.7% for T+U (ERK1/2 y_max to 0.3) and 8.4% T+SB (p38 y_max to 0.05) [76]. This shows that the model was able to closely predict the trends in α-SMA and fibronectin activity. Changes in the model structure may be required before collagen I expression can be predicted.

We compared the model with experiments in which TNFα was added to rat PAAFs [77] by increasing the TNFα node from 0.25 to 0.375. The error in the predicted increase in IL6 expression was only −1.1%, and the predicted effect of adding the ROS scavenger was qualitatively similar to observation, with an error of 128% (figure 2e).

All model results were significantly different (p < 0.05) than experimental means except those for α-SMA (figure 2d. A Student’s heteroscedastic t-test produced p-values of 0.06 for α-SMA stimulation and ERK inhibitor (T+U) and 0.16 for α-SMA stimulation and p38 inhibitor (T+SB) given the sample size (n = 3) and standard deviation reported in the original experimental paper [76].

(b). Sensitivity analysis

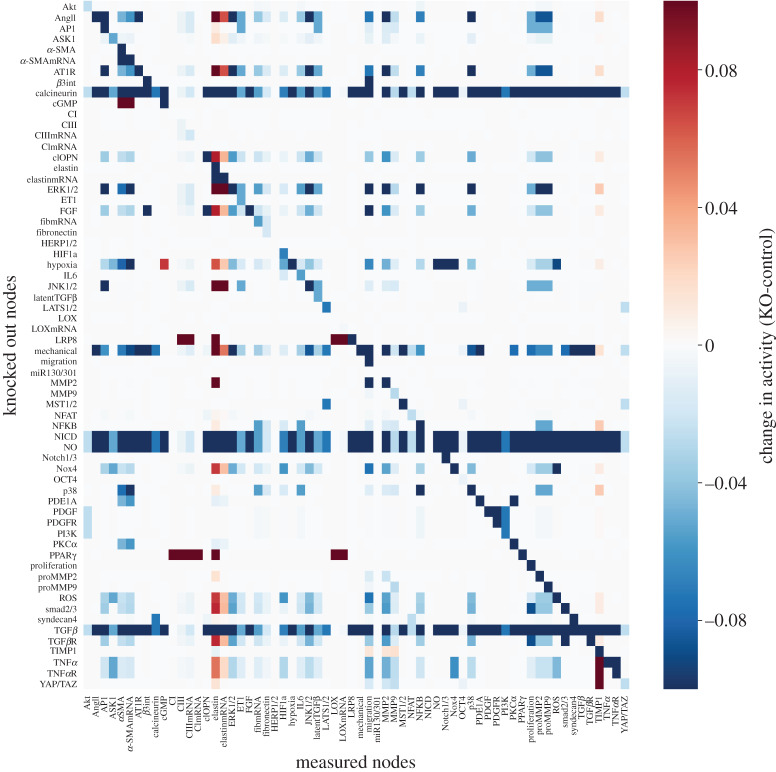
A sensitivity analysis was used to identify the nodes that are the most influential determinants of network state under baseline conditions and conditions of high mechanical stimulation as occurs in PAH. The change in the steady-state (200 min) response of each node in the network (columns) to 100% knockout of each node individually (rows) is displayed as a heat map in figure 3. The analysis shows that mechanical stimulation, hypoxia, angiotensin II and transforming growth factor β are the most important inputs. Important intermediate regulators include the MAPK (ERK1/2, JNK1/2 and p38), calcineurin, the Smads 2 and 3, cleaved osteopontin (clOPN), ROS, notch intracellular domain (NICD), nitric oxide (NO) and NADPH oxidase 4 (Nox4). This sensitivity analysis has thus revealed the larger influence of hypoxia and FGF in the PAAF model than in the model of CFBs [6]

Figure 3.

Heat map of the baseline sensitivity analysis showing changes in activity of all the nodes in the model (columns) in response to knocking out each node (rows), where red indicates an increase in activity over baseline and blue shades indicate a decrease in activity in response to the knockout. (Online version in colour.)

Given the importance of mechanical loading and vessel stiffening in the pathogenesis of pulmonary arterial fibrosis, we repeated the sensitivity analysis in the context of high mechanical load by increasing the input weight of the mechanical stimulation input node from the baseline value of 0.25 to a higher value of 0.9 as shown in electronic supplementary material, S3. Under these conditions, the most influential unique nodes were found to be α-SMA, cyclic guanosine monophosphate (cGMP), endothelin 1 (ET1), proteins in the Hippo pathway and syndecan4. These nodes are highly active in mechanotransduction, proliferation, vasoconstriction and activation of fibroblasts into the myofibroblast phenotype [3]. Knocking out these nodes generally resulted in a decrease in matrix proteins including collagen III and fibronectin. This global sensitivity analysis is also a way to elucidate the likely determinants of greatest structural and parameter uncertainty in the model. In the following sections, we investigated the effects of parameter and network uncertainty in the model.

(c). Quantification of parameter uncertainty

In order to examine the effect of propagated uncertainty of model parameters on the accuracy of the model, a validation table of the 39 experimental results was coded to compare results against. The accuracy was compared with the baseline 80% accuracy achieved with default model parameters.

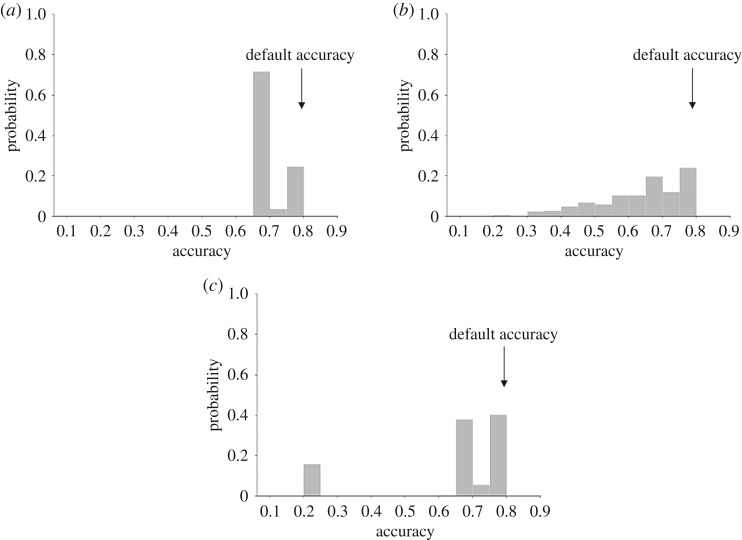
Each parameter was varied independently using a uniform distribution $n\sim (1.36-2.36)$, ${\text{EC}}_{50}\sim (0.4-0.7)$, $w\sim (0.1-0.4)$. A (quasi-)Monte Carlo method with 5000 model evaluations was used for UQ analysis of n and EC₅₀ to cover the 99 uncertain reactions, and a fourth-order polynomial chaos expansion was used for the weight w of the seven model inputs. As seen in figure 4, the distribution of model accuracy for input weight has a mean of 70.4%, standard deviation of 5.3%, a minimum accuracy of 66.67% and a maximum accuracy of 79.5%. For EC50, the mean of the distribution is 65.4% with a standard deviation of 19.2% and a minimum accuracy of 20.5% and maximum accuracy of 82%. For the Hill coefficient, the mean accuracy of the distribution was 63.9% with a standard deviation of 13.3%, a minimum accuracy of 20.5%, and a maximum accuracy of 79.5%. This indicates that network model accuracy was most vulnerable to uncertainty in n, somewhat vulnerable to uncertainty in EC₅₀ and relatively robust to input weight uncertainty.

Figure 4.

Quantification of the effects of model parameter uncertainty on the probability of qualitative model prediction accuracy assuming uniform random distributions of input weights w (a), Hill coefficients n (b), and half-maximal activations EC₅₀ (c). Accuracy with using default parameters is annotated. Varying input weight w randomly between 0.1 and 0.4 for seven inputs using polynomial chaos expansion with a fourth order produced accuracies between 70% and 80%, whereas varying the Hill coefficient n from 1.36 to 2.36 for all 99 reactions using the (quasi-)Monte Carlo method resulted in a much wider distribution of model accuracies ranging from 20% to 80%. Varying EC₅₀ randomly between 0.4 and 0.7 for all 99 reactions using the (quasi-)Monte Carlo method resulted in peaks in accuracy at around 20% and at 70–80%.

A subset of specific combinations of input weights over the range of 0.1–0.4 did result in a decrease in accuracy including a combination of low mechanical and low hypoxia or a combination of low AngII, TGFβ and FGF, but these did not decrease the model accuracy more than 13% (figure 4a).

There was a wide range of changes in model accuracy as shown in figure 4b, over the relatively large range of n of 1.36–2.36, showing increased uncertainty propagation. Lower model accuracy (less than 40%) was observed when more than 30% of the 99 reactions had Hill coefficients n exceeding 2.2. In order to allow EC₅₀ to vary, n was set to 2 as stated in §2 to avoid numerical errors [2].

Model accuracy was generally high and robust to varying EC₅₀ from 0.4 to 0.7, but there was a secondary peak at 20% as seen in figure 4c. The low peak occurred when the reactions of MST1/2 activating LATS1/2 and miR130/301 inhibiting LRP8 both had EC₅₀ values greater than 0.68. Both reactions are involved in the Hippo pathway, which is activated by mechanical stimulus. Finally, there was a set of EC₅₀ values that led to an increased model accuracy of 82%. When compared with thousands of combinations that produced an 80% accuracy. This result is unique in that all of the inputs and hypoxia → Nox4 were not extreme values (0.42 < EC₅₀ < 0.68) combined with a high EC₅₀ (greater than 0.68) for the reaction: MMP9 and latent TGFβ activating TGFβ and a low EC₅₀ (less than 0.42) for the reaction: proMMP9 activating MMP9 and TIMP1 inhibiting MMP9. This finding demonstrates how further tuning can be done by optimizing model parameters.

The 11 inhibition results seen in figure 2b–e (activation by TGFβ and TNFα then inhibition of p38, ERK1/2 or ROS) were coded with a threshold of 0.05, and UQ was repeated using polynomial chaos expansion with a fourth order varying the seven input weights from 0.1 to 0.4. Electronic supplementary material, S5 shows that the predicted results of inhibition experiments were relatively robust to this change, accurately predicting 9/11 (82%) or 8/11 (73%) of the activation by TGFβ and TNFα and inhibition of p38, ERK1/2 and ROS. However, the model was not able to capture the inhibition of collagen I by p38 or ERK1/2.

(d). Quantification of epistemic uncertainty of network structure

To use UQ to evaluate the level of uncertainty associated with the cell type used in the model construction, a reduced version of the model was created with only experimental data reported for fibroblast cells from the cardiovascular system, specifically PAAFs and CFBs. This new criterion led to a reduced model with 82 reactions and 62 nodes, due to the removal of ET1 and latent TGFβ, versus the 92 reactions and 64 nodes in the original model (electronic supplementary material, S4). The reduced model was qualitatively validated against the same independent set of data as the full model. Here, the accuracy went down to 24/38 (63%) compared to 31/39 (80%) for the original model. The number of experiments compared against drops down from 39 to 38 as a result of ET1 being a node in the input–output comparison.

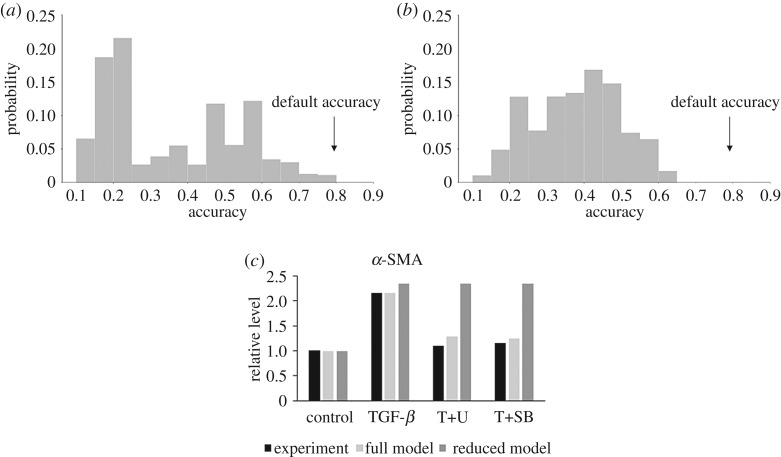
We ran a (quasi-)Monte Carlo simulation with 10 000 model evaluations where n was given a uniform distribution from 2 to 2.4, EC₅₀ was given a uniform distribution of 0.4 to 0.7 (default value of 0.6), and the input weight w was given a uniform distribution of 0.1 to 0.4 (default value of 0.25) as depicted in figure 5a.

Figure 5.

Results of a 10 000 model evaluation run using the (quasi-)Monte Carlo simulation where the Hill coefficient n was a uniform random variate between 2 and 2.4, EC₅₀ was given a uniform distribution of 0.4 to 0.6, and w was varied according to a uniform random distribution of 0.1 to 0.4. The two models being compared are the UQ results for the full model (a) versus the reduced model (b) based only on literature data from cardiovascular cells (PAAFs and CFBs) with accuracy using default parameters annotated. Inhibition results for α-SMA using the reduced model were run under the same conditions used to produce figure 2d (c). Results remained unchanged for the other outputs (collagen I, fibronectin, IL6) as seen in electronic supplementary material, S5.

We further compared the two models by varying all three parameters at once: n ∼ U(2, 2.4), EC₅₀ ∼ U(0.4, 0.6) and w ∼ U(0.1, 0.4) (figure 5). The mean accuracy of the baseline model (figure 5a) was 35.7% with a standard deviation of 18% and reaches a maximum accuracy of 80%, while the mean accuracy of the reduced model (figure 5b) was 38.4% with a standard deviation of 12% and a maximum accuracy of 63%. Overall, this result suggests that while using data from non-cardiovascular cell types is a source of epistemic uncertainty, the additional model components and reactions deduced from these other cell types can improve prediction accuracy without significantly compromising robustness. These results may help to prioritize new in vitro experiments in PAAFs that are not available in the literature but are important to the accuracy of the model. This includes experiments on the feedback from and activation of latent TGFβ, activation of TIMP1 and ET1 by AP1, activation of elastin mRNA by PKCα, activation of HIF1α by ROS and activation of α-SMAmRNA by p38.

To examine the effects of only including cardiovascular fibroblast data (PAAFs and CFBs) on the inhibition results, simulations were rerun with the same conditions as in figure 2b–e. Briefly, input TGFβ = 0.475, and TNFα = 0.375, ERK1/2 y_max = 0.3, p38 y_max = 0.05, ROS y_max = 0, and at 24 h and 8 h, respectively. While other trends remained the same as shown in electronic supplementary material, S5, the reduced model resulted in a qualitative reversal of the accuracy for α-SMA predicted by the full PAAF model. As shown in figure 5c, there was no longer a decrease in activity in α-SMA due to ERK and p38 inhibitors as originally observed. The reduced form of the model only agrees with the increase in α-SMA due to TGFβ stimulation. The results also no longer match the experiment, producing p values that were less than 0.05 with a heteroscedastic Student’s t-test, rejecting the null hypothesis that the model results lie in the same distribution as the experimental ones [76]. Thus, the full model, despite including some information from non-cardiovascular fibroblasts, better captures the complex regulation of α-SMA expression.

4. Conclusion

We created a novel network model of cell signalling in PAAFs that integrates seven signalling modules known to be involved in pulmonary arterial fibrosis. This model was qualitatively consistent with experimentally measured input–output relationships and the results from inhibition experiments all from independent papers not used to formulate the model originally. To determine the specificity of the model to fibroblasts from the pulmonary arterial adventitia, we ran a simulation using only nodes also included in the CFB model developed by Zeigler et al. Here, the CFB model with 40 reactions significantly underpredicted by almost threefold the PAAF input–output experiments. This indicates the important role played by the 52 added reactions in our fibroblast model to describe the signalling pathway representing PAAF properties in PAH. Sensitivity analysis showed that model-predicted PAAF network state was most sensitive to TGFβ, MAPK and hypoxia signalling pathways. The sensitivity analysis for the CFB model showed similar importance of TGFβ pathways and MAPK pathways, but mechanical stimulus had a higher impact. By using UQ, we determined the robustness of the model with respect to input weight and EC₅₀, but found that parameter uncertainty propagation was increased significantly with increased n.

This paper takes similar approaches to those previously undertaken in other logic-based network models including those done by Zeigler et al. [6] and Kraeutler et al. [2]. The Zeigler model has been shown to be similarly robust to this PAAF model, with an accuracy of 80% and similarly predicts a strong influence of TGFβ [6]. Our model uses the same default parameters and also includes analysis of variation in baseline input. This is in contrast to the Kraeutler model, where the model is fully parameterized and the authors carried out a sensitivity analysis on the Hill coefficient, EC₅₀, and y_max [2]. We have further varied the Hill coefficient and EC₅₀ using a uniform distribution via UQ.

We also identified the areas of epistemic uncertainty inherent in network construction that will need further confirmation, revision and comparison with future experiments done specifically in PAAFs by running a three parameter UQ analysis on the model with and without the pathways derived from non-cardiovascular fibroblasts. In some cases, information from non-cardiovascular cell types were shown not to highly affect input–output prediction accuracy but did improve the accuracy of predictions on the effects of inhibitors as seen in the predictions of how α-SMA responds to TGFβ when ERK or ROS were inhibited. Thus, the full model, despite including some information from non-cardiovascular fibroblasts, better recapitulated the regulation of α-SMA expression. In this way, UQ was able to capture the levels to which the output of model accuracy could vary given changes in large ranges of parameters and in the absence of pathways elucidated by non-cardiovascular fibroblasts. This analysis was crucial to a system that has so little certainty in model construction and literature data such as in PAAFs. With directions for optimization given by UQ, this model can be improved to help the scientific community understand the complex interplay of pathways in pulmonary arterial remodelling in order to identify treatments that can better target adventitial fibrosis.

5. Limitations and future directions

There is very little literature from which to determine specific model parameters, so we have not attempted to identify individual parameters and instead used constant values for every node and explored parameter uncertainty over a wide range. For example, all reactions are at a default weight of 1; however, the literature data could suggest that some reactions are more important than others in determining fibrosis. These findings are consistent with the conclusion that capturing the molecular interactions within the network topology is more important for reproducing the qualitative features revealed by typical cell biological experiments than the particular choice of parameters. This property explains why this class of network model is often preferred to more biochemically detailed models with fewer interacting pathways for interpreting the frequently more qualitative conclusions of many cell biological studies. The analyses suggested that the model is quite robust to parameter uncertainty at least when using qualitative experimental criteria. When varying input weight (w) the model accuracy ranged from 67% to 80%, when varying half-maximal effective concentration (EC₅₀) the accuracy generally ranged from 60% to 80% though the model accuracy was highly affected by changes in the Hill coefficient (n). Given that the UQ results depend on the ranges chosen for the model parameters, in this case n, EC₅₀ and w, caution should be taken in making too many biological conclusions based on this analysis.

A critical next step identified by UQ is to fill in the areas where there are no in vitro experiments in PAAFs both to refine the model and acquire more validation data so one can be more confident in the results. For example, there are no literature data on how stimulation of PAAFs with TNFα affect phenotypic outputs, only on intermediates in the model. There is some data uncertainty in the literature, as a low sample size and power in typical cell biology experiments means there is less confidence in experimental findings concluding no significant change versus those reporting significant changes.

The model is currently only shown to be qualitatively consistent with input–output experiments and normalized from 0 to 1 as the range is unknown and many reported experimental results are not quantitative. In the future, we can implement mass-action equations with kinetic rates to create a more quantitative and realistic measure of matrix remodelling that we can validate through experimentation. We can also integrate paracrine signalling with other cell types, as PAAFs are known to activate macrophages and smooth muscle cells surrounding them in the pulmonary arterial wall [59] Another future direction is to reformulate the model by adding exogenous stimulation for ET1 and IL6 and feedback, which could increase model accuracy.

Data accessibility

This article has no additional data.

Authors' contributions

A.W. curated the data for network construction, created the network, performed the validation and sensitivity analysis and drafted and edited the manuscript. S.C. developed the Python code and methodology for uncertainty analysis. Y.A. conceived of applying UQ to the network model and edited the manuscript. D.V.-J. conceived of the project idea, acquired funding, administered and supervised the project, and edited the manuscript. All authors read and approved the manuscript.

Competing interests

None.

Funding

This work was partially funded by the American Heart Association Scientist Developmentgrant no. 16SDG29670010, and the National Institutes of Health grant nos¡/GRANTSPONSOR¿2NHLBI 1 T32 HL105373 and NHLBI 1 R01 HL137100.