Uncertainty quantification and sensitivity analysis of left ventricular function during the full cardiac cycle

Abstract

Patient-specific computer simulations can be a powerful tool in clinical applications, helping in diagnostics and the development of new treatments. However, its practical use depends on the reliability of the models. The construction of cardiac simulations involves several steps with inherent uncertainties, including model parameters, the generation of personalized geometry and fibre orientation assignment, which are semi-manual processes subject to errors. Thus, it is important to quantify how these uncertainties impact model predictions. The present work performs uncertainty quantification and sensitivity analyses to assess the variability in important quantities of interest (QoI). Clinical quantities are analysed in terms of overall variability and to identify which parameters are the major contributors. The analyses are performed for simulations of the left ventricle function during the entire cardiac cycle. Uncertainties are incorporated in several model parameters, including regional wall thickness, fibre orientation, passive material parameters, active stress and the circulatory model. The results show that the QoI are very sensitive to active stress, wall thickness and fibre direction, where ejection fraction and ventricular torsion are the most impacted outputs. Thus, to improve the precision of models of cardiac mechanics, new methods should be considered to decrease uncertainties associated with geometrical reconstruction, estimation of active stress and of fibre orientation.

This article is part of the theme issue ‘Uncertainty quantification in cardiac and cardiovascular modelling and simulation’.

1. Introduction

The advances in computational modelling of the heart have enabled more realistic simulations of its activity [1], which can be useful for medical applications. Patient-specific simulations where personalized information from the patient are used as input for the simulation provide an individual understanding of the organ and its functions and can support diagnostics and treatments [2,3]. Simulations can also estimate important quantities that are difficult to be measured directly in patients, such as strain in fibre direction [4], and also myofibre stress, which is an important indicator of disease progression [5]. However, the translation of these simulations to a clinical context depends on the reliability of the model predictions. In turn, these are hampered by uncertainties, which come from measurement techniques, biological variability, estimation of model parameters and other model uncertainties. Therefore, an important step in the translation of computer simulations to clinical application is to quantify how uncertainties can impact relevant model predictions. This investigation must be carried out with uncertainty quantification (UQ) techniques, and supplemented with a sensitivity analysis (SA) to identify the input parameters which most impact on the outputs.

The process of constructing patient-specific models involves several sources of uncertainty. Personalized geometries are generated from the segmentation of medical images, which is a semi-manual process that may induce variability in the resultant geometry [6]. Another input with significant uncertainty is the fibre orientation, which can only be obtained from ex vivo experiments using diffusion tensor magnetic resonance or through atlas-based methods. Both strategies have reported significant variation due to image acquisition and biological variability, which can significantly impact tissue deformation [7]. Furthermore, to match experimental data, studies have performed parameter estimation for constitutive models [8,9], which is also subject to uncertainties and where a high variability of parameter values is described in the literature.

Recent works have studied the impact of uncertainties in models of cardiac activity, ranging from electrophysiology [10], where the uncertainty in the activation time at a specific location of the left ventricle (LV) was studied, to coupled electromechanical simulations [11], where the parametric uncertainty of the excitation–contraction model was assessed. Other studies have reported how uncertainties can impact cardiac mechanics predictions, such as [12], which considered uncertainties in parameters of a constitutive model and assessed the influence in outputs of simulations of the LV passive filling phase. An extension of this work was reported in [7], where uncertainties in the fibre orientation field were also included and treated as an approximated random field using a truncated Karhunen–Loéve expansion. However, their analysis was limited to simulations during the passive filling phase of the LV only. The influence of left-ventricular shape on end-diastolic fibre stress and strain was studied in [13] for the passive filling phase. The study was performed for different shapes of the LV based on properties such as sphericity (short-to-long axes ratio) and wall volume (wall-to-cavity volume ratio), where five cases of sphericity and three cases of wall volumes were studied considering a uniform thickness. The effect of geometry on cardiac mechanics has also been studied in [14], where it has been shown that the end-systolic shear strains are more sensitive to geometry than normal strains. To obtain end-systolic strains, a simplified approach was adopted, where preload and afterload were applied to simulate the LV mechanics. In particular, the results presented in our previous work [15] showed that predictions of passive filling simulations such as stress, strain and torsion are highly impacted due to uncertainties in personalized geometries of the LV.

A limited number of studies in cardiac mechanics have considered the entire cardiac cycle for performing UQ and SA of input parameters of the model. In particular, a simulation study of the entire cardiac cycle to investigate the impact of passive material parameters and a single contractility parameter was presented in [4], where the impact on myocardial stress and strains of a set of 21 material parameters from the literature was studied. However, the effects of other important input parameters such as fibre orientation, geometry, circulatory model and active stress still need to be investigated for the entire left ventricular cycle using modern and efficient techniques for UQ and SA.

The present work considers cardiac mechanics simulations of LV function during the full cardiac cycle. The simulations take into account uncertainties in the ventricular geometry, fibre orientation, constitutive parameters, active stress magnitude and in parameters of the coupled circulatory model. UQ and sensitivity analyses are performed to determine how important quantities of clinical interest, such as ejection fraction (EF), blood pressure and tissue stress, are affected by these uncertainties and which model inputs have the highest impact on each quantity. The sensitivities of systolic quantities like fibre stress, strain and torsion were assessed at different stages of the full cardiac cycle, such as at the early ejection as well as end-systole stages.

This paper extends our previous work [15] in two ways. First, we perform simulations of the full LV cycle, which allows computing clinically relevant quantities of interest (QoI), such as EF. This is a significant step from [15], where only the simpler case of the passive filling phase of the LV was studied. Second, to describe the mechanical activity of the LV during the full cycle, two additional models were considered: a lumped-parameter circulatory model describing haemodynamic conditions [16] and a model of the active stress [17] during the cycle. Consequently, the addition of these two models in the framework of cardiac mechanics simulation allowed us to incorporate their input parameters in the UQ and SA analyses together with parameters from the constitutive model, fibre orientation and parametrized geometry.

2. Methods

In this section, we introduce the mathematical model that describes the mechanical behaviour of the LV through the full cardiac cycle, as well as the techniques for UQ and SA.

(a). Cardiac mechanics

Cardiac tissue deformation is described by a quasi-static mechanical problem which is governed by the following equilibrium equation:

$$\mathrm{\nabla }\cdot (\mathbf{\text{FS}})=0,\text{in}\hspace{0.17em}{\mathit{\Omega }}_0,$$ 2.1

where F is the deformation gradient tensor, S is the second Piola–Kirchhoff stress tensor and Ω₀ is the undeformed configuration. The equation is solved to find the displacement field u compatible with external loads and kinematic boundary conditions.

Active contraction of the tissue is incorporated by dividing the stress tensor into passive and active parts

$$\mathbf{\text{S}}={\mathbf{\text{S}}}_p+{\mathbf{\text{S}}}_a,$$ 2.2

where the passive part S_p describes the passive behaviour of the tissue when subjected to loading and can be derived from a strain energy function, that is S_p = ∂Ψ/∂E. The active part S_a represents the tissue contraction due to the active force generated at the cellular level. Here, the active stress is considered anisotropic and applied in the fibre direction only, that is

$${\mathbf{\text{S}}}_a=T_{\text{ref}}{T}_a{\mathbf{\text{f}}}_{\mathbf{0}}\otimes {\mathbf{\text{f}}}_{\mathbf{0}},$$ 2.3

where T_a is the normalized active tension generated by cellular model, T_ref is a constant reference value for the active stress and f₀ is the unit vector that defines the fibre direction in the undeformed configuration.

(i). Constitutive model

The transversely isotropic model proposed by Guccione et al. [18] was used in the present work to represent the passive behaviour of cardiac tissue. The strain energy function is given by

$$\begin{array}{rl}& \mathit{\Psi }=\frac{C}{2}(e^Q-1)+\frac{\kappa }{2}{(J-1)}^2\\ \text{and}& Q=b_f{E}_{11}^2+b_t(E_{22}^2+E_{33}^2+E_{23}^2+E_{32}^2)+b_{fs}(E_{12}^2+E_{21}^2+E_{13}^2+E_{31}^2),\end{array}$$ 2.4

where J = det(F), E_ij are the Green–Lagrange strain tensor components, C is a factor that scales the stress, while b_f, b_t and b_fs are parameters related to the stiffness in the fibre direction, perpendicular to the fibre and shear parallel to the fibres, respectively. The parameter κ controls the compressibility of the tissue.

(ii). Active stress model

The active stress developed in a cardiac myocyte was described through an arrangement of a contractile element in series with an elastic element, as presented in [17]. It is written in terms of the elapsed time since depolarization t_a, the sarcomere length l_s and a contractile element length l_c, i.e.

$$T_a=\frac{l_s}{l_{s0}}{f}_{\text{iso}}(l_c)f_{\text{twitch}}(t_a,l_s)E_a(l_s-l_c),$$ 2.5

where l_s0 is the reference length of the sarcomere and E_a is the elastic element stiffness. The function f_iso describes the isometric stress, whereas the function f_twitch describes the myofibre stress dependence on t_a and l_s. The contractile element length varies with time according to the following first-order differential equation:

$$\frac{\text{d}{l}_c}{\text{d}t}=v_0(E_a(l_s-l_c)-1),$$ 2.6

where v₀ is the unloaded shortening velocity. More details of this model can be found in [17].

(iii). Circulatory model

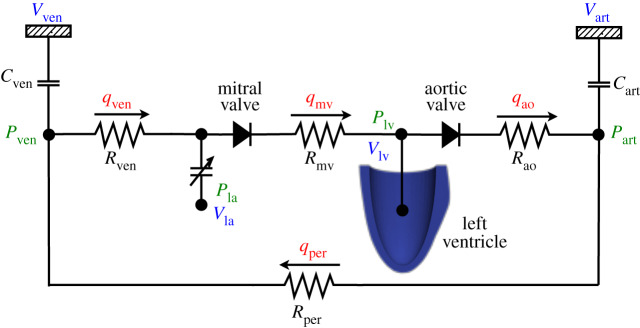
During the cardiac cycle, the endocardial surface of the LV is subjected to the dynamic loading of blood pressure which is described by a lumped parameter model of the circulatory system. Figure 1 presents a schematic for the circulatory model used in this work, which is based on [16].

Figure 1.

Schematic of the lumped parameter model used to describe the time varying pressure in the left ventricular cavity. (Online version in colour.)

In the model, arterial and venous pressures are related to volume via compliance

$$P_{\text{art}}=\frac{V_{\text{art}}-V_{\text{art},0}}{C_{\text{art}}}\text{and}{P}_{\text{ven}}=\frac{V_{\text{ven}}-V_{\text{ven},0}}{C_{\text{ven}}},$$ 2.7

where V_art,0 and V_ven,0 are the resting volumes for the arterial and venous systems, while C_art and C_ven are the arterial and venous compliances, respectively. The pressure in the left atrium is given by a time varying elastance function and the pressure in the LV is estimated through the coupling with the mechanical problem solver, as described in [19].

The left atrium dynamics is described by a time varying elastance function that relates the atrial pressure P_LA to its volume V_LA using the equation

$$P_{\text{LA}}(t)=e(t)P_{\text{es, LA}}(V_{\text{LA}})+(1-e(t))P_{\text{ed, LA}}(V_{\text{LA}}),$$ 2.8

with

$$P_{\text{es, LA}}(V_{\text{LA}})=E_{\text{es, LA}}(V_{\text{LA}}-V_{0,\text{LA}})$$ 2.9

and

$$P_{\text{ed, LA}}(V_{\text{LA}})=A_{\text{LA}}(e^{B_{\text{LA}}(V_{\text{LA}}-V_{0,\mathrm{LA}})}-1),$$ 2.10

where E_es, LA is the end-systolic elastance, V_0,LA is the volume axis intercept of the end-systolic pressure relation (ESPVR), while A_LA and B_LA are parameters of the end-diastolic pressure volume relation (EDPVR). The driving function e(t) is written in terms of the time point of maximal chamber elastance t_max, the time constant of relaxation τ and the time t within the cardiac cycle

$$e(t)=\{\begin{array}{ll}\frac{1}{2}(\sin [\left(\frac{\pi }{t_{max}}\right)t-\frac{\pi }{2}]+1)& \mathrm{if}\hspace{0.17em}0<t\le \frac{3}{2}{t}_{max}\\ \frac{1}{2}{\mathrm{e}}^{-(t-\frac{3}{2}{t}_{max})/\tau }& \mathrm{if}\hspace{0.17em}t>\frac{3}{2}{t}_{max}\end{array}.$$ 2.11

The flow rates through the aortic and mitral valves are

$$q_{\mathrm{ao}}=\{\begin{array}{ll}0& \mathrm{if}\hspace{0.17em}{P}_{\mathrm{LV}}<P_{\mathrm{art}}\\ \frac{P_{\mathrm{LV}}-P_{\mathrm{art}}}{R_{\mathrm{ao}}}& \mathrm{if}\hspace{0.17em}{P}_{\mathrm{LV}}\ge P_{\mathrm{art}}\end{array}\mathrm{and}{q}_{\mathrm{mv}}=\{\begin{array}{ll}0& \mathrm{if}\hspace{0.17em}{P}_{\mathrm{LA}}<P_{\mathrm{LV}}\\ \frac{P_{\mathrm{LA}}-P_{\mathrm{LV}}}{R_{\mathrm{mv}}}& \mathrm{if}\hspace{0.17em}{P}_{\mathrm{LA}}\ge P_{\mathrm{LV}}\end{array},$$ 2.12

where P_LV is the pressure in the left ventricle cavity, R_ao is the aortic valve resistance and R_mv is the mitral valve resistance. The flow rates for peripheral and venous systems are proportional to the pressure difference, i.e.

$$q_{\text{per}}=\frac{P_{\text{art}}-P_{\text{ven}}}{R_{\text{per}}}\text{and}{q}_{\text{ven}}=\frac{P_{\text{ven}}-P_{\text{LA}}}{R_{\text{ven}}},$$ 2.13

with R_per being the peripheral resistance and R_ven the venous resistance. Finally, conservation of the total blood volume gives the rate of change of volume in each compartment by

$$\frac{\text{d}{V}_{\text{LA}}}{dt}=q_{\text{ven}}-q_{\text{mv}},\hspace{0.17em}\frac{\text{d}{V}_{\text{LV}}}{dt}=q_{\text{mv}}-q_{\text{ao}},\hspace{0.17em}\frac{\text{d}{V}_{\text{art}}}{\text{d}t}=q_{\text{ao}}-q_{\text{per}},\hspace{0.17em}\frac{\text{d}{V}_{\text{ven}}}{\text{d}t}=q_{\text{per}}-q_{\text{ven}}.$$ 2.14

The solution of the circulatory model provides the blood volume in the ventricular cavity, but this volume cannot be prescribed as a boundary condition in the cardiac mechanics solver. Therefore, given a volume V_LV obtained from the lumped parameter model, a pressure value corresponding to this volume is estimated and applied at the endocardial surface via the cardiac mechanics solver.

The approach presented in [19] was used in this work to estimate the pressure, which is based on a method that minimizes the difference between the cavity volumes found from the cardiac mechanics model (2.1) and the lumped parameter model.

(iv). Left ventricle geometry

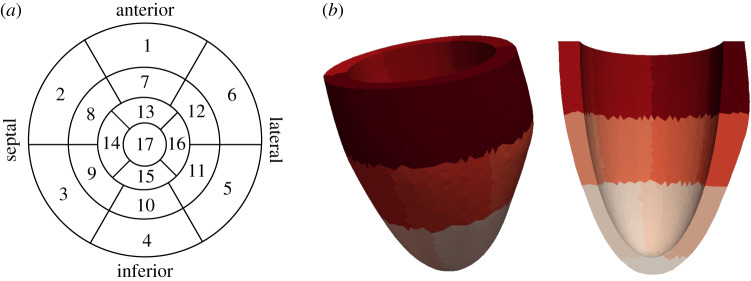
We considered personalized LV geometries constructed through a parametrized approach based on wall thickness measurements from the 17 AHA (American Heart Association) segment diagram [15]. This diagram divides the LV in 17 segments: six segments in the basal region, six in the medial, four in the apical region and one segment for the apex, as shown in figure 2a. The algorithm presented in [15] was applied to generate LV geometries, such as the one presented in figure 2b, using the values of wall thickness measured in each segment and the lengths of the short and long axis. This parametrization of the LV geometry allows incorporating different wall thickness for each segment, where the modification of the thickness is incorporated via the epicardial surface. For the UQ and SA analyses, this guarantees that all the geometrical samples have the same LV cavity volume in the unloaded state.

Figure 2.

Left ventricle geometry created with the mesh generator based on the 17 AHA diagram. (a) 17 AHA Diagram. (b) A sample LV geometry with AHA segments marked with different colours. (Online version in colour.)

Boundary conditions for the LV were applied in the basal plane, where the points at the epicardium ring were restricted to move in all directions and the remaining points in the base were fixed only in z-direction, as in previous studies [15].

The fibre orientation of the cardiac tissue was assigned to the geometry through the Laplace–Dirichlet rule-based algorithm [20]. In this approach, the fibre direction rotates clockwise from an angle α_endo on the endocardial surface to an angle α_epi on the epicardial surface. The transverse direction is considered perpendicular to the fibre direction and varies from β_endo to β_epi, while the sheet normal direction is orthonormal to the fibre and transverse directions.

(v). Numerical solution

The cardiac mechanics problem is solved using the finite-element method based on a mixed three field variational formulation. The nonlinear systems were solved using Newton’s method and the associated linear systems were solved by the generalized minimal residual method with a multigrid preconditioner, as described in [21]. The lumped parameter model was solved by the midpoint method and the LV pressure estimation is performed at each time step following the method described in [19].

(b). Uncertainty quantification

Surrogate models were generated via the polynomial chaos expansion (PCE) approach to accelerate the UQ analysis. In the PCE approach, the QoI are approximated through orthogonal polynomials in terms of the uncertain inputs considered as scalar random variables.

Let Z be a vector of independent random variables, then the mapping Y = f(Z) can be approximated by a finite PCE [22] of the form

$$\overline{Y}(\mathbf{\text{Z}})=\sum _{i=1}^P{b}_i{\mathit{\Phi }}_i(\mathbf{\text{Z}}),$$ 2.15

where Φ_i are the basis functions of orthogonal polynomials in terms of the random variables and b_i are the polynomial coefficients that need to be determined. The number of terms P required in the expansion for a polynomial degree d with N input parameters is P = (N + d)!/N!d!

The coefficients of the polynomial expansion were found through the probabilistic collocation method [7], which enforces that the polynomial evaluation in the collocation points is equal to the deterministic model in the same points. The number of collocation points employed is usually chosen as N_s = k P, for an integer k ≥ 1. The use of N_s > P gives a better approximation of the statistics measures and results in a least-squares problem to be solved [23].

After constructing the surrogate polynomial model, it can be used to evaluate the QoI for different values of the inputs with a low computational cost when compared to the cost of the full cardiac mechanics forward model. Moreover, statistical measures such as mean and standard deviation can be computed directly from the polynomial expansion.

(c). Sensitivity analysis

To study the contribution of each input parameter in the observed variability of the outputs we performed SA based on the Sobol sensitivity indices [24]. The sensitivity indices enable the identification of inputs Z_i that cause more variability in the outputs Y, which should, therefore, be prioritized in the measurements, and also to identify inputs with low impact on the QoI, which can be fixed in their range of uncertainty.

The main Sobol index $S_m^i$ is the ratio between the variance of Y when only Z_i is allowed to vary and the total variance of Y. It represents the portion of the variance of Y caused by the uncertain input Z_i and is given by

$$S_m^i=\frac{\mathbb{V}[\mathbb{E}[Y|Z_i]]}{\mathbb{V}[Y]},i=1,\dots ,N,$$ 2.16

where $\mathbb{V}$ is the variance and $\mathbb{E}$ the expected value. The total Sobol index considers the effects included in the main Sobol index plus possible effects due to high order interactions of Z_i with the remaining inputs. It is computed by

$$S_t^i=\frac{\mathbb{V}[Y]-\mathbb{V}[\mathbb{E}[Y|Z_{i\ast }]]}{\mathbb{V}[Y]},i=1,\dots ,N,$$ 2.17

where Z_i* is the set of all uncertain inputs except Z_i, then $\mathbb{V}[\mathbb{E}[Y|Z_{i\ast }]]$ is the variance due to the interactions among the inputs where Z_i is involved. When $S_t^i\approx 0$, it means that Z_i has low influence in the QoI and could be fixed in its range of uncertainty.

The presented Sobol indices are used to assess the sensitivity of scalar quantities, but for non-scalars such as time-varying quantities they are not the best choice since these indices are scaled by the variance, which is not constant for all points of a time series [25]. Therefore, for time-varying quantities, we computed the time-averaged sensitivity indices, proposed in [25]. The main time-averaged sensitivity ${\text{TAS}}_m^i$ and the total time-averaged sensitivity ${\text{TAS}}_t^i$ indices are given by

$${\text{TAS}}_m^i=\frac{{\int }_{t_0}^{t_1}{S}_m^i(t)\mathbb{V}{[Y]}_t\hspace{0.17em}\text{d}t}{{\int }_{t_0}^{t_1}\mathbb{V}{[Y]}_t\hspace{0.17em}\text{d}t}\text{and}{\text{TAS}}_t^i=\frac{{\int }_{t_0}^{t_1}{S}_t^i(t)\mathbb{V}{[Y]}_t\hspace{0.17em}\text{d}t}{{\int }_{t_0}^{t_1}\mathbb{V}{[Y]}_t\hspace{0.17em}\text{d}t}.$$ 2.18

(d). Quantities of interest

Six measurements were considered as QoI in the analyses. The LV torsion, mean fibre stress and strain in the entire mid-ventricular region were measured at the early ejection and end-systole stages of the cycle. Other quantities such as EF, end-systolic pressure (ESP) and maximal variation of pressure over time were computed from the pressure volume (PV) loop.

The normalized LV torsion denoted by T describes the twist of the ventricle in some time instant and it is based on the rotation between basal and apical slices. In this work, it was computed as [16]

$$T=\frac{({\varphi }_{\text{apex}}-{\varphi }_{\text{base}})({\rho }_{\text{apex}}+{\rho }_{\text{base}})}{2D},$$ 2.19

where ρ_apex and ρ_base are the mean radius of the basal and apical slices, respectively, and D is the distance between the slices. The rotation angles at apical and basal slices are ϕ_apex and ϕ_base. Owing to the variation of twist across the wall, an average value of T was computed using points on endocardial and epicardial surfaces, as suggested in [16].

The fibre stress σ_f is calculated using the Cauchy stress tensor σ and the fibre direction in the deformed configuration f. Whereas the fibre strain e_f is computed through the Green–Lagrange strain tensor E and undeformed fibrel direction f₀. These quantities are given by

$${\sigma }_f={\mathbf{\text{f}}}^T\mathit{\sigma }\mathbf{\text{f}}\text{and}{e}_f={\mathbf{\text{f}}}_{\mathbf{0}}^T{\mathbf{\text{Ef}}}_{\mathbf{0}}.$$ 2.20

To simplify the analysis, the averages of stress and strain over the entire mid-ventricular region, composed of segments 7–12, were considered as QoIs in all experiments.

The EF represents the percentage of blood that is pumped each time the ventricle contracts and characterizes the LV function. It is defined as

$$\text{EF}=\frac{\text{EDV - ESV}}{\text{EDV}},$$ 2.21

where EDV is the end diastolic volume and ESV is the end-systolic volume.

The maximal rate of change in pressure, denoted by dP/dt_max, is a common indicator of cardiac contractility and was computed by a first-order finite difference scheme. The ESP was also considered as a QoI, which is the pressure measured in the end of the ejection phase.

(e). Numerical experiments

UQ and sensitivity analyses were performed for LV simulations during the cardiac cycle in a series of four experiments. A cardiac cycle of 900 ms was considered, where the active stress was applied simultaneously in all points at time 200 ms. Uncertainties were considered in the parameters of the constitutive model, regional wall thickness, fibre angles, maximum value for active stress and in the parameters of the circulatory model. The uncertain inputs were described through normal distributions with 5% coefficient of variation (COV), where COV = 100 × (Std/mean)%.

The geometrical samples were constructed using the parametrized approach [15] based on the 17 AHA segments. The long and short axis lengths were fixed to 60 mm and 40 mm, respectively. The uncertainty in wall thickness was considered through a scalar random variable. For this, a multiplicative factor was introduced to change the wall thickness baseline value of each AHA segment as follows:

$$s_i=s_i\ast (1+w{t}_s),i=1,\dots ,17.$$ 2.22

where s_i represents the baseline value for wall thickness in the i_th segment and wt_s is a sample of the random variable wt.

Table 1 presents the values of the parameters used for the numerical experiments, which are detailed next. Most of the parameters were used as in our previous work [15]. However, some parameters were adjusted to obtain a baseline physiological output for the coupled model: R_ven and R_ao were reduced to 70% of their original values [16]; T_ref was adjusted to 75 kPa; C parameter was adapted to 60% from the value reported in [7] and finally b was increased in 40%.

• Experiment 1. In the first experiment, the uncertain inputs were the constitutive parameters of the passive tissue, wall thickness, fibre angles and the maximum value for active stress, while the parameters for the circulatory model were fixed to reference values. The mean value of wall thickness in all segments s_i of equation (2.22) was 6.4 mm, resulting in simplified LV geometries with constant wall thickness throughout the domain.

• Experiment 2. This experiment considers the same set of uncertain inputs as the previous, except for wall thickness. Here, the mean value for wall thickness in each AHA segment s_i followed the baseline values reported in the atlas [26] (table 2) to generate more realistic geometries of the LV.

• Experiment 3. In this case, the wall thickness uncertainty was considered only in segments of the lateral region which corresponds to the segments 5, 6, 11, 12, 16 and 17 (figure 2b). Thus, asymmetric uncertainty in wall thickness is considered within the physiological range as presented in [26]. This experiment also adds uncertainty in the parameters of the circulatory model, that is all parameters presented in table 1 are considered in this analysis.

• Experiment 4. The setting of this experiment is same of Experiment 2, but here an increase in the uncertainty of wall thickness is considered. Here, we represent errors during the segmentation process as described in [27], where measurements of left ventricular mass or volumes obtained by different groups for the same MR images of patients differ in average by 20% when compared with consensus measurements. Thus, in this experiment, we assume a coefficient of variation for wall thickness of 20%, while for all the other uncertain inputs COV was 5%.

Table 1.

Uncertain model inputs, described through Normal distribution with 5% for the coefficient of variation.

model input	unit	mean value	model input	unit	mean value
C	kPa	0.66	aortic valve resistance (Rao)	kPa ms ml−1	3.85
bf		6.6	peripheral resistance (Rper)	kPa ms ml−1	140
bt		4.0	venous resistance (Rven)	kPa ms ml−1	1.4
bfs		2.6	mitral valve resistance (Rmv)	kPa ms ml−1	1.75
wall thickness factor (wt)	mm	0	aortic compliance (Cart)	ml kPa−1	14
longitudinal fibre angle (αendo)	degrees	60	venous compliance (Cven)	ml kPa−1	300
longitudinal fibre angle (αepi)	degrees	-60	end-systolic elastance (Ees, LA)	kPa ml−1	0.06
transverse fibre angle (βendo)	degrees	-65	scaling factor for EDPVR (ALA)	kPa	0.05867
transverse fibre angle (βepi)	degrees	25	exponent for EDPVR (BLA)	ml−1	0.049
maximum active stress (Tref)	kPa	75	time to end-systole (tmax)	ms	200
			time constant of relaxation (τ)	ms	25

Table 2.

Baseline values of ventricular wall thickness for each AHA segment reported in [26].

segment	region	value (mm)	segment	region	value (mm)
1	basal anterior	6.21	10	mid inferior	6.64
2	basal anteroseptal	6.38	11	mid inferolateral	5.94
3	basal inferoseptal	6.23	12	mid anterolateral	6.92
4	basal inferior	5.82	13	apical anterior	5.47
5	basal inferolateral	5.38	14	apical septal	6.19
6	basal anterolateral	6.66	15	apical inferior	5.40
7	mid anterior	6.40	16	apical lateral	5.87
8	mid anteroseptal	7.06	17	apex	4.37
9	mid inferoseptal	8.41

(f). Surrogate model calibration

The quality of the surrogate model was assessed using the leave-one-out (LOO) cross validation test [24]. We generated N_s + 1 samples and one point Zⁱ is taken out of the construction of the surrogate model ${\hat{f}}^{(-i)}$, which is created using N_s = kP samples. The prediction error at Zⁱ is computed as ${\mathrm{\Delta }}^{(i)}=f({\mathbf{\text{Z}}}^{(i)})-{\hat{f}}^{(-i)}({\mathbf{\text{Z}}}^{(i)})$, where f(Z⁽ⁱ⁾) denotes the quantity computed by the forward problem and ${\hat{f}}^{(-i)}({\mathbf{\text{Z}}}^{(i)})$ the one estimated by the surrogate model constructed without the i-th sample. Then, after computing Δ⁽ⁱ⁾ for all Z⁽ⁱ⁾, the LOO error and the Q² coefficient are computed as

$$Er{r}_{\text{LOO}}=\frac{1}{n}\sum _{i=1}^n{({\mathrm{\Delta }}^{(i)})}^2\text{and}{Q}^2=1-\frac{Er{r}_{\text{LOO}}}{\text{Var}(\mathbf{\text{Z}})},$$ 2.23

where the closer Q² is to 1, the better is the approximation of the model.

3. Results

This section presents the results of UQ and sensitivity analyses for all experiments. For the sake of compactness, we chose to present and compare only the experiments where relevant differences appear.

(a). Calibration

The analyses were performed using second order polynomial chaos constructed with N_s = 3 P samples. Table 3 presents Q² for the considered QoI in each experiment, where torsion, stress and strain were measured at the early ejection stage. The values for the coefficient Q² from the cross validation tests were greater than 0.9 for most of the quantities, except for torsion. Considering a trade-off between computational cost and accuracy of the surrogate model, this setting for the construction of the polynomial chaos was chosen for the experiments presented next.

Table 3.

Q² coefficient obtained by the leave-one-out cross validation test for the QoIs in each experiment.

	early ejection			end-systole
experiment	torsion	σf	ef	torsion	σf	ef	ESP	EF	dP/dtmax
1	0.92	0.98	0.99	0.87	0.90	0.94	0.95	0.99	0.99
2	0.85	0.99	0.99	0.89	0.98	0.98	0.99	0.99	0.99
3	0.88	0.99	0.99	0.90	0.98	0.99	0.99	0.99	0.99
4	0.75	0.99	0.95	0.85	0.98	0.96	0.96	0.97	0.99

(b). Uncertainty propagation

Table 4 presents the uncertainty propagation results for all experiments considering QoIs at both early ejection and end-systole. In Experiment 1, the most impacted QoI during early ejection were ventricular torsion and stress, with 19.2% and 7.2% of variability, respectively, whereas at end-systole the outputs torsion, strain and stress were highly affected displaying significant variations. The outputs EF and dP/dt_max had a variability greater than 5% considered for the uncertain inputs. Moreover, the ESP was the quantity less impacted by the uncertainties.

Table 4.

Mean value, s.d. and the corresponding coefficient of variation (COV) of the quantities of interest for all experiments.

		early ejection			end-systole
exp.	QoI	torsion	σf	ef	torsion	σf	ef	ESP	EF	dP/dtmax
1	mean	7.16	101.02	0.207	5.16	40.84	-0.123	95.75	0.59	1171.76
	s.d.	1.37	7.3	0.011	1.75	7.05	0.032	2.97	0.06	75.25
	COV	19.2	7.2	5.40	33.9	17.3	26.0	3.1	9.6	6.40
2	mean	9.92	102.32	0.192	9.29	46.41	-0.102	94.00	0.56	1104.47
	s.d.	1.58	7.36	0.011	3.02	10.19	0.043	3.94	0.07	71.94
	COV	16.0	7.20	5.6	32.5	22.0	42.2	4.2	13.4	6.5
3	mean	9.73	102.05	0.192	9.15	45.34	-0.105	94.18	0.56	1104.71
	s.d.	2.11	4.45	0.01	3.33	7.39	0.035	3.24	0.06	58.19
	COV	21.7	4.4	5.2	36.4	16.3	33.5	3.4	10.9	5.3
4	mean	10.6	108.0	0.194	9.98	60.63	-0.069	91.51	0.51	1101.42
	s.d.	2.72	29.91	0.024	5.45	39.54	0.11	9.51	0.19	188.27
	COV	25.7	27.7	12.3	54.6	65.2	160.8	10.4	36.7	17.1

For Experiment 2, the uncertainty propagation results show that torsion and strain were also the most impacted quantities with COV = 32% and 42%, respectively. There was a significant increase in the variation of EF when compared to the previous experiment. The mean value of torsion increased, while its variability was lower than in Experiment 1. The behaviour for the remaining quantities was similar to the previous experiment.

The most impacted quantities in Experiment 3 were torsion, strain (at end-systole) and EF, as in the previous cases. The coefficient of variation for T increased to 21.7%, while for EF it decreased to 10.9%. The variability of fibre stress and fibre strain slightly decreased at both early ejection and end-systole, while the remaining observable outputs had similar variability in comparison to Experiments 1 and 2.

In Experiment 4, all quantities were very impacted by the uncertainties considered in wall thickness, where the lowest COV was obtained in ESP (10%). Stress and strain were considerably affected by the high dispersion imposed on wall thickness.

To show the uncertainties in volume and pressures curves, we chose Experiment 2 as an illustrative case. Figure 3 shows the variability of pressure and volume during the cardiac cycle from the 90% prediction interval, where it is notable that end-systolic volume is highly impacted by the uncertainties. The most significant change in the pressure profile is the peak value, while in the PV-loop, it is possible to observe high variations in the beginning of ejection phase and also at the end of systole, which impacts the EF. Results for Experiment 1 and 3 showed the same patterns as the results of Experiment 2.

Figure 3.

Mean value and variations in the 90% prediction interval for volume and pressure profiles as a function of time and PV-loop, respectively, for Experiment 2. (Online version in colour.)

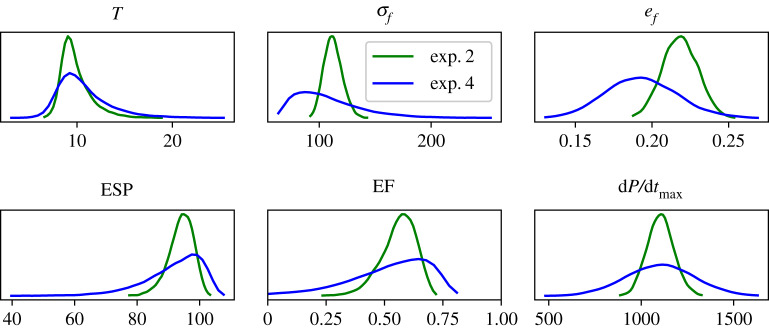
Figure 4 shows the density distribution estimated for each quantity of interest in Experiments 2 and 4, where torsion, stress and strain were estimated at the early ejection. The distributions are near symmetric in fibre strain and dP/dt_max, indicating they could be described by normal distributions, while the remaining quantities presented significant asymmetry. Comparing both experiments, it is clear that variability is higher in Experiment 4, as expected due to the high COV for the parameters, resulting in more dispersion in the curves for this case.

Figure 4.

Probability densities of QoIs for Experiments 2 and 4. (Online version in colour.)

(c). Sensitivity analysis

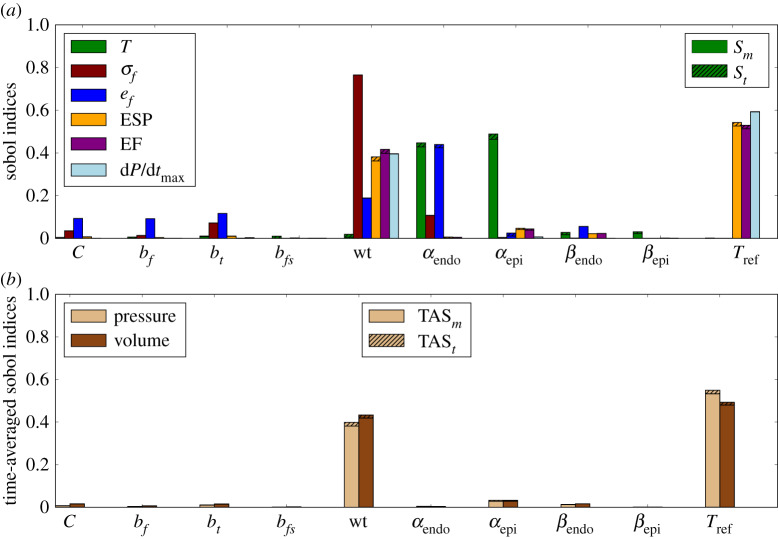
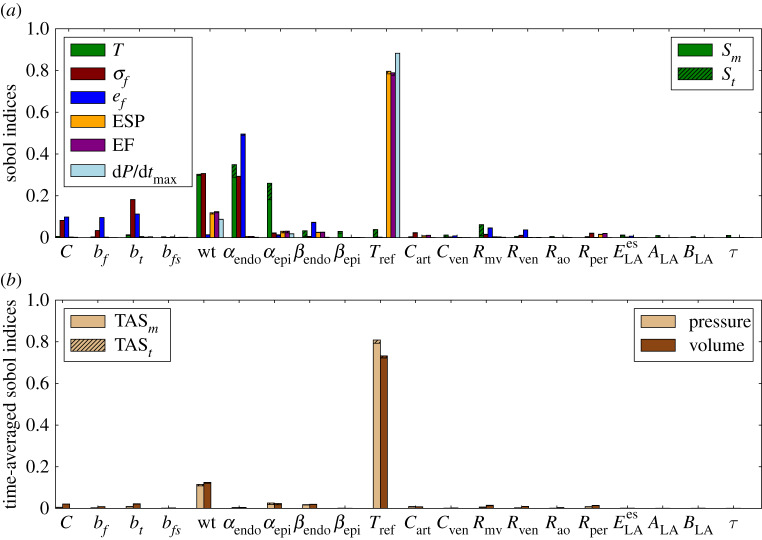
The Sobol sensitivity indices were computed for all QoI, and the results are shown in figure 5a for Experiment 1. The sensitivities of torsion, stress and strain were measured at the early ejection phase. The results show that most outputs are strongly influenced by wall thickness, while parameters of the passive constitutive model have low impact on the outputs. The magnitude of the active stress, T_ref, also has significant impact on the ESP, EF and dP/dt_max, but a low impact on the other quantities. Variation in fibre angles mainly affects LV torsion and fibre strain.

Figure 5.

Experiment 1: sensitivity analysis with main and total Sobol indices (a) and time-averaged indices (b). Striped bars represent the total Sobol indices while the solid bars show the main indices. (Online version in colour.)

The time-averaged Sobol sensitivity indices (figure 5b) show that the wall thickness and T_ref are the input parameters with the highest impact in pressure and volume as a time series. This result confirms the influence of both model inputs in the quantities extracted from the PV-loop, presented in figure 5a, such as ESP, EF and dP/dt_max. The SA for Experiment 2, where regional differences in wall thickness were incorporated in the geometries, showed a pattern similar to Experiment 1, which considers constant wall thickness.

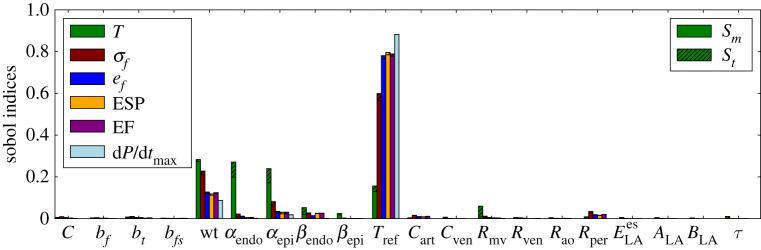
Figure 6a reports the main and total Sobol sensitivity indices obtained for Experiment 3, considering the sensitivities of torsion, stress and strain at early ejection phase. Comparing the results of Experiment 3 to those of Experiments 1 and 2, we note that the impact of T_ref in the selected outputs increases. The sensitivity of torsion to wall thickness increased significantly in this case, where this input shows to be as important as fibre angles. Wall thickness and fibre angle α_endo were the quantities that most impacted on torsion and fibre stress, whereas fibre strain was most influenced by α_endo. These results show that asymmetric uncertainties in wall thickness and fibre orientation are the parameters that cause more impact on torsion, fibre stress and strain measured at early ejection, whereas active stress magnitude T_ref dominates the impact on EF, ESP and dP/dt_max. It is also possible to observe from the total Sobol indices some high-order interactions between the fibre orientation parameters α_endo and α_epi.

Figure 6.

Experiment 3: sensitivity analysis with main and total Sobol indices (a) and time-averaged indices (b).

The time-averaged Sobol indices in figure 6b show that wall thickness and T_ref are still the inputs with the highest impact on pressure and volume time series. However, for Experiment 3, these quantities were more sensitive to T_ref than to wall thickness.

In Experiment 4, it was observed that wall thickness dominates the influence in all QoIs, as expected, since a large variation of wall thickness parameter was considered with COV = 20%. In this case, the Sobol indices for wall thickness were greater than 0.7 for all quantities and about 0.6 for torsion. The fibre angles still have an impact on torsion, whereas the remaining uncertain inputs have low impact on the QoI. The time-averaged Sobol index related to wall thickness was greater than 0.9 for pressure and volume times series.

(d). Sensitivity analysis at end-systole

QoI like torsion, stress and strain, as defined previously, are time-dependent. The previous results considered torsion, stress and strain measured only at the early ejection phase. To evaluate the sensitivities at other stages of the cardiac cycle, these quantities were measured at end-systole. Figure 7 presents the sensitivities of these quantities when they are measured at the end-systole for Experiment 3.

Figure 7.

Sensitivity analysis for Experiment 3 with torsion, stress and strain measured at end-systole. (Online version in colour.)

Comparing the sensitivities from early ejection to end-systole it is clear that the Sobol indices of torsion with respect to T_ref increased, whereas it slightly decreased with respect to wt and fibre angles (α_endo and α_epi). The Sobol indices of stress and strain with respect to T_ref also increased, whereas for the other parameters they decreased. In particular, the sensitivity of torsion with respect to the contractility state (modelled here by T_ref), fibre orientation and wall thickness corroborates with the existing literature [28–30].

(e). Stress and strain time series

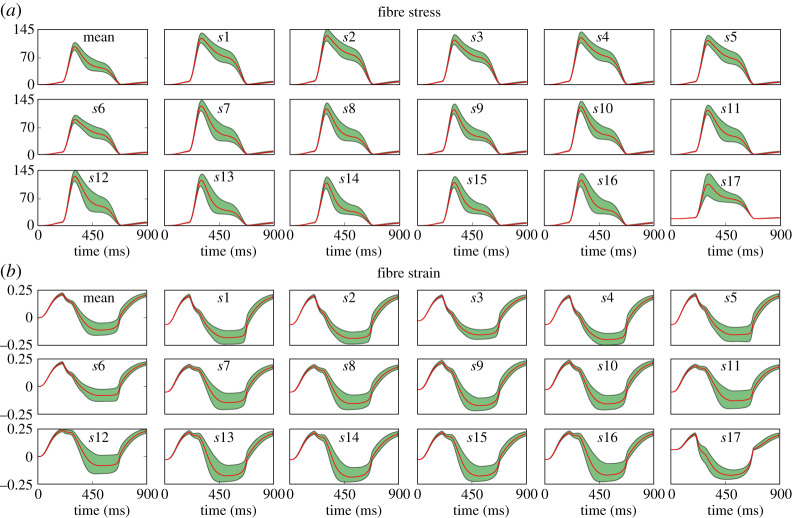
The previous experiments considered fibre stress and strain as scalar QoI extracted in the beginning of ejection phase at the mid-ventricular region. Figure 8 shows stress and strain time series to analyse the uncertainty of these quantities during the entire cycle.

Figure 8.

Experiment 2: uncertainty propagation for (a) stress and (b) fibre strain time series in each AHA segment s_i, for i = 1, …, 17. The figures also show the mean stress and fibre strain over the whole ventricle (top left). (Online version in colour.)

Figure 8a presents the mean stress for the whole ventricle over time, followed by the stress time series in each AHA segment. The segments of the medial region presented the largest values of stress and the variability is also larger in medial and apical regions, whereas basal segments presented a lower deviation from the mean. Furthermore, the significant variation is located in the time interval of the ejection phase. Figure 8b presents the time series for the mean fibre strain, where it can be noted that the more significant variability is also during the ejection phase. The time-averaged Sobol indices for these quantities showed that wall thickness and T_ref are the uncertain inputs with the highest impact on both time series.

4. Discussion

The aim of this work was to study the impact of uncertainties in different inputs and also to determine the most important parameters with respect to the outputs of a cardiac mechanics model for full cycle simulations. The model parameters considered in this study were geometry (regional wall thickness), fibre orientation, constitutive model properties, active stress magnitude and the parameters of the circulatory model used to reproduce the time-varying pressure in the LV cavity. Then, UQ and sensitivity analyses were performed to assess the impact on quantities that are important in clinical use.

A parametrized approach based on the 17 AHA segments diagram was used to incorporate uncertainties in the LV geometry, through the wall thickness value in each segment. This approach allows changes in the LV shape based on quantities with a direct clinical interpretation. Uncertainties can be incorporated in the entire ventricle to represent uncertainties, for instance in image segmentation, or regionally to represent pathology or some region of increased variability. Furthermore, this strategy enables the use of scalar random variables for wall thickness instead of random fields [7,31], which are more complex to be performed. LV wall thickness measurement in the 17 AHA segments can be found in the literature, as in [26] that present the wall thickness values and the variability among patients for each AHA segment.

All uncertain inputs were described by normal distribution with 5% coefficient of variation, which is within the range of uncertainty usually considered. The experiments showed that torsion and EF were the most affected quantities by the uncertain inputs. The main responsible inputs to their variability were the wall thickness, the magnitude of the active stress and the angles related to the longitudinal fibre direction.

Different tests were performed to incorporate uncertainty in wall thickness, where Experiments 1 and 2 obtained similar results, showing that variations in the mean values of wall thickness do not cause a different behaviour in the analyses when uncertain wall thickness is considered in a homogeneous manner. However, when wall thickness is varied only in the lateral region of the ventricle as in Experiment 3, torsion and fibre strain become more sensitive to this input, whereas ESP, EF and dP/dt_max become less sensitive to wall thickness and more sensitive to active stress. Experiment 4 considered a large variability in wall thickness and it was observed that uncertainties from this input dominates the impact on all QoI. This case reflects a variability caused by errors during the segmentation process, as presented in [27]. The propagation of segmentation errors used to reconstruct LV geometry can substantially affect the models predictions.

It was verified that parameters of the circulatory model have a small contribution in the variability of the observed quantities, including the time-series quantities. Therefore, these parameters could be fixed in a value within their range of uncertainty. However, a larger variability for these inputs is yet to be tested. In the near future, we plan to perform new experiments, including larger uncertainties on different parameters to study how this would affect forward UQ and SA.

An interesting result was presented in the time-averaged Sobol sensitivity indices, where the magnitude of the active stress has shown high impact in the pressure and volume time series. Consequently, the quantities computed from the PV-loop, such as EF, were very sensitive to uncertainties in active stress. T_ref changes the level of contractility, which in turn affects the pressure and volume of the LV cavity, as reported in [4].

Other works [7,15] have also used the Laplace–Dirichlet algorithm to assign the fibre orientation in LV geometries and reported that uncertainty in these angles did not impact significantly QoI extracted at the end of the passive filling phase. However, the present work which considered the full cardiac cycle showed that LV torsion and fibre strain extracted at early ejection are very sensitive to the angles related to fibre direction, which is expected due to the LV contraction caused by the active stress applied in the fibre direction.

As reported in [13,15], it was observed that wall thickness has the largest impact on fibre stress. The analysis of uncertainty propagation for fibre stress and strain time series showed that these quantities presented significant variability at the ejection phase. The deviation are larger in the medial and apical region than basal region. The SA showed that these time series are more sensitive to wall thickness and the magnitude of active stress.

In the case of an asymmetric LV geometry (Experiment 3), we observed that wall thickness and fibre orientation were the parameters that most influenced torsion. As presented in [30], the LV torsion is the result of the balance of mechanical forces between the endocardial and epicardial fibres. Typically, fibres from the epicardial surface contribute more to this force interplay due to their increased lever arm [30]. Pathological conditions of the LV, such as hypertrophic cardiomyopathy, typically show an increased torsion due to the increased wall thickness. In this case, the role of the epicardial fibres on the force balance that causes torsion is significantly increased, which contributes to greater torsion. The SA results of Experiment 3 correctly captured this behaviour since the Sobol indices of torsion with respect to wt, α_endo and α_epi have a significant value.

EF is usually within the range of 0.48–0.69, as presented in [32], whereas values below 0.25 represent cases of heart failure [33]. Figure 4 shows the constructed distributions for all the QoI in Experiments 2 and 4. In particular, for EF, it is clear that most of the samples are within this physiological range. As presented before in table 4 and shown in figure 4, the mean values of EF are 0.56 and 0.51 for Experiments 2 and 4, respectively. Only the tail of the constructed probability density function captures values below the normal physiological range, while for Experiment 4 about 11% of the samples used to generated the surrogate model resulted in an EF below 0.25 for EF.

The present study has some limitations which are worth mentioning. Long and short axis lengths were not considered in the geometrical parametrization, and as reported in [14] the LV size can influence strain. Only models of the mechanical function were considered, and further investigation of strongly coupled electromechanical models [11], where tissue will locally contract at different times and the electrical activity can impact in the active stress, can further advance this study. The variability used for input parameters was limited to 5% of coefficient of variation in all the parameters, except in the case of Experiment 4, where 20% was used for wall thickness. We observed that increasing the dispersion for all parameters (such as COV = 20%), resulted in a large number of model failure. Neglecting these samples in the construction of the surrogate model via polynomial chaos and performing the UQ and SA analysis, we observe that the mean values of the QoIs are similar, whereas s.d. and COV increase, as expected. The results presented in the electronic supplementary material show that there are no qualitative differences between the sensitivity indices if more dispersion is adopted equally for all parameters. Furthermore, the scatterplots presented in the electronic supplementary material suggest that there is no particular region of parameter values that lead to model failure. Considering the results mentioned above, we decided to conduct the numerical experiments using a lower dispersion for the parameters aiming for a robust response, instead of dealing with a high number of model failures.

In summary, the present work showed that the geometrical reconstruction and fibre orientation assignment are more important than parameters of the constitutive and circulatory models, highlighting the need of an accurate process in the generation of geometrical models. Uncertainties in these inputs have significant impact in important quantities such as EF and fibre stress. The magnitude of the active stress is also very important and can cause significant variations in the ventricular function during the cardiac cycle. Furthermore, the presented analyses can guide other works in the construction of simplified models with lower computational cost, where geometrical aspects should be prioritized.

5. Conclusion

The present work performed UQ and sensitivity analyses to verify how uncertainties in input parameters and geometry of a cardiac mechanics computational model of the full cycle can influence the prediction of quantities of clinical interest. The input parameters considered were the regional wall thickness of the LV geometries, fibre orientation, constitutive material properties, active stress and parameters of the coupled circulatory model used to prescribe pressure loading. A parametrized approach based on wall thickness measurements in the 17 AHA segments was used to generate geometrical samples that enabled the study of how uncertainties in the geometry of the heart affect the simulation results. The results showed that torsion and EF are the quantities most impacted by the uncertain inputs and all quantities are very sensitive to the active stress magnitude as well as by wall thickness. When wall thickness varies only in the LV lateral region, the outputs become less sensitive to these uncertain inputs, except for torsion which becomes more sensitive to wall thickness. Furthermore, the volume and pressure over time were very sensitive to the magnitude of the active stress and wall thickness. Therefore, the results have shown that patient-specific simulations requires accuracy in the processes of geometry reconstruction, fibre orientation assignment and the choice of active stress magnitude.

Data accessibility

This article does not contain any additional data.

Authors' contributions

J.O.C. carried out the experiments, whereas all authors participated in the study design, data analysis and manuscript drafting. All authors read and approved the manuscript.

Competing interests

We declare we have no competing interest.

Funding

We received no funding for this study.