Abstract
Seasonal environments vary in their amplitude of oscillation but the effects of this temporal heterogeneity for host–parasite coevolution are poorly understood. Here, we combined mathematical modelling and experimental evolution of a coevolving bacteria–phage interaction to show that the intensity of host–parasite coevolution peaked in environments that oscillate in their resource supply with intermediate amplitude. Our experimentally parameterized mathematical model explains that this pattern is primarily driven by the ecological effects of resource oscillations on host growth rates. Our findings suggest that in host–parasite systems where the host's but not the parasite's population growth dynamics are subject to seasonal forcing, the intensity of coevolution will peak at intermediate amplitudes but be constrained at extreme amplitudes of environmental oscillation.
Keywords: host–parasite, coevolution, Pseudomonas fluorescens, adaptive dynamics, mathematical modelling, oscillating environment
1. Introduction
It has long been recognized that environmental factors affect host–parasite coevolution, with experimental evidence showing that host defence, parasite transmission and the type of evolutionary dynamics observed can be influenced by the environment [1–5]. One important feature of many ecosystems is that the environment is heterogeneous, often varying in both space and time. This heterogeneity has been shown to have direct implications for host–parasite coevolution both empirically [6–10] and theoretically [11–14]. While the impact of spatial heterogeneity on host–parasite coevolution has been intensively studied [6,12,15–19], the effects of temporal heterogeneity have received less attention. This is despite the fact that many species experience seasonal oscillations in environment, which can lead to time-dependent effects upon infection rates [20–22], and life-history traits [23–29].
In host–parasite systems, temporally heterogeneous seasonal environments can affect coevolution in a number of different ways. For example, hosts may evolve greater resistance against a parasite when exposed to oscillating temperatures [30], but this may come at a cost to host survival [31]. However, different types of environmental oscillations can result in other evolutionary outcomes, and it has been reported that oscillations in resources can constrain antagonistic coevolution in two different predator–prey systems [32,33], and that such oscillations may skew the symmetry/asymmetry of coevolution by imposing stronger selection on one of the species [34]. Even within the same study system, different environmental oscillations can change how the interacting species evolve. For the bacterium Pseudomonas fluorescens SBW25 and its associated lytic bacteriophage SBW25φ2, Harrison et al. [35] showed that rapidly oscillating nutrient resource levels constrained coevolution, whereas Duncan et al. [36] showed the opposite effect for this interaction in oscillating temperature environments. Many of these studies consider how different periods of oscillation in environmental variables affect evolutionary outcomes for fixed amplitudes; however, natural seasonal variations are also likely to differ in amplitude, yet the effect of the latter is untested. An important unanswered question is, therefore, how the amplitude of environmental oscillation affects host–parasite coevolution.
There is a growing body of mathematical modelling of host–parasite coevolution in temporally heterogeneous seasonal environments. Ecology-based models have shown that oscillating environments implemented through host birth rate or parasite transmission can affect both host [37] and parasite evolution [38–40], with amplitude and period impacting evolutionary outcomes. For example, Donnelly et al. [40] found that parasite evolution is not affected by fluctuations in the host birth rate in a standard model, but the inclusion of density-dependent virulence leads to an increase in the parasite's transmission as the amplitude of oscillations increases. Elsewhere, coevolution of hosts and parasites with seasonal interactions has been considered using genetic based methods that do not account for ecological factors ([13,41]; but see [14]). Of particular relevance, Poisot et al. [14] showed that, for stepwise environmental oscillations implemented through a dynamic resource which impacts host birth rate, the host evolved lowest resistance for intermediate amplitudes. This is in contrast with results from Ferris & Best [37], where for a continuously varying host birth rate in the presence of recovery, they found that the host evolves monotonically decreasing resistance as amplitude increases. The differences between these predictions is probably owing to how increasing the amplitude changes the environmental oscillations: in Ferris & Best [37], the average birth rate stays the same while both the minimum and maximum change with amplitude; in Poisot et al. [14], the minimum resource input remains the same for all amplitudes while the maximum, and therefore the average, increases with amplitude. Either prediction could be correct for different species under certain environmental oscillations, but the effect of amplitude on evolution has yet to be explored thoroughly in an experimental context.
In this study, we consider how a seasonal, temporally oscillating nutrient resource affects coevolution of the bacterium P. fluorescens SBW25 with the lytic phage SBW25φ2 [42,43]. We focus on the effect of changing the amplitude of environmental oscillations on coevolution of bacterial resistance and phage infectivity, using constant and oscillating treatments with the same mean resource level but increasing difference between the high and low nutrient concentrations. Recent theory predicts that the bacterial host would evolve monotonically decreasing resistance as amplitude increases [37], and that the effect of resource oscillations on parasitic phage evolution would be indirect and mediated via the effect on the host [40,44]. We also extend the model by Ferris & Best [37] to include coevolution and growth rate parameters from the experiment, then compare our new predictions with the experimental results. We found that, in the experiment and the coevolutionary model, the amplitude of environmental oscillations determines the degree of host resistance evolution and thus counter adaptation through infectivity evolution by the phage, with greatest resistance and infectivity evolving at intermediate amplitudes of resource oscillation.
2. Methods
(a). Culture techniques
Cultures were grown in 30 ml glass microcosms with loose plastic lids containing 6 ml of King's Media B (KB) in M9 salt solution, incubated at 28°C with orbital shaking at 180 rpm. A gradient of nutrient concentrations, chosen by influence on growth kinetics (electronic supplementary material, Appendix A.1), were prepared by diluting KB into M9 salt solution. Bacterial densities were measured as colony forming units (CFU ml−1) by plating diluted cultures on standard KB agar plates, and phage densities as plaque forming units (PFU ml−1) by plating a serial dilution of phage filtrate on a soft agar (0.8% agar) lawn of ancestral bacteria.
(b). Experiment design
We used five treatments consisting of one constant (0.5 KB constant) and four oscillating treatments with the same mean resource level but different magnitudes of oscillation between high and low nutrient levels, alternating every transfer (0.25/0.75 KB, 0.1/0.9 KB, 0.05/0.95 KB, 0.01/0.99 KB). These treatments were chosen to maximize the range of growth kinetics across resource concentrations, with no amplitudes chosen between 0 and 0.5 as the growth kinetics were not significantly different to those in the constant resource concentration (0.5 KB, electronic supplementary material, Appendix A.1). Independent clones of P. fluorescens SBW25 and bacteriophage SBW25φ2 were used to inoculate initial populations (six replicates) with approximately 108 P. fluorescens SBW25 cells and approximately 107 SBW25φ2 particles. Phage were isolated from entire populations by filtration (0.22 µm). One per cent of the volume (60 µl) was serially transferred every 48 h into new media, for a total of 24 transfers. Population densities were measured every third transfer, whereupon samples of the whole population, phage population and 20 bacterial clones were collected from each replicate and frozen at −80°C in 20% glycerol.
During the course of the experiment, some phage populations fell below detection levels (minimum 200 PFU ml−1) and densities could not be measured by plaque assay. These are shown as having zero phage particles in plots. In some cases, these phage populations later recovered to densities above the detection threshold. Phage populations that recovered in a later transfer were re-isolated from the undetectable time point for use in cross-infection assays by growth from frozen stocks with ancestral bacteria for 24 h.
(c). Cross-infection resistance assay
Cross-infection assays were conducted to compare the resistance of the bacteria to phage from different treatments. As phage survival was variable across treatments (electronic supplementary material, Appendix A.2), we selected four treatments where phage survived to the endpoint in at least 4 out of 6 replicates. For four replicates per treatment, we measured the resistance of endpoint bacterial clones against whole phage populations from each treatment and replicate (16 phage populations in total).
To measure resistance, 20 bacterial clones and whole phage populations were grown in 96-well microtitre plates containing the standard concentration of KB media in M9 salts (final volume 150 µl). Bacterial overnight cultures were prepared directly from glycerol stocks by inoculation into KB 96-well microtitre plates and incubated for 24 h at 28°C, 80% humidity, static. Phage cultures were inoculated from glycerol stocks into microcosms containing ancestral bacteria for 24 h (180 rpm, 28°C) then filtered (0.22 µm) to prepare phage stocks. Bacteria were added to achieve a 10−2 dilution and phage a 10−1 dilution from overnight cultures, to ensure phage density was greater than bacterial density (i.e. multiplicity of infection > 1). Bacterial growth was measured as the change in absorbance at optical density (OD) 600 nm over 20 h. Relative bacterial growth (RBG, equation (2.1)) for bacteria i and phage j provides a metric of resistance to phage infection by describing growth in the presence versus absence of phage [45,46]. RBG values were adjusted to restrict values to [0,1] to keep within biologically meaningful ranges (negative values suggest negative growth, while values greater than 1 suggest growth higher than the reference bacteria without phage):
| 2.1 |
(d). Growth curves
To assess the impact of phage resistance on adaptation to different resource levels, we compared growth kinetics of the ancestral bacteria to phage-resistant mutants of SBW25 (previously isolated by Harrison et al. [35]). Three independent clones of each strain were pre-conditioned in 12 different resource concentrations for 48 h, then diluted by 10−2 in these KB concentrations into a 96-well microtitre plate (150 µl final volume). The absorbance at OD600 nm was measured every 30 min, after 1 min of shaking, for 48 h. The maximum growth rate was calculated as the maximum rate of increase in OD within 48 h.
(e). Statistical analysis
The fluctuations in bacteria and phage population densities were analysed for magnitude of variation using the fluctuation index (FI, [47]):
| 2.2 |
where N(t) is the population density at transfer t, and is the mean population density over T transfers. We also analysed the synchrony between replicates for the bacteria and phage population densities [48]:
| 2.3 |
where is the population density time series (i = 1, 2, …, S), S is the number of populations being compared (here S = 2, see the electronic supplementary material, Appendix A.3), and is the variance of . These quantities were statistically analysed with linear mixed effect models, with FI or synchrony as the response variables, resource amplitudes fitted as fixed effects, and replicate as a random effect (Akaike information criterion (AIC) values are given in the electronic supplementary material, Appendix A.3).
Linear mixed effect models were used to analyse the resistance assay data with RBG or 1-RBG as the response variable. Resource amplitudes were fitted as linear and quadratic fixed effects with no interaction, and replicate as a random effect, with phage replicate nested within bacteria replicate. A quadratic model was chosen based on the data and AIC values (electronic supplementary material, Appendix A.4). Post-hoc tests were conducted using a contrast matrix with the glht program in R, and pairwise comparisons are given in the electronic supplementary material, Appendix A.4.
The maximum growth rates were analysed using a mixed effects model, with maximum growth rate as the response, resource concentration and phage resistance as fixed effects, and replicate as a random effect (no interaction term was included as the model fit was better without it: AIC = −474.4 with interaction, AIC = −474.6 without interaction).
(f). Mathematical model
As the bacterial population dynamics are affected by the amplitude of resource oscillations (figure 1), we use an ecological model for this interaction. We use a standard susceptible-infected-susceptible (SIS) infection model [37,49], which is described by the following equations:
| 2.4 |
and
| 2.5 |
where S, I are the susceptible and infected populations, and N = S + I is the total population. We assume all new hosts are born susceptible at rate a, subject to population crowding q, and that the parasite renders the host temporarily sterile so only susceptible hosts reproduce. All hosts die at rate b, with additional mortality rate α for infected individuals. Hosts are infected at rate βI on contact with infected individuals, but can recover from infection and return to the susceptible class at rate γ. Default parameter values are given in the electronic supplementary material, table SB1 in Appendix B.1. Our assumptions of infected sterility and recovery are appropriate for our experimental study system, as bacteria infected with actively replicating phage are unlikely to divide (but see [50]), and bacteria can ‘recover' from infection [8,51]. We checked the case where the bacteria cannot recover from infection (γ = 0; electronic supplementary material, Appendix B.7), finding the same results as in the presence of recovery.
Figure 1.
Effect of resource oscillation amplitude on the ecological dynamics of bacteria and phage. (a,b,c) Bacterial population dynamics. (d,e,f) Phage population dynamics. (a,d) Mean log10 population densities per ml ± s.e. Grey shading indicates timepoints with high resource levels, whereas white shading indicates timepoints with low resource levels. (b,d) Mean fluctuation index ± s.e. (equation (2.2); [47]). (c,f) Mean synchrony between replicates ± s.e. (equation (2.3); [48]). Analysis of phage densities omitted extinct phage replicates. (Online version in colour.)
To imitate the oscillating media used in the experiment, we let the birth rate, a, depend on time through a periodic step function:
| 2.6 |
where a0 is the baseline birth rate and the function births(t) is a step function between a minimum and maximum (representing the low and high resource environments), which are defined as functions of the amplitude δ, figure 4a; electronic supplementary material, Appendix B.2. An equal amount of time is spent in each environment, with period of the oscillations equal to ε. We assume that seasonality impacts host birth rate, but recognize that it could also appear in other life-history processes such as death or competition.
Figure 4.
(a) Change in the maximum/minimum of the oscillating birth rate births(t), corresponding to growth in the high and low resource environments, as the amplitude of oscillations δ varies (blue). Maximum = 0.3684δ; minimum = −0.0699 δ/(1–0.9225δ). The black dashed line shows the average birth rate at amplitude δ. Insert: step function between minimum and maximum, with an equal amount of time spent in each environment. (b) Evolved host resistance u* and (c) evolved parasite infectivity v* as amplitude δ increases. (Online version in colour.)
To model the coevolution of the host and parasite, we use a range model that has been used previously to model eco-evolutionary dynamics with specificity in infection [44,52,53]. We use the following form for the transmission coefficient, incorporating the host defence u and parasite infectivity v:
| 2.7 |
where β0(v) describes a trade-off between broadness of infection and efficacy of transmission for the parasite. See the electronic supplementary material, Appendix B.3 for more information about the transmission coefficient β(u, v) and the trade-off functions β0(v), a0(u) (electronic supplementary material, figure SB2).
In this study, we use the adaptive dynamics method to model coevolution [54], which involves repeatedly adding a rare mutant with similar resistance/infectivity to the current population and following the progression of the traits through time. Here, we investigate how the endpoint of evolution varies with amplitude, i.e. we only consider ‘singular points' in the trait space that are both convergence stable and evolutionarily stable [54] and are thus long-term attractors of evolution. In a coevolutionary context, a singular point (u*, v*) is defined as the point where both the host and parasite fitness gradients with respect to a rare mutant are zero, i.e.:
| 2.8 |
and
| 2.9 |
where rH = host fitness, rP = parasite fitness, um = mutant host resistance and vm = mutant parasite infectivity [44]. Second-order conditions on the two fitnesses for evolutionary and convergence stability can be found in [44]. The host fitness is found in the same way as by Ferris & Best [37] (electronic supplementary material, Appendix B.5), using numerical Lyapunov exponents for 0 ≤ δ ≤ 1 [55]. For the parasite fitness, we use the averaging method from [40] and the average susceptible population size to find:
| 2.10 |
for all values of amplitude δ in [0,1] (see the electronic supplementary material, Appendix B.4 for full derivation). Note that the parasite's evolution only depends on seasonality through the host's resistance, u.
3. Results
(a). Bacterial population dynamics were affected by resource amplitude
To quantify the effect of resource oscillations on the ecological dynamics of bacteria and phage populations, we measured population densities of both species every third transfer. The extent of fluctuation in bacterial population densities varied according to the amplitude of resource oscillations, such that density fluctuations increased with the amplitude of resource oscillations (figure 1; amplitude effect on bacteria density fluctuations: t = 14.171, p < 10−16) while also becoming more synchronous among replicate populations (figure 1; amplitude effect on bacteria replicate synchrony: t = 10.35, p < 10−16). By contrast, phage population densities were not significantly affected by resource amplitude either in terms of fluctuation (amplitude effect on phage density fluctuations: t = 1.103, p = 0.27) or synchrony (amplitude effect on phage replicate synchrony: t = 0.547, p = 0.585). Taken together, these data show that bacterial population densities were driven by the resource oscillations, whereas phage population densities were not, suggesting that resource oscillations had a more direct effect on bacterial ecological dynamics.
(b). Resistance and infectivity ranges peak at intermediate resource amplitude
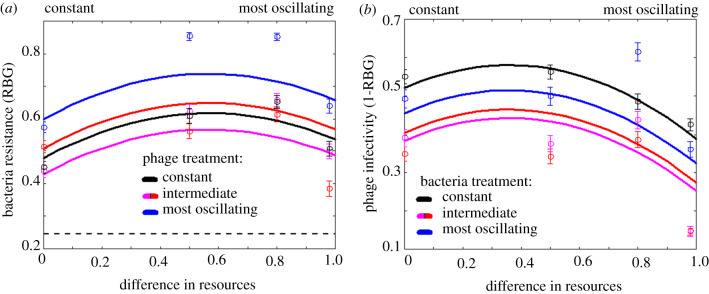
To explore how the amplitude of resource oscillations affected bacterial resistance evolution, we performed a cross-infection experiment using bacteria and phage isolated from the end of the coevolution experiment. Specifically, for each population we tested the resistance of multiple bacterial clones against infection by phage populations from all other treatments, thus gaining an overall measure of the extent of evolution in resistance and infectivity traits that occurred during the experiment. We found that bacteria from intermediate amplitude treatments evolved greater resistance against phage compared to bacteria from constant or high-amplitude oscillating environments (figure 2a; effect of quadratic bacteria resource amplitude term: t = −2.334, p = 0.0499; effect of linear term: t = 2.666, p = 0.0197; see also Appendix A.4). Phage evolved to counteradapt against increased bacterial resistance, figure 2b, such that the highest infectivity arose in phage evolved under intermediate amplitude resource oscillations (effect of quadratic phage resource amplitude term: t = 2.639, p = 0.022; effect of linear term: t = −1.911, p = 0.1345), with the lowest infectivity observed in phage evolved under the highest amplitude oscillations.
Figure 2.
(a) Bacterial resistance (RBG) against phage populations evolved under four resource oscillation amplitude regimens. The black dashed line indicates the mean RBG for ancestral bacteria against all phage populations. (b) Phage infectivity (1-RBG) against bacterial populations evolved under four resource oscillation amplitude regimens. Circles mark mean resistance/infectivity ± s.e. for each bacteria and phage treatment. (Online version in colour.)
(c). Modelling the evolutionary results
In order to model the experimental system, we adapted an SIS model with fluctuating growth rates [37] to include coevolution by way of a range model [44,52,53]. Initially, we assumed that the maximum (minimum) birth rates increased (decreased) linearly with resource concentrations. This model predicted monotonically decreasing investment in resistance and infectivity as the amplitude of the birth rate oscillations increased (electronic supplementary material, Appendix B.6). However, the patterns of evolved resistance and infectivity traits observed in the experiments were non-monotonic, and therefore this initial model did not capture the evolutionary behaviour of the system.
To better parameterize the model for the experimental system, because resource oscillations affected only the bacterial ecological dynamics, we next experimentally measured the effect of resource level on the growth rates of phage-sensitive and phage-resistant genotypes of P. fluorescens (figure 3). The phage-resistant genotypes had lower growth across resource environments (figure 3; effect of phage resistance: t = −3.849, p = 0.0002), but more importantly, the growth rates of both genotypes increased with resource level (resource effect on bacterial growth rate: t = 10.447, p < 10−10) but not linearly––the growth rate gradient is much steeper at low resource levels (figure 3). Hence we incorporated the bacterial growth rates into the oscillating birth rate in the model by fitting functions for the high and low resource birth rates, that is, the maxima and minima of the function in equation (2.6) that correspond to this trend of bacterial growth rate with resource as per figure 3 (figure 4a for varying amplitude δ). Specifically, we set the high resource birth rate in the model to increase linearly with amplitude, as this resembles the changes in bacterial growth rate in the high resource concentrations (resource concentrations ≥0.5 in figure 3, method in the electronic supplementary material, Appendix B.2). However, for the low resource birth rate, we found the best-fit function decreases slowly at low-amplitude oscillations (resource concentrations 0.25–0.5 in figure 3), but rapidly declines at high-amplitude oscillations (i.e. as the resource level decreases further; resource concentrations < 0.25 in figure 3, method in the electronic supplementary material, Appendix B.2). Having chosen the general functional forms for the high and low birth rate functions, parameters within these functions were found by minimizing the sum of squares error with the bacterial growth data of both genotypes. Resistance costs were incorporated through a trade-off in the baseline birth rate a0 which does not depend on amplitude/resource (electronic supplementary material, Appendix B.3).
Figure 3.

Mean maximum growth rate of ancestral (blue) and phage-resistant mutant (red) bacteria in the absence of phage grown under different resource concentrations ± s.e. Black lines show the statistically fitted curves used for the mathematical model in terms of resource concentration (see also figure 4a and the electronic supplementary material, Appendix B.2). Grey stripes indicate the resource concentrations used in the coevolution experiment. (Online version in colour.)
We found that as the amplitude of oscillations increases, the model predicts that the host evolves resistance non-monotonically, with highest resistance evolving for intermediate amplitudes, figure 4b. This behaviour is similar to that found in the experiment, figure 2a, and can be explained by considering the effect of the oscillating birth rates as amplitude increases.
For low amplitudes in the model, the birth rate in the high resource environment increases faster than it decreases in the low environment (figure 4a). Therefore the average birth rate over one oscillation increases with amplitude (figure 4a), and so the host can afford to invest more in resistance. Crucially, the increase in the average birth rate also increases the size of the infected population [37,56], which further amplifies selection for resistance. A similar argument follows through to the experimental data: at low amplitudes, the low resource environment has similar growth and resistance costs compared to the high environment (figure 3, resource concentrations 0.25 and 0.75), so average growth is greater than in the constant environment. As in the model, this results in a high infected population density [37,56] and so greater selection for resistance. Therefore, we find higher resistance evolving for intermediate amplitude oscillations owing to increased selection for resistance, which is (relatively) cheap when amplitudes are low, boosting the response to this selection.
For high-amplitude oscillations in the model, the birth rate in the low resource environment decreases faster than it increases in the high resource environment as the amplitude is increased further, giving an overall decrease in the average birth rate (figure 4a). This leads to a lower infected density, and so there is less selection for resistance. Therefore, as there is also a decrease in reproduction, the host invests more in growth, and so resistance decreases. For the bacteria, low resource concentrations at high amplitudes hindered growth in ancestral and spontaneous phage-resistant mutants (figure 3). This reduced growth means that the infected density is low and so there is less selection for resistance, but also that bacteria with high resistance will be selected against in the periodically low resource environment. Hence, the overall bacterial resistance decreases at high amplitudes.
Our model shows that parasite evolution depends on the oscillations in host birth rate through the host's resistance, u (equation (2.10)), hence the parasite evolves only in response to the host's resistance evolution, with highest infectivity evolving for intermediate amplitudes (figure 4c). This is similar to what we found for the phage (figure 2b), where phage population sizes were unaffected by the oscillating resource (figure 1) and fluctuations in phage density did not significantly affect infectivity (effect of phage FI on phage infectivity: t = −0.779, p = 0.920).
4. Discussion
In this study, we investigated how the amplitude of environmental oscillations affected the coevolution of host resistance and parasite infectivity experimentally and theoretically. We showed that the bacterium P. fluorescens and its lytic phage SBW25φ2 evolved highest resistance and infectivity for intermediate amplitude oscillations in nutrient resources. We also developed a coevolutionary model that incorporates evidence-based assumptions on the impact of seasonality on growth, which supported our empirical data by showing maximum investment in host resistance and parasite infectivity for intermediate amplitudes. By comparing different seasonality functions, the model shows that the coevolutionary results are owing to how the host growth dynamics change with amplitude in the high- and low-quality environments.
We used our theoretical model to explain the empirical results for varying amplitude when we include evidence-based growth rates in the oscillating birth rate function. The key to explaining the non-monotonicity in resistance evolution lies in how host growth rates in the constituent environments change with amplitude. At low amplitudes, the average birth rate increases with amplitude, giving higher infected population densities and thus greater selection for resistance. At high amplitudes, the average birth rate decreases with amplitude and thus selection for resistance decreases owing to lower infected population sizes, allowing for greater investment in births. We found this behaviour for a range of parameter values (electronic supplementary material, Appendix B.7) and so it is not limited to the example shown. These arguments from the model explain the experimental pattern for bacterial resistance. Nutrient level determines the growth rate of the bacteria, with highest average growth rate occurring for intermediate amplitudes in the oscillating treatments. This, along with low competition for resources between the bacteria, leads to a greater infected population and therefore increased selection for resistance [37,56]. These factors combine such that bacteria in resource environments with intermediate oscillations benefit from high nutrient levels (greater selection for resistance), but are not as limited by low resources (low costs at low amplitudes), hence resistant mutants are able to survive better than in populations experiencing high-amplitude oscillations of resource levels. This result, that the bacteria evolve higher resistance in an oscillating environment with intermediate amplitude, may appear contrary to existing evidence that a temporal environment constrains or has no effect on coevolution [35,36], including predator–prey interactions [32–34]. These studies, however, all use a fixed amplitude of oscillation, while we use a fixed period, and so there is likely to be an interacting effect of period and amplitude of oscillating environments on coevolution, although this has yet to be studied empirically.
For the phage, we found that highest infectivity evolved at intermediate amplitudes and was limited by very high-amplitude oscillations. The phage population sizes were unaffected by the amplitude of the resource oscillations, which suggests that phage infectivity was more strongly influenced by the strength of bacterial resistance than by nutrient availability. Therefore, we find theoretically that a non-linear response in phage infectivity as the amplitude of resource oscillations increases is owing to the behaviour of the evolved bacterial resistance. Parasite fitness is only affected by the oscillating environment through evolution of the host (equation (2.10), see also [40,44]), and so maximum infectivity evolves for intermediate amplitudes. A similar pattern was observed by Harrison et al. [35], in that the phage population densities were not affected by the oscillating resource level and the evolved bacteria resistance and phage infectivity ranges were correlated (broader range of resistance and infectivity in a constant environment). This experimental system and model are asymmetric in terms of how the oscillating environment impacts the ecology of each species, because only the host densities are strongly affected. This in turn influences how evolution depends on the environment, leading to imbalances in coevolution and producing the correlated evolutionary profiles with resource amplitude. However, this effect, where only the host population is strongly impacted by the oscillations, is unlikely to be universal. In fact, there are many instances of environmental variation that strongly affect the parasite only [1,2,36,57,58], both species [33], or their interaction [31,59]. In these cases, we may instead expect resistance and infectivity evolutionary profiles to become decoupled, and mathematical models have already shown that such oscillations in environmental conditions can have a direct effect on parasite evolution [38,39,60,61]. Hence we need to understand how the environment influences each partner and their interaction in order to accurately predict the effect on coevolution, especially for use in theoretical models.
Previously, theoretical models have predicted that hosts evolved highest resistance for either constant or high-amplitude oscillations in the environment [14,37]. Despite including a stepped resource and coevolution, previous models [14] and our initial model extension (electronic supplementary material, Appendix B.6) failed to fully replicate our experimental setup well enough to reproduce the experimental results. This is primarily owing to how the minimum environment changes with amplitude. Poisot et al. [14] keep the minimum constant while the maximum resource input increases, which does not match either the resource concentrations or growth rates in our experiment. For our initial model extension, we assumed that the maximum and minimum environments changed symmetrically, as this is how we alter the nutrient concentrations, and the average birth rate remains constant for all amplitudes. Again, this is not the case in the experiment, as we showed that growth rates decrease more rapidly as the resource concentration decreases. However, by incorporating experimentally derived growth kinetics, our coevolutionary model predicts evolution of highest resistance and infectivity at intermediate amplitudes, supporting the experimental results. While we did not experimentally test the effects of lower amplitude environments, results from the theoretical model support our predictions in that region. Owing to the default behaviour of the model, which produces a monotonic decrease in both traits for symmetric seasonality over a range of parameters (electronic supplementary material, Appendix B.7), the main difference between the experimental and theoretical results is the predicted large drop in both resistance and infectivity for very high amplitudes. This could be owing to the experimental oscillations being less extreme than the largest amplitude used in the model, and in fact the experimental data does suggest such a drop-off may occur, especially for the phage. We could test this using an even lower concentration of resource in the maximum amplitude environment, although this may come with an increased risk of phage extinction [46]. The model could also be made more specific to our study system, for example, by including free-living phage, more details about the lytic cycle or more realistic parameter values derived from experimental data.
The vast majority of natural biological systems experience environmental oscillations owing to a range of biotic and abiotic factors, not least regular seasonal variation of climate. The impact of this seasonality on population dynamics in infectious disease systems has received considerable attention [20]. Population densities are crucial to shaping host–parasite coevolution [62], yet until recently we have had little understanding of how fluctuating population densities, in any biological context, impact selection. This is now an emerging field of study; recent theoretical work [14,37,38,40] has laid the groundwork for us to be able to explore these impacts theoretically, and experimental tests of coevolution in oscillating environments are also emerging [35,36]. This study has emphasized the importance of understanding the effect of oscillations on ecological dynamics and identifying underlying fitness costs to better predict coevolution in a temporally oscillating environment.
Supplementary Material
Supplementary Material
Data accessibility
The data for this article is provided as the electronic supplementary material.
Authors' contributions
All authors designed the study, C.F. and R.W. carried out the experimental work; C.F. analysed the data; C.F. and A.B. performed the modelling work. All authors contributed towards the manuscript.
Competing interests
We declare we have no competing interests.
Funding
This study was funded by The Leverhulme Trust, Leverhulme Centre for Applied Biological Modelling, NERC Environmental Bioinformatics Centre (grant no. NE/R008825/1) to M.A.B. and NERC ACCE DTP studentship (grant no. 1517986) to R.W.
References
- 1.Fels D, Kaltz O. 2006. Temperature dependent transmission and latency of Holosporaundulata, a micronucleus-specific parasite of the ciliate Paramecium caudatum. Proc. R. Soc. B 273, 1031–1038. ( 10.1098/rspb.2005.3404) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Vale PF, Stjernman M, Little TJ. 2008. Temperature dependent costs of parasitism and maintenance of polymorphism under genotype-by-environment interactions. J. Evol. Biol. 21, 1318–1427. ( 10.1111/j.1420-9101.2008.01555.x) [DOI] [PubMed] [Google Scholar]
- 3.Lopez-Pascua L, Gandon S, Buckling A. 2012. Abiotic heterogeneity drives parasite local adaptation in coevolving bacteria and phages. J. Evol. Biol. 25, 187–195. ( 10.1111/j.1420-9101.2011.02416.x) [DOI] [PubMed] [Google Scholar]
- 4.Lopez-Pascua L, Hall AR, Best A, Morgan AD, Boots M, Buckling A. 2014. Higher resources decrease fluctuating selection during host–parasite coevolution. Ecol. Lett. 17, 1380–1388. ( 10.1111/ele.12337) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Zeller M, Koella JC. 2017. The role of the environment in the evolution of tolerance and resistance to a pathogen. Am. Nat. 190, 389–397. ( 10.1086/692759) [DOI] [PubMed] [Google Scholar]
- 6.Laine A-L. 2009. Role of coevolution in generating biological diversity: spatially divergent selection trajectories. J. Exp. Bot. 60, 2957–2970. ( 10.1093/jxb/erp168) [DOI] [PubMed] [Google Scholar]
- 7.Wolinska J, King KC. 2009. Environment can alter selection in host–parasite interactions. Trends Parasitol. 25, 236–244. ( 10.1016/j.pt.2009.02.004) [DOI] [PubMed] [Google Scholar]
- 8.Koskella B, Brockhurst MA. 2014. Bacteria–phage coevolution as a driver of ecological and evolutionary processes in microbial communities. FEMS. Microbiol. Rev. 38, 916–931. ( 10.1111/1574-6976.12072) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Brunner FZ, Eizaguirre C. 2016. Can environmental change affect host/parasite-mediated speciation? Zoology 119, 384–394. ( 10.1016/j.zool.2016.04.001) [DOI] [PubMed] [Google Scholar]
- 10.Parratt SR, Numminen E, Laine A-L. 2016. Infectious disease dynamics in heterogeneous landscapes. Annu. Rev. Ecol. Evol. Syst. 47, 283–306. ( 10.1146/annurev-ecolsys-121415-032321) [DOI] [Google Scholar]
- 11.Hochberg ME, van Baalen M.. 1998. Antagonistic coevolution over productivity gradients. Am. Nat. 152, 620–634. ( 10.1086/286194) [DOI] [PubMed] [Google Scholar]
- 12.Best A, Webb S, White A, Boots M. 2011. Host resistance and coevolution in spatially structured populations. Proc. R. Soc. B 278, 2216–2222. ( 10.1098/rspb.2010.1978) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Mostowy R, Engelstadter J. 2011. The impact of environmental change on host- parasite coevolutionary dynamics. Proc. R. Soc. B 278, 2283–2292. ( 10.1098/rspb.2010.2359) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Poisot T, Thrall PH, Hochberg ME. 2012. Trophic network structure emerges through antagonistic coevolution in temporally varying environments. Proc. R. Soc. B 279, 299–308.( 10.1098/rspb.2011.0826) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Rand DA, Keeling M, Wilson HB. 1995. Invasion, stability and evolution to criticality in spatially extended, artificial host-pathogen ecologies. Proc. R. Soc. Lond. B 259, 55–63. ( 10.1098/rspb.1995.0009) [DOI] [Google Scholar]
- 16.Haraguchi Y, Sasaki A. 2000. The evolution of parasite virulence and transmission rate in a spatially structured population. J. Theor. Biol. 203, 85–96. (doi:0.1006/jtbi.1999.1065) [DOI] [PubMed] [Google Scholar]
- 17.Thompson JN. 2005. The geographic mosaic of coevolution. Chicago, IL: University of Chicago Press. [Google Scholar]
- 18.Gandon S, Buckling A, Decaestecker E, Day T. 2008. Host–parasite coevolution and patterns of adaptation across time and space. J. Evol. Biol. 21, 1861–1866 ( 10.1111/j.1420-9101.2008.01598.x) [DOI] [PubMed] [Google Scholar]
- 19.Debarre F, Lion S, van Baalen M, Gandon S.. 2012. Evolution of host life-history traits in a spatially structured host-parasite system. Am. Nat. 179, 52–63. ( 10.1086/663199) [DOI] [PubMed] [Google Scholar]
- 20.Altizer S, Dobson A, Hosseini P, Hudson P, Pascual M, Rohani P. 2006. Seasonality and the dynamics of infectious diseases. J. Anim. Ecol. 9, 467–484. ( 10.1111/j.1461-0248.2005.00879.x) [DOI] [PubMed] [Google Scholar]
- 21.Fine PEM, Clarkson JA. 1982. Measles in England and Wales. I: an analysis of factors underlying seasonal patterns. Int. J. Epidemiol. 11, 5–14. ( 10.1093/ije/11.1.15) [DOI] [PubMed] [Google Scholar]
- 22.Finkenstadt BF, Grenfell BT. 2000. Time series modelling of childhood diseases: a dynamical systems approach. Appl. Stat. 49, 182–205. ( 10.1111/1467-9876.00187) [DOI] [Google Scholar]
- 23.Rowan W. 1938. Light and seasonal reproduction in animals. Biol. Rev. 13, 374–401. ( 10.1111/j.1469-185X.1938.tb00523.x) [DOI] [Google Scholar]
- 24.Summers-Smith D. 1956. Mortality of the house sparrow. Bird Study. 3, 265–270. ( 10.1080/00063655609475858) [DOI] [Google Scholar]
- 25.Gehrt SD. 2005. Seasonal survival and cause-specific mortality of urban and rural striped skunks in the absence of rabies. J. Mammal. 86, 1164–1170. ( 10.1644/04-MAMM-A-173R2.1) [DOI] [Google Scholar]
- 26.Gogarten JF, et al. 2012. Seasonal mortality patterns in non-human primates: implications for variation in selection pressures across environments. Evolution 66, 3252–3266. ( 10.1111/j.1558-5646.2012.01668.x) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Stawski C, Willis CKR, Geiser F. 2014. The importance of temporal heterothermy in bats. J. Zool. 292, 86–100. ( 10.1111/jzo.12105) [DOI] [Google Scholar]
- 28.Ketterson ED, Fudickar AM, Atwell JW, Greives TJ. 2015. Seasonal timing and population divergence: when to breed, when to migrate. Curr. Opin. Behav. Sci. 6, 50–58. ( 10.1016/j.cobeha.2015.09.001) [DOI] [Google Scholar]
- 29.Furness AI. 2016. The evolution of an annual life cycle in killifish: adaptation to ephemeral aquatic environments through embryonic diapause. Biol. Rev. 91, 796–812. ( 10.1111/brv.12194) [DOI] [PubMed] [Google Scholar]
- 30.Blanford S, Thomas M, Pugh C, Pell JK. 2003. Temperature checks the red queen? Resistance and virulence in a fluctuating environment. Ecol. Lett. 6, 2–5. ( 10.1046/j.1461-0248.2003.00387.x) [DOI] [Google Scholar]
- 31.Dallas T, Drake JM. 2016. Fluctuating temperatures alter environmental pathogen transmission in a Daphnia–pathogen system. Ecol. Evol. 6, 7931–7938. ( 10.1002/ece3.2539) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Friman V-P, Laakso J. 2011. Pulsed-resource dynamics constrain the evolution of predator-prey interactions. Am. Nat. 177, 334–345. ( 10.1086/658364) [DOI] [PubMed] [Google Scholar]
- 33.Hiltunen T, Ayan GB, Becks L. 2015. Environmental fluctuations restrict eco-evolutionary dynamics in predator–prey system. Proc. R. Soc. B 282, 20150013 ( 10.1098/rspb.2015.0013) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Friman V-P, Laakso J, Koivu-Orava M, Hiltunen T. 2011. Pulsed-resource dynamics increase the asymmetry of antagonistic coevolution between a predatory protist and a prey bacterium. J. Evol. Biol. 24, 2563–2573. ( 10.1111/j.1420-9101.2011.02379.x) [DOI] [PubMed] [Google Scholar]
- 35.Harrison E, Laine A-L, Hietala M, Brockhurst MA. 2013. Rapidly fluctuating environments constrain coevolutionary arms races by impeding selective sweeps. Proc. R. Soc. B 280, 20130937 ( 10.1098/rspb.2013.0937) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Duncan AB, Dusi E, Jacob F, Ramsayer J, Hochberg ME, Kaltz O. 2017. Hot spots become cold spots: coevolution in variable temperature environments. J. Evol. Biol. 30, 55–65. ( 10.1111/jeb.12985) [DOI] [PubMed] [Google Scholar]
- 37.Ferris C, Best A. 2018. The evolution of host defence to parasitism in fluctuating environments. J. Theor. Biol. 440, 58–65. ( 10.1016/j.jtbi.2017.12.006) [DOI] [PubMed] [Google Scholar]
- 38.Koelle K, Pascual M, Yunus M. 2005. Pathogen adaptation to seasonal forcing and climate change. Proc. R. Soc. B 272, 971–977. ( 10.1098/rspb.2004.3043) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Sorrell I, White A, Pedersen AB, Hails RS, Boots M. 2009. The evolution of covert, silent infection as a parasite strategy. Proc. R. Soc. B 276, 2217–2226. ( 10.1098/rspb.2008.1915) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Donnelly R, Best A, White A, Boots M. 2013. Seasonality selects for more acutely virulent parasites when virulence is density dependent. Proc. R. Soc. B 280, 20122464 ( 10.1098/rspb.2012.2464) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Nuismer SL, Gomulkiewicz R, Morgan MT. 2003. Coevolution in temporally variable environments. Am. Nat. 162, 195–204. ( 10.1086/376582) [DOI] [PubMed] [Google Scholar]
- 42.Buckling A, Rainey PB. 2002. Antagonistic coevolution between a bacterium and a bacteriophage. Proc. R. Soc. Lond. B 269, 931–936. ( 10.1098/rspb.2001.1945) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Brockhurst MA, Morgan AD, Fenton A, Buckling A. 2007. Experimental coevolution with bacteria and phage: the Pseudomonas fluorescens - Phi2 model system. Infect Genet. Evol. 7, 547–552. [DOI] [PubMed] [Google Scholar]
- 44.Best A, White A, Kisdi E, Antonvics J, Brockhurst MA, Boots M. 2010. The evolution of host-parasite range. Am. Nat. 176, 63–71. ( 10.1086/653002) [DOI] [PubMed] [Google Scholar]
- 45.Poullain V, Gandon S, Brockhurst MA, Buckling A, Hochberg ME. 2008. The evolution of specificity in evolving and coevolving antagonistic interactions between a bacteria and its phage. Evolution 62, 1–11. ( 10.1111/j.1558-5646.2007.00260.x) [DOI] [PubMed] [Google Scholar]
- 46.Wright RCT, Brockhurst MA, Harrison E. 2016. Ecological conditions determine extinction risk in co-evolving bacteria-phage populations. BMC Evol. Biol. 16, 227 ( 10.1186/s12862-016-0808-8) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Vogwill T, Fenton A, Brockhurst MA. 2009. Dispersal and natural enemies interact to drive spatial synchrony and decrease stability in patchy populations. Ecol. Lett. 12, 1194–1200. ( 10.1111/j.1461-0248.2009.01374.x) [DOI] [PubMed] [Google Scholar]
- 48.Loreau M, de Mazancourt C.. 2008. Species synchrony and its drivers: neutral and nonneutral community dynamics in fluctuating environments. Am. Nat. 172, E48–E66. ( 10.1086/589746) [DOI] [PubMed] [Google Scholar]
- 49.Anderson RM, May RM. 1981. The population dynamics of microparasites and their invertebrate hosts. Phil. Trans. R. Soc. B 291, 451–524. ( 10.1098/rstb.1981.0005) [DOI] [Google Scholar]
- 50.Ripp S, Miller RV. 1997. The role of pseudolysogeny in bacteriophage-host interactions in a natural freshwater environment. Microbiology 143, 2065–2070. ( 10.1099/00221287-143-6-2065) [DOI] [PubMed] [Google Scholar]
- 51.Westra ER, Swarts DC, Staals RH, Jore MM, Brouns SJ, van der Oost J.. 2012. The CRISPRs, they are a-changin’: how prokaryotes generate adaptive immunity. Annu. Rev. Genet. 46, 311–339. ( 10.1146/annurev-genet-110711-155447) [DOI] [PubMed] [Google Scholar]
- 52.Best A, Ashby B, White A, Bowers R, Buckling A, Koskella B, Boots M. 2017. Host–parasite fluctuating selection in the absence of specificity. Proc. R. Soc. B 284, 20171615 ( 10.1098/rspb.2017.1615) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Boots M, White A, Best A, Bowers R. 2014. How specificity and epidemiology drive the coevolution of static trait diversity in hosts and parasites. Evolution 68, 1594–1606. ( 10.1111/evo) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Geritz SAH, Kisdi E, Meszena G, Metz JAJ. 1998. Evolutionarily singular strategies and the adaptive growth and branching of the evolutionary tree. Evol. Ecol. 12, 35–57. ( 10.1023/A:1006554906681) [DOI] [Google Scholar]
- 55.Metz JAJ, Nisbet RM, Geritz SAH. 1992. How should we define ‘fitness’ for general ecological scenarios? Trends Ecol. Evol. 7, 198–202. ( 10.1016/0169-5347(92)90073-K) [DOI] [PubMed] [Google Scholar]
- 56.Boots M, Haraguchi Y. 1999. The evolution of costly resistance in host-parasite systems. Am. Nat. 153, 359–370. ( 10.1086/303181) [DOI] [PubMed] [Google Scholar]
- 57.Mitchell SE, Rogers ES, Little TJ, Read AF. 2005. Host–parasite and genotype-by-environment interactions: temperature modifies potential for selection by a sterilizing pathogen. Evolution 59, 70–80. ( 10.1111/j.0014-3820.2005.tb00895.x) [DOI] [PubMed] [Google Scholar]
- 58.Laine A-L. 2007. Pathogen fitness components and genotypes differ in their sensitivity to nutrient and temperature variation in a wild plant–pathogen association. J. Evol. Biol. 20, 2371–2378. ( 10.1111/j.1420-9101.2007.01406.x) [DOI] [PubMed] [Google Scholar]
- 59.Zhang Q-G, Buckling A. 2011. Antagonistic coevolution limits population persistence of a virus in a thermally deteriorating environment. Ecol. Lett. 14, 282–288. ( 10.1111/j.1461-0248.2010.01586.x) [DOI] [PubMed] [Google Scholar]
- 60.Hamelin FM, Castel M, Poggi S, Andrivon D, Mailleret L. 2011. Seasonality and the evolutionary divergence of plant parasites. Ecology 92, 2159–2166. ( 10.1890/10-2442.1) [DOI] [PubMed] [Google Scholar]
- 61.van den Berg F, Bacaer N, Metz JAJ, Lannou C, van den Bosch F. 2011. Periodic host absence can select for higher or lower parasite transmission rates. Evol. Ecol. 25, 121–137. ( 10.1007/s10682-010-9387-0) [DOI] [Google Scholar]
- 62.Papkou A, Gokhale GS, Traulsen A, Schulenberg H. 2016. Host-parasite coevolution: why changing population size matters. Zoology 119, 330–338. ( 10.1016/j.zool.2016.02.001) [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
The data for this article is provided as the electronic supplementary material.