Behavioural syndromes shape evolutionary trajectories via conserved genetic architecture

Abstract

Behaviours are often correlated within broader syndromes, creating the potential for evolution in one behaviour to drive evolutionary changes in other behaviours. Despite demonstrations that behavioural syndromes are common, this potential for evolutionary effects has not been demonstrated. Here we show that populations of field crickets (Gryllus integer) exhibit a genetically conserved behavioural syndrome structure, despite differences in average behaviours. We found that the distribution of genetic variation and genetic covariance among behavioural traits was consistent with genes and cellular mechanisms underpinning behavioural syndromes rather than correlated selection. Moreover, divergence among populations' average behaviours was constrained by the genetically conserved behavioural syndrome. Our results demonstrate that a conserved genetic architecture linking behaviours has shaped the evolutionary trajectories of populations in disparate environments—illustrating an important way for behavioural syndromes to result in shared evolutionary fates.

1. Introduction

Behaviour is frequently assumed to have been shaped by selection [1] and thus populations are expected to differ in a range of behaviours based on local selective pressures. This implies that behaviours are able to evolve independently, an assumption increasingly challenged by the ubiquity of behavioural syndromes—correlations among behaviours (table 1) [2,3]—which have been documented across taxonomic groups [4,5] and are composed of both genetic and environmental contributions [6–8].

Table 1.

Terms and symbol definitions.

term or symbol	definition
behavioural syndrome	Among-individual correlations of behaviour. For example, individuals that are on average more aggressive also, on average, show a higher degree of exploratory propensity.
G	Additive genetic covariance matrix.
gmax	The dominant eigenvector of G, describes the dimension in multivariate trait space with the highest additive genetic variance.
D	Among-population divergence matrix describing patterns of population divergence in average phenotype.
di	Eigenvectors of D, d1 represent the dimension capturing most of the divergence in average phenotype among populations.
H	Common subspaces of genetic variation for all four populations, describes the trait combinations that share the most genetic variation among populations.
hi	Eigenvectors of H, h1 is analogous to gmax and describe the major axis of shared genetic variance among populations.
Ei	Eigentensors describing subspaces for which G varies among populations.
eij	jth eigenvector of the ith eigentensor, describes the trait combinations for which genetic divergence has occurred among populations.
r	Correlation among eigenvectors, values close to 0 indicate independence of eigenvectors, values close to 1 indicate alignment of eigenvectors.
$\overline{a}$	Autonomy of G, indicates the proportion of genetic variation unconstrained by covariance among traits. Values closer to 0 indicate stronger evolutionary constraints and values closer to 1 indicate complete autonomy of genetic variation, meaning that each trait can evolve independently in response to future selection.

Given the contribution of genetic correlations to behavioural syndromes, these syndromes potentially constrain the ability of populations to diverge and respond to local selective pressures [9]. Specifically, if syndromes stem from pleiotropic effects—wherein a single gene affects multiple behaviours—populations will be constrained to diverge along shared evolutionary pathways. Further, this divergence is predicted to occur in the direction in trait space that contains the most variation (figure 1) [10]. Therefore, if syndromes have a constraining effect on evolution, the pattern of correlations among traits will be conserved among populations (figure 1). Alternatively, if genetic correlations underpinning syndromes are the result of historical selection favouring particular trait combinations (i.e. selection-induced linkage disequilibrium [11,12]), the divergence of populations will be generally unconstrained and genetic correlations should rapidly break down [11–13].

Figure 1.

Two contrasting hypotheses can explain the presence of genetic correlations among behavioural traits (i.e. behavioural syndromes): genetic constraints arising from pleiotropy and shared molecular mechanisms should lead to the expression of the same behavioural syndrome (a). As a result, the vector correlations (r) between major axes of genetic variation (g_max) are predicted to be approaching 1 (c). Alternatively, selection-induced linkage disequilibrium should lead to differing orientation and strength of behavioural syndromes when selective pressures differ among populations (b). The vector correlation between g_maxs should therefore be below 1 (d). (Online version in colour.)

These quantitative genetic explanations for behavioural syndromes have explicit analogues in the behavioural literature: whether syndromes emerge from pleiotropy, tight genetic linkage or other shared physiological and cellular effects has been termed the ‘constraints hypothesis', as opposed to selection-induced linkage disequilibrium, which has been termed the ‘adaptive hypothesis' (figure 1; sensu Bell [14]). While some studies have compared phenotypic or among-individual correlations across populations (e.g. [15–18]), only population comparisons of behavioural syndromes at the additive genetic level permit proper testing of these competing hypotheses. Unfortunately, data at the additive genetic level has been restricted to two population comparisons [14,19]. Consequently, the role of behavioural syndromes in shaping population divergence is unknown, and the constraints and adaptive hypotheses remain insufficiently tested.

Knowing whether behavioural syndromes emerge from genetic constraints or selection-induced linkage disequilibrium is significant because these mechanisms differentially affect evolutionary outcomes [12]. Potential effects are wide ranging, from altering responses to environmental changes to influencing speciation. For example, in Anolis lizards, constraints imposed by genetic correlations on morphological traits have shaped divergence and what phenotypes can be expressed during adaptive radiations [20]. Behavioural syndromes may have an even stronger effect: Dochtermann & Dingemanse [9] reported that the magnitude of genetic correlations between behaviours is sufficient to constrain evolutionary responses to a greater degree than expected for life-history or morphological traits. Unfortunately, this study could not distinguish between the constraints and adaptive hypotheses. If indeed the constraints hypothesis underpins behavioural syndromes, then syndromes will reduce the rate of adaptation and the rate at which populations and species diverge. Evaluating evidence for the constraints and adaptive hypotheses is therefore necessary to properly understand the role of behavioural syndromes in evolution.

Here, we evaluated predictions of the adaptive and constraints hypotheses (figure 1) by testing whether behavioural syndromes have diverged at the genetic level among populations of the field cricket, Gryllus integer. Specifically, according to the constraints hypothesis, we predicted that genetic variation would be consistent among populations and genetic correlations would be maintained across generations. The adaptive hypothesis was simultaneously assessed indirectly because it predicts divergence will not be constrained and that correlations will rapidly degrade. We evaluated these predictions via estimation and comparisons of behavioural genetic (co)variance matrices, i.e. G (table 1), for multiple populations of G. integer (figure 2).

Figure 2.

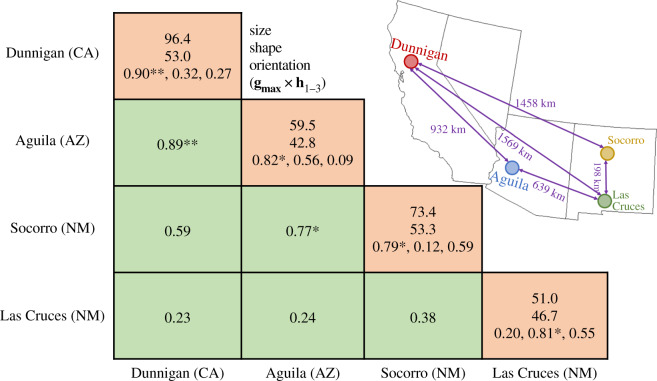
The genetic architecture of behavioural syndromes is shared in four isolated populations of Gryllus integer. Values along the diagonal (peach shading) describe the multivariate structure of behavioural variation: first row the size (total genetic variance), second the shape (per cent of variance explained by the major axis of genetic variation, g_max) and, third, orientation (vector correlation between g_max and conserved genetic subspaces h_1–3). Off-diagonal elements represent the correlation between the g_max of each population (top row) and the probability that alignment differed from 0: **p < 0.01, *p < 0.05. (Online version in colour.)

2. Material and methods

(a). Cricket collection

G. integer is ideal for evaluating the constraints and adaptive hypotheses as it exhibits population differences in ecologically relevant behaviours that can be assayed in the laboratory (e.g. [21–23]) and can be bred in the laboratory according to quantitative genetic designs [24].

We collected about 50 adult females from each of four populations located in the United States: Socorro, NM; Las Cruces, NM; Aguila, AZ; and Dunnigan, CA (electronic supplementary material, table S1; figure 2) during the summer of 2017. These populations are geographically distant from each other (figure 2) and vary in predator and parasitoid abundance [21]. Crickets from these locations are historically recognized as members of Gryllus integer but additional splitting out of subspecies or different species based on population genetic structure was recently proposed [25]. Collected individuals were sent to animal housing facilities at North Dakota State University. We housed females individually in 0.71 l containers provided with ad libitum food (Purina Chick Starter) and water (provided in glass vials capped with cotton) and shelter made of a small piece of cardboard egg carton. We maintained the cricket housing room at approximately 27°C and on a 12 : 12 dark : light cycle reversed such that the room was dark during daytime hours.

(b). Breeding design

We allowed females collected from the field (generation P) to oviposit in water vials while in their containers. Offspring of these females were designated generation F₀ as sires were unknown: mating occurred prior to capture and multiple mating is common in the genus [26]. When F₀ offspring hatched in their dams' containers, we moved them to individual housing prior to maturation. We assayed the behaviour of 387 F₀ individuals (see below) upon maturation (electronic supplementary material, table S1). After behavioural trials, F₀ individuals were assigned to breeding pairs such that individual males were mated to randomly assigned females from the same population but different dams. We mated individuals according to a standard full-sib, half-sib breeding design [27] but, based on the available crickets, some males could only be mated to a single female. We moved breeding pairs into larger containers (34.6 × 21 × 12.4 cm) along with their respective food dish, water vial and egg carton shelter for 24 h. After 24 h, we returned the male and female crickets to their original containers. If males were to be mated with additional females, we allowed a minimum break of 24 h before repeating the above procedure. F₀ females were subsequently allowed to oviposit into water vials within their containers and we moved the resulting F₁ offspring to individual housing prior to maturation. We assayed F₁ individuals' behaviours upon maturation and then repeated the mating procedure by pairing individuals from the same population. We repeated the behavioural assays once more for the F₂ offspring. In total, we tested the behaviours of 946 individual crickets: 387 F₀ individuals, 395 F₁ individuals and 163 F₂ individuals (electronic supplementary material, table S1).

(c). Behavioural testing

All behavioural tests followed standard procedures previously validated in the literature for gryllid crickets [23,28–33]. These assays encompass how individuals vary in risk-taking behaviour [29], exploratory propensity [31–33] and response to predation threat [31,32]. Based on the known relatedness among individuals, we then estimated G—the matrix of additive genetic behavioural variances and covariances—for each population. Below, we describe these behavioural assays and their ecological relevance.

(i). Latency to emerge from shelter

Gryllid crickets, including G. integer, use small burrows and cracks for refuge from predators, refuges to which they retreat when threatened. Consequently, latency to emerge from shelter after disturbance is a proxy for risk-taking behaviour or ‘boldness' [29]. Here, we conducted latency tests by transferring individuals from their home containers into small artificial burrows (40 cm³) placed within a 34.6 × 21 cm arena. These artificial burrows were capped so that individuals could not immediately emerge. Crickets remained in the artificial burrow for 2 min after which we removed the cap. We then allowed crickets to emerge from the artificial burrow for the next 6 min and 30 s and recorded time to emergence (in seconds).

(ii). Open-field exploratory behaviour

Open-field tests are a classic behavioural assay across taxa [34] and measure the exploratory propensity of individuals [35], including crickets [31–33]. Individuals that move through more of an area are considered more thorough explorers [35]. Here we used open-field tests to measure activity and exploratory propensity in a 30 × 30 cm Plexiglas arena. We placed individuals into the arena under a small container and allowed them to rest for 30 s. We then removed the container and let the cricket explore the arena for 3 min and 40 s. We cleaned the arena with isopropyl alcohol between trials to remove any chemosensory cues. We used Ethovision XT to estimate the total distance the individual moved during the trial (cm), the number of unique zones of the arena an individual visited during the trial [32,36] and the variance in velocity of individuals. This latter measure indicates whether an individual's speed of exploration was constant (low variance) or whether individuals had periods of inactivity punctuated by bouts of activity (high variance).

(iii). Response to cues of predator presence

How individuals respond to cues of predator presence varies within and among populations and likely covaries with fitness [37]. Crickets respond to cues of predator presence by either freezing or increasing activity depending on whether confronted by predator cues of sit-and-wait or active predators [38,39]. Here we used a behavioural assay to measure response to cues of predator presence previously used with another Gryllid species [31,32]. Specifically, we introduced individuals into a 15 cm diameter circular arena (7.5 cm height), covered with dry filter paper that had been soaked with diluted excreta from leopard geckos (Eublepharis macularius). Crickets respond to exposure to leopard gecko cues by increasing activity [31,32]. We fed leopard geckos a diet of G. integer with occasional supplementation with mealworms (larval Tenebrio molitor) and decorated crickets (Gryllodes sigillatus).

We introduced crickets to a portion of the arena without predator cue under a small shelter. After a 30 s rest period, we removed the shelter and let the individual to freely move throughout the arena for 3 min and 40 s. We then used Ethovision XT to estimate total distance moved during the predator cue trial (cm), the latency to first movement (in seconds) and the variance in velocity.

(d). Statistical analyses

(i). G matrix estimation

We used multi-response mixed effect animal models [40] implemented using the MCMCglmm package in R [41] to estimate genetic variances and covariances (i.e. G matrces). We included the effects of temperature, day and time of testing in the behavioural arena room along with sex, life-stage and mass of the individual as fixed effects. We used the individual relatedness matrix (based on the known pedigree) as a random effect. Traits for which variances and covariances were estimated were (i) the latency that an individual emerged from the shelter during the trial (modelled as censored Gaussian), (ii) the distance moved during the open-field trial (Gaussian), (iii) the number of unique zones an individual visited during the open-field trial (Poisson), (iv) the log-transformed variance in velocity during the open-field trial (Gaussian), (v) the square-root-transformed distance an individual moved during the predator cue response trial (Gaussian), (vi) the latency to initiate movement in the antipredator response trial (Poisson) and (vii) the log-transformed variance in velocity during the antipredator response trial (Gaussian). The inclusion of dam ID as a random effect did not improve model fit, indicating negligible maternal effects and was not included in final model runs. Multi-response models were fit individually by population with each population's variances and covariances estimated from the posterior of an MCMC chain of 4.8 × 10⁶ iterations, with an 800 000 burn-in period and a thinning interval of 4000. A prior that was minimally informative for both variances and covariances was used. All variances and covariances were estimated at the additive genetic level and on the latent scale (electronic supplementary material, table S4).

(ii). Evaluating the constraints and adaptive hypotheses

The location, orientation and distribution of genetic variation in multivariate space—in our case seven-dimensional space—can differ among groups in a variety of complex ways [42–46]. We therefore used a suite of statistical approaches to compare the orientation of genetic variation and evaluated agreement among approaches in support for either the constraints or adaptive hypothesis.

To determine whether behavioural syndrome structure at the additive genetic level was shared among populations, we used two approaches:

• (i)testing whether populations exhibited shared subspaces (dimensions) of G based on Krzanowski's common subspace analysis [46]; and
• (ii)comparing alignment of dominant eigenvectors among populations (i.e. g_max; table 1 [10]).

Krzanowski's common subspace analysis determines whether genetic variation is expressed in the same dimensions and direction across groups [46]. This is analogous to asking whether the populations shared principal components [45]. In two dimensions, this is represented by the directions ellipses point in figure 1, with shared subspaces when the ellipses overlap and point in the same direction. For our data, there were seven possible dimensions of overlap but some dimensions may not possess substantive variation (electronic supplementary material, table S4). Following Aguirre et al. [46] we considered those subspaces that contained greater than 90% of the genetic variation and summarized them in matrix form (H) [46]. Here, this included three possible shared subspaces (h₁, h₂ and h₃; table 1), and we tested whether these subspaces were shared among populations to a degree greater than expected by chance. Under the constraints hypothesis, we expect genetic variation to be expressed in the same dimensional direction among populations (i.e. shared genetic subspaces). A lack of shared subspaces would therefore contradict the predictions of the constraints hypothesis. However, shared subspaces can be observed under the adaptive hypothesis if selective pressures are the same across populations.

Because evolutionary trajectories are biased by the dimensional direction (vector) in which most genetic variation is expressed, we also compared this vector, i.e. g_max [10], among populations. This approach is similar to Krzanowski's common subspace analysis but focuses on the dimension in which most variation is expressed. Here we calculated the vector correlation between the g_maxs of each population and, via randomization testing, determined whether these correlations significantly differed from 0.

Even if genetic covariances are shared across populations, as evaluated by the above analyses, average behaviours can nonetheless differ. Therefore, we estimated ‘D' (table 1)—a matrix that describes the phenotypic divergence among populations and was here estimated as the (co)variance of species means [10,20]. The eigenvectors (d, table 1) of this matrix describe the direction in multivariate space in which most divergence has occurred. If behavioural syndromes have constrained the evolution of populations, the direction of most phenotypic divergence in average behaviour (d₁) will be correlated with shared subspaces identified by Krzanowski's common subspace analysis [20]. Here we calculated the vector correlation between d₁ and h_1:3. Non-zero correlations between d₁ and any of the shared subspaces would be consistent with the constraints hypothesis.

As with average behaviours, genetic variances may differ among populations even while populations share a genetic behavioural syndrome. We therefore asked whether genetic variances have been constrained by a conserved behavioural syndrome. Following Hine et al. [47], we calculated genetic covariance eigentensors (E, table 1). This approach calculates the variances and covariances of G matrices across populations followed by further eigen analysis, producing eigentensor matrices (E) and eigenvectors (e, table 1) describing in which dimensions Gs differ the most. If a conserved genetic behavioural syndrome, consistent with the constraints hypothesis, has affected the divergence of Gs among populations, we would expect correlations between the eigenvectors of eigentensors (e) and any shared subspaces (h_1:3). Put another way, if populations share genetic variation in the same dimension in which most of the genetic divergence occurred, this would be evidence that syndromes channel behavioural evolution along a line of least resistance.

For the above approaches, we followed the recommendations of Aguirre et al. [46] in that all tests were based on the full MCMC posterior distributions and null distributions for population comparisons were based on randomizations of breeding values. To compare whether eigenvectors were significantly aligned, we also generated a random distribution of vector correlations following McGlothlin et al. [20]. The critical values of vector correlations based on this distribution were 0.93 (p < 0.001), 0.85 (p < 0.01), 0.71 (p < 0.05) and 0.62 (p < 0.1). To assess the significance of eigenvalues of H and E against random expectations, we calculated the largest posterior quantiles for which these distributions did not overlap (electronic supplementary material, figures S2 and S3, respectively). This threshold serves as a Bayesian probability in favour of the observed distribution being generated by patterns other than chance (hereafter, P_mcmc). Because there are no clear-cut rules for interpreting these Bayesian probabilities, we provide the following scale to indicate how we interpreted support for inferences: P_mcmc < 0.7: poor evidence of difference compared to random expectations; P_mcmc > 0.8: moderate evidence of difference compared to random expectations; P_mcmc > 0.9 strong evidence of difference compared to random expectations; P_mcmc > 0.95: very strong evidence of difference compared to random expectations. Other reported probabilities were interpreted according to standard criteria.

To further assess support for the adaptive and constraints hypotheses, we also compared genetic correlations across generations. Genetic correlations due to selection-induced linkage disequilibrium are expected to decline across generations with random mating. Specifically, Conner [13] argued that with random mating and in the absence of physical linkage, the magnitude of genetic correlations should decrease by up to half every generation. Because of our breeding design, we were able to separately estimate phenotypic and genetic correlations among behaviours by generation. Here, while mating was restricted to be within populations, mating was random with regard to behaviour and we expect both genetic correlations (r_A) and phenotypic correlations (r_P) to decrease during the duration of the experiment under the adaptive hypothesis. We generated expected genetic and phenotypic average absolute correlations under these assumptions (electronic supplementary material, appendix S1) which we compared to the observed estimates. According to the constraints hypothesis, we expect correlations to remain stable across generations while under the adaptive hypothesis we expect them to degrade towards a correlation of zero.

Finally, we calculated ‘autonomy' following Hansen & Houle [48] ($\overline{a}$, table 1) to understand whether the constraint on future evolutionary trajectories was equivalent among populations. Autonomy provides an estimate of the ‘fraction of genetic variation that is independent of potentially constraining characters'[48] from complete independence ($\overline{a}=1$) to an absolute evolutionary constraint ($\overline{a}=0$).

3. Results

Behavioural syndromes were genetically conserved among populations. Based on Krzanowski's common subspace analysis (H; table 1) [46], the behavioural syndrome of G. integer was characterized by three dimensions of genetic covariance (h_1–3, table 1). These dimensions, and thus the overall syndrome, were shared among populations, as indicated by all Bayesian probabilities, P_mcmc, being less than 0.65 (electronic supplementary material, figure S1). The shared behavioural syndrome was composed of (i) genetic covariation between shelter emergence time and predator cue responsiveness (h₁; table 2); (ii) a genetic boldness-activity syndrome in which active individuals were more prone to ignore predator cues and were quicker to exit from their shelter (h₂, table 2) and (iii) genetic covariance between activity and shelter emergence (h₃; table 2). Each of these axes explained around one-third of the observed genetic variance (table 2).

Table 2.

Eigenvectors of phenotypic divergence (d), conserved genetic variation (h) and divergence in G (e). These vectors can be interpreted in the same manner as loadings from a principal components analysis. Traits legend: latency = latency to exit from the shelter, OF.Dist = distance travelled in the open-field test, UZ = number of unique zones explore in the open-field arena, OF.Var.Velo = variance in velocity in the open-field test, AP.Dist = distance travelled in the antipredator response test, AP.Lat.Mov = latency to initiate movement in the antipredator response test, AP.Var.Velo = variance in velocity in the antipredator response test. Loadings greater than 0.25 are shown in italics.

traits	d1	d2	h1	h2	h3	E1 (53%)	E2 (31%)
						e11	e21	e22
latency	−0.32	0.90	−0.31	0.86	0.47	0.63	0.08	0.77
OF.Dist	−0.80	−0.34	0.18	−0.37	0.88	−0.13	−0.79	0.42
UZ	−0.02	−0.06	0.02	−0.02	0.06	−0.01	−0.08	0.06
OF.Var.Velo	−0.09	−0.06	0.02	−0.02	0.07	−0.02	−0.10	0.06
AP.Dist	−0.48	−0.04	0.93	0.35	0.02	−0.74	−0.59	−0.45
AP.Lat.Mov	−0.05	0.24	−0.10	−0.01	0.02	0.16	0.07	0.15
AP.Var.Velo	−0.07	−0.03	0.05	0.02	0.01	−0.05	−0.05	−0.02
% variance explained	58.2	31.4	33.1	33.0	32.9	97.4	69.5	30.4

Following the demonstration of genetic conservation of behavioural syndromes, we determined whether genetic variation was primarily expressed in the same direction in multivariate space across populations (g_max alignment; table 1). Put another way, given the general conservation of behavioural syndrome structure at the genetic level, we tested whether populations expressed most genetic variation in the same combination of traits. Indeed, the g_maxs of the Aguila & Dunnigan and Socorro & Dunnigan populations were strongly correlated with each other (vector correlation r > 0.7, p < 0.05) (figure 2). Moreover, the g_maxs of each population were aligned with one of the shared axes (figure 2). This alignment confirmed that the orientation of genetic variation in multivariate space was conserved among the populations.

Despite the genetic conservation of behavioural syndrome structure, the examined populations have diverged in their multivariate behavioural averages (i.e. ‘D'; figure 3, table 1; electronic supplementary material, table S2) and in the magnitude of genetic variation present in each population (electronic supplementary material, figure S3). Importantly, however, the direction of divergence in both means and variances was aligned with the shared behavioural syndrome (e.g. r_d1,h3 = 0.85, p < 0.01; r_h1,e11 = 0.92, p < 0.01; electronic supplementary material, table S2). This alignment demonstrates that population divergence has been constrained by a shared behavioural syndrome.

Figure 3.

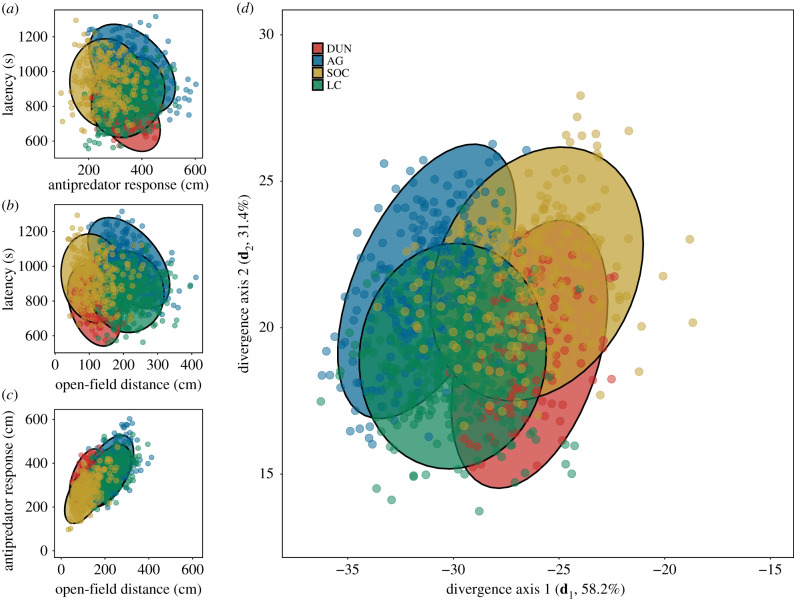
Evolutionary divergence in the structure of behavioural syndromes occurs along shared axes of genetic variation. (a–c) Correlations between pairs of traits that exhibit the greatest variation in divergence (electronic supplementary material, table S2). Points represent breeding values for each individual within a population centred around the population mean for that trait. More than 50% of divergence was in latency to emerge from shelter by antipredator response activity. (d) Population-specific divergence in average behaviours. Population-specific G matrices were visualized by transforming estimated breeding values for each trait based on the divergence among populations. Ellipses represent the 95% confidence ellipses for each population centred at the multivariate species mean (DUN: Dunnigan, CA; AG: Aguila, AZ; SOC: Socorro, NM; LC: Las Cruces, NM). (Online version in colour.)

Behavioural syndromes emerging from either the adaptive or constraints hypotheses are expected to respond differently to random mating. Specifically, under the adaptive hypothesis, genetic correlations are expected to erode by 50% every generation. Because we mated individuals at random, we were able to compare the observed average genetic and phenotypic correlations (r_A and r_P) with their expected values under the adaptive hypothesis (see electronic supplementary material, appendix S1 for details). As predicted by the constraints hypothesis, average genetic and phenotypic correlations remained stable over the course of three successive laboratory generations (posterior mean and 95% credible intervals; r_{A Observed} F₁ = 0.36 [0.23; 0.52], r_{A Observed} F₂ = 0.38 [0.23; 0.53]; figure 4).

Figure 4.

(a) Additive genetic (r_A) and (b) phenotypic correlations (r_P) remained stable over the course of three successive generations compared to theoretical expectations based on selection-induced linkage disequilibrium and random mating (r_{A observed} = 0.38, r_{A expected} = 0.18, P_mcmc for difference from expectations under selection-induced linkage disequilibrium greater than 0.85; r_{P observed} F₀ = 0.32, r_{P observed} F₂ = 0.33, r_{P expected} F₀ = 0.35, r_{P expected} F₂ = 0.26, P_mcmc F₂ > 0.80). Error bars correspond to 95% credibility intervals around the posterior mean. (Online version in colour.)

Finally, for each population, we calculated autonomy (table 1), which estimates the degree of constraint on evolutionary outcomes imposed by the genetic architecture connecting traits. Autonomy varies between 0 and 1, with higher values indicating greater potential for independent evolution. Autonomy varied between 0.47 and 0.61 with no marked difference among populations (DUN: $\overline{a}=0.48\hspace{0.17em}[0.31;0.68]$, SOC: $\overline{a}=0.47\hspace{0.17em}[0.32;0.67]$, AG: $\overline{a}=0.60\hspace{0.17em}[0.44;0.78]$, LC: $\overline{a}=0.61\hspace{0.17em}[0.43;0.76]$, all populations combined: $\overline{a}=0.57\hspace{0.17em}[0.43;0.70]$). This suggests that the constraining effect of behavioural syndromes is likely to persist over future generations.

4. Discussion

Three key results demonstrate conservation of behavioural syndromes at the genetic level despite differences among populations in average behaviour, providing strong support for the constraints hypothesis. This support for the constraints hypothesis is unexpected given that a previous study with stickleback [14] found that two populations differed in the magnitude of heritabilities and genetic correlations between two behaviours providing support for the adaptive hypothesis. Here, the conservation of behavioural syndrome structure has also had the effect of channelling population divergence. Our results therefore suggest that studying a broader suite of behavioural traits may reveal evolutionary constraints not apparent from pair-wise correlations.

Our first major result supporting the constraints hypothesis was that the genetic variation among the four populations was shared along three dimensions. These dimensions describe the shared genetic structure of the species' behavioural syndromes and demonstrate that the orientation of genetic variation was conserved among populations. The overall behavioural syndrome consisted of a boldness-activity dimension (h₂; table 2) frequently described in the literature. This dimension genetically links activity, exploration and risk-prone behaviours. This dimension has been described at the phenotypic level [49,50] but demonstrations at the genetic level are rare (see Bell [14] for one example). The other conserved dimension (h₁ and h₃) represents potential trade-offs between risk management strategies, in which individuals either compensate for risk during foraging by being less prone to resume activity when threatened (h₃; table 2), or take risks in one context (not moving away from a predator cue) while avoiding risk in another (taking longer to emerge from shelter) (h₁; table 2). Alternatively, dimension h₁ might indicate that individuals with long latencies are less active. As a result, these individuals may encounter fewer predator cues resulting in weaker antipredator responses.

Our second major result supporting the constraints hypothesis was that the g_maxs of the Aguila & Dunnigan and Socorro & Dunnigan populations were strongly correlated, and all g_maxs were aligned with the shared behavioural syndrome. This validates that the behavioural syndrome structure is shared among populations. Schluter [10] demonstrated that morphological divergence among several pairs of populations and species of vertebrates is constrained by g_max. Specifically, evolutionary divergence was greatest when populations and species shared a common g_max, and there was directional selection for morphological trait combinations in this same direction in phenotypic space [10]. Besides g_max being conserved, divergence in both average behaviour and genetic (co)variance among the four populations was aligned with g_max.. This demonstrates that behavioural syndromes affect population divergence in a manner similar to that observed for morphology.

Our third result in support of the constraints hypothesis stems from the prediction that, under the adaptive hypothesis, genetic correlations are expected to decrease by about 50% each generation due to the effects of recombination [13]. This prediction assumes an absence of genetic linkage and random mating (electronic supplementary material, appendix S1). However, genetic linkage sufficiently strong to resist recombination is also consistent with the constraints hypothesis—see, for example, the effects of supergenes [51,52]—and so we consider this assumption appropriate. In contrast with this prediction of declining correlations, we found that the average genetic correlation did not change across generations (figure 4). Similarly, phenotypic correlations did not decrease according to predictions (figure 4). Because we were not able to study replicate lines under random mating, this finding is not conclusive on its own. Instead the result is one additional line of evidence consistent with the constraints hypothesis and in contradiction of the adaptive hypothesis.

Importantly, the first two results—shared dimensions of genetic variation and correlated g_maxs—could also be observed under the adaptive hypothesis if the selective pressures each of the populations experienced were the same. We consider this unlikely for three reasons. First, the degree of geographic separation among populations was extensive, totalling more than 1500 km in some cases (figure 2). This degree of geographic separation makes it unlikely that the populations experienced the exact same selective regime. Moreover, climate (electronic supplementary material, table S5) as well as predation and parasitism regimes are highly variable among the populations [21]. Second, if similarity in selection regimes was the driving force behind these converging patterns of genetic covariance, we would expect the geographically closest populations to have the greatest similarity in g_max. This was not the case and, in fact, g_max was most similar among populations that were geographically most separated (figure 2). Finally, our third main result directly contradicts the adaptive hypothesis: if trait correlations arise due to the adaptive hypothesis and selection-induced linkage disequilibrium, they are expected to rapidly degrade under random mating [11,13]. In direct contradiction to this expectation we observed that correlations did not decrease across generations (figure 4). Put another way, our first two results—which showed that the multivariate composition of behavioural syndromes was shared among populations—are consistent with the predictions of the constraints hypothesis. Next, our third result—the maintenance of behavioural correlations despite random mating—demonstrates the failure of predictions made by the adaptive hypothesis.

Our results indicate that the conserved genetic architecture of behavioural syndromes quantitatively constrained evolutionary trajectories [53] and that syndromes have limited population divergence. This quantitative constraint and resulting limitation on divergence is also expected to persist into the future due to the behavioural syndrome structure imposed by each population's G matrix. Based on the observed G matrices, we found similar degrees of autonomy [48] among populations ranging from 0.47 to 0.61, a stronger constraint than observed for life-history or morphological traits [9]. These autonomies indicate that behaviours will rarely evolve independently and the observed genetic behavioural syndrome will affect future evolution.

Despite the conservation of behavioural syndrome structure at the genetic level across populations, G. integer populations did exhibit divergence in both mean behaviours and magnitudes of genetic variation present in each population. The divergence of both means and variances was strongly aligned with the shape of the shared behavioural syndrome, demonstrating that the syndrome itself was channelling the evolutionary divergence of the populations (electronic supplementary material, table S2). The divergence in means was most strongly related to differences in latency and distance moved in both the open-field and antipredator assays (table 2). Specifically, the Dunnigan, CA and Aguila, AZ populations exhibited the greatest differences in average behaviours (figure 3). Similarly, the divergence in magnitude of genetic variation was driven by the three easternmost populations having less genetic variation than the Dunnigan, CA population (electronic supplementary material, figure S1). Whether this represents a loss of variation due to selection, stochastic effects on the three eastern populations, or the accumulation of variation for the western population is not currently clear.

Throughout we have referred to the adaptive and constraints hypothesis as competing hypotheses for the expression of behavioural syndromes. However, we note two caveats: First, within a Tinbergian framework [54], these hypotheses are not addressing questions at the same level. The constraints hypothesis is a proximate causation question, reduces to a question about molecular mechanisms and is agnostic regarding selection. By contrast, the adaptive hypothesis is an ultimate question and would be assessed by determining the alignment between G and selection gradients. By contrast, in the quantitative genetics literature, selection-induced linkage disequilibrium and molecular mechanisms such as pleiotropy are considered competing explanations (e.g. [11]). As a second caveat, it is important to note that the hypotheses are not strictly mutually exclusive [12,55]. It is possible that some portion of an estimated genetic covariance might stem from pleiotropy while some other portion stems from linkage disequilibrium. Nonetheless, our results consistently supported the predictions of the constraints hypothesis across several lines of evidence.

The surprising degree of shared genetic variation in behavioural syndrome reported here suggests an unrecognized and important role for behavioural syndromes in the evolution of populations. Behaviours such as those measured here—exploratory behaviours and responses to predation threat—are frequently assumed to have been under selection and that their responses to selection have been unconstrained. By contrast, we have shown that the genetic contribution to behavioural expression is conserved, that populations share evolutionary fates, and that conserved behavioural covariation may be a driver of population divergence and perhaps even speciation.

Data accessibility

All relevant data are archived at Dryad Digital Repository [56]. All relevant code and analyses are available at https://github.com/DochtermannLab/G-PopComparison.

Authors' contributions

N.A.D. and A.H. conceived the project and supervised the gathering of data; R.R supervised and conducted behavioural trials and analysed the data. N.A.D., A.H. and R.R. wrote the manuscript.

Competing interests

We declare we have no competing interests.

Funding

This work was supported by US NSF IOS grant nos. 1557951 and 1558069 to N.A.D. and A.H. respectively.