Tractable calculation of the Green’s tensor for shear wave propagation in an incompressible, transversely isotropic material

Abstract

Assessing material properties from observations of shear wave propagation following an acoustic radiation force impulse (ARFI) excitation is difficult in anisotropic materials because of the complex relations among the propagation direction, shear wave polarizations, and material symmetries. In this paper, we describe a method to calculate shear wave signals using Green’s tensor methods in an incompressible, transversely isotropic (TI) material characterized by three material parameters. The Green’s tensor is written as the sum of an analytic expression for the SH propagation mode, and an integral expression for the SV propagation mode that can be evaluated by interpolation within precomputed integral functions with an efficiency comparable to the evaluation of a closed-form expression. By using parametrized integral functions, the number of requried numerical integrations is reduced by a factor of 10² − 10⁹ depending on the specific problem under consideration. Results are presented for the case of a point source positioned at the origin and a tall Gaussian source similar to an ARFI excitation. For an experimental configuration with a tilted material symmetry axis, results show that shear wave signals exhibit structures that are sufficiently complex to allow measurement of all three material parameters that characterize an incompressible, TI material.

1. Introduction

Elastic properties of materials can be measured by observing shear wave propagation following an acoustic radiation force impulse (ARFI) excitation and relating the propagation speed to a model of the material. For example, linear, elastic, homogeneous, and isotropic materials can be characterized using two elasticity constants such as the Lamé parameters λ and μ. For nearly incompressible materials, including many soft biological tissues, these parameters differ by a factor on the order of 10⁶, and the corresponding difference in longitudinal and shear wave speeds is on the order of 10³. Typically, ultrasonic tracking methods observe only shear wave propagation and calculate the shear modulus μ from the wave speed c and material density ρ by the relation (Graff 1991, Lai et al 2010)

$$\mu =\rho c^2.$$ (1)

The relation between wave speed and material properties is more complicated in anisotropic materials because of the complex dependence of the velocity relative to the propagation direction, material symmetries, and wave polarizations. For example, in a linear, elastic, transversely isotropic (TI) material, a symmetry axis exists and the material can be characterized by five elasticity constants (Lai et al 2010). Skeletal muscle is an example of a TI material with the symmetry axis defined by the direction of the muscle fibers (Gennisson et al 2010, Wang et al 2013). Stretched or compressed polyvinyl alcohol phantoms also have TI symmetry with the symmetry axis determined by the axis of deformation (Gennisson et al 2007, Chatelin et al 2014, Urban et al 2015). Measurements of shear wave propagation in these materials are typically performed using the experimental geometry shown in figure 1(a) (see, also, figure 2 of Chatelin et al (2014)) and observe propagation in the horizontal (Z = 0) plane in the $\widehat{n}$ direction at an angle θ relative to the symmetry axis. These measurements observe the SH propagation mode with displacements in the $\widehat{Z}$ direction so that the wave polarization is perpendicular to the Z = 0 plane. The phase velocity v_SH (θ) for this propagation mode is given by the relation (Wang et al 2013)

$$\rho v_{SH}^2(\theta )={\mu }_L{\cos }^2\theta +{\mu }_T{\sin }^2\theta$$ (2)

where μ_L and μ_T are shear moduli for wave propagation in the longitudinal and transverse directions relative to the material symmetry axis. The corresponding group velocity V(θ) has an elliptical shape (Wang et al 2013),

$$\rho V^2(\theta )=\frac{{\mu }_L{\mu }_T}{{\mu }_L{\sin }^2\theta +{\mu }_T{\cos }^2\theta }.$$ (3)

Figure 1.

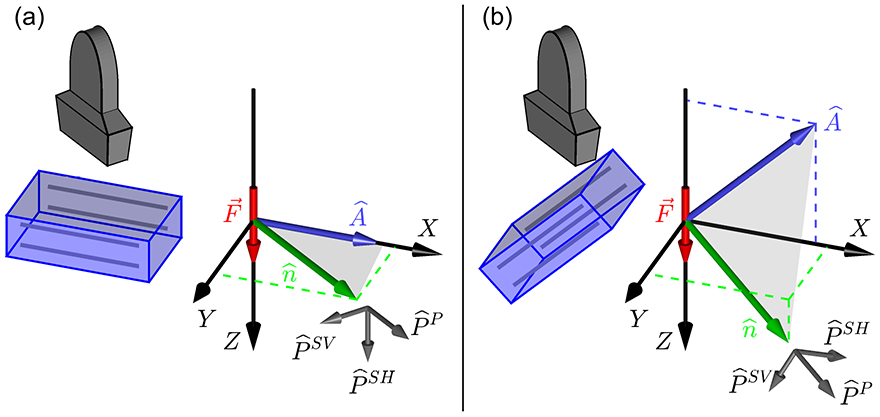
(a) Experimental configuration commonly used for investigations of shear wave propagation in an incompressible, TI material (see, also, figure 2 of Chatelin et al 2014). The left side shows a sketch of a linear ultrasound transducer and transversely isotropic material with the material symmetry indicated by the gray lines respresenting, for example, skeletal muscle fibers. The transducer can rotate about a vertical axis to observe shear waves for a range of propagation directions. The experimental X, Y, Z coordinate system shows the ARFI excitation force $\overrightarrow{F}$ along the Z axis and the material symmetry axis $\widehat{A}$ and propagation direction $\widehat{n}$ in the X − Y (Z = 0) plane. Polarization vectors for the SH (slow shear), SV (fast shear), and P (longitudinal) propagation modes are defined relative to the $\widehat{A}$ − $\widehat{n}$ plane shown in gray. Ultrasonic tracking measures the Z component of the shear wave displacement signal and is sensitive only to the SH propagation mode. (b) A more complicated experimental configuration in which the material symmetry axis $\widehat{A}$ and propagation direction $\widehat{n}$ are not restricted to the X − Y plane. Measurements of the Z component of shear wave displacement are sensitive to both the SH and SV propagation modes.

Experimental observations of shear wave propagation typically measure the group shear wave speed and determine μ_L and μ_T from the axes of the ellipse.

The relation between shear wave speed and propagation direction is even more complicated for experimental configurations such as figure 1(b) where the material symmetry axis is not oriented perpendicular to the excitation axis, or where waves are tracked in three dimensions including axial positions above and below the Z = 0 plane. For example, using finite element simulations, Rouze et al (2013) observed complicated shear wave signals for an excitation and tracking configuration with a symmetry axis tilted at an angle of 45° relative to the horizontal plane. The advantage of these geometries is that they allow experimental measurements of both the SH and SV propagation modes and are sensitive to more material properties than can be measured from just the SH propagation mode. However, analysis of these shear wave signals is difficult because the group propagation speeds do not reduce to simple expressions such as (3). Instead, this analysis is typically performed by calculating the shear wave signals using either finite element simulations (Palmeri et al 2005, Rouze et al 2013) or Green’s tensor calculations (Bercoff 2004, Chatelin 2015) and comparing the calculated and measured signals.

In this paper, we use Green’s tensor calculations to model shear wave propagation in an incompressible, TI material. This process calculates the shear wave signal $\overrightarrow{u}$(${\overrightarrow{r}}_{obs}$, t) at an observation position ${\overrightarrow{r}}_{obs}$ and time t by dividing the excitation force $\overrightarrow{f}$(${\overrightarrow{r}}_s$, t_s) into spatial and temporal source voxels s and summing the contributions from each voxel. The Green’s tensor G_in (${\overrightarrow{r}}_{obs}$ − ${\overrightarrow{r}}_s$, t − t_s) gives the relative contribution to the signal from each source voxel. Often, these calculations are performed in the temporal frequency domain with angular frequency ω = 2π f so that, assuming the force can be factored into a spatial function $\overrightarrow{f}$(${\overrightarrow{r}}_s$) and temporal window W(t), components u_i(${\overrightarrow{r}}_{obs}$, ω) of the shear wave signal can be written as

$$u_i({\overrightarrow{r}}_{obs},\omega )=\sum _s{G}_{in}(\overrightarrow{r},\omega )f_n({\overrightarrow{r}}_s)W(\omega )$$ (4)

where $\overrightarrow{r}={\overrightarrow{r}}_{obs}-{\overrightarrow{r}}_s$ is the relative position between the source and observation positions, the indices i and n take on the values 1, 2, and 3 corresponding to the x, y, and z vector components, and summation over the component index n of the force is implied.

One difficulty with Green’s tensor calculations of shear wave signals using (4) is that, for typical calculations, G_in($\overrightarrow{r}$, ω) must be evaluated for 10⁸ − 10¹⁵ combinations of r_s, r_obs, and ω. Thus, these calculations have been used primarily for linear, isotropic materials (Bercoff 2004, Rouze 2018) where the Green’s tensor is given by a closed-form expression (Aki and Richards 2002, Kausel 2006). Unfortunately, for more complicated materials, closed-form expressions for the Green’s tensor are known only for a few special-case materials (Vavryčuk 2001, 2007), and are not known for the case of a TI material, or an incompressible TI material. Instead, the Green’s tensor can be evaluated using integral expressions (Willis 1980, Wang and Achenbach 1995), including the specific case of a TI material (Gridin 2000). However, these expressions must be evaluated using numerical integration, and because the integrand in these expressions can oscillate rapidly, it is necessary to sample the integrand on a dense mesh. Thus, these calculations are too slow to be practical for applications involving a large number of combinations of r_s, r_obs, and ω.

In this paper, we describe a tractable method to perform integral calculations of the Green’s tensor for an incompressible, TI material. This process allows the Green’s tensor to be expressed as the sum of two terms, each given by the product of multiplicative factors and a relatively simple, parametrized integral. Numerical integration can be used to precompute the integral factors. Then, when calculating the shear wave signal using the sum (4), interpolation can be used to evaluate the integral factors efficiently. This procedure allows the Green’s tensor to be evaluated with an efficiency comparable to the evaluation of a closed-form expression. Furthermore, the number of numerical integrations required to precompute the integral factors is typically reduced by a factor of 10² − 10⁹ depending on the number of combinations of r_s, r_obs, and ω that would be required if numerical calculations were used to evaluate the Green’s tensor for each combination. This reduction in computational complexity is the key factor that allows tractable calculation of shear wave displacements using Green’s tensor methods.

2. Background

2.1. Incompressible, transversely isotropic (TI) materials

In Sections 2 and 3, we use a Cartesian x, y, z coordinate system such as shown in figure 2 to model the material, wave propagation, and Green’s tensor. This coordinate system is distinct from the X, Y, Z coordinate system used in figure 1 to describe the experimental configuration. The calculation of shear wave signals for a specific experimental configuration is described in Section 4.2.

Figure 2.

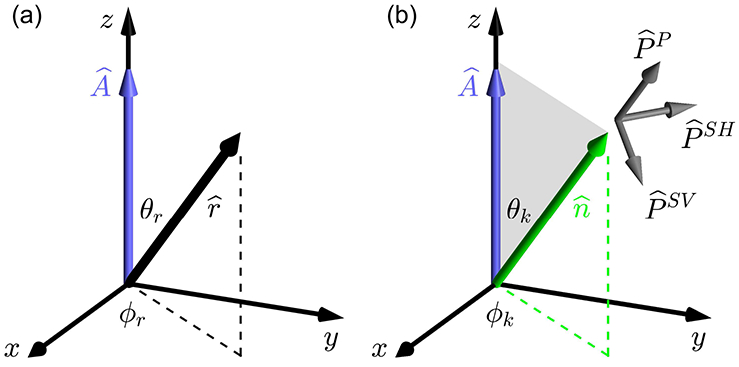
Coordinate system with x, y, and z axes used for the analysis of the material, wave propagation, and Green’s tensor in Sections 2 and 3. This coordinate system is distinct from the experimental XYZ coordinate system in figure 1. The relation between the xyz and XYZ coordinate systems is described in Section 4.2. (a) The xyz coordinate system is oriented so that the z axis is aligned with the material symmetry axis $\widehat{A}$, and the position vector $\overrightarrow{r}$ is specified by the angles θ_r and ϕ_r. To simplify the analysis in Section 3.1, the axes are rotated so that ϕ_r = 0. (b) Wave propagation is in the $\widehat{n}$ direction with wave vector $\overrightarrow{k}$ = k$\widehat{n}$ at an angle θ_k relative to the material symmetry axis $\widehat{A}$. The polarization vectors are defined relative to the $\widehat{A}$ − $\widehat{n}$ plane shown in gray with the SH polarization perpendicular to the $\widehat{A}$ − $\widehat{n}$ plane, and the SV and P polarizations in the $\widehat{A}$ − $\widehat{n}$ plane. Explicit expressions for polarization vectors are given in terms of θ_k and ϕ_k in (24).

In the limit of small displacements, the stress-strain relationship in an anistropic material is linear and can be described by a generalized Hooke’s law as

$${\sigma }_{ij}=c_{ijkl}{\epsilon }_{kl}$$ (5)

where σ_ij and ε_kl are components of the time-dependent stress and strain tensors, respectively, and c_ijkl are the components of a time-independent, fourth-order stiffness tensor. Each index can assume the value 1, 2, or 3, and summation over repeated indices is implied. Symmetries of the stress and strain tensors and the existence of a strain energy allow the stiffness tensor to be expressed in terms of 21 independent elements (Lai et al 2010). For the case of a TI material with symmetry axis $\widehat{A}$, rotation and reflection symmetries allow the stiffness tensor to be expressed in terms of five independent elements. By orienting the coordinate system so that $\widehat{z}=\widehat{A}$, the stress strain relation (5) can be expressed using Voigt notation as a matrix product with the stiffness matrix C (Lai et al 2010),

$$\left(\begin{array}{c}\hfill {\sigma }_{11}\hfill \\ \hfill {\sigma }_{22}\hfill \\ \hfill {\sigma }_{33}\hfill \\ \hfill {\sigma }_{23}\hfill \\ \hfill {\sigma }_{31}\hfill \\ \hfill {\sigma }_{12}\hfill \end{array}\right)=\left(\begin{array}{cccccc}\hfill C_{11}\hfill & \hfill C_{11}-2C_{66}\hfill & \hfill C_{13}\hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill \\ \hfill C_{11}-2C_{66}\hfill & \hfill C_{11}\hfill & \hfill C_{13}\hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill \\ \hfill C_{13}\hfill & \hfill C_{13}\hfill & \hfill C_{33}\hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill \\ \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill C_{44}\hfill & \hfill \hfill & \hfill \hfill \\ \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill C_{44}\hfill & \hfill \hfill \\ \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill C_{66}\hfill \end{array}\right)\left(\begin{array}{c}\hfill {\epsilon }_{11}\hfill \\ \hfill {\epsilon }_{22}\hfill \\ \hfill {\epsilon }_{33}\hfill \\ \hfill 2{\epsilon }_{23}\hfill \\ \hfill 2{\epsilon }_{31}\hfill \\ \hfill 2{\epsilon }_{12}\hfill \end{array}\right)$$ (6)

where missing elements are zero.

The stress-strain relation (6) can also be written in terms of the compliance matrix S = C⁻¹ using Young’s moduli E_L and E_T, shear moduli μ_L and μ_T, and Poisson’s ratios ν_LT and ν_TT where the longitudinal (L) and transverse (T) directions are defined relative to the material symmetry axis (Lai et al 2010),

$$\left(\begin{array}{c}\hfill {\epsilon }_{11}\hfill \\ \hfill {\epsilon }_{22}\hfill \\ \hfill {\epsilon }_{33}\hfill \\ \hfill 2{\epsilon }_{23}\hfill \\ \hfill 2{\epsilon }_{31}\hfill \\ \hfill 2{\epsilon }_{12}\hfill \end{array}\right)=\left(\begin{array}{cccccc}\hfill 1∕E_T\hfill & \hfill -{\nu }_{TT}∕E_T\hfill & \hfill -{\nu }_{LT}∕E_L\hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill \\ \hfill -{\nu }_{TT}∕E_T\hfill & \hfill 1∕E_T\hfill & \hfill -{\nu }_{LT}∕E_L\hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill \\ \hfill -{\nu }_{LT}∕E_L\hfill & \hfill -{\nu }_{LT}∕E_L\hfill & \hfill 1∕E_L\hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill \\ \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill 1∕{\mu }_L\hfill & \hfill \hfill & \hfill \hfill \\ \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill 1∕{\mu }_L\hfill & \hfill \hfill \\ \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill 1∕{\mu }_T\hfill \end{array}\right)\left(\begin{array}{c}\hfill {\sigma }_{11}\hfill \\ \hfill {\sigma }_{22}\hfill \\ \hfill {\sigma }_{33}\hfill \\ \hfill {\sigma }_{23}\hfill \\ \hfill {\sigma }_{31}\hfill \\ \hfill {\sigma }_{12}\hfill \end{array}\right)$$ (7)

with the relation

$${\mu }_T=\frac{E_T}{2(1+{\nu }_{TT})}.$$ (8)

Explicit relations for the elements C₁₁, C₁₃, C₃₃, C₄₄, and C₆₆ in (6) can be expressed in terms of E_L, E_T, μ_L, μ_T, ν_LT, and μ_TT through the relation S = C⁻¹,

$$\begin{gathered} C_{11}=\frac{E_T}{1+{\nu }_{TT}}\frac{1-{\nu }_{LT}^2{E}_T∕E_L}{1-{\nu }_{TT}-2{\nu }_{LT}^2{E}_T∕E_L},C_{44}={\mu }_L,C_{66}={\mu }_T \\ {C}_{13}=\frac{E_T{\nu }_{LT}}{1-{\nu }_{TT}-2{\nu }_{LT}^2{E}_T∕E_L},\text{and}{C}_{33}=\frac{E_L(1-{\nu }_{TT})}{1-{\nu }_{TT}-2{\nu }_{LT}^2{E}_T∕E_L}. \end{gathered}$$ (9)

For the case of an incompressible TI material, the fractional volume change, or dilation, of an infinitesimal volume subjected to stresses is zero. The dilation is given by the trace of the strain tensor (Lai et al 2010) so that, using (7)

$$\begin{gathered} \text{Tr}\{ϵ\}=\frac{1}{E_T}\left(1-{\nu }_{TT}-{\nu }_{LT}\frac{E_T}{E_L}\right)({\sigma }_{11}+{\sigma }_{22})+\frac{1}{E_L}(1-2{\nu }_{LT}){\sigma }_{33} \\ =0. \end{gathered}$$ (10)

Both terms in this expression must be zero, and the Poisson ratios for an incompressible TI material are given by

$${\nu }_{LT}=\frac{1}{2}\text{and}{\nu }_{TT}=1-\frac{E_T}{2E_L}.$$ (11)

Thus, three material parameters are required to characterize an incompressible, TI material. In this study, we use the parameters μ_L, μ_T, and E_T/E_L as used previously by Rouze et al (2013). However, with the relations (8) and (11), these parameters are not unique, and any three independent combinations of the parameters μ_L, μ_T, E_T, and E_L can be used. In particular, muscle strength, characterized by the longitudinal Young’s modulus E_L, can be determined from the three material parameters.

In addition, using the Poisson ratios (11) in expressions (9) indicates that the C₁₁, C₃₃, and C₁₃ elements of the stiffness matrix diverge in the limit of an incompressible, TI material. However, differences between pairs of these elements remain finite,

$$\begin{gathered} C_{11}-C_{13}\to \frac{{\mu }_T}{2}\left(1+4\frac{E_L}{E_T}\right),C_{11}-C_{33}\to {\mu }_T, \\ \text{and}{C}_{13}-C_{33}\to \frac{{\mu }_T}{2}\left(1-4\frac{E_L}{E_T}\right). \end{gathered}$$ (12)

As indicated in figure 1, wave propagation in a TI material can be described in terms of the P (longitudinal), SH (slow shear), and SV (fast shear) propagation modes identified by their polarization relative to the propagation direction $\widehat{n}$ and material symmetry axis $\widehat{A}$ (Tsvankin 2012, Carcione 2015). Polarization of the P mode is quasi-longitudinal and corresponds to the acoustic wave. The SH propagation mode corresponds to shear wave motion with a purely transverse polarization perpendicular to the to the $\widehat{A}$ − $\widehat{n}$ plane. The SV propagation mode has shear wave propagation with a quasi-transverse polarization in the $\widehat{A}$ − $\widehat{n}$ plane. Note that Rouze et al (2013) refer to these modes as the QL, PT, and QT modes, respectively. For plane wave propagation in a direction oriented at an angle θ relative to the symmetry axis, the phase velocity v_SH of the SH propagation mode is given by (2). In the limit of an incompressible TI material, the polarization of quasi-longitudinal P mode becomes purely longitudinal, and the propagation velocty v_P diverges. Similarly, for an incompressible TI material, the polarization of the quasi-transverse SV mode is purely transverse, and the propagation velocty v_SV is given by (Chadwick 1993, Papazoglou et al 2006, Rouze et al 2013)

$$\rho v_{SV}^2={\mu }_L{\cos }^{2}2\theta +{\mu }_T\frac{E_L}{E_T}{\sin }^{2}2\theta ={\mu }_L+4\left(\frac{E_L}{E_T}{\mu }_T-{\mu }_L\right){\sin }^2\theta {\cos }^2\theta .$$ (13)

Thus, all three parameters required to characterize an incompressible TI material can be measured by observing SH and SV shear wave propagation in the material.

2.2. Green’s tensors for constrained TI materials

Chatelin et al (2015) analyzed their measurements of shear wave propagation in a transversely isotropic material using the “Anisotropy III” special-case Green’s tensor from Vavryčuk (2001) and Vavryčuk (2007). The stiffness matrix for this case is given by expression (25) of Vavryčuk (2001) and also in the text just above expression (B3) of Vavryčuk (2007). This expression indicates that the stiffness matrix for the special-case Green’s tensor is similar to the stiffness matrix (6) for a general TI material with two additional assumptions,

$$C_{33}=C_{11}\text{and}{C}_{13}=C_{11}-2C_{44}.$$ (14)

The explicit expression for the Green’s tensor in this special case is given by expression (B3) of Vavryčuk (2007) and expresion (5) of Chatelin et al (2015) and will not be reproduced here. Note that the expressions from Vavryčuk (2007) and Chatelin et al (2015) are presented for the case of viscoelastic materials with complex, frequency-dependent moduli. We do not consider viscoelastic materials in this paper and will assume the moduli are real. However, because our development is presented in the temporal frequency domain, it can easily be extended to the case of viscoelastic materials by considering complex, frequency-dependent moduli.

The two constraints (14) on elements of the stiffness matrix imply that three parameters characterize the TI material for this special case. Chatelin et al (2015) analyzed their experimental measurements using the acoustic wave speed and the two wave speeds for shear wave propagation along and across the material symmetry axis. These parameters were sufficient to analyze the wave speeds for shear wave propagation in their experimental setup where the material symmetry axis was oriented perpendicular to the excitation axis, and only the SH propagation mode was observed, see figure 1(a) or figure 2 of Chatelin et al (2014). However, this analysis is not sensitive to all three material properties that are needed to characterize shear wave propagation in an incompressible, TI material because these measurements are not sensitive to the ratio E_T/E_L in the phase velocity for the SV propagation mode in (13). Thus, in the incompressible limit, the Green’s tensor used by Chatelin et al (2015) does not fully characterize an incompressible, TI material specified by three independent parameters.

In addition to the special-case Green’s tensors described by Vavryčuk (2007), several studies (Payton 1975, 1983, Chadwick and Norris 1990, Burridge et al 1993) have investigated the Green’s tensor for a TI material described by a stiffness matrix with four independent parameters and the constraint

$$C_{44}=\frac{C_{11}{C}_{33}-C_{13}^2}{C_{11}+C_{33}+2C_{13}}.$$ (15)

For the case of an incompressible, TI material considered in this study, this relation can be simplified by substituting the relations (9) for each term C_ij and evaluating the result using the Poisson ratios (11) for an incompressible, TI material. The result of this process demonstates that the constraint (15) is equivalent to the relation

$$\frac{{\mu }_T}{{\mu }_L}=\frac{E_T}{E_L}.$$ (16)

Thus, the ratio E_T/E_L is not an independent material parameter, and the expression for the Green’s tensor based on the relation (15) cannot fully describe shear wave propagation in an incompressible, TI material.

3. Green’s tensor for an incompressible, TI material

3.1. Integral expression for the Green’s tensor

Assuming a stress-strain relation of the form (5), the equation of motion for the Green’s tensor G_in($\overrightarrow{r}$, t) for the i^th component of displacement due to a spatial and temporal Dirac delta distribution in the x_n direction is given by (Kim et al 1994, Červený 2001)

$$-c_{ijkl}\frac{{\partial }^2}{\partial x_j\partial x_l}{G}_{kn}(\overrightarrow{r},t)+\rho \frac{{\partial }^2}{\partial t^2}{G}_{in}(\overrightarrow{r},t)={\delta }^3(\overrightarrow{r})\delta (t){\delta }_{in}$$ (17)

where δ_in is the Kronecker delta symbol.

In this paper we define the sign convention for the Fourier transform so that the forward transform from the coordinate to frequency domain is given by the relation

$$f(\omega )={\int }_{-\infty }^{\infty }f(t)e^{-i\omega t}dt$$ (18)

and the inverse transform is given by

$$f(t)=\frac{1}{2\pi }{\int }_{-\infty }^{\infty }f(\omega )e^{+i\omega t}d\omega .$$ (19)

This sign convention agrees with the MATLAB convention for the forward and reverse transforms. Also note that we use the symbol i to denote $\sqrt{-1}$ as in (18) and (19), and as an index as in (5). The specific meaning should be clear from the context.

Calculating the 4-dimensional Fourier transform of (17) with spatial frequency $\overrightarrow{k}$ and temporal frequency ω = 2πf gives

$$(c_{ijkl}{k}_j{k}_l-\rho {\omega }^2{\delta }_{ik})G_{kn}(\overrightarrow{k},\omega )=L_{ik}{G}_{kn}(\overrightarrow{k},\omega )={\delta }_{in}$$ (20)

where the matrix L has elements L_ik = c_ijklk_j k_l − ρω²δ_ik. This expression can be solved for G_in ($\overrightarrow{r}$, ω) by multiplying by L⁻¹ and calculating the inverse Fourier transform,

$$G_{in}(\overrightarrow{r},\omega )=\frac{1}{8{\pi }^3}{\int \int \int }_{}(L^{-1}{)}_{in}{e}^{i\overrightarrow{k}\cdot \overrightarrow{r}}{d}^3\overrightarrow{k}.$$ (21)

The inverse matrix L⁻¹ in (21) can be expressed as the sum of three terms using the eigenvectors ${\widehat{P}}^N$ and eigenvalues λ_N of L,

$$(L^{-1}{)}_{in}=\sum _{N=1}^3\frac{{\widehat{P}}_i^N{\widehat{P}}_n^N}{{\lambda }_N}.$$ (22)

The eigenvectors ${\widehat{P}}^N$ in (22) correspond to the polarization vectors for the SH, SV, and P propagation modes. As shown in figure 2(b), for plane wave propagation with wave vector $\overrightarrow{k}$ = $k\widehat{n}$, the propagation direction is given by

$$\widehat{n}=\widehat{k}=\left(\begin{array}{c}\hfill \sin {\theta }_k\cos {\varphi }_k\hfill \\ \hfill \sin {\theta }_k\sin {\varphi }_k\hfill \\ \hfill \cos {\theta }_k\hfill \end{array}\right)$$ (23)

and the polarization vectors are given by

$${\widehat{P}}^{SH}=\left(\begin{array}{c}\hfill -\sin {\varphi }_k\hfill \\ \hfill \cos {\varphi }_k\hfill \\ \hfill 0\hfill \end{array}\right),{\widehat{P}}^{SV}=\left(\begin{array}{c}\hfill \cos {\theta }_k\cos {\varphi }_k\hfill \\ \hfill \cos {\theta }_k\sin {\varphi }_k\hfill \\ \hfill -\sin {\theta }_k\hfill \end{array}\right),\text{and}{\widehat{P}}^P=\left(\begin{array}{c}\hfill \sin {\theta }_k\cos {\varphi }_k\hfill \\ \hfill \sin {\theta }_k\sin {\varphi }_k\hfill \\ \hfill \cos {\theta }_k\hfill \end{array}\right).$$ (24)

The eigenvalues λ_N of L are related to the phase velocities of the SH, SV, and P propagation modes. For the case of an incompressible, TI material, the phase velocity v_P diverges, and λ_SH and λ_SV are given by

$${\lambda }_N=\rho k^2{v}_N^2-\rho {\omega }^2$$ (25)

with v_SH and v_SV given by (2) and (13), respectively. Here, we neglect the P propagation mode in (21) and (22) due to its large speed and only consider the Green’s tensor describing shear wave motion. Then, from (21) and (22), G_in($\overrightarrow{r}$, ω) can be written as the sum of two terms corresponding to the SH and SV propagation modes,

$$\begin{gathered} G_{in}(\overrightarrow{r},\omega )=G_{in}^{SH}(\overrightarrow{r},\omega )+G_{in}^{SV}(\overrightarrow{r},\omega ) \\ =\sum _{N=SH,SV}\frac{1}{8{\pi }^3}{\int \int \int }_{}\frac{{\widehat{P}}_i^N{\widehat{P}}_n^N}{\rho k^2{v}_N^2-\rho {\omega }^2}{e}^{i\overrightarrow{k}\cdot \overrightarrow{r}}{d}^3\overrightarrow{k}. \end{gathered}$$ (26)

As shown in the Appendix, $G_{in}^{SH}$($\overrightarrow{r}$, ω) in (26) can be evaluated in closed-form using tabulated integrals. For indices i = 1, 2 and n = 1, 2,

$$G_{in}^{SH}(\overrightarrow{r},\omega )=\frac{1}{4\pi {\mu }_T}\left({\delta }_{in}-\frac{r_i{r}_n}{r_{\perp }^2}\right)\frac{e^{-i{k}_0{r}^{\prime }}}{r^{\prime }}-\frac{i}{4\pi {\mu }_L}\left({\delta }_{in}-\frac{2r_i{r}_n}{r_{\perp }^2}\right)\frac{e^{-i{k}_0{r}^{\prime }}-e^{-i{k}_0\mid z\mid }}{k_0{r}_{\perp }^2}$$ (27)

where $r_{\perp }^2=x^2+y^2$, $r^{\prime 2}=r_{\perp }^2{\mu }_L∕{\mu }_T+z^2$, $k_0^2=\rho {\omega }^2∕{\mu }_L$, and the sign of k₀ has been chosen to give outgoing waves when combined with the e^+iωt time dependence. For i = 3 or n = 3, ${\widehat{P}}_3^{SH}=0$ in (24) and $G_{in}^{SH}(\overrightarrow{r},\omega )=0$. After accounting for the sign convention used in the Fourier transform in (18) and (19), this result agrees with expression (4.14) from Gridin (2000) that was obtained using a different approach.

We have not found a closed-form expression similar to (27) for the SV propagation mode in (26). Instead, we can obtain an expression for $G_{in}^{SV}$($\overrightarrow{r}$, ω) suitable for numerical integration by writing the expression in spherical coordinates,

$$G_{in}^{SV}(\overrightarrow{r},\omega )=\frac{1}{8{\pi }^3}{\int }_0^{2\pi }{\int }_0^{\pi }{\int }_0^{\infty }\frac{{\widehat{P}}_i^{SV}{\widehat{P}}_n^{SV}}{\rho k^2{v}_{SV}^2-\rho {\omega }^2}{e}^{ikr(\widehat{k}\cdot \widehat{r})}{k}^{2}dk\sin {\theta }_{k}d{\theta }_{k}d{\varphi }_k$$ (28)

where $\overrightarrow{k}$ = k$\widehat{k}$ from (23), components of $\overrightarrow{r}$ are shown in figure 2(a),

$$\overrightarrow{r}=\left(\begin{array}{c}\hfill r\sin {\theta }_r\cos {\varphi }_r\hfill \\ \hfill r\sin {\theta }_r\sin {\varphi }_r\hfill \\ \hfill r\cos {\theta }_r\hfill \end{array}\right),$$ (29)

and

$$\widehat{k}\cdot \widehat{r}=\cos {\theta }_k\cos {\theta }_r+\sin {\theta }_k\sin {\theta }_r\cos ({\varphi }_k-{\varphi }_r).$$ (30)

Following the procedure described by Kim et al (1994), this expression can be simplified by extending the k integration to the range −∞ ≤ k ≤ ∞ and performing the θ_k integration over the range 0 ≤ θ_k ≤ π/2. The same result can be obtained using the θ_k integration range π/2 ≤ θ_k ≤ π, or as one-half the result using the full range 0 ≤ θ_k ≤ π. Then, using the full θ_k range and evaluating the k integration using equation (14) of Kim et al (1994), $G_{in}^{SV}$($\overrightarrow{r}$, ω) is given by the sum of two terms,

$$\begin{gathered} G_{in}^{SV}(\overrightarrow{r},\omega )=\frac{-i\omega }{16{\pi }^2\rho }{\int }_0^{2\pi }{\int }_0^{\pi }\frac{{\widehat{P}}_i^{SV}{\widehat{P}}_n^{SV}}{v_{SV}^3}{e}^{-i\omega r\mid \widehat{k}\cdot \widehat{r}\mid ∕v_{SV}}\sin {\theta }_{k}d{\theta }_{k}d{\varphi }_k \\ +\frac{1}{8{\pi }^2\rho r}{\int }_0^{2\pi }{\int }_0^{\pi }\frac{{\widehat{P}}_i^{SV}{\widehat{P}}_n^{SV}}{v_{SV}^2}\delta \left(\widehat{k}\cdot \widehat{r}\right)\sin {\theta }_{k}d{\theta }_{k}d{\varphi }_k. \end{gathered}$$ (31)

In this expression, the integral in the first term is over the surface of the unit sphere. The delta function in the second term reduces the integration range to a line integral over a great circle of the unit sphere in a plane perpendicular to $\widehat{r}$. Both of these integrals have a finite range and can be evaluated using numerical integration. After accounting for the sign convention used in the Fourier transform in (18) and (19), the result (31) is equivalent to the results from Gridin (2000), Willis (1980), and Wang and Achenbach (1995) that were obtained using forward and inverse Radon transformations instead of the Fourier transforms used here. Expression (31) is also equivalent to equation (15) of Kim et al (1994) which involves integrals over a hemisphere of the unit sphere.

3.2. Efficient calculation of the Green’s tensor

Using (26), components of the Green’s tensor are expressed in terms of seven parameters; four dynamic variables r, θ_r, ϕ_r, and ω, and three variables which characterize the material, μ_L, μ_T, and E_T/E_L. Here, we assume that $G_{in}^{SH}$(${\overrightarrow{r}}_{obs}$, ω) is evaluated using the closed-form expression (27). For the evaluation of $G_{in}^{SV}$(${\overrightarrow{r}}_{obs}$, ω), only the product μ_TE_T/E_L appears in the phase velocity v_SV in (13), and six parameters are needed to evaluate the integral expression (31). To reduce this number further, we can orient the coordinate system so that ϕ_r = 0. Also, the phase velocity v_SV from (13) can be written as

$$v_{SV}=v_0\sqrt{1+{\Delta }_{SV}{\sin }^{2}2{\theta }_k}$$ (32)

where $v_0=\sqrt{{\mu }_L∕\rho }$ is the phase velocity along the symmetry axis at θ_k = 0, and

$${\Delta }_{SV}={\mu }_T{E}_L∕{\mu }_L{E}_T-1.$$ (33)

After inserting this expression in (31), the first integral can be parametrized using the phase α = rω/v₀ so that $G_{in}^{SV}$($\overrightarrow{r}$, ω) can be written as

$$G_{in}^{SV}(\overrightarrow{r},\omega )=\frac{-i\omega }{16{\pi }^2\rho v_0^3}{I}_{in}^S(\alpha ,{\theta }_r,{\Delta }_{SV})+\frac{1}{8{\pi }^2\rho r{v}_0^2}{I}_{in}^L({\theta }_r,{\Delta }_{SV})$$ (34)

where the surface and line integrals are given by

$$I_{in}^S(\alpha ,{\theta }_r,{\Delta }_{SV})={\int }_0^{2\pi }{\int }_0^{\pi }\frac{{\widehat{P}}_i^{SV}{\widehat{P}}_n^{SV}}{(1+{\Delta }_{SV}{\sin }^{2}2{\theta }_k{)}^{3∕2}}{e}^{-i\alpha \mid \widehat{k}\cdot \widehat{r}\mid ∕\sqrt{1+{\Delta }_{SV}{\sin }^{2}2{\theta }_k}}\sin {\theta }_{k}d{\theta }_{k}d{\varphi }_k$$ (35)

and

$$I_{in}^L({\theta }_r,{\Delta }_{SV})={\int }_0^{2\pi }{\int }_0^{\pi }\frac{{\widehat{P}}_i^{SV}{\widehat{P}}_n^{SV}}{1+{\Delta }_{SV}{\sin }^{2}2{\theta }_k}\delta \left(\widehat{k}\cdot \widehat{r}\right)\sin {\theta }_{k}d{\theta }_{k}d{\varphi }_k.$$ (36)

These integrals can be precomputed for materials with specific values of Δ_SV using a dense grid of values of α and θ_r. Then, when summing over combinations of r_s, r_obs, and ω in (4), $I_{in}^S$(α, θ_r, Δ_SV) and $I_{in}^L$(θ_r, Δ_SV) can be evaluated efficiently by interpolation, and these values can easily be combined with the multiplicative factors in (34). With this procedure, the Green’s tensor can be calculated with an efficiency comparable to the evaluation of a closed-form expression.

4. Methods

4.1. Precomputation of the surface and line integrals

The surface integral (35) was evaluated by tabulating the integrand on a two dimensional mesh and using the trapezoidal rule to evaluate the integrals for both θ_k and ϕ_k numerically. The mesh used a step size of 0.005 rad for both Δθ_k and Δϕ_k. This step size was selected after varying the size and comparing the calculated Green’s tensor to exact results, see section 5.1. The surface integral was evaluated using phase angles α in the range 0 ≤ α ≤ α_max with a step size Δα = 0.2 rad, and angles θ_r in the range 0° ≤ θ_r ≤ 180° with a step size of Δθ_r = 0.5°. For negative values of α, the surface integral was evaluated using the relations Re [$I_{in}^S$(−α, θ_r, Δ_SV)] = Re [$I_{in}^S$(α, θ_r, Δ_SV)] and Im [$I_{in}^S$(−α, θ_r, Δ_SV)] = −Im [$I_{in}^S$(α, θ_r, Δ_SV)]. The value of α_max was set to 400 rad based on the maximum values of ω and r and the minimum value of v₀ for the materials and propagation geometries considered.

The line integral (36) was evaluated using the procedure described by Kim et al (1994). For this approach, the k_z axis is rotated so that it is oriented in the $\overrightarrow{r}$ direction with the great circle of the unit sphere in a plane perpendicular to $\overrightarrow{r}$. The integration is performed as a one dimensional integral using a single variable ϕ around the rotated k_z axis. However, when performing this integration, the phase velocity v_SV and polarization vectors ${\widehat{P}}^{SV}$ in the integrand of (36) are evaluated relative to the (unrotated) $\widehat{A}$ axis. This process was performed by defining a set of points {x_i, y_i, z_i} distributed around the unit circle in the z = 0 plane, and then rotating these points to the positions {$x_i^R$, $y_i^R$, $z_i^R$} using a rotation matrix determined from the angles θ_r and ϕ_r with the specific value ϕ_r = 0 from section 3.2,

$$\left(\begin{array}{c}\hfill x_i^R\hfill \\ \hfill y_i^R\hfill \\ \hfill z_i^R\hfill \end{array}\right)=\left(\begin{array}{ccc}\hfill \cos {\theta }_r\hfill & \hfill 0\hfill & \hfill \sin {\theta }_r\hfill \\ \hfill 0\hfill & \hfill 1\hfill & \hfill 0\hfill \\ \hfill -\sin {\theta }_r\hfill & \hfill 0\hfill & \hfill \cos {\theta }_r\hfill \end{array}\right)\left(\begin{array}{c}\hfill x_i\hfill \\ \hfill y_i\hfill \\ \hfill 0\hfill \end{array}\right).$$ (37)

These coordinates were used to calculate the polar angle ${\theta }_i^R$ and azimuthal angle ${\varphi }_i^R$ for each of the rotated points, and these angles were used to evaluate the phase velocity v_SV and polarization vectors ${\widehat{P}}^{SV}$ in the integrand of (36). The integration was performed using the trapezoidal rule for the same values of θ_r as used to evaluate the surface integral.

Results are presented in section 5 for materials with μ_L = 25 kPa, μ_T = 9 kPa, and E_T/E_L = 0.16, 0.36, and 0.64. These are the same materials considered by Rouze et al (2013). All calculations were performed on a Linux cluster with an average CPU speed of 2.6 GHz using Matlab (The MathWorks, Natick, MA). For each material, and for the range of variables α and θ_r described above, the (non-optimized) computation time for the surface and line integral data was roughly 128 minutes.

4.2. Calculation of shear wave signals

Shear wave signals were calculated by dividing the excitation force into voxels and performing the Green’s tensor sum (4) over the source positions ${\overrightarrow{r}}_s$ for each desired observation position ${\overrightarrow{r}}_{obs}$. In this sum, the force $\overrightarrow{f}$(r_s), relative position $\overrightarrow{r}$ = ${\overrightarrow{r}}_{obs}$ − r_s, and shear wave displacement $\overrightarrow{u}$(${\overrightarrow{r}}_{obs}$, ω) are defined relative to an experimental XYZ coordinate as shown in figure 1. However, the Green’s tensors $G_{in}^{SH}$($\overrightarrow{r}$, ω) and $G_{in}^{SV}$($\overrightarrow{r}$, ω) have been calculated using the xyz coordinate system shown in figure 2. To transform between these two coordinate systems, we define a rotation matrix R with components R_Ai = ${\widehat{X}}_A$ · ${\widehat{x}}_i$ so that, for example, the vector $\overrightarrow{r}$ can be written as

$${\overrightarrow{r}}_{XYZ}=\left(\begin{array}{c}\hfill X\hfill \\ \hfill Y\hfill \\ \hfill Z\hfill \end{array}\right)=R\left(\begin{array}{c}\hfill x\hfill \\ \hfill y\hfill \\ \hfill z\hfill \end{array}\right)=R{\overrightarrow{r}}_{xyz}.$$ (38)

Then, shear wave displacements in the XYZ coordinate system can be calculated using the Green’s tensor sum (4) as

$$u_A({\overrightarrow{r}}_{obs},\omega )=\sum _s{R}_{Ai}\left[G_{in}^{SH}(\overrightarrow{r},\omega )+G_{in}^{SV}(\overrightarrow{r},\omega )\right](R^{-1}{)}_{nB}{f}_B({\overrightarrow{r}}_s)W(\omega ).$$ (39)

The rotation matrix in (38) and (39) can be calculated by expressing $\widehat{x}$, $\widehat{y}$, and $\widehat{z}$ in terms of the X, Y, Z coordinates as follows. First, in figure 2(a), the z axis is aligned with the material symmetry axis so that $\widehat{z}$ = $\widehat{A}$. Also from figure 2(a), with the xyz coordinate system oriented so that ϕ_r = 0 as in Section 3.2, the y axis is perpendicular to the $\widehat{A}$ − $\widehat{r}$ plane and $\widehat{y}=\left(\widehat{A}\times \widehat{r}\right)∕\mid \widehat{A}\times \widehat{r}\mid$. Finally, $\widehat{x}=\widehat{y}\times \widehat{z}$. Then, elements R_Ai of the rotation matrix can be calculated using the relation R_Ai = ${\widehat{X}}_A$ · ${\widehat{x}}_i$ with each unit vector expressed relative to the XYZ coordinate system. For the sums in (39), the symmetries of $G_{in}^{SH}$($\overrightarrow{r}$, ω) and $G_{in}^{SV}$($\overrightarrow{r}$, ω) with respect to the indices i and n, and the choice ϕ_r = 0 from section 3.2 imply that it is only necessary to calculate the (i, n) = (1, 1) and (2, 2) components of $G_{in}^{SH}$($\overrightarrow{r}$, ω), and the (i, n) = (1, 1), (2, 2), (3, 3), and (1, 3) components $G_{in}^{SV}$($\overrightarrow{r}$, ω). In addition, for the results presented in section 5, the ARFI force is assumed to be directed along the Z axis, and only the Z component of the shear wave displacement is measured. Thus, the component sums in (39) can be simplified to include only these components.

Components of the Green’s tensors in (39) were calculated using (27) for $G_{in}^{SH}$($\overrightarrow{r}$, ω) and (34) for $G_{in}^{SV}$($\overrightarrow{r}$, ω) using the surface and line integral functions (35) and (36), respectively. These integral functions were precomputed for the specific materials described in the last paragraph of section 4.1, and the functions were evaluated for specific combinations of ${\overrightarrow{r}}_{obs}$, ${\overrightarrow{r}}_s$ and ω in the sum (39) by interpolation at the coordinates α = ωr/v₀ and θ_r within these functions. For the line integral, a linear interpolation was used to evaluate the function for a specific value of θ_r. For the surface integral, the interpolation was performed in two steps. First, a linear interpolation was used for the θ_r variable to obtain a function of α, and then spline interpolation was performed in this function for specific values of α. For this last step, the spline interpolation was performed once to find the piecewise interpolation polynomial, and then this polynomial was evaluated for all required values of ω.

The excitation window function W(t) was assumed to be a rectangular function with duration T = 200 μs so that the Fourier transform W(ω) in (39) is given by

$$W(\omega )=\frac{i}{\omega }(e^{-i\omega T}-1).$$ (40)

Calculations were carried out using frequencies in the range −10 kHz ≤ f ≤ 10 kHz with a step size Δf = 20 Hz corresponding to a temporal step size of 50 μs. After calculation of u_A(${\overrightarrow{r}}_{obs}$, ω) using (39), the time-dependent shear wave signal u_A(${\overrightarrow{r}}_{obs}$, t) was calculated using a discrete, inverse Fourier transform.

Results are presented in section 5 for the case of two force functions, a point source located at the origin, and a tall Gaussian source similar to an ARFI excitation described by the relation

$$\overrightarrow{f}({\overrightarrow{r}}_s)=e^{-X^2∕2{\sigma }_X^2}{e}^{-Y^2∕2{\sigma }_Y^2}{e}^{-Z^2∕2{\sigma }_Z^2}\widehat{Z}$$ (41)

with σ_X = 0.4 mm, σ_Y = 0.4 mm, and σ_Z = 7.5 mm. For the case of the tall Gaussian source, the force function was divided into 0.33×0.33×0.33 mm³ voxels, and the Green’s tensor sum (39) was truncated to include only the source voxels with an amplitude greater than 5% of the maximum force (Rouze et al 2018).

Results are presented in section 5 for the two possible experimental configurations shown in figure 1 with the symmetry axis oriented in a plane perpendicular to the excitation axis as in figure 1(a), and with the symmetry axis tilted at an angle of 45° in the X − Z plane as in figure 1(b). These results show shear wave signals in the X = 0, Y = 0, and Z = 0 planes for the case of the three materials described in the last paragraph of section 4.1. These planes are divided into 160 × 160 pixels, each with a dimension of 0.25 × 0.25 mm for a total of 25,600 observation positions ${\overrightarrow{r}}_{obs}$ in each plane. For the case of the tall Gaussian source, the (non-optimized) computation time for the shear wave signals in each plane was roughly 16 hr.

5. Results

5.1. Validation of the numerical integration procedure

The numerical integration procedure used to calculate the Green’s tensor for the SV propagation mode was validated by applying exactly the same procedure to the case of the SH propagation mode and comparing the results with the analytic, closed-form expression (27) for $G_{in}^{SH}$($\overrightarrow{r}$, ω). The surface and line integral functions in (35) and (36) were calculated using the same values of α and θ_r as used for the SV calculations, with the only changes being the replacement of the SV polarization vectors by the SH polarization vectors from (24), and the replacement of v_SV from (32) and (33) with v_SH given by (2),

$$v_{SH}=v_0\sqrt{1+({\mu }_T∕{\mu }_L-1){\sin }^2{\theta }_k}.$$ (42)

Interpolation within the tabulated integral functions was performed using exactly the same procedure described in section 4.2 for the calculation of shear wave signals.

Figure 3 shows a comparison of the analytic (true) results (black line) using (27) with results from the numerical calculation (dashed red line) over the frequency range 0 ≤ f ≤ 5 kHz for the specific case of the position r = 10 mm and angle θ_r = 45°. Comparisons are presented for the real (top row) and imaginary (bottom row) parts of the $G_{11}^{SH}$($\overrightarrow{r}$, ω), $G_{12}^{SH}$($\overrightarrow{r}$, ω), and $G_{22}^{SH}$($\overrightarrow{r}$, ω) components. The signals have MKS units of mN⁻¹ or Pa⁻¹ m⁻¹. These results show nearly perfect agreement between the numeric and analytic signals. Differences between these results can be quantified using the RMS percentage difference Δ_RMS defined as

$${\Delta }_{\text{RMS}}=\frac{\text{RMS}\left\{G_{in,\text{numeric}}^{SH}(\overrightarrow{r},\omega )-G_{in,\text{analytic}}^{SH}(\overrightarrow{r},\omega )\right\}}{\text{RMS}\left\{G_{in,\text{analytic}}^{SH}(\overrightarrow{r},\omega )\right\}}\times 100\%.$$ (43)

Figure 3.

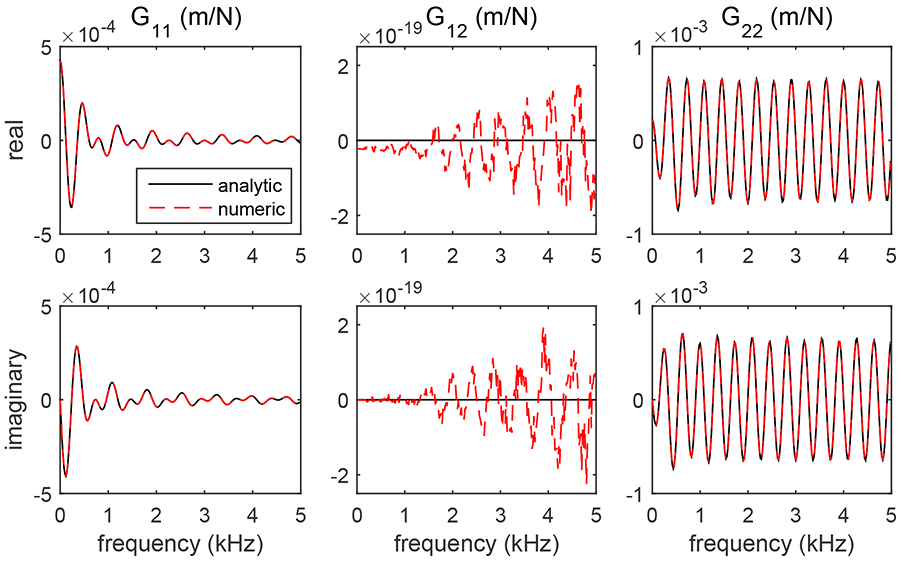
Validation of the numerical integration procedure by comparison of the analytic results (black lines) calculated using (27) with results from the numerical calculations (dashed red lines) for the real (top row) and imaginary (bottom row) parts of the $G_{11}^{SH}$($\overrightarrow{r}$, ω), $G_{12}^{SH}$($\overrightarrow{r}$, ω), and $G_{22}^{SH}$($\overrightarrow{r}$, ω) components of the Green’s tensor for the SH propagation mode. The signals have MKS units of mN⁻¹ or Pa⁻¹ m⁻¹. Results are shown for a material with μ_L = 25 kPa and μ_T = 9 kPa for the specific position r = 10 mm and angle θ_r = 45°. Near perfect agreement is observed for the $G_{11}^{SH}$($\overrightarrow{r}$, ω) and $G_{22}^{SH}$($\overrightarrow{r}$, ω) components. For the $G_{12}^{SH}$($\overrightarrow{r}$, ω) component, the analytic value is zero, and any nonzero signal from the numerical calculation is the result of numerical inaccuracies from the use of finite step sizes in the numerical integrations (35) and (36), or from roundoff errors.

This calculation gives Δ_RMS = 0.392% and Δ_RMS = 0.012% for the real and imaginary parts of $G_{11}^{SH}$($\overrightarrow{r}$, ω), respectively, and Δ_RMS = 0.008% and Δ_RMS = 0.002% for the real and imaginary parts of $G_{22}^{SH}$($\overrightarrow{r}$, ω), respectively. For the case of $G_{12}^{SH}$($\overrightarrow{r}$, ω), the choice ϕ_r = 0 from section 3.2 requires the analytic result (27) to be zero, and any nonzero signal calculated numerically is the result of numerical inaccuracies that result from the use of finite step sizes for the angles θ_k and ϕ_k in the numerical integrations (35) and (36), or from roundoff errors. The results shown in figure 3 indicate that these effects give very small errors on the order of 10⁻¹⁵ of the calculated signals.

5.2. Shear wave signals calculated using a point source excitation

Figure 4 shows an example of shear wave signals in the X = 0, Y = 0, and Z = 0 planes calculated using a point source excitation located at the origin. The three planes overlap and are shown with semi-transparency in the center, and are also duplicated without transparency at positions displaced from the center. The excitation configuration is shown in figure 1(a) with the material symmetry axis oriented along the X axis and the excitation axis in the $\widehat{Z}$ direction. The images show the $\widehat{Z}$ component of displacement at time t = 2.2 ms. These signals are shown for a material with μ_L = 25 kPa, μ_T = 9 kPa, and E_T/E_L = 0.16, and an excitation duration T = 200 μs. A movie showing the time evolution of these signals is included with supplementary material associated with this paper.

Figure 4.

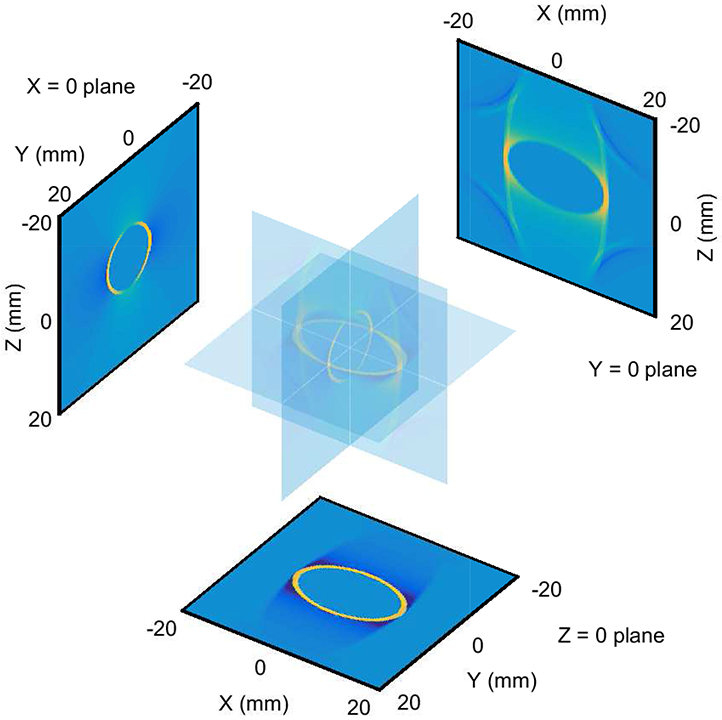
Views of shear wave signals in the X = 0, Y = 0, and Z = 0 planes at time t = 2.2 ms from a point source excitation located at the origin. The planes overlap and are shown with semi-transparency in the center, and are also duplicated without transparency at positions displaced from the center. The experimental configuration is shown in figure 1(a) with the material symmetry axis positioned along the X axis and the excitation force directed along the $\widehat{Z}$ direction. The $\widehat{Z}$ component of displacement is shown. Signals are shown for the case of a 200 μs excitation duration in a material with μ_L = 25 kPa, μ_T = 9 kPa, and E_T/E_L = 0.16. A movie showing the time evolution of these signals is included with supplementary material associated with this paper.

The shear wave signals in the Z = 0 plane of figure 4 are determined only by the SH propagation mode and show the expected elliptical shape from (3) with semi-major and semi-minor axes determined from the μ_L = 25 kPa and μ_T = 9 kPa shear moduli. However, for shear wave signals observed at axial positions above and below the Z = 0 plane, the $\widehat{A}$ − $\widehat{n}$ plane in figure 1 is tilted, and both the SH and SV propagation modes contribute to the shear wave signals.

Figure 5 shows shear wave signals in the X = 0, Y = 0, and Z = 0 planes as shown in figure 4 for experimental configurations with the symmetry axis oriented (a) along the X axis as in figure 1(a), and (b) tilted at an angle of 45° relative to the X axis as in figure 1(b). As in figure 4, these signals are shown for the case of a point source excitation located at the origin at time t = 2.2 ms. Signals are shown for materials with μ_L = 25 kPa, μ_T = 9 kPa, and E_T/E_L = 0.16, 0.36, and 0.64, and an excitation duration T = 200 μs. The top row of figure 5 shows the same signals as in figure 4. Movies showing the time evolution of these signals are included with supplementary material associated with this paper.

Figure 5.

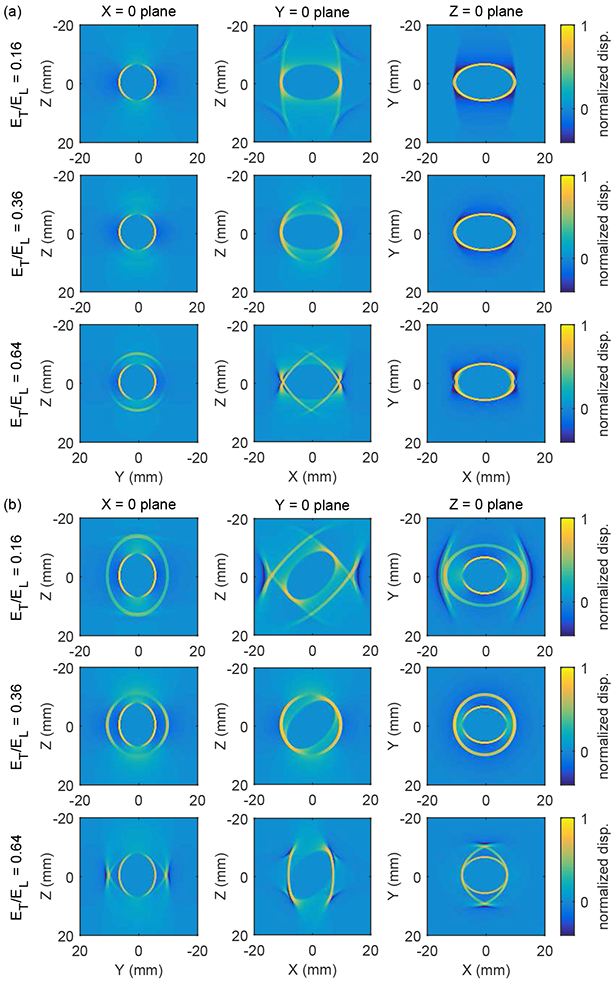
Normalized shear wave displacement signals in the X = 0, Y = 0, and Z = 0 planes (see figure 4) from a point source excitation located at the origin for cases with the material symmetry axis oriented (a) along the X axis as in figure 1(a), and (b) tilted at an angle of 45° relative to the X axis in the $\widehat{X}$ − $\widehat{Z}$ plane as in figure 1(b). The excitation force is oriented in the $\widehat{Z}$ direction, and the $\widehat{Z}$ component of displacement is shown. Signals are shown at a time t = 2.2 ms for materials with μ_L = 25 kPa, μ_T = 9 kPa, and E_T/E_L = 0.16, 0.36, and 0.64. The top row of signals are the same as the signals in figure 4. Movies showing the time evolution of these signals are included with supplementary material associated with this paper.

As with figure 4, the signals in the Z = 0 plane in figure 5(a) with the symmetry axis directed along the X axis show the expected elliptical shape from (3) with the same semi-major and semi-minor axes. However, we note that for the case with E_T/E_L = 0.64, structure from the SV propagation mode contributes to the signals and distorts the elliptical shape near Y = 0. For the case of the symmetry axis tilted at an angle of 45° relative to the X axis in figure 5(b), both the SH and SV propagation modes contribute to the signals and give more complicated shapes as compared to figure 5(a).

5.3. Shear wave signals calculated using a tall Gaussian excitation

Figure 6 shows shear wave signals in the X = 0, Y = 0, and Z = 0 planes as shown in figure 4 for the case of a tall Gaussian excitation source and experimental configurations with the symmetry axis oriented (a) along the X axis as in figure 1(a), and (b) tilted at an angle of 45° relative to the X axis as in figure 1(b). The size of the source was determined using σ_X = 0.4 mm, σ_Y = 0.4 mm, and σ_Z = 7.5 mm in (41). As described in section 4.2, the source was divided into 0.33 × 0.33 × 0.33 mm³ voxels, and the Green’s tensor sum (39) was truncated to include only the source voxels with an amplitude greater than 5% of the maximum force. As in figures 4 and 5, the signals in figure 6 are shown at time t = 2.2 ms for materials with μ_L = 25 kPa, μ_T = 9 kPa, and E_T/E_L = 0.16, 0.36, and 0.64, and an excitation duration T = 200 μs. Movies showing the time evolution of these signals are included with supplementary material associated with this paper.

Figure 6.

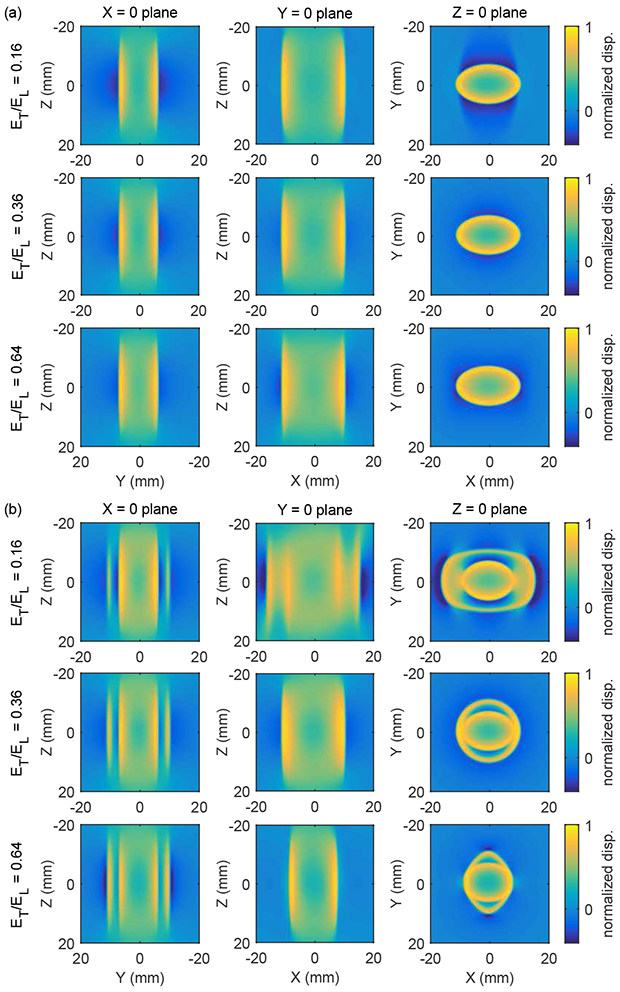
Normalized shear wave displacement signals in the X = 0, Y = 0, and Z = 0 planes (see figure 4) from a tall Gaussian source for cases with the material symmetry axis oriented (a) along the X axis as in figure 1(a), and (b) tilted at an angle of 45° relative to the X axis in the $\widehat{X}$ − $\widehat{Z}$ plane as in figure 1(b). The excitation force is oriented in the $\widehat{Z}$ direction, and the $\widehat{Z}$ component of displacement is shown. The source had dimensions σ_X = 0.4 mm, σ_Y = 0.4 mm, and σ_Z = 7.5 mm in (41) with an excitation duration of 200 μs. Signals are shown at a time t = 2.2 ms for materials with μ_L = 25 kPa, μ_T = 9 kPa, and E_T/E_L = 0.16, 0.36, and 0.64. Movies showing the time evolution of these signals are included with supplementary material associated with this paper.

The shear wave signals obtained using the tall Gaussian excitation in figure 6 show two key differences compared to the signals from the point source excitation in figures 4 and 5. First, the width of the shear wave signals in the Z = 0 plane from the tall source is greater than from the point source due to contributions from source points at positions above and below the Z = 0 plane that arrive in the Z = 0 plane at times later than contributions from a point source at the origin. Second, the Z-dependent structure seen in the point source calculations with the tilted excitation in figure 5(b) is washed out in figure 6 due to the tall source. Nevertheless, structure remains in the Z = 0 plane of figure 6(b) and can be used to distinguish among the signals obtained with different values of E_T/E_L.

6. Discussion

In this paper, we have described a method for the tractable calculation of the Green’s tensor for shear wave propagation in an incompressible, TI material, and have presented sample shear wave signals for the case of a point source, and a tall Gaussian source similar to an ARFI excitation. The motivation for this work is based on two key factors. First, previous applications of the Green’s tensor methods in TI materials have been based on special-case solutions of the equation of motion where closed-form expressions were available so that the sum over source voxels in (4) or (39) could be performed efficiently. However, these solutions only depend on the shear moduli μ_L and μ_T, and not on the ratio of Young’s moduli E_T/E_L, and thus, are not sensitive to all three material parameters needed to characterize an incompressible, TI material. In the current work, we have described a procedure to calculate the Green’s tensor and shear wave signals that is sensitive to all three of these material parameters. Thus, these techniques can be used to analyze shear wave signals in nearly incompressible TI materials such as skeletal muscle, and thereby allow the measurement of material properties such as the longitudinal Young’s modulus E_L which characterizes muscle strength.

The second key factor described in this work is a tractable method to calculate the Green’s tensor. Integral expressions for G_in($\overrightarrow{r}$, ω) have been described previously, but have been used sparingly, because of the large computational effort to evaluate the integral numerically due, in part, to the rapid oscillation of the integrand in (28). For the case of an incompressible, TI material considered here, it is possible to obtain relatively simple expressions for the phase velocity v_SV in (13) and polarization vectors ${\widehat{P}}^{SV}$ in (24). Then, the integral expression (34) for $G_{in}^{SV}$($\overrightarrow{r}$, ω) can be written in terms of integral functions $I_{in}^S$(α, θ_r, Δ_SV) and $I_{in}^L$(θ_r, Δ_SV) that are parametrized in terms of a small number of variables. After precomputing these functions, components of the Green’s tensor can be evaluated by interpolation within these functions and combining the results with multiplicative factors as in (34). This interpolation can be performed with an efficiency that is comparable to the evaluation of a closed-form expression.

Of course, this procedure also requires the numerical computation of the integral functions $I_{in}^S$(α, θ_r, Δ_SV) and $I_{in}^L$(θ_r, Δ_SV). However, because these functions are parametrized, they only need to be calculated for a relatively small number of parameter values. For the calculations reported here, the integral functions are calculated for 7.2 × 10⁵ combinations of α and θ_r. Without this parametrization, the numerical integration would need to be performed for each combination of ${\overrightarrow{r}}_{obs}$, ${\overrightarrow{r}}_s$, and ω used in the Green’s tensor sum (4) or (39). For example, a typical ARFI excitation force might be divided into 10³ − 10⁴ voxels and calculations might be performed using 10³ − 10⁴ frequencies. Also, the number of observation points might vary from 10² positions along a single axis, to 10⁷ positions throughout a volume. Then, it would be necessary to perform numerical integrations for 10⁸ − 10¹⁵ combinations of ${\overrightarrow{r}}_{obs}$, ${\overrightarrow{r}}_s$, and ω depending on the specific problem under consideration. Thus, by using parametrized integral functions, the number of required numerical integrations is reduced by a factor of 10² − 10⁹. This reduction in computational complexity is the key reason that allows the tractable calculation of shear wave displacement signal using the Green’s tensor procedure described herein.

Finally, we note that only elastic materials have been considered in this study. However, soft biological tissues are typically viscoelastic (Fung 1993), and it is common to model shear wave propagation in these materials using viscoelastic materials (Bercoff 2004, Gennisson 2010, Chatelin 2015). Characterization of viscoelastic materials is often done by working in the temporal frequency domain and using a stress-strain model that includes a loss mechanism dependent on the viscosity of the material. A common material model is the Voigt model with a frequency dependent shear modulus μ(ω) = μ₀ + iωη where μ₀ is the material stiffness and η is the viscosity. Other material models include the fractional Kelvin model (Zhang et al 2007) and models with attenuation expressed as a power-law function of frequency (Waters et al 2000, Rouze et al 2018). Because the Green’s tensor model considered in this study has been presented in the temporal frequency domain, it would be straightforward to extend the model to include viscoelastic materials with frequency-dependent material properties.

7. Conclusion

This paper describes a method for the tractable calculation of the Green’s tensor for shear wave propagation in an incompressible, transversely isotropic (TI) material following an acoustic radiation force impulse (ARFI) excitation. Wave propagation is modeled using SH and SV propagation modes defined by the wave polarization relative to the plane determined by the propagation direction and the material symmetry axis. Components of the Green’s tensor are written as the sum of an analytic expression for the SH propagation mode, and an expression involving numerically calculated integral functions for the SV propagation mode. These integral functions are parametrized in terms of two dynamic parameters and can be precomputed for each material under consideration. Then, interpolation within these functions allows the Green’s tensor to be calculated with an efficiency comparable to the evaluation of a closed-form expression. The numerical integration procedure is validated by applying it to the SH propagation mode and comparing the calculations to the known analytic results. Parametrization of the integral functions reduces the computational complexity by a factor on the order of 10² − 10⁹ depending on the specific problem under consideration, and thereby makes the Green’s tensor approach tractable. Results are presented for the case of a point source positioned at the origin and a tall Gaussian source similar to an ARFI excitation. For an experimental configuration with the material symmetry axis tilted relative to the excitation axis, results show that shear wave signals exhibit structure that are sufficiently complex to allow measurement of all three material parameters that characterize an incompressible, TI material.

Appendix

This appendix derives the closed-form expression (27) for $G_{in}^{SH}$($\overrightarrow{r}$, ω) using tabulated integrals. Using (2) and writing the integral (26) in cylindrical coordinates gives

$$G_{in}^{SH}(\overrightarrow{r},\omega )=\frac{1}{8{\pi }^3}{\int }_0^{\infty }{\int }_0^{2\pi }{\int }_{-\infty }^{\infty }\frac{{\widehat{P}}_i^{SH}{\widehat{P}}_n^{SH}}{{\mu }_L{k}_z^2+{\mu }_T{k}_{\perp }^2-\rho {\omega }^2}{e}^{i{k}_{z}z}{e}^{i{k}_{\perp }{r}_{\perp }\cos ({\varphi }_k-{\varphi }_r)}d{k}_{z}d{\varphi }_k{k}_{\perp }d{k}_{\perp }$$ (A.1)

where $\overrightarrow{k}$ and $\overrightarrow{r}$ are given by (23) and (29), $k_{\perp }^2=k_x^2+k_y^2=k^2{\sin }^2{\theta }_k$, and $r_{\perp }^2=x^2+y^2=r^2{\sin }^2{\theta }_k$.

The k_z integral can be evaluated using 3.354.5 of Gradshteyn and Ryzhik (2015),

$${\int }_{-\infty }^{\infty }\frac{e^{i{k}_{z}z}}{{\mu }_L{k}_z^2+{\mu }_T{k}_{\perp }^2-\rho {\omega }^2}d{k}_z=\frac{\pi }{{\mu }_L}\frac{e^{-\mid z\mid {\left(k_{\perp }^2{\mu }_T∕{\mu }_L-k_0^2\right)}^{1∕2}}}{(k_{\perp }^2{\mu }_T∕{\mu }_L-k_0^2{)}^{1∕2}}$$ (A.2)

where $k_0^2=\rho {\omega }^2∕{\mu }_L$. Even though this result diverges when $(k_{\perp }^2{\mu }_T∕{\mu }_L-k_0^2{)}^{1∕2}=0$, it can be used in the integrand for the k_⊥ integral in (A.6) below.

The ϕ_k integral can be evaluated using the substitution ${\varphi }_k^{\prime }={\varphi }_k-{\varphi }_r$ so that ${\widehat{P}}^{SH}$ in (24) is given by

$${\widehat{P}}^{SH}=\left(\begin{array}{c}\hfill -\sin ({\varphi }_k^{\prime }+{\varphi }_r)\hfill \\ \hfill \cos ({\varphi }_k^{\prime }+{\varphi }_r)\hfill \\ \hfill 0\hfill \end{array}\right)=\left(\begin{array}{c}\hfill -\sin {\varphi }_k^{\prime }\cos {\varphi }_r-\cos {\varphi }_k^{\prime }\sin {\varphi }_r\hfill \\ \hfill \cos {\varphi }_k^{\prime }\cos {\varphi }_r-\sin {\varphi }_k^{\prime }\sin {\varphi }_r\hfill \\ \hfill 0\hfill \end{array}\right).$$ (A.3)

Also, because the integrand for the ${\varphi }_k^{\prime }$ integral is periodic in 2π, the integration range can be shifted to the range 0 ≤ ${\varphi }_k^{\prime }$ ≤ 2π. Then, using 3.915.2 and 3.915.5 of Gradshteyn and Ryzhik (2015), the ϕ_k, integral in (A.1) is given by

$${\int }_0^{2\pi }{\widehat{P}}_i^{SH}{\widehat{P}}_n^{SH}{e}^{i{k}_{\perp }{r}_{\perp }\cos {\varphi }_k^{\prime }}d{\varphi }_k^{\prime }=A_{in}{J}_0(k_{\perp }{r}_{\perp })+B_{in}\frac{J_1(k_{\perp }{r}_{\perp })}{k_{\perp }{r}_{\perp }}$$ (A.4)

where J₀ and J₁ are Bessel functions of the first kind of order 0 and 1, respectively, and the coefficients A_in and B_in are given by

$$A_{in}=2\pi \left({\delta }_{in}-\frac{r_i{r}_n}{r_{\perp }^2}\right)\text{and}{B}_{in}=-2\pi \left({\delta }_{in}-\frac{2r_i{r}_n}{r_{\perp }^2}\right)$$ (A.5)

for indices i = 1, 2 and n = 1, 2, and A_in = 0 and B_in = 0 for i = 3 or n = 3. The components r_i and r_n of $\overrightarrow{r}$ are given by (29).

Finally, the the k_⊥ integral can be evaluated using 8.2(24) and 8.4(10) of Erdélyi et al (1954),

$$\begin{gathered} G_{in}^{SH}(\overrightarrow{r},\omega )=\frac{1}{8{\pi }^3}{\int }_0^{\infty }\frac{\pi }{{\mu }_L}\frac{e^{-\mid z\mid {\left(k_{\perp }^2{\mu }_T∕{\mu }_L-k_0^2\right)}^{1∕2}}}{(k_{\perp }^2{\mu }_T∕{\mu }_L-k_0^2{)}^{1∕2}}\left[A_{in}{J}_0(k_{\perp }{r}_{\perp })+B_{in}\frac{J_1(k_{\perp }{r}_{\perp })}{k_{\perp }{r}_{\perp }}\right]k_{\perp }d{k}_{\perp } \\ =\frac{1}{8{\pi }^2{\mu }_T}{A}_{in}\frac{e^{-i{k}_0{r}^{\prime }}}{r^{\prime }}+\frac{i}{8{\pi }^2{\mu }_L}{B}_{in}\frac{e^{-i{k}_0{r}^{\prime }}-e^{-i{k}_0\mid z\mid }}{k_0{r}_{\perp }^2} \end{gathered}$$ (A.6)

where $r^{\prime 2}=r_{\perp }^2{\mu }_L∕{\mu }_T+z^2$ and the sign of k₀ has been chosen so that the result gives outgoing waves when combined with the e^+iωt time dependence in (19). Note that 8.2(24) and 8.4(10) of Erdélyi et al (1954) require Re (ik₀) > 0. To meet this condition, a positive real part can be added to ik₀ using the subsitution $i{k}_0\to i{k}_0^{\prime }=\eta +i{k}_0$ with η > 0 to give an exponential decay in the result with $e^{-i{k}_0^{\prime }{r}^{\prime }}=e^{-\eta r^{\prime }}{e}^{-i{k}_0{r}^{\prime }}$ and $e^{-i{k}_0^{\prime }\mid z\mid }=e^{-\eta \mid z\mid }{e}^{-i{k}_0\mid z\mid }$. After the integrals are evaluated, the limit η → 0 gives (A.6). Combining (A.5) and (A.6) gives (27).