Abstract

Quantum-chemical calculations and classical and ab initio molecular dynamics simulations have been performed to study the Mg2+-conducting electrolytes based on Mg(TFSI)2/MgCl2 solutions in dimethoxyethane. It has been shown that depending on the TFSI/Cl– ratio, the Mg2Cl22+ or Mg3Cl42+ complexes are preferred as stable ion aggregates. In the initial stages of the ion association process, MgCl+, MgCl2, and Mg2Cl3+ are formed as intermediate species. Calculations of harmonic frequencies and simulations of the IR spectrum of the electrolyte from the ab initio MD trajectories have been used to identify the spectral range of vibrations of ion aggregates found in the modeled electrolyte. The results have been discussed in the context of experimental data.
1. Introduction
Challenges related to increasing power demand in industrial societies and concerns about environmental costs of energy production stimulate research on electrical energy storage technologies. Despite the great commercial success of lithium-ion devices, there is growing interest in “beyond Li” chemistries, based on other metals, also including multivalent ions. In the latter context, rechargeable magnesium batteries seem to be a promising alternative, offering high energy densities. Therefore, significant attention has been paid to experimental and computational studies on the development of Mg-based devices.1−5
An important component of an efficient battery is the electrolyte. Continuous interest in Mg-ion batteries, therefore, results in ongoing research on appropriate magnesium-conducting electrolytes.6 Several of these studies focus on Mg salt solutions in organic liquids, for example, ether-like solvents, including dimethoxyethane (DME) or higher glymes..7−16 Interactions between ions and solvent molecules in the electrolyte are often studied via the analysis of vibrational spectra.10,12,16−18 Experiments are supplemented and elucidated by quantum-chemical (QC) calculations9,10,12,17,19,20 and molecular dynamics (MD) simulations.9,20−22
Experiments on Mg(TFSI)2 solutions in DME show that the properties of an electrolyte may be improved by the addition of chloride anions, for example, in the form of MgCl2.23 In a recent work,24 Mg2+ solutions in DME with different TFSI/Cl ratios were studied. A variety of experimental techniques, including Raman spectroscopy and structural analysis by X-ray diffraction, were applied to investigate the formation of possible complexes of Mg2+ ions with Cl– anions. The results indicated that the DME solvent promotes the formation of multi-ionic aggregates, such as Mg2Cl22+ and Mg3Cl42+, stabilized by the interactions with solvent molecules. It was concluded that in the solution with a 1:1 Mg/Cl ratio, the main species are the Mg2Cl22+ complexes, possibly in equilibrium with MgCl+. In the case of 3:4 Mg/Cl ratio, the existence of Mg3Cl42+ was postulated, whereas the coexistence of MgCl+ and Mg2Cl3+ was considered as rather unlikely, based on the lack of signatures of the latter aggregate in the Raman spectrum.
In this work, we would like to apply the computational methodology to the electrolytes investigated experimentally in ref (24) in order to study the process of ion association and the stability of different complexes. QC calculations will be used to obtain the binding energies of aggregates and their vibrational spectra. Classical MD simulations for different compositions of electrolytes will be used to trace the evolution of systems. An MD study of ion agglomeration was recently used to investigate a similar problem for the MgCl2 electrolyte in tetrahydrofuran.22 Finally, we will use first-principles MD simulations to compare some structural data with classical MD simulations and to assess the vibrational spectrum in the condensed phase. The results will be discussed in the context of experimental findings of ref (24).
2. Computational Methods
Gaussian 09 rev. D0125 was used for optimization of the structure of complexes and calculations of harmonic vibrational frequencies. The DFT methodology using the PBE or B3LYP functionals with Grimme’s dispersion correction26 and the aug-cc-PVDZ basis set was applied. QC calculations were performed in vacuum and in the implicit solvent, modeled using the IEFPCM method with the dielectric constant of the medium set to ε = 7.2. Structures containing only ions were modeled from scratch, whereas for three systems containing DME molecules as the explicit solvent, we used the crystallographic data from ref (24) as initial structures for geometry optimization.
Classical MD simulations reported in this work were performed using the NAMD v. 2.12 simulation package.27 The polarizable force field (FF) was based on the parameterization used in our study on Mg(TFSI)2 solutions in DME.21 FF parameters for the TFSI anion were based on the OPLS parameterization28 with bonded parameters taken from the Lopes/Pádua force field29 and the nonbonded from Köddermann’s work.30 Parameters for DME molecules were adapted from the work of Anderson and Wilson,31 except for parameters describing the C–C–O–C and O–C–C–O torsional angles, which were taken from the GAFF parameterization.32 Nonbonded parameters for Mg2+ and Cl– ions were adapted from the AMOEBA-PRO-13 force field33 with slight modifications to improve the agreement of Mg2+–anion interaction energies with the QC results. Polarization effects were included via Drude oscillators.34 Drude particles were attached to all nonhydrogen atoms of DME molecules and to TFSI and Cl– anions; we did not use Drude oscillators for cations because the polarizability of the Mg2+ ion is small. Atomic polarizabilities and charges of TFSI anions were based on the APPLE&P force field,35 the polarizability of Cl– was based on AMOEBA FF, and the parameters of DME molecules were taken from the work on poly(ethylene oxide)36 with polarizabilities scaled by a factor of 0.7 to improve the Mg2+–DME interaction energies. FF parameters are listed in the Supporting Information. NAMD simulations were performed in the NpT ensemble at p = 1 atm and T = 298 K with Langevin dynamics and the modified Nose–Hoover Langevin barostat.37,38 A time step of 0.5 fs was used to integrate the equations of motion. Periodic boundary conditions were used, and electrostatic interactions were taken into account using the particle mesh Ewald algorithm.39
The systems simulated in the classical MD correspond to the electrolytes studied in the experimental work.24 Three electrolytes, denoted here I, II, and III, were 0.5 M Mg(TFSI)2/0.25 M MgCl2, 0.5 M Mg(TFSI)2/0.5 M MgCl2, and 0.5 M Mg(TFSI)2/1 M MgCl2 solutions in DME, respectively. Systems I–III initially contained randomly distributed Mg2+ and Cl– ions. The aggregation process may be too slow to be completed during a limited time of an MD run, therefore to assess the stability of ion aggregates, we prepared a set of systems with the same salt concentrations as in II or III, but with ions introduced as aggregates. In this way, we were able to check whether the aggregates dissociate or, on the contrary, tend to form larger ion clusters. System IIa contained initially the Mg2Cl22+ complexes; system IIIa was a 1:1 mixture of MgCl2 and Mg2Cl22+; and systems IIIb and IIIc contained Mg3Cl42+ complexes of type I and II (C.f. Section 3.1). Compositions of all electrolytes are listed in Table S1 in the Supporting Information. The classical MD simulations for all systems were performed for 400 ns.
For selected systems, we performed ab initio molecular dynamics (AIMD) simulations in the CP2K package.40,41 The PBE functional with empirical dispersion correction and Goedecker’s pseudopotentials42 were used for calculations with a molecularly optimized DZVP basis set. Simulations with a time step of 1 fs were performed for 35 ps in the NVT ensemble at T = 298 K using the Nosé–Hoover thermostat. The size of the periodic simulation cell was set to reproduce the densities of electrolytes obtained in classical MD simulations. The electrolytes modeled in AIMD simulations were systems III, IIIa, IIIb, and IIIc. The sizes of the systems were reduced, and all simulation boxes contained three Mg2+ cations, two TFSI anions, and four Cl– anions in 30 DME molecules. In system III, the ions were distributed randomly, and in systems IIIa–c as MgCl2 + Mg2Cl22+, Mg3Cl42+ (I), or Mg3Cl42+ (II) complexes, respectively. AIMD simulations were initiated from the structures equilibrated in classical MD runs. The Fourier tool43 from CPMD contributed programs was used to perform the Fourier transform (FT) of the autocorrelation function of the dipole moment and to calculate the infrared (IR) spectra from AIMD trajectories. Although, in the experiment, the Raman spectra were measured, we did not calculate Raman activity from AIMD because this requires calculations of the polarizability of the system, largely increasing the computational effort.
3. Results and Discussion
3.1. QC Calculations—Structures and Binding Energies
Geometries of complexes investigated by quantum-chemical calculations are shown in Figure 1. The distances between selected pairs of atoms obtained in the PBE calculations in vacuum and in the PCM solvent are listed in Table S2 in the Supporting Information. In this section, we will discuss the PBE results because this functional was used in AIMD; for comparison, the data for the B3LYP functional are also collected in Table S2. In the case of the Mg3Cl42+ complex, we found two stable forms: a linear structure and the other with a triangular arrangement of Mg2+ ions; these structures will be denoted structures I and II, respectively (Cf. Figure 1). Nevertheless, only the linear geometry of the [Mg3Cl4(DME)5]2+ complex was investigated, based on the structure experimentally determined in ref (24).
Figure 1.

Structures of investigated complexes.
Typical Mg–Mg distances are in the range of 3.2–3.6 Å, except for Mg2Cl3+ and Mg2Cl5– complexes in which they are significantly smaller (2.7–3.0 Å). Most of the Mg–Cl distances are between 2.2 and 2.5 Å. It may be easily seen in Table S2 that these distances become larger in the solvent. For isolated MgxCly complexes, the Mg–Mg and Mg–Cl distances increase by about 0.2 and 0.1 Å between the vacuum and the implicit solvent. The explicit solvent used in vacuum calculations (in the complexes with DME molecules) has an even greater impact on the geometry and increases the Mg–Mg distances by 0.3–0.35 Å and the Mg–Cl distances by 0.15 Å with respect to the “bare” complex. On the other hand, Mg–Mg and Mg–Cl distances in the MgxCly complexes with DME molecules do not increase further, or even slightly decrease, when the system is embedded in the PCM solvent, suggesting that the explicit solvent molecules will suffice to capture the major part of the solvent effect on the Mg–Mg/Cl distances. The Cl–Cl distances (mostly about 3.5 Å) are much less affected by the solvent, except for MgCl2, in which case the explicit solvent molecules change the geometry of the system from linear to bend. Finally, we note that the Mg–OE (where OE stands for the oxygen atom from the DME molecule) distances in the complexes containing explicit DME molecules decrease slightly in the implicit solvent with respect to vacuum values. Conversely, the PCM solvent increases by 0.05–0.1 Å the Mg–OT (OT denotes the oxygen atom from the TFSI anion) distances in the Mg2+ complexes with TFSI anions. The results obtained in the B3LYP calculations (C.f. Table S2) are similar to the PBE observations.
Table 1 presents the binding energies Eb of the studied complexes obtained in vacuum and in the implicit solvent. The Eb values were calculated with respect to the optimal geometries of free DME molecules and TFSI anions. In both functionals, geometry II of the Mg3Cl42+ complex has a lower energy than structure I, leading to a slightly larger binding effect. In the PCM solvent, the stabilization of geometry II is about 1–2 kcal/mol larger than for structure I. As expected, the binding effect increases with the number of ions or/and molecules in the complex. The implicit solvent reduces the stabilization, typically by a factor of about 5 or 4 for “bare” ion complexes or for the structures with explicit DME molecules, respectively. In the latter case, the effect of the implicit solvent is smaller because the ions are screened from the effective medium by the explicit solvent molecules.
Table 1. Binding Energies (in kcal/mol) Calculated using the aug-cc-pVDZ Basis Seta.
| PBE |
B3LYP |
|||
|---|---|---|---|---|
| vac | PCM | Vac | PCM | |
| MgCl+ | –338.5 | –59.7 | –336.7 | –59.3 |
| MgCl2 | –541.2 | –106.7 | –539.8 | –105.9 |
| MgCl3– | –606.8 | –132.1 | –605.2 | –130.4 |
| Mg2Cl22+ | –668.6 | –135.1 | –665.1 | –133.3 |
| Mg2Cl3+ | –942.1 | –186.7 | –935.4 | –182.0 |
| Mg2Cl5– | –1202.7 | –260.3 | –1197.0 | –254.4 |
| Mg3Cl42+ (I) | –1283.9 | –265.0 | –1277.8 | –261.1 |
| Mg3Cl42+ (II) | –1284.0 | –266.3 | –1279.4 | –263.8 |
| MgCl2·2E | –604.3 | –150.6 | –608.4 | –155.5 |
| [Mg2Cl2·4E]2+ | –981.9 | –268.8 | –995.2 | –283.0 |
| [Mg3Cl4·5E]2+ | –1617.9 | –428.2 | –1634.1 | –444.2 |
| [MgTFSI]+ | –338.0 | –51.9 | –336.9 | –54.3 |
| MgTFSI2 | –504.3 | –96.0 | –508.9 | –100.5 |
E stands for DME.
To obtain some clues about the relative stability of electrolytes with different complexes, we collected in Table 2 the total binding energies for different possible compositions of aggregates with the Mg/Cl ratio equal to 1:1 or 3:4; the definition of the binding effect is provided in the Supporting Information. In the case of 1:1 systems, the binding energy of the Mg2Cl22+ aggregate in the PCM calculations is 15 kcal/mol larger than the net binding effect of two MgCl+ complexes. Likewise, the Mg3Cl42+ complex is about 20 kcal/mol more stable than the pair of Mg2Cl22+ and MgCl2 aggregates or a pair of Mg2Cl3+ and MgCl+ complexes. The fourth possible 3:4 composition, MgCl2 + 2 × MgCl+ aggregates, is the least stable, with the net binding effect almost 40 kcal/mol smaller than that of Mg3Cl42+. It is an indication that Mg2Cl22+ and Mg3Cl42+ may be the preferred complexes in electrolytes with the Mg/Cl ratio of 1:1 and 3:4, respectively. A similar clue about Mg3Cl42+ stability is also obtained from binding energies of complexes with explicit solvent molecules: the binding energy of [Mg3Cl4(DME)5]2+ is 20 kcal/mol more negative (more stabilizing) than the sum of binding energies of MgCl2(DME)2 and [Mg2Cl2(DME)4]2+.
Table 2. Binding Effect (in kcal/mol) for Possible Aggregates Calculated at the PBE/aug-cc-pVDZ Level in Vacuum and in the PCM Solventa.
| PBE |
B3LYP |
||||
|---|---|---|---|---|---|
| Mg/Cl ratio | Eb (vac) | Eb (PCM) | Eb (vac) | Eb (PCM) | |
| 2MgCl+ | 1:1 | –677.0 | –119.3 | –673.4 | –118.6 |
| Mg2Cl22+ | 1:1 | –668.6 | –135.1 | –665.1 | –133.3 |
| 2MgCl+ + MgCl2 | 3:4 | –1218.2 | –226.0 | –1213.2 | –224.5 |
| Mg2Cl3+ + MgCl+ | 3:4 | –1280.6 | –246.4 | –1272.1 | –241.4 |
| Mg2Cl22+ + MgCl2 | 3:4 | –1209.8 | –241.8 | –1204.9 | –239.2 |
| Mg3Cl42+ (I) | 3:4 | –1283.9 | –265.0 | –1277.8 | –261.1 |
The most stable form for a given system composition is indicated in boldface.
3.2. MD Simulations
The radial distribution functions (RDFs) were averaged over the last 20 ns of classical MD simulations and over 30 ps of AIMD trajectories. Mg–Cl and Mg–O RDFs are shown in Figure 2; the plots of Mg–Mg, Cl–Cl RDFs, and integrated RDFs (running coordination numbers) are included in the Supporting Information (Figures S1–S3). When comparing the RDFs obtained from the classical and ab initio MD simulations, one should take into account that the AIMD runs were initialized from the equilibrated classical trajectories. The length of AIMD simulations was much too short to make possible any major changes in the coordination of the ions, but was sufficient to observe the differences in interatomic distances.
Figure 2.

RDFs for Mg–Cl and Mg–O pairs obtained from the classical (top) and ab initio (bottom) MD simulations. Oxygen atoms from TFSI anions and DME molecules are marked as OT and OE, respectively.
The first maximum in the Mg–Cl RDF in classical MD simulations (Figure 2) appears between 2.4 and 2.6 Å; larger values are observed for systems IIIa–c in accord with the QC-calculated distances which increase in complexes with a larger number of Mg2+ ions (Table S2). AIMD data follow the same pattern, with the maximum for system III observed at a distance 0.1–0.15 Å shorter than that of IIIa–IIIc. For all systems, the position of the maximum in the Mg–Cl RDF in AIMD shifted to distances that are 0.1 Å shorter with respect to FF-MD. RDFs for Mg–O pairs were calculated separately for OE and OT oxygen atoms. In the relatively large systems simulated by classical MD, both kinds of coordination are observed, with the Mg–OT maxima at about 2 Å and the Mg–OE maxima between 2.15 and 2.25 Å, in agreement with the QC data. The integrated Mg–O RDFs (Figure S2) show that the number of O atoms coordinating the metal cation is the largest in the most diluted electrolyte I and the smallest in electrolytes IIIa–IIIc, in which there is an increasing Mg2+ coordination by Cl– anions. The latter conclusion is confirmed by the integrated Mg–Cl and Cl–Cl RDFs for different electrolytes (Figure S3), exhibiting a trend opposite to that observed for Mg–O in Figure 2. In the AIMD trajectories, the position of the Mg–OE maximum located between 2.12 and 2.2 Å agrees well with the Mg–OE distances calculated in the PCM solvent. In two (III and IIIb) of the four electrolytes investigated via AIMD, one of the two TFSI anions is coordinated to one of the Mg2+ cations. The corresponding maximum in the Mg–OT RDF is at the distance of the Mg–OE maximum, despite the fact that the QC calculations predict shorter Mg–OT distances. The discrepancy may presumably originate from the effect of the explicit solvent in AIMD.
The Mg–Mg and Cl–Cl RDFs from FF-MD simulations (Figure S1) are more complicated, because interatomic distances differ depending on the composition of the aggregate. The main maximum in the Cl–Cl RDFs in electrolytes I and II appears at distances significantly higher than for systems IIIa–IIIc. This effect can be related to the QC results showing that the Cl–Cl distance in Mg2Cl22+ is substantially larger than in other complexes. From these data, we may expect that systems I and II contain a relatively larger amount of Mg2Cl22+ than systems IIIa–IIIc. Positions of the maxima of Mg–Mg and Cl–Cl RDFs in AIMD generally agree with QC-calculated distances. On the other hand, there is a difference between FF-MD and AIMD. In FF-MD, the Mg–Mg maximum appears at distances shorter than in AIMD, whereas for the Cl–Cl RDF the difference is opposite. As there is no major difference between FF-MD and AIMD for Mg–Cl RDF, we can infer that the shape of the Mg2Cl22+ rhombus is different in two types of MD, with the Mg–Mg diagonal longer and the Cl–Cl shorter in the AIMD structures.
We will start our analysis of ion aggregation in electrolytes with a check of the relative stabilities of the systems. The two electrolytes II and IIa contain the same number of ions and solvent molecules, and the same is true for four systems III and IIIa–c. Therefore, we can compare the energies of systems within sets IIx and IIIx, and the differences may provide some information on their relative stability: with all other things being equal, the differences in the energy arise from the differences in binding energies of ion aggregates, and the lower potential energy suggests that the aggregates contained in the system are more stable. In Figure 3, we show the changes in the potential energy Epot calculated per Mg2+ ion for the last 40 ns of the FF-MD trajectories. To make the plot less noisy, a moving average over 0.5 ns was applied to the data. The energy of the electrolyte IIa is lower than that of system II (about 0.9 kcal/mol per cation), indicating that the ion aggregation into Mg2Cl22+ is favorable. Likewise, the average Epot per ion decreases in the order of III > IIIa > IIIb > IIIc, suggesting again that ion complexation into Mg2Cl22+ and Mg3Cl42+ is preferred. In particular, system IIIc has a lower energy than IIIb, in agreement with the QC results that type II of the Mg3Cl42+ complex is slightly more stable than the linear form I. The difference between IIIc and IIIb is 0.7 kcal/mol per cation, which was recalculated as that every three Mg2+ ions yield 2.1 kcal/mol per Mg3Cl42+ aggregate, which was almost the same as the difference in QC energies between Mg3Cl42+ (I) and Mg3Cl42+ (II) (however, one should not directly compare these values because not all the Mg2+ ions in IIIb and IIIc form the Mg3Cl42+ aggregates).
Figure 3.

Relative potential energies Epot per Mg2+ ion of systems II, IIa, and III, IIIa–c (with respect to the energies of systems II or III, respectively) obtained from the last 40 ns of MD simulations.
To trace the changes in ion aggregation along the classical MD trajectories, in Figure 4 we plotted the changes in the average number of Mg2+ ions at the 4 Å distance from the central Mg2+ cation (NMg), that is, the value of the integrated Mg–Mg RDF at 4 Å. Similar plots for Mg–Cl and Cl–Cl RDFs are shown in the Supporting Information (Figure S4). The “ideal” values for Mg2Cl22+, Mg3Cl42+ (I), and Mg3Cl42+ (II) are 1, 1.33, and 2, respectively (C.f. Figure S3).
Figure 4.
Changes in the average number of Mg2+ ions found at the distance of 4 Å from the Mg cation. Initial arrangements of Mg2+ and Cl– ions are schematically depicted on the left side of the plot.
In Figure 4, there are only small changes for systems IIa, IIIb, and IIIc, that is, for these electrolytes, which initially contained aggregated ions. No decrease in NMg shows that there is not much dissociation of these complexes. For other systems, NMg increases with time, indicating the ion aggregation processes occurring in the electrolyte. The speed of aggregation decreases (especially for system I) because the larger the aggregates become, the lower their mobility is and the larger the average distances between them, therefore the waiting time for the next possible aggregation event increases.
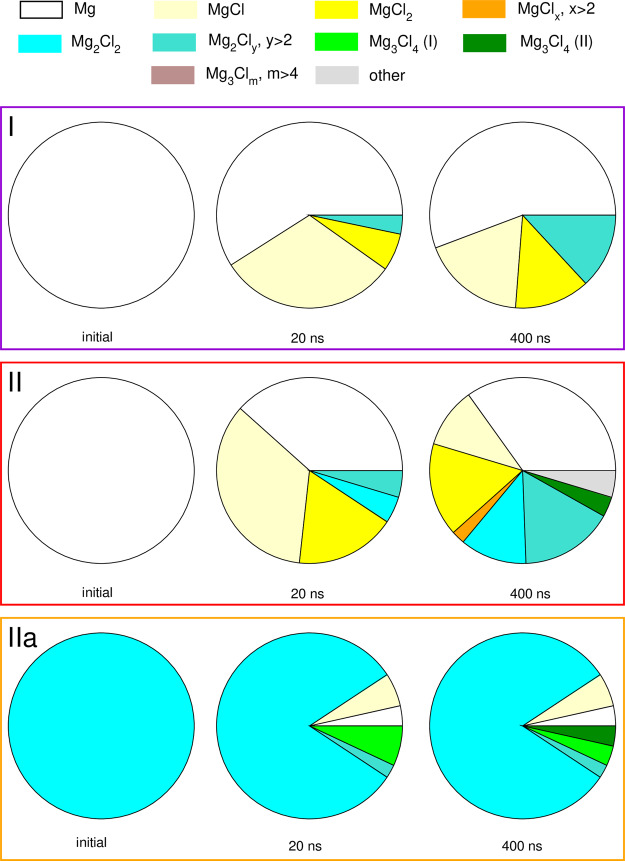
We performed the analysis of Mg2+ speciation for all systems I–IIIc at the beginning of the MD run and after 400 ns. For this purpose, we counted different aggregates formed by Mg2+ and Cl– ions, defining that the ion X belongs to an aggregate if its distance to any counterion in the aggregate is less than the threshold value of 3 Å. In Figures 5 and 6 we display the abundance of Mg2+ ions in different MgxCly complexes in the initial system, at about 20 ns of the simulation and at the end of the trajectory. In the statistics, we also include “free” cations, that is, cations not interacting with any of the Cl– anions.
Figure 5.
Abundance of Mg2+ ions in different complexes at different stages of MD simulations for systems I, II, and IIa.
Figure 6.
Abundance of Mg2+ ions in different complexes at different stages of MD simulations for systems III and IIIa–c.
System I, with the Mg(TFSI)2/MgCl2 ratio of 2:1, contains less Cl– anions than metal cations, therefore at any time there must be some “free” Mg2+ ions present. Accordingly, after 400 ns, more than 50% of Mg2+ cations are not coordinated to chlorine anions. Within the first few ns of the simulation, some amount of MgCl+ is formed, which then aggregates slowly yielding MgCl2 and Mg2Cly4–y (y > 2) complexes.
Electrolytes II and IIa contain Mg(TFSI)2 and MgCl2 with a 1:1 ratio. In system II (initially containing only “free” Mg2+), MgCl+ and MgCl2 are produced at the beginning of the simulation. After 400 ns, these species and “free” Mg cations are still present in the electrolyte, but the amount of MgCl+ is much smaller. Instead, Mg2Cly4–y aggregates with y = 2 and y = 3 are produced. Very few larger aggregates can also be found at this stage. Conversely, system IIa initially contained all the Mg ions as Mg2Cl22+ complexes. Within the first 20 ns, some of them dissociated, and some associated into larger aggregates, but there are no significant further changes. After 400 ns, the speciation of Mg2+ is similar to that at 20 ns, with more than 80% of Mg ions forming the Mg2Cl22+ aggregates.
The Mg(TFSI)2/MgCl2 ratio in the systems III and IIIa–IIIc is 1:2, therefore it is possible that all Mg cations exist as Mg3Cl42+. In systems III and IIIa, aggregation processes are observed. In system III, MgCl+ and MgCl2 are produced within 20 ns from initially “free” Mg2+ and then gradually condense into Mg2Cl22+, other Mg2Cly4–y aggregates, and some amount of Mg3Cl42+ or larger complexes. Production of Mg3Cl42+ is faster in electrolyte IIIa. The amount of MgCl2 and Mg2Cl22+ complexes, initially present in the system, decreases, and both types (I and II) of Mg3Cl42+ are formed. Therefore, system III, containing mainly MgCl2 and Mg2Cly4–y (y ≥ 2) after 400 ns, seems to be at a less advanced stage of the process. Electrolytes IIIb and IIIc initially contained only Mg3Cl42+ complexes of types I and II, respectively. During the first nanoseconds of MD simulations, a small fraction of these aggregates dissociates or associates into larger complexes, but then the amount of Mg3Cl42+ remains approximately constant for the next 400 ns. The major change occurring in electrolyte IIIb is the conversion of Mg3Cl42+ (I) aggregates into type II, in agreement with larger stability of the latter indicated by QC calculations.
We can conclude from the classical MD simulations that the initially “free” Mg2+ ions tend to form stable Mg2Cl22+ or Mg3Cl42+ complexes, depending on the Mg(TFSI)2/MgCl2 ratio being 1:1 or 1:2, respectively. In the initial stage of the process, intermediate aggregates: MgCl+, MgCl2, or Mg2Cly4–y, are produced.
Analysis of Mg2+ speciation agrees with Figure 4. The NMg value increases in systems in which the association process takes place, and conversely, NMg is approximately constant in electrolytes IIa, IIIb, and IIIc, which do not undergo significant changes. Electrolyte IIa contains mainly Mg2Cl22+ aggregates; consistently, NMg for this system is close to 1. At the end of the simulation, about 50 and 30% of Mg2+ ions in system IIIa form Mg2Clx and Mg3Cly aggregates, respectively. Together with other species present in the electrolyte, this composition leads to NMg of about 1.2. Systems IIIb and IIIc contain a mixture of Mg3Cl42+ complexes of types I and II, therefore the NMg values are between 1.33 and 2, corresponding to pure (I) or (II) aggregates, respectively. For example, in system IIIb, there is a similar amount of complexes (I) and (II), yielding the NMg close to 1.5. On the other hand, almost 70% of Mg2+ in system IIIc is in the form of Mg3Cl42+ (II), therefore the NMg is 1.77, quite close to 2, that is, the value of pure (II) complexes. Similar conclusions may be drawn from the integrated Mg–Cl or Cl–Cl RDFs and their changes with time (Figures S3 and S4 in the Supporting Information).
3.3. Vibrational Spectra
Raman scattering and IR spectra calculated for selected individual complexes in the PBE functional in vacuum and in the implicit PCM solvent are shown in Figure 7; a full set of data for all complexes is shown in Figure S5 in the Supporting Information. Changes in the activity and positions of peaks in the Raman spectrum between vacuum and the PCM are quite large. In the solvent, vibrations of MgxCly complexes investigated in this work are active in the range of 300–400 cm–1. The interpretation of the experimental spectra and their relation to QC calculations will be made more difficult not only by the small differences between different aggregates but also by the overlap with vibrations of the TFSI anion active in the same region.
Figure 7.

Raman (top) and IR (bottom) spectra calculated at the PBE/aug-cc-pVDZ level in vacuum and in the PCM solvent.
The difference between vacuum and PCM is smaller for IR spectra; the IR spectra of explicitly solvated [Mg2Cl2(DME)4]2+ and [Mg3Cl4(DME)5]2+ complexes are very little affected by the implicit solvent. The IR active vibrations of solvated aggregates are located mainly between 300 and 400 cm–1 with more intense peaks close to 300 cm–1. The IR bands originating from TFSI anions (free or interacting with Mg2+ cations) appear at about 500 cm–1, therefore they are higher than the vibrations of Mg2+ complexes.
In Table S3 in the Supporting Information, we try to relate the Raman active modes calculated in the PCM solvent for MgCl2, Mg2Cl22+, and Mg3Cl42+ aggregates and their complexes with DME to the experimental data presented in ref (24). The agreement between experiment and calculations is quite satisfactory. It may be noted that in the range of 300–400 cm–1 there are some bands computed for [Mg2Cl2(DME)4]2+ and [Mg3Cl4(DME)5]2+ complexes (i.e. without the TFSI anions) which correspond to experimental frequencies assigned in ref (24) to TFSI vibrations. Indeed, as seen in the Raman spectra in Figure 7, some bands of MgxCly complexes coincide with the positions of TFSI (or Mg-TFSI, C.f. Figure S5) modes. Therefore, the band assignment to MgxCly solvates or TFSI anions in some regions of the spectrum may be difficult.
Using the last 30,000 steps of the recorded AIMD trajectories for systems III and IIIa–IIIc, we calculated the corresponding IR spectra as the FT of the autocorrelation function of the total dipole moment of the system. The results are displayed in Figure 8. In the range 300–450 cm–1, there is an increase in the IR intensity of systems IIIa–c (with aggregated ions) with respect to system III. Based on the QC results, we may attribute this increase to vibrations of Mg2Cl22+ and Mg3Cl42+ aggregates. The band at ca. 550 cm–1 can be assigned to TFSI anions; it is the most prominent band (within the displayed energy range) shown at about 520 cm–1 in the TFSI IR spectrum in the lower panel of Figure 7.
Figure 8.

IR spectra obtained from the AIMD trajectories for systems III and IIIa–c.
Seeking confirmations of these conclusions, we applied the method used to analyze the effects of ion complexation in our recent work.44 We monitored the oscillations of Mg–Mg and Mg–Cl distances along the trajectory and calculated their FTs, obtaining the information on normal modes to which local oscillations contribute. Selected results are shown in Figure 9. The modes changing the Mg–Mg distances have low frequencies, <100 cm–1, but in IIIa and IIIc, they also have some contributions at about 350 cm–1. Therefore, the increase in the IR intensity in the spectra in Figure 8 may be attributed to vibrations involving displacements of Mg2+ ions. The vibrations changing the Mg–Cl distances appear between 150 and 250 cm–1 for all three systems IIIa–c. In the plots for systems IIIa and IIIb, one may easily note the difference between frequencies of Mg–Cl vibrations in different environments. For IIIa, the frequencies in MgCl2 are higher than for Mg2Cl22+. Likewise, in the case of the linear Mg3Cl42+ complex (system IIIb), frequencies of Mg–Cl stretches differ between the inner and the two outer Mg2+ ions.
Figure 9.

Fourier transforms of Mg–Mg and Mg–Cl interatomic distances (shown schematically in the plot) obtained from the AIMD simulations for systems IIIa–IIIc.
To prove the assignment of the 550 cm–1 band to TFSI anions, we calculated FTs of selected geometrical parameters of the anions: the S–O and S–N distances and the S–N–S angle; the plots are shown in the Supporting Information (Figure S6). The contributions to modes at 550–600 cm–1 come from bending the S–N–S angle and stretching the S–N bond. An interesting case is the plot of the FT of the S–O distances in the range 1000–1200 cm–1. The vibrational pattern obtained for some bonds in system IIIb apparently differs from the other two systems and, unlike other systems and frequency ranges, there are large differences between individual bonds within the same sample. Therefore, we analyzed this system in more detail in Figure 10.
Figure 10.

FTs of S–O bond lengths in TFSI anions obtained from AIMD trajectories. Curves for systems IIIa and IIIc are averaged over all S–O bonds in the system; transformations for individual bonds are shown for system IIIb.
In each system of IIIa–IIIc, there are two TFSI anions and 8 S–O bonds. For IIIa and IIIc, the power spectra do not differ much between bonds; therefore, for these systems, we plotted the average curves. In the case of IIIb, curves for all the eight S–O distances are displayed. Four of them are close to the average of IIIa and IIIc, but in addition, there are two other S–O pairs with significantly affected power spectra. The effect is related to TFSI–Mg2+ interactions. As shown by the RDFs, IIIb is the sole system in which one of the TFSI anions is coordinated to the Mg cation. The data for IIIa and IIIc are therefore for free TFSI anions. The four S–O stretches in the free anion in sample IIIb give the four curves close to average, and the two different pairs corresponding to two S–O bonds were either coordinated to the Mg cation or point in the opposite direction (as identified in Figure 10). This example shows that the coordination of the TFSI ion not only changes its vibrations but also allows discerning between coordinated and free bonds. In such a way, analysis of vibrational spectra obtained from AIMD simulations helps to get an atomistic insight into relations between interactions in the electrolyte and the resulting spectral changes.
3.4. Discussion
The results described in the preceding sections generally agree with the findings of ref (24) that multicationic species are formed in Mg(TFSI)2/MgCl2 solutions in DME. Depending on the electrolyte composition, solvated Mg2Cl22+ or Mg3Cl42+ complexes are predicted as stable aggregates. In the case of Mg3Cl42+, both QC-calculated energies and classical MD simulations predict the coexistence of two forms: linear and triangular; the latter form is slightly more stable and therefore dominates in simulated electrolytes. There are no experimental indications of the existence of the triangular aggregate, and the structure obtained from the single-crystal X-ray diffraction shows the linear Mg3Cl42+ complex. However, the energy difference between the two forms of Mg3Cl42+ obtained from QC calculations is 2 kcal/mol, therefore it is of the order of accuracy of computations and may be reversed, for example, by the solvent effect in the electrolyte, leading to the presence of only the linear form in real systems. Unfortunately, the attainable length of AIMD simulations is too short to observe major structural reorganization and verify this supposition.
Analysis of the abundance of different species found in the electrolytes during 400 ns of classical simulations led us to the conclusion that MgCl+ and MgCl2 appear as intermediate species in the route to Mg2Cl22+ formation. Likewise, in system IIIa, the Mg3Cl42+ complexes were effectively produced from MgCl2 and Mg2Cl22+, suggesting these two aggregates as the intermediates in the process. Such pathways agree with the reaction schemes proposed in ref (24). MD also supports the assumptions of ref (24) that the possibility of the existence of highly charged complexes may be excluded: in the simulations, we did not find aggregates with charges higher than +2. On the other hand, in our simulations, a significant amount of Mg2Cl3+ can be found during the ion association process, whereas based on Raman spectra, the presence of this aggregate as a major species was excluded in the experiment. Indeed, the calculated Raman activities show that the Mg2Cl3+ peak is distinct from the bands of other relevant MgxCly complexes, and therefore, should be easily detectable. However, we studied only 400 ns of ion aggregation, and it is possible that the intermediate Mg2Cl3+, present at this stage, will be eventually consumed in the process, and only small amounts of this complex will remain in equilibrium with Mg3Cl42+ in the final solution. Such a possibility was not excluded in ref (24).
The MD simulations and QC modeling therefore supplement the experiment by providing information on the stability of ion aggregates or their complexes with solvent molecules. Simulations also give some clues about possible intermediate species which may be present in the electrolyte at different stages of ion aggregation.
QC calculations of vibrational spectra in the implicit solvent show that most of the aggregates of interest contribute to the spectra in the same frequency range; therefore a direct comparison with experiment is not easy because the effect of a real solvent in the electrolyte may change the spectral features (frequency shifts). Analysis of changes in the spectrum for different compositions and concentrations of the electrolyte is, therefore, necessary to assign the spectral bands. QC computations combined with AIMD simulations can help in this task providing information on possible parentages of the observed bands.
4. Conclusions
Quantum chemical calculations and classical MD simulations presented in this work show that the aggregates with two or three Mg2+ ions are formed in Mg(TFSI)2/MgCl2/DME electrolytes. Mg2Cl22+ or Mg3Cl42+ are preferred as stable aggregates in solutions with the Mg(TFSI)2/MgCl2 ratio equal to 1:1 and 1:2, respectively. In the aggregation process, MgCl+, MgCl2, and Mg2Cl3+ are formed as intermediate species. Complexes of Mg2+ with Cl– anions are solvated by DME molecules, which facilitates their dissolution.
Calculations of IR and Raman spectra identified the spectral ranges in which signals of different MgxCly complexes may appear. Computation of the IR spectrum from AIMD trajectories and the analysis of possible contributions of local vibrations to the normal modes of the whole system were used to compare the results obtained for the bulk electrolyte to the data for individual complexes.
The results support the conclusions of the experimental work24 about the possible processes of ion association occurring in the electrolyte and give some insights into interactions and structure of the solution at the atomistic scale. We hope that further modeling on this subject will continue to assist the interpretation of experimental data.
Acknowledgments
This work was supported by the National Science Centre (Poland) grant no. UMO-2016/21/B/ST4/02110. The PL-Grid infrastructure was used in computations.
Supporting Information Available
The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acsomega.0c00594.
Compositions of investigated systems, structural data for investigated complexes, definition of the net binding effect for aggregates, RDFs, and integrated RDFs for selected atom pairs, changes in coordination numbers during the MD simulations, IR and Raman spectra, FT analysis of geometrical parameters of TFSI anions, and parameters of the polarizable FF (PDF)
The authors declare no competing financial interest.
Supplementary Material
References
- Aurbach D.; Gofer Y.; Lu Z.; Schechter A.; Chusid O.; Gizbar H.; Cohen Y.; Ashkenazi V.; Moshkovich M.; Turgeman R. A Short Review on the Comparison Between Li Battery Systems and Rechargeable Magnesium Battery Technology. J. Power Sources 2001, 97–98, 28–32. 10.1016/s0378-7753(01)00585-7. [DOI] [Google Scholar]
- Yoo H. D.; Shterenberg I.; Gofer Y.; Gershinsky G.; Pour N.; Aurbach D. Mg Rechargeable Batteries: an On-Going Challenge. Energy Environ. Sci. 2013, 6, 2265–2279. 10.1039/c3ee40871j. [DOI] [Google Scholar]
- Mohtadi R.; Mizuno F. Magnesium Batteries: Current State of the Art, Issues and Future Perspectives. Beilstein J. Nanotechnol. 2014, 5, 1291–1311. 10.3762/bjnano.5.143. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bucur C. B.; Gregory T.; Oliver A. G.; Muldoon J. Confession of a Magnesium Battery. J. Phys. Chem. Lett. 2015, 6, 3578–3591. 10.1021/acs.jpclett.5b01219. [DOI] [PubMed] [Google Scholar]
- Song J.; Sahadeo E.; Noked M.; Lee S. B. Mapping the Challenges of Magnesium Battery. J. Phys. Chem. Lett. 2016, 7, 1736–1749. 10.1021/acs.jpclett.6b00384. [DOI] [PubMed] [Google Scholar]
- Muldoon J.; Bucur C. B.; Oliver A. G.; Sugimoto T.; Matsui M.; Kim H. S.; Allred G. D.; Zajicek J.; Kotani Y. Electrolyte roadblocks to a magnesium rechargeable battery. Energy Environ. Sci. 2012, 5, 5941–5950. 10.1039/c2ee03029b. [DOI] [Google Scholar]
- Lapidus S. H.; Rajput N. N.; Qu X.; Chapman k. W.; Persson K. A.; Chupas P. J. Solvation Structure and Energetics of Electrolytes for Multivalent Energy Storage. Phys. Chem. Chem. Phys. 2014, 16, 21941–21945. 10.1039/c4cp03015j. [DOI] [PubMed] [Google Scholar]
- Ha S.-Y.; Lee Y.-W.; Woo S. W.; Koo B.; Kim J.-S.; Cho J.; Lee K. T.; Choi N.-S. Magnesium(II) Bis(trifluoromethane sulfonyl) Imide-Based Electrolytes with Wide Electrochemical Windows for Rechargeable Magnesium Batteries. ACS Appl. Mater. Interfaces 2014, 6, 4063–4073. 10.1021/am405619v. [DOI] [PubMed] [Google Scholar]
- Rajput N. N.; Qu X.; Sa N.; Burrell A. K.; Persson K. A. The Coupling between Stability and Ion Pair Formation in Magnesium Electrolytes from First-Principles Quantum Mechanics and Classical Molecular Dynamics. J. Am. Chem. Soc. 2015, 137, 3411–3420. 10.1021/jacs.5b01004. [DOI] [PubMed] [Google Scholar]
- Kimura T.; Fujii K.; Sato Y.; Morita M.; Yoshimoto N. Solvation of Magnesium Ion in Triglyme-Based Electrolyte Solutions. J. Phys. Chem. C 2015, 119, 18911–18917. 10.1021/acs.jpcc.5b04626. [DOI] [Google Scholar]
- Cheng Y.; Stolley R. M.; Han K. S.; Shao Y.; Arey B. W.; Washton N. M.; Mueller K. T.; Helm M. L.; Sprenkle V. L.; Liu J.; Li G. Highly Active Electrolytes for Rechargeable Mg Batteries Based on a [Mg2(μ-Cl)2]2+ Cation Complex in Dimethoxyethanre. Phys. Chem. Chem. Phys. 2015, 17, 13307–13314. 10.1039/c5cp00859j. [DOI] [PubMed] [Google Scholar]
- Terada S.; Mandai T.; Suzuki S.; Tsuzuki S.; Watanabe K.; Kamei Y.; Ueno K.; Dokko K.; Watanabe M. Thermal and Electrochemical Stability of Tetraglyme–Magnesium Bis(trifluoromethanesulfonyl)amide Complex: Electric Field Effect of Divalent Cation on Solvate Stability. J. Phys. Chem. C 2016, 120, 1353–1365. 10.1021/acs.jpcc.5b09779. [DOI] [Google Scholar]
- Tsuzuki S.; Mandai T.; Suzuki S.; Shinoda W.; Nakamura T.; Morishita T.; Ueno K.; Seki S.; Umebayashi Y.; Dokko K.; Watanabe M. Effect of the Cation on the Stability of Cation–Glyme Complexes and their Interactions with the [TFSA]− Anion. Phys. Chem. Chem. Phys. 2017, 19, 18262–18272. 10.1039/c7cp02779f. [DOI] [PubMed] [Google Scholar]
- Salama M.; Shterenberg I.; Gizbar H.; Eliaz N. N.; Kosa M.; Keinan-Adamsky K.; Afri M.; Shimon L. J. W.; Gottlieb H. E.; Major D. T.; Gofer Y.; Aurbach D. Unique Behavior of Dimethoxyethane (DME)/Mg(N(SO2CF3)2)2 Solutions. J. Phys. Chem. C 2016, 120, 19586–19594. 10.1021/acs.jpcc.6b07733. [DOI] [Google Scholar]
- He S.; Luo J.; Liu T. L. MgCl2/AlCl3 Electrolytes for Reversible Mg Deposition/Stripping: Electrochemical Conditioning or not?. J. Mater. Chem. A 2017, 5, 12718–12722. 10.1039/c7ta01769c. [DOI] [Google Scholar]
- Shimokawa K.; Matsumoto H.; Ichitsubo T. Solvation-Structure Modification by Concentrating Mg(TFSA)2–MgCl2–Triglyme Ternary Electrolyte. J. Phys. Chem. Lett. 2018, 9, 4732–4737. 10.1021/acs.jpclett.8b02209. [DOI] [PubMed] [Google Scholar]
- Fujii K.; Sogawa M.; Yoshimoto N.; Morita M. Structural Study on Magnesium Ion Solvation in Diglyme-Based Electrolytes: IR Spectroscopy and DFT Calculations. J. Phys. Chem. B 2018, 122, 8712–8717. 10.1021/acs.jpcb.8b05586. [DOI] [PubMed] [Google Scholar]
- Chaffin V. O.; Pessanha M. C.; Alves W. A. Solvation Structures Formed in the MgCl2:AlCl3 -Dimethoxyethane System: A Look Through Raman and IR Spectroscopies. Vib. Spectrosc. 2019, 100, 167–171. 10.1016/j.vibspec.2018.12.004. [DOI] [Google Scholar]
- Baskin A.; Prendergast D. Exploration of the Detailed Conditions for Reductive Stability of Mg(TFSI)2 in Diglyme: Implications for Multivalent Electrolytes. J. Phys. Chem. C 2016, 120, 3583–3594. 10.1021/acs.jpcc.5b08999. [DOI] [Google Scholar]
- Qu X.; Zhang Y.; Rajput N. N.; Jain A.; Maginn E.; Persson K. A. Computational Design of New Magnesium Electrolytes with Improved Properties. J. Phys. Chem. C 2017, 121, 16126–16136. 10.1021/acs.jpcc.7b04516. [DOI] [Google Scholar]
- Kubisiak P.; Eilmes A. Solvation of Mg2+ Ions in Mg(TFSI)2 −Dimethoxyethane Electrolytes - A View from Molecular Dynamics Simulations. J. Phys. Chem. C 2018, 122, 12615–12622. 10.1021/acs.jpcc.8b02460. [DOI] [Google Scholar]
- Vasudevan V.; Wang M.; Yuwono J. A.; Jasieniak J.; Birbilis N.; Medhekar N. V. Ion Agglomeration and Transport in MgCl2 -Based Electrolytes for Rechargeable Magnesium Batteries. J. Phys. Chem. Lett. 2019, 10, 7856–7862. 10.1021/acs.jpclett.9b03023. [DOI] [PubMed] [Google Scholar]
- Shterenberg I.; Salama M.; Yoo H. D.; Gofer Y.; Park J.-B.; Sun Y.-K.; Aurbach D. Evaluation of (CF3SO2)2N–(TFSI) based electrolyte solutions for Mg batteries. J. Electrochem. Soc. 2015, 162, A7118–A7128. 10.1149/2.0161513jes. [DOI] [Google Scholar]
- Salama M.; Shterenberg I.; J.W. Shimon L.; Keinan-Adamsky K.; Afri M.; Gofer Y.; Aurbach D. Structural Analysis of Magnesium Chloride Complexes in Dimethoxyethane Solutions in the Context of Mg Batteries Research. J. Phys. Chem. C 2017, 121, 24909–24918. 10.1021/acs.jpcc.7b05452. [DOI] [Google Scholar]
- Frisch M. J.; Trucks G. W.; Schlegel H. B.; Scuseria G. E.; Robb M. A.; Cheeseman J. R.; Scalmani G.; Barone V.; Mennucci B.; Petersson G. A.; et al. Gaussian 09, Revision D.01; Gaussian, Inc.: Wallingford CT, 2009.
- Grimme S.; Antony J.; Ehrlich S.; Krieg H. A Consistent and Accurate Ab Initio Parametrization of Density Functional Dispersion Correction (DFT-D) for the 94 Elements H-Pu. J. Chem. Phys. 2010, 132, 154104. 10.1063/1.3382344. [DOI] [PubMed] [Google Scholar]
- Phillips J. C.; Braun R.; Wang W.; Gumbart J.; Tajkhorshid E.; Villa E.; Chipot C.; Skeel R. D.; Kalé L.; Schulten K. Scalable Molecular Dynamics with NAMD. J. Comput. Chem. 2005, 26, 1781–1802. 10.1002/jcc.20289. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jorgensen W. L.; Maxwell D. S.; Tirado-Rives J. Development and Testing of the OPLS All-Atom Force Field on Conformational Energetics and Properties of Organic Liquids. J. Am. Chem. Soc. 1996, 118, 11225–11236. 10.1021/ja9621760. [DOI] [Google Scholar]
- Canongia Lopes J. N.; Deschamps J.; Pádua A. A. H. Modeling Ionic Liquids Using a Systematic All-Atom Force Field. J. Phys. Chem. B 2004, 108, 2038–2047. 10.1021/jp0362133. [DOI] [Google Scholar]
- Köddermann T.; Paschek D.; Ludwig R. Molecular Dynamic Simulations of Ionic Liquids: A Reliable Description of Structure, Thermodynamics and Dynamics. ChemPhysChem 2007, 8, 2464–2470. 10.1002/cphc.200700552. [DOI] [PubMed] [Google Scholar]
- Anderson P. M.; Wilson M. R. Developing a Force Field for Simulation of Poly(ethylene oxide) Based upon ab Initio Calculations of 1,2-Dimethoxyethane. Mol. Phys. 2005, 103, 89–97. 10.1080/00268970412331293811. [DOI] [Google Scholar]
- Wang J.; Wolf R. M.; Caldwell J. W.; Kollman P. A.; Case D. A. Development and Testing of a General Amber Force Field. J. Comput. Chem. 2004, 25, 1157–1174. 10.1002/jcc.20035. [DOI] [PubMed] [Google Scholar]
- Shi Y.; Xia Z.; Zhang J.; Best R.; Wu C.; Ponder J. W.; Ren P. Polarizable Atomic Multipole-Based AMOEBA Force Field for Proteins. J. Chem. Theory Comput. 2013, 9, 4046–4063. 10.1021/ct4003702. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lamoureux G.; Roux B. Modeling Induced Polarization with Classical Drude Oscillators: Theory and Molecular Dynamics Simulation Algorithm. J. Chem. Phys. 2003, 119, 3025–3039. 10.1063/1.1589749. [DOI] [Google Scholar]
- Borodin O. Polarizable Force Field Development and Molecular Dynamics Simulations of Ionic Liquids. J. Phys. Chem. B 2009, 113, 11463–11478. 10.1021/jp905220k. [DOI] [PubMed] [Google Scholar]
- Borodin O.; Smith G. D. Development of Quantum Chemistry-Based Force Fields for Poly(ethylene oxide) with Many-Body Polarization Interactions. J. Phys. Chem. B 2003, 107, 6801–6812. 10.1021/jp027537e. [DOI] [Google Scholar]
- Feller S. E.; Zhang Y.; Pastor R. W.; Brooks B. R. Constant Pressure Molecular Dynamics Simulation: The Langevin Piston Method. J. Chem. Phys. 1995, 103, 4613–4621. 10.1063/1.470648. [DOI] [Google Scholar]
- Martyna G. J.; Tobias D. J.; Klein M. L. Constant Pressure Molecular Dynamics Algorithms. J. Chem. Phys. 1994, 101, 4177–4189. 10.1063/1.467468. [DOI] [Google Scholar]
- Darden T.; York D.; Pedersen L. Particle Mesh Ewald: An Nlog(N) Method for Ewald Sums in Large Systems. J. Chem. Phys. 1993, 98, 10089–10092. 10.1063/1.464397. [DOI] [Google Scholar]
- VandeVondele J.; Krack M.; Mohamed F.; Parrinello M.; Chassaing T.; Hutter J. QUICKSTEP: Fast and Accurate Density Functional Calculations Using a Mixed Gaussian and Plane Waves Approach. Comput. Phys. Commun. 2005, 167, 103–128. 10.1016/j.cpc.2004.12.014. [DOI] [Google Scholar]
- Hutter J.; Iannuzzi M.; Schiffmann F.; VandeVondele J. CP2K: Atomistic Simulations of Condensed Matter Systems. Wiley Interdiscip. Rev.: Comput. Mol. Sci. 2014, 4, 15–25. 10.1002/wcms.1159. [DOI] [Google Scholar]
- Goedecker S.; Teter M.; Hutter J. Separable Dual-Space Gaussian Pseudopotentials. Phys. Rev. B: Condens. Matter Mater. Phys. 1996, 54, 1703–1710. 10.1103/physrevb.54.1703. [DOI] [PubMed] [Google Scholar]
- Forbert H.; Kohlmeyer A.. Fourier: Power Spectrum of Autocorrelation Function. http://cpmd.org/ last accessed 31 Jan, 2020.
- Wróbel P.; Kubisiak P.; Eilmes A. Interactions in Sodium Bis(fluorosulfonyl)imide/1-Ethyl-3-methylimidazolium Bis(fluorosulfonyl)imide Electrolytes for Na-Ion Batteries: Insights from Molecular Dynamics Simulations. J. Phys. Chem. C 2019, 123, 14885–14894. 10.1021/acs.jpcc.9b01208. [DOI] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.