Abstract

After large-scale and long-term waterflooding, reservoir physical properties such as the pore throat structure and rock wettability may change. In this paper, the relative permeability curves under different water injection volumes through core-flood experiments were used to characterize the comprehensive changes of various reservoir physical properties at high water-cut stage. The novel concept of “water cross-surface flux” was proposed to characterize the cumulative flushing effect on the reservoir by injected water, and a novel method for inverted five-spot reservoir simulation at high water-cut stage based on time-varying relative permeability curves was established. From the relative permeability curves measured through two cores from the X oilfield under different water injection volumes (100, 500, 1000, 1500, and 2000 PV), it is found that with the increase of injected water volume, the two-phase co-flow zone becomes wider, the water permeability under residual oil saturation increases, and the residual oil saturation decreases. A waterflooding core model was established, simulated, and verified by the method proposed in this paper. It is found that using time-varying permeability curves for simulation, the highest oil recovery factor (61.58%) can be obtained with injected water volume up to 2000 PV, and the purpose of improved oil recovery (IOR) can be achieved by high water injection volume, but the increment is only approximately 10%. Besides, a waterflooding model of an inverted five-spot reservoir unit based on the X oilfield was also established, simulated, and analyzed. Simulation results have shown that no matter which set of core permeability curves measured from 100 to 2000 PV is directly used alone, the oil recovery factor will be simulated inaccurately. The findings of this study can help in better understanding the quantitative description of the oil recovery changes with time-varying reservoir physical properties in high water-cut reservoirs during waterflooding.
1. Introduction
Waterflooding is by far the most widely applied method in improving oil recovery.1−7 However, large-scale and long-term water injection will cause reservoirs to enter the high water-cut stage, even the extra-high water-cut stage, and the yield will seriously drop in the meantime.8−11 For decades, the oilfield development industry in China has gradually formed a technology series featuring water injection technology.12 Meanwhile, most oilfields in China have entered the stage of high water-cut and high oil recovery. According to statistics, most of the large old oilfields (Daqing oilfield, Shengli oilfield, and Zhongyuan oilfield) have entered or approached the ultrahigh water-cut stage, and the average water-cut in these oilfields is above 90%.13,14
Many scholars15−23 have found that after large-scale and long-term waterflooding, reservoir physical properties such as the pore throat structure and rock wettability may change, thus leading to the increase of displacement efficiency and the decrease of residual oil saturation, which can usually improve the development effect on reservoirs. Through a number of waterflooding experiments on different types of cores, Loahardjo et al.24 confirmed that in the process of sequential waterflooding, the residual oil saturation decreased significantly from one flood to the next. Loahardjo et al.25 also demonstrated the systematic decrease of residual oil saturation during sequential waterflooding by nuclear magnetic resonance imaging measurements of in situ saturations. Laboratory tests on sandstone and limestone also showed that, even without changing the salinity, the oil recovery also increased from one flood to the next. Yang et al.26 conducted several waterflooding experiments with long cores taken from the production wells at ultrahigh water-cut period (average water-cut 91.6%) in the Shuanghe oilfield and found that with the increase of flooding degree, the overall porosity and permeability of the reservoir became higher and the wettability changed to be more hydrophilic. Comparing the relative permeability curves under different water injection volumes (10 vs 1400 PV, PV is the short form of pore volume), they found that the water saturation of the oil–water crossover point increased from 51.19 to 55.63%, the oil–water co-flow zone increased from 52.42 to 55.63%, and the water relative permeability under residual oil saturation increased from 16.63 to 28.36% on the map of relative permeability curves. Wu27 also conducted the experimental research on reservoir cores from the Shengtuo oilfield (average water-cut, 96%), which had been developed with waterflooding for 39 years, and revealed that a number of solid particles in the sandstone reservoir were flushed out during long-term waterflooding, which led to a better permeability. She also found that the rock wettability changed from lipophilic to strongly hydrophilic, which, as a result, increased the displacement efficiency and oil recovery. Han et al.28 had selected 12 cores from the Fuyu oilfield at high water-cut stage (average water-cut, 86.55%) for experimental research and found that with the increase of injected water volume (10–100 PV), the oil–water co-flow zone on the map of relative permeability curves became wider with an average increase of 20.25%, the residual oil saturation reduced with an average decrease of 20.78%, and the endpoint value of the water phase slightly increased with an average increase of 10.71%. By summing up these studies, it can be concluded that with the increase of water injection volume, rock solid particles and cement between pores may fall off, the pore throat sizes become larger and larger, and the wettability may change to be more hydrophilic, which eventually leads to a great decrease of residual oil saturation and a significant increase of displacement efficiency.
Although lots of studies have confirmed that reservoir properties may alter during the process of high-volume water injection, the current commercial simulators fail to quantitatively describe the oil recovery changes with time-varying reservoir physical properties,29−31 which cannot adapt to the actual demand of effective waterflooding for reservoir development at high water-cut stage and also increases the difficulty for history matching.32,33 Therefore, it is urgent to carry out research on the simulation method that can characterize the effects of time-varying reservoir physical properties on the development of high water-cut reservoirs.
Based on statistical analysis of the actual production performance data and field core plugs, some researchers29,30,45,47,48,50,51 intended to find the time-varying relationships between different reservoir physical parameters by fitting analysis and then establish a specific model to simulate the developing process of high water-cut reservoirs during waterflooding. However, most of the statistical analysis data are obtained from core-flood experiments; whether the micro laboratory data can be directly applied to the macro actual reservoir may need further demonstration. Moreover, the statistical analysis data are usually obtained from and applied for a specific reservoir; thus, the specific model cannot be directly extended to other reservoirs for simulation applications.
Through the experimental analysis, Zhang et al.34 summarized six main factors that may affect oil recovery of high-volume water injection reservoirs, including three microscopic factors and three macroscopic factors. The three microscopic factors are the mineral composition, the pore throat structure, and the rock wettability, and the three macroscopic factors are the residual oil saturation, the oil displacement efficiency, and the relative permeability. They referred that it was the above three microscopic mechanisms that led to the changes of the three macroscopic properties, and the changes of the other five factors above can be fully embodied in the changes of relative permeability curves. Relative permeability is a function of the wetting phase saturation, which is also affected by petrophysical properties (including pore throat structure and wettability), fluid properties, and experimental conditions (including saturation history, temperature, and displacement pressure difference).35−40 Under the same fluid properties and experimental conditions, the influence of petrophysical property changes on fluid flow can be reflected in different relative permeability curves synthetically, which are able to characterize the relative transport capability of each fluid.41−43 Therefore, the authors consider that the changing characteristics of different reservoir physical properties during the high-volume water injection process can be characterized by different relative permeability curves comprehensively.
Relative permeability curves can be estimated by laboratory experiments or prediction models.44 In the lab, the oil–water relative permeability curves under different water injection volumes can be easily measured, and the comprehensive time-varying characteristics of reservoir physical properties can be characterized by different relative permeability curves. If relative permeability curves corresponding to different water injection volumes measured through core-flood experiments can be reasonably used in the simulation process of actual high water-cut reservoirs, then the characterization problem of time-varying reservoir properties can be solved. Guided by this train of thought, taking the inverted five-spot reservoir unit at high water-cut stage as an example, the novel concept of “water cross-surface flux (CF)” was first proposed to characterize the cumulative flushing effect on the reservoir by injected water, the conversion relationship of water injection volume between the laboratory core and actual inverted five-spot reservoir was deduced, and a universal reservoir simulation method was established to realize characterization of time-varying physical properties in high water-cut reservoirs based on time-varying relative permeability curves by interpolating calculation in the simulator, which can not only avoid errors of the statistical analysis data but also be easily applied to other waterflooding reservoirs. Then, a waterflooding core model was established and simulated to verify the reliability and accuracy of using time-varying relative permeability curves for simulation, and a waterflooding model of an inverted five-spot reservoir unit based on the X oilfield was also established, simulated, and analyzed for an application using the new simulation method proposed in this paper.
2. Computational Methods
2.1. Method Overview
A new component is set in the simulator to receive time-varying values from interpolating calculation with different relative permeability curves. For a specific reservoir (or core), in addition to setting the initial water component WATER-INI (corresponding to the irreducible water saturation Swc), injected water WATER-INJ is regarded as a new water component. Before simulation, it is necessary to input a series of mole fractions of injected water component (M1, M2, M3, ...) and the corresponding series of relative permeability curves (KR1, KR2, KR3, ...) under the different mole fractions as the basis for interpolating calculation. The variable PV is generally used to measure the volume of injected water, defined as the ratio of cumulative water volume injected into the reservoir (or core) to its total pore volume. In the oil–water system, assuming that the molar volume for both initial and injected water components is equal at all temperatures and pressures, the mole fraction M of the injected water component for the oil zone can be calculated by PV, and the expression is as follows
| 1 |
For core-flood simulation, the mole fraction of the injected water component can be calculated directly by eq 1 above. It should be noted that due to the huge size difference between the core and the reservoir, the water injection volume in core-flood experiments can reach dozens, hundreds, or even thousands of PV, but in actual waterflooding reservoirs, the water injection volume is always much smaller, which is usually less than 1 PV. Therefore, the water injection volume of the laboratory core (PVc) cannot be directly equivalent to that of the actual reservoir (PVr). Generally, a series of core-scale relative permeability curves (KR1, KR2, KR3, ...) under different water injection volumes (PVc1, PVc2, PVc3, ...) can be obtained directly from laboratory core-flood experiments. If the conversion relationship between PVc and PVr can be established, then the different relative permeability curves can be used in the simulation process of the actual reservoir based on time-varying relative permeability curves by interpolating calculation in the simulator.
2.2. Establishment of the Conversion Relationship between PVr and PVc
The variable PV is a macroscopic characterization about the cumulative water injection volume, which cannot describe the cumulative flushing effect by water injection at the micro level. Lots of scholars45−47 tended to use the water crossing ratio (R) to characterize the cumulative flushing intensity in high water-cut reservoirs, which is defined as the ratio of total water volume flowing through one certain grid cell to the pore volume of the grid cell, namely
| 2 |
The author holds that there are three shortcomings of using R to characterize the cumulative flushing intensity of reservoirs by injected water:
-
(1)
The calculation results will heavily depend on the size of the meshing grid. If the grid is meshed too large, it will not be able to accurately reflect the flushing effect by injected water.
-
(2)
The actual water flow rate nearby the injection wells is certainly far larger than that away from the well. If the grid is meshed too small, unrealistic calculation values will be obtained.
-
(3)
The calculation results will be meaningful only under appropriate size of grid cells; besides, the simulation of refined blocks cannot be performed as well.48
Thus, based on the previous studies,48−51 the novel concept of water cross-surface flux (CF) is proposed to characterize the cumulative flushing effect of high-volume water injection on the reservoir, defined as the cumulative injected water volume through a unit water cross-surface, namely
| 3 |
For simplification, it is assumed that the volume of injected water flowing through each cross-surface is stable, and the oil saturation before the cross-surface has reduced to the residual oil saturation.
For laboratory cores, assuming they are homogeneous and the waterflooding front advances evenly, a one-dimensional waterflooding core model is established as shown in Figure 1.
Figure 1.
One-dimensional waterflooding core model.
In the one-dimensional coordinate system shown in Figure 1, taking the integral average
value of the water cross-surface flux along the x direction as the average water cross-surface flux 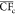 of the entire core, eq 4 can be obtained after t min
of flooding.
of the entire core, eq 4 can be obtained after t min
of flooding.
 |
4 |
Then, eq 4 can be solved to yield the following expression
| 5 |
For actual reservoirs, the determination of water cross-surface flux is related to the pattern of wells. Taking the typical inverted five-spot reservoir with vertical wells as an example, assuming that the formation is homogeneous, isopachous, and isotropic, an ideal unit model is established as shown in Figure 2.
Figure 2.
Ideal inverted five-spot reservoir unit model.
In the polar coordinate system shown in Figure 2, there is one injection well (Wellinj) and four production wells (Wellpro1, Wellpro2, Wellpro3, and Wellpro4) in the unit and the
injected water flows radially along the r direction.
Taking the integral average value of the water cross-surface flux
in the direction r as the average water cross-surface
flux  of the whole reservoir, eq 6 can be obtained after waterflooding
for time t (days)
of the whole reservoir, eq 6 can be obtained after waterflooding
for time t (days)
 |
6 |
Then, eq 7 can be obtained by integration
| 7 |
Since Lw ≫ rw
| 8 |
Generally, the cores used for flooding experiments are always from the corresponding actual reservoirs, so their porosity, irreducible water saturation, and residual oil saturation can be regarded as the same.
According to the equivalent average water cross-surface flux of the core and the reservoir, eq 9 can be obtained
| 9 |
Since Lw ≫ Lc, eq 9 can be simplified as
| 10 |
As eq 10 shows, the conversion relationship between PVc and PVr in inverted five-spot reservoirs based on equivalent water cross-surface flux has been established and obtained.
In practical applications, different relative permeability curves (KR1, KR2, KR3, ...) under different water injection volumes (PVc1, PVc2, PVc3, ...) can be first measured in the laboratory with core-flood experiments, and the corresponding water injection volume of the actual inverted five-spot reservoir (PVr1, PVr2, PVr3, ...) can be obtained by eq 10. Then, the corresponding series of mole fractions of the injected water component (M1, M2, M3, ...) can be calculated according to eq 1. Finally, the different mole fractions of the injected water component (M1, M2, M3, ...) and the corresponding relative permeability curves (KR1, KR2, KR3, ...) are input into the simulator for interpolating calculation and simulation. Using this method, the changes of various physical properties in high water-cut reservoirs during the waterflooding process can be characterized by time-varying relative permeability curves measured with core-flood experiments.
3. Results and Discussion
3.1. Relative Permeability Curves Measured by Core-Flood Experiments
In this study, the relative permeability curves of two cores from the X oilfield under water injection volumes of 100, 500, 1000, 1500, and 2000 PV are measured respectively, the detail of which is explained in Section 5. Based on the experiments and calculation results, two series of relative permeability curves related to two cores under different water injection volumes are plotted respectively as shown in Figure 3.
Figure 3.
Relative permeability curves under different water injection volumes for (a, b) core no. 01 and (c, d) core no. 02.
According to Figure 3, the residual oil saturation of two cores under different water injection volumes is recorded and the corresponding water permeability under residual oil saturation is calculated, as listed in Table 1 below.
Table 1. Residual Oil Saturation and the Corresponding Water Permeability under Residual Oil Saturation of Two Cores and under Different Water Injection Volumes.
| core no. | irreducible water saturation (%) | water injection volume (PV) | residual oil saturation (%) | water permeability under residual oil saturation (mD) |
|---|---|---|---|---|
| 01 | 20.1 | 100 | 34.6 | 25.0 |
| 20.1 | 500 | 32.0 | 30.6 | |
| 20.1 | 1000 | 31.4 | 33.4 | |
| 20.1 | 1500 | 30.8 | 35.6 | |
| 20.1 | 2000 | 29.8 | 50.1 | |
| 02 | 21.2 | 100 | 35.2 | 53.8 |
| 21.2 | 500 | 25.4 | 56.4 | |
| 21.2 | 1000 | 21.7 | 59.0 | |
| 21.2 | 1500 | 18.5 | 65.4 | |
| 21.2 | 2000 | 15.9 | 69.2 |
It can be seen in Figure 3 and Table 1 that for a certain core, with the increase of injected water volume, the two-phase co-flow zone becomes wider, the water permeability under residual oil saturation increases, and the residual oil saturation decreases, which are consistent with former scholars’ conclusions mentioned before. Meanwhile, due to the increase of water injection rate, the decrease of residual oil saturation of core no. 02 is significantly greater than that of core no. 01. In addition, it is obvious that the water relative permeability of two cores under residual oil saturation in Figure 3 is quite low, which reflects the poor flow capability of two-phase fluids in the reservoir.
3.2. Core Simulation
To preliminarily verify whether the proposed simulation method is reliable, a model of core no. 01 is established as an example using the five sets of relative permeability curves under different water injection volumes determined through the core-flood experiments as shown in Figure 3a and the corresponding mole fractions of the injected water component are calculated by eq 1. The basic parameters of the core no. 01 model are listed in Table 2, and the schematic diagram is shown in Figure 4 below.
Table 2. Basic Parameters of the Core No. 01 Model.
| parameters | values |
|---|---|
| grid length | 53 × 1 mm |
| grid width | (9–25) × 1 mm |
| grid height | (9–25) × 1 mm |
| porosity | 35.6% |
| permeability | 2460.8 mD |
| temperature | 32 °C |
| water injection rate | 1.0 mL/min |
| injected water volume | 2000 PV |
| viscosity of injected water and formation water | 0.88 mPa·s (32 °C) |
| density of injected water and formation water | 1.00 g/cm3 |
| oil viscosity | 397.26 mPa·s (32 °C) |
| oil density | 0.88 g/cm3 |
Figure 4.
Schematic diagram of the core no. 01 model.
To compare the simulation differences between using time-varying relative permeability curves and a certain set of relative permeability curves measured under the corresponding different water injection volumes (100, 500, 1000, 1500, and 2000 PV), the core-flood simulation process only changing relative permeability curves is conducted. After six various kinds of relative permeability curves are used for simulation respectively, the corresponding curves of the oil recovery factor are compared and shown in Figure 5 below.
Figure 5.
Simulated oil recovery factor curves for core no. 01 using different permeability curves: (a) 0% ≤ oil recovery factor ≤ 25% and (b) 25% ≤ oil recovery factor ≤ 65%.
It can be seen in Figure 5 that obviously different oil recovery factors can be obtained using time-varying relative permeability curves and using a certain set of relative permeability curves measured under the corresponding water injection volume for simulation. When the water injection volume is only 1 PV, the oil recovery factor is nearly 20%, and when the water injection volume reaches 50 PV, the oil recovery factor is more than 50%. According to the simulation results, it is apparent that the purpose of improved oil recovery (IOR) can be achieved by high water injection volume, but the increment is only approximately 10%, and the main growth stage of oil recovery factor is still concentrated upon the low water injection volume stage (<100 PV). Obviously, only using the relative permeability curves measured at PVcore1 = 100 for simulation, whose actual injected water volume is up to 2000 PV, may result in a lower oil recovery factor, which is only 56.68%. Meanwhile, when using time-varying permeability curves for simulation, the highest oil recovery factor, 61.58%, can be obtained with the injected water volume up to 2000 PV.
Since the core size is quite small, the mole fraction of the injected water component rises very fast, and the time-varying relative permeability curves are quickly interpolated depending on the relative permeability curves measured at PVcore1 = 2000. Thus, the simulation result of the oil recovery factor obtained using time-varying relative permeability curves is very close to that obtained using the relative permeability curves measured at PVcore1 = 2000.
For ease of observation, three oil recovery factor curves simulated using the time-varying relative permeability curves and another two relative permeability curves measured at PVcore1 = 100 and 2000 under the low water injection volume stage (<4 PV) are shown in Figure 6.
Figure 6.
Comparison of different oil recovery factor curves using different sets of relative permeability curves under the low water injection volume stage (<4 PV).
It can be inferred from Figure 6 that when the water injection volume is less than 1 PV, the time-varying relative permeability curves mainly depend on the relative permeability curves measured at PVcore1 = 100 for interpolating calculation. When the water injection volume is more than 1 PV, the time-varying relative permeability curves mainly depend on the relative permeability curves measured at PVcore1 = 2000 for interpolating calculation.
Generally, oil recovery ER can be expressed as the product of sweep efficiency EV and displacement efficiency ED, namely
| 11 |
In eq 11, displacement efficiency ED can be determined by relative permeability curves and calculated by eq 12 as follows
| 12 |
According to eq 12 and Table 1 above, the actual displacement efficiency for core no. 01 under different water injection volumes is calculated, as given in Table 3.
Table 3. Actual Displacement Efficiency for Core No. 01 under Different Water Injection Volumes.
| core no. | PVcore1 | Swc (%) | Sor (%) | ED (%) |
|---|---|---|---|---|
| 01 | 100 | 20.1 | 34.6 | 56.696 |
| 500 | 20.1 | 32.0 | 59.950 | |
| 1000 | 20.1 | 31.4 | 60.701 | |
| 1500 | 20.1 | 30.8 | 61.452 | |
| 2000 | 20.1 | 29.8 | 62.703 |
As shown in Figure 7 below, two oil recovery factor curves simulated using time-varying relative permeability curves and another relative permeability curve measured at PVcore1 = 100 are plotted and the actual displacement efficiency values listed in Table 3 are marked.
Figure 7.
Comparison of different oil recovery factor curves and the actual displacement efficiency points.
Since the core size is quite small and the water injection volume is quite huge comparatively, the sweep efficiency of the small core is close to 100%, and the oil recovery of the waterflooding core is approximately equal to the displacement efficiency. It can be seen from Figure 7 that when the water injection volume is less than 1000 PV, the actual displacement efficiency points are closer to the oil recovery curve simulated using the relative permeability curves measured at PVcore1 = 100. Apparently, this is also because the size scale of the experimental core is quite small, the mole fraction of the injected water component and the water-cut rise very fast, and the time-varying relative permeability curves are quickly interpolated and calculated mainly depending on the relative permeability curves measured at PVcore1 = 2000, however, which is quite different from the water-cut rising process in the actual reservoir, which is quite lager in size scale. Therefore, it also indirectly illustrates the necessity and significance of establishing the conversion relationship between PVc and PVr proposed in this paper. When the water injection volume is greater than 1000 PV, the oil recovery factor curve simulated based on time-varying relative permeability curves is significantly close to the actual displacement efficiency points corresponding to different water injection volumes. However, the oil recovery factor curve simulated based on the relative permeability curves measured at PVcore1 = 100 clearly deviates from the actual displacement efficiency points. Moreover, the degree of deviation gradually increases with the increase of injected water volume. Therefrom, the results have proven that simulation for high water-cut reservoirs based on time-varying relative permeability curves proposed in this paper is necessary and more accurate from the core scale.
3.3. Inverted Five-Spot Reservoir Simulation
Taking the inverted five-spot reservoir unit of the X oilfield as an example, the simulation method based on time-varying relative permeability curves proposed in this paper is also used for application. The physical parameters of the actual reservoir are the same as those of core no. 01, and other basic parameters are mentioned in Table 4 below. The schematic diagram of the inverted five-spot reservoir unit model of the X oilfield is shown in Figure 8.
Table 4. Basic Parameters of the Inverted Five-Spot Reservoir Unit of the X Oilfield.
| parameters | values |
|---|---|
| grid length | 29 × 4 m |
| grid width | 29 × 4 m |
| grid height | 5 × 1 m |
| injector–producer spacing | 82 m |
| wellbore radius | 0.10 m |
| water injection rate | 100 m3/day |
Figure 8.
Schematic diagram of the inverted five-spot reservoir unit model of the X oilfield.
According to the simulation method proposed in this paper, the different water injection volumes between the laboratory core and the actual reservoir based on equivalent water cross-surface flux are converted with eq 10, and the corresponding mole fractions of the injected water component are calculated by eq 1, as listed in Table 5.
Table 5. Conversion of Simulation Parameters.
| PVc | Lc (m) | Lw (m) | Sor (%) | Swc (%) | rw (m) | PVr | M |
|---|---|---|---|---|---|---|---|
| 100 | 0.053 | 82 | 0.346 | 0.201 | 0.10 | 0.0833 | 0.2930 |
| 500 | 0.053 | 82 | 0.32 | 0.201 | 0.10 | 0.2074 | 0.5078 |
| 1000 | 0.053 | 82 | 0.314 | 0.201 | 0.10 | 0.3594 | 0.6413 |
| 1500 | 0.053 | 82 | 0.308 | 0.201 | 0.10 | 0.5114 | 0.7179 |
| 2000 | 0.053 | 82 | 0.298 | 0.201 | 0.10 | 0.6639 | 0.7676 |
It can be seen from the conversion results that under the premise of equivalent water cross-surface flux, when the water injection volume in the laboratory core reaches 2000 PV, the corresponding water injection volume in the actual inverted five-spot reservoir unit is only less than 0.7 PV, which is consistent with the conclusion summarized in the practical waterflooding oilfields. In other words, if the same residual oil saturation in cores and actual reservoirs is reached, a very huge amount of water, which is up to thousands of times or even tens of thousands of times of PV, must be injected into cores.
The converted series of mole fractions of the injected water component and the corresponding series of relative permeability curves are input into the simulator by means of component interpolation calculation, and only the relative permeability curves are changed in the simulation process. Like the core simulation before, six different kinds of relative permeability curves are used for simulation respectively, and various simulated oil recovery factor curves and water-cut curves are compared and shown in Figure 9 below.
Figure 9.
Simulated oil recovery factor curves for the inverted five-spot reservoir unit of the X oilfield using different permeability curves: (a) 0 ≤ injected water volume ≤ 0.7, (b) 0 ≤ injected water volume ≤ 0.2, and (c) 0.2 ≤ injected water volume ≤ 0.7. (d) Simulated water-cut curves for the inverted five-spot reservoir unit of the X oilfield using different permeability curves.
It can be seen in Figure 9a–c that the oil recovery factor curve simulated based on time-varying relative permeability curves is quite different from that simulated using a certain set of relative permeability curves measured under the corresponding water injection volume. Simulation results have shown that no matter which set of core permeability curves measured from 100 to 2000 PV is directly used alone, the oil recovery factor will be simulated inaccurately. In Figure 9d, when the water injection volume reaches 0.7 PV, the water-cut in the production well is greater than 90%, which illustrates that this reservoir unit has entered the ultrahigh water-cut stage. Apparently, the water breakthrough time simulated based on time-varying relative permeability curves is between other simulated values. When the water injection volume is greater than 0.4 PV, the water-cut curve obtained using time-varying relative permeability curves tends to the water-cut curve obtained using relative permeability curves measured at PVcore1 = 2000. This indicates that the time-varying relative permeability curves mainly depend on the relative permeability curves measured at PVcore1 = 2000 for interpolating calculation, which is consistent with the water-cut change law during the later period of core-flood simulation above.
However, it can be seen that the change laws of various oil recovery factor curves simulated in the actual reservoir unit are different from that of core simulation, and the oil recovery factor simulated using the relative permeability curves measured at PVcore1 = 2000 is significantly the lowest. In fact, this is due to the differences in the range of water saturation between the reservoir unit and the core. As mentioned before, the experimental results have shown poor flow capability of two-phase fluids in the reservoir. Because the core size is very small, the water saturation of any simulated grid cell is greater than 0.6 when the injected water volume is up to 2000 PV. As shown in Figure 3a,b, when water saturation is greater than 0.6, the water relative permeability measured at PVcore1 = 2000 is obviously the highest, and the mobility of water is relatively the best. Thus, the simulated oil recovery factor is also the highest. Nevertheless, as can be seen in Figure 10, when the water injection volume of the reservoir unit reaches 0.7 PV, the water saturation of each simulated grid cell is just between 0.3 and 0.6. Even the water saturations of most grid cells are below 0.4, where the corresponding water relative permeability measured at PVcore1 = 2000 is obviously the lowest, as shown in Figure 3a,b as well. Therefore, the mobility of water is relatively the worst, and the simulated oil recovery factor is naturally the lowest correspondingly.
Figure 10.
Water saturation distribution of the reservoir unit simulated based on time-varying relative permeability curves with water injection volume of 0.7 PV.
4. Summary and Conclusions
Based on time-varying relative permeability curves, this paper proposed, validated, and applied a simulation method for an inverted five-spot reservoir at high water-cut stage. By summarizing the research process, the following significant conclusions have been obtained:
-
(1)
The comprehensive changes of various reservoir physical properties at the high water-cut stage during waterflooding can be characterized by measuring different relative permeability curves under different water injection volumes through laboratory core-flood experiments.
-
(2)
The novel concept of water cross-surface flux (CF) was proposed to characterize the cumulative flushing effect on the reservoir by injected water, the conversion relationship of water injection volume between the laboratory core and the actual inverted five-spot reservoir was deduced, and a simulation method for an inverted five-spot reservoir at high water-cut stage based on time-varying relative permeability curves was established.
-
(3)
The relative permeability curves of two cores from the X oilfield under different water injection volumes (100, 500, 1000, 1500, 2000 PV) were measured respectively. It is found that for a certain core, with the increase of injected water volume, the two-phase co-flow zone becomes wider, the water permeability under residual oil saturation increases, and the residual oil saturation decreases.
-
(4)
A waterflooding core model was established, simulated, and verified by the method proposed in this paper. It is found that using time-varying permeability curves for simulation, the highest oil recovery factor (61.58%) can be obtained with injected water volume up to 2000 PV.
-
(5)
According to the core-flood simulation results, it is apparent that the purpose of IOR can be achieved by high water injection volume, but the increment is only approximately 10%, and the main growth stage of oil recovery factor is still concentrated upon the low water injection volume stage (<100 PV).
-
(6)
A waterflooding inverted five-spot reservoir unit model of the X oilfield was also established, simulated, and analyzed. Under the premise of equivalent water cross-surface flux, when the water injection volume in the laboratory core reaches 2000 PV, the corresponding water injection volume in the actual inverted five-spot reservoir unit is only less than 0.7 PV.
-
(7)
Actual reservoir simulation results have shown that no matter which set of core permeability curves measured from 100 to 2000 PV is directly used alone, the oil recovery factor will be simulated inaccurately. When the water injection volume reaches 0.7 PV, the water-cut in the production well is greater than 90%, which illustrates that the reservoir has entered the ultrahigh water-cut stage.
5. Experimental Section
According to the national standard GB/T 28912-2012 in China,52 the relative permeability curves are usually measured in the laboratory by the unsteady-state method with water injection volume less than 30 PV. To study the change law of relative permeability curves under high-volume water injection, the relative permeability curves of two cores from the X oilfield under water injection volumes of 100, 500, 1000, 1500, and 2000 PV are measured respectively.
5.1. Experimental Instruments
The experimental instruments include an incubator, a high-pressure plunger pump (accuracy: ≤1%), two six-way valves, four pressure gauges (accuracy: ≤0.5%), an oil container, a water container, a core holder, a hand pump, a measuring cylinder, a thermometer, an electronic balance (sensitivity value: 0.01 g), a stopwatch (division value: 0.01 s), and a caliper (division value: 0.02 mm). The experimental process for relative permeability curve measurement is shown in Figure 11 below.
Figure 11.
Experimental process for relative permeability curves measurement.
5.2. Experimental Samples and Fluids
Two cores from the X oilfield are selected for waterflooding experiments. The basic parameters of two cores and designed experimental parameters are given in Table 6 below.
Table 6. Basic Parameters of Cores and Designed Experimental Parameters.
| parameters | core no. 01 | core no. 02 |
|---|---|---|
| well depth (m) | 1247.71 | 1287.93 |
| length (cm) | 5.319 | 4.445 |
| diameter (cm) | 2.442 | 2.433 |
| porosity (%) | 35.6 | 38.1 |
| gas permeability (mD) | 2460.8 | 2482.4 |
| experimental temperature (°C) | 32 | 32 |
| water injection rate (mL/min) | 1 | 1–7.5 |
| total water injection volume (PV) | 2000 | 10–1990 |
| confining pressure (MPa) | 2 | 2 |
The simulated formation water with salinity of 10 000 mg/L is selected as the experimental water, whose viscosity is 0.88 mPa·s at the test temperature. The simulated reservoir oil is selected as the experimental oil, and its viscosity is 397.26 mPa·s at the test temperature.
5.3. Experiment Procedures
The detailed procedure for measurement experiments is as follows:
-
(1)
After washing, drying, and cooling two cores, measure their lengths, radii, and absolute permeability.
-
(2)
Saturate two cores with the simulated formation water, weigh, and calculate the pore volume and porosity.
-
(3)
Put two cores into the core holder respectively, establish the irreducible water saturation with the oil-flooding method, and calculate the irreducible water saturation and the corresponding oil phase permeability.
-
(4)
Perform waterflooding experiments according to the designed flow rate of displacement.
-
(5)
Accurately record the water breakthrough time, the cumulative oil/liquid production, and the corresponding displacement pressure difference.
-
(6)
Record the oil output volume continuously.
-
(7)
When the total injected water volume reaches 2000 PV, calculate the corresponding water phase permeability under residual oil saturation and complete the experiments.
-
(8)
Calculate relative permeability curves according to the national standard GB/T 28912-2012:
| 13 |
| 14 |
| 15 |
| 16 |
| 17 |
| 18 |
| 19 |
The relative permeability data are computed through the above formulas when measured by means of the unsteady-state method.
Acknowledgments
The authors would like to acknowledge the National Natural Science Foundation of China (Grant No. 51974331) and the National Science and Technology Major Project (Grant No. 2017ZX05009004) for their financial support.
Glossary
Nomenclature
- WATER-INI
initial water component
- WATER-INJ
injected water component
- nWATER-INJ (mol)
total moles of injected water
- nWATER-INI (mol)
total moles of initial water
- M
mole fraction of injected water component
- KR
a set of relative permeability curves
- PVc
ratio of cumulative water volume injected into the core to its total pore volume
- PVr
ratio of cumulative water volume injected into the reservoir to its total pore volume
- Swc
irreducible water saturation
- Soi
initial oil saturation
- Sor
residual oil saturation
- R
water crossing ratio
- Areal (m2)
area of one certain water cross-surface
- Winj (m3)
cumulative injected water volume through one certain water cross-surface
- Wgrid (m3)
total water volume flowing through one certain grid cell
- CF
water cross-surface flux
- VWATER-INJ (m3)
total volume of injected water
- Vpgrid (m3)
pore volume of the grid cell
- Vp (m3)
pore volume of reservoir/core
- Vpc (m3)
pore volume of the core
- Vpr (m3)
total pore volume of the reservoir unit
- O
origin of the coordinate system
- x,r
coordinate along flowing direction
- t (min or day)
flooding time
- Lc (m)
core length
- Lw (m)
distance between the injection well and production wells
- rw (m)
radius of the wellbore
- Dc (m)
core diameter
- h (m)
thickness of the reservoir
- ϕ
porosity of the core/reservoir
- qr (m3/day)
flow rate of injected water in the reservoir
- qc (m3/min)
flow rate of injected water in the core

average water cross-surface flux of the entire core

average water cross-surface flux of the whole reservoir
- ER
oil recovery
- EV
sweep efficiency
- ED
displacement efficiency
- Kro(Swe)
relative permeability to oil at the outflow-end saturation
- Krw(Swe)
relative permeability to water at the outflow-end saturation
- V̅(t)
dimensionless cumulative water injected
- Vt (m3)
cumulative water injected
- V̅o(t)
dimensionless cumulative oil produced
- Vo (m3)
cumulative oil produced
- fo(Swe)
oil-cut at the outflow end
- fw(Swe)
water-cut at the outflow end
- Swe
water saturation at the outflow end
- Swi
connate-water saturation of the core
- μo (mPa·s)
viscosity of oil
- μw (mPa·s)
viscosity of water
- I
ratio of the flowing ability at a certain time to that at the initial time
- K (μm2)
absolute permeability of the core
- A (cm2)
cross-sectional area of the core
- L (cm)
length of the core
- Q(t) (cm3/s)
fluid production rate at the outflow end at the time t
- Δp(t) (10–1 MPa)
pressure difference between the two core-ends at the time t
- u (cm/s)
velocity of seepage flow
The authors declare no competing financial interest.
References
- Wei M.; Ren K.; Duan Y.; Chen Q.; Morteza D. Production decline behavior analysis of a vertical well with a natural water influx/waterflood. Math. Probl. Eng. 2019, 1683989 10.1155/2019/1683989. [DOI] [Google Scholar]
- Olayiwola S. O.; Dejam M. A comprehensive review on interaction of nanoparticles with low salinity water and surfactant for enhanced oil recovery in sandstone and carbonate reservoirs. Fuel 2019, 241, 1045–1057. 10.1016/j.fuel.2018.12.122. [DOI] [Google Scholar]
- Rostami P.; Mohammad F.; Mehraban M. F.; Sharifi M.; Dejam M.; Ayatollahi S. Effect of water salinity on oil/brine interfacial behavior during low salinity waterflooding: A mechanistic study. Petroleum 2019, 5, 367–374. 10.1016/j.petlm.2019.03.005. [DOI] [Google Scholar]
- Mashayekhizadeh V.; Shahin K.; Morteza D.. EOR potential within Iran. In Special Topics & Reviews in Porous Media: An International Journal; Begell House, 2014; Vol. 5, pp 325–354. [Google Scholar]
- Wei B.; Liu J.; Zhang X.; Xiang H.; Zou P.; Cao J.; Bai M. Nuclear Magnetic Resonance (NMR) mapping of remaining oil distribution during sequential rate waterflooding processes for improving oil recovery. J. Pet. Sci. Eng. 2020, 190, 107102 10.1016/j.petrol.2020.107102. [DOI] [Google Scholar]
- Shaker Shiran B.; Skauge A. Enhanced oil recovery (EOR) by combined low salinity water/polymer flooding. Energy Fuels 2013, 27, 1223–1235. 10.1021/ef301538e. [DOI] [Google Scholar]
- Morrow N.; Buckley J. Improved oil recovery by low-salinity waterflooding. J. Petrol. Technol. 2011, 63, 106–113. 10.2118/129421-JPT. [DOI] [Google Scholar]
- Feng Q.; Zhang J.; Wang S.; Wang X.; Cui R.; Wang D.; Bing S.; Rui Z. Unified relative permeability model and waterflooding type curves under different levels of water cut. J. Pet. Sci. Eng. 2017, 154, 204–216. 10.1016/j.petrol.2017.04.031. [DOI] [Google Scholar]
- Wang D.; Tand J. In Production Technology of Daqing Oil-Field during Its High Water-Cut Stage, International Meeting on Petroleum Engineering, Paper SPE-14847-MS; Beijing, China, March 17–20, 1986.
- Su Y.; L Y.; Li Y. In Practical Experiences of Improvement of Oil Recovery for SZ Heavy Oil Reservoir in the Stage of High Water-Cut, SPE Heavy Oil Conference Canada, SPE-146672-MS; Calgary, Alberta, Canada, June 12–14, 2012.
- Qin W.; Luo P.; Meng J.; Li H.; Mao T.; Wojtanowicz A. K.; Feng M.. Successful Field Trials of Water Control in High Water Cut Wells Using an Improved Downhole Water Sink/Drainage System, International Petroleum Exhibition & Conference, Paper SPE-188958-MS; Abu Dhabi, UAE, Nov 13–16, 2017.
- Dakuang H. Discussions on concepts, countermeasures and technical routes for the redevelopment of high water-cut oilfields. Pet. Explor. Dev. 2010, 37, 583–591. 10.1016/S1876-3804(10)60055-9. [DOI] [Google Scholar]
- Hu W. Necessity and feasibility of PetroChina mature field redevelopment. Pet. Explor. Dev. 2008, 35, 1–5. 10.1016/S1876-3804(08)60001-4. [DOI] [Google Scholar]
- Li Y. Study on enhancing oil recovery of continental reservoir by water drive technology. Acta Pharmacol. Sin. 2009, 30, 396–399. 10.1038/aps.2009.2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sun S.; Han J.; Guo Y. Laboratory experiment on physical properties of flooding sandstone in Shengtuo oilfield. J. Univ. Pet. China 1996, 20, 33–35. [Google Scholar]
- Hongxing Z.; Liu Q.; Li F.; Lu Y. Variations of petrophysical parameters after sandstone reservoirs watered out in Daqing oil field. SPE Adv. Technol. Ser. 1997, 5, 128–139. 10.2118/30844-PA. [DOI] [Google Scholar]
- Cheng L.; Li L.; Li C. Reservoir numerical simulation with variable rock wettability. J. Hydrodynamics 2003, 18, 786–791. [Google Scholar]
- Li H.; Wang X.; Liu S. Variation law of parameters of reservoir physical property in old oilfield. J. Southwest Pet. Univ. 2009, 31, 85–89. [Google Scholar]
- Jin W.; Wang X.; He F.; Chen T. Characteristics of Chang-6 oil-bearing formation changes after long term waterflood development in Ansai oilfield. J. Earth Sci. Environ. 2010, 32, 239–244. [Google Scholar]
- Ji S.; Tian C.; Shi C.; Ye J.; Zhang Z.; Fu X. New understanding on water-oil displacement efficiency in a high water-cut stage. Pet. Explor. Dev. 2012, 39, 362–370. 10.1016/S1876-3804(12)60052-4. [DOI] [Google Scholar]
- Loahardjo N.; Xie X.; Winoto W.; Buckley J.; Morrow N. In Oil Recovery by Sequential Waterflooding the Effect of Aging at Residual Oil and Initial Water Saturation, SPE 18th Improved Oil Recovery Symposium, Paper SPE-154202; Tulsa, Oklahoma, USA, April 14–18, 2012. [Google Scholar]
- Zhou Y.; Wang D.; Wang Z.; Cao R. The formation and viscoelasticity of pore-throat scale emulsion in porous media. Pet. Explor. Dev. 2017, 44, 111–118. 10.1016/S1876-3804(17)30014-9. [DOI] [Google Scholar]
- Zhou Y.; Yin D.; Cao R.; Zhang C. The mechanism for pore-throat scale emulsion displacing residual oil after water flooding. J. Pet. Sci. Eng. 2018, 163, 519–525. 10.1016/j.petrol.2018.01.027. [DOI] [Google Scholar]
- Loahardjo N.; Xie X.; Morrow N. Oil recovery by sequential waterflooding of mixed-wet sandstone and limestone. Energy Fuels 2010, 24, 5073–5080. 10.1021/ef100729b. [DOI] [Google Scholar]
- Loahardjo N.; Morrow N.; Stevens J.; Howard J. In Nuclear Magnetic Resonance Imaging: Application to Determination of Saturation Changes in a Sandstone Core by Sequential Waterflooding, International Symposium of the Society of Core Analysts; Halifax, Nova Scotia, Canada, Oct 4–7, 2010.
- Yang X.; Feng Y.; Guo E.; Lu X.; Li B. Changes of reservoir characteristics during ultra-high water cut period: Shuanghe Oilfield. J. South. Petrol. Inst. 2000, 22, 22–25. [Google Scholar]
- Wu S. Variation rule of oil layer parameters washed by long term injected water and its impact on development effect. Pet. Geol. Oilfield Dev. Daqing 2006, 25, 35–37. [Google Scholar]
- Han J.; Song X.; Li J.; Ju B.; Li H. Experimental research on the changes in formation parameters during water flooding for oil production in Fuyu Oilfield. Sci. Technol. Eng. 2013, 13, 3846–3850. [Google Scholar]
- Cui C.; Zhao X. The reservoir numerical simulation study with the variety of reservoir parameters. J. Hydrodynamics 2004, 19, 912–915. [Google Scholar]
- Xu Q.; Chen Y.; Hou Y.; Li H. Research on numerical simulation processing mode based on reservoir time varying physical properties and seepage in extra high water cut stage. Drill. Prod. Technol. 2015, 38, 41–43. [Google Scholar]
- Xu J.; Guo C.; Jiang R.; Wei M. Study on relative permeability characteristics affected by displacement pressure gradient: experimental study and numerical simulation. Fuel 2016, 163, 314–323. 10.1016/j.fuel.2015.09.049. [DOI] [Google Scholar]
- Eydinov D.; Gao G.; Li G.; Reynolds A. Simultaneous estimation of relative permeability and porosity/permeability fields by history matching production data. J. Can. Pet. Technol. 2009, 48, 13–25. 10.2118/132159-PA. [DOI] [Google Scholar]
- Zahoor M. K.; Derahman M. N. New approach for improved history matching while incorporating wettability variations in a sandstone reservoir-field implementation. J. Pet. Sci. Eng. 2013, 104, 27–37. 10.1016/j.petrol.2013.03.025. [DOI] [Google Scholar]
- Zhang W.; Cao R.; Luo D.; Sun C.; Li W. Displacement characteristics of high-multiple water drive in marine sandstone reservoirs in the Pearl River Mouth Basin, South China Sea. Pet. Geol. Recovery Effic. 2018, 25, 64–71. [Google Scholar]
- Anderson W. Wettability literature survey---part 5: the effects of wettability on relative permeability, SPE. J. Pet. Technol. 1987, 39, 1453–1468. 10.2118/16323-PA. [DOI] [Google Scholar]
- Karabakal U.; Bagci S. Determination of wettability and its effect on waterflood performance in limestone medium. Energy Fuels 2004, 18, 438–449. 10.1021/ef030002f. [DOI] [Google Scholar]
- Nguyen V.; Sheppard A.; Knackstedt M.; Pinczewski W. The effect of displacement rate on imbibition relative permeability and residual saturation. J. Pet. Sci. Eng. 2006, 52, 54–70. 10.1016/j.petrol.2006.03.020. [DOI] [Google Scholar]
- Solbakken J.; Skauge A.; Aarra M. Foam performance in low permeability laminated sandstones. Energy Fuels 2014, 28, 803–815. 10.1021/ef402020x. [DOI] [Google Scholar]
- Mo S.; He S.; Lei G.; Gai S.; Liu Z. Effect of the drawdown pressure on the relative permeability in tight gas: a theoretical and experimental study. J. Nat. Gas Sci. Eng. 2015, 24, 264–271. 10.1016/j.jngse.2015.03.034. [DOI] [Google Scholar]
- Ren G.; Rafiee J.; Aryana S.; Younis R. A Bayesian model selection analysis of equilibrium and nonequilibrium models for multiphase flow in porous media. Int. J. Multiphase Flow 2017, 89, 313–320. 10.1016/j.ijmultiphaseflow.2016.11.006. [DOI] [Google Scholar]
- Aggelopoulos C.; Tsakiroglou C. The effect of micro-heterogeneity and capillary number on capillary pressure and relative permeability curves of soils. Geoderma 2008, 148, 25–34. 10.1016/j.geoderma.2008.08.011. [DOI] [Google Scholar]
- Akhlaghinia M.; Torabi F.; Chan C. Effect of temperature on two-phase relative permeabilities of heavy oil, water, carbon dioxide, and methane determined by displacement technique. Energy Fuels 2013, 27, 1185–1193. 10.1021/ef301248y. [DOI] [Google Scholar]
- Shojaei M.; Ghazanfari M.; Masihi M. Relative permeability and capillary pressure curves for low salinity water flooding in sandstone rocks. J. Nat. Gas Sci. Eng. 2015, 25, 30–38. 10.1016/j.jngse.2015.04.023. [DOI] [Google Scholar]
- Wang F.; Jiao L.; Zhao J.; Cai J. A more generalized model for relative permeability prediction in unsaturated fractal porous media. J. Nat. Gas Sci. Eng. 2019, 67, 82–92. 10.1016/j.jngse.2019.04.019. [DOI] [Google Scholar]
- Liu X. Study on numerical simulation technology based on time varying physical properties in mid-high permeability sandstone reservoirs. Pet. Geo. Recov. Effic. 2011, 18, 58–62. [Google Scholar]
- Chen F.; Jiang H.; Li J.; Bai X. Quantitative liquid field description method and its application. J. Oil Gas Technol. 2011, 33, 111–114. [Google Scholar]
- Xu J.; Guo C.; Wei M.; Jiang R. Impact of parameters’ time variation on waterflooding reservoir performance. J. Pet. Sci. Eng. 2015, 126, 181–189. 10.1016/j.petrol.2014.11.032. [DOI] [Google Scholar]
- Sun Z.; Li Y.; Ma K.; Xu J.; Zhang G.; Jiang R.; Pan S. In A Novel Method to Characterize Time-Variation of Reservoir Properties: Experimental Study, Simulator Development and its Application in Bohai Bay Oilfield, SPE/IATMI Asia Pacific Oil & Gas Conference and Exhibition, SPE-196282-MS; Bali, Indonesia, Oct 29–31, 2019.
- Lei X.; Zhang Q.; Luo J.; Sui B.; Yang Z. Fine characterization technique of remaining oil after water flooding for complex fault block reservoirs in Weizhou Oilfields and its application. China Offshore Oil Gas 2015, 27, 80–85. [Google Scholar]
- Jiang R.; Qiao X.; Teng W.; Xu J.; Sun Z.; Xie L. Impact of physical properties time variation on waterflooding reservoir development. Fault-Block Oil Gas Field 2016, 23, 768–771. [Google Scholar]
- Hong C.; Wang W.; Lu R.; Zhong J.; Ren C. A quantitative method to predict the dynamic variation in permeability of oil reservoirs during waterflooding and oil displacement. J. South. Petrol. Univ. 2018, 40, 113–121. [Google Scholar]
- General Administration of Quality Supervision, Inspection and Quarantine of the PRC & Standardization Administration of the PRC . Test Method for Two Phase Relative Permeability in Rock: GB/T 28912-2012[S]; Standards Press of China: Beijing, 2012. [Google Scholar]













