Assessing functional propagation patterns in COVID-19

Abstract

Among the many efforts done by the scientific community to help coping with the COVID-19 pandemic, one of the most important has been the creation of models to describe its propagation, as these are expected to guide the deployment of containment and health policies. These models are commonly based on exogenous information, as e.g. mobility data, whose limitedness always compromise the reliability of obtained results. In this contribution we propose a different approach, based on extracting relationships between the evolution of the disease in different regions through information theoretical metrics. In a way similar to what is commonly done in neuroscience, propagation is understood as information transfer, and the resulting propagation patterns are represented and studied as functional networks. By applying this methodology to the dynamics of COVID-19 in several countries and regions thereof, we were able to reconstruct static and time-varying propagation graphs. We further discuss the advantages, promises and open research questions associated with this functional approach.

1. Introduction

The severe acute respiratory syndrome coronavirus 2 (SARS-CoV-2) emerged in December, 2019, possibly at a wildlife trading market in Wuhan, China [5], and spread globally by the end of April, infecting more than 6 million individuals by the end of May, 2020. The resulting coronavirus disease 2019 (COVID-19) has made appearance in almost every country of the world, and has caused more than 350,000 deaths as of end of May 2020 [38]. In parallel of efforts to improve clinical treatment, the research community has focused on developing models able to describe and predict the propagation of the disease [16], [26], [35], [49]. Understanding the spreading patterns of the COVID-19 outbreak, and in fact of any large-scale epidemics, is critical to predicting its spatio-temporal dynamics and ultimately devising effective public health policies to control it.

Two main approaches are available to support such modelling. On one hand, the spatial characterisation of spreading can be dealt with in a completely data-driven approach, wherein the spreading map is analysed as a static image. For instance, recent studies addressed spatial spreading of COVID-19 [22] and comparable diseases, including severe acute respiratory syndrome (SARS) [17], [28] and Middle East respiratory syndrome coronavirus (MERS-CoV) [1], [2], by quantifying static spatial correlations in spreading maps.

On the other hand, a different approach involves modelling the spreading process dynamics [13]. This typically involves subdividing the studied population into subpopulations, e.g. susceptible, infected and recovered compartments in the SIR model [24]. Epidemic dynamics is then modelled by taking the continuous-time limit of difference equations for the evolution of the average number of individuals in each compartment. This approach is predicated upon a homogenous mixing approximation, according to which individuals are well mixed and interact in a random fashion, so that individuals in a given subpopulation are indistinguishable and the spreading probability is simply proportional to the number of infected individuals [6], [21]. This approach neglects the diffusion of individuals and assumes random and homogeneous mixing, i.e. all members of a given compartment are indistinguishable, a rather unrealistic assumption. This limitation can be overcome by modelling the space in which the spreading process takes place as a network. Early modelling in this vein mainly focused on a class of random networks entirely characterised by their degree distribution, all other properties being essentially random. However, disease spreading is typically spatially inhomogeneous with nonlocal interactions, so that a nonlocal mechanism must be taken into account for a realistic picture of the situation. The spreading process as a whole is affected by geographical heterogeneity in demographic, economic and sociological terms, so that spatially uniform models typically fail to give a realistic picture of disease diffusion. Thus, the space in which the spreading process takes place differs rather drastically from a random uncorrelated network, and higher-order properties of real networks have been shown to play an important role in theoretical models of epidemic spreading [33]. In more recent studies [23], [29], [32], the importance of interconnected groups with high numbers of contacts and long-range connections (linking otherwise distant parts of the network) in disease transmission has been highglighted.

In this latter modelling approach, mobility data are typically incorporated exogenously. Network information is gathered either by resorting to fundamental biological information, viz. genetic mutation analysis, or by using techniques such as infection tracing, complete contact tracing, diary-based studies, or detailed general statistical mobility data. This has recently been revolutionised by the availability of large-scale real data sets on mobility, for instance gathered through cell phones positioning, opening the door to unprecedented opportunities [7], [8]. However, such information is not always available, and may be outdated and lacunary. Even in the best conditions, individual people can be located with a limited resolution, and interactions (and hence contagios) can only be modelled in a statistical way.

In this contribution we explore a third approach, involving the extraction of spreading patterns from the local dynamics. It is based on the idea that the local dynamics of the disease, e.g. of the number of cases in a region or in a province, is the result of two contributions: an internal component, due to all cases already present in the region; and inputs from other regions. While the former contribution is expected to dominate, the second should also be reflected in the dynamics of each region, e.g. of the daily evolution of the number of cases. In a way similar to what is now common in neuroscience [12], [18], pairwise interactions between regions can then be made explicit by applying information theoretic metrics to the associated time series, the latter being a function of the former. Disease spreading is then described as an information process, in which information about cases is spread between and process at discrete spatial locations.

This third approach has some important advantages. First, the description of propagation patterns only relies on macro-scale information, dispensing with the reliance on mobility data. Secondly, insofar as it is not based on a model, but only relies on real data, no free parameter needs to be tuned. As a consequence, results validity does not depend on the quality and quantity of micro-scale mobility data, on the choice of model parameters, or on subjective hypotheses; but only on the availability of good representations of the macro-scale dynamics, something nowadays common. Thirdly, results can conveniently take the form of functional networks, which can then be analysed using the vast array of tools provided by complex networks theory [3], [11], [43].

Using daily data about the number of new cases and deaths, we here study the dynamics of COVID-19 in some of the countries most affected by the epidemics. We first show how these time series of macroscopic disease-related variables can be used to detect temporal relationships describing the evolution of patients, and how these could be related to national health policies. We then describe their spatial dynamics, by reconstructing functional networks representing disease spreading in Portugal, Spain, Italy and England. Finally, we show how the temporal evolution of this spatial dynamics can be sketched providing a more real-time description of the process.

Though standard in many scientific fields, including neuroscience [12], [18], economics [4] and transportation [47], to the best of our knowledge functional networks have never been applied to the problem of modelling epidemic processes. In synthesis, this contribution is a first test case, showing some basic applications and discussing some open problems that will have to be tackled in the future, which should hopefully motivate further research efforts.

2. Data and methods

2.1. Global data

Global data about the evolution of the pandemic, in terms of number of confirmed cases and number of death, have been obtained from the COVID-19 Data Repository [15], made public by the Center for Systems Science and Engineering (CSSE) at Johns Hopkins University, and retrieved from github.com/CSSEGISandData/COVID-19. This data set included information from January 22nd to May 15th at a country level - when a higher resolution was available, the time series corresponding to different regions of a country have been merged. The six countries with the higher number of cases per capita (as of mid March 2020) have here been considered, i.e. US, United Kingdom, Italy, France, Spain and Belgium.

Additionally, data about the day with the highest number of confirmed cases and deaths for each country have been obtained from the corresponding Wikipedia webpages - see en.wikipedia.org/wiki/COVID-19_pandemic_by_country_and_territory.

2.2. Local evolution

The regional propagation patterns of COVID-19 have been studies in four countries, i.e. Portugal, Spain, Italy and England. The first three have been chosen because of their similar cultural background, while displaying a substantially different evolution -  ≈ 0.13 deaths per thousands people for Portugal, as opposed to  ≈ 0.57 and  ≈ 0.55 for Spain and Italy. Additionally, England has been chosen for its clear propagation pattern, which started from the province of London.

Portugal. Data for Portugal were obtained from the Wikipedia page “Pandemia de COVID-19 em Portugal” (pt.wikipedia.org/wiki/Pandemia_de_COVID-19_em_Portugal), which in turns recompiles data from relatórios de situação (situation reports) published by the Direção-Geral da Saúde (covid19.min-saude.pt/relatorio-de-situacao/). Two time series were extracted for each one of the seven Portuguese regions (Norte, Lisboa e Vale do Tejo, Centro, Alentejo, Algarve, Açores and Madeira), i.e. the number of confirmed cases and the number of deaths per day. These time series span from March 23rd to May 15th - the first 20 days were discarded, as too few cases were for them reported.

Spain. Data for Spain were obtained from the Ministerio de Sanidad, and are available at cnecovid.isciii.es/covid19/resources/agregados.csv. They include daily numbers of confirmed cases and death for 19 regions (17 “comunidades autónomas”, plus the two cities of Ceuta and Melilla), and span from March 10th to May 15th - as in the previous case, the first days have been excluded due to low numbers.

Italy. Data for Italy were recompiled from the reports published by the Ministero della Salute, available at www.salute.gov.itnuovocoronavirus. Number of confirmed cases and deaths are reported on a daily basis at regional and province levels - here only the former has been considered. Data were extracted from March 10th to May 15th.

England. Data for England and its 9 regions were obtained from the Public Health England, at coronavirus.data.gov.uk. They cover from January 30th to May 15th; as in the previous cases, data for the first 30 days have been discarded due to the low number of reported cases.

2.3. Data pre-processing and causality assessment

For each country and region, two time series have been created: ΔC and ΔD, respectively representing the daily variation in the number of confirmed cases and deaths. The former one is calculated as:

$$\Delta C\left(t\right)={\log }_{2}C\left(t\right)/C(t-1),$$ (1)

C(t) being the cumulative number of cases reported until day t. Positive values of ΔC(t) thus indicate an increase in the number of cases, and specifically $\Delta C\left(t\right)=1$ implies a duplication in such number between the day $t-1$ and the day t. Note that negative values for ΔC can rarely been found, indicating a change in the way cases are accounted for. The same equation applies for ΔD, the only difference being that it is calculated over the cumulative number of deaths.

The relationships present between the extracted time series are afterward tested through the celebrated Granger causality (GC) test [19], [20]. This test is held to be one of the few tests able to detect the presence of causal relationships, i.e. beyond correlation or co-occurrence, between time series. It is an extremely powerful tool for assessing information exchange between different elements of a system, and understanding whether the dynamics of one of them is led by the other(s). Given two time series X and Y, X is said to Granger-cause Y if X values provide statistically significant information about future values of Y. This is usually calculated by means of univariate autoregressions, and tested through t-tests and F-tests. Note that here the term causality is used lato sensu, as Wiener’s principle of observational causality [45], upon which the GC test is based, should be strictly interpreted as an improvement of the predictive capacity [27]; assessing true causal interactions ultimately require interventions [34].

One important requirement for obtaining reliable results with the GC test is related to the stationarity of the data. Due to the natural evolution of any pandemic, ΔC and ΔD are not expected to be stationary. To illustrate, let us consider a very simplified scenario, in which the number of daily confirmed cases reaches a maximum at some point in time t_peak, and then decreases. This means that ΔC will have large values until t_peak, and smaller values afterwards. As a consequence, the result of the GC test applied on two time series of this type will be dominated by the difference in time between the two transition points. To solve this issue, we make the time series stationary by calculating the deviation with respect to the expected value of the evolution of the time series:

$$\Delta \tilde{C}\left(t\right)=\Delta C\left(t\right)-\frac{\Delta C(t-1)+\Delta C(t+1)}{2}.$$ (2)

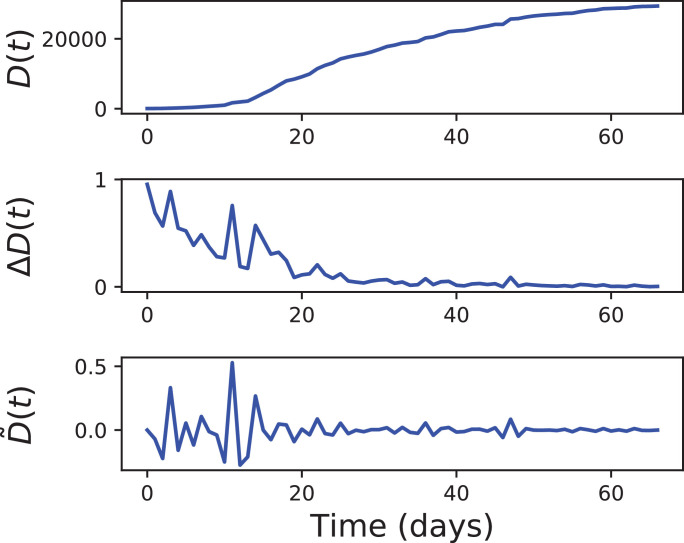
In other words, $\Delta \tilde{C}$ is a time series indicating, at each time point t, how the evolution of the number of confirmed cases deviates from the trend defined by the previous and the following days. The same transformation is applied to ΔD to obtain $\Delta \tilde{D}$. A graphical example of the pre-processing process is reported in Fig. 1 , depicting the evolution of D, ΔD and $\tilde{\Delta }D$ for one Spanish region. In all analyses reported below, the GC test is applied to $\Delta \tilde{C}$ and $\Delta \tilde{D}$.

Fig. 1.

Example of the process for obtaining stationary time series. The three panels, from top to bottom, depict respectively the evolution of D(t), ΔD and $\tilde{\Delta }D$ for the Spanish region of Catalunya. See main text for definitions.

2.4. Functional networks reconstruction and topological metrics

In order to obtain a representation of the spatial propagation patterns of COVID-19, functional networks have been reconstructed for the four countries previously listed. For each one of them, an adjacency matrix $\mathcal{A}$ of size n × n has been calculated, with n being the number of regions. Each element a _i,j is set to one if the GC test between the time series of regions i and j yields a statistically significant result ($\alpha =0.01,$ with a Šidák correction for multiple testing), and zero otherwise. The resulting networks have then been represented using the Cytoscape software [40], and their topological properties have been studied through the following metrics:

• •
  Link density. Fraction of active links, over the total number of possible links in the network:

  $$l_d=\frac{1}{n(n-1)}\sum _{i,j\ne i}{a}_{i,j}.$$ (3)

  The higher the link density, the more dense is the propagation of the disease between the considered regions.
• • Maximum k_out. The maximum out-degree is defined as the number of outbound links of the node with the maximum number of links coming out of it. A larger than expected k_out implies that a node is mostly responsible for the propagation of the disease, by acting like a hub.
• • Assortativity. Pearson correlation coefficient of the degrees of nodes at either ends of the links of the network [31]. Positive values are associated to assortative networks, in which nodes tend to connect to their connectivity peers; on the contrary, negative values are found in disassortative networks, where nodes with low degree are more likely connected with highly connected ones.
• • Transitivity. The transitivity, also known as the clustering coefficient, measures the presence of triangles in the network [30]. It is defined as the relationship between the number of triangles in the network (i.e. sets of three vertices with edges between each pair of them) and the number of connected triples (i.e. sets of three vertices where each vertex can be reached from each other, directly or indirectly). A large number of triangles implies that different regions are strongly inter-connected, with feedbacks and amplification of the number of cases.
• •
  Efficiency. The efficiency of a network represents how easily information can move between its nodes [25]. It is defined as the inverse of the harmonic mean of the distances between pairs if nodes:

  $$E=\frac{1}{N(N-1)}\sum _{i\ne j}\frac{1}{d_{i,j}},$$ (4)

  d _i,j being the distance between nodes i and j. A high efficiency indicates that the network is especially well-suited to the propagation of the disease, with a low number of bottlenecks that could be used to stop it.
• • Information Content (IC). Metric assessing the presence of regularities in the adjacency matrix of the network, i.e. of mesoscale structures. It is calculated as the amount of information encoded in the adjacency matrix, such that small values correspond to regular topologies, and large values to random-like structures [46], [48]. Low IC values thus indicate the presence of non-trivial structures, and can thus be used to confirm the statistical significance of the resulting network.

3. Global disease evolution

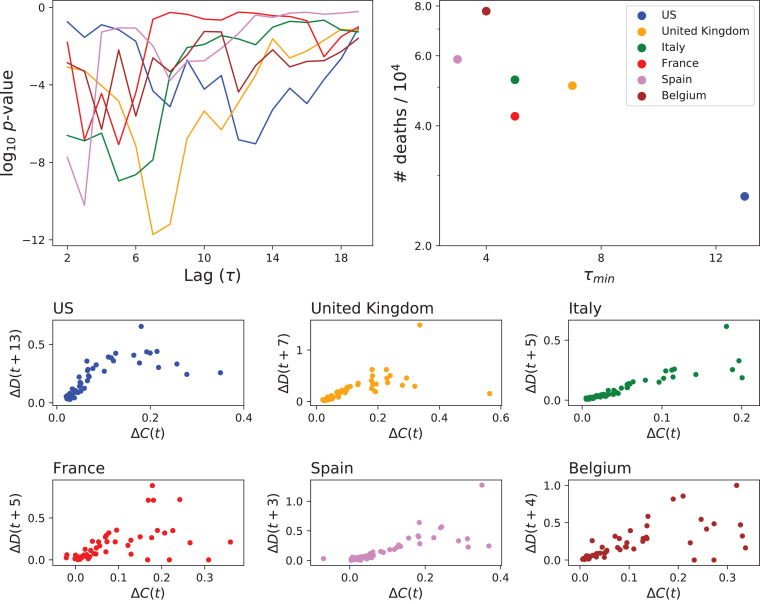
As an initial step towards the reconstruction of the local propagation patterns of COVID-19, we here analyse its global dynamics. Towards this aim, the top left panel of Fig. 2 depicts the evolution of the p-value yielded by the Granger Causality test between $\Delta \tilde{C}$ and $\Delta \tilde{D},$ by country (see color legend in right panel) and as a function of the lag τ. As expected, all curves reach a minimum that is always statistically significant (e.g. below $\alpha =0.01$), as clearly the evolution of the number of death must be driven by the evolution of infected people. On the other hand, it is interesting to see that the lags corresponding to such minima (τ _min) are clustered between 3 and 7 - the only exception being US, with ${\tau }_{\min }=13$. These numbers have to be understood in light of what currently known about COVID-19, and especially about the survival time of non-surviving patients, which is estimated to be around 14 - 16 days from the onset of symptoms and 3 - 5 days from hospitalisation [36], [37], [41]. This thus seems to indicate that countries like Spain and Belgium mostly report “confirmed cases” as those being hospitalised; or, in other words, that few confirmatory tests are performed outside hospitals.

Fig. 2.

Analysis of the global relationship between number of confirmed cases and deaths. (Top left panel) Evolution of the p-value of the GC test between ΔC and ΔD, for the six considered countries, as a function of the lag τ between both time series. (Top right panel) Scatter plot of the number of deaths per 10⁴ as a function of the value of τ minimising the p-value of the previous GC test. (Bottom panels) Scatter plots of ΔD as a function of ΔC, when the former is shifted τ_min points forward in time.

τ _min seems to be inversely correlated with the prevalence of the disease, and specifically with the number of deaths per capita - see top right panel of Fig. 2. This is confirmed by Table 1 , which reports the time between the day with the maximum number of reported new cases and the day with the higher number of deaths for different countries. Once again, countries that are reported as positive examples of the management of the pandemic, as Germany or South Korea, display larger values between peaks. These results thus seem to support the hypothesis that massive population testing, and especially testing of people who do not require hospitalisation, is an important element in the control of the spreading [10], [14], [39], [44].

Table 1.

Cases vs. death peaks. This table reports the approximate date of the day with most daily confirmed cases (second column) and with most deaths (third column) for different countries. The first six countries correspond to those that had a higher density of cases (see also Fig. 2; while the last three are examples of countries that have limited the propagation of the disease.

Country	Date of peak,	Date of peak,	Difference
	daily confirmed	daily deaths
Belgium	April 10th	April 12th	2
Spain	March 31st	April 2nd	2
United Kingdom	April 5th	April 9th	4
Italy	March 21st	27th March	6
France	March 31st	April 6th	6
US	April 24th	May 6th	12
Switzerland	March 23rd	March 31st	8
Germany	March 28th	April 16th	19
South Korea	March 1st	March 23rd	22

In order to further validate the obtained τ _min, and thus discard that they are only due to statistical fluctuations, the bottom panels of Fig. 2 report scatter plots of ΔD as a function of ΔC, with the former shifted τ _min days ahead in time. In all cases points form a straight line, more clear in the case of United Kingdom, Italy and Spain; and becoming fuzzy for extreme values of ΔC.

From the point of view of this study, results of Fig. 2 and Table 1 yield two important conclusions. Firstly, they confirm that the analysis of COVID-19 time series through causality metrics can yield non-trivial information about how different countries are managing the pandemic, information that in this case was possible to validate through more descriptive approaches. Secondly, that ΔC is less reliable than ΔD, as the former is strongly influenced by national testing protocols. Due to this, the analyses presented in the next section will be based on the time series of the number of deaths.

4. Local propagation patterns

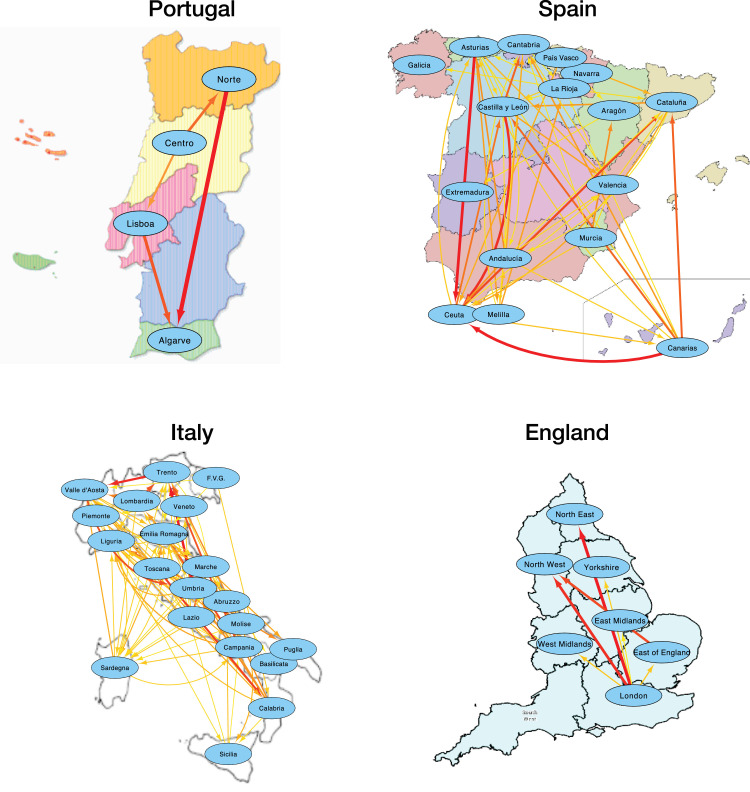
We then move to the analysis of local patterns of propagation, using four countries (i.e. Portugal, Spain, Italy and England) as test cases. More in details, time series of the number of deaths in each region composing those countries have been processed, and the GC test applied between pairs of them. Fig. 3 reports the resulting networks, where only links being statistically significant are plotted (significance level of $\alpha =0.01,$ with a Šidák correction for multiple testing). At a simple glance it can be appreciated that the Portuguese network is qualitatively different, with a sparser and simpler structure. This is further confirmed in Table 2 , reporting six classical topological metrics for the three networks. Spain and Italy are characterised by a stronger connectivity, thus by a stronger propagation of the disease between different regions; and by a large transitivity (see Z-Score for a comparison with random equivalent networks), i.e. by a larger than expected number of triangles between regions. Additionally, England displays a clear propagation pattern, in which most links depart from the region of London.

Fig. 3.

Functional propagation networks for Portugal, Spain, Italy and England. Link’s thickness and color indicates the strength of the causality link (from yellow for the weakest, to red for the strongest). (For interpretation of the references to colour in this figure legend, the reader is referred to the web version of this article.)

Table 2.

Topological metrics of the four networks represented in Fig. 3. Values in parenthesis indicates the corresponding Z-Score, calculated by comparing the obtained value of the topological metric with what expected in an ensemble of random networks with the same number of nodes and links.

Metric	Portugal	Spain	Italy	England
Link density	0.0952	0.155	0.199	0.0972
Max. kout	2 (0.570)	7 (1.24)	9 (1.05)	6 (7.16)
Assortativity	-1	0.0419 (0.699)	0.0459 (1.02)	-0.645
Transitivity	0.0 (-0.273)	0.399 (7.89)	0.434 (11.4)	0.0333 (-0.269)
Efficiency	0.107 (-0.457)	0.280 (-5.57)	0.380 (-13.3)	0.0972 (-1.78)
IC	4.35 (-1.68)	73.8 (-8.49)	134.1 (-11.4)	4.69 (-2.82)

Two additional conclusions can be drawn from the networks of Fig. 3. Firstly, islands (with the exception of Canary islands, in Spain) have been kept outside the propagation of the disease, or have very weak connections with the remainder of the country. This is to be expected, as their nature allows a simpler implementation of isolation policies. Secondly, the region of Madrid, which was the most important focus of COVID-19 in Spain, seems to have not propagated the disease to other parts of the country; this may be due to the strong isolation policies introduced by the Spanish government.

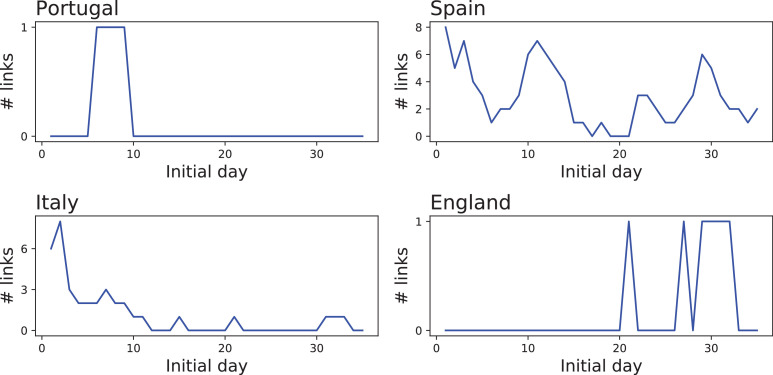
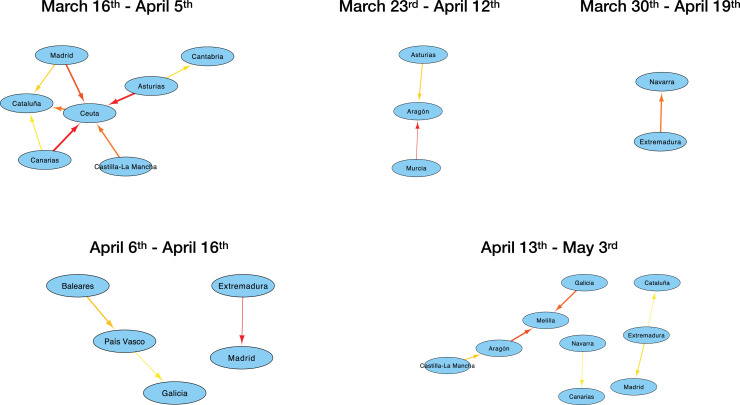
We finally study how functional networks can be used to monitor the progression of the epidemics on a shorter temporal scale. 35 networks were created for each country, by considering overlapping time windows of three weeks, with a starting point separated by one day. Fig. 4 reports the evolution of the number of links in each one of them. It can be appreciated that the evolution has been heterogeneous. Both Portugal and England show a static situation, with very few links appearing in an almost random fashion. Italy had most of its functional links at the beginning, for then reducing this number to almost zero. On the other hand, Spain displays a complex dynamics with multiple local maxima - see also Fig. 5 for a graphical representation of Spain’s networks.

Fig. 4.

Evolution of the number of inter-regional links for each of the four countries here considered, when networks are created using data from rolling windows of 3 weeks.

Fig. 5.

Functional networks of propagation for Spain, using data for five three-weeks-long time windows.

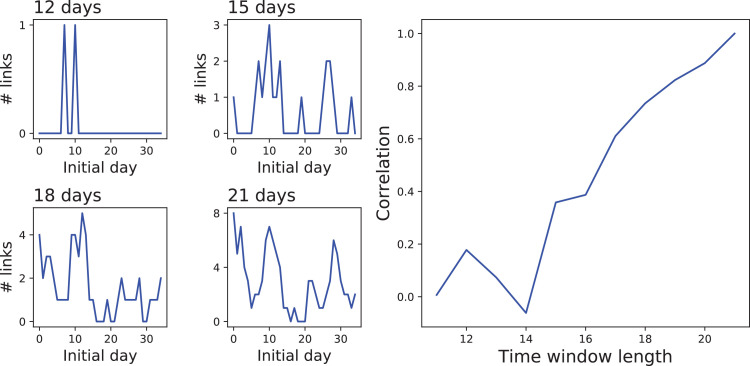
These last time-varying results should be interpreted with caution, as they are affected by two factors. First, the use of shorter time series implies a lower statistical significance of the results yielded by the GC test. Even though the same $\alpha =0.01$ threshold was used here, too short time series may introduce noise in the resulting functional structure. To illustrate this point, the four left panels of Fig. 6 report the evolution of the number of functional links for Spain according to the number of days considered in calculating the GC test. While the main trend is already visible with 15 days, some fine details are lost. The right panel of the same figure also depicts the correlation between the evolution of the number of links, calculated with 21 and n days, as a function of n; already for $n=16$ the correlation drops below 0.5, suggesting important information is lost. Second, weak connectivities that may be detected using the complete time series may disappear on shorter time windows, as they may not pass the significance threshold. This is probably the reason for the lack of links for England in Fig. 4, while propagation patterns clearly appear at a global level (see Fig. 3).

Fig. 6.

Information loss when considering short time series. The four left panels depict the evolution of the number of functional links for Spain according to the number of days considered in calculating the GC test - from left to right, top to bottom, 12, 15, 18 and 21. The right panel depicts the correlation between the evolution of the number of links for Spain, calculated with 21 and n days, as a function of n (the time window length).

5. Discussion and conclusions

In this contribution we presented a first test case and example of how functional relationships and networks can be used to describe the dynamics of an epidemic process, with a special focus on the case of COVID-19. The starting point is represented by time series of macroscopic variables describing the evolution of the disease, e.g. number of cases or deaths, in a geographic area of interest. After a suitable pre-processing, information theory metrics (here, the Granger Causality) can be applied to understand how these time series are interconnected or causally related.

Our results suggest that the functional approach allows extracting information about the propagation of a disease, a process that would usually require micro-scale information, e.g. following the movements of individual patients and their interactions. When the GC is applied to the time series of confirmed cases and deaths, it allows extracting aspects of public policies implemented by individual countries, specifically about when a case is confirmed. The time between confirmation and hospitalisation seems to be related to the effectiveness of spreading control. GC can also be applied to time series representing the evolution of the disease in different regions of the same country, yielding a network representation of the interregional propagation patterns. When these functional networks are made time-dependent, it is possible to detect trends and drifts, allowing a first evaluation of the effectiveness of containment policies.

The present study also highlights some limitations of the functional approach. The main one is related to the data temporal resolution: the small number of points in each time series is a challenge for methods such as GC, and precludes the use of other metrics e.g. Transfer Entropy [42]. Furthermore, in the presence of short time series, the dynamics of functional connectivity can only be analysed with low time resolution, as shown in Fig. 4. This drawback could be tackled in three ways. Firstly, longer time series may be studied in some specific case, e.g. contagious diseases that are endemic to a region or that do not have a seasonal evolution (like AIDS). Secondly, higher resolution time series may be used when available, e.g. of the number of deaths per hour; yet this information is seldom available, and it may represent an oversampling of the dynamics. Finally, tailored metrics could be devised, in line with what now common in neuroscience [9].

In parallel to the temporal resolution of data, one must be aware of the limitations of spatial resolution. The number of confirmed cases and deaths for some countries are relatively small, and hence the resulting time series can be quite noisy. This precludes the use of this method in very small countries or regions, or at least results ought to be interpreted with caution. Still, the results here obtained for countries like Spain and Italy are quite robust, as indicated by the very low p-values.

Finally, the quality of data also plays an important role. Different countries, or even different regions within a same country, may have different policies regarding testing procedures, data reporting or regarding when a death is attributed to the disease or to other comorbidities. These policies can also vary with time, such that adjustments can be made at any point. These factors act like noise in the analysis, lowering the confidence in the results.

In synthesis, we believe that the adaptation of the paradigm of functional analysis, a standard method in neuroscience, could yield an alternative and effective method for studying the dynamics of epidemic processes. By only relying on macroscopic data, nowadays published on a daily basis in most newspapers, this paradigm is impervious to the incomplete or unreliable micro-scale data at the basis of mobility-based models. At the same time, it is capable of providing synthetic descriptions of the propagation patterns, which could be used to assess the effectiveness of containment policies. In order to make this functional analysis effective and useful, several methodological challenges will have to be overcome, as here highlighted. Still, the potential gains justify future efforts on this topic.

Declaration of Competing Interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.