Toblerone: surface-based partial volume estimation

Abstract

Partial volume effects (PVE) present a source of confound for the analysis of functional imaging data. Correction for PVE requires estimates of the partial volumes (PVs) present in an image. These estimates are conventionally obtained via volumetric segmentation, but such an approach may not be accurate for complex structures such as the cortex. An alternative is to use surface-based segmentation, which is well-established within the literature. Toblerone is a new method for estimating PVs using such surfaces. It uses a purely geometric approach that considers the intersection between a surface and the voxels of an image. In contrast to existing surface-based techniques, Toblerone is not restricted to use with any particular structure or modality. Evaluation in a neuroimaging context has been performed on simulated surfaces, simulated T1-weighted MRI images and finally a Human Connectome Project test-retest dataset. A comparison has been made to two existing surface-based methods; in all analyses Toblerone’s performance either matched or surpassed the comparator methods. Evaluation results also show that compared to an existing volumetric method (FSL FAST), a surface-based approach with Toblerone offers improved robustness to scanner noise and field non-uniformity, and better inter-session repeatability in brain volume. In contrast to volumetric methods, a surface-based approach negates the need to perform resampling which is advantageous at the resolutions typically used for neuroimaging.

I. INTRODUCTION

PARTIAL volume effects (PVE) arise when an imaging matrix has low spatial resolution in relation to the structures of interest within the image, as is commonly the case for functional imaging techniques such as positron emission tomography (PET), blood oxygen-level dependent fMRI (BOLD) and arterial spin labelling (ASL). For example, ASL voxels typically have side lengths of 3–4mm whereas the mean thickness of the adult cortex is 2.5mm [1]. As such, voxels around the cortex will contain a mixture of cortical and non-cortical tissues, the proportions of which are termed partial volumes(PVs).PVE present a source of confound for functional imaging: whilst the objective is to obtain a measurement of function across some particular structure, the signal actually measured in each voxel is a sum, weighted by the partial volumes, of function both within and without said structure. This is a mixed-source problem in which the multiple tissues in each voxel constitute the sources. Partial volume effect correction (PVEc) uses voxel-wise estimates of PVs to separate out the signal arising from each tissue. Various PVEc methods have been developed, usually with a specific modality in mind (for example, Muller-Gartner for PET [2] and linear regression [3] or spatially-regularised variational Bayes for ASL [4]).

Estimation of PVs bears considerable similarity to volumetric segmentation and the two are typically performed concurrently on a structural image, as is demonstrated in [5]. In order to obtain PV estimates within the voxel grid of a functional image, estimates in the grid of a structural image must further be transformed. As each functional voxel corresponds to multiple smaller voxels on the structural image, the PVs of the former can be determined from the estimates of the latter. The efficacy of this approach is limited by the accuracy of the volumetric segmentation approach used. For complex geometries, such as the thin and highly folded structure of the cerebral cortex, the alternative of surface-based segmentation has gained widespread support (notably through FreeSurfer [6]). The advantage of such a segmentation method is twofold. Firstly, whereas volumetric segmentation is necessarily a discrete operation in terms of voxels, a surface approach is somewhat continuous as the surface vertices are placed with subvoxel precision. Secondly, anatomically-informed constraints can be enforced anisotropically when surfaces are used: for example, the constraint that tissues should be homogenous along a surface but heterogeneous across it. This is in contrast to a volumetric tool such as FSL FAST [7] which does enforce a similar tissue continuity constraint via the use of Markov random fields but only isotropically in the neighbourhood of each voxel. In principle, it should be possible to estimate PVs by considering the geometry of intersection between the individual voxels of an image and the surface segmentations of individual structures. Being a purely geometric construct, namely, given a surface that intersects a voxel, what is the volume within the voxel bounded by the surface, this is a fundamentally different approach to existing methods and it is expected that this will be reflected in the estimates produced.

Although surface-based PV estimation tools exist in the literature, past efforts have usually been designed with a specific modality in mind. Two notable examples for neuroimaging are the ribbon-constrained (RC) method used within the Human Connectome Project’s (HCP) fMRISurface pipeline [7] and PETSurfer [9], [10], a variant of FreeSurfer. The former is designed for use with BOLD and so distinguishes only between cortex and otherwise, not the grey matter (GM), white matter (WM) and non-brain required for ASL and PET; whereas the latter is both PET-specific and tightly integrated into FreeSurfer such that it is hard to use independently of that workflow. Furthermore, both methods deal exclusively with surfaces representing the cortex. The objective of this work was to develop an algorithm, named Toblerone¹, to estimate partial volumes for both cortical and subcortical structures (where such surfaces are available, for example via FSL FIRST [11]) for neuroimaging applications. The end result is highly general and could be used with images from multiple modalities and/or in other parts of the body.

II. THEORY

Voxelisation is the process of quantifying the volume contained within a surface and many algorithmic implementations are given in the computer graphics literature. The key step within this operation is determining if a point lies interior or exterior to a given surface; by repeating this test entire volumes can be built up. The ray intersection test outlined by Nooruddin and Turk [12] is widely used for this and requires only that the surfaces be contiguous (water-tight). The test is performed by projecting an infinite ray in any direction from the point under test and counting the number of intersections made with the surface. A ray from an interior point will make an odd number of intersections as it exits the surface (including folds within the surface, there will be one more point of exit than entry); conversely an exterior point will make an even number of intersections (balanced entries and exits), if at all. This test scales badly with increasing spatial resolution: for a linear resolution of n samples per unit distance, n³ tests per unit volume are required. Furthermore, as each ray must be tested against each surface element, the test also scales with surface complexity (linearly for a naïve implementation). For a typical functional image of 10⁵ voxels and 2.5×10⁵ surface elements in a FreeSurfer cortical surface, this is prohibitively computationally intensive.

The method adopted in this work is to only use the portion of surface that actually intersects a given voxel (termed the ‘local patch’) for ray intersection testing. The local patch is defined as all triangles that intersect the voxel or, equivalently, the minimal set of triangles that unambiguously divides the voxel into two regions. This patch is by definition non-contiguous, so it is necessary to modify the ray intersection test accordingly; the modified form is referred to as the ‘reduced’ test in contrast to the ‘classical’ test. Within each voxel, a ‘root point’ that is known to lie within the surface is identified via the classical ray test. Any other point within the voxel may then be tested by projecting the finite line segment r = p_t + λ(p_r − p_t), where p_t is the point under test, p_r is the root point and 0 ≤ λ ≤ 1 is a distance multiplier along the line. A parity test is then applied to the number of intersections identified between the root and test points. The fact that the line terminates at a point interior to the surface means that exterior points will lead to one more point of entry than exit; conversely interior points will lead to either zero or an even number of intersections. It is not necessary to test surface elements outside the voxel as the finite length of the line segment means it can never leave the voxel. Fig. 1 provides an illustration of the test in practice.

Fig. 1.

Reduced ray intersection test for non-contiguous surfaces. The root point (interior) is shown in magenta. A ray from an interior point (green) makes two intersections due to the presence of a fold; from an exterior point (yellow) there is one intersection.

In order to minimise the number of tests required per voxel, convex hulls (defined as the smallest possible region enclosing a set of points within which any two points can be connected without leaving the region) are used to estimate partial volumes wherever possible. The rationale for this is that if the extrema points of a region can be classified as interior/exterior to a surface then, to an approximation, all points lying within the convex hull of these points will share the same classification.

III. ALGORITHM

The following section addresses PV estimation for structures within the brain, for which the tissue classes of interest are GM, WM and non-brain. The same principles would apply to structures in other areas of the body, though the interpretation of tissue classes would differ.

A. Estimation for a single surface

The core algorithm within Toblerone estimates the voxel-wise interior/exterior PVs arising from the intersection of a single surface with an arbitrary voxel grid. Toblerone assumes cuboid voxels with a ‘boxcar’ point-spread function (PSF), which is to say that it does not allow for any mixing of signal between voxels. In reality, different modalities have differing PSFs and such effects may be separately accounted for via a convolution operation.

The first step is to identify and record the local patches of surface intersecting each voxel of the reference grid via Moller’s triangle-box overlap test [13]. The geometry of a surface within a voxel can frequently be complex: using a sulcus of the cortex as an example, the surface may intersect the voxel multiple times, with the opposite banks of the sulcus appearing as two unconnected patches of surface, illustrated in fig. 2. Accounting for the many possible surface/voxel configurations requires numerous specific tests that rapidly become excessively complex, so the approach taken in Toblerone is to divide and conquer each voxel as required. As the length scale of a voxel decreases, the complexity of the local surface configuration within the voxel will also decrease (for example, a sulcus is less likely to intersect the voxel multiple times). Each voxel of the reference image is therefore divided into a number of subvoxels which are processed individually. The subdivision factor has been set empirically as ceil (v/0.75) where v is the vector of voxel dimensions and 0.75 represents the lower limit of feature size found in the brain (in other contexts this parameter could be varied). Note that this subdivision factor transforms anisotropic voxels into approximately isotropic subvoxels. Subvoxels are then processed according to the following framework.

Fig. 2.

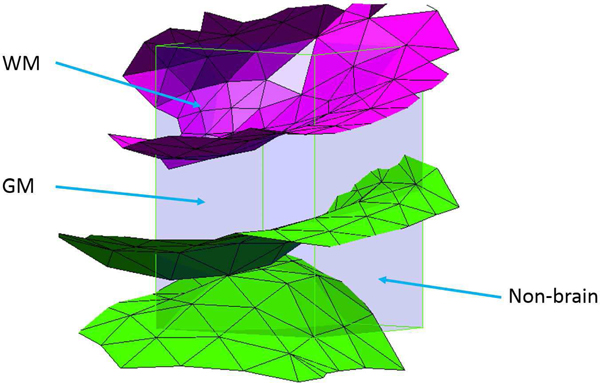
Intersection of inner (magenta) and outer (green) surfaces of the cortex with a voxel. The outer surface intersects twice with distinct patches of surface; this is likely due to the presence of a sulcus. Tissue PVs are labelled.

• If the subvoxel does not intersect the surface, it is assigned a single-class volume according to an interior/exterior classification of its centre. This is illustrated in fig. 3a.

• If the subvoxel intersects the surface, then it contains interior and exterior PVs. One of these will be estimated using a convex hull (via the Qhull implementation [14]) if the geometry of the surface is favourable, as follows:

  • If the surface intersects entirely through one face of the subvoxel, then it encloses a highly convex volume that may be reliably estimated. The other partial volume is calculated by subtraction from the total subvoxel volume. This is illustrated in fig. 3b.
  • If the surface is folded within the subvoxel (identified by multiple intersection of the surface along an edge or face diagonal of the subvoxel) then the subvoxel is subdivided a second time. This is because it is difficult to reliably identify which volume is interior or exterior in such a situation. This is illustrated in fig. 3c/d.
  • In all other cases, convex hulls are again used. In order to minimise the potential error associated with estimation of a non-convex volume via the use of a convex hull, it is important to identify which of the two PVs within the subvoxel is closer to being genuinely convex than the other. The proxy measure used for this is the number of subvoxel vertices lying on either side of the surface: the side with fewer vertices is assumed to enclose a more convex (and at any rate smaller) volume than the other. This is illustrated in fig. 3e.

• If the surface intersects the subvoxel multiple times (identified by the successful separation of surface nodes lying within the subvoxel into unconnected groups) then the voxel is subdivided a second time. This situation occurs for example when the opposite banks of a sulcus pass through a voxel. Although the reduced ray intersection test is accurate in such a situation, forming convex hulls is not, so subdivision is the safer option. This is illustrated in fig. 3f.

Fig. 3.

Various subvoxel/surface configurations. a) no intersection: whole-volume assignment; b) single intersection through one face: a small convex hull will be formed; c/d) two examples of single intersection, folded surface: further subdivision will be used; e) single intersection through multiple faces: a convex hull will be formed; f) multiple surface intersection (unconnected patches of surface, likely a sulcus): further subdivision will be used.

If required, the second subdivision is performed at a constant factor of 5 to yield sub-subvoxels of approximately 0.1 to 0.2mm side length isotropic. These are always assigned a single-class volume based on a classification of their centre points as their small size means that any PVE will be negligible. Finally, voxels that do not intersect the surface (fully interior or exterior) are given single-class volumes according to tests of their centre points. Structures defined by a single surface (e.g. the thalamus) require no further processing: the estimates produced by the aforementioned steps may be used directly for PVEc.

B. Multiple-surface structures

Structures that are defined by multiple surfaces require further processing to yield PV estimates for all tissues of interest. Using the cortex as an example, PVs within each hemisphere are obtained with the relations:

$$\begin{gathered} P{V}_{WM}=P_{inner} \\ P{V}_{GM}=\max \left(0,P_{outer}-P_{inner}\right) \\ P{V}_{NB}=1-\left(P{V}_{WM}+P{V}_{GM}\right) \end{gathered}$$

where P_inner and P_outer denote the interior/exterior PV fractions associated with the inner and outer surfaces of the cortex respectively and PV _WM, PV _GM and PV _NB denote the PV estimates for WM, GM and non-brain tissue (the latter including cerebrospinal fluid, CSF). These equations are structured to account for a potential surface defect whereby the surfaces of the cortex swap relative position (the inner lying exterior to the outer) around the corpus collosum.The structure of the above relations (N surfaces leading to N +1 tissue classes) could easily be generalised to structures defined by more than two surfaces (for example, sublayers of the cortex, as used in laminar fMRI). A similar set of equations is used to merge hemisphere-specific results to cover the whole cortex, accounting for voxels lying on the mid-sagittal plane that intersect both hemispheres.

C. Whole-brain PV estimation

Toblerone, as outlined above, operates on a structure-by-structure basis in which the output tissue types are dependent on the structure in question. A number of methods utilising this core functionality were implemented:

1. estimate_structure: estimate the inner and outer PVs associated with a structure defined by a single surface

2. estimate_cortex: estimate the GM, WM and non-brain PVs associated with the four surfaces of the cortex (l/r white/pial in the FreeSurfer terminology)

3. estimate_all: a combination of the structure and cortex methods above, this estimates PVs for the cortex and all subcortical structures identified by FIRST and combines them (with the exception of the brain stem) into a single set of GM, WM and non-brain PV estimates. The run-time for a typical subject was around 25 minutes.

The combination of FreeSurfer/FIRST and estimate_all provides a complete pipeline for obtaining whole-brain PV estimates in an arbitrary reference voxel grid from a single T1-weighted image that may be used as a replacement for existing volumetric tools such as FAST. There is however a key conceptual difference between surface and volumetric methods that concerns their interpretation of subcortical structures. Due to differences in tissue composition around the brain, cortical and subcortical GM have different intensities on a normal T1-weighted image and are accordingly assigned different GM PVs by volumetric tools such as FAST (whereby cortical GM is seen as more ‘grey’ than subcortical, as illustrated in fig. 12). Surface-based methods, by contrast, do not take a view on what tissue lies within a surface other than simply asserting that it is different to that which lies without. When combining the PVs of individual structures in Toblerone’s estimate_all function, all tissue within the cortex and subcortical structures is interpreted as pure GM. The practical implication of this is that Toblerone’s estimates for subcortical GM are higher than those produced by FAST. For this reason, the conventional GM/WM/CSF tissue classes used by volumetric tools may be better thought of within Toblerone’s framework as tissue of interest, other tissues and non-brain, though for the purposes of this article the familiar names GM and WM shall be used alongside non-brain. The inherent ambiguity in determining which tissues lie outside subcortical structures, which could be either WM or CSF depending on their location within the brain, was resolved using FAST’s segmentation results².

Fig. 12.

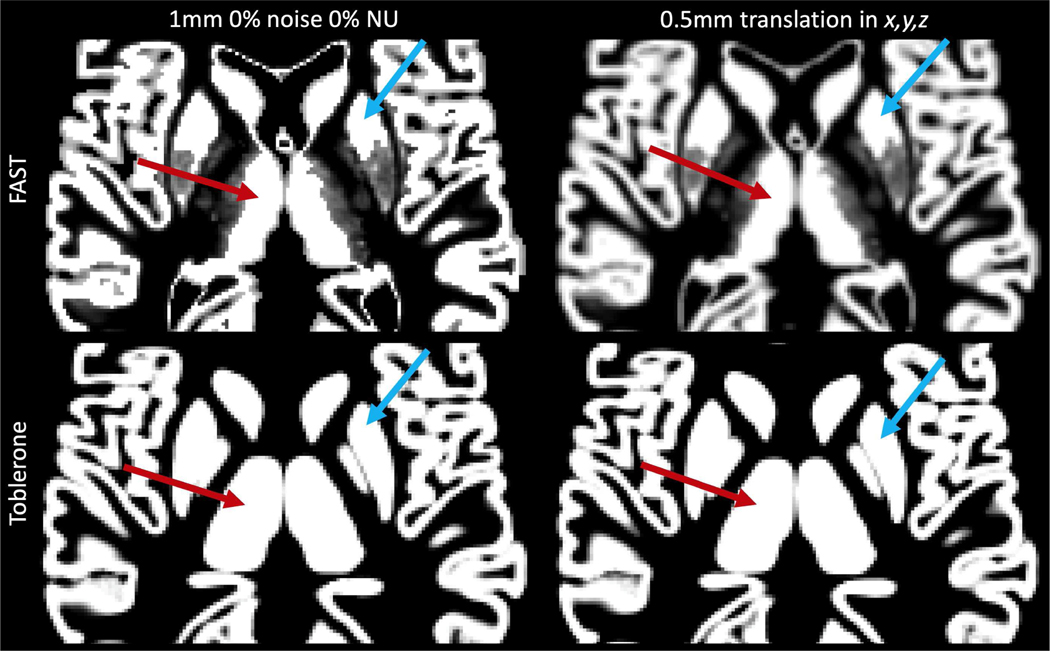
Illustration of resampling-induced blurring on the 1mm isotropic GM PV map from the 0% noise 0% NU BrainWeb image. The left column shows the original estimates produced by FAST and Toblerone, the right shows the result of a 0.5mm translation along each axis. The left thalamus (red) and right putamen (blue) are highlighted in each, showing how surface and volumetric methods differ markedly in their interpretation of subcortical structures (FAST does not regard them as pure GM, whereas Toblerone does for the analyses presented in this work).

IV. EVALUATION

Three datasets and three comparator methods were used, as summarised in Table I. The two surface-based comparator methods were restricted to use in the cortex only. Toblerone was run on both cortical and subcortical surfaces where appropriate to produce whole-brain PV estimates.

TABLE I.

DATASETS & METHODS USED.

name	Simulated surfaces	BrainWeb	HCP test-retest
type	S	V + S	V + S
resolution	-	1mm iso.	0.7mm iso.
size	1 cortical hemisphere	18 simulated T1 images	45 subjects, 2 sessions each
ground truth	numerical method	volumetric segmentation*	N/A
comparator methods	NeuroPVE (S) RC (S)	RC** (S) FAST (V)	RC** (S) FAST (V)

S surface, V volumetric, RC ribbon-constrained method

^*established via automatic segmentation with manual intervention

^**RC can only be run on the cortex for these datasets

A. Comparator methods

The first surface-based comparator method, the ribbon-constrained (RC) algorithm, was developed for use with BOLD data in the HCP’s fMRISurface pipeline [8] and is restricted to use in the cortex only. The method assumes vertex correspondence between the two surfaces of the cortex and works as follows. For each vertex in turn, the outermost edges of the triangles that surround said vertex are connected between the two surfaces to form a 3D polyhedron representing a small region of cortex. Nearby voxels are subdivided and the subvoxels centres tested to determine if they lie interior to the polyhedron. The subdivision factor used in this work was the higher value of either ceil (max (v) /0.4) or 4, where v is the vector of voxel dimensions. The fraction of subvoxel centres lying within any cortical polyhedron gives the cortical GM PV, which, as the BOLD signal is predominantly cortical in origin, is the quantity of interest for this modality. In order to obtain WM and non-brain PVs, the following post-processing steps were used. Firstly, the unassigned PV of each voxel was calculated as 1 − PV_GM, which was subsequently labelled as either WM or non-brain according to a signed-distance test of the voxel centre in comparison to the cortical mid-surface: for a voxel with centre point outside the mid-surface, the unassigned PV was labelled as non-brain. A weakness of this approach is that it is unable to faithfully capture a voxel in which all three tissues are present; only the combinations WM/GM or GM/non-brain are permitted. As voxel size increases, the probability of voxels containing multiple tissues also increases; testing on an image of 3mm isotropic resolution showed that around 30% of voxels intersecting the cortical ribbon contained three tissues. Resampling can be used to mitigate this effect so two variants of this method were tested: ‘RC’, direct estimation at each resolution, and ‘RC2’, estimation at 1mm followed by resampling to other resolutions via the process in section IV–B. The run-time for a typical subject was around 15 minutes.

This second surface method, NeuroPVE [15], uses a vox-elisation method based on the work of [9,12], applied in a brain-specific context and again restricted to use in the cortex only. Multiple expanded and contracted copies of each surface are created and the ratio of expanded to contracted surfaces intersecting a given voxel is used as a first approximation for partial volumes. This ratio is then mapped, along with surface orientation information, via trigonometric relations on the unit cube into a PV estimate. The estimates produced take discrete values according to the number of surfaces used (in this work the default of 5). The intended use of this tool was PV estimation at structural, not functional, resolution, so two variants were tested: ‘Neuro’, direct estimation at arbitrary resolutions, and ‘Neuro2’, estimation at structural resolution followed by resampling to other resolutions via the process in section IV–B. On the basis of NeuroPVE’s results on the simulated surfaces, it was excluded from further analysis. As the process of surface inflation is slow, the run-time for a typical subject was around 12 hours.

Finally, FSL’s FAST [7] is an established whole-brain volumetric segmentation tool that was used as a comparator for the surface methods. On both the BrainWeb and HCP test-retest datasets, FAST was run on the brain-extracted images at structural resolution (1mm and 0.7mm iso. respectively). PVs were then obtained at other resolutions via the resampling method detailed in section IV–B. The run-time for a typical subject was around 5 minutes.

B. Resampling

Resampling is an interpolation operation that is used to transform volumetric data between voxel grids (in this context, from structural to functional resolution). FSL’s applywarp tool was used with the -super flag for all resampling operations. This works by creating an up-sampled copy of the target voxel grid onto which values from the input image are sampled. The average is then taken across the voxel neighbourhoods of the high-resolution grid (sized according to the up-sampling factor) to obtain the result in the target voxel grid. Such an approach is appropriate when moving from fine to coarse as each output voxel corresponds to multiple input voxels, the individual contributions of which should be accounted for to preserve overall tissue proportions. When using applywarp a transformation matrix between the input and output voxel grids must be given as the -premat argument; to denote identity for the purposes of this work, the output of the HCP wb_command–convert-affine –from-world –to-flirt tool operating on I₄ was used as the -premat to correct for a subvoxel shift that arises due to FSL coordinate system conventions. Note that for perfectly aligned voxel grids with an integer ratio of voxel sizes, such as a 1mm and 2mm isotropic grid, this process is equivalent to averaging across blocks of the smaller grid (sized 2×2×2 in this case).

C. Simulated surfaces

A pair of concentric surfaces, illustrated fig. 4, were designed to capture geometric features relevant to the anatomy of a cortical hemisphere. These were produced by modulating the radius of a sphere as a function of azimuth θ and elevation φ to produce sulci and gyri-like features. The radius of the inner surface was defined as

$$r_{in}=60\left(1-0.1\max \left({\sin }^{20}5u,{\sin }^{20}5v\right)\right)$$

where 60 is the unmodulated radius of the sphere, 0.1 fixes the relative depth of sulci, the max function prevents sulci from constructively interfering to produce deep wells at points of intersection, the power of 20 produces broad gyri and narrow sulci, and the substitutionsu = φ+θ, v = φ−θ cause the sulci to spiral around the sphere in opposite directions. Modulation was restricted to the range −2π/5 ≤ θ ≤ 2π/5 to leave the poles smooth and suppress unrealistic features. The outer radius was set at r_out = 1.05 r_in, leading to a peak radial distance between surfaces of 3mm. The outermost region was taken to represent non-brain tissue, the innermost WM and the region in between GM. The use of analytic functions to define the surfaces permitted ground truth to be calculated using the following numerical method. Voxels were sampled at 4,096 elements per mm³ and the positions of these sample points expressed in spherical polar coordinates. By comparing the actual radius of each point to the calculated radius of the surface boundaries for the same azimuth and elevation, the tissue type of the sample point within the structure could be determined, and from there PVs obtained by aggregating results within voxels. This is referred to as the ‘numerical solution’ in the results section. All surface methods were used on this dataset to obtain PVs at voxel sizes of 1 to 3mm in steps of 0.2mm isotropic.

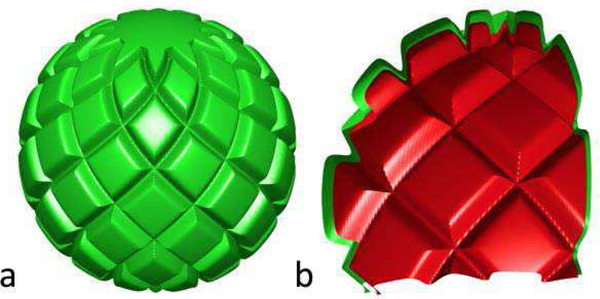
Fig. 4.

a) Simulated surfaces; b) cutaway showing inner (red) and outer (green) surfaces. Peak radial distance between the two was 3mm.

D. BrainWeb simulated T1 images

BrainWeb [16], [17] simulates whole-head T1 images at 1mm isotropic resolution with specified levels of random noise and field non-uniformity (NU). Eighteen images were produced to cover the available parameter space of noise levels {0, 1, 3, 5, 7, 9} and NU levels {0, 20, 40} (both quantities in percent). These were run through FIRST and FreeSurfer, after which Toblerone’s estimate_all and the RC method (cortex only) were used on the output. FAST was also used to enable a comparison between surface and volumetric methods. PVs were obtained at voxel sizes of 1 to 4mm in steps of 1mm isotropic. Although ground truth PV maps exist for this dataset (produced by automatic volumetric segmentation of T1 images with manual correction [16]), both surface and volumetric methods returned significantly different results to these, raising the complicated question of determining which set of results is correct. In order to avoid making this judgement, each method was instead referenced to its own results on the ideal T1 image (0% noise 0% NU) in the 1mm isotropic voxel grid of the structural images. The voxel grids associated with each voxel size were aligned such that results at 1mm could be used to calculate a reference at other sizes.

E. Human Connectome Project test-retest data

This dataset comprises 45 subjects from the main HCP cohort who underwent two separate structural scan sessions (mean age 30.2 years, mean time between sessions 4.8 months). Each session was processed using the pipeline in [8] to obtain cortical surfaces via FreeSurfer. Separately, the distortion-corrected T1 images were processed using FIRST to obtain subcortical surfaces. Toblerone’s estimate_all and the RC method (for the cortex only) were used on this dataset, as well as FAST for a comparison between surface and volumetric methods. PVs were obtained at voxel sizes of 1 to 3.8mm in steps of 0.4mm isotropic, as well as the native 0.7mm isotropic voxel grid of the structural images. Although a ground truth is not defined for this dataset, each method’s results from the first session were used as a reference for the second session.

F. Evaluation metrics

Errors were measured in both a per-voxel (root-mean-square, RMS, of individual voxel errors) and aggregate (total tissue volume) sense. The former basis is important as PVEc is locally sensitive to the PV estimates [18]; the latter basis reflects systematic bias at the aggregate level. All errors are expressed in percent and map directly to PV estimates without scaling: for example, a PV estimate of 0.5 against a reference value of 0.55 corresponds to an error of −0.05 or −5%.

A further analysis of voxel-wise differences between Toblerone and FAST was performed on the HCP dataset at multiple voxel sizes by sorting voxels into 5% width bins according to their Toblerone GM PV estimate. The difference (Toblerone – FAST) was calculated for each voxel and the mean taken across each bin. This quantity was then averaged across subjects and sessions (weighted to respect differences in brain volume).

V. RESULTS

A. Simulated surfaces

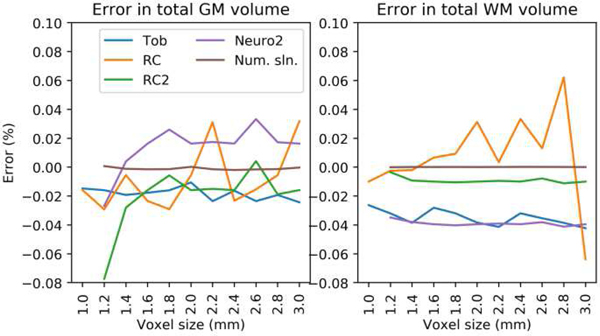
Fig. 5 shows the error in total tissue volume for the simulated surfaces. The numerical solution at 1mm was used as the reference. Toblerone showed consistency across voxel sizes, though with a small negative bias in both GM and WM. RC estimates showed variation in both. The resampling-based methods RC2 and Neuro2 showed high consistency in WM but less so in GM. The numerical solution was stable across voxel sizes. Neuro’s results are excluded from this and subsequent graphs for clarity; the full results are given in the supplementary material (figs. s5 and s6).

Fig. 5.

Simulated surfaces: error in total tissue volume. Toblerone showed consistency, though with small bias, for both GM and WM. RC1 errors were lower for GM than WM. Resampling-based methods (RC2, Neuro2) showed particular consistency in WM. [Full results in supplementary, fig. s5]

Fig. 6 shows per-voxel error for the simulated surfaces. Results were masked to consider voxels intersecting either surface of the cortex as only these contain PVs. Toblerone and RC produced the lowest errors at all voxel sizes in GM; in WM only Toblerone retained this behaviour. Resampling-based methods (RC2, Neuro2) produced lower errors as voxel size increased, and a characteristic notch in their results was observed at 2mm. Although RC initially performed better than RC2 in WM, the inverse was true above 2mm voxel size.

Fig. 6.

Simulated surfaces: per-voxel error. Toblerone and RC produced the lowest errors in GM; in WM there was a clear difference to Toblerone. RC2 and Neuro2’s errors both decreased with increasing voxel size, with a characteristic notch observed at 2mm. [Full results in supplementary, fig. s6]

B. BrainWeb simulated T1 images

Fig. 7 shows the difference in total tissue volume across the brain as a function of noise and NU levels, referenced to each method’s results at 0% noise and 0% NU. PV estimates at 1mm isotropic voxel size were used for this analysis. RC’s GM result was for the cortex only as it cannot process subcortical structures. In general, the surface-based methods showed more consistency in their estimates across all levels of noise and NU, with the notable exception of GM at 0% noise. FAST’s consistency was notably better in GM than WM.

Fig. 7.

BrainWeb: difference in total tissue volume referenced to each method’s 0% noise 0% NU result. Surface-based methods were more consistent at almost all noise and NU levels; FAST was more consistent in GM than WM.

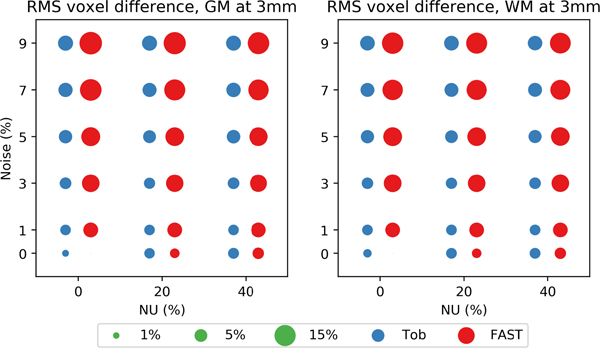
Fig. 8 shows the RMS per-voxel difference in PV estimates at 3mm voxel size as a function of noise and NU. Each method’s 1mm results at 0% noise 0% NU were used as the reference. Toblerone returned lower RMS voxel differences in both GM and WM at all levels of NU and noise except 0% noise 0% NU, a pattern that was repeated at other voxel sizes (given in supplementary fig. s8).

Fig. 8.

BrainWeb: RMS per-voxel differences at 3mm voxel size, referenced to each method’s 1mm 0% noise 0% NU results. Toblerone’s differences were smaller at almost all levels of noise and NU, as was also the case at other voxel sizes. [Results for other voxel sizes are given in supplementary fig. s8]

C. HCP test-retest subjects

Fig. 9 shows violin plots of inter-session difference (retest minus test) in tissue volume across the 45 subjects of the HCP dataset. PV estimates at 0.7mm isotropic voxel size were used for this analysis. RC’s GM result was for the cortex only. Both surface methods gave a tighter distribution than FAST, suggesting greater repeatability between sessions. All methods showed greater variability in GM than WM.

Fig. 9.

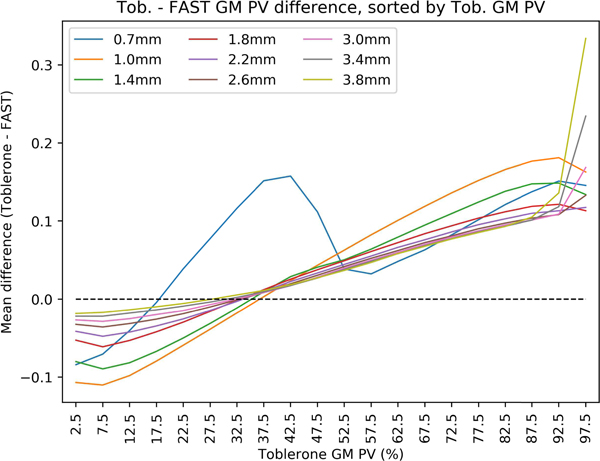
HCP test-retest: mean difference between Toblerone and FAST GM PVs, sorted into 5% width bins according to Toblerone’s GM PV. As Toblerone’s GM PV estimate in a given voxel increased, FAST was more likely to assign a smaller value, and vice-versa. The strength of this relationship decreased with increasing voxel size. An inverse, but weaker, effect was seen for WM (supplementary fig s9).

Fig. 10 shows the mean per-voxel difference between Toblerone and FAST’s GM PV estimates as a function of Toblerone’s GM PV estimate. Excepting the 0.7mm result, the positive slope of each line shows that in voxels with a low Toblerone GM PV estimate, FAST was more likely to assign a higher value, and vice-versa at high Toblerone GM PV estimates. The strength of this relationship decreased with increasing voxel size. It should be noted that the 0.7mm result was the only one not to make use of resampling (for all others, FAST’s 0.7mm estimates were resampled onto the target voxel grid).

Fig. 10.

HCP test-retest: inter-session (retest minus test) difference in total tissue volume. PVs were estimated in the native 0.7mm isotropic space of the structural images. RC’s result is for the cortex only. Both surface methods show a tighter distribution than FAST.

VI. DISCUSSION

Results from the simulated surfaces showed that Toblerone produced estimates with a comparatively low and consistent error. Although the RC method was able to perform similarly for GM, there was a clear advantage for Toblerone in WM. Results from the BrainWeb dataset suggested that a surface-based approach (the combination of FreeSurfer/FIRST and Toblerone) was more robust to random noise and field non-uniformity than FAST’s volumetric approach. In particular, the BrainWeb results showed that the consistency of FAST’s WM estimates suffered in the presence of these scanner imperfections. Finally, results from the HCP test-retest dataset showed that the surface-based approach provided better inter-session repeatability in estimates of total tissue volume.

The use of resampling – unavoidable for volumetric methods which must transform PV estimates from a structural voxel grid to a functional voxel grid – degrades data quality in an unpredictable and highly localised manner. This chiefly arises due to so-called subvoxel effects, which may be illustrated via the following 1D example. Consider a row of voxels of size 1mm that are to be resampled onto 1.4mm voxels. A larger voxel overlaps evenly onto two smaller voxels, covering 0.7mm of each. The resampled value will be the mean of the two smaller, on the implicit and unlikely assumption that the tissues within each are evenly distributed. Next, consider a row of 1mm voxels that are to be resampled onto 3.4mm voxels, whereby a larger voxel overlaps by 0.2, 1, 1, 1 and 0.2mm onto smaller voxels. Again, the resampled value will be a weighted mean of the smaller voxels, but as the central three voxels are included wholly in the new voxel, the spatial distribution of tissues within these voxels is irrelevant and the assumption of even distribution can safely be made. As the ratio of output voxel size to input voxel size increases, the significance of subvoxel effects is therefore reduced.

It is extremely difficult to quantitatively measure the impact of resampling, particularly on non-simulated data. To do so would require the ability to express some volumetric reference data in an arbitrary voxel grid without making use of resampling, otherwise a trap of circular reasoning results. Nevertheless, such an analysis can be performed using the simulated surfaces presented earlier. The key conceptual difference is that the ground truth for this dataset is defined by a surface and can therefore calculated in any voxel grid without resampling. Fig. 11 shows the results of resampling ground truth results from the numerical method at each resolution to all other resolutions above the one in question (for example, the 1.4mm truth was resampled to 1.6, 1.8, …etc). At each voxel size, the resampled results can be compared to a ground truth that has been calculated without the use of resampling. RMS per-voxel error was then measured using the same mask as before, namely all voxels intersecting either surface of the cortex, as only these contain PVs. Multiple trends were seen: firstly, as the input voxel size increased, error at all output voxel sizes increased. Secondly, as the ratio of output to input voxel size increased, the error decreased. Finally, the error fell to zero when this ratio took an integer value. This is due to the use of perfectly aligned voxel grids in this work (which would not be the case with patient data) and is discussed in section IV.B. These phenomena likely explain the interesting behaviour observed in various analyses, namely: the notches seen in fig. 6, as well as supplementary figs. s5 and s6 (perfect voxel correspondence means no subvoxel effects); the 0.7mm result in fig. 10 (for all other sizes, resampling by a non-integer ratio of voxel size blurs the FAST results, reducing image contrast and the number of high GM PV voxels); and the lack of error observed in FAST’s GM and WM results at 2, 3 and 4mm voxel size, 0% noise 0% NU in figs. 8 and s8 (again, perfect voxel correspondence with the reference set of 1mm estimates). These considerations do not apply to surface-based methods as they do not make use of resampling.

Fig. 11.

Simulated surfaces: error induced by resampling the ground truth GM PV map, masked to voxels intersecting either surface of the cortex. As the input voxel size increases, error increases, but as the ratio output / input voxel size increases, error falls. Finally, error falls to zero when the ratio takes an integer value.

A further advantage of surface-based methods concerns their application of transformations. Notwithstanding the fact that volumetric methods require resampling to transform data from one resolution to another, they also require it to apply a registration transformation between the structural voxel grid in which PVs are estimated and the functional voxel grid in which PVEc is to be performed. Once again, the impact of this upon data quality is highly localised and difficult to measure quantitatively. It can however be illustrated via the following experiment, illustrated in fig. 12. GM PV maps for the 0% noise 0% NU BrainWeb image were translated by 0.5mm in each of the x,y,z axes. For FAST, this translation took the form of an affine transformation applied during a resampling operation. Significant blurring is seen, particularly around the edges of structures where there was previously good edge definition. As these edge voxels by definition contain PVs this is a particularly undesirable outcome. By contrast, blurring within a structure is of little consequence as the tissue is already homogenous. For Toblerone, this translation was performed by shifting the surfaces into the new reference voxel grid represented by the translation and then estimating PVs afresh with no noticeable reduction in edge definition.

In its native form, the RC method is unable to correctly handle voxels in which all three tissue types are present (due to the fact that it estimates for GM first and then assigns the remainder to either WM or non-brain). The impact of this is seen in the positive relationship between per-voxel error in WM and voxel size in fig. 6. Resampling can help to minimise this error: at small voxel sizes, the probability of voxels containing three tissue types is smaller and so the error is minimised, but this does not hold true at larger voxel sizes. Accordingly, as output voxel size increases, it is increasingly beneficial to obtain PV estimates by resampling those from a smaller voxel size. Set against this, however, are the aforementioned problems introduced by resampling: when the ratio of output to input voxel size is small, subvoxel effects are significant and high per-voxel errors result (as seen in fig. 6). A threshold voxel value above which resampling is beneficial therefore results (at around 2mm in the figure). The exact value of this threshold would be difficult to predict in the general case (in particular, the use of aligned voxel grids in this work is both highly significant and extremely unrealistic). By contrast, Toblerone is able to produce consistent estimates in all tissue classes at arbitrary voxel sizes without the use of resampling.

We were unable to further analyse the HCP test-retest dataset in order to establish where in the brain the differences between Toblerone’s and FAST’s estimates arise. As this would require extensive use of non-linear registrations and resampling to transform all subjects onto a common template, it is likely that the artefacts imposed by this process would obscure the true methodological differences of interest. Furthermore, an analysis on the BrainWeb database would be of limited use as it only represents the cortical anatomy of a single subject and would therefore ignore population variability.

VII. CONCLUSION

Toblerone is a new method for estimating PVs using surface segmentations. Unlike existing surface-based tools, it is not closely tied to any specific modality or structure and can therefore be adapted to multiple use cases (notably, providing PV estimates for the whole brain). It is able to operate at arbitrary resolutions without recourse to resampling, thereby avoiding the highly localised degradation of image quality that this process entails. Three datasets have been used for evaluation of the method. Results from simulated surfaces show consistently low errors at both the voxel and aggregate level, either matching or surpassing other surface-based methods. Results on simulated T1 images from the BrainWeb database show that a FreeSurfer/FIRST/Toblerone surface-based pipeline used as an alternative to FAST is more robust in the presence of random noise and field non-uniformity. Finally, results from the HCP test-retest dataset of 45 subjects show that the surface-based pipeline produces a tighter distribution of inter-session tissue volumes than FAST, suggesting the surface approach has greater repeatability. The magnitude of methodological differences observed in this work, and related conceptual questions concerning the difference in interpretation of subcortical tissue between surface and volumetric methods, will have implications for the wider process of PVEc.