Three-Dimensional GRE T_1ρ mapping of the brain using tailored variable flip-angle scheduling

Abstract

Purpose:

To introduce a new approach called tailored variable flip-angle (VFA) scheduling for SNR-efficient 3D T_1ρ mapping of the brain using a magnetization-prepared gradient-echo sequence.

Methods:

Simulations were used to assess the relative SNR efficiency, quantitative accuracy, and spatial blurring of tailored VFA scheduling for T_1ρ mapping of brain tissue compared with magnetization-prepared angle-modulated partitioned k-space spoiled gradient-echo snapshots (MAPSS), a state-of-the-art technique for accurate 3D gradient-echo T_1ρ mapping. Simulations were also used to calculate optimal imaging parameters for tailored VFA scheduling versus MAPSS, without and with nulling of CSF. Four participants were imaged at 3T MRI to demonstrate the feasibility of tailored VFA scheduling for T_1ρ mapping of the brain. Using MAPSS as a reference standard, in vivo data were used to validate the relative SNR efficiency and quantitative accuracy of the new approach.

Results:

Tailored VFA scheduling can provide a 2-fold to 4-fold gain in the SNR of the resulting T_1ρ map as compared with MAPSS when using identical sequence parameters while limiting T_1ρ quantification errors to 2% or less. In vivo whole-brain 3D T_1ρ maps acquired with tailored VFA scheduling had superior SNR efficiency than is achievable with MAPSS, and the SNR efficiency improved with a greater number of views per segment.

Conclusions:

Tailored VFA scheduling is an SNR-efficient GRE technique for 3D T_1ρ mapping of the brain that provides increased flexibility in choice of imaging parameters compared with MAPSS, which may benefit a variety of applications.

1 |. INTRODUCTION

Quantitative mapping of spin-lattice relaxation in the rotating frame (T_1ρ) is an emerging brain imaging technique. The T_1ρ relaxation time may be useful to detect brain pathology, including abnormal metabolism and neurodegeneration, due to its sensitivity to both biochemical factors such as pH and microstructural factors including macromolecular content and cellular density.^1–5 Altered T_1ρ relaxation times have been observed in a number of neurological and psychiatric diseases including Parkinson’s disease,^6–8 Alzheimer’s disease,^8–12 multiple sclerosis,^13,14 bipolar disorder,^15,16 and Huntington’s disease.¹⁷ There is also interest in using T_1ρ mapping in the clinical management of stroke^18–22 and glioma.^23–27

However, the practical utility of brain T_1ρ mapping is limited by the relative slowness of the technique. Quantitative T_1ρ maps are typically generated by fitting spin lock–weighted images acquired with different spin-lock durations (TSLs) to a mono-exponential signal decay model. The need for multiple TSL images, recovery of longitudinal magnetization, and RF heating restrictions all contribute to long scan times. Furthermore, volumetric coverage is required to study progressive changes in the brain, to better understand normal development and aging as well as changes associated with neurological and psychiatric disorders. In some of these populations, head motion may be an issue. Given these limitations, it is critical that brain T_1ρ mapping be made as efficient as possible to provide the best trade-off among scan time, spatial resolution, volumetric coverage, and accuracy.

Recently developed segmented 3D-GRE and fast spin-echo (FSE) sequences are promising options for providing rapid 3D whole-brain quantitative T_1ρ mapping.^28–31 These techniques use long gradient-echo (GRE) or spin-echo trains with variable flip-angle (VFA) schedules for fast imaging with high spatial resolution. The 3D acquisition also provides an SNR advantage over 2D alternatives. In the case of 3D GRE, RF cycling can be applied to account for TSL-dependent signal evolution across the GRE train, thus improving accuracy over previous methods.²⁸ These sequences can be used with advanced spin-locking pulses that incorporate self-compensating,^32,33 refocusing,³⁴ RF cycling,³⁵ and/or adiabatic^36–38 methods to reduce sensitivity to B₁ and B₀ inhomogeneities. These methods can also incorporate fluid suppression, which may improve T_1ρ quantification in voxels with partial-volume averaging of brain tissue and CSF.^31,39 Using combinations of these strategies, the feasibility of whole-brain 3D T_1ρ mapping has recently been demonstrated.^{14,30,31,37,40}

In this work, a new VFA scheme called “tailored VFA scheduling” is introduced to further improve the SNR efficiency of 3D-GRE T_1ρ mapping of the brain. In simulations and in vivo experiments, the performance of tailored VFA scheduling was compared with the combined RF cycling and VFA approach used in the state-of-the-art magnetization-prepared angle-modulated partitioned k-space spoiled GRE snapshots (MAPSS) sequence.²⁸ This work demonstrates that tailored VFA scheduling can provide a significant gain in SNR efficiency with minimal loss in quantitative accuracy and spatial fidelity. This gain in SNR efficiency can be used to acquire T_1ρ maps of the brain with reduced scan time, higher spatial resolution, and/or reduced RF heating. Initial results for this study were reported in a conference abstract.⁴¹

2 |. METHODS

2.1 |. Pulse sequence components

This work builds upon a previously described segmented 3D pulse sequence framework for T_1ρ mapping.^28,30,31 This section reviews the sequence framework and defines the imaging parameters.

Each imaging segment consists of the components diagrammed in Figure 1. First, a magnetization saturation pulse is applied followed by a recovery time (T_rec) to ensure that the longitudinal magnetization (M_z) recovers to a consistent level before applying each T_1ρ preparation pulse. During T_rec, pulses for fluid suppression (i.e., CSF nulling) and/or fat saturation can optionally be applied. Note that fluid suppression is restrictive, requiring a particular TI as well as time for M_z recovery before the CSF nulling inversion pulse is applied (TI_prep), which limits settings for T_rec. A T₂ preparation pulse of duration TE_prep can be used before the inversion pulse to reduce the required TI.^31,42 Following T_rec, the T_1ρ preparation pulse is applied, which typically consists of (1) an excitation pulse to tip M_z from the +z axis to the x-y transverse plane; (2) a spin-lock pulse of duration TSL, during which the transverse magnetization (M_xy) decays with relaxation time T_1ρ; and (3) a second excitation pulse to return M_xy to either the +z or −z axis. Note that any magnetization-preparation pulse (e.g., T₂-prep,⁴³ adiabatic T_1ρ,³⁶ RAFF⁴⁴) can optionally be used instead of the spin-lock pulse. Following the T_1ρ preparation, a spoiler gradient is applied followed by additional dead time to eliminate any residual M_xy and reduce eddy current effects (total duration τ). Finally, a rapid 3D-GRE pulse sequence is played out to collect a train of phase-encoded readouts (i.e., views). Given a particular TR and views per segment (VPS), the total duration of the GRE train is TR × VPS. The GRE train is played out with a VFA schedule to reduce spatial blurring. This entire segment is repeated until all phase encodes of the 3D volume are acquired. This 3D acquisition is then repeated for each TSL to quantify T_1ρ.

FIGURE 1.

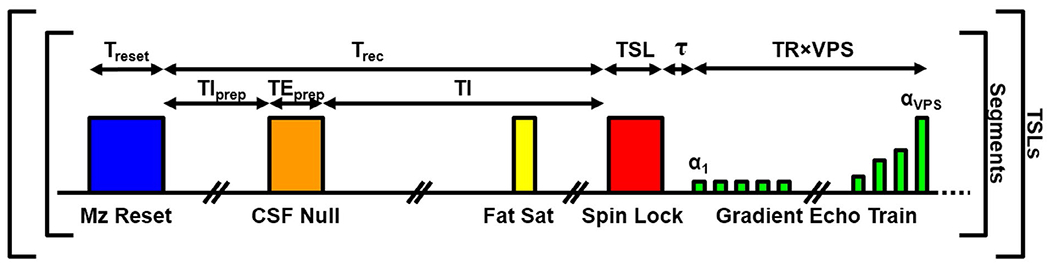
Three-dimensional spin lock–prepared pulse sequence components and imaging parameter definitions. Note that the durations and amplitudes are not drawn to scale. During the M_z recovery time (T_rec), CSF nulling and/or fat saturation can optionally be applied. The entire segment is repeated until all views are acquired for a given spin-lock time (TSL). The full 3D acquisition is then repeated for each unique TSL. α_n = flip angle of nth excitation pulse in the gradient-echo train; VPS, views per segment

In this study, spin-locked 2D-GRE and 3D-GRE sequences were implemented using the pulse-sequence components outlined in Figure 1 with the following details. The M_z reset component used either the approach described by Parker et al⁴⁵ or the pulse train approach described by Kim et al.⁴⁶ The CSF nulling component used a T₂-prep pulse with Malcolm-Levitt phase cycling⁴³ and adiabatic excitation pulses, similar to the approach used in Watts et al³¹ and Gai et al.⁴² The fat-saturation component was not applied. A spoiler gradient with amplitude of 15 mT/m and duration of 5.0 ms was applied following both the CSF nulling and T_1ρ preparation pulses. The value of τ was set to 7.0 ms. For spin-lock preparation, an approach similar to the B₁-compensated and B₀-compensated pulse proposed by Witschey et al³⁴ was updated to use adiabatic instead of hard pulses for the 90° excitations, to increase robustness to B₀ and B₁ inhomogeneities across the brain.⁴⁷ The adiabatic pulse parameters were B_1,max = 1000 Hz, pulse duration = 3.1 ms, and time-bandwidth product = 30. Furthermore, unlike the method by Witschey et al, which must prepare magnetization along the −z axis to account for B₁ sensitivity of the excitation pulses, the B₁-insensitive adiabatic pulses can accurately prepare magnetization along the −z or +z axis.

2.2 |. Tailored VFA scheduling

In this section, an SNR-efficient approach called tailored VFA scheduling is introduced to correct for TSL-dependent signal evolutions over the GRE train. If a constant flip angle is used for each excitation pulse of the GRE train, then the TSL-specific spin lock–prepared signal will approach a steady-state value that will be the same for each TSL (Figure 2A). This is undesirable for two reasons: (1) k-Space will be modulated by the signal evolution over the GRE train, resulting in TSL-dependent spatial blurring; and (2) the uniquely prepared signal level for each TSL will be altered over the course of the GRE train, resulting in quantification errors. The goal then is to preserve the prepared signal levels over the course of the GRE train.

FIGURE 2.

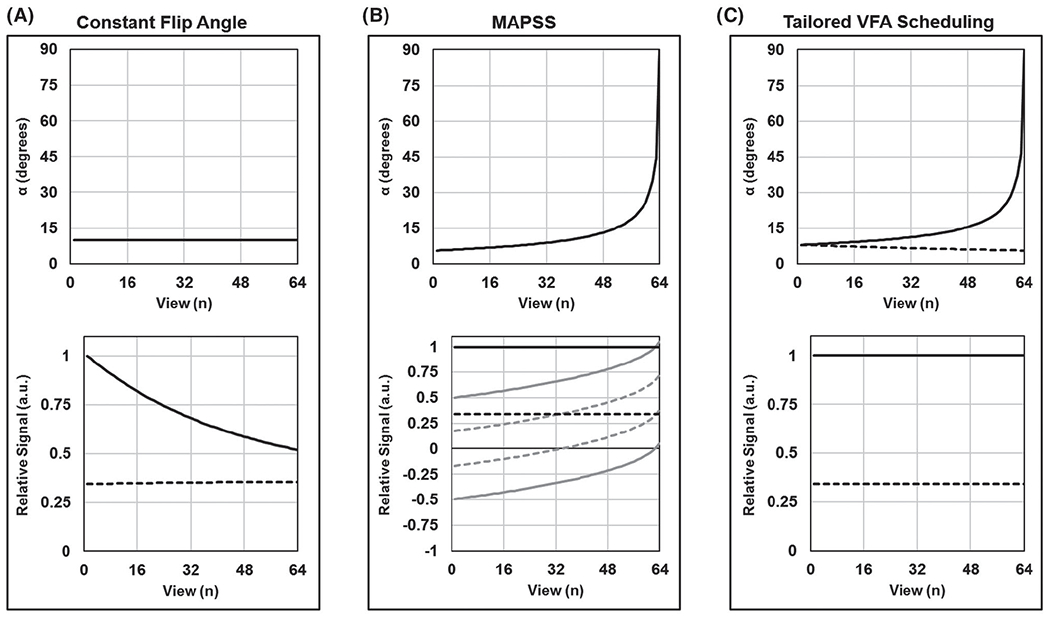
Comparison of variable flip angle (VFA) techniques for segmented gradient-echo (GRE) T_1ρ mapping. Results are simulated for VPS = 64 and TSL = 0 (solid lines) and 80 ms (dashed lines). Flip-angle schedules are shown in the top plots, and corresponding k-space signal modulations along the phase-encode dimension are shown in the bottom plots (each plot is individually normalized). A, If a constant flip angle is used to acquire all views following a spin-lock preparation pulse, then the measured signal will be modulated across the k-space phase-encoding plane. In this case (α_n = 10°), TSL = 0 ms will produce a low-pass filtered image and TSL = 80 ms will produce a slightly high-pass filtered image. B, Magnetization-prepared angle-modulated partitioned k-space spoiled GRE snapshot (MAPSS) corrects for the k-space signal modulation by combining RF cycling with a single VFA train that is the same for all TSLs. Each TSL image is acquired twice, with magnetization, respectively, prepared along the +z and −z axes (gray lines); these signals are then subtracted to yield constant signal amplitude across the k-space phase-encoding plane (black lines). C, Tailored VFA scheduling corrects for the k-space signal modulation by applying a unique VFA train for each TSL, which obviates the need for RF cycling. VFA trains are generated based on assumed brain-tissue T₁ and T_1ρ relaxation times, such that each TSL image ideally has a constant signal amplitude across its k-space phase-encoding plane. Note that the VFA trains at TSL = 0 are different for MAPSS and tailored VFA scheduling, with different α₁

The MAPSS approach is an accurate method to correct for the TSL-dependent signal evolutions; it combines RF cycling with a VFA schedule.²⁸ The RF cycling works by acquiring two images for each TSL: one with signal prepared along the +z axis and the other with signal prepared along the −z axis. Subtraction of these two images yields a TSL-independent signal evolution, which can be used in conjunction with a single VFA schedule to avoid k-space signal modulation (Figure 2B). The RF cycling has the additional advantage of eliminating T₁ contamination caused by recovery of longitudinal magnetization over the dead time σ (i.e., the T₁ contributions are subtracted out). Thus, MAPSS is an effective approach to generate quantitatively accurate T_1ρ maps without loss of spatial fidelity. However, this is accomplished at the expense of SNR efficiency, as discussed subsequently.

The tailored VFA scheduling approach calculates a unique VFA schedule for each TSL image as opposed to using one VFA schedule for all TSL images as in MAPSS (Figure 2C). Compared with MAPSS, this approach can provide greater T_1ρ map SNR efficiency with some loss of quantitative accuracy and spatial fidelity (e.g., spatial blurring due to k-space signal modulation). The gain in SNR is due to increased signal, as noise is not affected by the method. However, the SNR advantage of tailored VFA scheduling can be further enhanced by the fact that, without the RF cycling requirement that each TSL be acquired twice, a more SNR-efficient TSL sampling schedule can be used.⁴⁸ The TSL-specific VFA schedules are generated using Bloch simulations and a priori estimates of brain tissue T₁ and T_1ρ relaxation times. Referring to Figure 1, the Bloch simulations model signal recovery of M_z (with time constant T₁) over times T_rec and τ as well as signal decay of M_xy (with time constant T_1ρ) over time TSL to estimate the relative signal available at the time of the first excitation pulse of the GRE train (with flip angle α₁) for each TSL. Because views are acquired in an elliptical-centric fashion, α₁ determines the signal at the center of k-space, and the sine of α₁ is approximately proportional to the image SNR. The goal then is to choose a VFA schedule that maximizes α₁, while eliminating k-space signal modulation.

Tailored VFA schedules are generated as follows. For a given α₁, a VFA schedule can be calculated using Bloch simulations to keep the excitation signal constant across the GRE train (i.e., to avoid k-space signal modulation), and α₁ is maximized when α_VPS = 90°. Thus, the first step in generating the tailored VFA schedules is to select α₁ for the shortest TSL (typically TSL = 0 ms), such that α_VPS = 90° (it should be noted that this same strategy is used to determine α₁ in the MAPSS approach,²⁸ in which the VFA schedule is optimized for the subtracted RF-cycled signal evolution). The value of α₁ is then fixed for all other TSL images, such that the excitation flip angle when encoding the center of k-space is consistent between TSLs even if there is inhomogeneity in the transmit B₁ field. The unique VFA schedules for the longer TSLs are then generated using the fixed α₁, which will result in α_VPS less than 90° for these cases. Finally, to partially reduce the effect of T₁ contamination in tailored VFA scheduling, the signal intensity of each acquired TSL image is scaled to account for T₁ recovery over the dead time τ by simulating the TSL-dependent recovery of M_z using Bloch equations with an assumed T₁ value for brain tissue. The provided MATLAB (version 2019b; Math Works, Natick, MA) simulation code includes the algorithm to generate the tailored VFA schedules (see next section).

The SNR advantages of tailored VFA scheduling are achieved at the cost of T_1ρ quantification errors and loss of spatial fidelity, which will vary spatially depending on how the true T₁ and T_1ρ values of the tissue deviate from those assumed for the Bloch simulations used to generate the tailored VFA schedules. These costs increase as VPS increases, which must be traded off with the desired increase in SNR efficiency. Additionally, these costs are a function of TSL, as each TSL image is generated using a unique VFA schedule. In the following simulation and in vivo experiments, we analyze the advantages and costs of tailored VFA scheduling in comparison to MAPSS for 2D and 3D GRE T_1ρ mapping of the brain.

2.3 |. Simulation experiments

All simulations were conducted using MATLAB. The MATLAB simulation code is available online (github.com/mricpj/tailoredVFA), which includes code to generate tailored VFA schedules, assess the performance of tailored VFA scheduling, and optimize pulse-sequence parameters.

First, we simulated the relative SNR efficiency of tailored VFA scheduling compared with MAPSS using the imaging parameters for the in vivo 2D T_1ρ mapping experiment, which are listed in Table 1. We assumed brain-tissue relaxation times of T₁ = 1200 ms⁴⁹ and T_1ρ = 75 ms.³¹ The VFA schedules were generated for both approaches for VPS ranging from 1 to 256. We estimated relative SNR for each VPS by calculating the ratio of the signal encoded at the center of k-space (i.e., sine of α₁) using the two techniques.

TABLE 1.

Common imaging parameters for the in vivo 2D and 3D T_1ρ mapping experiments

Parameter	2D mapping	3D mapping
Orientation	Axial	Sagittal
Phase-encoding directions	R/L	A/P and R/L
FOV (cm)	22 × 22	24 × 24 × 16
Sampling matrix	256 × 256	256 × 128 × 80
Slice thickness (mm)	10	2
TR/TE (ms)	8.5/3.8	6.8/2.95
Bandwidth (Hz/px)	260	260
Fat saturation	Yes	Yes
GRAPPA acceleration	None	Table 2
VPS	32, 64, 128, 256	Table 2
No CSF nulling: Trec (ms)	2500	Table 2
CSF nulling: TIprep/TEprep/TI (ms)	1350/200/940	Table 2
TSLs (ms)	0, 20, 40, 60, 80	Table 2
Spin-lock pulse amplitude (Hz)	350	350
Assumed brain tissue T1 (ms)	1200	1200
Assumed brain tissue T2 (ms)	70	70
Assumed brain tissue T1ρ (ms)	75	75

Second, we characterized the degree to which deviations in true brain tissue T₁ and T_1ρ relaxation times from those assumed for generating tailored VFA schedules result in T_1ρ quantification errors and loss of spatial fidelity. The 2D T_1ρ mapping parameters listed in Table 1 were used to generate tailored VFA schedules for TSL = 0, 20, 40, 60, and 80 ms with VPS = 64, 128, and 256. We then used Bloch equations to simulate the k-space signal evolution during the GRE train, as the true T₁ was varied from 700 to 1900 ms and the true T_1ρ was varied from 60 to 90 ms. These T₁ and T_1ρ relaxation times cover the expected range for brain tissue.^31,49,50 For each pair of true T₁ and T_1ρ values, we simulated the k-space signal modulation across a central line in the phase-encoding direction for each TSL image. We then calculated the TSL point spread functions (PSFs) by taking the fast Fourier transform of the signal-modulated phase-encoding lines. The generated TSL PSFs were then convolved with a one-dimensional binary rectangular object to generate TSL images. To measure T_1ρ quantification error, we fit the centermost TSL image signals to a mono-exponential decay model using the Levenberg-Marquardt algorithm to compare the measured T_1ρ relaxation time to the true T_1ρ value. To measure spatial blurring, we calculated the FWHM) of each TSL PSF. We then qualitatively assessed the generated TSL image profiles and resultant T_1ρ map profiles at select pairs of true T₁ and T_1ρ values. We then repeated this analysis for (1) a broader range of true T₁ and T_1ρ values extending to 4300 and 2000 ms, respectively, to analyze the effect of CSF and other fluid; and (2) scaling of the flip angles by 0.8 and 1.2 to analyze the effect of transmit B₁ inhomogeneity.

Finally, we simulated and compared optimal 3D-GRE imaging parameters for tailored VFA scheduling and MAPSS. Specifically, we compared the relative SNR of the techniques using a previously described framework for estimating T_1ρ precision (σ_T1ρ), which is inversely proportional to T_1ρ SNR (SNR_T1ρ)⁴⁸ as follows:

$${\text{SNR}}_{\text{T}1\rho }={\text{T}}_{1\rho }/{\sigma }_{\text{T}1\rho },$$ (1)

where T_1ρ is the relaxation time at a given pixel, and σ_T1ρ is the precision of the measurement (i.e., SD). Specifically, this framework estimates T_1ρ precision as

$${\sigma }_{\text{T}1\rho }=\frac{1}{{\text{SNR}}_0}\text{f}\left({\text{T}}_{1\rho },\text{TSLs}\right),$$ (2)

where SNR₀ is the SNR of the sequence when no spin locking is applied (i.e., TSL = 0), and f(T_1ρ,TSLs) is a closed-form function of T_1ρ and the TSL sampling schedule (see Equation 3 in Johnson et al⁴⁸). For 3D-GRE T_1ρ mapping, Equation 2 can be expanded by solving for SNR₀ as a function of the pulse-sequence parameters defined in Figure 1:

$${\text{SNR}}_0=\left({\text{SNR}}_{\max }\right)\left({\text{S}}_{\text{rec}}\right)\left(\sin {\alpha }_1\right)\left(\frac{1}{\text{g}\sqrt{\text{R}}}\right),$$ (3)

where S_rec is the signal recovery that occurs over time T_rec; α₁ is the first flip angle of the elliptical-centric GRE train; R is the net acceleration factor (e.g., due to parallel imaging and partial Fourier); g is the g-factor noise amplification as a result of the applied acceleration; and SNR_max is the maximum achievable SNR for a given set of base sequence parameters (i.e., for T_rec >> T₁, α₁ = 90°, VPS = 1, and R = 1). If CSF nulling is not applied, then

$${\text{S}}_{\text{rec}}=1-{\text{e}}^{-{\text{T}}_{\text{rec}}/\text{T}1}.$$ (4)

If CSF nulling is applied, then

$${\text{S}}_{\text{rec}}=1-\left(1+\left(1-{\text{e}}^{-{\text{TI}}_{\text{prep}}/\text{T}1}\right)·{\text{e}}^{-{\text{TE}}_{\text{prep}}/\text{T}2}\right)·{\text{e}}^{-\text{TI}/\text{T}1}.$$ (5)

Ignoring the negligible short pulse durations, the total scan time of the sequence is

$${\text{T}}_{\text{acq}}=\sum _{i=1}^{\text{N}}\left[\left({\text{T}}_{\text{reset}}+{\text{T}}_{\text{rec}}+{\text{TSL}}_i+\tau +\text{TR}·\text{VPS}\right)\left(\frac{{\text{N}}_y·{\text{N}}_z}{\text{VPS}·R}\right)\right],$$ (6)

where N is the number of TSLs, and N_y and N_z are the total number of fully sampled phase and slice encoding lines, respectively. Using Equations 2 and 6, we calculated the optimal imaging parameters (TSLs, T_rec, TI_prep/TE_prep/TI, and R) at different VPS to minimize the T_1ρ map scan time for a given target T_1ρ precision (σ_T1ρ), both for tailored VFA scheduling and MAPSS. For these estimates, we assumed the common imaging parameters for the in vivo 3D T_1ρ mapping experiments (Table 1): CSF T₁ = 4300 ms and T₂ = 2000 ms,⁵¹ and g = 1.0, 1.2, 1.5, and 1.8, respectively, for R = 1.0, 2.0, 3.2, and 4.0 (GRAPPA acceleration with 24 calibration lines).

2.4 |. In vivo experiments

Four healthy volunteers were imaged under internal review board–approved protocols. One participant was imaged at the University of Iowa using a 3T-MRI system (Tim Trio; Siemens Healthcare, Erlangen, Germany) with a vendor-provided 12-channel receiver head coil and body transmit coil. The other 3 participants were imaged at the University of Minnesota using a 3T-MRI system (Prisma; Siemens Healthcare) with a vendor-provided 32-channel receiver head coil and body transmit coil. Quantitative T_1ρ brain maps were acquired using the GRE sequence framework outlined in Figure 1.

First, we compared the tailored VFA scheduling and MAPSS methods using a 2D-GRE implementation. A 2D implementation was used to acquire quantitative T_1ρ maps with relatively high SNR in a short scan time to most accurately compare the two methods. Each participant’s brain was imaged using both methods with an axial segmented 2D-GRE sequence with VPS = 32, 64, 128, and 256, both without and with application of CSF nulling. Sequence parameters were identical for the two methods and are listed in Table 1. The TSLs were acquired twice for both tailored VFA scheduling and MAPSS to yield equivalent scan times for the two techniques. The T_1ρ map scan times were 229, 125, 73, and 48 seconds for VPS = 32, 64, 128, and 256, respectively, both without and with CSF nulling.

We then conducted a second in vivo experiment to demonstrate the feasibility and flexibility of 3D T_1ρ mapping of the whole brain using tailored VFA scheduling. Four 3D T_1ρ maps were acquired for each of the 3 participants imaged at the University of Minnesota, each with a 10-minute scan time. The parameters given in Tables 1 and 2 were selected to produce optimized and comparable T_1ρ maps using (1) MAPSS with VPS = 64, (2) tailored VFA scheduling with VPS = 64, (3) tailored VFA scheduling with VPS = 64 and CSF nulling, and (4) tailored VFA scheduling with VPS = 256 and CSF nulling.

TABLE 2.

Unique imaging parameters and estimated relative SNR for the in vivo 3D T_1ρ mapping data sets

Data set	Method	Estimated relative SNR	Scan time	TSLs (ms)	VPS	Trec (ms)	TIprep/TEprep/TI (ms)	R
Without CSF nulling
1	MAPSS	1.0	10:16	0+, 0−, 80+, 80−	64	1100	-	2
2	Tailored VFA	1.6	10:16	0, 80, 80, 80	64	1100	-	2
With CSF nulling
3	Tailored VFA	1.1	9:45	0, 80	64	2540	1400/160/980	2
4	Tailored VFA	1.6	10:04	0, 80, 80, 80	256	1520	1000/180/750	-

2.5 |. In vivo data analysis

All data analyses were performed using MATLAB. For each participant, all 2D TSL images were co-registered; similarly, all 3D-TSL images were co-registered. To reduce Gibbs ringing artifact, the 2D-TSL images were sinc-interpolated to twice the acquired in-plane voxel size. The 3D-TSL volumes were sinc-interpolated to 0.94 mm isotropic spatial resolution. The T_1ρ maps were calculated by fitting the co-registered, sinc-interpolated TSL images to a mono-exponential signal decay model using the Levenberg-Marquardt algorithm on a voxel-by-voxel basis. The 2D T_1ρ maps for 1 participant were additionally calculated using the fitting approach described by Miller and Joseph,⁵² to determine whether the results varied with noise correction.

The 2D-GRE T_1ρ maps were used to measure the T_1ρ quantification error and SNR of tailored VFA scheduling relative to MAPSS. For each participant, eight regions of interest (ROIs) with observed relatively homogenous T_1ρ relaxation times were defined using the brain T_1ρ map generated by the MAPSS VPS = 32 acquisition (Supporting Information Figure S4). The same ROIs were then used to analyze all of the other maps. The T_1ρ percent error of the tailored VFA scheduling sequence was measured by comparing mean T_1ρ relaxation times in each ROI using the mean values for the MAPSS VPS = 32 acquisitions, without and with CSF nulling, as the references. Relative SNR was estimated by calculating the ratio of the SDs (i.e., precision) of the T_1ρ relaxation times in each ROI between each pair of MAPSS and tailored VFA scheduling acquisitions with the same VPS setting; it was assumed that brain-tissue T_1ρ relaxation times were homogeneous in each ROI, such that variations in T_1ρ were only due to noise.

The relative SNR values of the 3D-GRE T_1ρ maps were calculated in the same manner described previously for the 2D T_1ρ maps. For each participant, eight 2D ROIs with relatively homogeneous T_1ρ relaxation times were defined in a single axial brain slice (Supporting Information Figure S8). The T_1ρ quantitative accuracy was not measured for the 3D T_1ρ maps due to limitations of acquiring high-quality and high-SNR reference whole-brain T_1ρ maps using the 3D-MAPSS approach in a reasonable scan time; the 2D in vivo data were used for this purpose.

3 |. RESULTS

3.1 |. Simulation experiments

First, the relative SNR gains of tailored VFA scheduling compared with MAPSS were simulated. Figure 3A plots the VFA schedules needed for the two methods, given the imaging parameters in Table 1. At VPS = 64, α₁ = 8.0° for tailored VFA scheduling versus 5.6° for MAPSS, which corresponds to a relative SNR increase of 41%. Given the same imaging parameters, Figure 3B,C plots α₁ and the relative SNR of tailored VFA scheduling versus MAPSS as a function of VPS. As VPS increases, the SNR advantage of tailored VFA scheduling becomes more substantial. For example, at VPS = 128 and 256, the relative SNR increases of tailored VFA scheduling versus MAPSS are 104% and 346%, respectively. For the parameters given in Table 1, the relative SNR ratios of tailored VFA scheduling versus MAPSS are estimated to be 1.2, 1.4, 2.0, and 4.5 without CSF nulling, and 1.3, 1.7, 2.6, and 6.3 with CSF nulling for VPS = 32, 64, 128, and 256, respectively.

FIGURE 3.

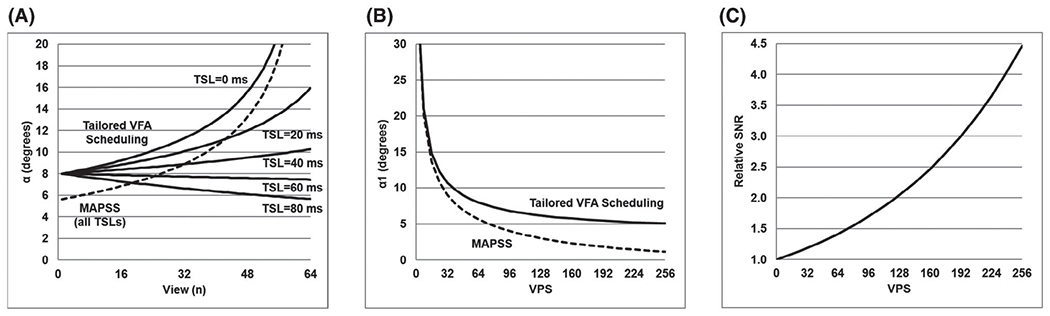
Relative SNR of tailored VFA scheduling compared with MAPSS. A, The VFA trains for tailored VFA scheduling (solid lines) and MAPSS (dashed line) at VPS = 64 for the imaging parameters listed in Table 1. The value of α₁ is greater for tailored VFA scheduling than MAPSS, which results in relatively greater signal. B, The difference in α₁ between the two methods becomes greater as VPS increases. C, Relative SNR of tailored VFA scheduling versus MAPSS, assuming that SNR is proportional to sin(α₁). At VPS = 32, 64, 128, and 256, tailored VFA scheduling has, respectively, 1.2×, 1.4×, 2.0×, and 4.5× greater SNR than MAPSS

Second, T_1ρ map quantification errors and loss of spatial fidelity when using tailored VFA scheduling were simulated as a function of true T₁ and T_1ρ relaxation times. The quantification percent errors are plotted in Figure 4A. For the set of simulated imaging parameters (Table 1), the maximum percent errors across the full range of true T₁ and T_1ρ values were limited to 0.87%, 1.06%, and 2.00% for VPS = 64, 128, and 256, respectively. To assess spatial fidelity, the maximum PSF FWHM values across all TSLs are plotted in Figure 4B. Over the full range of true T₁ and T_1ρ relaxation times and TSLs, the maximum FWHM values were 1.07, 1.05, and 1.05 pixels for VPS = 64, 128, and 256, respectively. In comparison, if no VFA scheduling was applied and a constant 10° excitation flip angle was instead used across the GRE train (as in Figure 2A), then the maximum FWHM values would be 1.16, 1.26, and 1.29 pixels, respectively. The TSL image profiles and corresponding T_1ρ map profiles for the one-dimensional binary rectangular object are plotted in Figure 4C for VPS = 64 (black lines) and VPS = 256 (red lines) at five different pairs of true T₁ and T_1ρ relaxation times: the assumed values used to generate the tailored VFA schedules (i.e., the ideal case) and the most extreme pairs of values (i.e., the worst cases). In general, the TSL image profiles and T_1ρ map profiles closely resembled the ideal case. In some cases, there was low-pass filtering (i.e., rounding of the image profile edges), and in other cases there was high-pass filtering (i.e., increased signal at the image profile edges). These filtering effects were somewhat more pronounced at VPS = 256. Analysis of the extended range of true T₁ and T_1ρ values for CSF are shown in Supporting Information Figure S1. The T_1ρ quantification errors and FWHM values generally increased over the range, with FWHM values reaching a maximum of 1.21 pixels at VPS = 256. The effect of B₁ inhomogeneity is shown in Supporting Information Figure S2. The B₁ inhomogeneity did not affect T_1ρ percent errors, but it did lead to an increase in FWHM values at all VPS to 1.15 pixels.

FIGURE 4.

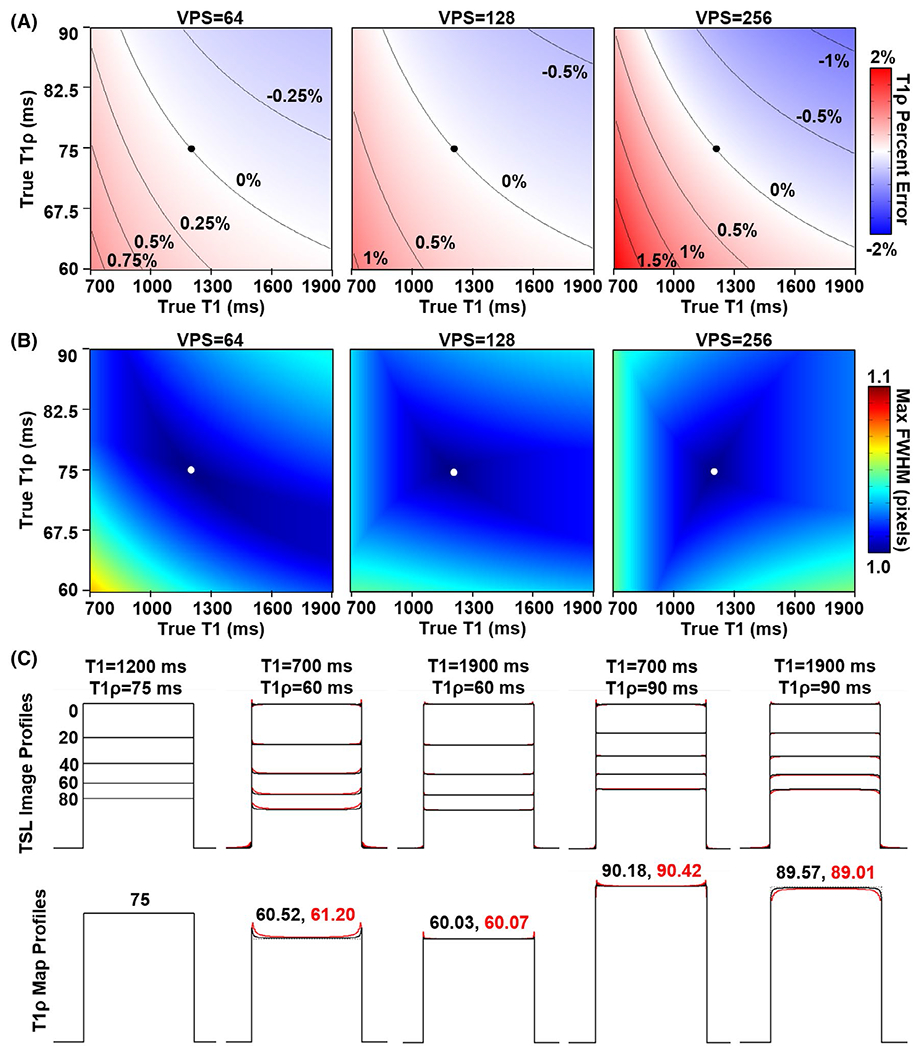
Simulated percent error in measured T_1ρ relaxation times and spatial blurring using tailored VFA scheduling. The dots mark the assumed T₁ (1200 ms) and T_1ρ (75 ms) relaxation times when calculating the tailored VFA schedules. A, Plots of T_1ρ percent error as a function of the true T₁ and T_1ρ relaxation times of brain tissue after fitting five TSLs (0, 20, 40, 60, and 80 ms) to a mono-exponential decay curve. The T_1ρ quantification error increases as VPS increases but is ≤ 2% up to VPS = 256. B, Plots of the maximum FWHM values across all TSL image point spread functions (PSFs). There is relatively little PSF blurring with FWHM ≤ 1.07 pixels for all cases. C, Simulated image and T_1ρ map profiles. The leftmost plot is for the ideal case, where the true T₁ and T_1ρ relaxation times match those assumed when generating the tailored VFA schedules (corresponding to the dots in [A] and [B]). The next four plots are the extreme pairs of T₁ and T_1ρ values used for the simulations (corresponding to the corners of the plots in (A) and (B)). Black lines are for VPS = 64 and red lines are for VPS = 256. The T_1ρ relaxation times in the middle of the map profiles are indicated above the plots for both VPS = 64 (black font) and VPS = 256 (red font)

Finally, optimal imaging parameters for tailored VFA scheduling and MAPSS to minimize the T_1ρ map scan time for a given target T_1ρ map precision were simulated. Plots of scan time versus relative SNR at VPS = 64, 128, and 256 are shown in Figure 5, both without and with application of CSF nulling. The optimal imaging parameters at each of the circled points along the curves are given in Table 2 and correspond to the 3D T_1ρ map data sets acquired for the in vivo experiment. The MAPSS data set (point 1 in Figure 5) was assigned a relative SNR of 1.0. For tailored VFA scheduling, the scan time needed to achieve a given SNR target decreases as VPS increases. Thus, SNR efficiency will be maximized for a single-shot acquisition (i.e., VPS = N_y*N_z/R). This is not the case for MAPSS, which reaches its maximum SNR efficiency near VPS = 64. The combination of greater α₁ and more flexible choice of TSLs for tailored VFA scheduling provides a significant gain in relative SNR efficiency versus MAPSS. For example, in Figure 5A, for a 10-minute scan time at VPS = 64, tailored VFA scheduling (point 2) provides a substantial gain in SNR versus MAPSS (point 1). Alternatively, tailored VFA scheduling can achieve the same SNR as MAPSS at point 1 in half the scan time or less. The same trends apply if CSF nulling is used (Figure 5B), which necessitates longer scans times and potentially makes MAPSS an impractical approach. However, using tailored VFA scheduling, CSF nulling can be achieved in 10 minutes (e.g., points 3 and 4) with similar SNR as the non-CSF-nulled acquisitions (e.g., points 1 and 2).

FIGURE 5.

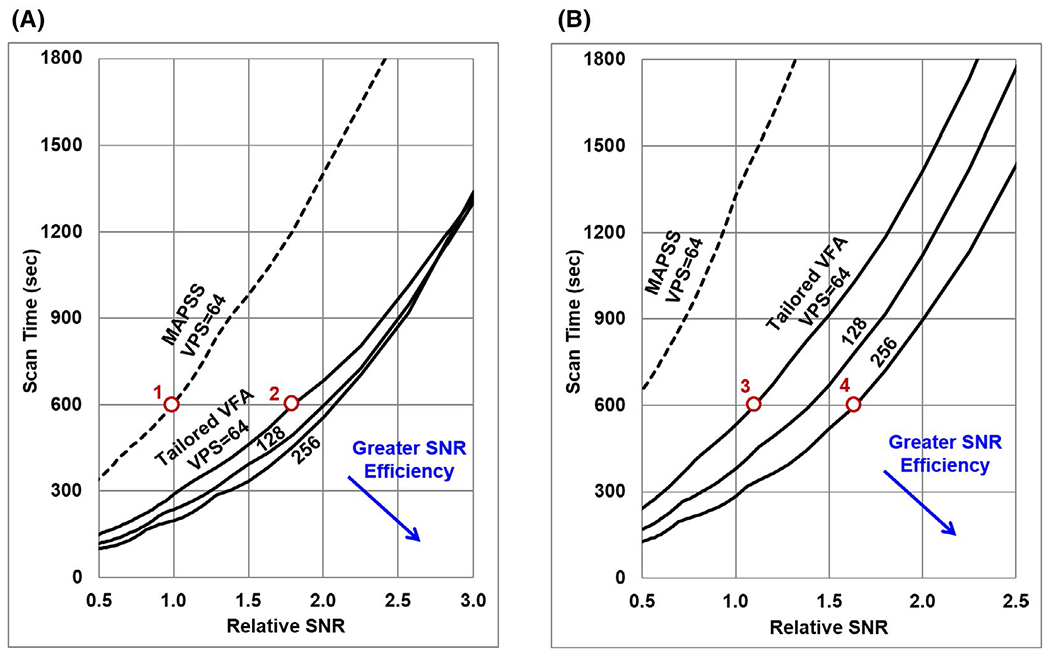
Simulated T_1ρ map relative SNR versus scan time for 3D T_1ρ mapping acquisitions, assuming the base 3D mapping parameters listed in Table 1. Results are plotted for acquisitions without (A) and with (B) CSF nulling applied. The MAPSS technique (dashed line) requires greater scan time than tailored VFA scheduling (solid lines) to achieve a given T_1ρ SNR. The SNR efficiency of tailored VFA scheduling improves as VPS increases (lines are shown for VPS = 64, 128, and 256), whereas the SNR efficiency of MAPSS is optimized near VPS = 64. Points along these curves corresponding to the data sets acquired for the in vivo 3D T_1ρ mapping experiment (Table 2) are indicated by the circles and labeled with the corresponding data set number

3.2 |. In vivo experiments

The 2D T_1ρ maps acquired for 1 participant using tailored VFA scheduling and MAPSS are shown in Figure 6, and data for all participants are shown in Supporting Information Figure S3. Qualitatively, at VPS = 32, the two methods produce visually similar T_1ρ maps. As VPS increases, the greater SNR efficiency of tailored VFA scheduling becomes increasingly apparent. Quantitative results of the ROI analysis are plotted in Figure 7 (the ROI locations are shown in Supporting Information Figure S4). The average relative SNR of tailored VFA scheduling versus MAPSS at VPS = 32, 64, 128, and 256 was, respectively, 1.2, 1.4, 1.9, and 4.5 without CSF nulling; with CSF nulling, the relative SNR was 1.3, 1.6, and 2.6 at VPS = 32, 64, and 128, respectively (MAPSS did not have sufficient SNR at VPS = 256 with CSF nulling to make a relative SNR measurement). At VPS = 32, 64, 128, and 256, respectively, the maps acquired with tailored VFA scheduling had, on average, absolute T_1ρ percent errors of 0.7%, 0.9%, 1.8%, and 3.2% without CSF nulling and 0.8%, 1.0%, 1.3%, and 2.0% with CSF nulling. On average, the absolute T_1ρ percent errors were lowest when the true T_1ρ value was near 75 ms (i.e., that assumed when generating the tailored VFA schedules) and increased slightly across the full range of observed T_1ρ values (62 to 83 ms; see plot of all ROI values in Supporting Information Figure S5). The primary drawback to tailored VFA scheduling is spatial blurring, which becomes more apparent as VPS increases. The results were the same whether the T_1ρ maps were generated using a mono-exponential fitting function with or without noise correction (data not shown).

FIGURE 6.

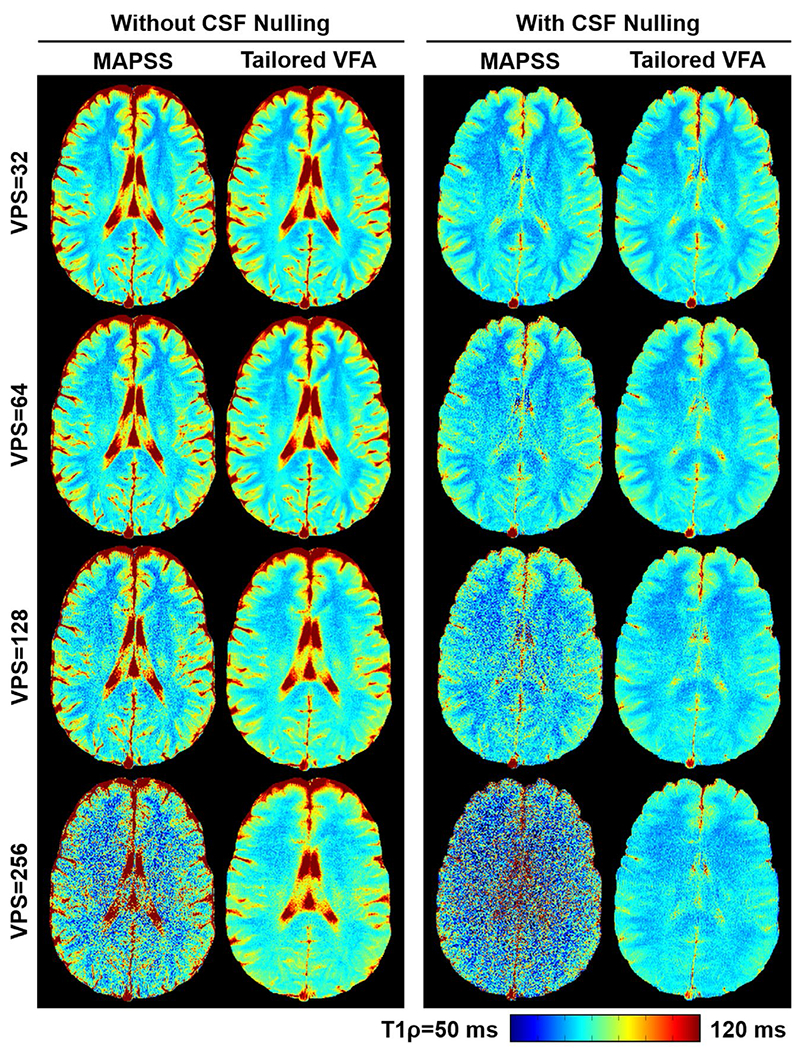
Comparison of 2D-GRE T_1ρ maps acquired in vivo for 1 participant using tailored VFA scheduling and MAPSS. The left-hand panel images were acquired without CSF nulling, and the right-hand panel images were acquired with CSF nulling. The scan time was the same for all T_1ρ maps acquired at a given VPS setting, and the phase-encoding direction was right/left. The improved SNR efficiency of tailored VFA scheduling is apparent and becomes more pronounced at higher VPS. Furthermore, there is no appreciable loss in quantitative accuracy of the T_1ρ maps using tailored VFA scheduling. However, there is some loss in spatial fidelity as VPS increases. The 2D T_1ρ maps for all participants are shown in Supporting Information Figure S3

FIGURE 7.

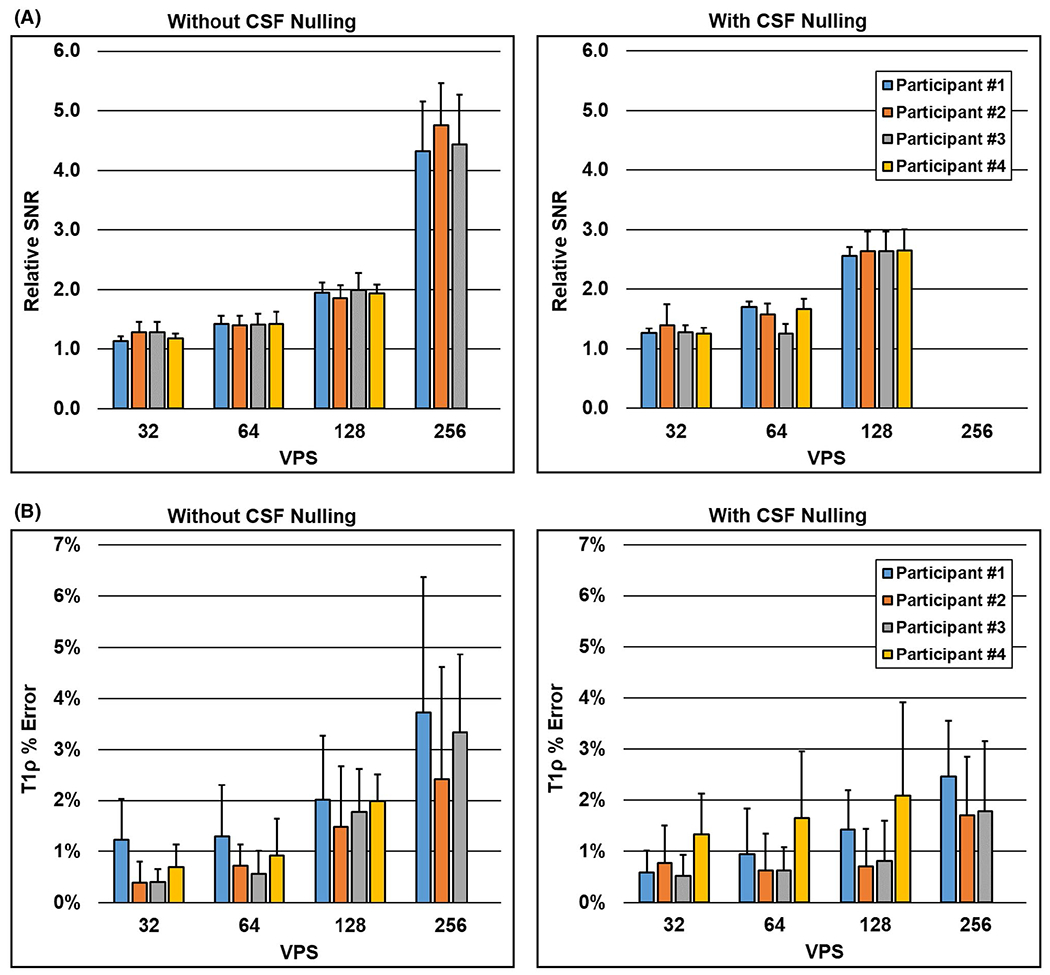
Region of interest (ROI) analysis of the relative SNR and T_1ρ percent error of the in vivo 2D T_1ρ maps acquired with tailored VFA scheduling versus MAPSS. Each colored bar is 1 of the 4 participants, and each bar plots the mean and SD across the eight ROIs (Supporting Information Figure S4). A, Relative SNR increased with VPS, yielding greater than 4× SNR using tailored VFA scheduling versus MAPSS at VPS = 256. B, Average absolute T_1ρ percent error was 2% or less up to VPS = 128. Furthermore, T_1ρ errors were generally lower when CSF nulling was applied

The 3D T_1ρ maps for 1 participant are shown in Figure 8, and maps for the other 2 participants are shown in Supporting Information Figures S6 and S7. Qualitatively, the improvement in T_1ρ map SNR efficiency provided by tailored VFA scheduling compared with MAPSS is evident, which enabled T_1ρ maps to be acquired with greater relative SNR and/or CSF nulling in an equivalent scan time. The ROI measurements found relative SNR to be, on average across participants, 1.5, 1.2, and 1.5 for the three maps acquired with tailored VFA scheduling (data sets 2, 3, and 4, respectively, in Table 2) versus the T_1ρ map acquired with MAPSS. The ROI locations and a plot of the data are shown in Supporting Information Figure S8. As expected from the simulations and quantitative 2D T_1ρ map analyses, the maps had comparable T_1ρ relaxation times and minimal loss of quantitative accuracy. However, there is some spatial blurring with tailored VFA scheduling, which is most apparent at VPS = 256.

FIGURE 8.

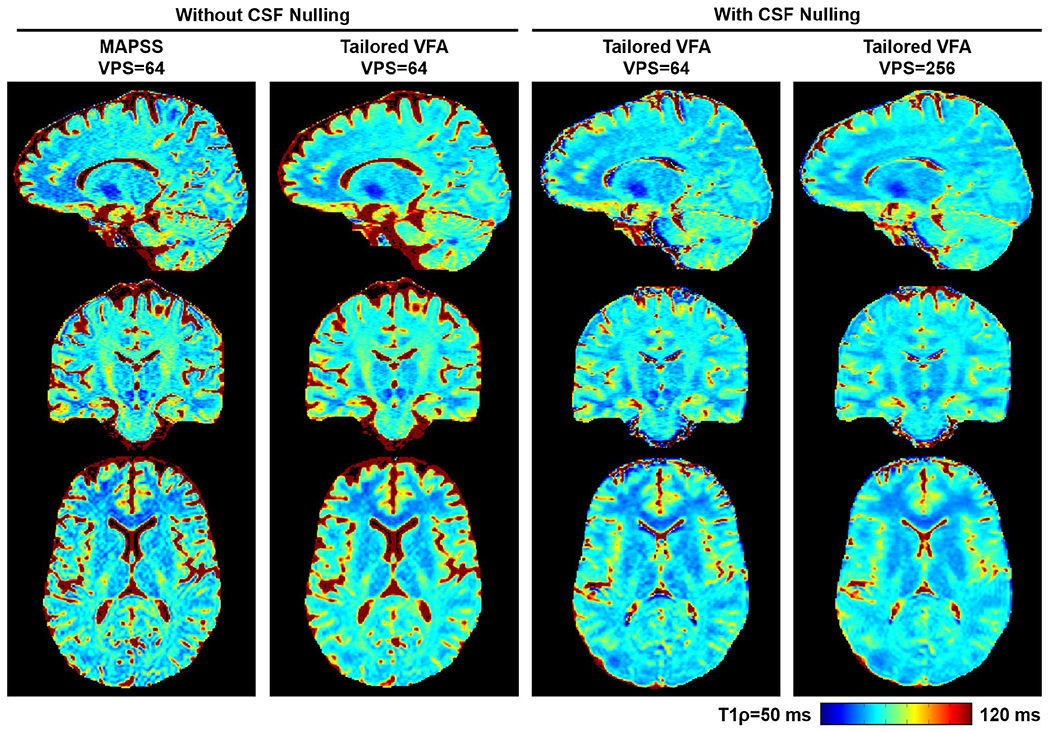
Comparison of 3D T_1ρ maps acquired with MAPSS and tailored VFA scheduling for 1 participant. The T_1ρ maps were sinc-interpolated to 0.94-mm isotropic resolution, and the three acquired orthogonal planes are shown (phase-encoding directions were anterior/posterior and right/left). The greater SNR efficiency of tailored VFA scheduling versus MAPSS is apparent, and there is no appreciable loss in T_1ρ quantitative accuracy. There is some spatial blurring at VPS = 256. The 3D T_1ρ maps for the other 2 participants are shown in Supporting Information Figures S5 and S6

4 |. DISCUSSION

Tailored VFA scheduling is introduced as an alternative approach for 3D-GRE T_1ρ mapping, which improves SNR efficiency compared with the state-of-the-art MAPSS technique. The potential gains of the method were demonstrated for application to the brain. Compared with MAPSS, tailored VFA scheduling provided a substantial gain in SNR of brain T_1ρ maps for an equivalent scan time with minimal loss in quantitative accuracy and some loss in spatial fidelity.

The primary advantage of tailored VFA scheduling is that it allows for additional flexibility in setting GRE T_1ρ mapping sequence parameters to more optimally trade off SNR efficiency, quantitative accuracy, and spatial fidelity for a given application. In this study we showed that VFA scheduling enabled T_1ρ maps of the brain to be acquired using long GRE trains with significantly greater relative SNR than MAPSS (e.g., >4× SNR for 256 views per segment), while limiting errors in T_1ρ quantification to about 2% when using CSF nulling. These results were supported by both the simulation and in vivo data analyses, which had good overall agreement. Relative SNR values of tailored VFA scheduling versus MAPSS for the 2D in vivo data were measured to be 1.2, 1.4, 1.9, and 4.5 for VPS = 32, 64, 128, and 256, respectively, compared with 1.2, 1.4, 2.0, and 4.5 estimated by simulation, and average T_1ρ quantification errors for VPS = 64, 128, and 256 were measured in vivo to be, respectively, 1.0%, 1.3%, and 2.0% with application of CSF nulling compared with the maximum errors of 0.9%, 1.1%, and 2.0% estimated by simulation. Note that tailored VFA scheduling is compatible with acceleration techniques such as partial Fourier, parallel imaging, and compressed sensing, which may be used to further improve SNR efficiency.^53–55

In addition to providing greater SNR efficiency for a given number of views per segment, tailored VFA scheduling also does not require two acquisitions for each TSL image as in MAPSS. As a result, more optimal TSL sampling schedules can be acquired, which further increases the overall SNR efficiency advantage of the method. By expanding on a framework to calculate optimal TSL sampling schedules based on target T_1ρ map precision,⁴⁸ to also account for the relative SNR of tailored VFA scheduling and MAPSS, we found that the SNR efficiency of tailored VFA scheduling improves with greater views per segment, while MAPSS is optimized near VPS = 64. Thus, depending on the degree of loss in T_1ρ map quantitative accuracy and spatial fidelity that can be tolerated for a particular application, tailored VFA scheduling can provide very large gains in SNR efficiency, which may enable sequence configurations that may not be practical with MAPSS, such as CSF nulling.

Although tailored VFA scheduling has advantages for T_1ρ mapping of the brain using a 3D-GRE sequence, an alternative option is to use a 3D-FSE sequence for the image readout.^30,31 A primary advantage of 3D-FSE approaches is their high SNR efficiency, given the use of long spin-echo trains that use large flip angles and refocusing pulses as well as their relative robustness to TSL-dependent k-space signal modulations.^56,57 In contrast, one significant benefit of GRE approaches is their relatively low RF heating requirements, which is potentially advantageous for applications using the body coil for transmit, rapid imaging, high spin-lock amplitudes, or ultrahigh field strengths (e.g., 7 T). Gradient-echo sequences like tailored VFA scheduling and MAPSS may also provide greater quantitative accuracy and spatial fidelity than the 3D-FSE sequences,⁵⁸ but further work is needed to directly compare the relative advantages of GRE and FSE T_1ρ mapping methods.

Tailored VFA scheduling may also have application beyond the brain. The method may be favorable for regions such as the liver and intervertebral disc, where RF heating can be problematic but some losses in quantitative accuracy and spatial fidelity are potentially tolerable. The SNR efficiency of tailored VFA scheduling may also be advantageous for T_1ρ mapping of articular cartilage, such as at the knee or hip; however, further investigation is needed to determine the fidelity of the method when imaging such thin structures with high spatial frequencies.

This study has two primary limitations that can be addressed in future work. First, while the tailored VFA scheduling method was characterized for a typical set of brain imaging parameters, there are many other variations that one could investigate (e.g., effect of varying TR, further extending the VPS beyond 256, and use of different assumed T₁ and T_1ρ relaxation times). These numerous combinations can be investigated for a given application, including for regions beyond the brain, using the provided MATLAB simulation code. Second, a limited number of in vivo experiments were performed to demonstrate the feasibility of the tailored VFA scheduling method and its relative advantages and costs compared with MAPSS. Further in vivo studies are needed to analyze the robustness and reproducibility of the method, which are beyond the scope of this initial feasibility study.

5 |. CONCLUSIONS

Tailored VFA scheduling is an SNR-efficient GRE technique for whole-brain 3D T_1ρ mapping. Tailored VFA scheduling provides increased flexibility in choice of T_1ρ mapping imaging parameters compared with MAPSS, which may benefit a variety of applications.

Supplementary Material

sup info

FIGURE S1 Simulated T_1ρ percent error (A) and spatial blurring (B) for an extended range of true T_1ρ and T₁ values up to those expected for CSF. Plots are shown in the same manner as Figure 4A,B. The value of T_1ρ is not accurately quantified for fluid, with errors increasing to 20% or more. Voxels with CSF also have increased spatial blurring compared to voxels with just brain tissue. Cerebrospinal fluid nulling may help reduce these confounding signals

FIGURE S2 Simulated T_1ρ percent error and spatial blurring over the range of typical brain tissue T_1ρ and T₁ values for three different flip-angle scaling factors due to transmit B₁-field inhomogeneity: 0.8 (A), 1.0 (B), and 1.2 (C). The plots in (B) are the same as those in Figure 4 (no B₁ inhomogeneity). The B₁ inhomogeneity in (A) and (C) does not affect the T_1ρ percent error, but it does increase spatial blurring

FIGURE S3 Two-dimensional T_1ρ maps for all 4 participants. The scan times were the same for a given VPS setting: 229, 125, 73, and 48 seconds for VPS = 32, 64, 128, and 256, respectively. The results are consistent across all 4 volunteers. The relative SNR efficiency of tailored VFA scheduling versus MAPSS increases with VPS, while quantitatively the maps appear similar. However, there is also gradual loss of spatial fidelity for tailored VFA scheduling as VPS increases. Note that data at VPS = 256 were not acquired for participant 4

FIGURE S4 Locations of the eight ROIs used to calculate the mean T_1ρ relaxation times for each participant’s 2D T_1ρ maps

FIGURE S5 The T_1ρ quantification error for tailored VFA scheduling versus true T_1ρ value (as measured by MAPSS at VPS = 32) for all ROIs for the 2D T_1ρ map data analyses (Supporting Information Figure S4). Data are included from T_1ρ maps acquired both with and without CSF nulling. Each point is a different ROI, and second-order polynomial trendlines are plotted for data at each VPS. For all VPS, errors are generally lowest near T_1ρ = 75 ms (the assumed value for T_1ρ when generating the tailored VFA schedules) and slightly increase over the full range of measured T_1ρ values

FIGURE S6 Three-dimensional T_1ρ maps for a second participant, shown in the same format as Figure 8

FIGURE S7 Three-dimensional T_1ρ maps for a third participant, shown in the same format as Figure 8. This participant had consistent respiratory motion, which led to some motion artifacts in the T_1ρ maps

FIGURE S8 Region of interest analysis of the relative SNR of the 3D T_1ρ data sets acquired with tailored VFA scheduling versus MAPSS. A, Locations of the eight 2D ROIs used to calculate mean T_1ρ relaxation times for each participant’s 3D T_1ρ maps. The ROIs were defined using the shown T_1ρ map 2D phase-encoding plane slices acquired with MAPSS. B, Average relative SNR for tailored VFA scheduling (data sets 2, 3, and 4) versus MAPSS (data set 1; see Table 2 and Figure 5 for data-set definitions) across the eight ROIs (error bars indicate the SD). Each bar is a different participant. The average relative SNR across the participants was 1.5, 1.2, and 1.5 for data sets 2, 3, and 4, respectively, which agrees well with the expected values from simulation (1.6, 1.1, and 1.6)