Marangoni flows drive the alignment of fibrillar cell-laden hydrogels

Cell-laden hydrogels can be engineered using evaporating droplets of collagen.

Abstract

When a sessile droplet containing a solute in a volatile solvent evaporates, flow in the droplet can transport and assemble solute particles into complex patterns. Transport in evaporating sessile droplets has largely been examined in solvents that undergo complete evaporation. Here, we demonstrate that flow in evaporating aqueous sessile droplets containing type I collagen—a self-assembling polymer—can be harnessed to engineer hydrated networks of aligned collagen fibers. We find that Marangoni flows direct collagen fiber assembly over millimeter-scale areas in a manner that depends on the rate of self-assembly, the relative humidity of the surrounding environment, and the geometry of the droplet. Skeletal muscle cells that are incorporated into and cultured within these evaporating droplets collectively orient and subsequently differentiate into myotubes in response to aligned networks of collagen. Our findings demonstrate a simple, tunable, and high-throughput approach to engineer aligned fibrillar hydrogels and cell-laden biomimetic materials.

INTRODUCTION

Evaporating sessile droplets that contain a solute and volatile solvent generate a myriad of solute deposition patterns that arise from evaporation-driven fluid flow. This phenomenon—first reported by Robert Brown (1, 2) and subsequently studied in the seminal work of Deegan and colleagues (3, 4)—has applications ranging from microfabrication (5) to ink-jet printing (6), nanochromatography (7), and low-cost diagnostics (8). In the evaporating droplet, fluid flow depends on the solute (9), solvent (10), droplet geometry (11), substratum hydrophobicity (12), and evaporation conditions (13), among other parameters. Outward radial flow—known as the coffee-ring effect—occurs when the solvent is volatile, the contact line is pinned, the contact angle is nonzero, and Marangoni flow driven by the latent heat of evaporation is suppressed (3, 10). In contrast, Marangoni flows that arise from thermal or solute-driven gradients in surface tension can generate recirculating flows (10).

Flow in evaporating droplets has largely been described for particles suspended in solvents that evaporate completely (14–17). In the context of polypeptides, capillary flow was found to generate dynamic crowded conditions that drive protein self-assembly (18). Studies of actin filaments in droplets that undergo complete evaporation revealed that flow can generate nematic-like structures and orient actin networks (19). In addition, nanoscale alignment of self-assembling peptides (20) and stretching and orienting of DNA molecules (21) has also been achieved using flow in evaporating droplets.

Here, we found that flow in evaporating droplets not only regulates the rate of protein self-assembly but also controls the alignment of fibrous cell-laden protein networks. We demonstrate that flow in evaporating aqueous droplets of neutralized type I collagen—a self-assembling protein—generates millimeter-scale aligned networks of collagen fibers. We find that thermal and solutal Marangoni effects generate radial flow in the evaporating droplet, which orients collagen fibers radially during self-assembly. The orientation of fibers can be tuned by changing the rate of self-assembly, the relative humidity (RH) of the surrounding environment, and the geometry of the droplet. Moreover, skeletal muscle cells that are incorporated into evaporating droplets collectively orient and differentiate into multinucleated myotubes in response to collagen fiber alignment. A key distinction of our approach is that only a fraction of the water evaporates from the droplet, which forms a cell-laden hydrogel. Marangoni flow in evaporating droplets is a simple, tunable, and high-throughput approach that can be used to fabricate cell-laden aligned fibrillar hydrogels. These hydrogels will have broad applications in the design of biomimetic scaffolds for studies in tissue engineering and developmental biology and for studies of self-assembling materials.

RESULTS

Self-assembly of collagen fibers in evaporating droplets of collagen

We began by drop casting neutralized solutions of type I collagen onto ultraviolet (UV)/ozone (UVO)–treated glass-bottom culture dishes. The RH in the culture dish was controlled using a saturated solution of MgCl₂, which was deposited inside the perimeter of the dish before drop casting collagen (Fig. 1A). After drop casting, the culture dish was sealed and placed into a larger sealed petri dish, which was subsequently incubated at 37°C to initiate self-assembly of collagen.

Fig. 1. Self-assembly of collagen in evaporating droplets generates aligned networks of collagen fibers.

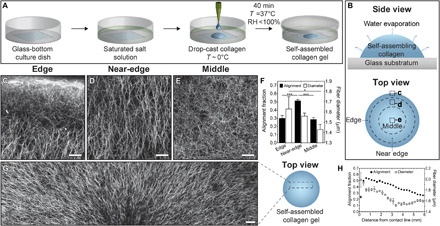
Schematic of (A) drop-casting procedure and (B) top and side views of an evaporating droplet of collagen. CRM images of self-assembled droplet of collagen in the (C) edge, (D) near-edge, and (E) middle regions of interest. Images are oriented such that the top of the image points toward the contact line of the droplet. The location for each image is highlighted in dashed boxes in (B). Scale bars represent 50 μm. (F) Alignment fraction and fiber diameter for drop-cast collagen gels. (G) CRM image of a self-assembled droplet of collagen. Five separate CRM images are stitched together to reveal the radial alignment of collagen fibers. Scale bar, 100 μm. (H) Alignment fraction and fiber diameter as a function of distance from the contact line for drop-cast collagen gels. Collagen solutions (pH 11) were gelled at controlled RH using a saturated solution of MgCl₂ (RH ~ 31%) on UVO-treated glass. *P ≤ 0.05 and ***P ≤ 0.001.

During incubation, collagen self-assembles as water simultaneously evaporates from the droplet (Fig. 1B, top). We hypothesized that evaporation-driven flow produced in the droplet might be sufficient to direct the self-assembly of collagen fibers. To test this hypothesis, we used confocal reflection microscopy (CRM) to visualize the orientation of collagen fibers in three concentric regions of the droplet, which we denoted as edge, near-edge, and middle (Fig. 1B, bottom). The edge region contains the droplet contact line, whereas the middle region represents the approximate center of the droplet. We defined the near-edge as an annular region with an outer boundary located ~500 μm inward from the droplet contact line. CRM images of these regions revealed fibrous networks of collagen throughout the droplet and bright regions along the contact line, indicating accumulation of collagen fibers (Fig. 1, C to E).

To directly compare collagen fiber alignment in the three regions of the droplet, we used our CRM images to calculate the alignment fraction, which represents the fraction of fibers oriented within 20° of the radial direction in the droplet. These calculations revealed anisotropic orientation of collagen fibers in the near-edge region of the droplet and isotropic orientation in the middle and edge regions (Fig. 1F). In the near-edge region, collagen fibers are oriented perpendicular to the contact line of the droplet, which is consistent with the expected radial direction of flow. Furthermore, collagen fiber alignment varies as a function of distance from the substratum in the edge region (fig. S1). We also found that the diameter of collagen fibers (Fig. 1F) and the pore size (fig. S2) in the middle region are smaller than in the near-edge region. Given that the diameter of collagen fibers is directly related to the duration of the nucleation phase during self-assembly (22, 23), our observations suggest that the rate of collagen self-assembly varies spatially within the evaporating droplet. Nevertheless, we observed that collagen fibers are oriented radially throughout millimeter-scale regions of the droplet (Fig. 1G). However, collagen fiber alignment and diameter both decrease with increasing distance from the contact line (Fig. 1H). Droplets that did not undergo partial evaporation during self-assembly contained isotropic networks of collagen in all regions (fig. S3). Together, these data confirm that the orientation and diameter of collagen fibers vary spatially within evaporating droplets.

Flow in the evaporating droplet aligns collagen fibers during self-assembly

To determine whether the orientation of collagen fibers correlates with the internal patterns of flow during evaporation, we incorporated fluorescent beads with a diameter of 1 μm into the droplets. Time-lapse CRM allowed us to simultaneously visualize the motion of the beads (movie S1) and the self-assembly of collagen (movies S2 and S3). This analysis revealed that beads in the near-edge region move radially inward during the early stages of evaporation (movie S1). Inward radial movement is consistent with the orientation of collagen fibers in this region (Fig. 1D) and suggests that Marangoni flow drives recirculation in these evaporating droplets. We also observed that beads in the middle region largely undergo random motion, while beads in the edge region move radially both to and from the contact line (movie S1). These bead movements are consistent with the patterns of collagen fiber alignment throughout the droplet (Fig. 1).

To obtain a quantitative description of the flow in evaporating droplets, we calculated the time- and ensemble-averaged mean-squared displacement (MSD), total displacement, and velocity of bead trajectories. We found that the power-law exponents for the MSD of beads in the edge, near-edge, and middle regions are 1.33 ± 0.03, 1.68 ± 0.12, and 1.36 ± 0.18, respectively (Fig. 2A). These measurements indicate that beads in the near-edge region of the droplet have increased mobility as compared to beads in the edge and middle regions. Consistent with these observations, the average velocity of beads is 5- to 10-fold higher in the near-edge region than in the edge or middle regions (Fig. 2B).

Fig. 2. Evaporation drives distinct regional patterns of flow, which are attenuated by the self-assembly of collagen.

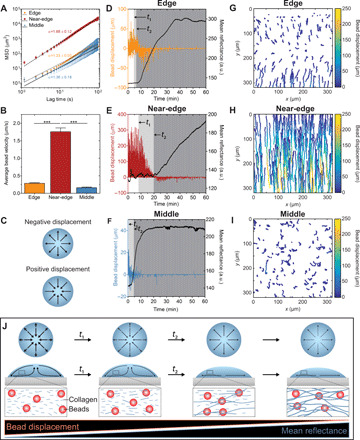
(A) Time- and ensemble-averaged MSD for bead trajectories. Trajectories in the middle region exceeding 300 frames in length were eliminated to improve computational efficiency. The slope, α, represents the power-law exponent that was fitted to the data. (B) Average radial bead velocity for 500 bead trajectories identified in each of three replicates. (C) Direction of radial flow corresponding to positive or negative displacement. Radial bead displacement in the (D) edge, (E) near-edge, and (F) middle regions of an evaporating droplet of collagen. Black lines represent mean reflectance at 488 nm. Characteristic times associated with the formation of free-flowing collagen fibers, t₁, and the formation of a stable network of collagen fibers, t₂, are annotated on plots (D to F). a.u., arbitrary units. Single-bead trajectories color-coded based on bead displacement for the (G) edge, (H) near-edge, and (I) middle regions of an evaporating droplet of collagen. The first 500 trajectories that exceeded 20 frames in length in each region of interest are plotted. (J) Flow fields observed in an evaporating droplet of collagen containing fluorescent beads. Collagen solutions were gelled at controlled RH using a saturated solution of MgCl₂ (RH ~ 31%) on UVO-treated glass. ***P ≤ 0.001.

To visualize temporal changes in flow, we plotted radial bead displacement and mean reflectance, which provides an indication of collagen fiber formation, as a function of time (Fig. 2, C to F). We defined two characteristic times: t₁, which corresponds to the formation of free-flowing collagen fibers, and t₂, which corresponds to the formation of a network of collagen fibers that do not move freely with the fluid flow. In the edge region, beads are simultaneously displaced radially toward and away from the contact line (Fig. 2D) due to regional vortices (movie S1). After t₁, the magnitude of displacement decreases until t₂, when beads in the edge region largely move toward the contact line before their motion becomes constrained. Given that mean reflectance increases as bead displacement decreases, we hypothesized that collagen fibers constrain the motion of the beads. Using time-lapse CRM, we observed that the beads colocalize with collagen fibers and that the formation of a stable network of fibers constrains bead movement (movie S3). In the near-edge region, beads initially move radially inward, and their displacement begins to decrease at t₁ (Fig. 2E). Subsequently, the displacement of beads is further attenuated, and the flow reverses direction at t₂ (Fig. 2E). Beads in the middle region initially move radially inward and then outward before largely undergoing random motion (Fig. 2F). Plots of representative trajectories revealed that beads experience a recirculating flow in the edge region of the droplet (Fig. 2G), while beads in the near-edge and middle regions undergo unidirectional (Fig. 2H) and random (Fig. 2I) motion, respectively. In each region, we observed distinct characteristic times and reflectance curves, which again suggest that the rate of self-assembly varies spatially within the droplet. Together, these data show that evaporation drives the radial displacement of beads. Bead displacement reverses direction during collagen self-assembly and is attenuated by the formation of a stable network of collagen fibers (Fig. 2J).

Flow in the evaporating droplet is driven by surface tension gradients

The patterns of flow observed in evaporating droplets of collagen are reminiscent of Marangoni flow, which can result from thermal (nonuniform temperature) or solutal (nonuniform solute) effects. Given that the rate of collagen self-assembly varies within the droplet, we hypothesized that the resulting nonuniform distribution of collagen monomers could generate a surface tension gradient. For this hypothesis to be correct, the surface tension of the solvent [phosphate-buffered saline (PBS)] must differ from that of the solute (collagen at a concentration of 0.8 mg/ml). As expected, we found that the surface tensions of the PBS solvent (74.5 mN/m) and collagen solute (67.9 mN/m) are different, which suggests that a nonuniform distribution of collagen can generate solutal Marangoni flows in evaporating droplets of collagen.

Collagen and PBS are initially well mixed before the droplet is cast on the glass, but our bead displacement data revealed that flow is induced immediately after heating the droplet. These observations suggest that a thermal Marangoni flow might be present at the earliest stages of evaporation. To determine whether thermal Marangoni effects are sufficient to induce fluid flow in this system, we incorporated fluorescent beads into droplets of collagen-free PBS and tracked their movements during evaporation. We observed flow patterns (figs. S4, A and B) in which the direction of flow was consistent with the initial flow observed in evaporating droplets of collagen (Fig. 2, G and H), but that did not reverse (fig. S4, C and D). These data suggest that thermal Marangoni flow drives the initial inward radial flow in evaporating droplets of collagen. This flow leads to a nonuniform distribution of collagen within the droplet, resulting in a solutal Marangoni effect that reverses the direction of flow.

We next considered how Marangoni flow could affect the alignment of collagen fibers during self-assembly. To estimate the strength of evaporation-driven flow in the droplet, we calculated the Weissenberg number (Wi) (table S1) (24), which is a dimensionless number defined as the product of the polymer relaxation time (τ) and the deformation rate. Because a shear flow is generated in the evaporating droplet, the deformation rate is given by the shear rate ($\stackrel{.}{\mathrm{\gamma }}$) (i.e., $\mathit{Wi}=\stackrel{.}{\mathrm{\gamma }}\mathrm{\tau }$). Under these conditions, large values of Wi would indicate that the shear rate is sufficient to deform and affect the orientation of a collagen molecule. However, using a previously reported estimate for the relaxation time of an individual collagen molecule (25), we find that Wi ≪ 1. This analysis suggests that the shear flow generated in evaporating droplets is not sufficient to align individual collagen molecules in the direction of flow. When we perform this calculation using previously reported parameters for collagen fibers (26) and the viscosity of collagen solutions (27), we find that Wi > 1 (table S1). Marangoni flow thus appears to orient larger assembles of collagen, not individual collagen molecules, in the direction of flow.

Tuning collagen fiber alignment and diameter

On the basis of these results, we further explored collagen fiber alignment in the near-edge region of the droplets. The velocity of a Marangoni flow is proportional to the evaporation rate (28), and the alignment of collagen fibers self-assembled under flow depends on the flow-induced shear rate (25). Therefore, we hypothesized that we could tune the alignment of collagen fibers by varying the RH and thus the evaporation rate. To test this hypothesis, we incorporated pure water (RH ~ 100%) or saturated solutions of NaCl (RH ~ 75%) or LiBr (RH ~ 6%) into the culture dish instead of the saturated solution of MgCl₂ (RH ~ 31%). Calculating alignment fraction from CRM images of the near-edge region revealed that collagen fiber alignment decreases under the higher RH conditions provided by pure water or NaCl (Fig. 3, A to E). These results are consistent with the average bead velocity in evaporating droplets, which generally decreases with increasing RH (Fig. 3F). We also observed increased accumulation of collagen along the contact line with decreased RH, which is consistent with the measured flow velocities (fig. S5). In the center of the droplets, we observed no change in the alignment fraction as a function of RH (fig. S6).

Fig. 3. RH affects the alignment fraction and geometry of collagen fibers.

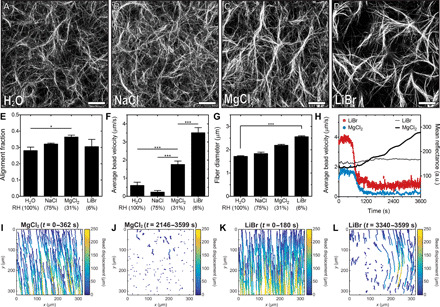
Representative CRM images in the near-edge region of droplets of collagen self-assembled in the presence of (A) water (RH ~ 100%) and saturated solutions of (B) NaCl (RH ~ 75%), (C) MgCl₂ (RH ~ 31%), or (D) LiBr (RH ~ 6%). Scale bars, 50 μm. (E) Alignment fraction of collagen fibers in the near-edge region of droplets of collagen. (F) Average radial bead velocity in the near-edge region of droplets of collagen. Velocity was determined from the average of 500 bead trajectories. (G) Average collagen fiber diameter in the near-edge region of droplets of collagen. (H) Average radial bead velocity as a function of time in the near-edge region of droplets of collagen. Bead velocity data were smoothed using a moving average of 10. The black lines represent mean reflectance at 488 nm. Bead displacement in the near-edge region of droplets incubated with saturated solutions of (I and J) MgCl₂ or (K and L) LiBr. (I) and (K) represent bead trajectories at the beginning of an experiment and (J) and (L) represent trajectories after the characteristic time t₂. The total time during which trajectories are plotted is noted above each plot. Collagen solutions were gelled on UVO-treated glass. *P ≤ 0.05 and ***P ≤ 0.001.

Decreasing the RH using LiBr decreases the alignment fraction (Fig. 3E) and increases collagen fiber diameter (Fig. 3G), which may be attributed to attenuated kinetics of collagen self-assembly under increased velocity of flow. RH thus appears to regulate the alignment fraction and diameter of collagen fibers by altering the rate of flow in the evaporating droplet. To understand why fiber alignment is reduced at the lowest RH condition, we plotted the average bead velocity and mean reflectance as a function of time (Fig. 3H). We observed that the bead velocity decreases rapidly during self-assembly before reaching a plateau, which is higher at lower RH. The rapid decrease in bead velocity is consistent with our observation that beads colocalize with collagen fibers, which are stationary after the formation of a stable network of fibers. Therefore, the higher bead velocity observed at the lower RH suggests that an unstable network of fibers has formed. This idea is supported by the lower mean reflectance values observed at lower RH (Fig. 3H). We also plotted bead trajectories at the beginning of evaporation and after the characteristic time, t₂ (Fig. 3, I to L). In the presence of saturated solutions of MgCl₂ (RH ~ 31%), the radial flow of beads (Fig. 3I) is followed by an attenuation of bead movement (Fig. 3J). In contrast, in the presence of saturated solutions of LiBr (RH ~ 6%), radial flow (Fig. 3K) is followed by distorted patterns of flow (Fig. 3L) that are caused by an unstable network of fibers. These data demonstrate that sufficiently large flow rates can disrupt the formation of a stable network of collagen, distort flow patterns, and reduce fiber alignment.

Given the suspected role of self-assembly kinetics in producing aligned networks of collagen, we proceeded to modify the rate of self-assembly by changing the pH of the solution. Decreasing the pH to 6.5, which decreases the rate of fibril formation (29), does not significantly affect the alignment fraction. Increasing the pH to 11, which increases the rate of fibril formation, significantly increases the alignment fraction (fig. S7, A to D). These data suggest that alignment fraction is a function of the rate of collagen self-assembly. Under the low RH provided by LiBr, we observed that the alignment fraction increases with decreasing pH (fig. S7, E to H). These data suggest that there is an optimal ratio between the rate of collagen self-assembly and the shear rate. We further observed that doubling the concentration of collagen, which increases both the rate of self-assembly (29) and the viscosity of the solution (30), decreases collagen fiber alignment (fig. S7, I to L). Halving the collagen concentration has the opposite effect. These results are consistent with previous studies, which have demonstrated that evaporation-driven flows can be attenuated by increasing viscosity (31). Together, these data demonstrate that collagen fiber alignment is a function of the kinetics of self-assembly in an evaporating droplet.

It is also well appreciated that the contact angle of an evaporating droplet can affect the velocity and direction of Marangoni flow (32). However, there is no significant difference in the orientation or alignment fraction of collagen fibers in the near-edge region of droplets that are drop cast on substrata with different surface chemistries (fig. S8). In these samples, there are modest differences in collagen fiber alignment as a function of distance from the substratum in the edge region of the droplets (fig. S9). These results suggest that the droplet contact angle does not affect flow over the time scales and RHs investigated. Alternatively, interactions between the hydrophobic silane coating and collagen molecules may affect flow in the droplet.

Droplet geometry dictates the pattern of collagen fiber alignment

We next investigated the effects of droplet geometry on the pattern of collagen fiber alignment and accumulation. We laser etched glass surfaces to control the geometries of droplets of collagen (Fig. 4, A to C). Using CRM, we observed distinct radial patterns of collagen fibers aligned perpendicular to the contact line of the droplet for each geometry (Fig. 4, D to G). We also acquired CRM images of collagen fibers along the long (Fig. 4H) and short (Fig. 4I) axes of an oval droplet of collagen. Quantification of fiber orientation in these images demonstrates that the radius of curvature of the contact line alters the pattern of fiber alignment (Fig. 4, H′ and I′). In the absence of Marangoni flow, droplet geometry did not affect collagen fiber orientation (fig. S10). In addition to fiber alignment, we observed an increase in the pore size of networks of collagen in square and oval droplets as compared to circular droplets (Fig. 4J). Droplet geometry is also known to affect evaporation-driven flow, with convex regions along the contact line experiencing a higher evaporative flux (3, 11). Using CRM, we acquired images of collagen fibers along curved (Fig. 4K) and straight (Fig. 4L) regions of the contact line for square droplets. We observed increased collagen fiber accumulation along curved edges of the square droplet of collagen (Fig. 4M), consistent with enhanced flux at these edges. The pattern of collagen alignment can therefore be tuned by controlling the geometry of the droplet.

Fig. 4. Droplet geometry affects collagen fiber alignment and accumulation.

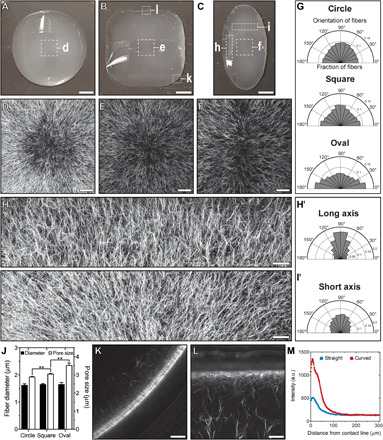
(A) Circular, (B) square, or (C) oval droplets of collagen. Scale bars, 2 mm. CRM images of the center of (D) circular, (E) square, and (F) oval droplets. Scale bars, 200 μm. (G) Collagen fiber orientation in the middle region of droplets. CRM images of the (H) long and (I) short axes of an oval droplet. Representative regions of the oval droplet are highlighted with white boxes in (C). (H) has been rotated 90° clockwise relative to the orientation in (C). Scale bars, 150 μm. Orientation of collagen fibers along the (H′) long and (I′) short axes of an oval droplet. (J) Collagen fiber diameter and pore size. CRM images of (K) curved and (L) straight regions of the contact line of a square droplet. Representative regions of the square droplet are highlighted in white boxes in (B). Images represent a single confocal slice. Scale bars, 100 μm. (M) Average collagen intensity as a function of distance from the contact line. (D) to (F) and (H) and (I) were obtained by stitching multiple images together. Collagen solutions (pH 11) were gelled at controlled RH using a saturated solution of MgCl₂ (RH ~ 31%) on UVO-treated glass. **P ≤ 0.01.

Patterning cell alignment and differentiation

Aligned networks of collagen fibers influence cell and tissue behavior in vivo and regulate biological processes including epithelial tissue morphogenesis (33) and cancer cell migration (34). Aligned collagen fibers can also affect the orientation (35) and differentiation (36) of cells in culture, which offers a promising avenue for engineering aligned tissue constructs such as those found in skeletal muscle. To determine whether cells remain viable and respond to fiber alignment that results from evaporating droplets of collagen, we incorporated human breast cancer or skeletal muscle cells into the solution of collagen before drop casting and evaporation. As expected (34), quantitative image analysis revealed that breast cancer cells orient radially along collagen fibers in the droplet (fig. S11). Similarly, we observed that skeletal muscle cells orient in the direction of collagen fiber alignment (Fig. 5 and figs. S12 and S13). To promote differentiation, skeletal muscle cells in droplets of collagen were cultured in differentiation medium. After 4 days in differentiation medium, skeletal muscle cells fuse together into multinucleated myotubes oriented in the direction of collagen fiber alignment throughout the droplet (Fig. 6 and fig. S14). Analysis of the collagen fiber orientation demonstrated that cells remodel collagen fibers and disrupt the initial collagen alignment pattern in the droplet (fig. S15).

Fig. 5. Evaporating droplets of collagen pattern mammalian cell alignment.

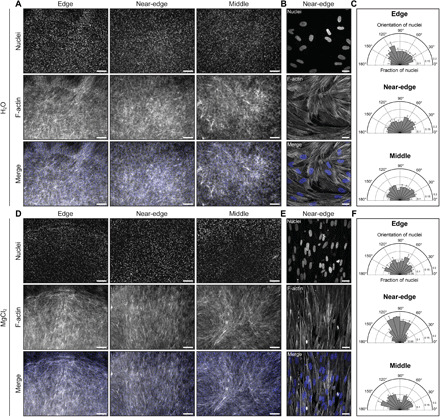
Representative (A) low and (B) high magnification fluorescence images of human skeletal muscle cells in each region of interest of a self-assembled droplet of collagen after 3 days in differentiation medium. The concentration of collagen was 2 mg/ml. RH was controlled using water (RH ~ 100%). (C) Orientation of nuclei in the edge (n = 2511), near-edge (n = 2148), and middle (n = 1767) regions of the droplet, where n represents the number of nuclei analyzed. Representative (D) low and (E) high magnification fluorescence images of human skeletal muscle cells in each region of interest of a self-assembled droplet of collagen after 3 days in differentiation medium. The concentration of collagen was ~2.3 mg/ml. RH was controlled using a saturated solution of MgCl₂ (RH ~ 31%). (F) Orientation of nuclei in the edge (n = 2928), near-edge (n = 2381), and middle (n = 2638) regions of the droplet, where n represents the number of nuclei analyzed. Panels (B) and (E) represent the maximum-intensity z projection of a 7.8-μm-thick stack and a 10-μm-thick stack, respectively. Scale bars, 250 μm (A and D) and 25 μm (B and E). Cells are stained with Hoechst 33342 to label nuclei (blue) and phalloidin to label F-actin (gray). Collagen solutions were gelled on UVO-treated glass.

Fig. 6. Evaporating droplets of collagen pattern the orientation of differentiated skeletal muscle cells.

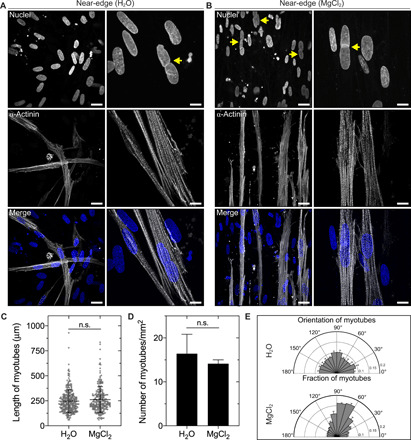
Representative fluorescence images of human skeletal muscle cells in the near-edge region of a self-assembled droplet of collagen after 4 days in differentiation medium. RH was controlled using (A) water (RH ~ 100%) or (B) a saturated solution of MgCl₂ (RH ~ 31%). Yellow arrows denote multinucleated cells. Cells are stained with Hoechst 33342 to label nuclei (blue) and an antibody against sarcomeric α-actinin (gray). Scale bars in the left and right columns of (A) and (B), 25 and 10 μm, respectively. Fluorescent images represent maximum-intensity z projections of 3.3 μm [(A), left column], 6.9 μm [(A), right column), 8 μm [(B), left column], or 7 μm [(B), right column] stacks. The concentration of collagen was 2 or 2.1 mg/ml for droplets self-assembled in the presence of water or a saturated solution of MgCl₂, respectively. Average (C) length and (D) density of myotubes in the near-edge region of droplets of collagen self-assembled in the presence of water or a saturated solution of MgCl₂. Error bars for myotube length represent SD. (E) Orientation of myotubes in the near-edge region of droplets of collagen. Collagen solutions were gelled on UVO-treated glass. n.s., not significant.

To confirm that droplets of collagen influence differentiation, we cultured cells on a glass substratum under the same conditions and observed that sarcomeric structures are smaller and randomly oriented (fig. S16). We also incorporated skeletal muscle cells into droplets of collagen without any fiber alignment (self-assembled in the presence of water). We observed that skeletal muscle cells were randomly oriented throughout these droplets (Fig. 5). As compared to cells in droplets of collagen with fiber alignment, skeletal muscle cells formed randomly oriented myotubes with a similar length and density (Fig. 6, C to E). Lastly, in addition to pure collagen gels, we found that collagen fibers in mixtures of collagen and Matrigel, which are used to study epithelial tissue morphogenesis, are aligned by evaporation-driven flow (fig. S17). Together, these data demonstrate that evaporating droplets of collagen can pattern cell alignment and differentiation over millimeter length scales.

DISCUSSION

Flow in evaporating droplets has emerged as a versatile approach for patterning solutes ranging from polymeric colloids to self-assembling proteins. Solutes are typically suspended in solvents that completely evaporate, giving rise to thin dehydrated patterns of solute on a surface. Here, we demonstrate that Marangoni flows generated in evaporating droplets of type I collagen can precisely regulate the hierarchical self-assembly of collagen and generate three-dimensional (3D) networks with tunable fiber alignment, fiber diameter, and porosity. By preventing complete evaporation, we demonstrate that the resulting droplets contain hydrated 3D collagen fiber networks that can support mammalian cell growth and differentiation over millimeter length scales.

Under the conditions used in this study, more than 50% of collagen fibers were oriented within 20° of the radial direction in the droplet. We identified that the direction and speed of fluid flow, pH, and collagen concentration affect fiber alignment in evaporating droplets. However, it is likely that additional experimental parameters, such as temperature, ionic strength, and molecular crowding, may be used to further tune the structure and alignment of the collagen fiber networks. In future work, the spatial control of Marangoni flows (37) may permit the generation of more complex patterns of collagen fiber alignment, fiber diameter, and porosity. Given that CRM is unable to detect collagen fibers oriented more than ~50° from the imaging plane (38), alternative imaging techniques such as confocal fluorescence microscopy may be needed to more completely characterize the resulting networks of collagen.

In contrast to existing approaches for aligning collagen, evaporating droplets spontaneously generate radial fiber alignment under conditions that are compatible with cell culture and without any specialized equipment. However, while aligned collagen fibers are largely oriented in the radial direction, we observe random fiber alignment along the contact line and in the middle of the droplet. We also observe variations in the fiber diameter and pore size at different radial positions within the droplet. This spatial heterogeneity might have implications for the mechanical properties of collagen gels, and further analysis is required to assess how mechanical properties vary throughout the droplet.

Using our approach, mammalian cells that are incorporated into neutralized solutions of collagen before drop casting orient in the direction of collagen fiber alignment throughout the droplets of collagen. We find that cells can be incorporated into evaporating droplets at high densities (~500,000 cells/ml) and cultured for times exceeding 1 week. Our approach offers several advantages for generating cell-laden networks of aligned type I collagen fibers. As compared to bioprinting, cells within the evaporating droplet are subject to minimal shear flow (table S1), which may allow the incorporation of and limit the damage to shear-sensitive cells. In contrast to strained elastomeric molds, cells are not subjected to external compression or global densification of the collagen network. However, one fundamental limitation of our approach is that cell sedimentation within drop-cast collagen gels can occur at low concentrations owing to the slow rate of collagen self-assembly. In addition, droplets with low collagen concentrations (~2 mg/ml) can be mechanically deformed by contractile cells during extended periods of culture. Covalently bonding collagen to an underlying substratum (39) might reduce the extent of deformation, but it is unclear how this would affect the patterns of collagen fiber alignment within the droplet.

Evaporating droplets represent a widely accessible and powerful platform for engineering networks of collagen. Droplets of collagen can be used to address a wide range of questions as to how aligned fiber networks influence the behavior of mammalian cells. This system could also provide a simple high-throughput approach for incorporating tissue explants or organoids into aligned networks of collagen. Ultimately, our approach may enable the fabrication of aligned tissue constructs at physiologically relevant length scales for applications in developmental biology and tissue engineering.

MATERIALS AND METHODS

Collagen gel preparation

Unless stated otherwise, solutions of acid-solubilized bovine type I collagen (Advanced Biomatrix, Carlsbad, CA) were prepared to obtain a final collagen concentration of 0.8 mg/ml at pH ~8. The collagen concentration was tuned using PBS, and the pH of the resulting mixture was adjusted using the manufacturer-provided neutralizing solution (Advanced Biomatrix). Growth factor–reduced Matrigel (Corning, Corning, NY) had an initial protein concentration of 8.2 mg/ml. Fluorescent carboxylate–modified polystyrene beads (1 μm in diameter; Thermo Fisher Scientific, Waltham, MA) were incorporated into neutralized collagen at a density of ~3.0 × 10⁷ beads/ml for time-lapse experiments. Cells were incorporated into neutralized solutions of collagen at a concentration of ~500,000 cells/ml.

Drop casting

Custom culture dishes with a diameter of 35 mm with no. 1 glass coverslip bottoms were used for all experiments (Fig. 1A). Before drop casting, glass-bottom culture dishes were rinsed with 100% ethanol, air dried, and subsequently treated with UVO (Jelight Company, Irvine, CA) for 7 min. The hydrophobicity of the glass surface was modified by treatment with 3,3,3-trifluoropropyl-trichlorosilane (Alfa Aesar, Haverhill, MA), trimethylchlorosilane (Sigma-Aldrich), or trichloro(1H,1H,2H,2H-perfluorooctyl)silane (Sigma-Aldrich) as described previously (40). Advancing and receding contact angle data for these surface chemistries have been reported (40). The RH was controlled using saturated solutions of sodium chloride (RH ~ 75%; Sigma-Aldrich), magnesium chloride (RH ~ 31%; Sigma-Aldrich), or lithium bromide (RH ~ 6%; Sigma-Aldrich) (41). Saturated salt solution (~300 μl) was added uniformly around the perimeter of the culture dish immediately before drop casting. Neutralized solutions of collagen (150 μl) were then drop cast onto no. 1 glass coverslips at room temperature (~20°C). Before incubation at 37°C, cell-laden droplets of collagen were placed on ice for 20 min. Otherwise, drop-cast solutions of collagen were placed directly into a 37°C incubator at 5% CO₂ for 40 min.

Cell culture

Human skeletal muscle cells (CC-2561; BioWhittaker, Walkersville, MD) were cultured on collagen-coated tissue culture dishes in F-10 nutrient mixture medium (Thermo Fisher Scientific) supplemented with 20% fetal bovine serum (FBS; Atlanta Biologicals, Flowery Branch, GA), 0.5% chick embryo extract (MP Biomedicals, Santa Ana, CA), and 1% glutamine-penicillin-streptomycin (Thermo Fisher Scientific). To promote differentiation, skeletal muscle cells were subsequently cultured in 1:1 Dulbecco’s modified Eagle’s medium (DMEM)/F-12 medium (Thermo Fisher Scientific) supplemented with 2% horse serum (Thermo Fisher Scientific). Human breast cancer cells (MDA-MB-231; ATCC, Manassas, VA) were cultured in 1:1 DMEM/F-12 medium supplemented with 10% FBS and gentamicin (50 μg/ml; Sigma-Aldrich). Both cell lines were maintained in an incubator at 37°C under 5% CO₂.

Confocal reflection microscopy

Collagen fibers were imaged under reflection mode using a Nikon A1 laser-scanning confocal microscope equipped with a 488-nm argon laser and GaAsP detector. CRM images were acquired using a 10×/0.3 numerical aperture (NA) air, 20×/0.75 NA air, or 40×/1.3 NA oil-immersion objective. Unless stated otherwise, CRM images represent maximum-intensity z projections of 30-μm z stacks, which were scanned at ~2-μm intervals and centered 50 μm above the glass substratum. Time-lapse imaging was performed using a Nikon A1R-Si confocal microscope equipped with a stage-top incubator (Pathology Devices, Westminster, MD) maintained at 37°C. Time-lapse images were collected in a single plane at ~1.19-s intervals for a total time of 1 hour using a 40×/1.3 NA oil-immersion objective. Images of cells cultured within drop-cast networks of collagen were acquired using a Nikon Plan Apo 4×/0.2 NA air objective and ORCA-03G digital charge-coupled device camera (Hamamatsu Photonics, Japan) or 60×/1.4 NA or 100×/1.45 NA oil-immersion objective and Nikon A1 laser-scanning confocal microscope. Mean reflectance was obtained by measuring the mean gray value in ImageJ [National Institutes of Health (NIH)].

Immunofluorescence staining

Samples were fixed in a 4% (w/v) solution of paraformaldehyde (Alfa Aesar) in PBS for 15 min at room temperature and washed in PBS. To label nuclei, samples were incubated in a 1:5000 (v/v) solution of Hoechst 33342 (Invitrogen, Carlsbad, CA) in PBS for 15 min at room temperature and washed in PBS. To label F-actin, samples were permeabilized in 0.3% (v/v) Triton X-100 (Sigma-Aldrich) in PBS (PBST) for 15 min and then blocked in 10% (v/v) goat serum (Sigma-Aldrich) in PBST for 1 hour at room temperature. Blocked samples were incubated in a 1:200 (v/v) solution of Alexa Fluor 594 phalloidin (Thermo Fisher Scientific) in blocking solution for 2 hours at room temperature and washed with PBST. To label sarcomeric α-actinin, samples were fixed and blocked as described above and incubated in a 1:500 (v/v) solution of primary antibody against sarcomeric α-actinin (Thermo Fisher Scientific) overnight at 4°C and washed in PBST. Samples were then incubated in a 1:1000 (v/v) solution of Alexa Fluor 488 goat anti-mouse secondary antibody (Thermo Fisher Scientific) overnight at 4°C and washed in PBST.

Quantification of pore size and collagen fiber alignment and diameter

Collagen fiber alignment in drop-cast collagen gels was quantified as described previously (40). Briefly, the local gradient orientation plug-in (created by J.-Y. Tinevez) in ImageJ was used to quantify an alignment fraction, which represents the fraction of collagen fibers oriented within 20° of the radial direction in the droplet. The BoneJ plug-in (created by M. Doube) in ImageJ was used to quantify collagen fiber diameter and pore size (42).

Quantification of cell orientation

The orientation of human skeletal muscle cells was approximated on the basis of the orientation of F-actin fibers and nuclei. F-actin images were analyzed using the local gradient orientation plug-in in ImageJ. Images of nuclei were converted to binary images, and the analyze particles plug-in in ImageJ was used to calculate the angle of the maximum Feret diameter, which approximates the nuclear orientation. After differentiation, the orientation of myotubes was determined using the local gradient orientation plug-in in ImageJ. The orientation of human breast cancer cells was determined directly from phase-contrast images. Cell boundaries were outlined manually, and the angle of the maximum Feret diameter of the resulting outline was calculated.

Surface tension measurements

The surface tensions of solutions of collagen and PBS were determined using the pendant droplet method (43). All measurements were conducted at room temperature.

Laser etching glass

No. 1 glass coverslips were etched with a laser cutter (60 W, Helix; Epilog Laser, Golden, CO). The etching pattern was generated using Adobe Illustrator (Adobe, San Jose, CA). After etching, glass coverslips were incorporated into culture dishes and prepared as described above.

Particle tracking analysis

Fluorescent bead trajectories were obtained using the Particle Tracker plug-in (created by Mosaic group) in ImageJ (44). Beads were tracked in a single x-y plane at a frame rate of ~1.19 s for a total duration of 1 hour. The average velocity and the time- and ensemble-averaged MSD were calculated using a custom script written in MATLAB (R2015b, MathWorks, Natick, MA). MSD was calculated directly from x and y coordinates using Eq. 1, where τ represents the lag time

$$\mathit{MSD}(\mathrm{\tau })=\langle {(x(t+\mathrm{\tau })-x(t))}^2\rangle +\langle {(y(t+\mathrm{\tau })-y(t))}^2\rangle$$ (1)

The slope, α, of the log-log plot of MSD versus τ was determined by fitting MSD data to the power-law model shown in Eq. 2, where D is the apparent diffusion coefficient

$$\mathit{MSD}(\mathrm{\tau })=4D{\mathrm{\tau }}^{\mathrm{\alpha }}$$ (2)

Statistical analyses

Unless stated otherwise, data represent the average of three independent replicates, and error bars represent SEM. Statistical analysis was performed using GraphPad Prism (GraphPad Software, San Diego, CA). A Student’s t test or a one-way analysis of variance (ANOVA) with Tukey’s post hoc test was used for statistical comparison. P < 0.05 was considered to be statistically significant.

SUPPLEMENTARY MATERIALS

Supplementary material for this article is available at http://advances.sciencemag.org/cgi/content/full/6/24/eaaz7748/DC1

View/request a protocol for this paper from Bio-protocol.