Mapping the 3D orientation of nanocrystals and nanostructures in human bone: Indications of novel structural features

3D mapping of crystal and nanostructure orientation shows that bone contains a mineral fraction not aligned with the nanostructure.

Abstract

Bone is built from collagen fibrils and biomineral nanoparticles. In humans, they are organized in lamellar twisting patterns on the microscale. It has been a central tenet that the biomineral nanoparticles are co-aligned with the bone nanostructure. Here, we reconstruct the three-dimensional orientation in human lamellar bone of both the nanoscale features and the biomineral crystal lattice from small-angle x-ray scattering and wide-angle x-ray scattering, respectively. While most of the investigated regions show well-aligned nanostructure and crystal structure, consistent with current bone models, we report a localized difference in orientation distribution between the nanostructure and the biomineral crystals in specific bands. Our results show a robust and systematic, but localized, variation in the alignment of the two signals, which can be interpreted as either an additional mineral fraction in bone, a preferentially aligned extrafibrillar fraction, or the result of transverse stacking of mineral particles over several fibrils.

INTRODUCTION

Bone formation leads to a hierarchically structured composite material, whose outstanding mechanical properties are intimately linked to its nanostructure. Our aging society presents increasing problems of poor bone health due to changes in the bone structure resulting in impaired mechanical properties, yet an understanding of bone mechanics critically relies on understanding its architecture. The basic building blocks of bone comprise collagen fibrils reinforced by biomineral particles, predominantly carbonated hydroxylapatite (HAP) (1, 2), and are organized in various highly oriented twisting patterns. Recently, the understanding of bone constituents has advanced, with studies showing that the biomineral particles are composed of fractal aggregates rather than platelets as hitherto believed (3) or the discovery that the hydration of collagen fibrils may induce drastic tensile forces and consequently alter its mechanical properties (4). Furthermore, a rich variety of organization patterns on the microscale were identified (5), evidencing a fine-grained control of the fracture mechanical properties of bone (6). Essentially, all these investigations reflect an urgent need to understand the nanostructural and crystallographic organization at play. The orientation of the two constituents together within a large volume is especially important for placing results in a proper microstructural context in contrast to previous studies.

The mechanical properties of bone are connected to the orientation of the underlying microscale motifs (7–10). Human lamellar bone was traditionally believed to be formed by alternating orientations of two-dimensional (2D) co-aligned mineralized collagen fibrils (11, 12). Recently, however, focused ion beam-scanning electron microscopy (FIB-SEM) tomography on de-mineralized bone challenged this model, as it revealed distinctive zones of ordered, 3- to 7-μm-thick lamellae interlaced with disordered regions (5), allowing a better understanding of the mechanical properties of bone (6). Ordered fibrils show a discontinuous change in their orientation, due to their remodeling properties (13, 14). On the micro- and nanoscale, bone mechanical properties are defined by the mineralized collagen fibrils, noncollagenous matrix components, and the 3D arrangement of the constituents (15). The type I collagen fibrils contain molecules organized in a staggered, overlapping array of triple helices with ~67-nm periodicity (overlap region) and hole zones at the ends of the individual molecules that are believed to be sites of mineral nucleation and are thus thought to be co-aligned. The co-alignment of mineral and collagen has large implications for the mechanical performance of bone (16, 17). There is general agreement that the orientation of the crystallographic c axis follows the collagen fibrils on a submillimeter scale (18, 19), which is confirmed on a single fibril level by electron diffraction (20). However, probing single fibers is prone to sampling bias with severe limitations in field of view (FOV) and sample thickness. X-rays allow averaged sampling of functionally relevant volumes while retaining a sufficiently high resolution to resolve relevant motifs. On bone, small-angle x-ray scattering (SAXS) provides information on the nanostructural level where the contrast is based on electron density variations between the mineral nanoparticles and the organic matrix (21). Wide-angle x-ray scattering (WAXS) probes atomic scale (in angstrom) distances in bone mostly from the biomineral, that is, the HAP crystals contained in the collagen matrix of bone. In both cases, the orientation of the respective signal is directly related to the orientation of the scattering structures, either the orientation of the mineral particle shape, probed via SAXS as the signal from their thinnest dimension, or via WAXS as the orientation of their crystallographic c axis. Previous results obtained from SAXS/WAXS orientation analysis of the fibrous texture arrangement of HAP in human osteonal lamellae were consistent with co-alignment of the mineral particles long axis and their c axis (22, 23). A fiber texture is a rotationally random distribution of crystallites along an axis of preferred orientation, the fiber axis (24). The co-alignment of the collagen fibril and the c axis is assumed in all current bone models. We sample a signature of the nanostructure (mineral particle thickness) in SAXS/WAXS as azimuthally dependent scattering separated by 90° between SAXS and the biomineral (002) reflection (Fig. 1). Additional reports have found alignment of the crystalline c axis of HAP to be spread in a full width at half maximum range up to 15°, as determined by the azimuthal broadening of the (002) reflection in electron diffraction (25). Furthermore, in a perfectly aligned crystal, reflections such as (1 1 2), (2 1 1), and (3 0 0) would not be observed together, albeit they usually are observed together in the case of bone. This has been interpreted as an indicator of a tilting of the crystalline c axis of different mineral particles within a mineralized fibril.

Fig. 1. Experimental setup and the alignment of nanocrystal and crystal structure.

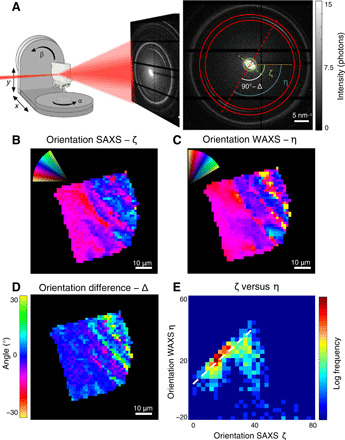
(A) The experimental setup comprised a μ-focused synchrotron x-ray beam and a sample, which is raster-scanned along the x and y directions. For a tensor tomography dataset, the sample is further rotated with the angles α and β. In each scattering pattern collected at each point, both SAXS (nanostructure) and WAXS (biomineral diffraction) are measured. The orientation difference of the SAXS signal (green dashed line) and the hydroxyapatite (002) reflection (red dashed line) is visible in the raw data. (B to D) Orientation of the nanostructure ζ (from2D SAXS) and crystallographic c axis η (from 2D WAXS) and their respective orientation difference Δ = 90° + ζ − η in a single projection of raw data. (E) 2D histogram of the alignment ζ versus η − 90°. It is clear that besides the major portion of co-aligned SAXS/WAXS signal (dashed line), a significant portion is oriented differently.

However, we observed several cases during scanning SAXS/WAXS investigations of bone where this orthogonality was broken in the scattering patterns. We hypothesized that this is evidence for an additional mineral fraction, not co-aligned with the “regularly” aligned mineral fraction. To test this hypothesis, it is essential to map orientations in 3D to ensure that the observed differences in alignment cannot result from accidental projection effects. Therefore, we extended the recently established small-angle scattering tensor tomography (26, 27) from the volumetric mapping of nanostructures based on SAXS (28) to the mapping of crystal orientations based on WAXS (Supplementary Materials) through an experimental setup that measured SAXS and WAXS simultaneously while collecting a tensor tomography dataset with a 700-nm synchrotron x-ray beam. Thereby, we simultaneously collected information on the nano- and crystal structure as well as their orientations in a single experiment with a spatial resolution allowing to resolve lamellae. This novel approach allows a direct and unambiguous comparison of the two and enables to address the question of bone architecture directly. An important implication of the 700 nm × 700 nm × 700 nm sampling size is that we are not sensitive to the orientation effects on the single fibril level but rather average over about 100 fibrils. Following the reasoning of Wagermaier et al. (22) on the number of illuminated HAP crystallites, this transfers to 1.2 × 10⁵ sampled crystallites per voxel. While a stacking of the mineral particles is reported within one individual fibril and beyond for mineralized turkey leg tendon (29), an aspect further exploited in some models of SAXS data (30), little to no correlation in the stacking between several fibrils in human bone was reported (31). Hence, we expect, and verified with other reconstruction methods as shown in the Supplementary Materials, that within one voxel, on average, there is a high degree of rotational invariance around the fibril bundle axis. This analysis, presented in fig. S4, allows to determine the degree of axial symmetry around the fiber axis. We found values of about 0.34 that did not vary across the different zones in the sample, meaning that the intensity around the fiber axis fluctuated by about 30% irrespective of whether the crystal structure and nanostructure displayed orientational differences.

We studied a 40 μm by 40 μm by 40 μm human lamellar bone cube from an iliac crest trabecula (Fig. 2A and fig. S1). The cube consisted of about three lamellae and a nonlamellar part as identified from synchrotron nanotomography (Fig. 2B or fig. S1). The data collection for tensor tomography requires scanning the sample across the beam for several rotations of the sample around two axes [α and β, Fig. 1A; Materials and Methods and (28)]. In the following, the 2D map of such an x/y scan in each sample orientation is referred to as a projection. The scattered intensity (movie S1) revealed a clear lamellar structure of oriented material interlaced with disordered regions as proposed by Reznikov et al. (5, 32). To extract 3D orientation information, we analyzed the intensity distribution in reciprocal space through tensor tomography (Fig. 1A and Supplementary Materials) (26, 28, 33) to reconstruct SAXS/WAXS orientation tensors in each voxel (Fig. 2). The orientation pattern follows the twisted plywood pattern of human lamellar bone (5). To the best of our knowledge, it is the first time that this motif is mapped in 3D at such high resolution.

Fig. 2. SAXS and WAXS tensor tomography of human bone.

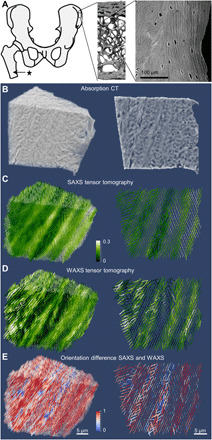
(A) The anatomical location of the sampling site of the bone cube, its hierarchical structure from laboratory microcomputed tomography (μCT) and SEM (13), and the anatomical location (*) of the 2D sample (Supplementary Materials). High-resolution absorption tomogram (B) with a cut through the middle of the sample and the corresponding reconstructed SAXS (C) and WAXS (D) tensor. Color code is degree of orientation. (E) Comparison of the SAXS versus WAXS orientation, with the orientation difference (calculated as squared dot product between SAXS and WAXS orientation) as color code with 1 (red) for orthogonal orientation, corresponding to co-alignment of the fibrils in SAXS and the mineral c axis in WAXS, and 0 (blue) for maximum orientation difference.

RESULTS

To introduce our results, we selected a measured 2D projection where the lamellae are oriented perpendicular to the x-ray beam so that any difference in orientation would be expected to be maximal. This difference between SAXS and WAXS signals is already evident from the raw data (Fig. 1A). The orientation projected in 2D of the nanostructure can be extracted from the azimuthal intensity distribution of the SAXS signal, resulting in the nanostructure orientation ζ (Fig. 1B). The direction of the c axis, η (Fig. 1C), was extracted from the (002) HAP reflection. A localized and notable alignment difference Δ = 90° + ζ − η was revealed (Fig. 1D). The alignment difference varied across the bone projection but reaches up to ~30°. A histogram of ζ versus η (Fig. 1E) shows not only that the majority of pixels display little to no alignment difference but also that a significant subfraction of pixels features larger alignment difference. This indicated that the crystals probed did not have their c axes (η) co-aligned with the nanostructure of the bone (ζ). An analysis of a 2D slice from human cortical femoral bone revealed the same pattern (fig. S2 and Supplementary Materials).

By extending the SAXS tensor reconstruction (Fig. 2C) to WAXS tensors (Fig. 2D and Supplementary Materials), we were able to compare and quantify differences in the alignment in 3D (Fig. 2E) as the squared dot product of the SAXS and WAXS tensor (see Materials and Methods). Figure 2E shows a slice through the volume of the sample, with cylinders representing the direction of highest SAXS orientation, the length as the summed SAXS intensity, and the color as the local difference in alignment. Voxels with large alignment differences were not randomly distributed but rather localized to zones of low degree of fibril orientation in SAXS (Fig. 2C). These stronger differences in alignment in the disordered zones can be understood as follows: One portion of mineral has the c axes symmetrically aligned around and roughly along the collagen fibril, encompassing not only mineral in the fibril gap zones but also symmetrically distributed extrafibrillar mineral from differently oriented mineral. This is consistent with all previously published bone models. However, we observe an additional portion of crystals whose c axes are preferentially aligned away from the collagen fibril axis. This could, for instance, be extrafibrillar mineral that is distributed asymmetrically around collagen fibrils. Note that other situations, like a very strong localized ordering, resulting in domains of iso-oriented stacking of mineral particles can be envisaged, albeit no experimental evidence supporting such motifs is known to the best of our knowledge. The part of bone containing a significant fraction of differently oriented mineral was estimated from voxels with an alignment dot product of <0.5. Extrapolating from the current 3D reconstruction, this suggests that ~30% of the bone volume may contain mineral with a difference in alignment. Note that this estimate is an upper bound for the volume fraction because each voxel contains an averaged signal and most likely also contains aligned mineral particles. If the volumes where this difference of orientation is present are significantly smaller than one of our voxels, then these numbers could be reduced. For example, variations in bone mineral crystallographic properties and matrix WAXS signals have been observed across lamellae in human osteons (34), suggesting that this is the case.

The observed localized difference in orientation and its correlation with intensity variations of the SAXS signal and the HAP reflections can also be observed directly in the measured data (projection). Figure 3 shows the SAXS/WAXS intensities across several lamellae, together with the difference in orientation obtained from 3D reconstruction (Fig. 2E) projected to 2D with the corresponding sample rotation. The positional variation of the HAP (002) intensity is anti-correlated with the SAXS signal and (310) reflection (Fig. 3B). An increased 3D alignment (i.e., larger squared dot product) seems to be correlated with the higher SAXS and (310) intensity. Scattering patterns from voxels with and without a difference of alignment are shown in Fig. 3 (C and D). Depending on the orientation of the minerals, the (002) intensity drops as the crystals are aligned in the beam direction, where the SAXS intensity is increased.

Fig. 3. Reflection intensities in one measured projection.

(A) Selected projection perpendicular to the lamellae orientation with position of the line profile (yellow line). (B) Integrated intensity along a line of the SAXS (green), HAP 002 (red), 310 reflection (blue), and the projected dot product indicating orientation differences (black). (C) Measured 2D scattering pattern of the lamellar zone. The HAP 002 is clearly visible and very intense. (D) Measured 2D scattering pattern from the misoriented zone. The 002 is still present but rather weak compared to the SAXS signal, shown in the insets with separate scaling.

The measured projections (Figs. 1 and 3) represent an average over the illuminated path through the sample. The fact that the orientation difference is seen in projections and in tensor tomography excludes that possible reconstruction artifacts affect our interpretation. With a 700-nm beam size, we collected statistical information on several hundreds of collagen fibrils and associated mineral. The statements here thus concern the ensemble averaged orientation within one voxel (Fig. 2) or its projections (Figs. 1 and 3). The observed orientation difference thus occurs on the microscale in bone beyond individual collagen fibrils, strongly suggesting that it is functionally relevant.

As our approach provides information on the ensemble average, unlike direct imaging techniques such as transmission electron microscopy (TEM), atomic force microscopy (AFM), ptychography, or x-ray holotomography (11), it does not allow proposing models on the single fibril level. Yet, we showed that a significant portion of the bone mineral is differently oriented with respect to the main collagen fibril orientation in the disordered zones. Several scenarios may explain these observations. First, the crystals extending outside the hole zones in collagen may have a different orientation within and outside of the collagen fibrils. A recent publication showed mineral lamellae extending between collagen fibrils (35). The collagen molecules within the fibrils are tilted by about ~5° (36) with respect to the fibril axis, meaning that the overlap zones are tilted with respect to the hole zones. As the hole zones make up most of the available space in the collagen fiber, they dominate the SAXS signal when filled with mineral. However, disorder within the crystals of the hole zones could reduce the diffraction contribution compared to the better ordered crystals in the overlap zones. This could account for the correlated occurrence of higher orientational difference in regions with lower SAXS signal but higher (002) intensity (Figs. 2 and 3). From the (002) intensity, about 30% of the mineral is not well aligned, which agrees with the SAXS/WAXS orientation difference.

A second possible scenario is the presence of another, extrafibrillar, less aligned mineral population that may be more crystalline and hence contribute stronger to WAXS. It is noteworthy that we find stronger differences in orientation in the interlamellar zones. These were described by Reznikov et al. (32) as zones of low collagen orientation between strongly aligned structural motifs, in agreement with our present SAXS tensor orientation results (Fig. 2C). Because the disordered zones have less densely packed collagen fibrils, it is likely that these zones leave room for extrafibrillar mineral, possibly in conjunction with other biomolecules. Such crystals would not be tightly associated with the collagen fibrils and would therefore not be subjected to lattice deformations from the fibrils. Remarkably, the (002) d-spacing, related to strain in the HAP crystal, is also correlated to the orientation difference (fig. S3). The average c axis of the HAP crystals was slightly shorter in the differently oriented zones, but we found a clear bimodal distribution of an intrafibrillar and extrafibrillar population, as shown in fig. S3C, as opposed to the ordered region, which features a monomodal distribution of c axis values. This supports the idea that the new disordered mineral component is uncoupled from the collagen fibrils.

A third interpretation of our results is possible, if the assumption of a fiber texture breaks down. This could be the case for transversally extended stacking of the minerals over several fibrils in the probed volume. In this case, the difference in alignment that we observe could as well be a misalignment between the mineral particles, as the SAXS signal in this case reflects the local disordering in the lateral arrangement of the mineral particles. It could be further envisaged that the asymmetry observed in the alignment of the crystal and nanostructure could be induced by the mineral particles bridging different collagen fibrils. As this could happen asymmetrically, the measured difference in the alignment could be a signature of the asymmetry of these mineral bridges. This behavior has been observed in mineralized turkey tendon (37, 38) but, to the best of our knowledge, not in human bone.

Our results have several implications for current models of bone structure and mechanics. To summarize, we revealed spatially localized differences between the orientation of the mineral particles and their respective crystalline signal by applying scattering tensor tomography with resolution on the single lamella level, a representative sampling volume over several dozens of collagen fibrils, and a large FOV. The difference in alignment was associated with the disordered zones of lamellar bone. Bone serves several functions, including mechanics, and its remarkable toughness is determined by its hierarchical structure (8–10). The lamellar structure of bone has been proposed as one such toughening mechanism (39) for which varying mechanical properties play a key role. Micropillar experiments have shown that lamellar bone in compression mostly fails by shear slip plane formation (6), in part with cracks forming at the interfaces between ordered and disordered regions of lamellar bone (40). Different mechanical properties for the ordered and disordered parts were described (41). The presence of an additional mineral fraction, differently aligned with respect to the main orientation, would provide a different means of mechanical optimization, specifically geared toward compressive loading as opposed to the more tensile-oriented load-bearing performance of mineralized collagen fibrils. We suggest that the mineral fraction described in this work might serve this purpose and thus adds an additional layer of mechanical adaptation. This observation can help in understanding the complex behavior of bone. The large change in fibril orientations between ordered and disordered zones is expected to increase fragility at this interface (40), and the extrafibrillar oriented mineral fraction observed here could provide a means to counteract this effect. In addition, water is crucial for bone mechanics, and hydration can lead to large stresses in nonmineralized collagen fibrils (4) even if the impact on the mineralized fibrils in bone is smaller. Because the mechanical properties of the mineral itself are insensitive to hydration and the differently aligned mineral may not be strongly coupled to collagen, it may not display the same anisotropic response to water as the collagen fibrils, suggesting that there may be localized, more homogenous, and less water-sensitive mechanical elements in the disordered parts of lamellar bone. Lastly, the research on biomineralization mechanisms of bone have been strongly focused on a tight interplay between collagen fibrils and the forming mineral (25, 42). Our results indicate that there might be an additional player, namely, orientation, to be considered when discussing the mechanical properties of bone. This has huge implications for the mechanical behavior of bone as well as for bone mineralization and the development of bone disorders. Fully understanding its microstructural organization is a fundamental step toward understanding the micromechanical behavior of lamellar bone and ultimately being able to predict and treat bone disease.

MATERIALS AND METHODS

Sample preparation

Two lamellar bone samples were prepared for scattering tensor tomography and scanning SAXS/WAXS, respectively. The former was taken from the trabecular part of a transiliac bone biopsy stemming from a 56-year-old female with hypoparathyroidism treated with subcutaneous injections of PTH(1–84) 100 μg a day for 6 months (43, 44). A rod was cut from the biopsy after poly(methyl methacrylate) embedding in which a region of interest of ~40 μm × 40 μm × 40 μm was identified and extracted by a combination of polishing, razor blade cutting, and FIB milling (Versa 3D, FEI, Eindhoven, The Netherlands). The sample for 2D scanning was prepared from male mid-femoral bone, also by a combination of polishing, razor blade cutting, and FIB milling to obtain a ~3-μm-thick section along the lamellae.

Small-angle scattering tensor tomography

Experiments were carried out at the ID13 beamline at the European Synchrotron Radiation Facility (ESRF), Grenoble, France, with the storage ring operated in full-hybrid mode with 200-mA initial ring current, topped up twice per day. The 13-keV x-ray beam was defined by a channel-cut Si(111) monochromator with a bandwidth of ~10⁻⁴. The beam was focused to a beam size of 700 nm × 700 nm by a pair of Pt-coated fixed elliptical curvature Kirkpatrick Baez (KB) mirrors. To increase the flux at the sample position, the beam was prefocused by a set of beryllium compound refractive lenses to the secondary KB optics. This configuration provided a flux of ~7 × 10¹¹ photons/s.

The sample was mounted on a goniometer composed of two SmarAct rotation stages, which was motorized by a three-axis linear scanning stage. A 65-mm-long helium flight tube was placed between the sample and the lead beam stop (200 μm diameter, 3 mm long) to reduce air scattering. Scattering patterns were recorded using a Dectris Eiger4M detector placed 150 mm downstream of the sample. The setup gave access to scattering vectors between 0.3 and 30 nm⁻¹. A total of 262 projections were taken at 10 β angles between 0° and 40° and α angles between 0° to 180° (β = 0°) and 0° to 360°. The rotational sampling was varied with a factor of cos(β) to provide equal angular sampling in the spherical 3D reciprocal space (28).

The sample was first pre-aligned with an overview scan with 0.002-s exposure time per frame, and the centroid of the total scattering was used to center the sample. Then, the sample was scanned with a step width of 1 μm and an exposure time of 0.01 s per point with an FOV of 100 μm × 80 μm. In total, 2,228,310 individual scattering patterns were collected. Each voxel was exposed for 3.144 s in total.

The total duration of the experiment was 24 hours, with a total exposure time of 6 hours and a motor movement and sample prealignment overhead of 18 hours. The exposure time is mostly limited by the data transfer of the detector and can be significantly reduced by the next generation of x-ray detectors.

As a bulk sample is investigated in a tomographic way, probing inside a biologically intact structural volume, artifacts induced by producing either very thin (TEM) or flat (AFM) surfaces are avoided. It is, however, important to note that due to the irradiation of the sample with x-rays, the properties might change. The samples were checked for radiation damage by comparing projections at the beginning and end of the experiment; no changes in neither the mineral structure nor the SAXS signal of the mineral could be detected, indicating that only minimal irradiation damage at a level acceptable for the purpose of this study had occurred during the experiment.

Scanning SAXS/WAXS experiments

The 2D scanning experiments on the healthy sample shown in fig. S3 were carried out at the ID13 beamline at the ESRF, Grenoble, France, with the storage ring operated in full hybrid mode with 200-mA ring current. The 15.2-keV x-ray beam was defined by a channel-cut Si(111) monochromator with a bandwidth of ~10⁻⁴. The beam was focused to a beam size of 200 nm × 200 nm by a pair of silicon compound refractive lenses (Si CRL). To increase the flux at the sample position, the beam was prefocused by a set of beryllium compound refractive lenses onto the Si CRL. This configuration delivered a flux of 5 × 10⁹ photons/s. The sample was aligned using an on-axis optical microscope and raster-scanned with 200-nm steps through the x-ray beam by a piezo-actuated xyz stage, with an exposure time of 0.2 s per point. A helium-flushed flight tube was used to reduce air scattering, and a 200-μm-diameter lead beam stop gave access to scattering vectors from 0.25 to 35 nm⁻¹. Scattered radiation was detected using a Dectris Eiger4M detector, placed 132 mm downstream of the sample.

Absorption tomography

Full-field absorption tomography data were collected on the TOMCAT beamline at the Swiss Light Source, Paul Scherrer Institute, Villigen, Switzerland. The x-ray energy was selected to 21.0 keV with a fixed-exit double-crystal multilayer monochromator. Projections were collected using a setup consisting of a 5-μm-thick LuAG:Ce scintillator, a standard high-resolution microscope from Optique Peter with a UPLAPO40x lens, and a PCO.Edge 5.5 camera to obtain a pixel size of 0.16 μm × 0.16 μm. The full tomogram consisted of 1801 projections/180°, measured with an exposure of 500 ms, and was reconstructed using the GridRec algorithm with a Parzen filter and FFT/Wavelet ring removal.

Small-angle scattering tensor tomography reconstruction

The data were reduced by integration in 16 azimuthal and 2000 radial bins. For the reconstruction of the SAXS signal, the q range from 0.3 to 0.5 nm⁻¹ was selected, and for WAXS, the q range from 18.1 to 18.3 nm⁻¹ [the HAP (002) reflection] was selected. The data were normalized on the basis of the air scattering surrounding the sample, and projections were aligned on the basis of their total SAXS scattering intensity. The SAXS signal was reconstructed as an equatorial ring in the 3D reciprocal space representation, whereas the WAXS reconstruction (owing to the orthogonality of the signal) was reconstructed as a signal on the poles of the 3D reciprocal space representation. Because of this reconstruction scheme, the dot product 1 is co-alignment.

A gradient-based optimization algorithm was used for reconstruction. The exact definition of the error metric and the optimization parameters are described elsewhere (28).

SAXS tensor tomography, as presented by Liebi et al. (26), ignores the curvature of the Ewald sphere. For WAXS, this is no longer a valid assumption; for this case, the curvature of the Ewald sphere is taken into account as an angular offset of the polar angle, in the experiment coordinates, at which the reciprocal space map is evaluated, namely, θ_det

$${\mathrm{\theta }}_{\text{det}}=\frac{\mathrm{\pi }}{2}+\mathrm{\theta }$$

where θ is the half scattering angle of the sample, directly derived from Bragg’s law as

$$\mathrm{\theta }={\text{sin}}^{-1}\left(\frac{\mathit{q}\mathrm{\lambda }}{4\mathrm{\pi }}\right)$$

where q is the scattering vector and λ is the wavelength of the incident beam.

The reconstructions were carried out with an optimized code presented by Liebi et al. (28), implemented in Matlab2018a and executed on a standard CPU server with 28 cores. The code took about 12 hours to complete a full optimization.

The orientation of the azimuthal intensity profiles from the measured 2D scattering patterns was determined by fitting a cosine with an added background, spaced by 180° to the data (45). The radial peak position was determined by fitting a Gaussian to the selected peak. An interactively defined grouping mask based on the misorientation was applied to calculate statistical parameters and the distribution of the d-spacing in the ordered and disordered zones.

SUPPLEMENTARY MATERIALS

Supplementary material for this article is available at http://advances.sciencemag.org/cgi/content/full/6/24/eaba4171/DC1

View/request a protocol for this paper from Bio-protocol.