Abstract
Although shown to have a great utility for a wide range of neuroscientific and clinical applications, diffusion-weighted magnetic resonance imaging (dMRI) faces a major challenge of low signal-to-noise ratio (SNR), especially when pushing the spatial resolution for improved delineation of brain’s fine structure or increasing the diffusion weighting for increased angular contrast or both. Here, we introduce a comprehensive denoising framework for denoising magnitude dMRI. The framework synergistically combines the variance stabilizing transform (VST) with optimal singular value manipulation. The purpose of VST is to transform the Rician data to Gaussian-like data so that an asymptotically optimal singular value manipulation strategy tailored for Gaussian data can be used. The output of the framework is the estimated underlying diffusion signal for each voxel in the image domain. The usefulness of the proposed framework for denoising magnitude dMRI is demonstrated using both simulation and real-data experiments. Our results show that the proposed denoising framework can significantly improve SNR across the entire brain, leading to substantially enhanced performances for estimating diffusion tensor related indices and for resolving crossing fibers when compared to another competing method. More encouragingly, the proposed method when used to denoise a single average of 7 Tesla Human Connectome Project-style diffusion acquisition provided comparable performances relative to those achievable with ten averages for resolving multiple fiber populations across the brain. As such, the proposed denoising method is expected to have a great utility for high-quality, high-resolution whole-brain dMRI, desirable for many neuroscientific and clinical applications.
Keywords: Denoising, Variance stabilizing transformation, Singular value decomposition, Simultaneous multi-slice, Diffusion MRI, High field MRI, Human connectome project
1. Introduction
Diffusion-weighted magnetic resonance imaging (dMRI) (Le Bihan et al., 1986, 1988) provides a unique, non-invasive means for the in-vivo mapping of the brain’s microstructure (Basser and Pierpaoli, 1996), tractography (Basser et al., 2000; Wedeen et al., 2012; Xue et al., 1999), and connectome (Craddock et al., 2013; Harms et al., 2018; Sporns et al., 2005; Van Essen et al., 2013). In its standard form, dMRI utilizes a pulsed-gradient, spin-echo sequence (Tanner and Stejskal, 1968) for data acquisition in which MR signals are sensitized to the diffusion of water molecules along different directions in biologic tissues. Since the multidimensional pattern of water diffusion is reflective of the surrounding microscopic environment, the dMRI signals carry the information that can be used to infer the microstructural and connective features of the biologic tissues. Although shown to have a great utility for a wide range of neuroscientific (Behrens et al., 2003a; Bullmore and Sporns, 2009; Catani et al., 2002; Snook et al., 2007; Thiebaut de Schotten et al., 2011) and clinical (Hugg et al., 1999; Krabbe et al., 1997; Lutsep et al., 1997; Werring et al., 1999) applications, dMRI faces various challenges (Jones and Cercignani, 2010; Tournier et al., 2011).
A major challenge for dMRI is the intrinsically low signal-to-noise ratio (SNR), especially when pushing the spatial resolution or increasing the diffusion weighting or both. It has been shown that dMRI with higher spatial resolutions can help improve the delineation of brain’s fine structure (McNab et al., 2013; Miller et al., 2011; Sotiropoulos et al., 2016; Uǧurbil et al., 2013). The use of higher diffusion weightings (i.e., higher b-values) for dMRI acquisition can help increase the angular contrast (Fan et al., 2014; Frank, 2001; Jensen et al., 2005), promoting the estimation of fiber crossing (Behrens et al., 2007; Descoteaux et al., 2009; Fan et al., 2016). However, increasing spatial resolutions and/or diffusion weightings will lead to decreased SNR, rendering the quantitative analysis of diffusion unreliable (Dietrich et al., 2001; Huang et al., 2004; Jones and Basser, 2004; Lori et al., 2002) and making the interpretation of the quantitative results difficult (Jones et al., 2013). The SNR can be increased by averaging. The averaging can be performed during image reconstruction (Eichner et al., 2015) or through diffusion model fitting, that is, to fit the model to more data measurements (or repetitions), which is shown to also help reduce the negative impact of noise on parameter estimations (Behrens et al., 2007; Jones, 2004). However, averaging usually demands prolonged scan time, limiting its utility in practice given the time constraint associated with dMRI acquisition. Therefore, it is more desirable to use a postprocessing method such as denoising that can improve the SNR without imposing an increase in scan time.
To date, a large variety of methods have been proposed for denoising of dMRI. Some methods are devised to minimize the effect of noise on diffusion parameter mapping by either incorporating an appropriate noise model during (Clarke et al., 2008; Fillard et al., 2007) or filtering the results after (Chen and Hsu, 2005; Coulon et al., 2004; Goh et al., 2011) the parameter estimation process. Meanwhile, many denoising methods are introduced to filter the diffusion images prior to any diffusion parameter estimation. These methods have been developed using algorithms based on nonlinear smoothing (Becker et al., 2014; Ding et al., 2005; Duits and Franken, 2011; Parker et al., 2000), non-local means (Manjon et al., 2010; Wiest-Daessle et al., 2008), wavelet transform (Nowak, 1999; Wirestam et al., 2006), Principle Component Analysis (PCA) (Bydder and Du, 2006; Manjon et al., 2013), maximum a posteriori formulation (Basu et al., 2006; Lam et al., 2014), LMMSE estimation (Aja-Fernandez et al., 2008), sparsity (Patel et al., 2011), regularized joint reconstruction in k-space (Haldar et al., 2013), higher order singular value decomposition (Rajwade et al., 2013; Zhang et al., 2017) and many others. Most notably, image denoising methods based on PCA (which can be viewed as a special case of a general low-rank model based denoising framework (Lam et al., 2012)) have recently gained increasing popularity in a large part because they leverage the data redundancy inherent to diffusion acquisition (Tristan-Vega and Aja-Fernandez, 2010). A PCA-based denoising method typically accomplishes the task of denoising by involving three steps: 1) perform the singular value decomposition (SVD) of the noisy data to obtain a principle component basis and associated singular values, 2) manipulate the singular values to minimize the impact of noise, and 3) reconstruct the denoised data by combining the original principle component basis with the manipulated singular values. The denoising performance of a PCA-based method is highly dependent on how the singular values are manipulated in step 2).
One simple yet effective way to manipulate singular values is by thresholding, i.e., nullifying all of the singular values less than a threshold. Thresholding is motivated by the fact that the principle components associated with the smallest singular values arise from noise contamination and the signal in the redundant data is only contained in a few principle components associated with the highest singular values. The use of a PCA-based approach for denoising of dMRI was pioneered by Manjon et al. (2013), who proposed a local PCA (LPCA) method which works by locally thresholding the singular values (i.e., thresholding the singular values obtained from the SVD of local patches). Although shown to outperform other non-PCA-based approaches when used to denoise magnitude diffusion images, the LPCA method requires the threshold to be empirically determined in order to account for the Rician bias (Gudbjartsson and Patz, 1995; Henkelman, 1985). Later, Veraart et al. (2016b) continued to introduce a Marchenko-Pastur (MP)-distribution-based PCA (MPPCA) method, in which the local thresholding of singular values is automatically determined by utilizing the knowledge that the eigenvalue spectrum (in its asymptotic limit) of a noise covariance matrix follows a universal Marchenko-Pastur distribution (Marčenko and Pastur, 1967). Despite that the MP distribution in theory is only applicable to Gaussian noises (Donoho et al., 2018), the use of MPPCA to denoise magnitude diffusion images where the noise are non-Gaussian (Constantinides et al., 1997; Dietrich et al., 2008; Gudbjartsson and Patz, 1995; Henkelman, 1985) is shown capable of only removing the variances that arise from the thermal noise, thereby providing a better performance of preserving fine structures in the images than using other existing methods. However, as will be shown later in this article, the use of MPPCA for denoising magnitude diffusion images will become less effective when SNR is so low (e.g., SNR < 3) that the data are far from being Gaussian-distributed (Gudbjartsson and Patz, 1995; Henkelman, 1985).
When the data to be denoised are Gaussian-distributed, it actually becomes straightforward to implement a PCA-based method with optimal singular value manipulation, thanks to the advances made in the field of matrix recovery (Cai et al., 2010; Eckart and Young, 1936). In the field of matrix recovery, great strides have been made to recover the underlying noise-free signal matrices from noisy data by developing optimal strategies for singular value manipulation. These strategies involve using analytically formulated algorithms that define such nonlinear manipulations of the singular values as optimal thresholding (Gavish and Donoho, 2014) and optimal shrinkage (Gavish and Donoho, 2017). However, the direct use of these optimal strategies to denoise magnitude diffusion images is not straightforward due to the data being non-Gaussian.
One way to capitalize on the optimal singular value manipulation strategies when denoising magnitude diffusion images is by variance stabilizing transformation (VST). The idea of using VST to preprocess the non-Gaussian data that have signal-dependent variances can date back to early 2000 (Huber et al., 2002; Rocke and Durbin, 2003) when researchers in the field of gene expression attempted to stabilize (or make constant) the variance of the microarray data so that a standard statistic method tailored for Gaussian data can be applied for data analysis. Later, Foi (2011) introduced this idea to the field of MRI and took the effort to derive the recipe of VST to transform Rician-distributed MRI data in a way that stabilizes the data variance to unity. Most recently, Zhang et al. (2017) have adopted this VST approach when proposing a two-stage denoising method based on the higher order SVD (HOSVD) (De Lathauwer et al., 2000; Rajwade et al., 2013). With the help of VST, the authors were able to demonstrate that their HOSVD-based method outperformed other competing methods when used to denoise magnitude diffusion images. However, like the LPCA approach (Manjon et al., 2013), the HOSVD-based denoising method had to rely on exhaustive search to empirically determine the thresholding of the singular values associated with the HOSVD.
Here, we introduce a comprehensive denoising framework for denoising magnitude dMRI. The framework is built based on the variance stabilizing transformation (Foi, 2011) that effectively transforms the Rician data to Gaussian-like data with the variance being stabilized to around unity. The framework accommodates the use of any standard denoising method optimized for denoising Gaussian data and therefore does not require any exhaustive search to be conducted to determine how to manipulate the singular values. More importantly, the framework is implemented in a patch-based fashion (Katkovnik et al., 2010), improving the denoising performance and allowing the estimation of spatially varying noise. The output of the framework is the estimated underlying diffusion signal for each voxel in the image domain. The usefulness of the proposed framework for denoising magnitude diffusion is demonstrated using both simulation and real-data experiments. The simulation experiment utilized synthetic diffusion-weighted images of a brain-like phantom (Maier-Hein et al., 2017a; Neher et al., 2014b) simulated by using Fiberfox (Maier-Hein et al., 2017a; Neher et al., 2014b), whereas the real-data experiment acquired in-vivo whole brain diffusion data following the 7 Tesla (7T) Human Connectome Project (HCP) diffusion protocol (Vu et al., 2015). Our results for both simulation and real-data experiments show that the proposed denoising framework can significantly improve SNR across the entire brain, leading to substantially enhanced performances for estimating diffusion tensor related indices and for resolving crossing fibers when compared to the noisy diffusion data. Further, the proposed denoising framework is shown to outperform the MPPCA approach, which serves to represent the state of the art. More encouragingly, the use of the proposed method for denoising a single average of in-vivo whole brain diffusion acquisition is found to provide comparable performances relative to those achievable with fitting the diffusion model to ten averages when resolving multiple fiber populations across the brain.
2. A variance-stabilizing-transformation-based denoising framework
At the heart of the proposed denoising framework (Fig. 1) are sequential applications of four operation modules: 1) noise estimation, 2) variance stabilizing transformation (VST), 3) denoising, and 4) exact unbiased inverse VST (EUIVST). The goal of the first module is to estimate the underlying Gaussian noise level (i.e. the standard deviation (std) of the Gaussian noise corrupting the data), which is required as priori knowledge by the subsequent VST and EUIVST modules. The noise estimation module can be implemented by incorporating any noise estimation method (such as those based on VST (Foi, 2011), MPPCA (Veraart et al., 2016a) and median absolute deviation (Coupe et al., 2010)) that can estimate the noise level directly from the Rician data.
Fig. 1.
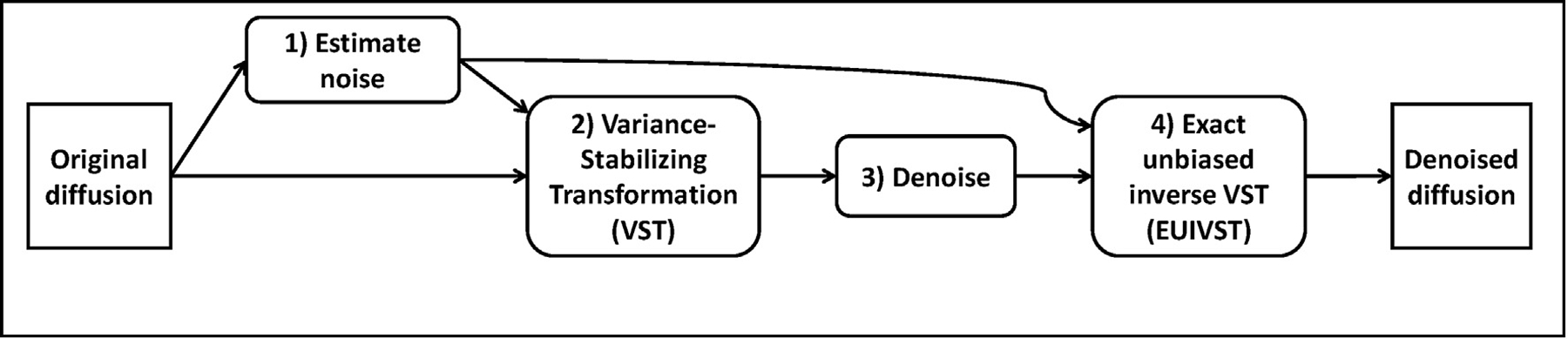
Flowchart of the proposed denoising framework. At the heart of this framework are sequential applications of four operation modules: 1) noise estimation, 2) variance stabilizing transformations (VST), 3) denoising and 4) exact unbiased inverse VST (EUIVST). The purpose of noise estimation is to estimate directly from the Rician distributed diffusion magnitude data the standard deviation (std) of the Gaussian noise (or noise level) corrupting the data, since both VST and EUIVST require priori knowledge on the noise level. The denoising module aims to reduce the noise from the transformed data by using a standard denoising algorithm. Implementation of all of these operation modules are patch-based for improved performance. The output images of this framework are estimates of the underlying noise-free diffusion signals.
The purpose of the second module is to stabilize the std of the data by transforming the Rician data through VST, such that the transformed data have a std confined to about 1. The VST is fulfilled by defining a nonlinear function, f(z), to map a Rican random variable z to new values. In his seminal paper (Foi, 2011), Foi presented two such nonlinear functions, “VST A″ and “VST B″, both obtained by solving an optimization problem formulated to have a main term ensuring accuracy of variance stabilization together with a few penalty terms enabling properties needed for practical use of the nonlinear function. The calculations of the “VST A″ and “VST B″ functions differ in how those penalty terms are incorporated in the optimization. Although leading to different transformed data, both functions appear effective for variance stabilization, giving rise to a std (of the transformed data) closer to 1 than that of the original Rician data, especially for extremely low SNR (i.e., SNR < 2) (Fig. S1). After VST, the transformed data behave more like Gaussian distributed and can be denoised using any standard denoising algorithm.
The third module in the denoising framework aims to minimize the negative impact of the noise on the transformed data by using any standard denoising algorithm tailored for reducing the noise variance in Gaussian data. Possible standard denoising algorithms include 1) truncated singular value decomposition (TSVD) (Eckart and Young, 1936), 2) soft thresholding of singular values (Cai et al., 2010), 3) hard thresholding of singular values (Gavish and Donoho, 2014), and 4) optimal shrinkage of singular values (Gavish and Donoho, 2017). While all of these standard algorithms follow a same multi-step procedure (Fig. S2) to estimate the signal matrix through manipulating the singular values of the noise-corrupted data matrix, they are different from each other in how they manipulate the singular values (Fig. S3). After the transformed data are denoised, the denoised data are further processed to produce the final denoised images.
The goal of the fourth and final module in the denoising framework is to produce the final denoised diffusion images by transforming the denoised data (obtained in the previous step) through EUIVST (Foi, 2011). The purpose of the EUIVST is to obtain a maximum likelihood estimate of the underlying noise-free MR signal by combining inverse VST with Rician bias elimination. Like VST, EUIVST is also fulfilled by defining a nonlinear function, vf(D), to map the denoised data, D, into new values. We note that the nonlinear function utilized for EUIVST must be coupled with the nonlinear function that has been utilized for VST. Therefore, there are two nonlinear functions (Fig. S4) for EUIVST, corresponding to the two functions (i.e., “VST A″ and “VST B″) that can be used for VST.
An important property of the proposed denoising framework is that each of the four operation modules aforementioned is implemented with a patch-based approach for enhanced performance (Katkovnik et al., 2010). The patch-based approach aims to estimate the parameter of interest (e.g., the noise std and the voxel value) at each voxel by aggregating multiple estimates of the parameter that have been obtained from a group of patches. Specifically, the patch-based implementation of each operation module can consist of three steps. The first step is to define a series of 4D patches of size x by y by z by t by sliding a 3D kernel (of size x by y by z) across the image field of view (FOV). Here x, y, and z denote the patch size (in voxels) in the three spatial dimensions, and t the patch size in the time dimension (which is usually set to the number of image volumes). The second step is to use each patch to obtain an estimate of the parameter for every voxel that resides within the patch, resulting in multiple estimates of the parameter at each voxel. The third and final step in the patch-based implementation is to aggregate the multiple estimates at each voxel to obtain final estimates of the parameter.
Mathematically, the final estimate, , of the parameter for a voxel at location, j, can be given by:
| (1) |
where K is the number of patches containing the voxel, the estimate of the parameter for the voxel obtained from the k-th patch, and wk the weight of the k-th patch. We note that the definition of the patch weights and the range of the voxel locations depend on which module (or which parameter) is under consideration. For all operation modules except for the denoising one, the weight can simply be set to unity for every patch, corresponding to taking the average of the multiple estimates of the parameter as the final estimate. However, for the denoising module, it is desirable to obtain the final estimate of the parameter by calculating a weighted average of the multiple estimates. This can be done by defining a weight for each patch in a way that reflects the quality of the corresponding estimates. Further, the voxel location ranges from 1 to xyz in steps of 1 (i.e., j = 1, 2, …,xyz) for noise estimation aimed at estimating the noise std for each voxel only in space, whereas it spans from 1 to xyzt in steps of 1 (i.e., j = 1, 2, …,xyzt) for all of the other modules that aim to estimate the voxel value for each voxel not only in space but also in time.
3. Methods
We implemented the proposed VST-based denoising method in MATLAB (The Mathworks Inc., Natick, MA). The source code is publically available at https://github.com/XiaodongMa-MRI/Denoising/releases. To demonstrate the usefulness of the proposed method, we performed both simulation and real-data experiments in which the proposed method was applied to double-shell diffusion data and the results were compared to those obtained without denoising as well as those with denoising but using the MPPCA approach (Veraart et al., 2016b). For both simulation and real-data experiments, the process of MPPCA denoising was performed by using the implementation in the MRtrix3 package (www.mrtrix.org).
3.1. Simulation experiment
We started by conducting a simulation experiment to evaluate the denoising performance of the proposed method. The simulated diffusion data including several noisy double-shell diffusion imagesets were synthesized by adding Gaussian noise of various levels to a noise-free imageset. The noise-free and artifact-free imageset (Fig. 2a) was created by simulating diffusion signals across a 3D brain-like phantom using Fiberfox (Neher et al., 2014a) (www.mitk.org33). The 3D brain-like phantom which was initially designed for the ISMRM tractography competition (tractometer.org/ismrm_2015_challenge) (Maier-Hein et al., 2017b) was synthesized by manually extracting 25 white matter fiber bundles from the tractography result for a high-quality 3T HCP dataset and by modeling four brain compartments (including intra- and inter-axonal white matter, gray matter and CSF). The diffusion model and relevant parameters (such as diffusivity and T2 relaxation values) assigned to each brain compartment are listed in Table S1 in the supporting materials. The simulation was run at 2-mm isotropic resolutions with a matrix size of 90×108×90, producing a total of 61 images including 30 diffusion-weighted (DW) images for b-value = 1000 s/mm2 (b1k) and 30 DW images for b2k and a single b0 image. The final noise-free imageset was formed by inserting a b0 image after every 9-th DW image, resulting in a series of 67 images including 7 b0 images interspersed between 60 DW images.
Fig. 2.
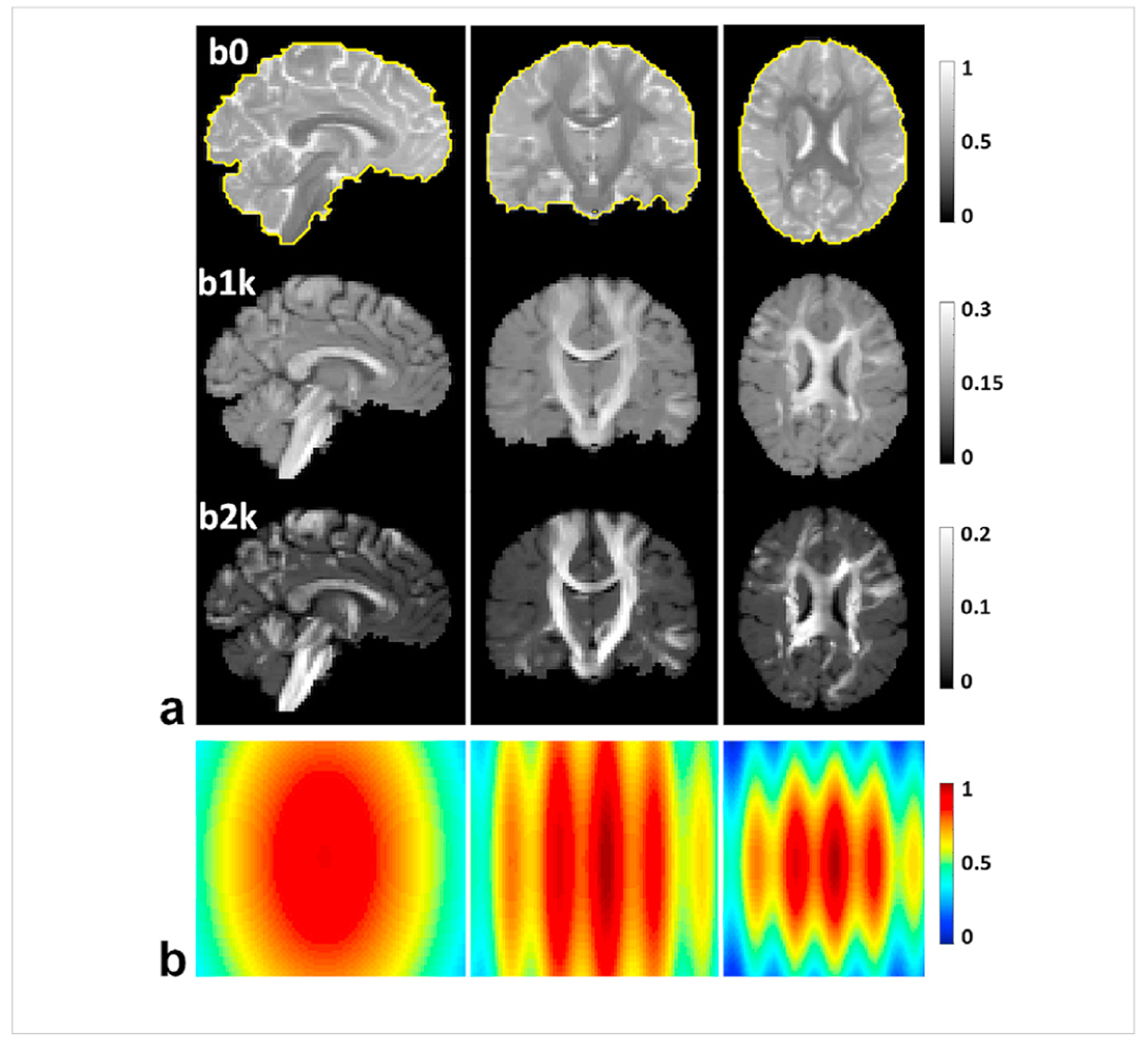
Simulation experiment: noise-free diffusion magnitude images serving as gold standard (a), alongside a 3D noise map (b) defining how the noise level (ie. the standard deviation of the Gaussian noise corrupting the data) would vary in space, displayed in axial, sagittal and coronal views. Shown are b0 images (overlaid with the brain mask as indicated by the yellow curves), and diffusion weighted images of one representative direction with b-values = 1000 and 2000 s/mm2. The dataset consists of a total of 67 images, including 7 b0 images interspersed between 60 diffusion weighted images (with one b0 image inserted after every 9th diffusion weighted image). The double-shell diffusion weighted images were created to sample the q-space on two shells with 30 randomly distributed samples on each shell and were ordered in an interleaved manner between the two shells. The noise map (normalized to unity) was scaled according to the desired noise level before being added to the gold standard to synthesize the noisy images.
The noisy magnitude diffusion imageset for a given noise level was synthesized by adding Gaussian noise to the noise-free imageset:
| (2) |
where Inoisy(r,m) and Igt(r,m) are the m-th noisy and noise-free images, respectively, and nre(r,m) and nim(r,m) are noises added to the real and imaginary channels, respectively. The noise terms nre(r,m) and nim(r,m) were independently created, each by drawing from a zero-mean Gaussian noise model defined as where σ(r) denotes the std of the Gaussian noise at location r. In the current study, σ(r) was further given by σ(r) = aσ0 (r) where the scalar a is the noise level, and σ0(r) is a noise std map normalized to 1 and prescribed to mimic a parallel imaging application in which the noise std would vary in space. The 3D normalized noise std map σ0(r) was synthesized (Fig. 2b) with characteristics of fast variations in x, and slow variations in y and z dimensions. The noise levels considered here ranged from 1% to 10% in steps of 1%. The noise level was defined by the ratio of the maximum std of the underlying Gaussian noise divided by the maximum signal intensity of the noise-free imageset. For example, the noisy imageset with a noise level of 5% was synthesized by setting the maximum std of the underlying spatially varying Gaussian noise to 5% of the maximum signal intensity (taking place in b0 images) of the noise-free imageset.
For each noise level, we evaluated the denoising performance of the proposed method by comparing the final denoised images against the noise-free images. In particular, the difference between the denoised and the noise-free images were quantified by calculating the peak SNR (PSNR),
| (3) |
where MSE is the mean squared error measuring the deviation of the denoised images from the noise-free images. Four PSNR values were calculated, including one “overall” PSNR (calculated by considering the entire imageset) and three “b-value-dependent” PSNR values (calculated by only accounting for images with a specific b-value). The PSNR values for the proposed method were compared against those for the noisy images and for the denoised images with the MPPCA approach.
We also conducted diffusion analysis to investigate how the proposed denoising method would improve diffusion tensor imaging (DTI) and enhance the performance for estimation of fiber crossing. For DTI, the diffusion tensor model was fit to the denoised double-shell diffusion data using FSL’s dtifit routine (Jenkinson et al., 2012) to derive such diffusion metrics as mean diffusivity (MD), fractional anisotropy (FA), axial diffusivity (AD) and radial diffusivity (RD). For each diffusion metric, the root mean square error (RMSE) was evaluated to measure the deviation from the gold standard as obtained by fitting the diffusion tensor model to the noise-free imageset.
For estimation of fiber crossing, an extended ball and stick diffusion model (Behrens et al., 2003b, 2007; Jbabdi et al., 2012) was fit to the denoised double-shell diffusion data using FSL’s bedpostx routine (Behrens et al., 2007) to estimate the existence of three fiber populations (i.e., the first, the second and the third fibers). For each fiber population, diffusion metrics such as the volume fraction, orientation vector and orientation dispersion (or uncertainty) were evaluated on a voxel-by-voxel basis and were visualized in FSLeyes (https://zenodo.org/record/2630502#.XNA9×45KiUn) to have a qualitative comparison against the respective gold standard as obtained by fitting the diffusion model to the noise-free imageset.
For each fiber population, the diffusion metrics derived were also quantitatively compared against the gold standard serving as the reference. In particular, fiber orientation vectors were compared by quantifying the angular difference across the brain. The other two diffusion metrics (i.e., volume fraction and orientation dispersion) were compared through Bland-Altman (BA) analysis (Bland and Altman, 1986) based on region-specific average values. For each diffusion metric, region-specific average values were calculated based on regions of interest (ROIs) that were defined by a standard atlas. Here, two standard atlases (Fig. S10) were considered: the MNI structural atlas (Mazziotta et al., 2001) that defines nine anatomic regions across the brain and the JHU white matter atlas (Wakana et al., 2007) that labels 48 white matter tracts. More details of how Bland-Altman analysis was done can be found in the supporting materials.
In all cases, the results were compared against those obtained for the noisy images and for the denoised images using the MPPCA approach. For estimation of fiber crossing, we only considered the noise level of 4% since it led to SNR levels comparable to what was estimated for the real data acquisition (see supporting materials for more details on SNR estimation).
3.2. Real-data experiment
We also conducted real-data experiment to evaluate the denoising performance of the proposed method. This was done by acquiring 7T HCP-style diffusion images in a healthy volunteer who signed a consent form approved by the local Institutional Review Board. The volunteer was scanned on a 7T MR scanner (Siemens, Erlangen, Germany) equipped with the Siemens SC72 body gradient (70 mT/m maximum strength and 200 T/m/s maximum slew rate) and 32 receive channels. The Nova single-channel transmit 32-channel receive head coil was used for RF transmission and signal reception. For improved transmit RF field in lower brain regions, dielectric padding was employed as in the 7T HCP dMRI protocol (Vu et al., 2015).
We acquired two datasets: a single average and ten averages. The single average was obtained by acquiring the first half of the HCP 7T diffusion acquisition (Vu et al., 2015). Briefly, it consisted of a pair of diffusion runs (or acquisitions), each obtained with matched imaging parameters and the same q-space sampling. For both runs, the same double-shell q-space sampling scheme (b-values = 1000 and 2000 s/mm2) was applied to obtain 71 image volumes (including 63 DW images plus 8 interspersed b0 images), leading to a total of 142 images. For either run, whole brain diffusion images were obtained with the following imaging parameters: 1.05-mm isotropic resolution, 7000-ms repetition time (TR), 71-ms echo time (TE), 3-fold in-plane GRAPPA (iPAT3), 2-fold slice acceleration (MB2), 6/8 partial Fourier, 132 oblique axial slices, 210 × 210 mm2 field of view (FOV), ½ FOV inter-slice shift, 0.82-ms echo spacing, 1388 Hz/pixel bandwidth. To allow for correction of EPI geometric distortions in the subsequent image preprocessing, the two runs of the single average were acquired with opposed phase encoding directions, i.e., one acquired with Anterior-Posterior (AP) and the other with PA phase encoding direction. The scan time of each run was ~10 min, leading to a total scan time of 20 min for the single average. The ten averages were obtained by acquiring 10 times the single average, leading to a total of 1420 image volumes acquired in 20 runs with a total scan time of ~200 min. The ten averages dataset was used as a bronze standard serving as the reference in the subsequent diffusion analysis. Note that all images of the ten averages dataset were treated as independent volumes with no prior averaging in the image domain when used to fit a diffusion model.
All original diffusion images were reconstructed online using an integrated image reconstruction program. The image reconstruction program first reconstructed multi-channel images of individual receive channels using the split slice GRAPPA algorithm (Cauley et al., 2014) to minimize inter-slice signal leakage, and then combined the reconstructed multi-channel images via the SENSE-1 method (Sotiropoulos et al., 2013) to form the final Rician image with a reduced noise floor. The final images saved in the DICOM format were exported for use in subsequent data processing and analysis.
We denoised the single average dataset at the run level, i.e., the two runs (of 71 image volumes each) were denoised separately. This was to improve the denoising performance by reducing the negative impact of the presence of large opposed distortions when denoising two runs together. Further, the background voxels were not included in the denoising process for improved computation efficiency.
The denoised single average dataset were then preprocessed by following the HCP pipelines (Glasser et al., 2013) to correct for head motion and geometric EPI distortions arising from susceptibility and eddy currents. The correction was achieved by combining FSL’s topup (Andersson et al., 2003) and eddy (Andersson and Sotiropoulos, 2016) routines. Further, the corrected diffusion images were registered to the volunteer’s native structural volume space by using the boundary-based registration method (Greve and Fischl, 2009; Jenkinson et al., 2002). The volunteer’s native structural volume space was defined by acquiring high-resolution structural T1-weighted (T1w) and T2w images as in our previous studies (Wu et al., 2018, 2019). Briefly, both T1w and T2w images were acquired at 0.7-mm isotropic resolutions with matched FOV. The T1w image was obtained with an MPRAGE sequence (Mugler and Brookeman, 1990), whereas the T2w image with a variable flip angle 3D turbo spin echo sequence (Mugler et al., 2000).
Using the preprocessed denoised single average dataset, we performed diffusion analysis to derive relevant diffusion metrics related to DTI and estimation of fiber crossing as in the simulation experiment. For angular difference evaluation and BA analysis, the results were compared against those derived from the ten averages dataset serving as the reference. In all cases, the diffusion analysis results for the single average without denoising and denoised with the MPPCA approach were also obtained for comparison.
3.3. Implementation of the proposed denoising method
We conducted a pilot study (see supporting materials) to optimize the implementation of the proposed denoising method. The purpose of this optimization was to determine what method or algorithm to use to implement each of the four operation modules involved in the denoising pipeline. For each module, different methods were compared and the one providing best performance was chosen. The result of this optimization was a finalized implementation utilized to denoise the double-shell diffusion data for both simulation and real-data experiments. The specific realization of each module in the finalized implementation was as follows.
The noise estimation module opted for the VST-based method with the “VST B” function since it appeared constantly effective in estimating the std of the underlying Gaussian noise (Fig. S6) in comparison to other noise estimation methods considered here including the MPPCA approach and the VST-based method with “VST A″ function. The VST module employed the “VST B″ function for transforming noisy diffusion data because it turned out to outperform the “VST A″ function in variance stabilization (Fig. S7). For consistency, the EUIVST module also utilized the “VST B″ function to estimate the underlying diffusion signal. The denoising module incorporated the standard singular value shrinkage algorithm (Gavish and Donoho, 2017) since it appeared to outperform any other standard denoising algorithm in reducing the negative impact of noise variance on the final denoised images (Fig. S8). Here, the singular value shrinkage was optimized for a cost function formed in the Frobenius matrix norm and the priori knowledge on the noise std after VST (as needed for data scaling) was estimated using a patch-based extension to the MPPCA method.
We also determined how best to estimate the underlying Gaussian noise given a series of double-shell diffusion magnitude images. Using the simulated data, we compared four strategies: 1) All: use the entire image set including b0 images; 2) b1k þ b2k: only use DW images with non-zero b-values; 3) b1k: only use DW images with b-value = 1000 s/mm2; 4) b2k: only use DW images with b-value = 2000 s/mm2. The third strategy using only b1k images appeared to outperform other strategies (Fig. S9) and therefore was chosen in both simulation and real-data experiments to estimate the underlying Gaussian noise level for use in subsequent VST and EUIVST modules.
Further, the patch-based implementation of each operation module involved using patches defined by a sliding kernel of size 5 × 5 × 5 (i.e., x = y = z = 5). For the noise estimation module, the noise std in each patch was assumed constant and was estimated through VST-based iterations (Foi, 2011). Each iteration involved two steps: 1) filter the voxel values in the patch using a high-pass convolutional kernel (Abdelnour and Selesnick, 2005) and 2) calculate the median of the absolute deviations of the filtered voxel values to estimate the noise std. The result of the noise estimation module was a noise map with spatially varying noise std values across the image FOV. For both VST and EUIVST modules, the data transformations in a patch were performed using the average noise std in the patch. For the denoising module, each patch was converted into a 2D data matrix of size M by N (where M = t and N = xyz) by concatenating the spatial dimensions before being denoised with a standard denoising algorithm. As a result, the aspect ratio, , (i.e., the only parameter defining the singular value manipulation function in a standard denoising algorithm (Fig. S3)) was 0.536 in the simulation experiment and 0.568 in the real-data experiment.
Moreover, the patch weights utilized to aggregate multiple estimates of parameters at each voxel were set to 1 for all modules except for the denoising module. For the denoising module, the weight for the k-th patch was defined by
| (4) |
where Rk is the rank (or the number of non-zero singular values) of the denoised data matrix (i.e., matrix in Fig. S2). This was to assign a higher weight to those estimates obtained from a denoised data matrix of a lower rank. Such weight definition was used in previous studies (Manjon et al., 2012, 2013; Zhang et al., 2017) to improve denoising performance and reduce Gibbs artifacts.
We implemented the proposed denoising method by integrating and modifying the source codes generously shared by authors of previous works (Foi, 2011; Gavish and Donoho, 2014, 2017; Lam et al., 2012; Veraart et al., 2016a; Zhang et al., 2017). In particular, the patch-based implementation of each operation module adapted the code shared by Zhang et al. (2017) (https://github.com/XinyuanZhang719/gl-hosvd). Along with both VST and EUIVST modules, the noise estimation module when using a VST-based noise estimator was built by incorporating the code shared by Foi (2011) (http://www.cs.tut.fi/~foi/RiceOptVST/). The denoising module using a standard denoising algorithm was fulfilled by integrating the code shared by Gavish and Donoho (Gavish and Donoho, 2014, 2017) (http://purl.stanford.edu/kv623gt2817). Further, the proposed denoising method was implemented to only process the voxels in a reduced FOV for improved computational efficiency. The reduced FOV was determined by creating a brain mask through optimum thresholding (Ridgway et al., 2009) to exclude the background voxels.
4. Results
4.1. Simulation experiment
The use of the proposed denoising method to denoise the noisy diffusion data largely enhanced image quality and outperformed the MPPCA approach (Figs. 3 and 4). Particularly, it improved both overall and b-value-dependent PSNR values across the noise levels investigated in this study (Fig. 3). The improvement in all PSNR values increased with increasing noise levels, with the greatest improvement observed at the highest noise level of 10%. At this high noise level, the overall PSNR increased by as high as ~52% (33.3 vs 21.9 dB) relative to the noisy data and by as high as ~28% (33.3 vs 26.0 dB) relative to the MPPCA approach. Similar results were observed for b-value-dependent PSNR values, with the greatest improvement in PSNR obtained for b2k images. The PSNR for b2k images at 10% noise level increased by as high as ~52% (32.6 vs 21.5 dB) relative to the noisy data and by as high as ~35% (32.6 vs 24.1 dB) relative to the MPPCA approach.
Fig. 3.
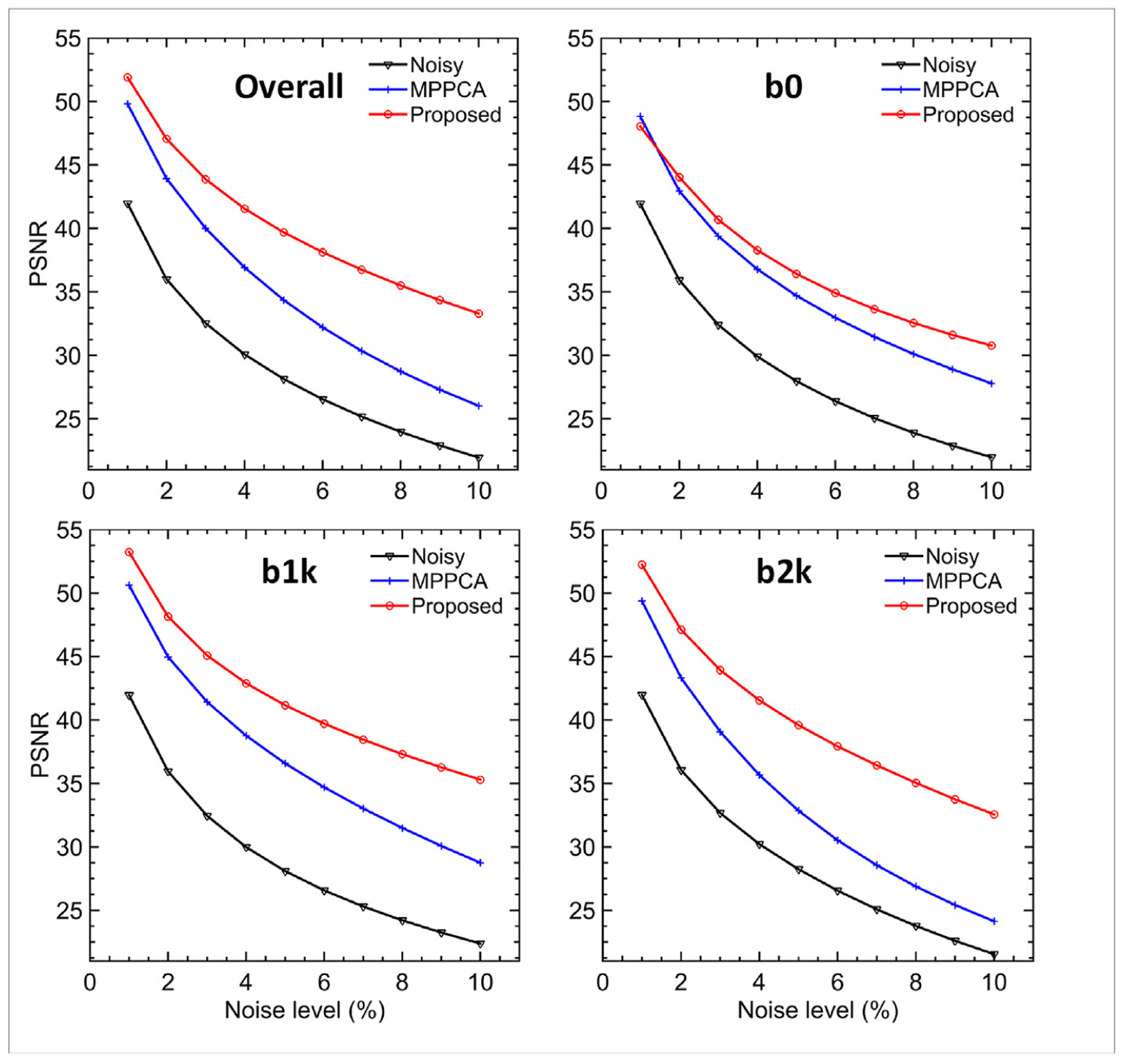
Simulation experiment: comparing denoising performances of the proposed method vs the MPPCA approach in terms of overall and b-value-dependent peak SNR (PSNR) in dB as a function of the noise level. The overall PSNR was calculated by considering whole-brain images including b0 and diffusion weighted images, whereas the b-value-dependent PSNR by only accounting for images of the specified b-value (e.g., b0 PSNR was evaluated by only considering b0 images). Note that the use of the proposed denoising method outperformed the MPPCA approach and substantially improved the image quality (especially for diffusion weighted images).
Fig. 4.
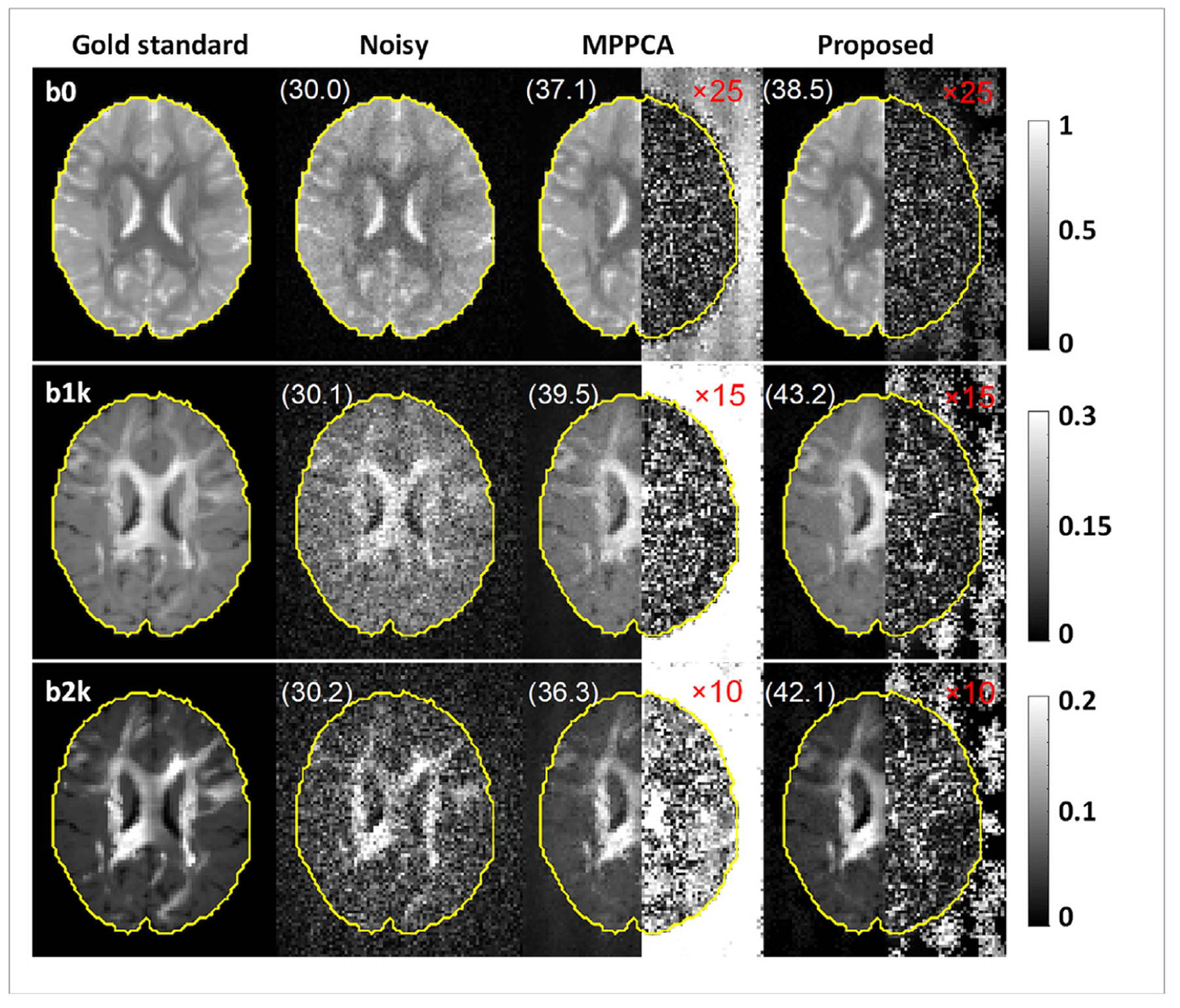
Simulation experiment: example denoised images at 4% noise level obtained using the proposed method vs the MPPCA approach, alongside the corresponding gold standard and noisy images for comparison. The right half of each denoised image shows the corresponding absolute difference image relative to the gold standard (amplified in magnitude by 25-fold for b0, 15-fold for b1k and 10-fold for b2k images for improved visualization), the numbers reported are b-value-dependent PSNR in dB, and the brain mask (yellow) defines the region of interest for all PSNR calculations. Note that the use of the proposed denoising method outperformed the MPPCA approach (especially for diffusion weighted images), producing images that were much closer to the gold standard.
Visual comparison of denoised images against the gold standard at 4% noise level (Fig. 4) further confirmed the effectiveness of the proposed method for noise reduction and revealed how the proposed method outperformed the MPPCA approach. The use of the proposed method substantially improved image quality when compared to noisy images, producing images similar to the gold standard. When compared to the MPPCA approach, the proposed method appeared more effective for noise reduction. While improving slightly the b0 images, the proposed method substantially improved DW images, increasing the PSNR values up to 43.2 dB for the b1k, and 42.1 dB for the b2k image. By contrast, the use of the MPPCA approach appeared to struggle with reducing the noise, especially for b2k images with extremely low SNR, giving rise to images far away from the gold standard as immediately identified by comparing the difference images.
The improvement in PSNR with the proposed denoising method directly translated into improvement in DTI (Fig. 5). Particularly, the use of the proposed method improved the estimation of diffusivity metrics (MD, AD and RD) and FA across the noise levels investigated in this study, with the greatest improvement mostly observed at the highest noise level of 10%. At this high noise level, the RMSE for estimation of MD, AD, RD and FA reduced by ~46%, ~24%, ~52% and ~51%, respectively, when compared to the noisy data, and by ~50%, ~43%, ~50% and ~5%, respectively, when compared to the MPPCA approach.
Fig. 5.
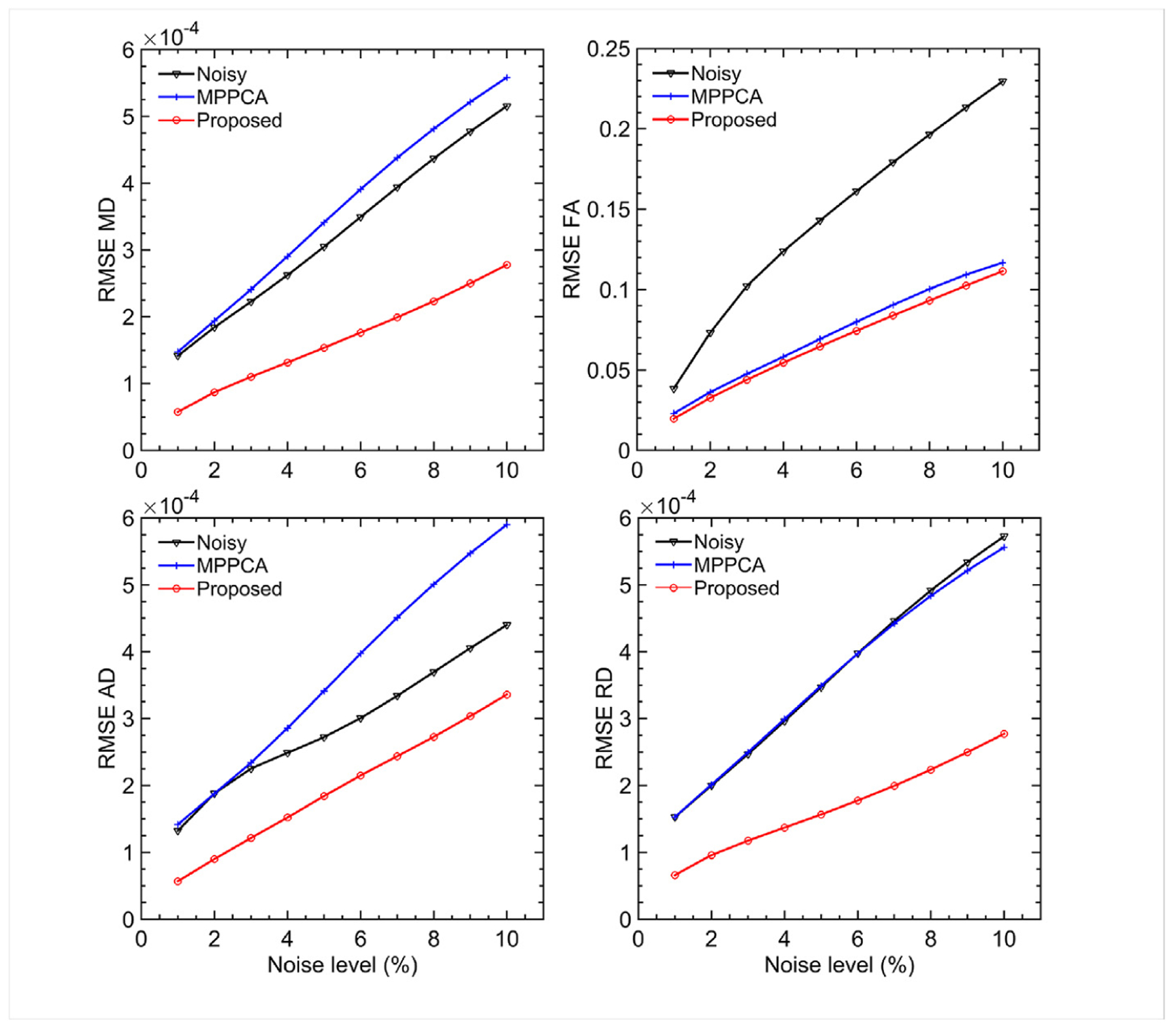
Simulation experiment: comparing denoising performances of the proposed method vs the MPPCA approach in terms of estimation of four diffusion metrics: mean diffusivity (MD), fractional anisotropy (FA), axial diffusivity (AD) and radial diffusivity (RD). The metric mapping was obtained by fitting a diffusion tensor model to the double shell diffusion data. For each case, we evaluated the respective estimation performances by calculating the root mean square error (RMSE) of the metric estimation relative to the gold standard obtained from the noise-free images, and compared to the metric estimation using the noisy images. Note that the use of the proposed denoising method substantially improved the estimation performances especially for intermediate and high noise levels (>5%), relative to the noisy images or the MPPCA approach.
Visual comparison of example diffusion metrics maps at 4% noise level (Fig. 6) further confirmed the efficacy of the proposed method for improving DTI and revealed how the proposed method outperformed the MPPCA approach. Specifically, all diffusion metrics maps (MD, AD, RD and FA) for the proposed method closely resembled the respective gold standard, preserving fine structures and tissue contrasts across the brain. By contrast, the maps for noisy images were noisy, presenting over- and under-estimation for FA and under-estimation for both MD and RD across the brain. Although appearing less noisy, the diffusivity maps (MD, AD and RD) for the MPPCA approach surprisingly exhibited even higher underestimation; the FA map however was visually comparable to that for the proposed method, with slightly increased RMSE (~0.06 vs ~0.05) when compared against the gold standard. The improvement in DTI with the proposed method was further verified by comparing the fitting errors; the whole brain average sum-of-square error for diffusion tensor fitting was 7.13 for noisy images, 0.97 for the MPPCA approach, 0.60 for the proposed method and 0.47 for the gold standard.
Fig. 6.
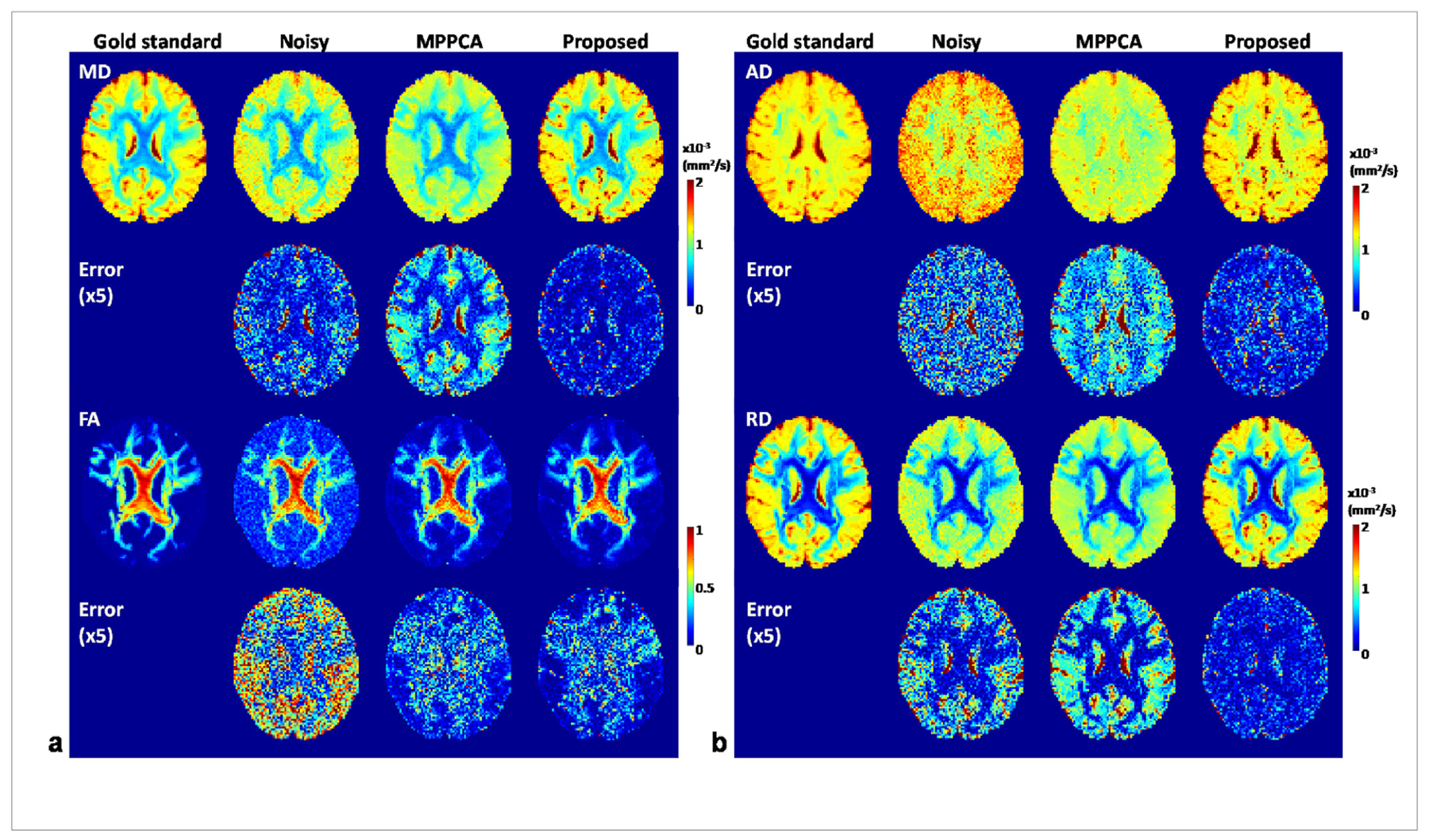
Simulation experiment: example diffusion tensor metric maps estimated from denoised images obtained at 4% noise level using the proposed method vs using the MPPCA approach, alongside the gold standard metric maps estimated from the corresponding noise-free images and those from the noisy images for comparison. The use of the proposed method largely improved the estimation of MD, AD and RD with increased values and clearer delineation of fine structures, and slightly improved estimation of FA with reduced noise.
The efficacy of the proposed denoising method was further confirmed by estimation of fiber crossing (Fig. 7). For all three fiber populations, the use of the proposed method substantially improved the estimation of volume fraction and orientation dispersion and outperformed the MPPCA approach, leading to volume fraction and dispersion maps most similar to the respective gold standard. The improvement was further quantitatively verified by examining the results of BA analysis (Fig. 8). For all three fiber populations, the use of the proposed method resulted in volume fraction and dispersion values that on average were closest to the respective gold standard. The average difference in volume fraction against the gold standard across all ROIs was reduced by ~95% (MNI atlas) and ~98% (JHU WM atlas) for first, ~85% (MNI atlas) and ~97% (JHU WM atlas) for second, and ~46% (MNI atlas) and ~57% (JHU WM atlas) for third fibers when compared to the noisy images, and by ~81% (MNI atlas) and ~95% (JHU WM atlas) for first, ~57% (MNI atlas) and ~85% (JHU WM atlas) for second, and ~34% (MNI atlas) and ~35% (JHU WM atlas) for third fibers when compared to the MPPCA approach. The average difference in dispersion across ROIs was reduced by ~97% (MNI atlas) and ~93% (JHU WM atlas) for first, ~95% (MNI atlas) and ~95% (JHU WM atlas) for second, and ~92% (MNI atlas) and ~94% (JHU WM atlas) for third fibers when compared to the noisy images, and by ~57% (MNI atlas) and ~41% (JHU WM atlas) for first, ~65% (MNI atlas) and ~61% (JHU WM atlas) for second, and ~55% (MNI atlas) and ~61% (JHU WM atlas) for third fibers when compared to the MPPCA approach.
Fig. 7.
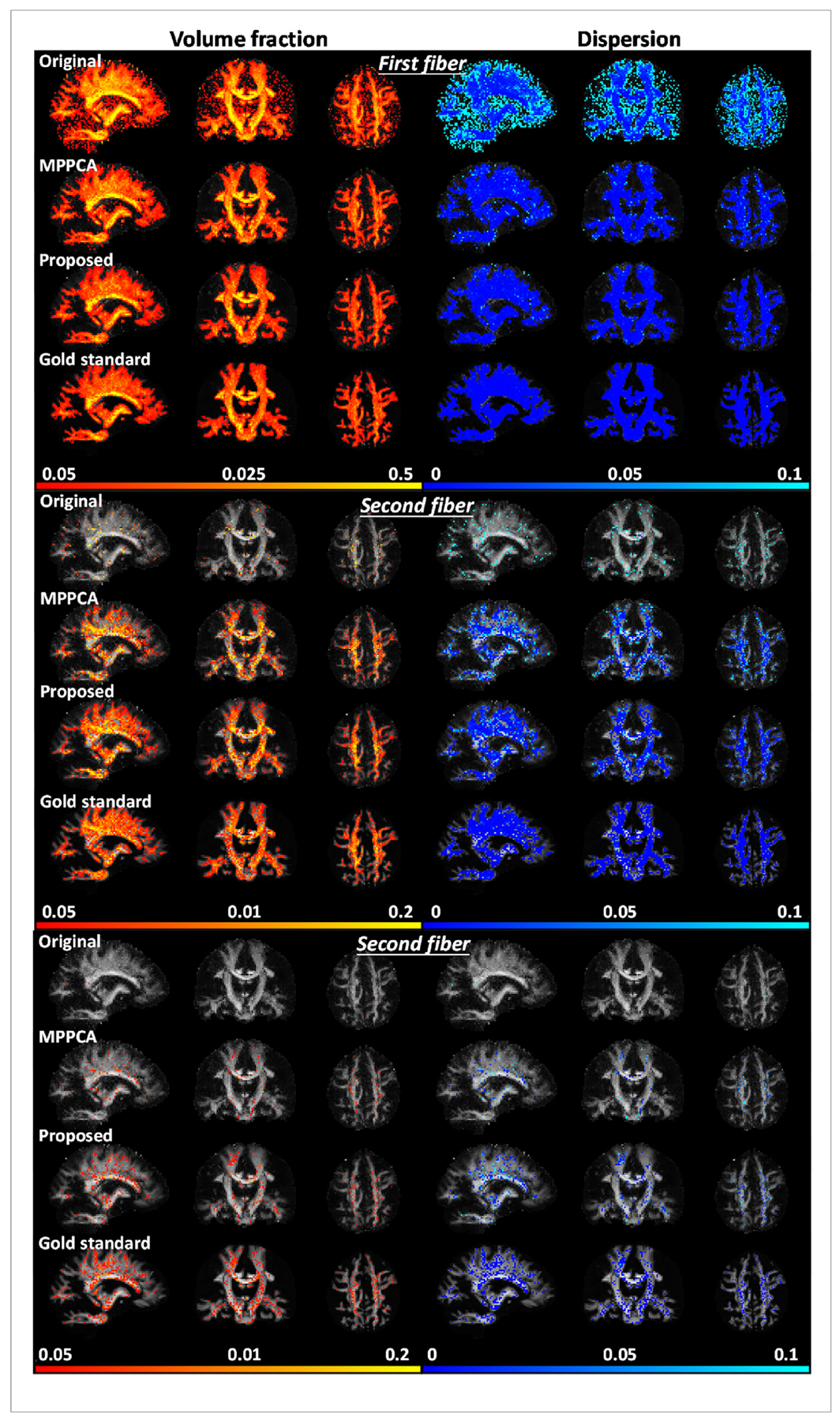
Simulation experiment: comparing performances for estimation of fiber crossing when fitting an extended ball and stick model. Shown are volume fraction and dispersion maps (shown for voxels of ≥0.05 vol fraction) for first (or principle), second and third fibers when estimated using noise-free images (Gold standard), noisy images (Original), denoised images with MPPCA (MPPCA) or the proposed method (Proposed). Results of noise level of 4% were shown for demonstration.
Fig. 8.
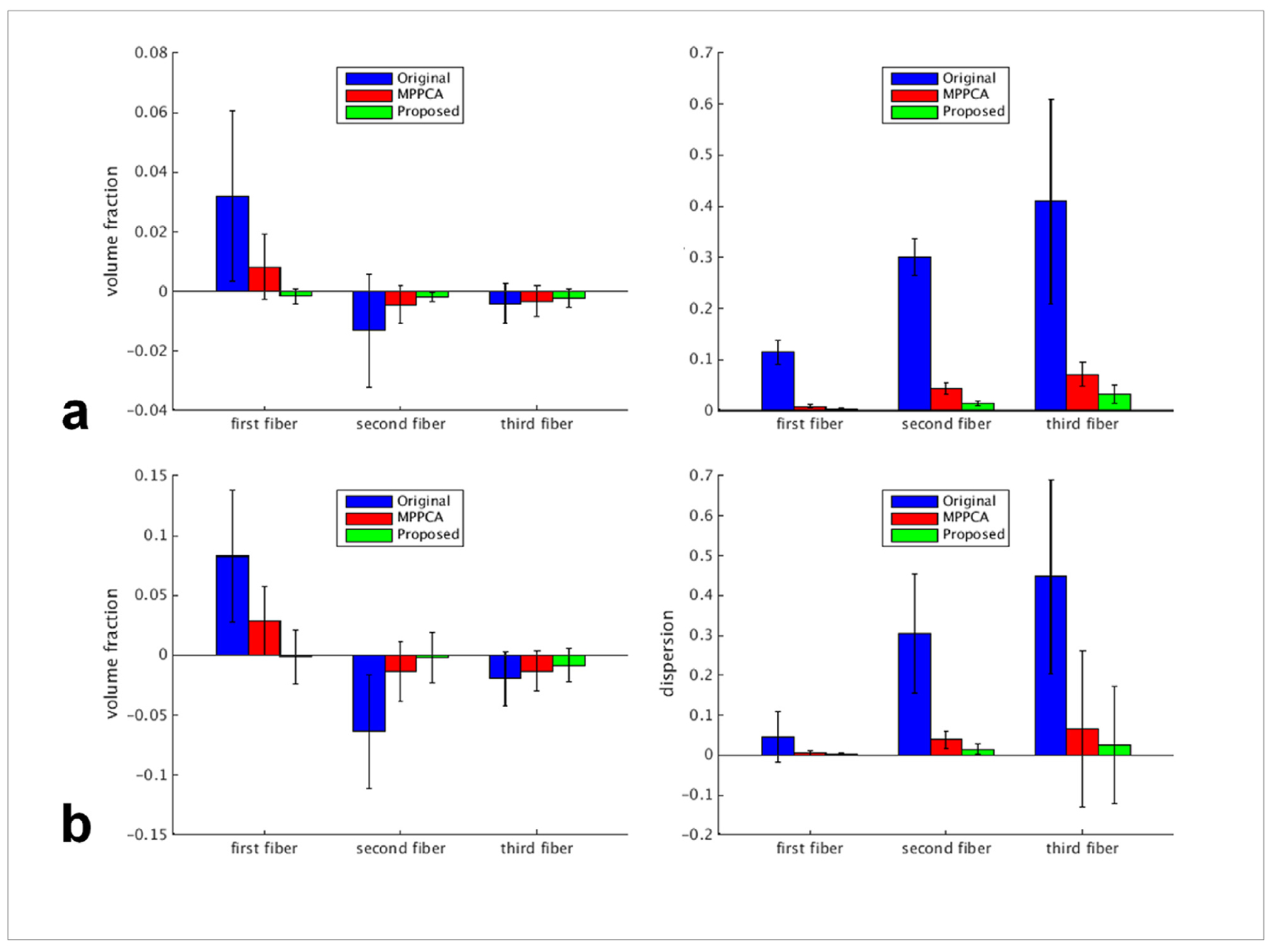
Simulation experiment: summary of Bland-Altman (BA) analysis results when using the MNI structural atlas (a) and the JHU white matter atlas (b) to define the regions of interest (ROIs) for comparison. Using each atlas, we compared each noisy or denoised imageset against the gold standard: 1) noisy images (Original), 2) images denoised with the MPPCA approach (MPPCA), and 3) images denoised with the proposed method (Proposed). Results of noise level of 4% were shown for demonstration. For each of the three fiber types (ie, first, second and third fiber), two diffusion metrics were compared: volume fraction (left column) and dispersion (right column). For each diffusion metric, region-specific average values for individual ROIs were calculated for each imageset and the results were compared against those of gold standard by calculating the region-specific difference values between each imageset and the reference. For each case, shown is the average difference across ROIs with the error bar corresponding to the reproducibility coefficient (ie, 1.96 standard deviation (SD) of the differences across ROIs).
Inspecting an exemplar region known to have multiple white matter bundles (Fig. 9), we found that the use of the proposed method resulted in orientation vectors that were most similar to the gold standard, especially for second and third fibers. Further, the orientation vectors for second and third fibers were best aligned with the respective gold standard across the brain, reducing the brain average angular differences (Fig. 10). The brain average angular difference was reduced by ~44% for second and ~16% for third fibers when compared to noisy images, and ~21% for second and ~12% for third fibers when compared to the MPPCA approach.
Fig. 9.
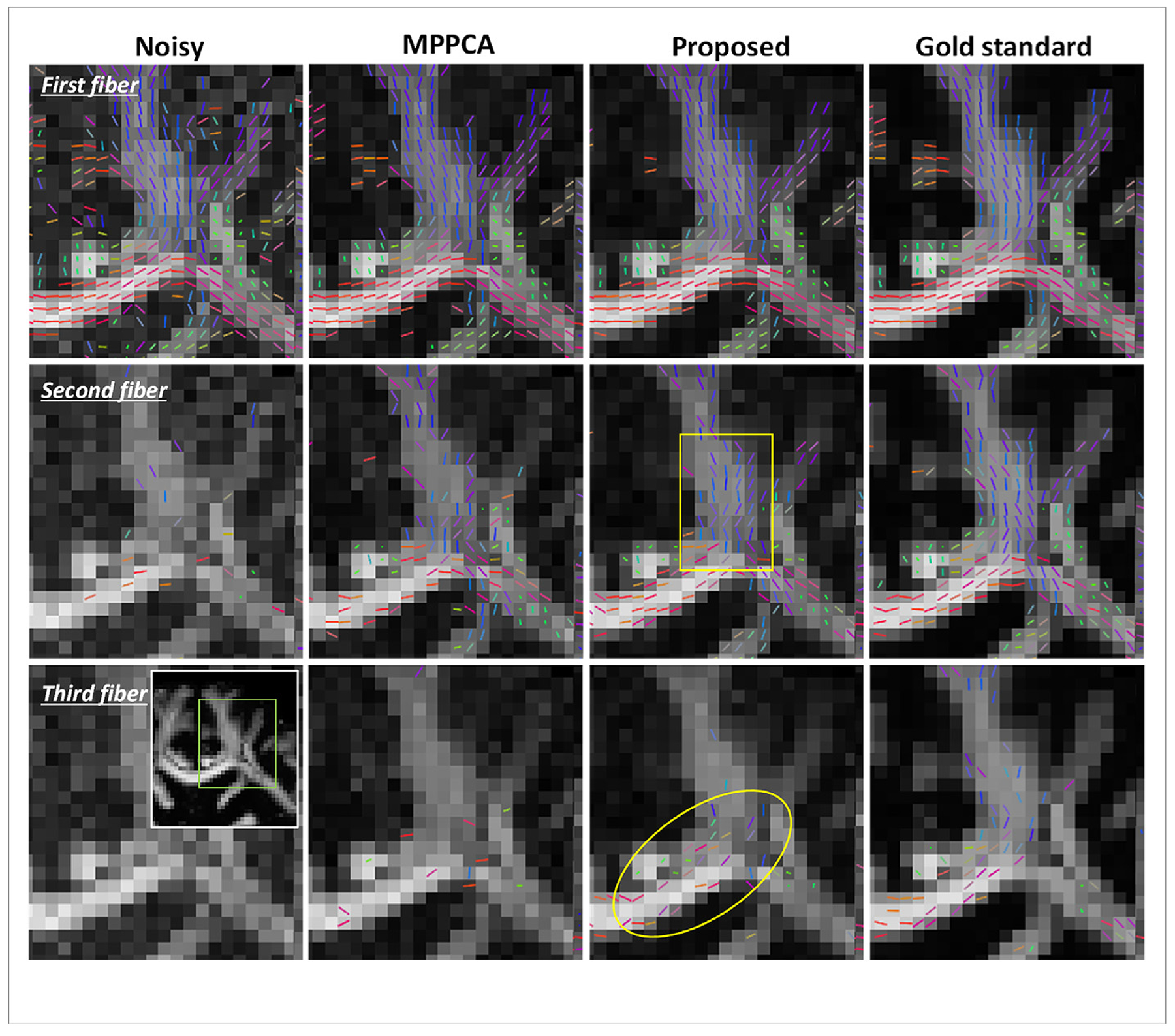
Simulation experiment: an exemplar region of the centrum ovale (as indicated by a green box in the inset) demonstrating the comparison of the original noisy images (noise level 4%), images denoised using MPPCA or the proposed method for estimation of fiber crossing, with gold standard images serving as the reference. In each case, shown are the estimated orientations for the first, second and third fibers (thresholded at 0.05 vol fraction) overlaid on the respective FA map, with the color representing the fiber orientation (red: left-right; green: anterior-posterior; blue: superior-inferior). Note that the fiber orientation maps resulting from the use of the proposed method were closer to those obtained with gold standard images compared to the noisy images and MPPCA, especially for second and third fibers, indicated by the yellow box and ellipse respectively.
Fig. 10.
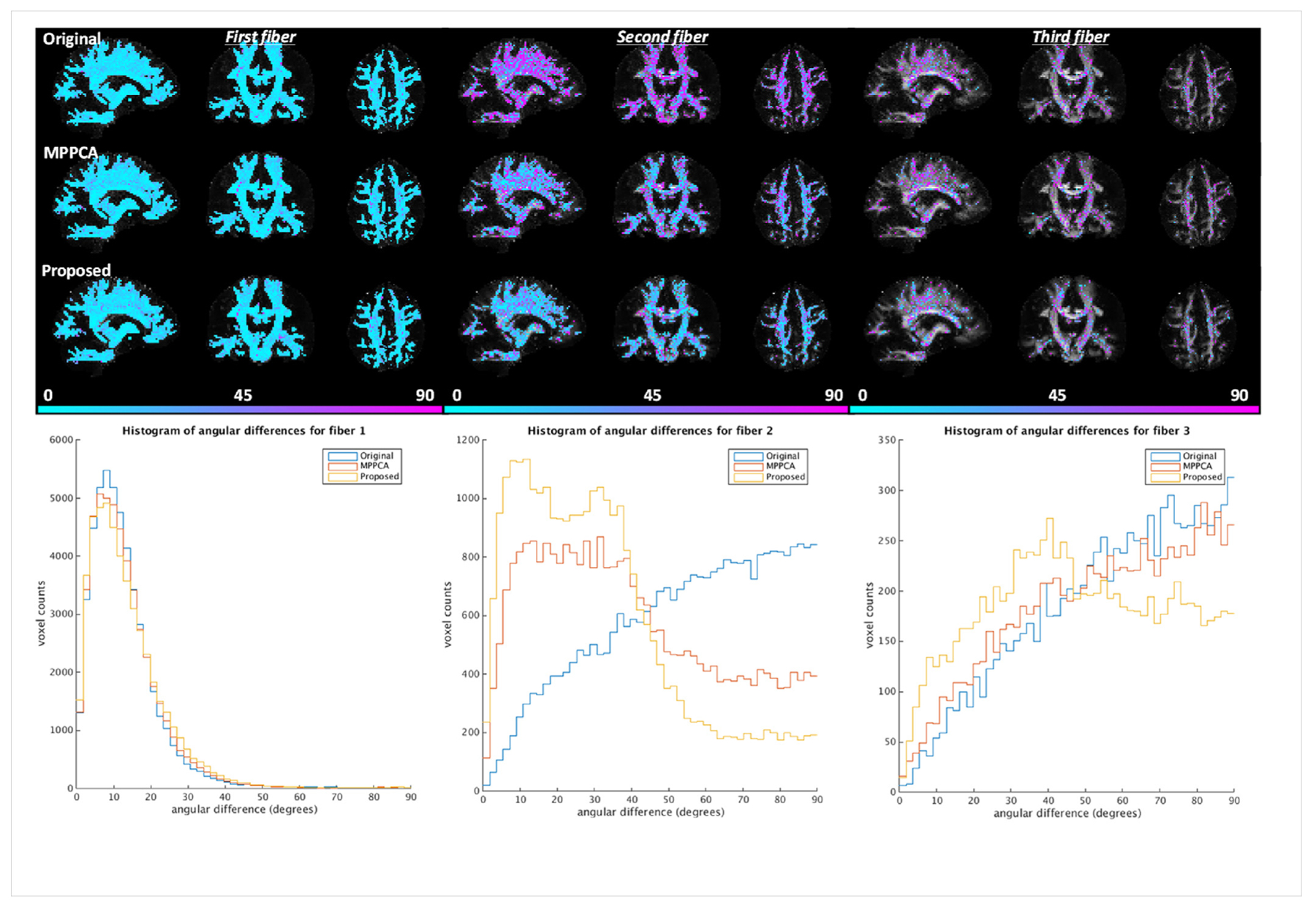
Simulation experiment: comparing angular differences for first, second and third fibers when fitting the ball and stick model to the double shell simulated diffusion data. Results of noise level of 4% were shown for demonstration. The angular differences for each fiber type were calculated by comparing the fiber orientation obtained with gold standard (serving as the reference) against that with noisy images (Original), images denoised with the MPPCA approach (MPPCA) or with the proposed method (Proposed). For each case, angular differences in degrees masked using the corresponding volume fractions thresholded at 0.05 are shown on top of the respective FA map in the top panel; the corresponding histograms of angular differences are plotted in the bottom panel.
4.2. Real data experiment
Similar to what was observed with the simulation experiment, the use of the proposed method to denoise the HCP-style diffusion largely improved the image quality relative to the original data and outperformed the MPPCA approach (Fig. 11). While improving b0 images subtly, the use of proposed method substantially improved the DW images as compared to the original data, leading to enhanced delineation of tissue boundaries between gray and white matters as easily identified across the entire brain. It also appeared more effective than the MPPCA approach in reducing noise levels especially for the DW images.
Fig. 11.
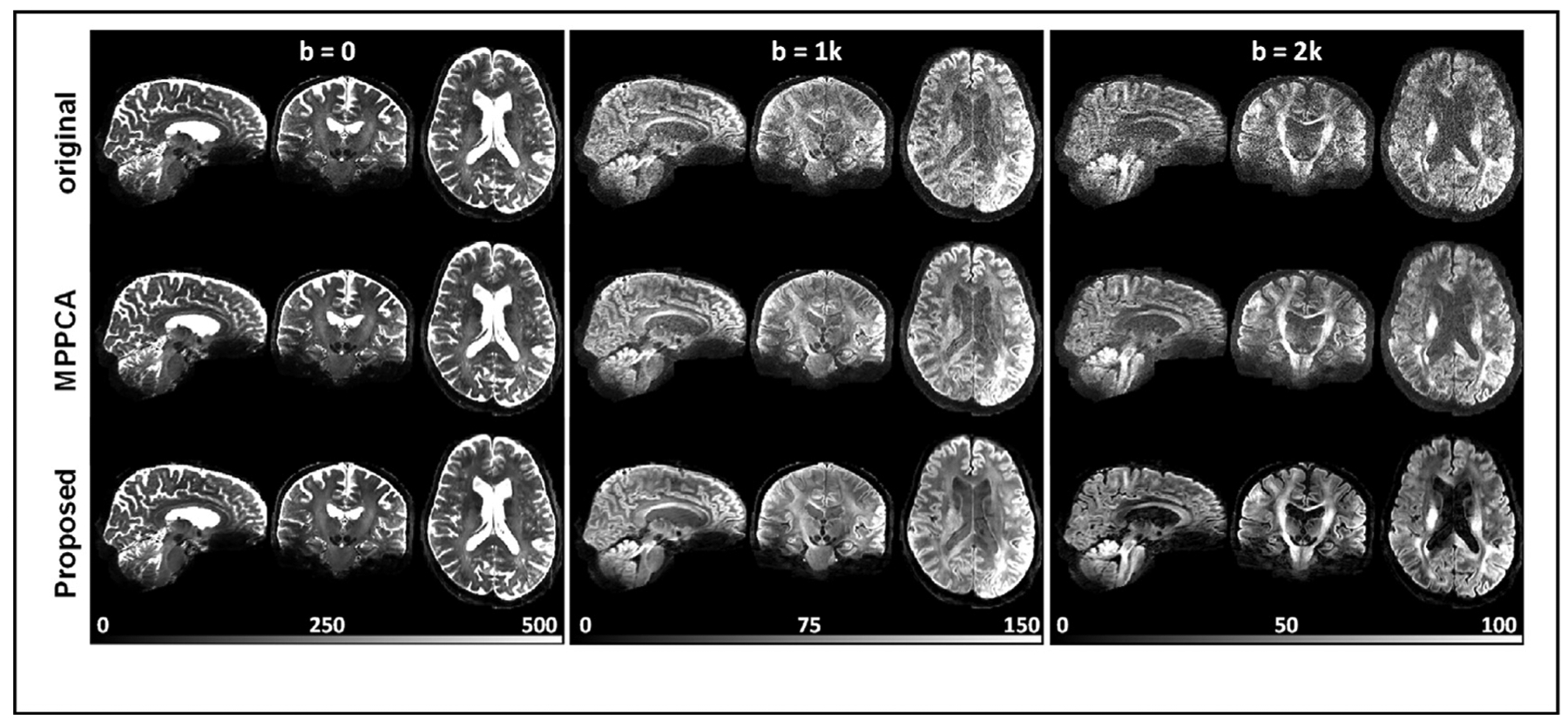
Real-data experiment: comparing HCP-style diffusion before (top) and after denoising using the MPPCA approach (middle) and using the proposed denoising method (bottom). In each case, shown are a set of three orthogonal views for b = 0, 1000, or 2000 s/mm2, obtained from a representative image volume after the respective entire dataset underwent the HCP 7T diffusion preprocessing pipeline to correct for motion and EPI geometric distortion. The whole-brain diffusion dataset was acquired following exactly the HCP 7T diffusion imaging parameters including 1.05-mm isotropic resolutions, 2-fold slice acceleration, 3-fold in-plane acceleration, and TE/TR = 71/7000 ms; it consisted of a series of 71 unique image volumes (including eight b0 images interspersed between 63 double-shell diffusion-weighted images), acquired twice with anterior-posterior (AP) and PA phase encode directions, leading to a total scan time of ~20 min. Note how the use of the proposed method substantially increased the signal to noise ratios (by effectively reducing the noise floor), giving rise to largely improved tissue contrasts especially for diffusion-weighted images.
The improvement in image quality with the proposed method immediately translated into improved DTI (Fig. 12). Consistent with simulation results, MD, AD and RD values were estimated to be higher across the brain (especially for CSF) than those obtained using the noisy images or the MPPCA approach. Further, FA values were estimated to be less noisy across the brain, especially in low-SNR regions (e.g., lower temporal lobes). The improvement of DTI with the proposed method was further confirmed by comparing the fitting errors; the whole brain average sum-of-square error for diffusion tensor fitting was reduced by as high as ~73% (0.84 vs 3.12) relative to the noisy images and by ~41% (0.84 vs 1.42) relative to the MPPCA approach.
Fig. 12.
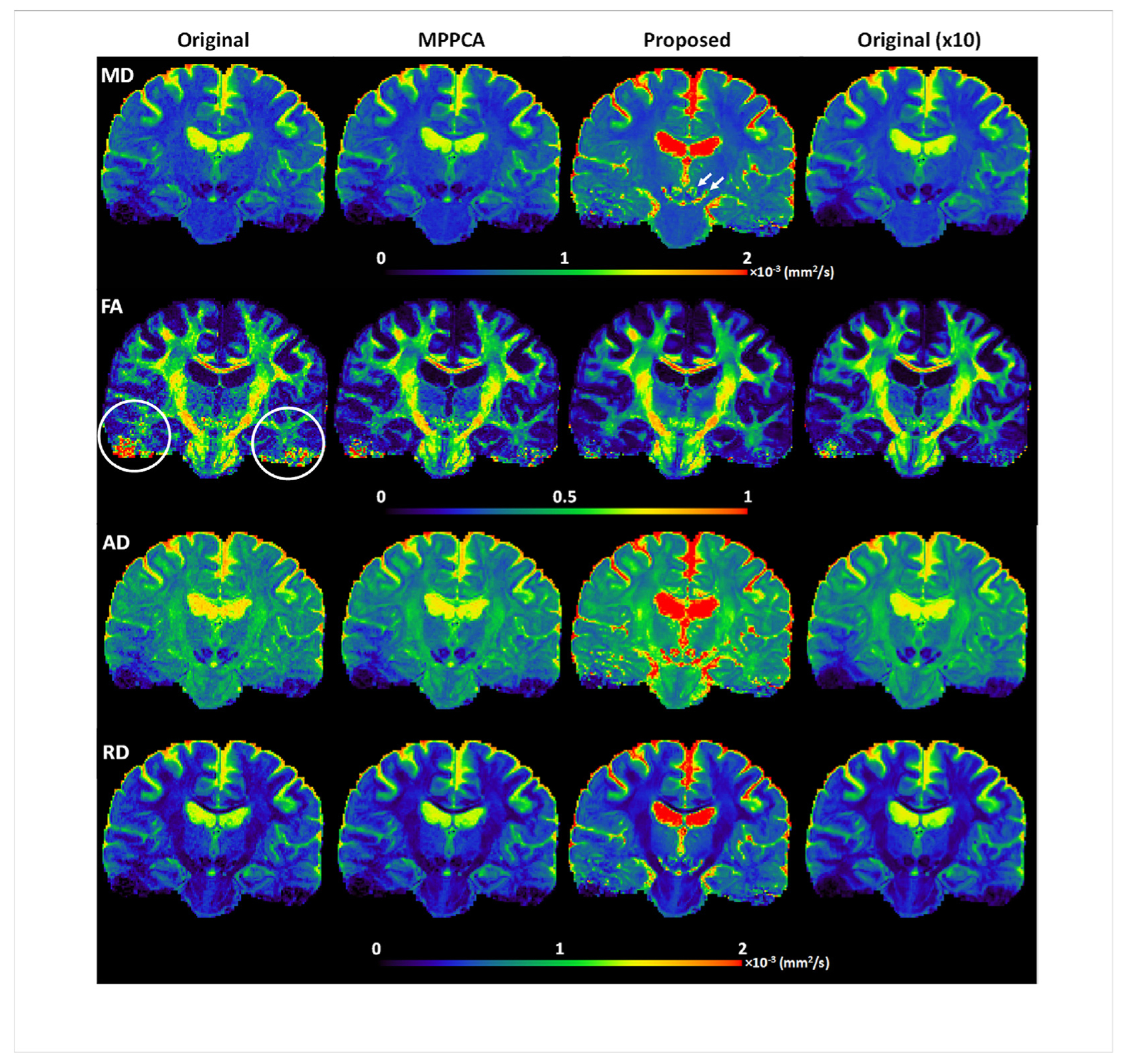
Real-data experiment: comparing performances for estimation of mean diffusivity (MD), fractional anisotropy (FA), radial diffusivity (RD) and axial diffusivity (AD) when fitting a diffusion tensor model to the HCP-style double-shell diffusion acquisition. Here, we compared 1) single average (Original), 2) single average denoised using the MPPCA approach (MPPCA), 3) single average denoised with the proposed method (Proposed), and 4) 10 averages (Original (x10). Note that the use of the proposed method substantially improved the estimation performances: it resulted in less underestimated MD in CSF (with average MD in CSF being ~1.8×10^−3 mm2/s as compared to ~1.3×10^3 mm2/s for all the other three cases) while providing more plausible non-zero MD values for subcortical nuclei (such as red nuclei and substantia nigra as indicated by white arrows); it also improved FA estimation, giving rise to FA values comparable to 10 averages, especially for regions (e.g., lower temporal lobes as indicated by white circles) where the initial signal to noise ratios were low due to RF inhomogeneity.
The efficacy of the proposed denoising method was further confirmed by estimation of fiber crossing (Fig. 13). In agreement with simulation results, the use of the proposed method reduced orientation dispersion for all three fiber populations and supported more voxels of fiber crossing, leading to volume fraction and dispersion maps most similar to the respective bronze standard. The improvement was further quantitatively verified by examining the results of BA analysis (Fig. 14). For all three fiber populations, the use of the proposed method resulted in volume fraction and dispersion values that on average were closest to the respective bronze standard. When using the JHU WM atlas, the average difference in volume fraction against the bronze standard across all ROIs was reduced by ~92% for first, ~88% for second, and ~79% for third fibers when compared to the noisy images, and by ~80% for first, ~75% for second, and ~68% for third fibers when compared to the MPPCA approach; the average difference in dispersion was reduced by ~93% and ~79% for first fiber when compared to the noisy images and the MPPCA approach, respectively, while becoming almost identical to the bronze standard for second and third fibers. Similar results were observed for when using the MNI structural atlas, except that the average difference in volume fraction was increased (by ~44%) for first fiber relative to the MPPCA approach; for all fiber populations, the average difference in dispersion became even smaller than the bronze standard.
Fig. 13.
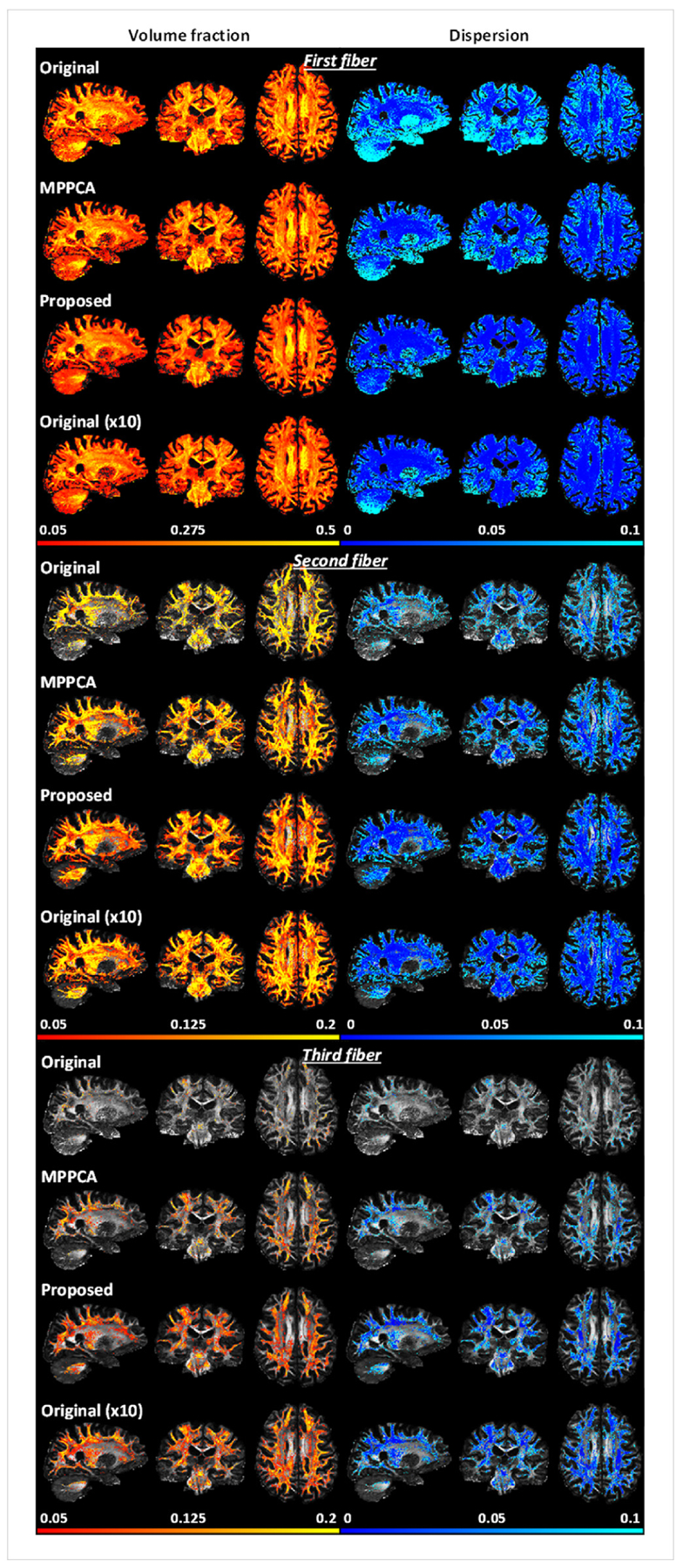
Real-data experiment: comparing performances for estimation of fiber crossing when fitting an extended ball and stick model to HCP-style double-shell diffusion acquisitions. Shown are volume fraction and dispersion maps (shown for voxels of ≥0.05 vol fraction) for first (or principle), second and third fibers when estimated using single average (original), single average denoised with MPPCA (MPPCA), single average denoised with the proposed method (Proposed), and 10 averages (Original (x10)).
Fig. 14.
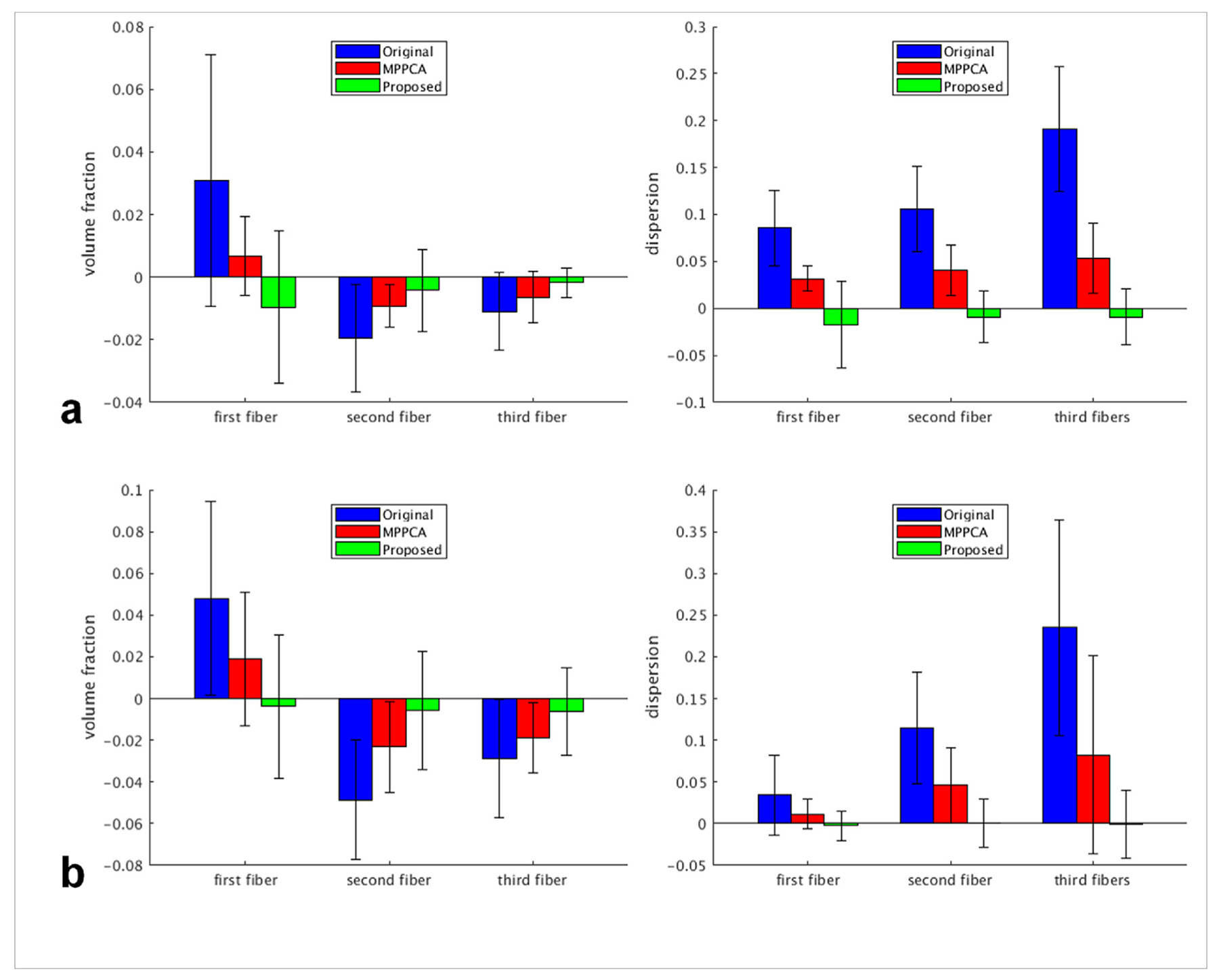
Real-data experiment: summary of Bland-Altman (BA) analysis results when using the MNI structural atlas (a) and the JHU white matter atlas (b) to define the regions of interest (ROIs) for comparison. Using each atlas, we compared the three single average scenarios against the 10 averages (serving as the reference): 1) single average (Original), 2) single average denoised with the MPPCA approach (MPPCA), and 3) single average denoised with the proposed method (Proposed). For each of the three fiber types (ie, first, second and third fiber), two diffusion metrics were compared: volume fraction (left column) and dispersion (right column). For each diffusion metric, region-specific average values for individual ROIs were calculated for each single average scenario and the results were compared against those of the reference by calculating the region-specific difference values between the single average scenario under consideration and the reference. For each case, shown is the average difference across ROIs with the error bar corresponding to the reproducibility coefficient (ie, 1.96 standard deviation (SD) of the differences across ROIs).
Examining an exemplar region of the centrum ovale known to have three-way white matter bundles (Fig. 15), we found that the use of the proposed method resulted in orientation vectors that were most similar to the bronze standard, especially for second and third fibers. Correspondingly, the orientation vectors were best aligned with the respective bronze standard across the brain, leading to reduced angular differences (Fig. 16). The brain average angular difference was reduced by ~10% for first, ~19% for second and ~25% for third fibers when compared to noisy images; when compared to the MPPCA approach, the brain average angular difference was reduced by ~7% for second and ~12% for third fibers while being comparable for first fiber.
Fig. 15.

Real-data experiment: comparing first, second and third fiber orientations when estimated using single average (original), single average denoised with MPPCA (MPPCA), single average denoised with the proposed method (Proposed), and 10 averages (Original (x10)). Shown are fiber orientations in a region of the centrum ovale (as indicated by a green box in the inset) known to have multi-way white matter fibers. In each case, voxel-wise color-coded fiber orientations, thresholded at 0.05 vol fraction and with the color representing the fiber orientation (red: left-right; green: anterior-posterior; blue), are displayed over the respective FA map. Note that when compared to using the single average without denoising superior-inferioror denoised with the MPPCA approach, the use of the proposed method to denoise the single average substantially improved the estimation of fiber orientations by giving rise to better-organized and better-aligned fibers (e.g., in a region as indicated by the ellipse) while supporting more voxels of three-way white matter fibers (e.g., in a region as indicated by the rectangle), which improvement appeared comparable to what was achievable with 10 averages.
Fig. 16.
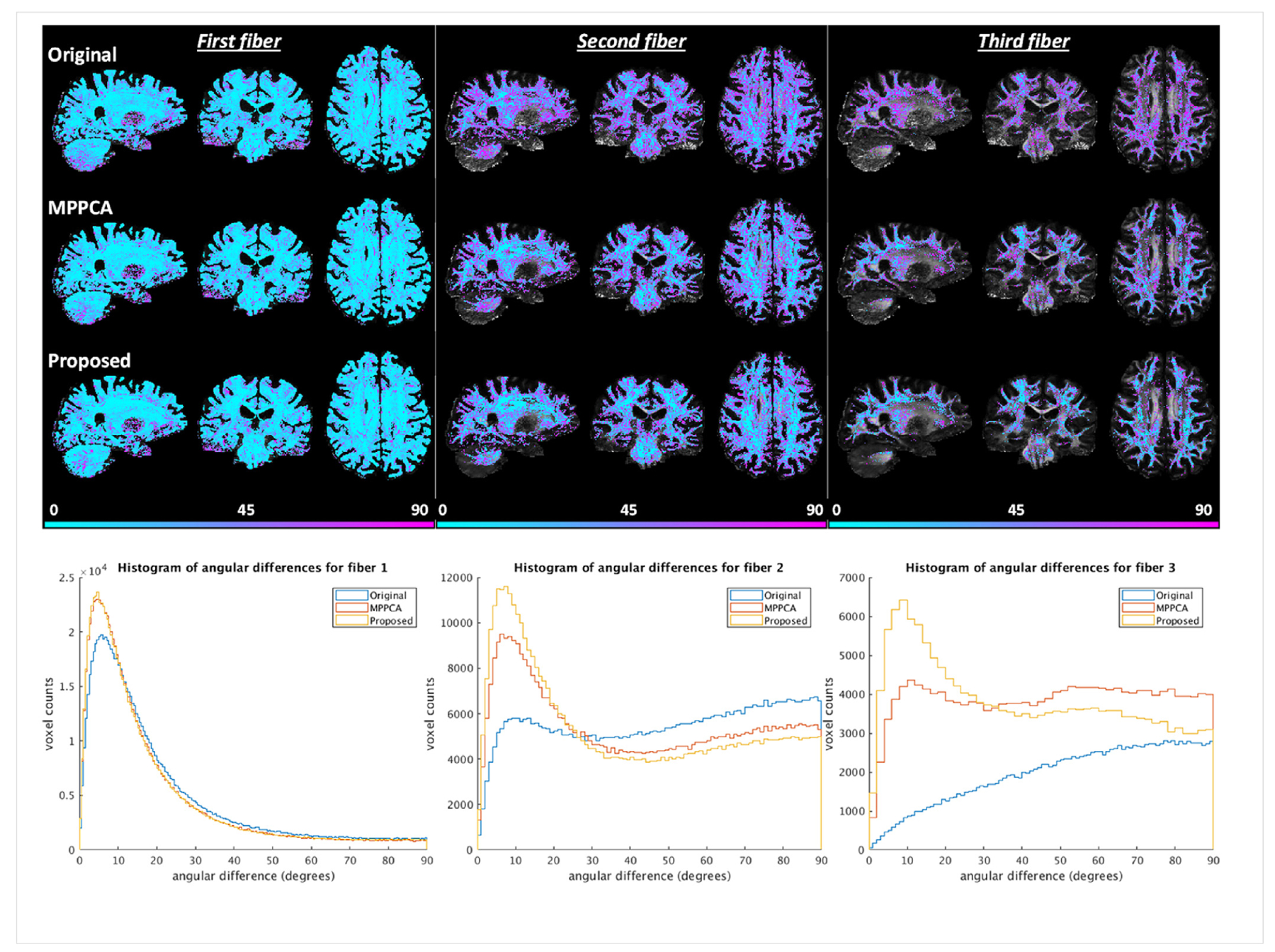
Real-data experiment: comparing angular differences for first, second and third fibers when fitting the ball and stick model to the HCP-style double shell diffusion data. The angular differences for each fiber type were calculated by comparing the fiber orientation obtained with 10 averages (serving as the reference) against that with single average (Original), single average denoised with the MPPCA approach (MPPCA), and single average denoised with the proposed method (Proposed). For each case, angular differences in degrees masked using the corresponding volume fractions thresholded at 0.05 are shown on top of the respective FA map in the top panel; the corresponding histograms of angular differences are plotted in the bottom panel.
5. Discussion
Here we proposed and demonstrated a denoising method that can be used to effectively improve the SNR for magnitude diffusion images. Critical to the efficacy of the new method for noise reduction is the realization of a VST-based denoising framework (Fig. 1) that synergistically combines various techniques including noise estimation, variance stabilization, standard denoising (with optimal singular value shrinkage) and patched-based implementation. The effectiveness of the proposed method for reducing the negative impact of Rician noise in magnitude diffusion images was demonstrated by performing both simulation and real-data experiments. The results of the simulation experiment using synthetic multi-shell diffusion images of a brain-like phantom (Figs. 2–10) show that the use of the proposed method can effectively estimate the underlying diffusion signals (despite the Rician noise characteristics), thereby substantially improving the peak SNR. The SNR improvement can in turn enhance DTI and estimation of fiber crossing when compared to using the original noisy diffusion images. Likewise, the results of the real-data experiment using 7T HCP-style diffusion acquisitions at ~1-mm isotropic resolutions (Figs. 11–16) show that the use of the proposed method to denoise a single average of data acquisition can largely enhance the SNR for whole brain diffusion images acquired with high spatial resolutions and high b values, giving rise to massively improved estimation of diffusion metrics in DTI and in resolving fiber crossings. Further, our results suggest that the large improvement in estimation of multiple fiber orientations globally is comparable to what is achievable with 10 averages (without denoising). In both simulation and real-data experiments, our results show that the proposed method outperforms the MPPCA approach (a current state of the art method for denoising in diffusion) when directly used to reduce the Rician noise in magnitude diffusion images.
Important to the success of the proposed VST-based denoising method are the two executions of noise estimation along the denoising pipelines: 1) the noise estimation right before the VST (Fig. 1) and 2) the noise estimation right after the VST (Fig. S2). The first noise estimation aims to provide the priori knowledge on the underlying Gaussian noises that is needed in the subsequent VST and EUIVST operations. For this first noise estimation, any method capable of estimating the underlying Gaussian noise levels directly from the Rician image data can be considered. Although the VST-based method with the “VST B″ function (Foi, 2011) was chosen in the current study because of its robustness for noise estimation across a wide range of noise levels (Fig. S6), alternative methods exist including the one in (Coupe et al., 2010) that combines the median absolute deviation with Koay’s inversion technique (Koay and Basser, 2006)), the method in (Manjon et al., 2015) that estimates noise levels based on non-local principle component analysis, and another approach in (Koay et al., 2009) which can also be used to identify noise-only voxels. The second noise estimation, which is executed after the VST and is also the first step in the application of standard denoising (Fig. S2), aims to estimate the noise levels directly from the transformed data in order for data scaling to be fulfilled before optimal singular value manipulation. For this second noise estimation, any method tailored for estimating the noise level given the Gaussian data can be considered. This includes the use of the MPPCA approach as adopted in the current study and alternative methods such as the one in (Gavish and Donoho, 2014, 2017) that estimates the Gaussian noise levels based on the median singular value of the noise-corrupted data matrix and the median of the Marcenko-Pastur distribution. Further, the implementation of both noise estimations follows a patch-based approach in order to not only improve the noise estimation performance (by aggregating multiple estimates at each image voxel) but also enable estimation of spatially varying noise levels (by capturing local noise characteristics around each image voxel). For both noise estimations, we note that the ability to estimate spatially varying noise levels is important. This is because diffusion images often do not present uniform noise levels across space due to the application of parallel imaging for improved acquisition efficiency. This is also because the VST is by no means perfect and the std of transformed data does not remain unchanged across space (although stabilized to being close to unity) (Fig. S7).
An interesting observation when using only b1k images to estimate the underlying Gaussian noise was that the estimation inaccuracy (in terms of RMSE) did not monotonically increase with noise levels (Fig. S9) – it decreased at the beginning for low to intermediate noise levels (up to ~4%). This can be explained by understanding how the VST-based method utilized for noise estimation works. The VST-based method works by estimating the noise std after high-pass filtering the image intensities, assuming that the high-frequency components of intensity changes across a patch are due to noise contamination. However, this assumption is not met at a low noise level, as the high-frequency components of intensity changes are mostly attributable to changes in tissue contrast. As a result, the VST-based method tends to over-estimate the noise std, leading to an increase in estimation error. The noise overestimation can readily be appreciated by examining the result at the 2% noise level (Fig. S9) and noticing that the noise std was estimated to be higher than the ground truth especially in white matter regions where the tissue contrast varies the most from one diffusion direction to another. Likewise, noise overestimation was also observed for when using only b2k images but now at a higher level as a result of increased variations in tissue contrast due to the doubled b-value. Such noise overestimation due to changes in tissue contrast is further confirmed by additional simulation using pure noises for noise estimation showing that the estimation error largely reduced at low noise levels and overall presents a monotonic increase with the noise level across the entire range of noise levels under consideration.
Another interesting observation associated with the VST-based noise estimation method is that the use of more data by including images of different b-values did not seem to help improve the performance for noise estimation in comparison to when using the b1k images alone (Fig. S9). This can also be explained by the fact that the changes in tissue contrast from image to image can bias the noise estimation. For example, in the case where all images (including b0, b1k and b2k images) are used for noise estimation, jumps in tissue contrast from one b-value to another would introduce additional bias to a level that outweighs the potential improvement provided by the increase in data quantity, thereby leading to substantially decreased estimation accuracy across the noise levels. This can be evidenced by comparing the noise estimation results at various noise levels and realizing how the use of all images have resulted in higher noise estimation than using only b1k images (Fig. S9).
In the current study, we incorporated the optimal singular value shrinkage algorithm (based on Frobenius norm) into the denoising module of the proposed framework to manipulate singular values. This shrinkage algorithm was found in our pilot study to provide best estimation of underlying diffusion signals in the presence of Rician noise when compared to other standard singular value manipulation algorithms including truncated SVD, hard thresholding and soft thresholding (Fig. S7). This finding is in consistency with the theoretical results (Gavish and Donoho, 2014, 2017) showing that the optimal singular value shrinkage when used to recover an n-by-n matrix of rank r observed in white noise with level σ would guarantee the least asymptotic mean squared error of 2nrσ2 vs 3nrσ2 for hard thresholding, 5nrσ2 for truncated SVD, and 6nrσ2 for soft thresholding. We also note that the MPPCA method is essentially the same as the truncated SVD when dealing with a Gaussian data matrix. This is evidenced by the results of our pilot study, showing that the two methods led to nearly identical results (Fig. S7) when integrated into the denoising module to estimate the underlying diffusion signals. This can be explained by the fact that both methods attempt to recover the signal matrix by nullifying singular values below a threshold and the threshold in both cases is determined based on the Marchenko-Pastur distribution (Eckart and Young, 1936; Marčenko and Pastur, 1967; Veraart et al., 2016b).
The results of our simulation experiment suggest that the direct use of the noisy magnitude diffusion images would lead to inaccurate estimations of diffusion metrics in DTI (Fig. 5). In particular, our results (Fig. 6) show that MD appeared under-estimated (due in large part to a substantial underestimation in RD), whereas both AD and FA under- and over-estimated across the region of interest. These findings are in agreement with the literature (Dietrich et al., 2001; Jones and Basser, 2004; Jones and Cercignani, 2010) showing how the presence of Rician noise can negatively influence the fitting of a diffusion tensor model. Surprisingly, although capable of improving the image quality in terms of PSNR (Figs. 3 and 4), the use of the MPPCA approach was found to provide even worse estimation of MD than the direct use of the noisy images, mostly due to a large underestimation in AD especially at low SNR levels. This can be explained by the fact that the MPPCA approach has the ability to reduce the variances in the data, thereby smoothing out the noise floor and increasing the Rician bias in the axial direction of the diffusion tensor where the diffusion signal profile presents minimum values. Imposing the Rician bias at a similar level in the radial direction of the diffusion tensor, the use of the MPPCA approach however leads to largely improved estimation of FA as compared to the direct use of the noisy images.
Likewise, the results for our real data experiment (Fig. 12) show that the use of the MPPCA approach does not necessarily improve the estimation of MD and may actually provide similar MD values to using the original noisy diffusion images. In both cases, the MD tends to be underestimated across the brain. By contrast, the use of our proposed denoising method effectively reduces the under-estimation of MD and improves the estimation of MD across the brain. This improvement can be appreciated by comparing the MD estimations for CSF and for subcortical nuclei such as red nuclei. The MD for CSF on average was estimated to increase from ~1.3e-3 mm2/s for using the noisy diffusion images or using the MPPCA approach to ~1.8e-3 mm2/s for using the proposed denoising method, which becomes closer to the MD value of ~3e-3 mm2/s for CSF reported in literature (Pierpaoli et al., 1996). Furthermore, the MD for red nuclei on average was estimated to increase from nearly zero for using the noisy diffusion images or using the MPPCA approach to ~0.7e-3 mm2/s for using the proposed denoising method. This nonzero MD value estimated for red nuclei is in line with the findings of previous work aimed at characterizing diffusion tensor metrics of red nuclei (Kim et al., 2018).
Both our simulation and real-data experiments show that the use of the proposed denoising method can improve the estimation of multiple fiber populations when fitting an extended ball and stick diffusion model to double-shell diffusion data, supporting more voxels of fiber crossing while increasing the accuracy and decreasing the uncertainty for each fiber orientation. These improvements in estimation of fiber crossing are further confirmed by comparing the results against a reference chosen to be the gold standard (obtained with noise-free images) in the simulation and the bronze standard (obtained with 10 averages dataset) in the real-data experiment. In both cases, our results show that the use of the proposed method can give rise to estimation results that are closest to the reference and outperform the MPPCA approach. Most encouragingly, our results for the real HCP-style diffusion at ~1 mm isotropic resolutions show that the use of the proposed method to denoise a single average can improve the performances for estimation of fiber crossing to a level comparable to what is achievable with 10 averages, enabling us to achieve what is attainable with 200-minute scan by only acquiring data for 20 minutes.
When estimating fiber crossing by fitting an extended ball and stick diffusion model to the synthetic gold standard dataset, we notice that the results (Fig. 7) (using FSL’s bedpostx rountine) support the existence of multiple fiber populations in many voxels in the corpus callosum where the existence of a single fiber population seems more plausible. A closer comparison of fiber orientations in those voxels reveals that the second and third fibers (when present) are mostly aligned with the first fiber (Fig. 9), with the angular differences between them being minimum. We consider this to be a feature of FSL’s bedpostx rountine which tends to overfit especially at high SNR. We note that this overfitting should not be viewed as a big problem for subsequent tractography analysis, since the existence of such multiple fiber orientations is still likely to give rise to fiber tracts that follow the pathway of the corpus callosum, thereby resembling the underlying ground truth.
To investigate how the proposed method would compare to a non-PCA-based alternative, we implemented another denoising approach based on the adaptive non-local means (ANLM) filtering (Manjon et al., 2010). We applied the ANLM filtering to the simulated double-shell diffusion data and compared the results to those obtained with the proposed method (see supporting materials for more details). Our data (Fig. S15) show that the proposed method outperformed the ANLM filtering, increasing PSNR and preserving fine brain structures. This is in agreement with previous studies (Manjon et al., 2013; Veraart et al., 2016b) showing that a PCA-based method usually provides better denoising performances than other non-PCA-based methods including the ANLM filtering.
In the current study, a constant kernel size of 5 × 5 × 5 was utilized for all the operation modules along the proposed denoising pipeline.Using the synthesized mouse data, we found that using a larger kernel size of 7 × 7 × 7 throughout the denoising pipeline resulted in comparable denoising performance, leading to nearly identical PSNR values across a range of noise levels. However, the use of a large kernel size would slow down the computation due to larger data matrices to deal with. For increased computation efficiency without a compromise on denoising performance, we decided to choose the kernel size of 5 × 5 × 5 for all of the denoising processes in the current paper. We note that the proposed denoising pipeline does not require a constant kernel size for all of its operation modules and in fact it allows a different kernel size to be used for each module. Part of our future work would be to examine how the kernel size of each module can be optimized and how this module-specific kernel size optimization would further improve the denoising performance of the proposed method. Additionally, for the denoising module (in which a standard denoising method is applied), we will consider using more advanced patch definitions (such as those through non-local spatial (Buades et al., 2005; Dabov et al., 2007; Maggioni et al., 2013; Manjon et al., 2015) and angular (St-Jean et al., 2016) matching and through structure adaptation (Bao et al., 2013; Foi et al., 2007)) to form the data matrices to be denoised and will explore how the combined use of these more advanced patch definitions would leverage the denoising performance of the proposed method by maximizing the information redundancy (thereby minimizing the rank) of the data matrices.
Incorporating Foi’s VST recipe (Foi, 2011), the proposed denoising method is specifically devised for denoising Rician images. In the context of parallel imaging, a Rician image is obtained by taking the magnitude of a single composite complex-valued Gaussian image (Dietrich et al., 2001). This single composite complex-valued Gaussian image can directly be reconstructed by using a SENSE-type algorithm (Pruessmann et al., 1999); alternatively, it can be obtained by using a GRAPPA-type interpolation (Griswold et al., 2002) in which case the GRAPPA-reconstructed multi-channel complex-valued images have to be combined using an intelligent multi-channel combination method such as spatial matched filtering (Roemer et al., 1990; Walsh et al., 2000) or SENSE-1 reconstruction (Sotiropoulos et al., 2013) (as employed in this study). If the GRAPPA-reconstructed multi-channel images are combined with the sum of squares approach, the resulting composite magnitude image may still be modelled to follow a non-central Chi distribution. However, it has been shown (Aja-Fernández et al., 2011) that the non-central Chi distribution in this case has to be characterized by effective parameters as determined by the GRAPPA interpolation and the coil-to-coil correlation and that the effective parameters (i.e., effective channel count and effective noise variance) are spatially dependent (meaning that they vary from one image voxel to another). We note that this spatial dependency of effective parameters will make it difficult in practice to accurately estimate the shape of the data distribution at each image voxel, posing a challenge to denoising. Therefore, we recommend that non-central Chi distribution be avoided through image reconstruction that aims to form a single composite complex-valued Gaussian image. Such composite complex-valued Gaussian images can also be denoised directly (Cordero-Grande et al., 2019), which is believed to hold potential to provide improved denoising performance, especially for low SNR regimes. Indeed, we have run additional simulation (data not shown) to investigate how our proposed VST-based denoising method would compare against denoising directly in the complex domain; we found that the direct use of the optimal shrinkage algorithm to denoise a Gaussian diffusion imageset outperformed the use of the proposed denoising method to denoise the corresponding Rician diffusion image-set, increasing the PSNR measures by ~4% at 5% noise level and by ~10% at 10% noise level.
One limitation of the current study is that the whole brain diffusion images were obtained using the Nova single-channel transmit RF coil which is known to present severe transmit RF inhomogeneity across the brain (Vu et al., 2015). Although reduced to some extent by using dielectric padding, the transmit RF inhomogeneity of the coil was still quite strong, leading to weak diffusion signal or even signal dropout in lower brain regions such as the cerebellum and the pole of temporal lobes. Our results (Figs. 12 and 13) show that the proposed denoising method has the ability to improve the SNR in these lower brain regions, resulting in enhanced estimation of diffusion metrics as compared to using the original noisy diffusion images. However, the improvement in estimation of diffusion metrics was limited mostly due to the extremely low SNR to begin with. On the other hand, it has been shown that RF parallel transmission (Katscher et al., 2003; Zhu, 2004) can be used to improve the image quality of HCP-style whole brain diffusion at 7T by effectively improving the RF uniformity across the brain and substantially enhancing the SNR in lower brain regions (Wu et al., 2018). Part of our future work therefore would be to combine RF parallel transmission with the proposed denoising method and evaluate how this synergistic combination would further improve the image quality when acquiring 7T whole brain diffusion at ~1-mm isotropic resolutions.
6. Conclusions
We have introduced and demonstrated a comprehensive denoising method that can be used to enhance the SNR for magnitude diffusion images. Critical to the efficacy of the new denoising method is the synergistic combination of various techniques including noise estimation, variance stabilization, standard denoising (e.g., with optimal singular value shrinkage) and patch-based implementation. The effectiveness of the proposed method for noise reduction is demonstrated by using both simulation and real-data experiments and by considering spatially varying noise levels. Our results obtained using synthetic diffusion data in a brain-like phantom and using ~1-mm isotropic HCP-style 7T dMRI show that the use of the proposed method can effectively remove Rician noise and improve the image SNR, thereby substantially increasing the performances for diffusion tensor imaging and the estimation of fiber crossing. Further, the results of our real-data experiment show that the use of the proposed method can improve the performances for estimation of fiber crossings to a level comparable to what is achievable with 10 averages. In addition, our results from both simulation and real-data experiments demonstrate that the proposed denoising method can outperform the MPPCA approach, an existing method representing the state of the art in denoising magnitude diffusion images. As such, we believe that the proposed denoising method will have a great utility for high-quality, high-resolution whole-brain diffusion MRI, desirable for many neuroscientific and clinical applications.
Supplementary Material
Acknowledgments
The authors would like to thank Steen Moeller and Mehmet Akçakaya for their stimulating discussions on denoising, Christophe Lenglet for his valuable comments on diffusion analysis, and John Strupp and Brian Hanna for their assistance in setting up computation resources. This work was supported by NIH grants including U01 EB025144, P41 EB015894 and P30 NS076408.
Footnotes
Appendix A. Supplementary data
Supplementary data to this article can be found online at https://doi.org/10.1016/j.neuroimage.2020.116852.
References
- Jones DK, Basser PJ, 2004. “Squashing peanuts and smashing pumpkins”: how noise distorts diffusion-weighted MR data. Magn. Reson. Med. : Off. J. Soc. Magn. Reson. Med./Soc. Magn. Reson. Med 52, 979–993. [DOI] [PubMed] [Google Scholar]
- Abdelnour AF, Selesnick IW, 2005. Symmetric nearly shift-invariant tight frame wavelets. IEEE Trans. Signal Process 53, 231–239. [Google Scholar]
- Aja-Fernandez S, Niethammer M, Kubicki M, Shenton ME, Westin CF, 2008. Restoration of DWI data using a Rician LMMSE estimator. IEEE Trans. Med. Imag 27, 1389–1403. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Aja-Fernández S, Trist an-Vega A, Hoge WS, 2011. Statistical noise analysis in GRAPPA using a parametrized noncentral Chi approximation model. Magn. Reson. Med 65, 1195–1206. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Andersson JLR, Sotiropoulos SN, 2016. An integrated approach to correction for off-resonance effects and subject movement in diffusion MR imaging. Neuroimage 125, 1063–1078. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Andersson JLR, Skare S, Ashburner J, 2003. How to correct susceptibility distortions in spin-echo echo-planar images: application to diffusion tensor imaging. Neuroimage 20, 870–888. [DOI] [PubMed] [Google Scholar]
- Bao LJ, Robini M, Liu WY, Zhu YM, 2013. Structure-adaptive sparse denoising for diffusion-tensor MRI. Med. Image Anal 17, 442–457. [DOI] [PubMed] [Google Scholar]
- Basser PJ, Pierpaoli C, 1996. Microstructural and physiological features of tissues elucidated by quantitative-diffusion-tensor MRI. J. Magn. Reson. B 111, 209–219. [DOI] [PubMed] [Google Scholar]
- Basser PJ, Pajevic S, Pierpaoli C, Duda J, Aldroubi A, 2000. In vivo fiber tractography using DT-MRI data. Magn. Reson. Med 44, 625–632. [DOI] [PubMed] [Google Scholar]
- Basu S, Fletcher T, Whitaker R, 2006. Rician noise removal in diffusion tensor MRI. Med. Image Comput. Comput.-Assist. Interv. - Miccai 117–125, 2006, Pt 1 4190. [DOI] [PubMed] [Google Scholar]
- Becker SMA, Tabelow K, Mohammadi S, Weiskopf N, Polzehl J, 2014. Adaptive smoothing of multi-shell diffusion weighted magnetic resonance data by msPOAS. Neuroimage 95, 90–105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Behrens TEJ, Johansen-Berg H, Woolrich MW, Smith SM, Wheeler-Kingshott CAM, Boulby PA, Barker GJ, Sillery EL, Sheehan K, Ciccarelli O, Thompson AJ, Brady JM, Matthews PM, 2003a. Non-invasive mapping of connections between human thalamus and cortex using diffusion imaging. Nat. Neurosci 6, 750–757. [DOI] [PubMed] [Google Scholar]
- Behrens TEJ, Woolrich MW, Jenkinson M, Johansen-Berg H, Nunes RG, Clare S, Matthews PM, Brady JM, Smith SM, 2003b. Characterization and propagation of uncertainty in diffusion-weighted MR imaging. Magn. Reson. Med 50, 1077–1088. [DOI] [PubMed] [Google Scholar]
- Behrens TEJ, Berg HJ, Jbabdi S, Rushworth MFS, Woolrich MW, 2007. Probabilistic diffusion tractography with multiple fibre orientations: what can we gain? Neuroimage 34, 144–155. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bland JM, Altman DG, 1986. Statistical methods for assessing agreement between two methods of clinical measurement. Lancet 1, 307–310. [PubMed] [Google Scholar]
- Buades A, Coll B, Morel JM, 2005. A review of image denoising algorithms, with a new one. Multiscale Model. Simul 4, 490–530. [Google Scholar]
- Bullmore ET, Sporns O, 2009. Complex brain networks: graph theoretical analysis of structural and functional systems. Nat. Rev. Neurosci 10, 186–198. [DOI] [PubMed] [Google Scholar]
- Bydder M, Du J, 2006. Noise reduction in multiple-echo data sets using singular value decomposition. Magn. Reson. Imag 24, 849–856. [DOI] [PubMed] [Google Scholar]
- Cai JF, Candes EJ, Shen ZW, 2010. A singular value thresholding algorithm for matrix completion. SIAM J. Optim 20, 1956–1982. [Google Scholar]
- Catani M, Howard RJ, Pajevic S, Jones DK, 2002. Virtual in vivo interactive dissection of white matter fasciculi in the human brain. Neuroimage 17, 77–94. [DOI] [PubMed] [Google Scholar]
- Cauley SF, Polimeni JR, Bhat H, Wald LL, Setsompop K, 2014. Interslice leakage artifact reduction technique for simultaneous multislice acquisitions. Magn. Reson. Med 72, 93–102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chen B, Hsu EW, 2005. Noise removal in magnetic resonance diffusion tensor imaging. Magn. Reson. Med 54, 393–401. [DOI] [PubMed] [Google Scholar]
- Clarke RA, Scifo P, Rizzo G, Dell’Acqua F, Scotti G, Fazio F, 2008. Noise correction on rician distributed data for fibre orientation estimators. IEEE Trans. Med. Imag 27, 1242–1251. [DOI] [PubMed] [Google Scholar]
- Constantinides CD, Atalar E, McVeigh ER, 1997. Signal-to-noise measurements in magnitude images from NMR phased arrays. Magn. Reson. Med 38, 852–857. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cordero-Grande L, Christiaens D, Hutter J, Price AN, Hajnal JV, 2019. Complex diffusion-weighted image estimation via matrix recovery under general noise models. Neuroimage 200, 391–404. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Coulon O, Alexander DC, Arridge S, 2004. Diffusion tensor magnetic resonance image regularization. Med. Image Anal 8, 47–67. [DOI] [PubMed] [Google Scholar]
- Coupe P, Manjon JV, Gedamu E, Arnold D, Robles M, Collins DL, 2010. Robust Rician noise estimation for MR images. Med. Image Anal 14, 483–493. [DOI] [PubMed] [Google Scholar]
- Craddock RC, Jbabdi S, Yan CG, Vogelstein JT, Castellanos FX, Di Martino A, Kelly C, Heberlein K, Colcombe S, Milham MP, 2013. Imaging human connectomes at the macroscale. Nat. Methods 10, 524–539. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dabov K, Foi A, Katkovnik V, Egiazarian K, 2007. Image denoising by sparse 3-D transform-domain collaborative filtering. IEEE Trans. Image Process 16, 2080–2095. [DOI] [PubMed] [Google Scholar]
- De Lathauwer L, De Moor B, Vandewalle J, 2000. A multilinear singular value decomposition. SIAM J. Matrix Anal. Appl 21, 1253–1278. [Google Scholar]
- Descoteaux M, Deriche R, Knosche TR, Anwander A, 2009. Deterministic and probabilistic tractography based on complex fibre orientation distributions. IEEE Trans. Med. Imag 28, 269–286. [DOI] [PubMed] [Google Scholar]
- Dietrich O, Heiland S, Sartor K, 2001. Noise correction for the exact determination of apparent diffusion coefficients at low SNR. Magn. Reson. Med 45, 448–453. [DOI] [PubMed] [Google Scholar]
- Dietrich O, Raya JG, Reeder SB, Ingrisch M, Reiser MF, Schoenberg SO, 2008. Influence of multichannel combination, parallel imaging and other reconstruction techniques on MRI noise characteristics. Magn. Reson. Imag 26, 754–762. [DOI] [PubMed] [Google Scholar]
- Ding ZH, Gore JC, Anderson AW, 2005. Reduction of noise in diffusion tensor images using anisotropic smoothing. Magn. Reson. Med 53, 485–490. [DOI] [PubMed] [Google Scholar]
- Donoho D, Gavish M, Johnstone I, 2018. Optimal shrinkage of eigenvalues in the spiked covariance model. Ann. Stat 46, 1742–1778. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Duits R, Franken E, 2011. Left-Invariant diffusions on the space of positions and orientations and their application to crossing-preserving smoothing of HARDI images. Int. J. Comput. Vis 92, 231–264. [Google Scholar]
- Eckart C, Young G, 1936. The approximation of one matrix by another of lower rank. Psychometrika 1, 211–218. [Google Scholar]
- Eichner C, Cauley SF, Cohen-Adad J, Möller HE, Turner R, Setsompop K, Wald LL, 2015. Real diffusion-weighted MRI enabling true signal averaging and increased diffusion contrast. Neuroimage 122, 373–384. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fan Q, Nummenmaa A, Witzel T, Zanzonico R, Keil B, Cauley S, Polimeni JR, Tisdall D, Van Dijk KRA, Buckner RL, Wedeen VJ, Rosen BR, Wald LL, 2014. Investigating the capability to resolve complex white matter structures with high b-value diffusion magnetic resonance imaging on the MGH-USC connectom scanner. Brain Connect 4, 718–726. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fan Q, Witzel T, Nummenmaa A, Van Dijk KRA, Van Horn JD, Drews MK, Somerville LH, Sheridan MA, Santillana RM, Snyder J, Hedden T, Shaw EE, Hollinshead MO, Renvall V, Zanzonico R, Keil B, Cauley S, Polimeni JR, Tisdall D, Buckner RL, Wedeen VJ, Wald LL, Toga AW, Rosen BR, 2016. MGH-USC Human Connectome Project datasets with ultra-high b-value diffusion MRI. Neuroimage 124, 1108–1114. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fillard P, Pennec X, Arsigny V, Ayache N, 2007. Clinical DT-MRI estimation, smoothing, and fiber tracking with log-euclidean metrics. IEEE Trans. Med. Imag 26, 1472–1482. [DOI] [PubMed] [Google Scholar]
- Foi A, 2011. Noise estimation and removal in mr imaging: the variance-stabilization approach. In: 2011 8th Ieee International Symposium on Biomedical Imaging: from Nano to Macro, pp. 1809–1814. [Google Scholar]
- Foi A, Katkovnik V, Egiazarian K, 2007. Pointwise shape-adaptive DCT for high-quality denoising and deblocking of grayscale and color images. IEEE Trans. Image Process 16, 1395–1411. [DOI] [PubMed] [Google Scholar]
- Frank LR, 2001. Anisotropy in high angular resolution diffusion-weighted MRI. Magn. Reson. Med 45, 935–939. [DOI] [PubMed] [Google Scholar]
- Gavish M, Donoho DL, 2014. The optimal hard threshold for singular values is 4/root 3. IEEE Trans. Inf. Theor 60, 5040–5053. [Google Scholar]
- Gavish M, Donoho DL, 2017. Optimal shrinkage of singular values. IEEE Trans. Inf. Theor 63, 2137–2152. [Google Scholar]
- Glasser MF, Sotiropoulos SN, Wilson JA, Coalson TS, Fischl B, Andersson JL, Xu J, Jbabdi S, Webster M, Polimeni JR, Van Essen DC, Jenkinson M, 2013. The minimal preprocessing pipelines for the Human Connectome Project. Neuroimage 80, 105–124. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Goh A, Lenglet C, Thompson PM, Vidal R, 2011. A nonparametric Riemannian framework for processing high angular resolution diffusion images and its applications to ODF-based morphometry. Neuroimage 56, 1181–1201. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Greve DN, Fischl B, 2009. Accurate and robust brain image alignment using boundary-based registration. Neuroimage 48, 63–72. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Griswold MA, Jakob PM, Heidemann RM, Nittka M, Jellus V, Wang J, Kiefer B, Haase A, 2002. Generalized autocalibrating partially parallel acquisitions (GRAPPA). Magn. Reson. Med 47, 1202–1210. [DOI] [PubMed] [Google Scholar]
- Gudbjartsson H, Patz S, 1995. The Rician distribution of MRI data. Magn. Reson. Med 34, 910–914. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Haldar JP, Wedeen VJ, Nezamzadeh M, Dai GP, Weiner MW, Schuff N, Liang ZP, 2013. Improved diffusion imaging through SNR-enhancing joint reconstruction. Magn. Reson. Med 69, 277–289. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Harms MP, Somerville LH, Ances BM, Andersson J, Barch DM, Bastiani M, Bookheimer SY, Brown TB, Buckner RL, Burgess GC, Coalson TS, Chappell MA, Dapretto M, Douaud G, Fischl B, Glasser MF, Greve DN, Hodge C, Jamison KW, Jbabdi S, Kandala S, Li X, Mair RW, Mangia S, Marcus D, Mascali D, Moeller S, Nichols TE, Robinson EC, Salat DH, Smith SM, Sotiropoulos SN, Terpstra M, Thomas KM, Tisdall MD, Ugurbil K, van der Kouwe A, Woods RP, Zollei L, Van Essen DC, Yacoub E, 2018. Extending the human connectome Project across ages: imaging protocols for the lifespan development and aging projects. Neuroimage 183, 972–984. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Henkelman RM, 1985. Measurement of signal intensities in the presence of noise in MR images. Med. Phys 12, 232–233. [DOI] [PubMed] [Google Scholar]
- Huang H, Zhang JY, van Zijl PCM, Mori S, 2004. Analysis of noise effects on DTI-based tractography using the brute-force and multi-ROI approach. Magn. Reson. Med 52, 559–565. [DOI] [PubMed] [Google Scholar]
- Huber W, von Heydebreck A, Sultmann H, Poustka A, Vingron M, 2002. Variance stabilization applied to microarray data calibration and to the quantification of differential expression. Bioinformatics 18 (Suppl. 1), S96–S104. [DOI] [PubMed] [Google Scholar]
- Hugg JW, Butterworth EJ, Kuzniecky RI, 1999. Diffusion mapping applied to mesial temporal lobe epilepsy: preliminary observations. Neurology 53, 173–176. [DOI] [PubMed] [Google Scholar]
- Jbabdi S, Sotiropoulos SN, Savio AM, Graña M, Behrens TEJ, 2012. Model-based analysis of multishell diffusion MR data for tractography: how to get over fitting problems. Magn. Reson. Med 68, 1846–1855. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jenkinson M, Bannister P, Brady M, Smith S, 2002. Improved optimization for the robust and accurate linear registration and motion correction of brain images. Neuroimage 17, 825–841. [DOI] [PubMed] [Google Scholar]
- Jenkinson M, Beckmann CF, Behrens TEJ, Woolrich MW, Smith SM, 2012. Fsl. NeuroImage 62, 782–790. [DOI] [PubMed] [Google Scholar]
- Jensen JH, Helpern JA, Ramani A, Lu HZ, Kaczynski K, 2005. Diffusional kurtosis imaging: the quantification of non-Gaussian water diffusion by means of magnetic resonance imaging. Magn. Reson. Med 53, 1432–1440. [DOI] [PubMed] [Google Scholar]
- Jones DK, 2004. The effect of gradient sampling schemes on measures derived from diffusion tensor MRI: a Monte Carlo study. Magn. Reson. Med 51, 807–815. [DOI] [PubMed] [Google Scholar]
- Jones DK, Cercignani M, 2010. Twenty-five pitfalls in the analysis of diffusion MRI data. NMR Biomed 23, 803–820. [DOI] [PubMed] [Google Scholar]
- Jones DK, Knösche TR, Turner R, 2013. White matter integrity, fiber count, and other fallacies: the\ndo’s and don’ts of diffusion MRI. Neuroimage 73, 239–254. [DOI] [PubMed] [Google Scholar]
- Katkovnik V, Foi A, Egiazarian K, Astola J, 2010. From local kernel to nonlocal multiple-model image denoising. Int. J. Comput. Vis 86, 1–32. [Google Scholar]
- Katscher U, Börnert P, Leussler C, Van den Brink JS, 2003. Transmit SENSE. Magnetic resonance in medicine, 49, 144–150. [DOI] [PubMed] [Google Scholar]
- Kim H, Lee H, Jung KI, Ohn SH, Yoo WK, 2018. Changes in diffusion metrics of the red nucleus in chronic stroke patients with severe corticospinal tract injury: a preliminary study. Ann. Rehabil. Med 42, 396–405. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Koay CG, Basser PJ, 2006. Analytically exact correction scheme for signal extraction from noisy magnitude MR signals. J. Magn. Reson 179, 317–322. [DOI] [PubMed] [Google Scholar]
- Koay CG, Ozarslan E, Pierpaoli C, 2009. Probabilistic identification and estimation of noise (PIESNO): a self-consistent approach and its applications in MRI. J. Magn. Reson 199, 94–103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Krabbe K, Gideon P, Wagn P, Hansen U, Thomsen C, Madsen F, 1997. MR diffusion imaging of human intracranial tumours. Neuroradiology 39, 483–489. [DOI] [PubMed] [Google Scholar]
- Lam F, Babacan SD, Haldar JP, Schuff N, Liang ZP, 2012. Denoising diffusion-weighted mr magnitude image sequences using low rank and edge constraints. In: 2012 9th Ieee International Symposium on Biomedical Imaging (Isbi), pp. 1401–1404. [Google Scholar]
- Lam F, Babacan SD, Haldar JP, Weiner MW, Schuff N, Liang ZP, 2014. Denoising diffusion-weighted magnitude MR images using rank and edge constraints. Magn. Reson. Med 71, 1272–1284. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Le Bihan D, Breton E, Lallemand D, Grenier P, Cabanis E, Laval-Jeantet M, 1986. MR imaging of intravoxel incoherent motions: application to diffusion and perfusion in neurologic disorders. Radiology 161, 401–407. [DOI] [PubMed] [Google Scholar]
- Le Bihan D, Breton E, Lallemand D, Aubin ML, Vignaud J, Laval-Jeantet M, 1988. Separation of diffusion and perfusion in intravoxel incoherent motion MR imaging. Radiology 168, 497–505. [DOI] [PubMed] [Google Scholar]
- Lori NF, Akbudak E, Shimony JS, Cull TS, Snyder AZ, Guillory RK, Conturo TE, 2002. Diffusion tensor fiber tracking of human brain connectivity: acquisition methods, reliability analysis and biological results. NMR Biomed 15, 493–515. [DOI] [PubMed] [Google Scholar]
- Lutsep HL, Albers GW, DeCrespigny A, Kamat GN, Marks MP, Moseley ME, 1997. Clinical utility of diffusion-weighted magnetic resonance imaging in the assessment of ischemic stroke. Ann. Neurol 41, 574–580. [DOI] [PubMed] [Google Scholar]
- Maggioni M, Katkovnik V, Egiazarian K, Foi A, 2013. Nonlocal transform-domain filter for volumetric data denoising and reconstruction. IEEE Trans. Image Process 22, 119–133. [DOI] [PubMed] [Google Scholar]
- Maier-Hein KH, Neher PF, Houde JC, Cote MA, Garyfallidis E, Zhong J, Chamberland M, Yeh FC, Lin YC, Ji Q, Reddick WE, Glass JO, Chen DQ, Feng Y, Gao C, Wu Y, Ma J, He R, Li Q, Westin CF, Deslauriers-Gauthier S, Gonzalez JOO, Paquette M, St-Jean S, Girard G, Rheault F, Sidhu J, Tax CMW, Guo F, Mesri HY, David S, Froeling M, Heemskerk AM, Leemans A, Bore A, Pinsard B, Bedetti C, Desrosiers M, Brambati S, Doyon J, Sarica A, Vasta R, Cerasa A, Quattrone A, Yeatman J, Khan AR, Hodges W, Alexander S, Romascano D, Barakovic M, Auria A, Esteban O, Lemkaddem A, Thiran JP, Cetingul HE, Odry BL, Mailhe B, Nadar MS, Pizzagalli F, Prasad G, Villalon-Reina JE, Galvis J, Thompson PM, Requejo FS, Laguna PL, Lacerda LM, Barrett R, Dell’Acqua F, Catani M, Petit L, Caruyer E, Daducci A, Dyrby TB, Holland-Letz T, Hilgetag CC, Stieltjes B, Descoteaux M, 2017a. The challenge of mapping the human connectome based on diffusion tractography. Nat. Commun 8, 1349. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Maier-Hein KH, Neher PF, Houde JC, Cote MA, Garyfallidis E, Zhong JD, Chamberland M, Yeh FC, Lin YC, Ji Q, Reddick WE, Glass JO, Chen DQ, Feng YJ, Gao CF, Wu Y, Ma JY, Renjie H, Li Q, Westin CF, Deslauriers-Gauthier S, Gonzalez JOO, Paquette M, St-Jean S, Girard G, Rheault F, Sidhu J, Tax CMW, Guo FH, Mesri HY, David S, Froeling M, Heemskerk AM, Leemans A, Bore A, Pinsard B, Bedetti C, Desrosiers M, Brambati S, Doyon J, Sarica A, Vasta R, Cerasa A, Quattrone A, Yeatman J, Khan AR, Hodges W, Alexander S, Romascano D, Barakovic M, Auria A, Esteban O, Lemkaddem A, Thiran JP, Cetingul HE, Odry BL, Mailhe B, Nadar MS, Pizzagalli F, Prasad G, Villalon-Reina JE, Galvis J, Thompson PM, Requejo FD, Laguna PL, Lacerda LM, Barrett R, Dell’Acqua F, Catani M, Petit L, Caruyer E, Daducci A, Dyrby TB, Holland-Letz T, Hilgetag CC, Stieltjes B, Descoteaux M, 2017b. The challenge of mapping the human connectome based on diffusion tractography. Nat. Commun 8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Manjon JV, Coupe P, Marti-Bonmati L, Collins DL, Robles M, 2010. Adaptive nonlocal means denoising of MR images with spatially varying noise levels. J. Magn. Reson. Imag 31, 192–203. [DOI] [PubMed] [Google Scholar]
- Manjon JV, Coupe P, Buades A, Collins DL, Robles M, 2012. New methods for MRI denoising based on sparseness and self-similarity. Med. Image Anal 16, 18–27. [DOI] [PubMed] [Google Scholar]
- Manjon JV, Coupe P, Concha L, Buades A, Collins DL, Robles M, 2013. Diffusion weighted image denoising using overcomplete local PCA. PloS One 8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Manjon JV, Coupe P, Buades A, 2015. MRI noise estimation and denoising using nonlocal PCA. Med. Image Anal 22, 35–47. [DOI] [PubMed] [Google Scholar]
- Marčenko VA, Pastur LA, 1967. Distribution OF eigenvalues for some sets OF random matrices. Math. USSR Sbornik 1, 457–483. [Google Scholar]
- Mazziotta J, Toga A, Evans A, Fox P, Lancaster J, Zilles K, Woods R, Paus T, Simpson G, Pike B, Holmes C, Collins L, Thompson P, MacDonald D, Iacoboni M, Schormann T, Amunts K, Palomero-Gallagher N, Geyer S, Parsons L, Narr K, Kabani N, Le Goualher G, Boomsma D, Cannon T, Kawashima R, Mazoyer B, 2001. A probabilistic atlas and reference system for the human brain: international Consortium for Brain Mapping (ICBM). Phil. Trans. Biol. Sci 356, 1293–1322. [DOI] [PMC free article] [PubMed] [Google Scholar]
- McNab JA, Polimeni JR, Wang R, Augustinack JC, Fujimoto K, Stevens A, Triantafyllou C, Janssens T, Farivar R, Folkerth RD, Vanduffel W, Wald LL, 2013. Surface based analysis of diffusion orientation for identifying architectonic domains in the in vivo human cortex. Neuroimage 69, 87–100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Miller KL, Stagg CJ, Douaud G, Jbabdi S, Smith SM, Behrens TEJ, Jenkinson M, Chance SA, Esiri MM, Voets NL, Jenkinson N, Aziz TZ, Turner MR, Johansen-Berg H, McNab JA, 2011. Diffusion imaging of whole, post-mortem human brains on a clinical MRI scanner. Neuroimage 57, 167–181. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mugler JP, Brookeman JR, 1990. Three-dimensional magnetization-prepared rapid gradient-echo imaging (3D MP RAGE). Magn. Reson. Med 15, 152–157. [DOI] [PubMed] [Google Scholar]
- Mugler JP, Bao S, Mulkern RV, Guttmann CRG, Robertson RL, Jolesz FA, Brookeman JR, 2000. Optimized single-slab three-dimensional spin-echo MR imaging of the brain. Radiology 216, 891–899. [DOI] [PubMed] [Google Scholar]
- Neher PF, Laun FB, Stieltjes B, Maier-Hein KH, 2014a. Fiberfox: facilitating the creation of realistic white matter software phantoms. Magn. Reson. Med 72, 1460–1470. [DOI] [PubMed] [Google Scholar]
- Neher PF, Laun FB, Stieltjes B, Maier-Hein KH, 2014b. Fiberfox: facilitating the creation of realistic white matter software phantoms. Magn. Reson. Med 72, 1460–1470. [DOI] [PubMed] [Google Scholar]
- Nowak RD, 1999. Wavelet-based Rician noise removal for magnetic resonance imaging. IEEE Trans. Image Process 8, 1408–1419. [DOI] [PubMed] [Google Scholar]
- Parker GJM, Schnabel JA, Symms MR, Werring DJ, Barker GJ, 2000. Nonlinear smoothing for reduction of systematic and random errors in diffusion tensor imaging. J. Magn. Reson. Imag 11, 702–710. [DOI] [PubMed] [Google Scholar]
- Patel V, Shi Y, Thompson PM, Toga AW, 2011. K-SVD for HARDI denoising. In: 2011 IEEE International Symposium on Biomedical Imaging: from Nano to Macro, pp. 1805–1808. [Google Scholar]
- Pierpaoli C, Jezzard P, Basser PJ, Barnett A, Di Chiro G, 1996. Diffusion tensor MR imaging of the human brain. Radiology 201, 637–648. [DOI] [PubMed] [Google Scholar]
- Pruessmann KP, Weiger M, Scheidegger MB, Boesiger P, 1999. SENSE: sensitivity encoding for fast MRI. Magn. Reson. Med 42, 952–962. [PubMed] [Google Scholar]
- Rajwade A, Rangarajan A, Banerjee A, 2013. Image denoising using the higher order singular value decomposition. IEEE Trans. Pattern Anal. Mach. Intell 35, 849–862. [DOI] [PubMed] [Google Scholar]
- Ridgway GR, Omar R, Ourselin S, Hill DLG, Warren JD, Fox NC, 2009. Issues with threshold masking in voxel-based morphometry of atrophied brains. Neuroimage 44, 99–111. [DOI] [PubMed] [Google Scholar]
- Rocke DM, Durbin B, 2003. Approximate variance-stabilizing transformations for gene-expression microarray data. Bioinformatics 19, 966–972. [DOI] [PubMed] [Google Scholar]
- Roemer PB, Edelstein WA, Hayes CE, Souza SP, Mueller OM, 1990. The NMR phased array. Magn. Reson. Med 16, 192–225. [DOI] [PubMed] [Google Scholar]
- Snook L, Plewes C, Beaulieu C, 2007. Voxel based versus region of interest analysis in diffusion tensor imaging of neurodevelopment. Neuroimage 34, 243–252. [DOI] [PubMed] [Google Scholar]
- Sotiropoulos SN, Moeller S, Jbabdi S, Xu J, Andersson JL, Auerbach EJ, Yacoub E, Feinberg D, Setsompop K, Wald LL, Behrens TEJ, Ugurbil K, Lenglet C, 2013. Effects of image reconstruction on fiber orientation mapping from multichannel diffusion MRI: reducing the noise floor using SENSE. Magn. Reson. Med 70, 1682–1689. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sotiropoulos SN, Hernández-Fernández M, Vu AT, Andersson JL, Moeller S, Yacoub E, Lenglet C, Ugurbil K, Behrens TEJ, Jbabdi S, 2016. Fusion in diffusion MRI for improved fibre orientation estimation: an application to the 3T and 7T data of the Human Connectome Project. Neuroimage 134, 396–409. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sporns O, Tononi G, Kötter R, 2005. The human connectome: a structural description of the human brain. PLoS Comput. Biol 1, 0245–0251. [DOI] [PMC free article] [PubMed] [Google Scholar]
- St-Jean S, Coupe P, Descoteaux M, 2016. Non Local Spatial and Angular Matching: enabling higher spatial resolution diffusion MRI datasets through adaptive denoising. Med. Image Anal 32, 115–130. [DOI] [PubMed] [Google Scholar]
- Tanner JE, Stejskal EO, 1968. Restricted self-diffusion of protons in colloidal systems by pulsed-gradient spin-echo method. J. Chem. Phys 49, 1768. [Google Scholar]
- Thiebaut de Schotten M, Ffytche DH, Bizzi A, Dell’Acqua F, Allin M, Walshe M, Murray R, Williams SC, Murphy DG, Catani M, 2011. Atlasing location, asymmetry and inter-subject variability of white matter tracts in the human brain with MR diffusion tractography. Neuroimage 54, 49–59. [DOI] [PubMed] [Google Scholar]
- Tournier JD, Mori S, Leemans A, 2011. Diffusion tensor imaging and beyond. Magn. Reson. Med 65, 1532–1556. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tristan-Vega A, Aja-Fernandez S, 2010. DWI filtering using joint information for DTI and HARDI. Med. Image Anal 14, 205–218. [DOI] [PubMed] [Google Scholar]
- Uǧurbil K, Xu J, Auerbach EJ, Moeller S, Vu AT, Duarte-Carvajalino JM, Lenglet C, Wu X, Schmitter S, Van de Moortele PF, Strupp J, Sapiro G, De Martino F, Wang D, Harel N, Garwood M, Chen L, Feinberg DA, Smith SM, Miller KL, Sotiropoulos SN, Jbabdi S, Andersson JLR, Behrens TEJ, Glasser MF, Van Essen DC, Yacoub E, 2013. Pushing spatial and temporal resolution for functional and diffusion MRI in the Human Connectome Project. Neuroimage 80, 80–104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Van Essen DC, Smith SM, Barch DM, Behrens TEJ, Yacoub E, Ugurbil K, 2013. The Wu-minn human connectome Project: an overview. Neuroimage 80, 62–79. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Veraart J, Fieremans E, Novikov DS, 2016a. Diffusion MRI noise mapping using random matrix theory. Magn. Reson. Med 76, 1582–1593. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Veraart J, Novikov DS, Christiaens D, Ades-aron B, Sijbers J, Fieremans E, 2016b. Denoising of diffusion MRI using random matrix theory. Neuroimage 142, 394–406. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vu AT, Auerbach E, Lenglet C, Moeller S, Sotiropoulos SN, Jbabdi S, Andersson J, Yacoub E, Ugurbil K, 2015. High resolution whole brain diffusion imaging at 7T for the Human Connectome Project. Neuroimage 122, 318–331. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wakana S, Caprihan A, Panzenboeck MM, Fallon JH, Perry M, Gollub RL, Hua KG, Zhang JY, Jiang HY, Dubey P, Blitz A, van Zijl P, Mori S, 2007. Reproducibility of quantitative tractography methods applied to cerebral white matter. Neuroimage 36, 630–644. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Walsh DO, Gmitro AF, Marcellin MW, 2000. Adaptive reconstruction of phased array MR imagery. Magn. Reson. Med 43, 682–690. [DOI] [PubMed] [Google Scholar]
- Wedeen VJ, Rosene DL, Wang R, Dai G, Mortazavi F, Hagmann P, Kaas JH, Tseng WYI, 2012. The geometric structure of the brain fiber pathways. Science 335, 1628–1634. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Werring DJ, Clark CA, Barker GJ, Thompson AJ, Miller DH, 1999. Diffusion tensor imaging of lesions and normal-appearing white matter in multiple sclerosis. Neurology 52, 1626–1632. [DOI] [PubMed] [Google Scholar]
- Wiest-Daessle N, Prima S, Coupe P, Morrissey SP, Barillot C, 2008. Rician noise removal by non-local means filtering for low signal-to-noise ratio MRI: applications to DT-MRI. Med. Image Comput. Comput.-Assist. Interv. - Miccai 5242, 171–179, 2008, Pt Ii, Proceedings. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wirestam R, Bibic A, Latt J, Brockstedt S, Stahlberg F, 2006. Denoising of complex MRI data by wavelet-domain filtering: application to high-b-value diffusion-weighted imaging. Magn. Reson. Med 56, 1114–1120. [DOI] [PubMed] [Google Scholar]
- Wu X, Auerbach EJ, Vu AT, Moeller S, Lenglet C, Schmitter S, Van de Moortele P-F, Yacoub E, Uğurbil K, 2018. High-resolution whole-brain diffusion MRI at 7T using radiofrequency parallel transmission. Magn. Reson. Med 80, 1857–1870. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wu X, Auerbach EJ, Vu AT, Moeller S, Van de Moortele P-F, Yacoub E, Uğurbil K, 2019. Human Connectome Project-style resting-state functional MRI at 7 Tesla using radiofrequency parallel transmission. Neuroimage 184, 396–408. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Xue R, van Zijl PCM, Crain BJ, Solaiyappan M, Mori S, 1999. In vivo three-dimensional reconstruction of rat brain axonal projections by diffusion tensor imaging. Magn. Reson. Med 42, 1123–1127. [DOI] [PubMed] [Google Scholar]
- Zhang XY, Peng J, Xu M, Yang W, Zhang Z, Guo H, Chen WF, Feng QJ, Wu EX, Feng YQ, 2017. Denoise diffusion-weighted images using higher-order singular value decomposition. Neuroimage 156, 128–145. [DOI] [PubMed] [Google Scholar]
- Zhu Y, 2004. Parallel excitation with an array of transmit coils. Magn. Reson. Med 51, 775–784. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


