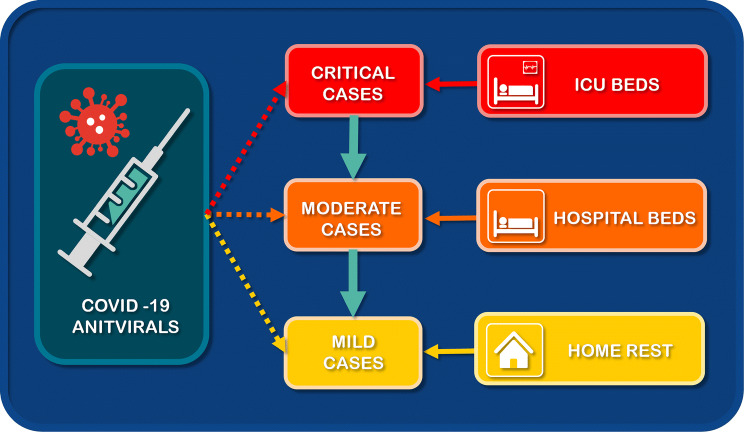
Abstract
Abstract
The global scientific community has intensified efforts to develop, test, and commercialize pharmaceutical products to deal with the COVID-19 pandemic. Trials for both antivirals and vaccines are in progress; candidates include existing repurposed drugs that were originally developed for other ailments. Once these are shown to be effective, their production will need to be ramped up rapidly to keep pace with the growing demand as the pandemic progresses. It is highly likely that the drugs will be in short supply in the interim, which leaves policymakers and medical personnel with the difficult task of determining how to allocate them. Under such conditions, mathematical models can provide valuable decision support. In particular, useful models can be derived from process integration techniques that deal with tight resource constraints. In this paper, a linear programming model is developed to determine the optimal allocation of COVID-19 drugs that minimizes patient fatalities, taking into account additional hospital capacity constraints. Two hypothetical case studies are solved to illustrate the computational capability of the model, which can generate an allocation plan with outcomes that are superior to simple ad hoc allocation.
Graphic abstract
Keywords: Pharmaceutical shortage, Resource allocation, COVID-19, Mathematical programming, Disease outbreak, Sustainable Development Goals
Introduction
The COVID-19 pandemic has escalated dramatically in the span of just a few months into the worst health crisis of the twenty-first century (Bandyopadhyay 2020). According to the World Health Organization (WHO 2020), the disease has now infected more than 7 million people and killed over 400,000 victims worldwide. The USA, Brazil, Mexico, Spain, Italy, Germany, France, the UK, China, Iran, and Turkey have been hit particularly hard. In contrast, some smaller countries, such as Taiwan, Singapore, and New Zealand, have demonstrated relatively successful control safety measures. The situation in highly populated developing countries (e.g., India) and regions (e.g., Southeast Asia) is still unfolding and uncertain.
The pandemic has adverse implications on international progress toward most of the Sustainable Development Goals (SDGs). Ferguson et al. (2020) reported simulations showing that the COVID-19 pandemic, left unchecked, can rapidly overwhelm the healthcare systems of even affluent countries. They also showed how aggressive suppression measures—i.e., lockdowns with stringent restrictions on the mobility of the public—can delay the progress of the pandemic to minimize the strain on healthcare capacity. Numerous countries responded by imposing lockdowns and other nonpharmaceutical interventions (NPIs) to “flatten the curve” and spread out COVID-19 cases over a more extended period (Ferguson et al. 2020).
In addition to health issues, COVID-19 has links to different dimensions of sustainability. The virus is believed to have originated via cross-species transmission from bats (Zhou et al. 2020) or pangolins (Zhang et al. 2020). Genetic analysis of the virus suggests that it may have been spreading more extensively in humans in late 2019 than previously thought (Andersen et al. 2020). The emergence of this novel pathogen underscores the risks resulting from human encroachment on natural habitats (Cunningham et al. 2017). The origin of this virus and the response of governments have mixed implications for ecosystems. On the one hand, the post-COVID-19 era may see more stringent regulations on the capture and consumption of wildlife (Yuan et al. 2020). On the other hand, ubiquitous lockdown measures have effectively put a stop to many conservation efforts (Corlett et al. 2020). The biosphere will also be affected by environmental impacts resulting from healthcare measures. For example, the sheer volume of hazardous medical waste from hospitals threatens to overwhelm waste treatment capacity in the same manner that the pandemic surge threatens to overwhelm healthcare systems (Klemeš et al. 2020). Air emissions from the cremation of the remains of COVID-19 victims will also escalate. Once effective drugs are found for the treatment for COVID-19, metabolites in human waste will become an issue (Celiz et al. 2009). Such trace pollutants cannot be destroyed by sewage treatment systems and require novel processing technologies for proper waste management (Majumdar and Pal 2020).
The suppression measures being implemented in most parts of the world, while necessary, also come with adverse socioeconomic consequences. Reduced economic output creates upstream and downstream cascading effects that can cross national boundaries (Yu and Aviso 2020). These impacts are then felt by workers in different economic sectors as loss of income (Santos 2020). The pandemic has also led to an increase in the level of output in other industries, such as those providing medical supplies, delivery services, and Web-based communication platforms to facilitate remote work and education. Some of these responses may eventually persist in the post-COVID-19 world as permanent post-disaster structural changes in economic systems (Okuyama 2014). These changes will have mixed positive and negative environmental impacts. For example, more extensive use of work-from-home arrangements after the pandemic will reduce greenhouse gas emissions and air pollution generated from daily commuting.
In response to the pandemic, efforts to develop pharmaceutical interventions for COVID-19 have been intensified. New vaccines and dedicated antivirals are currently under development, but such products are unlikely to be available within 2020. Repurposing existing drugs offers the promise of a more timely solution. The World Health Organization (WHO) is currently running the SOLIDARITY trials to find therapeutic drugs for COVID-19. The candidate drugs in the trial are already commercially available for the treatment for other diseases. These can, in principle, be administered sooner than other antivirals and vaccines, which will still need to pass regulatory hurdles (Kupferschmidt and Cohen 2020). However, it has also been pointed out by Yu et al. (2020) that ramping up the production capacity of these drugs will be a serious engineering and business challenge for pharmaceutical supply chains. Potential roadblocks include bottlenecks in drug synthesis or the sourcing of specialty chemical precursors. There is also a clear risk of countries imposing barriers to the trade of critical products or raw materials.
In the likely event of future shortages of COVID-19 drugs, mathematical models can be used to aid decision-makers in developing rational allocation policies that are superior to ad hoc or heuristic triage approaches. Such models can be used for the allocation of vaccines and antivirals (Medlock and Galvani 2009; Koyuncu and Erol 2010; Tuite et al. 2010) and can provide a computational framework for developing policies that respond dynamically to demand surge and shifting conditions (Arora et al. 2010; Yaesoubi and Cohen 2016). They can be used to provide a rigorous basis for government regulations to manage drug shortages (Musazzi et al. 2020).
The field of process integration (PI) offers a practical engineering toolbox for dealing with such problems. PI was developed initially as a systematic and holistic approach for designing sustainable, resource-efficient industrial systems (El-Halwagi 2006). It uses computational techniques such as pinch analysis (Klemeš et al. 2018), mathematical programming (Klemeš and Kravanja 2013), and process graphs (Friedler et al. 2019) to aid in the design or retrofit of industrial plants and planning of larger-scale systems such as industrial parks and supply chains. While the original purpose was to economize on the use of industrial inputs such as fuel and water, there has been notable diversification in the literature in recent years, demonstrating the use of core PI principles for the efficient use of resources in general (Klemeš et al. 2018; Friedler et al. 2019). Recent studies have applied PI principles as a decision-support tool on a pandemic outbreak. Liu et al. (2019) developed a mixed-integer nonlinear programming (MINLP) model to determine when to open and close newly isolated wards while quantifying the capacity and the budget requirement for the H1N1 outbreak. Aviso et al. (2018) developed a fuzzy input–output optimization model for the allocation of medical personnel in a hospital during a pandemic. Sun et al. (2014) developed a multiobjective optimization model for patient and resource allocation in hospitals to minimize the distance traveled by patients in an influenza outbreak. However, no studies have been found which consider supply and hospital constraints while determining the optimal drug allocation.
In this paper, we develop a linear programming (LP) model based on PI principles to determine the optimal allocation of future COVID-19 drugs considering constraints on their supply, as well as hospital capacity. There is still considerable uncertainty in the state of scientific knowledge on COVID-19, which makes it impossible to obtain clear-cut data on case fatality rates and responses to treatment. Nevertheless, the principle of allocating scarce resources to achieve maximum benefit can be demonstrated with a representative example. Thus, our work emphasizes the model’s general capacity to compute solutions, rather than the specific numerical values of model parameters. The capabilities of the model are illustrated using two hypothetical case studies. In both examples, it is shown that the LP model can reduce patient fatalities compared to ad hoc or heuristic allocation policies. The rest of the paper is organized as follows: The next section gives the formal problem statement that the LP addresses. Then, the model formulation is given. A simple illustrative and hypothetical example meant for pedagogical purposes is solved first, followed by a simulated scenario based on the projected near-future situation in the National Capital Region (NCR) of the Philippines. The practical implications of the use of the model are discussed. Finally, the conclusions and prospects for future work are discussed.
Problem statement
The formal problem addressed by the model is as follows: given the following user-specified inputs:
A limited amount of antivirals that can be given to an infected population;
m severity levels of infection each requiring a specific level of health care;
n population groups with a known case fatality rate of patients in each severity level when receiving or not receiving appropriate health care;
o regions where there are cases of infection;
p types of hospital resources with known availability for each region;
Efficacy of antivirals, as quantified by the average transfer rate of patients between severity levels upon receipt of treatment;
The model determines the optimal allocation of available antivirals and the corresponding minimum number of total deaths. The model is static and assumes a fixed set of patients and resources for a given planning time frame. In practice, it can be applied sequentially to a given cohort of patients using resource data available then. Input data can be subsequently updated as new data are acquired for replanning.
Model formulation
| Sets | |
| M | Set of severity levels |
| N | Set of population age-group |
| O | Set of regions |
| P | Set of available hospital resources |
| W | Set of available antiviral types |
| Indices | |
| i | Index for severity level |
| j | Index for population group |
| k | Index for region |
| r | Index for resource type |
| v | Index for antiviral type |
| Parameters | |
| Case fatality rate of individuals in severity level i who did not get needed resource | |
| Case fatality rate of individuals in severity level i who received proper resources | |
| Total number of antiviral type v available | |
| Probability that group j will be in severity level i for antiviral given | |
| Amount of hospital resource r needed by individual in severity level i | |
| Total available resource r in region k | |
| Total number of infected symptomatic individuals in population group j in region k | |
| Variables | |
| Actual number of resource type r used in region k | |
| Number of individuals in population group j in region k that were given antiviral v | |
| Number of individuals in severity level i in region k after they were given antiviral v | |
| Number of individuals in severity level i, in region k who did not receive required hospital resources | |
| Number of individuals in severity level i in region k who received required hospital resources | |
| Total number of individuals in severity level i in region k | |
| Total number of deaths in region k among those who had access to hospital resources | |
| Total number of deaths in region k among those who did not have access to required hospital resources | |
The overall objective is to minimize the total number of deaths as given by Eq. 1 where is the total number of deaths among those who had access to hospital resources in region k, and is the total number of deaths among those who did not have access to hospital resources in region k:
| 1 |
The sum of infected symptomatic individuals classified as those not given antivirals and those given antiviral of a certain type () for each population group j, region k, and antiviral type v should equal the total number of infected symptomatic individuals for each population group and region (), as shown in Eq. 2. For an infected symptomatic individual in group j, the probability of getting an infection severity level i will depend on whether the person was given an antiviral or not, and if yes, the type of antiviral v given as defined in . For each drug, these parameters summarize how treatment reduces symptom severity. The total number of individuals from region k who received antiviral type v and experienced a severity level i is obtained using Eq. 3; are the total number of individuals in severity level i for region k after getting the treatment for antiviral v. The total number of infected individuals in each severity level for each region () is then given by Eq. 4:
| 2 |
| 3 |
| 4 |
The total number of individuals to be given the antiviral should not exceed the total number of antivirals available (Eq. 5):
| 5 |
Individuals who experience severity level i will require resource type r as indicated in . Thus, region k can only provide for a limited number of infected individuals () based on how much resource type r is available in region k (), as shown in Eq. 6. All other infected individuals will not be able to access the required hospital resource (), as shown in Eq. 7. The actual number of resource type r used in region k () is given by Eq. 8:
| 6 |
| 7 |
| 8 |
The case fatality rate will then depend on the severity level and whether the infected individual was given access to the required hospital resources as deemed necessary by the infection severity where is the case fatality rate for severity level i for individuals with no access to resource and is the case fatality rate for severity level i for individuals with access to hospital resources. The total number of deaths in region k for those who did not have access to the resources is given by Eq. 9, while the total number of deaths in region k even with access to resources is shown in Eq. 10:
| 9 |
| 10 |
This formulation is an LP model that can be solved for global optimality with no computational difficulties. The next two sections apply the model to case studies implemented using the commercial optimization software LINGO 18.0. However, the model itself is generic and can be implemented in other software, including spreadsheet applications.
Case study 1
In this section, a simple hypothetical example is given to illustrate the capabilities of the model. Given that there is one region with individuals infected by a particular epidemic and that the cases can be grouped into mild, moderate, and critical cases, the total number of infected individuals for each population group is summarized in Table 1.
Table 1.
Number of infected symptomatic individuals per region and population group (
| Severity level | Number of cases |
|---|---|
| Mild | 800 |
| Moderate | 150 |
| Critical | 50 |
| Total | 1000 |
Three different treatments are possible: any given patient can be given Antiviral A, Antiviral B, or none. The probability of each risk group falling under infection severity levels based on the treatment received is given in Table 2. Note that these probabilities do not include the probability of being infected and being asymptomatic. The effectiveness of the antivirals is quantified by the transition rate of patients to lower severity levels. It can be seen that if an individual is administered with antiviral, the severity of the infection can be reduced. For example, without treatment, the patients remain in their original severity level (as signified by values of 1 in the diagonal of the transfer matrix and 0 in all other cells) and suffer the same mean case fatality rate. On the other hand, if Antiviral A is given to patients that initially require ICU confinement (or critical severity), the treatment is sufficiently effective to allow 80% of such patients to require less resource-intensive regular hospital care, i.e., regular hospital beds. It should be noted that Antivirals A and B are hypothetical, and the efficacy figures shown here are hypothetical and purely for illustrative purposes. However, the model can use empirical parameters for future COVID-19 drugs once the results of ongoing trials are published.
Table 2.
Probability of infection severity due to the risk group and administration of antiviral
| Group severity | No antiviral | With antiviral A | With antiviral B | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Mild | Moderate | Critical | Mild | Moderate | Critical | Mild | Moderate | Critical | |
| Mild | 1 | 0 | 0 | 1 | 0.6 | 0 | 1 | 0.75 | 0 |
| Moderate | 0 | 1 | 0 | 0 | 0.4 | 0.8 | 0 | 0.25 | 0.6 |
| Critical | 0 | 0 | 1 | 0 | 0 | 0.2 | 0 | 0 | 0.4 |
The following tables are illustrative and use hypothetical data. For each severity level, the resource requirements are shown in Table 3. For this example, there are three types of health facilities considered as resources: home care, regular hospital beds, and intensive care unit (ICU) beds. An individual with mild severity requires only one home care resource, those with moderate severity requires only one regular hospital bed resource, and those with critical severity requires only one ICU resource. The total number of each resource type available in the region is given in Table 4. The case fatality rate of an individual is affected by whether they receive the necessary care depending on the severity of their illness. The assumed case fatality rates are summarized in Table 5. Furthermore, only 100 treatment courses of Antiviral A are available, while there are 200 treatment courses of Antiviral B. Each treatment course corresponds to daily dosage multiplied by the total duration of treatment, which is assumed to be the same for all patients.
Table 3.
Health facility requirement based on infection severity level ()
| Severity | Home care | Regular hospital bed | Intensive care unit |
|---|---|---|---|
| Mild | 1 | 0 | 0 |
| Moderate | 0 | 1 | 0 |
| Critical | 0 | 0 | 1 |
Table 4.
Available health facilities
| Health facility | Number of units |
|---|---|
| Home care | Unlimited |
| Hospital beds | 100 |
| Intensive care units | 20 |
Table 5.
Case fatality rates by severity level and health facility access
| Severity | No appropriate health facility | With appropriate health facility |
|---|---|---|
| Mild | 0.0 | 0.0 |
| Moderate | 0.2 | 0.05 |
| Critical | 1.0 | 0.50 |
Different scenarios were considered for this example: Scenario 1.1: No antivirals are available; Scenario 1.2: Both antivirals are available and used interchangeably; Scenario 1.3: Allocation is optimized based on antiviral availability and known efficacy. This particular case study results in 150 variables, and all cases were solved in a negligible computational time of 0.01 s using a laptop running on Windows 10 using the Intel® Core™ i7-6500 CPU Processor at 2.50 GHz.
Scenario 1.1
This scenario assumes the baseline case where no drugs are available to treat COVID-19. Solving Eq. 1 subject to the constraints outlined in Eqs. 2 to 10 with Eq. 5 indicates that there are no antivirals available (. Table 6 shows the number of individuals who receive access to the health facility appropriate to the severity of their symptoms, as well as those who do not. Since the total number of hospital beds available is only 100, 50 other patients suffering from moderate severity do not get access to this resource. Similarly, only 20 critical patients can be prioritized for the 20 ICU facilities available, while 30 others do not. The patients that do not get access to the health facility appropriate to the severity of their symptoms suffer higher case fatality rates, as shown in Table 5. As a result, a total of 55 deaths are experienced.
Table 6.
Severity of infected individuals and their access to the appropriate health facility for Scenario 1.1
| Severity | With appropriate health facility | No appropriate health facility | Total |
|---|---|---|---|
| Mild | 800 | 0 | 800 |
| Moderate | 100 | 50 | 150 |
| Critical | 20 | 30 | 50 |
Scenario 1.2
For Scenario 1.2, an ad hoc allocation plan is assumed where the two antivirals are used interchangeably and prioritized for use by patients depending on severity level. The allocation of the antivirals is shown in Table 7. A total of 300 individuals are given antivirals, and as a result, the number of mild cases increases to 905 patients (13.1% more than Scenario 1.1), while the moderate cases reduced to 78 patients (48.0% lower than Scenario 1.1) and the critical cases to 17 patients (67% lower than Scenario 1.1). In addition, all patients are able to get access to the appropriate resources within the limits of the hospital. As a result, the number of deaths is reduced to 12, which is a 78.2% reduction compared to Scenario 1.1 (Table 8).
Table 7.
Allocation of antivirals for Scenario 1.2
| Mild | Moderate | Critical | Total antiviral used | |
|---|---|---|---|---|
| No antiviral | 700 | 0 | 0 | NA |
| Antiviral A | 33 | 50 | 17 | 100 |
| Antiviral B | 67 | 100 | 33 | 200 |
| Total infected | 800 | 150 | 50 |
Table 8.
Severity of infected symptomatic individuals and their access to the appropriate health facility for Scenario 1.2
| Severity | With appropriate health facility | No appropriate health facility | Total |
|---|---|---|---|
| Mild | 905 | 0 | 905 |
| Moderate | 78 | 0 | 78 |
| Critical | 17 | 0 | 17 |
Scenario 1.3
For Scenario 1.3, the LP model is applied to determine the best drug allocation. There is enough Antiviral A for 100 patients and enough Antiviral B for 200 patients. Instead of using the two drugs interchangeably, the model assigns them to patients based on quantitative measures of their efficacy for patients at different severity levels. The optimal result of antiviral allocation is shown in Table 9, while the number of cases with respect to severity is shown in Table 10. It can be seen that Antiviral A is prioritized for the critical cases, while Antiviral B is only used for moderate cases. This allocation follows logically from performance parameters defined in Table 2, which shows that Antiviral A is the superior product for critical cases, while Antiviral B is superior for moderate cases. All surplus doses of the two drugs can then be given to patients with mild cases or, alternatively, held in reserve for future patients. The option not to administer medication to mild cases can also reduce downstream environmental impacts from trace pollutants from drug metabolization. As in Scenario 2, all individuals are able to receive access to the appropriate health facilities because the antivirals allow patients to be moved to facilities that fall within hospital resource limits. The total number of mild cases increases to 912 (14.0% more than Scenario 1.1), the moderate case reduces to 78 patients (48.0% less than Scenario 1.1), and the critical cases also reduce to ten patients (80% less than Scenario 1.1). As a result, the total number of the expected number of deaths is further reduced to nine individuals, which is an 83.6% reduction from Scenario 1.1. This figure is also 25% lower than the fatality level in Scenario 1.2.
Table 9.
Allocation of antivirals for Scenario 1.3
| Mild | Moderate | Critical | Total antiviral | |
|---|---|---|---|---|
| No antiviral | 700 | 0 | 0 | NA |
| Antiviral A | 50 | 0 | 50 | 100 |
| Antiviral B | 50 | 150 | 0 | 200 |
| Total infected symptomatic | 800 | 150 | 50 |
Table 10.
Severity of infected symptomatic individuals and their access to appropriate resources for Scenario 1.3
| Severity | With appropriate health facility | No appropriate health facility | Total |
|---|---|---|---|
| Mild | 912 | 0 | 912 |
| Moderate | 78 | 0 | 78 |
| Critical | 10 | 0 | 10 |
A comparative summary of all three scenarios is shown in Table 11.
Table 11.
Summary of results
| Scenario 1.1 | Scenario 1.2 | Scenario 1.3 | ||||
|---|---|---|---|---|---|---|
| Antiviral A | Antiviral B | Antiviral A | Antiviral B | Antiviral A | Antiviral B | |
| Mild | 0 | 0 | 33 | 67 | 50 | 50 |
| Moderate | 0 | 0 | 50 | 100 | 0 | 150 |
| Critical | 0 | 0 | 17 | 33 | 50 | 0 |
| With appropriate health facility | 920 | 1000 | 1000 | |||
| No appropriate health facility | 80 | 0 | 0 | |||
| Deaths | 55 | 12 | 9 | |||
Case study 2
Case study 2 builds upon the previous set of computational experiments by considering multiple regions in the National Capital Region (NCR). The densely populated NCR has a daytime population of 12.88 million and accounts for 12.8% of the 100.98 million total Philippine population, according to the Philippine Statistics Authority’s 2015 census (PSA 2020a, b). It is the economic and political capital of the Philippines and is currently the country’s epicenter of COVID-19 infections. For this example, each of the 16 component cities and one municipality in the NCR are considered distinct regions. The subsequent set of computations uses the same set of parameters from the first case study, namely the probability of infections (Table 2), resource requirement based on infection severity level (Table 3), and the case fatality rates (Table 5). However, hospital resource availability was obtained from official statistics of the Philippine Department of Health (DoH 2020). Detailed data for the component cities and municipality of NCR are given in “Appendix.” This subsequent case study results in a model with 1003 continuous variables, with a computation time of 2.89 s using a laptop running on Windows 10 using the Intel® Core™ i7-6500 CPU Processor at 2.50 GHz.
Scenario 2.1: Availability of antiviral drugs
This scenario considered how drug availability affects the number of deaths and the number of patients that would need access to health facilities. This was implemented by varying the percentage from 10 to 100% of those patients that would be given either Antiviral A or B. Table 12 shows the number of deaths alongside how the Antiviral A and Antiviral B will be allocated to the infected population. It can be seen that the number of deaths decreases with the increasing availability of the two drugs. However, the number begins to plateau once drug availability reaches about 70%, as shown in Fig. 1. This is primarily because of the large proportion of the infected population with mild cases of the disease. No added benefit is seen even if they take these drugs since they will remain under the same severity level. Hence, they need not be given any antiviral drugs, regardless of availability. It is assumed here that any surplus is stockpiled in reserve for a future surge of serious COVID-19 cases. Furthermore, as in Case Study 1, for critical cases, Antiviral A had a higher efficacy level than Antiviral B. Figures 2 and 3 show how Antiviral A is allocated to critical cases, while Antiviral B is allocated to moderate cases.
Table 12.
Optimal allocation of antivirals at different levels of supply availability in Scenario 2.1
| Fractional availability | Deaths | Mild | Moderate | Critical | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| No antiviral | Antiviral A | Antiviral B | No antiviral | Antiviral A | Antiviral B | No antiviral | Antiviral A | Antiviral B | ||
| 0.1 | 16,527 | 32,577 | 0 | 0 | 45,087 | 0 | 0 | 8708 | 9597 | 0 |
| 0.2 | 10,841 | 32,577 | 0 | 0 | 44,094 | 0 | 994 | 105 | 18,200 | 0 |
| 0.3 | 9421 | 32,577 | 0 | 0 | 34,602 | 0 | 10,486 | 0 | 18,305 | 0 |
| 0.4 | 8217 | 32,577 | 0 | 0 | 25,005 | 0 | 20,083 | 0 | 18,305 | 0 |
| 0.5 | 7076 | 32,577 | 0 | 0 | 15,408 | 0 | 29,680 | 0 | 18,305 | 0 |
| 0.6 | 6030 | 32,577 | 0 | 0 | 5811 | 0 | 39,276 | 0 | 18,305 | 0 |
| 0.7 | 5400 | 32,577 | 0 | 0 | 42 | 0 | 45,046 | 0 | 18,305 | 0 |
| 0.8 | 5397 | 32,577 | 0 | 0 | 0 | 0 | 45,087 | 0 | 18,305 | 0 |
| 0.9 | 5397 | 32,577 | 0 | 0 | 0 | 0 | 45,087 | 0 | 18,305 | 0 |
| 1 | 5397 | 32,577 | 0 | 0 | 0 | 0 | 45,087 | 0 | 18,305 | 0 |
Fig. 1.
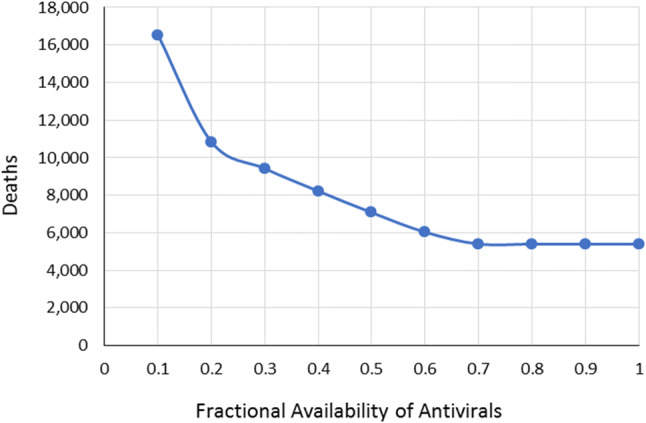
Variation in the number of deaths relative to the availability of antivirals
Fig. 2.
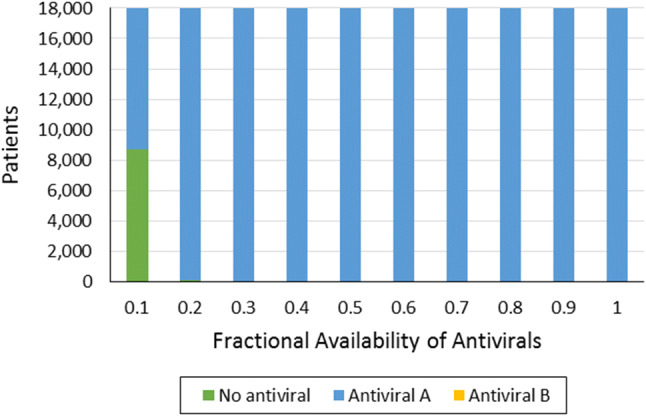
Allocation of antivirals to critical-case patients
Fig. 3.

Allocation of antivirals to moderate-case patients
It is interesting to note that when the fractional availability of antivirals was at 0.2, 105 critical patients were not provided with an antiviral even when 994 patients of moderate severity were given antiviral B. This result is primarily due to the efficiency of the antiviral on a particular severity group. Based on Table 2, it can be seen that antiviral B had a better efficiency at reducing the severity of individuals in the moderate severity group such that 75% will now experience mild symptoms. In contrast, providing antivirals to the critical severity group only results in 60% of critical cases being reduced to moderate severity. As a result, individuals who were initially in the moderate severity group will have a higher chance of recovering and a greater contribution toward lowering case fatality rates.
Figure 4 shows the proportion of patients who were able to gain access to the hospital facility that they need, which are appropriate to the severity of the infection. The results highlight how antiviral drugs decrease the burden on hospital resources, which may be needed for patients with other ailments. At 100% antiviral availability, most of those infected will now be classified as mild cases that only need home care. Conversely, the need for health facilities (i.e., regular hospital beds and ICU beds) increases as drug availability decreases.
Fig. 4.

Distribution of patients at different levels of antiviral availability
Scenario 2.2: Availability of health facilities dedicated to COVID-19 patients
The second scenario alternatively considers how the availability of appropriate health facilities affects the number of deaths and access to the needed level of care with respect to the severity of the infection. In this scenario, it was assumed that drug availability is 100%, i.e., all patients can get the antiviral drugs they need. As in the first scenario, the number of deaths decreases as more hospital health facilities get assigned specifically for COVID-19 patients (Fig. 5). This result is due to patients falling under the different severity levels being able to get appropriate treatment. For instance, critical patients are able to access ICU beds, while those classified under moderate severity are assigned to regular beds inside the hospital (Fig. 6). Another key observation here is that the number of deaths, even with only 10% availability, is still lower than the number recorded from Scenario 2.1. Again, this is because the antiviral drugs lower the severity levels of the infections—allowing some of the patients to become mild cases that will only require home care (Table 13).
Fig. 5.
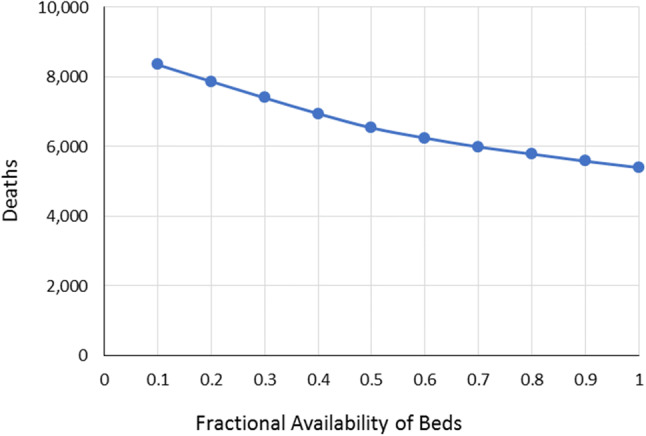
Variation in the number of deaths relative to the availability of health facility
Fig. 6.
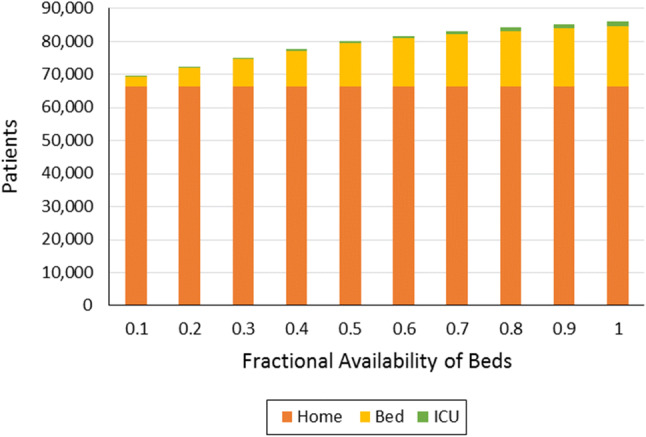
Distribution of patients at different levels of health facility availability
Table 13.
Optimal patient outcomes at different levels of health facility availability in Scenario 2.2
| Fractional availability | Deaths | Access to health facility | ||
|---|---|---|---|---|
| 0.1 | 8349 | Home | Bed | ICU |
| 0.2 | 7868 | 66,392 | 2806 | 149 |
| 0.3 | 7397 | 66,392 | 5534 | 291 |
| 0.4 | 6945 | 66,392 | 8209 | 432 |
| 0.5 | 6538 | 66,392 | 10,751 | 572 |
| 0.6 | 6246 | 66,392 | 12,996 | 713 |
| 0.7 | 5991 | 66,392 | 14,473 | 854 |
| 0.8 | 5786 | 66,392 | 15,712 | 992 |
| 0.9 | 5581 | 66,392 | 16,633 | 1126 |
| 1 | 5397 | 66,392 | 17,553 | 1259 |
Practical implications
The search for effective antivirals to treat COVID-19 is a scientific process, which will eventually have to be followed by the business and engineering problem of production scale-up (Yu et al. 2020). Drug shortages are a plausible scenario due to the scale of the pandemic. There is a risk that these scarce resources may not be optimally allocated. Experience with the scarcity of human resources, hospital beds, and other supplies in Italy illustrates that the patient-centric outlook of frontline medical personnel may fail to take into account critical system-level features of the pandemic (Ferrari et al. 2020). In other words, decisions that may seem optimal for individual patients, or for small groups of patients, may lead to nonoptimal outcomes for the entire healthcare system.
The holistic perspective that underlies PI methodology lends itself to addressing this problem. The LP model developed in this work can optimize drug allocation at the system level, taking into account background conditions such as disease incidence and the local availability of various health system resources. Given data on such conditions, the model can generate a drug allocation plan that minimizes total fatalities by reducing disease severity or by assigning appropriate levels of care. The two hypothetical case studies in the previous sections demonstrate this capability. The model outputs can be readily translated into practical allocation rules to guide medical personnel at the frontlines. These rules will vary depending on the prevailing conditions—i.e., specific numerical values of the model parameters may vary with location or with time—but the general principle of providing the capability to compute for the best allocation remains constant across all instances.
Conclusions
An LP model has been developed for optimizing the allocation of future COVID-19 drugs under conditions of a supply shortage. The model also accounts for hospital capacity due to limits on space, vital life support equipment, and medical personnel. Two case studies were solved to illustrate how the model can generate allocation policies that outperform ad hoc or heuristic triage policies using patient fatalities as a metric. The model can provide strategic insights for government planners and healthcare administrators to complement the operational view of frontline medical personnel. The LP formulation is flexible, and it can be readily updated once published data on drug efficacy become available. As an LP, it can also be readily implemented and solved in commonly available software such as spreadsheets applications. This simple model can also serve as the core model for future extensions. In particular, robust, multiperiod, and multiobjective variants should be prioritized for development to account for uncertainties, dynamics, and conflicting goals, respectively.
Appendix
Table 14.
Number of patients categorized in the different severity levels in Case Study 2
| Region | Low | Medium | High |
|---|---|---|---|
| 1 | 613,790 | 852,926 | 354,586 |
| 2 | 112,590 | 177,221 | 75,059 |
| 3 | 154,560 | 216,156 | 99,684 |
| 4 | 244,945 | 356,378 | 135,084 |
| 5 | 1,042,956 | 1,437,646 | 549,412 |
| 6 | 38,006 | 66,532 | 31,900 |
| 7 | 598,550 | 740,827 | 286,933 |
| 8 | 136,246 | 177,469 | 74,862 |
| 9 | 102,102 | 121,449 | 48,396 |
| 10 | 221,055 | 300,631 | 106,951 |
| 11 | 207,692 | 282,448 | 118,715 |
| 12 | 169,671 | 295,306 | 124,973 |
| 13 | 162,512 | 247,780 | 97,488 |
| 14 | 211,903 | 312,244 | 124,592 |
| 15 | 140,649 | 213,381 | 77,965 |
| 16 | 23,870 | 32,464 | 14,609 |
| 17 | 249,035 | 341,851 | 110,450 |
Table 15.
Available hospital resources in Case Study 2
| Region | Home | Bed | ICU |
|---|---|---|---|
| 1 | No limit | 4028 | 208 |
| 2 | No limit | 807 | 42 |
| 3 | No limit | 1041 | 54 |
| 4 | No limit | 1629 | 84 |
| 5 | No limit | 6702 | 345 |
| 6 | No limit | 302 | 16 |
| 7 | No limit | 3598 | 185 |
| 8 | No limit | 859 | 44 |
| 9 | No limit | 601 | 31 |
| 10 | No limit | 1391 | 72 |
| 11 | No limit | 1346 | 69 |
| 12 | No limit | 105 | 67 |
| 13 | No limit | 1123 | 58 |
| 14 | No limit | 1435 | 74 |
| 15 | No limit | 955 | 49 |
| 16 | No limit | 157 | 8 |
| 17 | No limit | 1551 | 80 |
Footnotes
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
References
- Andersen KG, Rambaut A, Lipkin WI, Holmes EC, Garry RF. The proximal origin of SARS-CoV-2. Nat Med. 2020 doi: 10.1038/s41591-020-0820-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Arora H, Raghu TS, Vinze A. Resource allocation for demand surge mitigation during disaster response. Decis Support Syst. 2010;50:304–315. doi: 10.1016/j.dss.2010.08.032. [DOI] [Google Scholar]
- Aviso KB, Mayol AP, Promentilla MAB, Santos JR, Tan RR, Ubando AT, Yu KDS. Allocating human resources in organizations operating under crisis conditions: a fuzzy input-output optimization modeling framework. Resour Conserv Recycl. 2018;128:250–258. doi: 10.1016/j.resconrec.2016.07.009. [DOI] [Google Scholar]
- Bandyopadhyay S. Coronavirus Disease 2019 (COVID-19): we shall overcome. Clean Technol Environ Policy. 2020 doi: 10.1007/s10098-020-01843-w. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Celiz MD, Tso J, Aga DS. Pharmaceutical metabolites in the environment: analytical challenges and ecological risks. Environ Toxicol Chem. 2009;28:2473–2484. doi: 10.1897/09-173.1. [DOI] [PubMed] [Google Scholar]
- Corlett RT, Primack RB, Devictor V, Maas B, Goswami VR, Bates AE, Koh LP, Regan TJ, Loyola R, Pakeman RJ, Cumming GS, Pidgeon A, Johns D, Roth R. Impacts of the coronavirus pandemic on biodiversity conservation. Biol Conserv. 2020 doi: 10.1016/j.biocon.2020.108571. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cunningham AA, Dazak P, Wood JLN. One health, emerging infectious diseases and wildlife: two decades of progress? Philos Trans R Soc B Biol Sci. 2017;372:20160167. doi: 10.1098/rstb.2016.0167. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Department of Health (2020) The Philippine health system at a glance. https://www.doh.gov.ph/sites/default/files/basic-page/chapter-one.pdf. Accessed 14 April 2020
- El-Halwagi MM. Process integration. Amsterdam: Elsevier; 2006. [Google Scholar]
- Ferguson NM, Laydon D, Nedjati-Gilani G, Imai N, Ainslie K, Baguelin M, Bhatia S, Boonyasiri A, Cucunubá Z, Cuomo-Dannenburg G, Dighe A, Dorigatti I, Fu H, Gaythorpe K, Green W, Hamlet A, Hinsley W, Okell LC, van Elsland S, Thompson H, Verity R, Volz E, Wang H, Wang Y, Walker PGT, Walters C, Winskill P, Whittaker C, Donnelly CA, Riley S, Ghani AC (2020) Impact of non-pharmaceutical interventions (NPIs) to reduce COVID-19 mortality and healthcare demand. COVID-19 reports. Faculty of Medicine, Imperial College, London, UK. 10.25561/77482
- Ferrari R, Maggioni AP, Tavazzi L, Rapezzi C. The battle against COVID-19: fatality in Italy. Eur Heart J. 2020 doi: 10.1093/eurheartj/ehaa326. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Friedler F, Aviso KB, Bertok B, Foo DCY, Tan RR. Prospects and challenges for chemical process synthesis with P-graph. Curr Opin Chem Eng. 2019;26:58–64. doi: 10.1016/j.coche.2019.08.007. [DOI] [Google Scholar]
- Klemeš JJ, Kravanja Z. Forty years of heat integration: pinch analysis (PA) and mathematical programming (MP) Curr Opin Chem Eng. 2013;2:461–474. doi: 10.1016/j.coche.2013.10.003. [DOI] [Google Scholar]
- Klemeš JJ, Varbanov PS, Walmsley TG, Jia X. New directions in the implementation of Pinch Methodology (PM) Renew Sustain Energy Rev. 2018;98:439–468. doi: 10.1016/j.rser.2018.09.030. [DOI] [Google Scholar]
- Klemeš JJ, Fan YV, Tan RR, Jiang P. Minimising the present and future plastic waste, energy and environmental footprints related to COVID-19. Renew Sustain Energy Rev. 2020;127:109883. doi: 10.1016/j.rser.2020.109883. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Koyuncu M, Erol R. Optimal resource allocation model to mitigate the impact of pandemic influenza: a case study for Turkey. J Med Syst. 2010;34:61–70. doi: 10.1007/s10916-008-9216-y. [DOI] [PubMed] [Google Scholar]
- Kupferschmidt K, Cohen J. WHO launches global megatrial of the four most promising coronavirus treatments. Science. 2020 doi: 10.1126/science.abb8497. [DOI] [Google Scholar]
- Liu M, Xu X, Cao J, Zhang D. Integrated planning for public health emergencies: a modified model for controlling H1N1 pandemic. J Oper Res Soc. 2019 doi: 10.1080/01605682.2019.1582589. [DOI] [Google Scholar]
- Majumdar A, Pal A. Recent advancements in visible-light-assisted photocatalytic removal of aqueous pharmaceutical pollutants. Clean Technol Environ Policy. 2020;22:11–42. doi: 10.1007/s10098-019-01766-1. [DOI] [Google Scholar]
- Medlock J, Galvani AP. Optimizing influenza vaccine distribution. Science. 2009;325:1705–1708. doi: 10.1126/science.1175570. [DOI] [PubMed] [Google Scholar]
- Musazzi UM, Di Giorgio D, Minghetti P. New regulatory strategies to manage medicines shortages in Europe. Int J Pharm. 2020;579:119171. doi: 10.1016/j.ijpharm.2020.119171. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Okuyama Y. Disaster and economic structural change: case study on the 1995 Kobe earthquake. Econ Syst Res. 2014;26:98–117. doi: 10.1080/09535314.2013.871506. [DOI] [Google Scholar]
- Philippine Statistics Authority (2020a) National Quickstat for 2020. https://psa.gov.ph/statistics/quickstat/national-quickstat/all/*. Accessed 14 April 2020
- Philippine Statistics Authority (2020b) 2018 Quickstat of National Capital Region. https://psa.gov.ph/statistics/quickstat/regional-quickstat/2018/National%20Capital%20Region. Accessed 14 April 2020
- Santos JR. Reflections on the impact of “flatten the curve” on interdependent workforce sectors. Environ Syst Decis. 2020 doi: 10.1007/s10669-020-09774-z. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sun L, Depuy GW, Evans GW. Multi-objective optimization models for patient allocation during a pandemic influenza outbreak. Comput Oper Res. 2014;51:350–359. doi: 10.1016/j.cor.2013.12.001. [DOI] [Google Scholar]
- Tuite AR, Fisman DN, Kwong JC, Greer AL. Optimal pandemic influenza vaccine allocation strategies for the Canadian population. PLoS ONE. 2010;5:e10520. doi: 10.1371/journal.pone.0010520. [DOI] [PMC free article] [PubMed] [Google Scholar]
- World Health Organization (2020) WHO COVID-19 Dashboard, https://covid19.who.int/. Accessed 22 May 2020
- Yaesoubi R, Cohen T. Identifying cost-effective dynamic policies to control epidemics. Stat Med. 2016;35:5189–5209. doi: 10.1002/sim.7047. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yu KDS, Aviso KB. Modelling the economic impact and ripple effects of disease outbreaks. Process Integr Optim Sustain. 2020 doi: 10.1007/s41660-020-00113-y. [DOI] [Google Scholar]
- Yu DEC, Razon LF, Tan RR. Can global pharmaceutical supply chains scale up sustainably for the COVID-19 crisis? Resources. Conserv Recycl. 2020;159:104868. doi: 10.1016/j.resconrec.2020.104868. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yuan J, Lu Y, Cao X, Cui H. Regulating wildlife conservation and food safety to prevent human exposure to novel virus. Ecosyst Health Sustain. 2020;6:1741325. doi: 10.1080/20964129.2020.1741325. [DOI] [Google Scholar]
- Zhang T, Wu Q, Zhang Z. Probable pangolin origin of SARS-CoV-2 associated with the COVID-19 outbreak. Curr Biol. 2020 doi: 10.1016/j.cub.2020.03.022. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhou P, Yang X-L, Wang X-, Hu B, Zhang L, Zhang W, Si H-R, Zhu Y, Li B, Huang C-L, Chen H-D, Chen J, Luo Y, Guo H, Jiang R-D, Liu M-Q, Chen Y, Shen X-R, Wang X, Zheng X-S, Zhao K, Chen Q-J, Deng F, Liu L-L, Yan B, Zhan F-X, Wang Y-Y, Xiao G-F, Shi Z-L. A pneumonia outbreak associated with a new coronavirus of probable bat origin. Nature. 2020;579:270–273. doi: 10.1038/s41586-020-2012-7. [DOI] [PMC free article] [PubMed] [Google Scholar]