Finite element models for fracture prevention in patients with metastatic bone disease. A literature review

Abstract

Patients with bone metastases have an increased risk to sustain a pathological fracture as lytic metastatic lesions damage and weaken the bone. In order to prevent fractures, prophylactic treatment is advised for patients with a high fracture risk. Mechanical stabilization of the femur can be provided through femoroplasty, a minimally invasive procedure where bone cement is injected into the lesion, or through internal fixation with intra- or extramedullary implants. Clinicians face the task of determining whether or not prophylactic treatment is required and which treatment would be the most optimal. Finite element (FE) models are promising tools that could support this decision process. The aim of this paper is to provide an overview of the state-of-the-art in FE modeling for the treatment decision of metastatic bone lesions in the femur. First, we will summarize the clinical and mechanical results of femoroplasty as a prophylactic treatment method. Secondly, current FE models for fracture risk assessment of metastatic femurs will be reviewed and the remaining challenges for clinical implementation will be discussed. Thirdly, we will elaborate on the simulation of femoroplasty in FE models and discuss future opportunities. Femoroplasty has already proven to effectively relieve pain and improve functionality, but there remains uncertainty whether it provides sufficient mechanical strengthening to prevent pathological fractures. FE models could help to select appropriate candidates for whom femoroplasty provides sufficient increase in strength and to further improve the mechanical benefit by optimizing the locations for cement augmentation.

1. Introduction

1.1. Metastatic bone disease increases fracture risk

Metastatic bone disease is a progressive disease state of cancer, which results when a primary tumor spreads to the skeleton. Especially breast, prostate and lung cancers show a preference to metastasize to the bone (Body et al., 2013; Gendi et al., 2016; Coleman et al., 2006; Van Den Hurk et al., 2011). An evaluation on a large cohort of 33.771 patients with primary breast cancer demonstrated that 16% metastasized within 5 years after the initial diagnosis, 57% of which were bone metastases (Van Den Hurk et al., 2011). Worldwide, >1.5 million patients are affected by bone metastases (Body et al., 2013; Jasmin et al., 2005) and this number is increasing along with the increasing number of cancer diagnoses (Gendi et al., 2016). Patients are also living longer with the disease due to the improved treatment methods (O'Shaughnessy, 2005; Ratasvuori et al., 2013), which has led to an increase in secondary complications caused by the disease or its treatment as well (Ratasvuori et al., 2013).

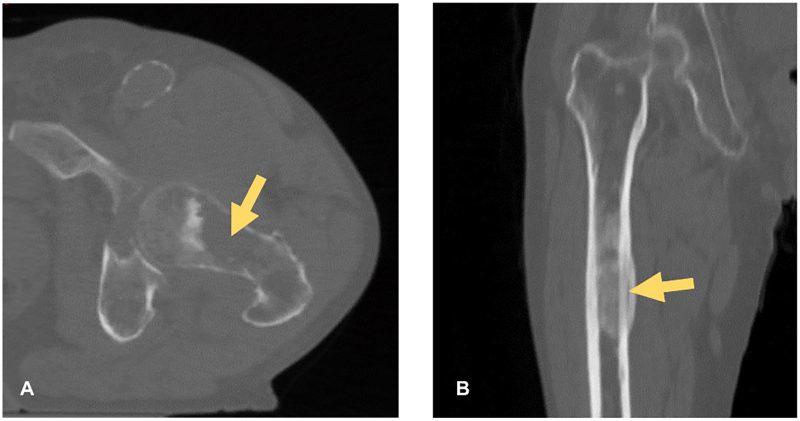
Common complications associated with bone metastases are pain and pathological fractures (Gendi et al., 2016; Mavrogenis et al., 2012). Metastatic bone lesions damage and weaken the bone, resulting in micro-fractures that initially can cause pain and eventually may lead to a pathological fracture (Ratasvuori et al., 2013). Metastatic lesions can be classified as lytic or blastic lesions based upon their radiographic appearance that demonstrates predominant bone destruction or deposition of new bone (Fig. 1). A mixture of both lesions may also occur. The majority of the lesions are lytic and these are also associated with the highest risk for fracture (Benca et al., 2016; Mirels, 1989). Such fractures have a significant impact on the quality of life since they lead to a loss of mobility and shorten survival (Ratasvuori et al., 2013; Mavrogenis et al., 2012; Hansen et al., 2009). Moreover, pathological fractures often require complex surgical procedures, after which complete healing is still not assured since fracture healing is limited in this patient group (Mavrogenis et al., 2012).

Fig. 1.

Two examples of metastatic bone lesions in the femur: (a) a lytic lesion in the femur neck and (b) a blastic lesion in the femur shaft.

1.2. Prophylactic treatment to prevent fracture

Given the severe consequences of pathological fractures, prophylactic (preventive) surgery is advised for patients with a high risk for fracture. The most common location for surgery of impending fractures is the proximal femur (Ratasvuori et al., 2013), not only because the incidence of bone metastases is high at this site (Gendi et al., 2016; Mavrogenis et al., 2012), but also because it suffers from a high fracture risk (Tian et al., 2016). Mechanical stabilization of the femur is typically provided by intra- or extramedullary implants, such as intramedullary rods (Ormsby et al., 2016; Kim et al., 2016; Swanson et al., 2000) or plates and/or screws (Swanson et al., 2000; Pusceddu et al., 2017; Mavrovi et al., 2017), often in combination with cement augmentation. Some lesions are solely treated with cement augmentation through a minimally invasive procedure called femoroplasty (Cazzato et al., 2015; Plancarte et al., 2014; Feng et al., 2016a; Anselmetti, 2010; Feng et al., 2016b). In this procedure, bone cement, typically polymethylmethacrylate (PMMA), is injected through a needle inserted percutaneously from the lateral aspect of the greater trochanter.

Most current literature supports prophylactic fixation of impending fractures since it is less complex and has better survival rates compared to the treatment of pathological fractures (Ratasvuori et al., 2013; Mavrogenis et al., 2012; Hansen et al., 2009). Yet, prophylactic surgery of all patients will cause overtreatment, and will put patients at risk because of unnecessary surgery. Lesions that do not seem to jeopardize the mechanical integrity of the bone are therefore treated conservatively with the aim to relieve pain, with a combination of radiotherapy, analgesics, chemotherapy, hormonal therapy or bisphosphonates (Derikx et al., 2015).

1.3. Fracture risk assessment

Radiologists and clinicians face the task of evaluating the fracture risk to decide whether prophylactic surgery is necessary. Several clinical guidelines have been formulated to provide an indication of fracture risk. Among them, the Mirels' scoring system (Mirels, 1989) seems to be the most used. This scoring system takes size, appearance and site of the lesion into account, as well as the presence of pain. A score higher than 8 is associated with an impending fracture and indicates the need for prophylactic surgery. Another commonly used guideline is the threshold of 30 mm axial cortical involvement (Fig. 2) (Van Der Linden et al., 2003), which proved to have an improved specificity over the Mirels' score (Van der Linden et al., 2018). Nevertheless, a study comparing several of these conventional guidelines, among others the Mirels' scoring system and the 30 mm threshold, demonstrated that none of these guidelines were accurate enough to predict the actual occurrence of a fracture (Van der Linden et al., 2018). The need for a more accurate tool has been widely recognized.

Fig. 2.

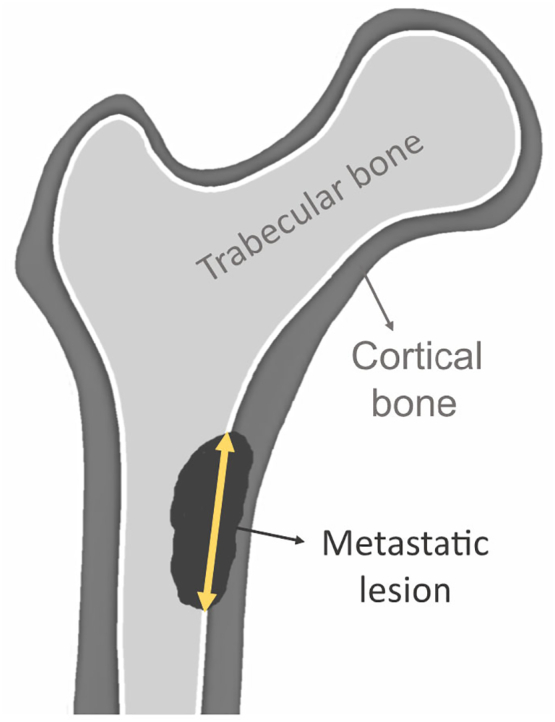
Illustration of the measurement of the axial cortical involvement of a metastatic lesion.

More recently, the focus has shifted towards mechanical models for fracture risk assessment (Derikx et al., 2015). Today, two image-based computational tools are under development. The first approach, computed-tomography-based rigidity analysis (CTRA), makes use of composite beam theory to evaluate bone rigidity in two-dimensional (2D) cross-sections (Anez-Bustillos, 2014). The axial, bending or torsional rigidities are calculated for all 2D-sections in a three-dimensional (3D) CT scan by summing the rigidity of all bone pixels in the section. The pixel rigidity is based on the corresponding bone density in the CT scan and the distance of the pixel to the geometrical centroid of the bone cross-section. The section with the lowest rigidity then represents the strength of the femur (the weakest link in the chain). Recently, an improvement of the method has been introduced by making use of curved instead of straight beam theory (Oftadeh et al., 2016). In contrast to traditional CTRA, curved CTRA takes into account the influence of the intrinsic bone curvature by measuring the rigidity in new cross-sections perpendicular to the curved centroidal axis.

The second approach is finite element (FE) modeling, a computational method that enables a three-dimensional analysis of bone strength. Just as in CTRA, FE models are also based on CT scans, from which the bone geometry and density are retrieved. This information is then joined together to create a 3D computer model, representing the geometry of the bone. The model consists of a large number of small elements with material properties based on the bone densities. Varying loading conditions can be simulated in the model by applying external forces and displacements.

Both curved CTRA and FE have shown to outperform the Mirels' score and/or the 30 mm axial cortical involvement threshold when predicting fracture risk in vivo (Damron et al., 2016; Goodheart et al., 2015; Eggermont et al., 2019a). A recent head-to-head comparison of both techniques evaluated the methods on an identical dataset to directly compare their accuracy in quantifying bone strength. Both models exhibited a strong level of correlation with mechanical testing results, yet with a slightly better subject-specific accuracy for FE models (Oftadeh et al., 2016). Although these results indicate only a minimal accuracy benefit for FE, its more intricate methodology might offer more flexibility. CTRA is not suited to assess more complex loading modes, such as the inclusion of muscle forces. Especially in cases where the metastatic lesion is located close to a muscle attachment point, this could pose a limitation for CTRA (Oftadeh et al., 2016). Furthermore, an accurate evaluation of the trochanteric region is problematic, if not impossible, with CTRA because of the 2D nature of the technique. Specifically, the irregular geometry in this region largely deviates from the concept of a beam, hence the criteria to use beam theory, the theory underlying CTRA, are not fulfilled. It can thus be expected that in this region in particular, which accounts for 20% of proximal femoral metastases (Feng et al., 2016b; Guzik, 2018), FE models will outperform CTRA.

1.4. Role of finite element models in the treatment of metastatic bone disease

FE models are thus promising tools that could improve fracture risk assessment in patients with metastatic bone disease relative to the currently used clinical guidelines. They provide an objective, biomechanics-based assessment of fracture risk that could support clinicians in deciding whether a patient should be treated prophylactically. In addition, FE models could potentially be extended to also simulate prophylactic treatment and thereby evaluate the mechanical effects of treatment. This way they could aid in selecting the most optimal treatment method for a specific patient. Currently, the optimal type of surgery is still unclear (Ratasvuori et al., 2013; Mavrogenis et al., 2012) and is decided based on the individual judgement of the surgeon and/or oncologist. Here too, FE models could support the decision process by offering an objective, biomechanics-based assessment of the fracture risk after treatment. In this paper, we will specifically focus on the evaluation of femoroplasty. An FE analysis of the latter procedure could aid clinicians in evaluating whether this minimally invasive procedure would suffice in improving bone strength or whether a more rigid fixation with implants is required.

The aim of this paper is to provide an overview of the state-of-the-art in FE modeling for the treatment decision of bone metastases in the femur. First, we will summarize the clinical and mechanical results of femoroplasty as a prophylactic treatment method. Secondly, current FE models for fracture risk assessment of metastatic femurs will be reviewed and the remaining challenges for clinical implementation will be discussed. Thirdly, we will elaborate on the simulation of femoroplasty in FE models and discuss future opportunities.

2. Femoroplasty as a prophylactic treatment method

Femoroplasty is a minimally invasive procedure, which provides important benefits for the patient compared to conventional surgical fixation, such as a shorter and less invasive procedure, less pain and discomfort, and reduced hospital stay and recovery time (Deschamps et al., 2012). Especially for patients with bone metastases who have a relatively higher mortality and morbidity of surgery, the reduced risk for infections and blood loss associated with a minimally invasive procedure are important (Deschamps et al., 2012).

The procedure has evolved from vertebroplasty, which is now widely performed to stabilize osteoporotic fractures or lesions in the spine. Vertebroplasty was applied for the first time in the late 1980s to treat a painful vertebral body hemangioma and was later extended to extraspinal lesions (Cazzato et al., 2015; Anselmetti, 2010). It has proven to be an effective method to offer immediate pain relief and improved functionality for metastatic disease patients (Cazzato et al., 2015; Anselmetti, 2010). However, some controversy still exists about the application in the femur, i.e. femoroplasty. Although it also proved to effectively relieve pain and improve functionality (Plancarte et al., 2014; Feng et al., 2016a; Deschamps et al., 2012), uncertainty remains whether it provides sufficient mechanical strengthening of the femur (Deschamps et al., 2012). As one of the long weight-bearing bones, the femur is vulnerable to fracture (Tian et al., 2016) and some reports indicate a substantial risk of fracture even after femoroplasty (Tian et al., 2016; Anselmetti, 2010; Deschamps et al., 2012). Besides the risk for revision, there are also biological risks associated with femoroplasty, such as thermal necrosis, allergic reactions and fat embolism (Feng et al., 2016a; Varga et al., 2016). Yet, clinical studies on femoroplasty reported a high technical success rate with only few complications (Tian et al., 2016; Plancarte et al., 2014; Anselmetti, 2010; Deschamps et al., 2012).

The mechanical improvement that can be gained with femoroplasty has been investigated in biomechanical studies mainly in the application of prophylactic augmentation for osteoporotic femurs (reviewed by Varga et al. (2016)). Varga et al. divided these studies in ‘first and second generation studies’ based on the evolution in the volume of injected cement. In ‘first generation studies’, large amounts of cement up to 40–50 ml were injected, while ‘second generation’ studies realized the biological risks associated with large cement volumes and reduced them to 10–15 ml. Yet, the second generation studies aimed to achieve a similar improvement in strength as the ‘first generation studies’ by injecting the cement at an optimal location in the femur. These studies found that, on average, femoroplasty could increase strength by 30–40% and energy to failure by 120–150%, while the stiffness remained unaffected. However, a large amount of scatter was present in the data; most likely this is related to the important role of the cement location (Varga et al., 2016); the best results were often found for cement injections close to the cortex in the femoral neck (Basafa and Armand, 2014; Varga et al., 2017).

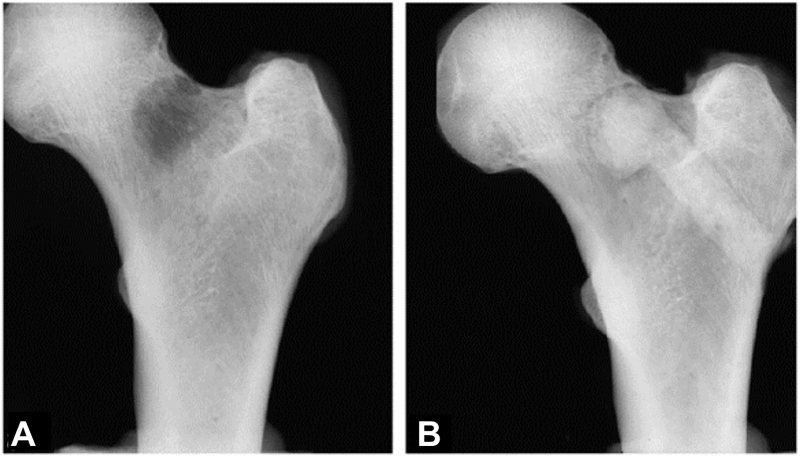
The femoroplasty technique used in metastatic proximal femurs is very similar, but injecting cement into a local metastasis is likely to have a different effect than injecting cement in broad regions of osteoporotic bone (Kaneko et al., 2007). Only limited data is available on the mechanical improvement in metastatic femurs (Kaneko et al., 2007; Palumbo et al., 2014). Kaneko et al. (2007) conducted a mechanical experiment on cadaver femurs where they created artificial lesions in the femur neck and subsequently filled them with PMMA bone cement (Fig. 3). They compared the strength of the augmented femurs against the strength of contralateral femurs that were left intact and found that, on average, femoroplasty could recover 94.7% of the intact strength. Similarly, Palumbo et al. (2014) evaluated the performance of femoroplasty on cadaver femurs with artificial neck lesions; however, instead of comparing the strength of augmented femurs against the strength of intact femurs, they compared it against the strength of internally fixated femurs with a compression screw. No significant differences in failure load were observed between the two procedures. Yet, they did observe a relation between failure load and the cement distribution. Specifically, and in line with the studies on osteoporotic femurs (Varga et al., 2016; Basafa and Armand, 2014; Varga et al., 2017), increased strength was observed if the cement extended to the cortex in the femoral neck.

Fig. 3.

Radiograph of a femur with an artificial defect in the neck, before (a) and after (b) augmenting the lesion with bone cement injected from the lateral aspect of the greater trochanter. Reprinted from Kaneko et al. (2007) with permission from Elsevier.

To conclude, femoroplasty has proven to be a safe and effective method to relieve pain and restore function, however only limited data is available on the mechanical improvement in femurs with bone metastases. More data are needed to determine the gain in mechanical efficacy. Yet, the preliminary data indicate that some patients may definitely benefit from femoroplasty, but at the same time the substantial scatter in the data suggests the need for developing strategies to identify patients whom will benefit the most from the procedure. E.g., Dechamps et al. suggested to only apply femoroplasty when lesions have <30 mm cortical involvement and when there is no history of fracture in the lesser trochanter (Deschamps et al., 2012). It should be noted that, similarly to the assessment of fracture risk, it is likely that such clinical guidelines are not accurate enough and could be improved with biomechanics-based models such as FE analysis.

3. FE models for fracture risk assessment

3.1. Overview of FE models for fracture risk assessment in metastatic femurs

In the last 30 years, several groups have developed FE models to assess fracture risk in metastatic bone disease patients (Table 1) (Yosibash et al., 2014; Tanck et al., 2009; Keyak et al., 2005a; Derikx et al., 2012; Benca et al., 2019; Alexander et al., 2013; Keyak et al., 2005b; Spruijt et al., 2006; Cheal et al., 1993). The very first FE model to predict bone strength in femurs with metastatic lesions was developed by Cheal et al. (1993). However they found only a poor agreement with experimental results due to their rather primitive FE model (550 linear isoparametric elements) based on data from an “average” femur.

Table 1.

Overview of FE models for strength assessment in metastatic femurs, validated with experiments on human cadaver femurs (Yosibash et al., 2014; Tanck et al., 2009; Keyak et al., 2005a; Derikx et al., 2012; Benca et al., 2019; Alexander et al., 2013; Keyak et al., 2005b; Spruijt et al., 2006; Cheal et al., 1993).

Study		No. of femurs	Lesion		Mechanical test	FEA		Validation
			Type	Location		Meshing	Material	Parameter	R2
Cheal et al., 1993		1	Simulated	Neck	Compression	Geometry	Linear	Failure force	“poor”
Keyak et al., 2005a, Keyak et al., 2005b	2005a	24	Real and simulated	Shaft	4 point-bending	Voxel	Linear	Failure force	0.88-0.95
	2005b	44	Real	Proximal femur	Compression	Voxel	Nonlinear	Failure force	0.83-0.88
Spruijt et al., 2006		11 pairs	Simulated	Shaft	Torsion	Voxel	Linear	Failure moment	0.68-0.82
Tanck et al., 2009		5 pairs	Simulated	Proximal femur	Compression	Voxel	Nonlinear	Failure force	0.92
Derikx et al., 2012		10 pairs	Simulated	Proximal femur	Compression	Geometry	Nonlinear	Failure force	0.90-0.93
Alexander et al., 2013		8 pairs	Simulated	Neck	Compression	Geometry	Linear	NA
Yosibash et al., 2014		7 pairs	Real	Proximal femur	Compression	Geometry	Linear	Yield force	0.78
Benca et al., 2019		16 pairs	Simulated	Neck	Compression	Voxel	Nonlinear	Failure force	0.77-0.98
								Stiffness	0.47-0.94

NA = Not Applicable.

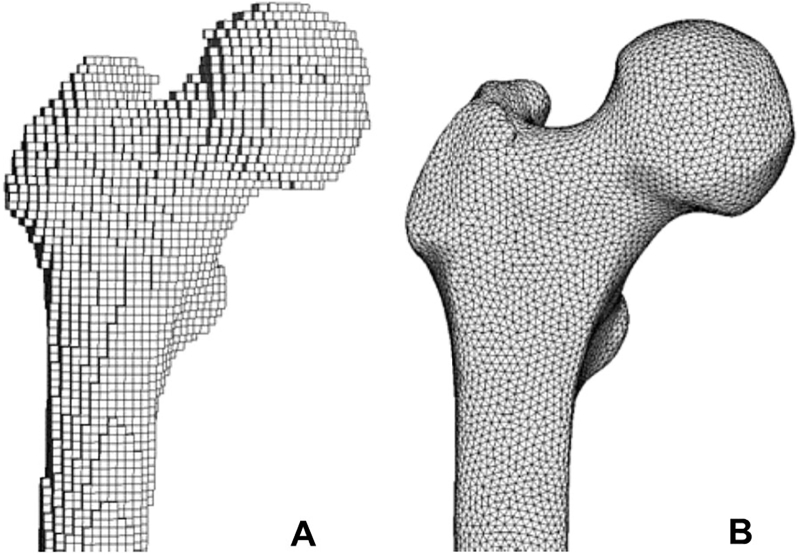
Keyak et al. (Keyak et al., 2005a; Keyak et al., 2005b; Kaneko et al., 2003; Kaneko et al., 2004; Keyak et al., 1996; Keyak et al., 2007) were the first to have built a complete workflow to develop accurate subject-specific FE models from quantitative computed tomography (QCT) images. In their workflow, Keyak et al. first established relationships between the densities as determined from QCT images and bone material properties for specimens with and without bone metastases (Kaneko et al., 2003; Kaneko et al., 2004; Keyak et al., 1996). Subsequently, they used these material relationships in FE models of the femoral shaft and proximal femur to predict bone strength (Keyak et al., 2005a; Keyak et al., 2005b). To create these FE models from QCT scans, the scans were first segmented to separate the femur from the remaining parts present in the scan. The segmented voxel data were then converted into a 3D representation of the femur, from which an FE model could be built. Keyak et al. made use of a voxel-based meshing approach (Fig. 4a), where the voxels from the scan were directly converted into cube shaped elements (shaft: size 1.5 mm, proximal femur: size 3 mm). Material properties were assigned to each element based on the bone densities of the corresponding voxels in the QCT images and the established relations with the material properties. Bone densities (ρ) can be directly extracted from the QCT scan using the calibration phantom with known densities, which is scanned along with the patient to set up a reference between the Hounsfield units in the CT scan and the bone densities.

Fig. 4.

Illustration of the two meshing approaches: (a) voxel-based FE mesh with brick shaped elements and (b) geometry-based mesh with tetrahedral elements.

For the FE model of the femoral shaft (Keyak et al., 2005b), Keyak et al. used linear material properties, which assumes a linear stress-strain relationship for each element in the FE model. In this case, the only material parameter that needs to be assigned to each element is the elastic modulus E, capturing the element stiffness. For all bone tissue, an identical ρ-E relationship could be used regardless of whether metastases were present or not, since adapting the relationship for metastatic bone showed almost no difference in results (Keyak et al., 2005b). To predict bone strength with this linear FE model, a criterion needed to be defined to determine failure. Keyak et al. defined the failure force as the force where the first non-surface element reached a von Mises stress value beyond its ultimate strength S, with S defined in function of ρ. To validate these FE models, they compared the FE predicted failure force against the maximal force measured during mechanical experiments on human cadaver femurs. A good correspondence (R² = 0.88–0.95) with the experiment was found, yet the slope of the relation was almost equal to 2, indicating that FE underestimated the maximal experimental force. A probable reason for this is that linear FE models can only capture the onset of failure, while actual fractures occur well beyond that point.

Nonlinear FE models on the other hand do allow including the mechanical behavior past the onset of local material failure. As proven earlier, such models can improve the precision of FE models in predicting femoral bone strength over linear models (Keyak, 2001). Yet, they make the simulations computationally more expensive. In Keyak's FE model of the proximal femur (Keyak et al., 2005a), they made use of nonlinear material properties after failure occurred according to the von Mises criterion (σ_VM > S). The post-failure behavior was modeled as a perfectly plastic phase at the ultimate stress value S, followed by a strain softening phase until the stress was equal to a minimal value. In this model, the failure force was simply defined as the maximal force applied in the FE model. Validation of the model against experiments on cadaver femur showed again a strong correspondence between the FE and experimental failure force (R² = 0.83–0.88) with a slope close to 1 and an intercept not different from 0.

Tanck et al. (Tanck et al., 2009; Derikx et al., 2012) built further on this workflow by using the same nonlinear material properties of the proximal femur. Initially, they also developed voxel-based FE models of the proximal femur consisting of brick shaped elements (0.94 × 0.94 × 3 mm) (Tanck et al., 2009), but some years later they switched to a geometry-based model (Fig. 4b) with tetrahedral elements (mean edge length 2 mm) (Derikx et al., 2012). This transition towards geometry-based meshes is a general trend that has been observed in macro-FE analyses of bone since it enabled a more accurate representation of the bone surface (Lenaerts and Van Lenthe, 2009; Viceconti et al., 1998). Geometry-based meshes are generated in two steps: (1) reconstruction of the femur surface based on the contours in the segmented CT scan and (2) conversion of the surface geometry into a volumetric mesh with tetrahedral or hexahedral elements. In contrast, voxel-based mesh generation is simpler, requiring only a single step where voxels from the CT scan are directly converted into brick-shaped elements. Moreover, the method is fully robust to mesh distortion since it makes use of identical brick shaped elements, which have the “perfect” shape by definition. However, the disadvantage of voxel-based meshes is the jagged surface representation, which has drawn some criticism as it may give rise to inaccurate stress concentrations at the surface (Lenaerts and Van Lenthe, 2009; Viceconti et al., 1998; Marks and Gardner, 1993). Currently, the vast majority of FE models of the femur make use of geometry-based meshes, likely supported by the increased availability of automated geometry-based meshing algorithms in commercial FE pre-processors (Viceconti et al., 1998).

Both the voxel-based and the tetrahedral FE model from Tanck et al. were validated against experiments on cadaver femurs with simulated lesions of varying size and location (Tanck et al., 2009; Derikx et al., 2012). The FE models predicted the experimental failure force slightly better (R² = 0.90–0.93) compared to the proximal femur model of Keyak et al. (2005a), which was likely related to the smaller element sizes. To prove that FE models are better at predicting fracture risk than the existing clinical guidelines, they compared the FE predictions against predictions from clinicians, who were asked to rank the tested femurs in terms of strength (Derikx et al., 2012). The results demonstrated that FE models (Kendall rank correlation τ = 0.87) outperformed the predictions by clinicians (τ = 0.11–0.42).

Recently, Benca et al. (2019) switched back towards voxel-based meshes (3 mm cubes) under the rationale that this meshing approach allows a high level of automation and is robust for mesh distortion. It enabled them to perform a complete analysis in less than half an hour, with minimal manual workload, while Derikx et al. (2012) reported a duration of 8 h to generate and simulate their tetrahedral FE model. However, the accuracy of Benca's nonlinear, voxel-based model needs improvement since it underestimated the fracture load with a factor of two. This underestimation is likely caused by the differing material relationships compared to Keyak et al. (2005a), since the latter did not observe this problem with their voxel-based model of the proximal femur. Firstly, there is the difference in the material constants of the ρ-E and ρ-S relationships which obviously influence the stiffness and strength values. Secondly, Benca et al. made use of an asymmetric failure criterion (piecewise Hill criterion), which accounts for a lower strength of bone in tension than compression, while Keyak et al. assumed equal tensile and compressive strengths.

Besides the accuracy in predicting failure load, most studies also evaluated the ability of FE models to predict the location of fracture. In general, FE models better predicted the fracture location in femurs with metastatic lesions than intact femurs (Derikx et al., 2012; Benca et al., 2019). The prediction of the location in metastatic femurs is likely simplified due to the structural damage induced by the lesion, which creates an obvious weak spot that can be easily detected by the FE model. In these cases, the predicted and actual fracture lines mostly agreed very well, passing through the lesion itself. Instead, FE models of the intact femurs mainly predicted subcapital fractures (Tanck et al., 2009; Keyak et al., 2005a; Derikx et al., 2012; Benca et al., 2019), while during the experiment mostly intertrochanteric fractures were observed.

Finally, it should be highlighted that directly comparing studies on metastatic femurs is difficult as they all evaluate different types of lesions. These varying lesion types can results in different prediction accuracies, even within one study, as clearly demonstrated by Benca et al. (2019). They observed large site-specific differences in the correlation between FE computed and experimentally measured stiffness and failure load; superolateral neck lesions showed a better correspondence in stiffness compared to inferomedial neck lesions (superolateral R² = 0.94, inferomedial R² = 0.47), while the opposite was observed for the failure load (superolateral R² = 0.77, inferomedial R² = 0.98).

3.2. In vivo assessment of fracture risk

To demonstrate the predictive power in a clinical setting, the FE modeling approach should not only be validated on cadaver femurs, but also on in vivo CT scans of patients with femur metastases (Goodheart et al., 2015; Eggermont et al., 2019a; Eggermont et al., 2018; Sternheim et al., 2018). A recent retrospective study (Sternheim et al., 2018) evaluated the ability of FE models to predict the occurrence of a fracture for metastatic patients who were recommended for prophylactic surgery, but declined it. Yet, the usable dataset to evaluate the accuracy was limited (11 patients, no fractures) and the CT scans were not optimal, because no calibration phantoms were included, different filters were used, and in some cases only a small part of the femur was imaged. Prospective studies with standardized CT protocols would therefore be more appropriate. Two groups have presented data from prospective studies to compare the predictive power of FE models against two clinical guidelines, the Mirels' score (Goodheart et al., 2015) and the 30 mm threshold of axial cortical involvement respectively (Eggermont et al., 2019a; Eggermont et al., 2018). More specifically, Goodheart et al. (2015) included 38 patients with metastatic femoral lesions, who were followed over a period of 4 months. FE models simulating walking conditions showed a similar accuracy as the Mirels' score in identifying patients sustaining a fracture (sensitivity 80%), but demonstrated an improved ability to identify non-fracture patients (specificity 86% vs 43%). Analogously, Eggermont et al. (2019a) evaluated 39 patients with femoral metastases who were referred for palliative therapy and were followed for 6 months. Their FE models proved to have an improved sensitivity and specificity over the guideline of 30 mm cortical involvement (sensitivity 100% vs 86%, specificity 74% vs 42%). Larger datasets should be analyzed in the future to confirm the improved predictive power of FE models (Eggermont et al., 2018).

3.3. Challenges for entering clinical practice

Although these results are very promising and demonstrate that FE models improve fracture risk prediction over clinical guidelines, some challenges still remain before entering clinical practice. A major limitation is that FE models are too time-consuming, require expert knowledge and necessitate specific modeling software. To turn this method into a time- and cost-effective clinical tool, a high level of automation is necessary and the simulations should be robust and fast. As depicted earlier, voxel-based models might be of interest in this aspect since they enable a fully automated mesh generation and are robust for mesh distortion (Benca et al., 2019). Yet, their accuracy should be further demonstrated for varying types of lesions.

Another challenge is to improve the accuracy on a subject-specific level (Derikx et al., 2015). Although FE predictions show strong correlations with actual failure load, the under- and overestimation on a subject-specific level can still be quite large. A possible improvement would be to account for tissue anisotropy (Derikx et al., 2015; Lenaerts and Van Lenthe, 2009; Viceconti et al., 2018). It is well known that cortical as well as trabecular bone are orthotropic materials in nature (Lenaerts and Van Lenthe, 2009). Yet, FE models typically make use of isotropic material properties since anisotropy is not detectable from the current resolution of clinical QCT. Alternatively, models based on high-resolution peripheral QCT (HR-pQCT) are able to include bone anisotropy and these models have already proven to improve strength predictions compared to isotropic models (Luisier et al., 2014). One way to incorporate anisotropy as obtained from high-resolution HR-pQCT or micro-CT scans into clinical QCT scans is to apply image registration to map the bone anisotropy from a template image to the clinical dataset (Taghizadeh et al., 2016). Another way would be a direct incorporation of anisotropy from improved CT resolutions which may become available in the near future thanks to the steadily improving imaging techniques (Derikx et al., 2015). However, the downside of incorporating anisotropy is that it requires to formulate and validate new material relationships, and this takes time. It would result in slowing down the clinical implementation, while current isotropic FE models could already offer an improvement for the treatment of patients with bone metastases. Therefore, we should rather move forward in introducing current FE models in clinical practice, and perform further research to improve the models in parallel.

4. FE models for prophylactic treatment evaluation

Since metastatic bone disease patients are living substantially longer than before due to improved cancer treatment methods, selecting an adequate prophylactic treatment that endures the remaining life span is getting more important (Ratasvuori et al., 2013). FE models could support the selection process by offering a biomechanics-based evaluation of the treatment effects. For femoroplasty specifically, FE models could help to select appropriate candidate patients for whom femoroplasty provides sufficient increase in strength. Moreover, FE models could be used to further improve the mechanical benefit of femoroplasty by optimizing the locations for and mechanical properties of cement augmentation.

4.1. Decision support to select appropriate candidates

FE models have already been used to quantify the effect of cement augmentation in osteoporotic (Varga et al., 2017; Basafa et al., 2013; Kok et al., 2019) and in metastatic (Palumbo et al., 2014; Kaneko et al., 2008) proximal femurs. However, only few studies have validated these FE models against data from in vitro experiments on human cadaver femurs to determine the accuracy in predicting bone strength (Basafa et al., 2013; Kaneko et al., 2008). In the application of femoroplasty for osteoporotic femurs, Basafa et al. (2013) validated a hexahedral FE model of the proximal femur with linear material properties. They simulated cement augmentation by assigning cement material properties (Young's modulus 1.2 GPa) to the elements corresponding to the locations of injected bone cement. A good agreement was found between the experimental and FE predicted yield force with an R² of 0.72, mean accuracy error of 0.29 kN and 95% confidence interval of ±0.45 kN. In the application of metastatic femurs, Kaneko et al. (2008) extended the nonlinear voxel-based model of Keyak et al. (2005a), as discussed earlier for fracture risk assessment, by including PMMA material properties (Young's modulus 2.72 GPa, strength 98 MPa) at the location of the augmented, artificial lesions. They compared the experimental and FE predicted maximal failure force and found an agreement with an R² of 0.88, mean accuracy error of −0.11 kN and 95% confidence interval of ±2.01 kN.

The accuracy of these models could be improved in a similar way as discussed for the FE models in fracture risk assessment, i.e. by including tissue anisotropy. Another potential for improvement is a more appropriate method to model the augmented trabecular bone. Typically, perfect bonding is assumed between the bone and the cement (Varga et al., 2017; Palumbo et al., 2014; Basafa et al., 2013; Kok et al., 2019; Kaneko et al., 2008); furthermore, material properties are modeled as pure bone cement (Basafa et al., 2013), as perfect bone-cement composite with no porosity (Varga et al., 2017) or as bone with the stiffness increased by the stiffness of pure cement (Kok et al., 2019). These methods likely overestimate the real stiffness and strength of the augmented femur. On the other hand, Kaneko et al. (2008) ignored the interdigitation of cement in the surrounding trabecular bone and only replaced the lesion itself with cement, which would rather cause an underestimation of strength. An additional error will be introduced when the FE models will be used for predicting the effect of augmentation in patients because the distribution of the injected cement will be unknown as opposed to experimental cadaver studies. Hence, it remains to be evaluated how deviations between the simulated and real cement distribution would impact the accuracy of the prediction.

Another remaining uncertainty is the level of strength improvement that is required to prevent actual fractures and thereby enable to select appropriate candidates (Varga et al., 2016; Kok et al., 2019). One suggested way of quantifying this is to look at the load-to-strength ratio, where the load can be estimated from the patient's weight and height and the strength can be predicted with FE analysis (Keaveny and L. Bouxsein, 2008; Orwoll et al., 2009). In theory, cement augmentation would be effective when it would reduce this ratio to a value smaller than 1. Based on the results from a prospective case study by Orwoll et al. (2009), who found an average load-to-strength ratio of 1.13 for fracture cases, this would mean that on average a 13% increase would suffice. Yet, there was a wide range in the load-to-strength ratios (from 0.2 up to 2.4), indicating that many patients would require a larger increase in bone strength. Hence, this load-to-strength ratio provides a useful concept to quantify the effectiveness of prophylactic treatment in preventing fractures, but it requires further refinement to improve the accuracy (Keaveny and L. Bouxsein, 2008).

Analogously to the FE models for fracture risk prediction, the FE models for evaluation of femoroplasty should not only be validated on cadaver femurs, but also on in vivo CT scans of patients with femur metastases. The predictive power could be assessed through retro- or prospective studies on patients treated with femoroplasty by comparing the predicted outcome from the FE analysis with the actual occurrence/absence of a fracture. For now, this is rather a future perspective since only limited clinical cases of femoroplasty are currently available with insufficient statistical power. Nevertheless, preliminary analyses could already be performed on the large existing CT datasets of patients diagnosed with bone metastases (Eggermont et al., 2018; Sternheim et al., 2018; Eggermont et al., 2019b). These datasets do not allow to validate the predictive power, but do enable an evaluation of femoroplasty on clinically relevant cases. The results could be used to evaluate the mechanical improvement on a large number of cases and explore potential relations with the lesion characteristics, such as size, location, and type.

4.2. Optimizing the location for cement augmentation

Due to the risks associated with femoroplasty such as thermal necrosis and embolism, it is desirable to use a minimal, yet sufficient, amount of cement (Basafa and Armand, 2014). To achieve substantial improvement in mechanical strength, the location of cement injection has been shown to play a key role (Varga et al., 2017; Basafa et al., 2013; Kok et al., 2019). Hence, it has raised the idea to use FE modeling to identify the optimal cement location (Basafa and Armand, 2014; Varga et al., 2017; Santana Artiles and Venetsanos, 2017).

The most advanced methodology in this area has been implemented by Basafa and Armand (2014). They used a bi-directional evolutionary structural optimization approach in combination with an FE modeling framework to determine the subject-specific ideal cement location. Through a series of iterations, PMMA was removed from the FE model at elements of low strain energy and added at elements of large strain energy until the yield force reached a threshold value (Fig. 5). To convert this optimal pattern into a practically feasible injection, they simulated 3 ml cement injections at pre-defined locations using a particle diffusion approach and combined the locations that best matched the optimal pattern. Through an experimental study they showed that their methodology can increase yield load by 33% and yield energy by 118% with, on average, only 9.5 ml cement (Basafa et al., 2015).

Fig. 5.

Basafa's optimization approach for cement placement. A representative model demonstrates the evolution of the cement distribution, starting from a completely filled proximal femur until the optimal distribution. Reprinted from Basafa and Armand (2014) with permission from Elsevier.

A different approach was taken by Varga et al. who attempted to identify generalizable patterns of optimal cement location that could be applied via simple surgical guidelines (Varga et al., 2017). In their opinion the detailed preoperative planning and controlled injection techniques proposed by Basafa et al. are not realistic for present clinical practice. They developed an injection pattern based on the principles of Wolff's law and reported an increase of 64% in yield force and 156% in yield energy with 12 ml cement. However, they did not validate the FE approach against experiments. A recent head-to-head comparison of both methodologies (Farvardin et al., 2019), patient-specific versus generalized, simulated both cement injection patterns via particle diffusion and showed favorable results for the patient-specific approach with a significantly higher increase in yield load.

Similar methodologies could be applied to femurs with bone metastases to identify optimal locations for cement injection next to the lytic lesions. It is hypothesized that such a strategic injection can improve strength upon solely filling of the lesions itself (Palumbo et al., 2014), while keeping the cement volume within an acceptable range.

Besides optimization of location, FE models also offer the possibility to insert various cement properties and thereby compare the spectrum of bone cements that are commercially available or under development. PMMA is the most widely used material, but also composite cements (Katsanos et al., 2010), calcium phosphate cements (Katsanos et al., 2010) and elastomers (Van Der Steenhoven et al., 2011) have been suggested as filler materials. These different materials can be included in FE models by adapting the stiffness and strength properties of the modeled cement. Even varying viscosity properties of cement have recently been compared (Ramos-Infante and Pérez, 2019).

5. Conclusion

Although it has been demonstrated that FE models for fracture risk prediction of proximal femurs with metastatic bone lesions outperform current clinical guidelines, the models are not integrated in the clinical workflow. Only a cautious start has been made at few places to introduce these models in clinical practice. Important barriers are the need for more automation to reduce the analysis time and the need to eliminate expert knowledge in developing and interpreting FE models. In addition to fracture risk assessment, FE models can be used to quantify the mechanical effects of prophylactic femoroplasty. Specifically, FE models could serve to select appropriate candidates who will benefit the most from the procedure and to improve the increase in mechanical strength by optimizing the location for cement augmentation. We conclude that when FE models would find their way into clinical practice, they could offer an improved, biomechanics-based tool to predict bone fracture risk on a subject-specific basis; furthermore, these models offer great potential to improve prophylactic treatment.

Transparency document

Transparency document.

CRediT authorship contribution statement

Amelie Sas: Conceptualization, Writing - original draft, Visualization, Project administration, Funding acquisition. Esther Tanck: Conceptualization, Writing - review & editing, Supervision. An Sermon: Conceptualization, Writing - review & editing, Supervision, Funding acquisition. G. Harry van Lenthe: Conceptualization, Writing - review & editing, Supervision, Funding acquisition.

Declaration of competing interest

None.