Solidarity and disparity: declining labor union density and changing racial and educational mortality inequities in the United States Solidarity and disparity

Abstract

Background:

Recently, U.S. life expectancy has stagnated or declined for the poor and working class and risen for the middle and upper classes. Declining labor-union density – the percent of workers who are unionized – has precipitated burgeoning income inequity. We examined whether it has also exacerbated racial and educational mortality inequities.

Methods:

From CDC, we obtained state-level all-cause and overdose/suicide mortality overall and by gender, gender-race, and gender-education from 1986–2016. State-level union density and demographic and economic confounders came from the Current Population Survey. State-level policy confounders included the minimum wage, AFDC/TANF generosity, and unemployment-insurance generosity. To model the exposure-outcome relationship, we used marginal-structural-modeling. Using state-level inverse-probability-of-treatment-weighted Poisson models with state and year fixed effects, we estimated three-year-moving-average union-density’s effects on the following year’s mortality rates. Then, we tested for gender, gender-race, and gender-education effect-modification. Finally, we estimated how racial and educational all-cause mortality inequities would change if union density increased to 1985 or 1988 levels respectively.

Results:

Overall, a 10% increase in union density was associated with a 17% relative decrease in overdose/suicide mortality (95% CI: 0.70, 0.98), or 5.7 lives saved per 100,000 person-years (95% CI: −10.7, −0.7). Union density’s absolute (lives-saved) effects on overdose/suicide mortality were stronger for men than women, but its relative effects were similar across genders. Union density had little effect on all-cause mortality overall or across subgroups, and modeling suggested union-density increases would not affect mortality inequities.

Conclusions:

Declining union density (as operationalized in this study) may not explain all-cause mortality inequities, although increasing union density may reduce overdose/suicide mortality.

1. Introduction

Over the last several decades in the U.S., life expectancy has stagnated or declined for the poor and working class and risen for the middle and upper classes.¹ The decline among those at the bottom of the class structure has precipitated an overall decline in U.S. life expectancy each of the last three years,² eroding a century of general improvement and suggesting a fundamental fracturing of society. Increased mortality from drug overdoses and suicides (often called “deaths of despair”) among the white working class has contributed to the growing socioeconomic inequities in mortality among white people, and fatal-overdose and suicide rates are increasing across racial groups.^1,3,4 However, despite the considerable amount of research documenting the widening inequities, few studies have sought to identify the widening’s causes. Moreover, studies that have tend to focus on changes in the class distribution of “risk behaviors”, like drug use, which provide only partial explanations.¹ The concurrent rise of health and income⁵ inequities suggests that structural factors – the economic, social, and political environments that drive social outcomes⁶ – have exacerbated inequities across multiple domains. One such structural factor – declining labor union density – has precipitated burgeoning income inequity.⁷ Unionism’s disproportionate decline among less-educated and blue-collar workers, and the well-documented relationship between unions and wages, benefits, occupational safety, and protective policies suggests a connection with growing mortality inequities.^8,9 Thus, in this state-level study, we analyzed union density’s relationship with all-cause mortality and overdose/suicide mortality, and tested whether declining union density has exacerbated racial and educational mortality inequities.

Today, income inequity is greater than any time since the Great Depression. In 1980, the average pretax earnings of the top 1% of Americans were 27 times more than those of the bottom 50%, whereas in 2015, they were 81 times more.⁵ Income inequities across social classes have also grown: from the 1970s to the 2000s, the household-income gap between the large-business-owning class and the working class increased 2.5-fold.¹⁰ Meanwhile, racial inequities in family incomes have remained largely unchanged since the late 1960s.¹¹

Mortality inequities have grown alongside the income inequities. For example, period life expectancy inequities between high and low socioeconomic groups (defined by education or income) have increased 1–2 years since the 1980s, due in part to increases in overdose and suicide rates among the marginalized.¹ Among certain demographics, inequities have grown more sharply. One study estimated that among white women, the life-expectancy gap between those with a college degree and those without a high-school (HS) degree increased by 2.2 years from 1991 to 2005; among those without a HS degree, life expectancy declined by 0.7 years.¹² Cohort inequities have also increased. The National Academies of Sciences, Engineering, and Medicine predicts the age-50 life expectancy gap between those in the top and bottom lifetime-income quintiles will increase from 3.9 years among women born in 1930 to 13.6 years among women born in 1960, while among men, they predict the gap will increase from 5.1 years to 12.7 years.¹³ Although racial mortality disparities have narrowed, substantial inequities persist.¹⁴ For example, in 2015, the white-Black life expectancy gap was 2.6 years among women and 4.1 years among men.¹⁵ One study estimated racial survival inequities precipitated 2.7 million excess Black deaths from 1970 to 2004.¹⁶

Falling relative incomes among the poor and working class and a strengthening income-mortality relationship have contributed to the growing SES-related mortality inequities.¹ Social-service cuts,¹⁷ increasing costs of necessities like health care,¹⁸ and mass incarceration¹⁹ may have strengthened the income-mortality relationship. Furthermore, income inequity itself may worsen health inequities by undermining social cohesion among the marginalized and by giving the wealthy more political power.¹ For example, societies with greater income inequity tend to spend less on income redistribution, which may undermine the ability of those in the poor and working class to satisfy their material needs.^20,21

The proportion of U.S. wage and salary workers ages 25-to-64 covered by labor union contracts (i.e., labor union density) decreased from 27.1% to 13.1% from 1983 to 2017, including from 36.3% to 14.9% among Black workers (compared with 25.9% to 13.5% among white workers) and from 29.7% to 11.4% among workers with a HS degree or less (compared with 24.1% to 13.9% among workers with more than a HS degree).²² Several factors have precipitated this decline, including the hostile business and political opposition faced by unions following the 1970s and 1980 recessions.^23,24 For example, the number of unfair labor practices and illegal firings by employers doubled from 1970 to 1980.²⁴ In response to the opposition, many union leaders pursued labor-management partnerships, suppressing the workplace organizing and direct action undergirding organized labor’s historical successes;^23–25 from the 1970s to the 2010s, the number of strikes involving at least 1,000 workers decreased from approximately 300 per year to fewer than 20.²⁶ In this context of declining density and militancy, unions have grown increasingly likely to grant concessions to employers like benefit cuts in exchange for promises of job security.^27,28

Multiple studies have connected declining union density to growing income inequity.⁷ Low union density undermines worker power over wages, which has spillover effects for prevailing norms in non-unionized workplaces,²⁹ and undermines union organizing for redistributive policies, like a higher minimum wage.³⁰ For example, one study estimated that declining union membership from 1973 to 2007 explained a third of the rise of wage inequity among men and a fifth of the rise among women,²⁹ an effect size similar to that found in more-recent research.^7,31 Declining union density has also exacerbated racial income inequities: Rosenfeld et al. estimated that Black-white wage inequity in 2007 would have been 3%−10% lower among men and 13%−30% lower among women if union membership had remained at 1973 levels.³²

Unions may also protect health and reduce health inequities. At the workplace level, by regulating the balance of power between workers and management, unionization may reduce exposure to material deprivation (e.g., inadequate wage and non-wage benefits, including access to health insurance and drug treatment),^7,27 occupational hazards (e.g., toxic chemicals),^8,9 and stressors (e.g., job instability or a lack of job autonomy),²⁷ which can cause chronic disease and occupational injury, as well as mental illness, drug use, and their sequelae, like suicide and fatal overdose.³³ For example, Hagedorn et al. found that collectively-bargained, legally-binding union contracts tend to contain provisions promoting workers’ income, benefits, working-time arrangements, safety, and decision-making power.⁸ The workplace-level health benefits of unionization may be stronger for less-educated, racialized, and otherwise marginalized workers, a finding demonstrated for economic outcomes like the union wage premium.⁷ Similarly, at the societal level, by regulating the balance of power between the working class and owning class, unionism may improve working-class health by advancing economy-wide compensation norms, labor rights, and progressive social protections and public-health programs, reducing material deprivation and psychosocial stressors throughout the working class, union membership aside.^9,29,30,34 For example, Feigenbaum et al. found that state-level right-to-work laws, which weaken unions by allowing workers in unionized businesses to opt out of paying union dues, reduce state-level policy progressivism, such as the strength of redistributive social programs.³⁰ Additionally, by fostering solidarity among workers and their broader communities, unionism may reduce alienation and feelings of powerlessness, factors associated with mental illness and drug use.^35,36 For example, DeFina et al. found that higher state-level union density was associated with lower state-level overdose death rates from 1999–2016.³⁵

Despite these potential mechanisms, few US-based studies aside from DeFina et al.’s have analyzed unionism’s relationship with non-occupational health outcomes or inequities in those outcomes, although several have identified a protective effect of unionization on occupational fatalities.^37–39 Regarding non-occupational health outcomes, Reynolds et al. identified a cross-sectional association between union membership and better self-rated health among workers who were men, had less than a college degree, or had incomes below the 75^th percentile,²⁷ while Waitzman found that union membership was associated with reduced mortality among men in the 1960s and 1970s.⁴⁰ Given the limited prior research, the relationship between union density and mortality, as well the role of declining union density in growing mortality inequities, remains understudied.

Using a longitudinal, ecological study of U.S. states, we tested the relationships between union density, mortality rates, and racial and educational mortality inequities. Our specific goals were to estimate state-level union density’s effects on all-cause mortality rates and overdose/suicide (“despair”) mortality rates from 1986 to 2016, and to test for effect modification of these estimates by gender, gender-race, and gender-education. Additionally, we estimated how racial and educational mortality inequities would change if union density increased from 2015 levels to 1985 or 1988 levels respectively. We hypothesized that increases in union density would have small protective effects on all-cause mortality and stronger protective effects on despair mortality (because despair mortality may be more immediately affected by changes in union density than other types of mortality). We also hypothesized that increases in union density would be more protective for men (given their stronger attachment to the waged labor force throughout the study period), as well as for Black and less-educated people (given findings from prior research on unionism and economic outcomes), than for women, white people, and more-educated people. Finally, because of union density’s disproportionate decline among Black and less-educated workers, as well as our hypothesis that union density would be most protective for those groups, we hypothesized that racial and educational inequities would lessen if union density increased to earlier levels.

2. Methods

a. Data

Exposure

Beginning in 1983 (the first year union status was available), we calculated overall and demographic-specific (gender, gender-race, and gender-education) state-level union density among 25-to-64-year-olds using the Merged Outgoing Rotation Group files of the Current Population Survey (CPS) maintained by the Center for Economic Policy Research.⁴¹ The Census Bureau cleans CPS data and imputes missingness. Using the year-specific estimates, we created a three-year moving average union density variable using a given state’s union density in that year and each of the two preceding years. We used a moving average to reduce sampling error and because average union density over several years may be more mortality-relevant than union density in a single year. We excluded respondents ages 65 and older to focus on populations with high labor-force participation, as union density may be most relevant to their health. We excluded respondents below age 25 not only because of their lower labor-force participation, but also because education level at death, which we used in the gender-education effect-modification analyses, may not accurately proxy socioeconomic status in this group.

The overall state-level union density measure was the exposure for our primary analyses, while the gender, gender-race, and gender-education specific state-level union density measures were the exposures for each of the effect-modification analyses. In the effect-modification analyses, we defined race as white or Black (the only consistently-coded races in the outcome data) and education as ≤ HS or > HS educated. Because decedents with < HS education are sometimes misclassified as having a HS degree on death certificates, our chosen categories minimized misclassification.⁴²

Mortality counts

Annual overall, gender-, and gender-race-specific state-level all-cause mortality counts among 25-to-64-year-olds from 1986 to 2016 came from CDC’s Compressed Mortality Files (CMF).⁴³ Due to small counts, CDC suppressed 307 Black-female-state-year observations and 231 Black-male-state-year observations, including all Black-state observations from MT, ND, SD, VT, and WY. Gender-education specific state-level all-cause mortality counts from 1989 to 2004 (1989 was the first year death certificates recorded education) came from CDC’s publicly-available Multiple Cause of Death (MCD) files maintained by the National Bureau of Economic Research.⁴⁴ Counts from 2005 to 2016 came from CDC’s restricted MCD files. Twenty-one states recorded no education information on their death certificates in at least one year; we excluded these state-year observations from our analyses. In other state-years, a fraction of deaths lacked education (the mean state-level proportion of deaths lacking education information was 3.8%). For these state-years, we used hot-deck imputation to impute missing values assuming the missingness was random conditional on state, year, gender, race, and age.⁴⁵

Using the same sources, we also obtained annual overall and gender-specific state-level counts of deaths with underlying causes of drug and alcohol poisoning and suicide (“deaths of despair”).^46,47 CDC suppressed 31 female-state-year observations due to small counts. We did not obtain gender-race- and gender-education-specific state-level despair-deaths due to small counts. Appendix A1 discusses the ICD codes used in these analyses.

Population denominators

For analyses of overall, gender-, and gender-race-specific state-level mortality, population denominators came from CDC WONDER, which provided estimates from the decennial census for 1990, 2000, and 2010 and interpolated estimates for intercensal years.⁴³ For analyses of gender-education-specific state-level mortality, we estimated the denominators using decennial census and American Community Survey (ACS) data maintained by IPUMS.⁴⁸

Confounders

Potential time-varying state-level confounders identified a priori included: 1) the distribution of age, race, and education, 2) social/labor policies (the minimum wage, the AFDC/TANF-to-poverty ratio – an indicator of welfare generosity, and the unemployment insurance recipiency rate – an indicator of unemployment insurance generosity), 3) economic conditions (unemployment rate, mean hourly wage, and per-capita GDP), and 4) industrial structure (percent of workforce employed in: a) manufacturing, b) transportation and utilities, c) construction, and d) the public sector). State and year, which we modeled as fixed effects, were also confounders due to time-invariant differences across states in confounding factors (e.g., labor laws), as well as secular trends across states in such factors (e.g., recessions or the fatal-overdose epidemic). Table I displays how we specified the time-varying confounders; Appendix A2 displays their sources. In our primary analyses, we measured non-policy confounders at the state-level among 25-to-64-year-olds, while in our effect-modification analyses, we measured non-policy confounders at the state-demographic level among 25-to-64-year-olds. The confounders did not contain any missingness.

Table I.

Mean (SD) of three-year moving average state-level variables, as well as state-level mortality rates, in 1985 (top) and 2015 (bottom) across year-specific union-density quartiles.^a

			Quartile 1	Quartile 2	Quartile 3	Quartile 4
1985	Age	% 25–34 years old	0.35 (0.02)	0.36 (0.02)	0.35 (0.02)	0.35 (0.03)
		% 35–44 years old	0.27 (0.01)	0.26 (0.01)	0.26 (0.01)	0.27 (0.01)
		% 45–54 years old	0.19 (0.01)	0.19 (0.01)	0.19 (0.01)	0.19 (0.01)
		% 55–64 years old	0.19 (0.02)	0.18 (0.02)	0.19 (0.01)	0.19 (0.03)
Gender		% women	0.51 (0.01)	0.51 (0.01)	0.51 (0.01)	0.51 (0.01)
Race		% white	0.79 (0.11)	0.89 (0.08)	0.83 (0.20)	0.84 (0.17)
		% Black	0.11 (0.10)	0.07 (0.09)	0.11 (0.19)	0.06 (0.04)
		% other	0.09 (0.12)	0.04 (0.03)	0.06 (0.07)	0.10 (0.18)
Education		% < HS	0.23 (0.06)	0.19 (0.08)	0.18 (0.03)	0.18 (0.06)
		% HS	0.36 (0.02)	0.39 (0.03)	0.38 (0.06)	0.41 (0.04)
		% some college	0.21 (0.04)	0.22 (0.05)	0.20 (0.04)	0.20 (0.05)
		% college	0.20 (0.03)	0.20 (0.04)	0.24 (0.05)	0.21 (0.04)
Econ. conditions		% unemployed	0.06 (0.01)	0.06 (0.02)	0.06 (0.01)	0.08 (0.02)
		GDP per capita ($10k)b	3.40 (0.44)	3.71 (0.78)	4.28 (1.84)	4.26 (2.13)
		Mean wage ($)b	19.26 (1.82)	19.47 (1.85)	21.16 (2.31)	22.02 (3.00)
Ind. structure		% agriculture	0.04 (0.02)	0.06 (0.05)	0.03 (0.03)	0.03 (0.02)
		% services	0.75 (0.06)	0.75 (0.04)	0.77 (0.09)	0.75 (0.07)
		% manufacturing	0.21 (0.07)	0.19 (0.06)	0.20 (0.09)	0.22 (0.08)
		% public sector	0.18 (0.04)	0.18 (0.02)	0.19 (0.07)	0.18 (0.04)
Policies		State - federal MW ($)c	0.00 (0.00)	0.00 (0.00)	0.08 (0.27)	0.09 (0.33)
		AFDC/TANF:povertyd	0.40 (0.13)	0.48 (0.14)	0.73 (0.28)	0.72 (0.16)
		UI recipiency ratee	0.21 (0.04)	0.27 (0.08)	0.31 (0.06)	0.31 (0.09)
Mortality		All-cause per 100k	441.75 (60.04)	405.08 (79.40)	447.53 (91.65)	416.24 (70.89)
		Despair per 100k	20.27 (3.00)	18.74 (3.84)	18.73 (6.21)	16.86 (3.85)
2015	Age	% 25–34 years old	0.27 (0.02)	0.27 (0.04)	0.24 (0.02)	0.26 (0.02)
		% 35–44 years old	0.25 (0.01)	0.24 (0.01)	0.23 (0.01)	0.24 (0.01)
		% 45–54 years old	0.25 (0.01)	0.25 (0.02)	0.27 (0.01)	0.26 (0.01)
		% 55–64 years old	0.23 (0.02)	0.24 (0.02)	0.27 (0.02)	0.24 (0.01)
Gender		% women	0.51 (0.01)	0.50 (0.01)	0.50 (0.01)	0.50 (0.01)
Race		% white	0.67 (0.13)	0.70 (0.16)	0.84 (0.12)	0.63 (0.18)
		% Black	0.16 (0.12)	0.12 (0.12)	0.07 (0.08)	0.08 (0.05)
		% other	0.17 (0.12)	0.18 (0.13)	0.08 (0.05)	0.29 (0.19)
Education		% < HS	0.10 (0.03)	0.07 (0.02)	0.06 (0.02)	0.07 (0.02)
		% HS	0.31 (0.04)	0.30 (0.05)	0.33 (0.05)	0.28 (0.03)
		% some college	0.29 (0.03)	0.29 (0.06)	0.27 (0.04)	0.29 (0.04)
		% college	0.30 (0.04)	0.34 (0.10)	0.34 (0.07)	0.36 (0.05)
Econ. conditions		% unemployed	0.05 (0.01)	0.05 (0.01)	0.04 (0.01)	0.06 (0.01)
		GDP per capita ($10k)b	4.90 (0.76)	6.66 (3.71)	5.26 (0.87)	6.13 (0.96)
		Mean wage ($)b	22.54 (2.18)	23.95 (3.48)	23.94 (2.75)	25.73 (1.98)
Ind. structure		% agriculture	0.02 (0.02)	0.02 (0.02)	0.02 (0.02)	0.01 (0.01)
		% services	0.86 (0.03)	0.86 (0.06)	0.85 (0.05)	0.88 (0.05)
		% manufacturing	0.12 (0.02)	0.11 (0.05)	0.13 (0.04)	0.11 (0.05)
		% public sector	0.16 (0.02)	0.18 (0.05)	0.16 (0.03)	0.15 (0.04)
Policies		State - federal MW ($)c	0.09 (0.23)	0.39 (0.62)	0.42 (0.53)	1.10 (0.54)
		AFDC/TANF:povertyd	0.10 (0.07)	0.22 (0.24)	0.27 (0.10)	0.33 (0.14)
		UI recipiency ratee	0.16 (0.04)	0.22 (0.08)	0.28 (0.07)	0.29 (0.07)
Mortality		All-cause per 100k	437.23 (96.55)	433.29 (73.54)	425.74 (91.85)	349.85 (46.77)
		Despair per 100k	45.32 (10.51)	48.10 (11.41)	57.92 (15.29)	44.04 (11.07)

Notes:

^aQuartile ranges: 1985: 7.3–16.9%, 16.9–23.6%, 25.6–29.0%, 30.2–39.5%; 2015: 3.9–7.4%, 8.2–12.6%, 12.8–16.5%, 16.9–28.0%.

^b2017 dollars.

^bMW is the minimum wage.

^cProportion of families receiving AFDC/TANF benefits out of all impoverished families with children.

^dShare of unemployed workers receiving unemployment insurance (UI) benefits from regular state programs.

b. Statistical analyses

We hypothesized prior union density affected prior socioeconomic conditions and policies (because unionization may immediately affect factors like wages), as well as current socioeconomic conditions and policies (because union organizing may take time to affect factors like policies), and mortality (Figure 1). In turn, current socioeconomic conditions and policies affected future union density (because certain conditions and policies may make it easier to unionize) and mortality. Thus, given that policies and socioeconomic conditions were confounders and mediators of the union density-mortality relationship, we used a marginal structural modeling (MSM) approach to estimate the relationship between state-level union density and state-level mortality rates.⁴⁹

Figure 1.

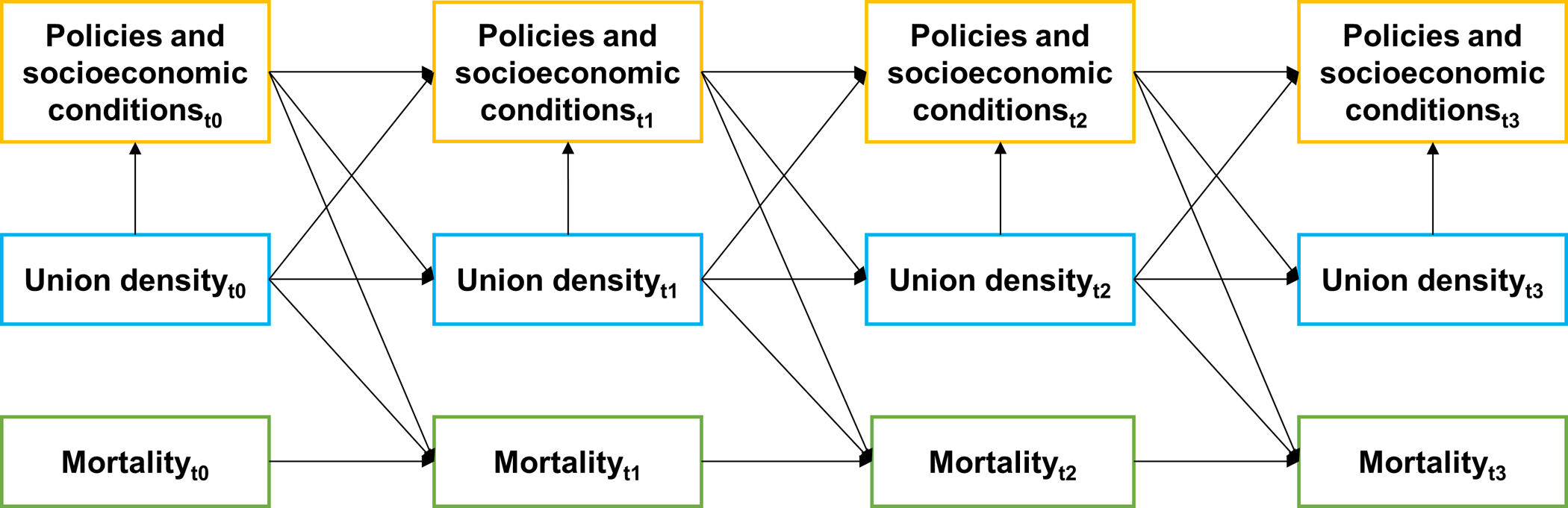
Directed acyclic graph depicting hypothesized relationship between union density, mortality, and time-varying confounders. Policies and socioeconomic conditions are confounders and mediators of the union density-mortality relationship.

First, we calculated stabilized inverse-probability-of-treatment weights (IPTW) for each state-year observation. We defined the stabilized weight (SW) for state i at time t as:

$$S{W}_{it}=\frac{f_{E_{it}|I_i{T}_t}\left(E_{i,t},I_i,T_t\right)}{f_{E_{it}| C_{i,t-1},E_{i,t-3},I_i,T_t}\left(E_{i,t,t-3},C_{i,t-1},I_i,T_t\right)}$$

where $f(\cdot )$ is the probability density function for the exposure E, I is state, T is year, and C is a vector of time-varying confounders. The weight denominator for state i in year t was the density of the exposure model at the observed exposure value E_it given prior time-varying confounders C_it-1, prior exposure E_it-3, state I_i, and year T_t. Using R code from Hazelbag et al.,⁵⁰ we estimated this probability-density function using a pooled gamma linear model that had three-year moving average state-level union density as the outcome and the aforementioned time-varying confounders (lagged one year), prior exposure (lagged three years to reduce collinearity), and state and year fixed effects as predictors. Not lagging the time-varying confounders did not meaningfully affect the estimated weights. To estimate the weight numerator, we used the same gamma linear model but included only state and year fixed effects as predictors. The final stabilized weight for each observation was the product of the state’s weight in a given year and each of the two preceding years. This approach assumed that a state’s probability of receiving its union density value in a given year was independent of exposure and confounder history beyond the two preceding years;⁵⁰ we were unable to include more years without the weight range growing large. Large estimated weights, which often result from non-positivity, make certain observations exert undue influence in the outcome model, causing imprecision and bias.⁵¹ Following standard practice, we used weight truncation to ensure the weights had a mean of approximately 1 and a small range.⁵¹ For the main analyses, we truncated the weights at the 5^th and 95^th percentiles (i.e., weights smaller than the 5^th percentile or larger than the 95^th percentile were set equal to the 5^th percentile or 95^th percentile weight values respectively). Appendix A3 shows the weight distribution.

Next, in Stata, we used log-linear Poisson models with IPTW weights, state and year fixed effects (modeled using dummy variables), an offset of log(population size), and state-level cluster-robust standard errors to estimate the effects of a 10% (interquartile range) increase in one-year lagged, three-year moving average state-level union density on the following year’s state-level all-cause and despair mortality rates;^52,53 ordinary least squares models weighted by state-population size and the IPTW with mortality rates as the outcome yielded similar estimates (Appendix A4). Because state and year fixed effects were in the numerator and denominator of the IPTW, we included them in the outcome models to adjust for confounding by those factors.⁵¹ The Poisson models directly estimated the relative effects of union density on mortality (i.e., risk ratios or RRs). We also estimated absolute effects (i.e., risk differences or RDs) using Stata’s “margins” command.⁵⁴ We conducted the analyses on a sample of 1,581 observations (51 states – including D.C. – observed for 31 years each).

To test for effect modification of the union-density-mortality relationship by gender, we calculated IPTW using a similar approach. However, in addition to the aforementioned time-varying confounders, the denominator model included gender by state-fixed-effect and gender by year-fixed-effect interaction terms as predictors (i.e., gender-state and gender-year fixed effects), due to time-invariant state-level differences in gender disparities in union density and mortality, as well as strong gender-specific temporal trends in such factors across states. In addition, we included the preceding year’s union density exposure among the complementary gender (e.g., for a given woman-state-year observation, the preceding year’s union density exposure among men in that state). We included the complementary gender’s union density because it may affect the given gender’s propensity to unionize, as well as their access to health-promoting resources. The numerator model included gender-state and gender-year as predictors. We truncated the final weights at the 4th and 96th percentiles (Appendix A3). We then tested whether the relationship between union density and mortality varied by gender by including a union density by gender interaction term in the IPTW log-linear Poisson models, which also included gender-state and gender-year fixed effects. The models provided evidence about multiplicative effect modification directly. We tested for additive effect modification using “margins”. We conducted the analyses on a sample of 3,162 observations for all-cause mortality and 3,131 observations for despair mortality.

To test for effect modification of the union-density-mortality relationship by race, we first stratified the data by gender, due to gender differences in levels of union density and mortality, as well as in the hypothesized relationship between the variables. Next, we calculated stabilized IPTW. The denominator models included the time-varying confounders as predictors, as well as race-state and race-year fixed effects. We also included the union density exposures among the complementary gender-races. The numerator models included race-state and race-year as predictors. We truncated the final weights at the 4th and 96th percentiles for women and men (Appendix A3). We then tested whether the relationship between union density and all-cause mortality varied by race by including a union density by race interaction term in the IPTW log-linear Poisson models, which also included race-state and race-year fixed effects. To reduce exposure measurement error, we excluded gender-Black-state-year observations with fewer than 50 Black respondents surveyed about their union-contract coverage on average over the prior three years; increasing the cutoff to 100 did not change our effect estimates. We also excluded gender-race-state-year observations that had estimated complementary gender-race union densities of 0% or 100%; these values resulted from small cell sizes in the CPS and caused the IPTW models to fit poorly. Excluding the complementary gender-race union densities as predictors in the IPTW models did not affect the estimated weights. Overall, the exclusions reduced the sample size from 2,855 to 2,347 observations among women and from 2,931 to 2,279 observations among men. After the exclusions, certain states lacked Black observations throughout follow-up: AL, AZ, HI, ID, IA, ME, MT, NE, ND, NH, NM, OR, SD, UT, VT, WV, WY, and, among women, WA.

To test for effect modification of the union-density-mortality relationship by education, we used a similar approach to the racial effect-modification analyses. However, to reduce misclassification, we excluded state-year observations in which more than 20% of death certificates lacked education information (n=266); increasing the threshold to 30% did not meaningfully change our estimates, nor did excluding the 21 states that recorded no education information on their death certificates in at least one study year. We truncated the final weights at the 4^th and 96^th percentiles for women and men (Appendix A3). For each gender, we conducted the analyses on a sample of 2,590 observations.

Finally, to estimate counterfactual racial and educational mortality inequities, we used parameter estimates from the IPTW log-linear Poisson models to compare how state-level all-cause mortality rates would change for Black people versus white people and the less-educated versus the more-educated if three-year moving average union density increased from mean 2015 levels to mean 1985 or 1988 levels respectively for each group across all states. Regarding racial inequities, this corresponded to an increase in union density from 14.7% to 29.4% among Black women, 13.2% to 18.3% among white women, 17.2% to 38.4% among Black men, and 14.6% to 29.1% among white men). Regarding educational inequities, this corresponded to an increase in union density from 9.2% to 15.6% among less-educated women, 14.8% to 19.9% among more-educated women, 13.5% to 31.6% among less-educated men, and 14.4% to 21.4% among more-educated men. Our approach assumed union density’s mortality effects did not change temporally.

c. Sensitivity analyses

We tested our results’ robustness to three specific concerns.

First, we tested the sensitivity of our results to the estimated weights. In MSM analyses, obtaining asymptotically unbiased estimates requires correct specification of the weighting model.⁵⁵ In settings with continuous exposures, this can be complicated by the need to identify the exposure’s correct distributional form.⁵⁵ Our primary analyses used gamma models to generate the weights rather than linear models because weighting by gamma IPTW may lead to less-biased estimates for skewed exposures.⁵⁵ We tested the sensitivity of our results to this choice by re-estimating the IPTW using linear models (with R code from Hernan et al.⁵⁶) prior to fitting the outcome models.

Second, we tested whether lagging the exposure three years rather than one year affected our results. Although certain health-related factors may be immediately affected by changes in union density, others may remain unaffected for several years. Moreover, changes in such factors may take several years to affect health.

Finally, we tested for nonlinear union density-mortality relationships. Unions could plausibly have stronger mortality effects at higher densities if unions at lower densities lack the power to organize workers and change working conditions. Contrarily, unions could have stronger mortality effects at lower densities given diminishing returns to improving such factors. We tested for nonlinear relationships by modeling union density with 3-knot restricted cubic splines (with knots at the 10^th, 50^th, and 90^th union-density percentiles) in the outcome analyses. We estimated RRs from the spline terms using Stata’s “xblc” command.⁵⁷

d. Institutional review board approval

This study used publicly-availably, de-identified data. Thus, it was exempt from IRB review. However, this study falls under a broader research project that the University of Washington Institutional Review Board approved.

3. Results

Three-year moving average union density among 25-to-64-year-olds decreased from 25.4% in 1985 to 13.6% in 2015 (Figure 2). This decrease did not distribute evenly across genders, races, or education groups, but rather concentrated among Black and less-educated workers, particularly Black and less-educated male workers (Figure 2). The decrease did not distribute evenly across states either; in New Hampshire, union density decreased from 15.4% to 12.8%, whereas in Michigan, it decreased from 38.0% to 18.5%, including from 72.3% to 28.0% among Black male workers and from 57.6% to 20.8% among ≤ HS-educated male workers. Compared to state-year observations with lower union density, state-year observations with higher union density tended to be less Black, more educated, and have higher mean wages, minimum wages, AFDC/TANF-to-poverty ratios, and unemployment insurance recipiency rates (Table I).

Figure 2.

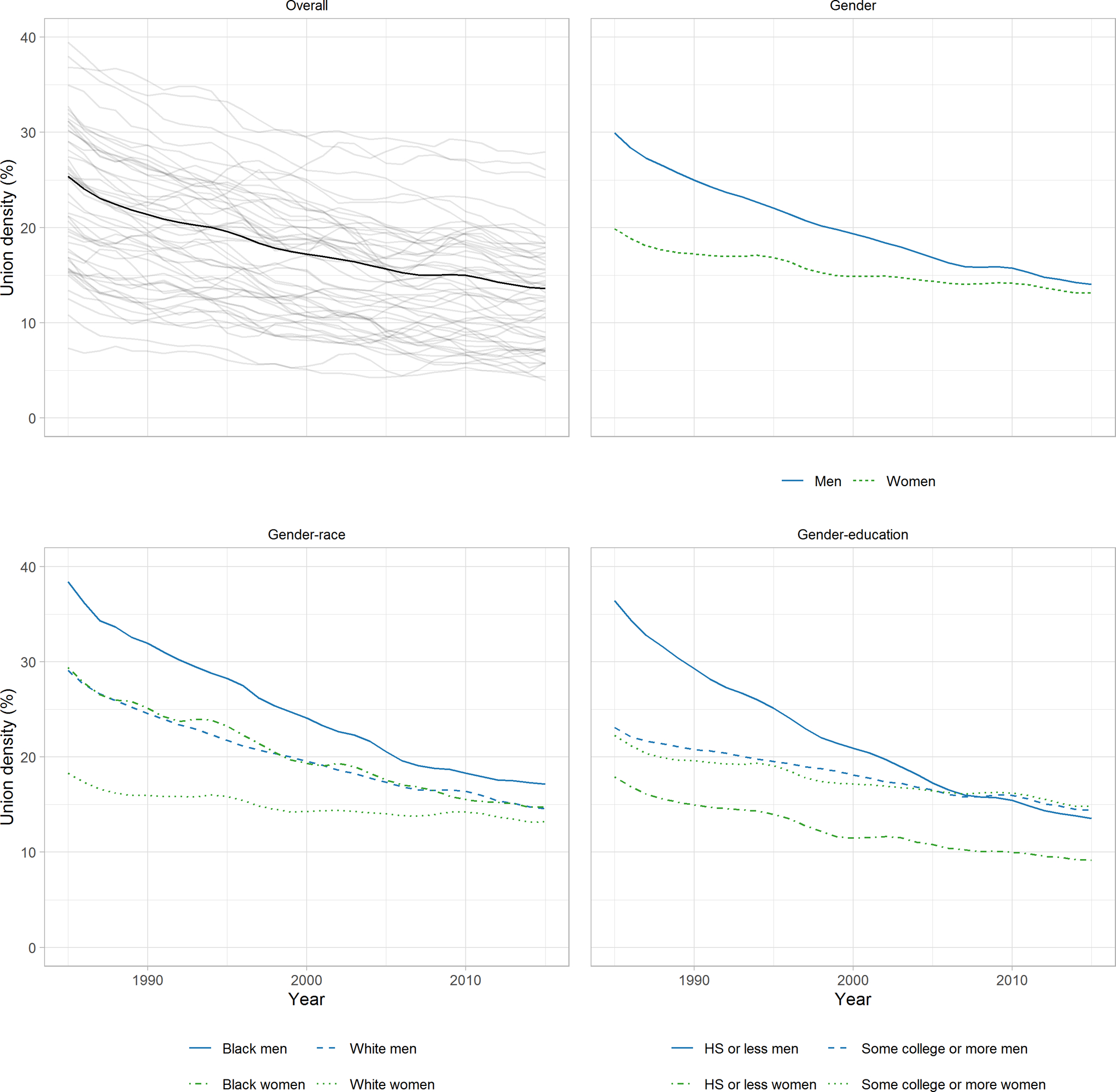
Three-year moving average union density in the United States from 1985 to 2015 among 25-to-64-year-old wage and salary workers overall (with state-specific trends shown in grey), as well as by gender, gender-race, and gender-education. Note: Union density is the proportion of wage and salary workers covered by a labor-union contract, which we estimated from the Current Population Survey’s Merged Outgoing Rotation Group files maintained by the Center for Economic Policy Research.

A 10% increase in one-year lagged, three-year moving average union density was not associated with all-cause mortality (RR: 0.99 [95% CI: 0.91, 1.08]; RD per 100,000: −3.2 [95% CI: −36.3, 29.8]) (Table II). However, it was associated with a 17% decrease in despair mortality (95% CI: 0.70, 0.98), which corresponded to a 5.7 per 100,000 person-years decrease in the outcome (95% CI: −10.7, −0.7). We found little evidence that union density’s effect on all-cause mortality varied by gender on the additive or multiplicative scales (Table II). However, although its effect on despair mortality did not vary by gender on the multiplicative scale, it did vary by gender on the additive scale (Table II). Specifically, among women, a 10% increase in one-year lagged, three-year moving average union density was associated with a 2.3 per 100,000 person-years decrease in despair mortality (95% CI: −6.0, 1.3), while among men, it was associated with an 11.0 per 100,000 person-years decrease (95% CI: −16.8, −5.1); the difference in these RDs was 8.6 (95% CI: 3.5, 13.8). Finally, we found no evidence that union density’s effect on all-cause mortality varied by gender-race or gender-education (Table III). Rather, across genders, races, and education groups, its effects were null.

Table II.

Relationship between 10% increase in 1-year lagged, 3-year moving average state-level union density and state-level mortality rates from 1986 to 2016 overall and by gender.^a

	Unweighted				Weightedb
	RR	95% CI	RD	95% CI	RR	95% CI	RD	95 % CI
Overall
All-cause mortality	0.92	0.84, 1.01	−30.7	−65.9, 4.5	0.99	0.91, 1.08	−3.2	−36.3, 29.8
Despair mortality	0.69	0.56, 0.85	−10.8	−17.1, −4.6	0.83	0.70, 0.98	−5.7	−10.7, −0.7
Gender
All-cause mortality
Women	0.89	0.79, 1.01	−32.1	−66.2, 1.9	0.96	0.81, 1.12	−13.2	−60.2, 33.8
Men	0.95	0.89, 1.03	−23.6	−60.2, 13.1	1.00	0.92, 1.08	−0.1	−41.8, 41.6
Interaction	0.93	0.83, 1.06	−8.6	−49.7, 32.6	0.96	0.78, 1.17	−13.1	−84.0, 57.9
Despair mortality
Women	0.65	0.48, 0.89	−6.4	−10.7, −2.0	0.86	0.68, 1.09	−2.3	−6.0, 1.3
Men	0.78	0.68, 0.89	−11.5	−18.1, −4.9	0.79	0.70, 0.89	−11.0	−16.8, −5.1
Interaction	0.84	0.66, 1.07	5.2	0.4, 10.0	1.10	0.89, 1.34	8.6	3.5, 13.8

Notes:

^aRisk ratio (RR) and risk difference (RD, per 100,000 person-years) estimates calculated using log-linear Poisson models with state-level cluster-robust standard errors, state and year fixed effects, and where appropriate, union density*gender interaction terms. RD is average marginal effect of union density on mortality.

^bModels weighted by gamma inverse probability of treatment weights.

Table III.

Relationship between 10% increase in 1-year lagged, 3-year moving average state-level union density and state-level mortality rates from 1986 to 2016 by gender-race and from 1989 to 2016 by gender-education.^a

	Unweighted				Weightedb
	RR	95% CI	RD	95% CI	RR	95% CI	RD	95 % CI
Gender-race
All-cause mortality
Women
Black	1.00	0.95, 1.04	−1.0	−20.6, 18.6	0.99	0.95, 1.04	−2.4	−21.0, 16.3
White	0.82	0.73, 0.92	−53.0	−82.0, −23.9	0.93	0.82, 1.05	−20.0	-52.4, 12.3
Interaction	1.22	1.09, 1.37	52.0	20.6, 83.4	1.07	0.95, 1.21	17.6	−17.2, 52.5
Men
Black	1.00	0.94, 1.07	3.5	−42.6, 49.5	1.00	0.92, 1.08	−1.5	−59.4, 56.4
White	0.92	0.87, 0.97	−39.0	−63.9, −14.0	0.95	0.90, 1.01	−22.6	−47.8, 2.6
Interaction	1.09	1.03, 1.16	42.4	3.2, 81.6	1.05	0.98, 1.13	−21.1	−30.3, 72.6
Gender-education
All-cause mortality
Women
≤ HS	0.89	0.78, 1.02	−50.5	−109.0, 8.1	0.96	0.86, 1.07	−18.6	−68.9, 31.7
> HS	0.91	0.85, 0.98	−16.7	−29.4, −3.9	0.96	0.90, 1.03	−6.4	−18.7, 5.9
Interaction	0.98	0.90, 1.08	−33.8	−83.4, 15.8	1.00	0.90, 1.10	−12.2	−57.7, 33.4
Men
≤ HS	0.94	0.88, 1.01	−44.1	−99.6, 11.4	0.96	0.90, 1.03	−30.9	−85.8, 24.1
> HS	0.93	0.87, 1.00	−19.3	−39.4, 0.8	0.95	0.87, 1.03	−15.3	−39.8, 9.3
Interaction	1.01	0.92, 1.11	−24.8	−80.3, 30.7	1.01	0.93, 1.11	−15.6	−67.2, 36.0

Notes:

^aRisk ratio (RR) and risk difference (RD, per 100,000 person-years) estimates calculated using log-linear Poisson models with state-level cluster-robust standard errors, state and year fixed effects, and union density*race or union density*education interaction terms. RD is average marginal effect of union density on mortality.

^bModels weighted by gamma inverse probability of treatment weights.

Modeling suggested that Black-white all-cause mortality inequities would remain largely unchanged if one-year lagged, three-year moving average union density increased to baseline levels. Specifically, among women, modeling suggested inequities would increase by 3% (95% CI: 0.95, 1.12), a 6.8 per 100,000 person-years increase in the inequity (95% CI: −22.9, 36.4). Among men, meanwhile, modeling suggested inequities would increase by 7% (95% CI: 0.92, 1.24), a 26.1 per 100,000 person-years increase in the inequity (95% CI: −82.5, 134.8) (Table IV).

Table IV.

Change in state-level all-cause mortality rates among Black people versus white people and the less-educated versus the more-educated if 1-year lagged, 3-year moving average union density increased from 2015 levels to 1985 or 1988 levels respectively.^a

	Women				Men
	RR	95% CI	RD	95% CI	RR	95% CI	RD	95 % CI
Raceb
Black	0.99	0.93, 1.06	−3.5	−30.7, 23.7	1.00	0.84, 1.17	−6.8	−127.6, 114.0
White	0.96	0.90, 1.03	−10.3	−26.8, 6.3	0.93	0.86, 1.01	−33.0	−69.5, 3.5
Ratio/difference	1.03	0.95, 1.12	6.8	−22.9, 36.4	1.07	0.92, 1.24	26.1	−82.5, 134.8
Educationc
≤ HS	0.97	0.91, 1.05	−12.0	−44.7, 20.6	0.93	0.82, 1.06	−54.8	−150.7, 41.1
> HS	0.98	0.95, 1.02	−3.2	−9.3, 2.9	0.96	0.91, 1.02	−10.7	−28.0, 6.5
Ratio/difference	0.99	0.93, 1.06	−8.8	−38.9, 21.4	0.97	0.86, 1.09	−44.1	−135.3, 47.1

Notes:

^aRisk ratio (RR) and risk difference (RD, per 100,000 person-years) estimates calculated using linear combinations of parameters from inverse probability of treatment weighted log-linear Poisson models with state-level cluster-robust standard errors, state and year fixed effects, and union density*race or union density*education interaction terms. RD is average marginal effect of union density on mortality.

^bModels run on outcome data from 1986–2016. Counterfactual union density set to 1985 levels.

^cModels run on outcome data from 1989–2016. Counterfactual union density set to 1988 levels.

Modeling also suggested educational inequities would be largely unaffected if union density increased to baseline levels. Specifically, among women, modeling suggested educational inequities would decrease by 1% (95% CI: 0.93, 1.06), an 8.8 per 100,000 person-years reduction in the inequity (95% CI: −38.9, 21.4), while among men, modeling suggested educational inequities would decrease by 3% (95% CI: 0.86, 1.09), a 44.1 per 100,000 person-years reduction in the inequity (95% CI: −135.3, 47.1) (Table IV).

Our results were somewhat sensitive to the estimated IPTW, particularly in despair-death analyses (Appendix A5). For example, in models weighted by linear IPTW, a 10% increase in one-year lagged, three-year moving average union density was associated with just an 11% decrease in despair mortality (95% CI: 0.72, 1.09), smaller than the estimate produced by models weighted by gamma IPTW. Nonetheless, lagging the exposure three years instead of one year did not meaningfully change most of the effect estimates, although increases in three-year lagged union density appeared to be protective for white men (Appendix A6). Finally, there were nonlinear relationships between union density and all-cause mortality for the overall and effect-modification analyses (Appendix A7). Specifically, increases in union density tended to be more protective at lower densities than at higher densities (although the estimates were imprecise), and increases in union density appeared to be most protective for white men. Nonetheless, modeling union density with a spline term did not appreciably change estimates from the counterfactual racial- and educational-inequity analyses. Meanwhile, for despair mortality, increases in union density tended to be more protective at higher densities than at lower densities.

4. Discussion

In our primary analyses, we found that increases in union density had protective effects on despair mortality but little effect on all-cause mortality. Moreover, union density’s effects did not vary substantially by gender, gender-race, or gender-education, and modeling did not suggest relative or absolute racial and educational all-cause mortality inequities would meaningfully change if union density increased to 1985 or 1988 levels. Across subgroups, weighted estimates tended to be smaller than unweighted estimates (sometimes considerably), suggesting that time-varying confounding of the union density-mortality relationship by economic, political, and demographic factors may have been considerable, even after adjusting for state and year fixed effects. Given the potential non-recursive relationship between union density and these time-varying confounders, our MSM approach to confounder-adjustment may have been less biased than traditional covariate-adjustment approaches. Although we did identify a protective effect of union density on all-cause mortality in certain sensitivity analyses – particularly among white men – we believe these estimates should be interpreted cautiously given the large number of statistical tests performed, generally small effect sizes, and our approach’s limitations (described below).

Several factors may explain our largely null findings. First, while unionization can improve working conditions, its effects – like a 15–20% wage premium⁷ – may be too weak to lower mortality rates, particularly given weakening union power. Second, SES inequities in mortality have primarily grown in recent decades, which is well after union density began precipitously declining,¹ suggesting other factors have played a larger role in the trend. That some of the largest inequity increases have occurred among women suggests that explanations focused solely on changes in the organization of wage labor, like declining union density, may be inadequate, particularly given patterns of sexism in the labor movement.⁵⁸ Third, although prior research has shown that the union wage and benefit premium is larger for Black workers than for white workers,⁷ racism in the union movement^59,60 may undermine the health benefits of unionization for Black workers. Although many unions today do work to protect members against workplace harassment and discrimination, some have ignored or been hostile to such concerns, particularly unions dominated by white workers.⁸ Fourth, because some union hierarchies have grown detached from their rank-and-file membership,^23,25 the solidarity-promoting and alienation-reducing effects of union membership and high union density may have weakened. Finally, we may not have identified the relevant etiologic period for the exposure. For example, average union density throughout one’s lifetime may be more relevant to health than the short-term changes we analyzed.⁶¹ Relatedly, certain outcomes that could be affected by union density, like stress-related cardiovascular disease, may not strike until older ages.⁶²

To our knowledge, no prior research has analyzed the effects of union density on these mortality outcomes. A recent instrumental-variable analysis using data from 1992 to 2016 found that a 1% increase in union density was associated with a 5% (95% CI: 0.93, 0.97) decrease in occupational fatalities.³⁷ Given that occupational fatalities constitute a small proportion of all-cause mortality, these findings do not contradict our own. Another recent study using data from 1999 to 2016 found that a 10% increase in union density was associated with a 2.7 per 100,000 person-years (95% CI: 0.5, 4.9) decrease in the overdose mortality rate.³⁵ Coupled with ours, these latter findings – and those of other studies⁴⁶ – point to the potential alleviation of overdose and suicide mortality with more robust social and economic protections for marginalized populations. Nonetheless, a recent study by Ruhm suggests that worsening economic conditions (and attendant increases in “despair”) have played a relatively small role in the fatal-overdose epidemic compared with changes in the drug environment, namely the cost, composition, and availability of drugs.⁶³ Other researchers have also challenged the “deaths of despair” framing, arguing that rather than “despairing”, marginalized groups in the U.S. have long struggled against their oppression, a stressful coping process which itself can harm health.³ Critics have further argued that excessive focus on “deaths of despair” has led researchers to overlook the primary causes of premature death among Black people and ignore other diseases contributing to widening SES inequities in mortality.³ More research is needed to disentangle the relative contributions of various social and economic factors to these phenomena.

Our analyses had several limitations, including potential violations of the strong MSM assumptions, which are: 1) no unmeasured confounding, 2) positivity (non-zero probability of all exposure-confounder combinations), 3) counterfactual consistency (states’ counterfactual outcomes under their observed exposure histories equal their observed outcomes), 4) no interference (states’ potential outcomes do not depend on other states’ exposures), and 5) no model misspecification.^51,64 Regarding the no-unmeasured-confounding assumption, our estimates may have been biased by time-varying confounding due to the exposure-outcome relationship’s complexity and our inability to incorporate states’ complete confounding histories into the IPTW. One potential unmeasured confounder was an indicator of state-level health-insurance generosity, such as the percent insured, consistent data on which was not available for all study years. Although estimates from models adjusted for percent insured for the years a consistent measure was available (1988 to 2013 in the CPS) closely resembled estimates from models unadjusted for the variable (Appendix A8), there may be other unmeasured confounders. Regarding the positivity assumption, our analyses had no structural positivity violations, given that each observation could have theoretically received any value of the exposure and confounders. Nonetheless, random positivity violations can cause unstable weights, a problem we observed.⁵¹ Although we used weight truncation to reduce bias and variance from weight variability, such truncation may have decreased control of confounding bias.⁵¹ Regarding the consistency assumption, our analyses assumed union density’s effects on mortality were independent of how union density changed. This assumption would be violated if, for example, increases in union density driven by rank-and-file organizing have different mortality effects than increases driven by labor-law changes. Nonetheless, we think meaningful consistency violations are unlikely given our largely null overall findings. Regarding the no-interference assumption, in preliminary analyses we found no evidence that union density in one state affected mortality rates in another state (Appendix A9), although more rigorous approaches are needed to rule interference out. Finally, regarding the no-model-misspecification assumption, our results’ sensitivity to the choice of IPTW, as well as the large range of weights, raises concerns about possible misspecification of the weighting model, which could have biased our estimates.

In addition to potential violations of certain MSM assumptions, our analyses may have suffered from sampling error, particularly in the race by union density analyses, despite our use of moving averages and sample-size restrictions. For Black-state-year observations, we based the CPS-derived exposure and confounding variables on responses from just 241 Black women and 195 Black men on average per year. For approximately ¼ of Black-state-year observations, we based the exposure and confounding variables on responses from fewer than 100 Black respondents of each gender on average per year. These small sample sizes increased the risk of random error in our union-density estimates. Sample size aside, nondifferential exposure measurement error may have also biased our density estimates. For example, Card found that 2.5% of CPS respondents in 1977 misreported their union status.⁶⁵ Although sampling error had an unpredictable effect on our estimates, measurement error may have biased them away from the null.⁶⁶

Despite these limitations, our analyses had several strengths. First, few studies have used MSM approaches in ecological settings with continuous exposures and extensive follow-up. We demonstrated the feasibility of using MSMs in such settings, as well as the potential pitfalls, like unstable weights. Second, our 30 years of follow-up was much longer than the few prior studies on union density and health.^35,37,38 Third, we collected comprehensive time-varying confounder data, which we drew from a variety of sources. Thus, we may have more thoroughly adjusted for time-varying confounding than prior studies on the topic, particularly because our MSM approach accommodated the non-recursive relationships between union-density and the time-varying confounders. Finally, to our knowledge, this is one of few empirical studies to examine the role of structural factors – rather than behavioral ones – in explaining recent increases in mortality inequities across socioeconomic groups.

5. Conclusion

In summary, we found that increases in state-level union density were associated with reductions in despair mortality. However, we found little consistent evidence that state-level union density affected state-level all-cause mortality rates overall or among subgroups.

Given the important roles of unions in wages, working conditions, and political-economic factors, our largely null findings raise questions that should be pursued in future research. First, researchers should examine these associations at the individual-level, including how individual-level union membership interacts with area- or industry-level union density to produce health outcomes. Individual-level data could also allow researchers to analyze interactions between union membership and relational social class measures based on property ownership and supervisory authority, which may more strongly interact with union membership than SES-based measures like education.⁶⁷ Second, researchers should test how long-term changes in union density affect health outcomes; states’ cumulative union density over several decades may have stronger mortality effects than the short-term changes we analyzed. Finally, researchers should examine how alternative measures of labor-movement and working-class power, like the strike rate, affect health and health inequities, both independently and through their interactions with union density.