Use of Normalized Prediction Distribution Errors for Assessing Population Physiologically-Based Pharmacokinetic Model Adequacy

Abstract

Currently employed methods for qualifying population physiologically-based pharmacokinetic (Pop-PBPK) model predictions of continuous outcomes (e.g., concentration-time data) fail to account for within-subject correlations and the presence of residual error. In this study, we propose a new method for evaluating Pop-PBPK model predictions that account for such features. The approach focuses on deriving Pop-PBPK-specific normalized prediction distribution errors (NPDE), a metric that is commonly used for population pharmacokinetic model validation. We describe specific methodological steps for computing NPDE for Pop-PBPK models and define three measures for evaluating model performance: mean of NPDE, goodness-of-fit plots, and the magnitude of residual error. Utility of the proposed evaluation approach was demonstrated using two simulation-based study designs (positive and negative control studies) as well as pharmacokinetic data from a real-world clinical trial. For the positive-control simulation study, where observations and model simulations were generated under the same Pop-PBPK model, the NPDE-based approach denoted a congruency between model predictions and observed data (mean of NPDE = −0.01). In contrast, for the negative-control simulation study, where model simulations and observed data were generated under different Pop-PBPK models, the NPDE-based method asserted that model simulations and observed data were incongruent (mean of NPDE = −0.29). When employed to evaluate a previously developed clindamycin PBPK model against prospectively collected plasma concentration data from 29 children, the NPDE-based method qualified the model predictions as successful (mean of NPDE = 0). However, when pediatric subpopulations (e.g., infants) were evaluated, the approach revealed potential biases that should be explored.

Introduction

In recent years, utilization of physiologically-based pharmacokinetic (PBPK) modeling analyses by pharmaceutical sponsors has dramatically increased, as evidenced by the number of regulatory submissions employing PBPK modeling techniques received by the United States (U.S.) Food and Drug Administration (FDA). Between 2004 and 2014, the U.S. FDA received 39 new drug application (NDA) submissions incorporating PBPK modeling techniques; whereas, in the following three-year period (2015 to 2017), 55 submissions were received [1]. Despite the increased use of PBPK modeling analyses in regulatory submissions, to date no clear standards for evaluating the adequacy of model predictions have been adopted by key regulatory agencies such as the U.S. FDA and the European Medicines Agency (EMA). In 2016, draft documents providing prospective guidance for reporting the results of PBPK model analyses were circulated by the U.S. FDA and EMA [2,3]. Though both documents highlighted the importance of establishing confidence in model predictions with respect to the study’s purpose/question, this notion was weakened by the lack of clear criteria for assessing the quality of model predictions. This omission likely is due to the limited amount of literature devoted to PBPK model evaluation methods. Considering the diverse utilization of PBPK models (e.g., prediction of drug-drug interactions, pediatric dose selection, assessing impact of hepatic disease), as well as the type and availability of clinical information on-hand to facilitate model evaluation, application of a single standardized metric and criteria for all cases is likely untenable. Nevertheless, assessments of a model’s capacity to recapitulate continuous (e.g., time-based) drug concentration data from specific biological matrices (e.g., plasma) is a common approach for evaluating PBPK model performance [4–6]. Pharmacokinetic (PK) datasets used to facilitate such evaluations can range in terms of size (e.g., number of subjects/samples) and sample collection intervals (e.g., sampling time). Larger PK datasets consisting of multiple, timed samples per patient are common among adult subjects [7]. In contrast, for specialized populations such as pediatrics, where sparse and opportunistic PK sampling designs are employed, disparately collected plasma-concentration-time datasets may represent the only measure available for PBPK model evaluation [8,9].

In addition to providing predictions towards a typical individual, PBPK models can be used to generate predictions for specific populations through the use of stochastic population algorithms. Such algorithms allow for the creation of virtual populations of subjects whose anatomy and physiology (e.g., system-specific parameters) differ based on inferences and knowledge of real-world biological variability [10]. By characterizing differences in simulated drug disposition among virtual population members, population-PBPK (Pop-PBPK) models can provide users with realistic estimates of the average tendency and range of inter-subject variability in compound PK. To assess Pop-PBPK model performance against observed concentration-time data, one commonly used approach is to compute the proportion of observed data that corresponds with model-derived prediction intervals (PI) [5,6,9,11]. Though convenient to compute, such numerical predictive checks (NPC) can provide erroneous conclusions regarding model performance as they fail to account for within-subject correlations (e.g., multiple samples per subject) and the presence of residual error [12]. Furthermore, most studies fail to define thresholds for the proportion of observed data falling outside model generated percentiles for model acceptance/rejection, making it difficult to assess if the modeling exercise was successful [9,13].

In this study, we propose a new paradigm for assessing the adequacy of Pop-PBPK model predictions for continuous PK data (e.g., plasma concentration-time values). The approach focuses on deriving Pop-PBPK-specific normalized prediction distribution errors (NPDE), a metric that is commonly used for population PK model validation [14]. NPDE are simulation-based metrics that are computed using a decorrelation step. Correspondingly, they are assumed to have improved properties for evaluating models against datasets containing correlated observations (i.e., multiple observations per subject) [15,16]. We first introduce the aforementioned model evaluation technique and then demonstrate its functionality using a simulation-based study design. We then provide a real-world example of the utility of the proposed technique for evaluating a previously published pediatric PBPK model for clindamycin [9].

Methods

Software

PK-Sim® (version 7.2, http://open-systems-pharmacology.org) was used for development of all Pop-PBPK models. Data management (e.g., formatting) and graphical plots were conducted/produced in R (version 3.4.3, R Foundation for Statistical Computing, Vienna, Austria) and RStudio (version 1.1.383, RStudio, Boston, MA, USA) with the ggplot2, cowplot, xlsx, and rlist packages. NPDE were computed in R using the npde package [15]. The piecewise cubic hermite interpolating polynomial (pchip) function from the pracma package in R was used for all data interpolations. Visual predictive checks were generated in R using the vpc package [17].

NPDE evaluation methodology

In their original conception, NPDE were formulated to evaluate the performance of mixed-effect models defined by the following general structure [14]:

$$y_{ij}=f\left(t_{ij},{\theta }_i\right)+{\epsilon }_{ij}$$ (Equation 1)

Where y_ij is the observed value for subject i at time t_ij, (t_ij, θ_i) is the model predicted value for subject i, which is a function of time (t_ij) and individual subject parameters (θ_i), and ε_ij is the stochastic residual error component. Monte-Carlo simulations based on the above statistical model that introduce variability towards inter-individual (e.g., θ_i) and error (e.g., ε_ij) components are used to generate a distribution of K-simulated values for each observation (i.e., individual predictive distributions). Following a decorrelation step, where both observed data and model simulations are decorrelated based on the empirical covariance matrix of model simulations, NPDE values can be obtained by Equations 2 and 3 [15]:

$$pd{e}_{ij}=\frac{1}{k}{{\sum }_{k=1}^{k}1}_{y_{ij}{}^{sim(k)*}<y_{ij}{}^{*}}$$ (Equation 2)

$$npd{e}_{ij}={\varphi }^{-1}\left(pd{e}_{ij}\right)$$ (Equation 3)

Where pde_ij is the prediction discrepancy error, y_ij* is decorrelated observed value, y_ij ^sim(k)* is the decorrelated simulated value, and ϕ⁻¹ is the inverse of the cumulative normal density function for N(0,1). pde defines the decorrelated quantile of an observation within an individual predictive distribution. For a formal description of relevant formula associated with the decorrelation process, the reader is referred to a previous publication by Comets et al. [15]. By forgoing the decorrelation step, indices such as prediction discrepancies (pd) and normalized prediction discrepancies (npd) can be computed using similar processes as described in Equations 2 and 3, respectively. For graphical depictions of trends over time or across predicted values, use of npd are sometimes preferred due to the tendency of the decorrelation process to introduce graphical artifacts within npde based plots [18].

In order to compute Pop-PBPK specific NPDE values, PBPK generated individual predictive distributions that incorporate inter-subject and residual variability are required. To generate such distributions, PBPK modeling software (e.g., PK-Sim®) is used to produce individualized-populations (number of individuals = K) for each observed subject based on their age, weight, height, race, and sex. Population algorithms incorporated into PBPK modeling platforms introduce stochastic variability toward system-specific model parameters (e.g., organ volumes, perfusion rates, plasma protein concentrations, enzyme abundance, etc.) based on knowledge or inferences of biological variability specific to the organism of interest [10,19]. In addition, during the model development process, users may choose to introduce or modify variability towards relevant system-specific parameters. Based on this approach, generated individualized-populations will consist of subjects who share the same demographic quantifiers (e.g., age, weight, height, race), but exhibit unique differences in terms of their underlying anatomic/physiologic parameter values (e.g., liver blood flow, liver weight, plasma protein abundance, hepatic enzyme abundance, etc).. Conceptually, PK variability associated system-specific parameters introduced by population algorithms or the user can be viewed as model-based approximations of inter-subject variability. Pop-PBPK models for each subject are parameterized with drug-specific properties (e.g., lipophilicity, LogP; molecular weight, MW; acid-base dissociation constant, pKa); absorption, distribution, metabolism, and excretion (ADME) data (e.g., fraction unbound in plasma, fu_p; intrinsic clearance towards specific enzymes; CL_int); and subject-specific dosing information to generate K sets of concentration-time estimates.

Concentration-time estimates produced by the PBPK modeling software are read into R where simulated concentrations from each individualized-population are interpolated at congruent time points to those depicted in the observed dataset (e.g., actual sampling times). Interpolated concentrations are formatted into a simulated dataset using a similar structure to that of the observed dataset. NPDE are computed using the npde package in R based on observed and interpolated (i.e., simulated) datasets [15]. The inverse method (eigenvalue decomposition) was used to decorrelate observed and simulated concentration values [20]. For models that appropriately describe observed data, NPDE should conform to a normal distribution with a mean of 0 and variance of 1 [14]. Unlike real-world (observed) datasets, where residual error is assumed to be present, Pop-PBPK model predictions do not include residual variability. To define the extent of residual variability associated with Pop-PBPK model predictions, we propose an iterative workflow (Fig. 1). During the initial NPDE assessment, the simulated dataset is created by directly interpolating Pop-PBPK model predictions (i.e., no residual variability added). Expectedly, the estimated variance of initially generated NPDE values will be considerably higher than the nominal value (i.e., 1), indicating that the degree of variability associated with Pop-PBPK model predictions is under-estimated. By defining an error sub-model, such as that depicted by Equation 4, residual error can be introduced into simulated datasets in R.

$$C_{sim,\mathit{\text{error}}}=C_{\mathit{\text{sim}}}*{\text{e}}^{\epsilon };\epsilon ~N(0,SD)$$ (Equation 4)

In the above equation, C_sim,error is the simulated concentration value with residual error added, C_sim is the simulated concentration value without error, and ε is a random error term, which follows a normal distribution with a mean of 0 and standard deviation of SD. Following a repetitive process of increasing the magnitude of residual variability associated with model simulations, re-computing NPDE values, and assessing their variance, the residual error component of the model can be approximated. Based on the proposed workflow, the magnitude of residual error is increased until the variance of NPDE approximates a value of 1 (i.e., standard deviation ~ 1). For information on appropriate data formatting and use of the npde R package, the reader is referred to the npde user guide [20].

Figure. 1.

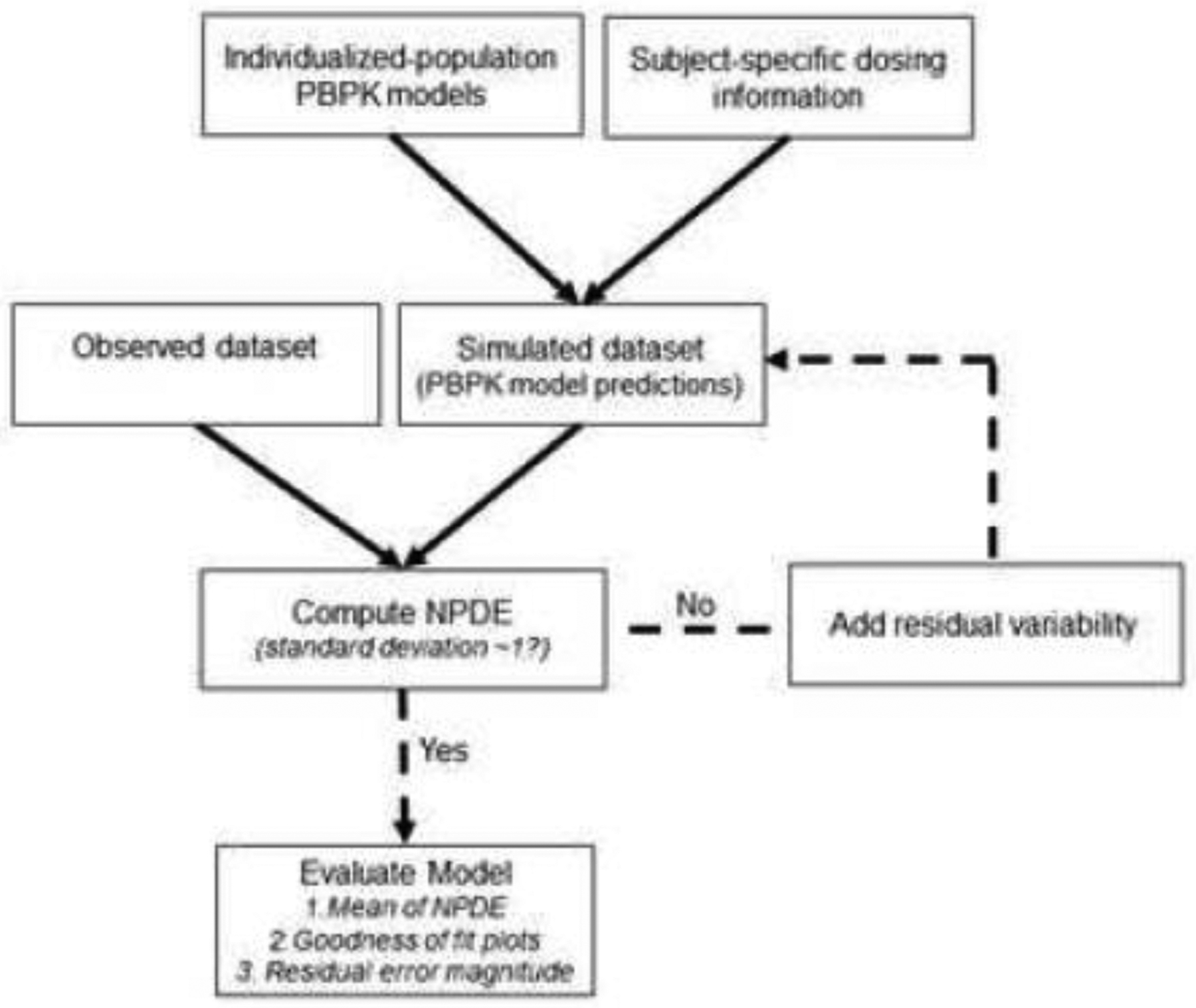
NPDE model evaluation workflow.

NPDE, normalized prediction distribution errors; PBPK, physiologically-based pharmacokinetic

Using the proposed NPDE-based approach, assessments of Pop-PBPK model quality can be facilitated using a variety of measures: 1) the mean of NPDE; 2) goodness-of-fit plots; and 3) the magnitude of residual error. A Student’s t-test (two-sided) can be used to evaluate if the mean of NPDE values statistically differ from the theoretical value of 0 (p-value <0.05). Goodness-of-fit plots can be constructed to assess for the presence of systematic trends associated with model predictions. Lastly, the magnitude of residual variability, as approximated by the proposed workflow (Fig. 1), provides a quantitative measure of the magnitude of unspecified variability required for model simulations to recapitulate the observed PK data.

Assessment of NPDE for qualifying PBPK model predictions using simulation-based study designs

The utility of the proposed NPDE-based approach for evaluating the quality Pop-PBPK model predictions was demonstrated using two simulation-based study designs. Both studies assessed model performance among neonates. The first was a positive-control study, whereby the ability of the NPDE-based workflow to identify a case where observed data and model simulations were derived from the same Pop-PBPK model was assessed. The second was a negative-control study that assessed the ability of the NPDE-based workflow to identify a case where observed data and model simulations were generated from different Pop-PBPK models. Specific details pertaining to the design and analysis of the positive and negative control studies are denoted below.

Positive-control study

Compound physico-chemistry and ADME

For the positive-control study, Pop-PBPK models were developed for a theoretical compound whose physico-chemical and ADME properties are denoted in Table 1 [12]. Tissue-to-plasma partition coefficients (Kp) were estimated in-silico according to the tissue-composition based approach presented by Rodgers and Rowland [21–23]. The compound, which exhibited affinity for albumin, displayed a high degree of plasma protein binding in adults (fraction unbound in plasma, fu_p = 0.1). Hepatic CYP3A4 was solely responsible for compound clearance. A preliminary simulation assessing administration of a 100 mg intravenous (IV) bolus dose of the theoretical compound to a 30 year-old White American male (80.4 kg, 178.5 cm) displayed a hepatic extraction ratio (ER) of 0.17 (i.e., low ER compound).

Table 1.

Theoretical compound physico-chemistry and ADME information [12]

Physico-chemistry	LogP	2.5
	pKa	NA (neutral)
	MW	350 g/mol (0 halogens)
ADME	Fup	0.1
	Binding protein	albumin
	CLint,3A4 (hepatic)	0.25 1/min/umol CYP3A4

CLint,3A4, intrinsic clearance intrinsic clearance of (hepatic) isozyme CYP3A4; fup, plasma fraction unbound; LogP, logarithm of the octanol-water partition coefficient (lipophilicity); MW, molecular weight; pKa, negative logarithm of the acid dissociation constant; NA, not applicable

Observed subjects

Using PK-Sim’s® population module, demographics information for 30 unique neonatal subjects (postnatal age < 30 days) were generated based on a White American population with a male:female ratio of 50:50. Generated subject demographics included postnatal age, weight, height, and sex. In addition, each subject was stochastically assigned 9 unique PK sampling times over a 24 hour period. Sample times were defined for different collection intervals as described in Supplementary Table S1, with each interval-specific sampling time being randomly selected. The ontogeny for hepatic CYP3A4 as defined by PK-Sim® is displayed in Supplementary Table S2. These proportional scalers define the effect of maturation on isozyme function with a value of 1 signifying complete maturation (i.e., adult values).

Individual predictive distributions (individualized-population PBPK simulations)

Individual predictive distributions of plasma concentrations for each observed subjects were generated using PK-Sim’s® population module. For each observed subject, a virtual population consisting of 500 individuals was created with the same postnatal age, weight, height, sex, and race. The population algorithm introduced stochastic variability towards organ weights, blood flows, plasma albumin concentrations, and hepatic CYP3A4 abundances between members of the same individualized-population [10, 19]. Resulting individualized-populations consisted of subjects with the same gross demographic measures but with underlying inter-subject anatomical and physiological differences capable of perpetuating PK alterations. Pop-PBPK model simulations were generated in PK-Sim® for each of the 30 individualized-populations following administration of a 1.5 mg/kg IV bolus dose of the above defined theoretical compound (Table 1). For each individualized-population, model simulated peripheral venous plasma concentrations were interpolated at the 9 sampling times points defined for each observed subject. This process created individual predictive distributions for each subject-specific sampling time consisting of 500 simulated concentration values, one for each individualized-population member.

NPDE-based model evaluation

Assessment of Type-I-error.

To explore the influence of different numbers of subjects and samples per subject on performance of the proposed NPDE-based model evaluation approach, assessments were performed over 12 separate study designs with over 500 iterations for each design (Table 2). The frequency of type-I-errors (i.e., incorrectly asserting observations and models simulations are divergent) associated with use of the proposed NPDE-based model evaluation approach was assessed for the positive-control study (observations and model simulations were derived from the same Pop-PBPK model). For each iteration, observed datasets were created based on the following process. First, single individuals from each individualized-population were selected and their interpolated concentration-time values were combined to form an observed dataset. Next, to provide a resemblance to a real-world PK data, which implicitly contains residual variability, an exponential residual error with a standard deviation (SD) of 0.20 was stochastically added onto interpolated concentration values using Equation 4.

Table 2.

Evaluated study designs for positive and negative-control studies

Number of Subjectsa	Samples per Subjectb
5	3	6	9
10	3	6	9
20	3	6	9
30	3	6	9

^aSuccessive (subject) groups contain observed subjects from previous groupings in addition new subjects

^bCollection intervals for the 3 sample time points were 10–15 minutes, 60–70 minutes, and 8–8.5 hours. For 6 sample time points, collection intervals were 10–15 minutes, 25–30 minutes, 60–70 minutes, 120–140 minutes, 8–8.5 hours, and 12–13 hours. For 9 sample time points, collection intervals were 1–3 minutes, 10–15 minutes, 25–30 minutes, 60–70 minutes, 120–140 minutes, 4–4.5 hours, 8–8.5 hours, 12–13 hours, and 22–24 hours (post-dose administration).

Simulated datasets were created by combining interpolated concentrations over all individualized-populations. The resulting dataset contained individual predictive distributions for each subject-specific sampling time point (500 concentrations per sampling time), albeit without residual error. The magnitude of residual error associated with model simulations was algorithmically estimated using the optimize function in R (one dimensional optimization). Example code for this optimization process has been provided in the supplementary materials. Using the estimated residual variability, PBPK model specific NPDE values were computed. The proportion of iterations where the mean of NPDE was asserted to be statistically different than 0 (p-value <0.05; two-sided Student’s t test) provided an estimate of the type-I-error for the proposed model evaluation approach.

To evaluate the influence of misspecification of the magnitude of residual error on the frequency of type-I-errors, NPDE values were computed for different scenarios where the magnitude of residual error added onto model simulations varied. For each iteration, the mean NPDE value was statistically evaluated under a scenario where no residual error was added onto model simulations. Two additional scenarios where excess residual error was added onto model simulations to provide NPDE distributions with SD of less than the ideal value (i.e., 1) were evaluated. Under these scenarios, the magnitude of residual error was optimized to provide NPDE with SD of 0.75 and 0.5. Statistical evaluations for the mean of NPDE values under these scenerios were conducted in a similar manner as described above.

Additionally, for each iteration, a conventional NPC was performed to assess Pop-PBPK model performance [12]. Under this approach, the proportion of observed concentrations falling outside a Pop-PBPK model defined 90% PI generated for 100 virtual neonates whose distribution of postnatal age, sex (i.e., 50:50), and race mirrored that of observed subjects was calculated. The PI was generated for simulated plasma concentrations following administration of a 1.5 mg/kg IV bolus dose of the theoretical compound described in Table 1. In a manner congruent to current PBPK modeling practices, no residual error was added to model simulations for construction of the 90% PI. The exact binomial test was used to evaluate if the proportion of observations falling outside the model’s 90% PI was statistically greater than the expected proportion (0.10). Statistical significance was asserted using a p value<0.05.

Descriptive Example.

Following the workflow depicted in Figure 1, NPDE-based model evaluation measures (i.e., mean of NPDE, goodness-of-fit plots, and magnitude of residual variability) were computed for a single iteration of the positive-control study consisting of 10 subjects with 6 samples per subjects. Generated goodness-fit-plots consisted of npd vs time, npd vs predicted concentrations, normal quantile-quantile (Q-Q), and prediction-corrected visual predictive check (pc-vpc) plots [24]. pc-vpc represent a modification of traditional visual predictive checks whereby observed and simulated concentrations are normalized by their expected model simulated value (i.e., typical value). This modification reduces the magnitude variability that occurs when data from subjects receiving dissimilar dosages or who differ in terms influential covariates are binned together, enhancing the ability of these plots to detect model misspecifications. Goodness-of-fit plots were developed based on simulated datasets with added residual error, as defined by the evaluation workflow (Fig. 1).

For comparison, conventional metrics employed for PBPK model evaluation including residual plots, bias and precision indices, and NPC of the proportion of data falling outside the model’s 90% PI were computed/generated. Conventionally computed residuals (RES) were calculated according to Equation 5.

$$RES=OB{S}_{i,t}-PRE{D}_{ME{D}_{i,t}}$$ (Equation 5)

Where OBS_i,t is the observed concentration-time value for subject, i, at time, t, and $PRE{D}_{ME{D}_{i,t}}$ represents the median simulated concentration (without added residual error) corresponding to the individual predictive distribution for subject, i, at time, t. In this context, $PRE{D}_{ME{D}_{i,t}}$ provides an approximation of the expected concentration from model simulations (i.e., the typical value). Conventional measures of bias included mean error (ME; Equation 6) and average-fold error (AFE; Equation 7); whereas, conventional measures of precision included root mean squared error (RMSE; Equation 8) and absolute average-fold error (AAFE; Equation 9).

$$ME=\frac{1}{n}\sum \left(OB{S}_{i,t}-PRE{D}_{ME{D}_{i,t}}\right)$$ (Equation 6)

$$AFE={10}^{\frac{1}{n}\sum \text{log}\left(\frac{PRE{D}_{ME{D}_{i,t}}}{OB{S}_{i,t}}\right)}$$ (Equation 7)

$$\mathit{\text{RMSE}}=\sqrt{\frac{1}{n}\sum {\left(OB{S}_{i,t}-PRE{D}_{ME{D}_{i,t}}\right)}^2}$$ (Equation 8)

$$\mathit{\text{AAFE}}={10}^{\frac{1}{n}\Sigma \left|\text{log}\left(\frac{PRE{D}_{ME{D}_{i,t}}}{OB{S}_{i,t}}\right)\right|}$$ (Equation 9)

Lastly, we performed a NPC to evaluate if the proportion of observations falling outside the Pop-PBPK model’s 90% PI was statistically greater than the expected proportion (0.10). As described above, the 90% PI was generated based on a 100 virtual neonates whose demographics distribution (i.e., age, race, and sex) mirrored that of observed subjects.

Negative-control study

Compound physico-chemistry and ADME

For the negative-control study, observed and simulated datasets were generated using Pop-PBPK models for two different, albeit similar, theoretical compounds. To generate the observed dataset, a modified compound was created whose physico-chemical and ADME properties were similar to that displayed in Table 1 with one alteration; the reference (adult) fu_p was increased to 0.13. In contrast, the simulated dataset was derived based on Pop-PBPK model simulations for the unaltered theoretical compound with a reference fu_p of 0.10 (Table 1).

Observed subjects

Observed subject demographics and PK sampling times were the identical to those defined for the positive-control study. Thus, analysis of the negative-control study was based on 30 neonatal subjects, each assigned a unique PK sampling scheme comprised of 9 sample times over 24 hours.

Individual predictive distributions (individualized-population PBPK simulations)

Using a similar methodology as described for the positive-control study, two sets of individual predictive distributions were generated for each of the 30 observed subject. The first set was comprised of Pop-PBPK simulations for the theoretical compound described in Table 1 (i.e., fu_p = 0.10) and was identical to the distributions generated for the positive-control study. The second set was comprised of Pop-PBPK simulations for the above-defined modified theoretical compound (fu_p = 0.13). Accordingly, two competing individual predictive distributions, one for the unaltered theoretical compound (fu_p = 0.10; Table 1) and one for modified theoretical compound (fu_p = 0.13), were generated for each subject-specific sampling time.

NPDE-based model evaluation

Power.

Model-based statistical evaluations for power were performed over 12 separate study designs (Table 2) using 500 iterations per design. Power (i.e., correctly asserting observations and models simulations are divergent) associated with use of the proposed NPDE-based model evaluation approach was assessed for a case where observations and model simulations were derived from different Pop-PBPK model simulations.

For each iteration, observed datasets were created from individual predictive distributions for the modified theoretical compound (fu_p = 0.13) using a similar approach as described for the positive control study. Exponential residual error with a SD of 0.20 was stochastically added onto concentrations from the observed dataset using Equation 4. Simulated datasets were based on the unmodified theoretical compound (fu_p = 0.10; Table 1) and were identical those created for the positive control study.

At each iteration, PBPK model derived NPDE values were computed using the proposed model evaluation workflow (Fig. 1). Power was computed as the proportion of iterations where the mean of NPDE values was asserted to be statistically different than 0 (p-value <0.05). The influence of misspecification of the magnitude of residual error on the power the proposed model evaluation approach was assessed in a similar manner as described for the positive-control study. A conventional NPC evaluating the proportion of observed data that coincides with a Pop-PBPK model defined 90% PI generated for 100 virtual neonates receiving a 1.5 mg/kg IV bolus dose of the unmodified theoretical compound (fu_p = 0.10; Table 1) was computed.

Descriptive Example.

The model evaluation workflow was conducted for a single representative iteration of the negative-control study consisting for 10 subject with 6 samples per subject.

Evaluation of a previously developed pediatric PBPK model for clindamycin using the proposed NPDE-based approach

Pediatric PBPK model description

The proposed NPDE-based model evaluation approach was used to qualify predictions from a published pediatric PBPK model for IV clindamycin [9]. The model was originally developed using 68 opportunistically collected clindamycin plasma concentration samples from 48 subjects, who ranged in postnatal age from 1 month to 19 years. As IV preparations of clindamycin are formulated using its prodrug, clindamycin-phosphate, the model was developed to simulate exposures of both compounds. Elimination pathways for clindamycin-phosphate include conversion to clindamycin by plasma alkaline phosphatase and renal filtration. For clindamycin, elimination is modulated by both hepatic (CYP3A4 and CYP3A5) and renal processes (filtration and tubular secretion). Specific details pertaining to drug-physico-chemistry and PBPK model parametrization (e.g., ontogeny functions, partition coefficients) are denoted in the published manuscript [9].

Observed subjects

Clindamycin plasma-concentration samples were collected from children enrolled in a prospective phase-I clinical trial (NCT02475876). Study inclusion was confined to children with postnatal ages between 1 month to 17 years receiving IV clindamycin for prophylaxis or treatment of a confirmed or suspected infection. Patients concomitantly receiving medications known to inhibit or induce hepatic CYP3A4 were excluded from the analysis. Up to 7 PK samples were collected per patient over one or two occasions (i.e., doses). Samples were collected pre-dose, 0–10 minutes after the end of the infusion, 2–4 hours after start of the dose infusion, and 30 minutes prior to the next dose. Records pertaining to the complete dosing history for the current course of clindamycin were available for each patient. Of note, the abovementioned represents the ideal PK sampling scheme; however, as sampling was conducted during the course of clinical care, deviations with respect to the timing and number of samples collected per patient were observed.

Individual predictive distributions (individualized-population PBPK simulations)

Simulated clindamycin peripheral venous plasma concentrations were computed using the previously developed clindamycin pediatric PBPK model [9]. For each subject, individualized-populations consisting of 500 virtual individuals with the same demographic quantifiers (e.g., age, sex, weight, height, and race) were created using PK-Sim’s® population module. Pop-PBPK model simulations were generated for each individualized-population using each subject’s recorded dosing scheme. Model simulated peripheral venous concentrations were interpolated at identical time points that PK samples were collected for each respective subject. This process created individual predictive distributions for each subject-specific sampling time that consisted of 500 simulated concentrations.

Model evaluation

The NPDE-based model evaluation workflow (Fig. 1) was employed to qualify Pop-PBPK model predictions. Evaluations were conducted based on two approaches. The first approach was a full analysis where the entire study cohort (i.e., PK data from all subjects) was evaluated together. The second was a segmented analysis that grouped subjects using the following age classifications: infant (>1 month–2 years), young children (2–6 years), and children/adolescent (6–18 years) [25]. Children and adolescent were evaluated as single group as physiological processes modulating PK (e.g., clearance) were inferred to be fully mature beyond 6 years of age [26, 27]. Observed datasets were created by combining observed clindamycin plasma concentrations from subject belonging to each age-group of interest into a single dataset. Simulated datasets were created by combining model generated individual predictive distributions of plasma concentrations over each age-group of interest. Dissimilar to our developed simulation-based studies, clindamycin PK samples were permitted to be collected over two occasions (e.g. samples collected over intervals that spanned >1 dose). Owing to temporal changes in PK parameters (e.g., clearance or volume of distribution), plasma concentrations within the same individual may exhibit interoccasion differences [28]. In general practice, PBPK model simulations do not account for interoccasion variability. However, calculated NPDE values based on simulations that lack interoccasion variability and observed datasets where interoccasion variability is prevalent will typically exhibit inflated variances. Consequently, the defined evaluation workflow (Fig. 1) will necessitate that larger (i.e., inflated) residual errors be apportioned toward model simulations. To circumvent this issue, NPDE were computed separately for each occasion among subjects where PK samples were collected over multiple occasions. This was achieved by assigning unique identification numbers for PK samples collected around different doses (e.g., after the first dose [occasion 1]; and around the sixth dose [occasion 2]). This modification was instituted in both observed and simulated datasets.

Conventional metrics for qualifying PBPK models, as described previously for simulation-based studies, were also examined. 90% PI(s) for clindamycin plasma concentrations were computed using Pop-PBPK simulations pertaining to three separate virtual populations (i.e., infants, young children, and children/adolescents). Populations, consisting of 100 virtual subjects each, were generated based on the demographic distributions (i.e., age, race, and sex) of observed subjects falling into each of the abovementioned age classifications. Separate simulations were conducted using each individual’s specific dosing regimen in conjunction with the applicably aged virtual population. NPC were computed using the same methodology as described for simulation-based studies.

Results

Evaluation of simulation-based study designs using an NPDE-based approach

Simulated neonatal plasma concentration-time profiles for the two theoretical compounds used to facilitate model evaluations for the positive and negative-control simulation studies are depicted in Figure 2. Median plasma concentrations corresponding to the unmodified theoretical compound (fu_p = 0.10; Table 1) were greater than concentrations for the modified compound (fu_p=0.13). This finding was unsurprising considering anticipated increases in systemic clearance and volume of distribution associated with increases in fu_p for a low extraction ratio compound.

Figure. 2.

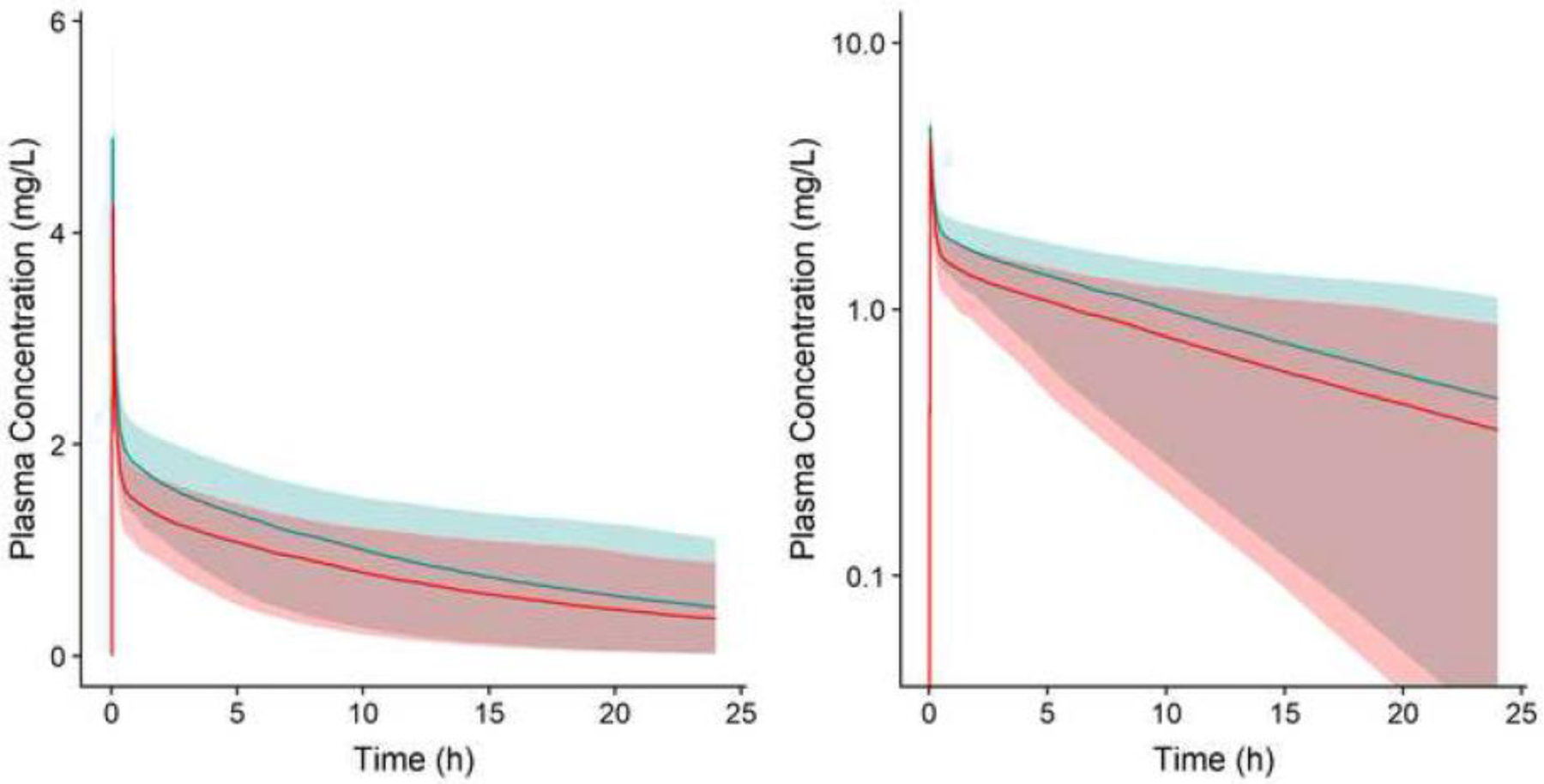
Simulated plasma concentration-time profiles (linear, A; semi-logarithmic, B) for two theoretical hepatic isozyme CYP3A4 substrates with different fractions unbound in plasma [0.10 (blue) and 0.13 (red)]. Shaded regions depict 90% PI for Pop-PBPK model simulations following administration of 1.5 mg/kg IV doses of each theoretical compound to a population of 100 virtual neonates. Solid lines depict median concentration-time values.

IV, intravenous; PI, prediction interval; Pop-PBPK, population physiologically-based pharmacokinetic

For the positive-control study, where both observed and simulated datasets were based on the theoretical compound described in Table 1 (fu_p = 0.10), assessments of the mean of NPDE values were associated with type-I-error rates ranging from 0.026 to 0.06 among the examined study designs (Table 3). These values approximate the expected type-I-error rate of 0.05. In contrast, use of a NPC based on the proportion of data exceeding the model’s 90% PI was associated with higher type-I-error rates, ranging between 0.61 to 1 (Table 3). Under this approach, type-I-error rates increased with increasing subject numbers and samples per subject. The influence of misspecification of the magnitude of residual error is depicted in Supplementary Table S3. For workflows where no residual error was added onto model simulations, evaluations of the mean of NPDE values were associated with suppressed type-I-error rates (~ 0). Conversely, for workflows where excessive residual error was added onto model simulations to provide NPDE distributions with SD of 0.75 and 0.5, inflated type-I-error rates ranging between 0.056 to 0.222 and 0.1 to 0.678, respectively, were observed.

Table 3.

Type-I-error for the NPDE-based model evaluation approach (positive-control simulation study)

Number of Subjects	Samples per Subject	Total Samples	Iterationsa	P-value (μNPDE)b	P-value (NPC)c
5	3	15	467	0.028	0.61
10	3	30	491	0.047	0.894
20	3	60	498	0.042	1
30	3	90	500	0.06	1
5	6	30	493	0.053	0.85
10	6	60	496	0.026	0.974
20	6	120	498	0.038	0.998
30	6	180	497	0.038	1
5	9	45	492	0.03	0.868
10	9	90	497	0.054	0.988
20	9	180	499	0.036	1
30	9	270	499	0.056	1

μ_NPDE mean of normalized prediction distribution errors; NPC, numerical predictive check

^aIterations (out of 500) where the standard deviation of NPDE were not optimized to within ±0.01 of the target value (i.e., 1) by the developed fitting algorithm were excluded from the analysis.

^bType-I-error for the NPDE-based model evaluation approach. Computed as the proportion of iterations where the μ_NPDE was statistically different than 0 (p-value<0.05; two-sided Student’s t-test).

^cType-I-error for the conventional evaluation approach. Computed as the proportion of iterations where the proportion of observed data exceeding the model’s 90% prediction interval was statistically > 0.10 (p-value < 0.05; exact binomial test)

NPDE-based model evaluation measures computed for a single iteration of the positive-control study (10 subjects; 6 samples per subject) depicted a similarity between model simulations and observed data. The mean of NPDE values was −0.01, a value that was not statistically different than 0 (p-value = 0.952). Goodness-of-fit plots generated for the proposed model evaluation approach were devoid of systematic trends (Fig. 3). An exponential residual error of 0.181 was estimated using the NPDE-based methodology, a value that is in close agreement to the theoretical value of 0.20. The visual impact of adding varying magnitudes of residual error onto model simulations for the positive-control study is depicted in Supplementary Figure S1. Normal quantile-quantile plots demonstrate that increasing the magnitude of residual error redistributes the NPDE density away from the tails. When the magnitude of residual error is approximately estimated (e.g., 0.15 to 0.25; Supplementary Fig. S1D–F), visual agreement between distributions for NPDE values and a standard normal random variable were observed.

Figure. 3.

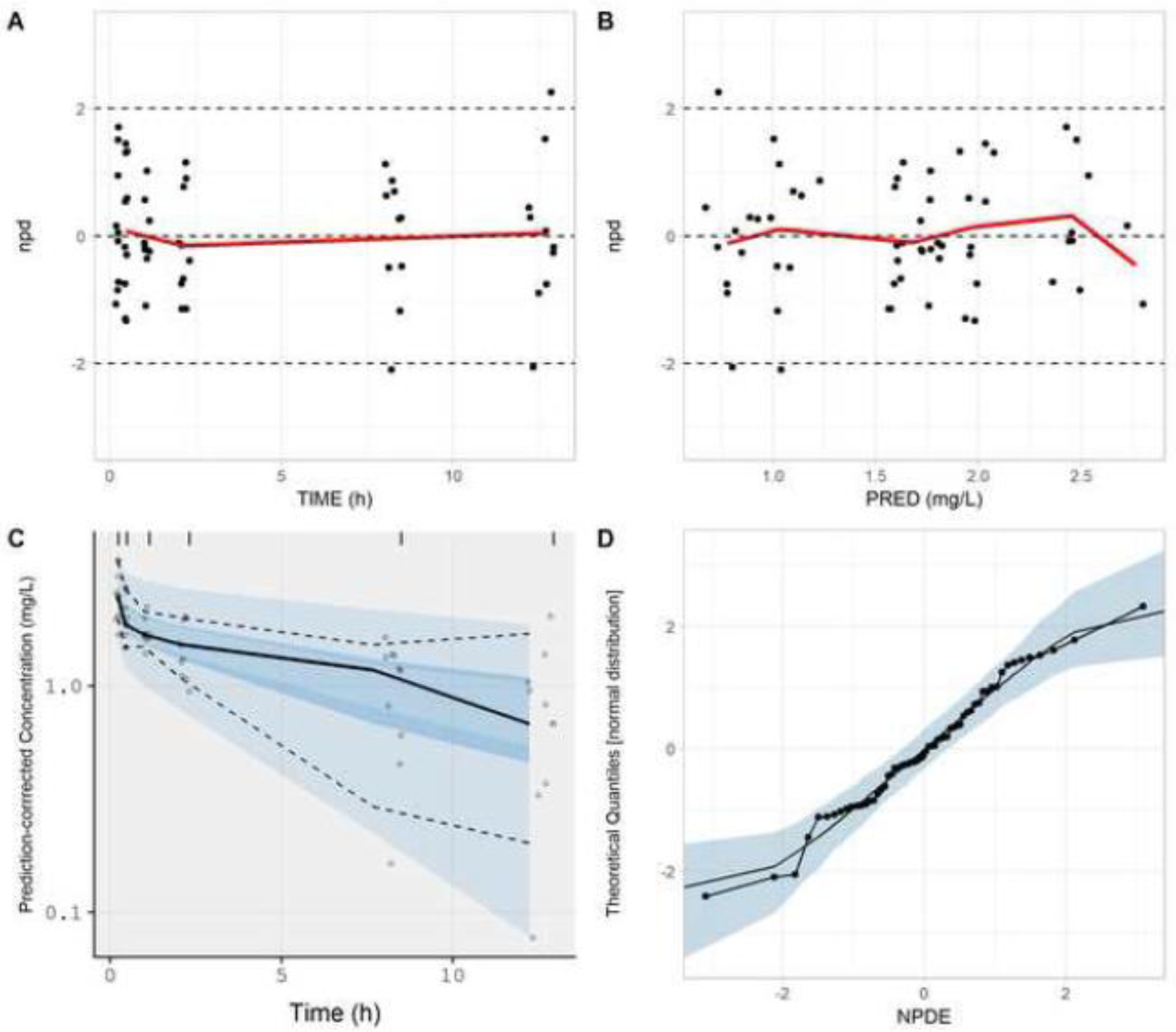
Goodness-of-fit plots generated from the NPDE-based model evaluation workflow corresponding to the positive-control study. Model simulations incorporated a residual error (exponential) of 0.181. Plots include npd vs. time (A); npd vs. PRED (B); a prediction-corrected visual predictive check (C); and a normal quantile-quantile plot of NPDE values (D). In A and B, red lines represent moving (local) averages. In C, the light blue shaded regions represent 90% prediction bands associated with the 5^th and 95^th percentiles of PBPK model simulations. The dark blue region represents the 90% prediction band associated with the 50^th percentile of PBPK model simulations. Dashed lines represent the 5^th and 95^th percentiles of observed data; whereas, the solid line represents the 50^th percentile of observed data. In D, the light blue shaded region represents the 95% prediction interval for a standard normal random variable (based on 1000 iterations). The solid line represents the 50^th percentile of the standard normal random variable.

npd, normalized prediction distribution errors; NPDE, normalized prediction distribution errors; PRED, median simulated concentration

Conventional model evaluation metrics provided contrasting depictions of model performance for the positive-control study. AFE (bias) was 1.08, indicating agreement between observations and model simulations, albeit with a minute positive bias (over-prediction). AAFE (precision) was 1.34 (Table 4). Conventional residual plots were free of systematic trends (Supplementary Fig. S2). However, a NPC based on the model’s 90 % PI indicated a discrepancy between observed and simulated datasets. The proportion of observed data exceeding the model’s 90% PI was 0.27 - a value that was statistically greater than the nominal rate of 0.10 (Table 4).

Table 4.

Conventional model evaluation metrics for the positive and negative-control simulation studies

Variable	Positive-control study	Negative-control study
Number of subjects	10	10
Samples per Subject	6	6
Total Samples	60	60
ME (mg/L)	0.025	−0.207
RMSE (mg/L)	0.445	0.472
AFE	1.08	1.26
AAFE	1.34	1.39
Number of samples outside the model’s 90 PI (N [%])	16 (26.67%)*	19 (31.67%)*

ME, mean error; RMSE, root mean squared error; AFE, average fold-error ; AAFE, absolute average fold-error ; PI, prediction interval; PK, pharmacokinetic

^*Proportion of observed data exceeding model’s 90% PI is statistically greater than 0.10 (p-value<0.05, exact binomial test)

For the negative-control study, observed datasets were generated using a Pop-PBPK model for the modified theoretical compound (fu_p = 0.13); whereas, simulated datasets were generated using a Pop-PBPK model for the unmodified theoretical compound (fu_p = 0.10; Table 1). The power of statistical tests for the mean of NPDE increased with increasing subject numbers. For 5, 10, 20, and 30 subjects, power ranged between 0.43 to 0.511, 0.79 to 0.869, 0.98 to 0.996, and 1, respectively (Table 5). Power estimates for study designs with the same amount of subjects but varying number of samples per subject were relatively similar. For a NPC based on the Pop-PBPK model’s 90% PI, power ranged between 0.735 to 1 (Table 5). NPC-based power estimates increased with increasing subject numbers and samples per subject. Supplementary Table S4 depicts the influence of misspecification of the magnitude of residual error on the power of the proposed NPDE-based model evaluation approach. Low power estimates (0–0.07) were associated with workflows where no residual error was added onto model simulations. In general, the addition of excessive residual error onto model simulations had a minimal impact on the power of the proposed model evaluation approach.

Table 5.

Power of the NPDE-based model evaluation approach (negative-control simulation study)

Number of Subjects	Samples per Subject	Total Samples	Iterationsa	P-value (μNPDE)b	P-value (NPC)c
5	3	15	446	0.43	0.735
10	3	30	485	0.79	0.973
20	3	60	492	0.98	1
30	3	90	495	1	1
5	6	30	487	0.511	0.891
10	6	60	498	0.869	0.998
20	6	120	500	0.996	1
30	6	180	499	1	1
5	9	45	497	0.503	0.942
10	9	90	499	0.866	0.998
20	9	180	499	0.984	1
30	9	270	499	1	1

μ_NPDE, mean of normalized prediction distribution errors; NPC, numerical predictive check

^aIterations (out of 500) where the standard deviation of NPDE were not optimized to within ±0.01 of the target value (i.e., 1) by the developed fitting algorithm were excluded from the analysis.

^bPower of the NPDE-based model evaluation approach. Computed as the proportion of iterations where the μ_NPDE was statistically different than 0 (p-value<0.05; two-sided Student’s t-test).

^cPower of the conventional evaluation approach. Computed as the proportion of iterations where the proportion of observed data exceeding the model’s 90% prediction interval was statistically > 0.10 (p-value < 0.05; exact binomial test)

For single representative iteration of the negative-control study (10 subjects; 6 samples per subject), the NPDE-based model evaluation approach depicted a divergence between model simulations and observed data. The mean of NPDE was −0.29, a value that was statistically different than 0 (p-value = 0.0308). Goodness-of-fit plots generated for the proposed model evaluation approach were indicative of a discrepancy between observed and simulated datasets (Fig. 4). npd based plots (versus time and predicted concentrations) indicated a tendency of model simulations to over-predict observed values (Fig. 4A, B). pc-vpc and normal quantile-quantile plots also depicted a tendency towards model over-prediction (Fig. 4C,D). Using the NPDE-based methodology, an exponential residual error of 0.184 was estimated. Supplementary Fig. S3 depicts the impact of adding varying magnitudes of residual error onto model simulations for the negative-control study. For all magnitudes of residual error depicted (0 to 0.30; Supplementary Fig. S3A–G), distributional differences between NPDE values and a standard normal random variable were observed.

Figure. 4.

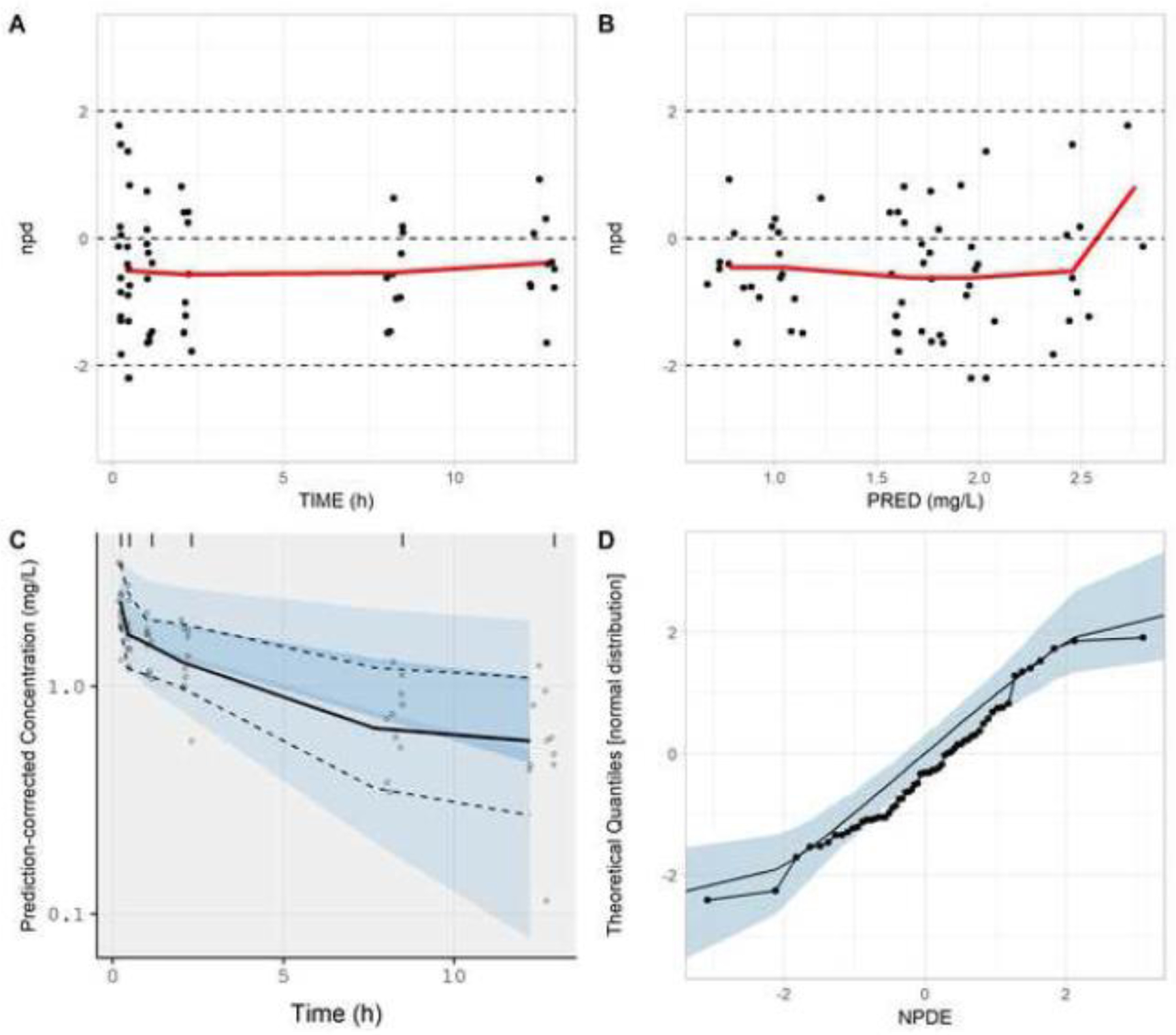
Goodness-of-fit plots generated from the NPDE-based model evaluation workflow corresponding to the negative-control study. Model simulations incorporated a residual error (exponential) of 0.184. Plots include npd vs. time (A); npd vs. PRED (B); a prediction-corrected visual predictive check (C); and a normal quantile-quantile plot of NPDE values (D). In A and B, red lines represent moving (local) averages. In C, the light blue shaded regions represent 90% prediction bands associated with the 5^th and 95^th percentiles of PBPK model simulations. The dark blue region represents the 90% prediction band associated with the 50^th percentile of PBPK model simulations. Dashed lines represent the 5^th and 95^th percentiles of observed data; whereas, the solid line represents the 50^th percentile of observed data. In D, the light blue shaded region represents the 95% prediction interval for a standard normal random variable (based on 1000 iterations). The solid line represents the 50^th percentile of the standard normal random variable.

npd, normalized prediction distribution errors; NPDE, normalized prediction distribution errors; PRED, median simulated concentration

The majority of conventional PBPK model evaluation metrics for the negative-control study depicted the presence of a mismatch between observed data and model simulations. The AFE (bias) was 1.26, indicating the presence of an over-prediction bias associated with model simulations. However, AAFE (precision) was only 1.39 - a value that was similar to that computed for the positive-control study (Table 4). Conventional residual-based goodness-of-fit plots exhibited trends indicative of model over-prediction (Supplementary Fig. S4). Application of a NPC to the negative control study indicated that the proportion of observed data exceeding the model’s 90% PI was 0.32 - a value that was statistically greater than the nominal value of 0.10 (Table 4)

Evaluation of a previously developed pediatric PBPK model for clindamycin using the proposed NPDE-based approach

Demographics of the 29 children who participated in the prospective clindamycin PK study are displayed in Table 6. Subjects ranged in postnatal age from 3 months to 16 years. Gestational age (GA) was reported for 7 infants less than 1 year postnatal age, four of whom were premature at birth (GA <37 weeks). However, specific modeling considerations for prematurity were not considered since the postnatal age of all premature subjects was greater than 7 months. A total of 157 samples were available for clindamycin PK analysis; the median (range) number of samples per subject was 6 (2–7). Samples were collected on one occasion (i.e., dose) in 8 subjects. The remaining 21 subjects provided samples over two occasions. PK samples corresponding to the first occasion were collected after a median (range) of 5 (1–7) doses. For the cohort of subjects who contributed samples over two occasions, samples corresponding to the second occasion were collected after a median (range) of 8 (4–13) doses. The median (range) administered clindamycin dosage was 12.6 mg/kg (9.1–16.4). Notably, two subjects received single oral doses of clindamycin over the course of their sampling interval. However, PK samples were not collected over the interval immediately following oral dose administration. Considering the high oral bioavailability of clindamycin (~90%) [29], these doses were modeled by administration of the complete dose via an IV intermittent infusion over 30 minutes.

Table 6.

Demographic characteristics of children who contributed clindamycin PK data for the analysis

Variable	Median (Range) or N (%)
	1 month-2 years	2–6 years	6–18 years
Number of subjects	10	6	13
Gestational age (weeks)	37 (33–40)a	-	-
Postmenstrual age (weeks)	67 (51–78)b	-	-
Postnatal age (years)	0.64 (0.27–1.45)	4 (3.56–5.93)	9.18 (6.06–15.98)
Body weight (kg)	8.45 (5.5–11.7)	16.3 (14.7–21.1)	41.2 (16.9–72.7)
Female	4 (40)	2 (33)	7 (54)
Race
White	5 (50)	5 (83)	11 (84)
Black or African American	2 (20)	1 (17)	1 (8)
Asian	2 (20)	0	0
More than one race	1 (10)	0	0
Other or not reported	0	0	1 (8)

PK, pharmacokinetic

^aGestational age reported for subjects with postnatal age <1 year (N=7 subjects).

^bPostmenstrual age computed for subjects with postnatal age <1 year as the sum of gestational and postnatal age (N=7 subjects).

Application of the presented NPDE-based model evaluation approach (Fig. 1) towards the entire clindamycin PK dataset (i.e., 29 children; 157 samples) indicated that model simulations adequately reproduced observed data. A mean NPDE value of 0 (p-value = 0.99) was computed. The estimated magnitude of residual error (exponential) to provide NPDE values with a SD of 1 was 0.42 (Table 7). Figure 5 displays goodness-of-fit plots generated for the proposed model evaluation approach. npd and pc-vpc plots displayed a adequate fit between model simulations and observed data, though minor trends towards model over-prediction at higher concentrations (collected post-drug infusion) and under-prediction at sampling times 2–4 hours post-drug infusion were observed. Trough concentrations were well predicted (Fig. 5A, B, C). In addition, the distribution of NPDE values were similar to that of a standard normal random variable (Fig. 5D). The AFE was computed to be 1, indicating a lack of bias associated with model predictions. Precision (AAFE) was computed to be 1.95, indicating that on-average observed data fell within 1.95-fold of simulated values (Table 8).

Table 7.

NPDE-based model evaluation metrics for the previously developed pediatric clindamycin PBPK model [9]

Variable	1 month–2 years	2–6 years	6–18 years	All
Number of subjects	10	6	13	29
Number of PK samples	48	37	72	157
Residual (exponential) variability	0.26	0.43	0.5	0.42
Mean of NPDE	−0.36*	0.21	0.08	0

NPDE, normalized prediction distribution errors; PBPK, physiologically-based pharmacokinetic; PK, pharmacokinetic

^*mean of NPDE is statistically different than 0 (p-value < 0.05, two-sided Student’s t-test)

Figure. 5.

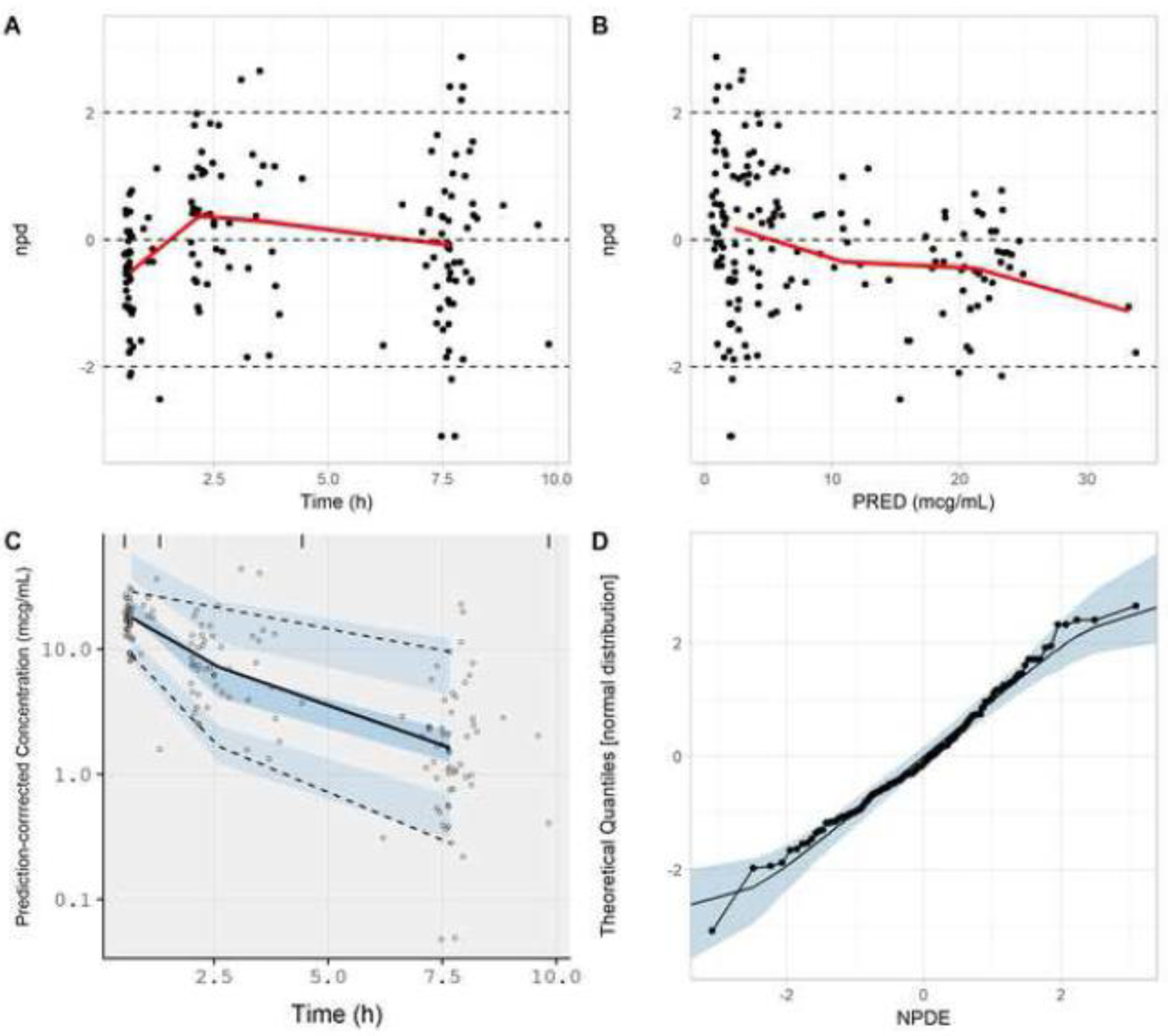
Goodness-of-fit plots generated from the NPDE-based model evaluation workflow corresponding to all subjects (N=29) from whom clindamycin concentrations were collected. Model simulations incorporated a residual error (exponential) of 0.422. Plots include npd vs. time (A); npd vs. PRED (B); a prediction-corrected visual predictive check (C); and a normal quantile-quantile plot of NPDE values (D). In A and B, red lines represent moving (local) averages. In C, the light blue shaded regions represent 90% prediction bands associated with the 5^th and 95^th percentiles of PBPK model simulations. The dark blue region represents the 90% prediction band associated with the 50^th percentile of PBPK model simulations. Dashed lines represent the 5^th and 95^th percentiles of observed data; whereas, the solid line represents the 50^th percentile of observed data. In D, the light blue shaded region represents the 95% prediction interval for a standard normal random variable (based on 1000 iterations). The solid line represents the 50^th percentile of the standard normal random variable.

npd, normalized prediction distribution errors; NPDE, normalized prediction distribution errors; PRED, median simulated concentration

Table 8.

Conventional model evaluation metrics for the previously developed pediatric clindamycin PBPK model [9]

Variable	1 month–2 years	2–6 years	6–18 years	All
Number of subjects	10	6	13	29
Number of PK samples	48	37	72	157
ME (mcg/mL)	−0.82	1.7	0.06	0.18
RMSE (mcg/mL)	4.2	5.68	6.45	5.66
AFE	1.31	0.73	0.98	1.00
AAFE	1.84	1.76	2.14	1.95
Number of samples outside the model’s 90 PI (N [%])	3 (6.25 %)	6 (16.22 %)	27 (37.5%)*	36 (22.93 %)a,*

ME, mean error; RMSE, root mean squared error; AFE, average fold-error; AAFE, average absolute fold-error; PBPK, physiologically-based pharmacokinetic; PI, prediction interval.

^aSummary of age-segmented analyses.

^*Proportion of observed data exceeding model’s 90% PI is statistically greater than 0.10 (p-value<0.05, exact binomial test)

Conversely, age-segmented evaluations of PBPK model performance displayed dissimilar results between age-groups. For infants (1 month–2 years; 10 subjects; 48 PK samples), the proposed NPDE-based model evaluation approach indicated the presence of a discrepancy between model simulations and observed data. Computed NPDE values exhibited a mean of −0.36 (p-value = 0.015; Table 7), indicating a trend towards model over-prediction. Goodness-of-fit plots also supported the presence of an over-prediction bias associated with model predictions (Supplementary Fig. S5). Conventionally computed bias (AFE) and precision (AAFE) measures were 1.31 (i.e., over-prediction bias) and 1.84, respectively. However, a NPC for the proportion of data exceeding the model’s 90% PI (0.0625) did not exceed the nominal value of 0.10 (Table 8).

In young children (2–6 years; 6 subjects; 37 PK samples), evaluation measures from the proposed model evaluation approach provided conflicting findings. NPDE values exhibited a mean of 0.21 - a value that was not significantly different than 0 (p-value = 0.211; Table 7). However, goodness-of-fit plots indicated a trend towards model under-prediction for samples collected between 2–4 hours (Supplementary Fig. S6). The computed AFE (0.73) indicated a bias towards model under-prediction. However, precision (AAFE) associated with model predictions was less than 2-fold (1.76; Table 8). Furthermore, the proportion observed data exceeding the model’s 90% PI (0.1622) was not statistically greater than the nominal value of 0.10 (Table 8).

For children between 6–18 years (13 subjects; 72 PK samples), the proposed model evaluation workflow depicted an adequate fit between model simulations and observed data. NPDE values exhibited a mean value of 0.08 (p-value = 0.522; Table 7). Goodness-of-fit plots indicated that model simulations adequately recapitulated the observed data. Although, for concentrations post-drug infusion (i.e., high concentrations), a minor over-prediction bias was observed (Supplementary Fig. S7). The estimated residual variability (exponential) associated with model predictions was 0.50 (Table 7). AFE was 0.98, indicating a lack of bias associated with model predictions. However, AAFE (precision) was greater than 2-fold (2.14). In addition, a statistically greater proportion of observed data fell outside the model’s 90% PI (0.375) compared to the nominal value of 0.10 (Table 8).

Discussion

The current study introduces a new approach for evaluating Pop-PBPK model predictions against time-based observations (i.e., continuous data) that are commonly collected during clinical investigations. Though the examples presented here were specifically tailored towards PK data, the depicted methodology could equally be applied to other continuous data types, such as pharmacodynamic measures. The proposed approach focuses on deriving Pop-PBPK specific NPDE. Rather than providing an indication of the absolute difference between model simulations and observed data, NPDE provide a normalized approximation of the percentile that decorrelated observations fall in terms of model simulations. For example, a NPDE value of 0 would indicate that the decorrelated observation falls on the 50^th (i.e., median) percentile of docorrelated model simulations. Furthermore, statistical analysis of the first two moments (i.e., mean and variance) for derived NPDE distributions provide an understanding of the model’s ability to recapitulate observed datasets in terms of bias and variability. Though commonly employed for population PK model validation [30, 31], to our knowledge, this presents the first instance where NPDE have been appropriated for Pop-PBPK model evaluation.

Due to their varied scope of utilization, as well as lack of clear guidance from regulatory authorities [2, 3], PBPK models are commonly evaluated using a diverse set of quantitative metrics. For continuous data, such as concentration-time measurements, evaluations traditionally include summative metrics of bias (e.g., AFE, mean percentage error) and precision (e.g., AAFE, root-mean squared error, mean absolute percentage error) [32, 33], as well as NPC (e.g., proportion of observed data falling outside the model’s 90% PI) [9, 13]. Of note, such metrics fail to account for within-subject correlations (i.e., multiple observations per subject) and the presence of residual error. As a result, derived conclusions may be biased [12]. For example, the NPC based on the 90% PI from the presented positive-control study indicated that the proportion of data exceeding the model’s PI (0.27) was statistically greater than the nominal value of 0.10 (Table 4). This is a notable finding, considering that observations and simulations were generated under the same PBPK model, albeit with a 0.20 exponential error added to observed concentrations.

The proposed NPDE-based model evaluation approach offers several distinct advantages compared to conventionally employed metrics. First, the approach allows for the development of goodness-of-fit plots that aid in the identification of model misspecifications similar to those used for population PK analyses [34]. Generated plots allows for data from individuals administered a drug at dissimilar dosages or frequencies to be combined and displayed using a discrete set of graphs. Such visual depictions are particularly advantageous for opportunistically collected PK datasets, where dosing schemes and timing of samples can vary considerably between subjects. Additionally, through creation of individual predictive distributions for each observed value, the proposed workflow permits for Pop-PBPK model specific pc-vpc plots to be generated. These plots offer an enhanced ability to detect model misspecifications by normalizing data to account for differences in dosages or influential covariates between subjects [24]. Second, unlike summative metrics (e.g., AFE), which are derived based on model predictions for a typical subject (i.e., without consideration of inter-subject variability), NPDE are computed based on simulations that encapsulate the range of expected variability (e.g., inter-individual variability and residual error) associated with each prediction [14]. As such, NPDE-based analyses provide an important conceptual shift from conventional summative metrics. Rather than focusing on how far observations lie with respect to a single simulated (typical) individual, the proposed approach focuses on where observations fall within the range of variability proposed by the model, which permits NPDE-based analyses to provide simultaneous assessments of the adequacy of model predictions in terms of bias and variability. Lastly, the proposed evaluation approach incorporates residual variability into its qualification process. To our knowledge, this is one of the first instances where consideration of residual error has been incorporated into the PBPK model evaluation process. As pediatric PK studies are frequently conducted during the course of clinical care, obtained PK datasets are inferred to embody higher degrees of residual error in comparison to prototypical phase-I PK studies performed in adults. Therefore, to facilitate appropriate model evaluations against such observed datasets, evaluation techniques capable of accounting for residual error are required.

Pre-established thresholds for assessing the quality of PBPK model predictions are not well-defined within the literature. For example, a systematic review of published PBPK models indicated that for 56% of modeling exercises, a priori criteria for qualifying models as successful was not listed [35]. This finding is likely a reflection of the difficulty associated with establishing thresholds that are of clinical relevance. As opposed to evaluating models based on pre-specified clinically relevant thresholds, which vary between compounds and study populations, the proposed model evaluation workflow permits for a statistical assessment of similarity between observations and model simulations. For example, statistical evaluations of the mean of NPDE values provides an explicit quantitative assessment of model bias. However, it can be conceded that specific thresholds for acceptable goodness-of-fit plots and magnitudes of residual error are less well-defined. For the magnitude of residual error, estimates should be within a reasonable range with respect to the compound’s efficacy/safety profile and source of data. Though the safety of clindamycin in children has yet to widely investigated, a previously published safety analysis of 21 preterm and term infants receiving clindamycin for treatment of a suspected systemic infection or as part of standard of care found that 9 (43%) experienced adverse events, none of which were inferred to be related to clindamycin [36]. Additionally, a previously conducted population PK analysis of opportunistically collected clindamycin plasma PK data from 125 children, characterized a proportional residual error of 0.40 [37]. Of note, for smaller magnitudes of variance, proportional and exponential error functions introduce similar degrees of variability. Consequently, exponential residual error estimates from the developed pediatric clindamycin Pop-PBPK model were deemed acceptable as they approximated or were less than the population PK model defined value (Table 7) [9, 37].

PBPK model evaluations should be conducted in a manner that demonstrates the model’s applicability towards study populations of interest [3]. The importance of this concept was highlighted through our evaluation of the previously developed pediatric Pop-PBPK model for clindamycin [9]. When model simulations were evaluated against observed data from all subjects, spanning from infants to adolescents, a suitable fit between model simulations and observed data was depicted (Table 7; Figure 5). However, when analyses were segregated between different age-specific cohorts, differences in model performance were observed. In young children (2–6 years), evaluation measures offered contrasting findings. Goodness-of-fit plots indicated the presence of model under-prediction, yet the mean of NPDE values was not statistically significant (Table 7; Supplementary Figure S6). This discrepancy may be a result of the low number of subjects within this cohort (i.e., 6), reducing the power for tests associated with the mean of NPDE values. Furthermore, in infants (1 month – 2 years), model simulations were found to over-predict observed concentrations (Table 7; Supplementary Figure S5). These results support the use of segmented analyses of Pop-PBPK model performance within specific study populations of interest. Subject segregation should be conducted with careful consideration as the creation of too heterogeneous groups may mask the ability to detect model misspecifications within specific sub-groups. Regulatory guidance and pre-existing knowledge of patient populations where PK differences are anticipated (e.g., neonates vs infants; males vs females) could be used to formulate groups for such analyses.

The proposed NPDE-based evaluation approach is not without limitations. Computation of NPDE uses a process whereby observations are decorrelated based on model simulations [16]. However, this process does not necessarily render NPDE as completely independent [38]. As a consequence, statistical tests based on NPDE can be associated with slightly higher type I error rates (i.e., erroneously asserting that model predictions and data are divergent). Therefore, it is recommended that goodness-of-fit plots also be considered as part of the model evaluation process [15]. Although the negative-control study was designed to assess the power of the proposed NPDE-based model evaluation approach to detect differences between two theoretical compounds whose PK profiles were slightly different, it should be noted that these computations were specific to the presented example. With use of Pop-PBPK models for an alternative set of compounds, different results would have been obtained. Despite their complexity, PBPK models are still simplified representations of complex biological systems. Consequently, the residual error computed using the defined workflow should be viewed as a composite of several sources including inappropriate model structure, misspecification of drug and system-specific parameters in addition to study execution and drug measurement errors. Although we assessed the influence of misspecifications of the magnitude of residual (exponential) error on type-I-error and power (Table 3 and Table 5), this work does not provide an understanding of the impacts of misspecification of the error model type (e.g., additive vs. proportional vs. auto-correlated, etc.). The most notable limitation of the proposed evaluation approach is its need for patient-specific PK and demographic data; this represents a departure from currently employed metrics such as NPC that can be employed based on tertiary demographic information (e.g., age and weight range of observed subjects) [39]. Nonetheless, considering the advantages associated with use of the proposed model evaluation approach in comparison to conventionally utilized evaluation metrics, further development of NPDE-based methods for Pop-PBPK model evaluation is warranted.

Conclusions

The presented work introduces a new paradigm for qualifying Pop-PBPK model predictions of continuous outcomes (e.g., concentration-time values) that accounts for within-subject correlations (i.e., multiple observations per subject) and the presence of residual error. The novel approach focuses on deriving Pop-PBPK model specific NPDE, a metric that is commonly utilized for population PK model validation. Using simulation-based study designs, the performance of the proposed NPDE-based model evaluation approach was demonstrated through statistical assessments of power and type-I-error . When employed to evaluate a previously developed clindamycin PBPK model against prospectively collected plasma concentration values from 29 children, the NPDE-based approach asserted that, on average, the model predictions were unbiased; however, when pediatric subpopulations were evaluated, the approach revealed potential biases that should be explored.