Significance
We propose a general framework for population viability analysis aimed at near-term ecological forecasting of suitable focus species’ presence in heterogeneous landscapes. Our method is based on remotely acquired and objectively manipulated Earth observations, coupled with hard-gained field evidence and landscape-explicit stochastic models of population dynamics. The integration of field data on the geographical niche plays a major role in calibration and in defining the impact of imperfect detection of species’ presence. Our case study deals with the persistence of two carabid species in the Gran Paradiso National Park (Italy), singled out as important biodiversity indicators. Results suggest the effectiveness of our framework in near-term forecasting the dynamics of species presence in space/time, leading to testable predictions of ecological responses.
Keywords: species distribution models, metapopulation ecology, landscape matrix, Earth observation, carabids
Abstract
Understanding risks to biodiversity requires predictions of the spatial distribution of species adapting to changing ecosystems and, to that end, Earth observations integrating field surveys prove essential as they provide key numbers for assessing landscape-wide biodiversity scenarios. Here, we develop, and apply to a relevant case study, a method suited to merge Earth/field observations with spatially explicit stochastic metapopulation models to study the near-term ecological dynamics of target species in complex terrains. Our framework incorporates the use of species distribution models for a reasoned estimation of the initial presence of the target species and accounts for imperfect and incomplete detection of the species presence in the study area. It also uses a metapopulation fitness function derived from Earth observation data subsuming the ecological niche of the target species. This framework is applied to contrast occupancy of two species of carabids (Pterostichus flavofemoratus, Carabus depressus) observed in the context of a large ecological monitoring program carried out within the Gran Paradiso National Park (GPNP, Italy). Results suggest that the proposed framework may indeed exploit the hallmarks of spatially explicit ecological approaches and of remote Earth observations. The model reproduces well the observed in situ data. Moreover, it projects in the near term the two species’ presence both in space and in time, highlighting the features of the metapopulation dynamics of colonization and extinction, and their expected trends within verifiable timeframes.
Monitoring, understanding, and predicting changes in biodiversity and in the geographical distribution of species have become increasingly important to mainstream ecology (1–6). As climate change, possibly human induced (7), redefines the geographical distribution of species (8, 9), alterations in habitat structures appear ubiquitously as dominant drivers (10, 11). Improving our capability to reliably describe and monitor the changes in biodiversity, species distribution, and habitat in space and time is thus fundamental toward informed decisions on landscape, biodiversity, and conservation management (12–14). To that end, theory can be instructive (1, 15–25), in particular if meant to link directly Earth observations (EOs) to in situ ecological data on presence, absence, and abundance providing estimates of the geographical distribution of a species within a landscape (12, 26, 27). Wherever the movement of individuals across structured habitats is concerned, by necessity metapopulation dynamics are relevant. Within that context, understanding the links between a complex and heterogeneous landscape acting as the ecological substrate and the hosted population dynamics is central (4, 28–31). In complex topographies such as mountainous regions shaped by fluvial processes (32) the core of landscape ecology has been on spatial patterns, and therein the need for integration of ecological processes and population dynamics has been convincingly advocated (20, 33). Moreover, it has been compellingly claimed that refocusing ecological forecasting on the near term lies at the core of the scientific method because it allows one to contrast predictions with actual observations (14).
The main drivers of the geographic distribution of a species are 1) the set of abiotic factors characterizing its fundamental niche (34), 2) the interactions with other individuals (biotic interactions and demography) (21, 35), and 3) the accessibility of geographical regions where species movement is not impaired [e.g., mountain tops, valleys, or man-made dams and roads (23, 36–38)]. The combination of the fundamental niche with the species interactions defines the realized niche (39), i.e., the fraction of the fundamental niche which shows a positive population growth rate despite competition (40). Species distribution models (SDMs) (41) concern the modeling of the landscape-explicit probability of presence of a species based on the realized niche. This occurs by relying primarily on the habitat suitability (42) given its biotic and abiotic factors. Habitat suitability drives the probability of presence of a species at equilibrium (43, 44), implying that the presence of a species in the landscape reflects its niche while other processes, like dispersal, colonization, or migration, do not have major effects (45). In species distribution models, most processes are implicitly incorporated into the habitat suitability and hence into the species’ niche (46). Physical barriers, sources–sinks, and population and metapopulation dynamics are thus not modeled explicitly (45), although models have been developed to integrate certain features of the relevant dynamics with SDMs (21, 35, 47, 48).
Here, we focus explicitly on the linkage of attributes of the landscape matrix with stochastic metapopulation dynamics (6, 16, 20, 25, 49) where the landscape is subdivided into cells, as is commonplace when EO rasters are used. Each cell constitutes a patch sensu Hanski, from which a focus species can colonize other empty patches or go extinct. This allows us to characterize precisely the abiotic conditions within each cell based on EO data and derive a species’ fitness, i.e., the local habitat suitability. Once the niche of species is estimated, the metapopulation model can, in time, reflect the unfolding colonization of geographical regions and account explicitly for physical barriers that prevent it. Moreover, a method estimating this niche by calibrating the parameters driving processes relevant to metapopulations has to account for the gaps in data in space and time as well as the imperfect detection of species (31, 50, 51). Our method merges the use of SDMs (52) with the demands of stochastic metapopulation models (1, 15) (see SI Appendix, Fig. S14 for an overview of the general scheme; see also Materials and Methods). EO data are employed to characterize habitat suitability in space and time by reproducing observed spatial and temporal presences of the in situ data for the focus species. As SDMs prove particularly apt at depicting a species’ static probability of presence, we make use of a reasoned (Materials and Methods) generalized linear model (GLM) to estimate the initial presence in the landscape. A stochastic metapopulation framework (spatially explicit patch occupancy model [SPOM]) (6, 16, 25, 49, 53) (Materials and Methods) is employed to dynamically model the presence of the focus species in time (23, 52). A suitably modified metapopulation fitness (i.e., suitability of the habitat for the focus species) is defined based on the core concept of GLMs, which we calibrate by using an iterated filtering (IF) scheme (54), a technique particularly powerful when applied to partially observed Markov processes, tailored to accommodate partial and imperfect observation data in space and time (50, 51, 53), without the need for observations in each modeled path or timestep. An application to a case study then showcases the capabilities of the framework by replicating the observed spatial and temporal dynamics of two species of carabids viewed as significant biodiversity indicators—an outcome of a large field observations program in the Gran Paradiso National Park in the Italian Alps (Materials and Methods) (Figs. 1 and 2).
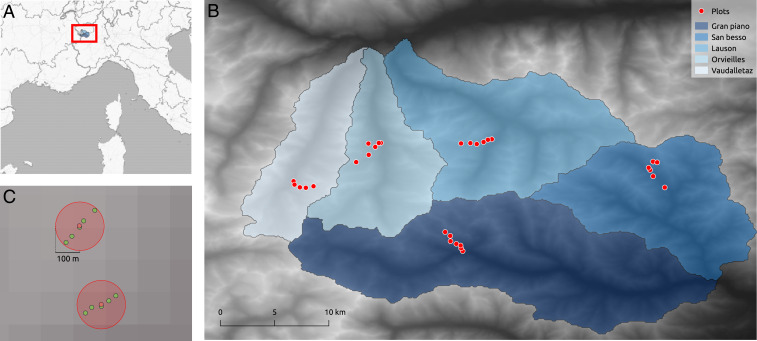
Fig. 1.
Overview of the study area and setup. (A) Location of the GPNP. (B) Overview of the GPNP’s five valleys with the location of the 30 plots in the valleys. (C) Example of traps aggregated in a 100-m radius forming 2 plots. The 2 plots are separated by 200 m in elevation.
Fig. 2.
EO data used in the study to define the species’ fitness. Dynamic data with one map per year (2006 shown): (A) temperature, (B) greenness, (C) wetness, and (D) brightness. Static data: (E) aspect, (F) slope, and (G) forest presence. The resolution of all rasters is 180 m.
Results
The output of the model (Materials and Methods) is shown for both focus species, Pterostichus flavofemoratus and Carabus depressus, simulated via properly calibrated parameters (Table 1 and Materials and Methods) contrasting field sampling and by layers of a filtering algorithm (SI Appendix, section 4 and Materials and Methods). Note that the process-based results on the species are to be read with caution given the relatively short case study (Discussion) and mainly show the possible extent of interpretation of the method.
Table 1.
Calibrated parameter values for the two species of interest
| P. flavofemoratus | C. depressus | |
| 79% | 63% | |
| 1% | 1% | |
| 187.6 | 733.1 | |
| 1.5 | 1.2 | |
| 189.9 | 173.0 | |
| 2.1 | 3.4 | |
| 3.6 | ||
| 3.2 | ||
| 0.4 | 0.8 | |
| 1.54 | ||
| 1.4 | ||
| 0.1 |
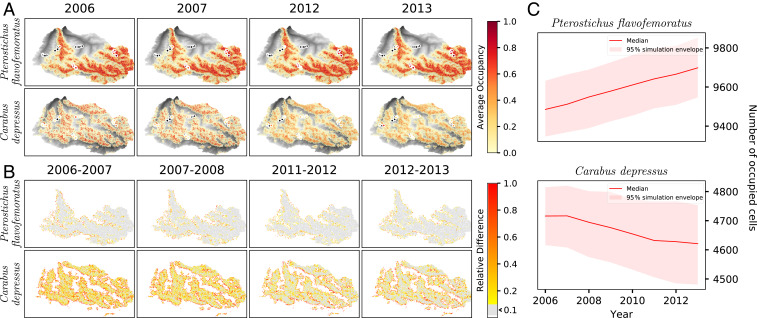
Fig. 3 shows the two species’ simulated average occupancy in the landscape for the sampled years, computed from 480 replicas of the stochastic algorithm tackling metapopulation dynamics (Materials and Methods), along with the relative changes in occupancy highlighting possible differences arising in time.
Fig. 3.
Output of the filtering algorithm for the calibrated parameters. (A) Average occupancy in time with the ratio of number of times a species was observed vs. the number of times it was sampled displayed at the sampling location. (B) Relative difference in average occupancy computed from one year to the next. The relative difference is computed as which highlights large changes compared to the initial value. The color code is as follows: white, no change occurs; gray, less than 10% difference is observed; and a scale endowed with a linear gradient capped at 100% for the values above. (C) Time series of the median number of occupied cells with a simulation envelope. The full time series of A and B from which C is derived are shown in SI Appendix, section 5.
For both species, the modeled average occupancy matches systematically the observed ratios from pitfall trapping samples (Materials and Methods) in nearly all plots. This suggests that the calibration process identified a parameter combination that results in an appropriate fitness function driving the metapopulation dynamics. Fluctuations occur around multiple stable cores, where the pressure of colonization lessens. The presence of C. depressus appears more patchy than the one of P. flavofemoratus, with clusters of high occupancy and surrounding lower occupancy maintained by the colonization process.
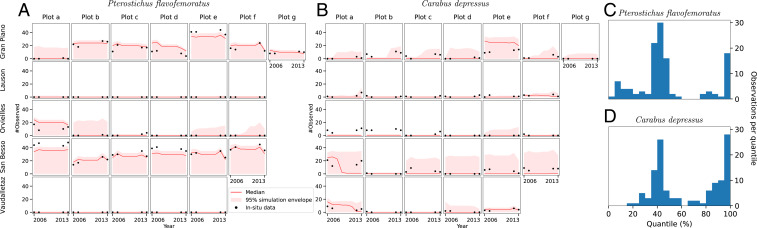
Fig. 4 A and B shows a comparison between the modeled (, red line with simulation envelope) and in situ (black dots) number of times the species was observed in each plot and year. The modeled (the number of times per year and plot a species is counted) is derived by drawing 1,000 samples from the binomial distribution for each particle, plot, and year (with the values of estimated true positive [] and false positive [] displayed in Table 1), knowing the output of the model (, the binary occupancy state) and the number of times the plot was sampled in the given year (). The displayed median and the simulation envelope are computed from the joint distribution.
Fig. 4.
(A and B) Modeled (red with simulation envelope) and in situ (black dots) number of times the two species were observed () in each plot and year. The modeled is generated by sampling from a binomial distribution (Materials and Methods). For the years 2008 to 2011 the average is taken. (C and D) Histogram of the quantiles in which the in situ data are located within the model result (A and B). Values on the right side of the 50% mark show where the model underestimates the occupancy, and those on the left side show where the model overestimates the chances of occupancy.
The modeled of P. flavofemoratus encapsulates the in situ data within errors in almost all of the plots, with a few plots displaying a large envelope, but with the median usually close to the observed data. Because for C. depressus the uncertainty on the false negative data (, Table 1) is higher, this translates directly into higher uncertainty above the median in the modeled value of . Decreasing and successively increasing trends in the observations, as seen in Fig. 4 A and B, plot for the Gran Piano site and plot for Vaudalletaz, are well captured by the modeled ones through changes in the simulation envelope and, in some cases, by significant variations in the median.
Fig. 4 C and D shows the distribution of the data within the modeled simulation envelope. For both species, most of the data are around the 50% quantile, with 88.3% (P. flavofemoratus) and 85.0% (C. depressus) of the observations within 95% of the model envelope. For P. flavofemoratus, the highest source of deviation from the median is at quantile 100%, where the model underestimates the certainty of occupancy of the plot. Overestimation of the presence (left-hand side of the plot in Fig. 4 C and D) is less frequent. For C. depressus there appears to be a notable underestimation of the occupancy (right-hand side of the plot in Fig. 4D).
Fig. 3C shows the two focus species’ occupancy of the landscape in time. Overall, the two species appear to be stable, as expected over these timescales of observations, with a significant increase in presence over time for P. flavofemoratus and a decrease for C. depressus. The observed trends can mostly be related to the changes in fitness (SI Appendix, section 5), although they may be observed only at the landscape level, with little to no trends observed at the pixel level. The average occupancy appears to be lower for C. depressus than for P. flavofemoratus, owing to a more clustered fitness function along with a lower base fitness.
As all cofactors have been normalized (SI Appendix, section 2), a unit change in a parameter directly influences the change in the contribution of the cofactors to the fitness relative to the other explanatory variables. For P. flavofemoratus, most of the variables contribute to the fitness, although brightness and greenness do so to a lesser extent. The increase in presence observed in Fig. 3C can be related to high parameter values multiplying temperature, brightness, and greenness, which have significantly increased in time (SI Appendix, section 2). C. depressus appears to be most sensitive to the presence of vegetation (greenness), with a negative parameter value explaining the observed trend.
Discussion
The proposed framework shows how EO data can be selected and used in conjunction with partially observed in situ data to model the presence of a metapopulation in space and time. The resulting calibration process converges to parameter combinations that generate initial spatial occupancy comparable to the one proposed by the SDM (SI Appendix, Fig. S15) and subsume the spatial dynamics of the metapopulation processes.
Static variables such as slope and aspect (northness and eastness) appear to be essential for characterizing the species’ niche. However, temporally varying state variables emerge as key players in predicting temporal trends in species occupancy. Because the static variables do not change in time, the observed changes are stemming only from two sources: 1) colonization and extinction processes related to the metapopulation parameters [c, e, and D (c.f. Materials and Methods, Metapopulation model - SPOM)], and 2) time-varying climatic drivers. The metapopulation parameters explain most of the stochastic variations, given that the observed trends are not due to the model rebalancing the occupancy to match parameter fluctuations (see SI Appendix, section 4 and Materials and Methods on model spin-up). The observed trends are therefore related to the variation of the time-dependent drivers. At the plot level, the simulated results show that the model is capable of reproducing, within a 95% simulation envelope, most of the species’ dynamics (Fig. 4). Similarly, the modeled envelope is produced by the SPOM stochastic structure, and the variations are induced by the variation in time of the covariates. An example is given in plot of the valleys of Gran Piano and Lauson (Fig. 4 A and B), where the model envelope increases as the observed presence increases.
The results at plot level corroborate the assumption that simulations reflect rather closely the observations, yielding a global interpretation of the species presence. The stochastic variations in occupancy occur around stable cores, which calls to mind the classic metapopulation approach centered around patches, but highlights the importance of modeling the landscape explicitly, as most of the changes occur at the edge of the stable cores or between them and not within a patch of homogeneous quality. These fluctuations, occurring in the marginal areas of habitat patches, could lead to the identification of leading and trailing edges if propagated in time (25, 55, 56). At a landscape level, little changes are observed considering the time frame and the domain’s scale. In a period of 8 y, perturbations of the environment in a protected area are hardly extreme and mostly observed in terms of variations in the number of individuals captured (to be interpreted with caution because of the imperfect detection) and not in terms of major shifts in geographical space of the species’ distribution. This is precisely what is expected from near-term ecological predictions (14).
The species’ calibrated initial spatial presence is maintained throughout the simulation and so the occupancy in 2013 resembles the occupancy imposed in 2006. The trends, however weak, reflect the two species’ long-term fate in the landscape and allow us to draw early warning of impending change. As mentioned above, P. flavofemoratus is mostly sensitive to temperature, wetness, and to some extent greenness, while C. depressus almost exclusively reacts to changes in greenness (Table 1). The decreasing trend in C. depressus (Fig. 3C) could therefore be explained by a parallel increase in the greenness values (see data analysis in SI Appendix, section 3 and Fig. S11) as the relation proves to be of inverse proportionality. This could also explain, at least in part, the trend for P. flavofemoratus since greenness is the variable with the strongest increase over time. All parameters multiplying the time-variant covariates are positive, explaining the trend in occupancy observed in Fig. 3C.
In terms of observation uncertainty, the model evaluates the probability of false negative C. depressus to be quite high (37%) compared to the one of P. flavofemoratus (21%). The model here reflects the sampling (SI Appendix, Fig. S8), where C. depressus has been observed fewer times than P. flavofemoratus. Nevertheless, a question remains on whether the occurrences of species not observed reflect true absence or undersampling. Because sampling reflects the species’ activity–density, a species less active at certain times of the year will be less present in the observations. However, the model is meant to reflect the species average presence in the landscape during the year, regardless of its level of activity. Here, the model follows the assumption that in 37% of the cases C. depressus was indeed present but not observed and accounts for this in the calibration. This problem is less evident the case of P. flavofemoratus, where over all plots the largest ratio of observed to sampled is higher.
The two species’ fitness (SI Appendix, Figs. S19 and S24) inform us about the ecology of the focus species. With a comparably more homogeneous fitness and a higher average value in the whole domain, P. flavofemoratus appears to be—relatively—a generalist, whereas C. depressus, with its more refined fitness and patchy occupancy, can be classified more as a specialist species.
Our study presents limitations and opportunities. Although the effort involved in the collection of these data has been major, the time series of in situ data are relatively short. This is often the case in practical conservation studies. The temporal dynamics of the species, especially the long-term landscape-wide trends, are difficult to detect from observed data. Relatively little change in the descriptors occurs, and the spatial distribution of the species does not drastically change in time. Further studies should perhaps be attempted on long-term ecological time series to validate the proposed method. The importance of long-term sampling of these habitats and the importance of continuing the efforts as done in the context of the data provided for this study are hardly overestimated. Obtaining consistently long time series of EO data is uncommon. Landsat, for instance, is one the longest and most consistent time series of EO data, but even this dataset suffers from failures (SI Appendix, section 2), and matching the different datasets of different Landsat missions is a demanding task. Other sources of errors or missing data arise when the weather corrupts images, e.g., when clouds obstruct the satellite image. Parts of the image therefore cannot be used and must be gap filled, because the captured signal does not reflect the actual conditions on the ground. In mountainous regions this can be quite problematic as clouds are frequent. On given bad years, almost all images are clouded to some extent, and a reconstruction of the image is inevitable. Taking the median value over the year for each pixel as done here can mitigate this problem, at the cost of limiting the modeling to a yearly dynamic.
The spatial distribution of the sampling points, arranged in transects, is most suited for the studies of the species–elevation relationship and identifying trends in altitudinal gradients, but inadequate for spatially explicit modeling. To do so, a random distribution of the sampling points would be most useful (57). The sampling scheme chosen here informs on the species’ presence on one side of the valley, but leaves out the presence on the other. The model then has to extrapolate from the climatic data in other valleys which have been sampled in similar conditions. Even though the data analysis suggests that the climatic data in the plots are representative of the whole domain, this might not be the case for the presence of the species, which depends not only on climatic data but also on the dispersal and metapopulation dynamics. Specialist species, with small, patchy presence, or generalists with lower activity or limited in time, might especially be misrepresented by this sampling scheme. The impact of the sampling scheme on the results of this framework could constitute an interesting follow-up of the present analysis.
Although widely used in species distribution modeling and shown to be performing relatively well compared to other SDM techniques (46), the fitness function as proposed here, based on the same concept as generalized linear models, obviously has limitations. Here, the response curve of the species to the environmental drivers is by definition monotonic. This means that, for a positive relationship between parameter and covariate, a covariate increasing in time (say, for instance, temperature) will increase the fitness of the species and then plateau, but never decrease again. In reality, species have a certain range of tolerance to an environmental factor, with an optimal value and decreasing slope on both sides of the optima, often hump shaped (23, 58) (see ref. 25 for an example), or a smooth function as in generalized additive models (GAMs) (59) (but see ref. 46 for a summary of response curves). This might not be an issue with SDMs where the parameters are calibrated once against a static presence. However, with dynamic models as presented here, the monotonicity would possibly be an issue if longer time series were to be considered or if the result would have to be propagated in time to simulate climate change or identify leading and trailing edges (see, e.g., ref. 25 for a methodology on identifying species fates). In such cases, the number of parameters would be doubled, and choice would therefore have to be made based on the number of relevant drivers, and longer time series with possibly more sampling points would be needed for the calibration.
Finally, the focus species must be ecologically relevant and suitable to metapopulation analyses that neglect ecological interactions with other species (as is the case for carabids) (SI Appendix, section 1). This means that observations must not provide the basis for describing their demography and interactions, including the role/functions of the various species competing in the ecosystems in which they are embedded. Inferring species functionality and recovery sensu ref. 60 is thus complementary to this approach. This general framework, however, is based on much easier to collect Earth observations and presence/absence data and resolves a number of practical and theoretical issues for the generalized application of the metapopulation approach. Unlike recovery targets for a focus species (60), which involve the need to gather notable ecological information, like size, density, and demographic structure of its population, this framework does not require the kind of intensive field work necessary should ecological species interactions be defining. In this framework, the role of the paths of species recovery is surrogated by the probability of occupancy, the end result of our framework, which also provides opportunities for letting ecological theory inform conservation practice.
Conclusions
The framework shown here must be seen as a proof of concept of a dynamic landscape-explicit metapopulation model driven by Earth observations intended for mountain species epitomizing, however, complex landscapes (i.e., substrates for ecological interactions). The proposed framework allows the estimation of the initial distribution of the species in the landscape. In a first step the initial occupancy is obtained by an SDM and, then, by calibrating the metapopulation model through the iterated filtering process, ensuring the occupancy in the landscape to be at equilibrium for the chosen fitness and metapopulation parameters. The calibration process identifies the parameters most suited for the species, which, in turn, permits the identification of trends in the spatial variability of the species. The framework permits the simulation of the spatial occupancy of a calibrated species in years when the species was not sampled, thus filling the spatiotemporal gaps between in situ observations. The proposed method permits us to extrapolate the information from sampled sites to unsampled sites and to capture the process in time. The method does not require all modeled sites to be observed as was previously the case in other studies (50, 51) and offers an integrated method to estimate the uncertainty of the observations (similar to ref. 50). Here, for instance, the metapopulation results are the only source of information for the occupancy from years 2008 to 2011, with the years 2006, 2007, 2012, and 2013 serving as reference for the calibration. Additionally, the framework manages to capture the metapopulation process of the species, thus potentially, with only EO data available, or with projected simulated EO data, permitting one to project the presence of these species into the future. Given the dynamical nature of the model, the presented spatial distribution serves as starting point for the simulation, which would then be driven by the EO data and the model dynamics.
Materials and Methods
The developed framework is demonstrated on data originating from a large ecological monitoring program called the “Biodiversity Monitoring Project” performed in the Gran Paradiso National Park (GPNP), a protected area located in the Italian Alps (Fig. 1A). In this study, data on invertebrates (Coleoptera Carabidae, Coleoptera Staphylinidae, Araneae, Hymenoptera Formicidae, Orthoptera, Lepidoptera Rhopalocera) and birds (Aves) have been routinely gathered since 2006 to gain an extended understanding on elevation-driven biodiversity patterns (12). The data have been gathered in the park’s five valleys (Gran Piano, San Besso, Lauson, Orvieilles, Vaudalettaz; Fig. 1B), in a 2-y sampling, 4-y break scheme; i.e., the processed data are available in 2006, 2007, 2012, and 2013. The project monitors species presence and abundance by considering a series of circular plots (5 to 7 in each valley, for a total of 30; Fig. 1B) of a radius of 100 m. These plots are separated by 200 m in elevation along a transect of the valley (Fig. 1C).
We here focus on carabids, one of the collected taxon. Carabids, or ground beetles, are a family of terrestrial arthropods (Carabidae taxon) composed of more than 40,000 species worldwide (61). Carabids are among the best-studied taxons in entomology (61), in part because of their commonplace use as bioindicators and in agriculture (SI Appendix, section 1A). Their study has significantly advanced our understanding of conservation biology and landscape and population ecology (SI Appendix, section 1B). Carabids have been confirmed as a taxon following metapopulation dynamics (61), which frame them as good candidates for this study (SI Appendix, section 1E). It has been shown that environmental drivers such as temperature, humidity, or presence of vegetation drive these species (61). EO data capturing these landscape features are therefore good candidates to model their niche.
During the 4 y of sampling, 90 different species of carabids have been identified, in various frequencies of occurrence and plots. We here focus on 2 species, which display different occurrence dynamics: P. flavofemoratus, relatively stable in terms of occurrences, and C. depressus, with more fluctuations (62). The analyses of the 2 species’ in situ data are presented in SI Appendix, section 3.
We aim at modeling near-term, interannual dynamics of the carabids, rather than seasonal ones. This choice for the temporal resolution of the model output is justified by three reasons: First, carabids have a life cycle which spans over 1 y (SI Appendix, section 1C), and most changes in density are observed between years. Second, the main drivers of the model are EO data, and obtaining accurate EO data multiple times a year is challenging due to cloud covering and possible sensor failures. Third, the carabids are collected by pitfall trapping, which produces estimates of the activity–density of individuals in a region. It is widely accepted as a good estimate of density fluctuations between years, but not within a single season (SI Appendix, section 1D). We have thus aggregated the field data by plots and year, focusing on presence rather than density, and as such reduce the uncertainty associated with categorizing each individual. For each year and plot, the number of times a certain species is found is counted () along with the number of times the plot was sampled (), which corresponds to the number of times each trap in a plot was visited in a given year. This provides a good estimate of the reliability with which a species has been identified and captured in a given plot, assuming that the species have the same activity during the sampling period. Issues on imperfect detection have been considered (50, 51).
The raster EO data have been selected based on the carabid ecology described in the literature (SI Appendix, section 1E) to best portray the carabids’ niche, i.e., a multidimensional function describing the suitability of the habitat (34, 40, 42, 45). The data collection raster scale imposes a natural constraint on the choice of pixel size of 180 m, taken as the fundamental surrogate for unit range (patch) size, thus neutralizing geometric uncertainty (63).
Because carabids are quite sensitive to temperature (61), this climatic driver is the first environmental descriptor to be considered (64), with complementary topographic data (slope and aspect) to characterize the niche allowed by the local terrain (however rugged). Additionally, carabids are affected by humidity, light, and the presence of vegetation (12, 61). To quantify these factors, we consider the tasseled cap indexes (65), which are a series of transformations (linear combinations) of the Landsat bands (66) designed to best quantify the degree of greenness, wetness, and brightness present in each pixel. Greenness is linked to the amount of vegetation present, wetness to humidity, and brightness to solar radiation. The tasseled cap indexes have recently been proposed as an interesting candidate to represent the variables of interest in the context of modeling beetle presence (67). Finally, forest presence has been mentioned multiple times as an important descriptor of carabid presence (61, 68) and is therefore included among explanatory variables (69). The preprocessing and generation of EO data are detailed in SI Appendix, section 2 (with final product displayed in Fig. 2), along with a data analysis in SI Appendix, section 3 which did not yield the necessity to remove any covariate beforehand, letting the calibration process decide their individual importance (cf. calibration below and results).
Modeling Framework.
Metapopulation model—SPOM.
Metapopulation theory is concerned with the persistence of a focus species in a given landscape, assumed to either survive due to the balance between colonization and extinction processes or go extinct. In SPOM (6, 16, 31, 53), each species is characterized by a set of parameters that defines its traits and the fitness function (performance of the species). SPOM is a Markov chain, where, for each cell and simulation time , the probabilities of colonization and extinction events are computed from the current presence as
| [1] |
| [2] |
where is the simulation timestep and and are the extinction and colonization rates (with dimension ) for cell at time . The colonization and extinction mechanisms are directly related to a fitness function, (see below), which measures the suitability of patch for the species. The local extinction rate on a cell is inversely proportional to the fitness; i.e., , where is the extinction constant. The colonization rate of an unoccupied cell is driven by the sum of the contributions from surrounding occupied cells,
| [3] |
where is the distance between cells and , the dispersal distance, and the colonization constant.
Fitness.
We represent the species suitability at cell and time by the fitness function (performance of the species) inspired by the nonlinear logistic regression functions adopted in GLMs (16, 49),
| [4] |
where is the value of the EO cofactor at position and time , the intercept, and the parameter associated with the EO cofactor .
Initial distribution estimation.
Given the discrete nature of spatial sampling, the carabid’s initial (2006) distribution in the GPNP needs to be estimated, for which an SDM is used. SDMs are a range of statistical models used to assess the probability of presence of a focus species in a landscape given in situ data and, often, EO data (41, 46).
Here, a subtype of the SDM, a GLM, is used (52, 70). A GLM attempts to model the presence and absence data by linearly combining explanatory variables (71) as
| [5] |
where and are the GLM’s parameters. We then use a logit link function to link the linear predictor () to the probability of presence (), assuming a binomial distribution (71):
| [6a] |
| [6b] |
The species presence is estimated based on the 2006 sampled vs. observed carabids data and the EO data. The sampled and observed data describe the number of times a species was sampled in a plot, vs. the number of times it was actually found in the given plot, and permit us to use a binomial distribution for the calibration of the probability of presence,
| [7] |
where is the probability of the species predicted by the GLM, the number of times the species was observed in the plot in times the plot was sampled, and the number of times the plot was found empty. The values of and are calibrated by maximum-likelihood estimation (70, 71).
Once the GLM is calibrated, the output probability of presence is used (SI Appendix, Fig. S15). Random initial occupation landscapes are generated by sampling the produced probability of presence. These initial occupancy maps are then further refined through the iterated filtering algorithm (see below) and spin-up period, as it is important to ensure that the initial presence is relaxed around the quasi-equilibrium imposed by the metapopulation parameters (ref. 72 and SI Appendix, section 4C).
Iterated filtering algorithm.
The IF algorithm has been proposed as a way to calibrate partially observed Markov processes (POMP) (54) using a frequentist approach based on maximum-likelihood estimation. Here, we make use of algorithm IF2 described in ref. 54. IF2 proposes to search for the maximum likelihood by spawning a given number of particles which all perform the Markov process multiple times (called iterations; SI Appendix, Fig. S16). Each particle is associated with certain values for each parameter. At each step of the Markov process, the parameters are first perturbed, and then the step is performed. After the step, if in situ data are available, a new set of particles is drawn by randomly sampling from the pool of particles based on a weighted distribution proportional to the likelihood, meaning one particle can be selected multiple times if it outperforms the other particles, or by randomness (73). A measurement model then links the model states to the observations (see below). The process then goes on by perturbating the parameters and running the Markov step.
The perturbation of the parameters is done by sampling from a Gaussian distribution around the values of the parameters (transformation of the sampling space can be performed for only positive parameters (log), bounded parameters (logistic), etc.) and with an SD which decreases in time to ensure the convergence of the parameters. The convergence of IF2 to the maximum likelihood estimation has been proved (54).
IF2 Applied to SPOM.
We here sought to apply IF2 to SPOM. We propose a likelihood function which takes advantage of the in situ data structure, capitalizing on the yearly sampled vs. observed data. We make use of a binomial function with a probability depending on the model prediction and integrating imperfect detection:
| [8a] |
| [8b] |
with the parameters of the model, the binomial distribution as described above at time , the state of the model at time and in patch , and the species misidentification (probability of false positive) and the detection probabilities (probability of true positive), respectively. Note that corresponds to , the probability of true negative and hence the probability of correctly measuring the absence of the species, and corresponds to , the probability of missing the species in the sampling. Note that the likelihood is computed in each pixel and year where and when in situ data are available (one pixel per plot per year). The model itself does not require observation data in each modeled pixel or year to generate a presence value. The two probabilities described here are considered as two parameters calibrated along the other parameters of the model.
We here add the initial occupancy of the landscape to the particle definition. At the beginning of each iteration, for each particle the spin-up is run with the initial presence contained in each particle, and the final state is conserved for the next iteration. The spin-up period ensures that the observed trends in species presence stem from stochastic fluctuations or environmental forcing, i.e., temporal changes in the cofactors, and not from the model transitioning to a quasi-equilibrium imposed by the parameters (SI Appendix, section 4C). Since the parameters change at each step and iteration, it is important to rerun the spin-up at the beginning of the iteration to ensure the pseudo-equilibrium, but with the parameter change being slow over the calibration process, the final state of the previous iteration is already close to the new pseudo-equilibrium imposed by the sampled parameters, and thus this state is used as initial occupancy for the new parameters and spin-up, whose final state then becomes the new initial presence for the particle. To summarize, each particle contains parameter values (, , , , ) and an initial presence . SI Appendix, section 4 further details the application.
Data and Model Accessibility.
The EO data accessibility is detailed in SI Appendix, section 2. The in situ data are available on Dryad: https://doi.org/10.5061/dryad.9zw3r22b9. The model implementation can be found on GitHub: https://github.com/GieziJo/SPOM-P.
Supplementary Material
Acknowledgments
This work was supported by the European Union’s Horizon 2020 Research and Innovation Program under Grant 641762 (Project ECOPOTENTIAL: Improving Future Ecosystem Benefits through Earth Observations). A.R. acknowledges the spinoffs of his European Research Council Advanced Grant RINEC-227612. We thank Ruth Sonnenschein for interesting discussions on Earth observation data, with regard to tasseled cap indexes in particular. We further thank Yoni Gavish and Guy Ziv for interesting discussions and insights on the species distribution modeling tools, as well as Enrico Bertuzzo and Lorenzo Mari for exchanges on population dynamics.
Footnotes
The authors declare no competing interest.
Data deposition: The in situ data are available on Dryad: https://doi.org/10.5061/dryad.9zw3r22b9. The model implementation can be found on GitHub: https://github.com/GieziJo/SPOM-P.
This article contains supporting information online at https://www.pnas.org/lookup/suppl/doi:10.1073/pnas.1919580117/-/DCSupplemental.
References
- 1.Hanski I., Metapopulation dynamics. Nature 396, 41–49 (1998). [Google Scholar]
- 2.Hanski I., Habitat connectivity, habitat continuity, and metapopulations in dynamic landscapes. Oikos 87, 209–219 (1999). [Google Scholar]
- 3.Hanski I., Alho J., Moilanen A., Estimating the parameters of survival and migration of individuals in metapopulations. Ecology 81, 239–251 (2000). [Google Scholar]
- 4.Ricketts T. H., The matrix matters: Effective isolation in fragmented landscapes. Am. Nat. 158, 87–99 (2001). [DOI] [PubMed] [Google Scholar]
- 5.Ries L., Fletcher R., Battin J., Sisk T., Ecological responses to habitat edges: Mechanisms, models and variability explained. Annu. Rev. Ecol. Evol. 35, 491–522 (2004). [Google Scholar]
- 6.Rybicki J., Hanski I., Species-area relationships and extinctions caused by habitat loss and fragmentation. Ecol. Lett. 16, 27–38 (2013). [DOI] [PubMed] [Google Scholar]
- 7.Neukom R., Steiger N., Gómez-Navarro J. J., Wang J., Werner J. P., No evidence for globally coherent warm and cold periods over the preindustrial Common Era. Nature 571, 550–554 (2019). [DOI] [PubMed] [Google Scholar]
- 8.Lenoir J., Svenning J. C., Climate-related range shifts–A global multidimensional synthesis and new research directions. Ecography 38, 15–28 (2015). [Google Scholar]
- 9.Rumpf S., et al. , Range dynamics of mountain plants decrease with elevation. Proc. Natl. Acad. Sci. U.S.A. 115, 1–6 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Parmesan C., Yohe G., A globally coherent fingerprint of climate change impacts across natural systems. Nature 421, 37–42 (2003). [DOI] [PubMed] [Google Scholar]
- 11.Parmesan C., Ecological and evolutionary responses to recent climate change. Annu. Rev. Ecol. Evol. Syst. 15, 365–377 (2006). [Google Scholar]
- 12.Viterbi R., et al. , Patterns of biodiversity in the northwestern Italian Alps: A multi-taxa approach. Community Ecol. 14, 18–30 (2013). [Google Scholar]
- 13.Acevedo P., et al. , Population dynamics affect the capacity of species distribution models to predict species abundance on a local scale. Divers. Distrib. 23, 1008–1017 (2017). [Google Scholar]
- 14.Dietze M. C., et al. , Iterative near-term ecological forecasting: Needs, opportunities, and challenges. Proc. Natl. Acad. Sci. U.S.A. 115, 1424–1432 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Hanski I., Metapopulation Ecology (Oxford University Press, 1999). [Google Scholar]
- 16.Purves D. W., Zavala M. A., Ogle K., Prieto F., Benayas J. M. R., Environmental heterogeneity, bird-mediated directed dispersal, and Oak Woodland dynamics in Mediterranean Spain. Ecol. Monogr. 77, 77–97 (2007). [Google Scholar]
- 17.Ovaskainen O., Sato K., Bascompte J., Hanski I., Metapopulation models for extinction threshold in spatially correlated landscapes. J. Theory Biol. 215, 95–108 (2002). [DOI] [PubMed] [Google Scholar]
- 18.Fletcher R., Multiple edge effects and their implications in fragmented landscapes. J. Anim. Ecol. 74, 1173–1181 (2005). [Google Scholar]
- 19.Bascompte J., Sole R. V., Habitat fragmentation and extinction thresholds in spatially explicit models. J. Anim. Ecol. 65, 465–473 (1996). [Google Scholar]
- 20.Fahrig L., “Landscape heterogeneity and metapopulation dynamics” in Key Topics and Perspectives in Landscape Ecology, Wu J., Hobbs R. J., Eds. (Cambridge University Press, 2007), pp. 78–89. [Google Scholar]
- 21.Keith D. A., et al. , Predicting extinction risks under climate change: Coupling stochastic population models with dynamic bioclimatic habitat models. Biol. Lett. 4, 560–563 (2008). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Rota C., Fletcher R., Dorazio R., Betts M., Occupancy estimation and the closure assumption. J. Appl. Ecol. 46, 1173–1181 (2009). [Google Scholar]
- 23.Bertuzzo E., et al. , Geomorphic controls on elevational gradients of species richness. Proc. Natl. Acad. Sci. U.S.A. 113, 1737–1742 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Pasetto D., et al. , Integration of satellite remote sensing data in ecosystem modelling at local scales: Practices and trends. Methods Ecol. Evol. 9, 1810–1821 (2018). [Google Scholar]
- 25.Giezendanner J., Bertuzzo E., Pasetto D., Guisan A., Rinaldo A., A minimalist model of extinction and range dynamics of virtual mountain species driven by warming temperatures. PLoS One 14, 1–19 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Burel F., Butet A., Delettre Y. R., Millàn De La Peña N., Differential response of selected taxa to landscape context and agricultural intensification. Landsc. Urban Plan. 67, 195–204 (2004). [Google Scholar]
- 27.Jacquin A., et al. , Habitat suitability modelling of Capercaillie (Tetrao urogallus) using earth observation data. J. Nat. Conserv. 13, 161–169 (2005). [Google Scholar]
- 28.Urban D., Keitt T., Landscape connectivity: A graph-theory perspective. Ecology 82, 1205–1218 (2001). [Google Scholar]
- 29.With K. A., “Metapopulation dynamics: Perspectives from landscape ecology” in Ecology, Genetics and Evolution of Metapopulations, Hanski I., Gaggiotti O. E, Eds. (Academic Press, 2004), pp. 23–44. [Google Scholar]
- 30.Fahrig L., Nuttle W. K., “Population ecology in heterogeneous environments” in Ecosystem Function in Heterogeneous Landscapes, Lovett G. M., Turner M. G., Jones C. G., Weathers K. C., Eds. (Springer, 2005), pp. 95–118. [Google Scholar]
- 31.Ovaskainen O., Saastamoinen M., Frontiers in metapopulation biology: The legacy of Ilkka Hanski. Annu. Rev. Ecol. Evol. Syst. 49, 231–252 (2018). [Google Scholar]
- 32.Rodriguez-Iturbe I., Rinaldo A., Fractal River Basins: Chance and Self-Organization (Cambridge University Press, 2001). [Google Scholar]
- 33.Wu J., Hobbs R., Key issues and research priorities in landscape ecology. Landscape Ecol. 17, 355–365 (2002). [Google Scholar]
- 34.Hutchinson G. E., “Concluding remarks: The demographic symposium as a heterogeneous unstable population” in Foundations of Ecology: Classic Papers with Commentaries, L. A. Real, J. H. Brown, Eds. (University of Chicago Press, 1957), vol. 22, pp. 415–427. [Google Scholar]
- 35.Akçakaya H. R., Viability analyses with habitat-based metapopulation models. Res. Popul. Ecol 42, 0045 (2000). [Google Scholar]
- 36.Colwell R. K., Hurtt G. C., Nonbiological gradients in species richness and a spurious Rapoport effect. Am. Nat. 144, 570–595 (1994). [Google Scholar]
- 37.Economo E., Keitt T., Network isolation and local diversity in neutral metacommunities. Oikos 119, 1355–1363 (2010). [Google Scholar]
- 38.González-Ferreras A. M., et al. , Effects of altered river network connectivity on the distribution of Salmo trutta: Insights from a metapopulation model. Freshw. Biol. 64, 1877–1895 (2019). [Google Scholar]
- 39.Soberón J., Peterson A. T., Interpretation of models of fundamental ecological niches and species’ distributional areas. Biodivers. Inf. 2, 1–10 (2005). [Google Scholar]
- 40.Pearman P. B., Guisan A., Broennimann O., Randin C. F., Niche dynamics in space and time. Trends Ecol. Evol. 23, 149–158 (2008). [DOI] [PubMed] [Google Scholar]
- 41.Guisan A., Thuiller W., Predicting species distribution: Offering more than simple habitat models. Ecol. Lett. 8, 993–1009 (2005). [DOI] [PubMed] [Google Scholar]
- 42.Kearney M., Porter W., Mechanistic niche modelling: Combining physiological and spatial data to predict species’ ranges. Ecol. Lett. 12, 334–350 (2009). [DOI] [PubMed] [Google Scholar]
- 43.Busby J. R., “Potential impacts of climate change on Australia’s flora and fauna” in Greenhouse: Planning for Climate Change, Pearman G. I., Ed. (CSIRO, Canberra, Australia, 1988), pp. 387–398. [Google Scholar]
- 44.Booth T. H., Nix H. A., Busby J. R., Hutchinson M. F., Bioclim: The first species distribution modelling package, its early applications and relevance to most current MaxEnt studies. Divers. Distrib. 20, 1–9 (2014). [Google Scholar]
- 45.Thuiller W., et al. , Does probability of occurrence relate to population dynamics? Ecography 37, 1155–1166 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Guisan A., Zimmermann N. E., Predictive habitat distribution models in ecology. Ecol. Modell. 135, 147–186 (2000). [Google Scholar]
- 47.Kéry M., Guillera-Arroita G., Lahoz-Monfort J. J., Analysing and mapping species range dynamics using occupancy models. J. Biogeogr. 40, 1463–1474 (2013). [Google Scholar]
- 48.Gavish Y., et al. , Accounting for biotic interactions through alpha-diversity constraints in stacked species distribution models. Methods Ecol. Evol. 8, 1092–1102 (2017). [Google Scholar]
- 49.García-Valdés R., Zavala M. A., Araújo M. B., Purves D. W., Chasing a moving target: Projecting climate change-induced shifts in non-equilibrial tree species distributions. J. Ecol. 101, 441–453 (2013). [Google Scholar]
- 50.Mackenzie D. I., Nichols J. D., Hines J. E., Knutson M. G., Franklin A. B., Estimating site occupancy, colonization, and local extinction when a species is detected imperfectly. Ecology 84, 2200–2207 (2003). [Google Scholar]
- 51.Royle J. A., Kéry M., A Bayesian state-space formulation of dynamic occupancy models. Ecology 88, 1813–1823 (2007). [DOI] [PubMed] [Google Scholar]
- 52.Guisan A., Thuiller W., Zimmermann N., Habitat Suitability and Distribution Models with Applications in R (Cambridge University Press, 2017). [Google Scholar]
- 53.Moilanen A., SPOMSIM: Software for stochastic patch occupancy models of metapopulation dynamics. Ecol. Modell. 179, 533–550 (2004). [Google Scholar]
- 54.Ionides E. L., Nguyen D., Atchadé Y., Stoev S., King A. A., Inference for dynamic and latent variable models via iterated, perturbed Bayes maps. Proc. Natl. Acad. Sci. U.S.A. 112, 719–724 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55.Thuiller W., et al. , Predicting global change impacts on plant species’ distributions: Future challenges. Perspect. Plant Ecol. Evol. Syst. 9, 137–152 (2008). [Google Scholar]
- 56.Anderson B. J., et al. , Dynamics of range margins for metapopulations under climate change. Proc. Biol. Sci. 276, 1415–1420 (2009). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 57.Woodcock B. A., “Pitfall trapping in ecological studies” in Insect Sampling in Forest Ecosystems, Leather S. R., Ed. (John Wiley & Sons, Ltd, 2007), vol. 3, pp. 37–57. [Google Scholar]
- 58.Moilanen A., Hanski I., Metapopulation dynamics: Effects of habitat quality and landscape structure. Ecology 79, 2503–2515 (1998). [Google Scholar]
- 59.Guisan A., Edwards T. C., Hastie T., Generalized linear and generalized additive models in studies of species distributions: Setting the scene. Ecol. Modell. 157, 89–100 (2002). [Google Scholar]
- 60.Akçakaya H. R., et al. , Assessing ecological function in the context of species recovery. Conserv. Biol., 10.1111/cobi.13425 (2019). [DOI] [PubMed] [Google Scholar]
- 61.Kotze D. J., et al. , Forty years of carabid beetle research in Europe–From taxonomy, biology, ecology and population studies to bioindication, habitat assessment and conservation. Zookeys 100, 55–148 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 62.Giezendanner J., et al. , Carabids data of Pterostichus flavofemoratus and Carabus depressus in the Gran Paradiso National Park (2006, 2007, 2012, 2013). Dryad. 10.5061/dryad.9zw3r22b9. Deposited 5 May 2020. [DOI]
- 63.Keith D. A., Akçakaya H. R., Murray N. J., Scaling range sizes to threats for robust predictions of risks to biodiversity. Conserv. Biol. 32, 322–332 (2017). [DOI] [PubMed] [Google Scholar]
- 64.Haylock M. R., et al. (2008) A European daily high-resolution gridded data set of surface temperature and precipitation for 1950–2006. J Geophys Res-Atmos 113, D20119. [Google Scholar]
- 65.Kauth R. J., Thomas G. S., “Tasselled cap–A graphic description of the spectral-temporal development of agricultural crops as seen by Landsat” in Proceedings of the Symposium on Machine Processing of Remotely Sensed Data (Purdue University, West Lafayette, IN: ) (1976), vol. 59, pp. 41–51. [Google Scholar]
- 66.Gorelick N., et al. , Google Earth Engine: Planetary-scale geospatial analysis for everyone. Remote Sens. Environ. 202, 18–27 (2017). [Google Scholar]
- 67.Dittrich A., et al. , Modelling distributions of rove beetles in mountainous areas using remote sensing data. Rem. Sens. 12, 80 (2020). [Google Scholar]
- 68.Lövei G. L., Sunderland K. D., Ecology and behavior of ground beetles. Annu. Rev. Entomol. 41, 231–256 (1996). [DOI] [PubMed] [Google Scholar]
- 69.Kempeneers P., Sedano F., Seebach L., Strobl P., San-Miguel-Ayanz J., Data fusion of different spatial resolution remote sensing images applied to forest-type mapping. IEEE Trans. Geosci. Remote Sens. 49, 4977–4986. [Google Scholar]
- 70.Yee T. W., Vector Generalized Linear and Additive Models with Implementation in R (Springer-Verlag, New York, 2013). [Google Scholar]
- 71.Fox J., “Generalized linear models” in Applied Regression Analysis and Generalized Linear Models, Fox J., Ed. (SAGE Publications, Inc, 2015), ed. 3, pp. 379–424. [Google Scholar]
- 72.Moilanen A., Patch occupancy models of metapopulation dynamics: Efficient parameter estimation using implicit statistical inference. Ecology 80, 1031–1043 (1999). [Google Scholar]
- 73.Arulampalam M. S., Maskell S., Gordon N., Clapp T., A tutorial on particle filters for online nonlinear/non-Gaussian Bayesian tracking. IEEE Trans. Signal Process. 50, 174–188 (2002). [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.