Comparison of Cox proportional hazards regression and generalized Cox regression models applied in dementia risk prediction

Abstract

Introduction

The frequently used Cox regression applies two critical assumptions, which might not hold for all predictors. In this study, the results from a Cox regression model (CM) and a generalized Cox regression model (GCM) are compared.

Methods

Data are from the Survey of Health, Ageing and Retirement in Europe (SHARE), which includes approximately 140,000 individuals aged 50 or older followed over seven waves. CMs and GCMs are used to estimate dementia risk. The results are internally and externally validated.

Results

None of the predictors included in the analyses fulfilled the assumptions of Cox regression. Both models predict dementia moderately well (10‐year risk: 0.737; 95% confidence interval [CI]: 0.699, 0.773; CM and 0.746; 95% CI: 0.710, 0.785; GCM).

Discussion

The GCM performs significantly better than the CM when comparing pseudo‐R² and the log‐likelihood. GCMs enable researcher to test the assumptions used by Cox regression independently and relax these assumptions if necessary.

1. INTRODUCTION

Dementia is one of the leading causes of dependency and disability in older individuals, with no cure yet. ¹ , ² However, evidence from recent studies shows the protective effects of lifestyle changes (eg, healthy diet and physical activity), regardless of genetic risk, have opened opportunities for dementia risk reduction via the implementation of behavioral interventions. ³ , ⁴ Hence, the identification of individuals at high risk of developing dementia is pivotal to apply preventive programs and to inform selection into clinical trials.

Multiple dementia risk prediction models have been developed in the last decade. ⁵ , ⁶ , ⁷ However, only a few have been recommended for clinical use, largely due to their multiple methodological weaknesses. For instance, some of the methodological limitations of the models reviewed include the overreliance on one data source and lack of internal and external validation; important concerns about the analytical techniques used were also highlighted. ⁶ , ⁸ , ⁹ The review of Goerdten et al. ⁹ summarizes the analytical techniques commonly used to derive dementia risk prediction models. Cox proportional hazards regression was one of these frequently used techniques. It belongs to the class of survival models, where the time until the event of interest, for example, death or disease diagnosis, is analyzed. With Cox regression, the influence of multiple predictors on the hazard, that is, risk of death or the disease, can be modeled. But this model relies on two critical assumptions: the proportional hazards (PH) and the log‐linearity (LL) of covariates. The PH assumption supposes that the ratio of hazards between two individuals remains constant over the studied period. However, in dementia studies in which the effects of risk factors are observed over two or three decades certain individual factors may be of benefit at a time and disadvantage at another time. For instance, in a recent study Ritchie et al. ¹⁰ showed that high plasma beta amyloids were associated with an increased risk in the preclinical phase only and tended to flatten out in the approach to diagnosis while performances of cognitive tests were lowered across the 10 years before diagnosis.

Published Cox regression analyses typically impose a priori the assumption that continuous covariates have a linear effect on the logarithm of the hazard. This LL assumption implies that dementia risk changes gradually with increasing value of the prognostic factor, so that, for example, the relative risk for a 60‐year‐old subject compared to a 50‐year‐old is the same as that when comparing subjects aged 80 versus 70 years. However, if the true relationship between the continuous independent variable and the outcome does not fulfil the LL assumption, then the conventional log‐linear model may result in incorrect identification of high‐risk subgroups and biased prognosis.

In this article, we use generalized Cox regression models, which can incorporate non‐linear and/or time‐dependent effects of variables to model dementia risk. ¹¹ To demonstrate the benefits of this modeling approach for dementia risk prediction, we compare results obtained from this methodology to results obtained from Cox regression, which is used frequently in the field. ⁹

2. METHODS

2.1. Study population

The Survey of Health, Ageing and Retirement in Europe (SHARE) is a multidisciplinary and cross‐national panel database with data collected on health, socio‐economic status, and social and family networks. SHARE comprises approximately 140,000 participants aged 50 and older from 27 European countries and Israel. Follow‐up of respondents was carried out in waves (Wave 1 to 7). SHARE was described elsewhere in more detail. ¹² We use information from Wave 2 to 7, ¹³ , ¹⁴ , ¹⁵ , ¹⁶ , ¹⁷ , ¹⁸ as from Wave 2 forward the information regarding dementia diagnosis was collected from respondents aged 60 and older. Wave 3 was not included, as it focused on the childhood of respondents. ¹⁴ In SHARE participants with only baseline measures, a dementia diagnosis at baseline and/or missing information for the predictor variables were excluded, which resulted in a cohort of 11,603 participants.

2.2. External validation sample

The Aging, Demographics, and Memory Study (ADAMS) is a supplementary study of the Health and Retirement Study (HRS). ¹⁹ The HRS is a longitudinal panel study, looking into the changing health and economic circumstances of adults over age 50 in the United States. In ADAMS, in‐person clinical assessments were conducted to gather information on the cognitive status of the participants over four waves (Wave A to D). Participants are aged 70 and older. The design and methods of ADAMS are described elsewhere in more detail. ²⁰

HIGHLIGHTS

• The frequently used Cox regression employs two crucial assumptions, which might not hold for all predictor variables, and can lead to incorrect predictions of dementia risk.

• Generalized Cox regression can relax the assumptions made by Cox regression.

• Generalized Cox regression performs better than Cox regression in predicting dementia risk.

• Generalized Cox regression is an interesting extension of Cox regression, and should be used more frequently in dementia risk research.

RESEARCH IN CONTEXT

1. Systematic review: The authors reviewed the literature using traditional sources (PubMed) and references from previous publications.

2. Interpretation: The presented findings show the improvements made through the incorporation of splines in the model, and the relaxation of the assumptions used by Cox regression. Importantly, none of the continuous predictor variables obeyed the crucial PH assumption. Generalized Cox regression enables researchers to test the assumptions independently and relax the assumptions of Cox regression if necessary.

3. Future directions: We would like to encourage researchers to adapt the use of splines in dementia risk prediction research.

2.3. Assessment of dementia and predictors

Dementia diagnosis was recorded by self‐report in SHARE. The participants were asked if a doctor ever diagnosed them/told them they have Alzheimer's disease, dementia, or senility. ²¹ , ²² , ²³ , ²⁴ , ²⁵

To have a close and in‐depth look at the variables selected as predictors, we chose to focus on modifiable risk factors identified by Livingston et al. ² and age. We selected age, years of education, body mass index (BMI), hearing loss, high blood pressure, smoking status, depression, physical activity, and diabetes. The information regarding disease status and behavioral risk were collected by self‐report. ²¹ BMI was calculated from height and weight reported by the participants. Hearing was recorded as “excellent,” “very good,” “good,” “fair,” and “poor.” It was categorized into 0/1, where “excellent” to “good” was coded as 0 and “fair” to “poor” as 1. For the diagnoses of high blood pressure and diabetes the participants were asked if a doctor ever told them they have high blood pressure/hypertension or high glucose level/diabetes. For the diagnosis of depression, the participants were asked if they suffered ever/since last wave from symptoms of depression which lasted at least 2 weeks. Physical activity was recorded as “more than once a week,” “once a week,” “one to three times a month,” and “hardly ever, or never.” It was categorized into 0/1, where “more than once a week” to “one to three times a month” was coded as 0 and “hardly ever, or never” as 1.

2.4. Generalized Cox regression

Cox proportional hazard regression is commonly used to model censored survival data. The purpose of the Cox proportional hazards regression model (CM) is to model the simultaneous effect of multiple factors on the survival. ²⁶ The CM aims to estimate hazard ratios over time. ²⁶ The model equation is written as follows:

$$h(t|z_1,\dots ,z_p)=h_0\left(t\right)\exp \left(\sum _i{\beta }_i{z}_i\right)$$

where${(z_i)}_{\mathrm{i}=1,\dots ,p}$ are the values of the covariates $Z_1,\dots ,Z_p$ on which the hazard may depend and $h_0(t)$ represents the baseline hazard. The baseline hazard is defined as the value of the hazard when $z_i=0$, for$i$in$1,p$.

In this study, three flexible models proposed by Mahboubi et al. ²⁷ were used, which are generalizations of the CM. With these flexible models, one or both assumptions used by Cox regression can be relaxed and tested independently. Cox regression employs the PH and LL assumption. With the generalized Cox regression model (GCM) it is possible to model time dependent hazard ratios and/ or non‐linear effects of the predictor variables.

The first flexible model relaxes the proportional hazards assumption (NPH):

$$h(t|z_1,\dots ,z_p)=h_0\left(t\right)\exp \left(\sum _i{\beta }_i\left(t\right)z_i\right)$$

The second flexible model relaxes the log‐linearity assumption (NLL):

$$h(t|z_1,\dots ,z_p)=h_0\left(t\right)\exp \left(\sum _i{r}_i\left(z_i\right)\right)$$

Last, the third flexible model relaxes both assumptions simultaneously (NPHNLL):

$$h(t|z_1,\dots ,z_p)=h_0\left(t\right)\exp \left(\sum _i{\beta }_i\left(t\right)r_i\left(z_i\right)\right)$$

The function $r_i$is a spline function of $z_i$modeling the non log‐linear effect of $z_i$ and $\beta i(t)$ is a spline function of t modeling the time dependent effect of$z_i$. Estimations of these functions are based on the full likelihood.

The flexible models use B‐splines, which are piecewise polynomials, where the pieces are joint by knots. Here, the splines are allowed to have one or two knots. The knot selection has to follow one criterion: there must be roughly the same number of events in the subintervals defined by the selected knots. The decision if one or two knots are used is based on a goodness of fit test. For example, models with one and two knots are computed and compared in terms of the Akaike information criterion (AIC). The model that produces the smallest AIC is selected. It can be tested if a variable obeys the assumptions by comparing the models described before using likelihood ratio tests (see Figure 1) ²⁷ and by this deciding which of the four models (CM, NPH, NLL, NPHNLL) models the variable best.

FIGURE 1.

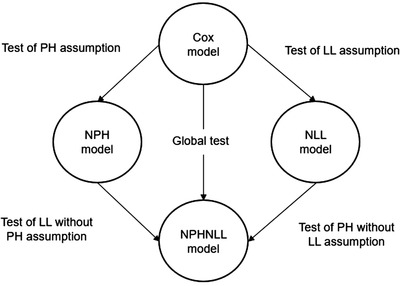
Testing of assumptions and finding best model. Arrows represent likelihood ratio test. Comparing models by likelihood ratio tests the assumptions of proportional hazards (PH) and log‐linearity (LL), and the best fitting model for the predictor is identified. This figure is adapted from Mahboubi et al ²⁷

2.5. Statistical analyses

A CM and a GCM were fitted to data from SHARE to predict dementia risk. Study time was used as time scale for all analyses. Study time was calculated from study entry (Wave 2, 2007) until study exit—wave of dementia diagnosis, wave in which participant died, wave in which participant was lost to follow‐up, or the end of the study (Wave 7, 2017), whichever came first. In the survival time analyses, dementia diagnosis was treated as the failure event.

To compute the full GCM, first, we tested if each predictor variable complied with the PH assumption and/or the LL assumption. To test these assumptions each predictor variable was modeled in a CM, an NPH model, an NLL model, and in an NPHNLL model. The computed models were compared by likelihood ratio test, and the best fitting model for each predictor variable was selected. All predictor variables were entered into the full model, while modeling each predictor with the best‐identified knot and spline combination. Last, after fitting the model with all identified splines and knots, spline coefficients were eliminated systematically. We reduced spline coefficients if more than one coefficient was non‐significant for a predictor, while comparing the smaller model with the previous one by likelihood ratio test—until the best fitting model was found. For the full CM, all predictor variables were entered into the model. To determine which model fits the data better, the model derived from Cox regression or generalized Cox regression, likelihood ratio tests were performed and the computed pseudo‐R² proposed by Nagelkerke and Cragg and Uhler were compared. ²⁶ C‐statistics adapted for survival analyses were calculated to assess predictive ability. ²⁶ The C‐statistic is a discrimination measure for binary outcomes, and it ranges from below 0.5 (indicating very poor model discrimination) to 1 (indicating perfect model discrimination). Bootstrapping with 1000 repetitions was performed to compute 95% confidence intervals (CI) for the C‐statistics and the pseudo‐R².

SHARE was used as the development sample and ADAMS as the external validation sample.

All analyses were performed in R Studio (Version 3.5.1) ²⁸ and the packages flexrsurv, ²⁹ survival, ³⁰ , ³¹ Hmisc, ³² and ggplot2 ³³ were used.

3. RESULTS

Among the 11,603 SHARE participants, 757 (6.5%) reported that they had received a diagnosis of dementia during 10 years of follow‐up. The mean age of diagnosis was 75.4 (7.2 standard deviation [SD]). Baseline characteristics for SHARE and ADAMS are presented in Table 1.

TABLE 1.

Baseline characteristics of SHARE and ADAMS

	SHAREN = 11,603	ADAMSN = 410
Dementia (%)	757 (6.5)	102 (24.9)
Age mean (SD a )	69.7 (7.2)	79.1 (6.1)
Years of education (SD)	10.2 (4.4)	10.71 (4.3)
Body mass index (SD)	26.7 (4.2)	26.9 (4.9)
Sex (%)
Female	6283 (54.1)	210 (51.2)
Male	5320 (45.9)	200 (48.8)
Depression (%)	1866 (16.1)	107 (26.1)
Diabetes (%)	1354 (11.7)	86 (20.98)
High blood pressure (%)	4647 (40.1)	257 (62.7)
Poor hearing (%)	2464 (21.2)	122 (29.8)
Ever smoker (%)	1532 (13.2)	117 (28.5)
No physical activity (%)	5424 (46.8)	257 (62.7)

^aStandard deviation (SD).

Abbreviations: ADAMS, Aging, Demographics, and Memory Study; SHARE, Survey of Health, Ageing and Retirement in Europe.

In SHARE none of the variables obeyed the PH assumption, when modeled alone (crude model). Two (years of education and BMI) of three continuous variables additionally did not obey the LL assumption. Comparisons of the estimated log hazards of dementia risk for age, years of education, and BMI in SHARE from the crude CMs (Figure 2 parts A, C, E) and GCMs(Figure 2 parts B, D, F) are presented in Figure 2.

FIGURE 2.

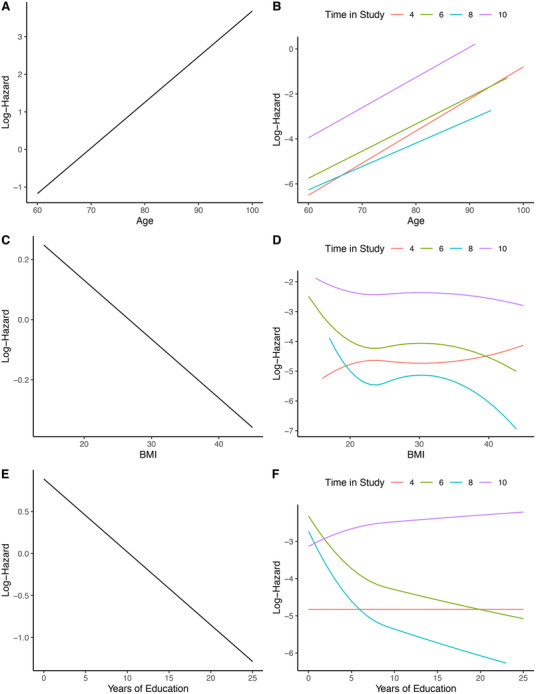
Estimated log‐hazards from crude Cox models (CMs) and generalized Cox models. Graphs A, C, and E show estimated log‐hazards for age, body mass index (BMI), and years of education from crude CMs; graphs B, D, and F show estimated log‐hazards, for each follow‐up time point, for age from a crude non proportional hazards model (NPH), BMI, and years of education from crude non proportional hazards and non log linear models (NPHNLL)

The following section discusses the full prediction model derived from Cox regression and generalized Cox regression; both include the same predictor variables (age, years of education, BMI, depression, diabetes, high blood pressure, hearing, smoking status, and physical activity). In the full GCM, age, years of education, and BMI were modeled non‐proportional with time (NPH). When comparing the CM and GCM in terms of the log‐likelihood, the test results in a P‐value of <.001. The pseudo‐R² for the CM is 0.06 (95% CI: 0.048, 0.062) and for the GCM 0.493 (95% CI: 0.460, 0.506). The C‐statistic for the predicted 10‐year dementia risk is 0.737 (95% CI: 0.699, 0.773; CM) and 0.746 (95% CI: 0.710, 0.785; GCM). The C‐statistic for the predicted 4‐year dementia risk is 0.711 (95% CI: 0.678, 0.74; CM) and 0.709 (95% CI: 0.673, 0.74; GCM). Within ADAMS the two models generate a C‐statistic for the predicted 6‐year dementia risk of 0.743 (95% CI: 0.58, 0.924; CM) and 0.764 (95% CI: 0.607, 0.952; GCM). All computed C‐statistics for the time points from the models are presented in Table 2.

TABLE 2.

C‐statistics for SHARE models

	Number of cases	Cox regressionC‐statistic (95% CI)	Generalized Cox regressionC‐statistic (95% CI)
In SHARE
10 years	177	0.737 (0.699, 0.773)	0.746 (0.710, 0.785)
8 years	173	0.658 (0.616, 0.699)	0.659 (0.616, 0.698)
6 years	150	0.735 (0.693, 0.773)	0.736 (0.695, 0.775)
4 years	257	0.711 (0.678, 0.74)	0.709 (0.673, 0.74)
In ADAMS
≥6 years	13	0.747 (0.601, 0.917)	0.805 (0.695, 0.942)
6 years	10	0.743 (0.58, 0.924)	0.764 (0.607, 0.952)
5 years	23	0.51 (0.367, 0.652)	0.517 (0.368, 0.659)
4 years	23	0.592 (0.436, 0.768)	0.589 (0.430, 0.775)
3 years	4	1.0	1.0
2 years	16	0.708 (0.558, 0.869)	0.708 (0.555, 0.865)
1 years	23	0.602 (0.45, 0.765)	0.62 (0.468, 0.795)

Abbreviations: ADAMS, Aging, Demographics, and Memory Study; CI, confidence interval; SHARE, Survey of Health, Ageing and Retirement in Europe.

The regression coefficients computed by CM and GCM from SHARE are presented in Appendix A in supporting information. The computed overall C‐statistics for the CM and GCM in SHARE and ADAMS are presented in Appendix B in supporting information.

4. DISCUSSION

In this study, we compared dementia risk prediction models derived from generalized Cox regression and Cox regression. Our results show that the model derived from the generalized Cox regression fits the data significantly better than the model derived from Cox regression. The predictive ability of the CM and GCM range from moderate to good.

4.1. Cox regression versus generalized Cox regression

The GCM performs in the development sample and in the validation sample better than the CM. Both GCM and CM reach moderate to good predictive ability, which is in line with previous dementia risk prediction models. ⁷

The overall estimated C statistic for SHARE and ADAMS from the GCM shows an interesting problem: the C‐statistic is lower than 0.5, which would mean the model performs worse than chance (see Appendix B). However, this is not the case when looking at the estimated C‐statistics for the follow‐up time points. The C‐statistic is a rank correlation test; a high C‐statistic translates to a model which is able to estimate higher risks for individuals experiencing the outcome than individuals who did not during follow‐up. ²⁶ In this case—in which we relaxed the PH assumption for all three continuous predictors—the C‐statistic test is not able to rank the estimated risks correctly, because the GCM estimates time dependent risks. The overall risk of individuals who had a follow‐up of 10 years is higher than for example of individuals who had a follow‐up of 4 years, regardless of dementia risk (Appendix C in supporting information). Hence, the test ranks all individuals who had a follow‐up of 10 years over individuals with a follow‐up of 4 years, which results in an incorrect low C‐statistic. It might be useful to evaluate in which time frame a dementia risk prediction model derived from a GCM performs best.

Additionally, it needs to be mentioned that the C‐statistic or area under the receiver operating characteristic curve (AUROC) is not recommended to compare models, as it is a low power procedure. ³⁴ They should only be used to describe the predictive ability of a model. Instead, a high‐power test should be carried out to asses which model fits the data better, for example, a likelihood ratio test and/or comparing R². In this study the likelihood ratio test suggests the GCM fits the data significantly better than the CM. The pseudo R² suggests that the GCM improves greater upon the null model than the CM and hence is better able to predict the outcome than the CM. When looking at the results from the likelihood ratio test and the pseudo R² we can conclude that the GCM performs better than the CM in modeling dementia risk in SHARE.

4.2. Improvements by generalization

As summarized by Goerdten et al., ⁹ most published dementia risk prediction studies overlook the fulfilment of the assumptions of the analytical technique used for the estimation of risk. Consistent testing of these assumptions is crucial, as their violation can lead to biased results. ³⁵ This is especially important for continuous variables (eg, age) as shown in our work. This problem might lead researchers to categorize continuous variables, a practice that in turn leads to information loss and residual confounding. ³⁶ Instead, Moons et al. ³⁷ recommend the incorporation of splines, if there are any uncertainties about whether a variable complies with the linearity assumption, as the incorporation of splines makes the categorization of continuous variables unnecessary.

In this study we incorporated splines to test and relax the two strong assumptions used by Cox regression: (1) assumption of LL, that is, a linear relationship between the independent variable and the log‐hazard of dementia and (2) assumption of PH, that is, the effect of a variable is constant over time. There are other (simpler) options to assess the PH assumption of Cox regression: an interaction term with time can be added to the model or stratification by time can be performed. But using simpler testing methods implies assuming the LL assumption while testing the PH assumption and assuming the PH assumption while testing the LL assumption. The GCM allows us to test both assumptions of Cox regression independently from each other.

None of the predictor variables included in our analyses fulfilled the PH assumption. Furthermore, two of the continuous variables did not fulfil the LL assumption either. Comparing the estimated log‐hazards for the three continuous variables (age, BMI, and years of education) from crude CMs and GCMs, the difference between the models becomes evident. While the CM computes linear declining or increasing log‐hazards for the continuous variables, GCM computes a great variety of curves (see Figure 2). For age the PH assumption was relaxed, hence the effect of this variable on dementia risk is not constant with time and the different lines for 4 to 10 years can be seen. For BMI and years of education additionally the LL assumption was relaxed, hence the effects of the variables are not constant with time and there are non‐linear relationships between the variables and the log‐hazard of dementia, and the different lines with curves for 4 to 10 years can be seen.

Comparing the presented methodology with for example the CAIDE score ³⁸ —a well‐known dementia risk prediction score, computed by logistic regression, that ignores the dependence on time of the event being modeled—the applied approach could in theory model more accurately dementia risk. The CAIDE score translates to risk percentages ranging from 1% (low risk) to 16.4% (high risk). The difference to a risk model derived from GCM would be that the prediction model could inform if this risk changes over time, as the effects of some or all predictors on dementia risk change with time. The generalized Cox regression is more flexible and able to pick up changes in the effect of a predictor variable on dementia risk over time.

4.3. Strengths and limitations

This study has several limitations. First, due to the design of the used datasets, interval censoring is present. This means that the exact date of diagnosis is not known and occurred at some point during the interval between the waves. This might have resulted in biased results, likely an overestimation of the predictor coefficients. ³⁹ Second, censoring due to death, which is a competing event, was not taken into account. There are existing methods to incorporate competing risks in survival analyses ⁴⁰ as well as generalizations of these models. ⁴¹ However, the information on death in SHARE are recorded by proxy questionnaire and the use of these information might have hampered the results even further. ²¹ Third, the quality of the data about dementia diagnosis in SHARE is not optimal, as it is only recorded by self‐report and no further testing of the diagnosis is made. A similar limitation of the data is that the predictor variables were also self‐reported. However, for the purpose of this paper, these limitations are not critical given the aims of our work.

This study has several strengths. SHARE offers a large sample size, which covers a wide range of European countries and Israel, making it representative of the European population. ¹² In ADAMS the diagnosis of dementia was made by professionals. Every predictor variable was tested for the assumptions used by Cox regression. Importantly, following recommended practice, the developed models were validated internally and externally.

5. CONCLUSION

With the generalized Cox regression, the assumptions of Cox regression can be tested thoroughly and independently, and relaxed if needed. However, while the generalized Cox regression offers advantages, such as avoiding categorization, the disadvantages need to be mentioned too: the flexible models can require long computation times and a bigger sample is needed than for a Cox regression. Additionally, the interpretation of the coefficients computed by GCMs are not straightforward and it is only possible to examine the effect of a variable visually. Taking all this into account the generalized Cox regression is an interesting option to extend a Cox regression. The possibility to add splines and herewith relax the assumptions is especially appealing when including continuous variables. We would like to encourage researchers to adapt the use of splines in dementia research, to increase the understanding of the relationship between potential predictors and dementia risk.

CONFLICTS OF INTEREST

The authors report no conflicts of interest.

Supporting information

Supplementary information

Supplementary information

Supplementary information

Goerdten J, Carrière I, Muniz‐Terrera G. Comparison of Cox proportional hazards regression and generalized Cox regression models applied in dementia risk prediction. Alzheimer's Dement. 2020;6:1–8. 10.1002/trc2.12041