Abstract
Recent advances in diffusion magnetic resonance imaging (dMRI) analysis techniques have improved our understanding of fibre‐specific variations in white matter microstructure. Increasingly, studies are adopting multi‐shell dMRI acquisitions to improve the robustness of dMRI‐based inferences. However, the impact of b‐value choice on the estimation of dMRI measures such as apparent fibre density (AFD) derived from spherical deconvolution is not known. Here, we investigate the impact of b‐value sampling scheme on estimates of AFD. First, we performed simulations to assess the correspondence between AFD and simulated intra‐axonal signal fraction across multiple b‐value sampling schemes. We then studied the impact of sampling scheme on the relationship between AFD and age in a developmental population (n = 78) aged 8–18 (mean = 12.4, SD = 2.9 years) using hierarchical clustering and whole brain fixel‐based analyses. Multi‐shell dMRI data were collected at 3.0T using ultra‐strong gradients (300 mT/m), using 6 diffusion‐weighted shells ranging from b = 0 to 6,000 s/mm2. Simulations revealed that the correspondence between estimated AFD and simulated intra‐axonal signal fraction was improved with high b‐value shells due to increased suppression of the extra‐axonal signal. These results were supported by in vivo data, as sensitivity to developmental age‐relationships was improved with increasing b‐value (b = 6,000 s/mm2, median R 2 = .34; b = 4,000 s/mm2, median R 2 = .29; b = 2,400 s/mm2, median R 2 = .21; b = 1,200 s/mm2, median R 2 = .17) in a tract‐specific fashion. Overall, estimates of AFD and age‐related microstructural development were better characterised at high diffusion‐weightings due to improved correspondence with intra‐axonal properties.
Keywords: apparent fibre density, constrained spherical deconvolution, development, diffusion MRI, fixel based analysis, white matter
1. INTRODUCTION
Diffusion magnetic resonance imaging (dMRI; Le Bihan & Breton, 1985) offers a magnified window into white matter by probing the tissue microstructure properties. Various dMRI modelling and analysis techniques are available, which aim to summarise the local architecture of white matter as a quantitative metric. However, the biological interpretations around commonly investigated dMRI metrics rest heavily on whether the acquisition protocol can capture the relevant microstructural attributes (Lebel & Deoni, 2018; Tournier, Mori, & Leemans, 2011).
Traditionally, studies have acquired dMRI data with one diffusion‐weighting (or b‐value shell), opting for either low b‐values (e.g., b = 1,000 s/mm2) for diffusion tensor imaging (DTI) analyses (Jones, Horsfield, & Simmons, 1999; Landman et al., 2007), or moderate‐to‐high b‐values (e.g., b ≥ 3,000 s/mm2) for probabilistic tractography (Tournier, Calamante, & Connelly, 2013). More recently, with the advent of multi‐slice accelerated imaging (Barth, Breuer, Koopmans, Norris, & Poser, 2016), the acquisition of multiple dMRI shells has become more feasible. This has considerably improved data acquisition capabilities for sensitive populations (such as children and clinical populations) which may not withstand long acquisition times (Kunz et al., 2014; Silk et al., 2016; Somerville et al., 2018).
Multi‐shell dMRI data has been used in conjunction with various analysis approaches (Novikov, Veraart, Jelescu, & Fieremans, 2018; Zhang, Schneider, Wheeler‐Kingshott, & Alexander, 2012) across a variety of applications (Genc, Malpas, Ball, Silk, & Seal, 2018; Kunz et al., 2014; Pines et al., 2019). Measures derived from constrained spherical deconvolution (CSD; Dell'Acqua & Tournier, 2019) can infer the intra‐axonal signal fraction along multiple fibre pathways (Dell'Acqua, Simmons, Williams, & Catani, 2013; Raffelt et al., 2012). One such measure of microstructural organisation, termed apparent fibre density (AFD), can indicate relative differences in the white matter fibre density per unit volume of tissue. Given that the specificity to the intra‐axonal water signal is maximised at high b‐values due to higher restriction of water diffusion (Figure 1), AFD can be sensitive to axon density at high diffusion‐weightings (Raffelt et al., 2012).
Figure 1.
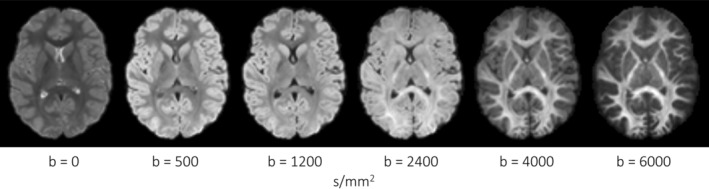
Spherical harmonics (zero order) maps derived from a representative participant (aged 8 years). Visually, increasing b‐value from 0 to 6,000 s/mm2 leads to greater specificity to the signal attributed to the intra‐axonal space
Analysis frameworks such as fixel‐based analysis (FBA; Raffelt et al., 2017) provide a means to test fibre‐specific differences in AFD within a population. FBA offers two major advantages over alternative dMRI analysis techniques: sensitivity to fibre properties (density and morphology), and specificity to fibre populations within voxels (or “fixels”). This combination of improved sensitivity and specificity increases the possibility of assigning group differences in fibre properties to specific fibre populations (Dimond et al., 2019; Gajamange et al., 2018; Genc et al., 2018; Mito et al., 2018).
In practise, FBA is compatible with both single‐shell (Dhollander, Raffelt, & Connelly, 2016) and multi‐shell (Jeurissen, Tournier, Dhollander, Connelly, & Sijbers, 2014) dMRI data. An intuitive choice might be to use all available dMRI data to compute fibre‐specific AFD. However, this might not be compatible with the underlying assumptions of AFD reflecting intra‐axonal properties. In addition, sensitivity to the extra‐axonal signal upon the inclusion of lower b‐values can influence the response function choice, resulting in a potential mismatch between the response function and the true underlying fibre properties.
Combining FBA with the very latest in MRI gradient hardware (300 mT/m) (Jones et al., 2018), we explore the impact of sampling scheme on AFD estimates using a rich developmental dataset comprising multi‐shell diffusion MRI data with b‐values ranging from 0 to 6,000 s/mm2. Firstly, we simulate multiple fibre geometries to showcase how discrepancies in “true” microstructural configurations can influence the interpretations of AFD generated from both single‐shell and multi‐shell dMRI data. We then conduct experiments to confirm the theory that AFD is more sensitive and specific to axon density at higher b‐values, demonstrated by sensitivity to detecting age‐relationships in a developmental population of children and adolescents.
2. METHODS
2.1. Simulations
Single fibre populations were simulated with the intra‐ and extra‐axonal spaces represented by axially symmetric tensors; the second and third eigenvalues were set to zero for the intra‐axonal tensor and equal but non‐zero for the extra‐axonal tensor (Jespersen, Kroenke, Ostergaard, Ackerman, & Yablonskiy, 2007; Kroenke, Ackerman, & Yablonskiy, 2004). The intra‐axonal and extra‐axonal parallel diffusivities were set to 1.9 μm2/ms, and 42 different combinations were simulated with intra‐axonal signal fraction f = [0.2,0.3,0.4,0.5,0.6,0.7,0.8] and extra‐axonal perpendicular diffusivity De,⊥ = [0.2,0.4,0.6,0.8,1, 1.2] μm2/ms. 100 Rician noise generalisations were computed with three different signal‐to‐noise ratio (SNR) values on the b = 0 signal (SNR = 50; 35; and 20). The response function, which should reflect the properties of a single fibre population (Tax, Jeurissen, Vos, Viergever, & Leemans, 2014), was set to have f = 0.3 and De,⊥ = 0.8 μm2/ms informed by values estimated from the group‐wise response function used in this study. These values are in the range of previously reported estimates of white matter in vivo (Fieremans, Jensen, & Helpern, 2011; Novikov et al., 2018).
2.2. Participants
We scanned a sample of typically developing children aged 8–18 years recruited as part of the Cardiff University Brain Research Imaging Centre (CUBRIC) Kids study (Genc et al., 2019; Raven et al., 2019). This study was approved by the School of Psychology ethics committee at Cardiff University. Participants and their parents/guardians were recruited via public outreach events. Written informed consent was provided by the primary caregiver of each child participating in the study, and adolescents aged 16–18 years additionally provided written consent. Children were excluded from the study if they had nonremovable metal implants, and if they reported history of a major head injury or epilepsy. All procedures were completed in accordance with the Declaration of Helsinki.
A total of 78 children between the ages of 8–18 years (Mean = 12.4, SD = 2.9 years) were included in the current study (45 female).
2.3. Diffusion magnetic resonance imaging
2.3.1. Image acquisition and pre‐processing
Diffusion MRI data were acquired on a 3.0T Siemens Connectom system with ultra‐strong (300 mT/m) gradients. Multi‐shell dMRI data were collected using the following parameters: TE/TR = 59/3000 ms; voxel size = 2 × 2 × 2 mm; b‐values = 0 (14 volumes, interleaved), 500 (30 directions), 1,200 (30 directions), 2,400 (60 directions), 4,000 (60 directions), and 6,000 (60 directions) s/mm2. The larger number of volumes across the higher diffusion weightings were to compensate for lower SNR and to capture the higher angular resolution present at higher b‐values (Tournier et al., 2013). Diffusion MRI data were acquired using electrostatic repulsion generalised across multiple shells (Caruyer, Lenglet, Sapiro, & Deriche, 2013). Data were acquired in an anterior–posterior (AP) phase‐encoding direction, with one additional PA volume. The total acquisition time (across four acquisition blocks) was 16 min and 14 s.
Pre‐processing of dMRI data involved steps largely in line with recommended steps for standard 3.0T systems, interfacing various tools such as FSL (Smith et al., 2004), MRtrix3 (Tournier et al., 2019), and ANTS (Avants et al., 2011). These steps included: denoising (Veraart, Fieremans, & Novikov, 2016), slicewise outlier detection (SOLID; Sairanen, Leemans, & Tax, 2018), and correction for drift (Vos et al., 2017); motion, eddy, and susceptibility‐induced distortions (Andersson, Skare, & Ashburner, 2003; Andersson & Sotiropoulos, 2016); Gibbs ringing artefact (Kellner, Dhital, Kiselev, & Reisert, 2016); bias field (Tustison et al., 2010); and gradient nonlinearities (Glasser et al., 2013; Rudrapatna, Parker, Roberts, & Jones, 2018). Root mean squared (RMS) displacement from eddy (Andersson & Sotiropoulos, 2016) was used as a summary measure of global head motion. Estimates of SNR were performed by taking the signal in the white matter and dividing this by the signal outside of the brain (for each b = 0 image). SNR estimates in the in vivo data were: mean = 48.02, SD = 7.46.
2.3.2. Image processing and analysis
To compare multiple sampling schemes, pre‐processed dMRI data were further processed and analysed separately for each sampling scheme in a common population‐template space, using a recommended framework (Raffelt et al., 2017). Firstly, data were intensity normalised and spatially upsampled to 1.3 mm3 isotropic voxel size to increase anatomical contrast and improve tractography (Dyrby et al., 2014). For single‐shell (ss) single‐tissue constrained spherical deconvolution (CSD), a fibre orientation distribution (FOD; Tournier, Calamante, & Connelly, 2007) was estimated in each voxel with maximal spherical harmonics order l max = 8 for shells with high angular resolution (b = 2,400, 4,000, 6,000 s/mm2 – 60 directions each) and l max = 6 for shells with lower angular resolution (b = 1,200 s/mm2 – 30 directions). Multi‐shell (ms) multi‐tissue CSD was performed using a separate framework (Dhollander et al., 2016; Jeurissen et al., 2014). Following FOD estimation, we derived a population template using all diffusion volumes (msall), and subsequently registered subject‐specific and sampling‐scheme‐specific FOD maps to this template (Figure S1). We then computed an apparent fibre density (AFD) map containing fibre‐specific AFD along each fixel for each subject (Raffelt et al., 2017).
In order to estimate AFD along various commonly investigated white matter fibre pathways, white matter tract segmentation was performed. We applied the automated TractSeg technique (Wasserthal, Neher, Hirjak, & Maier‐Hein, 2019; Wasserthal, Neher, & Maier‐Hein, 2018) in population template space, as this technique provides a balance between manual dissection and atlas‐based tracking approaches. Of the existing library of 72 tracts, we chose to delineate 38 commonly investigated fibre pathways bilaterally for the left (L) and right (R) hemisphere (Figure S2). This included: AF: arcuate fasciculus; ATR: anterior thalamic radiation; CA: anterior commissure; CC: corpus callosum [1 = rostrum, 2 = genu, 3 = rostral body, 4 = anterior midbody, 5 = posterior midbody; 6 = isthmus, 7 = splenium]; CG = cingulum; CST: corticospinal tract; FX: fornix; ICP: inferior cerebellar peduncle; IFOF: inferior fronto‐occipital fasciculus; ILF: inferior longitudinal fasciculus; MCP: middle cerebellar peduncle; MLF: middle longitudinal fasciculus; OR: optic radiation; superior longitudinal fasciculus: SLF [I, II, III]; and UF: uncinate fasciculus. Each tractography map was converted to a fixel map to segment fixels corresponding to streamlines, and AFD was computed within each tract‐specific fixel map for further statistical analysis.
2.4. Statistical analyses
2.4.1. Impact of b‐value sampling scheme
Statistical analyses were performed within R (v3.4.3) and visualisations were carried out in RStudio (v1.2.1335). The coefficient of determination (R 2) was computed to summarise the proportion of variance explained by age for each sampling‐scheme in each tract. Linear models were computed, whereby AFD in each tract was entered as the dependent variable, age was entered as the independent variable, and sex and RMS displacement were set as nuisance variables. To compare sampling schemes in terms of their relationship with age, the difference in R 2 was bootstrapped with 10,000 samples to compute 95% bias corrected accelerated (BCa) confidence intervals.
Hierarchical clustering was performed to discern clusters of sensitivity to age‐relationships across various combinations of b‐value sampling schemes and white matter tracts. These results were visualised as a heatmap with hierarchical clustering using the “gplots” package (Warnes et al., 2015) using Euclidean distance and complete agglomeration for clustering. To account for family‐wise error (FWE) we made use of a strict Bonferroni correction by adjusting our p‐value threshold by the 152 comparisons (38 tracts × 4 sampling schemes). As a result, our statistical significance was defined as p < 3.3e‐4.
2.4.2. Whole‐brain fixel‐based analysis
Separate statistical analyses were performed for each single‐shell sampling scheme (b = 1,200; 2,400; 4,000; 6,000 s/mm2) using connectivity‐based fixel enhancement (CFE), which provides a permutation‐based, family‐wise error (FWE) corrected p‐value for every individual fixel in the template image (Raffelt et al., 2015). For each sampling scheme, we tested the relationship between AFD and age, covarying for sex. For these whole‐brain analyses, statistical significance was defined as p FWE < .05. Statistically significant fixels were converted into binary fixel maps, and an intersection mask was computed to quantify the proportion of significant fixels overlapping between sampling schemes.
3. RESULTS
3.1. Simulations
The results of the simulations for AFD across various fibre geometries and sampling schemes is summarised in Figure 2. Compared to the highest single shell acquisition (ss6000), we observe a statistically significant three‐way interaction between De,⊥, f, and sampling‐scheme for ss1200: β [95% CI] = .80 [.44, 1.2]; ss2400: β [95% CI] = .55 [.19, .91]; msall: β [95% CI] = .83 [.47, 1.2]. These observed differences are visually reflected by a greater dependency of AFD and f on simulated De,⊥ as a result of the discrepancy with the response function.
Figure 2.
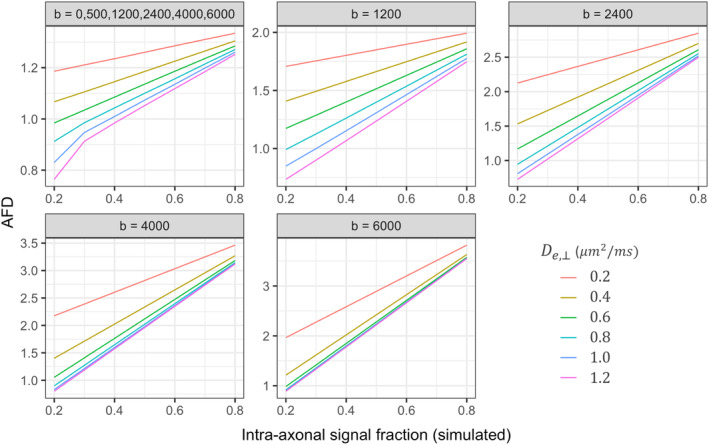
AFD for simulated fibre geometries across five sampling schemes. Variations to simulated intra‐axonal signal fraction and perpendicular diffusivity of the extra‐axonal space (De,⊥) were tested to compare AFD across multiple fibre geometries. Sampling schemes reflect the chosen b‐values, in s/mm2
When considering the full multi‐shell acquisition (msall) there are multiple degenerate scenarios whereby different combinations of f and De,⊥ could result in the same AFD, compared with high b‐value shells (i.e., ss4000 or ss6000). From the simulated scenarios for example, if AFD (msall) = 1.2, it can be seen that there are at least six combinations of f and De,⊥resulting in this value (Figure 2). Whereas a change in AFD computed from the highest b‐value shell could more directly reflect a change in the underlying f, reducing the potentially confounding effect of discrepancies with the response function.
The addition of noise had negligible effects on these relationships (Figure S3). However, we observed that with decreasing SNR (greater noise), the estimated AFD was more variable.
3.2. In vivo developmental data
3.2.1. Impact of b‐value sampling scheme
In order to assess the impact of b‐value sampling‐schemes on tract‐specific age relationships, we visualise our data as a heatmap (Figure 3; S4). The coefficient of determination (R 2) derived from the linear model for each tract is organised into hierarchical clusters with branching dendrograms.
Figure 3.
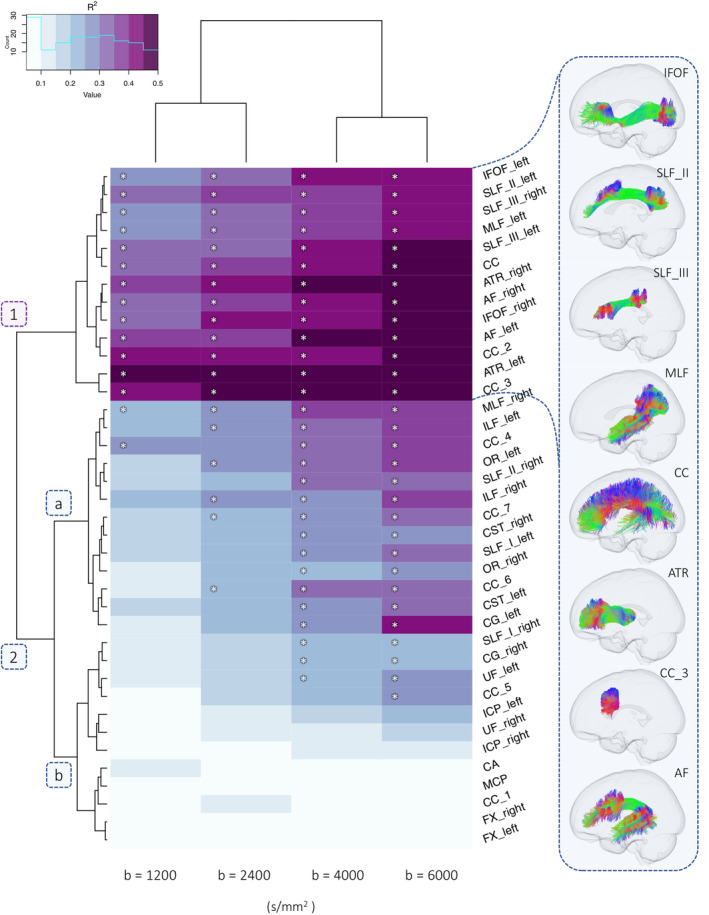
Dendrogram heatmap highlighting clusters of tracts which differentially describe age‐related differences in apparent fibre density (AFD) across various single‐shell b‐value sampling schemes. Heatmap colour intensity reflects range of R 2 values derived from a linear model including age, sex, and RMS displacement. Significant age‐effects (p < 3.3e‐4) are annotated with an asterisk (*). A depiction of several fibre pathways in one cluster is presented on the right
3.2.2. Single‐shell single‐tissue FBA
We observe two main clusters of single‐shell b‐value sampling‐schemes: the first including low and moderate diffusion‐weightings (b = 1,200; 2,400 s/mm2); and the second including high diffusion‐weightings (b = 4,000; 6,000 s/mm2). Secondly, two tract‐specific hierarchical clusters are observed, represented by branching dendrograms (Figure 3: clusters 1 and 2a,b). Sensitivity to age relationships was improved at high diffusion‐weightings (Table 1), whereby AFD exhibited a significantly stronger relationship with age at ss6000 compared with: ss4000 (6/38 tracts); ss2400 (25/38 tracts); and ss1200 (27/38 tracts).
Table 1.
Variance in AFD explained by age for each single‐shell sampling scheme across tracts
| Tracts | R 2 | R 2 difference [95% CI] | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| ss6000 | ss4000 | ss2400 | ss1200 | ss6000 > ss4000 | ss6000 > ss2400 | ss6000 > ss1200 | |||||
| AF | L | .50 | .49 | .39 | .35 | .01 | [−.11, .06] | .12 | [−.01, .18] | .15 | [.07, .23] |
| R | .46 | .43 | .37 | .33 | .02 | [−.08, .09] | .08 | [−.03, .13] | .13 | [.03, .21] | |
| ATR | L | .53 | .50 | .43 | .42 | .03 | [−.15, .11] | .11 | [−.05, .20] | .11 | [.02, .27] |
| R | .48 | .42 | .38 | .36 | .06 | [−.01, .13] | .10 | [.01, .21] | .12 | [−.05, .21] | |
| CA | .06 | .03 | .03 | .11 | .04 | [−.01, .12] | .03 | [−.06, .12] | −.05 | [−.17, .13] | |
| CC | Full | .44 | .39 | .32 | .31 | .04 | [−.07, .10] | .12 | [.03, .20] | .13 | [−.04, .21] |
| 1 | .05 | .02 | .02 | .05 | .03 | [−.04, .13] | .03 | [−.04, .17] | .01 | [−.12, .14] | |
| 2 | .45 | .43 | .38 | .38 | .03 | [−.13, .10] | .07 | [−.07, .17] | .07 | [−.04, .19] | |
| 3 | .48 | .46 | .43 | .42 | .02 | [−.03, .07] | .05 | [.01, .14] | .06 | [−.03, .14] | |
| 4 | .35 | .31 | .24 | .25 | .04 | [−.02, .08] | .11 | [.05, .21] | .10 | [−.03, .17] | |
| 5 | .22 | .16 | .11 | .06 | .06 | [.02, .10] | .12 | [.06, .19] | .16 | [.07, .23] | |
| 6 | .34 | .29 | .21 | .14 | .04 | [−.02, .08] | .13 | [.07, .20] | .19 | [.10, .31] | |
| 7 | .31 | .29 | .22 | .18 | .02 | [−.04, .08] | .09 | [.04, .15] | .13 | [.05, .20] | |
| CG | L | .38 | .27 | .18 | .10 | .11 | [−.03, .23] | .20 | [.06, .34] | .28 | [.11, .41] |
| R | .21 | .20 | .11 | .06 | .01 | [−.14, .10] | .10 | [−.02, .20] | .16 | [.05, .29] | |
| CST | L | .34 | .27 | .19 | .16 | .07 | [−.01, .15] | .15 | [.06, .21] | .18 | [.05, .27] |
| R | .29 | .28 | .20 | .15 | .01 | [−.08, .09] | .09 | [−.01, .17] | .14 | [.05, .26] | |
| FX | L | .06 | .03 | .01 | .01 | .02 | [−.04, .10] | .04 | [−.02, .12] | .05 | [−.01, .16] |
| R | .05 | .02 | .01 | .01 | .03 | [−.04, .10] | .05 | [−.04, .16] | .03 | [−.12, .18] | |
| ICP | L | .21 | .18 | .11 | .04 | .03 | [−.01, .14] | .11 | [.02, .23] | .17 | [.02, .31] |
| R | .11 | .11 | .07 | .08 | −.01 | [−.07, .07] | .03 | [−.07, .14] | .03 | [−.10, .16] | |
| IFOF | L | .44 | .40 | .34 | .29 | .03 | [−.02, .13] | .10 | [.01, .18] | .15 | [.09, .26] |
| R | .46 | .42 | .40 | .33 | .04 | [−.02, .12] | .06 | [−.01, .14] | .12 | [.02, .22] | |
| ILF | L | .39 | .34 | .27 | .22 | .05 | [−.02, .16] | .13 | [.05, .22] | .18 | [.10, .27] |
| R | .35 | .26 | .24 | .21 | .09 | [.01, .19] | .10 | [.04, .24] | .14 | [.05, .25] | |
| MCP | .07 | .06 | .05 | .08 | .01 | [−.03, .05] | .02 | [−.07, .10] | −.02 | [−.13, .15] | |
| MLF | L | .43 | .39 | .30 | .26 | .04 | [.01, .09] | .13 | [.06, .17] | .17 | [.10, .24] |
| R | .39 | .34 | .28 | .20 | .05 | [−.04, .09] | .11 | [.02, .18] | .19 | [.07, .25] | |
| OR | L | .36 | .30 | .25 | .18 | .05 | [.01, .13] | .11 | [.05, .21] | .17 | [.10, .28] |
| R | .28 | .25 | .19 | .13 | .03 | [−.04, .10] | .09 | [.02, .17] | .15 | [.05, .30] | |
| SLF_III | L | .47 | .44 | .33 | .30 | .04 | [.01, .08] | .14 | [.08, .19] | .18 | [.11, .26] |
| R | .41 | .38 | .31 | .28 | .04 | [−.09, .10] | .10 | [.01, .18] | .13 | [.01, .24] | |
| SLF_II | L | .41 | .40 | .32 | .29 | .01 | [−.04, .06] | .09 | [.02, .14] | .12 | [.06, .20] |
| R | .31 | .29 | .21 | .17 | .02 | [−.05, .05] | .10 | [.04, .15] | .13 | [.07, .22] | |
| SLF_I | L | .29 | .24 | .19 | .15 | .05 | [.01, .11] | .10 | [.05, .15] | .14 | [.05, .22] |
| R | .22 | .20 | .15 | .08 | .02 | [−.03, .06] | .07 | [.02, .13] | .14 | [.06, .24] | |
| UF | L | .27 | .23 | .11 | .10 | .04 | [−.05, .16] | .16 | [.07, .27] | .16 | [.03, .28] |
| R | .17 | .09 | .04 | .04 | .08 | [−.01, .21] | .13 | [.03, .26] | .13 | [.02, .32] | |
Note: R 2 represents the multiple coefficient of determination computed using a linear model for each tract, with age, sex and motion as predictors. Difference indicates difference between R 2 coefficients. Square brackets show 95% bias corrected accelerated (BCa) confidence intervals computed with 10,000 bootstrapped samples. Bold = differences in R 2 where 0 was not captured by the confidence intervals. Abbreviations: AF, arcuate fasciculus; ATR, anterior thalamic radiation; CA, anterior commissure; CC, corpus callosum [1 = rostrum, 2 = genu, 3 = rostral body, 4 = anterior midbody, 5 = posterior midbody; 6 = isthmus, 7 = splenium]; CG = cingulum; CST, corticospinal tract; FX, fornix; ICP, inferior cerebellar peduncle; IFOF, inferior fronto‐occipital fasciculus; ILF, inferior longitudinal fasciculus; MCP, middle cerebellar peduncle; MLF, middle longitudinal fasciculus; OR, optic radiation; superior longitudinal fasciculus: SLF [I, II, III]; UF, uncinate fasciculus.
The first tract cluster is composed of a sub‐cluster of regions where a high proportion of age‐related variance is described across all diffusion weightings (median R 2 = .40). The first sub‐cluster (Figure 3: cluster 1) includes several association tracts (left MLF, bilateral IFOF, left SLF II, bilateral SLF III, bilateral ATR, bilateral AF) and commissural tracts (corpus callosum: full extent, genu, rostral body). Significant age‐relationships are observed for all of the sampling schemes (b = 1,200; 2,400; 4,000; 6,000 s/mm2), with an increase in the estimated R 2 when going to higher diffusion weightings (Figure 4). The proportion of variance explained for the high diffusion‐weightings (b = 4,000 and 6,000 s/mm2) ranged from 38% to 53% (Table 1). Despite the consistent sensitivity to age‐related development in this tract cluster, a greater b‐value dependence on these relationships was observed when moving from low to high b‐values, particularly for association tracts such as bilateral SLF III, left SLF I, left IFOF and left MLF.
Figure 4.
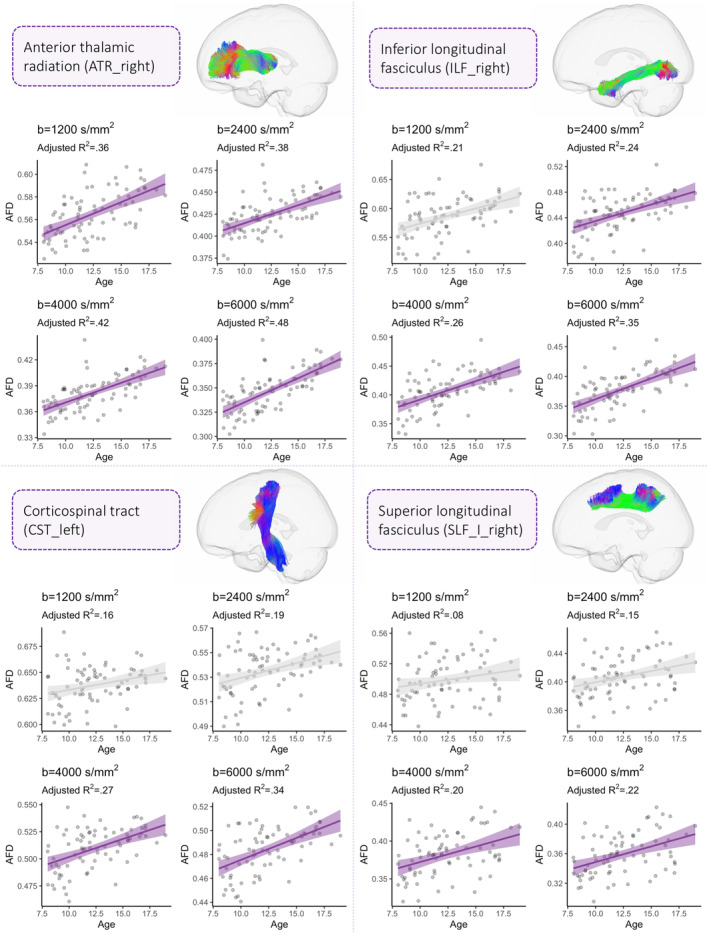
The relationship between AFD and age across four regions including: the right anterior thalamic radiation (ATR_right), inferior longitudinal fasciculus (ILF_right), corticospinal tract (CST_left), and superior longitudinal fasciculus I (SLF_I_right). Each region is representative of individual tract clusters where a progressive increase in the coefficient of determination (R 2) is observed when moving from low to high diffusion‐weightings. Sampling schemes whereby AFD was significantly associated with age are coloured in purple
The second tract cluster is composed of a sub‐cluster (Figure 3: 2a) of association tracts (left SLF_I, right SLF_II, bilateral ILF, right MLF, left CG, bilateral OR), projection tracts (bilateral CST), and commissural tracts (corpus callosum: anterior midbody, isthmus). In this sub‐cluster, significant age‐relationships are predominantly observed at high diffusion‐weightings where the proportion of variance ranged from 24% to 39%, compared with at low‐to‐moderate diffusion‐weightings (10–28%). The second sub‐cluster (Figure 3: 2b) includes cerebellar tracts (MCP, bilateral ICP), rostrum of the corpus callosum, bilateral fornix, right SLF_I and bilateral UF. This represented a sub‐cluster of tracts which captured little‐to‐no variation across development across moderate‐low b‐values (1–15%).
3.2.3. Multi‐shell multi‐tissue FBA
Consistent with the single‐shell single‐tissue results, sensitivity to age relationships was improved at high diffusion‐weightings for multi‐shell analyses (Table S1). We observed two main clusters of multi‐shell b‐value sampling schemes; the first including multiple combinations of low, moderate, and high b‐value sampling schemes, and the second including various combinations of high b‐value sampling schemes (Figure S5). In addition, we observed two main tract‐clusters consistent with the single‐tissue results: the first including various left‐lateralised association tracts and corpus callosum projections; and the second including predominantly cerebellar tracts, projection tracts (CST) and association tracts (including right SLF_II, SLF_I, ILF, CG, and OR). Overall, we observed a general reduction in the proportion of detectable age‐related variance when adding multiple shells for AFD estimation (Figure S5) across various tracts.
3.2.4. Whole brain fixel‐based analysis
In order to evaluate the sensitivity of FBA to age‐related microstructural development across sampling‐schemes, we performed four separate statistical analyses. For each single‐shell sampling scheme (b = 1,200; 2,400; 4,000; 6,000 s/mm2) we tested the relationship between age and AFD using the CFE method (Raffelt et al., 2015).
FBA revealed a significantly positive relationship between AFD and age across all b‐values (p FWE < .05). No significant age effects were observed in the opposite direction (p FWE > .05). We observed a general decrease in the number of significant fixels (n sig) when moving from high to low b‐values (ss6000: n sig = 13,382; ss4000: n sig = 10,070; ss2400: n sig = 7,283; ss1200: n sig = 5,506). In terms of anatomical overlap between results, 58% of significant fixels overlapped between ss6000 and ss4000, 43% of significant fixels overlapped between ss6000 and ss2400; and 20% of significant fixels overlapped between ss6000 and ss1200. Visualisations of significant and overlapping fixels across diffusion‐weightings are depicted in Figure 5. The core regions overlapping across all sampling schemes include the body and splenium of the corpus callosum, left IFOF, left ATR, left SLF, and right CST.
Figure 5.
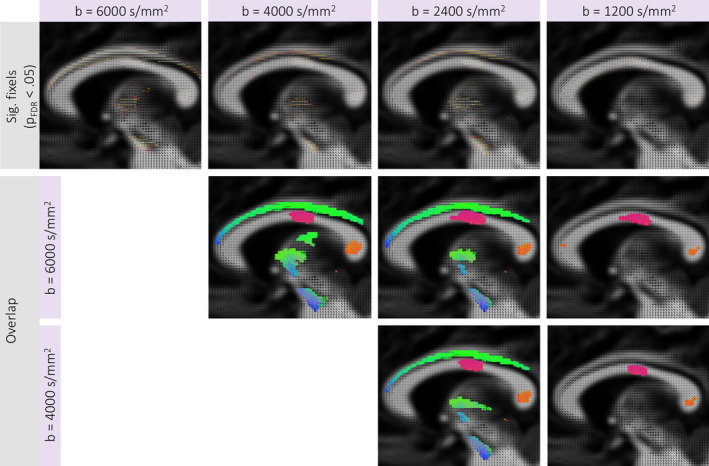
Fixel‐based analysis results. Top row displays fixels exhibiting a significantly positive relationship between age and AFD for each b‐value sampling scheme (p FWE < .05). The second (ss6000 vs. ss4000; ss6000 vs. ss2400; ss6000 vs. ss1200) (ss4000 vs. ss2400; ss4000 vs. ss1200) and third (ss vs. ss; ss vs. ss)(ss4000 vs. ss2400) rows display maps of the tracts traversing overlapping fixels between separate FBA results. Results are shown on a representative sagittal slice
4. DISCUSSION
In this study we demonstrate a b‐value dependence on estimates of apparent fibre density. Our results highlight that AFD more prominently reflects age‐related white matter development at high b‐values.
4.1. Simulations
The simulations for multiple sampling schemes revealed an improved correspondence between estimated AFD and the underlying intra‐axonal fibre properties when using high b‐value shells (b = 4,000 or b = 6,000 s/mm2). When moving to lower b‐values, or including the complete set of multi‐shell data, we observed a larger dependency of AFD on extra‐axonal perpendicular diffusivity. This could suggest that any changes in the true underlying fibre density could be camouflaged by concomitant changes in perpendicular diffusivity, whereby a simultaneous reduction of the intra‐axonal volume fraction and De,⊥ could result in the AFD remaining the same.
AFD is hypothesised to be proportional to the intra‐axonal signal fraction of a fibre population (Raffelt et al., 2012). With increasing b‐value, the intra‐ and extra‐axonal signal is differentially attenuated, leading to greater signal contribution from the intra‐axonal space (Tournier et al., 2013). Therefore, an increase in AFD can suggest alterations to axonal properties, such as axon count, packing density, and diameter (Raffelt et al., 2017). However, our results suggest that AFD is dependent on the extra‐axonal signal when including lower b‐values, as the mismatch between estimated AFD and simulated intra‐axonal signal fraction across varying De,⊥ is exaggerated.
As such, a change in AFD estimated at high diffusion‐weightings (in this case b = 4,000 or 6,000 s/mm2) could more directly reflect a change in the underlying axon density compared with lower b‐value shells or multi‐shell acquisitions, reducing the potential confounding effect of discrepancies with the response function.
4.2. In vivo developmental data
When considering in vivo developmental data, the dependence of b‐value on estimates of AFD was reflected by improved sensitivity to age relationships. Several association tracts consistently described age‐related differences in AFD across moderate to high diffusion‐weightings, including the left MLF, bilateral IFOF, left SLF II, bilateral SLF III, bilateral ATR, bilateral AF, and anterior segments of the corpus callosum. These regions, particularly the corpus callosum, arcuate and superior longitudinal fasciculus, appear to be sensitive to age‐related differences in microstructure regardless of dMRI acquisition scheme or analysis technique (Genc, Smith, et al., 2018; Ladouceur, Peper, Crone, & Dahl, 2012; Lebel & Beaulieu, 2011; Sawiak et al., 2018).
A group of left‐lateralised association tracts (e.g., left CG, MLF, OR, SLF_III, SLF_I, IFOF) better described age‐related variance in AFD when comparing the highest b‐value (b = 6,000 s/mm2) with high to moderate b‐values (b = 4,000 or 2,400 s/mm2). Left‐lateralisation of language has been well documented (Catani, Jones, & ffytche, 2005) and related to microstructure (Lebel & Beaulieu, 2009). The microstructure of lateralised association tracts is likely linked with the ongoing development of complex cognitive processes throughout childhood and adolescence (Blakemore & Choudhury, 2006; Jung & Haier, 2007). Our results suggest that lateralised association tracts linked with language and cognitive development are better characterised at high b‐values. This is likely due to improved sensitivity and specificity to axonal microstructure in the branching endpoints of these tracts integrating such higher order functions across fronto‐parietal, fronto‐occipital, and occipito‐temporal pathways. Future work should focus on investigating subject‐specific branching endpoints of these tracts, to assess individual variation in microstructure.
One key observation was that a higher proportion of age‐related variance was observed in the single‐tissue analyses compared with the multi‐tissue analyses. A decrease in discriminative power of age‐related development was observed across a number of multi‐shell configurations, more heavily weighted towards those which included low‐to‐moderate b‐values. It is possible that single‐shell analyses at higher b‐values may better isolate the true effect of changing intra‐axonal properties, and not clutter it with mismatches of the response function and/or other effects in the extra‐axonal space. Future work comparing the current approach with emerging methods such as single‐shell three‐tissue CSD (Aerts, Dhollander, & Marinazzo, 2019; Dhollander, Mito, Raffelt, & Connelly, 2019) and simultaneous voxel‐wise estimation of the response function and FOD (Jespersen et al., 2007) are warranted to explore this further.
The results of the whole‐brain FBA revealed a b‐value dependence on age‐related differences in AFD. Notably, more widespread associations with age were observed at high diffusion‐weightings, implicating a number of regions which were not found using other sampling‐schemes. This b‐value dependence suggests that whilst some core regions such as the body and splenium of the corpus callosum are clearly exhibiting strong age‐related development across all sampling schemes, a degree of anatomical sensitivity and specificity is lost at lower diffusion‐weightings. This is not to say that studies performing FBA with low‐to‐moderate b‐values will completely lose sensitivity to age‐related effects or clinical group differences. However, in conditions with subtle differences in underlying neurobiology or microstructure, going to higher b‐values may improve the characterisation of AFD and thus improve the detectability of clinically significant group differences.
Overall, AFD derived from high b‐values (b = 4,000 or 6,000 s/mm2) best modelled age‐relationships for the majority of white matter tracts tested. These results, combined with the simulations, suggest that axonal properties (such as axon density) dominate age‐related variance in AFD at high b‐values, whereas extra‐axonal signal contamination at decreasing diffusion‐weightings incrementally suppress this effect.
4.3. Implications
Our results bear implications for fixel‐based analysis applications using retrospectively collected dMRI data which may not be optimal for the estimation of AFD. The biological interpretation of group differences in AFD should be tailored to the acquisition scheme used. Relative differences in AFD at high b‐values could relate to the true underlying axon density; at moderate b‐values could relate to overall white matter fibre density; and at low b‐values could relate to white matter fibre density including potential extra‐axonal signal contamination.
Although we have demonstrated a clear b‐value dependence on developmental patterns of AFD, it is important to note that the in vivo results at high diffusion‐weightings are specific to the ultra‐strong gradient system used here, resulting in a higher SNR compared with what could be a achieved on a standard MR system. Promisingly, our simulation results suggest that the effect of b‐value and discrepancy with the response function dominates the effect of noise (Figure S3), even at a lower SNR which closely matched our in vivo data (SNR = 50). Therefore, we expect that our observations at high b‐values may be reproducible on a standard 3.0T system. As strong gradient systems become increasingly available, the practicalities of acquiring such high quality dMRI data at higher b‐values is becoming less cumbersome (Chamberland, Tax, & Jones, 2018; McKinnon & Jensen, 2019; Moss, McKinnon, Glenn, Helpern, & Jensen, 2019).
Whilst in this study we have used a developmental population of children and adolescents as an exemplar of a b‐value dependence on estimates of AFD, these findings can be applied more broadly and bear implications for a range of group studies (e.g., clinical groups or ageing adults).
4.4. Limitations and future directions
One limitation of the current study is that we have no ground truth on the development of axonal density over childhood and adolescence. Therefore, our interpretations of improved intra‐axonal signal sensitivity rests on age‐relationships investigated here, which has also been used previously (Maximov, Alnæs, & Westlye, 2019; Pines et al., 2019). Whilst we have attempted to understand how AFD can vary across multiple simulated fibre geometries, we do not know how the underlying fibre properties (such as axon diameter) vary with age. Despite this consideration, a recent study of histological validation suggests that AFD is a reliable marker of axonal density in the presence of axonal degeneration (Rojas‐Vitea et al., 2019). This is a promising indicator of the neurobiological properties proportional to AFD. Future work should adopt multi‐dimensional approaches to extract meaningful components (Chamberland et al., 2019), enhance data quality (Alexander et al., 2017) and harmonise existing data (Maximov et al., 2019; Tax et al., 2019).
5. CONCLUSION
We summarise our findings with three main conclusions: (a) the correspondence between apparent fibre density and simulated intra‐axonal signal fraction is improved with high b‐value shells; and (b) AFD better reflects age‐related differences in axonal microstructure with increasing b‐value (b = 4,000 or 6,000 s/mm2) over childhood and adolescence; and (c) these relationships differ across the brain, with a greater b‐value dependence in association tracts and posterior projections of the corpus callosum. Together, our results suggest that axonal properties dominate the variance in AFD at high b‐values.
CONFLICT OF INTEREST
All authors disclose no real or potential conflicts of interest.
Supporting information
Figure S1 Example of preprocessing and analysis outputs for representative participants aged 8, 13, and 18 years old: A) raw dMRI data; B) preprocessed dMRI data; C) fibre orientation distributions (FODs) pre‐ and post‐registration to the population‐based template.
Figure S2: Representative images of tract bundles extracted for statistical analysis, generated using TractSeg. The left view of the tract is presented in each case. Tracts are coloured by the direction of streamlines (red: left–right; green: anterior–posterior; blue: inferior–superior).
Figure S3: AFD for simulated fibre geometries across five sampling schemes with noise. Variations to simulated intra‐axonal signal fraction and perpendicular diffusivity of the extra‐axonal space (De,⊥) were tested to compare AFD across multiple fibre geometries. Simulations were performed with noise (SNR = 50 35 and 25) with 100 Rician noise generalisations (error bars denote mean ± 2SD). Sampling schemes reflect the chosen b‐values, in s/mm2. With lower SNR (greater noise), the estimated AFD was more variable indicated by a larger spread of values, particularly at smaller intra‐axonal signal fractions.
Figure S4: Dendrogram heatmap highlighting clusters of tracts which differentially describe age‐related differences in apparent fibre density (AFD) across various single‐shell b‐value sampling schemes. Heatmap colour intensity reflects range of R 2 values derived from a linear model including age and sex. A depiction of several fibre pathways in one cluster is presented on the right.
Figure S5: Dendrogram heatmap highlighting clusters of tracts which differentially describe age‐related differences in apparent fibre density (AFD) across various multi‐shell b‐value sampling schemes. Heatmap colour intensity reflects range of R 2 values derived from a linear model including age and sex. Note: datasets with two diffusion weightings (including the b = 0) were processed using the multi‐shell multi‐tissue FBA framework, thus resulting in separate but comparable results to the single‐shell single‐tissue FBA (presented in Figure 3).
Appendix S1: Supplementary Materials
ACKNOWLEDGMENTS
We are grateful to the participants and their families for their participation in this study. We would like to thank Umesh Rudrapatna, John Evans, Alison Cooper, Peter Hobden, Daniel Burley, and Isobel Ward (CUBRIC) for their support with data acquisition. We also thank Gareth Ball and Charles Malpas for statistical advice. These data were acquired at the UK National Facility for in vivo MR Imaging of Human Tissue Microstructure funded by the EPSRC (grant EP/M029778/1), and The Wolfson Foundation. DKJ is supported by a Wellcome Trust Investigator Award (096646/Z/11/Z) and a Wellcome Trust Strategic Award (104943/Z/14/Z). SG was supported by an International Society for Magnetic Resonance in Medicine (ISMRM) research exchange grant. CMWT was supported by a Rubicon grant (680‐50‐1527) from the Netherlands Organisation for Scientific Research (NWO). ER was supported by a Marshall Sherfield fellowship. MC was supported by the Postdoctoral Fellowships Program from the Natural Sciences and Engineering Research Council of Canada (PDF‐502385‐2017).
Genc S, Tax CMW, Raven EP, Chamberland M, Parker GD, Jones DK. Impact of b‐value on estimates of apparent fibre density. Hum Brain Mapp. 2020;41:2583–2595. 10.1002/hbm.24964
Funding information Postdoctoral Fellowships Program from the Natural Sciences and Engineering Research Council of Canada, Grant/Award Number: PDF‐502385‐2017; Marshall Sherfield; Netherlands Organisation for Scientific Research; International Society for Magnetic Resonance in Medicine; Wellcome Trust Strategic Award, Grant/Award Number: 104943/Z/14/Z; Wellcome Trust Investigator Award, Grant/Award Number: 096646/Z/11/Z; The Wolfson Foundation; EPSRC, Grant/Award Number: EP/M029778/1
DATA AVAILABILITY STATEMENT
The data that support the findings of this study are available on request from the corresponding author. The data are not publicly available due to privacy or ethical restrictions.
REFERENCES
- Aerts, H. , Dhollander, T. , & Marinazzo, D. (2019). Evaluating the performance of 3‐tissue constrained spherical deconvolution pipelines for within‐tumor tractography. bioRxiv, 629873 10.1101/629873 [DOI] [Google Scholar]
- Alexander, D. C. , Zikic, D. , Ghosh, A. , Tanno, R. , Wottschel, V. , Zhang, J. , … Criminisi, A. (2017). Image quality transfer and applications in diffusion MRI. NeuroImage, 152, 283–298. [DOI] [PubMed] [Google Scholar]
- Andersson, J. L. , Skare, S. , & Ashburner, J. (2003). How to correct susceptibility distortions in spin‐echo echo‐planar images: Application to diffusion tensor imaging. NeuroImage, 20, 870–888. [DOI] [PubMed] [Google Scholar]
- Andersson, J. L. R. , & Sotiropoulos, S. N. (2016). An integrated approach to correction for off‐resonance effects and subject movement in diffusion MR imaging. NeuroImage, 125, 1063–1078. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Avants, B. B. , Tustison, N. J. , Song, G. , Cook, P. A. , Klein, A. , & Gee, J. C. (2011). A reproducible evaluation of ANTs similarity metric performance in brain image registration. NeuroImage, 54, 2033–2044. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Barth, M. , Breuer, F. , Koopmans, P. J. , Norris, D. G. , & Poser, B. A. (2016). Simultaneous multislice (SMS) imaging techniques. Magnetic Resonance in Medicine, 75, 63–81. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Blakemore, S. J. , & Choudhury, S. (2006). Development of the adolescent brain: Implications for executive function and social cognition. Journal of Child Psychology and Psychiatry, and Allied Disciplines, 47, 296–312. [DOI] [PubMed] [Google Scholar]
- Caruyer, E. , Lenglet, C. , Sapiro, G. , & Deriche, R. (2013). Design of multishell sampling schemes with uniform coverage in diffusion MRI. Magnetic Resonance in Medicine, 69, 1534–1540. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Catani, M. , Jones, D. K. , & ffytche, D. H. (2005). Perisylvian language networks of the human brain. Annals of Neurology, 57, 8–16. [DOI] [PubMed] [Google Scholar]
- Chamberland, M. , Raven, E. P. , Genc, S. , Duffy, K. , Descoteaux, M. , Parker, G. D. , … Jones, D. K. (2019). Dimensionality reduction of diffusion MRI measures for improved tractometry of the human brain. NeuroImage, 200, 89–100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chamberland, M. , Tax, C. M. W. , & Jones, D. K. (2018). Meyer's loop tractography for image‐guided surgery depends on imaging protocol and hardware. Neuroimage: Clinical, 20, 458–465. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dell'Acqua, F. , Simmons, A. , Williams, S. C. , & Catani, M. (2013). Can spherical deconvolution provide more information than fiber orientations? Hindrance modulated orientational anisotropy, a true‐tract specific index to characterize white matter diffusion. Human Brain Mapping, 34, 2464–2483. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dell'Acqua, F. , & Tournier, J. D. (2019). Modelling white matter with spherical deconvolution: How and why? NMR in Biomedicine, 32, e3945. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dhollander, T. , Mito, R. , Raffelt, D. , & Connelly, A. Improved white matter response function estimation for 3‐tissue constrained spherical deconvolution. 0555. In 2019; Montreal, Canada.
- Dhollander, T. , Raffelt, D. , & Connelly, A. Unsupervised 3‐tissue response function estimation from single‐shell or multi‐shell diffusion MR data without a co‐registered T1 image. 2016.
- Dimond, D. , Schuetze, M. , Smith, R. E. , Dhollander, T. , Cho, I. , Vinette, S. , … Bray, S. (2019). Reduced white matter fiber density in autism spectrum disorder. Cerebral Cortex, 29, 1778–1788. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dyrby, T. B. , Lundell, H. , Burke, M. W. , Reislev, N. L. , Paulson, O. B. , Ptito, M. , & Siebner, H. R. (2014). Interpolation of diffusion weighted imaging datasets. NeuroImage, 103, 202–213. [DOI] [PubMed] [Google Scholar]
- Fieremans, E. , Jensen, J. H. , & Helpern, J. A. (2011). White matter characterization with diffusional kurtosis imaging. NeuroImage, 58, 177–188. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gajamange, S. , Raffelt, D. , Dhollander, T. , Lui, E. , van der Walt, A. , Kilpatrick, T. , … Kolbe, S. (2018). Fibre‐specific white matter changes in multiple sclerosis patients with optic neuritis. Neuroimage Clinical, 17, 60–68. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Genc, S. , Malpas, C. B. , Ball, G. , Silk, T. J. , & Seal, M. L. (2018). Age, sex, and puberty related development of the corpus callosum: A multi‐technique diffusion MRI study. Brain Structure & Function, 223, 2753–2765. [DOI] [PubMed] [Google Scholar]
- Genc, S. , Smith, R. E. , Malpas, C. B. , Anderson, V. , Nicholson, J. M. , Efron, D. , … Silk, T. J. (2018). Development of white matter fibre density and morphology over childhood: A longitudinal fixel‐based analysis. NeuroImage, 183, 666–676. [DOI] [PubMed] [Google Scholar]
- Genc, S. , Tax, C. M. , Raven, E. P. , Chamberland, M. , Parker, G. D. , & Jones, D.K. New insights into the development of white matter microstructure across childhood and adolescence from ultra‐strong gradients. 0381. In 2019; Montreal, Canada. p 0381.
- Glasser, M. F. , Sotiropoulos, S. N. , Wilson, J. A. , Coalson, T. S. , Fischl, B. , Andersson, J. L. , … Jenkinson, M. (2013). The minimal preprocessing pipelines for the human connectome project. NeuroImage, 80, 105–124. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jespersen, S. N. , Kroenke, C. D. , Ostergaard, L. , Ackerman, J. J. , & Yablonskiy, D. A. (2007). Modeling dendrite density from magnetic resonance diffusion measurements. NeuroImage, 34, 1473–1486. [DOI] [PubMed] [Google Scholar]
- Jeurissen, B. , Tournier, J. D. , Dhollander, T. , Connelly, A. , & Sijbers, J. (2014). Multi‐tissue constrained spherical deconvolution for improved analysis of multi‐shell diffusion MRI data. NeuroImage, 103, 411–426. [DOI] [PubMed] [Google Scholar]
- Jones, D. K. , Alexander, D. C. , Bowtell, R. , Cercignani, M. , Dell'Acqua, F. , McHugh, D. J. , … Tax, C. M. W. (2018). Microstructural imaging of the human brain with a 'super‐scanner’: 10 key advantages of ultra‐strong gradients for diffusion MRI. NeuroImage, 182, 8–38. [DOI] [PubMed] [Google Scholar]
- Jones, D. K. , Horsfield, M. A. , & Simmons, A. (1999). Optimal strategies for measuring diffusion in anisotropic systems by magnetic resonance imaging. Magnetic Resonance in Medicine, 42, 515–525. [PubMed] [Google Scholar]
- Jung, R. E. , & Haier, R. J. (2007). The Parieto‐frontal integration theory (P‐FIT) of intelligence: Converging neuroimaging evidence. The Behavioral and Brain Sciences, 30, 135–154 discussion 154‐87. [DOI] [PubMed] [Google Scholar]
- Kellner, E. , Dhital, B. , Kiselev, V. G. , & Reisert, M. (2016). Gibbs‐ringing artifact removal based on local subvoxel‐shifts. Magnetic Resonance in Medicine, 76, 1574–1581. [DOI] [PubMed] [Google Scholar]
- Kroenke, C. D. , Ackerman, J. J. H. , & Yablonskiy, D. A. (2004). On the nature of the NAA diffusion attenuated MR signal in the central nervous system. Magnetic Resonance in Medicine, 52, 1052–1059. [DOI] [PubMed] [Google Scholar]
- Kunz, N. , Zhang, H. , Vasung, L. , O'Brien, K. R. , Assaf, Y. , Lazeyras, F. , … Hüppi, P. S. (2014). Assessing white matter microstructure of the newborn with multi‐shell diffusion MRI and biophysical compartment models. NeuroImage, 96, 288–299. [DOI] [PubMed] [Google Scholar]
- Ladouceur, C. D. , Peper, J. S. , Crone, E. A. , & Dahl, R. E. (2012). White matter development in adolescence: The influence of puberty and implications for affective disorders. Developmental Cognitive Neuroscience, 2, 36–54. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Landman, B. A. , Farrell, J. A. D. , Jones, C. K. , Smith, S. A. , Prince, J. L. , & Mori, S. (2007). Effects of diffusion weighting schemes on the reproducibility of DTI‐derived fractional anisotropy, mean diffusivity, and principal eigenvector measurements at 1.5T. NeuroImage, 36, 1123–1138. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Le Bihan, D. , & Breton, E. (1985). In vivo magnetic resonance imaging of diffusion. Comptes Rendus Des Seances de l'Academie Des Sciences Serie, 2(301), 1109–1112. [Google Scholar]
- Lebel, C. , & Beaulieu, C. (2009). Lateralization of the arcuate fasciculus from childhood to adulthood and its relation to cognitive abilities in children. Human Brain Mapping, 30, 3563–3573. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lebel, C. , & Beaulieu, C. (2011). Longitudinal development of human brain wiring continues from childhood into adulthood. The Journal of Neuroscience: The Official Journal of the Society for Neuroscience, 31, 10937–10947. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lebel, C. , & Deoni, S. (2018). The development of brain white matter microstructure. NeuroImage, 182, 207–218. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Maximov, I. I. , Alnæs, D. , & Westlye, L. T. (2019). Towards an optimised processing pipeline for diffusion magnetic resonance imaging data: Effects of artefact corrections on diffusion metrics and their age associations in UKbiobank. Human Brain Mapping, 40(14), 4146–4162. [DOI] [PMC free article] [PubMed] [Google Scholar]
- McKinnon, E. T. , & Jensen, J. H. (2019). Measuring intra‐axonal T2 in white matter with direction‐averaged diffusion MRI. Magnetic Resonance in Medicine, 81, 2985–2994. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mito, R. , Raffelt, D. , Dhollander, T. , Vaughan, D. N. , Tournier, J. D. , Salvado, O. , … Connelly, A. (2018). Fibre‐specific white matter reductions in Alzheimer's disease and mild cognitive impairment. Brain, 141, 888–902. [DOI] [PubMed] [Google Scholar]
- Moss, H. , McKinnon, E. T. , Glenn, G. R. , Helpern, J. A. , & Jensen, J. H. (2019). Optimization of data acquisition and analysis for fiber ball imaging. NeuroImage, 200, 690–703. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Novikov, D. S. , Veraart, J. , Jelescu, I. O. , & Fieremans, E. (2018). Rotationally‐invariant mapping of scalar and orientational metrics of neuronal microstructure with diffusion MRI. NeuroImage, 174, 518–538. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pines, A. R. , Cieslak, M. , Baum, G. L. , Cook, P. A. , Adebimpe, A. , Davila, D. G. , … Satterthwaite, T. D. (2019). Advantages of multi‐shell diffusion models for studies of brain development in youth. bioRxiv, 611590 10.1101/611590 [DOI] [Google Scholar]
- Raffelt, D. , Tournier, J. D. , Rose, S. , Ridgway, G. R. , Henderson, R. , Crozier, S. , … Connelly, A. (2012). Apparent fibre density: A novel measure for the analysis of diffusion‐weighted magnetic resonance images. NeuroImage, 59, 3976–3994. [DOI] [PubMed] [Google Scholar]
- Raffelt, D. A. , Smith, R. E. , Ridgway, G. R. , Tournier, J. D. , Vaughan, D. N. , Rose, S. , … Connelly, A. (2015). Connectivity‐based fixel enhancement: Whole‐brain statistical analysis of diffusion MRI measures in the presence of crossing fibres. NeuroImage, 117, 40–55. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Raffelt, D. A. , Tournier, J. D. , Smith, R. E. , Vaughan, D. N. , Jackson, G. , Ridgway, G. R. , & Connelly, A. (2017). Investigating white matter fibre density and morphology using fixel‐based analysis. NeuroImage, 144, 58–73. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Raven, E. P. , Chamberland, M. , Genc, S. , Duffy, K. , Tax, C. M. , Parker, G. D. , …, Jones, D. K. Gradient profiles of myelin and microstructure metrics across the developing brain. 2618. In 2019; Montreal, Canada.
- Rojas‐Vitea, G. , Coronado‐Leijaa, R. , Narvaez‐Delgado, O. , Ramírez‐Manzanares, A. , Marroquín, J. L. , Noguez‐Imm, R. , … Conchaa, L. (2019). Histological validation of per‐bundle water diffusion metrics within a region of fiber crossing following axonal degeneration. Neuroimage, 201,116013. [DOI] [PubMed] [Google Scholar]
- Rudrapatna, S. , Parker, G. , Roberts, J. , & Jones, D. Can we correct for interactions between subject motion and gradient‐nonlinearity in diffusion MRI. 2018.
- Sairanen, V. , Leemans, A. , & Tax, C. M. W. (2018). Fast and accurate Slicewise OutLIer detection (SOLID) with informed model estimation for diffusion MRI data. NeuroImage, 181, 331–346. [DOI] [PubMed] [Google Scholar]
- Sawiak, S. J. , Shiba, Y. , Oikonomidis, L. , Windle, C. P. , Santangelo, A. M. , Grydeland, H. , … Roberts, A. C. (2018). Trajectories and milestones of cortical and subcortical development of the marmoset brain from infancy to adulthood. Cerebral Cortex, 28(12), 4440–4453. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Silk, T. J. , Genc, S. , Anderson, V. , Efron, D. , Hazell, P. , Nicholson, J. M. , … Sciberras, E. (2016). Developmental brain trajectories in children with ADHD and controls: A longitudinal neuroimaging study. BMC Psychiatry, 16, 59. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Smith, S. M. , Jenkinson, M. , Woolrich, M. W. , Beckmann, C. F. , Behrens, T. E. , Johansen‐Berg, H. , … Matthews, P. M. (2004). Advances in functional and structural MR image analysis and implementation as FSL. NeuroImage, 23(Suppl. 1), S208–S219. [DOI] [PubMed] [Google Scholar]
- Somerville, L. H. , Bookheimer, S. Y. , Buckner, R. L. , Burgess, G. C. , Curtiss, S. W. , Dapretto, M. , … Barch, D. M. (2018). The lifespan human connectome project in development: A large‐scale study of brain connectivity development in 5‐21 year olds. NeuroImage, 183, 456–468. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tax, C. M. W. , Grussu, F. , Kaden, E. , Ning, L. , Rudrapatna, U. , John Evans, C. , … Veraart, J. (2019). Cross‐scanner and cross‐protocol diffusion MRI data harmonisation: A benchmark database and evaluation of algorithms. NeuroImage, 195, 285–299. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tax, C. M. W. , Jeurissen, B. , Vos, S. B. , Viergever, M. A. , & Leemans, A. (2014). Recursive calibration of the fiber response function for spherical deconvolution of diffusion MRI data. NeuroImage, 86, 67–80. [DOI] [PubMed] [Google Scholar]
- Tournier, J. D. , Calamante, F. , & Connelly, A. (2007). Robust determination of the fibre orientation distribution in diffusion MRI: Non‐negativity constrained super‐resolved spherical deconvolution. NeuroImage, 35, 1459–1472. [DOI] [PubMed] [Google Scholar]
- Tournier, J. D. , Calamante, F. , & Connelly, A. (2013). Determination of the appropriate b value and number of gradient directions for high‐angular‐resolution diffusion‐weighted imaging. NMR in Biomedicine, 26, 1775–1786. [DOI] [PubMed] [Google Scholar]
- Tournier, J. D. , Mori, S. , & Leemans, A. (2011). Diffusion tensor imaging and beyond. Magnetic Resonance in Medicine, 65, 1532–1556. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tournier, J. D. , Smith, R. E. , Raffelt, D. A. , Tabbara, R. , Dhollander, T. , Pietsch, M. , … Connelly, A. (2019). MRtrix3: A fast, flexible and open software framework for medical image processing and visualisation. NeuroImage, 202, 116137. [DOI] [PubMed] [Google Scholar]
- Tustison, N. J. , Avants, B. B. , Cook, P. A. , Zheng, Y. , Egan, A. , Yushkevich, P. A. , & Gee, J. C. (2010). N4ITK: Improved N3 bias correction. IEEE Transactions on Medical Imaging, 29, 1310–1320. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Veraart, J. , Fieremans, E. , & Novikov, D. S. (2016). Diffusion MRI noise mapping using random matrix theory. Magnetic Resonance in Medicine, 76, 1582–1593. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vos, S. B. , Tax, C. M. , Luijten, P. R. , Ourselin, S. , Leemans, A. , & Froeling, M. (2017). The importance of correcting for signal drift in diffusion MRI. Magnetic Resonance in Medicine, 77, 285–299. [DOI] [PubMed] [Google Scholar]
- Warnes, G. R. , Bolker, B. , Bonebakker, L. , Gentleman, R. , Liaw, W. H. A. , Lumley, T. , … Venables, B. 2015. gplots: Various R Programming Tools for Plotting Data. Version R package version 2.17.0. https://www.scienceopen.com/document?vid=0e5d8e31‐1fe4‐492f‐a3d8‐8cd71b2b8ad9 [Google Scholar]
- Wasserthal, J. , Neher, P. , & Maier‐Hein, K. H. (2018). TractSeg – Fast and accurate white matter tract segmentation. NeuroImage, 183, 239–253. [DOI] [PubMed] [Google Scholar]
- Wasserthal, J. , Neher, P. F. , Hirjak, D. , & Maier‐Hein, K. H. (2019) Combined tract segmentation and orientation mapping for bundle‐specific tractography. arXiv [cs.CV], 1901.10271. [DOI] [PubMed]
- Zhang, H. , Schneider, T. , Wheeler‐Kingshott, C. A. , & Alexander, D. C. (2012). NODDI: Practical in vivo neurite orientation dispersion and density imaging of the human brain. NeuroImage, 61, 1000–1016. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Figure S1 Example of preprocessing and analysis outputs for representative participants aged 8, 13, and 18 years old: A) raw dMRI data; B) preprocessed dMRI data; C) fibre orientation distributions (FODs) pre‐ and post‐registration to the population‐based template.
Figure S2: Representative images of tract bundles extracted for statistical analysis, generated using TractSeg. The left view of the tract is presented in each case. Tracts are coloured by the direction of streamlines (red: left–right; green: anterior–posterior; blue: inferior–superior).
Figure S3: AFD for simulated fibre geometries across five sampling schemes with noise. Variations to simulated intra‐axonal signal fraction and perpendicular diffusivity of the extra‐axonal space (De,⊥) were tested to compare AFD across multiple fibre geometries. Simulations were performed with noise (SNR = 50 35 and 25) with 100 Rician noise generalisations (error bars denote mean ± 2SD). Sampling schemes reflect the chosen b‐values, in s/mm2. With lower SNR (greater noise), the estimated AFD was more variable indicated by a larger spread of values, particularly at smaller intra‐axonal signal fractions.
Figure S4: Dendrogram heatmap highlighting clusters of tracts which differentially describe age‐related differences in apparent fibre density (AFD) across various single‐shell b‐value sampling schemes. Heatmap colour intensity reflects range of R 2 values derived from a linear model including age and sex. A depiction of several fibre pathways in one cluster is presented on the right.
Figure S5: Dendrogram heatmap highlighting clusters of tracts which differentially describe age‐related differences in apparent fibre density (AFD) across various multi‐shell b‐value sampling schemes. Heatmap colour intensity reflects range of R 2 values derived from a linear model including age and sex. Note: datasets with two diffusion weightings (including the b = 0) were processed using the multi‐shell multi‐tissue FBA framework, thus resulting in separate but comparable results to the single‐shell single‐tissue FBA (presented in Figure 3).
Appendix S1: Supplementary Materials
Data Availability Statement
The data that support the findings of this study are available on request from the corresponding author. The data are not publicly available due to privacy or ethical restrictions.


