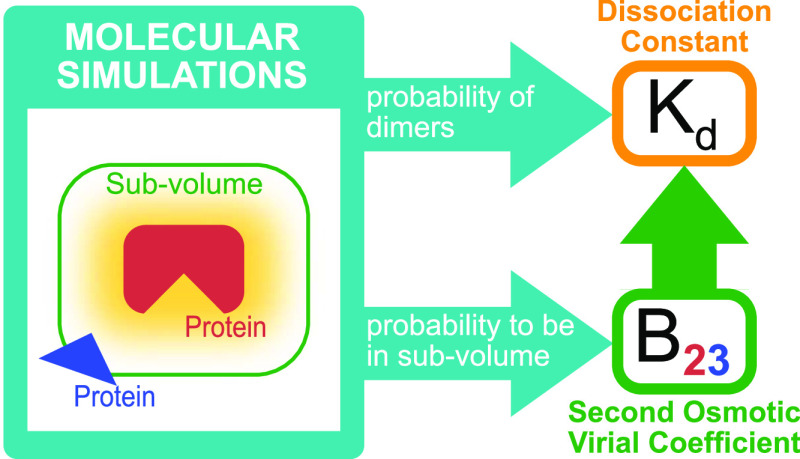
Abstract
Interactions among proteins, nucleic acids, and other macromolecules are essential for their biological functions and shape the physicochemcial properties of the crowded environments inside living cells. Binding interactions are commonly quantified by dissociation constants Kd, and both binding and nonbinding interactions are quantified by second osmotic virial coefficients B2. As a measure of nonspecific binding and stickiness, B2 is receiving renewed attention in the context of so-called liquid–liquid phase separation in protein and nucleic acid solutions. We show that Kd is fully determined by B2 and the fraction of the dimer observed in molecular simulations of two proteins in a box. We derive two methods to calculate B2. From molecular dynamics or Monte Carlo simulations using implicit solvents, we can determine B2 from insertion and removal energies by applying Bennett’s acceptance ratio (BAR) method or the (binless) weighted histogram analysis method (WHAM). From simulations using implicit or explicit solvents, one can estimate B2 from the probability that the two molecules are within a volume large enough to cover their range of interactions. We validate these methods for coarse-grained Monte Carlo simulations of three weakly binding proteins. Our estimates for Kd and B2 allow us to separate out the contributions of nonbinding interactions to B2. Comparison of calculated and measured values of Kd and B2 can be used to (re-)parameterize and improve molecular force fields by calibrating specific affinities, overall stickiness, and nonbinding interactions. The accuracy and efficiency of Kd and B2 calculations make them well suited for high-throughput studies of large interactomes.
1. Introduction
In biological cells, most protein, DNA, and RNA molecules have to bind to specific binding partners to perform their biological functions. These specific interactions compete with nonspecific interactions, and cells have evolved various mechanisms to minimize wasteful nonspecific binding.1,2 However, nonspecific interactions shape the physicochemical properties of the crowded environments inside cells.3 The quantification of binding affinities and interaction strengths of biological macromolecules is thus crucial for the understanding and modeling of cellular processes. In the following, we focus on protein–protein interactions, but all of our results are generally applicable to other specific and nonspecific binding interactions.
Experimentally, protein interactions are quantified by the dissociation constants Kd and the second osmotic virial coefficient Bij of protein species i and j. We follow the common convention and use B22 for self-interactions and B23 for cross-interactions. The dissociation constant Kd quantifies the amount of bound proteins and can be measured in isothermal titration calorimetry, surface plasmon resonance, or analytical ultracentrifugation experiments, for example.4 The interaction strength of pairs of proteins in binding and nonbinding configurations can be quantified by measuring the second osmotic virial coefficient Bij, which relates the microscopic protein interactions to the macroscopic osmotic pressure.5−7 Moreover, the second osmotic virial coefficient is related to solubility and used as a predictor for protein crystallization conditions.8,9 In experiments, Bij is measured by sedimentation10−12 and size-exclusion chromatography.8 Scattering experiments, such as static light scattering (SLS) and small-angle X-ray scattering (SAXS) experiments, can provide approximate estimates for Bij.13,14
Kd and Bij are crucial quantities to relate molecular simulations of interacting proteins to the experiment. Such comparisons become increasingly important as molecular simulations of crowded cell-like environments have become computationally feasible, even in full atomic detail.15,16 In simulations of strong binders, Kd is usually determined by calculating the binding free energy to specific binding interfaces.17 If binding interfaces are unknown, Kd values are often calculated from the ratio of bound and unbound populations,18 as recently applied to RNA–RNA binding.19 As we will discuss here, this approximation is accurate only for special cases. Bij can be estimated by integration over the configuration space,20−22 by Mayer sampling,23,24 from molecular simulations using radial distribution functions or potentials of mean force,25−28 and by simply counting all configurations in which proteins do not interact.29,30
Here, we show that Kd is fully determined by Bij and the fraction pb(V) of bound proteins estimated from molecular simulations of two proteins in a box with volume V, i.e.
| 1 |
Here NA is Avogadro’s constant. In the derivation of this equation, we do not make any assumptions about the interaction strength or about the degrees of freedom of proteins or the solvent. Thus, it is generally applicable and valid not only for coarse-grained simulations using implicit solvents but also for fully atomistic molecular dynamics simulations using explicit solvents. We present two different routes to calculate Bij and thus Kd.
For simulations using implicit solvents, we can apply protein insertion and removal moves to estimate the free energy that corresponds to the two-particle partition function determining Bij. The insertion ensemble can be generated with any Monte Carlo or molecular dynamics code to sample from the canonical ensemble without modification. We estimate the partition function by combining the insertion and removal ensemble using either Bennett’s acceptance ratio (BAR) method31 or the binless weighted histogram analysis method (WHAM).32−34 In contrast to the Mayer sampling method,23,24 which uses molecular Monte Carlo integration to calculate virial coefficients even of higher orders, here, we use exactly the same simulation system for the calculation of Bij as we use to sample from the canonical ensemble.
For simulations using either implicit or explicit solvents, Bij can be calculated accurately by estimating the probability that the two proteins are outside of their interaction range.29 We present mathematically simple expressions for Bij and Kd in terms of this probability, which provide insights into their physical interpretations complementary to more common formulations based on radial distribution functions or potentials of mean force.
We quantify the interactions of the two proteins when they are not bound using Kd and Bij. Previously, theoretical models for excluded volumes have been used to extract nonbinding interactions from experimentally measured Bij values.35 Here, we use the fact that the contributions of bound configurations to Bij are completely determined by Kd and show that the remaining contributions have a simple and clear interpretation. Moreover, we propose that these contributions of nonbinding interactions can be estimated in experiments.
The article is organized as follows. In Section 2, we derive expressions to calculate the dissociation constant and the second osmotic virial coefficient from simulations. We present the details of our methods in Section 3 and a validation of our methods and results for three weekly binding proteins using coarse-grained simulations in Section 4. We end with conclusions in Section 5.
2. Theory
For simulations of two proteins in a box, we show that the dissociation constant Kd is determined by the binding probability and the second osmotic virial coefficient Bij of protein species i and j. The latter is determined by the two-particle partition function, which in general can be estimated from the fraction of states where proteins are outside of their interaction range29 or, for implicit solvents, by performing a free energy calculation using insertion and removal moves.
2.1. Preliminaries
McMillan and Mayer5 have shown how we can apply results of statistical mechanics to describe osmotic properties of solutions. Integrating out solvent degrees of freedom, only solute degrees of freedom remain and solutes interact with each other via effective potentials. For such a system with m solute species, the virial equation of state36,37 becomes the osmotic virial equation of state, i.e.
| 2 |
where Π is the osmotic pressure, Vm is the molar volume, R is the gas constant, T is the temperature, xi is the mole fraction of species i, and Bij is the osmotic second virial coefficient of proteins of species i and j.
We can express the second virial coefficients Bij of an arbitrarily shaped particle of species i and an arbitrarily shaped particle of species j, via one- and two-particle configurational partition functions. To do so, we extend the derivation by McQuarrie to nonspherical particles7 and start from the grand canonical partition function
| 3 |
where V is the volume, Ni is the number of molecules of species i containing ni atoms each, and zi = exp(βμi) is the fugacity determined by the chemical potential μi of species i and the inverse temperature β = 1/(kbT). kb is Boltzmann’s constant. The osmotic pressure is a function of the fugacities and given by βΠV = ln Ξ(T,V, z1,...,zm).38,39 Here, we write the canonical partition function Q(N1,...,Nm) of m species of arbitrarily shaped particles as
| 4 |
where 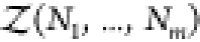 is the
corresponding configurational partition
function
is the
corresponding configurational partition
function
| 5 |
where the potential
energy U(X) depends on the set X of all |X| = ∏iNini atom positions.
In eq 4, we introduced 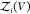 for the
single-particle canonical partition
function, e.g.,
for the
single-particle canonical partition
function, e.g., 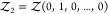 . For spherically symmetric particles,
. For spherically symmetric particles, 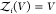 and we recover McQuarrie’s
expression7 for Q(N1, ..., Nm). For
rigid cylindrically symmetric and asymmetric particles,
and we recover McQuarrie’s
expression7 for Q(N1, ..., Nm). For
rigid cylindrically symmetric and asymmetric particles, 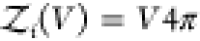 and
and 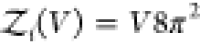 , respectively.
Note that in the following,
we use “Z” instead of “
, respectively.
Note that in the following,
we use “Z” instead of “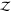 ” for
these expressions for rigid
molecules to distinguish them from the full configurational partition
function of flexible molecules written as calligraphic “
” for
these expressions for rigid
molecules to distinguish them from the full configurational partition
function of flexible molecules written as calligraphic “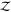 ”. We
obtain for the second osmotic
virial coefficients
”. We
obtain for the second osmotic
virial coefficients
| 6 |
where we introduced 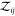 for the two-particle
partition function,
e.g.,
for the two-particle
partition function,
e.g., 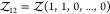 for a pair of particles of species 1 and
2 or
for a pair of particles of species 1 and
2 or 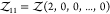 for a pair of particles of species 1.
for a pair of particles of species 1.
2.2. Estimating the Dissociation Constant
We show how to obtain a box-size-independent estimate of the dissociation constant Kd from simulations of two proteins in a box. Kd is related to the Gibbs binding free energy ΔG via
| 7 |
where c0 = 1M is the standard concentration and Δp is the pressure difference between bound and unbound states.40 The last term is usually small and can be neglected.
For large enough box volumes V, one would be tempted to estimate the dissociation constant of two proteins A and B directly from the binding probability pb(V). For a discussion of suitable definitions of bound states, see Section 2.7. Using the concentrations of free proteins [A] = [B] = (1 – pb(V))/(NAV) and the concentration of bound protein [AB] = pb(V)/(NAV), a first rough estimate of the dissociation constant is given by
| 8 |
For small box sizes typically used in simulations, this estimate suffers from finite-size effects. Accurate estimates using eq 8 would require unusually large boxes, as we show in Section 4, which makes sampling highly inefficient.
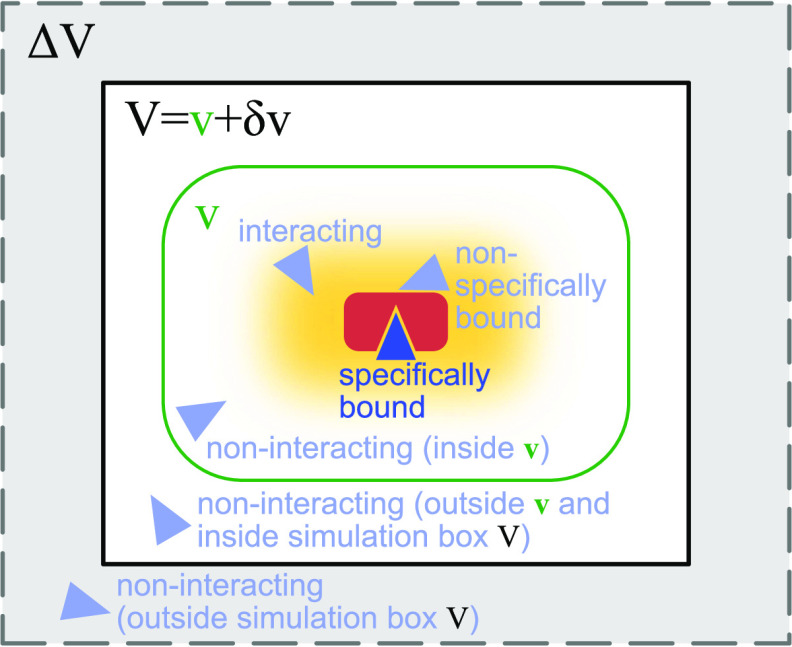
To overcome this finite-size effect, we effectively extend the box volume analytically and calculate Kd in the limit of infinite volume (Figure 1). We emphasize here that in the following derivation, we consider fully flexible proteins without any restrictions on their internal degrees of freedom. We remove the translational and rotational degrees of freedom of the protein of species i, which correspond to a factor Zi(V) = 8π2V in the partition function for asymmetric proteins. That is, we fix the position and orientation of the protein of species i, which leaves the internal degrees of freedom due to the flexibility of the protein unchanged. The corresponding partition function of j in the presence of i, with i fixed in position and orientation but internally flexible, is given by
| 9 |
We extend this system with a fixed position and orientation of the flexible protein i by an additional volume ΔV accessible to the second protein. The contribution to the partition function of a protein of species j being in this additional volume ΔV is given by
| 10 |
where Zj(ΔV) = 8π2ΔV gives the contribution due to the
translational and rotational
degrees of freedom of an asymmetric protein to the partition function. 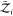 and
and 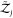 are the partition functions of individual
proteins i and j, whose positions
and orientations are fixed in space. That is,
are the partition functions of individual
proteins i and j, whose positions
and orientations are fixed in space. That is, 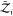 and
and 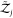 contain only contributions
due to the respective
internal degrees of freedom of free proteins and due to the degrees
of freedom of solvent molecules in the vicinity of the proteins, which
differ from the bulk due to the presence of the protein. For rigid
protein models in implicit solvents,
contain only contributions
due to the respective
internal degrees of freedom of free proteins and due to the degrees
of freedom of solvent molecules in the vicinity of the proteins, which
differ from the bulk due to the presence of the protein. For rigid
protein models in implicit solvents, 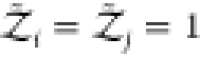 .
.
Figure 1.
Calculating the dissociation constant Kd and the second osmotic virial coefficient Bij from simulations of two proteins in a box of volume V. The red protein has a single specific wedge-shaped binding site for the triangular blue protein. The light-blue protein configurations illustrate different interaction modes of the two proteins considered in the derivation of eqs 1 and 28. To obtain a Kd estimate independent of box size, we analytically extend the two-particle partition function for the simulation box by the contributions of an extension volume ΔV (gray shaded area) and perform the limit ΔV → ∞. We calculate Bij from the probability pv(V) that the two proteins are within a subvolume v (green), which is at least large enough to cover all protein–protein interactions (yellow shaded area).
The probability pb(Vex) that the two proteins are bound in the extended volume Vex = V + ΔV is now given by the ratio of the partition function 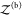 of the bound
proteins to the partition
function of the extended system
of the bound
proteins to the partition
function of the extended system 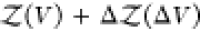 . With the position of
protein i fixed,
. With the position of
protein i fixed, 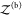 is independent of the size of the volume V and
thus the same for the simulation box and for the extended
system, i.e.,
is independent of the size of the volume V and
thus the same for the simulation box and for the extended
system, i.e., 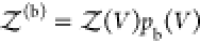 . Consequently
. Consequently
| 11 |
To calculate a Kd value unaffected by the finite size of the simulation box, we now substitute eq 11 into eq 8. We then take the limit ΔV → ∞ and use that Zj(V)/V = 8π2 to obtain
| 12 |
We can rewrite
this equation realizing that
the partition function of all bound states of the system, where also
protein i can move and rotate, is given by 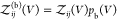 . Note that
. Note that 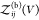 is proportional to V. Equation 12 becomes
is proportional to V. Equation 12 becomes
| 13 |
Expressing 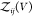 by the second osmotic virial coefficient
defined in eq 6
by the second osmotic virial coefficient
defined in eq 6
| 14 |
and inserting the resulting expression in eq 12, we obtain the relationship between Kd and Bij given in eq 1
As a corollary, the volume dependence of the fraction of bound proteins
| 15 |
is parameterized by Kd and Bij.
As we derive in the following, Kd and Bij fulfill the approximate relation
| 16 |
This approximate relationship becomes an exact
relationship if we define all interacting states as bound states41,42 or for proteins that do not interact when they are not bound (see Section 2.4). We write 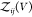 as a sum of the partition functions
as a sum of the partition functions 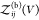 for the bound and
for the bound and 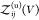 for the unbound states, i.e.,
for the unbound states, i.e., 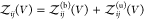 , and insert this expression
in eq 14. We then obtain
, and insert this expression
in eq 14. We then obtain
| 17 |
If unbound interactions are weak, then
| 18 |
such that
| 19 |
where we used eq 13. Rearranging this equation, we arrive at eq 16. We can now insert this expression into eq 15 and obtain
| 20 |
from which we can express Kd to obtain an approximate estimate for Kd, which we call Kd′, i.e.
| 21 |
Here, we introduced the fraction of unbound protein configurations as pu(V) = 1 – pb(V). Note that eq 21 corresponds to eq 13 of de Jong et al.18 For the exact relationship between Kd and Kd′, see Section 2.4.
2.3. Estimating the Second Osmotic Virial Coefficient
As we have shown above, we have to estimate Bij to accurately estimate Kd. To do so, we apply the same concepts as we have used for the calculation of Kd. We first remove contributions to the partition function due to the translational and rotational freedom of the whole system by keeping the position and the orientation of the otherwise flexible protein i fixed (eq 9). Around this protein, we define a subvolume v < V, which has to be big enough such that it captures all protein–protein interactions (Figure 1). Outside this subvolume, protein–protein interactions can be neglected. That is, the flexible protein j moves freely when it is in volume δv = V – v.
The probability pv(V) that protein j is in subvolume v is given by
| 22 |
where 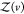 is given analogous to eq 9 and Zj(δv) = 8π2δv for asymmetric proteins. We can express
is given analogous to eq 9 and Zj(δv) = 8π2δv for asymmetric proteins. We can express 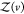 from eq 22 as
from eq 22 as
| 23 |
Usiing eq 9 for 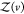 , it follows that
, it follows that
| 24 |
1 – pv(V) is the probability that protein j is in volume δv. Consequently
| 25 |
Using that Zj(v) and Zj(δv) are proportional to their arguments with the same prefactor (see Section 2.1) and that δv = V – v, where V is the box volume, we obtain
| 26 |
Solving for pv(V), we obtain
| 27 |
which describes the dependence of pv(V) on the box volume V and the subvolume v.
We emphasize that eq 26 is generally valid for arbitrary binding partners, without making any assumptions about symmetry or the number of internal degrees of freedom of the binding partners or of the solvent. The only condition is that interactions between binding partners are negligible outside of the volume v. We can introduce correction terms based on an effective pairwise potential acting between the binding partners if this condition is not fulfilled (see Section 2.7).
To motivate the interpretation of eq 26, we rewrite it as
| 28 |
Note that the prefactor in eq 28 contains the box volume V, whereas the prefactor in eq 26 contains the subvolume v. The first term in the brackets, determining the two-particle partition function, is the ratio of the probability of finding one protein outside of the subvolume v for the ideal system, 1 – v/V, to the corresponding probability for the interacting proteins, 1 – pv(V). This ratio, which is the inverse of the quantity f2(V) of Ashton and Wilding,29 is independent of the subvolume v, chosen to be just large enough to cover the interaction range. Consequently, the first term in the brackets in eq 28 can be written as 1/exp[−βFo(ex)(V)], where we introduced the excess free energy of finding the two proteins outside of their interaction range in the box of volume V as
| 29 |
We express Kd as a function of pv(V) by inserting eq 28 into eq 1 and obtain
| 30 |
We next establish the commonly used relationship of Bij to the partial radial distribution function g(r).7 The ratio of pv(V)/(1 – pv(V)) can be estimated from the probability density of center-of-mass distances p(r) of two proteins in a box, for instance, which is itself related to the radial distribution function g(r). To do so, we define a spherical volume v = 4πR3/3 and a spherical shell around this sphere with volume δv = 4π[(δR + R)3 – R3]/3. The ratio is then given by
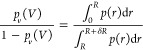 |
31 |
We define a radial distribution function g(r) through
| 32 |
We can choose the proportionality constant such that g(r) = 1 for r > R, where p(r) ∝ r2. Then, 4π ∫RR+δRg(r)r2 dr = δv and we may write
| 33 |
Inserting this expression in eq 26 and using that ∫0R 4πr2dr = v, we obtain
| 34 |
By introducing an effective interaction potential βw(r) = −ln g(r), we can write eq 34 as it is commonly presented
| 35 |
Using eq 28 instead of eq 34 or 35, we can avoid the computation of distance distribution functions and potentials of mean force, respectively, and the subsequent integration. Importantly, we also do not have to estimate the plateau value of g(r), which in simulations is different from one and which depends on system size and the thermodynamic ensemble.29,43 Although these differences might be viewed only as a minor simplification, eq 28 emphasizes that Bij is independent of the detailed shapes of g(r) and w(r) and determined by the excess free energy Fo(ex)(V) of finding the two proteins outside of their interaction range. Note that our results also apply to the infinite dilution limits of the Kirkwood–Buff integrals Gij = 4π ∫r=0[g(r) – 1]r2 dr = 2Bij.13,44,45
2.4. Contribution of Nonbinding Interactions to Bij
We can use Kd and Bij to quantify the nonbinding interactions of two proteins. Let
us first consider two nonbinding proteins for which 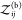 (V) = 0. Consequently, eq 17 becomes
(V) = 0. Consequently, eq 17 becomes
| 36 |
where we use the superscript “(u)” to indicate contributions of the unbound states. For binding proteins, Bij(u) is given by the difference between Bij = Bij + Bij(b) and the contributions to Bij due to binding
| 37 |
i.e., we can quantify the nonbinding interactions for two binding proteins via
| 38 |
which becomes
| 39 |
For hard spheres, pu(V) = 1 and pv(V) = (v – vexc)/(V – vexc), where vexc is the excluded volume, such that Bij(u) = vexc/2. For attractive nonbinding interactions Bij < vexc/2, and for repulsive nonbinding interactions Bij(u) > vexc/2. Note that for asymmetric proteins, vexc corresponds to an excluded region in the configuration space, which, for instance, is spanned by Cartesian coordinates and Euler angles in the case of rigid proteins. Thus, in general, vexc should be viewed as an effective volume corresponding to a thermodynamic free energy.
We now show that Bij(u) quantifies the difference between the approximate expression for Kd in eq 21 and the box-size-independent expression for Kd in eq 1. Inserting eq 11 into eq 21, we obtain
| 40 |
such that the relative difference is given by
| 41 |
Consequently, the approximate estimate Kd′ deviates systematically from the true value Kd, with deviations proportional to Bij, but converges to the true value with increasing box volume as 1/V.
2.5. Indistinguishable Binding Partners (Homodimers)
So far, we have assumed that the proteins are distinguishable, i.e., that they form heterodimers, but all expressions derived here are also valid for indistinguishable binding partners forming homodimers. To consider the case of two identical binding partners, we rewrite eq 13 as
| 42 |
where
we introduced 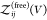 for the
partition function of two free
proteins, which is determined by the product of two single-protein
partition functions. For indistinguishable binding partners forming
homodimers, both
for the
partition function of two free
proteins, which is determined by the product of two single-protein
partition functions. For indistinguishable binding partners forming
homodimers, both 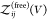 and
and 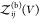 would have to be multiplied by a factor
1/2 to account for the indistinguishablity of the proteins. However,
these factors then cancel in the ratio in eq 42.
would have to be multiplied by a factor
1/2 to account for the indistinguishablity of the proteins. However,
these factors then cancel in the ratio in eq 42.
2.6. Kd and Bij from a Single Simulation
We can estimate Kd and Bij from the fraction of bound protein pb(V) and the probability pv(V) of one protein being located in a subvolume v around the other. The latter determines Bij according to eq 28, which we then insert into eq 1 to obtain the finite-size corrected estimate of Kd. We call this method the subvolume method. To calculate Bij, we can also estimate the two-particle partition function Zij(V), now for simplicity but without loss of generality only considering rigid molecules, using free energy methods.46 For implicit solvents, we can use insertion and removal moves of the proteins to efficiently estimate Zij(V), as explained in the following. We call this method the insertion/removal method.
2.6.1. Estimating Two-Particle Configurational Partition Functions for Implicit Solvents
A simulation of a pair of proteins in a box of volume V at reciprocal temperature β gives us immediately the particle-removal energy distribution as the normalized distribution of potential energies. We define xi = (ri,Ωi), where ri are the Cartesian coordinates of the geometric center of protein i and Ωi are its Euler angles defining its orientation. We denote the configuration space as W = V × Ω to simplify the notation. The particle-removal energy distribution is then given by
| 43 |
where Z23(β) = ∫W2 dx2dx3e–βU(x2,x3) and δ[·] is Dirac’s delta function.
The particle-insertion energy distribution pins(E) is formally given by
| 44 |
where Zi(β = 0) = ∫W dxi. Sampling the particle-insertion energy distribution pins(E) for a given box size is straightforward. All one needs is a replica with reciprocal temperature β = 0 exactly. All moves will then be accepted, and the energies saved are those of random insertions. Alternatively, one could make trial moves of the two proteins with Monte Carlo move widths ±L/2, where L is the box length, and the orientation changes about random axes by ±π, and to write out the absolute trial (!) energies (not the energy differences or the accepted energies). With such a move protocol, it would not matter if one or both particles were moved and if moves are accepted or not. It also does not matter what the “acceptance rate” is (i.e., it can be zero!). What is important, though, is that the box volumes in insertion and removal runs are the same.
The normalized removal and insertion energy distributions are related to each other by
| 45 |
which follows from
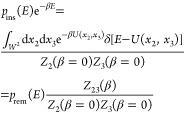 |
46 |
The ratio of partition functions defines the free energy of going from a system of two noninteracting particles to a system in which they interact
| 47 |
Note that F = −Fo(ex)(V) (see eq 29). An efficient way of determining this free energy is to use the Bennett acceptance ratio (BAR) estimator31
| 48 |
where Ei are the uncorrelated (by construction) insertion energies and Ei are the uncorrelated removal energies. However, it is clear that this is problematic in cases where the proteins are strongly bound (forming a dimer!) because then one would have very little information about higher energies.
This problem can be remedied using all of the data in a temperature replica exchange simulation. In effect, the high-temperature runs allow us to estimate an accurate density of states to a pretty high energy. The particle-insertion energies complement this density of states on the high-energy side. All of the runs at different temperatures can be combined with the list of insertion energies using binless WHAM. As a reference, we take the temperature of interest (β = β1 without loss of generality). The bias energies at replicas with reciprocal temperature βi are then ΔU = (βi/β – 1)U. This formula works also for the insertion energies coming from a run with βi = 0. The insertion energies can be thought of as coming from a run with the bias potential ΔU = −U, i.e., on potential zero. A binless-WHAM analysis using these bias energies as input will produce the required free energy F as the difference between the reference state and the insertion run.
2.7. Practical Considerations
In the derivation
of Kd and Bij, we have assumed that the volume is large enough
such that interactions between the protein with a fixed position and
orientation and the protein in the extended volume can be neglected.
If this condition is not fulfilled, then we can correct for residual
interaction energies using a simple distance-dependent interaction
potential ϕ(r) in the calculation of 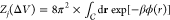 , where
, where 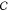 denotes the
Cartesian space defining ΔV. For example, at
large distances, the interaction of charged
proteins can be approximated by (screened) Coulomb interactions of
the total charges located at the centers of charge. In such a case,
we would include for the calculation of the fraction bound only configurations
of the simulation where the two proteins are separated less than a
cutoff distance, usually given by half the shortest box length. Such
a system corresponds to a spherical volume with one protein at its
center and the other one moving unrestrained. Doing so, we assume
that the residual interaction modeled as a simple pair-potential has
a negligible effect on the internal degrees of freedom and the degrees
of freedom of the surrounding solvent, i.e.,
denotes the
Cartesian space defining ΔV. For example, at
large distances, the interaction of charged
proteins can be approximated by (screened) Coulomb interactions of
the total charges located at the centers of charge. In such a case,
we would include for the calculation of the fraction bound only configurations
of the simulation where the two proteins are separated less than a
cutoff distance, usually given by half the shortest box length. Such
a system corresponds to a spherical volume with one protein at its
center and the other one moving unrestrained. Doing so, we assume
that the residual interaction modeled as a simple pair-potential has
a negligible effect on the internal degrees of freedom and the degrees
of freedom of the surrounding solvent, i.e., 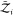 and
and 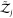 are unchanged.
are unchanged.
Suitable definitions of bound states will depend on the molecular model we use for simulations. In our simulations of rigid proteins in implicit solvents, we consider a state as bound if the interaction energy of the two proteins is smaller than −2kbT. Additionally demanding that two proteins have to have a minimum Cα distance smaller than 0.8 nm to be counted as bound does not have a noticeable effect on the binding probability. For molecular dynamics simulations using explicit solvents, a combination of distance- and energy-based criteria and using transition-based-assignment of states47 might be necessary to reliably distinguish bound states from spurious contacts.
In simulations of two proteins in a box, we can estimate pv(V) using a distance-based criterion as has been introduced by Ashton and Wilding.29 We define a distance between the two proteins, e.g., the center-of-mass distance r. We introduce a distance R such that interactions between proteins are negligible for distances r > R. For an ensemble of N structures, we count the number of structures Nv for which r ≤ R. In these structures, the center-of-mass of protein 2 lies within a spherical volume v = 4πR3/3 centered at the center-of-mass of protein 1. We then estimate pv(V) = Nv/N.
For strong binders and in boxes of typical size, pv(V) is close to one. For pv(V) = 1, (1 – v/V)/(1 – pv(V)) in eq 28 diverges. Consequently, pv(V) has to be determined with sufficient numerical precision to obtain accurate estimates. For example, if we sample 10 000 configurations, then the numerical precision of pv(V) is limited to 1/10 000. The precision can be increased by sampling more configurations or, in the case of replica simulation, by including additional replicas using WHAM when calculating pv(V). For weak binders with Kd ≳ 100 μM, 10 000 configurations are sufficient to estimate Kd and Bij even without applying WHAM.
3. Methods
We chose three weakly binding protein pairs with experimental Kd values covering 3 orders of magnitude from ∼μM to ∼mM. The lysozyme homodimer has an experimental Kd value of Kd ≈ 2710 ± 240 μM48 (PDB 6LYZ49), the ubiquitin/CUE dimer (PDB 1OTR50) has a Kd ≈ 155 ± 9 μM,50 and the dimer of the uracil-DNA glycosylase UDG and its uracil-DNA glycosylase inhibitor protein (Ugi) has a Kd ≈ 1. 3 ± 0.3 μM51 (PDB 1UUG52).
To simulate these protein pairs, we use the amino-acid-level coarse-grained model developed by Kim and Hummer for weakly binding proteins53 implemented in the Complexes++ software (https://www.github.com/bio-phys/complexespp). We treat all proteins as rigid bodies. In contrast to the original model, which is called the KH-model, we shift the original Miyazawa and Jernigan parameters54,55 by e0 = −1.875 kbT, where T = 300 K, to account for the solvation energy and we scale the resulting parameters by λ = 0.1243 to balance them with the electrostatic interactions. In the original model, e0 = −2.27 kbT and λ = 0.159. The new values have been chosen to better reproduce the B22 value of lysozyme and the Kd value of the ubiquitin/UIM1 complex. We chose residue charges of −1.0e for Asp and Glu, +1.0e for Arg and Lys, and +0.5e for His because its isoelectric point is at pH 7. e is the elementary charge. Consequently, the total charges of the proteins are +8.5e for lysozyme, +0.5e for ubiquitin, −4.5e for CUE, +7.5e for UDG, and −11.5e for Ugi. We set the dielectric constant to 80 and the Debye length to 1 nm, corresponding to the conditions in an aqueous solution of 100 mM NaCl.
To generate Boltzmann ensembles of configurations, which also provide the removal energy distributions defined in eq 43, we perform temperature replica exchange Monte Carlo (REMC) simulations using 24 replicas. Temperatures were equally spaced between 300 and 530 K. In a Monte Carlo sweep, each protein performs one trial move on average, which can be translation or rotation. Replica exchanges are attempted every 10 sweeps. For the rotation move, a rotation axis is randomly generated by drawing a point from a sphere. Then, we rotate around this axis by an angle, which we draw from a box distribution with a width given by twice the maximum angle. This maximum angle is set to 0.1 rad for the coolest replica and to 1.25 rad for the hottest replica and spaced equidistantly in between. Similarly, we set the maximum displacement for the translation move to 0.2 nm in the coolest replica and to 1.35 nm in the hottest replica, with equal spacing in between. In our simulations, we use a cutoff radius of 3 nm to truncate our interaction potentials.
To sample the insertion energy distribution defined in eq 44 in simulations, we switch off all interactions by setting all interaction parameters and residue charges to zero. We use a maximum displacement of half the box length and a maximum rotation angle of π. We accept and sample all configurations to generate the insertion ensembles, for which we then recalculate all energies for switched-on potentials.
To estimate the two-particle partition function, we combine results from REMC simulations (removal ensemble) and the energies calculated for the ensemble of noninteracting proteins (insertion ensemble) using binless WHAM.32−34 To avoid numerical problems, we clip interaction energies at 100 kbT. We define two proteins as being bound if their total interaction energy is below −2kbT.
For equilibration, we performed 106 Monte Carlo sweeps in each replica. For production, we performed 107 sweeps and we sampled every 100th sweep, yielding 105 structures for each protein pair per replica. We also performed 106 insertion moves for each pair, which by design creates uncorrelated configurations.
To study the box volume dependence of the fraction bound pb(V), we calculated for the coolest replica pb = NE≤−2kbT/N. NE≤−2kbT is the number of structures with energies E ≤ −2kbT, and N = 105 is the total number of structures. To study the box volume dependence of the subvolume probability pv(V), we calculated for the coolest replica pv = Nv/N, where Nv is the number of structures within the subvolume v. We defined this volume as a spherical volume with a radius given by the sum of (Di + Dj)/2, where Di and Dj are the largest diameters of proteins of species i and j, respectively, and our cutoff radius of 3 nm. The resulting radii are between ∼6.7 and ∼7.4 nm for the three proteins. For each protein pair, we performed simulations for 17 box sizes with volumes ranging from 3375 to 106 nm3. We calculated the standard errors of the mean by block averaging.56,57
We validate the insertion/removal method and the subvolume
method
for the smallest boxes used here with volume 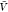 = 153 nm3 = 3375
nm3. With uniform probability, we selected at random 10 000
of the N = 105 samples and chose for each
replica the configurations corresponding to the same 10 000
indices. We also drew 10 000 configurations of the 106 configurations in the insertion ensemble with uniform probability.
In the insertion/removal method, we then applied WHAM using these
250 000 configurations in total to calculate pb(
= 153 nm3 = 3375
nm3. With uniform probability, we selected at random 10 000
of the N = 105 samples and chose for each
replica the configurations corresponding to the same 10 000
indices. We also drew 10 000 configurations of the 106 configurations in the insertion ensemble with uniform probability.
In the insertion/removal method, we then applied WHAM using these
250 000 configurations in total to calculate pb(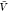 ) and
) and 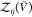 , from which we then estimated Kd and Bij. We repeated this procedure 1000 times and calculated the averages
of Kd and Bij and their covariance matrices. We confirmed visually
that the distributions of the estimates of Kd and Bij are
distributed according to two-dimensional Gaussians with the estimated
covariance matrices. We use the same protocol to obtain estimates
and uncertainties from resampling for the subvolume method, in which
we do not use the insertion ensemble.
, from which we then estimated Kd and Bij. We repeated this procedure 1000 times and calculated the averages
of Kd and Bij and their covariance matrices. We confirmed visually
that the distributions of the estimates of Kd and Bij are
distributed according to two-dimensional Gaussians with the estimated
covariance matrices. We use the same protocol to obtain estimates
and uncertainties from resampling for the subvolume method, in which
we do not use the insertion ensemble.
4. Results
We calculated Kd and Bij using the insertion/removal method and the subvolume method for three protein pairs, i.e., the lysozyme homodimer and the heterodimers ubiquitin/CUE and UDG/Ugi. As we will show, these estimates allow us to quantify the contributions due to binding and nonbinding interactions to Bij.
In the insertion/removal method, we determine Kd and Bij from replica exchange simulations at a box volume 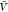 and from insertion ensembles. We first
estimated pb(
and from insertion ensembles. We first
estimated pb(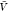 ) and Zij(
) and Zij(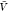 ) by combining the insertion ensemble and
the replicas of our temperature REMC simulations using WHAM. We then
evaluated eq 14 to obtain Bij and used this value together
with our estimate for pb(
) by combining the insertion ensemble and
the replicas of our temperature REMC simulations using WHAM. We then
evaluated eq 14 to obtain Bij and used this value together
with our estimate for pb(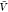 ) in eq 1 to obtain Kd. By resampling,
we estimated the covariance matrix.
) in eq 1 to obtain Kd. By resampling,
we estimated the covariance matrix.
In the subvolume method,
we first estimated pv(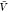 ) and pb(
) and pb(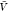 ) from all replicas using WHAM. We used eq 26 to calculate Bij from pv(
) from all replicas using WHAM. We used eq 26 to calculate Bij from pv(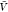 ) and used this estimate together with pb(
) and used this estimate together with pb(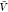 ) to estimate Kd using eq 1.
) to estimate Kd using eq 1.
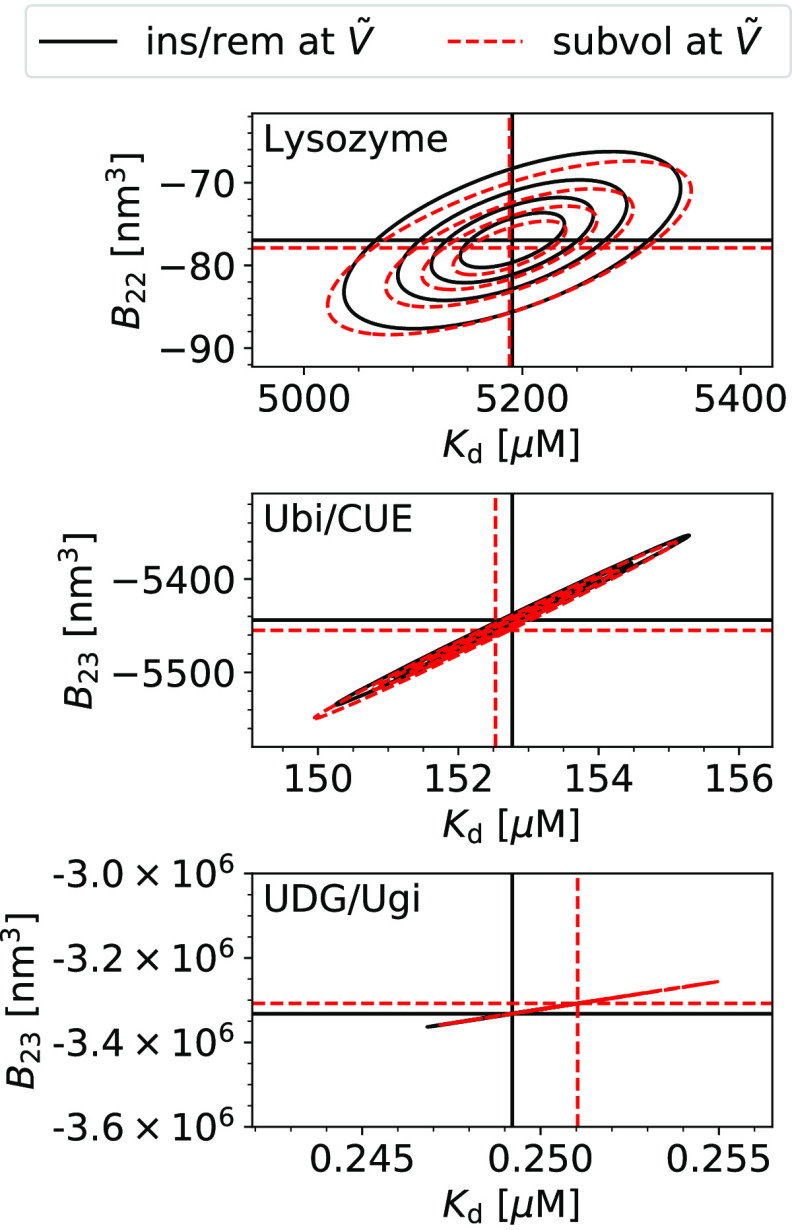
We find that the estimates for Kd and Bij from the insertion/removal method and the subvolume method agree excellently with each other (Figure 2 and Table 1). Moreover, the estimates have similar uncertainties. Kd values and Bij values calculated by resampling are correlated for both methods (Figure 2). A smaller value of Bij, i.e., a more negative value, leads to a smaller value of Kd according to eq 1.
Figure 2.
Comparison of the accuracy of the insertion/removal method (ins/rem, black, solid lines) and the subvolume method (subvol, red, dashed lines) to estimate Kd and Bij for three different protein pairs (top to bottom). The most likely estimates are indicated by horizontal and vertical dashed lines. The contour lines indicate the limits of the 25, 50, 75, and 95% confidence regions. The insertion/removal method (eqs 14 and 1 and the two-particle partition function from WHAM (Section 2.6.1), black) and the subvolume method (eqs 26 and 1, red) agree excellently with each other, and they have similar uncertainties. For UDG/Ugi, contour lines collapse on to a single line due to the strong correlation between the estimates for Kd and Bij.
Table 1. Kd, Bij, and the Contributions of Binding Interactions, Bij(b), and Nonbinding Interactions, Bij, to Bij for Three Protein Complexes (PDB codes 6LYZ, 1OTR, 1UUG) for the Insertion/Removal Method (“ins/rem”) and the Subvolume Method (“subvol”)a.
| lysozyme | method | Kd [μM] | B22 [nm3] | B22(b) [nm3] | B22(u) [nm3] |
|---|---|---|---|---|---|
| ins/rem | 5191 ± 63 | –77 ± 4 | –160 ± 2 | 83 ± 4 | |
| subvol | 5188 ± 68 | –78 ± 4 | –160 ± 2 | 82 ± 3 |
| Ubi/CUE | method | Kd [μM] | B23 [nm3] | B23(b) [nm3] | B23(u) [nm3] |
|---|---|---|---|---|---|
| ins/rem | 153 ± 1 | –5444 ± 37 | –5435 ± 37 | –9 ± 3 | |
| subvol | 153 ± 1 | –5455 ± 39 | –5444 ± 38 | –11 ± 3 |
| UDG/Ugi | method | Kd [μM] | B23 [nm3] | B23(b) [nm3] | B23(u)[nm3] |
|---|---|---|---|---|---|
| ins/rem | 0.25 ± 0.002 | –3 332 000 ± 27 000 | –3 332 000 ± 27 000 | –94 ± 5 | |
| subvol | 0.25 ± 0.002 | –3 308 000 ± 27 000 | –3 308 000 ± 27 000 | –81 ± 7 |
Errors are standard errors of the mean.
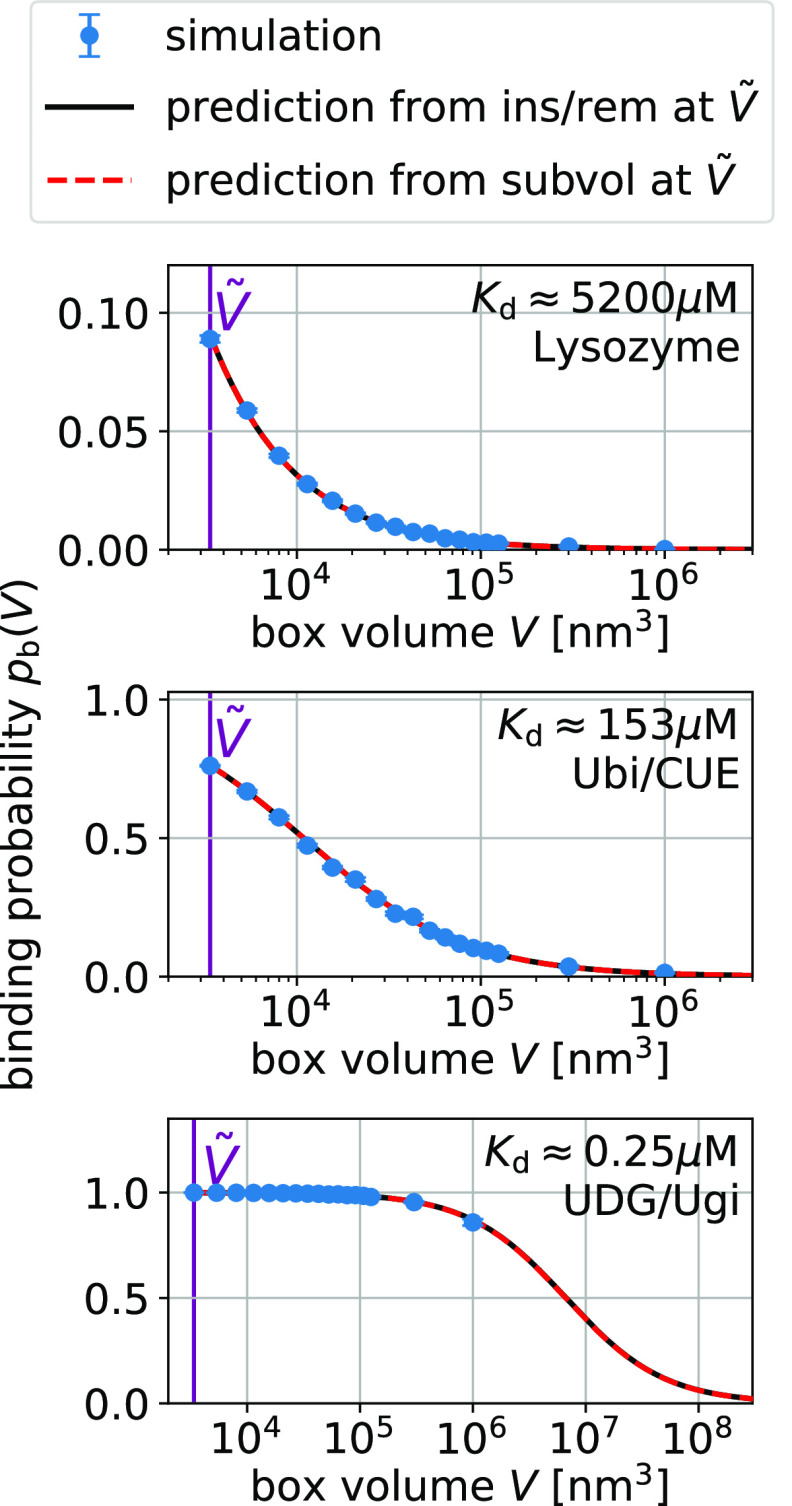
For additional validation,
we use the results for Kd and Bij obtained at the box volume 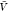 to predict the box-size dependence of the
fraction bound pb(V)
and the subvolume probability pv(V). We use eq 15 and our estimates for Kd and Bij obtained at
a box volume
to predict the box-size dependence of the
fraction bound pb(V)
and the subvolume probability pv(V). We use eq 15 and our estimates for Kd and Bij obtained at
a box volume 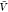 to calculate pb(V) (Figure 3). We use eq 27 and our estimates for Bij obtained at a box volume
to calculate pb(V) (Figure 3). We use eq 27 and our estimates for Bij obtained at a box volume 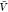 to calculate pv(V) (Figure 4). The resulting
curves reproduce the box
volume dependencies of pb(V) and pv(V) observed in the entire range of simulations, covering nearly 3
orders of magnitude in volume.
to calculate pv(V) (Figure 4). The resulting
curves reproduce the box
volume dependencies of pb(V) and pv(V) observed in the entire range of simulations, covering nearly 3
orders of magnitude in volume.
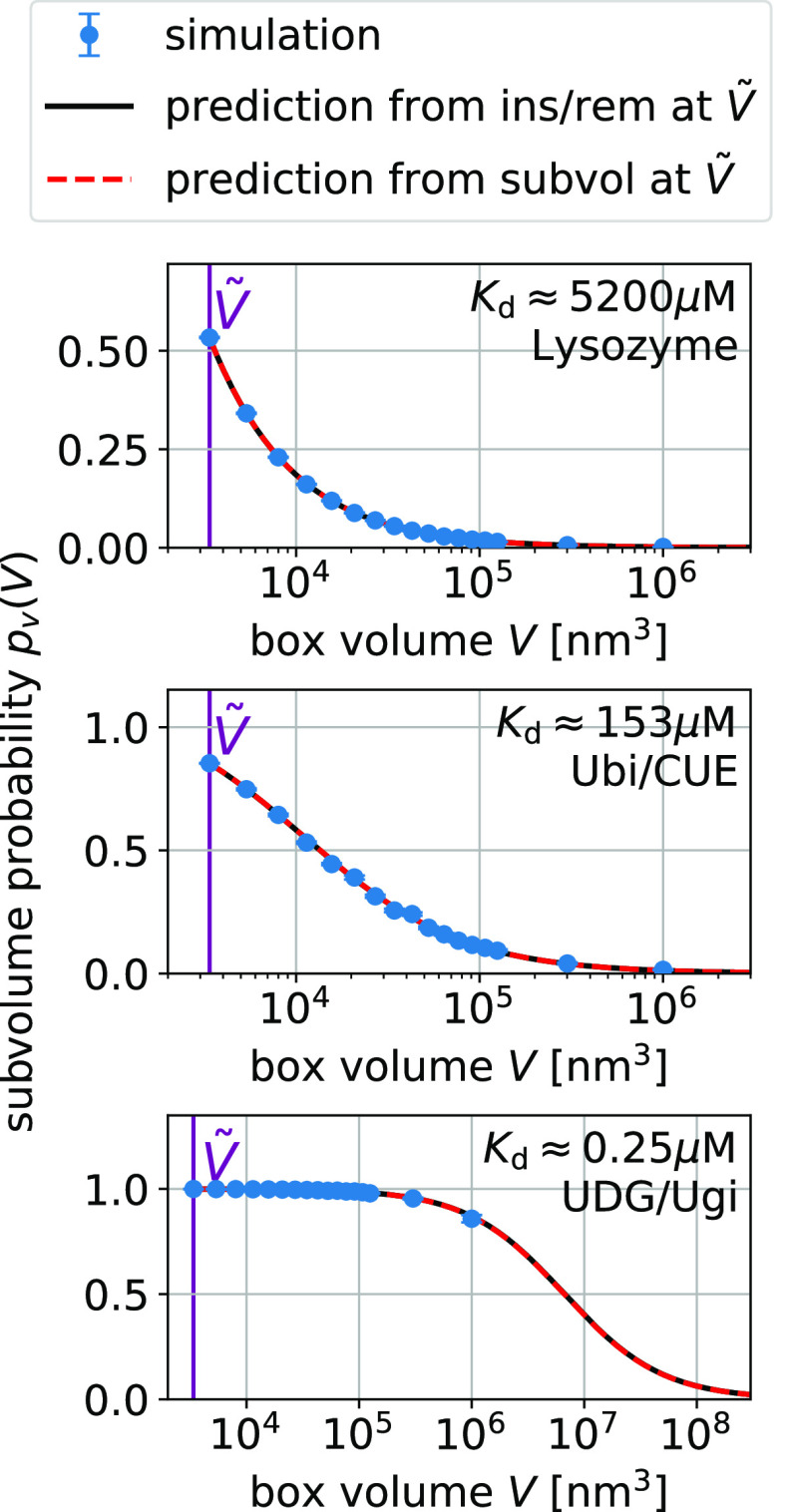
Figure 3.
Box-size dependence of the binding probability pb(V) is determined by Bij and Kd via eq 15.
We show
simulation results (blue) for three protein pairs (top to bottom).
Error bars indicate the blocked standard errors of the mean. The lines
are predictions using eq 15 and estimates for Kd and Bij obtained at a box volume 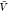 = 3375 nm3 (magenta vertical
line) using the insertion/removal method (black, solid lines) and
the subvolume method (red, dashed lines).
= 3375 nm3 (magenta vertical
line) using the insertion/removal method (black, solid lines) and
the subvolume method (red, dashed lines).
Figure 4.
Box-size
dependence of the subvolume probability pv(V) is determined by Bij via eq 27. We show simulation results (blue) for three
protein pairs (top to bottom). Error bars indicate the blocked standard
errors of the mean. The lines are predictions using eq 27 and estimates of Bij obtained at a box volume 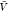 = 3375 nm3 (magenta vertical
line) using the insertion/removal method (black, solid lines) and
the subvolume method (red, dashed lines).
= 3375 nm3 (magenta vertical
line) using the insertion/removal method (black, solid lines) and
the subvolume method (red, dashed lines).
For strong binders, the fraction bound pb(V) and the subvolume probability pv(V) take on similar values (compare Figures 3 and 4). In these cases, pv(V) is dominated by binding. For small boxes, pb(V) is close to one and consequently so is pv(V). For box sizes large enough such that pb(V) is significantly below one, the contribution of the size of the subvolume v to pv(V) is small. For UDG/Ugi, the strongest binding complex considered here, the fraction bound dominates pv(V) such that the pv(V) curve in Figure 4 looks nearly identical to the corresponding pb(V) curve in Figure 3. However, the differences in these curves are significant as they are not only determined by the size of the subvolume v but also by the nonbinding interactions.
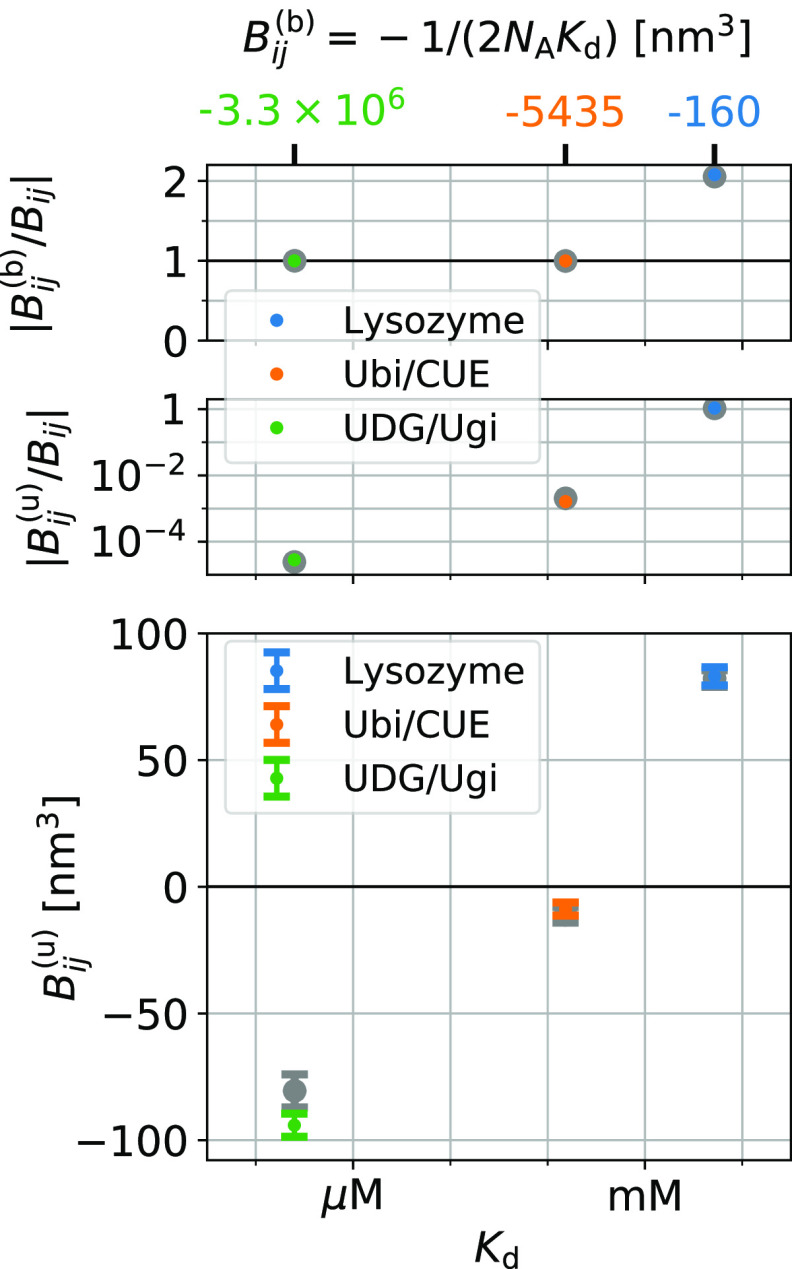
We can extract the contributions Bij(u), eq 38, of nonbinding interactions to Bij. We can do so even in the case of strong binders for which the Kd value is close to Bij = −1/(2NAKd) according to eq 16 (Figure 5, top). With the estimates provided by either the insertion/removal method or the subvolume method, we can resolve the small difference Bij(u) = Bij – Bij (Figure 5, center). Focusing on the results from the insertion/removal methods, we find that for lysozyme Bij(u) ≈ 83 ± 4 nm3 > 0. This value is close to what one would expect for hard spheres of equal volume, i.e., Bij = vexc/2 ≈ 70 nm3. For ubiquitin/CUE, the interactions are clearly attractive, but Bij(u) ≈ −9 ± 3 nm3 nearly vanishes. For UDG/Ugi, Bij ≈ −94 ± 5 nm3 indicates attractive interactions (Figure 5 and Table 1).
Figure 5.
Contributions of binding and nonbinding interactions to Bij = Bij(b) + Bij for three protein pairs. We show estimates from the insertion/removal method in color and estimates from the subvolume method using larger symbols in gray. Bij of the strongest binders is dominated by contributions of binding Bij(b) = −1/(2NAKd) such that the ratio of |Bij/Bij| is close to one (top). In these cases, nonbinding contributions to Bij are relatively small, i.e., |Bij(u)/Bij| ≪ 1 (center).
Note that for Ubi/CUE and UDG/Ugi, the estimates for B23(u) = B23 – B23 are much smaller than the individual errors of B23 and B23(b) (∼27 000 nm3 for UDG/Ugi and ∼40 nm3 for Ubi/CUE; Table 1). Naively, one would think that these large uncertainties preclude reliable estimates for the comparably small difference B23 in such a situation. However, the estimates for B23 and B23(b) from resampling are highly correlated because of the strong correlation of B23 and Kd (Figure 2). That is, the individual errors of B23 and B23 do not determine the errors of their difference.
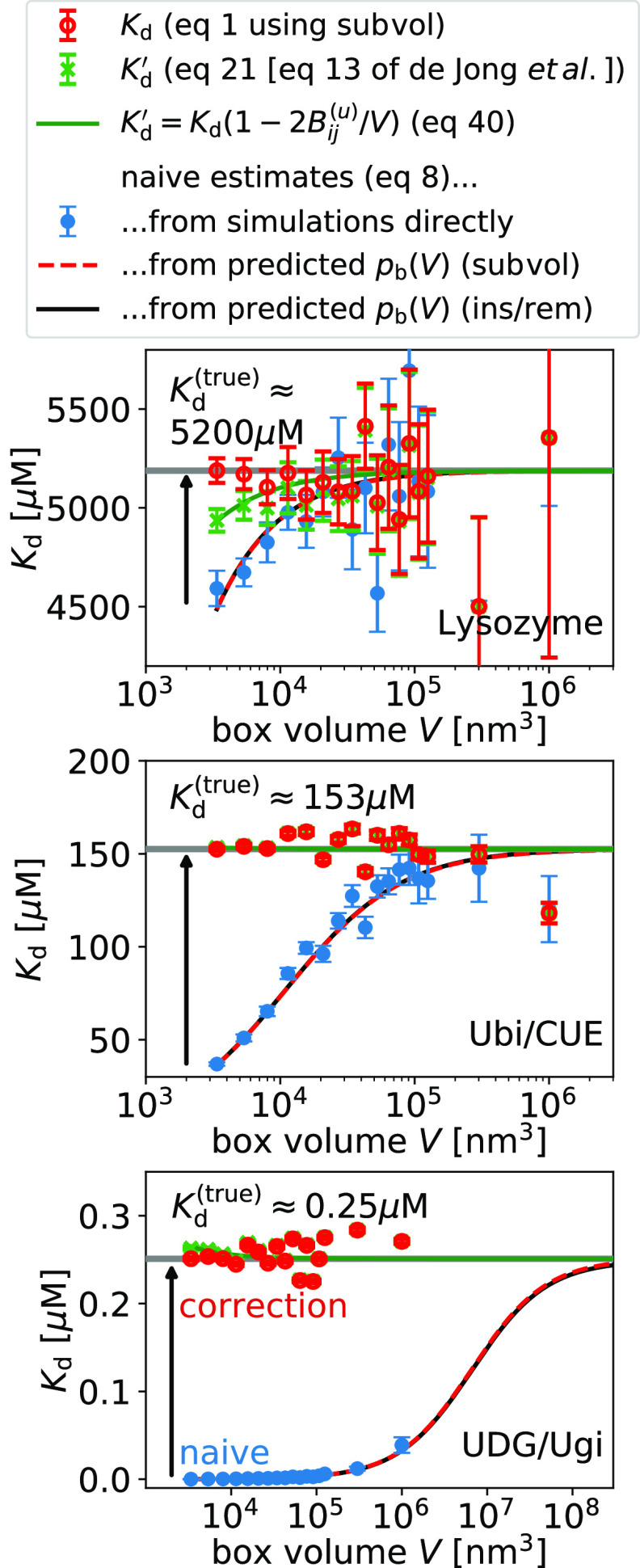
Next, we
show that the naive estimate of Kd from
concentrations using eq 8 actually suffers from a finite-size effect and that
it converges to the estimates obtained with the insertion/removal
and subvolume methods for large system sizes (Figure 6). For comparison only, we evaluate eq 8 for our predictions of pb(V) obtained at a volume 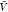 (Figure 3) and extrapolate the naive estimates for Kd until convergence is reached. For typical box sizes
used in simulations, Kd is underestimated
by about 10% for the lysozyme homodimer, the weakest binder considered
here, and by 3 orders of magnitude for UDB/Ugi, the strongest binder
considered here. To reach convergence when using eq 8, the box volumes have to be increased by
a factor ∼100 for the weakest binder and by a factor ∼100 000
for the strongest binder compared to typical box sizes.
(Figure 3) and extrapolate the naive estimates for Kd until convergence is reached. For typical box sizes
used in simulations, Kd is underestimated
by about 10% for the lysozyme homodimer, the weakest binder considered
here, and by 3 orders of magnitude for UDB/Ugi, the strongest binder
considered here. To reach convergence when using eq 8, the box volumes have to be increased by
a factor ∼100 for the weakest binder and by a factor ∼100 000
for the strongest binder compared to typical box sizes.
Figure 6.
Finite-size correction gives box-size-independent dissociation constants Kd (eq 1, red symbols). The naive estimate of Kd (eq 8, blue symbols) suffers from finite-size effects and converges to the true value (gray horizontal line) for increasing box size. We illustrate this convergence by evaluating eq 8 for the predictions for pb(V) from the insertion/removal method (black solid line) and the subvolume method (red dashed line). Approximately corrected estimates (eq 21, eq 13 of de Jong et al.,18 green symbols) suffer from finite-size effects and converge to the true value for increasing box volume. Error bars have been obtained by resampling.
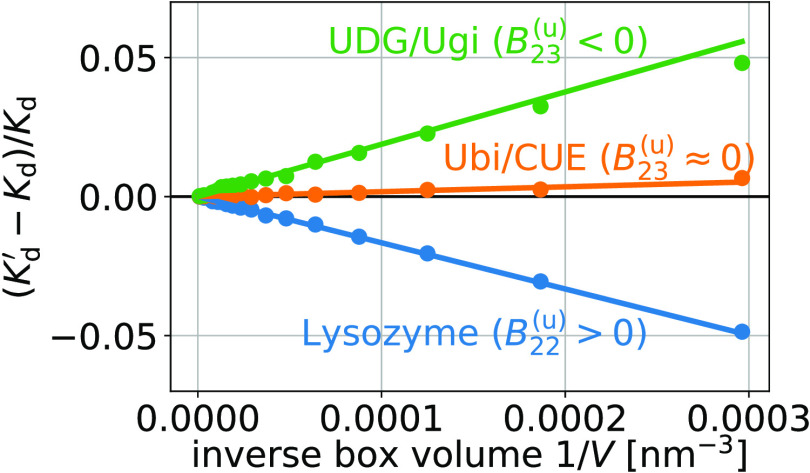
Using eq 1, we obtain finite-size effect-free estimates for Kd at all box volumes (see Figure 6). In contrast, the estimates obtained using the approximate relation given by eq 21 (eq 13 of de Jong et al.18) show small but systematic deviations determined by Bij(u) (eq 41); (see Figure 6). These systematic deviations decrease with increasing box volume as 1/V (Figure 7). For the three dimers considered here, these differences are in the range of ±5% for the smallest box sizes used here.
Figure 7.
Relative difference between the approximate estimates Kd′ (eq 21, eq 13 of de Jong et al.18) and the box-size-independent estimates Kd (eq 1) for the dissociation constant as shown in Figure 6 (discs) as functions of the inverse box volume 1/V. This difference is proportional to 1/V and to the contribution of unbound states to the second osmotic virial coefficient, Bij (eq 41, lines).
5. Conclusions
We have shown how to calculate the dissociation constant Kd of two proteins in a box from the fraction of protein dimers and the second osmotic virial coefficient Bij. We derived and validated two methods to calculate Bij: For implicit solvents, we can use standard Monte Carlo or molecular dynamics simulations of two proteins in a box and determine insertion and removal energy distribution functions. From the latter, we determine the two-particle partition function and thus Bij using BAR/WHAM. For implicit and explicit solvents, we can calculate the probability that the two proteins are within a volume at least covering the interaction range of the two proteins.29 Calculating Bij from the radial distribution function or equally the potential of mean force via an integral is equivalent to this method. For the coarse-grained simulations performed here, both methods provide accurate results with comparable uncertainties.
The relationship between Kd and Bij given by eq 1 is also well suited for the quantification of protein interactions in molecular dynamics simulations using explicit solvents. Fully atomistic simulations of concentrated protein solutions in explicit solvents have become computationally feasible on the microsecond scale.15,16 These studies have been facilitated by recent improvements in molecular force fields, which correct, among other things, for an increased stickiness of protein surfaces.58−61 These parameterization efforts can benefit from comparisons of Kd and Bij to the experiment.
Fully atomistic simulations are within
reach for the protein pairs
considered here. The box volume 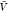 used here corresponds to about 300 000
particles in fully atomistic simulations using explicit solvents.
The binding and unbinding of weakly binding proteins like lysozyme
can be simulated atomistically without bias.15 For more strongly binding proteins, enhanced sampling techniques
have to be applied.62 Binding and unbinding
events of proteins and other molecules can be simulated efficiently
without bias also in molecular dynamics simulations using explicit
solvents using the MARTINI model, for example.63−65
used here corresponds to about 300 000
particles in fully atomistic simulations using explicit solvents.
The binding and unbinding of weakly binding proteins like lysozyme
can be simulated atomistically without bias.15 For more strongly binding proteins, enhanced sampling techniques
have to be applied.62 Binding and unbinding
events of proteins and other molecules can be simulated efficiently
without bias also in molecular dynamics simulations using explicit
solvents using the MARTINI model, for example.63−65
The sampling strategy used here for weak binders is different from the sampling strategy commonly used for strong binders. Strong binders usually have specific interfaces, and the dissociation constant is determined by the binding free energy to these specific interfaces. If these interfaces are known, then we only have to calculate the binding free energy for these specific binding poses dominating Kd.17 For weak binders, also nonspecific binding can contribute significantly to Kd and thus has to be sampled.
Bij also plays an important role in understanding phase separation by which liquid droplets are formed within cells.66 Specifically, the Flory–Huggins solution theory is used to model liquid–liquid phase separations.67,68 In this framework, the Flory interaction parameter χ is determined by Kd and Bij.69Bij also determines the “effective solvation volume” up to a proportionality constant, a quantity commonly used in polymer science.70
The interactions of proteins in nonbinding configurations can be quantified by Bij(u), which is fully determined by Kd and Bij and which is thus a well-defined thermodynamic quantity. These interactions shape the physicochemical properties of the crowded environments inside cells. For example, nonbinding interactions can lead to demixing and therefore to colocalization of binding partners. This colocalization effectively increases the binding probability.
In principle, the contributions Bij(u) of nonbinding interactions to Bij can be determined experimentally. SAXS experiments provide information about Bij in the forward scattering intensities as well as information about dimerization, and thus Kd, encoded in the radius of gyration. Varying protein concentrations in equilibrium sedimentation experiments can provide estimates for Kd and Bij.10 The latter is used to correct for the nonideality of the protein solution. Equation 1 can be viewed as such a correction for nonideality. Especially for weak binders, we expect that Kd and Bij can be estimated accurately enough such that the contributions Bij of nonbinding conformations to Bij can be determined. Similar to the calculations performed here, we expect that in sedimentation experiments, the uncertainties in the estimates for Bij(u) will be much smaller than the individual uncertainties in the estimates for Kd and Bij.
Complexes++ simulation software and the binless-WHAM code can be downloaded free of charge at https://www.github.com/bio-phys/complexespp and at https://github.com/bio-phys/binless-wham, respectively.
Acknowledgments
We thank Drs. Mateusz Sikora, Jakob T. Bullerjahn, Roberto Covino, and Attila Szabo for insightful discussions. We acknowledge the financial support by the Max Planck Society.
Author Present Address
§ Institute of General, Inorganic and Theoretical Chemistry, University of Innsbruck, Innrain 80-82, A-6020 Innsbruck, Austria.
The authors declare no competing financial interest.
References
- Johnson M. E.; Hummer G. Nonspecific binding limits the number of proteins in a cell and shapes their interaction networks. Proc. Natl. Acad. Sci. U.S.A. 2011, 108, 603–608. 10.1073/pnas.1010954108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Johnson M. E.; Hummer G. Evolutionary Pressure on the Topology of Protein Interface Interaction Networks. J. Phys. Chem. B 2013, 117, 13098–13106. 10.1021/jp402944e. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Qin S.; Zhou H.-X. Protein folding, binding, and droplet formation in cell-like conditions. Curr. Opin. Struct. Biol. 2017, 43, 28–37. 10.1016/j.sbi.2016.10.006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kastritis P. L.; Bonvin A. M. J. J. On the binding affinity of macromolecular interactions: daring to ask why proteins interact. J. R. Soc., Interface 2013, 10, 20120835 10.1098/rsif.2012.0835. [DOI] [PMC free article] [PubMed] [Google Scholar]
- McMillan W. G.; Mayer J. E. The Statistical Thermodynamics of Multicomponent Systems. J. Chem. Phys. 1945, 13, 276–305. 10.1063/1.1724036. [DOI] [Google Scholar]
- Hill T. L. Theory of Protein Solutions. I. J. Chem. Phys. 1955, 23, 623–636. 10.1063/1.1742068. [DOI] [Google Scholar]
- McQuarrie D. A.Statistical Mechanics; Harper & Row: New York, 1976. [Google Scholar]
- Tessier P. M.; Vandrey S. D.; Berger B. W.; Pazhianur R.; Sandler S. I.; Lenhoff A. M. Self-interaction chromatography: a novel screening method for rational protein crystallization. Acta Crystallogr., Sect. D: Biol. Crystallogr. 2002, 58, 1531–1535. 10.1107/S0907444902012775. [DOI] [PubMed] [Google Scholar]
- George A.; Chiang Y.; Guo B.; Arabshahi A.; Cai Z.; Wilson W.. Macromolecular Crystallography Part A. Methods in Enzymology Academic Press: 1997; Vol. 276, pp 100–110. [DOI] [PubMed] [Google Scholar]
- Harding S. E.; Rowe A. J. Insight into protein–protein interactions from analytical ultracentrifugation. Biochem. Soc. Trans. 2010, 38, 901–907. 10.1042/BST0380901. [DOI] [PubMed] [Google Scholar]
- Deszczynski M.; Harding S. E.; Winzor D. J. Negative second virial coefficients as predictors of protein crystal growth: Evidence from sedimentation equilibrium studies that refutes the designation of those light scattering parameters as osmotic virial coefficients. Biophys. Chem. 2006, 120, 106–113. 10.1016/j.bpc.2005.10.003. [DOI] [PubMed] [Google Scholar]
- Winzor D. J.; Deszczynski M.; Harding S. E.; Wills P. R. Nonequivalence of second virial coefficients from sedimentation equilibrium and static light scattering studies of protein solutions. Biophys. Chem. 2007, 128, 46–55. 10.1016/j.bpc.2007.03.001. [DOI] [PubMed] [Google Scholar]
- Blanco M. A.; Sahin E.; Li Y.; Roberts C. J. Reexamining protein-protein and protein-solvent interactions from Kirkwood-Buff analysis of light scattering in multi-component solutions. J. Chem. Phys. 2011, 134, 225103 10.1063/1.3596726. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wills P. R.; Winzor D. J. Rigorous analysis of static light scattering measurements on buffered protein solutions. Biophys. Chem. 2017, 228, 108–113. 10.1016/j.bpc.2017.07.007. [DOI] [PubMed] [Google Scholar]
- von Bülow S.; Siggel M.; Linke M.; Hummer G. Dynamic cluster formation determines viscosity and diffusion in dense protein solutions. Proc. Natl. Acad. Sci. U.S.A. 2019, 116, 9843–9852. 10.1073/pnas.1817564116. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nawrocki G.; Karaboga A.; Sugita Y.; Feig M. Effect of protein-protein interactions and solvent viscosity on the rotational diffusion of proteins in crowded environments. Phys. Chem. Chem. Phys. 2019, 21, 876–883. 10.1039/C8CP06142D. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Woo H.-J.; Roux B. Calculation of absolute protein–ligand binding free energy from computer simulations. Proc. Natl. Acad. Sci. U.S.A. 2005, 102, 6825–6830. 10.1073/pnas.0409005102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- De Jong D. H.; Schäfer L. V.; De Vries A. H.; Marrink S. J.; Berendsen H. J. C.; Grubmüller H. Determining equilibrium constants for dimerization reactions from molecular dynamics simulations. J. Comput. Chem. 2011, 32, 1919–1928. 10.1002/jcc.21776. [DOI] [PubMed] [Google Scholar]
- Yesselman J. D.; Denny S. K.; Bisaria N.; Herschlag D.; Greenleaf W. J.; Das R. Sequence-dependent RNA helix conformational preferences predictably impact tertiary structure formation. Proc. Natl. Acad. Sci. U.S.A. 2019, 116, 16847–16855. 10.1073/pnas.1901530116. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zimm B. H. Application of the Methods of Molecular Distribution to Solutions of Large Molecules. J. Chem. Phys. 1946, 14, 164–179. 10.1063/1.1724116. [DOI] [Google Scholar]
- Neal B.; Asthagiri D.; Lenhoff A. Molecular Origins of Osmotic Second Virial Coefficients of Proteins. Biophys. J. 1998, 75, 2469–2477. 10.1016/S0006-3495(98)77691-X. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kim B.; Song X. Calculations of the second virial coefficients of protein solutions with an extended fast multipole method. Phys. Rev. E 2011, 83, 011915 10.1103/PhysRevE.83.011915. [DOI] [PubMed] [Google Scholar]
- Singh J. K.; Kofke D. A. Mayer Sampling: Calculation of Cluster Integrals using Free-Energy Perturbation Methods. Phys. Rev. Lett. 2004, 92, 220601 10.1103/PhysRevLett.92.220601. [DOI] [PubMed] [Google Scholar]
- Benjamin K. M.; Singh J. K.; Schultz A. J.; Kofke D. A. Higher-Order Virial Coefficients of Water Models. J. Phys. Chem. B 2007, 111, 11463–11473. 10.1021/jp0710685. [DOI] [PubMed] [Google Scholar]
- Grünberger A.; Lai P.-K.; Blanco M. A.; Roberts C. J. Coarse-Grained Modeling of Protein Second Osmotic Virial Coefficients: Sterics and Short-Ranged Attractions. J. Phys. Chem. B 2013, 117, 763–770. 10.1021/jp308234j. [DOI] [PubMed] [Google Scholar]
- Qin S.; Zhou H.-X. Calculation of Second Virial Coefficients of Atomistic Proteins Using Fast Fourier Transform. J. Phys. Chem. B 2019, 123, 8203–8215. 10.1021/acs.jpcb.9b06808. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mereghetti P.; Gabdoulline R. R.; Wade R. C. Brownian Dynamics Simulation of Protein Solutions: Structural and Dynamical Properties. Biophys. J. 2010, 99, 3782–3791. 10.1016/j.bpj.2010.10.035. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mereghetti P.; Martinez M.; Wade R. C. Long range Debye-Hückel correction for computation of grid-based electrostatic forces between biomacromolecules. BMC Biophys. 2014, 7, 4 10.1186/2046-1682-7-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ashton D. J.; Wilding N. B. Three-body interactions in complex fluids: Virial coefficients from simulation finite-size effects. J. Chem. Phys. 2014, 140, 244118 10.1063/1.4883718. [DOI] [PubMed] [Google Scholar]
- Ashton D. J.; Wilding N. B. Quantifying the effects of neglecting many-body interactions in coarse-grained models of complex fluids. Phys. Rev. E 2014, 89, 031301 10.1103/PhysRevE.89.031301. [DOI] [PubMed] [Google Scholar]
- Bennett C. H. Efficient estimation of free energy differences from Monte Carlo data. J. Comput. Phys. 1976, 22, 245–268. 10.1016/0021-9991(76)90078-4. [DOI] [Google Scholar]
- Souaille M.; Roux B. Extension to the Weighted Histogram Analysis Method Combining Umbrella Sampling With Free Energy Calculations. Comput. Phys. Commun. 2001, 135, 40–57. 10.1016/S0010-4655(00)00215-0. [DOI] [Google Scholar]
- Shirts M. R.; Chodera J. D. Statistically Optimal Analysis of Samples from Multiple Equilibrium States. J. Chem. Phys. 2008, 129, 124105 10.1063/1.2978177. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rosta E.; Nowotny M.; Yang W.; Hummer G. Catalytic Mechanism of RNA Backbone Cleavage by Ribonuclease H from Quantum Mechanics/molecular Mechanics Simulations. J. Am. Chem. Soc. 2011, 133, 8934–8941. 10.1021/ja200173a. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Harding S. E.; Horton J. C.; Jones S.; Thornton J. M.; Winzor D. J. COVOL: An Interactive Program for Evaluating Second Virial Coefficients from the Triaxial Shape or Dimensions of Rigid Macromolecules. Biophys. J. 1999, 76, 2432–2438. 10.1016/S0006-3495(99)77398-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Onnes H. K.Through Measurement to Knowledge: The Selected Papers of Heike Kamerlingh Onnes 1853-1926; Gavroglu K.; Goudaroulis Y., Eds.; Springer Netherlands: Dordrecht, 1991; pp 146–163. [Google Scholar]
- Kamerlingh Onnes H. In Expression of the Equation of State of Gases and Liquids by Means of Series. KNAW Proceedings, Amsterdam, 1902; pp 125–147.
- Hill T. L. Theory of Solutions. II. Osmotic Pressure Virial Expansion and Light Scattering in Two Component Solutions. J. Chem. Phys. 1959, 30, 93–97. 10.1063/1.1729949. [DOI] [Google Scholar]
- Widom B.; Underwood R. C. Second Osmotic Virial Coefficient from the Two-Component van der Waals Equation of State. J. Phys. Chem. B 2012, 116, 9492–9499. 10.1021/jp3051802. [DOI] [PubMed] [Google Scholar]
- Gilson M.; Given J.; Bush B.; McCammon J. The statistical-thermodynamic basis for computation of binding affinities: a critical review. Biophys. J. 1997, 72, 1047–1069. 10.1016/S0006-3495(97)78756-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Woolley H. W. The Representation of Gas Properties in Terms of Molecular Clusters. J. Chem. Phys. 1953, 21, 236–241. 10.1063/1.1698866. [DOI] [Google Scholar]
- Schröer W.; Weiss V. C. Molecular association in statistical thermodynamics. J. Mol. Liq. 2015, 205, 22–30. 10.1016/j.molliq.2014.08.013. [DOI] [Google Scholar]; Global Perspectives on the Structure and Dynamics of Liquids and Mixtures: Experiment and Simulation 9–13 September, 2013.
- Lebowitz J. L.; Percus J. K.; Verlet L. Ensemble Dependence of Fluctuations with Application to Machine Computations. Phys. Rev. 1967, 153, 250–254. 10.1103/PhysRev.153.250. [DOI] [Google Scholar]
- Kirkwood J. G.; Buff F. P. The Statistical Mechanical Theory of Solutions. I. J. Chem. Phys. 1951, 19, 774–777. 10.1063/1.1748352. [DOI] [Google Scholar]
- Ben-Naim A.; Navarro A. M.; Leal J. M. A Kirkwood-Buff analysis of local properties of solutions. Phys. Chem. Chem. Phys. 2008, 10, 2451–2460. 10.1039/b716116f. [DOI] [PubMed] [Google Scholar]
- Singh J. K.; Kofke D. A. Mayer Sampling: Calculation of Cluster Integrals using Free-Energy Perturbation Methods. Phys. Rev. Lett. 2004, 92, 220601 10.1103/PhysRevLett.92.220601. [DOI] [PubMed] [Google Scholar]
- Buchete N.-V.; Hummer G. Coarse Master Equations for Peptide Folding Dynamics. J. Phys. Chem. B 2008, 112, 6057–6069. 10.1021/jp0761665. [DOI] [PubMed] [Google Scholar]
- Sophianopoulos A. J. Association Sites of Lysozyme in Solution: I. THE ACTIVE SITE. J. Biol. Chem. 1969, 244, 3188–3193. [PubMed] [Google Scholar]
- Diamond R. Real-space refinement of the structure of hen egg-white lysozyme. J. Mol. Biol. 1974, 82, 371–391. 10.1016/0022-2836(74)90598-1. [DOI] [PubMed] [Google Scholar]
- Kang R. S.; Daniels C. M.; Francis S. A.; Shih S. C.; Salerno W. J.; Hicke L.; Radhakrishnan I. Solution Structure of a CUE-Ubiquitin Complex Reveals a Conserved Mode of Ubiquitin Binding. Cell 2003, 113, 621–630. 10.1016/S0092-8674(03)00362-3. [DOI] [PubMed] [Google Scholar]
- Bennett S. E.; Schimerlik M. I.; Mosbaugh D. W. Kinetics of the uracil-DNA glycosylase/inhibitor protein association. Ung interaction with Ugi, nucleic acids, and uracil compounds. J. Biol. Chem. 1993, 268, 26879–26885. [PubMed] [Google Scholar]
- Putnam C. D.; Shroyer M. J. N.; Lundquist A. J.; Mol C. D.; Arvai A. S.; Mosbaugh D. W.; Tainer J. A. Protein mimicry of DNA from crystal structures of the uracil-DNA glycosylase inhibitor protein and its complex with Escherichia coli uracil-DNA glycosylase. J. Mol. Biol. 1999, 287, 331–346. 10.1006/jmbi.1999.2605. [DOI] [PubMed] [Google Scholar]
- Kim Y. C.; Hummer G. Coarse-grained Models for Simulations of Multiprotein Complexes: Application to Ubiquitin Binding. J. Mol. Biol. 2008, 375, 1416–1433. 10.1016/j.jmb.2007.11.063. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Miyazawa S.; Jernigan R. L. Estimation of effective interresidue contact energies from protein crystal structures: quasi-chemical approximation. Macromolecules 1985, 18, 534–552. 10.1021/ma00145a039. [DOI] [Google Scholar]
- Miyazawa S.; Jernigan R. L. Residue - Residue Potentials with a Favorable Contact Pair Term and an Unfavorable High Packing Density Term, for Simulation and Threading. J. Mol. Biol. 1996, 256, 623–644. 10.1006/jmbi.1996.0114. [DOI] [PubMed] [Google Scholar]
- Efron B. Bootstrap Methods: Another Look at the Jackknife. Ann. Stat. 1979, 7, 1–26. 10.1214/aos/1176344552. [DOI] [Google Scholar]
- Straatsma T.; Berendsen H.; Stam A. Estimation of statistical errors in molecular simulation calculations. Mol. Phys. 1986, 57, 89–95. 10.1080/00268978600100071. [DOI] [Google Scholar]
- Best R. B.; Zheng W.; Mittal J. Balanced Protein-Water Interactions Improve Properties of Disordered Proteins and Non-Specific Protein Association. J. Chem. Theory Comput. 2014, 10, 5113–5124. 10.1021/ct500569b. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Piana S.; Donchev A. G.; Robustelli P.; Shaw D. E. Water Dispersion Interactions Strongly Influence Simulated Structural Properties of Disordered Protein States. J. Phys. Chem. B 2015, 119, 5113–5123. 10.1021/jp508971m. [DOI] [PubMed] [Google Scholar]
- Robustelli P.; Piana S.; Shaw D. E. Developing a molecular dynamics force field for both folded and disordered protein states. Proc. Natl. Acad. Sci. U.S.A. 2018, 115, E4758–E4766. 10.1073/pnas.1800690115. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Piana S.; Robustelli P.; Tan D.; Chen S.; Shaw D. E. Development of a Force Field for the Simulation of Single-Chain Proteins and Protein-Protein Complexes. J. Chem. Theory Comput. 2020, 16, 2494–2507. 10.1021/acs.jctc.9b00251. [DOI] [PubMed] [Google Scholar]
- Siebenmorgen T.; Engelhard M.; Zacharias M. Prediction of protein-protein complexes using replica exchange with repulsive scaling. J. Comput. Chem. 2020, 41, 1436–1447. 10.1002/jcc.26187. [DOI] [PubMed] [Google Scholar]
- Marrink S. J.; Risselada H. J.; Yefimov S.; Tieleman D. P.; de Vries A. H. The MARTINI Force Field: Coarse Grained Model for Biomolecular Simulations. J. Phys. Chem. B 2007, 111, 7812–7824. 10.1021/jp071097f. [DOI] [PubMed] [Google Scholar]
- Stark A. C.; Andrews C. T.; Elcock A. H. Toward Optimized Potential Functions for Protein-Protein Interactions in Aqueous Solutions: Osmotic Second Virial Coefficient Calculations Using the MARTINI Coarse-Grained Force Field. J. Chem. Theory Comput. 2013, 9, 4176–4185. 10.1021/ct400008p. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schmalhorst P. S.; Deluweit F.; Scherrers R.; Heisenberg C.-P.; Sikora M. Overcoming the Limitations of the MARTINI Force Field in Simulations of Polysaccharides. J. Chem. Theory Comput. 2017, 13, 5039–5053. 10.1021/acs.jctc.7b00374. [DOI] [PubMed] [Google Scholar]
- Brangwynne C.; Tompa P.; Pappu R. Polymer physics of intracellular phase transitions. Nat. Phys. 2015, 11, 899–904. 10.1038/nphys3532. [DOI] [Google Scholar]
- Huggins M. L. Solutions of Long Chain Compounds. J. Chem. Phys. 1941, 9, 440. 10.1063/1.1750930. [DOI] [Google Scholar]
- Flory P. J. Thermodynamics of High Polymer Solutions. J. Chem. Phys. 1941, 9, 660. 10.1063/1.1750971. [DOI] [Google Scholar]
- Wei M.-T.; Elbaum-Garfinkle S.; Holehouse A. S.; Chen C. C.-H.; Feric M.; Arnold C. B.; Priestley R. D.; Pappu R. V.; Brangwynne C. P. Phase behaviour of disordered proteins underlying low density and high permeability of liquid organelles. Nat. Chem. 2017, 9, 1118–1125. 10.1038/nchem.2803. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Harmon T. S.; Holehouse A. S.; Rosen M. K.; Pappu R. V. Intrinsically disordered linkers determine the interplay between phase separation and gelation in multivalent proteins. eLife 2017, 6, e30294 10.7554/eLife.30294. [DOI] [PMC free article] [PubMed] [Google Scholar]