Value-Related Neuronal Responses in the Human Amygdala during Observational Learning

Abstract

The amygdala plays an important role in many aspects of social cognition and reward learning. Here, we aimed to determine whether human amygdala neurons are involved in the computations necessary to implement learning through observation. We performed single-neuron recordings from the amygdalae of human neurosurgical patients (male and female) while they learned about the value of stimuli through observing the outcomes experienced by another agent interacting with those stimuli. We used a detailed computational modeling approach to describe patients' behavior in the task. We found a significant proportion of amygdala neurons whose activity correlated with both expected rewards for oneself and others, and in tracking outcome values received by oneself or other agents. Additionally, a population decoding analysis suggests the presence of information for both observed and experiential outcomes in the amygdala. Encoding and decoding analyses suggested observational value coding in amygdala neurons occurred in a different subset of neurons than experiential value coding. Collectively, these findings support a key role for the human amygdala in the computations underlying the capacity for learning through observation.

SIGNIFICANCE STATEMENT Single-neuron studies of the human brain provide a unique window into the computational mechanisms of cognition. In this study, epilepsy patients implanted intracranially with hybrid depth electrodes performed an observational learning (OL) task. We measured single-neuron activity in the amygdala and found a representation for observational rewards as well as observational expected reward values. Additionally, distinct subsets of amygdala neurons represented self-experienced and observational values. This study provides a rare glimpse into the role of human amygdala neurons in social cognition.

Introduction

Acquiring new information about rewards associated with different stimuli is at the core of an animal's ability to adapt behavior to maximize future rewards (Sutton and Barto, 2018). In many organisms, reinforcement learning (RL) can take place through taking actions and experiencing outcomes but also indirectly through observing the actions taken and outcomes obtained by others, in a form of learning known as observational learning (OL; Cooper et al., 2012; Van Den Bos et al., 2013; Dunne et al., 2016; Charpentier and O'Doherty, 2018). The computational and neural basis of reinforcement-learning through direct experience has been the focus of intense study, and much is known about its neural underpinnings (Doya, 1999; Daw et al., 2005; Lee et al., 2012; O'Doherty et al., 2017). In contrast, the neural mechanisms of OL have been much less well studied, especially in humans.

A core feature of RL models is that to decide whether or not to choose a particular stimulus or action, it is first necessary to consider the expected future reward associated with that option. Consistent with this, neuronal activity has been found in the amygdala as well as elsewhere in the brain, which tracks the expected future reward associated with various options at the time of decision making (Gottfried et al., 2003; Holland and Gallagher, 2004; Hampton et al., 2006; Salzman and Fusi, 2010; Rudebeck et al., 2017; Wang et al., 2017). Lesions of the amygdala have shown it is necessary for guiding behavior on the basis of expected future outcomes learned about through experience (Málková et al., 1997; Bechara et al., 1999; Schoenbaum et al., 2003; Hampton et al., 2007; De Martino et al., 2010), suggesting that value representations in this area are causally relevant for driving value-related behavior. The amygdala performs these functions in concert with a broader network that regulates reward learning, memory, and emotion (Murray, 2007). Adaptive responses to reward cues and devaluation depend on amygdala-orbitofrontal cortex (OFC) connections in monkeys (Baxter et al., 2000) and mice (Lichtenberg et al., 2017). The amygdala also receives significant dopaminergic projections from the ventral tegmental area (VTA) and the substantia nigra pars compacta (SNc; Aggleton et al., 1980).

On the role of the amygdala in OL specifically, recent evidence has suggested a role for amygdala neurons in non-human primates in responding to the rewards obtained by others (Chang et al., 2015) as well as to others' choices (Grabenhorst et al., 2019). However, much less is known about the role of the amygdala in the human brain in processes related to OL. One human single-neuron study reported amygdala neurons which tracked observational outcomes (Hill et al., 2016), although the most robust signals were found in rostral anterior cingulate cortex (rACC). Building on evidence implicating the human amygdala not only in reward processing but also in social cognition more broadly (Rutishauser et al., 2015a), we aimed to address how neurons in the human amygdala are involved in OL. We asked a group of neurosurgery patients to perform an OL task while we performed single-neuron recordings from electrodes in the amygdala. This provided us with a rare opportunity to investigate the role of amygdala neurons in value prediction coding and updating during OL. Since observational and experiential learning differ in that learning by observation is necessarily passive, to control for equivalence between observational and experiential learning, our task consisted of a passive Pavlovian paradigm, including instrumental trials exclusively to test contingency learning. We hypothesized we would find evidence for reinforcement-learning signals in the amygdala during OL, especially concerning the representation of the value of stimuli learned through observation. Furthermore, we also contrasted the contribution of amygdala neurons to OL with that of the role of these neurons in experiential learning. Of particular interest was the question of whether an overlapping or distinct population of neurons in the amygdala contributes to encoding reinforcement-learning variables in observational compared with experiential learning.

Materials and Methods

Electrophysiology and electrodes

Broadband extracellular recordings were filtered from 0.1 Hz to 9 kHz and sampled at 32 kHz (Neuralynx Inc). The data reported here was recorded bilaterally from the amygdala, with one macroelectrode in each side. Each of these macroelectrodes contained eight 40-μm microelectrodes. Recordings were performed bipolar, with one microwire in each area serving as a local reference (Minxha et al., 2018). Electrode locations were chosen exclusively according to clinical criteria.

Patients

Twelve patients (four females) who were implanted with depth electrodes before possible surgical treatment of drug resistant localization related epilepsy volunteered to participate and gave informed consent. Four of the patients performed two recording sessions, and the others performed only one. One pilot session was not included in the analysis and one session was discarded due to technical error. Protocols were approved by the Institutional Review Boards of the California Institute of Technology, the Cedars-Sinai Medical Center, and the Huntington Memorial Hospital. Electrode location was determined based on preoperative and postoperative T1 scans obtained for each patient. We registered each patients postoperative scan to their preoperative scan, which we in turn registered to the CIT168 template brain (Tyszka and Pauli, 2016; which is in MNI152 coordinates) using previously published methods (Minxha et al., 2017).

Electrode localization, spike detection, and sorting

Spike detection and sorting was performed as previously described using the semiautomatic template-matching algorithm OSort (Rutishauser et al., 2006). Channels with interictal epileptic activity were excluded. Across all valid sessions, we isolated in total 202 putative single units in amygdala [135 in right amygdala (RA) and 67 in left amygdala (LA)]. We will refer to these putative single units as “neuron” and “cell” interchangeably. Units isolated from electrodes localized outside of the amygdala were not included in the analyses. Using the probabilistic CIT168 atlas of amygdala nuclei (Tyszka and Pauli, 2016), we determined the subnuclei from which the unit was recorded from: deep or basolateral (BL), with 117 units; superficial or corticomedial (CM), with 39 units; and remaining nuclei (R), with 46 units, which contained neurons from either the anterior amygdaloid area or the central nucleus (we were not able to distinguish between the two). We characterized the quality of the isolated units using the following metrics: the percentage of interspike intervals (ISIs) below 3 ms was 0.49 ± 0.63%; the mean firing rate was 1.98 ± 2.74 Hz; the SNR at the mean waveform peak, across neurons, was 5.12 ± 3.24; the SNR of the mean waveform across neurons was 1.87 ± 0.97; the modified coefficient of variation (CV2; Holt et al., 1996) was 0.95 ± 0.11; and the isolation distance (Schmitzer-Torbert et al., 2005) was 1.69 ± 0.59 for neurons in which it was defined.

Experimental design

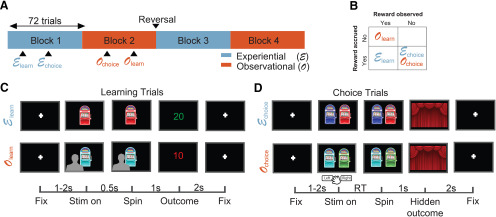
Patients performed a multiarmed bandit task (Dunne et al., 2016) with 288 trials in total, distributed across two experiential and two observational blocks. Block order was chosen to always interleave block types, and the type of the initial block was chosen randomly (Fig. 1A). Each block had 72 trials, out of which 48 were no-choice trials and 24 were binary choice trials. Choice and no-choice trials were randomly distributed across each block. Experiential no-choice trials began with the presentation of a single bandit, whose lever was pulled automatically 0.5 s after stimulus onset. Each block consisted of two possible bandits that were chosen randomly in every trial. Subjects were told that the color of a bandit allows them to differentiate between the different bandits. Bandits were repeated across blocks of the same type, with the possibility of contingency reversal. Reversals could happen only once in the entire task. For the sessions that did include a reversal (nine out of the 14 analyzed sessions), it always happened right before the beginning of the third block of trials, at the halfway point in the session. Patients were not told in advance about the reversals, but were fully instructed about the reward structure of the task (as explained below).

Figure 1.

OL task. A, Block structure. The task had 288 trials in total, in four blocks of 72 trials. Each block contained either experiential or OL trials, as well as choice trials. Block order was interleaved, and bandit values were reversed after the end of block 2. B, Reward structure. Reward was accrued to subjects' total only in experiential trials, and reward feedback was only presented in learning trials, both in experiential and observational blocks. C, Learning trials structure. Top row, Experiential learning trials. After a fixation cross of jittered duration between 1 and 2 s, subjects viewed a one-armed bandit whose tumbler was spun after 0.5 s. After a 1-s spinning animation, subjects received outcome feedback, which lasted for 2 s. Bottom row, OL trials. Subjects observed a video of another player experiencing learning trials with the same structure. Critically, outcomes received by the other player were not added to the subject's total. Lower bar, Timing of trial events in seconds. D, Choice trials structure. Subjects chose between the two bandits shown in the learning trials of the current block. After deciding, the chosen bandit's tumbler spun for 1 s, and no outcome feedback was presented.

Outcome was presented 1 s after the automatic lever press, and subjects received feedback on the amount of points won or lost in the trial, which was added or subtracted to their personal total. The amount of points for each trial was selected from a normal distribution, with specific means and variances for each bandit, truncating at −50 and +50 points. Subjects could not see their added points total during the task, but were shown their overall points total after the end of the task.

Observational no-choice trials consisted in watching a prerecorded video of another player experiencing the same trial structure. These videos contained the back of the head of a person (always the same individual), as he watched a screen containing a bandit playing out a no-choice trial, including the outcome in points. The person did not move during the video, but the bandit on the screen was animated to display the lever press and outcome display, same as in experiential trials.

Points received by the other player in the prerecorded video were not added or subtracted to subjects' personal total, and subjects were informed of this fact. Choice trials started with the presentation of two bandits, and subjects had up to 20 s to select one via button press, which would cause the lever on the corresponding bandit to be pulled. If subjects failed to respond within 20 s, the trial was considered missed, and subjects received a penalty of 20 points. In choice trials, after a 1-s period, subjects observed closed curtains on the screen instead of outcome feedback. Subjects were told they should attempt to maximize the amount of received rewards and that they would still receive or lose the amount of points displayed behind the curtain, despite the lack of feedback. This was done to restrict learning to no-choice trials, to further dissociate the decision-making and reward-learning components of the task. The two bandits that could be chosen in choice trials were always the two possible bandits from no-choice trials in the current block. Intertrial intervals were jittered with a uniform distribution between 1 and 3 s regardless of block and trial type. To further motivate subjects, a leaderboard was shown in the end of the task, displaying the amount of points won by the subject, in comparison to amounts won by previous participants.

Statistical analyses

Computational modeling

We focused on the form of OL referred to as vicarious learning, which takes place when individuals observe others taking actions and experiencing outcomes, rather than doing so themselves (Charpentier and O'Doherty, 2018). At the computational level, we hypothesized that vicarious learning involves similar mechanisms to those used for experiential learning. To test this hypothesis, we adapted a simple model-free learning algorithm from the experiential to the observational domain (Cooper et al., 2012). For both observational and experiential learning, this model learns expected values (EVs) for each stimulus via a reward prediction error (RPE) that quantifies discrepancies between predicted values and experienced reward outcomes. This prediction error signal is then used to iteratively update the value predictions.

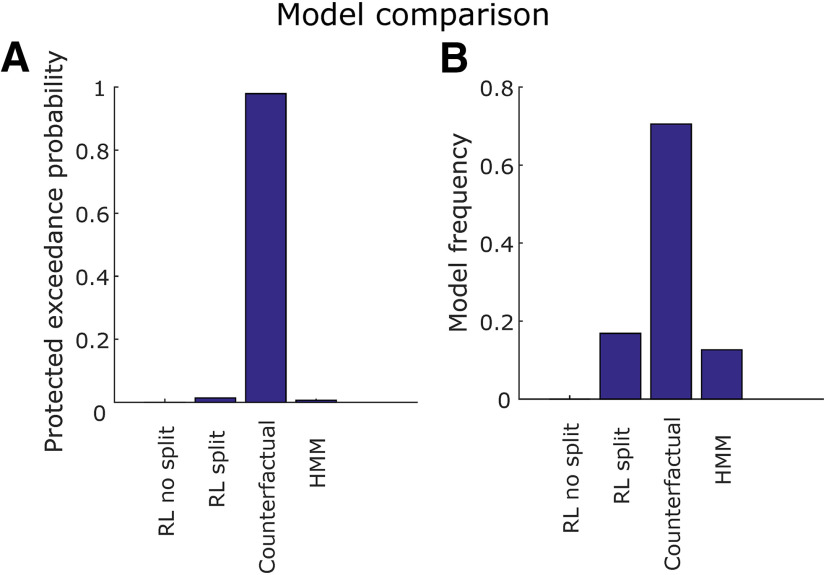
We used the behavior in the choice trials to fit four different types of computational models. We used a hierarchical Bayesian inference (HBI) framework to achieve both hierarchical model fitting and model comparison (Piray et al., 2019). This framework allowed us to infer a protected exceedance probability for each model, as well as individualized model parameters for each subject. The model with the largest protected exceedance probability was chosen for the model-based encoding and decoding analyses. The exceedance probability value expresses the probability that each model is the most frequent in the comparison set (Rigoux et al., 2014). Protected exceedance probability is a typically more conservative metric which takes into account the possibility that none of the compared models is supported by the data (Piray et al., 2019).

We first provide a brief summary of each of the computational models before describing each in detail. The first model was a simple RL model (Sutton and Barto, 2018) with a single learning rate parameter for both experiential and observational trials [RL (no split)]; the second model was the same, except that learning rates were split between observational and experiential trials [RL (split)]; the third model was a counterfactual RL model with a single learning rate in which EVs for played bandits were updated as usual, but EVs for the bandits that were not seen in a trial were also updated, in the opposite direction of the bandits that were actually played [RL (counterfactual)]. The last model was a hidden Markov model (HMM) with built-in reversals, with two states. The first state assumed one of the bandits in the block had a positive mean payout, while the other bandit had a negative mean payout with the same magnitude. The second state mirrored the first one, switching which bandits had the positive and negative payouts. This model allowed us to include inferred reversals between those two states, and to model the inferred reversal rate that patients assumed to be true. Expected values in all models were initialized to zero for all bandits.

The RL (no split) model keeps a cached value V for the EV of each bandit i, in every trial t, updated according to the following rule:

In this case, α represents the learning rate for both the experiential and observational cases, δ represents RPE, and R represents reward feedback value. The RL (split) model is identical, except that a learning rate α_exp is applied in experiential trials and another learning rate α_obs is applied in observational trials.

The RL (counterfactual) model is identical to RL (no split), except that both bandits are updated on every trial, in opposite directions. For the chosen and unchosen bandits in every trial, the EV updates are as follows:

The HMM has been formalized similarly to previous work (Prévost et al., 2013). An inferred state variable S_t represented the association between bandits and rewards at trial t. Assuming the two bandits in a block are arbitrarily indexed as A and B, that the magnitude of the inferred mean payout was a free parameter μ fixed throughout the task, and that mu_A and mu_B denote the mean payouts for bandits A and B, respectively,

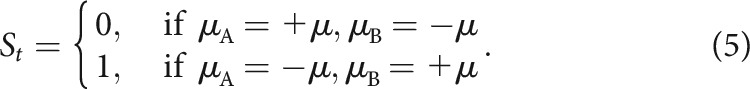This model allows for inferring reversals between states, which means the inferred mean payouts of the two bandits are swapped. The reversal structure is dictated by the following reversal matrix, assuming reversal rates were a free parameter r fixed throughout the task:

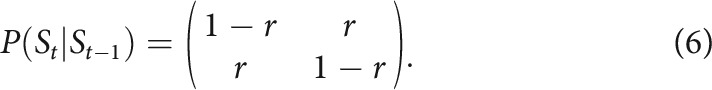Given this transition structure, the prior $Prior(S_t)$ would be updated in every trial as follows:

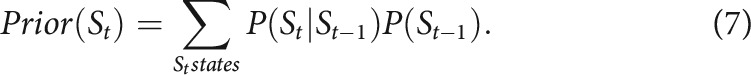Initial state probabilities were set to 0.5. Then, using Bayes' rule, the posterior would be updated using evidence from the outcome R_t:

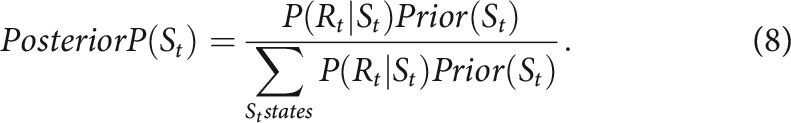Outcome variables were assumed to have a Gaussian distribution, with a fixed standard deviation free parameter σ:

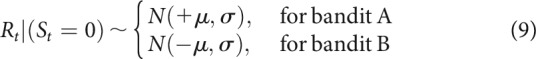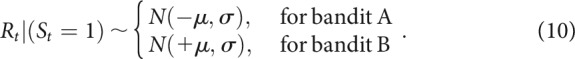This framework allowed for computing EVs in each trial t for each bandit j, taking into account the probability of being in each state:

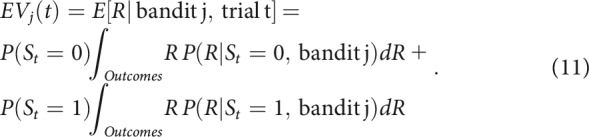Since outcomes were assumed to be normally distributed, for each bandit this reduced to

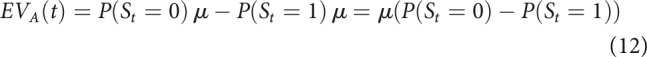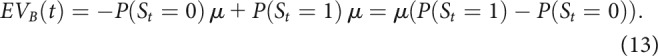This means that EVs for a certain bandit were larger if patients inferred they were more likely in the state in which that bandit was better. For example, if P(S_t = 0) = 0.9 and P(S_t = 1) = 0.1, then:

We used the cached value estimates of EV as parameters in a softmax function controlled by an inverse-temperature parameter β for each session, to generate decision probabilities in free-choice trials. For the RL models, we constrained α, α_exp, and α_obs in the (0,1) interval, and β in the (0,10) interval. In the HMM, we constrained r in the (0,1) interval, and both μ and σ in the (0,20) interval.

Model comparison was performed by computing the protected exceedance probability of each model and selecting the one with the largest value, which was RL (counterfactual; Fig. 3). For all subsequent model-based analyses, we display results using the EVs and RPEs produced by the RL (counterfactual) model. An example of how the EVs assigned to each bandit typically behave in a modeled session is displayed in Figure 2B.

Figure 3.

Model comparison. A, Protected exceedance probability. This is the probability that each one of the four models fit using HBI (RL split, RL no split, counterfactual, and HMM) was more likely than any other, taking into account the possibility that there is no difference between models. B, Model frequency. This is the proportion of individual patients whose behavior is better explained by each model. The counterfactual learning model outperforms the others both in terms of protected exceedance probability and model frequency.

Figure 2.

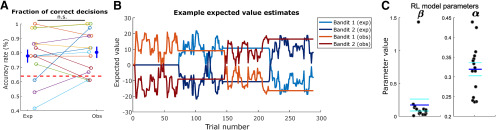
Behavior and RL model. A, Accuracy rate of all sessions as defined by the fraction of free trials in which a subject chose the bandit with highest mean payout, discarding the first 25% of trials in each block. Each color represents a different session, for experiential and observational trials, with average and standard error indicated on the left and right. Accuracy in experiential and observational trials was not significantly different (p < 0.66, two-sample t test), n.s., not significant. The dashed red line indicates the chance level estimated by the theoretical 95th percentile of correct proportions, obtained from an agent making random decisions with p = 0.5. B, Typical time course of modeled EVs throughout the task, using the RL (counterfactual) model. Bandit 1 (exp) and Bandit 2 (exp) indicate EVs for each of the two bandits shown in experiential blocks, respectively, whereas Bandit 1 (obs) and Bandit 2 (obs) indicate EVs for each of the two bandits shown in observational blocks, respectively. C, Parameter fits for each valid session, for the chosen RL model. The model contained a single learning rate (α) for experiential and observational trials and an inverse temperature β. Dark blue horizontal lines indicate parameter means, and cyan horizontal lines indicate SE.

Population decoding analysis

Population decoding was performed with the Neural Decoding Toolbox (Meyers, 2013) as described previously (Rutishauser et al., 2015b). We pooled neurons from all sessions into a single pseudopopulation with 202 amygdala neurons. To achieve this alignment on a trial by trial basis across sessions, we created discrete trial bins using quantiles of the decoded variable, with the same number of trials, for each session. For example, for outcome decoding, we found which trials for each session fit into each one of four quantiles of received outcomes and aligned trials that fell in the same bin across sessions, assuming all neurons belonged to the same session. This session-based trial binning meant the exact quantile boundaries were not necessarily the same across sessions. For example, a trial in which the outcome was 10 points might have been placed on bin 2 for one session and on bin three for another session, depending on the distribution of outcomes in each session. Finally, all learning trials across sessions had the same event timing, so no additional temporal alignment was needed.

We used this strategy to create a neural activity tensor of dimensions (n_neurons,n_trials), where n_trials is the number of trials in a single session. Decoding consisted of training and testing a classifier tasked with correctly predicting which bin of the variable of interest each trial belonged to, only from information contained in the neural activity tensor.

We used a maximum Pearson correlation classifier with access to spike counts binned in a time window of interest. This classifier learns by obtaining a mean representation x_c of each class c in the multidimensional neural population space, and assigns new data points y to a class c* corresponding to $c^{*}=argma{x}_c(corr(x_c,y))$.

We used 10-fold cross-validation and 20 cross-validation fold resample runs, which were averaged to generate a testing decoding accuracy score. Significance was determined via permutation test with 500 re-runs, shuffling regressor labels. Expected value decoding was only tested in the preoutcome period (300–1500 ms from trial onset), whereas outcome and prediction error decoding was only tested in the postoutcome period (300–2000 ms from outcome onset).

Single-neuron encoding analysis

For every tested neuron n, we used a Kruskal–Wallis test (Kruskal and Wallis, 1952) to fit binned spike counts y_n(t) (1200-ms bins for preoutcome, 1700-ms bins for postoutcome, 3500-ms bins for the whole trial), implemented with the MATLAB function kruskalwallis. Outcome and prediction errors were regressed only on the postoutcome period, and expected values were regressed only on the preoutcome period. Trial type regression was performed in the entire trial. Significance was determined through permutation tests by shuffling variable labels. For expected value and prediction error time series, in which trials might not be independent from each other, we performed variable shuffling using surrogate time series as described previously (Schreiber and Schmitz, 2000). For the other variables, we used standard random permutations. We then used χ² yielded by the Kruskal–Wallis test as a statistic for each regressor.

Simulation for comparing encoding and decoding

In order to better understand possible discrepancies between the encoding and decoding analyses, we set out to simulate a population of artificial neurons responding to a categorical variable, and to compare encoding and decoding analyses within this population for varying levels of noise. Each simulation contained a population of 200 Poisson point processes as artificial neurons in 96 trials. We created an artificial categorical variable X to be encoded and decoded, whose value would be sampled randomly with a uniform distribution in each trial from [1,2,3,4]. The latent firing rate λ_n of each neuron n was then given by:

The factor μ_n scales the influence of the categorical variable X over latent firing rates. For every neuron n, and for every simulation, we sampled μ_n from a normal distribution N(0,0.4). The factor ϵ controls the amount of random noise added to latent firing rates. For every trial, ϵ was sampled from a normal distribution N(0,0.4 σ), where σ is the noise factor variable. We ran 100 simulations with each one of the following noise factors σ: [1,5,20]. We included 0.4 as a factor in the distributions of μ_n and σ only with the intent of generating plausible spike counts.

Following the construction of latent firing rates, we simulated how many spikes occurred in a time window of 1 s and used these spike counts as the input for encoding and decoding analyses. We performed encoding by applying the previously described Kruskal–Wallis test, using the artificial spike counts and categories. We obtained chance levels for the encoding analysis theoretically, from an inverse binomial distribution, assuming a chance level of 0.05 and a total neuron population of 200. Additionally, we performed decoding of the variable X from spike counts with the previously described maximum Pearson correlation classifier, with a 75–25% split between training and testing trials, re-sampling cross-validation folds 10 times. Chance levels in decoding single test trials were obtained theoretically from an inverse binomial distribution, assuming a chance level of 0.25 (since X had four categories).

Finally, we compared how well decoding and encoding analyses performed for varying levels of the noise factor σ, in terms of decoding accuracy in single test trials, as well as significant neuron count.

Results

Behavioral performance

We obtained a behavioral metric of subject performance on choice trials (Fig. 2A): we defined “correct” trials as those in which the subject selected the bandit with the highest mean payout, disregarding the first 25% of trials in each block. The reason we excluded the first 25% of trials from accuracy analysis only was to get a coarse metric of overall accuracy discarding the transient initial period of learning. Note this transient period is still of interest in terms of measuring expected values and RPEs, so it is still included in the computational modeling and the neural analysis. We found that in 12 out of 15 recording sessions, performance was above the 95th percentile of a random agent, theoretically determined by a binomial distribution with success probability 0.5, thereby indicating that behavior in these sessions was significantly better than chance.

Overall, subjects performed well in both the experiential and observational condition (Fig. 2A): the proportion correct in all trials was 0.776 ± 0.038. Taking only experiential trials, the proportion correct was 0.763 ± 0.044; in observational trials, it was 0.789 ± 0.039. Experiential and observational correct proportions were not significantly different from each other across all sessions (two-sample t test, p = 0.6641 > 0.05). We estimated the chance level using the theoretical 95th percentile of correct proportions, obtained from an agent making random decisions with p = 0.5, assuming a binomial distribution. We also tested whether the correct proportions were different, in all the trials following a reversal, for the patients that did experience a reversal, between observed (0.78 ± 0.072) and experiential trials (0.800 ± 0.074), but found no evidence of a difference (two-sample t test, two-tailed, p = 0.894).

Computational model fitting

We fit four computational models to each subjects' behavior during choice trials (see Materials and Methods): a model-free RL model with one learning rate for experiential and observational trials [(RL (no split)]; a model-free RL model with separate learning rates split between experiential and observational trials [RL (split)]; a counterfactual RL model in which outcomes from the played bandit also were used to update EVs for the unseen bandit in each trial; and a HMM with an estimate of reversal rates on a trial-by-trial basis. In all models, we applied a softmax rule to generate probabilistic decisions. Model fitting and comparison were performed simultaneously with HBI (Piray et al., 2019), described in more detail in Materials and Methods.

Overall, the counterfactual RL model, with a single learning rate for experiential and observational trials, outperformed the others in both protected exceedance probability (Fig. 3A) and inferred model frequency among the patient population (Fig. 3B). The mean learning rate in the winning model was 0.31 ± 0.06, and the mean softmax inverse temperature β was 0.17 ± 0.35 (Fig. 2C). Using HBI, we also compared the single learning rate counterfactual model with a counterfactual model which had split learning rates between experiential and observational trials, finding a 99.9% protected exceedance probability for the single learning rate counterfactual model. Taken together, these behavioral findings suggest subjects employed a similar learning strategy for the valuation of each bandit regardless of trial type and were still engaged with the task when another person received rewards. Given that the counterfactual model was the best fitting model for explaining participants' behavior on the task, we used the variables generated by this model in the subsequent computational model-based analysis of the neuronal data.

Amygdala population decoding

We tested whether the activity of amygdala neurons was related to the following task and computational variables: trial type, EV, outcome, and RPE, during learning trials. Trial type decoding was performed in the whole trial; EV decoding was performed in a 1200-ms time bin starting 300 ms from stimulus onset, until outcome presentation; outcome and RPE decoding was performed in a 1700-ms time bin starting 300 ms after outcome presentation.

For each variable, we trained a maximum Pearson correlation classifier on a pseudopopulation of amygdala neurons (see Materials and Methods; Fig. 4). Cross-validated single-trial decoding accuracy was obtained for each tested variable, tested for significance through a permutation test with 500 shuffled label runs. The same procedure was repeated in 50 cross-validation randomly re-sampled folds. To perform decoding of continuous variables across sessions, we binned variables (EV, outcome, and RPE) into four bins (quantiles); p values were obtained by computing the proportion of shuffled instances in which decoding accuracy exceeded the real decoding accuracy. With this method, the smallest p value attainable was 1/n_permutations = 0.002.

Figure 4.

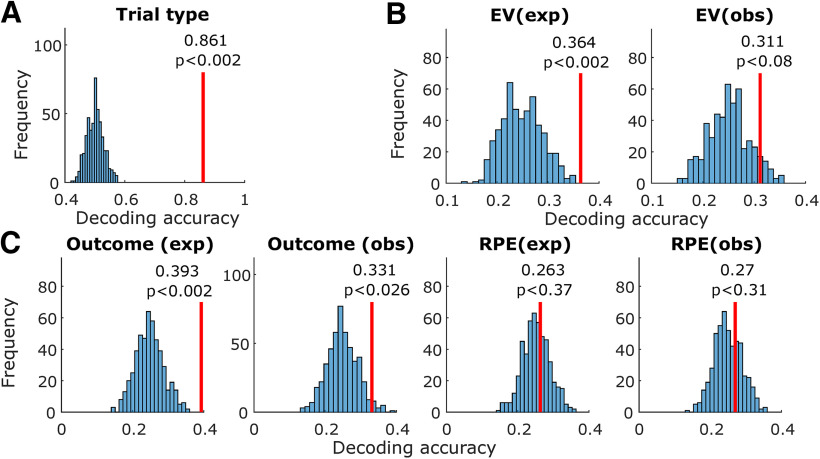
Amygdala population decoding analysis. A, Entire trial decoding. The tested variable was trial type (experiential vs observational). The vertical red line indicates average decoding accuracy in held-out trials after training with a maximum Pearson correlation classifier. The histogram indicates decoding accuracy in each instance of a permutation test, shuffling variable labels; p values were obtained by computing the proportion of permutation iterations in which the decoding accuracy exceeded the true decoding accuracy. B, Same, decoding within the preoutcome period. Decoded variables, from left to right, were EV (experiential) and EV (observational). C, Same, decoding within the postoutcome period. Decoded variables, from left to right, were outcome (experiential), outcome (observational), RPE (experiential), and RPE (observational).

Trial type decoding

Trial type (experiential vs observational) could be decoded from amygdala neurons with above chance accuracy (p < 0.002 < 0.05, permutation test; Fig. 4A). Average decoding accuracy in held-out trials was 86.1%. This indicates that amygdala neurons prominently tracked whether the current block was experiential or observational.

Expected value decoding

We next tested whether EV was decodable in the preoutcome period (300–1500 ms from bandit onset), separately for observational and experiential learning trials. We found better than chance decoding in experiential trials (p < 0.002 < 0.05, permutation test; Fig. 4B). Average experiential EV decoding accuracy in the preoutcome period was 36.4%. In contrast, observational EV decoding was within the chance boundaries of the permutation test (p < 0.08; Fig. 4B). This indicates that amygdala neuron populations contained more easily decodable information for keeping track of rewards received by oneself than by the other player.

Outcome decoding

Following outcome onset (300–2000 ms from outcome onset), outcome was decodable above chance in experiential trials (p < 0.002 < 0.05, permutation test; Fig. 4C), with an average decoding accuracy of 39.3%. Additionally, outcome was also decodable above chance in observational trials (p < 0.026 < 0.05, permutation test; Fig. 4C), with an average decoding accuracy of 33.1%. This indicates that amygdala populations represented both experienced and observed outcomes, but more strongly in the experienced case.

RPE decoding

We tested for decodability of RPEs during the outcome period (300–2000 ms from outcome onset), but did not find better decoding accuracy than expected by chance in the permutation test (Fig. 4C), both in the experiential (p < 0.37, permutation test) and the observational cases (p < 0.31, permutation test).

Single-neuron encoding analysis

In order to understand the relationship between the population decoding result and the activity of single neurons, we next tested the sensitivity of each amygdala neuron (n = 202 neurons) to each one of the decoded variables (Fig. 5). We used a Kruskal–Wallis analysis to compare every individual neuron's activity to the same variables used in decoding. We chose this method as opposed to a GLM analysis to encompass units whose activities might be non-linearly modulated by a variable of interest (e.g., being less active for intermediate levels of a variable of interest), such as the one displayed in Figure 6D.

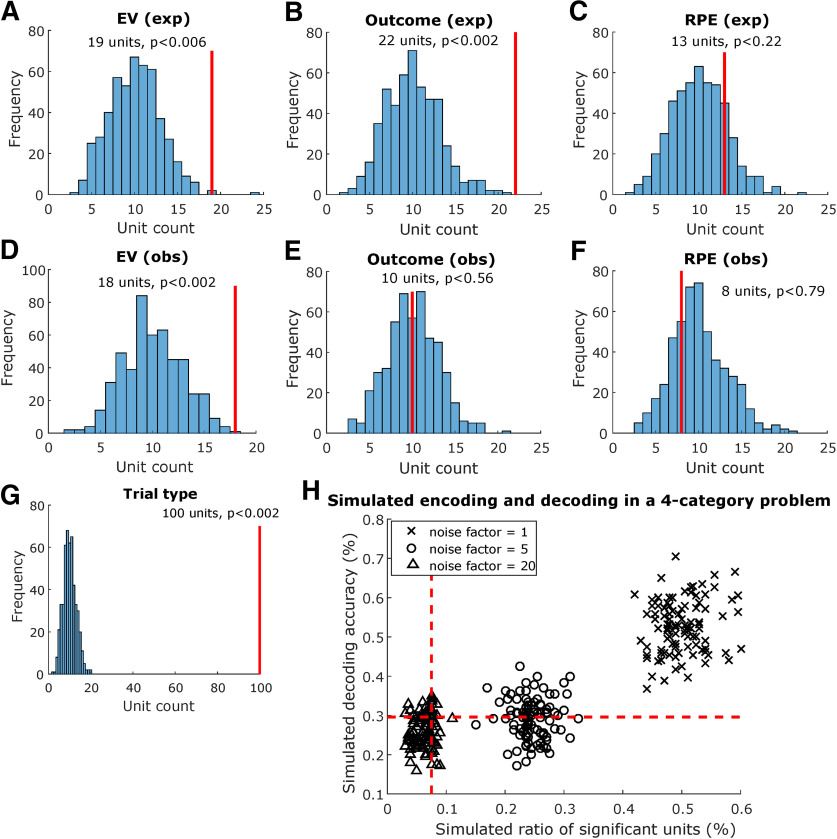
Figure 5.

Amygdala single-neuron encoding analysis. A, Preoutcome encoding of EV in experiential trials. Solid red lines indicate how many units were found to be sensitive to the tested variable within the preoutcome period. Histograms indicate how many units were sensitive to the tested variable in each iteration of the permutation test, shuffling variable labels; p values were obtained by computing the proportion of permutation iterations in which unit counts exceeded the true unit count. Similarly, we tested encoding for (B) experiential outcome in the postoutcome period, (C) experiential RPE in the postoutcome period, (D) observational EV in the preoutcome period, (E) observational outcome in the postoutcome period, (F) observational RPE in the postoutcome period, and (G) trial type in whole trials. H, Comparing encoding and decoding in a simulated four-category problem with varying noise levels. We simulated 96 trials with 200 artificial Poisson type neurons whose latent firing rate varied linearly as a function of an artificial categorical variable, chosen randomly between 1 and 4 for each trial. Noise was added to the latent firing rate of each neuron scaled by a noise factor of 1 (crosses), 5 (circles), or 20 (triangles), and simulations were repeated 100 times for each noise level. Each data point in the plot represents one individual simulation. Dashed red lines indicate theoretical chance levels for encoding (vertical) and decoding (horizontal).

Figure 6.

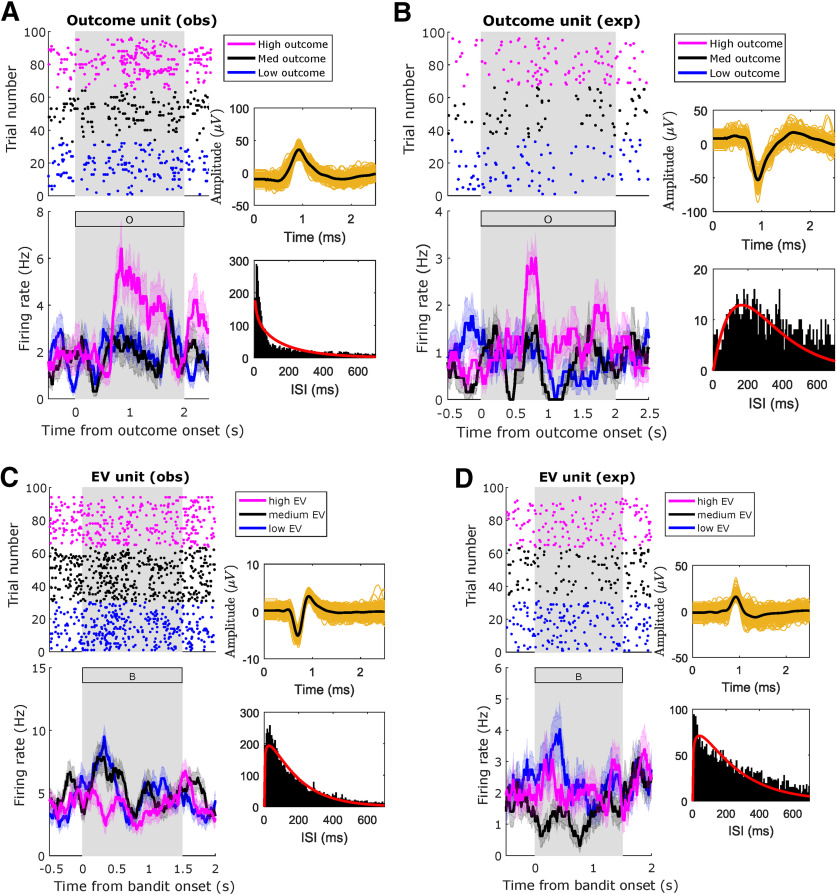
Amygdala neuron raster plot examples. Example amygdala units, significantly modulated by the indicated regressors, in the indicated conditions. A, Unit modulated by outcome in observational trials during postoutcome period. B, Unit modulated by outcome in experiential trials during postoutcome period. C, Unit modulated by EV in observational trials during preoutcome period. D, Unit modulated by EV in experiential trials during preoutcome period. Top, Raster plots. For plotting purposes only, we reordered trials by regressor levels by obtaining three quantiles from the variable of interest (magenta: high; black: medium; blue: low). Bottom, PSTH (bin size = 0.2 s, step size = 0.0625 s). The annex panels to the right of each raster display spike waveforms (top) and ISI histograms (bottom) from the plotted neuron. Background gray rectangles postoutcome periods (A, B) or preoutcome periods (C, D). Rectangles filled with a letter indicate which stimulus was present on the screen at that time (B: bandit; O: outcome).

Trial type neurons

We found 100 amygdala neurons whose activity is significantly different across experiential and observational trials (49.5%, p < 0.002 < 0.05, permutation test). Note this could partially be explained as an effect of the blocked design we chose, grouping all experiential trials and observational trials in distinct trial blocks. This result is also consistent with the high trial type decoding accuracy we found in left-out trials.

Expected value neurons

We tested amygdala neurons for experiential EV sensitivity and found 19 sensitive units (9.4%, p < 0.006 < 0.05, permutation test) during the preoutcome period (Fig. 5B, left). One experiential EV example unit is shown in Figure 5D. Conversely, observational EV sensitivity was found in 18 units (8.9%, p < 0.002 < 0.05, permutation test). An observational EV example unit is shown in Figure 5C. Taken together, these findings suggest that the expectation of outcomes is represented in a significant proportion of amygdala neurons, both for experienced and observed outcomes.

Outcome neurons

We also tested amygdala neurons for outcome sensitivity, in the postoutcome period. For experiential outcomes, we found a significant proportion (10.8%, p < 0.002 < 0.05, permutation test) of sensitive amygdala neurons (Fig. 5C, first panel). For observational outcomes (Fig. 5C, second panel), however, only 10 units were selected as sensitive (4.9%, p < 0.56, permutation test), despite better-than-chance observational outcome decoding. Example outcome neurons are displayed in Figure 6A (observational) and Figure 6B (experiential).

RPE neurons

Also, in the post outcome period, we found 13 (6.4%, p < 0.22, permutation test) experiential RPE units (Fig. 5C, third panel) as well as eight (3.9%, p < 0.76, permutation test) observational RPE units (Fig. 5C, fourth panel). Neither of these unit counts exceeded what is expected by chance in the permutation test. This finding is consistent with the low decoding accuracy we obtained for RPEs in the population decoding analyses.

Anatomical location

We used a χ² test of independence (1 degree of freedom) to determine whether units located in the RA or LA were more likely to be sensitive to each variable tested (Table 1). We found no evidence of lateralization for any of the tested variables. Similarly, we used a χ² test of independence (2 degrees of freedom) to test whether units were more likely to be sensitive to each variable in some amygdalar subnuclei group, the null hypothesis being that all groups were equally likely to contain units sensitive to each tested variable (Table 2). We found no evidence of any group being more likely than the others to contain sensitive units for any variable. Taken together, these findings provide no evidence for spatial specialization of value-related variables in amygdala, either by lateralization or by specialization within subnuclei. These findings must be interpreted cautiously, however, given our relatively low unit counts in each tested subset of amygdala neurons.

Table 1.

Sensitive units by side

	Right (n = 135)	Left (n = 67)	p value
Trial type	64	36	0.397
EV (exp)	11	8	0.384
EV (obs)	13	5	0.611
Outcome (exp)	14	8	0.736
Outcome (obs)	7	3	0.827
RPE (exp)	8	5	0.675
RPE (obs)	3	5	0.072

Testing the spatial specialization of value coding in amygdala. Number of sensitive units for each of the tested variables by side. We tested for independence between side and proportion of significant units by side using a χ² independence test (1 degree of freedom, p values indicated for each variable), and found no evidence of lateralization for any of the tested variables.

Table 2.

Sensitive units by major subnuclei group

	BL (n = 117)	CM (n = 39)	R (n = 46)	p value
Trial type	54	20	26	0.476
EV (exp)	12	2	5	0.590
EV (obs)	15	1	2	0.070
Outcome (exp)	12	2	8	0.184
Outcome (obs)	8	0	2	0.228
RPE (exp)	7	1	5	0.284
RPE (obs)	4	0	4	0.110

Testing the spatial specialization of value coding in amygdala. Number of sensitive units for each of the tested variables by major amygdalar subnuclei group (BL: deep and basolateral; CM: superficial or corticomedial; R: remaining nuclei). We tested for independence between major amygdalar subnuclei groups and proportion of significant units with a χ² test (2 degrees of freedom, p values indicated for each variable) and found no evidence for any subnuclei group being more likely to contain sensitive units for any tested variable.

Decoding generalization analysis

To test whether the same or different neurons encode experienced and observational variables, we performed a decoding generalization analysis (Wang et al., 2019). We trained decoders with neural activity in experiential trials and tested in observational trials (Fig. 7A) and vice versa (Fig. 7B). The method is otherwise identical to the previous decoding analysis. We tested generalization of EVs (Fig. 7A,B, left panels) in the preoutcome period and outcomes in the postoutcome period (Fig. 7A,B, right panels), since these variables were represented in the amygdala neuron population to some extent: outcome decoding was successful in both trial types, and despite weaker observational EV decoding, we did find a significant observational EV unit count through the encoding analysis.

Figure 7.

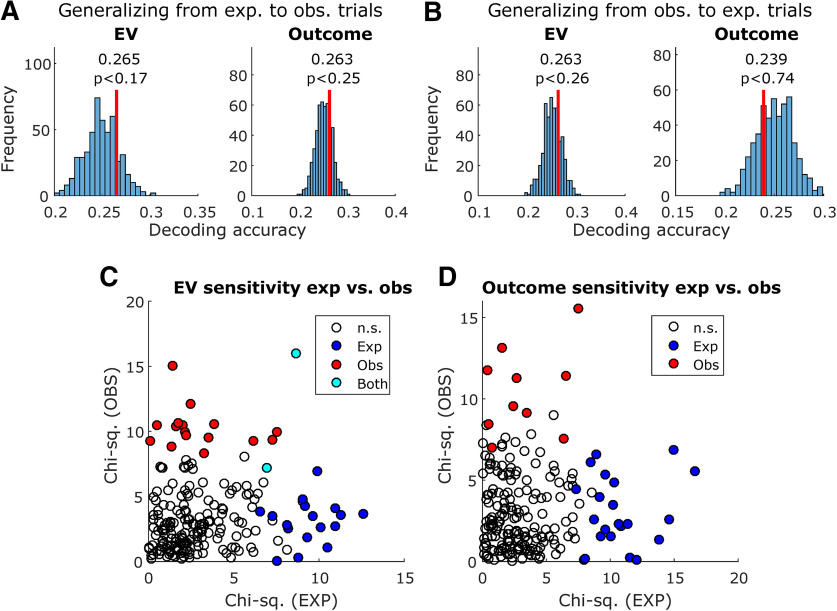
Comparing decoding and encoding across experiential and observational trials. A, Decoding generalization, training a decoder in experiential trials and testing in observational trials. Decoded variables were EV (left) and outcome (right). Vertical red lines indicate decoding accuracy, and histograms indicate decoding accuracy in each instance of the permutation test with shuffled variable labels; p values were obtained by computing the proportion of permutation iterations in which the decoding accuracy exceeded the true decoding accuracy. B, Same, but training in observational trials and testing in experiential trials. C, Sensitivity to EV in each unit, as obtained in the encoding analysis, plotted for experiential trials (x-axis) and observational trials (y-axis). Sensitivity was defined as the χ² value obtained from the Kruskal–Wallis test used in the encoding analysis. Unfilled data points indicate not sensitive units, blue data points indicate units only sensitive to experiential EV, red data points indicate units only sensitive to observational EV, and cyan data points indicate units sensitive to both experiential and observational EV. D, Same, but for outcome sensitivity.

None of the generalization decoding tests yielded better than chance decoding accuracy in the permutation test, regardless of which set of trials (experiential or observational) was used to train or test the decoder.

Additionally, we plotted the sensitivity of each individual amygdala neuron to EVs (preoutcome; Fig. 7C) and outcomes (postoutcome; Fig. 7D), contrasting experiential and observational trials. The sensitivity of each neuron is defined as the χ² value obtained from the previously described encoding Kruskal–Wallis test for differing levels of EV or outcome. The Pearson correlation between EV sensitivities was ρ = 0.10 (p < 0.14), and only 2 units were found to be sensitive in both trial types. Additionally, the Pearson correlation between outcome sensitivities was ρ = 0.02 (p < 0.77), and no units were found to be sensitive in both trial types.

These results indicate that despite evidence for successful outcome decoding in each condition separately, and significant unit counts for EV in both conditions, there is no evidence supporting a shared representation between experiential and observational trial conditions in amygdala.

Simulation for comparing encoding and decoding

We note that for some of the variables we investigated, the results of the encoding and decoding analysis differ such that one was above chance where the other was not (for an interpretation of this finding, see Discussion). To better understand how encoding and decoding analyses might differ in our data, we simulated the performance of these methods in characterizing the activity of an artificial neuron population whose activity correlates with an artificial four-category variable, with varying levels of noise. We used classification accuracy in test trials as the decoding metric, as well as the ratio of significant units as the encoding metric. For each noise factor level in [1,5,20], we ran 100 independent simulations and plotted decoding versus encoding performance for each simulation (Fig. 5H), as well as the theoretically estimated chance levels of 0.295 for decoding accuracy and 0.075 for significant unit ratios.

For the lowest noise factor, 1, decoding and encoding performances were highest, and always above the estimated chance levels for both analyses. The mean decoding accuracy was 0.52 ± 0.006, and the mean ratio of significant units was 0.50 ± 0.004. For a noise factor of 5, however, only 52% of the simulations performed better than the chance level for decoding, although all simulations performed better than chance in the encoding analysis. The mean decoding accuracy was 0.29 ± 0.005, and the mean ratio of significant units was 0.24 ± 0.003. Finally, for the highest noise factor, 20, in 3% of simulations both decoding and encoding performed better than chance; in 19% of simulations, decoding performed better than chance and encoding performed below chance levels; in 12% of simulations, decoding was below chance level and encoding performed better than chance; and in 66% of simulations, both analyses performed below chance. The mean decoding accuracy was 0.25 ± 0.004, and the mean ratio of significant units was 0.061 ± 0.001. This result, particularly in the high-noise condition, suggests that there is a diversity of neural population configurations in which decoding analyses might detect the presence of information for a variable of interest to an acceptable degree, but single unit counts might be below chance thresholds. Conversely, it is also possible that an above-threshold count of significant units might not translate into successful population decoding with the chosen method. Overall, this indicates that these analyses are complementary when trying to understand the information contained in single-neuron data, particularly in noisier conditions.

Discussion

In OL, an individual learns about the value of stimuli in the world not through direct experience, but instead through observing the experiences of others. Here, we investigated whether the human amygdala contains neuronal representations of key computational variables relevant for learning about the value of stimuli through observation. We found evidence for the encoding of the EV of a stimulus in amygdala neurons, at the time when participants are observing another agent choose that stimulus before this agent received an outcome, although on those specific trials no tangible reward outcome is obtained by the participant themselves. In addition, we found evidence that the amygdala contains decodable representations of outcomes during OL and experiential learning. Together, these results suggest that the human amygdala tracks several key RL variables that can be deployed for observational reward learning.

In addition, human amygdala neurons also strongly discriminated between whether or not a particular trial involved observational or experiential learning at the trial onset. This was the most robust signal found in the amygdala neurons, although this could at least in part be an effect of the distinct visual properties of experiential and observational trials (i.e., the presence of the face of the observed person, which can modulate amygdala cells; Minxha et al., 2017), or of the blocked task design. Still, taken together with the RL computations found in the amygdala that were related to OL, these findings support a contribution of the human amygdala to OL.

Consistent with a large literature describing the role of amygdala in anticipating rewards (Belova et al., 2008; Prévost et al., 2013; O'Doherty et al., 2017), we found evidence for experiential EV in both the single unit encoding analysis and the population decoding analysis, as well as for observational EV, in the single unit encoding analysis, further supporting the computational model as a meaningful description of behavior. Our findings in the experiential condition are compatible with results reported in monkey amygdala for expected values in the context of anticipating rewards for exploratory decision making (Costa et al., 2019).

An issue that requires further investigation is whether neurons encode experiential and observational expected value signals independently of the identity of the presented stimulus. Previous studies have reported stimulus identity encoding at the single-neuron level in amygdala, such as the identity of faces (Gothard et al., 2007), visual categories (Fried et al., 1997; Kreiman et al., 2000; Rutishauser et al., 2015b), but also identity-independent stimulus feature encoding, such as in familiarity/novelty tuning during memory retrieval (Rutishauser et al., 2015b) and ambiguity tuning during decision making (Wang et al., 2017).

A related question is whether the neural substrate representing value in amygdala neurons is the same or different for observational and experiential learning. That is, do EVs and outcomes activate amygdala neurons in a similar manner, whether it occurs in an OL situation or an experiential learning situation? To test this, we trained a classifier to decode these variables in OL and tested this classifier on the same neurons during the experiential learning condition and vice versa. In both cases, we could not successfully decode signals when training on one condition and testing on the other. These findings suggest that neuronal coding of OL EV and outcomes is distinct and not-overlapping with the neuronal code for experiential learning prediction errors. Additionally, we inspected the sensitivity of individual neurons while encoding EVs and outcomes, and found that, across the amygdala neuron population, experiential and observational sensitivities to these variables do not correlate. There is also little overlap between which neurons encode EV and outcomes in each condition. This does not preclude the existence of a distinct population of amygdala neurons, not found by this study, which encodes both experiential and observational values, as reported elsewhere (Chang et al., 2015). Our findings also support the argument that the subjects properly understood the task and knew that the observed rewards would not be given to them. If this were not the case, the neural representation for expected values and outcomes likely would not be separate.

The encoding and decoding analyses gave slightly divergent results for some of the variables in the OL condition. For instance, expected value signals during OL were detected at levels higher than chance in the single-unit encoding analysis but not in the decoding analysis (with the decoding accuracy bordering but not reaching statistical significance). Such divergent results can arise due to differences in the nature of the neural signals being detected by the two methods. Encoding analysis assesses information encoded on average by individual neurons, whereas decoding analysis assesses whether information can be read out at the population level in individual trials. It is possible to decode from a population from which individual neurons cannot be selected at levels above those expected by chance (as we reported for outcome in observational trials) if the underlying code isdistributed (Rumelhart and McClelland, 1986; Rogers and McClelland, 2014) and/or exhibits correlated variability between neurons (Stefanini et al., 2019). This is because from the point of view of a decoder, neurons that by themselves are not informative can still be useful in the context of the population. This has been demonstrated experimentally: a study on the distributed encoding of space in rodents (Stefanini et al., 2019) showed that cells which individually do not provide a significant amount of information were nevertheless highly informative at the population level as demonstrated by a high importance index. Conversely, it is possible that neurons can be selected at proportions higher than expected by chance while not being able to decode from individual trials. This may happen in a scenario where several units are considered sensitive but weakly so, not providing enough information for single-trial decoding. By simulating encoding and decoding in an artificial population of neurons, we showed situations where either of these discrepancies between encoding and decoding analyses are possible, depending on the levels of noise used in the simulation.

In the present study, we did not assess whether the OL signals we found in the amygdala are specifically recruited when observing another human agent, or rather are recruited when observing causal relationships between stimuli, actions, and outcomes regardless of the nature of the agent performing the actions. Thus, our design does not control for the social versus non-social learning component of OL. An important direction for future studies would be to compare and contrast neuronal effects in the amygdala during OL when the agent is human or a computer. There is no strong reason to assume a-priori that the responses detected in the amygdala should be specific only to observed human agents. However, it is possible that the presence of a human might enhance the salience of the observed stimuli compared with the situation where the agent is non-human, which could potentially increase the magnitude of neuronal responses. Adding to this argument, a study using a modified dictator game in monkeys found that amygdala neurons mirrored value representations between rewards received by oneself and given to others, but no such mirroring was observed when a computer was responsible for delivering rewards to another monkey (Chang et al., 2015).

One important caveat is that proportions of sensitive amygdala neurons for value related variables have been higher in the monkey literature (Chang et al., 2015; Costa et al., 2019) than in the present study. However, there are many differences between species, recording techniques and task preparation that could lead to such differences in encoding proportions. Unlike in animal studies, our participants performed the task for <1 h with no training, whereas training in animals is typically weeks to even months. Additionally, our recording electrodes were chronically implanted and could not be moved to search forresponsive neurons, thereby providing an unbiased estimate. Finally, it is plausible that neuronal representations in the human amygdala are more complex, processing rich forms of information such as social networks or deep and elaborate knowledge about stimuli in the world and their associated values, meaning that seeing a relatively smaller proportion of neurons dedicated to value coding would not be entirely surprising.

To conclude, our findings support a role for the human amygdala in OL, particularly under situations where associations between stimuli and outcomes are learned about through observing the experiences of another agent. The amygdala was found to contain neuronal representations depicting the expected future reward associated with particular stimuli when observing the experiences of another agent interacting with and obtaining rewards from those stimuli. Furthermore, amygdala neuron populations contained decodable information for outcomes whether the subject experienced them or passively observed another agent receiving them. The specific contributions we have uncovered for the amygdala in OL adds to a burgeoning literature highlighting a broad role for this structure in social cognition more generally (Adolphs et al., 1998; Gothard et al., 2007; Adolphs, 2010; Chang et al., 2015; Minxha et al., 2017; Taubert et al., 2018).

Code Availability

The analysis code is available on request to the authors.