Linear Time-Varying Model Characterizes Invasive EEG Signals Generated from Complex Epileptic Networks

Abstract

Electrocorticography (ECoG) and stereotactic electroencephalography (SEEG) are popular tools for studying neural mechanisms governing behavior and neural disorders, such as epilepsy. In particular, clinicians are interested in identifying brain regions that start seizures, i.e., the epileptogenic zone (EZ) from such invasive recordings. Currently, they visually inspect signals from each electrode to locate abnormal activity, and are not informed by predictive models that can characterize such recordings and potentially increase accuracy in localizing the EZ. In this paper, we test whether a simple linear time varying (LTV) model is sufficient to characterize both ECoG and SEEG activity. Specifically, we construct linear time invariant models in consecutive time windows before, during and after seizure events creating an LTV model from data collected in one ECoG and one SEEG patient. We find that these LTV models accurately reconstruct both ECoG and SEEG time series measured suggesting that these LTV models can be used for EZ localization.

I. Introduction

Over 20 million people in the world suffer from medically refractory epilepsy (MRE) [1]–[3], [9]. MRE patients are drug resistant and thus are frequently hospitalized and burdened by epilepsy-related disabilities, such as delay in neurocognitive development. Approximately 50% of MRE patients have focal epilepsy. Focal epilepsy is a neurological disorder, in which seizures originate within networks, often limited to one brain hemisphere [11]. The current treatment procedures are surgical resection of the EZ, and electrical stimulation of the EZ [14].

Despite the fact that successful treatment is life changing, surgical treatment utilization is minimal (~2%) because the clinical workflow to localize the EZ can be excessive invasive, long, complex, expensive and fraught with problems: (i) invasive electrode (e.g., subdural grids) are often required, with a high rate of morbidity and low efficiency in EZ localization (ii) the patient endures a prolonged hospital stay, risking infection and neurological comorbidities as the clinician waits for several seizure events to accrue sufficient data, (iii) specialized clinicians manually inspect individual EEG channels to localize the EZ. Despite large brain regions being removed, surgical success rates barely reach 60–65% [4]–[8], [12], [13]. Such variable and disappointing outcomes associated with high morbidity rates are often due to imprecise and/or inaccurate localization of the EZ in association with high invasiveness in the current diagnosis and treatment modalities.

In an era of big data, computational models should be used to assist clinicians in localizing the EZ. We seek to model the complexities of ECoG and SEEG activity that renders low reconstruction error. Linear models describe the evolution of a continuous response variable (e.g. ECoG channel activity) as a linear function of one or more predictor variables (e.g. prior ECoG activity). If we can develop a simple linear time varying (LTV) model that sufficiently captures the dynamics within ECoG and SEEG time series data, then we could use these models downstream for EZ localization, thus improving treatment outcomes of epileptic patients.

In this study, we take ECoG and SEEG data collected by the National Institute of Health (NIH) and Cleveland Clinic (CC), respectively, and compute a LTV multivariate model. We use different time windows and find an optimal window for having the lowest reconstruction error. We demonstrate that it is possible to represent the complex ECoG and SEEG time series as a simple LTV model. The paper is organized as follows. Section II describes the general LTV model, how we build it, and how we systematically determine the optimal window size for ECoG and SEEG data. Section III reports the results of our models versus empirical data. Section IV discusses possible extensions of LTV models for ECoG and SEEG data for epilepsy applications.

II. METHODS

In this section, we first describe the linear time varying model used for representing the ECoG/SEEG network, as introduced in [10]. Then we describe the specific methodology we apply to EEG data and how to obtain an optimal LTV model from recordings. All methods were run on MATLAB 2016b on a Linux 64-bit machine with an Intel Xeon 3.47 GHz processor with 6 cores.

A. Linear Time Varying (LTV) Model

To construct an LTV model, we concatenate a sequence of linear time-invariant (LTI) models. Specifically, for each window size T, we construct an LTI model. Consider a discrete time LTI system with a state evolution equation as (1) with state vector x(t) ∈ R^N, and state transition matrix A ∈ R^N×N.

$$\mathbf{x}(t+1)=\mathbf{Ax}(t)$$ (1)

The elements in the state vector represent activity for each EEG contact (node in EEG network). One can think of element A_ij as how activity of node j, x_j(t) affects the future activity of node i, x_i(t+1). Element A_ii is an autofeedback term, representing a first-order approximation to the internal dynamics of node i. The i^th row of A determines the network as the cumulative functional effect on node i, while the j^th column captures the functional effect of node j on the entire network.

The following variables describe a linear model for a multivariate time series:

• T = window size

• N = number of variables in multivariate system

• A ∈ R^N×N, being the state evolution matrix for the system

• x_i(t), t = 1, 2, …, T for variable i = 1, 2, …, N is the i^th component of the state vector.

A is estimated by solving a system of linear equations using least squares estimation. The following is the general system of linear equations that come directly from writing out recursions of the LTI model (1) for each time step:

$$\begin{gathered} x_1(2)=A_{1,1}{x}_1(1)+A_{1,2}{x}_2(1)+\dots +A_{1,N}{x}_N(1) \\ {x}_2(2)=A_{2,1}{x}_1(1)+A_{2,2}{x}_2(1)+\dots +A_{2,N}{x}_N(1) \\ ⋮ \\ {x}_N(2)=A_{N,1}{x}_1(1)+A_{N,2}{x}_2(1)+\dots +A_{N,N}{x}_N(1) \\ {x}_1(3)=A_{1,1}{x}_1(2)+A_{1,2}{x}_2(2)+\dots +A_{1,N}{x}_N(2) \\ {x}_2(3)=A_{1,1}{x}_1(2)+A_{1,2}{x}_2(2)+\dots +A_{1,N}{x}_N(2) \\ ⋮ \\ {x}_1(T)=A_{1,1}{x}_1(T-1)+\dots +A_{1,N}{x}_N(T-1) \\ ⋮ \\ {x}_N(T)=A_{N,1}{x}_1(T-1)+\dots +A_{N,N}{x}_N(T-1) \end{gathered}$$

Then for each arbitrary window of data, the above system is used to represent the multivariate system. Specifically, if we want to estimate an LTV model over 100×T seconds, we construct 100 LTI models with state evolution matrices {A_k} for k = 1, 2, …, 100, each with window size T. Note, that although each window is time invariant, the overall model across the entire multivariate time series is time varying.

B. LTV Model Applied to ECoG and SEEG Data

First, we introduce some additional definitions to simplify how this model is estimated from data.

• b ∈ R^(T−1)∗N, where b are the electrode recordings at the next time point

• $H\in R^{(T-1)*N\times N^2}$, where H is defined below as a system of linear equations

• $X\in R^{N^2}$, where X is the vectorized adjacency matrix, A, which we are interested in

The model for the state evolution matrix is constructed by transforming the LTI model into a linear system of equations: b = HX, and then solving the least squares problem in MATLAB using X = H \ b. Then X is transformed into the A matrix (note that X is the vectorized form of A).

$$\mathbf{b}={\left[x_1(2)x_2(2)\dots x_N(2)\dots x_1(T)x_2(T)\dots x_N(T)\right]}^T$$

$$\mathbf{H}=\left[\begin{array}{ccc}{x}_1(1)\dots x_N(1)& 0\dots 0& 0\dots 0\\ 0\dots 0& x_1(1)\dots x_N(1)& 0\dots 0\\ 0\dots 0& 0\dots 0& x_1(1)\dots x_N(1)\\ \dots & \dots & \dots \\ x_1(2)\dots x_N(2)& 0\dots 0& 0\dots 0\\ \dots & \dots & \dots \\ 0\dots 0& 0\dots 0& x_1(2)\dots x_N(2)\\ \dots & \dots & \dots \\ x_1(T-1)\dots x_N(T-1)& 0\dots 0& 0\dots 0\\ \dots & \dots & \dots \\ 0\dots 0& 0\dots 0& x_1(T-1)\dots x_N(T-1)\end{array}\right]$$

$$\mathbf{X}={\left[A_{11}{A}_{12}\dots A_{1N}{A}_{21}\dots A_{N,N-1}{A}_{NN}\right]}^T$$

We systematically determine an optimal window size for reconstructing A. We represent our entire dataset as x(t) ∈ R^N, with t = 1, …, S, S being the length of the entire ECoG, or SEEG time series. We then divide S into windows of length T and solve for matrices, A over time.

C. Comparing Reconstructed ECoG and SEEG with Real Recordings

The following process outlines the process to compare reconstructed data with actual ECoG/SEEG data:

1. Input arbitrary window T; initialize S (length of data time series)

2. For iWindow = 1 to S/T (assume integer)

   • Setup system of equations to solve equation (1)
   • Solve for A_k using procedure outlined in section B.

3. Reconstruct $\widehat{x}(t+1)=A_k\widehat{x}(t)$ for t=i,…i+T, k ≡ A for some window. With the initial condition, $\widehat{x}(0)$, for each window coming from empirical data.

4. Compute $ϵ(t)=MSE(\widehat{x}(t)-x(t))$ as the mean-squared error

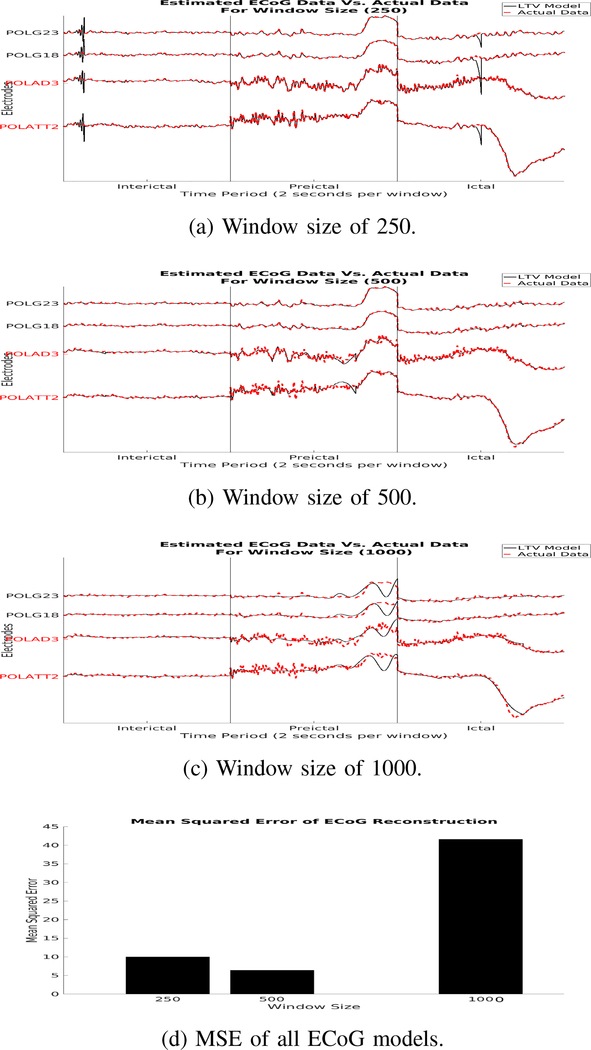
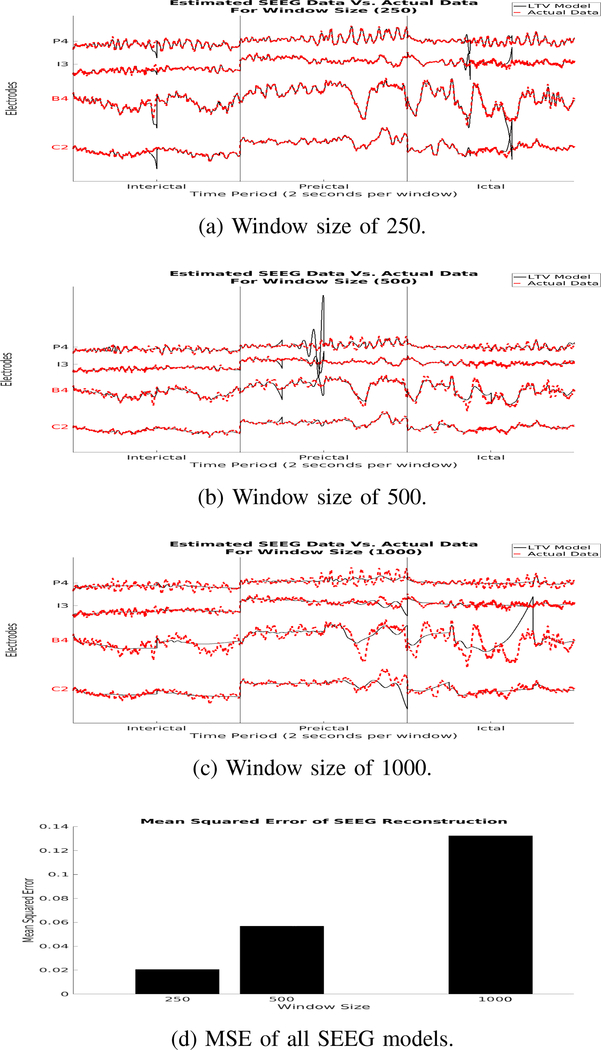
ϵ(t) is then analyzed to determine the optimal T to reconstruct the ECoG/SEEG time series with minimal error. We outline the above procedure in Fig. 1. We selected the window sizes 250, 500 and 1000 and compared their performances.

Fig. 1:

This figure outlines the linear time-varying process of reconstruction by first using data x(t) to generate a sequence of linear time-invariant models, which are then used in sequence to reconstruct $\widehat{x}(t)$ given the initial condition within each model window.

D. Intracranial Recordings - ECoG and SEEG

The ECoG patient included in this study was surgically treated for drug-resistant seizures at the National Institute for Health (NIH), and underwent invasive presurgical monitoring with subdural grid-and-strip arrays for seizure localization or mapping of eloquent areas. Clinical monitoring lasted five to seven days and included two to seven clinical seizures. Subdural grid arrays (SDE), strips, and depth-electrode arrays were implanted in various combinations as determined by clinical assessment for patients with temporal, occipital, or frontal lobe seizures. Subdural grids had 20–64 contacts per array and were used in combination with subdural strips (four to eight contacts) or depth arrays, thus having 80–120 electrodes per patient over all. Intracranial contact locations were documented by postoperative CT coregistration with preoperative MRI.

The SEEG patient included in this study SEEG placement, was surgically treated for drug-resistant seizures at the Cleveland Clinic (CC). The SEEG technique uses several small drill holes (1.8 mm in diameter), allowing many electrodes to be inserted (up to 20). SEEG may provide a more complete coverage of the brain, from lateral, intermediate and/or deep structures in a three-dimensional arrangement recorded over hundreds of channels. The number and location of implanted electrodes are pre-operatively planned based on a pre-implantation hypothesis, which is formulated in accordance with non-invasive pre-implantation data such as seizure semiology, ictal and inter-ictal scalp EEG, MRI images, PET and ictal SPECT scans.

Decisions regarding the need for invasive monitoring and the placement of electrode arrays were made independently of this work and solely based on clinical necessity. The research protocol was reviewed by the Institutional Review Board (IRB) at the NIH and CC. Recordings were acquired without interfering with the clinical procedures and length of patient’s stay after that informed consent was obtained.

Recordings were acquired with a Nihon Kohden system (Nihon Kohden Corp.) with 1,000-Hz sampling rate and 300-Hz antialiasing filter, and were converted to EDF format for storage and further processing. Digitized data were stored in an IRB-approved database compliant with Health Insurance Portability and Accountability Act (HIPAA) regulations. Board-certified electroencephalographers marked, by consensus, the unequivocal electrographic onset of each seizure and the period between seizure onset and termination. Data was then preprocessed as .mat files for analysis in MATLAB.

III. Results

In this section, we show results of our model reconstructions for different linear time-varying models of both ECoG and SEEG recordings. In our reconstructions of ECoG data, we see that there is a steady decrease in MSE as window sizes decrease. However, there is a slightly larger MSE for window size of 250 versus 500 due to the oscillations produced from the model, which could be due to the nonlinear nature of ECoG activity. We know that EEG activity is nonstationary and has time varying dynamics. This could be a window that is able to capture linear dynamics of the ECoG activity.

In the reconstruction of SEEG data, we also see a steady decrease in MSE as window sizes decrease. There are slight oscillations that appear in the reconstruction during seizure period, but none as drastic as the ECoG LTV model of window size 250. Although larger window sizes follow the general trend of the electrophysiological signals, they less incapable of following oscillations in the signals. Smaller window sizes are capable of following the signals very well throughout the time series, but have a higher tendency to produce large oscillatory reconstructions.

In both ECoG and SEEG data the LTV model reconstructions generally follow the trend in the empirical signals. This suggests that the complex and large time series of electrode recordings can be simplified to a LTV model.

IV. Discussion

In this study, we characterize complex multivariate ECoG time series as a LTV model. We hypothesize that ECoG and SEEG recordings can be accurately reconstructed using a simplified linear model, and demonstrate that one can use data to select an optimal time window for creating the time-varying models defined by a sequence of LTI models. This method is adaptive to the user. If one is only interested in following the general trend of the ECoG, or SEEG signals, then a higher window size can be used. However, if one is interested in having a model that represents the oscillatory patterns of the empirical signals, then perhaps a smaller window size should be used. Larger window sizes have decrease computational time, while smaller window sizes increase computational time. In order to further validate this methodology, we intend on expanding the analysis to more patients and different types of implanted electrodes (grid, subdural, depth, strip, etc.).

Fig. 2:

This figure shows reconstructed data (a-c) generated from our discrete LTV model overlaid on real ECoG data. It also shows the MSE for each model (d). The red electrode labels are electrodes within the clinically annotated EZ, while the other electrodes are some channels from outside the EZ.

Fig. 3:

Simulated data (a-c) generated from our discrete LTV model overlaid on real SEEG data with MSE for each model (d). The red electrode labels are electrodes within the clinically annotated EZ, while the other electrodes are some channels from outside the EZ.