Neural circuits for evidence accumulation and decision-making in larval zebrafish

Abstract

Making appropriate decisions requires the accumulation of sensory evidence. Simple integrator models can explain many aspects of such behavior, but it remains poorly understood how the underlying computations are mechanistically implemented in the brain. Here, we approach this problem by adapting the random dot motion discrimination paradigm, classically used in primate studies, to larval zebrafish. Using their innate optomotor response as a readout of decision-making, we find that larval zebrafish accumulate and remember motion evidence over many seconds and that the behavior is in close agreement with a bounded leaky integrator model. Through brain-wide functional imaging, we identify three neuronal clusters in the anterior hindbrain that are well suited to execute the underlying computations. Relating the dynamics within these structures to individual behavioral choices, allows us to propose a biophysically plausible circuit arrangement in which an evidence integrator competes against a dynamic decision threshold to activate a downstream motor command.

Introduction

Behaviorally relevant signals in the environment are rarely present all at once, they are often obscured by noise, and in many cases, they are even conflicting. To still be able to make reliable sensory-motor decisions, animals need to constantly integrate information from their senses, and they need to do this over space and time. Several of the behavioral features resulting from such integration, such as response accuracy and delay, can be faithfully explained by simple integrator models with a decision threshold, generally known as bounded drift-diffusion models^1,2. However, such models usually have integration time constants of many seconds, which are magnitudes larger than the milliseconds permitted by the biophysics of individual neurons. This poses the question of how such processes are mechanistically implemented on the level of the nervous system.

Sensory evidence accumulation over periods extending several seconds has been described in various animal species, ranging from flies^3–5 to rodents^6–8 to primates^9–12. However, these previous studies have mostly focused on individual neuronal response types within specific brain regions, and have largely ignored the possibility that the underlying processes might be distributed across large parts of the brain. A classical stimulus probing integration and decision-making mechanisms in the visual system of primates uses random dot motion kinematograms^13–15, where a fraction of flickering dots moves coherently over the screen, while the remaining elements are randomly redrawn across the visual field. This provides several benefits when dissecting the neuronal basis of spatiotemporal integration: First, dots have short lifetimes, making it impossible for the animal to track individual objects over the time course of stimulation. Second, adjusting coherence levels allows for regulation of stimulus strength without changing luminance, contrast, or speed. Third, motion strength is locally weak and equally distributed across the visual field, simplifying the identification of areas computing or further processing spatially pooled signals.

When stimulated with global motion drift, larval zebrafish follow the overall motion direction, a behavior that is called the optomotor response and that is thought to be important for counteracting involuntary displacements in flowing streams¹⁶. Moreover, larvae swim in discrete bouts where each bout can be considered the outcome of an individual decision, raising the possibility that animals accumulate sensory evidence during the time of quiescence¹⁷. Such behavioral reports are innate, do not require any training, and, therefore, greatly facilitate experimental procedures. Finally, larvae are transparent and it is possible to non-invasively image their entire brain at cellular resolution over many hours¹⁸. Previous brain--wide imaging in the context of moving gratings has suggested that the pretectum plays an important role in the computation of global motion signals from both eyes^16,19,20 and that signals are further processed downstream in the anterior hindbrain to eventually bias swimming^21,22.

Here we employ random dot motion stimuli to probe whether the larval zebrafish can accumulate sensory evidence and use such signals for decision-making. We find that larval zebrafish do indeed temporally integrate motion evidence over many seconds and that the behavior is in close agreement with a simple bounded leaky integrator model. Through brain-wide two-photon calcium imaging, we identify the anterior hindbrain as a prominent center presumably involved in the underlying computations, and we propose a biophysically plausible circuit model that captures the measured circuit dynamics as well as the recorded behavioral output.

Results

Freely swimming larval zebrafish can integrate motion coherence

To probe whether larval zebrafish can temporally integrate motion evidence, we presented random dot motion stimuli of different coherence levels onto the floor of an arena containing a freely swimming animal and tracked its behavior in real-time (Fig. 1a and Supplementary Video 1, world-centric view). We designed the stimulus in a closed-loop fashion such that it always moved perpendicularly to the animal, creating a constant sideways drift from the perspective of the fish irrespective of its body orientation and position in the dish (Supplementary Video 1, fish-centric view). Each elicited swim bout was labelled as either correct or incorrect depending on whether it followed or opposed motion direction, respectively, and we find, using this analysis, that larvae robustly followed coherent motion direction in this context (Extended Data Fig. 1a–e). Importantly, we show that with increasing coherence levels decision accuracy and the precision of correct bouts increased, and inter-bout intervals shortened (Fig. 1b and Extended Data Fig. 1b,c). Moreover, for each tested coherence level, accuracy improved over time and over consecutive swims (Fig. 1c,d), indicating that decisions are based on some form of temporal integration and that individual swim bouts do not fully reset the integrator. To test whether the integrator operates on the sensory or on the motor level, we next focused on the very first bout after stimulus onset in each trial. We found that performance improved with increase of the delay period (Fig. 1e). This can only be explained by sensory but not by motor integration since the previous bout, before stimulus onset, occurs in a random direction with respect to the stimulus. In a similar way, we quantified the first bout after the end of stimulation, and we show that motion memory slowly decays during quiescence (Fig. 1e). Finally, we found that at constant 0 % coherence animals display an increased probability of selecting consecutive turns in the same direction (Fig. 1f), which could be explained by a model in which decisions are based on the slowly fluctuating sign of a leaky integrator operating on noise.

Figure 1 |. Behavior and modeling in freely swimming larval zebrafish.

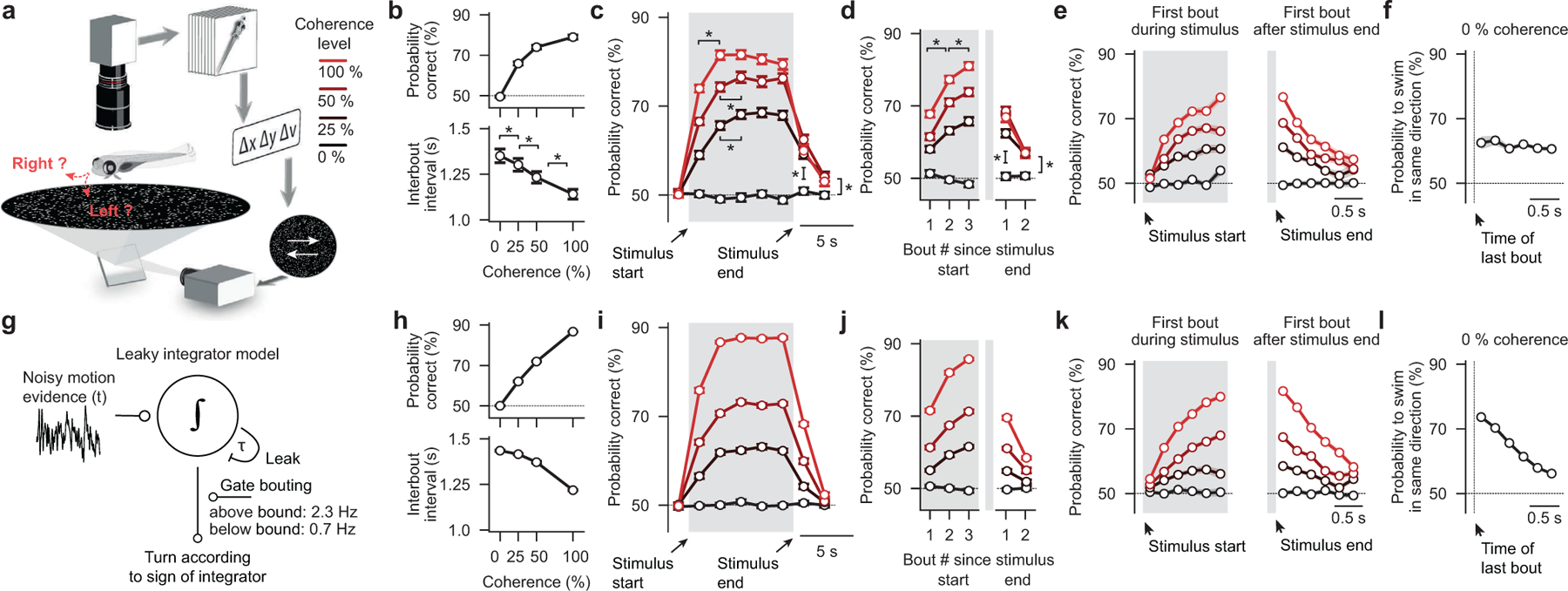
a, Random dot motion kinematograms presented from below to freely swimming larval zebrafish. After a few seconds of 0 % coherence (baseline stimulus, no motion, flickering dots), a certain percentage of the dots starts to move coherently either left- or right-ward at a constant speed until we switch coherence levels back to 0 %. Each dot, whether it is moving or not, has a lifetime of a few hundred milliseconds, making it impossible for larvae to track individual dots over the time course of the trial. The system operates in closed-loop so that dots always move perpendicularly to the fish no matter where animals are located and how they are oriented in the arena. Note that sizes are not to scale (the body length a larval zebrafish at this age is ~4 mm, the diameter of the visual arena is 12 cm). b, Accuracy and interbout interval as a function of coherence strength. c, Time-binned accuracy as a function of time (first bin during motion: *p < 0.001 for all coherence levels; second bin during motion: p = 0.9, *p < 0.05, *p < 0.01, for 100 %, 50 %, 25 % coherence level, respectively; first bin after stimulus: *p < 0.001 for all coherence levels; second bin after stimulus: *p < 0.05, *p < 0.01, *p < 0.01, for 100 %, 50 %, 25 % coherence level, respectively). d, Accuracy over consecutive bouts (first to second bout after stimulus start: *p < 0.001, for all coherences; second to third bout after stimulus start: *p < 0.001, *p < 0.01, *p < 0.05, for 100 %, 50 %, 25 % coherence level, respectively; first and second bout relative to 0 % control: *p < 0.001, for all coherences). e, Accuracy of the first bout during the stimulus and the first bout after the stimulus end as a function of delay. f, Probability to swim in the same direction as a function of interbout interval during 0 % coherence. g, Schematic of the bounded leaky integrator model. h–l, Quantification of model simulation results as in (b–f). N = 60 fish in (b–d,f) and N = 56 fish in (e). N = 16 model runs in (h–l). Gray shaded areas in (c–e,i–k) indicate time of motion coherence presentation, before and after coherence levels are at 0 %. All error bars are mean ± sem over fish. P-values are based on one-sided t-tests comparing response differences to zero. All asterisks (*) indicate significance (*p < 0.05, *p < 0.01, or *p < 0.001).

These findings indicate that freely swimming larval zebrafish can integrate motion evidence during quiescence and over consecutive swims, and we therefore sought to explore whether the behavior of freely swimming larvae could be modeled with a bounded integrator model (Fig. 1g and Supplementary Video 2). Further, since we found that accuracy over time follows the dynamics of a leaky integrator (Fig. 1c), we added a leak component to our model. Spontaneous swims bouts were implemented via a random bout clock at different probabilities depending on whether the integrator variable was below or above the bound. The sign of the integrator variable at the moment of a swim then determined the direction of turning. Finally, given our experimental findings (Fig. 1d), we did not fully reset the integrator at each swim. Instead, we reduced it by a small fixed amount, accounting for residual visual noise and optic flow opposite to the turning direction (visual feedback) that cannot be fully compensated in our assay. After applying a systematic strategy to fit model parameters to our experimental data, we find that our simple model faithfully captures all tested behavioral features (compare Fig. 1h–l and Fig. 1b–f).

We next sought to explore whether four alternative models of different complexity could also explain the behavior: 1) A stochastic model, in which decisions are made only according to the momentary noisy motion evidence, failed to reproduce the improvement of decision accuracy over time (Extended Data Fig. 2a and Supplementary Video 3). 2) The addition of an explicit motor memory to the stochastic model could only partly rescue the dynamics. This model failed, however, to capture the performance improvement with extended integration time (Extended Data Fig. 2b, Supplementary Video 4, and Fig. 1e). 3) A leaky integrator model, in which we did not include self-created visual feedback, could reproduce our experimental behavioral data but captured the dynamics less well (Extended Data Fig. 2c and Supplementary Video 5). 4) Finally, we tested a non-leaky integrator model (Extended Data Fig. 2d and Supplementary Video 6), where we fully reset the integrator at every bout. Interestingly, even without a leak component, the model could reproduce the apparent leaky integrator dynamics of the behavior. However, without additional memory components, the model could not capture the saving of information across consecutive bouts (Fig. 1d,f) and required the explicit addition of a motor memory. Even though such a significantly more complex model could reproduce our experimental findings, our later analyses of head-fixed larvae and of the actual neural circuit implementation (described below) favor a leaky integrator model as described in Fig. 1g–l. Notably, we developed a quantitative metric that allowed us to evaluate, rank, and compare the goodness of fit across all different models (Extended Data Fig. 2e), an analysis that also favors the proposed leaky integrator model.

Thus, our behavioral analyses and modeling suggest that freely swimming larval zebrafish do indeed temporally integrate motion evidence, that they use that information to guide swimming decisions and that the behavior can be well explained with bounded integrator models. However, the spontaneous and frequent occurrence of swim bouts in these experiments prevents us from further constraining model architecture and parameters, since integration times are limited to the short inter-bout intervals and since other sensory systems might potentially confound our interpretations.

Head-fixed larval zebrafish can integrate motion coherence

A common procedure to study larval zebrafish behavior under more controlled conditions is to embed them in transparent agarose, and leaving the tail free to move (Fig. 2a). In this preparation, behavior can be tracked in real-time while animals are fixed in place. Moreover, notably, larvae are in a state where they almost never swim spontaneously but still perform significantly delayed directional tail flicks in response to visual motion. Hence, self-induced optic flow and visual noise, as well as potential motor memories (Fig. 1g–l), are not a problem anymore, allowing us to explicitly focus on the mechanisms of sensory evidence accumulation during quiescence.

Figure 2 |. Behavior and modeling in head-fixed larval zebrafish.

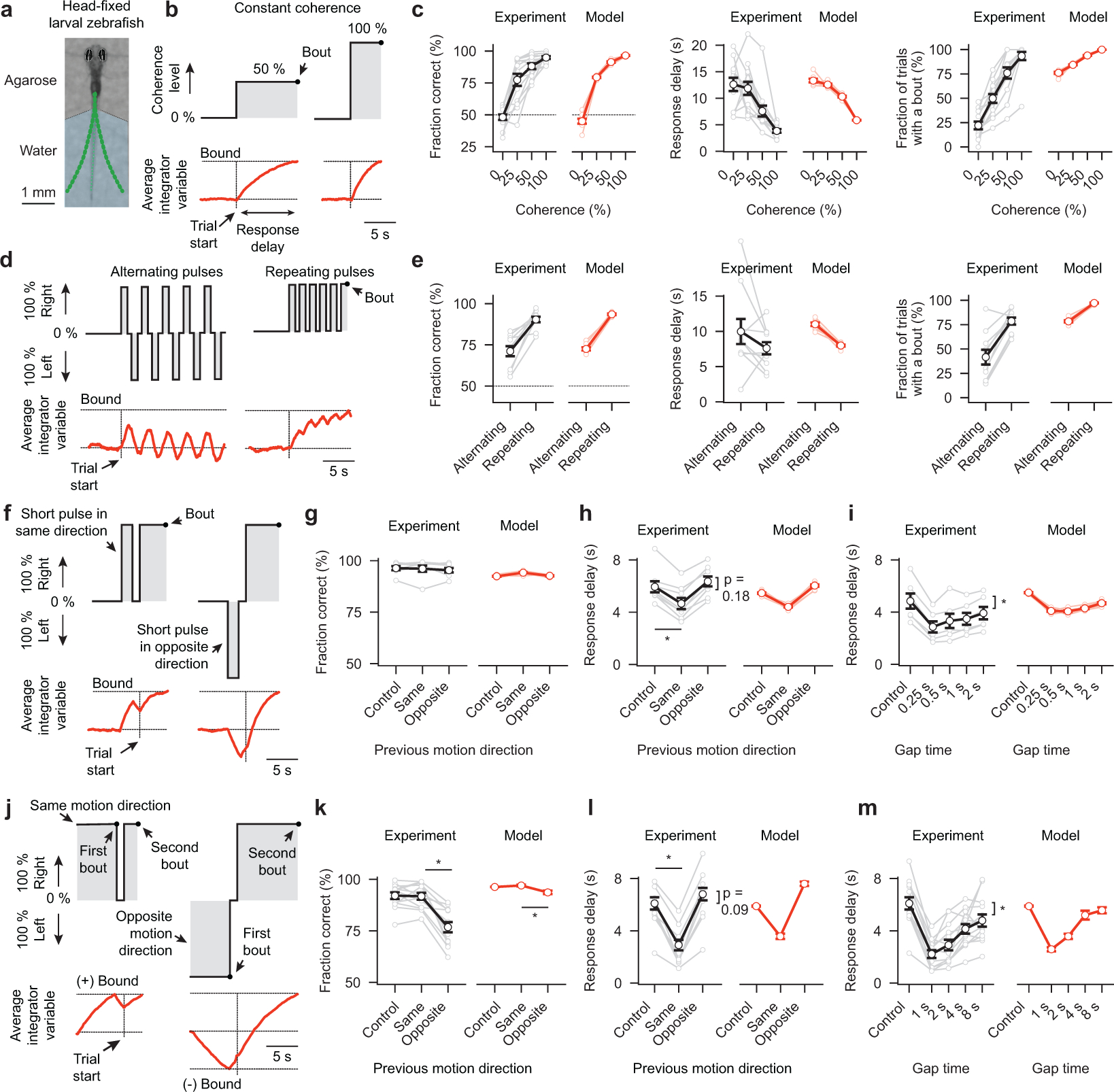
a, Photograph of a head-fixed larval zebrafish in transparent agarose with the tail free to move. Green dots indicate tail tracking points. In such a preparation, spontaneous swim rates are low, but animals still respond robustly to motion¹⁷. We track behavioral choices based on the first bout during the trial. b,d,f,j, Stimulation protocols used (black lines with shaded gray area) and cartoons depicting respective estimates of the average bounded leaky integrator variable (red traces). c, Accuracy, response delay, and fraction of trials with a bout as a function of coherence strength. e, Same as in (c) but for stimulation protocol with alternating and repeating motion pulses. g,h, Accuracy and response delay as a function of direction of a single motion pulse shown before the trial. Control conditions have no such pulse (*p < 0.001 for same direction against control). i, Response delay as a function of gap time (0 % coherence) since a same direction motion pulse (*p < 0.001 for gap times 0.25, 0.5, and 1 s; *p < 0.01 for gap time 2 s). k,l,m, Same is in (g,h,i) but with the previous motion stimulus presented until a first bout event (*p < 0.001 for all conditions). Gray and black lines in (c,e,g–i,k–m) indicate individual and average larvae responses, light red and red lines model evaluations, respectively. N = 13 fish in (c), N = 10 fish in (e), N = 8 fish in (g,h), N = 6 fish in (i), N = 13 fish in (k–m), N = 8 model evaluations (different noise seeds) in (c,e,g–i,k–m). All error bars are mean ± sem over fish or model runs. P-values are based on one-sided t-tests comparing response differences to zero. All asterisks (*) indicate significance (*p < 0.05, *p < 0.01, or *p < 0.001).

Analyzing the dynamics of the sensory variable in our bounded leaky integrator model in a trial average (Fig. 2b) as well as in individual example trials (Supplementary Video 7) allowed us to predict that the animal’s decision accuracy should increase, and its response delay decrease, with increasing levels of coherence. Moreover, we reasoned that the integrator variable might, especially under low coherence levels, often fail to reach the bound during the limited length of the trial. Furthermore, our leaky integrator model allowed us to make critical predictions about the shape of the response delay distributions of correct and incorrect bouts as well as about the relationship between response accuracy and delay. Experimental data were found to be in excellent agreement with all of these model predictions (Fig. 2c and Extended Data Fig. 3a–c).

To further probe the behavior and challenge our leaky integrator model, we next performed different kinds of motion pulse experiments where short periods of coherent motion alternate with periods of zero coherence (Fig. 2d). We first tested pulses in alternating directions. This should lead to an oscillating integrator variable of low amplitude and, hence, animals should behave approximately as if not stimulated at all. In contrast, when motion pulses repeatedly go in the same direction, the integrator variable should slowly ramp up, and the behavior should emulate conditions with continuous weak motion coherence. Here too, the behavioral data were found to be in agreement with our model (Fig. 2e).

We next sought to explore how short motion pulses, delivered at a specific interval before the actual trial, influence behavioral choices and response delay (Fig. 2f). We reasoned that such pulses should prime the initial state of the integrator variable, and decrease or increase response delays depending on whether they oppose or support the stimulus motion of the trial itself. We found that this was indeed the case and that our model could reproduce these effects (Fig. 2g,h). Moreover, we predicted that placing the motion pulse further into the past should allow the integrator variable to decay closer back to baseline before the start of the trial. We quantified how the length of such gaps influences response delay and found that larvae could remember such pulses for at least 2 s (Fig. 2i).

In a similar setting, we extended the length of the motion pulse until larvae initiated a first swim (Fig. 2j). We then immediately stopped the stimulus for variable amounts of time before starting the actual test trial. We reasoned that in such a paradigm the integrator variable should be pushed to the - maximal - bound and, after the first bout, decay back with its characteristic time constant. Quantification of the behavior revealed that this was indeed the case and that larvae could remember the previous motion stimulus for at least 8 s (Fig. 2j). Moreover, the dynamics of the motion memory decay allowed us to fit our bounded leaky integrator model, suggesting an integration time constant of the system of around 5 s.

These experiments in head-fixed larvae also allowed us to test the performance of the presented alternative models without the confound of spontaneous bouting (Supplementary Videos 7–9). This analysis revealed that all tested models could mimic the behavior in response to constant coherent motion (Extended Data Fig. 3d). However, the stochastic model failed to reproduce the response delay distribution difference between correct and incorrect bouts (Extended Data Fig. 3b), and couldn’t reproduce any of the motion pulse experiments (Extended Data Fig. 3e–g). The non-leaky integrator model could roughly mimic the relationship between response delay, pulse direction, and gap time (Extended Data Fig. 3e,f), but motion working memories decayed much slower in this model than in the experiment (Fig. 2i), as expected from a model without a leak component. Moreover, here, we reset the integrator variable at each bout and store a persistent working memory of the last behavioral action. Yet, when testing the paradigm in which we presented motion until a first bout before starting the actual test trial (Fig. 2j–m), the model could not capture the relationship between response delay and gap time (Extended Data Fig. 3g). This failure suggests that bouts, indeed, do not reset the integrator.

In summary, we have shown that, also when head-fixed, larval zebrafish temporally integrate motion evidence during quiescence, that they can keep a persistent motion memory for many seconds, that bouts do not reset the integrator, and that all measured behavior is in agreement with the predictions from a bounded leaky integrator model.

Several neuronal clusters show correlated activity with motion integration

Knowing that the animal can integrate motion, we next sought to explore where and how in the brain such a mechanism might be implemented. To this end, we used brain-wide two-photon calcium imaging to screen for areas whose temporal dynamics are aligned with our modeled leaky integrator time constant. We did this in larvae that were fully embedded in transparent agarose, expressing cytosolic GCaMP6s, a calcium level-dependent fluorophore, in most neurons. We presented animals with left- or right-ward moving 50 % or 100 % coherence interleaved with periods of 0 % coherence baseline, i.e. no motion (Fig. 3a). The absence of behavior in such a fully restrained preparation significantly simplifies the imaging procedure, allowing us to sequentially characterize many imaging planes over many hours. We then applied automatic segmentation and signal extraction techniques to obtain estimates of the cellular calcium dynamics²³. Mapping cells into the larval zebrafish reference brain atlas (z-brain²⁴) enabled us to further characterize neurons tied to precisely predefined volumetric anatomical masks.

Figure 3 |. Brain-wide and anterior hindbrain two-photon calcium imaging.

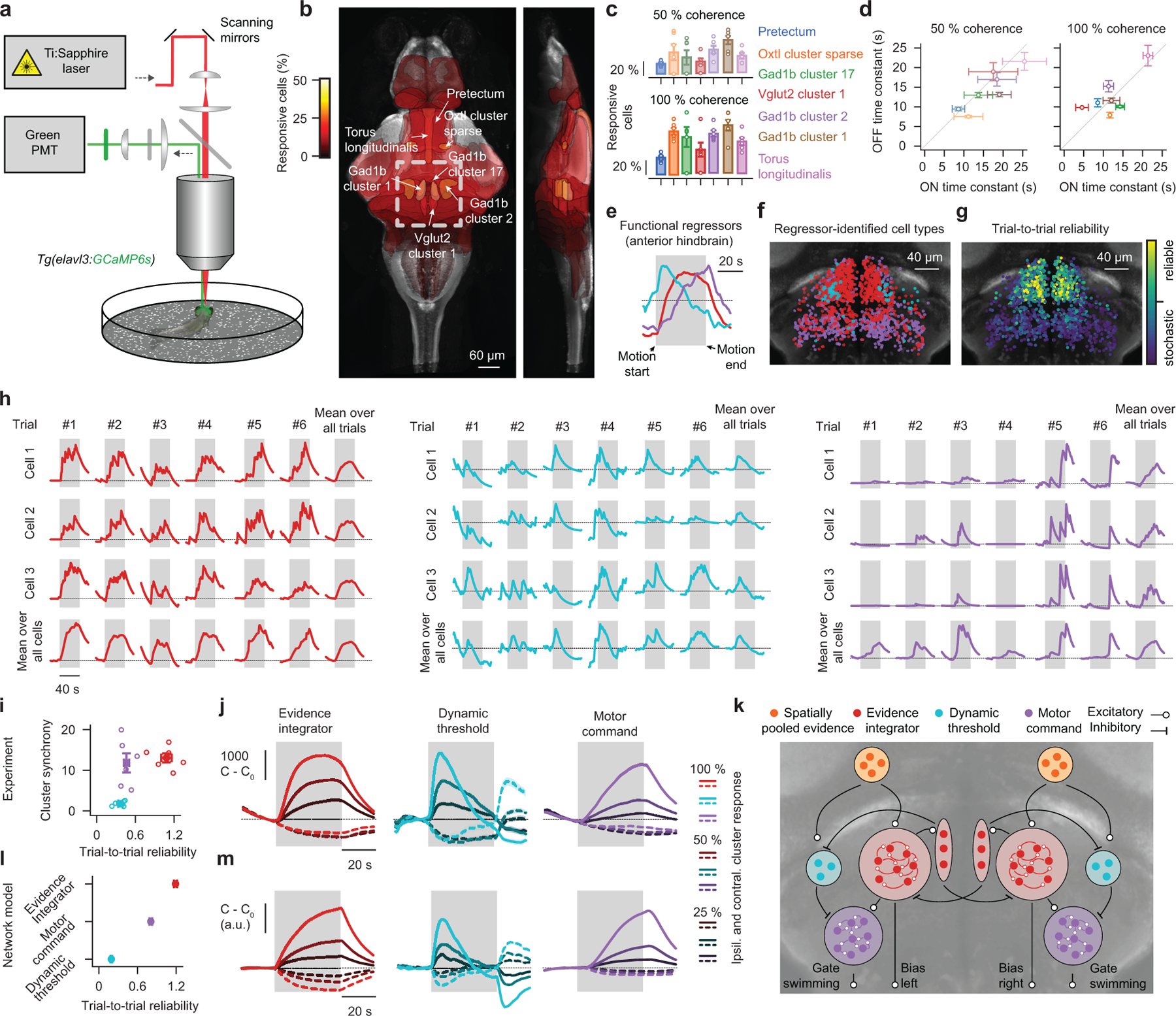
a, Schematic of the two-photon microscope. Fully agarose-embedded animals (no behavior) are presented with dot motion stimuli from below that either drift left- or right-ward. We either image across the entire brain (b–d) or focus on a single plane within the anterior hindbrain (e–j). b, Overlay of all brain regions where the fraction of responsive neurons is larger than 1 % during 50 % coherent motion, on top of z and x projections of the larval zebrafish reference brain. Colors indicate the fraction of responsive cells in the area. Region names follow reference brain (https://engertlab.fas.harvard.edu/Z-Brain) convention²⁴. The dashed square indicates where the anterior hindbrain resides. c,d, Quantification of the fraction of responsive cells within the identified brain areas (c) and of regional onset and offset time constant dynamics (d) for 50 % and 100 % coherence levels. e–g, Functional regressors found by k-means clustering (e) and spatial arrangement of clustered cell types (f) together with their trial-to-trial reliability at 50 % coherence (g) for the single plane anterior hindbrain imaging experiment. h, Single cell and trial example dynamics for each identified anterior hindbrain cluster and respective averages over trials and cells for 100 % coherent motion. i, Trial-to-trial reliability plotted against cluster synchrony for each cluster (see methods for metrics). j, Cluster average calcium dynamics, relative to baseline (C₀), for different coherence levels (moving right- or left-ward) over time. Ipsilateral indicates the left or the right hemisphere for left- or right-ward motion, respectively, contralateral the other side. k, Suggested network model. Each cluster is implemented as a single rate unit. l,m, Analysis as in (i,j) but for network model simulations. Cluster synchrony is not defined here as model clusters are single rate units. N = 6 fish for each coherence level in (b–d) and N = 6 fish in (e–j). N = 8 model simulations in (l,m). All error bars indicate mean ± sem over trials (j,m) or fish (c,d,i,l). Gray shaded areas in (e,h,j,m) indicate motion stimulation (before and after, 0 % coherence is shown). Open circles in (c,i) show individual fish.

We first presented larvae with 0 % and 50 % coherent motion and systematically searched for areas that could robustly distinguish between the two stimuli. As the tested motion strength was relatively weak and hard to detect, we argue that such regions should represent a spatially and/or temporally low-pass filtered version of the stimulus. Analyzing our brain-wide imaging data accordingly revealed seven brain regions (Fig. 3b and Extended Data Fig. 4a): the pretectum and an embedded oxytocin-like cluster (midbrain), Gad1b clusters 1, 2, and 17 (anterior hindbrain), a Vglut2 cluster 1 (anterior hindbrain), as well as the torus longitudinalis (midbrain). Further analysis of these areas showed that the fraction of active neurons as well as their response amplitudes became higher with increasing coherence levels and that all regions were direction-selective (Fig. 3c and Extended Data Fig. 4b). We next fitted onset and offset time constants to the dynamics of each region. This analysis revealed a brain-wide sensory processing hierarchy of temporal integration (Extended Data Fig. 4a), where early sensory structures, such as the pretectum, carry a rather instantaneous stimulus representation and where several motor-related brain areas respond with significant delays. Moreover, within most regions, we found that onset and offset time constants were not significantly different from one another and only mildly depended on the coherence level (Fig. 3d), which is all in agreement with the dynamics expected from leaky integration.

We further argue that integrators should act as low-pass filters and, hence, regions with longer time constants should be less noisy within individual trials. To test this idea, we calculated the activity variance over time for each cell in each trial during the 0 % baseline condition (Extended Data Fig. 4b). Averaging these numbers per region revealed that the fast responding pretectum and the embedded oxytocin-like cluster were relatively noisy and that some of the slower anterior hindbrain regions were almost noise-free. However, the torus longitudinalis, which had by far the slowest dynamics, was paradoxically much noisier than expected. Its single-trial dynamics are, hence, not in agreement with a leaky integrator model, which leads us to believe that this region is not directly involved in the behavior.

Thus, our analyses of brain-wide circuit dynamics suggest that pretectal regions provide a relatively fast but robust representation of the motion stimulus, probably performing spatial pooling from local motion cues^16,19,20, whereas multiple anterior hindbrain clusters temporally integrate over these signals.

Anterior hindbrain imaging reveals three functional cell types with distinct response dynamics

As the activity dynamics within the anterior hindbrain suggested that this is likely the site of temporal integration, we next wanted to explore this brain area in more detail (Supplementary Video 10). To obtain a sufficient number of trials for more rigorous statistical analyses, we focused on a single plane (Fig. 3b), and presented animals with left- or right-ward moving 25 %, 50 %, or 100 % coherence levels and 0 % baseline before and after the motion stimulus. K-means clustering on trial-averaged cell responses revealed three distinct functional cell types in the network and provided us with a set of regressors (Fig. 3e), which unbiasedly classified neurons based on their response dynamics (Extended Data Fig. 4c). These clusters spatially segregated and symmetrically tiled the anterior hindbrain (Fig. 3f). Two of the identified regressors had a rather similar shape with only a slight difference in their dynamics. We, therefore, sought to test if cells also spatially segregate based on other measures. To this end, we analyzed dynamics and trial-to-trial variability on the level of single cells, which revealed that neurons in the anterior part of this brain region responded more reliably than the ones in the posterior part (Fig. 3g and Extended Data Fig. 4d), a spatial arrangement that matched the cluster locations found by the regressor analysis.

To better understand the origin of these different dynamics, we next explored a few example cells and trials (Fig. 3h): We found that individual cells in the first cluster were responding together and showed ramping behavior in individual trials. Cells in the second cluster were noisier, less synchronous, and less reliable. Cells in the third cluster had more complex dynamics: While generally responding synchronously, responses were variable across trials. In many trials this cluster remained largely inactive during the stimulation period and occasionally responded in a step-like manner. To quantify these effects, we analyzed the identified clusters based on statistical measures for cell-to-cell synchrony and trial-to-trial reliability and found that clusters indeed segregated according to these features (Fig. 3i).

We next plotted the average response over cells and trials of each cluster to different coherence levels moving left- or right-ward (Fig. 3j), revealing that all identified clusters were direction-selective with distinct temporal dynamics: The first cluster followed the dynamics of a low-pass filter with a long time constant of ~11 s and the second cluster had more high-pass filter-like (or derivative-like) dynamics. The third cluster showed slow linearly increasing activity in a trial average whose dynamics, given the trial-to-trial dynamics of this cluster (Fig. 3h,i), should rather be interpreted as a response probability.

We next wanted to know whether the identified functional clusters might be excitatory or inhibitory. To this end, we compared their spatial arrangement with the expression patterns of two neurotransmitter-specific driver lines²⁵ (Extended Data. Fig. 5a,b). This analysis suggested that the low-pass filter cluster is likely composed of both excitatory and inhibitory cells, while the high-pass filter cluster appears to be exclusively inhibitory. To obtain an idea of the possible inputs and outputs, as well as the intrinsic connectivity, we used the individually traced neuronal morphologies available at the Max-Planck Zebrafish Brain Atlas²⁶. We find that of all these cells that have their soma in the anterior hindbrain, many form a dense cluster in the ventral area and branch out into the pretectum (oxytocin-like cluster) and towards premotor areas^27,28 and that local contralateral projections exist (Extended Data Fig. 5c).

Given the identified structural features, we next set out to generate a plausible network implementation (Fig. 3k). In line with our brain-wide imaging experiments (Fig. 3b–d) and previous imaging studies^16,19,20, we assume that spatially pooled motion cues are computed within pretectal circuits. Such signals are then further processed by the identified low-pass filter cluster in the anterior hindbrain. Long time constants within neural circuits can be obtained by densely coupling neurons of similar functional type and finely adjusting the balance of excitation and inhibition²⁹. In order for the low-pass filter cluster to be able to transmit excitatory and inhibitory signals while obeying Dale’s principle, we attached an inhibitory helper unit to it. The presence of excitatory and inhibitory neurons within this cluster is in agreement with the identified neurotransmitter distribution (Extended Data. Fig. 5a,b). We speculate that the observed high-pass filter properties of the second cluster could simply arise by subtracting the original signal from the pretectum with its low-pass filtered version – which is already computed by the first cluster. Based on our neurotransmitter analyses (Extended Data Fig. 5a,b), we modeled the high-pass filter cluster as purely inhibitory. Finally, we observed that the response dynamics in the third cluster roughly followed the difference between the low-pass and high-pass filter clusters (Fig. 3j). Following these observations, we suggest that both clusters converge in a push-pull configuration onto the third cluster such that whenever excitation exceeds inhibition, a step-like response is initiated. Finally, following the general pattern of cell morphologies in this area (Extended Data Fig. 5c), we fashioned the network in a bilaterally symmetric way and added inhibitory contralaterally projecting connections between the two hemispheres. We then systematically tuned model parameters to the experimental data and found that our network model could faithfully mimic trial-to-trial cluster properties (Fig. 3l) as well as the response dynamics in a trial average (Fig. 3m).

We, therefore, propose that the low-pass filter cluster represents a motion evidence integrator and that the high-pass filter cluster represents a dynamic decision threshold. We further propose that both clusters compete, in a push-pull configuration, for activating the third cluster, a motor command unit. The resulting step-like response then leads to swimming decisions where turning directions are controlled by the lateral left-right bias of the two integrator clusters (Fig. 3k).

Dynamics in the anterior hindbrain relate to behavioral choices in single trials

We next wanted to relate our imaging data to the behavior. To this end, we imaged the anterior hindbrain in head-fixed larvae with the tail free to move, allowing us to simultaneously observe neural activity and motor decisions (Fig. 4a). To automatically assign functional labels to imaged cells, we designed a behavior-based classification approach. To this end, we first used our network model to simulate bout-aligned circuit dynamics (Extended Data Fig. 6b,c), allowing us to formulate a set of heuristic rules for clustering neurons (Extended Data Fig. 6d). Notably, the spatial arrangement of the clusters resulting from this alternate classification approach (Fig. 4a) resembled the one we had found in fully embedded larvae using classical regressor-based analysis (Fig. 3e,f). We first wanted to know if our network model could, in principle, capture the experimentally measured behavioral response delay distributions. To test this, we grouped bouts based on whether they were correct or incorrect and compared data and model results, revealing a remarkable agreement between the two (Extended Data Fig. 6e).

Figure 4 |. Neural correlates of behavioral choices in the anterior hindbrain.

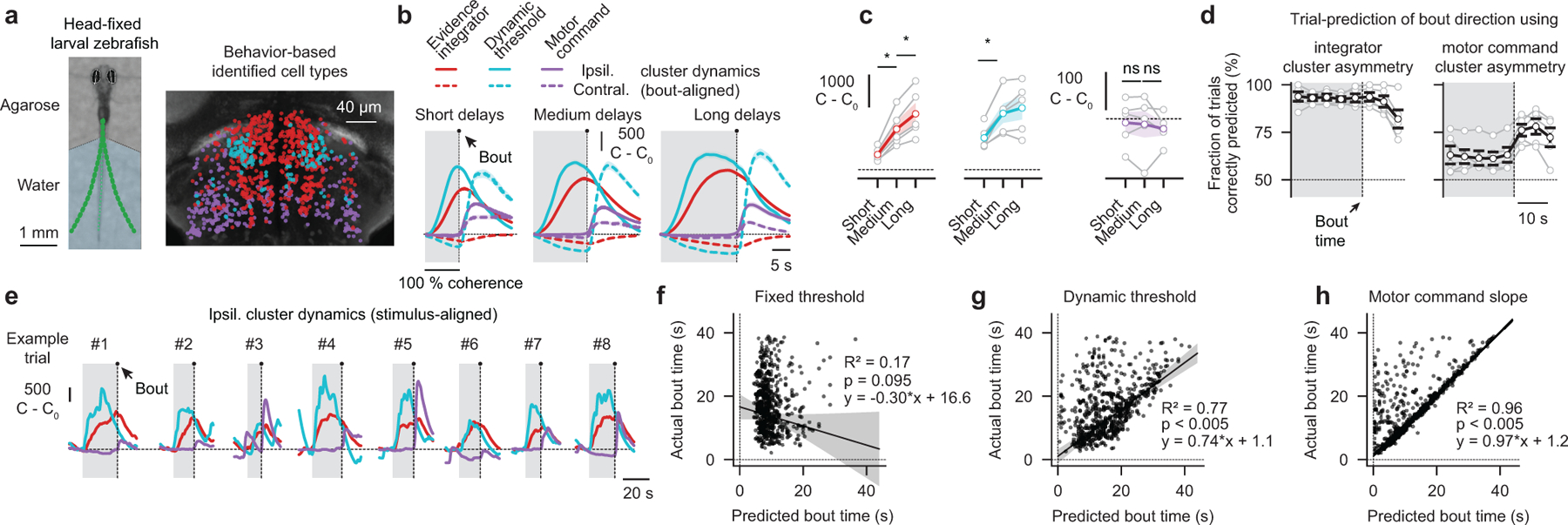
a, Photograph of a head-fixed larval zebrafish in the two-photon microscope (left panel). Green dots indicate tail tracking points. In each trial, we presented 0 % coherence as a baseline, followed by left- or right-ward moving 100 % coherence until the animal initiated a swim bout. Whenever we detected such an event, we immediately dropped coherence levels to 0 %, which was necessary to prevent vigorous movements and struggles. We used a behavior-based classification approach to determine the functional identity of cell types (right panel). b, Experimentally obtained bout-aligned cluster averages, grouped by response delay (short: 4–10 s, medium: 10–16 s long: 16–22 s). Ipsilateral indicates the left or the right hemisphere for left- or right-ward motion, respectively, contralateral the other side. Gray shaded areas indicate motion stimulation. c, Quantification of ipsilateral cluster activity at bout time as a function of delay (*p < 0.01 for both integrator cluster comparisons; *p < 0.05 for the dynamic threshold cluster comparison; p = 0.72 and p = 0.61 for the motor command cluster comparisons). See Extended Data Fig. 6b,c for model simulations. d, Trial-to-trial prediction of swimming direction, based on the integrator or motor command cluster dynamics, as a function of time relative to bout. e, Example trials of stimulus-aligned ipsilateral cluster dynamics. f,g,h, Trial-to-trial bout time predictions (black dots indicate individual bouts) based on three threshold models and respective robust linear regression analyses (RANSAC, see methods). Gray shaded areas indicate confidence intervals of the regression fits. N = 5 fish in (a–d,f–h) and N = 1 fish in (e). Gray lines with open circles in (c,d) are individual fish, colored or black lines in (c,d) are fish averages. All error bars indicate mean ± sem over trials (b) or fish (c,d). P-values in (c) are based on one-sided t-tests comparing response differences to zero. All asterisks (*) indicate significance (*p < 0.05, *p < 0.01, or *p < 0.001).

Assuming that the integrator cluster always integrates with a given time constant, a prediction of a push-pull competition between this cluster and the dynamic threshold cluster is that both activities should scale with response delay (Extended Data Fig. 6b,c). Only then would the integrator cluster activity reach sufficiently high levels to overcome the stronger inhibition from the dynamic threshold cluster and trigger a swim. To explicitly test this idea in our experimental data, we grouped short, medium and long trials, and found, indeed, that activity in both clusters was correlated with delay time (Fig. 4b,c).

In our network model, we further propose that a decision is made whenever the activity of the evidence integrator cluster exceeds the activity of the dynamic threshold cluster. This implies that calcium signals should converge and cross around the time of a bout (Extended Data Fig. 6b). Indeed, we could observe such crossing events in our bout-aligned data irrespectively of response delay (Fig. 4b and Extended Data Fig. 6a). Moreover, the motor command cluster should only engage after such events and remain silent beforehand, which we found to be the case (Fig. 4b,c). Thus, our analysis of bout-aligned circuit dynamics provides additional evidence for the suggested push-pull organization between evidence integrator cluster, dynamic threshold cluster, and motor command cluster. Notably, the small delay between the crossing event and the actual swimming decision is likely due to the low-pass filter properties of GCaMP6s that add an estimated 1–3 s³⁰ to any measured neural activity dynamics.

We next sought to use the activity of the identified clusters to predict behavioral choices on the level of single trials. We first tried to predict swimming direction and found that by calculating which of the evidence integrator hemispheres was more active allowed us to faithfully predict this feature many seconds before the actual swim (Fig. 4d). Similarly, we tried to estimate swimming directions based on the activity in both motor command cluster hemispheres. Such predictions were largely unsuccessful, which is in agreement with the idea that these units are only responsible for releasing motor decisions, rather than providing an anticipatory bias.

We next tested what features of the circuit activity best predicted response delay. Our network model allowed us to formulate two parallel hypotheses: First, bouts are initiated whenever activity in the evidence integrator cluster exceeds activity levels in the dynamic threshold cluster (Extended Data Fig. 6f). Second, bouts are triggered when the slope in the motor command cluster turns positive (Fig. 4e). We also wanted to test a third, alternative, hypothesis, namely that bouts might be initiated whenever the integrator value crosses a fixed threshold (Extended Data Fig. 6f). We analyzed our neural data in all trials according to these predictors and compared our predicted delay with the actually measured one (Fig. 4f–h and Extended Data Fig. 6g,h). We found that the fixed threshold predictor performed poorly and that predictions significantly improved using the dynamic threshold (Fig. 4f,g and Extended Data Fig. 6g,h). In the latter, the predictive quality was surprisingly high, considering that we likely subsample both neuronal populations, and given that we operate in a regime of significant measurement noise. Finally, we find that the sudden rise in slope in the motor command cluster was an almost perfect predictor of bout events (Fig. 4h and Extended Data Fig. 6g), providing additional confirmation that this cluster is involved in executing swimming decisions.

Thus, by imaging anterior hindbrain dynamics in behaving animals, we found, in close agreement with our proposed network model, that the three identified clusters are good predictors of upcoming behavioral choices on the level of individual trials.

Finally, we tested if our network model could reproduce also the behavior of freely swimming larvae (Fig. 1a–f and Extended Data Fig. 7a). However, to allow for spontaneous bouts in the absence of motion stimulation, we needed to add an additional component to the model. Here, a rapidly triggered collapse of the dynamic threshold offered an intriguing possibility for spontaneous bout generation, since the high-pass filter characteristics of this structure readily allows for its rapid adjustment. For example, it might be targeted by other brain regions that measure balance³¹, water flow³², or that detect predators and, if such signals are inhibitory, they could shunt the dynamic threshold cluster and gate a premature readout of the integrator cluster in the case of urgency. We found that such a model could, in principle, reproduce the behavior of freely swimming larvae (Extended Data Fig. 7b,c). Thus, our network model of the anterior hindbrain could indeed represent a plausible circuit implementation that can mechanistically describe how freely behaving animals accumulate evidence from, and dynamically interact with, a complex sensory environment.

Discussion

We have here provided the first evidence that larval zebrafish can temporally integrate noisy coherent motion stimuli over many seconds, that this behavior can be explained by bounded leaky integrator models, and that the dynamics in the anterior hindbrain can predict swimming decisions. Our study brings the powerful toolkits of the larval zebrafish animal model to the field of sensory integration and decision-making, creating thereby new opportunities for brain-wide and local circuit analyses of the precise neural processes controlling such behaviors.

The swim bout as a decision event has been recently explored in head-fixed larval zebrafish¹⁷, where the authors analyzed response delay distributions of forward swims, triggered by back-to-front motion. The preferred interpretation here was that larvae respond stochastically to the stimulus rather than temporally integrate information, which is in contrast to our findings. We attribute these differences mostly to the non-directional decision criterion used in the previous work. Further, in these, like in most other comparable studies, larval zebrafish visual behavior is normally studied using moving gratings^16,19,28,33. Such stimuli have strong local motion energy across the visual field, making it difficult to explore aspects of spatial and temporal integration. Here, we use dot motion kinematograms which present weaker and noisier motion stimuli. Combining these stimuli with brain-wide calcium imaging, allows us to search for the relevant neuronal structures on the level of almost the entire nervous system. Our findings suggest that pretectal circuits perform spatial pooling of local motion cues while the anterior hindbrain temporally integrates these signals. Both ideas are in agreement with recent studies in zebrafish that argue that the pretectum computes direction-selective global motion signals^16,19,20 and that the anterior hindbrain is a center of sensory-motor convergence^21,22,34,35. Moreover, such a twostep computational arrangement is reminiscent of the middle temporal visual area (MT) and lateral intraparietal cortex (LIP), which are thought to have similar roles during evidence integration and decision-making in primates¹¹. We also identified further brain regions with slow integration dynamics during motion processing, such as the torus longitudinalis. In fish, this brain region has been attributed to processes related to prediction and attention³⁶ but its role during motion processing remains unclear. We speculate that the torus longitudinalis might allow for persistent working memory storage of the more distant sensory history that can potentially help to refine and bias future integration and decision-making processes, a role that has recently been proposed for the mouse posterior parietal cortex³⁷.

Investigating trial-by-trial dynamics of the identified neuronal ensembles in the anterior hindbrain allowed us to propose a biophysically plausible circuit arrangement in which one cluster represents the accumulated evidence while a second cluster represents a dynamic threshold. We further propose that the two clusters converge, in a push-pull configuration, onto a third, motor command, cluster, which executes swimming events whenever the evidence cluster activity exceeds the one from the dynamic threshold cluster. Similar models have been explored in computational studies^38,39, but the precise advantages over simpler implementations using fixed decision criteria remain to be elucidated. We speculate that the proposed arrangement might allow for rapid adjustments of the decision threshold, for example through urgency-related signals^40,41, which could lead to a rapid collapse of the threshold. This might be useful in decision-making scenarios where the need for response speed outweighs the importance of response accuracy⁴². Both conditions occur frequently in moving animals, such as a freely swimming larval zebrafish, that have to interact adaptively with a constantly changing environment.

As the integrator cluster is composed of a large number of neurons that respond in synchrony within single trials, we propose that the integration dynamics within that structure arises through local dense circuit coupling. Yet, it remains unclear whether such dynamics require an intricate balance of excitation and inhibition within the network^29,43,44 or whether these neurons employ certain specialized biophysical features^3,6 allowing them to operate with slower time constants. To test these, and many other possibilities of concrete circuit implementation, further studies involving cell physiology⁴⁵, anatomy⁴⁶, connectivity⁴⁷, ablations, and optogenetics⁴⁸ are required to challenge, constrain, and further expand our network model. This should help to uncover and mechanistically describe general computational principles underlying sensory evidence accumulation and decision-making also in other organisms.

Online methods

Zebrafish

To obtain larvae, we incrossed adult transgenic zebrafish of the elavl3:GCaMP6s line⁴⁹. We raised small groups of 20–30 larvae in filtered facility water in Petri dishes (diameter: 9 cm) on a 14 h light, 10 h dark cycle at constant 28 °C. From 4 days post-fertilization (dpf) onwards, we fed larvae with paramecia once per day. We performed experiments with larvae at ages 5–7 dpf. Sex cannot be determined at this developmental stage. In our purely behavioral experiments (Fig. 1 and Fig. 2), we did not sort larvae based on fluorescence or pigmentation. We did not observe any difference in behavior based on the genetic background. For all imaging experiments (Fig. 3 and Fig. 4), we screened larvae to have strong GCaMP6s fluorescence and no pigmentation (mitfa^−/−). In the imaging experiment where we explored the distribution of inhibitory neurons in the anterior hindbrain (Extended Data Fig. 5b), we used double transgenic Tg(elavl3:GCaMP6s); Tg(gad1b:loxP-DsRed-loxP-GFP)²⁵ larvae. All experiments were approved by Harvard University’s standing committee on the use of animals in research and training.

Visual stimuli

In all experiments, we used random dot motion kinematograms as visual stimuli (Fig. 1a and Supplementary Video 1) which consisted of ~1000 dots (diameter: 2 mm), projected (60 Hz, AAXA P300 Pico Projector) from below onto a circular arena (diameter: 12 cm) of mildly light-scattering parchment paper. Based on visual acuity considerations⁵⁰, we roughly estimate the behaviorally relevant visual field to have a radius of ~5 cm around the animal. We first showed 0 % coherence as a baseline stimulus (no movement) and then abruptly switched coherence levels, letting dots translate continuously (speed: 1.8 cm/s), either right- or left-ward relative to the body orientation of the fish. After some time, coherence levels dropped to 0 % again. Each dot, no matter if static or moving, had a short lifetime (200 ms mean), stochastically disappeared and immediately reappeared at a random location. This ensured that our experiments are not confounded by animals potentially tracking individual dots. In the purely behavioral experiments (Fig. 1 and Fig. 2), dots were white on a black background (average luminance of the scene: ~120 Lux, Extech Instruments Light Meter LT300). In the imaging experiments (Fig. 3 and Fig. 4), to prevent bleed-through into the green photomultiplier, dots were red on a black background (average luminance of the scene: ~20 Lux). We rendered stimuli online using programs custom-written in Python 3.7 and Panda3D 1.10 with GLSL vertex shaders running on Nvidia GPUs (GTX 970).

Behavior experiments in freely swimming larval zebrafish

We placed larvae in custom-designed acrylic dishes (diameter: 12 cm, height: 5 mm, rim: black, bottom: transparent) filled with filtered facility water. We illuminated the scene from below using infrared LED panels (940 nm panel, Cop Security). For tracking, we used a camera (Grasshopper3-NIR, FLIR Systems) with a zoom lens (Zoom 7000, 18–108 mm, Navitar) and a long-pass filter (R72, Hoya). We performed posture analysis in real-time at ~100 Hz using custom-written software based on Python 3.7 and OpenCV 4.1. In brief, we determined the position of the fish from the center of mass in the background-subtracted image and used second-order image moments to determine its body orientation. We then computed a rolling variance (50 ms window size) of body orientation, identifying events of high activity (bouts). Running the analysis online allowed us to store a highly compressed version of the data set rather than raw movies. Moreover, it allowed us to always align coherent motion direction to the body orientation of the fish (Supplementary Video 1). To increase throughput, we used 2 computers, each connected to 4 cameras and 2 projectors, allowing for independent stimulation and closed-loop tracking of 8 individual fish at once. As a stimulus protocol, we presented 5 s of 0 % coherence, followed by 0 %, 25 %, 50 %, or 100 % coherence moving right- or left-ward, followed by 5 s of 0 % coherence. The stimulation order was random.

Behavior experiments in head-fixed larval zebrafish

We embedded larvae in freshly made 1.8 % agarose (Invitrogen, UltraPure™ Low Melting Point Agarose, 16520–100), at ~35 °C, on a microscope glass slide. After solidifying (~20 s), we cut out a small block of agarose containing the fish, transferred it to the center of a Petri dish (diameter: 9 cm, VWR®), surrounded the block with a thin layer of agarose, and filled the dish with filtered facility water. We then used a fine scalpel to remove the agarose around the eyes and tail. We performed experiments immediately after the embedding using the same 8 setups as used for the freely swimming fish. Using another custom-written Python 3.7-based software package, we tracked ~30 points along the tail as well as the angle of both eyes at ~360 Hz. Bouts were detected online whenever the rolling variance (50 ms window size) of the tail tip deflection (angle relative to the swim bladder) crossed a threshold (1.5).

We performed two prescreening steps before all our experiments in head-fixed larvae: First, we tested fish under freely swimming conditions and presented them with 0 % coherence as well as 4 directions of motion (100 % coherence moving right- or left-ward, front-to-back or back-to-front). Using this stimulus, we discarded fish if they did not swim spontaneously or did not show a clear optomotor response (approximately 30 % of the tested fish). We then embedded the remaining fish, following the procedure described above. Second, we presented the same visual stimuli to head-fixed larvae again. We discarded fish if we did not observe robust (within 10 s) directional tail flicks of roughly the same delay and amplitude between right- and left-ward 100 % coherent motion (approximately 60 % of the head-fixed larvae). We attribute the low yield to the fact that animals might get harmed by the embedding procedure.

In all experiments with head-fixed larvae, in each trial, we first presented 0 % motion coherence (baseline) before starting the actual stimulus. Whenever we detected a bout, we immediately set the coherence level to 0 % and started the next trial. This prevented larvae from performing vigorous and exhaustive tail movements and significantly increased the number of measurable trials. If the animal did not respond after a maximum of 30 s of stimulus presentation, we also initiated a new trial. As a stimulation protocol for the experiments shown in Fig. 2b,c, we presented animals with 8 s of 0 % coherence, followed by 0 %, 25 %, 50 %, or 100 % coherent motion right- or left-ward. Pulse lengths in Fig. 2d,e were 1 s (100 % coherent motion right- or left-ward) and interleaved with 0 % coherence. Pulses in Fig. 2f–i were 2 s, followed by variable periods of 0 % coherence, followed by 100 % coherent motion right- or left-ward. If a bout occurred during the motion pulse or during the gap period, we discarded that trial. In Fig. 2j–m, we presented 100 % coherent motion until the detection of the first bout. We then showed variable gaps of 0 % coherence and then started the test stimulus (100 % coherent motion right- or left-ward). If additional bouts occurred during the gap period, we discarded that trial.

Two-photon calcium imaging

For in vivo-imaging experiments, we prescreened and head-fixed larvae as explained above. In the experiments that did not require behavioral readout, we fully embedded larvae in agarose (Fig. 3). In imaging experiments with behavioral readout (Fig. 4), we removed the agarose around the tail as described for the head-fixed behavior. Immediately after embedding, we transferred animals into the measurement chamber of a custom-built two-photon microscope, operated by custom-written Python 3.7-based software (PyZebra2P). In brief, we used a femtosecond-pulsed MaiTai Ti:Sapphire laser (Spectra Physics, USA) tuned to 950 nm for GCaMP6s imaging or to 1040 nm for DsRed imaging, a set of x/y-galvanometers (Cambridge Technology, USA), and a 20x Olympus infrared-optimized objective (XLUMPLFLN) to scan over the brain. We collected fluorophore emission using two photomultipliers (green and red), amplified by two current preamplifiers (Stanford SR570). We used frame acquisition rates of around 1 Hz in all imaging experiments. We adjusted laser power to ~13 mW at the specimen, a low enough value that did not seem to interfere with the behavior of larvae.

In our brain-wide imaging experiments (Fig. 3a–d), we imaged each plane at a spatial resolution of ~0.7 μm per pixel (700 × 700 pixels) for 16 minutes, while presenting ~8 trials of 40 s of coherent motion (50 % or 100 %, moving right- or left-ward) interleaved by 20 s of 0 % coherence. We then moved the objective 6 μm to the next imaging plane and repeated the procedure. We acquired ~23 planes, resulting in a total imaging time of around 6 hours per fish. Because of time concerns, we only presented one of the two coherence levels in a given fish.

In our imaging experiments of the anterior hindbrain (Fig. 3e–j and Fig. 4), we imaged a single plane at higher spatial resolution (0.35 μm per pixel, 700 × 700 pixels) for a total time of ~4 hours. In the experiments without behavior (Fig. 3), we presented ~40 trials of 40 s of motion coherence (25 %, 50 %, and 100 %, right- or left-ward), interleaved with 20 s of 0 % coherence baseline. We presented all three coherence levels to a given fish. For the imaging experiments with simultaneous behavioral readout (Fig. 4), we installed a camera below the fish (Grasshopper3-NIR, FLIR Systems), a custom-built lens array, and infrared illumination, allowing for tail tracking as described above. We first presented 0 % coherence for 30 s and then switched to a higher coherence level (only 100 %) for up to 40 s. Whenever we detected a bout, we immediately dropped the coherence level to 0 %. In addition to the reasons stated above, this procedure was of particular importance during our long imaging experiments as it reduced motion artifacts and prevented drift.

Preprocessing and anatomical mapping of two-photon imaging data

We implemented a three-step pipeline for preprocessing imaging data, combining the computational toolbox for large scale calcium imaging data analysis (CaImAn²³) and the computational morphometry toolkit (CMTK⁵¹).

First step: We used the CaImAn framework to perform piecewise rigid motion correction (NoRMCorre⁵²), using standard parameters.

Second step: We applied the CaImAn framework-based segmentation algorithm (constrained non-negative matrix factorization, CNMF), using standard parameters adjusted for frame rate and cell size. We then temporally aligned the extracted calcium dynamics of segmented cells based on stimulus onset (Fig. 3h,j and Fig. 4e) or bout time (Fig. 4b). In all trials, we subtracted the estimated baseline calcium level (C₀), averaged 10 s before the onset of motion, giving us a relative measure of the dynamics (C – C₀). We did not calculate a ΔC / C₀ because estimated baseline values were often zero. We also sought to ensure that CaImAn’s estimate of the calcium dynamics was compatible with previously used analysis techniques performing segmentation and signal extraction based on local pixel correlation⁵³. These techniques found much fewer units than CaImAn but identified the same brain areas to be involved in the integration process with similar temporal dynamics.

Third step: We mapped the coordinates of all identified cells into the larval zebrafish reference brain using CMTK, allowing us to assign anatomical labels based on well-defined anatomical masks²⁴. Mapping a single plane from the anterior hindbrain (Fig. 3e–j and Fig. 4) into the reference brain required an additional step: After the experiment, we quickly acquired a volume stack and used template matching in OpenCV 4.1 to find a transformation of our plane to this stack.

Anatomical mapping of cell morphologies

To map all cell morphologies from the Max-Planck Zebrafish Brain Atlas²⁶ to the z-brain altas²⁴, we first created a bridge transform between the two coordinate systems. To this end, we mapped the available immunostained t-erk reference stacks from the two atlases to one another using the Advanced Normalization Tools (ANTs)⁵⁴ following standard procedures^26,55. We then used the function antsApplyTransformsToPoints to convert the available cell morphology swc files.

Analysis of brain-wide imaging data

To create a catalog of brain regions involved in the integration process (Fig. 3b and Extended Data Fig. 4a), we first grouped neurons based on their responsiveness to coherent motion (50 % or 100 %, right- or left-ward). We considered a neuron responsive if its activity to either motion direction was significantly different from zero (one-sided t-test, p < 0.05) and if its response was at least 100 C - C₀. This analysis allowed us to calculate the fraction of responsive cells in a given area. We discarded brain areas containing less than 10 cells in total or where the fraction of responsive neurons was less than 1 %.

We estimated regional time constants based on all responsive cells in an area. To this end, we grouped neurons according to their directional preference and averaged over cells and trials. To calculate onset and offset time constants, we fitted two exponential functions, $A_1\cdot \left(1-e^{-t/{\tau }_{\mathit{\text{onset}}}}\right)$ and $A_2\cdot e^{-t/{\tau }_{\mathit{\text{offset}}}}$, to the area’s preferred direction dynamics during and after coherent motion stimulation, respectively. For some brain areas either fitting function sometimes did not converge and, hence, regional sample numbers are variable across fish (Fig. 3c,d and Extended Data Fig. 4a). We discarded areas for which we could not determine any time constant in any fish. Notably, because of the relatively slow GCaMP6s kinetics³⁰, we estimate the actual time constants to be ~1–3s faster than what we report (Fig. 3d and Extended Data Fig. 4a).

Functional clustering of anterior hindbrain neurons

In our imaging experiments in fully embedded larvae (Fig. 3e–j), we used a regressor-based method for clustering neurons. We only used neurons from anterior hindbrain rhombomeres 1–3. To this end, we first analyzed all identified cells from the left hemisphere that had a maximum trial-averaged activity of at least 200 C - C₀ when stimulated with 100 % coherence in preferred direction. We then clustered these traces using Python 3.7 and scikit-learn k-means, revealing three functional regressors (Fig. 3e). We next determined the correlation coefficient between the trial-averaged preferred-direction activity of each cell in both hemispheres and each regressor and assigned functional labels based on the maximum correlation value. If this value was lower than 0.8, we labeled neurons as “not assigned” (Extended Data Fig. 4c).

Since in the imaging experiments with simultaneous behavioral readout (Fig. 4) stimulation times depend on the variable response delay, we could not easily employ a regressor-based clustering strategy here. Instead, we formulated a set of heuristic rules based on the bout-aligned dynamics predicted from our network model (Extended Data Fig. 6b,c): We labeled a cell as an integrator neuron if its activity was larger than 150 C - C₀ within 5 s before and after bouts for ipsilateral motion (for cells in the left and right hemisphere, left- and right-ward motion, respectively). For contralateral motion, its activity needed to be smaller than 150 C - C₀ within 5 s before and after bouts. We labeled a cell as a dynamic threshold neuron if its activity was larger than 150 C - C₀ within 5 s after motion onset for ipsilateral motion. For contralateral motion, its activity needed to be smaller than 150 C - C₀ within 5 s after motion onset but larger than 150 C - C₀ within 5 s after bouts (= stimulus offset, which induces an activity rebound). We labeled a cell as a motor command neuron if its activity within 5 s before bouts was smaller than 150 C - C₀ for ipsilateral and contralateral motion. For ipsilateral motion, its activity within 5 s after bouts needed to be larger than 150 C - C₀. Also, activity within 5 s after bouts for ipsilateral motion needed to be larger than the one for contralateral motion. If neurons had multiple labels after this procedure, we prioritized the integrator cluster label over the dynamic threshold cluster label over the motor command cluster label. If neurons had no label, we considered them as “not assigned” (Extended Data Fig. 6d).

Analysis of anterior hindbrain neurons

We determined cell-to-cell synchrony (Fig. 3i) by dividing the variance over time of the response mean over cells by the mean of the response variance over time of all cells⁵⁶. This measure gives an index ranging from zero for asynchronous networks to one for networks in perfect synchrony. As it depends on the network size, we repeated the process for time-shuffled data, allowing us to calculate a normalized index. We calculated trial-to-trial reliability (Fig. 3g,i,l and Extended Data Fig. 4d) by dividing, per time bin, the absolute mean response over trials by the standard deviation over trials, and then averaged those values during stimulus presentation. Using this metric, cells that have large response means and small standard deviations over trials will be considered reliable. The exact value of this index can go from zero to infinity. Neurons whose raw data suggested almost perfect trial-to-trial reliability (such as the example cells of the integrator cluster in Fig. 3h) had values of around 2.

Prediction of behavioral choices

To estimate the upcoming turning direction, we analyzed the left and right integrator cluster activity in individual trials and predicted that animals would turn according to the bias of the two hemispheres. To ensure that all time points reported in Fig. 4d reflect situations where motion was present, we introduced nans before the onset of motion before averaging. In the same way, we analyzed turning direction based on the left and right motor command cluster.

To predict bout timing, we tested three different threshold models, one using a fixed threshold, one using the measured dynamic threshold cluster, and one looking for the first occurrence of a small positive slope in the motor command cluster. For the first two models, we first smoothed and extrapolated the integrator activity. To this end, we fitted an exponential $A\cdot \left(1-e^{-t/{\tau }_{\mathit{\text{onset}}}}\right)$ to the left and to the right integrator cluster activity in each trial, considering only the time of motion stimulation before the bout (Extended Data Fig. 6f). We set τ_onset to 11 s based on the observed trial-average cluster dynamics (Fig. 3j). In the model with fixed thresholds, we determined, in every trial, when the left or the right smoothed and extrapolated integrator cluster activity would cross the threshold (Extended Data Fig. 6f). We tested three fixed threshold levels (low, medium, high), chosen based on the average integrator level activity in bouts with short, medium, or long delays, respectively, in a given fish. In the model with the dynamic threshold, we also smoothed the activity from the left and the right measured dynamic threshold cluster, using a Gaussian filter with a standard deviation of 1 s. Next, we determined when the left or right smoothed extrapolated integrator cluster activity would be larger than 200 C - C₀ and cross the left or right smoothed dynamic threshold cluster activity from below. The first moment this happened on either hemisphere, we predicted a bout (Extended Data Fig. 6f). In the third threshold model, we only used the motor command cluster activity on the left and right side. Here we first applied a Gaussian filter with a standard deviation of 1 s to each activity trace. We then searched for the first occurrence of a slope larger than 50 C - C₀ per second.

We applied these predictors in each trial and fish and then compared the predicted bout times with the actually measured ones (Fig. 4f–h and Extended Data Fig. 6g,h), allowing for further statistical quantification. To this end, we applied a robust linear regression algorithm from the Python 3.7 package sklearn.linear_model (random sample consensus; RANSAC⁵⁷). We chose robust linear regression because standard linear regression algorithms appeared to be sensitive to the skewness of our bout time distributions and outliers. We ran the RANSAC algorithm 200 times. In each iteration, we calculated the coefficient of determination (R²) and the estimated linear slope and offset. We then averaged these values to obtain a single estimate for the dataset. To test the statistical significance of the obtained R² values, we repeated the process 20 times on shuffled data. This allowed us to calculate the probability of an estimated R² value to arise by chance (p-values reported in Fig. 4f–h and Extended Data Fig. 6h).

Statistical comparisons

We used one or two-sided t-tests (Python 3.7 scipy ttest_1samp and ttest_ind) in all statistical comparisons. Prior to testing, visual inspection of our data indicated that the underlying distributions were approximately Gaussian, but we did not formally test for this feature. In general, we had performed several pilot experiments identifying the best concepts for our experimental paradigms and to obtain an idea of response variability. To obtain convincing statistical power, we concluded that sample numbers for the freely swimming fish should at least be around 30 (Fig. 1). For the head-fixed behavioral experiments (Fig. 2) and our imaging experiments (Fig. 3 and Fig. 4), variability between fish was low and, hence, we planned experiments for around N = 6 fish. We then performed experiments in batches according to these numbers and analyzed the data automatically, only discarding fish based on the criteria described above.

Algorithmic modeling

We implemented all algorithmic models (Fig. 1, Extended Data Fig. 2, Fig. 2, and Extended Data Fig. 3) using the following equations:

Leaky integrator models:

$$\tau \frac{dX(t)}{dt}=-X(t)+C(t)+N\left(0,{\sigma }^2\right).$$

Stochastic models:

$$X(t)=C(t)+N\left(0,{\sigma }^2\right).$$

Non-leaky integrator models:

$$X(t)=X(t-1)+C(t)+N\left(0,{\sigma }^2\right).$$

X(t) represents the sensory variable at time point t, τ the leak time constant, C(t) the timedepended coherence level, and N(0,σ²) is a random Gaussian variable with standard deviation σ. Coherence levels were between 0 and 1 (corresponds to 0 and 100 %) and follow exactly the respective experimental stimulus protocol. We initiated bouts at different probabilities (r_{| X(t) | < B} and r_{| X(t) | > B}) depending on whether the absolute value of X(t) was below or above the bound (B), respectively. We did prevent bouting if the last bout was less than 200 ms ago, mimicking biological constraints on motor behavior. At each bout, model fish decided to swim right or left depending on the sign of X(t). We performed all simulations in Python 3.7 and numba using forward Euler with dt = 0.01 and put the results in the same file format as our experimentally measured data, allowing for the same analysis and plotting scripts to run on experimental and model data.

We call models in agreement with experimental data when they could qualitatively capture the critical features tested in the experiment, such as an increase in accuracy over time (Fig. 1d,j). Specifically, we quantified these effects by calculating the correlation coefficient for each feature between model and experiment (Extended Data Fig. 2e and Extended Data Fig. 3h), rejected all models where any correlation coefficient was smaller than 0.5, and then picked the model with highest overall correlation score. In order to tune model parameters, we employed systematic and objective step-by-step fitting strategies (explained below for each model).

For the freely swimming larvae (Fig. 1g–l, and Extended Data Fig. 2), we chose model parameters as follows:

Leaky integrator model with visual feedback (Fig. 1g–l and Supplementary Video 2): τ = 2 s; σ = 15; B = 0.9; $r_{|X(t)|<B}=0.6\frac{1}{s};r_{|X(t)|>B}=2.3\frac{1}{s}$. In order to mimic self-created optic flow created by each bout, we increased (for left bouts) or decreased (for right bouts) the coherence level at the next stimulation time point C(t + 1) by $0.70\frac{1}{s}$. For simplicity, we implemented this mechanism only in this model and not in any of the alternative models (Extended Data Fig. 2). We tuned model parameters in a systematic way: 1) We determined σ by fitting an exponential function to the time-binned accuracy over time at 50 % coherence (Fig. 1c). 2) We chose σ such that the simulated time-binned accuracy over time for 100 % coherence peaked at around 80 % (Fig. 1c). 3) We varied B, r_{| X (t) | <B}, and r_{| X (t) | > B} to match the experimentally measured relationship between interbout interval and coherence strength (Fig. 1b). 4) We adjusted the visual feedback strength such that the probability to swim in the same direction approximated the corresponding experimental data (Fig. 1f).

Stochastic model without motor memory (Extended Data Fig. 2a and Supplementary Video 3): σ = 1.2; B = 1,8; $r_{|X(t)|<B}=0.7\frac{1}{s};r_{|X(t)|>B}=2.0\frac{1}{s}$. We tuned σ, B, r_{| X(t) | < B}, and r_{| X(t) | > B} as described above.

Stochastic model with motor memory (Extended Data Fig. 2b and Supplementary Video 4): σ = 1.2; B = 1,8; $\sigma =1.2;B=1,8;r_{|X(t)|<B}=0.36\frac{1}{s^{\prime }};r_{|X(t)|>B}=2.5\frac{1}{s}$. In this model, we implemented an additional bout initiation probability, i.e. to repeat the last motor action²¹, $r_M=0.3\frac{1}{s}$. We determined parameters as follows: 1) We chose σ as described above. 2) We tuned r_M to mimic the dynamics of the time-binned accuracy over time for 50 % coherence (Fig. 1c). 3) We varied B, r_{| X(t) | < B}, and r_{| X(t) | > B} as described above.

Leaky integrator model without visual feedback (Extended Data Fig. 2c and Supplementary Video 5): τ = 2 s; σ = 20; B = 1.5; $r_{|X(t)|<B}=0.7\frac{1}{s};r_{|X(t)|>B}=2.0\frac{1}{s}$. We tuned parameters as described above.

Non-leaky integrator model with reset and motor memory (Extended Data Fig. 2d and Supplementary Video 6): σ = 10; B = 220; $r_{|X(t)|<B}=0.4\frac{1}{s}$. In this model, we initiated about whenever the integrator variable reached the bound, i.e. $r_{|X(t)|>B}=100\frac{1}{s}$ and did then reset the integrator variable to zero. To capture the accuracy improvements and memory over consecutive bouts (Fig. 1c,d,f), we also implemented an explicit motor memory. To this end, we added an additional bout initiation probability, $r_M=0.3\frac{1}{s}$, i.e. to repeat the last motor action²¹. We determined parameters as follows: 1) We chose r_M such that the probability to swim in the same direction approximated the experimental data (Fig. 1f). 2) σ, B and r_{| X(t) | < B} were all varied together in order to capture the dynamics of the time-binned accuracy over time at 50 % coherence (Fig. 1c).

For the head-fixed larvae, we chose model parameters as follows:

Head-fixed larval zebrafish with the tail free to move almost never swim spontaneously but still robustly respond when stimulated with motion¹⁷ (Extended Data Fig. 3a,b). We model this effect by switching off the spontaneous bout clock (r_{| X(t) | < B} = 0) and by initiating bouts whenever the sensory variable reaches the bound $\left(r_{|X(t)|>B}=100\frac{1}{s}\right)$. Moreover, we did not implement visual feedback in any of these models as head-fixed fish do not create self-induced optic flow or visual noise.

Leaky integrator model (Fig. 2b–m, Extended Data Fig. 3b–h and Supplementary Video 7): τ = 5 s; σ = 15; B = 1. Parameters were tuned as follows: 1) We determined τ using the motion pulse and gap experiments presented in Fig. 2j,m. Based on the timing of the first bout, which occurs after ~5 s, we could constrain the relationship between bound and time constant, i.e. B = (1 −exp^−5s/τ). After the first bout at time point t₀, the integrator variable X(t) is located at the bound and then decays over time. Hence, X(t₀ + gap) = B · exp^−gap/τ. After the gap time, the new motion stimulus starts, and the integrator variable starts to rise again. The relationship between response delay relative to control (Δ) and the gap time is given by B · exp^−gap/τ = (1 − exp^−Δ/τ). Solving that equation, we obtain Δ = − log (1 − B · exp^−5s/τ) · σ). Inserting B, we obtain Δ = − log (1 − (1 − exp^−5s/τ) · exp^−5s/τ) · τ). As the gap time and Δ are known from the experiment (Fig. 2m), we can fit the equation to measured data, resulting in τ = 5 s. This also allowed us to calculate B = 1. 2) We determined σ to match the response delay in Fig. 2c for 0 % coherence.

Stochastic model (Extended Data Fig. 3b–h and Supplementary Video 8): σ = 2; B = 7.2. Parameters were systematically tuned as follows: 1) We determined the ratio between both parameters to obtain a response delay of ~5 s, following our experimental data (Fig. 2c). 2) We varied σ while keeping the ratio between σ and B the same until we approximated the response delay for 0 % coherence (Fig. 2c).

Non-leaky integrator model with reset and motor memory (Extended Data Fig. 3b–h and Supplementary Video 9): σ = 10; B = 500. In this model, we did reset the integrator after each bout to zero and added an explicit motor memory, i.e. the probability to perform the last motor action again, $r_M=0.3\frac{1}{s}$. Resetting and motor memory were only relevant for the experiments with two bouts (Fig. 2j–m). Parameters were tuned as follows: 1) We tuned σ and B as for the stochastic model. 2) We set r_M to approximate the accuracy as a function of the previous motion direction (Fig. 2k).

Anterior hindbrain network modeling

We modeled the units that spatially pool motion evidence (Fig. 3k) as being proportional to the coherence level plus noise. As suggested by our brain-wide imaging data (Fig. 3a–d and Extended Data Fig. 4b), we assumed that for left-ward coherent motion, activity increases on the left, but slightly decreases on the right side:

$$I_{\mathit{\text{left}}}(t)=0.5\cdot C(t)+N\left(\mu ,{\sigma }^2\right),$$

$$I_{\mathit{\text{right}}}(t)=-0.25\cdot C(t)+N\left(\mu ,{\sigma }^2\right).$$

For right-ward coherent motion, we assumed the opposite:

$$I_{\mathit{\text{left}}}(t)=-0.25\cdot C(t)+N\left(\mu ,{\sigma }^2\right),$$

$$I_{\mathit{\text{right}}}(t)=0.5\cdot C(t)+N\left(\mu ,{\sigma }^2\right).$$

C(t) represents the time-dependent coherence level, ranging from 0 to 1 (corresponds to 0 and 100 %) and N(μ, σ²) Gaussian noise with μ = 0.4 and σ = 13. We used independent noise in both hemispheres. We modeled all units as individual rate units, following the network connectivity diagram presented in Fig. 3k. We did not allow firing rates to become negative. We performed all simulations in Python 3.7 and numba using forward Euler with dt = 0.01. In each case, we ran the process 500 times for different random seeds, following the stimulation protocols as used in the experiments. To approximate the GCaMP6s calcium dynamics from the simulated firing rates, we applied a first-order temporal low-pass filter with a time constant of 1 s³⁰. We then multiplied signals with 4000 to approximate the calcium range measured in the experiments (Fig. 3j,m). We used the same analysis scripts for model quantification and experimental data, allowing us to compare model performance and experiment. Notably, we used a single parameter set to simulate all presented imaging and behavior data (Fig. 3l,m, Extended Data Fig. 6b,c,e, and Extended Data Fig. 7c). We call models in agreement with experimental data when they could qualitatively capture the critical features tested in the experiment, such as the general activity dynamics of the measured clusters (Fig. 3j,m). We modeled the left evidence integrator unit (X_left(t)) by

$${\tau }_x\frac{d{X}_{\mathit{\text{left}}}(t)}{dt}=-X_{\mathit{\text{left}}}(t)+I_{\mathit{\text{left}}}(t)-I_{\mathit{\text{right}}}(t),$$

where τ_x = 12 s. We did not model a helper unit reading out the integrator (as displayed in Fig. 3k), allowing X_left(t) to be excitatory and inhibitory.

We modeled the left dynamic threshold unit (Y_left(t)) by

$${\tau }_y\frac{d{Y}_{\mathit{\text{left}}}(t)}{dt}=-3.6\cdot Y_{\mathit{\text{left}}}(t)+3\cdot I_{\mathit{\text{left}}}(t)-{\delta }_y(t),$$

where τ_y = 7 s. δ_y(t) is an inhibitory shunting pulse, spontaneously applied (only for freely swimming fish, Extended Data Fig. 7a), with a probability of $0.4\frac{1}{s}$.

We modeled the left motor command unit Z_left(t) by

$${\tau }_z\frac{d{Z}_{\mathit{\text{left}}}(t)}{dt}=-Z_{\mathit{\text{left}}}(t)+1.1\cdot X_{\mathit{\text{left}}}(t)-0.44\cdot Y_{\mathit{\text{left}}}(t),$$

where τ_z = 3.

We implemented units in the right hemisphere in the same way. If the slope of either motor command unit, $\frac{d{Z}_{\mathit{\text{left}}}(t)}{dt}$ or $\frac{d{Z}_{\mathit{\text{right}}}(t)}{dt}$ exceeded $0.06\frac{1}{s}$, we allowed bouts to occur, with a high probability of $4\frac{1}{s}$. For each bout, we then chose turning direction based on whether X_left(t) or Y_right(t) was more active.

Finally, we sought to mimic visual feedback in freely swimming fish (Extended Data Fig. 7c) as we have done in the leaky integrator model (see above and Fig. 1g–l). To this end, we increased (for left bouts) or decreased (for right bouts) the input signals (I_left(t) and I_right(t)) by $0.1\frac{1}{s}$, for the next 10 frames.

We tuned model parameters as follows: 1) We chose the conversation factors between C(t) and I(t) as well as the noise μ to obtain a dynamic range between approximately 0 and 1 for motion the left and right on both sides. 2) We tuned the noise σ to mimic the experimentally observed trial-to-trial reliability of each unit (Fig. 3i). 3) We varied τ_x, τ_y, and τ_z in the integrator unit, the dynamic threshold cluster, and the motor command cluster as well as respective connectivity weights until we approximated the experimentally measured calcium dynamics (Fig. 3j). 4) We chose the motor command unit slope threshold such that we obtained response delays of ~15 s for 0 % coherence (Fig. 2c). 5) For the freely swimming fish, we chose δ_y(t) to reproduce the experimentally observed reduction in interbout interval as a function of coherence level (Fig. 1b) and adjusted visual feedback strength such that we roughly obtained the dynamics of the accuracy over time (Fig. 1c).

Extended Data

Extended Data Fig. 1. Behavior in freely swimming larval zebrafish.

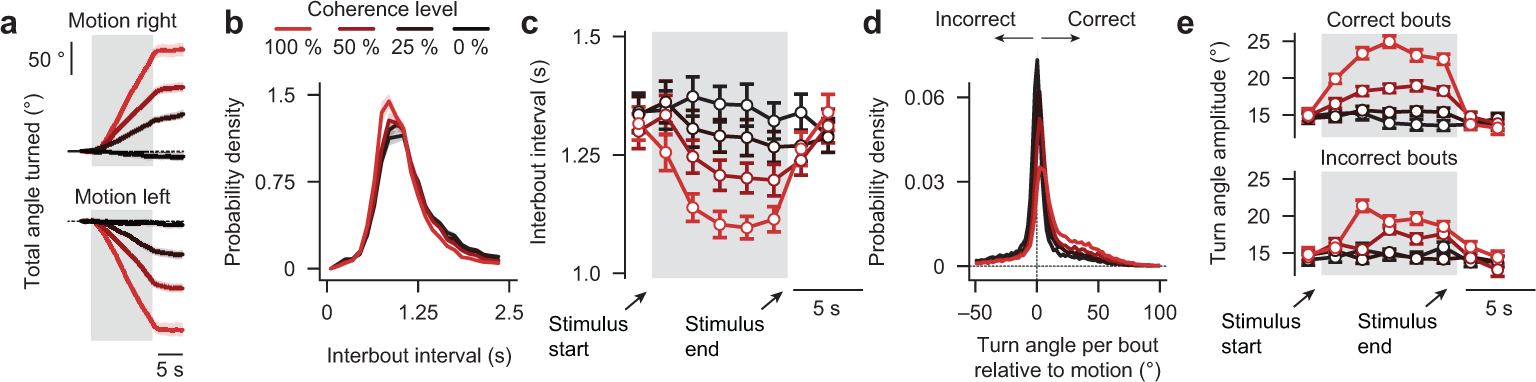
a, Turn angle larvae accumulate over time (positive, right; negative, left). b, Probability distribution of interbout intervals during presentation of different coherence levels. c, Time-binned interbout intervals as a function of time. d, Probability distributions of turn angles per bout relative to motion direction. Bouts are defined as correct when they follow motion direction (= positive) and incorrect otherwise (= negative). e, Time-binned precision (absolute turn angle) of correct and incorrect bouts over time. Gray shaded areas in (a,c,e) indicate motion presentation. Before and after, we always show 0 % coherence. Bin sizes in (c,e) are 2 s. All error bars are mean ± sem over fish. N = 60 fish in (a–e), same fish as in Fig. 1b–d.

Extended Data Fig. 2. Model alternatives for freely swimming larval zebrafish.

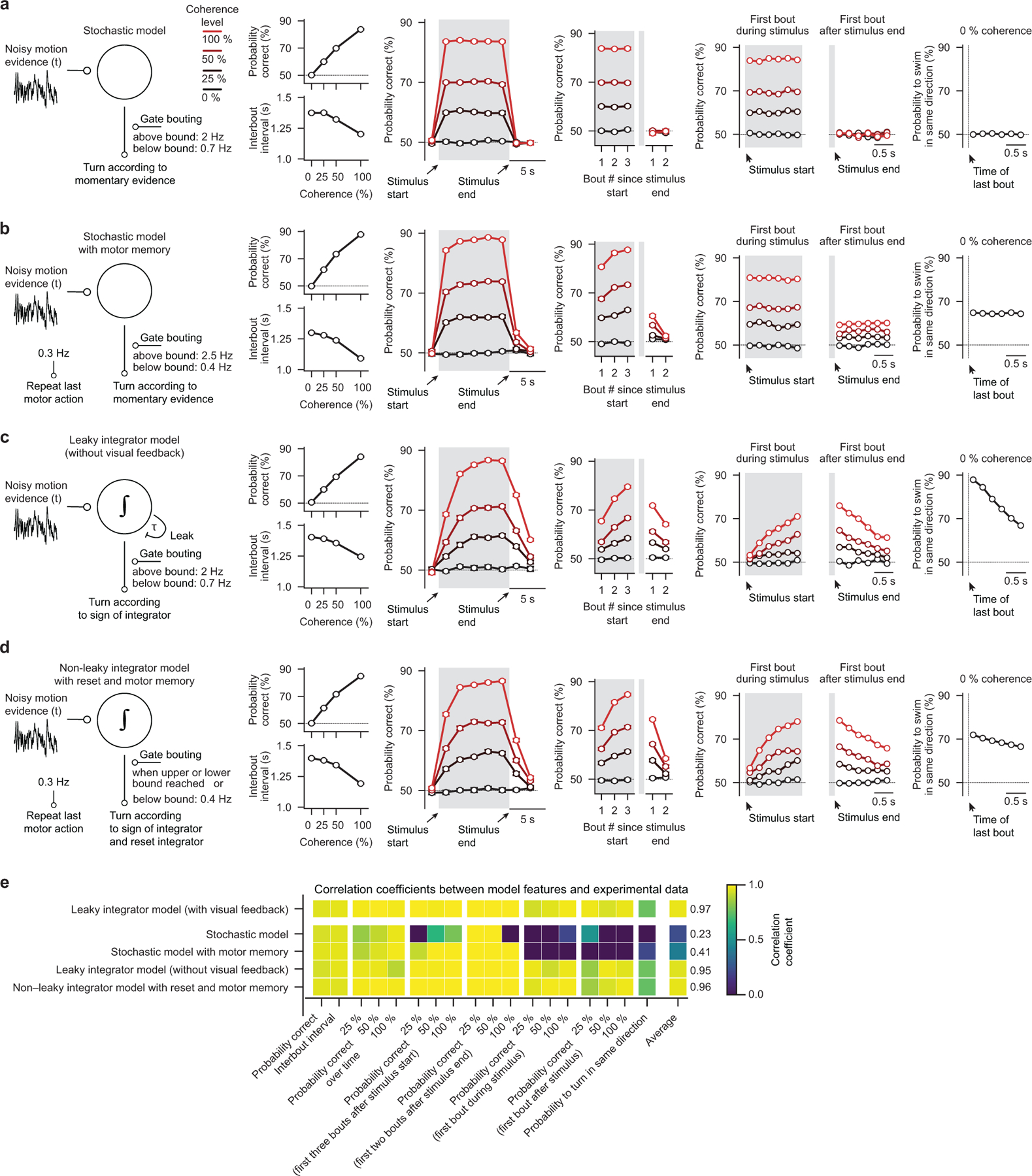
a–d, Schematics and simulation results of alternative models. For simplicity, none of these models had visual feedback. Quantification as in Fig. 1b–f,h–l. N = 16 model runs for each model. e, Pearson’s correlation coefficient between each model feature and the respective experimental data. We use the average of these values to rank the models. All error bars in (a–d) are mean ± sem over model runs.

Extended Data Fig. 3. Behavior and modeling in head-fixed larval zebrafish.

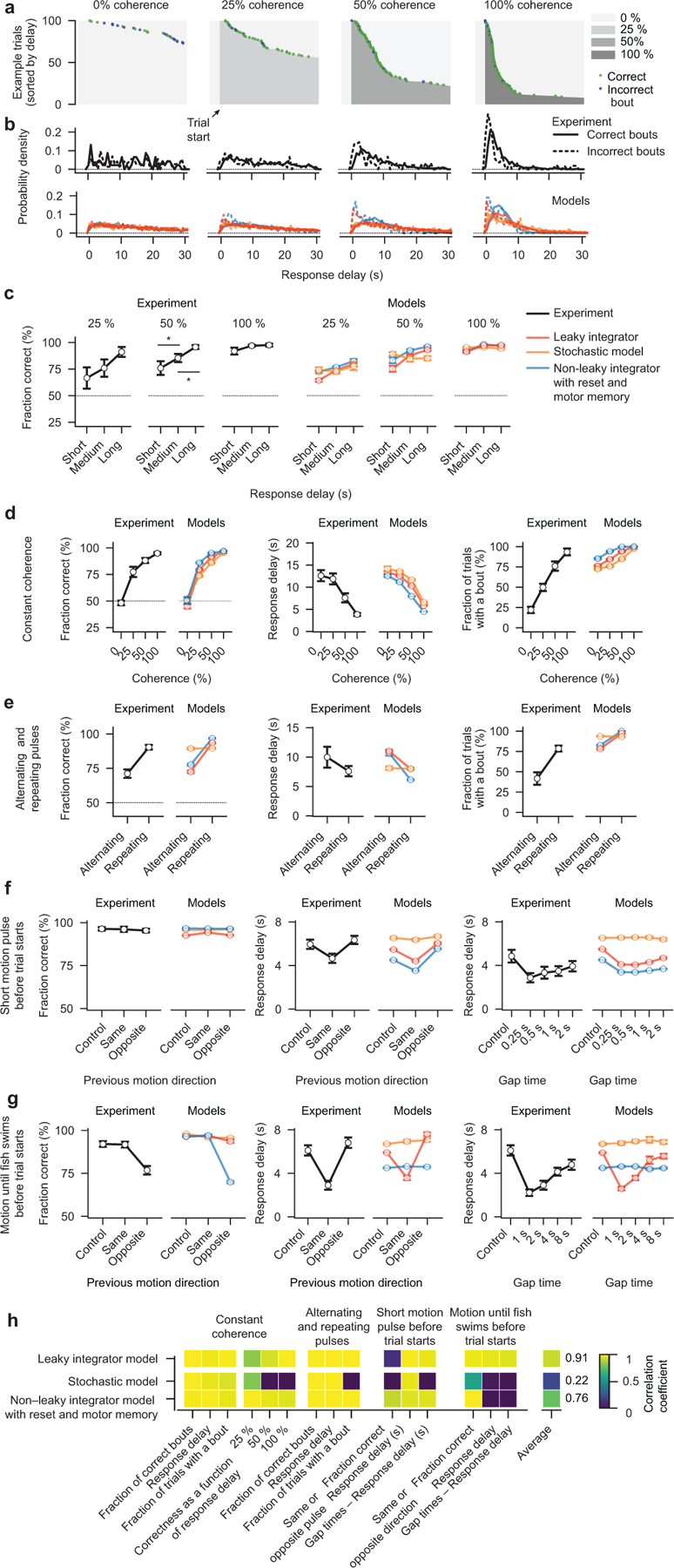
a, 100 randomly selected experimental example trials with periods of coherent motion (shades of gray) and 0 % coherence (lightest gray), sorted by response delay. Note that after each correct (green dots) or incorrect (blue dots) bout, coherence levels are immediately set to 0 %. b, Probability density distributions of response delays for correct (solid lines) and incorrect (dashed lines) bouts, for experiment (black lines) and models (red, orange, and blue lines). Models have the same structure as in Extended Data Fig. 2a,c,d but without spontaneous bouts below the bound and different parameters. c, Accuracy as a function of response delay (short: 0–2 s, medium: 2–4 s, long: 4–6 s) for experiment (*p < 0.05 for both comparisons at 50 % coherence) and models. Behavioral data in (a–c) comes from the experiment with constant motion coherence (Fig. 2b). d,e,f,g, Behavior quantification for experiment and models, as in Fig. 2c,e,g–i,k–m. h, Pearson’s correlation coefficient between each model feature and the respective experimental data. We use the average of these values to rank the models. N = 13 fish in (a–d), N = 10 fish in (e), N = 8 fish (left panels) and N = 6 fish (right panel) in (f), N = 13 fish in (g), same fish as in Fig. 2c,e,g–i,k–m. N = 8 model runs for each model in (b–h). All error bars are mean ± sem over fish. P-values in (c) are based on one-sided t-tests comparing response differences to zero. Asterisks (*) in (c) indicate significance (*p < 0.05).

Extended Data Fig. 4. Detailed quantification of responsive brain areas identified during brain-wide calcium imaging.

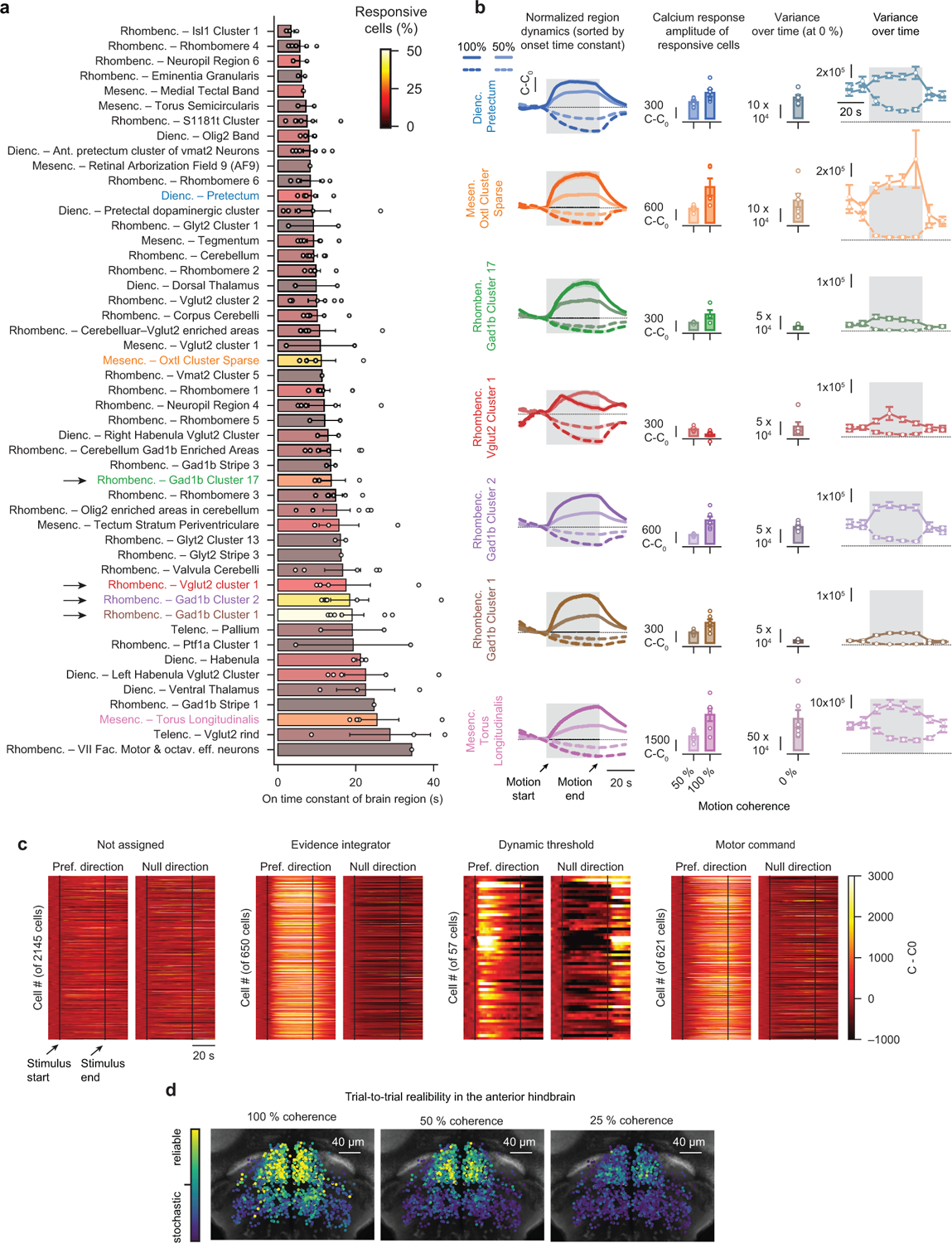
a, All brain areas with >1 % responsive cells, sorted by fitted onset time constant during 50 % coherent motion. Text label colors relate to colors in (b) and Fig. 3c,d. Bar colors represent fraction of responsive cells within a brain region. Black arrows indicate anterior hindbrain regions with slow dynamics and a large fraction of responsive cells. b, Brain areas with >15% responsive cells sorted by temporal dynamics (top, fast; bottom, slow) characterized from left to right. Column 1: Peak-normalized calcium dynamics, relative to baseline (C0) averaged over all cells responding to coherent motion in preferred- (PD) or null-direction (ND), respectively. Column 2: Average (last 5 s of coherent motion) calcium response amplitude (comparisons between 50 % and 100 %, from top to bottom: p = 0.05, p = 0.06, p = 0.16, p < 0.05, p < 0.01, p < 0.05, p < 0.05). Column 3: Variance (over time), calculated in individual cells and trials, then averaged, during 0 % coherence Column 4: Same as column 3 but time-binned for region’s preferred- and null-direction. As variances for preferred- and null-direction motion quickly converge after motion stimulation, the last time bin reflects a motion-memory independent variance at 0 % coherence. c, Preferred- and null-direction dynamics of all identified anterior hindbrain cells functionally clustered by regressor analysis (Fig. 3e). Preferred motion direction refers to motion to the left or right for cells in the left or right hemisphere, respectively, null-direction motion the other way around. d, Spatial arrangement of trial-to-trial reliability for all cells without functional clustering, as in Fig. 3g but for all three coherence levels. N = 6 fish for 50 % and N = 6 fish for 100 % motion coherence stimulation in (a,b). Open circles in (a,b) indicate individual fish. Note that in some fish not all brain areas were imaged and, hence, fish number per brain regions is variable. N = 6 fish in (c,d). All error bars in (a,b) indicate mean ± sem over fish. Shaded gray areas in (b) and dashed vertical lines in (c) indicate motion stimulation. Before and after 0 % coherence is shown. All p-values are based on two-sided t-tests.

Extended Data Fig. 5. Neurotransmitter identity and neuronal morphology in the anterior hindbrain.

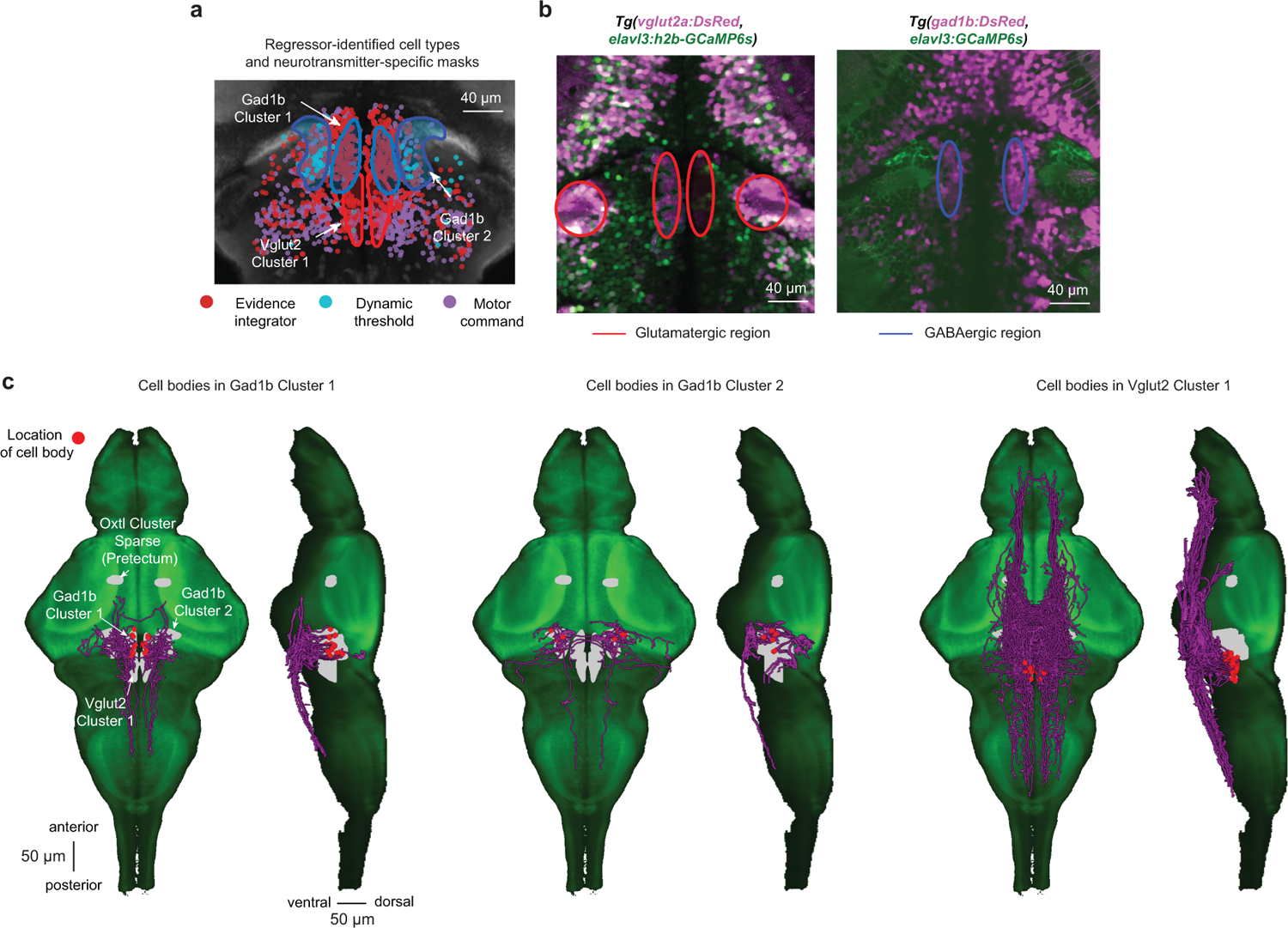
a, Overlay of neurotransmitter type-specific masks from the z-brain atlas (refs. 24 and 25) (glutamate = red outline; GABA = blue outline) with the functionally characterized cell types (same cells as in Fig. 3f) in the same coordinate system. Note that almost all identified dynamic threshold neurons lie within the Gad1b Cluster 2 and are, therefore, likely inhibitory. Please also note that the expression pattern of the vglut2a-driver line (ref. 25) suggests that the anatomical mask of the VGlut2 Cluster 1 likely extends even further into the anterior part of the hindbrain. b, Simultaneous imaging of DsRed (pink), expressed only in excitatory vglut2a+ neurons (left panel) or of DsRed expressed only in inhibitory gad1b+ neurons (right panel), and cytosolic or nuclear-localized GCaMP6s (green, pan-neuronal expression). Colored ellipses are manually added to highlight regions of interest. c, Single-cell morphologies with somata in the identified regions in the anterior hindbrain. Cells were mapped from the Max-Planck Zebrafish Brain Atlas (ref. 26) into the z-brain coordinate system and overlaid with the available masks (gray) on a GCaMP5G reference larval zebrafish (green). N = 6 fish in (a), same data as in Fig. 3f. N = 1 fish for each plot in (b).

Extended Data Fig. 6. Neural correlates of behavioral choices.

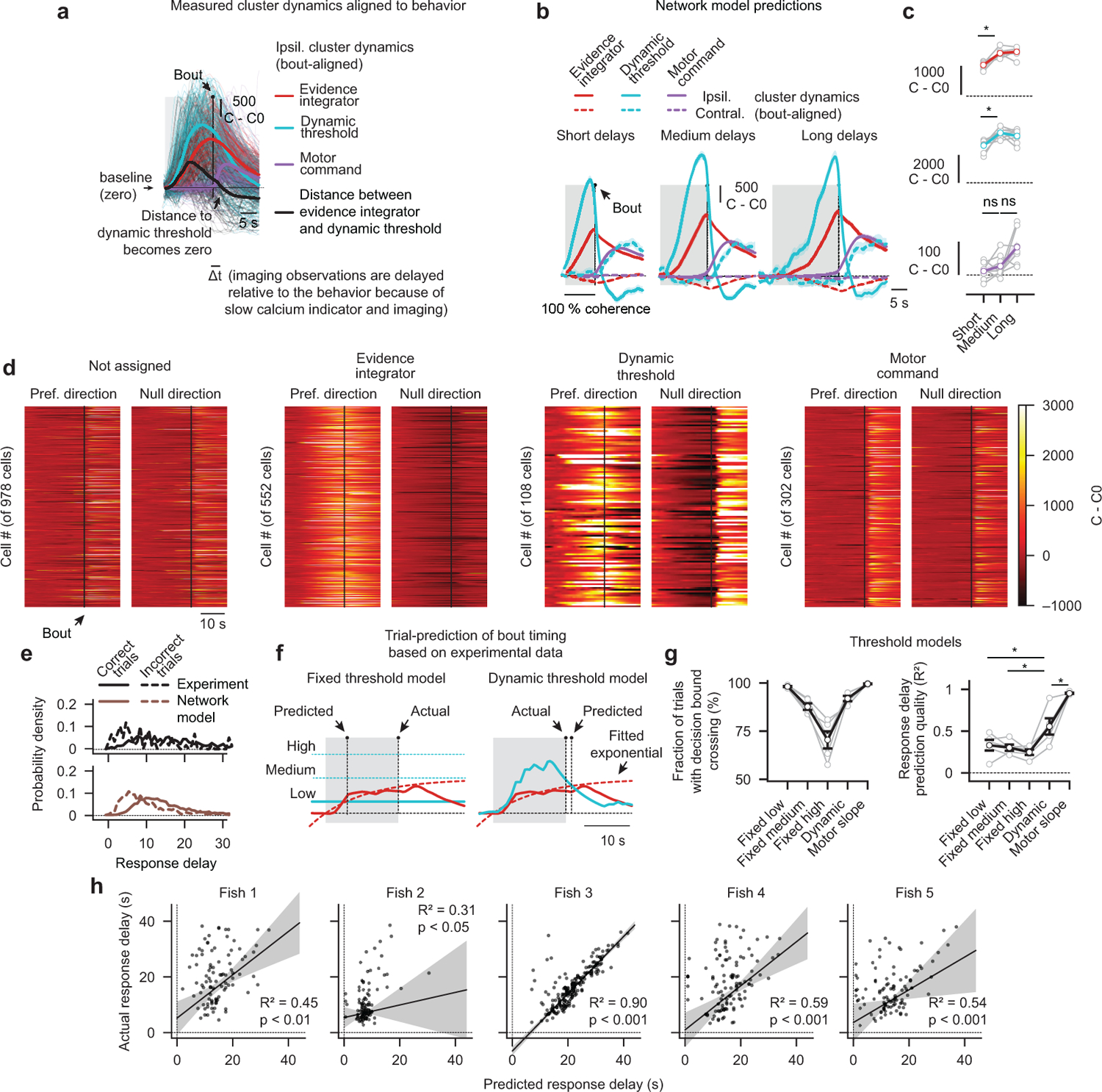
a, Measured cluster dynamics aligned to swim bouts (same data as in Fig. 4b but as a reduced version only showing ipsilateral dynamics for medium response delays). The thick black line illustrates the difference between the dynamic threshold cluster and the evidence integrator cluster, which crosses zero (baseline) around the same time the motor command cluster reaches its maximum. This event occurs slightly after the bout likely due to delays introduced by the relatively slow dynamics of the GCaMP6s indicator (ref. 30). The transparent thin lines are single-trial responses. b,c Same analysis as in Fig. 4b,c but for bout-aligned network model simulations (*p < 0.001 for the integrator and dynamic threshold unit comparisons; p = 0.58 and p = 0.06 for the motor command cluster comparisons). d, Bout-aligned preferred- and null-direction dynamics of all identified cells from all N = 5 fish, functionally clustered by the behavior-based classification method. Preferred motion direction refers to motion to the left or right for cells in the left or right hemisphere, respectively, null-direction motion the other way around. e, Probability density distributions of response delays for correct (solid lines) and incorrect (dashed lines) bouts, for experiment (black) and network model (brown). f, Illustration of two methods for trial-by-trial prediction of individual behavioral choices based on the experimentally obtained cluster dynamics. Bouts are predicted when the smoothed and extrapolated integrator cluster activity (red dashed lines are exponential fits of the experimental data, solid red lines) crosses the threshold (cyan lines). Three fixed thresholds (left panel) and the dynamic threshold (right panel) are tested. The third method, which uses a sudden rise in the motor command slope as a predictor, is not illustrated. g, Quantification of the fraction of trials in which a threshold crossing event is detected and quantification of predictive quality (coefficient of determination, R2) for the different threshold models (*p < 0.05 for each model compared to the dynamic threshold model). Gray lines are individual fish, black lines are fish averages. h, Individual fish trial-by-trial predictions of bout-timing using the dynamic threshold, and robust linear regression analysis results (RANSAC, see methods). Gray shaded areas indicate confidence intervals of the regression fits. N = 5 fish in (a,d,e,g,h), same fish as in Fig. 4. N = 8 model runs in (b,c,e). All error bars are mean ± sem over simulated trials in (b), model runs in (c), or fish in (g). P-values in (c,g) are based on one-sided t-tests comparing differences to zero. Asterisks (*) in (c,g) indicate significance (*p < *0.05, or *p < 0.001).

Extended Data Fig. 7. Speculative network model implementation of urgency-related signals in freely swimming larval zebrafish.

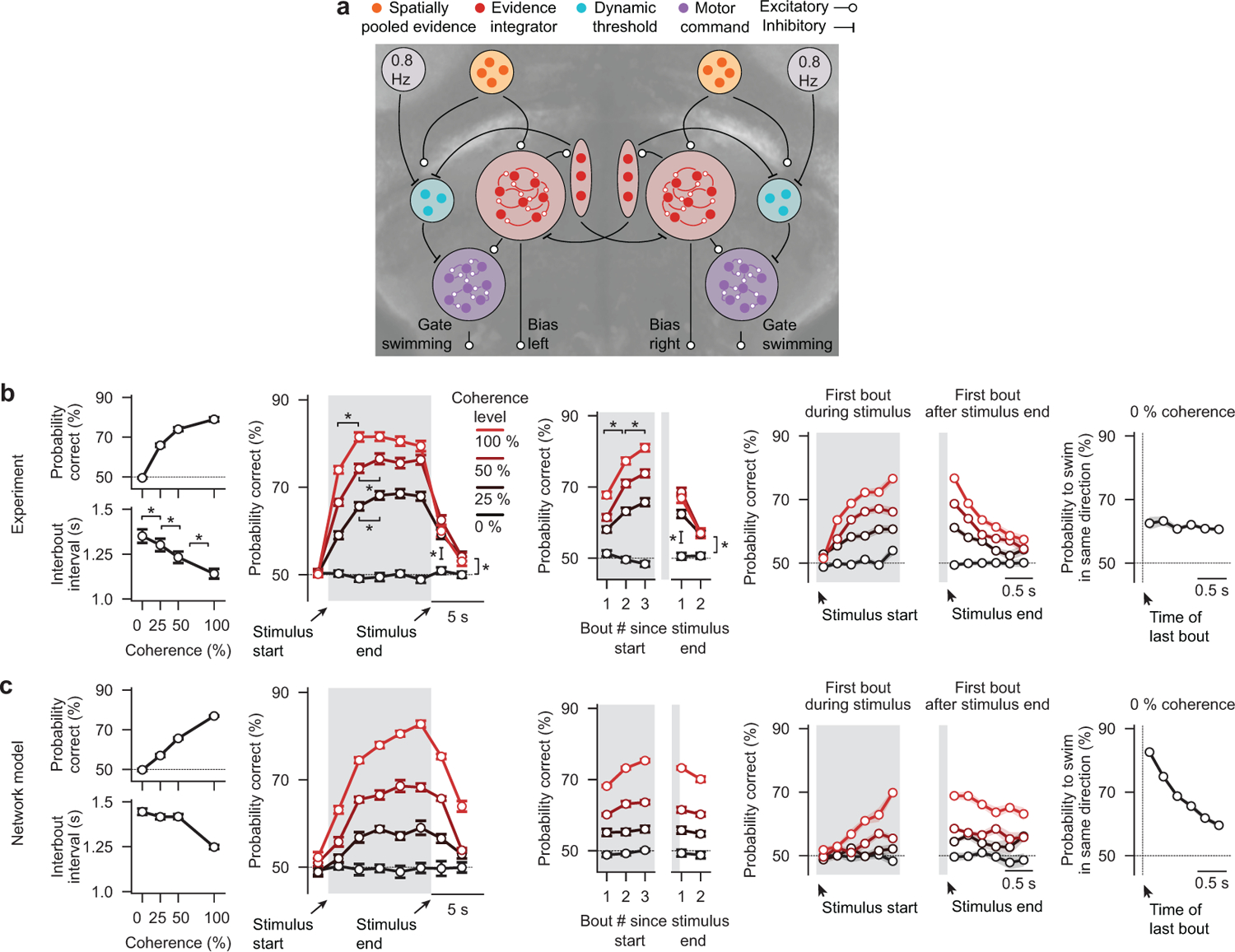
a, Network model as in Fig. 3k but with inhibitory bout clock attached to the dynamic threshold clusters. We speculate that the bout clock or the system for keeping balance act as urgency-related signals here. These signals lead to rapidly collapsing bounds, allowing for spontaneous swimming. Also, in this model, each simulated bout induced opposing visual feedback, as in Fig. 1g–l. b, Copy of behavior data from Fig. 1b–f. c, Network model simulation results, quantified as in Fig. 1b–f,h–l. N = 8 model runs in (c). All error bars are mean ± sem over fish in (b) or model runs in (c). Asterisks (*) in (b) indicate significance (*p < 0.05, *p < 0.01, or *p < 0.001). See Fig. 1b–f for more details on p-values and statistics.

Supplementary Material

Video 1

Supplementary Video 1 Freely swimming larval zebrafish with example dot motion stimulus. We present 5 s of 0 % coherence, followed by 10 s of 25 % coherence and 5 s of 0 % coherence. Dot motion is always perpendicular (right- or left-ward) locked to the body orientation of the fish. Dots have a short lifetime and stochastically disappear and reappear at a random location within the arena. Left panel shows the perspective of the experimenter (world-centric view). Right panel shows the visual stimulus from the perspective of the fish (fish-centric view). Note that sizes are not to scale. The body length of a larva zebrafish at this age (6 days post fertilization) is about 4 mm. The diameter of the visual arena is 12 cm.

Video 5

Supplementary Video 5 Simulation of the leaky integrator model without visual feedback for freely swimming larval zebrafish. Same as in Supplementary Video 2 but for a simpler version of the bounded leaky integrator model in which we did not include self-created optic flow or visual noise.

Video 4

Supplementary Video 4 Simulation of the stochastic model with motor memory for freely swimming larval zebrafish. Same as in Supplementary Video 2 but for the stochastic model with motor memory. Bouts are initiated according to the same rules as in the stochastic model. Additionally, a motor memory component allows larvae to sometimes simply repeat the last motor action.

Video 3

Supplementary Video 3 Simulation of the stochastic model for freely swimming larval zebrafish. Same as in Supplementary Video 2 but for the stochastic model. Note that threshold crossing events are rarely visible because we slightly low-pass filter the sensory variable over time. Otherwise, the trace would not be resolvable in the movie.

Video 2

Supplementary Video 2 Simulation of the leaky integrator model with visual feedback for freely swimming larval zebrafish. We present different levels of coherence (moving right- or left-ward), indicated by the orange and blue shaded areas. Bouts are initiated by a stochastic bout clock operating at a low probability below the threshold and a higher probability above it. Orange dots indicate bouts to the right, blue dots indicate bouts to the left. Note that in this model, each bout slightly resets the integrator, mimicking self-created optic flow and visual noise.

Video 6

Supplementary Video 6 Simulation of the non-leaky integrator model with reset and motor memory for freely swimming larval zebrafish. Same as in Supplementary Video 2 but for an integrator model without a leak component in which bouts completely reset the sensory variable to zero. Similarly, as in Supplementary Video 4, an additional motor memory component allows larvae to sometimes repeat the last motor action.

Video 10

Supplementary Video 10 Denoised activity in the anterior hindbrain during motion integration. We created the video by reconstituting fluorescent activity from the segmented and calcium-extracted neuronal activity using the CaImAn framework. The video is not aligned to visual stimulation onset or bout events and is slightly sped up to enhance the visibility of bilateral circuit dynamics.

Video 9

Supplementary Video 9 Simulation of the non-leaky integrator model with reset and motor memory for head-fixed larval zebrafish. Same as in Supplementary Video 7 but for an integrator model without a leak component in which bouts completely reset the sensory variable to zero.

Video 7

Supplementary Video 7 Simulation of the leaky integrator model for head-fixed larval zebrafish. Following the behavior of head-fixed larvae, bouts (orange and blue dots) are only triggered when the integrator variable reaches the threshold and not stochastically. We present different levels of coherence (moving right- or left-ward), indicated by the orange and blue shaded areas. Note that whenever we detect a bout, we immediately set coherence levels to zero, as in the experiments.

Video 8

Supplementary Video 8 Simulation of the stochastic model for head-fixed larval zebrafish. Same as in Supplementary Video 7 but for the stochastic model. Note that threshold crossing events are rarely visible because we slightly low-pass filter the sensory variable over time. Otherwise, the trace would not be resolvable in the movie.