Improving Language Comprehension to Enhance Word-Problem Solving

Abstract

The focus of this article is the role of language comprehension within word-problem solving (WPS). The role of the language comprehension in WPS is explained, and an overview of research illustrating language comprehension’s contribution to WPS is described. Next, an innovative intervention that embeds WP-specific language comprehension instruction within a validated form of schema-based WP intervention is described, and the methods and results of a randomized controlled trial assessing the added value of embedding WP-specific language comprehension instruction are outlined. Implications for practice and future research are drawn.

Word-problem solving (WPS) reflects understanding of and the capacity to apply mathematical ideas in everyday life and in the service of science, technology, engineering, and advanced mathematics. It is not surprising therefore that WPS is a strong school-age predictor of employment and wages in adulthood (Every Child a Chance Trust 2009; Batty, Kivimäki, & Deary, 2010). Yet, difficulty with WPs is widespread (Daroczy, Wolska, Meurers, & Nuerk, 2015). The idea that WPS is important but challenging is highlighted in a large national survey of U.S. Algebra I teachers, who rated the importance of 15 math skills potentially foundational for algebra success. Results indicated that of all 15 skills, student preparation on WPS is weakest, and poor WPS constrains algebra success more than any other skill deficit (Hoffer, Venkataraman, Hedberg, & Shagle, 2007).

The most transparent distinction between WPs and other forms of mathematics performance is that text processing is required. Beyond executing computational skill to find solutions, students must build textual representations, as they decipher the problem’s central mathematical event and the relationships among the numbers provided in the WP statement and the missing quantity. This means building a problem model and setting up the equation that represents the information in the text.

The challenges of text processing are highlighted in studies showing that WPS difficulty can occur even when computational skill is intact (Cummins, Kintsch, Ruesser, & Wiener, 1988; Fuchs et al., 2008; Koedinger & Nathan, 2004). WPS difficulty, in the face of intact computation skill, may reflect the fact that WPS, with its combined focus on text, mathematical ideas, and computational skill, engages more cognitive resources than computational skill does (Daroczy et al., 2005; Swanson & Beebe-Frankenberger, 2004).

A recurring finding in the literature concerns the role of language comprehension in WPS. This is the focus of the present article. We begin by explaining the role of language comprehension in WPS and then providing an overview of research that illustrates the unique contribution language comprehension makes in WPS. We next describe an approach to intervention that embeds WP-specific language comprehension instruction within a validated form of WP intervention. This is followed by an outline of the structure and a summary of results of a highly relevant study in which we assessed the added value of embedded language comprehension instruction on WP outcomes. We conclude by drawing implications for practice and future research. Note that the purpose of this article is not to provide a research report of the study we outline. Instead, the purpose is to provide an overview on the role of language comprehension in WPS. (For a full research report of that study, see Fuchs et al., 2019.)

The Role of Language Comprehension in Word-Problem Solving

Some teachers believe that teaching students arithmetic will translate into improved WPS. A recent study, however, illustrates that this is not the case for many struggling learners. Fuchs et al. (2013) randomly assigned at-risk first graders to a control group and two versions of an arithmetic intervention focused strongly on number knowledge. Results indicated dramatically superior arithmetic outcomes (more fluent and accurate addition [sums from 5 to 12] and subtraction [minuends from 5 to 12]) for both number knowledge intervention conditions compared to the control group condition.

Because arithmetic is a critical pathway to WP competence (Fuchs et al., 2010; 2016), one might expect this number knowledge intervention, with its dramatic effects on arithmetic, to simultaneously build WPS performance. Yet, effects for number knowledge intervention in that first-grade study (Fuchs et al., 2013) were substantially lower on WP outcomes than on arithmetic outcomes. Also, although intervention eliminated the posttest arithmetic achievement gap between at-risk intervention students and not-at-risk classmates, intervention students’ posttest WP achievement gap remained large. This suggests that although arithmetic is foundational to WPS, it is not a sufficient pathway.

An increasing WPS gap in the face of a narrowing arithmetic gap should not, however, be surprising, when considering that WPS, but not arithmetic, requires text processing to build problem models and generate number sentences (text processing is necessary even when students listen to WPs, as in the study just described). Further, language comprehension is necessary for text comprehension (Catts, Hogan, & Adolf, 2005). In fact, although arithmetic is also associated with language ability (Dehaene, Spelke, Pinel, Stanescu-Cosson, & Tsivkin, 1999; Powell, Driver, Roberts, & Fall, 2017; Purpura & Ganley, 2014), studies that formally contrast pathways for both outcomes against each other show that language is more strongly related to WPS than to arithmetic (Fuchs et al., 2008, 2016).

Walter Kintsch and his colleagues (Cummins et al., 1988; Kintsch & Greeno, 1985) originally hypothesized that WPS relies on a combination of language comprehension processes and mathematical problem-solving processes. Based on theories of discourse processing (van Dijk & Kintsch, 1983), their model assumes that memory representations of WPs have three components. The first involves constructing a coherent representation of the essential ideas directly expressed in the text. The second, the situation model, requires supplementing the text with inferences based on the WP solver’s world knowledge. This includes knowledge about relations among quantities. The WP solver coordinates this information with the third component, knowledge about WP models, or schemas, to formalize conceptual relations among quantities and guide application of solution strategies.

In the primary grades, the three main schemas are combine WPs (i.e., quantities are combined to form a total), compare WPs (i.e., quantities are compared to find a difference), and change WPs (i.e., an action triggers an increase or decrease in a starting amount). These WP types are operationalized further in subsequent sections of this article. For information on problem models in the intermediate grades, see Powell and Fuchs (2018).

Kintsch and colleagues (Cummins et al., 1988; Kintsch & Greeno, 1985) posited that this process of building the propositional text structure, inferencing, identifying schema and applying solution strategies makes strong demands on short-term memory. In our work (e.g., Fuchs, Fuchs, Seethaler, & Barnes, 2019), we reframed short-term memory as working memory, because WPS requires not only briefly storing information but also sequentially updating that information in memory as the problem solver processes subsequent segments of the WP statement. This revision is grounded in studies showing that working memory is engaged in WPS (Anderson 2007; Lee et al. 2004; Peng et al., in press; Raghubar et al. 2010; Swanson, 2016; Swanson & Beebe-Frankenberger, 2004; Swanson, Jerman, & Zheng, 2008; Swanson, Moran, Lussier, & Fung, 2014; Swanson, & Sachse-Lee, 2001).

To appreciate the cognitive demands involved in WPS, consider a text-processing scenario for a combine problem (Part 1 plus Part 2 equals Total): Freddie has 4 spinners. Hollis has 2 spinners. Hollis also has 9 jump ropes. How many spinners do the children have in all? A competent WP solver processes sentence 1 to identify that the object is spinners; the quantity is 4; the actor is Freddie; but Hollis’s role is to be determined (TBD). These pieces of information are stored in working memory. In sentence 2, propositions are similarly coded and stored (object = spinners; quantity = 2; actor = Hollis; Hollis’s role = TBD). In sentence 3, jump ropes fails to match the object code in the first two sentences, signaling 9 may be irrelevant. This is stored in working memory. In sentence 4 (the question), how many spinners and the phrase in all cue the problem solver to identify the combine schema; assign the role of superset (Total) to the question; assign subset roles (Parts 1 and 2) to the TBD information; and reject 9 jump ropes as irrelevant. Filling in these slots of the schema triggers a set of strategies to solve for the missing information (Total). Errors are viewed as failures to produce the intended mental representations or to manage working memory demands. (Note that, when considered in the context of processing the complete WP text, in all can be productively used to help identify the operation needed to solve problem. However, in all does not necessarily indicate addition, and when used in isolation, without reliance on the full text, often leads to incorrect operations. We return to this point later, when we explain why relying on key words – without processing the full WP text, is error fraught.)

Yet, according to Kintsch and colleagues (Cummins et al., 1988; Kintsch & Greeno, 1985), WPS not only requires building mental representations of the text and managing working demands, it also relies on language comprehension. Cummins et al. (1988) computationally modeled incorrect WPS as a function of incorrect mathematical problem-solving processing versus faulty language comprehension. Problem representation depended more on language comprehension. In describing language comprehension’s contribution to WPS, Kintsch and Greeno (l985) noted that children understand important word meanings and syntax prior to entering school and learn to treat these words in a task-specific way via arithmetic and WP instruction. This includes extensions to ordinary word usage (e.g., all or more) to constructions involving sets (in all and more than).

This suggests that two forms of language comprehension are involved in WPS: general language comprehension and WP-specific language comprehension. To think about how WPS taxes both forms of language comprehension, consider this revised combine problem: Coronado has 5 puppies. Soledad has 5 kittens. Soledad also has 2 older dogs. How many young pets do the children have in all? Objects in this text increase demands on language comprehension for assigning roles for the propositional text structure. This is due to more sophisticated representations of vocabulary involving taxonomic relations at superordinate levels and subtle distinctions between categories (puppies + kittens = young pets; older dogs are not young pets). Further, because older is often used to frame comparisons between quantities, its use in this combine problem complicates demands for inducing the schema.

Evidence on the Contribution of Language Comprehension to Word-Problem Solving

Evidence on the contribution of language comprehension to WPS is found in two types of studies. Experiments demonstrate that seemingly minor changes in the wording of WPs affects problem-solution accuracy. For example, in a study conducted with preschoolers, Hudson (1983) contrasted two versions of a WP: One version was, “There are 5 birds and 3 worms. How many more birds are there than worms?”; the other version was, “There are 5 birds and 3 worms. How many more birds don’t get worms?” This rewording resulted in an 83% increase in performance. Other studies (Cummins, 1991; Davis-Dorsey et al., 1991; De Corte, Verschaffel, & De Win, 1985) demonstrate this effect in older children when WPs are altered to reveal semantic relations between sets more clearly. Vicente, Orarntia, and Verschaffel (2007) extended this literature by showing that rephrasing conceptual wording improves performance more for younger than older children (for third more than fifth graders) and for more difficult problems.

The second type of study is correlational. This literature demonstrates that individual differences in language comprehension uniquely account for individual differences in WPS development. For example, we (Fuchs, Gilbert, Fuchs, Seethaler, & Martin, 2018) assessed second graders representing high, average, and low reading and mathematics performance at the start of the school year on text comprehension, general language comprehension, non-linguistic reasoning, working memory, and foundational skill (word identification, arithmetic). Near the end of the year, we tested the same children on WPS, WP-language comprehension (i.e., understanding WP statements, without performing calculations), and calculations. Results indicated that start-of-year language comprehension was a significantly stronger predictor of year-end WP outcomes than of year-end arithmetic. By contrast, start-of-year arithmetic was a significantly stronger predictor of year-end computational skill than of year-end WPS or WP- language comprehension. Another example of correlational study is Schumacher and Fuchs (2012), who found that second graders’ understanding of relational terms, like more, less, and fewer, mediated (accounted for) the effects of WP intervention on some difference WPs. (Note that although the Schumacher & Fuchs study focused specifically on relational terminology, the randomized controlled trial described later in this article expands the focus to include other types of WP language.)

Across such WP rewording experiments and correlational prediction studies of individual difference in WPS, results suggest a role for language comprehension in WP intervention. Even so, to demonstrate the need for WP language instruction within WP intervention and to establish a causal role for language comprehension in WPS, a randomized controlled trial, which contrasts the effects of WP intervention with versus without embedded language comprehension instruction, is needed.

Embedding WP-Language Instruction in WP Intervention

In our WP intervention research, we have relied on an approach to WP intervention known as schema-based instruction. In multiple randomized controlled trials conducted by our research group and in randomized controlled trials conducted by other research groups, schema-based intervention has proven efficacious for enhancing WP performance (Fuchs et al., 2008; Fuchs, Fuchs, Finelli, Courey, & Hamlett, 2004; Jitendra, Star, Rodriguez, Lindell, & Someki, 2011; Jitendra et al., 2009; Powell, Berry, & Barnes, 2019; Powell & Fuchs, 2010). The commonality across the Jitendra, the Powell, and the Fuchs research groups is that, with schema-based instruction, students learn strategies that support thinking about and classifying WPs into problem types and then solving WPs according to the identified problem type’s solution method.

In our research, we have developed three schema-based WP interventions: Pirate Math (so named because it incorporates a pirate theme, such as pirates find x!), Hot Math (so named because it encourages students to “get hot” in mathematics), and Super Solvers (so named because it invokes super heroes to motivate students). Evidence of validity from randomized controlled trials is available for each program at each grade level for which it was developed.

Pirate Math focuses on the three major WP types addressed in the primary grades (combine WPs, compare WPs, and change WPs, explained below). We developed three Pirate Math programs: one at first grade, another at second grade, and the other at third grade. Hot Math addresses four WP types, which involve finding half or combining multiple quantities each costing a different price or using a pictograph with icons representing different values, or step-up functions (e.g., you need 7 brownies, but brownies are only sold in dozens). Hot Math is designed for third graders. Super Solvers addresses fraction WPs. At third grade, this includes compare, order, and change WP types. At fourth and fifth grades, Super Solvers addresses these same WP types as well as WPs with multiplicative relations, ratios, and proportions. In each program, 2-step problems are taught, in which a single WP incorporates more than one of the taught problem types. For information on how to obtain manuals, go to https://vkc.mc.vanderbilt.edu/frg.

Schema-Based WP Intervention

In this article, we illustrate our approach to schema-based intervention using first-grade Pirate Math. After describing this schema-based WP intervention, we explain how we embed language comprehension instruction within the Pirate Math programs.

The content of first-grade Pirate Math (Fuchs, Seethaler, & Fuchs, 2019) is organized in five units. Unit 1 (lessons 1–9) addresses adding and subtracting concepts, addition and subtraction counting strategies, and solving for a missing number represented by the letter x. Unit 2 (lessons 10–18) focuses on total problems (also known as combine WPs). Total problems combine two or three quantities; for example, There are 5 girls on the playground and 3 girls in the yard. How many girls are there? Unit 2 also includes instruction on 3-addend addition and 3-part total problems. Unit 3 (lessons 19–27) focuses on difference problems (also known as compare WPs). Difference problems compare a larger and a smaller quantity to find the difference; for example, At the picnic, the kids ate 5 hotdogs. They ate 3 hamburgers. How many more hot dogs did they eat than hamburgers? Unit 4 (lessons 28–36) focuses on change problems, in which start quantity increases or decreases a start quantity to produce a new end amount; for example, Jamarius baked 6 cookies. Then, he gave 3 of them to his friend. How many cookies does Jamarius still have? Cumulative review across foundational skills (Unit 1) and WP types (Units 2–4) is incorporated throughout. Unit 5 (lessons 37–45) introduces a sorting game with which students decide whether problems fit the total, difference, or change categories, without finding solutions, while provides cumulative review.

Units 2–4 begin by teaching the mathematical structure of that unit’s focal WP type. This involves role playing the problem type’s central mathematical event using an intact number story (i.e., without a missing quantity), concrete objects, and the child’s and tutor’s names. Tutors next use the intact story to connect the mathematical central event to (a) a visual schematic (into which story quantities are written) and (b) a hand gesture, which is used across lessons to quickly remind children of the three problem types’ central events. Then tutors connect the problem’s central event to a problem-model number sentence: for total, P1 + P2 = T (Part 1 plus Part 2 equals Total; also 3-part problems); for difference, B – s = D (bigger quantity minus smaller quantity equals difference); for change, St +/− C = E (for change increase, start number plus change number equals end number; for change decrease, start number minus change number equals end number).

In the problem type’s same introductory lesson, tutors present the first WP, using the same cover story with which the problem type was introduced, but with a missing quantity. The problem is enacted via role playing with concrete objects and the child’s/tutor’s names; the problem type’s schematic and hand gesture are applied; and the problem model number sentence is introduced with × standing for the missing quantity. In each WP unit, the idea of irrelevant information is explicitly taught.

Similarly, throughout this lesson and throughout the program, tutors rely on explicit instruction. This includes step-by-step strategies, designed to reduce demands on reasoning and working memory, to structure students’ WP processing in terms of WP types (schemas or problem models) and help them systematize the process of building WP models. These strategies involve naming the problem type, representing that problem model with that problem type’s number sentence, and entering relevant quantities from the WP statement into the problem type’s number sentence while crossing out “extra” (irrelevant) numbers in the text. Students then solve for the missing quantity.

More specifically, Students RUN through the problem: They Read it (as they listen to the tutor read it, and students then do a quick retell; this is to encourage careful attending); students Underline what the problem is mostly about (i.e., the word(s) in which the problem’s object code; this becomes the number answers’ label); and they Name the problem type. Next, they write T, D, or C next to the problem to help them remember the problem type they just identified, and they write the problem type’s number sentence in the work space. Then next re-read the problem as they substitute known quantities from the WP statement into the appropriate slots of the problem-type number sentence and enter × into the appropriate slot of the problem-type number sentence to denote the missing quantity.

For example, for the tutor reads, Today, there are 6 dogs at the park and 5 cats at the park. There are also 7 kids at the park. How many pets are at the park today?, as the student follows along on paper. The student does a quick retell of key content; underlines pets; identifies the problem as total and writes T; writes the problem type’s number sentence, P1 + P2 = T; re-reads and listens to the problem while replacing 6 for P1, 5 for P2, and × for T; and crosses out 7. To solve 6 + 5 = ___, the student retrieves the answer or uses counting strategies (these counting strategies, which are taught in Unit 1, are described below).

Each Pirate Math lesson is organized into three major activities. The bulk (the middle 20 minutes) of each 30-minute lesson involves the “instructional segment” that teaches the problem types’ ideas and the associated problem-solving strategies just explained. Within a given unit, the dominant focus of each day’s instructional segment is the unit’s main focus (e.g., change problems in Unit 4). However, after Unit 2, the instructional segment usually includes two or three problems, one of which is a review problem type. Each lesson begins with a 5-minute warm-up activity, called Meet or Beat Your Score (MOBYS), which provides students speeded strategic arithmetic practice (explained below). Each lesson concludes with 5 minutes of independent practice on finding the unknown in number sentences and solving a WP aligned with that day’s lesson focus or a review WP. Tutors provide corrective feedback throughout.

Each Lesson’s First Activity: MOBYS on Speeded Strategic Arithmetic Practice

The first activity in each Pirate Math lesson is speeded strategic practice, which is referred to as Meet or Beat Your Score (MOBYS). Students have 60s to answer flash cards, a shuffled deck of all combinations of sums and minuends up to 18. Students are taught to “know the answer right off the bat” (retrieve from memory) if confident; otherwise, they use the taught counting strategies. Students answer each presented problem correctly because, as soon as an error occurred, the tutor requires them to use the taught counting strategy to produce the correct response. To discourage guessing or careless application of counting strategies, seconds elapse as students execute the counting strategy as many times as needed to produce the correct answer. In this way, careful but quick responding increases the number of correct responses. Students have a chance to meet or beat the first score, and the day’s higher score is plotted.

The efficient counting strategies are taught in Unit 1. Tutors first address the conceptual bases using manipulatives and the number line and then teach how to use fingers to execute these strategies. For addition, students “count-in.” For 3 + 4 =, they hold 3 fingers up on one hand to represent the smaller quantity; then they put 4 remaining fingers down in a fist to note the 4 in hand and count 5 (putting another finger down with the other down fingers), 6 (putting another finger down), and 7 (putting the last finger down). The last number counted is the answer. For subtraction, they “count-up.” For 5 – 2 = 3, they count the difference between the numbers, saying 2 with a closed fist first; then they count 3 (hold up a finger), 4 (hold up a finger), 5 (hold up a finger). The number of raised fingers is the answer. (Note that at higher grades, a variation of these counting strategies, which requires more finger dexterity, is used.)

Student Work Illustrating the Pirate Math WP Strategies

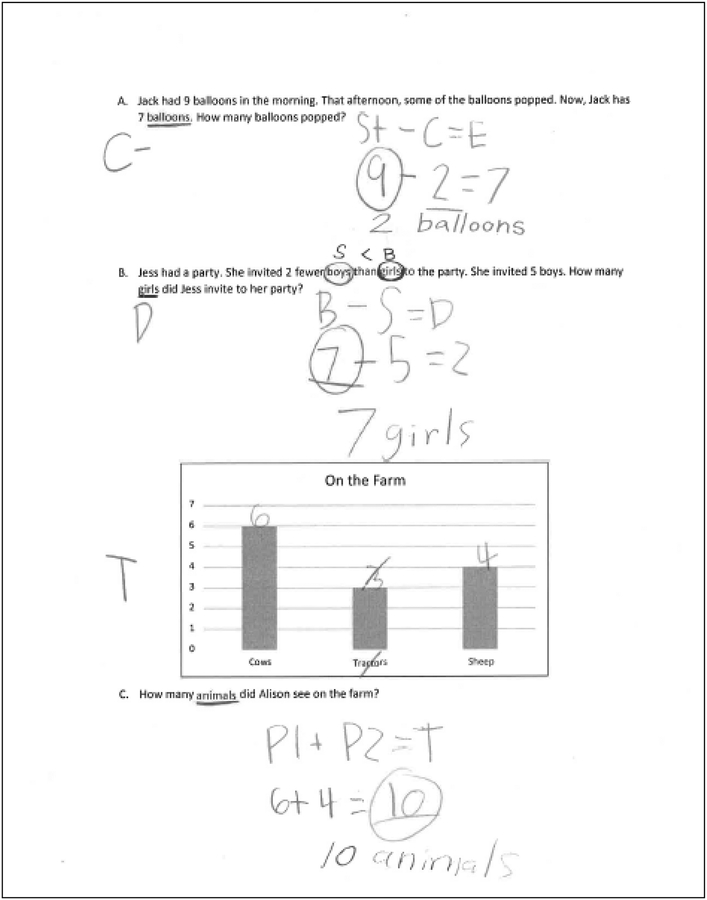
Figure 1 shows examples of intervention students’ post-intervention work at first grade; Figure 2, at second grade. We include examples of the three taught problem types, with and without irrelevant information and with and without graphs or charts displaying relevant information. Also, because second-grade Pirate Math explicitly teaches students about missing information in any of the three slots of problem-type number sentences (this is also the case in our grades 3–5 schema-based instruction programs), two of the three examples in Figure 2 have missing information in the first or second slot of the problem type’s number sentence. (In Figure 1, missing information in all three problems falls in the final slot, because first-grade Pirate Math does not address missing information in the first or second slot.)

Figure 1:

Examples of first-grade Pirate Math work.

Figure 2:

Examples of second-grade student work.

Embedding Language Comprehension Instruction into WP Intervention

Across Pirate Math and Super Solvers WP intervention, language comprehension instruction is embedded within WP intervention. We embed language comprehension instruction within WP intervention, rather than teaching WP-vocabulary and syntax within more conventional language therapy, because although language comprehension is associated with WPS, the literature suggests that domain-general cognitive training or language therapy often fails to transfer to academic skill. In Melby-Lervag and Hulme’s meta-analysis (2013), for example, the mean ES on verbal working memory tasks was 0.55, but the ES for transfer to computational skill among at-risk learners was 0.25. Research on language therapy in the area of reading comprehension, which also is associated with language comprehension, indicates a similar pattern of effects (Catts & Kamhi, 2017; Schleppegrell, 2007). That is, language therapy improves language, but transfer to reading comprehension is disappointing.

Inadequate transfer from working memory training or language therapy to academic performance is not, however, surprising. This is because at-risk learners experience substantial challenge with transfer (Haskell, 2001; National Research Council, 2000). Moreover, expecting domain-general cognitive training or language therapy to boost academic performance in this population seems unrealistic because at-risk learners, as operationalized in the intervention literature, have a poor foundation of academic skill. This argues for embedding such training in the context of academic intervention to facilitate transfer of improved domain-general resources, while building the academic skill to which improved domain-general resources may be applied.

In Pirate Math, the embedded language instructional component addresses WP language relevant to total, different, and change problems. In Unit 2, the meaning and application of vocabulary are taught in the context of total problems: joining words (e.g., altogether, in all) and superordinate categories (e.g., animals = dogs + cats). In Unit 3, the meaning and application of vocabulary and syntax are taught in the context of difference problems: compare words (e.g., more, fewer, than, -er words) and adjective -er versus verb -er words (e.g., bigger vs. teacher). In change problems, the meaning and application of vocabulary and syntax are taught in the context change problems: cause - effect conjunctions (e.g., then, because, so), implicit quantity change verbs (e.g., cost, ate, found), and time passage phrases (e.g., 3 hours later, the next day). Other focal points apply across problem types: for example, confusing cross-problem constructions (e.g., more than vs. then … more) and “tricky” labels (e.g., questions with superordinate category words, without a label, noun that’s the wrong label [as in money questions]).

The embedded language comprehension instructional methods are explicit, designed to support students’ understanding and correct application of these ideas in the context of solving WPs. For example, in teaching superordinate categories (e.g., animals = dogs + cats), the tutor uses photographs of dogs and cats to discuss with the student differences between dogs versus cats that help us know which are which. Then the tutor discusses with the student similarities between same across dogs and cats that help us know dogs and cats are both animals.

After practice with corrective feedback on dogs versus cats and animals versus not-animals, the tutor introduces a total problem with animals as a superordinate category in the question: Celia has 3 cats, and LaRashia has 6 dogs. How many animals do the children have? The tutor and student RUN through the problem. When it comes time to identify what the problem is mostly about (the U in RUN), the tutor and students work together to extend the ideas developed about dogs and cats as examples of animals and think about how the word animals in the WP’s question captures what the problem is mostly about. Extensive practice with a variety of similar categories is provided throughout Unit 2’s lessons, and theses ideas are intertwined and regularly reviewed throughout Units 3–5.

Why Embedded Language Comprehension Instruction Is Not Keyword Instruction

It is important to note that embedded language instruction does not teach children to rely on key words. Instead, students are explicitly taught how and why “grabbing numbers and key words” to identify a number sentence frequently produces, and this is why they must read WPs problems to meaningfully derive the problem’s central mathematical event. To help children appreciate this, they check the work of “other children” (prepared worked problems). Students find errors and explain how and why errors occurred. Worked examples rely on key words to select the wrong operation. They also include misusing irrelevant numbers or failing to recognize 3-part total problems.

Another reason why embedded language instruction is not keyword instruction is that identifying problem types within schema-based instruction does not tell the problem solver what operation to use to solve the problem. Instead, schema-based instruction provides problem solvers with a framework for systematically representing the mathematical structure of WPs. This is illustrated in Figure 3‘s first three WPs. In the first problem, altogether is associated with a total problem and addition. However, in the second problem, although altogether is associated a total problem, subtraction is required to find the solution to this total problem. By contrast, the third problem includes no possible keyword on which a problem solver might superficially rely to identify the problem type or the operation. The last problem illustrates why relying on other “extraneous tips” to “grab numbers” without processing WP text is fraught with errors.

Figure 3.

Four total problems illustrating why problem solvers need to process the word problem’s text to build a word-problem model and why instead relying on keywords or other extraneous information to solve word problems is error fraught.

A Randomized Controlled Trial Isolating the Added Value of Embedded Language Comprehension Instruction on WP Outcomes

As mentioned, in the context of a Pirate Math study, Schumacher and Fuchs (2012) found that second graders’ understanding of relational terms, like more, less, and fewer, mediated the effects of WP intervention on some difference WPs. This suggests that teaching and improving understanding of WP-specific language may be a valuable addition to WP intervention. But because mediation analysis is correlational, a randomized controlled trial is needed to establish a causal role for language comprehension in WPS and to demonstrate the added value of WP language instruction. Also the Schumacher and Fuchs (2012) study only addressed relational terminology. The randomized controlled trial we describe next adopted the greater variety of WP language explained above.

Study Methods

In this section of the present article, we provide a brief overview of a 2019 study’s methods and results for the purpose of highlighting the causal role language comprehension plays within WPS. (For a full study report, see Fuchs et al., 2019.)

In this randomized controlled trial, we identified first-grade students with risk in terms of low arithmetic skill and low performance on math concepts and applications. Although we did not identify children for inclusion in this study due to poor language skill, standard scores on a measure of general language comprehension (Woodcock Diagnostic Reading Battery (WDRB) - Listening Comprehension, Woodcock, 1997) for the sample fell 1.67 SDs below the test’s normative framework.

Within each classroom, we randomly assigned the at-risk students identified to participate in the study to four conditions: WP intervention with embedded language comprehension instruction, the same WP intervention without language comprehension instruction, number knowledge intervention, and control (the schools’ business-as-usual program, including classroom instruction and, for most students, school-based intervention). We included the number knowledge intervention condition to assess whether improved arithmetic skill from number knowledge intervention is sufficient to support WP development.

The three intervention conditions shared four commonalities. (1) Forty-five 30-minute intervention sessions were conducted over 15 school weeks outside the classroom in the child’s school. (2) Instruction was explicit. (3) Because at-risk first graders often display attention, motivation, and self-regulation difficulties that may affect learning (e.g., Fuchs et al., 2013), intervention included a self-regulation component centered on four rules: use an inside voice; stay in seat; follow directions; and try hard to answer problems correctly. (4) Each session comprised three segments: speeded practice on arithmetic problems (MOBYS; 5 minutes); the instructional segment, in which tutors introduced and systematically reviewed concepts and strategies (20 minutes); and practice (5 minutes). (5) Throughout these segments, tutors required children to know the answer or use taught counting strategies to solve arithmetic problems.

The two WP conditions relied on the first-grade Pirate Math schema-based intervention approach just described. One of the WP conditions, embedded the language comprehension instruction just described. Number knowledge intervention followed the program known as Galaxy Math, described in Fuchs et al. (2013). This included basic number knowledge, adding and subtracting concepts and principles, counting strategies, doubles concepts, number sets, and writing, counting and reading numbers 0–99, 3-addend problems, and double-digit adding and subtracting.

What We Found

The main conclusion from this randomized controlled trial, which is central to this article’s focus, is that embedding language comprehension instruction within WP intervention produces stronger WPS outcomes than does the same WP intervention without language comprehension instruction. The effect for this contrast was almost one-half standard deviation (SD). This is considerable given that intervention time was held constant across the two WP conditions, resulting in less direct skills WP instruction in the embedded condition than was provided in the WP intervention condition without language comprehension instruction (approximately 5 minutes less per session).

So although both WP intervention conditions significantly enhanced WPS over the control group, the effect for schema-based WP intervention with embedded language comprehension instruction (effect size = 1.75) was considerably larger than for WP schema-based intervention without embedded language comprehension instruction (effect size = 1.08). This demonstrates the added value of language comprehension instruction. It also reveals a causal role for language comprehension in WPS.

It is also interesting to consider at-risk children’s post-intervention WP achievement gaps. Over the course of intervention, the gap substantially narrowed for children in the condition that received WP intervention without language comprehension instruction, from 1.69 SDs below not-at-risk classmates at pre-intervention to a small gap of only 0.11 SDs at post-intervention. However, for students who did receive WP intervention with embedded language comprehension instruction, the gap more than closed: It decreased from 1.65 SDs below not-at-risk classmates at start of intervention to 0.52 SDs above not-at-risk classmates at the end of intervention. This provides students who received WP intervention with embedded language comprehension instruction a cushion of additional WP skill, compared to students in the WP intervention without language comprehension instruction, for weathering the transition from supplemental intervention support to general classroom programming.

It is also interesting to note that improvement in arithmetic skill, realized via number knowledge intervention, was not sufficient to address at-risk learners’ WP learning challenges. Although number knowledge intervention substantially improved arithmetic skill, with a moderate to large effect size of 0.59 SDs over at-risk control group students, this did not translate into superior WP performance. In fact, the effect size for number knowledge intervention on WPS was low (0.09 SDs). Moreover, the pre- to posttest WP achievement for the number knowledge condition remained sizeable at the end of intervention and similar to what occurred for control group children.

Implications for Research and Practice

Results of the Fuchs et al. (2019) randomized controlled trial clearly reveal that we cannot simply focus on number knowledge intervention, as so many early intervention programs do, hoping that its effects on arithmetic skill will transfer to improved WP performance. Instead, results demonstrated that an explicit focus on WP intervention is required.

The need to improve WP performance is pressing, because WPS, which is expected in almost every strand of the mathematics curriculum, is critical for school success even as it serves as a strong school-age predictor of employment and wages in adulthood (Every Child a Chance Trust 2009; Batty et al., 2010). Yet, WP difficulty is widespread (Daroczy et al., 2015), and teachers often view and structure WP instruction as if WPs are arithmetic tasks (Daroczy et al., 2015). Findings should alert teachers, teacher preparation faculty, and textbook developers to the need for research-based WP instructional and intervention methods. Unfortunately, WP instruction in the U.S. is commonly fraught with error-producing methods by teaching children to link keywords to mathematical operations and by providing children practice that requires application of the same solution method across all WPs on the practice sheet. These methods discourage the mathematical reasoning required for WPs (Powell & Fuchs, 2018).

Perhaps the most instructive finding from the Fuchs et al. (2019) randomized controlled trial is that embedding language comprehension within schema-based WP intervention provides students with an additional boost in WP performance, over the same schema-based WP intervention without embedded language comprehension instruction. This carries important implications for designing WP intervention and for supporting children’s language development. With respect to language development, results suggest that parents and preschool teachers be alert to and act on opportunities to extend children’s ordinary word usage to include mathematical contexts. In terms of WP intervention, it appears that WP instruction should incorporate a strong and explicit focus on language, including WP-specific vocabulary and syntactic knowledge. In terms of research, this randomized controlled trial motivates additional studies designed to isolate the effects of embedded language comprehension component within schema-based WP intervention with older and younger samples.