Impact of parameter selection on estimates of motoneuron excitability using paired motor unit analysis

Abstract

Objective.

Noninvasive estimation of motoneuron excitability in human motoneurons is achieved through a paired motor unit analysis (ΔF) that quantifies hysteresis in the instantaneous firing rates at motor unit recruitment and de-recruitment. The ΔF technique provides insight into the magnitude of neuromodulatory synaptic input and persistent inward currents (PICs). While the ΔF technique is commonly used for estimating motoneuron excitability during voluntary contractions, computational parameters used for the technique vary across studies. A systematic investigation into the relationship between these parameters and ΔF values is necessary.

Approach.

We assessed the sensitivity of the ΔF technique with several criteria commonly used in selecting motor unit pairs for analysis and methods used for smoothing the instantaneous motor unit firing rates. Using high-density surface EMG and convolutive blind source separation, we obtained a large numberof motor unit pairs (5409) from the triceps brachii of ten healthy individuals during triangular isometric contractions.

Main results.

We found an exponential plateau relationship between ΔF and the recruitment time difference between the motor unit pairs and an exponential decay relationship between ΔF and the de-recruitment time difference between the motor unit pairs, with the plateaus occurring at approximately 1 s and 1.5 s, respectively. Reduction or removal of the minimum threshold for rate-rate correlation of the two units did not affect ΔF values or variance. Removing motor unit pairs in which the firing rate of the control unit was saturated had no significant effect on ΔF. Smoothing the filter selection had no substantial effect on ΔF values and ΔF variance; however, filter selection affected the minimum recruitment and de-recruitment time differences.

Significance.

Our results offer recommendations for standardized parameters for the ΔF approach and facilitate the interpretation of findings from studies that implement the ΔF analysis but use different computational parameters.

1. Introduction

Initial investigations of motoneuron firing patterns proposed that the firing rate of a motoneuron bears a linear relation to the net excitatory synaptic input that the motoneuron receives. However, in recent decades, studies have shown that this relationship is non-linear due to the influence of monoaminergic neuromodulatory synaptic inputs (Bennett et al 1998, Lee et al 2003). Serotonin (5-HT) and norepinephrine (NE) are robust monoaminergic neuromodulators that act through G-protein coupled receptors to dramatically change motoneuron excitability by adjusting the response of the motoneuron to excitatory and inhibitory ionotropic input (Heckman and Enoka 2012). These monoamines have a prominent effect on motoneuron dendrites by activating persistent inward currents (PICs), comprised of slow L-type Ca + currents and fast persistent Na + currents, which evoke a sustained depolarization in the cell (Hounsgaard et al 1984, Bennett et al 1998). This depolarization leads to amplified and prolonged responses in motoneuron output in relation to excitatory synaptic inputs, creating the distinctive firing patterns we see in motoneurons.

There is a small but growing body of recent work in humans that is beginning to reveal the importance that PICs have in both typical and pathological motor control. In the intact nervous system, the influence of PICs likely varies among muscles throughout the body and may be crucial in the control of muscles with different functions. For example, because the prolonged motoneuron output elicited by PICs is advantageous for muscles that must be activated for extended periods, postural and anti-gravity muscles are likely to have larger PICs than muscles specialized for fine motor control (Binder and Powers 2001, Heckman and Enoka 2012, Wilson et al 2015). Additionally, abnormal neuromodulatory synaptic input and/or PICs may underlie motor deficits seen in pathological states. In individuals with a chronic spinal cord injury, uncontrolled muscle spasms and hyperactive reflexes have been linked to PICs elicited by constitutively active serotonin receptors (Gorassini et al 2004, Li et al 2004, Murray et al 2010, 2011). In individuals with chronic stroke, increased monoaminergic drive and PICs may be partially responsible for hyperactive stretch reflexes and for facilitating the upper extremity flexion synergy (McPherson et al 2008, 2018a, 2018b, 2018c, Karbasforoushan et al 2019, Mottram et al 2009). Weakness associated with sepsis may be related to impaired PICs, as serotonin agonist-induced PICs have also been shown to ameliorate motor neuron firing deficits in a preclinical model of sepsis (Nardelli et al 2017). This work in pathological populations emphasizes the role that neuromodulatory inputs and PICs play in the control of movement and the importance of their study. Nonetheless, much is still unknown and further study of neuromodulatory inputs and PICs is necessary.

Although PICs cannot be directly measured from human motoneurons, experimental techniques have been developed to estimate the size of PICs in humans via motor unit recordings. Currently, the standard method for estimating PIC amplitude (thus allowing for inference of neuromodulatory synaptic input) is the ΔF technique developed by Gorassini and colleagues (Gorassini et al 2002). With this technique, PIC amplitude is estimated by quantifying motor unit recruitment/de-recruitment hysteresis (ΔF) using pairs of motor units firing during slow linear ‘triangle’ contractions. The hysteresis of the higher threshold motor unit, as compared to a lower threshold unit, is thought to represent the decrease in excitatory synaptic input between the level of input at motor unit recruitment and the level of input at motor unit derecruitment. Such a decrease would then be indicative of the contribution of the PIC to motor unit firing. The ΔF metric has been validated through both animal and simulation work (Powers et al 2008, Powers and Heckman 2015) and has shown sensitivity to increased monoaminergic drive in humans given amphetamines (Udina et al 2010).

Conventionally, the ΔF technique requires that motor unit pairs meet certain criteria based on assumptions related to the underlying physiology. For example, the difference in recruitment time between the control (lower threshold) and test (higher threshold) unit must be long enough to ensure that the PIC in the control unit is fully active before test unit recruitment. The control and test units must have sufficient correlation of their firing rates (i.e. the instantaneous firing rate time series of each motor unit, calculated as the inverse of the inter-spike interval of the time series of motor unit action potentials), as the firing rate of the control unit is used as an approximation of the ionotropic excitatory synaptic input to the test unit. Firing rate saturation in the control unit may also bias the ΔF calculation and is often controlled for in these analyses. Despite the use of these standard criteria, the specific parameter values for each criterion vary across studies. Further, there are differences in computational factors across studies, such as the type of filter used to provide a smoothed instantaneous motor unit firing rate time series.

The purpose of the present study is to determine the sensitivity of the ΔF technique to differences in (1) minimum recruitment and derecruitment time difference, (2) minimum rate-rate slope correlation, (3) control unit firing rate modulation, and (4) filter selection. Such a robust sensitivity analysis is now possible as we can obtain spike trains from large populations of motor units using high-density surface EMG (HD-sEMG) decomposition approaches (Holobar and Zazula 2007, Chen and Zhou 2015, Negro et al 2016). Previous work with ΔF has largely used intramuscular recordings and has therefore been limited by the number of motor units that can feasibly be recorded. Here, we present motor unit data obtained using convolutive blind source separation of HD-sEMG signals (Negro et al 2016) recorded from the human triceps.

2. Methods

2.1. Participants

Ten adults (three female, seven male) ranging in age from 22 to 31 (mean ± SD age: 26.2 ± 2.4) completed the study. For inclusion in this study all participants were required to have: (1) no known neurological injury or disease, (2) no musculoskeletal impairment of the upper extremity, and (3) no significant visual or auditory impairments. All participants provided written informed consent prior to participation in this experiment which was approved by the Institutional Review Board of Northwestern University.

2.2. Experimental apparatus

Participants were seated in a Biodex experimental chair (Biodex Medical Systems, Shirley, NY) and secured with shoulder and waist straps to minimize trunk movement. In order to measure isometric elbow torques, the participant’s dominant forearm was placed in a fiberglass cast and rigidly fixed to a six degree-of-freedom load cell (JR3, Inc., Woodland, CA). The six degree-of-freedom load cell had an input range of 1115 N for forces in the x and y directions, 2230 N for forces in the z direction, and 127 Nm for torques about the x, y, and z axes. The data recorded across all participants had a maximum force of 539.8 N, and a maximum torque of 83.0 Nm. The arm was positioned at a shoulder abduction angle of 75° and an elbow flexion angle of 90°. The fingers were secured to a custom hand piece at 0° wrist and finger (metacarpophalangeal) flexion/extension (Stienen et al 2011, Miller and Dewald 2012, Miller et al 2014) (figure 1).

Figure 1.

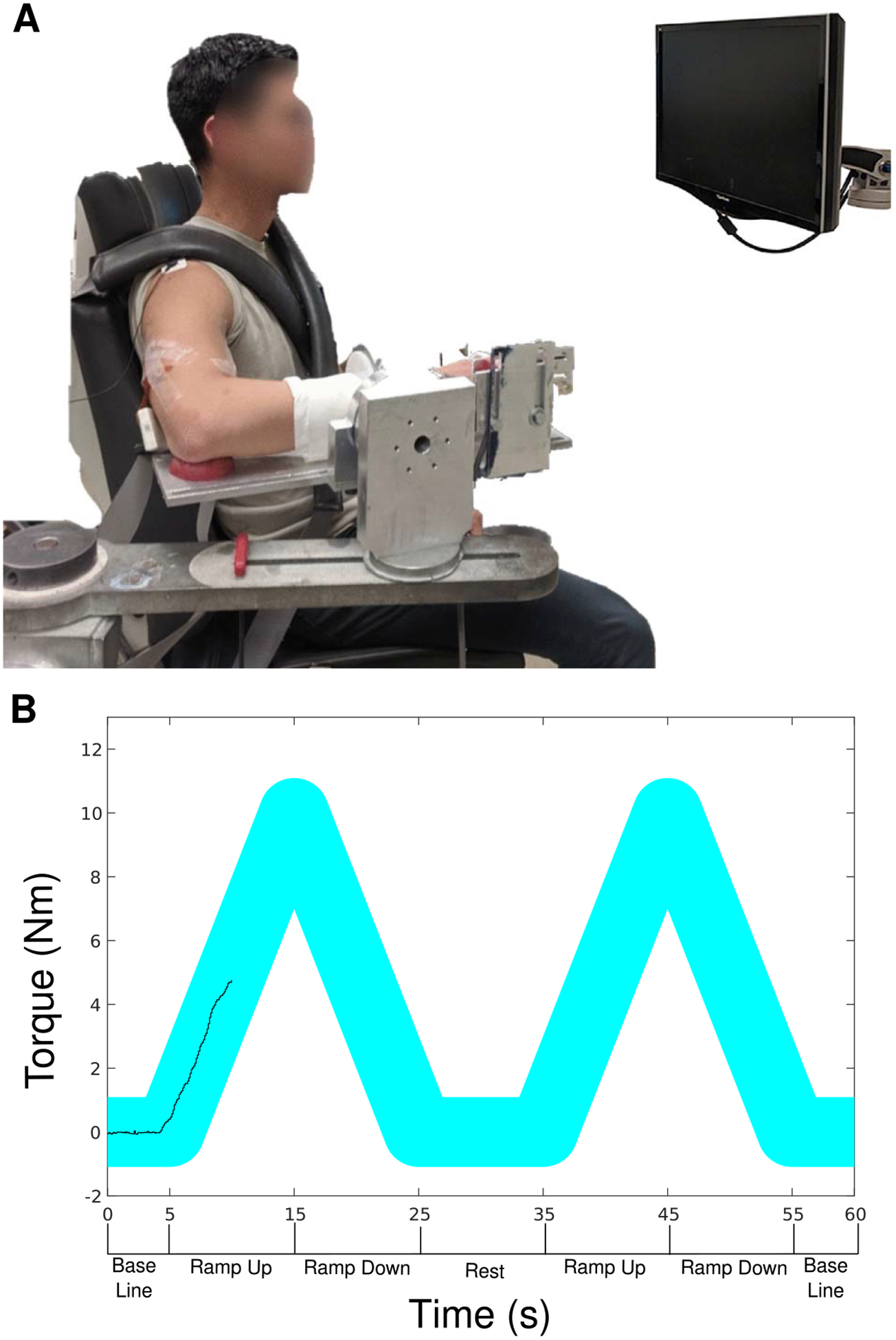
Isometric joint torque recording device with high-density surface EMG grids on the biceps brachii and triceps brachii (A). An example of the visual feedback provided to a subject, with the desired torque profile as the wide cyan line, and the generated torque as the black line, along with a timeline of key phases of a typical trial below the x-axis (B).

Forces and torques measured at the forearm-load cell interface were recorded at 1024 Hz and, along with limb segment lengths and joint angles, converted into elbow flexion and extension torques using a Jacobian based algorithm implemented by custom MATLAB software (The MathWorks).

Multi-channel surface EMG recordings were collected in a single differential mode from the lateral head of the triceps brachii using a grid of 64 electrodes with 8mm inter-electrode distance (GR08MM1305, OT Bioelettronica, Inc., Turin, IT) (figure 1). For two of the ten participants, EMG data were collected using the EMG-USB2+ signal amplifier (OT Bioelettronica, Inc., Turin, IT). For the other eight participants, EMG data were collected on the Quattrocento signal amplifier (OT Bioelettronica, Inc., Turin, IT), the newer model of the EMG-USB2+. EMG signals were amplified (Quattrocento: ×150; EMG-USB2 + : ×1 k− × 10 k), band-pass filtered (10–500 Hz) and sampled at 2048 Hz. For the data collected using the EMG-USB2+, the gain was manually set to maximize signal amplitude without saturating the A/D board (±5 V). Data recorded on the Quattrocento had a maximum range of 3.85 mV (Quattrocento input range: 33 mVpp). Because the EMG recordings and the force/torque recordings were collected on separate comp uters, a 1 s TTL pulse was transmitted to both comp uters for use as a marker, and each trial was temporally synced offline using cross-correlation of the TTL pulses.

2.3. Protocol

First, participants were asked to generate maximum voluntary torques (MVTs) in the direction of elbow extension. Real-time visual feedback of torque performance was provided on a computer monitor. Trials were repeated until three trials in which the peak torque was within 10% of each other were collected. If the final trial had the highest peak torque, a subsequent trial was collected. Participants were provided with enthusiastic vocal encouragement during MVT trials and were given adequate rest breaks between trials to prevent fatigue.

Experimental trials entailed the generation of triangular isometric torque ramps using real-time visual feedback of elbow flexion/extension torque, shown in figure 1(B). Participants were instructed to gradually increase their elbow extension torque to ~20% MVT over 10 s and then gradually decrease their torque back to 0% MVT over the subsequent 10 s. To facilitate accurate completion of the task, the desired time-torque profile was displayed on the monitor with an overlay of real-time torque performance. Each trial consisted of either two or three ramps in succession, with ten seconds of rest between ramps and five seconds of baseline at the beginning and end of each trial, where no torque generation was required. Participants were given at least several minutes of rest between trials. Participants were given several practice trials with verbal coaching to become comfortable with the task, followed by five to six experimental trials that were used for subsequent analysis. Torque traces were visually inspected. Trials that did not exhibit smoothly increasing torque from 0% to 20% and smoothly decreasing torque 20% to 0% MVT over the appropriate timeline were discarded, as were trials that exhibited any sudden increases or decreases in torque.

2.4. Motor unit decomposition and selection

All surface EMG channels were visually inspected and channels showing substantial artifacts, noise, or saturation of the A/D board were removed (typically zero to five channels were removed per trial). The remaining surface EMG channels were decomposed into motor unit spike trains based on convolutive blind source separation (Negro et al 2016) and successive sparse deflation improvements (Martinez-Valdes et al 2017). The silhouette threshold for decomposition was set to 0.85. However, even with this high threshold of decomposition accuracy, the blind source separation algorithm may still extract some solutions which deviate from physiological motor unit firing patterns. To address these errors, we supplemented the automatic decomposition with visual inspection of the motor unit firings. When potential errors were noted, a local re-optimization of the decomposition parameters was performed by experienced investigators with the use of a custom-made graphical user interface. This approach has been previously applied (Boccia et al 2019) and provides a high degree of accuracy in the estimated discharge patterns. While the automatic blind source separation does not produce any duplicate motor units, the visual inspection and iterative improvement process occasionally leads to duplicate units due to the separation of merged motor units or removal of erroneous firing times. For this reason, after the visual inspection, all duplicate motor units were detected by cross-correlation and the unit with a higher coefficient of variation in the inter-spike intervals was eliminated. The instantaneous motor unit firing rates were calculated as the inverse of the inter-spike intervals of the motor unit spike trains. Figure 2 displays raw EMG traces (A), along with the decomposed motor unit spike trains (B).

Figure 2.

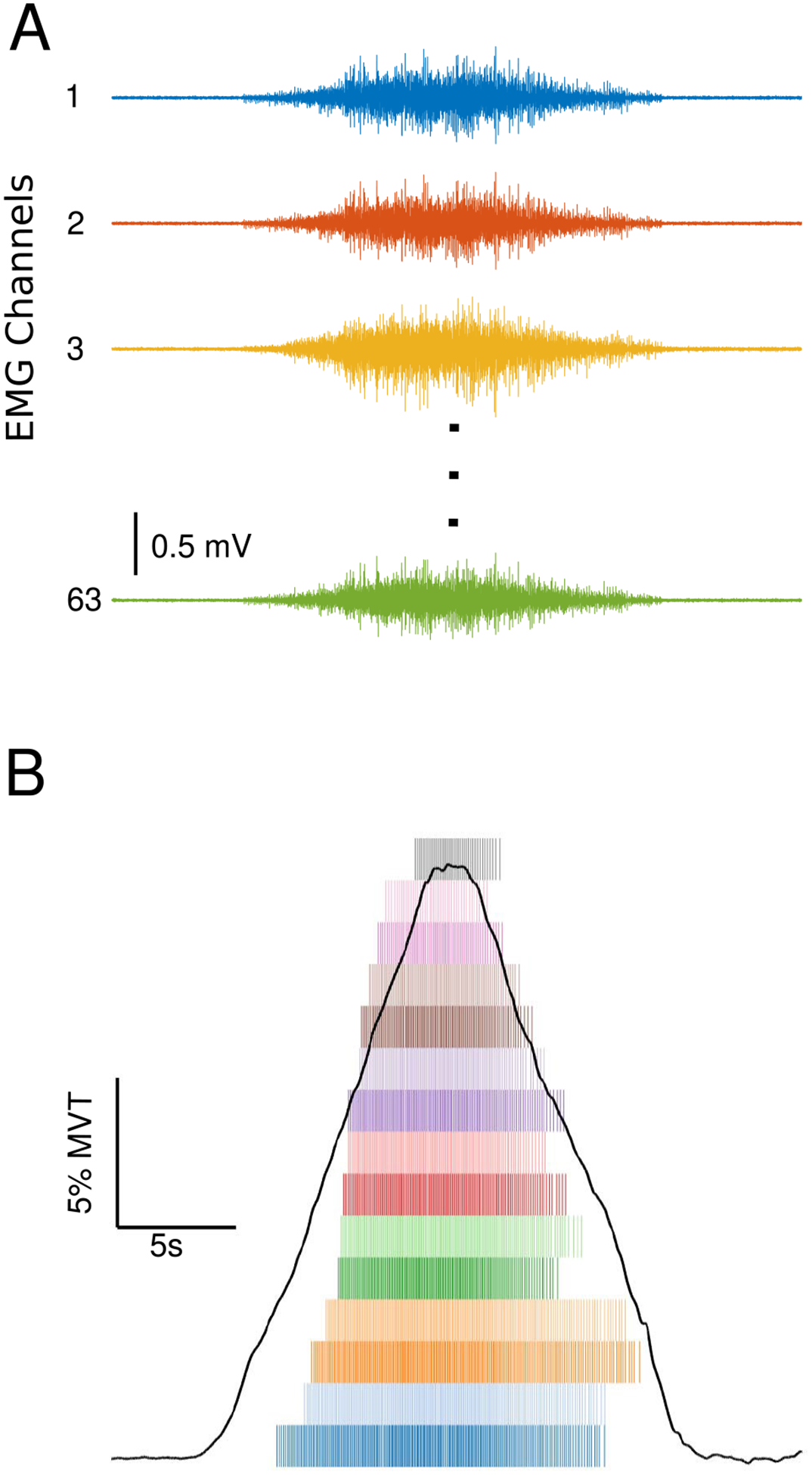
Raw EMG traces from the high-density electrode placed on the triceps brachii of one participant (A). Elbow extension torque trace and a spike raster plot of MU firings from the same trial (B).

2.5. Paired motor unit analysis

The ΔF technique is a paired motor unit analysis that quantifies the effects of PICs on motoneuron firing patterns by measuring the discharge hysteresis of a higher threshold motor unit (test) with respect to the firing rate of a lower threshold motor unit (control) (Gorassini et al 2002). Specifically, the ΔF value of the test motor unit is calculated as the difference in the firing rate of the control motor unit between the time of recruitment and de-recruitment of the test motor unit. Figure 3 illustrates this method of analysis.

Figure 3.

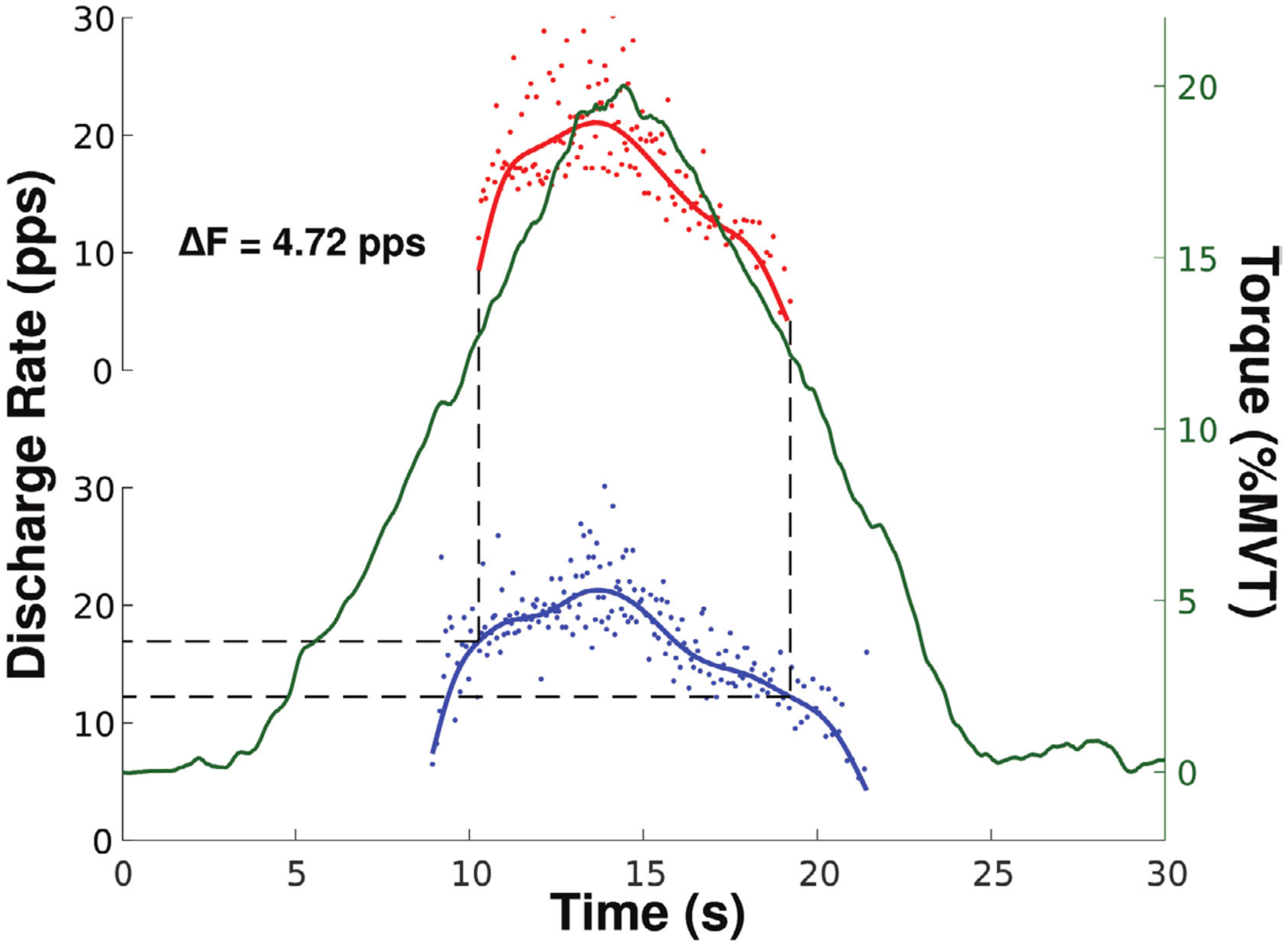
An example of the ΔF technique where the change in firing rate of the control unit (blue) is measured at the recruitment (16.93 pps) and de-recruitment (12.21 pps) of the test unit (red) taken from the triceps brachii of one participant. The solid blue and red lines represent the smoothed firing rates. The solid green line shows the torque trace for this trial, plotted against the right y-axis.

The ΔF technique first considers every combination of motor unit pairs in which the lower threshold control unit fires through both recruitment and derecruitment of the higher threshold test unit. The test unit must fire for at least 2 s to ensure the PIC can be fully activated (Stephenson and Maluf 2011). Then, the motor unit pairs must meet additional criteria to be appropriate for further analysis.

Criteria commonly used for the ΔF technique are the following: (1) a minimum time difference between recruitment of the motor unit pairs, (2) a minimum rate-rate slope (reflecting sufficient shared synaptic input), and (3) sufficient rate modulation in the control unit. Here, we assess the sensitivity of the ΔF calculation to various parameter values of these criteria.

2.5.1. Recruitment time difference

The criterion of a minimum recruitment time difference between the control and test motor units is based on the idea that the PIC in the control unit must be fully activated prior to the recruitment of the test unit. Thus, any further changes in the control unit firing rate will reflect a change in excitatory synaptic drive rather than changes in the activation of its PIC. Early work required a minimum of 2 s between recruitment of the control and test unit based on initial literature showing the PIC can take up to 2 s to fully activate (Hounsgaard and Kiehn 1989, Bennett et al 2001, Li et al 2004). However, simulation work by Powers and Heckman (2015) has suggested that the effect of recruitment time difference on ΔF and its variance across motor unit pairs diminishes greatly after 0.5 s.

2.5.2. Derecruitment time difference

The minimum de-recruitment time difference between the control and test units may also have a substantial effect on ΔF due to the rapid decrease in firing rate typical of motor units at de-recruitment. Previous work has not investigated the effect of derecruitment time difference on the ΔF analysis; however, deactivation of the PIC in the control unit very close in time to deactivation of the test unit may lead to overestimation of PICs.

2.5.3. Rate-rate relationship

The ΔF calculation relies on the assumption that both the control and test unit share substantial synaptic input as quantified using correlation of their rate-rate relationship (firing rate of the test unit as a function of the firing rate of the control unit during test unit firing). A consistent minimum for the rate-rate correlation has not been established. The initial threshold of r² ⩾ 0.7 used by Gorrassini and colleagues (Bennett et al 2001, Gorassini et al 2002) has been used extensively (Udina et al 2010, Stephenson and Maluf 2011, Wilson et al 2015). However, other work has used more lenient limits on rate-rate correlation including r² ⩾ 0.6 (Mottram et al 2009) and r² ⩾ 0.5 (Powers et al 2008), and r² ⩾ 0.3 (Zijdewind et al 2014). We investigated the effect of 8 different rate-rate correlation minima (r²˃ 0, 0.25, 0.5, 0.7, 0.75, 0.8, 0.85, 0.9) on the ΔF calculation.

2.5.4. Rate modulation of the control unit

If the firing rate of the control unit does not reflect the net ionotropic excitatory synaptic drive (e.g. due to decreased rate modulation of that unit), then the PIC amplitude using the ΔF method could be underestimated. Rate modulation in the control unit is here defined as the range of firing rates of the control unit during the time the test unit is active. Previous work (Stephenson and Maluf 2011, Wilson et al 2015) has excluded motor unit pairs in which the rate modulation of the control unit is within 0.5 pps of the calculated ΔF, to ensure rate saturation of the control unit is not limiting ΔF. Here we evaluated the effect of removing motor unit pairs which showed control unit saturation on the ΔF calculation.

2.5.5. Filter selection

Variation in computational methods used to prepare motor unit firing patterns for the ΔF analysis may affect the results. Gorassini and colleagues’ original implementation of the ΔF method fit a 5th-order polynomial to the instantaneous firing rates (Gorassini et al 2002) while previous motor unit work has filtered instantaneous firing rates using a Hanning window (De Luca and Erim 1994, de Luca et al 1996, De Luca and Contessa 2012) or a Gaussian window (Powers et al 2008). Due to the use of these smoothing methods in previous ΔF and other motor unit analyses, we have chosen to investigate the effect of these methods on the ΔF results. These smoothing methods have different effects on the firing patterns, particularly as a result of edge effects at motor unit recruitment and de-recruitment. The shape of Hanning and Gaussian filters produce sharper downward edges, while the 5th-order polynomial is more sensitive to doublets and errors, which may disproportionally skew the polynomial fit at recruitment and de-recruitment. Here we compare ΔF values, as well as the relationship between recruitment/de-recruitment time difference and ΔF, calculated using a 1 s Hanning window, a 2 s Hanning window, a 2 s Gaussian window, and a 5th order polynomial to smooth instantaneous firing rates.

2.6. Statistical analysis

Values are presented as mean ± SD. For group means, the mean ΔF was calculated for each participant before averaging across participants. A paired t-test was used to determine whether group mean ΔF was different when removing motor unit pairs with control unit rate saturation compared to not removing those pairs. Separate one-way repeated measures ANOVAs were used to determine the effect of filter type on ΔF values and on the individual participant variance in ΔF. When the effect of filter was significant, post-hoc tests were conducted to compare values between each pair of filter types using the Tukey correction for multiple comparisons. All statistical tests were calculated using GraphPad Prism (version 8.2.0 for macOS, GraphPad Software, San Diego, California USA). Statistical significance was set at p ˂ 0.05.

2.7. Approach to sensitivity analysis

We first examined the effect of recruitment and de-recruitment time difference on ΔF using three different rate-rate correlation thresholds and a 2s Hanning window. The Hanning window was chosen to start because it has been used extensively by our group and others (De Luca and Erim 1994, De Luca and Contessa 2012) to smooth motor unit firing patterns. For the subsequent analysis of the effect of various rate-rate correlation thresholds, we applied the recruitment and de-recruitment time difference parameters obtained from the first analysis. Then, the recruitment and de-recruitment time difference and rate-rate correlation parameters were used for both the analyses of control unit saturation and filter selection.

3. Results

In total, 1576 motor unit spike trains were decomposed from the triceps brachii of ten participants. Each participant completed at least eight isometric elbow extension triangle contractions with an average yield of 10.4 ± 4.3 motor units per trial. We considered 5409 motor unit pairs for the ΔF analysis. A small number of these pairs (106) were excluded because the test unit was active for less than 2 s.

3.1. Relation of ΔF values to recruitment and derecruitment time difference

Figures 4(a)–(c) shows the relationship between ΔF values and the time difference between control and test unit recruitment with three different thresholds for rate-rate correlation (r² ˃ 0.5, 0.7, 0.9). With all three rate-rate correlation thresholds, the ΔF values demonstrated an exponential plateau behavior, rapidly increasing along with recruitment time difference values before plateauing. This exponential relationship has not been previously presented in the literature but was more apt for our data than the previously demonstrated linear and second order polynomial fits (Stephenson and Maluf 2011, Wilson et al 2015). To approximate the minimum recruitment time difference at which ΔF values no longer varied, we fit the data using an exponential plateau function and identified where the exponential fit had grown three half-lives, reaching 87.5% of its asymptotic value. This resulted in a recruitment time difference cutoff of 0.92 s, 0.95 s, and 0.91 s for the motor unit pairs with r² ˃ 0.5, 0.7, and 0.9, respectively.

Figure 4.

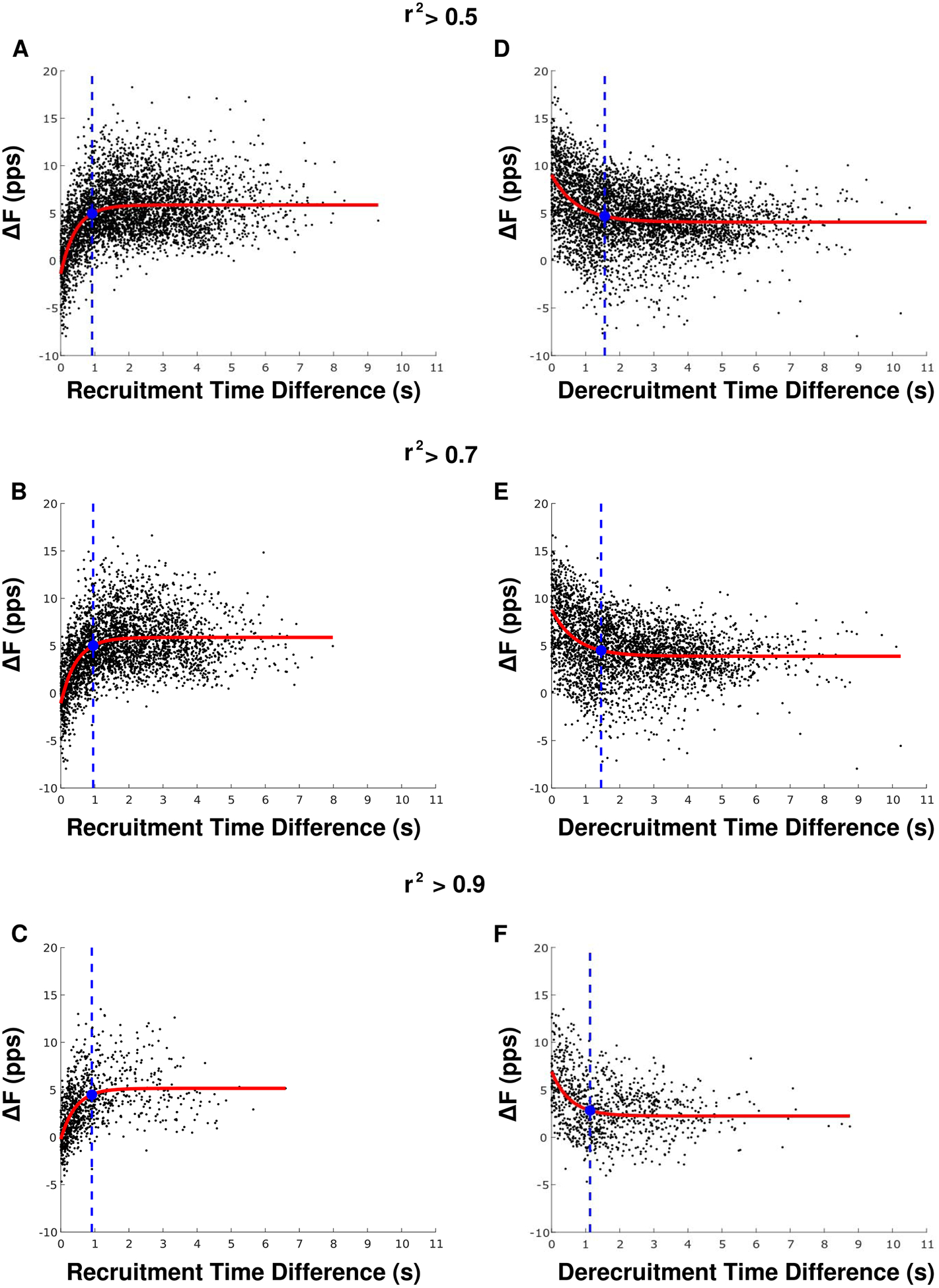
The relationship between recruitment time difference (A)–(C) and ΔF as well as de-recruitment time difference (D)–(F) and ΔF is shown for three different rate-rate correlation thresholds. The red lines denote exponential plateau (A)–(C) or decay (D)–(F) fits. The blue filled circles indicate where the exponential model is 87.5% from the value at t = 0 to the asymptote value. The blue dotted lines indicate the minimum recruitment/de-recruitment time difference used for further analyses.

Figures 4(d)–(f) shows the relationship between ΔF values and the time difference between test and control unit de-recruitment, with three different thresholds for rate-rate correlation (r² ˃ 0.5, 0.7, 0.9). A decaying exponential plateau function was used to fit the data, and the minimum de-recruitment time difference was determined as the point where the exponential fit had decayed 87.5% from the value at de-recruitment time difference = 0 to its asymptotic value. The minimum de-recruitment time difference was 1.56 s, 1.45 s, and 1.13 s for the motor unit pairs with r² ˃ 0.5, 0.7, and 0.9, respectively.

Based on these results, we restricted our following analyses to motor unit pairs with at least 1 s difference between control and test unit recruitment times and 1.5 s difference between test and control unit derecruitment times, which yielded 3041 motor unit pairs (304.1 ± 178.4 pairs per participant) across all contractions.

3.2. Dependence of ΔF on rate-rate correlation

The average number and percentage of motor unit pairs with rate-rate correlation values above each threshold (r² ˃ 0, 0.25, 0.5, 0.7, 0.75, 0.8, 0.85, 0.9) are shown in table 1. The percentage of retained motor unit pairs decreased dramatically when the r² threshold increased beyond 0.5, dropping from 76.1% (2320 motor unit pairs) with r² ˃ 0.5% to 49.8% (1602 motor unit pairs) with r² ˃ 0.7 to only 6.5% (197 motor unit pairs) with r² ˃ 0.9.

Table 1.

Number and percentage of motor unit pairs at various rate-rate correlation thresholds (group mean ± SD).

Minimum r2	Number of pairs	% of pairs
0.00	304.1 ± 178.4	100 ± 0.0
0.25	276.6 ± 164.8	90.7 ± 0.1
0.50	232.0 ± 146.7	76.1 ± 0.1
0.70	160.2 ± 124.2	49.8 ± 0.2
0.75	133.1 ± 110.8	40.9 ± 0.2
0.80	98.8 ± 83.9	30.5 ± 0.2
0.85	55.8 ± 49.7	17.6 ± 0.1
0.90	19.7 ± 17.5	6.5 ± 0.0

Figure 5(A) shows the relationship between group mean ΔF value and each rate-rate correlation threshold. Figure 5(B) displays the group mean individual participant variance in ΔF across the different thresholds for rate-rate slope correlation. At the majority of the rate-rate slope correlation thresholds (below 0.85), both the group mean ΔF values and group mean individual participant variance remained constant. The group mean ΔF values of ~5 pps are comparable to results from previous work that calculated ΔF in the triceps brachii using motor unit data obtained using intramuscular EMG decomposition (Wilson et al 2015). At the strictest r² thresholds (r² ˃ 0.85 and r² ˃ 0.9), the group mean ΔF value decreased, and the group mean individual participant variance increased.

Figure 5.

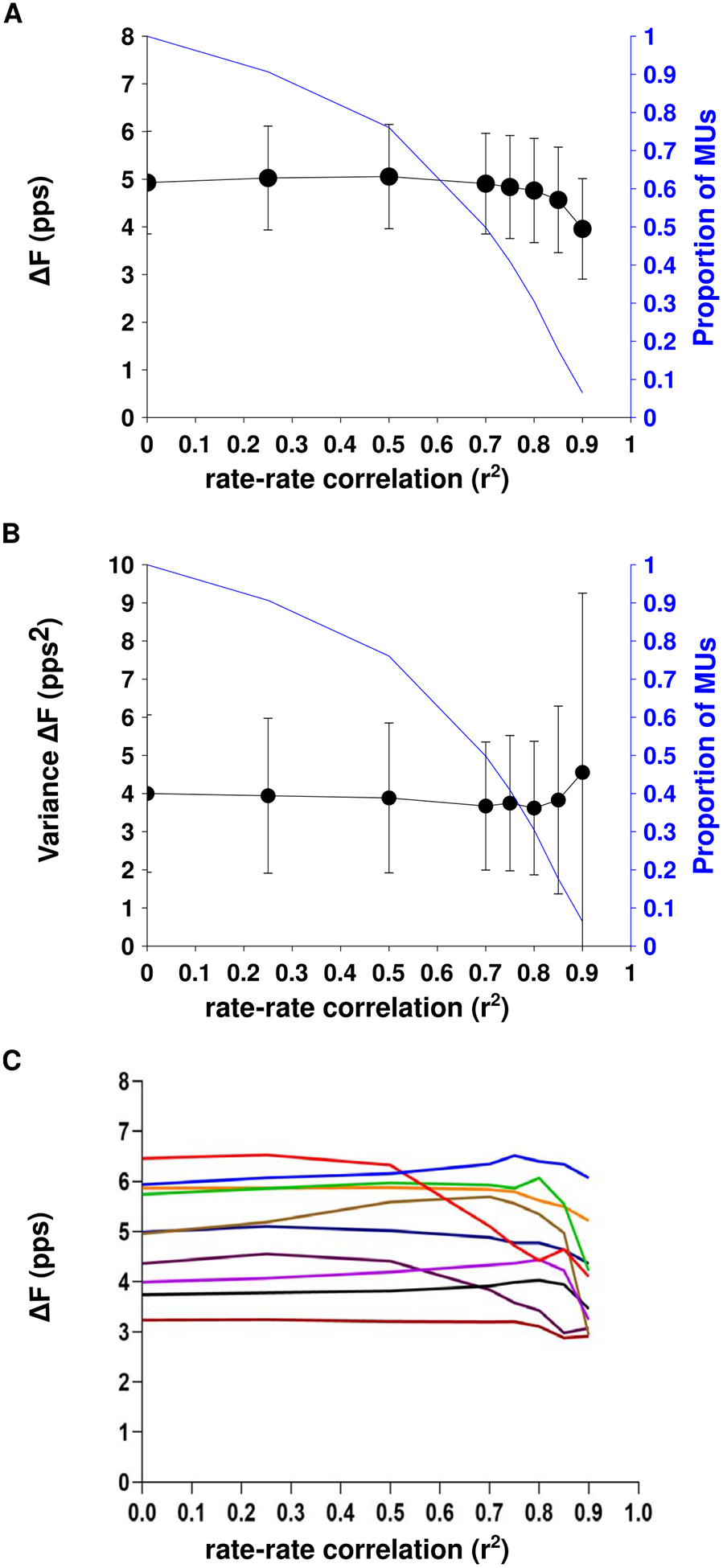
The group mean ± SD ΔF values (A) and group mean ± SD individual participant variance in ΔF (B) across three different thresholds for rate-rate correlation. The relationship between ΔF and rate-rate correlation threshold for each of the ten participants is shown in part C.

Figure 5(C) shows the relationship between ΔF value and minimum rate-rate correlations for each participant. ΔF values for all participants were relatively stable for r² thresholds of up to 0.5. For three participants, ΔF decreased markedly with higher r² thresholds whereas values for the other participants fluctuated to a lesser degree.

Similar ΔF values and variance were obtained when using no rate-rate correlation threshold as were obtained when using threshold of r² ˃ 0.7 that has been most commonly used in the literature. Based on this consistency, as well as the higher number of motor unit pairs afforded by removing the rate-rate correlation restriction, we removed the rate-rate correlation criterion in our following analyses.

3.3. Dependence of ΔF on control unit firing rate modulation

The maximum ΔF value of a motor unit pair is limited by the amount of rate modulation in the control unit during test unit firing. In order to avoid underestimation of ΔF due to insufficient rate modulation in the control unit, previous studies have removed motor unit pairs in which the ΔF value was within 0.5 pps of the control unit rate modulation (Stephenson and Maluf 2011, Wilson et al 2015). Figure 6(A) shows the relationship between ΔF and the firing rate modulation of the control unit; motor unit pairs that fit the criteria for control unit saturation are shown in blue. The group mean ΔF was 4.9 ± 1.1 pps before removal of pairs which exhibited control unit saturation, and the group mean ΔF was 4.7 ± 1.0 pps following the removal of those pairs. There was no significant change in subject mean ΔF after removal of pairs that fit the saturation criterion (p = 0.17). Figure 6(B) shows the mean ΔF per subject before and after the removal of motor unit pairs that exhibited possible saturation.

Figure 6.

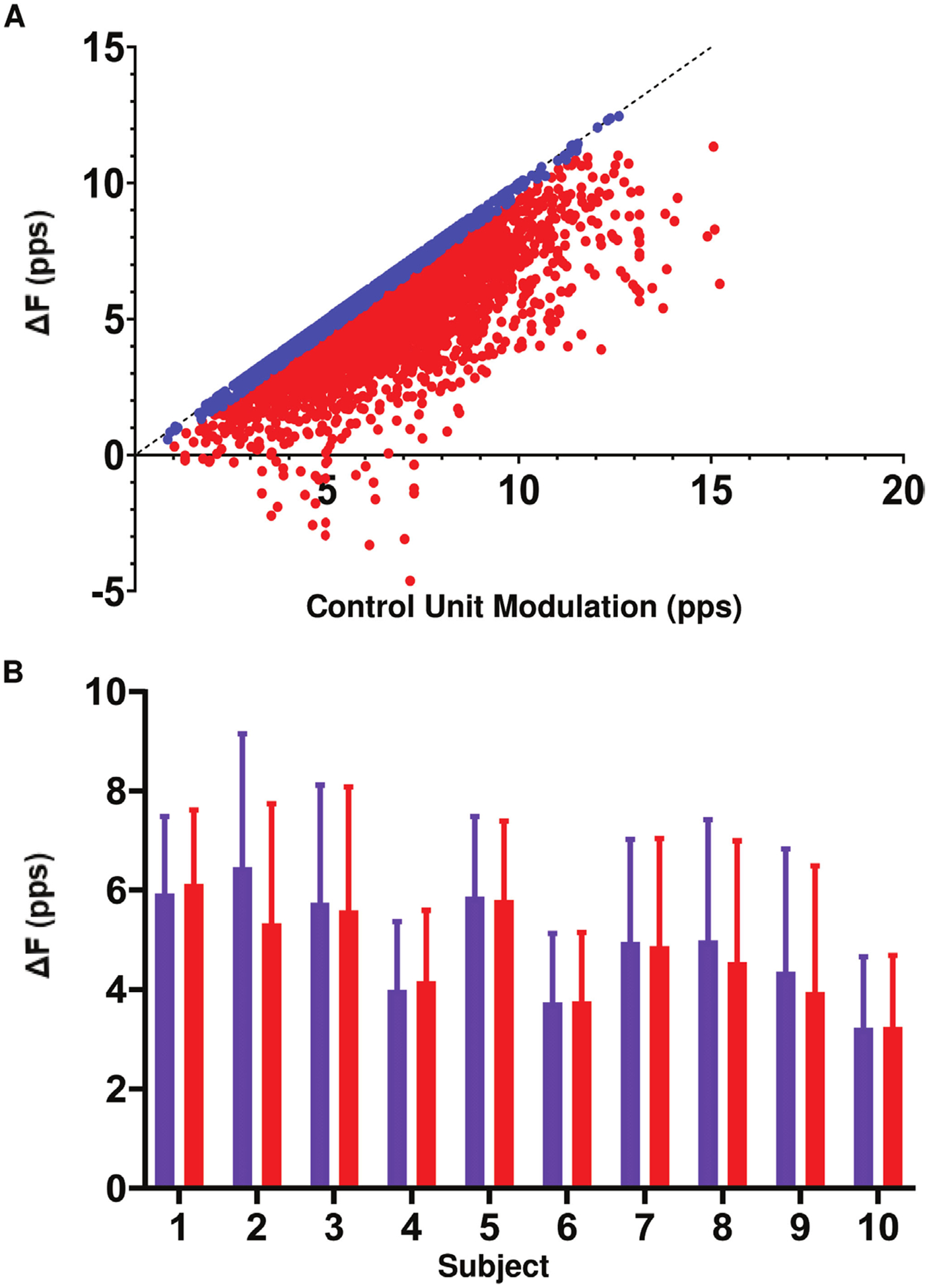
(A) The relationship between ΔF and control unit firing rate modulation. Motor unit pairs matching the criteria for control unit saturation are shown in blue. (B) The mean ± SD ΔF per subject before (purple) and after (red) the removal of motor unit pairs with control unit saturation.

3.4. Effect of filter selection on ΔF results

The ΔF technique requires filtering of instantaneous motor unit firing rates to provide smoothed continuous firing rates. Figure 7(A) shows the change in each subject’s mean ΔF across 4 different filter methods. The group mean ΔF was 5.1 ± 1.1 pps for the 1 s Hanning window, 4.9 ± 1.1 pps for the 2 s Hanning window, 4.9 ± 1.1 pps for the 2 s Gaussian window, and 5.0 ± 1.1 pps for the fifth-order polynomial fit. The one-way repeated measures ANOVA revealed a significant effect of filter type on ΔF (P ˂ 0.0001, F(3,27) = 11.96). Post-hoc tests revealed that the 1 s Hanning window resulted in mean ΔF values that were significantly higher than those obtained using the 2s Hanning window (+0.18, p = 0.002), the 2 s Gaussian window (+0.25, p ˂ 0.0001), and the fifth-order polynomial (+0.15, p = 0.011). However, these increases are unlikely to be meaningful given their small magnitudes. The remaining comparisons were not significantly different.

Figure 7.

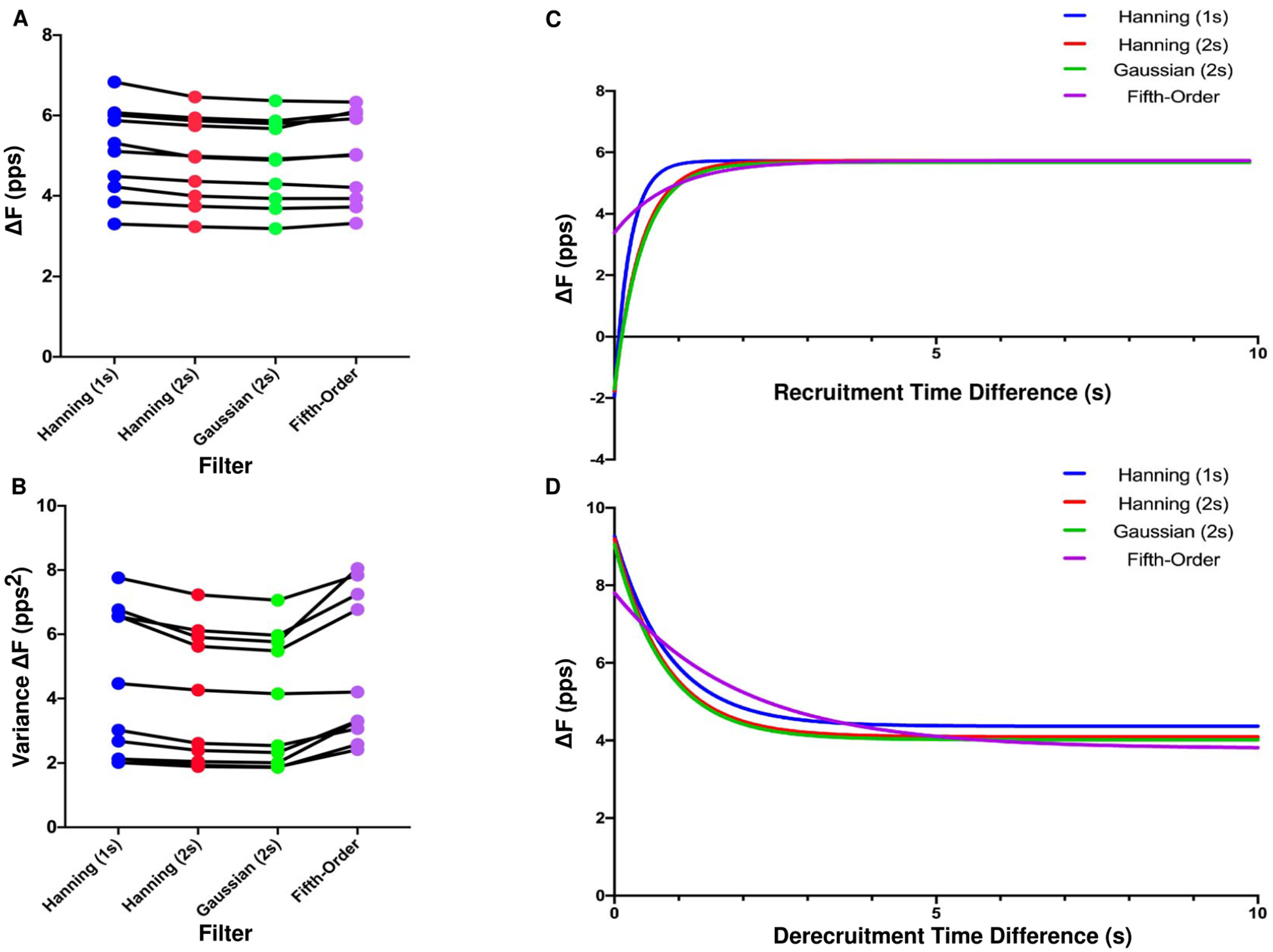
Mean ΔF (A) and variance in ΔF (B) for each participant plotted across four filter types. An exponential plateau function showing the relationship between ΔF and recruitment time difference (C) and de-recruitment time difference (D) for the same four filter types.

Figure 7(B) shows the relationship between each participant’s variance in ΔF values and filter type. The mean individual participant variance was 4.4 ± 2.3 pps² for the 1 s Hanning window, 4.0 ± 2.0 pps² for the 2 s Hanning window, 3.9 ± 2.0 pps² for the 2 s Gaussian window, and 4.9 ± 2.3 pps² for the fifth-order polynomial fit. The one-way repeated measures ANOVA revealed a significant effect of filter type on individual participant variance in ΔF (P ˂ 0.0001, F(3,27) = 20.20). Post-hoc tests revealed that the fifth-order polynomial resulted in individual participant variances that were higher than for the 1 s Hanning window (+0.47, p = 0.01), the 2 s Hanning window (+0.88, p ˂ 0.0001), and the 2 s Gaussian window (+0.98, p ˂ 0.0001). The 1 s Hanning window led to more variability than the 2 s Hanning window (+0.41, p = 0.034) and the 2 s Gaussian window (+0.51, p = 0.006). There was no significant difference in variability between the 2 s Hanning window and the 2 s Gaussian window (p = 0.10).

Figure 7(C) shows the relationship between ΔF and recruitment time difference for each filter type. Based on the previous analysis of ΔF vesus recruitment time difference using a 2 s Hanning window (figure 4), these relationships were modeled as exponential plateau functions. The recruitment time difference at which the exponential fit reached 87.5% of its asymptotic value was smaller for the data smoothed with the 1 s Hanning window (0.50 s) than with the 2 s Hanning window (0.87 s), 2 s Gaussian window (0.91 s), and the fifth-order polynomial, (1.82 s). Additionally, ΔF calculated using a fifth order polynomial was less sensitive to the recruitment time difference parameter, with a range of 2.36 pps for the exponential function across the range of observed recruitment time differences, compared to 7.70 pps, 7.53 pps, and 7.39 pps for the 1 s Hanning window, 2 s Hanning, and 2 s Gaussian window, respectively.

Figure 7(D) shows the relationships between ΔF and de-recruitment time difference, modeled using an exponential decay function. The de-recruitment time difference at which the exponential fit had decayed 87.5% from the value at de-recruitment time difference = 0 to its asymptotic value was similar for the data smoothed with a 1 s Hanning window, 2 s Hanning window, and 2 s Gaussian window (1.78 s, 1.63 s, and 1.65 s, respectively) but was much later for the data smoothed with the fifth-order polynomial (4.09 s). As with recruitment time difference, the fifth order polynomial was least sensitive to the de-recruitment time difference parameter. The range of the exponential decay function was 4.02 pps compared with 4.90 pps for the 1 s Hanning window, 5.11 pps for the 2 s Hanning window, and 5.04 pps for 2 s Gaussian.

4. Discussion

In this study we quantified the relationship between values of ΔF and the methods used to calculate them. By utilizing HD-sEMG and motor unit decomposition, we were able to obtain a much larger sample of motor unit pairs than previous studies, enabling us to systematically explore the sensitivity of the ΔF calculation to different computational parameters.

4.1. Effect of recruitment and derecruitment time difference on ΔF

The ΔF technique requires that the PIC of the control unit be active for the duration of test unit firing, to ensure the control unit firing rate varies linearly in response to changes in net excitatory input. If the PIC in the control unit has not been fully activated before the recruitment of the test unit ΔF may be underestimated. Previous studies have controlled for this by discarding motor unit pairs with recruitment time differences below a certain minimum, however, these thresholds vary across studies from 0.5 to 2 s.

In alignment with previous work (Powers et al 2008, Stephenson and Maluf 2011, Wilson et al 2015), we observed a reduction in ΔF values for motor unit pairs with closely recruited control and test units. Further, we found an exponential plateau relationship between ΔF and recruitment time difference (figure 4). While previous work has modeled this relationship with linear (Wilson et al 2015) or quadratic (Stephenson and Maluf 2011) fits, data from the current study demonstrated an exponential plateau function. Because we measured a vastly larger number of motor unit pairs across a wider range of recruitment time differences compared with previous studies, we were able to characterize this relationship in a robust manner, which may explain the differences in type of model fit. Based on the exponential plateau relationship, we identified that a recruitment time difference of ~1 s is an appropriate minimum for use in the ΔF calculation. This time course is similar to that of PIC activation recorded from intracellular recordings in rat motoneurons (Bennett et al 2001).

Examining the relationship between ΔF and the de-recruitment time difference of the test and control units, an exponential decay relationship was observed. When control units that are de-recruited closely after the test unit are included in the ΔF calculation, the ΔF value may be overestimated. This finding suggests that the effect of de-recruitment time difference on ΔF should be considered and/or controlled for in future studies. The increased ΔF for motor unit pairs with short de-recruitment time differences is likely due to the deceleration of the control unit firing rate that typically occurs just prior to de-recruitment. PIC inactivation near de-recruitment could be one contributor to this rapid deceleration, as could prolongation of the after hyperpolarization (Wienecke et al 2009). Additionally, the edge effects of filters used to smooth instantaneous firing rates may enhance the deceleration near de-recruitment. A reduced de-recruitment time difference may be due to PIC induced onset/offset hysteresis in the test unit, and is accurately reflected by an increase in ΔF. However, the tail end of the control unit may not be an accurate reflection of synaptic input.

4.2. Relation between ΔF and rate-rate slope correlation

As the ΔF technique uses the control unit as an estimate of the excitatory synaptic drive to the test unit, previous studies use only motor unit pairs that have a strong correlation between their firings rates. Previous work has commonly used rate-rate correlation thresholds of r² ˃ 0.5–0.7.

The present study found that reducing or removing the minimum threshold for rate-rate slope correlation did not affect ΔF value or its variance. These results are consistent with findings from the decerebrate cat (Powers et al 2008). As previously posited, one possible explanation for these results is that the ΔF calculation only measures the control unit firing at two points, test recruitment and de-recruitment (Powers et al 2008). Differences in modulation of the test and control unit that do not occur at test recruitment and de-recruitment would affect the rate-rate slope correlation, but not the ΔF value, as long as the control unit is a sensitive indicator of synaptic input at the onset and offset of discharge of the test unit.

While ΔF values were stable across lower minimum correlation thresholds, our results suggest putting stricter limitations on firing rate correlation leads to a decrease in ΔF value and an increase in variance. The increased variance is likely due to the substantially reduced number of motor units available for these analyses. Selection bias may also play a role in the reduced ΔF values observed with higher rate-rate correlation threshold. Motor unit pairs with higher firing rate correlation are often recruited closely together, which can lead to reduced ΔF if a sufficient minimum recruitment time difference is not used. Additionally, only test units with minimal PIC-induced firing rate nonlinearities would have a sufficiently high correlation with control units that have fully activated PICs, limiting the selection to units with lower ΔF.

The ability to relax the rate-rate correlation threshold without affecting ΔF values may enable a more robust implementation of the ΔF technique in pathological conditions that may alter motor unit firing rate correlation, such as individuals with chronic spinal cord injury (Zijdewind et al 2014).

4.3. Effect of control unit firing rate modulation on ΔF

Due to the nature of the ΔF calculation, the ΔF value for any motor unit pair is limited by the firing rate modulation of the control unit while the test unit is active. Limited rate modulation in the control unit relative to the excitatory synaptic input may lead to an underestimation of ΔF. To address this possible underestimation, previous work has excluded motor unit pairs in which the rate modulation of the control unit during test unit firing was within 0.5 pps of ΔF (Stephenson and Maluf 2011, Wilson et al 2015).

The present study found that removing possibly saturated motor unit pairs had no significant effect on group mean ΔF. This result is consistent with findings from intramuscular recordings (Wilson et al 2015) and suggest that control unit saturation does not have a substantial influence on ΔF value. However, identifying possibly saturated control units using the current method (Stephenson and Maluf 2011), may also lead to underestimation of ΔF. Pairs with saturated control units often have higher ΔF values due to the mathematical constraints inherent in this method for determining saturation. One possible solution is to quantify rate modulation in the control unit using a method that is independent of the ΔF calculation. Additionally, the ΔF technique only requires that the control unit be a sensitive indicator of synaptic input at the recruitment and de-recruitment time of the test unit, and saturation of the control unit that does not occur at test unit onset or offset would not affect ΔF values.

4.4. Influence of smoothing method on ΔF

The ΔF calculation requires a smoothed instantaneous firing rate time series for each motor unit. A variety of different smoothing methods have been previously used, and the method chosen to smooth the instantaneous firing rates may influence the ΔF calculation.

While our results show a significant effect of filter type on ΔF value, the range of group mean ΔF across the smoothing methods (0.25 pps) was negligible relative to the magnitude of ΔF and the only filter to differ from the rest was a 1 s Hanning window. Filter type also had a significant effect on individual participant variance in ΔF, which was highest when using the fifth-order polynomial. This could be attributed to due to this filter’s increased sensitivity to doublets and erroneous spikes, particularly at onset and offset, when compared to Hanning or Gaussian filters. Additionally, some units displayed non-physiological increases in firing rates at recruitment or derecruitment when smoothed using the fifth-order polynomial.

There is also an effect of filter type on the ΔF vesus recruitment/derecruitment time difference relationship. When a fifth-order polynomial is used, ΔF varies to a lesser extent across recruitment time difference values compared with the other filter types. Additionally, data smoothed using the shorter 1 s Hanning window reached a plateau in ΔF value at a shorter recruitment time difference than data smoothed using the longer 2 s Hanning and Gaussian windows. These results suggest that a portion of the observed relationship between recruitment time difference and ΔF is due to the smoothing of instantaneous firing rates, in addition to the rapid firing rate acceleration associated with PIC activation. Data smoothed with the fifth-order polynomial were also less sensitive to de-recruitment time difference, though to a lesser extent than recruitment time difference. There was minimal difference between smoothing firing rates with the shorter 1 s Hanning window and the 2 s Hanning or Gaussian window. This is possibly due to the slower time course and smaller magnitude of the effect of de-recruitment time difference on ΔF compared with recruitment time difference.

5. Conclusions, limitations, and future directions

Previous studies utilizing the ΔF technique have required motor unit pairs to meet certain criteria based on physiological assumptions. This study assessed the relationship between ΔF values and the commonly used criteria and smoothing filters. The data presented here indicate that the following methodological considerations may enable more accurate estimation of PIC amplitude using the ΔF technique: (1) the control unit should be recruited a sufficient time (~1 s) before the test unit to avoid underestimation of ΔF; (2) the control unit should also be derecruited a sufficient time (~1.5 s) after the test unit to avoid overestimation of ΔF; (3) reduction or removal of rate-rate correlation restrictions does not affect ΔF values or variance; (4) Filter selection for smoothing instantaneous firing rates has little effect on ΔF values, however, the fifth-order polynomial showed increased individual participant variance compared with the Hanning and Gaussian filters, and therefore may not be the best smoothing option. Additionally, filter selection may affect the minimum recruitment and de-recruitment time difference function shown in figure 4 for the Hanning window, and therefore a suitable minimum value should be determined for the specific filters being used; (5) Removal of possibly saturated control units had no effect on ΔF values.

Limitations and Future Work:

This work was conducted in one muscle of young healthy participants which may affect the generalizability of findings. It is possible that the relationships between ΔF and the criteria and filters investigated here may vary in different muscles or populations. Additionally, while this work evaluated the influence of several common smoothing filters on ΔF, there are a number of additional smoothing methods, as well as a larger range of filter window lengths, that could still be explored. Future work will continue to compare methods for the comprehensive quantification of PICs in humans. The results of this robust sensitivity analysis allow for comparison between the paired motor unit analysis and any novel methods to characterize PIC behavior.