Development and Validation of Early Warning Score System: A Systematic Literature Review

Abstract

Objectives

This review aims to: 1) evaluate the quality of model reporting, 2) provide an overview of methodology for developing and validating Early Warning Score Systems (EWSs) for adult patients in acute care settings, and 3) highlight the strengths and limitations of the methodologies, as well as identify future directions for EWS derivation and validation studies.

Methodology

A systematic search was conducted in PubMed, Cochrane Library, and CINAHL. Only peer reviewed articles and clinical guidelines regarding developing and validating EWSs for adult patients in acute care settings were included. 615 articles were extracted and reviewed by five of the authors. Selected studies were evaluated based on the Transparent Reporting of a multivariable prediction model for Individual Prognosis Or Diagnosis (TRIPOD) checklist. The studies were analyzed according to their study design, predictor selection, outcome measurement, methodology of modeling, and validation strategy.

Results

A total of 29 articles were included in the final analysis. Twenty-six articles reported on the development and validation of a new EWS, while three reported on validation and model modification. Only eight studies met more than 75% of the items in the TRIPOD checklist. Three major techniques were utilized among the studies to inform their predictive algorithms: 1) clinical-consensus models (n=6), 2) regression models (n=15), and 3) tree models (n=5). The number of predictors included in the EWSs varied from 3 to 72 with a median of seven. Twenty-eight models included vital signs, while 11 included lab data. Pulse oximetry, mental status, and other variables extracted from electronic health records (EHRs) were among other frequently used predictors. In-hospital mortality, unplanned transfer to the intensive care unit (ICU), and cardiac arrest were commonly used clinical outcomes. Twenty-eight studies conducted a form of model validation either within the study or against other widely-used EWSs. Only three studies validated their model using an external database separate from the derived database.

Conclusion

This literature review demonstrates that the characteristics of the cohort, predictors, and outcome selection, as well as the metrics for model validation, vary greatly across EWS studies. There is no consensus on the optimal strategy for developing such algorithms since data-driven models with acceptable predictive accuracy are often site-specific. A standardized checklist for clinical prediction model reporting exists, but few studies have included reporting aligned with it in their publications. Data-driven models are subjected to biases in the use of EHR data, thus it is particularly important to provide detailed study protocols and acknowledge, leverage, or reduce potential biases of the data used for EWS development to improve transparency and generalizability.

1. Introduction

In the United States, over 200,000 patients die in the hospital each year due to cardiac arrest.[1] Additionally, an estimated 14% to 28% of ICU admissions are unplanned transfers to the ICU.[2] These outcomes are considered clinical deterioration events and many hospital practices are directed towards intervening before they occur. Multiple studies provide evidence that patients usually develop physiological instability preceding clinical deterioration.[3, 4] In response, early warning scores (EWSs) have been developed to assist clinicians in recognizing signs of early physiological deterioration, allowing them to intervene in a timely manner and provide more intensive care. EWSs generally take routinely measured physiological measurements (e.g., vitals signs, lab data) as input and evaluate patients’ risk of developing clinical deterioration events as output. When a patient’s score passes a certain threshold, an alarm may be sent to the corresponding clinicians for further evaluation and intervention.

The concept of EWSs dates back to the late 1990s when five physiological parameters were utilized for bedside evaluation: 1) systolic blood pressure, 2) pulse rate, 3) respiratory rate, 4) temperature, and 5) mental status based on expert opinion.[5] Developed by Subbe et al., the Modified Early Warning Score (MEWS) became one of the most cited models.[6] To date, EWSs are widely used internationally and various algorithms have been published. Several literature reviews compare and validate the predictive power of existing EWSs and their effects on clinical outcomes.[7–12] Since the development of MEWS, many more EWSs built with more complex statistical learning algorithms have been published. The Transparent Reporting of a multivariable prediction model for Individual Prognosis Or Diagnosis (TRIPOD) statement was published in 2015 in response to the rapid growth of clinical prediction models as well as the incomplete reporting of model development and validation studies. TRIPOD provides detailed guidance on the 37 key items to report in studies of developing, validating, or updating clinical prediction models.[13, 14] Complete reporting of research facilitates reproducibility of models, appraisal of model validity, and judgement of model generalizability to other clinical settings.[15] Given the evolving science, a thorough review of methods for developing and validating EWSs must first be conducted, and yet, such a systematic review does not exist to date. This review aims to: 1) evaluate the quality of model reporting, 2) provide an overview of methodology for developing and validating EWSs for adult patients in acute care settings, and 3) highlight the strengths and limitations of the methodologies, as well as identify future directions for EWS derivation and validation studies.

2. Material and Methods

To include all relevant scientific literature, a systematic search was performed within the PubMed, CINAHL, and Cochrane Library databases from their date of inception to March 2^nd, 2019. Search terms included free-text as well as controlled terms from MeSH in PubMed, and free-text only in Cochrane Library and CINAHL. A broad search strategy was applied in an attempt to include all available literature regarding EWSs. Search terms with wild cards “warning scor*” OR “warning system*” were used in combination with “validat*” (see Figure 1: search strategy). The results of the search were stored and managed in EndNote X9 (Thomson Reuters, New York, NY).

Figure 1.

PubMed search strategy

2.1. Study Selection

All potentially relevant titles and abstracts were independently screened by five reviewers (LH, AM, JS, MK, JG) for eligibility. Studies were included based on the following criteria: (i) the study used physiological measurements from adult human subjects in acute care units, (ii) the study was related to the development and validation of an EWS system, and (iii) the study was a peer-reviewed publication. Studies were excluded if they were: (i) studies restricted to pediatric, obstetric, or intra-operative units, or restricted to trauma patients or patients in an ICU or emergency room, (ii) studies restricted to a subgroup of patients with specified primary diseases, (iii) qualitative or implementation evaluation studies, (iv) pure validation studies testing an existing EWS without modification, (v) not accessible for full-text review, or (vi) not written in English. Studies selected by at least one reviewer were subjected to a full-text review, and consensus was reached by discussion. In addition, reference lists of selected literature and clinical guidelines were reviewed to identify studies that were not covered by initial search terms.

2.2. Analysis of EWS Development and Validation

Studies that met inclusion and exclusion criteria were first evaluated using the TRIPOD checklist.[14] We focused our analysis on study design, predictor selection, outcome measurement, modeling methodology, and validation strategy. In addition, we categorized the selected models into three classes by their scoring methods: unweighted activation criteria, aggregated weighted scores, and complex computerized scores. The unweighted activation criteria category was composed of a list of physiological criteria where one or more out-of-range variable(s) could trigger the activation. The aggregated weighted score is a multivariable function where vital signs and other predictors are categorized into different levels of abnormality and are assigned point values. The weighted model returns an aggregated score and is easy to calculate manually. The final class was comprised of complex computerized models, including more recently developed EWSs that used more complex statistical and machine learning methodologies. These models usually included feature engineering and are often not feasible to calculate manually.

3. Results

3.1. Search Results

The search generated a total of 615 references from PubMed (n=282), CINAHL (n=125), and Cochrane Library (n=208). Five-hundred thirty unique references were identified after removing duplicates. Since we were only interested in literature regarding the development and validation of EWSs, 471 references were excluded after screening titles and abstracts based on our criteria. Fifty-nine publications were considered relevant and were subjected to a full-text review. Twenty-nine were included for final analysis. The flowchart displays our search and selection process as recommended by PRISMA guidelines (Figure 2).[16]

Figure 2:

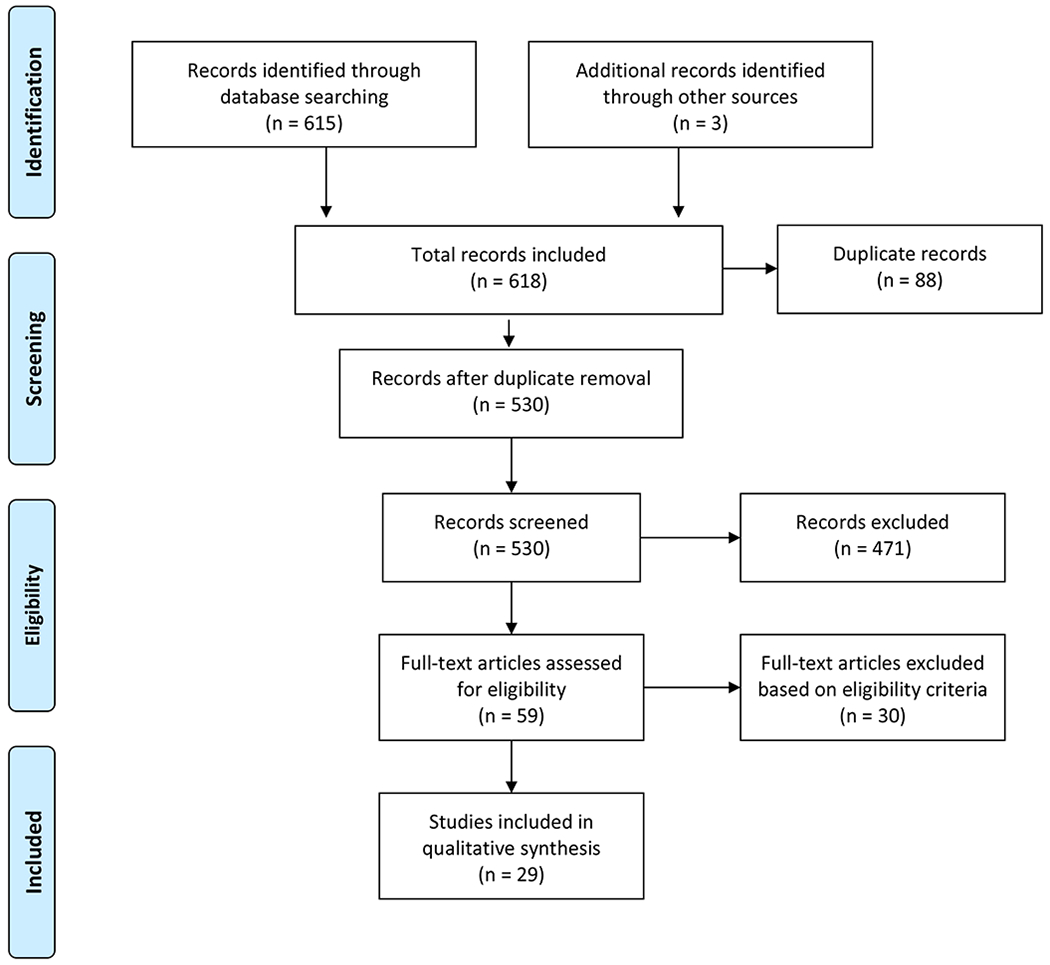
Search Diagram

3.2. Results of EWS Development and Validation Analysis

In total, 29 studies were included in our analysis (Table 1). Twenty-six were development and validation studies[6, 18, 20, 22–44] and three were validation studies of model modification.[17, 19, 21] Twenty-nine distinct EWSs, all published after the year 2000, were identified.

Table 1.

Overview of papers describing EWS development and validation

Authors	Study Design	Model Type Model Name	Participant Sample Size (n)	Outcomes
Expert opinion
Subbe et al. (2001) [6]	Prospective cohort study; Single center	Aggregated weighted score; MEWS	Medical emergency admissions; n = 673	Mortality, ICU and HDU transfer, cardiac arrest, survival and hospital discharge; 60 days from admission
Cretikos et al. (2007) [17]	Nested, matched case-control study; Multicenter	Unweighted activation criteria; Modified MET	General ward, CCU or HDU; 450 cases - 520 matched cases	Mortality, unplanned ICU admission, cardiac arrest; within 24 hrs of observation
Prytherch et al. (2010) [18]	Retrospective cohort study; Single center	Aggregated weighted score; ViEWS	Medical emergency admissions; n = 35585	Mortality; within 24 hrs of observation
Kellett et al. (2012) [19]	Retrospective cohort study; Single center	Aggregated weighted score; Abbreviated ViEWS	General Ward, ICU; n = 75419	Mortality; within 48 h of admission
Royal College of Physicians (2012) [20]	Retrospective cohort study; Single center	Aggregated weighted score; NEWS	Medical emergency admissions; n = 35585	Mortality; within 24 hrs of observation
Luis et al. (2018) [21]	Prospective cohort study; Single center	Aggregated weighted score; Short NEWS	General Ward; n = 330	Composite outcome: Mortality or Unplanned ICU admission; within 24 hrs of observation
Data-Driven
Duckitt et al. (2007) [22]	Retrospective cohort study; Single center	Aggregated weighted score; WPSS	Medical emergency admissions; n = 3184 (D); n = 1102 (V)*	Mortality; in-hospital
Cuthbertson et al. (2007) [23]	Comparative Cohort study; Single center	Computerized score	Surgical high-dependency units; 67 cases - 69 control	Unplanned ICU admission; in-hospital
Cuthbertson et al. (2010) [24]	Comparative Cohort study; Single center	Computerized score	Medical ward / respiratory unit; 61 case - 230 control / 68 case - 107 control	Unplanned ICU admission; in-hospital
Bleyer et al. (2011) [25]	Retrospective cohort study; Single center	Unweighted activation criteria	General ward; n = 42430	Mortality; in-hospital
Tarassenko et al. (2011) [26]	Retrospective cohort study; Multicenter	Aggregated weighted score; CEWS	Mixed database of medical and surgical ward, progressive care unit, and trauma step-down unit; n = 863	N/A
Churpek et al. (2012) [27]	Retrospective cohort study; Single center	Aggregated weighted score; CART	General Ward; n = 47427	Cardiac arrest, Unplanned ICU admission; within 48 hrs of observation
Escobar et al. (2012) [28]	Retrospective case-control study; Multicenter	Computerized score;	General Ward n = 130627 (Down sampling: 4036 events shift - 39782 control shift)	Unplanned ICU admission, Mortality; 24 hrs preceding the 12-hrs shift
Alvarez et al. (2013) [29]	Retrospective cohort study; Single center	Computerized score	Medical ward; 7466 patient, 46,974 patient-days.	Mortality, resuscitation events; within 24 hrs of observation
Jarvis et al. (2013) [30]	Retrospective cohort study; Single center	Aggregated weighted score; LDT-EWS	Medical ward; n = 86472	Mortality; in-hospital
Kirkland et al. (2013) [31]	Retrospective case-control study; Single center	Computerized score	Medical ward; n = 1882(D); n = 1946(V)*	Mortality, Unplanned ICU admission, or RRT call; within 48 hrs of observation
Mohammed et al. (2013) [32]	Retrospective cohort study; Single center	Computerized score	Emergency admissions; n = 23248	Mortality; in-hospital
Badriyah et al. (2014) [33]	Retrospective cohort study; Single center	Aggregated weighted score; DTEWS	Medical emergency admissions; n = 35585	Composite outcome: cardiac arrest, Unplanned ICU admission, Mortality; within 24 hrs of observation
Churpek et al. (2014) [34]	Retrospective cohort study; Single center	Computerized score	General Ward; n = 59301	Cardiac arrest, Unplanned ICU admission; within 48 hrs of observation
Churpek et al. (2014) [35]	Retrospective cohort study; Multicenter	Computerized score; eCART	General Ward; n = 269999	Composite outcome: cardiac arrest, Unplanned ICU admission, Mortality; within 24 hrs of observation
Churpek et al. (2016) [36]	Retrospective cohort study; Multicenter	Computerized score	General Ward; n = 269999	Composite outcome: cardiac arrest, Unplanned ICU admission, Mortality; within 24 hrs of observation
Churpek et al. (2016) [37]	Retrospective cohort study; Multicenter	Computerized score	General Ward; n = 269999; 10,309 time-windows with adverse events were randomly matched to 10,309 non-event windows	Composite outcome: cardiac arrest, Unplanned ICU admission, Mortality; within 24 hrs of observation
Kipnis et al. (2016) [38]	Retrospective cohort study; Multicenter	Computerized score; AAM	General Ward; n = 649418	Unplanned ICU admission, Mortality; within 24 hrs of observation
Moore et al. (2017) [39]	Retrospective cohort study; Multicenter	Aggregated weighted score; UVA	General Ward; n = 5573	Mortality; in-hospital
Dziadzko et al. (2018) [40]	Retrospective cohort study; Multicenter	Computerized score; APPROVE	General Ward; n = 68775 (I); n = 2258(E)$	Composite outcome: Mortality or intubation with MV > 48hrs; within 48hrs of observation
Faisal et al. (2018) [41]	Retrospective cohort study; Multicenter	Computerized score; CARM	Medical emergency admissions; n = 30996(I); n = 26247(E)	Mortality; in-hospital
Ghosh et al. (2018) [42]	Retrospective cohort study; Single center	Computerized score; EDI	General Ward; n = 14,282	Mortality, Unplanned ICU admission; within 24 hrs of observation
Redfern et al. (2018) [43]	Retrospective cohort study; Multicenter	Aggregated weighted score; LDTEWS-NEWS	Medical emergency admissions; n = 97933(I) ; n = 21028(E)	Composite outcome: Mortality or Unplanned ICU admission; within 24 hrs of observation
Watkinson et al. (2018) [44]	Retrospective cohort study; Multicenter	Aggregated weighted score; mCEWS	General Ward; n = 12153(V) ; n = 53395(D)	Composite outcome: cardiac arrest, Unplanned ICU admission, Mortality; within 24 hrs of observation

Authors	Predictors	Statistical Methods	Validation Performance assessment
Expert opinion
Subbe et al. (2001) [6]	SBP, PR, RR, BT, AVPU; Highest score within five days of admission for model validation	Clinical consensus-based model	Risk of death (OR 5.4, 95%CI 2.8–10.7), ICU admission (OR 10.9, 95%CI 2.2–55.6) and HDU admission (OR 3.3, 95%CI 1.2–9.2) at threshold of 5.
Cretikos et al. (2007) [17]	RR(U), HR(U), SBP(L)#, GCS;	Clinical consensus-based model	Apparent validation; AUC: 0.77(0.74—0.79); Against MET’s AUC: 0.71(0.69—0.74)
Prytherch et al. (2010) [18]	PR, SBP, RR, BT, SpO2, O2, AVPU; Final set of observation for derivation	Clinical consensus-based model	Apparent validation; AUC: 0.888(0.880–0.895); best against other 33 EWSs; efficiency curve
Kellett et al. (2012) [19]	PR, SBP, RR, BT, SpO2, O2	Clinical consensus-based model	AUC for all patients: 0.93; for medical patients: 0.89; for ICU patients: 0.73
Royal College of Physicians (2012) [20]	PR, SBP, RR, BT, SpO2, O2, AVPU	Clinical consensus-based model	Apparent validation; AUC: 0.89(0.880–0.895)
Luis et al. (2018) [21]	RR, PR, SBP, SpO2, O2, AVPU;	Multivariable logistic regression; Univariable logistic regression used for predictor selection; Developed two new aggregated scales	AUC for two modified models: 0.965 and 0.903, respectively
Data-Driven
Duckitt et al. (2007) [22]	BP, HR, SpO2, RR, AVPU; First observation for model derivation	Generalized additive model with a non- parametric spline smoother; Variables were partitioned by identifying cut-off points using the method of O’Brien; Weights were assigned according to the regression coefficients	Calibration: Hosmer-Lemeshow goodness-of-fit test; Temporally split validation set; AUC: 0.72(0.66–0.79), sensitivity: 0.63, specificity: 0.72 at threshold of 3 Apparent validation; AUC: 0.88(0.86—0.90); MEWS AUC: 0.85(0.83—0.86) Apparent validation; AUC for medical cohort: 0.91; AUC for respiratory cohort: 0.85 Apparent validation; AUC: 0.851; Against VIEWS’ AUC 0.862; MEWS’ 0.865 N/A
Cuthbertson et al. (2007) [23]	PR, RR, SpO2; Median of each variable were used for modeling	Linear discrimination analysis; Univariable logistic regression for predictor selection
Cuthbertson et al. (2010) [24]	PR, RR, SpO2; Median of each variable were used for modeling	Linear discrimination analysis; Univariable logistic regression for predictor selection
Bleyer et al. (2011) [25]	SBP, HR, BT, SpO2, RR, Level of consciousness	Multivariate logistic regression with backward elimination
Tarassenko et al. (2011) [26]	HR, RR, SpO2, SBP	Gaussian Kernel; Normalized histogram for each vital sign; Cut-off value and weights were set by centiles
Churpek et al. (2012) [27]	RR, PR, DBP, pulse pressure index (PPI), age; Max and Min values for model derivation; Missing value: impute with most recent or a normal value	Stepwise multivariable logistic regression with backwards elimination (AIC); Variables cut-off thresholds were chosen from locally weighted least squares regression (LOWESS) and refined by univariable analysis combining categories with similar odds ratio	Apparent validation; AUC: 0.84; Against MEWS’ AUC 0.76 for predicting cardiac arrest; AUC: 0.71; Against MEWS’ AUC 0.67 for predicting unplanned ICU transfer
Escobar et al. (2012) [28]	PR, SBP, DBP, RR, SpO2, BT, trend term (HR variability), level of consciousness, BUN, Lac, Hc, COPS (12months), LAPS (72hrs), sex, LOS, care directives; Missing data (<3%): drop NA shift or impute with mean	Multivariable logistic regressions on subgroups	Randomly split validation set; AUC: 0.775; Against MEWS’ AUC 0.698; Performed best in cohort of gastrointestinal diagnoses (0.841; 0.783–0.897) and worst among cohort of congestive heart failure (0.683; 0.610–0.755)
Alvarez et al. (2013) [29]	MEWS, SpO2, DBP, PCO2, K, WBC, Plt, AST, ABG, Age, EKG, Stat order, High risk floor assignment; Most abnormal values 24 hours prior to event day for model derivation; Missing data: compare and pool in values from appropriate reference group	Multivariable logistic regression Univariable logistic regression with spline and variable transformation for fitting non-linear variables Variable cut-off thresholds were set by recursive partitioning.	Calibration: Hosmer-Lemeshow goodness-of-fit test; AUC: 0.85 (0.82-0.87); sensitive: 51.6%, specific: 94.3%, PPV: 10%; Against MEWS’ AUC: 0.75 (0.71-0.78)
Jarvis et al. (2013) [30]	Hb, WBC, BUN, Alb, Cr, Na, K, Sex; Observation set within 24 hours of admission for model derivation	Decision trees; Each variable was recursively partitioned independently into decision tree and refined by combining categories with similar risk ratio	Temporally split validation sets; AUC (best): 0.801 (0.776–0.826); efficiency curve
Kirkland et al. (2013) [31]	RR, SpO2, Braden Scale, shock index (HR/SBP);	Multivariable logistic regressions with backward elimination; Generalized additive models using a cubic spline and univariable logistic regression with generalized estimating equations approach for predictors selection	Temporally split validation sets; AUC: 0.71 (0.68-0.74)
Mohammed et al. (2013) [32]	NEWS, age, Alb, Na, WBC, BUN; First set of observation for model derivation	Empirical decision tree models	Randomly split validation set; AUC: 0.853 (0.840 to 0.866);
Badriyah et al. (2014) [33]	PR, SBP, RR, BT, AVPU, SpO2, O2 supplement;	Decision trees; Each variable was recursively partitioned independently into decision tree and refined by combining categories with similar risk ratio; Weights were assigned according to the risk ratio	Apparent validation; AUC: 0.708 (0.669–0.747); Against NEWS’ AUC 0.722 (0.685–0.759) for predicting cardiac arrest; AUC: 0.862 (0.852–0.872); Against NEWS’ AUC 0.857 (0.847–0.868) for predicting unplanned ICU transfer; AUC: 0.899 (0.892–0.907); Against NEWS’ AUC 0.894 (0.887–0.902) for predicting mortality; AUC: 0.877 (0.870–0.883); Against NEWS’ AUC 0.873 (0.866–0.879) for predicting composite outcomes; efficiency curve
Churpek et al. (2014) [34]	RR, DBP, PR, SpO2, O2, level of consciousness, BT, Hb, Plt, WBC, BUN, K, AG, time, age, prior ICU admission; Variable values at the beginning of each time block were used for model derivation	Discrete time multinomial logistic regression model (8-hour time period) with backward selection;	Cross-validation; AUC: 0.88; Against ViEWS’ AUC 0.78 for predicting cardiac arrest; AUC: 0.77; Against ViEWS’ AUC 0.73 for predicting unplanned ICU transfer; efficiency curve
Churpek et al. (2014) [35]	BT, PR, SBP, DBP, RR, SpO2, AVPU; WBC, Hb, Plt, Na, K, Cl, HCO2, AG, BUN, Cr, Glu, Ca, TP, Alb, T.bil, AST, ALKP, age, number of prior ICU, LOS; Variable values at the beginning of each time block were used for model derivation; Missing value: previous data or median	Discrete time logistic regression model (8-hour time period); Fit non-linear variables with linear splines; Predictor selection by collinearity and backward elimination; Up-sampling for cardiac arrest patients by factor of 25	Temporally split validation set AUC: 0.83 (0.82–0.83); Against MEWS’ AUC 0.71 (0.70–0.73) for predicting cardiac arrest; AUC: 0.74 (0.74–0.75); Against MEWS’ AUC 0.68 (0.68–0.68) for predicting unplanned ICU transfer; AUC: 0.93 (0.93–0.93); Against MEWS’ AUC 0.88 (0.88–0.88) for predicting mortality; AUC: 0.77 (0.76–0.77); Against MEWS’ AUC 0.70 (0.70–0.70) for predicting composite outcomes; Net reclassification improvement (NRI): 0.28 (0.18–0.38)
Churpek et al. (2016) [36]	BT, PR, SBP, DBP, RR, SpO2, trend (delta, mean, standard deviation, slope, min, max, smoothed curve); Variable values at the beginning of each time block were used for model derivation; Missing value: previous data or median	Discrete time logistic regression model (4-hour time period); Trend variables: change in current value from the previous value (delta), mean of the previous six values (mean), standard deviation of the previous six values (SD), slope of the previous six values (slope), minimum value prior to current value (minimum), maximum value prior to current value (maximum), and an exponential smoothing method (smoothed) Restricted cubic splines with three knots, with knot placement; Univariable models: predictor trend variables alone; Bivariable models: trend variables plus the variables current value; Full model: the current value and all trend variables for each vital sign	Temporally split validation set Full model’s AUC: 0.78; Against model of only current value AUC: 0.74
Churpek et al. (2016) [37]	BT, PR, SBP, DBP, RR, SpO2, AVPU; WBC, Hb, Plt, Na, K, Cl, HCO2, AG, BUN, Cr, Glu, Ca, TP, Alb, T.bil, AST, ALKP, age, number of prior ICU, LOS, two-way interaction; Variable values at the beginning of each time block were used for model derivation; Missing data: forward fill or median	Discrete time analysis model (8-hour time period); Down-sampling: 10,309 time windows with adverse events - 10,309 non-event windows for model derivation; Multiple models were built and compared: random forest, gradient boosted machine, bagged-tree model, logistic regression with restricted cubic splines with three knots, simple logistic regression, k-nearest neighbors, support vector machines, and neural network	Calibration: Hosmer-Lemeshow goodness-of-fit test, Cox calibration; Temporally split validation set Random forest AUC 0.80 (0.80–0.80); Against MEWS’ AUC 0.70 (0.70-0.70)
Kipnis et al. (2016) [38]	SBP, DBP, PR, SpO2, RR, BT, level of consciousness, Trend; AG, HCO3, Glu, Lac, BUN, Cr, Trop, Na, WBC; COPS(12months), LAPS(72hrs), sex, LOS, care directives; Missing data: forward fill or median	Discrete time logistic regression model with backwards selection (1-hour time period); Variable transformation Down-sampling: all events episode to 10 times of uneventful episodes for model derivation; Truncated episodes with a length of stay greater than 15 days (3% of all episodes)	Calibration: Hosmer-Lemeshow goodness-of-fit test; Temporally split validation set; AUC 0.82; Against eCART’s AUC 0.79, NEWS’ 0.76; efficiency curve
Moore et al. (2017) [39]	BT, PR, RR, SBP, SpO2, GCS, HIV serostatus; Missing values: k-nearest neighbors single imputation method	Multivariable logistic regression; Univariable logistic regression with cut-off thresholds set by recursive partitioning used for predictor selection	Calibration: Brier score; Cross-validation; AUC: 0.77 (0.75 to 0.79); Against MEWS’ AUC 0.70 (0.67 to 0.71), qSOFA’s AUC 0.69 (0.67 to 0.72)
Dziadzko et al. (2018) [40]	PR, SBP,DBP, RR, BT, SpO2, O2, RASS; AG, pCO2, pO2, pH, HCO3, BUN/Cr, Hc, Hb, Lac, Alb, Ca, Cl, Glu, Na, K, T.bil, WBC; Age, Sex, Weight, Height, BMI; (transformation); A randomly selected observation over the hospital stay of each patient were used for model derivation; Missing data: imputed using a random forest algorithm to match patients having known values	Random forest model	External validation set; AUC: 0.86 (0.73–0.94) for predicting machine ventilation > 48 hours; AUC: 0.93 (0.89-0.97) for predicting mortality; Performed similarly against MEWS and NEWS; PPV 16%
Faisal et al. (2018) [41]	RR, PR, SBP, DBP, BT, SpO2, O2, AVPU; Cr, K, WBC, BUN, AKI score; age, sex; (transformation); First set of observation for model derivation	Multivariable logistic regression; Variable transformation and automatic selection of two-way interaction terms	Calibration: Hosmer-Lemeshow goodness-of-fit test; External validation; AUC: 0.86 (0.85 - 0.87)
Ghosh et al. (2018) [42]	PR, RR, SBP, BT, SPO2, age;	Naive Bayes classification; Risk curve generated for each variable and score by summing up the probabilities	Temporally split validation set; AUC: 0.7655; Against NEWS’ AUC: 0.6569, MEWS’ 0.6487
Redfern et al. (2018) [43]	NEWS, LDTEWS Using the most recent value of each variable at most 5 days or zero	Linear combination of two established EWS; Combined LDT-EWS and NEWS values using a linear time-decay weighting function; Weight chosen by grid-search approach	Calibration: Hosmer-Lemeshow goodness-of-fit test; External validation; AUC: 0.901 (0.898–0.905); Against NEWS’ AUC: 0.877 (0.873–0.882)
Watkinson et al. (2018) [44]	PR, SBP, RR, BT, AVPU, SpO2, O2 supplement; Missing data: more than two missing excluded imputed with population mean	Kernel-based density estimator; A smooth estimation of the distribution of each vital sign; Cut-off value and weights were set by centiles	Temporally split validation set; AUC: 0.868 (0.864–0.872); Against NEWS’ AUC: 0.867 (0.863–0.871)

HDU: high dependency unit; CCU: coronary care unit; RRT: rapid response team

AAM: Advanced Alert Monitor; APPROVE: Accurate Prediction of Prolonged Ventilation; CARM: Computer-Aided Risk of Mortality; CART: Cardiac Arrest Risk Triage; CEWS: centile-based EWS; DTEWS: Decision-tree early warning score; EDI: Early Deterioration Indicator; LDT-EWS: Laboratory Decision Tree EWS; MET: Medical Emergency Team; MEWS: Modified Early Warning Score; NEWS: National Early Warning Score; UVA: Universal Vital Assessment; ViEWS: VitalPACTM EWS; WPSS: Worthing Physiological Scoring System; eCART: electronic Cardiac Arrest Risk Triage; mCEWS: manual centile-based EWS

^*D: derivation set; V: validation set

^$I: internal database; E: external database

ABG: arterial blood gas; AKI: acute kidney injury; ALKP: alkaline phosphatase; AST: aspartate aminotransferase; AVPU: The Alert Verbal Painful Unresponsiveness scale; Alb: albumin; BMI: body mass index; BT: body temperature; BUN: blood urea nitrogen; COPS: Comorbidity Point Score; Ca: calcium; Cl: chloride; Cr: creatinine; DBP: diastolic blood pression; EKG: electrocardiogram; GCS: Glasgow Coma Scale; Glu: glucose; HCO2: formate ion, AG: anion gap; Hb: hemoglobin; Hc: hematocrit; K: potassium; LAPS: Laboratory-based Acute Physiology Score; LOS: length of stay; Lac: lactate; Na: sodium; O2: oxygenation; PR: pulse rate; Plt: platelet; RASS: The Richmond Agitation and Sedation Scale; RR: respiratory rate; SBP: systolic blood pressure; SpO2: saturation; T.bil: total bilirubin; TP: total protein; Trop: troponin; WBC: white blood cell

^#U: upper limit; L: lower limit

3.2.1. Reporting of Clinical Prediction Models

Of the 29 studies, only eight[17, 28, 38–41, 43, 44] met more than 75% of the items in the TRIPOD checklist, and two of those studies were published before the TRIPOD publication. In total, 19 studies were published before TRIPOD’s publication in 2015. Three studies explicitly stated that they followed the TRIPOD checklist to report their research. TRIPOD items from the abstract, introduction, source of data, participants, model performance, and discussion sections were reported in more than 75% of the studies. Items from the sample size and participants sections were reported in less than 25% of the studies (Table 2).

Table.2 –

TRIPOD Checklist

		Subbe 2001 [6]	Cretikos 2007 [17]	Duckitt 2007 [22]	Cuthbertson 2007 [23]	Prytherch 2010 [18]	Cuthbertson 2010 [24]	Bleyer 2011 [25]	Tarassenko 2011 [26]	Kellett 2012 [19]	Churpek 2012 [27]	Escobar 2012 [28]	RCP 2012 [20]	Alveraz 2013 [29]	Jarvis 2013 [30]	Kirkland 2013 [31]	Mohammed 2013 [32]	Badriyah 2014 [33]	Churpek 2014 [34]	Churpek 2014 [35]	Churpek 2016 [36]	Churpek 2016 [37]	Kipnis 2016 [38]	Moore 2017 [39]	Dziadzko 2018 [40]	Faisal 2018 [41]	Ghosh 2018 [42]	Luis 2018 [21]	Redfern 2018 [43]	Watkinson 2018 [44]
Model Type		D	V	D/V	D	D	D	D	D	V	D	D/V	D/V	D/V	D/V	D/V	D/V	D	D	D/V	D/V	D/V	D/V	D	D/V	D/V	D/V	V	D/V	D/V
Title and abstract
Title	1	0	0	0	0	0	0	0	0	0	0	1	0	0	1	0	1	0	0	0	0	0	1	1	1	1	0	0	1	0
Abstract	2	1	1	1	0	1	0	1	0	1	1	1	1	1	1	0	1	1	1	1	1	1	1	1	1	0	1	0	1	1
Introduction
Background and objectives	3a	1	1	1	1	1	1	1	0	1	1	1	1	1	1	1	1	1	1	1	1	1	1	1	1	1	1	1	1	1
	3b	1	1	1	1	1	1	1	1	1	1	1	1	1	1	1	1	1	1	1	1	1	1	1	1	1	1	1	1	1
Methods
Source of data	4a	1	1	1	1	1	1	1	1	1	1	1	1	1	1	1	1	1	1	1	1	1	1	1	1	1	1	1	1	1
	4b	1	1	1	1	1	1	1	1	1	1	1	0	1	1	1	1	1	1	1	1	1	1	1	1	1	1	1	1	1
Participants	5a	1	1	1	1	1	1	1	1	1	1	1	1	1	1	1	1	1	1	1	1	1	1	1	1	1	1	1	1	1
	5b	1	1	1	0	1	0	1	0	0	1	1	0	1	1	1	1	1	0	0	0	0	1	0	1	1	0	1	1	1
	5c	NA	NA	NA	NA	NA	NA	NA	NA	NA	NA	NA	NA	NA	NA	NA	NA	NA	NA	NA	NA	NA	NA	NA	NA	NA	NA	NA	NA	NA
Outcome	6a	1	1	0	1	1	1	0	0	0	1	1	1	1	0	1	0	1	1	1	1	1	1	0	1	1	0	1	1	1
	6b	NA	NA	NA	NA	NA	NA	NA	NA	NA	NA	NA	NA	NA	NA	NA	NA	NA	NA	NA	NA	NA	NA	NA	NA	NA	NA	NA	NA	NA
Predictors	7a	1	1	1	0	1	0	1	0	0	1	1	1	1	1	1	1	1	0	0	0	0	1	0	1	1	0	0	1	1
	7b	NA	NA	NA	NA	NA	NA	NA	NA	NA	NA	NA	NA	NA	NA	NA	NA	NA	NA	NA	NA	NA	NA	NA	NA	NA	NA	NA	NA	NA
Sample size	8	0	1	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0
Missing data	9	1a	1	1a	1	0	0	0	0	1a	1	1	0	0	0	0	1a	0	1	1	1	1	1	1	1	0	1	1a	1	1
Statistical analysis methods	10a	0	NA	1	1	1	1	1	1	NA	1	1	1	1	1	1	1	1	1	1	1	1	1	1	1	1	1	NA	1	1
	10b	1	NA	1	1	1	1	1	1	NA	1	1	1	1	1	1	1	1	1	1	1	1	1	1	1	1	1	NA	1	1
	10c	NA	1	1	NA	NA	NA	NA	NA	1	NA	1	1	1	1	1	1	NA	NA	1	1	1	1	NA	1	1	1	1	1	1
	10d	0b	0b	1	0b	0b	0b	0b	0	1	0b	0b	0b	1	0b	0b	0b	0b	0b	0b	0b	1	1	0b	0b	1	0b	1	1	1
	10e	NA	1	NA	NA	NA	NA	NA	NA	0	NA	NA	NA	NA	NA	NA	NA	NA	NA	NA	NA	NA	NA	NA	NA	NA	NA	1	NA	NA
Risk groups	11	NA	NA	NA	NA	NA	NA	NA	NA	NA	NA	NA	NA	NA	NA	NA	NA	NA	NA	NA	NA	NA	NA	NA	NA	NA	NA	NA	NA	NA
Development vs. validation	12	NA	0	1	NA	NA	NA	NA	NA	0	NA	0e	0	0e	0	1	0e	NA	NA	1	0	0	1	NA	1	1	1	0	1	1
Results
Participants	13a	0	0	0	0	0	0	0	0	0	0	1	0	0	0	0	0	0	0	0	0	0	0	1	0	1	0	0	1	0
	13b	0	1	1	0	0	0	0d	0	0d	0d	1	0	1	0	0	1	0	0	0	0	0	0d	1	1	0	0d	0d	0d	0d
	13c	NA	0	0	NA	NA	NA	NA	NA	0	NA	0e	0	0e	0	1	0e	NA	NA	1	0	0	1	NA	1	1	1	1	1	1
Model development	14a	0	NA	0	0	0	1	0	0	NA	1	1	0	1	0	0	0	0	0	1	0	0	1	1	1	1	1	NA	1	1
	14b	NA	NA	NA	1	NA	1	NA	0	NA	0	NA	NA	1	NA	1	NA	NA	NA	NA	0	NA	NA	NA	NA	NA	NA	NA	NA	NA
Model specification	15a	1	NA	1	1	1	1	1	1	NA	1	1	1	0f	1	1	1	1	0f	0f	0	0	0f	1	0	1	0	NA	1	1
	15b	1	NA	1	1	1	1	1	1	NA	1	1	1	0	1	1	1	1	0	0	0	0	0	1	0	1	0	NA	1	1
Model performance	16	1	1	1	1	1	0c	0c	0	1	0c	1	1	1	1	1	1	1	1	1	1	1	1	1	1	1	0c	1	1	1
Model-updating	17	NA	1	NA	NA	NA	NA	NA	NA	1	NA	NA	1	NA	NA	NA	NA	NA	NA	NA	NA	NA	1	NA	NA	NA	NA	1	NA	1
Discussion
Limitations	18	1	1	1	1	1	1	1	1	1	1	1	0	1	1	1	0	1	1	1	1	1	1	1	1	1	1	1	1	1
Interpretation	19a	NA	1	NA	NA	NA	NA	NA	NA	1	NA	NA	1	NA	NA	NA	NA	NA	NA	NA	NA	NA	NA	NA	NA	NA	NA	1	NA	1
	19b	1	1	1	1	1	1	1	1	1	1	1	1	1	1	1	1	1	1	1	1	1	1	1	1	1	1	1	1	1
Implications	20	1	1	1	1	1	1	1	1	1	1	1	1	1	1	1	1	1	1	1	1	0	1	1	1	1	1	1	1	1
Other information
Supplementary information	21	0	1	0	1	0	0	1	1	0	0	1	0	0	0	0	0	0	0	1	1	1	1	0	1	1	1	0	1	1
Funding	22	1	1	0	0	1	0	1	1	0	1	1	1	1	1	1	1	1	1	1	1	1	1	1	1	1	1	1	1	1

1: (D;V) Identify the study as developing and/or validating a multivariable prediction model, the target population, and the outcome to be predicted.

2: (D;V) Provide a summary of objectives, study design, setting, participants, sample size, predictors, outcome, statistical analysis, results, and conclusions.

3a: (D;V) Explain the medical context (including whether diagnostic or prognostic) and rationale for developing or validating the multivariable prediction model, including references to existing models.

3b: (D;V) Specify the objectives, including whether the study describes the development or validation of the model or both.

4a: (D;V) Describe the study design or source of data (e.g., randomized trial, cohort, or registry data), separately for the development and validation data sets, if applicable.

4b: (D;V) Specify the key study dates, including start of accrual; end of accrual; and, if applicable, end of follow-up.

5a: (D;V) Specify key elements of the study setting (e.g., primary care, secondary care, general population) including number and location of centres.

5b: (D;V) Describe eligibility criteria for participants.

5c: (D;V) Give details of treatments received, if relevant.

6a: (D;V) Clearly define the outcome that is predicted by the prediction model, including how and when assessed.

6b: (D;V) Report any actions to blind assessment of the outcome to be predicted.

7a: (D;V) Clearly define all predictors used in developing or validating the multivariable prediction model, including how and when they were measured.

7b: (D;V) Report any actions to blind assessment of predictors for the outcome and other predictors.

8: (D;V) Explain how the study size was arrived at.

9: (D;V) Describe how missing data were handled (e.g., complete-case analysis, single imputation, multiple imputation) with details of any imputation method.

10a: (D) Describe how predictors were handled in the analyses.

10b: (D) Specify type of model, all model-building procedures (including any predictor selection), and method for internal validation.

10c: (V) For validation, describe how the predictions were calculated.

10d: (D;V) Specify all measures used to assess model performance and, if relevant, to compare multiple models.

10e: (V) Describe any model updating (e.g., recalibration) arising from the validation, if done.

11: (D;V) Provide details on how risk groups were created, if done.

12: (V) For validation, identify any differences from the development data in setting, eligibility criteria, outcome, and predictors.

13a: (D;V) Describe the flow of participants through the study, including the number of participants with and without the outcome and, if applicable, a summary of the follow-up time. A diagram may be helpful.

13b: (D;V) Describe the characteristics of the participants (basic demographics, clinical features, available predictors), including the number of participants with missing data for predictors and outcome.

13c: (V) For validation, show a comparison with the development data of the distribution of important variables (demographics, predictors and outcome).

14a: (D) Specify the number of participants and outcome events in each analysis.

14b: (D) If done, report the unadjusted association between each candidate predictor and outcome.

15a: (D) Present the full prediction model to allow predictions for individuals (i.e., all regression coefficients, and model intercept or baseline survival at a given time point).

15b: (D) Explain how to the use the prediction model.

16: (D;V) Report performance measures (with CIs) for the prediction model.

17: (V) If done, report the results from any model updating (i.e., model specification, model performance).

18: (D;V) Discuss any limitations of the study (such as nonrepresentative sample, few events per predictor, missing data).

19a: (V) For validation, discuss the results with reference to performance in the development data, and any other validation data.

19b: (D;V) Give an overall interpretation of the results, considering objectives, limitations, results from similar studies, and other relevant evidence.

20: (D;V) Discuss the potential clinical use of the model and implications for future research.

21: (D;V) Provide information about the availability of supplementary resources, such as study protocol, Web calculator, and data sets.

22: (D;V) Give the source of funding and the role of the funders for the present study.

a: Complete-case analysis

b: Did not report calibration of models

c: Did not report confidence interval of AUC

d: Did not report the number of participants with missing data for predictors and outcome.

e: Randomly splitting a single data set into a development and a validation data set

f: Did not report intercept of the multivariable model

3.2.2. Study Designs

Twenty-two of the 29 models were developed utilizing a retrospective cohort study [18–20, 22, 25–27, 29, 30, 32–44] and 17 were conducted at a single center.[6, 18–25, 27, 29–34, 42] Fourteen models were derived from health records of general ward admissions.[17, 19, 21, 25, 27, 28, 34–40, 42, 44] Eleven models were limited to medical admissions only[6, 18, 20, 22, 24, 29–31, 33, 41, 43], while two studies extended their cohort to coronary care unit (CCU) or ICU patients.[17, 19] One study built a model based on surgical ward data.[23] The settings of the included studies varied from a single center containing several hundred beds to a multicentered health system encompassing 21 hospitals that provide healthcare to millions. Study cohort sizes varied greatly from hundreds[6, 17, 21, 23, 24, 26] to hundreds of thousands.[28, 35–38, 43]

3.2.3. EWS Development Approaches and Scoring Criteria

Three major techniques were utilized among the studies to inform their predictive algorithms: 1) clinical consensus (n=6)[6, 17–21], 2) regression models (n=15)[22–25, 27–29, 31, 34–36, 38, 39, 41], and 3) tree-based methods (n=5).[30, 32, 33, 37, 40]

Older EWSs were mainly developed using clinical consensus and informed by minimal statistical analysis. Well-known and widely used EWSs, such as the Medical Emergency Team activation criteria (MET), the Modified Early Warning Score (MEWS)[6], the VitalPAC Early Warning Score (ViEWS)[18], and the National Early Warning Score (NEWS)[20], were all developed according to that method. Three studies modified the existing clinical consensus models and validated them against original models.[17, 19, 21] Logistic regression[21, 22, 25, 27, 28, 39, 41] and linear discrimination analysis[23, 24] were found to be handy tools for binary classification. Six models utilized more flexible techniques, such as splines and the generalized additive model, to tackle non-linear relationships.[22, 29, 31, 35–37] The discrete time logistic regression, a survival analysis model, was used in five studies.[34–38] Decision trees were employed in three studies[30, 32, 33], while more advanced tree models using ensemble methods, such as bagging, boosting, and random forest, were utilized in two studies.[37, 40] Other statistical learning techniques, including Naive Bayes classification and Kernel-base density, were also applied for modeling in this review.[26, 42, 44] In total, we reviewed two studies that used unweighted activation criteria[17, 25], 13 studies that utilized aggregated weighted scores[6, 18–22, 26, 27, 30, 33, 39, 43, 44], and 14 studies that applied complex computerized scores.[23, 24, 28, 29, 31, 32, 34–38, 40–42]

3.2.4. EWS Predictors and Outcome Selections

The number of predictors included in the EWSs varied from 3 to 72 with a median of seven. Vital signs, like heart rate (n=28)[6, 17–32, 34–44], respiratory rate (n=28)[6, 17–32, 34–44], systolic blood pressure (n=24)[6, 17–22, 25, 26, 28, 29, 31–33, 35–44], diastolic blood pressure (n=13)[21, 27–29, 32, 34–38, 40, 41, 43], and body temperature (n=19)[6, 18–20, 25, 28, 29, 32, 33, 35–44], were commonly used as predictors. Three models used vital sign trends by studying the mean, standard deviation, maximum, minimum, or range of observations over a period of time.[28, 36, 38] Eleven studies utilized lab data for model derivation.[28–30, 32, 34, 35, 37, 38, 40, 41, 43] However, the lab items used varied greatly across studies. One model was derived purely on lab data[30], while two studies used the Laboratory-based Acute Physiology Score (LAPS), a composite score of 14 lab test results obtained in the 72 hours preceding hospitalization.[28, 38] Mental status (n=21)[6, 17, 18, 20–22, 25, 28, 29, 32–35, 37–44], pulse oximetry (SpO2) (n=25)[18–26, 28, 29, 31–44], and age (n=9)[27, 29, 34, 35, 37, 38, 40–42] were also frequently used in EWS models. More complex algorithms incorporated the comorbidity index[28, 38], length of stay[28, 34, 35, 37, 38], history of ICU stays[34, 35, 37], care directive status[28, 38], physician orders[29], and patient demographic data.[28, 38, 40, 41] Four studies applied feature engineering and used transformed terms as substitutes or in parallel to the originals.[28, 38, 40, 41] Only six studies reported predictor selection processes for their multivariable models. Three used simple backward selection[25, 34, 38], while the others utilized penalized model selection, such as Akaike information criterion (AIC)[27, 35] and Bayesian information criterion (BIC).[39]

In-hospital mortality (n=24)[6, 17–22, 25, 28–33, 35–44], unplanned transfer to the ICU (n=18)[6, 17, 21, 23, 24, 27–29, 31, 33–38, 42–44], and cardiac arrest (n=10)[6, 17, 27, 29, 33–37, 44] were the most commonly used clinical outcomes. In addition, Dziadzko et al. used respiratory failure requiring machine ventilation as a primary outcome[40], while Kirkland et al. included rapid response team (RRT) calls.[31] Ten studies used composite endpoints that included two or more outcomes.[21, 29, 31, 33, 35–37, 40, 43, 44] Outcome events within 24 hours or 48 hours preceding an observation were the most common timeframes established for evaluating outcomes (n=18).[17, 18, 20, 21, 27–29, 31, 33–38, 40, 42–44] The second most common timeframe was in-hospital mortality during a period of time following the time of admission (n=8).[6, 19, 22–25, 30, 32, 39, 41]

Several studies utilized a single set of observations for each patient at various time points for model training, like the first observation set since admission[22, 30], the maximum and minimum value of each vital sign within the 24 hours preceding outcomes[27], and a randomly chosen observation set per patient.[40] Kirkland et al.[31] used generalized estimating equations to account for multiple observations per patient while training logistic regression. Churpek et al.[34–36] and Kipnis et al.[38] introduced a discrete time logistic regression model for EWS derivation. This survival analysis approach involves fitting the occurrence of an outcome into discrete time intervals, taking the closest observation set to the beginning of each time interval for model training.

3.2.5. EWS Validation, and Performance Assessment

Twenty-eight studies conducted model validation either within study or against other widely-used EWSs.[6, 17–25, 27–44] Eight studies validated their model on the same dataset used for model derivation.[17, 18, 20, 23–25, 27, 33] Three studies also validated their model on the same dataset, but employed an internal validation technique, such as cross-validation[34, 39] or bootstrapping.[41] Four studies randomly split the dataset into a derivation set and a validation set.[28, 29, 32, 40] Ten studies validated their model on temporally-split datasets[22, 30, 31, 35–38, 42–44], while three studies additionally validated their model using an external database separate from the derivation database.[40, 41, 43]

Area Under the Curve (AUC) and Receiver Operating Characteristics (ROC) curves were the most widely used methods to assess model performance(n=28).[6, 17–25, 27–44] Seven studies used a decision curve or positive predictive value to evaluate the effectiveness of detecting a true positive case.[18, 28–30, 33, 34, 38]

4. Discussion

4.1. TRIPOD and Model Reporting

This systematic review identified 29 distinct EWSs that support early detection of clinical deterioration events in the adult acute care setting. Sufficiently detailed key information on how a model is built and validated is essential in order to appraise the risk of bias and generalizability of each published model, and to subsequently encourage reproducibility of results and the applicability of a model to other clinical settings. However, we found that only TRIPOD items from the abstract, introduction, source of data, participants, model performance, and discussion were generally well-reported. Similar findings were recorded by a recent study on clinical model reporting.[15] There is a need for greater awareness of the checklist, including awareness by journal editors and educational institutions. Only eight studies included in this review reported more than 75% of key information recommended by TRIPOD guidelines. Yet, we noted that two of those studies were published before the TRIPOD guidelines were published. Future studies are needed to evaluate the impact and limitations of the TRIPOD checklist on quality of clinical prediction model reporting.

4.2. From Clinical Consensus to Data-Driven Models

The characteristics of the cohort, predictors, outcome selection, as well as the metrics for model validation vary greatly across EWS studies. However, we found a paradigm shift in EWS development over the past two decades from clinical consensus to data-driven approaches. Five of the six models based on clinical consensus were built before 2013. Of the 24 data-driven models, 17 were published after 2013. Among clinical consensus models, the parameters and critical values were mainly set by existing knowledge of the relationship between physiology and adverse clinical events[4, 45, 46], literature review of previous EWSs[12], and clinical practice recommendations as well as meaningfulness.[47] The ViEWS study reported that the critical value and weighting for each of the parameters were then adjusted based on model performance.[18] Conversely, data-driven models rely on statistical methods for feature selection, engineering, and model derivation, which are often associated with increased complexity and flexibility. The performance of data-driven models is therefore strongly influenced by the database from which it derives. For instance, the Decision-Tree Early Warning Score (DTEWS) did not assign weights to low respiratory rate and set the critical value considerably high for high blood pressure compared to the NEWS. Such values were likely caused by low prevalence in the study cohort.[33] Data-driven approaches reflect the characteristics of a given dataset, while clinical consensus models consider the clinical importance of given values. The difference between the two approaches is also reflected in their modeling strategies. Earlier clinical consensus models were designed as paper-based standardized scoring systems aimed to be generalizable across all hospitals. Since patient care varies greatly between healthcare systems, researchers built parsimonious models based on measurements routinely collected in daily patient care across most healthcare systems. Therefore, such simple models could be easily adapted, and were shown to have acceptable generalizability on external databases in various validation studies.[9, 48, 49] Thus, they are commonly used as benchmarks in EWS validation. The NEWS further provides guidance for educational programs and implementation of standardized clinical response mechanisms according to the score.[20]

4.3. Approaches to Data-Driven EWS Derivation

Increasing availability of data and computational power in the past decade has allowed researchers to train models on larger datasets, with more predictors, and with more complex statistical and machine learning methods. The 2009 Health Information Technology for Economic and Clinical Health (HITECH) Act, which includes the concept of meaningful use of electronic health records, promoted the adoption and use of EHRs throughout healthcare systems in the United States. There was a significant increase in EHR integration from 2010 to 2013.[50] Escobar et al[28] and Kipnis et al[38] utilized huge databases that stored hundreds of thousands of general ward admissions from the EHRs of 14 hospitals and 21 hospitals within the Kaiser Permanente Northern California (KPNC) healthcare system for their research. Their models included 38 and 72 predictors respectively, including vital signs, lab results, length of stay, care directives, and other demographic information.

4.3.1. Predictor Selection

The goal of predictive models is to find the combination of predictors that results in optimal predictive accuracy; interpretability may be of secondary importance.[51] Luis et al. used simple logistic regression to evaluate each variable in NEWS and demonstrated that temperature and systolic blood pressure were not statistically significantly associated with mortality. Their final model dropped temperature but kept systolic blood pressure because of improved predictive power compared to the original NEWS.[21] This demonstrates that statistical significance between variables of a model does not necessarily reflect overall prediction performance. Similarly, multicollinearity is less of a problem for a predictive model since it does not affect the ability of prediction, unless the importance or contribution of individual independent variables to the dependent variables is of interest.[51] Researchers could explore a wide range of variables to capture relationships such as non-linearity and interactions. However, the inclusion of a large number of variables increases the risk of including spurious predictors and may lead to overfitting, especially in studies with a smaller sample size.[13] Backward selection is the most commonly used method for predictor selection. Yet, backward selection is particularly suboptimal for models with a large number of variables since many potential predictors are highly correlated. The use of penalized model selection methods, such as AIC, BIC, and least absolute shrinkage and selection operator (LASSO), are recommended for prediction model derivation.[13, 52]

4.3.2. Sample Size

There is no consensus on how to determine an adequate sample size for predictive modeling.[13] The optimal algorithm with small prediction error is often determined from the data, thereby requiring a sufficiently large sample for algorithm selection.[51] Therefore, it is reasonable to use an entire dataset for model building. Additionally, larger datasets enable more complex models to be built for specific patient cohorts. Escobar and colleagues further built sub-models for each of the 24 diagnosis groups included in their model.[28]

4.3.3. Sampling from Longitudinal Dataset

The database for EWS derivation usually involves a longitudinal dataset since most predictors are physiological measurements, which are repeatedly measured during hospital admission according to policy. However, most models were built by taking transactional data points from a series of observations and treating each observation as an independent trial process. This assumption allows researchers to apply regression and tree models during model derivation. Still, there is no consensus on which observation set to use for model derivation. Using a single data point could not capture the pattern of changes in physiological measurements over a period of time. These patterns typically provide valuable clinical information to clinicians when evaluating patient status. Nonetheless, several studies demonstrated that EWSs trained on transactional health data still display acceptable predictive accuracy.[22, 27, 30, 40] In order to take series of observations into account while modeling, four studies utilized discrete time survival analysis, a technique that can easily estimate time-varying covariates and produce competing risk models that are intuitive and easy to interpret.[34–36, 38] This method utilizes the same number of observations for each patient over the same period of time, removing the potential bias of sicker patients having a higher physiological measurement frequency.

4.3.4. Outcome Selection

The choice of study endpoints also influences the performance and generalizability of an EWS. Frequently used outcomes in the reviewed studies included in-hospital mortality, unplanned transfer to the ICU, and unexpected cardiac arrest, as well as composites of two or more outcomes. In-hospital mortality was the most commonly used outcome and was relatively more accessible from databases. However, this outcome, which includes expected mortality among those who had a do-not-resuscitate (DNR) order or end-stage diseases, may decrease a model’s discriminating power among deteriorating patients who are not expected to die. Some studies excluded admissions for comfort care, but not every study was able to retrieve such care directives from the database. Churpek et al conducted a sensitivity test on eCART by excluding patients who died without a resuscitation attempt, showing no significant changes in predictive accuracy.[35] Transfer to the ICU partially reflects clinical concerns for patients with worsening clinical presentations and may require more intensive management. But there is no general guideline for ICU admissions, so ICU patient cohorts have different characteristics across healthcare systems.[53] As a result, using unplanned transfer to the ICU as a primary outcome could make a model less generalizable to other hospitals. Unexpected cardiac arrest on wards represents a group of patients who develop cardiopulmonary collapse but fail to be noticed by the clinicians in advance. It is possible that this cohort may benefit greatly from EWSs due to early detection and timely treatment prior to cardiac arrest. However, the incidence of in-hospital cardiac arrest is relatively rare, with a mean of less than 1.6 per 1000 admissions in both the US and UK[1, 54], which can lead to imbalanced datasets. Several resampling techniques have been proposed to improve performance.[55] Models built upon in-hospital mortality, unplanned transfer to the ICU, and/or unexpected cardiac arrest may be intrinsically biased towards patients with severe conditions. These endpoints are not able to capture patients who had less severe vital sign derangement as a prodrome of a clinical deterioration event. If these patients’ derangement received timely treatment, they would not develop an endpoint. Other clinical outcomes have been proposed to identify patients with less severe though still critical conditions, like pulmonary failure, myocardial infarction, deep vein thrombosis, pulmonary embolism, acute renal failure, gastrointestinal hemorrhage, sepsis, and shock, that require timely elevation of care.[56–58] Moreover, different primary outcomes could result due to different patient cohorts. Churpek et al. built models on cardiac arrest and ICU transfer patients separately and demonstrated that the two subgroups gave different characteristics.[34]

4.3.5. Model Selection

Multiple studies have shown that aggregated weighted scores and computerized scores perform better in discriminating patients with higher risk of clinical deterioration than activation criteria. [29, 59, 60] Though easier to implement, simplified models using cut-points (e.g. respiratory rate > 35) for single parameters may result in information loss and diminished prediction power.[61, 62] Clinicians consider multiple predictors to make clinical decisions and predictors are not weighted with equal clinical importance. Therefore, the former two classes of models better reflect the clinical decision-making process.

Various algorithms have been applied and compared for EWS derivations. Kipnis et al. selected discrete time logistic regression as a final model because it outperforms other ensemble models.[38] While Churpek et al. tested several machine learning algorithms (i.e., logistic regressions, tree-based models, k-nearest neighbors, support vector machines, and neural network) and suggested that a random forest model was an ideal algorithm for EWS derivation.[37] Random forest algorithms generally perform well in classification problems and intrinsically capture non-linear and interactional relationships between variables. Several methods exist for the extraction of important features and interactions to help interpret models.[52] The “No-free-lunch” theory of statistics indicates that there is no ubiquitous model for all possible datasets.[63] Complex models built by feature engineering and elaborate machine learning algorithms do not guarantee superior performance. This is demonstrated by the random forest algorithm involving 42 variables proposed by Dziadzko et al. The algorithm displayed good predictive power but did not perform significantly better than MEWS and NEWS when externally validated.[40] Although the primary goal for predictive modeling is to optimize predictive power, there is growing concern about the ability of machine learning models to align with domain knowledge about relationships contained in data, often referred to as model interpretability.[52] Complex algorithms that fail to provide clear explanations for its predictors and outcomes are less appealing and less credible to many clinicians and patients.[64] Frameworks for discussing interpretability have been proposed recently as the debate continues on whether interpretability is an essential characteristic of clinical prediction models and there is no consensus on how to evaluate interpretation methods.[52, 65] Therefore, we recommend researchers should strike a balance between predictive accuracy and interpretability while building new EWSs.

4.3.6. Model Evaluation and Validation

Among earlier studies, EWSs were developed and validated on the same dataset. This “apparent validation” usually leads to overly optimistic performance. Several internal validation techniques can more honestly estimate model performance. For example, the split-data approach is commonly used in EWS validation. However, randomly splitting a dataset into derivation and validation sets is often sub-optimal. The difference between the two split datasets is a result of chance, and thus, the performance of the model is likely to be very similar on either set. A better alternative is splitting by time.[13] Recent studies validated their models on external datasets rather than on the original dataset from which the model was derived. Furthermore, EWS validation should not only consider accuracy, but also other clinically relevant metrics like positive predictive value (PPV) and sensitivity.[66] Repeated and inappropriate alerts resulting from poor PPV and sensitivity potentially lead to alert fatigue and poor clinical usability of the model.[67, 68] Only one third of the studies reviewed used PPV or predicting efficiency curve (PEV) to evaluate a model’s ability to identify positive cases.

4.4. Potential Bias in EWS Derivation Using EHR Data

EWSs are typically intended to be used in clinical decision support tools and therefore require stringent data quality. EHR data are not collected without reason, but their collection process can be highly complex and diverse. For example, some inpatient data are collected on all patients automatically (e.g., vital signs) whereas some data are collected only if required for treatment (e.g., a CT scan). EHR data can be noisy and wrong and are sometimes unfit for use for other purposes.[69–72] At a high level, EHR data are governed by physiology and the health care process.[73, 74] The data themselves are not independent of their existence and values, making their use complex[75]. The healthcare process encompasses how clinician judgment in relation to individual patients, clinical guidelines, reimbursement systems, EHR implementation, and risk of lawsuits triggers interventions, documentation, etc. This process induces differences in clinical practice across health systems, which could lead to selective recording in the EHR.[72, 76] Such biases can cause data to be incorrect, misrepresentative of their outfacing meaning, can confound the truth, but can also reveal much more than the data elements themselves. For example, patient measurements taken at night represent a different acuity level than patient data collected during the day. This difference in measurement representative of acuity level can generate a signal based entirely on the difference in health care process between night and day instead of a change in patient status.[77, 78] We can also leverage elements of the health care process, like nursing documentation[79, 80], to predict changes in the patient and outcomes. While such biases can be detected and removed, they can also be exploited to yield more information than is present in the data elements alone.[81] While it is important to exercise great care when using EHR data to create predictive models, this data is real-world data[82] and comes with substantial advantages when the processes that generate the data are taken into account. Because these data are special in this way, one should be aware of potential biases—both the benefits and limitations—when using EHR data for developing EWSs. As such, every decision made during data preparation, feature engineering, and analytic methods have an impact on modeling.[72, 83] Efforts must be taken to either leverage or remove the health care process bias.[84, 85]

Studies of more complicated models provide strategies and methodologies for healthcare systems to establish their own EWSs that reflect characteristics of their patient populations. However, they are subject to biases in the use of EHR data. Therefore, it is particularly important for studies on data-driven models to provide detailed study protocols and acknowledge, leverage or reduce[84, 85] potential biases in the data used for model development to improve transparency and generalizability.

4.5. Limitations

There are several limitations in this review. To the best of our knowledge, our criteria include an exhaustive list of original studies pertaining to the development and validation of new EWSs as well as validation and modification of existing EWSs for adult patients in acute care settings. Commercial clinical deterioration models that have only published about implementations and not development and validations of the underlying models are not included since implementation of EWSs and impacts on actual patient care are out of the scope of this review. The TRIPOD checklist is mainly designed for clinical prediction models using regression modeling and is not necessarily a suitable checklist for studies using more complicated machine learning algorithms. In response to the growing degree of clinical artificial intelligence research, a new initiative to develop an updated version of TRIPOD specific to machine learning algorithms was announced.[86]

5. Conclusion

This literature review demonstrates that the characteristics of the cohort, predictors, and outcome selection, as well as the metrics for model validation, vary greatly across EWS studies. There is no consensus on the optimal strategy for developing such algorithms since data-driven models with acceptable predictive accuracy are often site-specific. A standardized checklist for clinical prediction model reporting exists, but few studies have included reporting aligned with it in their publications. Data-driven models are subjected to biases in EHR data, thus it is particularly important to provide detailed study protocols and acknowledge, leverage, or reduce potential biases of the data used for EWS development to improve transparency and generalizability.

HIGHLIGHTS.

1. Most of the EWS derivation and validation studies failed to comply to the TRIPOD checklist in reporting their models. Incomplete reporting hinders the assessment of bias in and generalizability of EWSs, as well as validation and comparison between models.

2. The characteristics of the cohort, predictors, and outcome selection, as well as the metrics for model validation vary greatly across EWS studies. In the literature, there is no consensus on the optimal strategy for developing a ‘best’ EWS since a data-driven model with acceptable predictive accuracy is often site-specific.

3. Interpretability may increase EWSs credibility among end-users, though the balance to strike between interpretability and accuracy is often debated and frameworks for discussing interpretability have been recently proposed.

4. EWSs are intended as an algorithm to be used in clinical decision support, thus the models require stringent data quality. Therefore, one should be aware of potential biases—both the benefits and limitations—when using EHR data for developing an EWS.