Cone-beam breast computed tomography using ultra-fast image reconstruction with constrained, total-variation minimization for suppression of artifacts

Abstract

Compressed sensing based iterative reconstruction algorithms for computed tomography such as adaptive steepest descent-projection on convex sets (ASD-POCS) are attractive due to their applicability in incomplete datasets such as sparse-view data and can reduce radiation dose to the patients while preserving image quality. Although IR algorithms reduce image noise compared to analytical Feldkamp-Davis-Kress (FDK) algorithm, they may generate artifacts, particularly along the periphery of the object. One popular solution is to use finer image-grid followed by down-sampling. This approach is computationally intensive but may be compensated by reducing the field of view. Our proposed solution is to replace the algebraic reconstruction technique within the original ASD-POCS by ordered subsets-simultaneous algebraic reconstruction technique (OS-SART) and with initialization using FDK image. We refer to this method as Fast, Iterative, TV-Regularized, Statistical reconstruction Technique (FIRST). In this study, we investigate FIRST for cone-beam dedicated breast CT with large image matrix. The signal-difference to noise ratio (SDNR), the difference of the mean value and the variance of adipose and fibroglandular tissues for both FDK and FIRST reconstructions were determined. With FDK serving as the reference, the root-mean-square error (RMSE), bias, and the full-width at half-maximum (FWHM) of microcalcifications in two orthogonal directions were also computed. Our results suggest that FIRST is competitive to the finer image-grid method with shorter reconstruction time. Images reconstructed using the FIRST do not exhibit artifacts and outperformed FDK in terms of image noise. This suggests the potential of this approach for radiation dose reduction in cone-beam breast CT.

1. Introduction

Clinical translation of dedicated breast CT (BCT) is an area of active research [1–5]. Current dedicated BCT scanners either use flat-panel detectors with 300 [6] or 500 views [1,7,8] in a circular trajectory covering 360 degrees for cone-beam BCT [6] or use photon-counting detectors in a helical scan [5]. Typically, Feldkamp-Davis-Kress (FDK) algorithm [9] or its variants are used for image reconstruction in cone-beam breast CT using flat-panel detectors.

The average glandular dose (AGD) from dedicated breast CT for non-contrast diagnostic imaging was reported to be 12.6 mGy (median) and is approximately similar to four mammographic views [6]. However, for breast cancer screening, it is necessary to reduce the radiation dose to be comparable to a standard 2-view mammographic screening exam. Several studies have shown that iterative reconstruction (IR) algorithms can maintain or improve image quality compared to the analytical FDK [9] algorithm while enabling radiation dose reduction either by reducing the radiation dose per projection or by reducing the number of projections [10–17]. One approach is to reduce the number of projections, i.e., sparse-view data acquisition. Some groups have investigated sparse-view iterative image reconstruction algorithms based on the theory of compressed sensing [18–20]. Among them, the algorithm using total variation with projection onto convex sets (TV-POCS) [21] was initially developed for sparse-view data set and its improved version, adaptive steepest descent POCS (ASD-POCS) [22], has been explored for dedicated breast CT [8]. We are actively investigating the potential of sparse-view data acquisition and ASD-POCS reconstruction for radiation dose reduction in dedicated breast CT. Our motivation for this investigation includes the following: (1) a prior study [1] showed that the conspicuity of microcalcifications is reduced in FDK-reconstructed breast CT images. Both system resolution and image noise could contribute to reduced conspicuity. In cone-beam breast CT, there are ongoing efforts to improve system resolution by pulsing the x-ray source [2,7], by using high-resolution detectors [7], and by optimizing scintillator thickness [23]. We hypothesize that reducing the image noise without adversely affecting system resolution through iterative image reconstruction techniques could potentially improve visibility of microcalcifications. (2) For diagnostic imaging using dedicated cone-beam breast CT, it is important that the image reconstruction time is minimized. This is necessary for clinical practice so as to decide if the results from the breast CT exam indicate the need for follow-up imaging studies (e.g., targeted ultrasound), or biopsy during the same patient visit. (3) In order to translate dedicated breast CT for breast cancer screening, it is necessary to reduce the radiation dose to a level comparable to a standard 2-view mammographic screening exam. As stated earlier, the compressed-sensing based algorithms such as ASD-POCS are well suited for radiation dose reduction by employing sparse-view acquisition. Thus, our motivation for this study is based on the need to advance the role of cone-beam breast CT in diagnostic imaging of the breast and ultimately for breast cancer screening.

Interference-like artifacts have been reported with statistical image reconstruction [24]. We have also observed such artifacts in the ASD-POCS reconstructed clinical breast CT images with 1024 x 1024 in-plane voxel array of 0.273 mm voxel pitch. Although ASD-POCS greatly reduced the image noise, the severity of interference-like artifacts degrades the image quality. The objective is to suppress these interference-like artifacts. One common method is to use finer image-grid followed by down-sampling [24,25]. However, this method requires half- or quarter-original voxel size which results in at least 4-fold increase in image array size compared to the desired image size. Although this method can remove the interference-like artifacts, it incurs additional computational cost or reducing the field of view (FOV) with interior tomographic reconstruction. Our main goal is to find a solution to generate artifact free images with improved image quality within a clinically acceptable reconstruction time. In this work, we propose a computationally efficient method by modifying the ASD-POCS algorithm without sacrificing the FOV and without artifacts and is described in Section 2. In Section 3, the reconstruction time of different image reconstruction algorithms in full FOV were compared, and the proposed method is quantitatively evaluated by comparing it with FDK images. The FDK reconstructions are chosen as reference for image quality comparisons as a multi-reader, multi-case receiver operating characteristic (ROC) study with 235 cases interpreted by 18 radiologists showed that FDK-reconstructed non-contrast breast CT improved sensitivity over diagnostic digital mammography [26]. The clinical cases used in this study were part of the data used in the abovementioned reader study.

2. Materials and Methods

2.1. Human subjects

This study used de-identified projection datasets from women assigned American College of Radiology (ACR) Breast Imaging–Reporting and Data System (BI-RADS) 4 or 5 diagnostic assessment categories that participated in a prior institutional review board (IRB –approved, Health Insurance Portability and Accountability Act (HIPAA) - compliant clinical study with informed consent. BI-RADS 4 or 5 women have suspicious findings that require tissue diagnosis (biopsy). All study participants underwent the non-contrast diagnostic BCT of the breast with the suspicious finding prior to biopsy. This dataset was previously analyzed for volumetric fibroglandular fraction [27], skin thickness [28] and radiation dose [6]. Part of this dataset was also used for evaluating x-ray scatter-correction methods [29–31]. FDK reconstructions of this dataset was also included in the case mix, prior to random selection, for the multi-reader, multi-case ROC study [26].

2.2. Geometry of cone-beam breast CT scanner

The clinical breast CT datasets were acquired on a clinical-prototype cone-beam BCT system. Detailed description of the system and acquisition parameters were reported in prior publications [2,6,27]. Briefly, the cone-beam BCT system used a flat-panel detector (PaxScan 4030CB, Varian Medical Systems) operated at a pixel pitch of 0.388 x 0.388 mm² (after 2x2 hardware binning of 0.194 x 0.194 mm² pixels) and each projection comprised 1024 x 768 pixels. There were 300 projection views distributed uniformly over 360 degrees of a circular trajectory. The distances from the source to the isocenter and to the detector were 650 mm and 898 mm, respectively.

2.3. Iterative Reconstruction Algorithm – ASD-POCS

In this study, the theory of the iterative reconstruction algorithm is based on a constrained, total-variation minimization algorithm, referred to as adaptive steepest descent – projection onto convex sets (ASD-POCS) and was developed by Sidky and Pan [32]. It uses the projection onto convex sets (POCS) as image constraints to enforce data consistency and employs the steepest descent with an adaptive step-size to reduce the total-variation (TV) of the image. The inspiration for this algorithm originated from the compressed sensing work by Candès et al [18], for the exact recovery of the image, when samples of the discrete Fourier transform (DFT) of the image is sparse. Candès et al also pointed out that the constrained, TV-minimization can be applied for linear systems [20]. For non-orthogonal linear systems such as the cone-beam projections, the developments and implementations were performed by Sidky, Kao and Pan [32,33]. The derivation and determinations of the parameters of ASD-POCS is beyond the scope of this article, and we refer the interested readers to the aforementioned articles.

2.4. Artifacts on Large Field of View (FOV) Image

ASD-POCS has been applied on different computerized phantoms, such as the FORBILD jaw [32], and it outperformed the expectation-maximization (EM) algorithms. The potential of ASD-POCS to provide better image quality in breast CT at lower radiation dose than the FDK algorithm has been reported [8]. The dimensions of image array in their breast CT study was 380 x 380 and the voxel size was 0.33 mm which results in 125.4 mm FOV.

In our breast CT study, the dimension of the image array is 1024 x 1024 with in-plane voxel size of 0.2734 mm, resulting in 280 mm FOV. GPU-based image reconstruction software (Tomographic Iterative GPU-based Reconstruction Toolbox, TIGRE) was employed for our image reconstruction processes [34]. When the ASD-POCS as implemented in TIGRE toolbox is used, interference-like artifacts can be found in many samples. Zbijewski and Beekman showed that the discretization errors at the vicinity of the large gradient in linear attenuation coefficients contributes to these artifacts [24]. In breast CT, this occurs at the breast periphery due to large attenuation coefficient difference between skin and air. One example from our patient data is used for demonstrating these artifacts (Fig. 1). The reconstructed image array from the full FOV is shown in the left panel and the zoomed in view is shown in the right panel. The interference-like artifacts are indicated by arrows in the right panel. Hereon, only the zoomed-in images are shown for clarity.

Figure 1.

An example of breast CT image reconstructed using ASD-POCS algorithm implemented in the TIGRE toolbox. Left: original image array of the entire field of view. Right: image array with zoom in. Interference-like artifacts (indicated by red arrows) can be clearly observed. The display range is [0.20 0.40] cm⁻¹.

The clinically used FDK reconstruction is shown in Fig 2a. For statistical image reconstruction algorithms, finer image-grid followed by down-sampling, was proposed by Zbijewski and Beekman and is commonly used to overcome these interference-like artifacts [24,25]. This was also applied in a prior breast CT study [8]. We found that these interference-like artifacts persisted unless quarter in-plane voxel size (0.0683 mm, resulting in 4096 x 4096 image array) was used. Fig 2b and Fig 2c show the same sample case before and after implementation of the finer image-grid method using the TIGRE toolbox. Although using finer image-grid method with quarter in-plane voxel size is a potential solution, it is challenging for practical use, when a large FOV, like our case (280 mm), needs to be reconstructed. In spite of GPU acceleration (NVIDIA QUADRO P6000 with 3840 cores), for reconstructing a breast with 310 slices, it takes more than 238 hours to complete 100 iterations to obtain a 4096 x 4096 x 310 reconstructed image volume. It will take longer to reconstruct breasts with longer chest-wall to nipple length. Chest-wall to nipple length as long as 17.5 cm (640 slices) have been reported [27].

Figure 2.

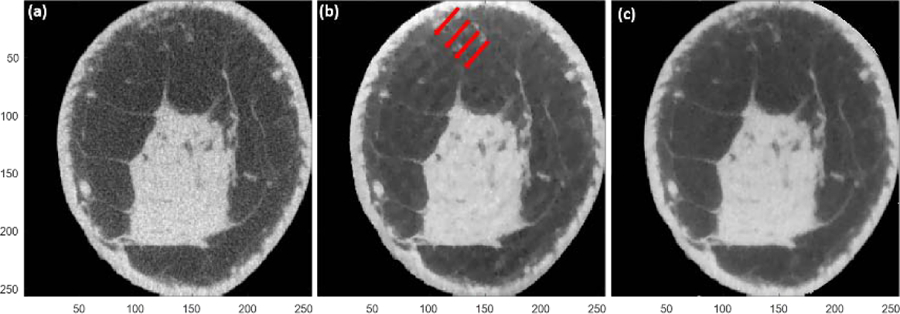
Image reconstruction of the same sample case in figure 1 using different methods. The full reconstruction FOV is 280 mm and the voxel size is 0.2734 mm. (a) The reference; FDK method using full FOV reconstruction FOV and zoom in. (b) ASD-POCS method as implemented in TIGRE toolbox using full FOV reconstruction and zoom in. Red arrows indicate the interference-like artifacts. (c) ASD-POCS as implemented in TIGRE toolbox with finer image-grid using quarter in-plane voxel size and quarter reconstruction FOV (69.99 mm) followed by down-sampling. The display range is [0.20 0.40] cm⁻¹.

2.5. Proposed Algorithm for Suppression of Artifacts

In this section, the proposed method using a modification to the ASD-POCS algorithm is described and the results using different methods were compared for the sample case shown in Fig. 1. The original ASD-POCS algorithm by Sidky and Pan [22] used the algebraic reconstruction technique (ART) [35] for the TV regularization step to solve the constrained minimization problem. In ART, the image is updated for each ray. Following the works of Censor and Elfving [36] and Jiang and Wang [37,38], the ART step have been replaced in many algorithms [39–45] and software [34] aimed for 3D CT image reconstruction with either simultaneous algebraic reconstruction technique (SART) [46] or with the ordered-subsets SART (OS-SART) [37], to accelerate the image reconstruction. In SART, the image is updated after each projection (view angle) and in OS-SART the image is updated after a subset of projections. Thus, SART is a special case of OS-SART, when the number of subsets is set to equal the number the projections. When the number of subsets in OS-SART is set to 1, then the image is updated after using all projections, and in this sense, is similar to simultaneous iterative reconstruction technique (SIRT) [47]. Initializing with non-zero image, such as with FDK reconstruction, have also been used in several iterative reconstruction algorithms [48–52]. Inspired by these studies, we investigated the combinations of the initial image and the algorithm used in the gradient descent steps for the TV penalty. For initialization, both zero-valued image and the FDK reconstructed image were considered. The ASD-POCS algorithm implemented in the TIGRE toolbox [34] uses SART for the TV regularization step. In order to distinguish this implementation using SART instead of ART, we refer to it as T-ASD-POCS. We modified T-ASD-POCS by retaining the adaptive steepest descent step from the original ASD-POCS algorithm and implemented OS-SART for the TV regularization step. In order to distinguish from the original ASD-POCS and the T-ASD-POCS, we refer to this method using OS-SART as Fast, Iterative, TV-Regularized, Statistical reconstruction Technique (FIRST). We investigated a range of ordered subsets (30 subsets to 1 subset) for the OS-SART. Hyper parameters used in this study are listed in Table 1. Other initial values [42,43] or filters [53,54] in FDK might work along with proper hyper parameters, but we focus on the use of FDK reconstruction with Ram-Lak filter, or the zero-valued image, as an initial image in this article. Hereon, we denote the investigated method as FIRST, when the number of subsets n = 1 and when initialized with FDK image. When n ≠ 1, then n is specified. If initialized with zero-valued image, then this is also specified.

Table 1.

Hyper parameters used in this study.

β	βred	α	αred	ng	rmax
1	0.995	0.001	0.95	30	0.95

2.6. Quantitative Image Quality Analysis

For quantitative comparison between the proposed method and the other methods described in the previous section, 15 clinical datasets, all with microcalcifications, were used in the analysis. The choice of using clinical datasets with microcalcifications is based on the observation that the conspicuity of microcalcifications is reduced in breast CT compared to mammography [1]. All analyses were performed on linear attenuation images (units of cm⁻¹). Signal-difference to noise ratio (SDNR) between adipose and fibroglandular tissues and its constituents, viz., the signal difference between adipose and fibroglandular tissue, and the noise (variance) within adipose and fibroglandular tissue regions were computed for both the FDK and the FIRST reconstructions. Additionally, the following metrics were calculated with the FDK reconstruction as the reference: root-mean-square error (RMSE), bias, percent difference in linear attenuation coefficients in fibroglandular and adipose tissue regions, and the percent difference in full-width at half-maximum (FWHM) for microcalcifications that were quantified along two orthogonal directions. The FDK reconstruction was chosen as the reference as it is used in the clinical breast CT system [26]. For microcalcifications, a single calcification from each case (n=15) was used to quantify the percent difference in FWHM. It is relevant to note that the SDNR is a commonly used image quality metric and is identical to the contrast-to-noise (CNR) metric used in a prior study to evaluate FDK and ASD-POCS reconstructions for sparse-view cone-beam CT [55]. The size of regions-of-interest (ROIs) for the SDNR, the percent difference in linear attenuation coefficients in adipose and fibroglandular tissue regions, and the variance in fibroglandular and adipose tissue regions were between 20 x 20 and 32 x 32 voxels and depended on the shape and size of the fibroglandular tissue regions. The RMSE and bias values were calculated based on the largest square ROI encompassing the breast tissue excluding the skin. This corresponded to approximately 80% of the image slice, and varied with breast size and shape. The slices containing the pectoralis muscle and the retro-areolar region were excluded for these quantitative measurements.

The obtained quantitative measures were statistically analyzed. All continuous variables for tested for normality assumption (Shapiro-Wilks test) and appropriate summary statistics were reported. For the metrics (SDNR, signal-difference and variance) with paired measurements from the FDK and the FIRST reconstructions, Wilcoxon signed rank sum test was used to test if they differed. For the percent difference in FWHM computed with FDK as the reference, one sample median test was used to test if the median significantly differed from zero. Effects associated with p<0.05 were considered statistically significant. All analyses were performed using statistical software (SAS version 9.4, SAS Institute Inc., Cary, NC).

3. Results

The results are organized as follows: The effect of number of subsets in FIRST algorithm is shown first. This is followed by showing the effects of initialization with zero-valued image and FDK reconstructed image. Finally, quantitative analysis and the reconstruction time are shown. It is relevant to note that all of the reconstructions presented in this manuscript reconstruct the full FOV and zoomed regions encompassing the breast are shown for clarity. Also, all reconstructed images are shown after 100 iterations. Figure 3 shows the results of the FIRST, when the number of subsets in the OS-SART is varied (30 to 6 subsets), and with FDK image initialization. Interference-like artifacts persisted until the number of subsets were reduced to 6 or less. Since the reconstruction time decreases with reducing number of subsets, subsequent evaluations using FIRST were performed with 1 subset as it provided the shortest reconstruction time.

Figure 3.

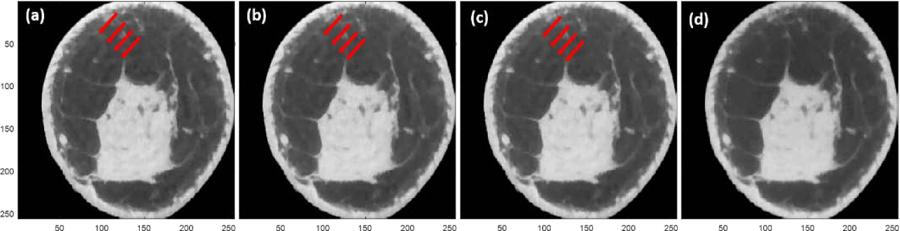
FIRST with FDK initialization for the same sample case in figure 1. The number of ordered subsets were varied: (a) 30; (b) 15; (c) 12; and, (d) 6 subsets. Red arrows indicate the interference-like artifacts. Interference-like artifacts persisted until the number of subsets was reduced to 6 or less. The display range is [0.20 0.40] cm⁻¹.

For the sample case shown in figure 1, the four combinations comprising two different initial images (zero and FDK) and the two algorithms (T-ASD-POCS and FIRST) are shown in figure 4. The number of iterations was fixed (100 iterations). Artifacts appear on reconstructed images for T-ASD-POCS with either zero (figure 4a) or FDK (figure 4b) as the initial value. When FIRST is initialized using zero-valued image, the resulting reconstruction is blurred (figure 4c). Initializing FIRST with FDK image provided an artifact free image.

Figure 4.

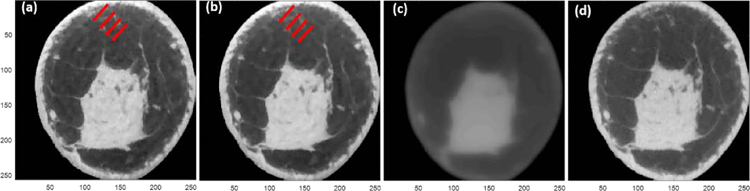
Image reconstruction of the same sample in figure 1 using four different combinations of the initial value and the implemented algorithms. T-ASD-POCS initialized with (a) zero-valued image and (b) FDK image. FIRST initialized with (c) zero-valued image and (d) FDK image. The display range is [0.20 0.40] cm⁻¹.

The average reconstruction time (seconds) per iteration per slice is summarized in Table 2. The reconstruction time, in this study, is inclusive of the computational time by the algorithm, hard disk access time for read/write operations, and any other sources of latency. All methods used full FOV reconstruction (1024 x 1024 in-slice pixel matrix) with GPU-based implementation (Quadro P6000, NVidia Corporation, Santa Clara, CA) on the same reconstruction workstation. Substantial improvement in reconstruction time is achieved with FIRST compared to T-ASD-POCS.

Table 2.

Average reconstruction time (seconds) per slice per iteration (if applicable) for full FOV reconstruction for each method studied here. The reconstruction time is inclusive of computational time by the algorithm, hard disk access time for read/write operations, and any other sources of latency. The finer image-grid uses T-ASD-POCS with quarter in-plane voxel size. All methods were implanted on a GPU (Quadro P6000, NVidia Corporation, Santa Clara, CA).

FDK	FIRST	T-ASD-POCS	Finer image-grid
0.029	0.034	1.25	20.85

It is relevant to note that the T-ASD-POCS with zero-valued initial image results in artifacts (Figure 4a). While FDK provided the fastest reconstruction, the resulting images are noisier compared to the proposed method. This is shown for the evaluation dataset of 15 cases with microcalcifications (Figure 5). The reference FDK reconstructions are shown in odd numbered rows in Figure 5. In each panel, the location of the microcalcification(s) are indicated by an arrow. The corresponding FIRST reconstructions are shown in even numbered rows. Qualitatively, a substantial reduction in image noise can be readily observed without a noticeable degradation in spatial resolution. Quantitative analyses are addressed below.

Figure 5.

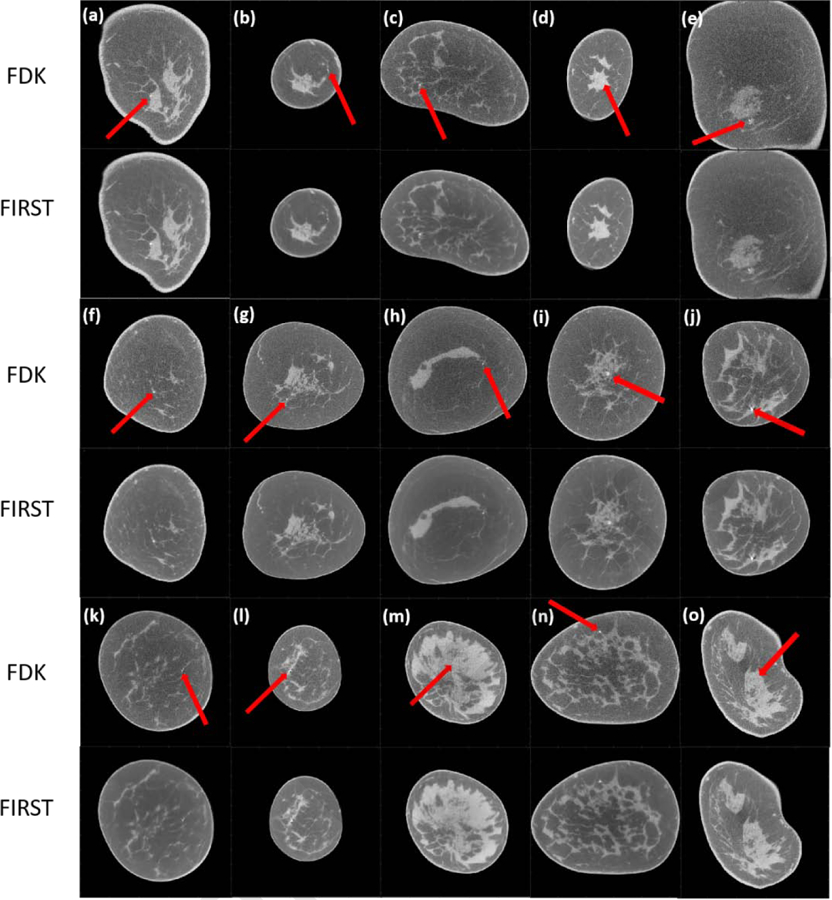
FDK and FIRST reconstructed images. In each panel of FDK images, the red arrow indicates the location of the microcalcification. The display range is [0.15 0.35] cm⁻¹.

Summary statistics of the image quality measures are shown in Table 3. All metrics are reported as median (inter-quartile range). SDNR computed between adipose and fibroglandular tissue regions and its constituents, viz., the signal-difference between adipose and fibroglandular tissue regions, the variance within adipose tissue region, and the variance within the fibroglandular tissue region were computed for both the FDK and FIRST reconstructions. RMSE, bias, percent difference in FWHM for microcalcifications along the two orthogonal directions were computed for the FIRST reconstruction with the FDK reconstruction as the reference.

Table 3.

Summary statistics [median (interquartile range)] of image quality measures from the FDK the FIRST reconstruction methods. All metrics were computed using linear attenuation coefficients and not HU. RMSE, bias and percent difference in FWHM for microcalcifications were computed with respect to the reference FDK reconstruction. [FWHM: Full-Width at Half-Maximum]

Metric	FDK	FIRST	P-value
Signal-difference to noise ratio, SDNR	59.15 (49.23–62.20)	119.86 (117.41–145.36)	P<0.0001
Signal-difference (cm−1)	0.0657 (0.0563–0.0675)	0.0652 (0.0596–0.0692)	P=0.18
Variance within fibroglandular region ( × 10−4 cm−2)	1.03 (0.88–1.12)	0.25 (0.16–0.35)	P=0.0001
Variance within adipose region ( × 10−4 cm−2)	0.65 (0.57–0.90)	0.09 (0.05–0.17)	P<0.0001
% FWHM (x)	Reference	0 (0 – 0)	P=0.25
% FWHM (y)	Reference	0 (0 – −0.06)	P=0.125
RMSE ( × 10−6 cm−1)	Reference	3.52 (3.29–4.31)	NA
Bias ( × 10−4 cm−1)	Reference	58.64 (49.70–57.41)	NA

For pairwise comparisons between FDK and FIRST reconstructions, SDNR showed a significant improvement (P<0.0001) for FIRST. Further analysis of the signal-difference and noise (variance) showed that the difference in signal-difference was not significant (P=0.18) and the variance was significantly reduced with FIRST (P≤0.0001). These results are in agreement with theoretical expectations of reduced variance with FIRST, while preserving the quantitative nature of breast CT. For the percent FWHM of microcalcifications calculated with respect to the reference FDK reconstruction, FIRST did not show a significant difference (P≥0.125) with a median of zero%. Thus, the investigated FIRST method showed a significant improvement in SDNR compared to the FDK reconstruction, while preserving the spatial resolution. Also, the reconstruction time is substantially reduced to make it practical for clinical use in diagnostic setting, which requires reconstructed images to be available in a timely manner for clinical workflow.

4. Discussion

This study describes an artifact-free, full FOV reconstruction without using finer image-grid for ASD-POCS based reconstruction. Although the finer image-grid method can remove the interference-like artifacts, it is computationally expensive even with GPU implementation. The investigated reconstruction method, FIRST, even in full FOV, achieves artifact-free reconstruction similar to the finer image-grid method and within a clinically acceptable reconstruction time. Using the same hardware and GPU implementation, FIRST reduced reconstruction time by 600-fold compared to the finer image-grid method using T-ASD-POCS, and by 30-fold compared to T-ASD-POCS with standard voxel size (Table 2). However, the T-ASD-POCS with standard voxel size suffers from artifacts and finer image-grid is needed (Figure 2). It is important to recognize that the reconstruction time includes the computational time by the algorithm, time to access the hard disk for any read/write operations, and any other latency that may be present. The TIGRE toolbox used for both T-ASD-POCS and FIRST algorithm performs all the computational steps in the GPU and the reconstructed image volume is stored in the hard disk. The FIRST reconstruction uses OS-SART with 1 subset. Hence, the image volume that is stored in the hard disk is updated once after using all projections per iteration. In comparison, T-ASD-POCS uses SART and the image volume is updated after each projection (300 projections in the studied breast CT cohort) per iteration. Additionally, the number of ray angles for forward and back projection is increased by a factor of 16 with the finer image-grid using quarter voxel size. Collectively, these factors contribute to the observation of substantial reduction in reconstruction time with the FIRST algorithm, making it practical for clinical use in a diagnostic setting.

The reconstructed images using FIRST outperformed the traditional FDK reconstruction in terms of image noise (variance) resulting in higher SDNR. We also found that the spatial resolution of the images reconstructed by FIRST is maintained compared to the FDK reconstruction, based on the measurements of FWHM of microcalcifications. Collectively, these factors could potentially improve the conspicuity of microcalcifications. Traditionally used metrics such as RMSE and bias were also computed with the FDK reconstruction as the reference. Regarding RMSE and bias, the observed median of 3.5x10⁻⁶ cm⁻¹ and 5.8x10⁻³ cm⁻¹ correspond to approximately 0.001% and 2%, respectively, for the range of linear attenuation coefficients expected for breast tissue. Although the FDK reconstruction was used as a reference to calculate bias and RMSE, it is far from an ideal reference standard due to substantial image noise. In FDK reconstructions, the standard deviation (square-root of variance, Table 3) for adipose and fibroglandular tissues were approximately 2–2.5% of the mean and is comparable to the observed bias.

Irrespective of initialization with zero-valued or FDK image, artifacts were present in T-ASD-POCS without finer image-grid. These artifacts can be attributed to the discretization errors described previously. For FIRST reconstruction with zero-valued image initialization, the resulting images are blurred. In general, the updates/changes to the image volume per iteration are smaller with OS-SART (with 1 subset) than with SART. While increasing the number of iterations may converge to a better solution, the increased computational time would make it challenging for practical use. Initializing with the FDK image enables the algorithm to converge to a better solution rapidly.

The primary reason for this study was to find a practical use of ASD-POCS in diagnostic setting, where the reconstruction time has to be compatible with clinical workflow, as the patient awaits the result from the breast CT exam. Our motivation was not to determine if replacing with OS-SART in ASD-POCS improves image quality, but whether using OS-SART (and number of subsets) could provide reconstruction times compatible with clinical workflow and if the image quality is comparable to FDK, with the added advantage of reduced image noise that may improve microcalcification visibility. The comparisons with ASD-POCS employing SART, i.e., T-ASD-POCS, with and without finer image-grid, are intended to show the presence of artifacts when finer image-grid is not employed, and the long reconstruction time when the finer image-grid is employed, both of which are detrimental for clinical adoption.

Our study had limitations. FDK is a naïve and straight forward option and it may not be the only option to be the initial value. Alternative initialization may be of value, but this was not the goal of this study. The primary aim of this study was to provide an easy implementation to suppress the interference-like artifacts, potentially improve the conspicuity of microcalcifications by reducing image noise, and to reduce the computational time so that it is clinically feasible. We also did not study the convergence with varying number of iterations. Considering that our proposed method, FIRST, after 100 iterations with FDK initialization showed reduction in noise, while preserving spatial resolution, it is possible that fewer than 100 iterations may be sufficient. This could further reduce reconstruction time. This is a subject of ongoing investigations and will be reported in future.

Based on the promising results obtained in terms of improved image quality, particularly in terms of image noise (variance) and SDNR, while maintaining spatial resolution as measured by FWHM of calcifications, future work will focus on reader studies to determine the improvements in lesion conspicuity (particularly calcified lesions) and in diagnostic performance through a receiver operating characteristic (ROC) study. Also, the FIRST algorithm is based on ASD-POCS and hence it could also be potentially used for sparse-view reconstruction, short-scan reconstruction, and for laterally-displaced detector reconstruction [56].

5. Conclusion

We report on the implementation of an effective artifact suppression method and apply this method on breast CT images. We demonstrated that our developed method provided images without interference-like artifacts and without using smaller pixel size resulting in full FOV reconstruction that is completed in a short time. Our results also show that the image quality is better than the FDK reconstruction without sacrificing the spatial resolution. Because the proposed method is based upon the theory of ASD-POCS, it can potentially be used in incomplete CT data acquired by sparse-view or by short-scan method for radiation dose reduction.

Highlights.

• Ultra-fast version of the ASD-POCS algorithm has been developed.

• Reconstruction speed was improved by 600 fold.

• Image reconstruction field of view and spatial resolution are preserved.

• Effective suppression of interference-like artifacts on the periphery.