Understanding factors governing distribution volume of ethyl cellulose-ethanol to optimize ablative therapy in the liver

Abstract

Objective:

Ethanol ablation, the injection of ethanol to induce necrosis, was originally used to treat hepatocellular carcinoma, with survival rates comparable to surgery . However, efficacy is limited due to leakage into surrounding tissue. To reduce leakage, we previously reported incorporating ethyl cellulose (EC) with ethanol as this mixture forms a gel when injected into tissue. To further develop EC-ethanol injection as an ablative therapy, the present study evaluates the extent to which salient injection parameters govern the injected fluid distribution.

Methods:

Utilizing ex vivo swine liver, injection parameters (infusion rate, EC%, infusion volume) were examined with fluorescein added to each solution. After injection, tissue samples were frozen, sectioned and imaged.

Results:

While leakage was higher for ethanol and 3%EC-ethanol at a rate of 10 mL/hr compared to 1 mL/hr, leakage remained low for 6%EC-ethanol regardless of infusion rate. The impact of infusion volume and pressure were also investigated, first in tissue-mimicking surrogates and then in tissue. Results indicated that there is a critical infusion pressure beyond which crack formation occurs leading to fluid leakage. At a rate of 10 mL/hr, a volume of 50 μL remained below the critical pressure.

Conclusions:

Although increasing the infusion rate increases stress on the tissue and the risk of crack formation, injections of 6%EC-ethanol were localized regardless of infusion rate. To further limit leakage, multiple low-volume infusions may be employed.

Significance:

These results, and the experimental framework developed to obtain them, can inform optimizing EC-ethanol to treat a range of medical conditions.

I. Introduction

ABLATION – minimally-invasive destruction of diseased tissue without removal from the body [1] – has the potential to be an effective treatment for many medical conditions and could be an effective adjunct or alternative to surgery. Common ablative technologies for superficial lesions include cryotherapy [2] and thermocoagulation [3]; deeper lesions are frequently treated with heat generated via electromagnetic radiation, e.g. via microwave [4] or radiofrequency ablation (RFA) [5].

Ethanol ablation is the direct injection of pure ethanol into tissue to induce cell death. Ethanol kills cells through protein denaturation and cytoplasmic dehydration [6]. Its cytotoxicity, and therefore therapeutic efficacy, are governed by ethanol concentration and exposure time [7]. Ethanol ablation was originally used in the treatment of inoperable hepatocellular carcinoma, with 5-year survival rates comparable to surgical resection [8]. While the liver was the first and remains the most common application, ethanol ablation has also been used in treatment of cardiomyopathies [9], parathyroid tumors [10], pancreatic tumors [11], and metastatic lymph nodes [12]. Conventionally, ethanol ablation involves injection of a high volume (often equal to or greater than the tumor volume) of pure ethanol at a high rate (≥100 mL/hr) [8, 13]. That rate can cause fracturing of the tissue and lead to ethanol leakage out of the target region, incomplete distribution within the tumor, and damage to surrounding tissue. Fluid leakage during ethanol ablation of hepatocellular carcinomas is well-documented, which results in vascular and bile duct injuries [14], coagulation necrosis outside of the target region of interest [15] and incomplete tumor coverage [6].

Modifying ethanol ablation to improve lesion coverage and decrease off-target effects has broad clinical implications in both high-income (HICs) and low- and middle-income countries (LMICs). Although surgical resection and transplantation are the most effective treatments for liver tumors in HICs, widespread liver damage often associated with liver tumors and limited donor availability preclude widespread use of these modalities leading to the use of either ablative or transarterial therapies [16]. Tumors under 3 cm are typically ablated while transarterial therapies are often employed for larger or more invasive tumors [17]. RFA has been demonstrated to require fewer treatment sessions and achieve better tumor control with fewer adverse events than ethanol ablation [18]. However, tumors near intestinal loops, along the liver capsules, or near large blood vessels complicate the use of RFA and are candidates for the use of ethanol ablation [19]. Additionally, other studies have indicated that combined use of ethanol ablation and RFA is more effective than RFA alone [20]. To treat larger or invasive more tumors, transarterial therapies in which embolic agents that may release chemotherapeutics (TACE) or radiation (TARE) are injected to occlude blood supply treat larger and more invasive tumors [21]. Ethanol ablation following a single session of TACE has been found to be more effective than repeat TACE without the added risk of developing resistance to cytotoxic drugs [22]. The complementary relationship be may the result of delayed ethanol clearance following embolization.

While there is a range of therapies available in HICs, their cost precludes their widespread use in LMICs. While LMICs are predicted to bear nearly two-thirds of the global cancer mortality burden by 2030 [23, 24], only 5% of global cancer resources are currently allocated to LMICs [25]. Currently, diagnostic capabilities for liver cancer in LMICs are limited, but this is likely to change with the advent of portable ultrasound and tele-medicine [26, 27]. While diagnosis may become more accessible, a majority of the world’s population – over 5 billion people – do not have access to basic surgical care [28]. Thus, it is crucial to expand access to treatment in LMICs. Ethanol ablation is appealing because it is low-cost and does not require hard-to-supply consumables, electricity, or specialized equipment. For ethanol ablation to have a renewed clinical impact in both HICs and LMICs, it is necessary to achieve controlled delivery by reducing leakage.

There are two major types of fluid leakage, which limit injection efficacy: (1) retrograde flow along a path proximate and parallel to the needle up to the tissue surface (“backflow”); and (2) flow in a high-permeability path within the tissue away from the needle tip (“crack formation”). Backflow occurs when injected fluid follows a path of least resistance between the surface of the needle and tissue that has separated from it [29]. The compressive stress exerted by the displaced tissue against the needle surface acts to diminish backflow by creating a seal. Dimpling or tissue deformation around the needle tip is correlated with decreased compressive stress, which leads to backflow [30, 31]. Thus, dimpling during needle insertion must be minimized. Crack formation occurs when fluid flowing into the tissue raptures its structure; this creates a high-permeability fluid flow path away from the injection site. Fluid flow through the interstitial space imparts a stress on the solid tissue network (comprised of cells and extracellular matrix). This deforms the network and forms of a fluid-filled cavity around the needle tip, which may rapture leading to leakage [32–34]. At relatively low fluid infusion rates (e.g. 1 mL/hr, steady flow can be achieved without substantially altering tissue structure. Faster infusion rates allow for shorter operation times, but also increases stress on the tissue and, ultimately, may cause tissue rupture [32]. Since rapture is most likely to occur at interfaces or brittle regions (e.g. along the vasculature or necrotic regions), the resulting fluid distribution is non-uniform. Previous studies in tumors found that the efficacy of fluid injections depended on infusion rate [35], and that rapid injection of ethanol in liver should be avoided to reduce its uncontrolled spread [36]. In order to contain injected fluid and ablate only diseased tissue while sparing surrounding tissue, the deleterious effects of crack formation and leakage must be minimized.

In addition to lowering the infusion rate, it has been demonstrated that in situ gelation of injected solutions could mitigate effects of backflow and crack formation [37]. The solvent transport is slowed due to the frictional resistance of the tight mesh formed in the gel network. To exploit this phenomenon, our group has utilized a formulation that combines ethanol with ethyl cellulose (EC), which forms a viscous solution without substantially diluting the ethanol [38]. EC is soluble in ethanol but forms a gel when it encounters an aqueous environment (e.g. in tissue). EC-ethanol has been used previously in treatment of venous malformations and herniated disks [39, 40]. The resulting gel serves to contain the mixture near the site of injection and induces sustained local ablative activity without systemic side effects [39, 40]. We tested the efficacy of EC-ethanol as a tumor ablation technique on squamous cell carcinomas in a hamster cheek pouch model [38]. Results showed that the normalized tumor volume (volume at 7 days/ volume at baseline) was significantly lower for animals treated with EC-ethanol compared to ethanol alone and was significantly lower for infusion rates of 1 and 10 mL/lir compared to manual injection (approximately 100 mL/hr).

Our previous study demonstrated proof-of-concept of mixing EC with ethanol for use in ablative therapy for local tumor control. A key step toward rendering EC-ethanol ablation a reliable therapeutic for liver cancers is to elucidate the relationship between salient parameters characterizing the injection and the resulting fluid distribution in liver tissue. Swine livers were selected for this study owing to the fact that they are similar in size and morphology to human livers [36]. The input parameters investigated in our study included needle insertion rate, needle insertion depth, concentration of EC, infusion rate, and infusion volume. The injected EC-ethanol distribution was imaged in serial sections of the liver, using a fluorescent dye that was added to each solution prior to delivery. To analyze the effect of infusion volume on crack formation, transparent tissue-mimicking mechanical surrogates were employed, and the upstream infusion pressure was monitored. Infusion pressure increased with infusion volume and reached a critical value in the surrogate, above which crack formation occurred. While results here are specific to healthy liver tissue, the framework for EC-ethanol formulation and delivery can be applied to tailor treatment to different tissue types and drug delivery applications.

II. METHODS

Salient characteristics of the injection process are: (1) concentration of EC mixed with ethanol; (2) needle insertion rate; (3) needle insertion depth; (4) infusion rate; and (5) volume of infused material. Since a full factorial design is unwieldy, parameters were systematically varied in a series of four experiments to reduce the parameter space, as summarized in Table I. Experiment 1 was designed to establish a standard needle insertion rate and depth of insertion. The former was chosen based upon maximizing the seal between the surface of the needle and the tissue (to diminish backflow along the needle). The latter was chosen based upon achieving a target net depth of insertion of 4 mm below the tissue surface. Specifically, 4 mm was selected because: (1) it is a common therapeutic depth achieved by other techniques (cryotherapy and thermocoagulation) used to treat superficial lesions, and (2) backflow is more likely in superficial injections [41], so by selecting a shallow injection depth, we were ensuring that our methods could be applicable to both shallow and deeper injections. Moving forward, needle insertion parameters were kept constant. Experiment 2 focused upon the roles of EC concentration and injection rate in maximizing injection depot volume. Then, experiments 3 and 4 investigated preventing crack formation by staying below the critical pressure (the pressure at which fracture occurs). Experiment 3 was performed in a transparent tissue-mimicking surrogates to allow direct visualization of crack formation and the role of infusion pressure, followed by validation in ex vivo liver tissue in Experiment 4. For experiments 1, 2, and 4, n=5 tissue samples for each experimental group were used from 5 separate livers in total. For experiment 3, n=4 surrogate samples were used for each infusion volume.

Table I.

Summary of experiments and key parameters varied in each experiment.

Exp.	Sample	Insertion rate (mm/s)	Insertion depth (mm)	EC %	Infusion rate (mL/hr)	Infusion volume (μL)	Key Results
1	Liver (n = 5)	0.2, 2, 10	4, 5.2, 8, 10	-	-	-	2 mm/s minimizes tissue damage and 5.2 mm programmed depth leads to 4 mm actual depth
2	Liver (n=5)	2	5.2	0, 3, 6	1, 10	100	6% at 10 niL/hr maximizes depot volume but forms cracks
3	Surrogate (n=4)	2	5.2	6	10	10, 25	There is a critical pressure at which crack formation occurs
4	Liver (n = 5)	2	5.2	6	10	50, 100, 200	50 μL stays below the critical pressure and maximizes normalized depot volume

A. Tissue Preparation

Freshly excised swine livers were obtained from Hampshire or Duroc cross-bred pigs aged 4 – 6 months (from Hatley farms in Hurdle Mills, North Carolina, USA). After excision, livers were stored in Krebs-Ringer Bicarbonate Buffer (Sigma Aldrich, K4002, St. Louis, MO) for approximately 2 hours during transport to our laboratory. Each liver was cut into approximately 2 cm x 2 cm x 1.5 cm (length x width x depth) pieces with operating scissors, and pieces with a visible vessel or duct were not used. Specimens were stored in Krebs-Ringer Bicarbonate Buffer until injections was performed. Twelve individual tissue specimens were typically prepared from each liver and used in experiments on the day of collection.

B. Selection of Needle Gauge and Insertion Rate, and Depth

Fig. 1a is a schematic summarizing the experimental methodology. A 27-gauge (with inner diameter of 0.21 mm and outer diameter of 0.41 mm) (G) needle size was selected for all injections. Larger needle diameters have been found to cause tissue damage leading to backflow along the needle pathway [41] while smaller needle diameters have been shown to reduce injection pain [42]. However, smaller 31G needles led to high pressures within the needle to inject the more viscous solutions (3 or 6% EC-ethanol), and therefore required high forces applied to the syringe. Since high forces on the syringe limit future applications in which fluid is manually injected, 27G needles were a preferred choice. They engendered less backflow vs. larger needles, but lower force required compared to smaller needles.

Fig. 1.

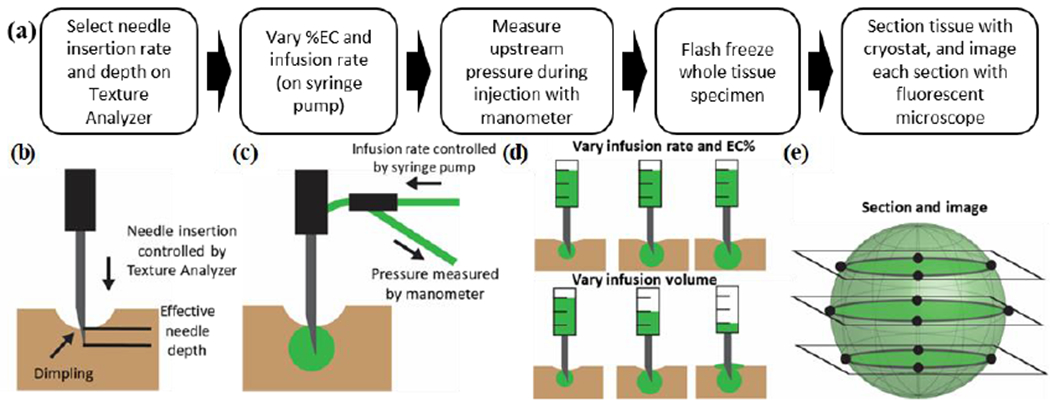
Overview of experimental methodology. (a) To standardize the injection process, the needle insertion rate and depth were selected to ensure the needle tip reached a consistent depth. Next, different infusion rates and EC concentrations were investigated. The infusion pressure was monitored both during the infusion and for a 5-minute monitoring period after the injection. Following the 5-minute monitoring period, tissue was flash frozen, sectioned, and imaged with a handheld fluorescent microscope to visualize the injected fluid distribution. (b) To select the optimal insertion rate, the effective needle depth was measured for insertion rates of 0.2, 2, and 10 mm/s. The degree of dimpling (reversible tissue deformation that occurs prior to puncture) depended on the insertion rate. (c) Fluid flowed from a syringe placed on the syringe pump, through an adaptor on the tip of the Texture Analyzer, through the needle, and finally into the tissue sample. (d) Infusion experiments investigated either the impact of infusion protocol for infusions of 100 μL or the effect of infusion volume for a single infusion protocol on both injected fluid distribution and infusion pressure. (e) Sectioning frozen tissue samples and imaging the 2D fluid distribution enabled 3D reconstruction of the injected fluid distribution.

Our initial Experiment 1 addressed the conditions leading to dimpling of the tissue surface and the seal between the needle and the tissue (which impacts backflow). The rate of needle insertion into the tissue and the net depth of insertion (net needle displacement) were controlled using a Texture Analyzer (model CT-3 with 4500 g load cell, 0.1 mm resolution, Brookfield Ametek, Middleboro, MA). We investigated a range of insertion rates (0.2 – 10 mm/s) and insertion depths (4 – 12 mm) suitable for treatment of superficial lesions. The needle was firmly attached to the Texture Analyzer brought into contact with the sample perpendicular to the surface. Recording of injection distance began once a load of 0.1 g was exceeded. While the Texture Analyzer could accurately lower the needle to a programmed depth, tissue dimpling (in which tissue deformed around the needle tip) led to a lower effective needle depth into the tissue than the programmed depth. We defined effective needle depth as the distance of the needle tip below the surface (Fig. 1b). To measure this, the needle was marked at the surface of the tissue after insertion. The distance between the mark and the tip of the needle (effective needle depth) was measured using digital calipers (with 0.01 mm resolution) after the needle was removed.

C. Solution Preparation and Use of Fluorescein to Visualize Injected Ethanol

Injectate solutions were prepared by mixing 200 proof ethanol (anhydrous ethanol, Koptec, King of Prussia, PA) with EC (Item: 247499, Sigma Aldrich, St. Louis, MO) using a magnetic stir bar at room temperature in a sealed container for 2-4 hours, within 24 horns preceding an experiment. Solutions were then loaded into a 3 mL syringe (BD Medical, Columbus NE). A 3-way stopcock with Luer lock connections (Cole Palmer, Vernon Hills, IL) was connected to the syringe. Both the pressure sensor (PX26030, Omega, Bridgeport, NJ) and rubber tubing (1/4” inner diameter, McMcmaster-Carr, Douglasville, GA) leading to the needle were connected to the other openings (Fig. 1c). To prevent damage to the pressure sensor from excessive pressure, the sensor was either removed from the stopcock or the outlet valve was closed whenever the syringe was operated manually or at a high infusion rate (> 10 mL/hr. Tubing was connected to the needle via a custom-made adaptor that attached to the Texture Analyzer. This controlled the needle insertion process and ensured stability of the needle.

The volume and distribution of the injected solution within the tissue are primary outcomes of the procedure. In principle, these could be measured by imaging serial sections of tissue after injection, e.g. using Raman spectroscopy (distinguishing unlabeled ethanol from tissue) [43]. However, such approaches with unlabeled materials were deemed too time-consuming, given the sample size and spatial resolution necessary for this study. In contrast, addition of a fluorophore (fluorescein) to the injection solution enabled adequate imaging time and spatial resolution, via quantitative fluorescence microscopy. Although fluorescein is slightly larger than ethanol (radii of gyration R_G = 4.8 Å [44] vs. 2.6 Å [45], respectively), since fluorescein is ethanol-soluble, but water-insoluble the motions of both molecules are similar following injection into tissue . Thus, it was deemed a suitable marker for the presence of ethanol in these experiments After the EC was fully dissolved in solution, fluorescein (Sigma Aldrich, Item: F2456, St. Louis, MO) was added and mixed until dissolved. Initially, visualization of our injections was optimized by preparing 6% EC-ethanol with a range of fluorescein concentrations (0.15% to 2% w/v). 1 mL of each solution was poured into a petri dish and then imaged with a custom fluorescent microscope described in section G below (with room lights off) to capture the fluorescent signal from the solution. Then, the average intensity in the green channel of the image was quantified in Matlab (R2018b, Mathworks Inc., Natick, MA) and plotted for each concentration. We found that 0.25% (w/v) fluorescein maximized image intensity, and this was used in all injections in our study (Fig S2).

D. Selection of EC Concentration and Infusion Rate

In Experiment 2 we began to evaluate dependence of the injected fluid distribution upon EC concentration and infusion rate. The selected infusion volume was 100 μL, based on the assumption that our target treatment volume of tissue is 500 μL (1 cm diameter) and given literature result that 10-minute exposure to 20% ethanol is cytotoxic [7]. Clinically, liver tumors 3 cm or smaller are candidates for ablation. The infusion rates tested were 1 and 10 mL/lir. While low infusion rates may produce a more favorable injected fluid distribution [46], their long infusion times preclude clinical adoption. Tested EC concentrations in ethanol were 0%, 3%, and 6%. The 3% EC concentration was used initially, since it marks the onset of a plateau in the ratio of gel mass to EC mass following mixing of EC-ethanol with water. Therefore, at a concentration of 3% or greater, a substantial mass of gel will form following injection into an aqueous tissue. The maximum concentration tested was 6%, which was informed by our prior study that found viscosity of EC-ethanol increases as the square of concentration below entanglement concentration of about 45 mg/mL (approximately 5%) and has a much stronger power-law dependence of viscosity on concentration beyond 45 mg/mL [38], and also the need to avoid high injection pressures that would be necessary to inject highly viscous solutions through narrow needles.

E. Normalizing Distribution Volume Measurements to Account for Tubing Compliance

In this study, infusion rate was controlled by a constant-rate syringe pump (NE-1000, New Era, Farmingdale, NY). Fluid flowed out of the syringe pump through approximately 25 cm of rubber tubing (Sigma Aldrich, ItemZ685631, St. Louis, MO) which exhibited some elasticity. While the flow rate of fluid leaving the syringe (Q_syringe) was controlled by the syringe pump, the rate of fluid passing through the needle (Q_infused) was affected by the elastic expansion of the tubing (Q_tubing, Fig. S1a). The volume of unpressurized tubing was approximately 500 μL and the tubing expanded with a compliance of 0.54 ± 0.04 μL/kPa (C_tubing, Equation 1). This compliance was determined by plugging the end of the tubing while infusing fluid and measuring the infusion pressure (data not shown). Actual infusion volumes are tabulated in Fig. S1b. To account for the effect of tubing expansion on measured injection distribution volumes, values of measured volumes were adjusted according to Equation 3.

$${\text{V}}_{\text{tubing}}{\text{(P) = V}}_{\text{tubing}}{\text{(P = 1 atm)+ ΔP/C}}_{\text{tubing}}$$ (1)

$$V_{infused,actual}=V_{infused,nominal}+V_{tubing}$$ (2)

$${\text{Vol}}_{\text{Distr}.,\text{adj}.}{\text{= Vol}}_{\text{Distr}.,\text{meas}.}*\frac{V_{infused,actual}}{V_{infused,nominal·}}$$ (3)

The average ± standard deviation of the ratio of the adjusted infused volume to the nominal infused volume were 0.90 ± 0.09 (n=40). Prior to beginning experiments, the pressure sensor was calibrated by applying a range of pressures with a water column. The sensor signal at each height (0, 50, 100, and 150 cm) was used to fit a linear calibration curve. This calibration curve was used to convert experimental measurements to pressure units. Infusion pressure was calculated by subtracting the pre-infusion pressure. The post-infusion pressure was normalized by dividing by the final infusion pressure.

F. Injection and Specimen Freezing Procedures

To initiate injection experiments, the needle was inserted at a predetermined rate and depth as controlled by the Texture Analyzer. Once the needle was inserted, fluid was infused via the syringe pump. The needle remained inserted for 5 minutes following the end of the fluid infusion phase, during which the upstream fluid pressure (at the top of the needle) was monitored. After the 5-minute post-infusion monitoring period, tissue was placed in a hand-folded aluminum foil (Genesee Scientific, Research Triangle Park, NC) container and covered in optimum cutting temperature (OCT) gel (Sakura Finetek, Torrance, CA). The sample was submerged in chilled 2-methylbutane (Sigma, Item: 277258, St. Louis, MO) in a −80°C freezer for 10 minutes. Then the sample was wrapped in aluminum foil and stored in the −80°C freezer.

G. Sectioning, Imaging, and Image Processing

Frozen samples were sectioned with a cryostat microtome (Microm HM 505 E, Walldorf, Germany) kept at −30°C. Prior to sectioning, the aluminum foil was removed, and excess OCT gel was shaved off. Samples were attached to the microtome chuck by applying room temperature OCT and placing them in the cryotome for 10 minutes until they solidified. Samples were then sectioned at a thickness of 500 μm. After a section was cut, the sample was removed from the cryotome and placed in a custom-made holder for the fluorescent microscope that blocked out ambient light and kept the working distance constant throughout the imaging process. Images were acquired with a custom hand-held fluorescent microscope developed by our group. Briefly, we redesigned the Pocket colposcope, previously described in [47], for fluorescence imaging of fluorescein. Specifically, we added blue LEDs (470 nm) at the tip of the probe to excite fluorescein. A band pass filter (535 nm with a 43 nm bandwidth) was added in front of the camera to ensure only fluorescence from fluorescein reached the camera without cutting off any of the illumination from the blue LEDs. After imaging, each sample was placed back into the cryostat, sectioned, and imaged again.

Two-dimensional images of each section were used to reconstruct the three-dimensional fluid distribution (Fig. 1e). Images were processed in Matlab to quantity distribution volumes from each injection. First, the images were cropped to 1000 x 1000 pixels to remove the edges of the tissue, which did not provide useful information. Then the green channel was thresholded to isolate the fluorescein signal. Specifically, the intensity at the edge of the depot was selected and used as a global threshold to create a binary image, which is a widely used technique to isolate features within an image based on intensity information [48]. The border of the binary image was then cleared and small regions less than 200 connected pixels were deleted to remove noise. Then the total area and area of the largest region (typically the depot) were quantified from the binary images using ‘regionprops’ within Matlab. To quantify the total volume, each slice from the 3D image stack was multiplied by the depth of the slice, and the sum of all slices was computed. Representative images that illustrate each step of the algorithm are included in Fig S3a–b. The algorithm was repeated 5 times on representative samples to demonstrate its reproducibility (Fig S3c–d).

H. Determination of Fracture Pressure

Experiments 3 and 4 addressed conditions giving rise to crack formation in the tissue during an injection. Crack formation occurred when the applied stress on the tissue was larger than the tissue tensile strength. When the applied stress was smaller than the tissue tensile strength, the tissue deformed creating a fluid-filled cavity. When the applied stress was larger than the tissue tensile strength, the tissue fractured and the infusion pressure decreased, as the tissue resistance dropped. The pressure at which fracture occurs is called the critical pressure. Keeping the infusion pressure below the critical pressure prevents crack formation, and presumably leads to a more symmetric fluid distribution.

These experiments used an EC concentration of 6% and an infusion rate of 10 mL/hr, based on results of Experiment 2. Since infusion pressure increases with infusion volume below the critical pressure due to fluid accumulation at the injection site, the infusion volume was varied in these experiments. First, in Experiment 3, a tissue surrogate material comprised of agarose was used to probe the dynamics of the injection process, and to demonstrate that there is a critical injection pressure above which crack formulation occurs. This material is transparent, which facilitated visualization of crack formation. Such material has been used previously in optimizing local drug delivery protocols [49, 50]. Surrogates were fabricated by dissolving agarose (UltraPure Agarose, Invitrogen, Carlsbad, CA) in deionized water over a hot plate until the solution was clear. Approximately 50 mL of this solution was then poured into vials (20 dram polystyrene containers, Fisher Scientific, Hampton NH), and allowed to cool at room temperature for 24 hours to solidify. In order to select the agarose concentration that most closely approximated tissue, the critical pressure during injection was measured for liver and for a range of agarose surrogates. This was done by using air infusion. The air was immiscible with the water inside the tissue and did not flow into the tissue. The applied stress was equal to the upstream infusion pressure, since there was no flow into the tissues/surrogate and the upstream pressure was the same as the downstream pressure due to the low viscosity of air. The tensile strength then corresponded to the critical pressure during the air infusion.

To visualize changes in agarose structure as a function of pressure during infusion of 6% EC-ethanol, both fluorescein (radius ~ 5x10⁻³ microns) and graphite (radius ~ 10 microns. Sigma Aldrich, Item: 282863, St. Louis, MO) were added to the solution. Since 1% agarose has a pore size of approximately 0.5 microns [51], only fluorescein could pass through intact agarose pores. Graphite could only flow out of the needle if the agarose gel were fractured allowing graphite to flow through the crack. This method enabled us to visualize the fracture of the gel as a result of exceeding its critical pressure and to correlate fracture with a decreasing post-infusion pressure.

I. Statistical Analysis

All statistical analysis was performed using R software (R Foundation for Statistical Computing, Vienna, Austria) [52]. For experiments 1, 2, and 4, a non-parametric two-way analysis of variance (Friedman test) was used, followed by a one-way analysis of variance (Kruskal-Wallis), and then a multiple comparisons test (Dunn’s test). For experiment 3, Dunn’s test was used. Non-parametric tests were used because of the extent of variability and small sample sizes. A significance level of p = 0.05 was applied to reject the null hypotheses in all analyses.

III. RESULTS

A. Selection of needle insertion rate and depth.

In this study, the needle insertion rate was selected to minimize dimpling, thereby maximizing the compressive stress between the tissue and needle interface and minimizing backflow. Specifically, the rate of needle insertion and the intended depth (“programmed depth”) were controlled with the Texture Analyzer. Then the actual needle depth was measured and compared to the programmed needle depth to calculate the amount of tissue dimpling. First, the insertion rate was varied for a programmed needle depth of 4 mm. Both needle insertion rates of 2 and 10 mm/s minimally influenced the actual depth in comparison to a rate of 0.2 mm/s as shown in Fig 2a (2.8 ± 0.2 and 2.7 ± 0.3 mm (mean ± s.d), respectively). However, 2 mm/s was chosen over 10 mm/s because tissue damage has also been demonstrated to increase with needle insertion rate, which leads to decreased compressive stress between the tissue and needle interface and increased backflow [30].

Fig. 2.

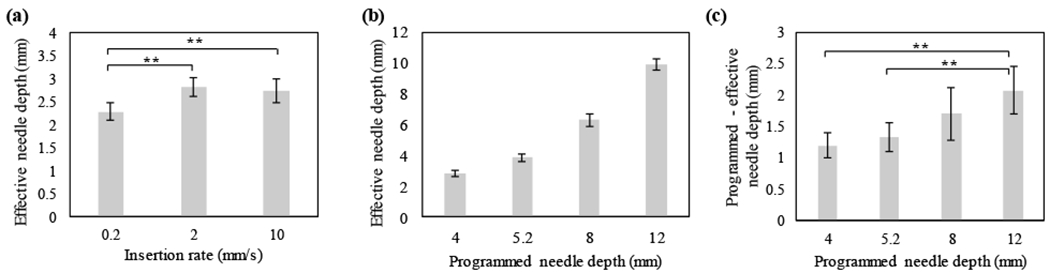
Relationship between insertion rate, programmed needle depth, and actual needle depth in liver. (a) Actual needle depth as a function of insertion rate for a programmed needle depth of 4 mm. Insertion rates ≥ 2 mm/s maximized actual needle depth (b) Actual needle depth increased with programmed needle depth for an insertion rate of 2 mm/s. (c) The difference between programmed and actual needle depth increased with programmed needle depth. All groups had a sample size of n = 5. ** = p<0.05.

Next, the programmed needle depth was selected to achieve the target effective needle depth of 4 mm. A target effective needle depth of 4 mm was chosen because it is the approximate therapeutic depth achieved by superficial ablative techniques (e.g. cryotherapy, thermocoagulation [53]). The effective needle depth in tissue increased non-linearly with programmed needle depth (Fig 2b). As the programmed needle depth increased, the deviation between the actual and programmed needle depth (i.e. amount of dimpling) also increased (Fig 2c). To achieve the target effective depth, a programmed needle depth of 5.2 mm was chosen (4.9 ± 0.2 mm).

B. Optimization of Infusion Rate and EC Concentration

Next, we evaluated the effect of EC concentration and infusion rate on the injected fluid distribution using a needle insertion rate of 2 mm/s and a programmed needle depth of 5.2 mm. Representative three-dimensional reconstructions resulting from each EC concentration-infusion rate groups investigated are compiled in Fig 3a. The XY, XZ, and YZ projections are shown in Figs. 3b, 3c, and 3d respectively. In all groups, the fluid distribution contained a roughly spherical region centered around the needle tip (referred to as the “depot volume”) above a narrow cylindrical region parallel with the initial fluid velocity as it exits the needle (the “non-depot volume”). Fig 3e illustrates the segmentation of the fluid distribution into depot (green) and non-depot (red) regions for an effective needle depth of approximately 4 mm. The transition depth between depot and non-depot volume was set at 10 mm, which was the approximate lower bound for the spherical region. The total distribution volume, the depot, non-depot and the ratio of depot to total distribution volume (referred to as the “normalized depot volume”) for each group are plotted in Figs. 3f, g, h, and i, respectively. While the nominal infusion volume for all groups was 100 μL, the actual infusion volume varied as a result of non-zero tubing compliance (described in Fig. S1) and distribution volume measurements were normalized to account for this. The total distribution volumes for all groups were less than the actual infusion volume. The total volume was larger for ethanol infusions compared to those for 3% and 6% EC-ethanol (83.2 ± 36.1 μL vs. 42.9 ±40.0 μL vs. 53.0 ±20.0 μL,p<0.05).

Fig. 3.

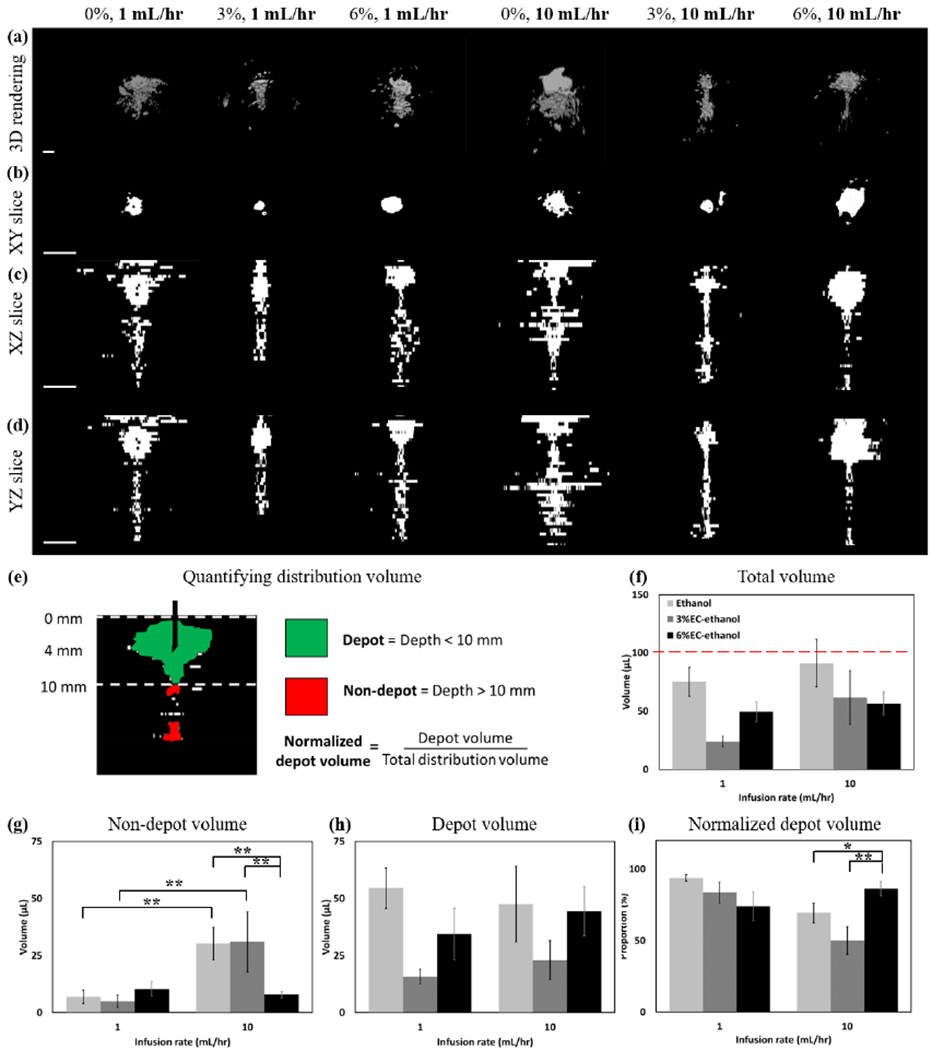
Representative images of 0%, 3%, and 6% EC dissolved in ethanol injected at both 1 and 10 mL/hr are shown in each column. A needle insertion rate of 2 mm/s and programmed needle depth of 5.2 mm were used for all experiments. (a) 3D representations of the distribution volume. (b) XY, (c) XZ, and (d) YZ slices taken through the center of the injection cloud. All scale bars are 5 mm. Each z-slice was adjusted to keep the segmented region in the center of the image. (e) To assess the amount of fluid localized the needle tip, fluid was segmented into the depot volume, which was defined as the largest region around the needle tip in the top 10 mm of the tissue, and non-depot volume, which was defined as the fluid below 10 mm into the tissue. Depot and non-depot are colored in green and red, respectively. (f) The total injected fluid distribution volume was quantified for infusions of 0, 3 and 6% EC dissolved in ethanol injected at a rate of either 1 or 10 mL/hr. The nominal infusion volume for all injections was 100 μL and is represented by the red dotted line. The total distribution volume was highest for pure ethanol (p<0.05) and a rate of 10 mL/hr (N.S.). (g) The non-depot volume was highest for pure ethanol and 3% EC-ethanol. 6% EC-ethanol was the only formulation in which non-depot volume did not depend on infusion rate. (h) The depot volume for each rate and EC concentration was quantified (i) The normalized depot volume (depot volume / total distribution volume) quantified the concentration of fluid within the depot. 6% EC-ethanol infused at 10 mL/hr had the largest proportion of injected fluid within the depot. All error bars depict standard error and all groups had a sample size of n = 5. * = p<0.1, ** = p<0.05.

The non-depot volumes for pure ethanol and 3% EC-ethanol were dependent on flow rate – the non-depot volume was greater for 10 mL/hr compared to 1mL/hr infusions (30.3 ± 16.0 μL vs. 7.0 ± 6.7 μL, p < 0.05 for pure ethanol and 31.0 ± 29.4 μL vs. 6.0 ± 5.0 μL, p < 0.1, for 3% EC-ethanol, respectively). The non-depot volumes for 6% EC-ethanol were not dependent on flow rate (10.4 ±7.1 μL vs. 8.0 ±3.3 μL, p=N.S). At a flow rate of 10 mL/hr, 6% EC-ethanol had a significantly lower non-depot volume compared to both pure ethanol and 3% EC-ethanol. The normalized depot volume, defined as the ratio of the depot volume to the total volume, represents the proportion of the injected fluid that is localized around the needle tip. A larger normalized depot volume is indicative of a more uniform distribution of ethanol around the needle tip and less fluid leakage. While pure ethanol infused at a rate of 10 mL/hr had the largest depot volume, it had a significantly larger non-depot volume than 6% EC-ethanol infused at 10 mL/hr (30.3 ± 16.0 μL vs.8.0 ± 3.3 μL, p < 0.05). Thus, at a rate of 10 mL/hr, the normalized depot was highest for 6% EC-ethanol (86.3 ± 11.0%) as compared to ethanol (69.5 ± 15.4%, p < 0.1) and 3% EC-ethanol (50.0 ± 21.6%, p <0.05).

C. Relationship of Crack Formation and Infusion Pressure

Although 6% EC-ethanol had the highest normalized depot volume, 13.6 ± 11.0% of the fluid was outside the depot. As noted above, when fluid is infused into a poroelastic material (e.g. tissue), it imposes stress on the solid network that increases with infusion volume [32]. As the stress increases, fracture may occur leading to the formation of a high-permeability path away from the injection site at a material-dependent critical pressure [54]. To demonstrate the effect of infusion pressure (as controlled by infusion volume) on crack formation, agarose surrogates were used because they are poroelastic (like tissue) and transparent, which enables visualization of fluid-material interactions. The agarose concentration was selected to match the critical pressure measured for liver tissue (Fig. S4).

To determine the effect of infusion pressure on crack formation, solutions composed of EC, fluorescein, and graphite mixed in ethanol were injected into agarose surrogates. While fluorescein (diameter = 1x10⁻³ μm) is substantially smaller than the pore size of agarose (0.5 μm [51]), graphite is substantially larger (~10 μm). Fluorescein traveled freely through the interstitial space, but graphite only left the needle if the agarose structure were fractured creating a channel larger than its diameter. When the infusion pressure remained below the critical pressure of agarose surrogates, no graphite was visible, but fluorescein could be seen emanating from the needle tip. (Fig. 4a). When the infusion pressure exceeded the critical pressure of agarose surrogates, both graphite and fluorescein were both visible (Fig. 4b). The infusion pressures for both the fractured and un-fractured cases in agarose surrogates relative to the measured critical pressure are shown in Fig 4c.

Fig. 4.

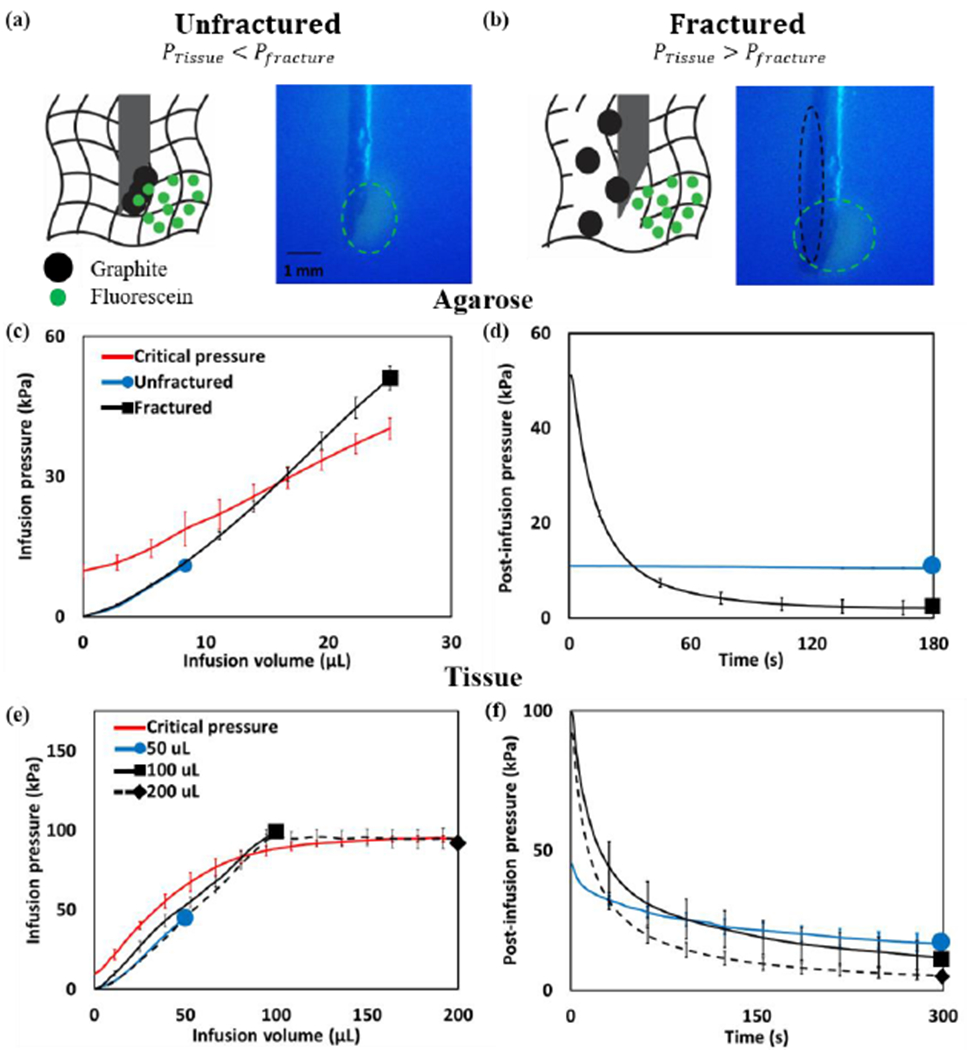
Infusion of fluid into a poroelastic material can cause fracture. To observe infusion-induced fracture, solutions containing ethyl cellulose, fluorescein (smaller than the agarose pore size), and graphite (larger than the agarose pore size) were infused into agarose surrogates at a rate of 10 mL/hr. (a) If the infusion pressure remained below the critical pressure, the gel remained unfractured and only fluorescein was visible (green circles). (b) If the infusion pressure exceeded the critical pressure, the gel fractured and both fluorescein and graphite were visible (black circles). (c) During the infusion, the infusion pressure increased monotonically for both the unfractured (blue) and fractured (black) groups. The red line illustrates the critical pressure, which depended on infusion volume (since the pressure gradient across the needle increased with infusion volume). (d) The post-infusion pressure remained elevated for the unfractured group but dropped for the fractured groups. (e) In tissue, the infusion pressure remained below the critical pressure for the infusion of 50 μL (blue), but infusions of 100 and 200 μL (black) exceeded the critical pressure (red). (f) The post-infusion pressure was highest for the 50 μL as compared to the 100 and 200 μL groups. The sample size for agarose experiments was n=4, and for tissue experiments, n=5. All error bars depict standard deviation.

When air (a compressible fluid) was infused into a material, fracture could be clearly detected by a decrease in infusion pressure coinciding with its expansion. A similar decrease could be observed for 6% EC-ethanol (an incompressible fluid) due to the formation of a high-permeability path at low infusion rates (0.1 mL/hr, Fig S4). At higher rates, this signal was obscured due to the increased pressure associated with fluid flowing through the needle. Fracture could also be detected by observing the pressure after fluid infusion had stopped (referred to as the “post-infusion pressure”), regardless of the infusion rate as observed in Fig. 4d, the post-infusion pressure dropped dramatically due to the formation of a crack in the agarose structure (illustrated by the spread of graphite). The final post-infusion pressure was 9.7 ± 0.4 kPa and 2.1 ± 0.2 kPa (Fig 4d) for the un-fractured and fractured groups, respectively. The normalized post-infusion pressure (final post-infusion pressure divided by final infusion pressure) was significantly higher for the un-fractured group compared to the fractured group (89.2 ± 2.1 % vs. 4.2 ± 3.6 %, p <0.01).

A similar relationship between infusion pressure and post-infusion pressure was observed in tissue. The nominal infusion volumes investigated were 50, 100 and 200 μL of 6% EC-ethanol infused at a rate of 10 mL/hr. The actual infusion volume during the infusion phase for these groups (accounting for tubing compliance as described in Fig. S1) was 26.6 ± 3.6 μL, 46.5 ± 15.0 μL, and 149.4 ± 17.6 μL, respectively. During the 50 μL infusion, the maximum infusion pressure remained below the critical pressure in tissue while at 100 and 200 μL, the maximum infusion pressure exceeded the critical pressure (Fig 4e). As observed in agarose, the post-infusion pressure in tissue remained elevated for sub-critical pressure infusions (Fig 4f). The final infusion pressures for the 50, 100, and 200 μL infusions were 45.1 ± 3.7 kPa, 99.2 ± 27.7 kPa, and 91.9 ± 33.4, respectively. The final post-infusion pressures for the 50, 100, and 200 μL infusions were 16.7 ± 8.3 kPa, are 11.6 ± 11.4 kPa and 5.1 ± 3.8 kPa, respectively. For 50 μL infusions, the normalized post-infusion pressure in tissue was significantly higher than those of 100 and 200 μL infusions (37.0 ± 16.0% vs. 11.7 ± 11.5% and 5.6 ± 4.1%, p < 0.05). Pressure curves for all injections where the concentration of EC, infusion rate, and infusion volume, were varied can be found in Figs. S5 and S6.

D. Relationship between Infusion and Depot Volume

Experiment 4 assessed the dependence of the fluid distribution on the infusion volume. Distribution volumes for infusions of 50, 100, and 200 μL of 6% EC-ethanol were quantified from fluorescein imaging of liver cross-sections. Representative three-dimensional reconstructions for each group are compiled in Fig 5a. Two-dimensional projections along the XY, XZ, and YZ planes are shown in Fig 5b, c, and d, respectively. While the total distribution volume increased with infusion volume (Fig 5e) the 50 μL group appeared to have a lower non-depot volume than either the 100 or 200 μL groups, which appeared to have a significant amount of fluid below 10 mm. To account for the difference in infusion volume, the ratio of the total distribution volume divided by the infusion volume is plotted in Fig 5f. The depot volume and the normalized depot volume (depot volume / total distribution volume) are plotted in Figs. 5g and 5h, respectively. The normalized depot volume was highest for the 50 μL (98.2 ± 2.0%) as compared to the 100 (86.3 ± 11.0%, p < 0.05) and 200 μL (73.8 ± 19.4%, p < 0.05) groups, indicating that an infusion volume of 50 μL achieved the largest normalized depot volume.

Fig. 5.

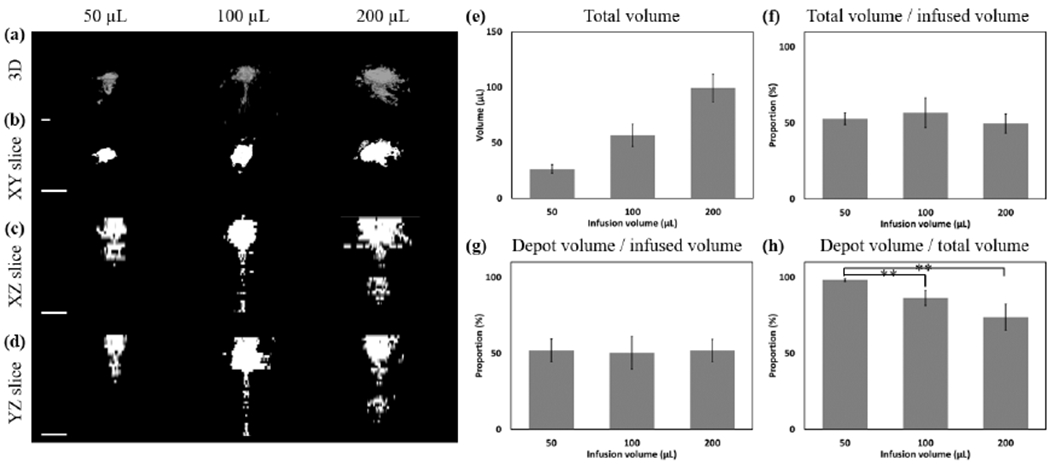
Representative injections of 6% EC injected at 10 mL/hr to different infusion volumes. Images of 50, 100, and 200 μL infusions are shown in each column. (a) 3D representations of the distribution volume. (b) XY, (c) XZ, and (d) YZ slices taken through the center of the injection cloud. All scale bars are 5 mm. (e) The total distribution volume is quantified for nominal infusion volumes of 50, 100, or 200 μL infusions of 6% EC-ethanol at 10 mL/hr. (f) The ratio of the total distribution volume divided by the infused volume had no clear dependence on infusion volume. (g) The absolute depot volume increased with infusion volume. (h) The normalized depot volume was highest for 50 μL infusions. All error bars depict standard error and all groups have a sample size of n = 5. ** = p<0.05.

IV. DISCUSSION

EC-ethanol ablation has the potential to be an effective ablation treatment with particular relevance to patients who already benefit from ethanol ablation, patients in LMICs without access to treatment, or to supplement existing therapies. While initial studies demonstrated enhanced efficacy against tumors with addition of EC to ethanol [38], clinical adaptation will require reliable treatment of diseased tissue while sparing surrounding healthy tissue. This study investigated the relationships amongst salient injection parameters and the injected fluid distribution. Ideally, this fluid should be localized around the needle tip to induce maximum cytotoxic effect in the target diseased tissue, with minimal damage to surrounding tissue. Experiments were performed in liver tissue because it was the initial site of clinical use for ethanol ablation [6].

Understanding and optimizing salient injection parameters requires relating them to key measures of injection performance. For the parameters tested, a full factorial experimental design is unwieldy and would require over 200 combinations. To systematically assess the parameter space, experiments were conducted in four separate phases (summarized in Table I). Here, this entailed mitigating the effects of backflow (defined as fluid flow along the needle to the tissue surface) and of crack formation (defined as the formation of high-permeability paths within the tissue emanating from the needle tip). In this study, the needle insertion rate was selected to minimize dimpling (i.e. tissue deformation during needle insertion), thereby reducing tissue damage and maximizing the compressive stress between the tissue and needle interface to minimize backflow [30, 31]. Our results indicated that for ex vivo swine liver, a slow insertion rate (0.2 mm/s) had the largest amount of dimpling compared to 2 and 10 mm/s rates (Fig 2a). Noting that high insertion rates could also cause tissue damage independent of dimpling, due to elevated shear stresses within the tissue, we selected a rate of 2 mm/s. As backflow is more likely in superficial injections [41], selecting a shallow injection depth ensures that our methods are applicable to shallow and deeper injections.

Crack formation was another source of fluid leakage away from the injection site and originated when the pressure exerted on tissue by the injected fluid exceeded a critical value. At the onset of injection, fluid flows into and through the porous tissue. This exerts a stress on the solid tissue components (cells and the extracellular matrix) and forms a fluid-filled cavity as fluid is infused [32–34]. At low infusion rates (approximately 10x slower than those investigated here), steady-state flow could be achieved with fluid flowing through the interstitial space without substantially altering tissue structure [32]. At high infusion rates, however, narrow tunnels (“micro-cracks”) of infused fluid have been observed when a radio-opaque dye has been injected into tissue [55]. Crack formation is most likely to occur in regions of decreased mechanical integrity of tissue (e.g. necrotic areas) and at interfaces (e.g. along vasculature) this process may eventually lead to the formation of a dominant crack (“macro-crack”) that substantially decreases fluid localization. Evidence of a macro-crack extending vertically from the injection site can be seen in Figs.3a–d and Figs. 5a–d. The formation of a macro-crack presents a challenge to achieving the localized fluid distribution necessary for ethanol ablation to achieve a therapeutic effect.

However, the addition of EC may mitigate the deleterious impact of crack formation. As previously reported, a gel forms when EC-ethanol is mixed with water due to the insolubility of EC in water [38]. As the fluid is injected into the tissue, the tissue is pressurized and water inside the tissue is squeezed out. The gel then forms around the needle tip as water diffuses in, which localizes the injected fluid due to the tight mesh in the cellulose gel network. The size of the mesh is quantified by the average distance between EC polymers as the correlation length in polymer physics. The correlation length is estimated to be 10 nm assuming it behaves as a freely jointed chain (estimated from a monomer size of 1 nm, 500 monomers [56] and a Kuhn length of 4 nm for cellulose [57, 58]).

In this study, the non-depot volume (fluid deeper than 10 mm in tissue) was low for all fluids at an infusion rate of 1 mL/hr. However, increasing the infusion rate from 1 mL/hr to 10 mL/hr led to significantly higher non-depot volumes for both ethanol and 3% EC-ethanol, but not for 6% EC-ethanol (Fig. 3g). Given that infusion pressure increases linearly with infusion rate [32], decreased fluid localization associated with higher rate infusions may have been the result of infusion-induced tissue deformation leading to the formation of a macro-crack. Our results suggest that the addition of an adequate amount of EC (6% in this case) may lead to accumulation of gel within the macro-crack, decreasing hydraulic conductivity and the rate of fluid leakage. To compare the efficacies of different injection protocols as quantified by the depot volume, we evaluated the injected fluid distribution for different injection parameters. To observe the fluid distribution, the fluorophore fluorescein was added to each solution. After injections, samples were frozen, cross-sectioned, and imaged. Fluorescein was selected because it is ethanol-soluble and water-insoluble, ensuring that it is present primarily in ethanol-rich regions.

The normalized depot volume, defined as the ratio of depot volume to total distribution volume, is the proportion of fluid that is localized around the needle tip. The normalized depot volumes were highest for either pure ethanol or 6% EC-ethanol infused at a rate of 1 mL/hr, and for 6% EC-ethanol infused at a rate of 10 mL/hr (Fig 3i). Since decreasing the infusion rate to 1 mL/hr would be more time-consuming and does not increase the normalized depot volume, infusing 6% EC-ethanol at 10 mL/hr is thus preferable. Further, although pure ethanol infused at a rate of 1 mL/hr had a high normalized depot volume, previous results indicate that it is significantly less effective than EC-ethanol in achieving tumor regression [38]. This was potentially due to the low resistance to clearance of pure ethanol, which may have led to shorter contact times with tissue in comparison to EC-ethanol.

Although the addition of EC reduced fluid leakage, avoiding infusion-induced fracture will further localize injected fluid, and could lead to improved therapeutic efficacy. The pressure-dependence of infusion-induced deformation has been explored in the development of a material characterization technique termed cavitation rheology, in which a fluid is infused until a maximum pressure is reached (“critical pressure”) [59]. Infusion of an immiscible fluid first leads to the expansion of a cavity via elastic deformation (“cavitation”) at the critical pressure and is followed by fracture as more fluid is infused.

We hypothesized that keeping the infusion pressure below the critical pressure would prevent fracture and decrease fluid leakage. We investigated this using agarose as a transparent tissue-mimicking surrogate. The use of a transparent material enabled real-time observation of fluid flow (as opposed to tissue in which only the final fluid distribution could be observed). The agarose concentration was selected to match the critical pressure of tissue (Fig S4). Including contrast agents smaller and larger than the agarose pore size (fluorescein and graphite, respectively) allowed us to discriminate between fluid flowing through intact agarose structure and fluid flowing through fractured agarose. When the pressure remained below the critical pressure, fluorescein was visible around the needle tip, but no graphite could be seen. In contrast, when the infusion pressure exceeded the critical pressure, the agarose fractured, and graphite was visible (Fig. 4a–b). In the unfractured case, the post-infusion pressure remained elevated in comparison to the fractured case (Fig 4d). Elevated post-infusion pressure may have been the result of low hydraulic conductivity, preventing fluid flow into the tissue. Although the specific mechanism of crack formation and its volume dependence vary between tissue and surrogates, these results establish that fracture may be detected by monitoring the post-infusion pressure. This is necessary because tissue is opaque preventing direct observation and the pressure drop across the needle is large the decrease in infusion pressure associated with crack formation cannot be detected during the infusion phase (as in Fig S4d).

A similar relationship between the infusion and post-infusion pressures was observed in tissue. Infusing a low volume (50 μL) ensured that the infusion pressure remained below the critical pressure, while infusing a larger volume (100 or 200 μL) exceeded the critical pressure (Fig 4e). As for agarose, exceeding the critical pressure led to a drop in the post-infusion pressure. For 50 μL, the normalized post-infusion pressure (defined as the ratio of the post-infusion pressure to the final infusion pressure) was significantly higher than the normalized post-infusion pressure for 100 or 200 μL infusions (Fig 4f). Representative fluid distributions illustrate the dependence of fluid localization on infusion volume (Fig 5a–d). As expected, the normalized depot volume was near 100% for 50 μL and was significantly larger than the normalized depot volume of 100 and 200 μL infusions (Fig 5h), demonstrating improved localization. This finding demonstrates that infusing low volumes may be advantageous when fluid localization is a priority. To treat a large volume of tissue, multiple infusions might therefore be considered. Although some leakage was seen with the 50 μL, this is likely because tissue is heterogenous and cracks may exist in the structure prior to the injection.

Limitations of this study warranting further investigation include the following. Although liver tissue was selected because it is relatively homogenous, ex vivo tissue has a collapsed vasculature, which allows for fluid flow through the vascular space as seen in Fig 3a–d and Fig 5a–d. The presence of collapsed vasculature makes fluid localization more challenging due to the presence of pre-existing channels in the tissue. Further, livers were cut into smaller pieces prior to injection, which decreased the distance from the injection site to the outside of each tissue piece, making leakage more likely. Additionally, ex vivo tissue does not account for clearance by either the vasculature or lymphatic systems, or for ischemia induced by damage to the vasculature. Although EC-ethanol separates into two phases upon mixing with water (a gel-phase with high EC concentration and a mobile phase with low EC concentration), the presence of EC likely slows vascular clearance. Conducting a similar study in vivo will likely further amplify the superiority of EC-ethanol over pure ethanol. Although healthy liver tissue was used for this study because it is more accessible than tumors, tumors are stiffer and contain necrotic regions that are more brittle, which may make crack formation more likely [60]. Further studies are necessary to investigate the effect of tissue type on injected fluid flow.

The use of non-zero compliance tubing presents another limitation. The elastic stretching of this tubing prevented direct control over the infusion rate of fluid into the tissue. While the impact of the actual infused volume on the distribution volume was taken into consideration by normalizing the distribution volumes, this approximation introduced a small source of error into our results because the exact infusion volume is not known and depends on flow resistance within the tissue. Additionally, we selected a shallower needle depth of 5.2 mm with an orthogonal needle insertion for our experiments. Future studies could investigate a larger range of needle depths and insertion angles, depending on the clinical application of interest. While this study utilized single injections through a conventional needle to better understand the relationship between fluid leakage, ethyl cellulose concentration, and infusion pressure, multiple injections or needles with multiple holes warrant investigation as they could produce a larger fluid distribution necessary for clinical translation.

V. Conclusion

In conclusion, the addition of EC increased the localization of an injected ethanol solution into ex vivo swine liver tissue. At the fluid infusion rates investigated here, the formation of cracks within the tissue could lead to substantial fluid leakage away from the injection site; however, EC formed a gel that may have occluded these cracks and reduced fluid leakage. We also evaluated injection parameters that minimized crack formation. Making use of a transparent tissue-mimicking surrogate material, we demonstrated that crack formation results from exceeding the critical pressure during infusion. Follow up experiments in liver tissue found that low infusion volumes resulted in an infusion pressure below the critical pressure, with minimal fluid leakage. While the results of this optimization are specific to ethanol injection to the liver, the framework may be applicable for other tissue types and for other types of drug delivery. Additionally, the methodological framework here could be used to optimize the distribution volume of ethanol to treat a variety of other medical conditions.