Abstract
To induce double-proton transfer (DPT) with guanine in a biological environment, 12 cytosine analogues (Ca) were formed by atomic substitution. The DPT reactions in the Watson–Crick cytosine–guanine model complex (Ca0G) and 12 modified cytosine–guanine complexes (Ca1-12G) were investigated using density functional theory methods at the M06-2X/def2svp level. The intramolecular proton transfers within the analogues are not facile due to high energy barriers. The hydrogen bond lengths of the Ca1-12G complexes are shorter than those in the Ca0G complex, which are conducive to DPT reactions. The DPT energy barriers of Ca1-12G complexes are also lower than that of the Ca0G complex, in particular, the barriers in the Ca7G and Ca11G complexes were reduced to −1.33 and −2.02 kcal/mol, respectively, indicating they are significantly more prone to DPT reactions. The DPT equilibrium constants of Ca1-12G complexes range from 1.60 × 100 to 1.28 × 107, among which the equilibrium constants of Ca7G and Ca11G are over 1.0 × 105, so their DPT reactions may be adequate. The results demonstrate that those cytosine analogues, especially Ca7 and Ca11, are capable of inducing DPT with guanine, and then the guanine tautomer will form mismatches with thymine during DNA replication, which may provide new strategies for gene therapy.
Subject terms: Density functional theory, DNA, Targeted gene repair
Introduction
Genetic mutations, alterations in the DNA sequence, have been identified as the cause of genetic disorders, tumor development and drug resistance in pathogenic microorganisms1–3. There are several types of mutations that can occur in DNA, such as copy number variations, duplications, deletions, insertion and single base substitutions, and the latter is the most common type (two-thirds of human genetic diseases are due to single-base alterations)4. Therefore, research on the mechanism of point mutations and single-base editing gene therapies has become an attractive topic4–6.
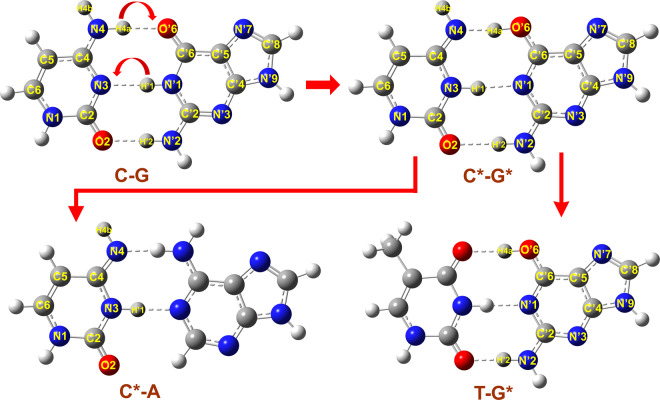
In double-helical DNA macromolecules, the complementarity between pyrimidines (cytosine and thymine) and purines (guanine and adenine) are due to hydrogen bonds. Each hydrogen bonding is essentially a proton trapped in an asymmetric double well potential between two electronegative atoms7. It has been hypothesized that proton transfer within the double well potential is an important mechanism of base substitution7,8. Tautomerism in guanine–cytosine base pairs resulting from intermolecular proton transfer has been suggested to be responsible for the universal guanine–cytosine to adenine–thymine mutation frequently observed in bacteria, fungi, plants, and animals9. The tautomers, indicated by an asterisks (C* and G*), resulting from the transfer of cytosine H4a to guanine and the back transfer from guanine H’1 to cytosine cannot form hydrogen-bonded complexes with their natural counterparts but can form mismatches with the bases A and T, respectively, during DNA replication (Fig. 1)7,10. Under normal circumstances, the relatively high energy barrier within the double well potential prevents the forward double-proton transfer (DPT) reaction, which accounts for the stability of DNA and the fidelity with which the genetic code is preserved and transmitted to daughter cells11,12. However, when the quantum nature of the proton is taken into account, the proton has a small yet finite probability of tunneling through the barrier12. When such double proton tunneling occurs during DNA synthesis, single base substitutions will occur. Fu et al. showed that among several possible DNA mutation processes, only the DPT mechanism could fully explain the universal mutation bias9.
Figure 1.
Structures and atomic numberings of the base pairs generated by GaussView 5.0. Top: Canonical C-G base pair and C*-G* base pair resulting from DPT; bottom: tautomers C* and G* mismatched to the bases A and T, respectively.
Previous studies have focused on various environmental factors that might facilitate intermolecular proton transfer within base pairs. Zhang, J. D. et al. showed that when an additional hydride is placed on the C6 and C4 positions of cytosine, the anionic complex formed, which facilitates guanine H1 transfer to the N3 site of cytosine13. Noguera, M. et al. found that protonation at the N7 and O6 sites of guanine, affording H+ GN7C and H+GO6C, strengthens the binding of the base pair and facilitates the N1–N3 single-proton-transfer reaction14. The influences of metal cation (Cu+, Ca2+ and Cu2+) coordination to the CG and AT base pairs on intermolecular proton transfer were studied using density functional theory (DFT) methods15,16. Alya, A. A. et al. investigated the DPT reaction of a GC base pair under the effect of uniform electric fields on the order of 108 to 109 Vm−1. They considered that fields applied along the axis of the double proton transfer in the -x (defined in the C to G direction) direction favor the canonical over the rare tautomers12. Chen, H. Y. et al.17 showed that the substantial effect of GC stacking originates from the electrostatic interactions between the dipoles of the outer GC base pairs and the middle GC•− base-pair radical anion, the extent of the charge delocalization is very small and has little effect on proton transfer in GC•−. The effect of the surrounding water molecules on the DPT in GC was investigated using DFT methods, and the results demonstrate that water is crucial to the proton reactions. It does not act as a passive element but actually catalyzes the DPT18.
Thus far, few studies have examined the effects of neutral cytosine analogues on the DPT reaction in CG base pare. The purpose of this study was to use existing physic-chemical understanding and predictive capability to identify neutral cytosine analogues that can induce DPT reactions with guanine under physiological conditions and provide new strategies for gene therapy.
Results and Discussions
Molecular structures of the modeled cytosine analogues
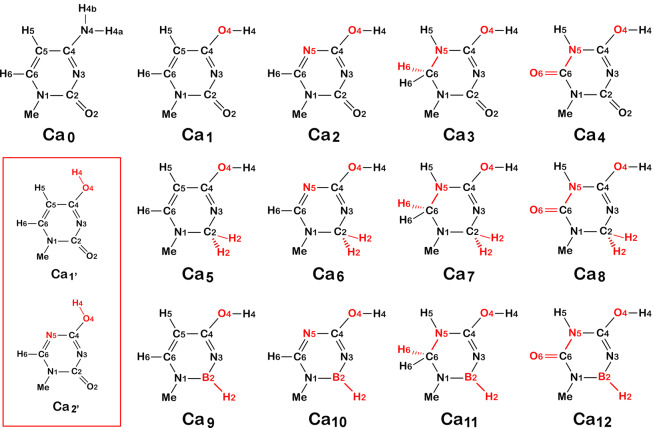
To provide minimized structures to mimic the Watson–Crick base pairing in duplex DNA or RNA, the sugar-attachment sites of cytosine and guanine were methylated19. To build a library of cytosine analogues, multiple atoms on the cytosine were replaced. To improve its ability to donate protons, the amino group at C4 was replaced by a hydroxy moiety. To improve the ability of N3 to accept protons, the carbonyl oxygen at C2 was replaced by a hydrogen, and separately, the C2 carbon atom was replaced by a boron atom. In addition, C5 was replaced by a nitrogen atom. The carbon atom at C6 was replaced with methine, methylene, and carbonyl moieties. A total of 12 cytosine analogues were modeled (Fig. 2).
Figure 2.
Molecular structures of the modeled cytosine analogues (Ca). The atoms that had being replaced were shown in red. The box showing the conformers of Ca1 and Ca2.
Energy barriers and rate constants of the intramolecular proton transfer
First, the structures of all the monomers, Ca0-12, were optimized by DFT M06-2X/def2svp method. The vibration analysis showed no imaginary frequencies in those monomers, indicating that the structures are stable at the current calculation level. Because both the O4 atom’s ability to provide protons and the N3 atom’s ability to acquire them are enhanced, the modeled cytosine analogues may undergo intramolecular proton transfer (H4 transfer from O4 to N3). Therefore, the intramolecular single proton transfer (SPT) reactions of all monomers were investigated. The calculated SPT energy barriers (ΔG≠) within the cytosine analogues ranged from 24.51 to 32.23 kcal/mol (Table 1). The forward reaction rate constants (calculated from ΔG≠) of the intramolecular proton transfer process range from 3.40 × 10−5 to 1.23 × 10−10 s−1, which indicate that the intramolecular SPT process are not facile. Therefore, the barriers of all cytosine analogues are relatively high for the proton to hop, indicating that these molecules can be used as candidate molecules to induce DPT reactions with guanine.
Table 1.
The values of the barrier of the intramolecular SPT reactions (ΔG≠), the energy difference between analogues and their conformers (ΔE), the forward and reverse barriers of the intermolecular DPT reactions (ΔG≠f and ΔG≠r), the forward and reverse reaction rate constants of intermolecular DPT reactions (kf and kr), and the equilibrium constants (Keq). All energy barrier values are given in kcal/mol.
| Can | ΔG≠ | ΔE | ΔG≠f | ΔG≠r | kf (s−1) | kr (s−1) | Keq |
|---|---|---|---|---|---|---|---|
| Ca0 | 43.13 | — | 8.31/8.80/7.60 | 0.22/0.71/−0.49 | 4.05 × 106 | 2.04 × 1012 | 1.99 × 10−6 |
| Ca1 | 30.71 | −2.99 | 1.07 | 1.60 | 1.14 × 1012 | 4.81 × 1011 | 2.37 × 100 |
| Ca2 | 32.23 | −0.49 | 0.87 | 1.16 | 1.57 × 1012 | 9.83 × 1011 | 1.60 × 100 |
| Ca3 | 28.19 | −4.45 | −1.20 | 3.79 | 4.53 × 1013 | 1.38 × 1010 | 3.28 × 103 |
| Ca4 | 31.50 | −4.59 | −1.54/−0.49/−1.15 | −0.08/0.97/0.31 | 1.43 × 1013 | 1.34 × 1012 | 1.07 × 101 |
| Ca5 | 29.86 | −2.97 | −0.62 | 4.24 | 1.77 × 1013 | 6.63 × 109 | 2.67 × 103 |
| Ca6 | 31.10 | −0.47 | −0.35 | 3.67 | 1.14 × 1013 | 1.67 × 1010 | 6.83 × 102 |
| Ca7 | 28.61 | −4.27 | −1.33 | 6.01 | 5.60 × 1013 | 3.75 × 108 | 1.49 × 105 |
| Ca8 | 31.68 | −4.55 | −0.48 | 4.95 | 1.41 × 1013 | 2.09 × 109 | 6.75 × 103 |
| Ca9 | 27.13 | −3.23 | 0.00 | 5.07 | 6.46 × 1012 | 1.72 × 109 | 5.09 × 103 |
| Ca10 | 28.19 | −0.52 | −0.20 | 5.22 | 8.94 × 1012 | 1.35 × 109 | 6.62 × 103 |
| Ca11 | 24.51 | −4.86 | −2.02 | 8.06 | 1.72 × 1014 | 1.34 × 107 | 1.28 × 107 |
| Ca12 | 28.36 | −4.89 | −0.74 | 5.62 | 2.15 × 1013 | 7.06 × 108 | 3.05 × 104 |
Due to the rotational orientation of the hydroxyl group, cytosine analogues have possible conformers in which the H4 atom is oriented toward the C5 or N5 atom, as shown in Fig. 2. The conformers were optimized by DFT at the current level and no imaginary frequencies were found. The present calculations show all the analogues have lower energy compared with their conformers (Table 1), indicating that these analogues are more stable than theirs conformers.
The vdW surfaces and ESP extrema of the cytosine analogues
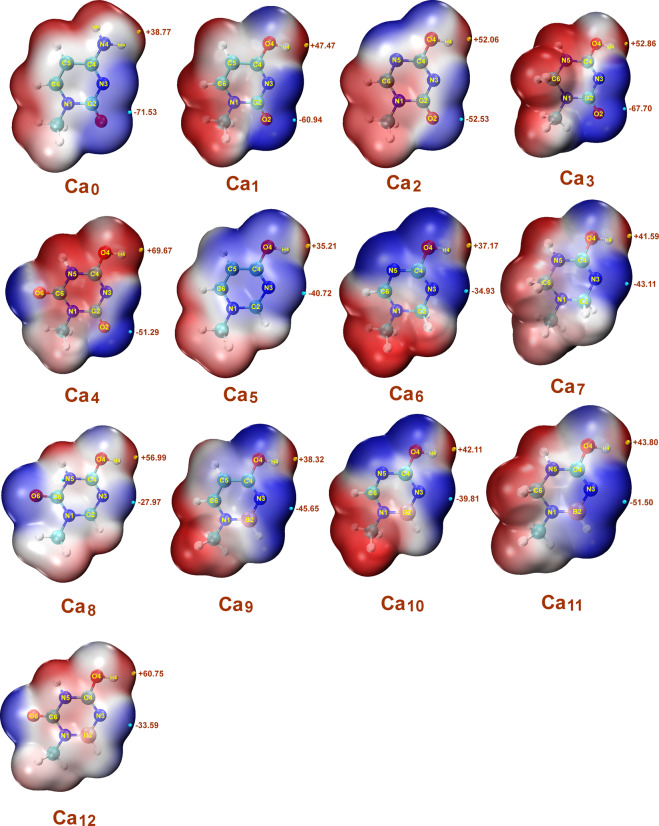
The electrostatic potential (ESP)-mapped van der Waals (vdW) surface has been used extensively for interpreting and predicting reactivity and intermolecular interactions of a wide variety of chemical systems20,21. The negative charge of the Ca0 molecule is concentrated on the O2 atom with an ESP extrema value of −71.53 kcal/mol. The positive electrostatic potential is centered around H4a of the amino group with an ESP extrema value of +38.77 kcal/mol (Fig. 3. Ca0). When the amino group at the C4 position of the cytosine was replaced by a hydroxy moiety, the ESP extrema value was increased to +47.47 kcal/mol, which is favorable for nucleophilic attack and release of the proton (Fig. 3. Ca1). Furthermore, when the C5 carbon atom was replaced by a nitrogen atom and the carbon atom at C6 was a methine, methylene, or carbonyl, the ESP extrema value of H4 was increased to +52.06 kcal/mol, +52.86 kcal/mol and +69.67 kcal/mol, respectively, which are all favorable for nucleophilic attack and release of the proton (Fig. 3. Ca2-Ca4). When the carbonyl oxygen at C2 was replaced by a hydrogen, the negative charges and the ESP extrema shift to the N3 atom, which is favorable for electrophilic attack and accepting a proton at the N3 site (Fig. 3. Ca5-Ca8). Furthermore, when the C2 carbon atom was replaced by a boron atom, the ESP extrema values of N3 are strengthen to −45.65 kcal/mol, −39.81 kcal/mol, −51.50 kcal/mol and −33.59 kcal/mol, which are all more favorable for electrophilic attack and accepting a proton at the N3 site (Fig. 3. Ca9-Ca12). So, these atomic substitutions, especially the substitutions of a hydroxy moiety for the amino group, a hydrogen for the carbonyl oxygen at C2 and a boron atom for the C2 carbon atom, are all favorable to induce DPT reactions with guanine.
Figure 3.
ESP-mapped vdW surfaces and ESP extrema of cytosine analogues generated by Multiwfn 3.6 and VMD 1.9.1 (http://www.ks.uiuc.edu/Research/vmd/). The red color indicates positive ESP regions on the vdW surface; the blue regions correspond to negative ESP regions of the vdW surface. The significant local maxima and minima of ESP on the vdW surfaces are represented as orange and cyan spheres, and labelled by values given in kcal/mol.
Energy barriers and equilibrium constants of the DPT reaction
The structures of all the CanG complexes were optimized by DFT at the current level. The vibration analysis showed no imaginary frequencies in these complexes, indicating that the structures are stable. Intermolecular DPT, which generates hydrogen-bonded pairs of tautomers, was computationally predicted for all the complexes. DPT can take place through a concerted DPT (Ca1-3G and Ca5-12G) or via a stepwise mechanism involving two distinct SPT steps (Ca0G and Ca4G). The vibration analysis of each proton transfer reaction showed one imaginary frequency, and the vibration mode of the imaginary frequency corresponds to the reactants and products assigned to the transition state. An intrinsic reaction coordinate was prepared to confirm the existence of the transition states.
The Gibbs free energies of the fully optimized Ca0G complexes were defined as having zero energy. The relative Gibbs free energies of the optimized reactants, the first and second single-proton transition states, the double-proton transferred states, the intermediate product of single proton transfer, and the product of double-proton transfer were calculated.
The Ca0G complex, the model of the Watson–Crick guanine–cytosine (GC) base pair, undergoes a stepwise DPT process. The dissociation energy (DE) of the Ca0G base pair at the current level of theory is 21.74 kcal/mol, which is in good agreement with the reported experimental value of 21.0 kcal/mol22. However, the previously calculated DE values were 25.4 kcal/mol23, 23.8 kcal/mol24, and 24.4 kcal/mol25. This result indicates that the present calculations are a better mimic of physiological conditions. The energy of the DPT product of Ca0G lies 9.15 kcal/mol above the reactant species, which is similar to previously calculated values of 9.8 kcal/mol14 and disfavors the DPT reaction. The Ca0G–Ca0*G* equilibrium (with a calculated equilibrium constant of 1.99 × 10−6, which is in good agreement with previously estimated values of 2.0 × 10−6)12 largely favors the reactants, so this double-proton-transfer reaction will rarely occur. In fact, we also calculated the dissociation energy of Ca0G and the equilibrium constant of the DPT reaction using the DFT B3LYP/6-311 + +G(d,p) method. And the calculated values were 13.25 kcal/mol and 4.53 × 10−8 respectively, which were quite different from the experimental values (21.0 kcal/mol) of the dissociation energy and the previously estimated values (2.0 × 10−6) of the equilibrium constant. So, these results calculated by the DFT M06-2X/def2svp method are in good agreement with previous findings related to the DPT reaction of GC base pairs, indicated the calculations are more reasonable.
The forward DPT free energy barriers of the 12 analogue complexes (ΔG≠f) range from −2.02 to 1.07 kcal/mol, which are significantly lower than the value of Ca0G (8.80 kcal/mol). The barriers increased in the order Ca11G < Ca7G < Ca3G < Ca12G < Ca5G < Ca4G < Ca8G < Ca6G < Ca10G < 0 < Ca9G < Ca2G < Ca1G<<Ca0G. Lower energy barriers favor the DPT reaction, especially for complexes with negative barriers. The forward rate constants (calculated from ΔG≠f) of the DPT process range from 1.14 × 1012 to 1.72 × 1014 s−1, which are significantly higher than the value of Ca0G (4.05 × 106 s−1). The reverse DPT free energy barriers of the 12 analogue complexes range from 0.97 to 8.06 kcal/mol, which are higher than the value of Ca0G (0.71 kcal/mol). In addition, the reverse rate constants (calculated from ΔG≠r) of the DPT process range from 1.34 × 107 to 1.34 × 1012 s−1, which are lower than the value of Ca0G (2.04 × 1012). The DPT equilibrium (keq = kf/kr) ranges from 1.60 × 100 to 1.28 × 107, which is significantly higher than the value of Ca0G (1.99 × 10−6). The DPT equilibrium constants increased in the order Ca0G<<0 < Ca2G < Ca1G < Ca4G < Ca6G < Ca5G < Ca3G < Ca9G < Ca8G < Ca10G < Ca12G < Ca7G < Ca11G. For all 12 analogue complexes with positive equilibrium constants, the reaction may occur in the DPT direction. In particular, the DPT equilibrium constants of Ca7G and Ca11G (1.49 × 105 and 1.28 × 107) are over 1.0 × 105, which indicates that these two proton transfer reactions will occur adequately. All the values are shown in Table 1.
Geometries of the DPT reactions of the analogue complexes
In the Ca0G complex, the intermonomer N3 − N′1 distance (as labeled in Fig. 1) is 2.92 Å. This distance is consistent with the calculated distance (2.95 Å) and the experimental distance (3.09 Å)12, as is the distances of N4 − O′6. As the reaction progresses from the reactant to transition state 1 (TS1), the intermediate product of the single proton transfer (SPT) and TS2, the guanine and cytosine monomers approach each other. The N3 − N′1 distances in TS1, SPT and TS2 are 2.65 Å, 2.72 Å and 2.78 Å, respectively. As the reaction proceeds, the N′1 − H′1 bond stretches faster than the N4 − H4a bond and completes the proton transfer first. In the products, the N3 − N′1 bridge elongates again to 2.86 Å, which is close to their original separation in the reactants.
In the Ca1-12G analogue complexes, the intermonomer N3 − N′1 distance and O4-O′6 distance range from 2.70 to 2.81 Å and 2.46 to 2.61 Å, respectively, which are all shorter than those in the Ca0G complex (2.92 Å and 2.85 Å), indicating that the forward DPT reaction of those complexes is more favorable than that of the Ca0G complex. As the reaction progresses from the reactant to TS, most of the N3 − N′1 distances and O4-O′6 distances are shorter than the distance in the Ca0G complex and favor the DPT reaction. In the products, the N3 − N′1 and O4-O′6 bridges elongate again, and more than half of these bridges are longer than the distance in the Ca0G DPT product, which indicates that the DPT reverse reaction in those complexes is more difficult than it is in the Ca0G DPT product (Table 2).
Table 2.
Distances (in Å) between the electronegative atoms involved in the two H-bonds in CanG during the DPT process.
| CanG | Electronegative Atoms | Reactant | TS (TS1/SPT/TS2) | Product |
|---|---|---|---|---|
| Ca0G | N3-N′1 | 2.92 | 2.65/2.72/2.78 | 2.86 |
| N4-O′6 | 2.85 | 2.62/2.59/2.48 | 2.58 | |
| Ca1G | N3-N′1 | 2.81 | 2.61 | 2.84 |
| O4-O′6 | 2.54 | 2.43 | 2.59 | |
| Ca2G | N3-N′1 | 2.79 | 2.60 | 2.82 |
| O4-O′6 | 2.52 | 2.46 | 2.61 | |
| Ca3G | N3-N′1 | 2.77 | 2.61 | 2.87 |
| O4-O′6 | 2.50 | 2.43 | 2.60 | |
| Ca4G | N3-N′1 | 2.76 | 2.71/2.69/2.60 | 2.81 |
| O4-O′6 | 2.46 | 2.40/2.45/2.50 | 2.65 | |
| Ca5G | N3-N′1 | 2.74 | 2.57 | 2.92 |
| O4-O′6 | 2.61 | 2.52 | 2.52 | |
| Ca6G | N3-N′1 | 2.80 | 2.56 | 2.94 |
| O4-O′6 | 2.60 | 2.49 | 2.53 | |
| Ca7G | N3-N′1 | 2.72 | 2.57 | 2.93 |
| O4-O′6 | 2.58 | 2.49 | 2.51 | |
| Ca8G | N3-N′1 | 2.78 | 2.56 | 2.89 |
| O4-O′6 | 2.52 | 2.41 | 2.59 | |
| Ca9G | N3-N′1 | 2.78 | 2.59 | 2.94 |
| O4-O′6 | 2.58 | 2.45 | 2.54 | |
| Ca10G | N3-N′1 | 2.78 | 2.58 | 2.91 |
| O4-O′6 | 2.56 | 2.44 | 2.57 | |
| Ca11G | N3-N′1 | 2.70 | 2.59 | 2.95 |
| O4-O′6 | 2.53 | 2.47 | 2.55 | |
| Ca12G | N3-N′1 | 2.77 | 2.65 | 2.91 |
| O4-O′6 | 2.49 | 2.40 | 2.62 |
Effects of cytosine atom substitution on the DPT reaction
When the amino group at the C4 position of the cytosine was replaced by a hydroxy moiety and the other conditions were held constant, the energy barrier of the DPT reaction decreased by 7.73 kcal/mol. This result indicates that the hydroxy group significantly favored the DPT reaction. Since the electronegativity of oxygen atom is lower than that of nitrogen atom, the attraction of oxygen to proton is less than that of nitrogen, which is the possible reason that favors the transfer of H4 from O4 to N′6.
When the C2 carbonyl oxygen atoms of the cytosine analogues were replaced by hydrogen, the energy barriers of the DPT decreased by an average of 1.01 kcal/mol. Replacing C2 with a boron atom further decreased the energy barriers of the DPT by an average of 0.06 kcal/mol, further favoring the DPT reaction. Removing the carbonyl group from C2 and replacing C2 with a less electronegative boron atom can transfer the negative charge to N3, which is conducive to the ability of N3 to acquire proton and favors the transfer of H’1 from N′1 to N3. A large number of BN-containing heterocycles have been developed by means of the substitution of a carbon-carbon double bond with an isoelectronic boron-nitrogen bond (BN-substitution)26,27. BN-substituted nucleobases are very attractive BN-substituted heterocyclic compounds. Bielawski et al.28 reported the synthesis of B(6)-phenyl-BN-uracil, which was characterized by mass spectrometry, IR spectroscopy and elemental analysis. It is interesting to note that Hiroshi et al.26 also reported the synthesis of B(6)-substituted 5-aza-6-borauracils (BN-substituted uracils) and -thymines (BN-substituted thymines). The structures of these BN-substituted nucleobases are similar to the cytosine analogues in present study. Therefore, these boron-containing cytosine analogues can be synthesized as realistic candidates.
When the C5 carbon atom of the cytosine analogues was replaced by a nitrogen atom, the energy barriers of the DPT decreased by an average of 0.03 kcal/mol. When the double bonds between N5 and C6 of these analogues were hydrogenated to single bonds, the energy barriers of the DPT further decreased by an average of 1.62 kcal/mol. However, when the hydrogen on C6 was exchanged for a carbonyl oxygen, the energy barriers of the DPT increased again. Therefore, the second result seemed to indicate that the DPT reaction was favored. Replacing C5 with highly electronegative nitrogen atom may transfer the negative charge from O4 to N5, which will reduce the attraction of O4 to proton and favors the transfer of H4 from O4 to N′6.
Conclusions
The abilities of 12 modified cytosine–guanine complexes to undergo DPT were predicted and compared using theoretical calculations. The DE value, DPT barriers, hydrogen bond lengths and equilibrium constants of the Ca0G complex are similar to previously calculated values and experimental values, indicating that the present calculation method is reasonable. Because of the intramolecular SPT process are not facile, the 12 modeled cytosine analogues can be used as candidate molecules to induce DPT reactions with guanine. Eight modified complexes (Ca3G, Ca5G and Ca7-12G) were significantly more prone to undergo DPT reactions than Ca0G. In particular, Ca7G and Ca11G may undergo sufficient DPT reactions under physiological conditions according to the present calculations. Here, we present the part of the study on theoretical calculations and predictions of candidate molecules. Next these analogues are expected to be synthesized for incorporation into single-stranded RNAs and to be validated in in-vivo model. By binding such modified RNA to DNA or RNA, DPT reactions of guanine may be induced at a fixed point. If cytosine analogues that can spontaneously induce DPT reactions of guanine under physiological conditions are identified experimentally, targeted pathogenic mutations can be used to restore original functions at the level of DNA or RNA.
Theoretical Methods
DFT with the M06-2X functional and the def2svp basis set has been the primary research method used to investigate proton transfer reactions between cytosine analogues and guanine. The M06-2X functional is a high nonlocality functional with twice the nonlocal exchange (2X), and it is considered suitable for the study of main-group thermochemistry, thermochemical kinetics, noncovalent interactions, and electronic excitation energies to the valence and Rydberg states. The M06-2X functional also gives the best performance for hydrogen-transfer barrier calculations and the lowest values of balanced mean unsigned error (BMUE), which means it gives the best overall performance for barrier calculations29–31. The D3 dispersion correction was used in this study to improve the accuracy of the energy and structure calculations32–35. To simulate the DNA surroundings in a biological environment, all the calculations were carried out with water solvation at T = 310.15 K (37 °C) and p = 1 atm. The sophisticated polarizable continuum model36 has been used to investigate solute–solvent interactions in water using the scrf = (solvent = water, pcm) keyword. The Gaussian 09 program package was used throughout this study37. The structures of all the monomers and complexes were optimized by DFT at the current level. The vibration analyses were performed to determine whether the molecular structures were stable. The H4 and H’1 hydrogen atoms of the optimized complexes were placed in the middle points between two electronegative atoms (N3-N′1, N4-O′6 or O4-O′6) and then the structures of the transition states were optimized using the opt = (calcall, ts, noeigen) keyword. The vibration analyses were performed to determine the existence of the transition states. The forward energy barrier, ΔG≠f, is the difference between the Gibbs free energy of the transferred states and the reactants. The reverse energy barrier, ΔG≠r, is the difference between the Gibbs free energy of the transferred states and the products.
The GaussView 5.038 was used to create molecular structures of the modeled cytosine analogues. The molecular structure of classic cytosine, at first, was created and optimized by the program package. And then the 12 modeled cytosine analogues were created by replacing the atoms in the classic cytosine and optimized by the program package.
To investigate the ability of N3 to accept protons and O4 to donate protons, the ESP-mapped vdW surfaces and ESP extrema were rendered using the VMD 1.9.1 program39 based on the outputs from the Multiwfn 3.6 program40,41.
To investigate the equilibrium of the DPT reactions and chemical reactions of the analogue complexes, the forward and reverse rate constants (kf and kr) were given by the following equation42
| 1 |
Where k is the forward or reverse rate constants, T=310.15 K (37 °C), ΔG≠ is the forward or reverse energy barriers. The equilibrium constants (Keq values) of the DPT reactions are the quotients of kf and kr (Keq= kf/kr).
Acknowledgements
We are grateful to Jiahui Xia, Huanxiao An, Lingqian Wu, Desheng Liang, Jigeng Bai, Yongxin Yang, Yu Wang, Wei Wei and the March of dimes birth defects foundation of Shanxi for their support in this study.
Author contributions
Conceptualization: Jinjie Xue. Methodology: Jinjie Xue, Xingbao Wang and Yafeng Xiao. Investigation: Jinjie Xue and Xingping Guo. Writing Original Draft: Jinjie Xue. All authors reviewed and approved the manuscript.
Competing interests
The authors declare no competing interests.
Footnotes
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
References
- 1.Bailey MH, et al. Comprehensive Characterization of Cancer Driver Genes and Mutations. Cell. 2018;173:371–385. doi: 10.1016/j.cell.2018.02.060. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Martinez JL, Baquero F. Mutation frequencies and antibiotic resistance. Antimicrob. Agents. Ch. 2000;44:1771–1777. doi: 10.1128/AAC.44.7.1771-1777.2000. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Milholland B, Suh Y, Vijg J. Mutation and catastrophe in the aging genome. Exp. Gerontol. 2017;94:34–40. doi: 10.1016/j.exger.2017.02.073. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Eid A, Alshareef S, Mahfouz MM. CRISPR base editors: genome editing without double-stranded breaks. Biochem. J. 2018;475:1955–1964. doi: 10.1042/BCJ20170793. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Qin W, et al. Precise A•T to G•C base editing in the zebrafish genome. BMC. Biol. 2018;16:139. doi: 10.1186/s12915-018-0609-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Gaudelli NM, et al. Programmable base editing of A•T to G•C in genomic DNA without DNA cleavage. Nature. 2017;551:464–471. doi: 10.1038/nature24644. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Löwdin PO. Proton Tunneling in DNA and its Biological Implications. Rev. Mod. Phys. 1963;35:724–732. doi: 10.1103/RevModPhys.35.724. [DOI] [Google Scholar]
- 8.Hideo I, Yoshimasa K. Direct proton exchange between complementary nucleic acid bases. Nature. 1978;271:277–278. doi: 10.1038/271277a0. [DOI] [PubMed] [Google Scholar]
- 9.Fu LY, Wang GZ, Ma BG, Zhang HY. Exploring the common molecular basis for the universal DNA mutation bias: revival of Löwdin mutation model. Biochem. Biophys. Res. Commun. 2011;409:367–371. doi: 10.1016/j.bbrc.2011.05.017. [DOI] [PubMed] [Google Scholar]
- 10.Radek P, et al. Proton transfer in guanine-cytosine base pair analogues studied by NMR spectroscopy and PIMD simulations. Faraday Discuss. 2018;212,:331–344. doi: 10.1039/C8FD00070K. [DOI] [PubMed] [Google Scholar]
- 11.Floria J, Leszczyn J. Spontaneous DNA Mutations Induced by Proton Transfer in the Guanine·Cytosine Base Pairs: An Energetic Perspective. J. AM. CHEM. SOC. 1996;118:3010–3017. doi: 10.1021/ja951983g. [DOI] [Google Scholar]
- 12.Alya AA, Chérif FM. Effects of Intense Electric Fields on the Double Proton Transfer in the Watson–Crick Guanine–Cytosine Base Pair. J. Phys. Chem. 2018;122:8631–8641. doi: 10.1021/acs.jpcb.8b05053. [DOI] [PubMed] [Google Scholar]
- 13.Zhang JD, Chen Z, Schaefer HF. Electron attachment to the hydrogenated Watson-Crick guanine cytosine base pair (GC+H): conventional and proton-transferred structures. J. Phys. Chem. A. 2008;112:6217–6226. doi: 10.1021/jp711958p. [DOI] [PubMed] [Google Scholar]
- 14.Noguera M, Sodupe M, Bertrán J. Effects of protonation on proton-transfer processes in guanine–cytosine Watson–Crick base pairs. Theor. Chem. Acc. 2004;112:318–326. doi: 10.1007/s00214-004-0591-2. [DOI] [Google Scholar]
- 15.Noguera M, Bertran J, Sodupe M. A Quantum Chemical Study of Cu2+ Interacting with Guanine−Cytosine Base Pair. Electrostatic and Oxidative Effects on Intermolecular Proton-Transfer Processes. J. Phys. Chem. A. 2004;108:333–341. doi: 10.1021/jp036573q. [DOI] [Google Scholar]
- 16.Noguera M, Bertran J, Sodupe M. Cu2+/+ cation coordination to adenine-thymine base pair. Effects on intermolecular proton-transfer processes. J. Phys. Chem. B. 2008;112:4817–4825. doi: 10.1021/jp711982g. [DOI] [PubMed] [Google Scholar]
- 17.Chen HY, Kao CL, Hsu SC. Proton transfer in guanine-cytosine radical anion embedded in B-form DNA. J. Am. Chem. Soc. 2009;131:15930–15938. doi: 10.1021/ja906899p. [DOI] [PubMed] [Google Scholar]
- 18.Ceron-Carrasco JP, Requena A, Zuniga J. Intermolecular Proton Transfer in Microhydrated Guanine-Cytosine Base Pairs: a New Mechanism for Spontaneous Mutation in DNA. J. Phys. Chem. A. 2009;113:10549–10556. doi: 10.1021/jp906551f. [DOI] [PubMed] [Google Scholar]
- 19.Ko YJ, et al. Barrier-free proton transfer induced by electron attachment to the complexes between 1-methylcytosine and formic acid. Mol. Phys. 2010;108:2621–2631. doi: 10.1080/00268976.2010.515623. [DOI] [Google Scholar]
- 20.Gautam BP, Srivastava M, Prasad RL, Yadav RA. Synthesis, characterization and quantum chemical investigation of molecular structure and vibrational spectra of 2, 5-dichloro-3, 6-bis-(methylamino) 1, 4-benzoquinone. Spectrochim. Acta. A. Mol. Biomol. Spectrosc. 2014;129:241–254. doi: 10.1016/j.saa.2014.02.082. [DOI] [PubMed] [Google Scholar]
- 21.Tao YP, Li XF, Han LG, Zhang WY, Liu ZJ. Spectroscopy (FT-IR, FT-Raman), hydrogen bonding, electrostatic potential and HOMO-LUMO analysis of tioxolone based on DFT calculations. J. Mol. Struct. 2016;1121:188–195. doi: 10.1016/j.molstruc.2016.05.077. [DOI] [Google Scholar]
- 22.Yanson IK, Teplitsky AB, Sukhodub LF. Experimental studies of molecular interactions between nitrogen bases of nucleic acids. Biopolymers. 1979;18:1149–1170. doi: 10.1002/bip.1979.360180510. [DOI] [PubMed] [Google Scholar]
- 23.Richardson NA, Wesolowski SS, Schaefer HF. Electron Affinity of the Guanine−Cytosine Base Pair and Structural Perturbations upon Anion Formation. J. Am. Chem. Soc. 2002;124:10163–10170. doi: 10.1021/ja020009w. [DOI] [PubMed] [Google Scholar]
- 24.Sponer J, Leszczynski J, Hobza P. Structures and Energies of Hydrogen-Bonded DNA Base Pairs. A Nonempirical Study with Inclusion of Electron Correlation. J. Phys. Chem. 1996;100:1965–1974. doi: 10.1021/jp952760f. [DOI] [Google Scholar]
- 25.Zhang RB, Eriksson LA. Effects of OH Radical Addition on Proton Transfer in the Guanine-Cytosine Base Pair. J. Phys. Chem. B. 2007;111:6571–6576. doi: 10.1021/jp071772l. [DOI] [PubMed] [Google Scholar]
- 26.Ito H, Yumura K, Saigo K. Synthesis, characterization, and binding property of isoelectronic analogues of nucleobases, B(6)-substituted 5-aza-6-borauracils and -thymines. Org. Lett. 2010;12:3386–3389. doi: 10.1021/ol1012058. [DOI] [PubMed] [Google Scholar]
- 27.Braunschweig H, Krummenacher I, Mailänder L, Rauch F. O,N,B-Containing eight-membered heterocycles by ring expansion of boroles with nitrones. Chem. Commun. 2015;51:14513–14515. doi: 10.1039/C5CC05368D. [DOI] [PubMed] [Google Scholar]
- 28.Bielawski J, Niedenzu K, Weber A, Weber W. Cyclic Boron Derivatives of Biurets. Z. Naturforsch. 1981;36b:470–473. doi: 10.1515/znb-1981-0413. [DOI] [Google Scholar]
- 29.Zhao Y, Truhlar DG. The M06 suite of density functionals for main grou, thermochemical kinetics, noncovalent interactions, excited states, and transition elements: two new functionals and systematic testing of four M06-class functionals and 12 other functionals. Theor. Chem. Acc. 2008;120:215–241. doi: 10.1007/s00214-007-0310-x. [DOI] [Google Scholar]
- 30.Yan Z, Truhlar DG. Density functionals with broad applicability in chemistry. Acc. Chem. Res. 2008;41:157–167. doi: 10.1021/ar700111a. [DOI] [PubMed] [Google Scholar]
- 31.Marciniak H, et al. Dynamics of Excited State Proton Transfer in Nitro Substituted 10-Hydroxybenzo [h] quinolines. Phys. Chem. Chem. Phys. 2017;19:26621–26629. doi: 10.1039/C7CP04476C. [DOI] [PubMed] [Google Scholar]
- 32.Goerigk L, Grimme S. Efficient and Accurate Double-Hybrid-Meta-GGA Density Functionals-Evaluation with the Extended GMTKN30 Database for General Main Group Thermochemistry, Kinetics, and Noncovalent Interactions. J. Chem. Theory. Comput. 2011;7:291–309. doi: 10.1021/ct100466k. [DOI] [PubMed] [Google Scholar]
- 33.Holger K, Marek H, Jiřı Š. QM Computations on Complete Nucleic Acids Building Blocks: Analysis of the Sarcin-Ricin RNA Motif Using DFT-D3, HF-3c, PM6-D3H, and MM Approaches. J. Chem. Theory Comput. 2014;10:2615–2629. doi: 10.1021/ct500183w. [DOI] [PubMed] [Google Scholar]
- 34.Daniel GAS, Lori AB, Konrad P, David SC. Revised Damping Parameters for the D3 Dispersion Correction to Density Functional Theory. J. Phys. Chem. Lett. 2016;7:2197–2203. doi: 10.1021/acs.jpclett.6b00780. [DOI] [PubMed] [Google Scholar]
- 35.Thomas S, Patrik E. The effect of density functional dispersion correction (DFT-D3) on lignans. Comput. Theor. Chem. 2015;1067:60–63. doi: 10.1016/j.comptc.2015.05.023. [DOI] [Google Scholar]
- 36.Romero EE, Hernandez FE. Solvent effect on the intermolecular proton transfer of the Watson and Crick guanine-cytosine and adenine-thymine base pairs: a polarizable continuum model study. Phys. Chem. Chem. Phy. 2018;20:1198–1209. doi: 10.1039/C7CP05356H. [DOI] [PubMed] [Google Scholar]
- 37.Frisch, M.J. et al. Gaussian 09, Revision D.01, Gaussian, Inc., Wallingford CT (2013).
- 38.Roy D. D. et al. GaussView 5.0, Semichem, Inc., Wallingford CT (2008).
- 39.Humphrey W, Dalke A, Schulten K. VMD: visual molecular dynamics. J. Mol. Graph. 1996;14:33–38. doi: 10.1016/0263-7855(96)00018-5. [DOI] [PubMed] [Google Scholar]
- 40.Lu T, Chen F. Multiwfn: a multifunctional wavefunction analyzer. J. Comput. Chem. 2012;33:580–592. doi: 10.1002/jcc.22885. [DOI] [PubMed] [Google Scholar]
- 41.Xiao M, Lu T. Generalized Charge Decomposition Analysis (GCDA) Method. J. Adv. Phys. Chem. 2015;4:111–124. doi: 10.12677/JAPC.2015.44013. [DOI] [Google Scholar]
- 42.Lu, T. How to judge whether a reaction is easy to occur through barrier? Network, http://sobereva.com/506 (2019).