Complex dynamics and control of a novel physical model using nonlocal fractional differential operator with singular kernel

Graphical abstract

Abstract

Fractional calculus (FC) is widely used in many interdisciplinary branches of science due to its effectiveness in describing and investigating complicated phenomena. In this work, nonlinear dynamics for a new physical model using nonlocal fractional differential operator with singular kernel is introduced. New Routh-Hurwitz stability conditions are derived for the fractional case as the order lies in [0,2). The new and basic Routh-Hurwitz conditions are applied to the commensurate case. The local stability of the incommensurate orders is also discussed. A sufficient condition is used to prove that the solution of the proposed system exists and is unique in a specific region. Conditions for the approximating periodic solution in this model via Hopf bifurcation theory are discussed. Chaotic dynamics are found in the commensurate system for a wide range of fractional orders. The Lyapunov exponents and Lyapunov spectrum of the model are provided. Suppressing chaos in this system is also achieved via two different methods.

Introduction

Fractional calculus (FC) has recently been considered to be one of the powerful tools to describe a complex dynamical phenomenon [1], [2], [3] and is widely applied in different fields including physics, economics, combustion science, biology and engineering [4], [5], [6], [7], [8], [9], [10], [11], [12], [13], [14], [15]. Indeed, FC provides a realistic description of a physical phenomenon and also helps to achieve greater degrees of freedom in physical models because the analysis in FC provides a generalization of the classical differentiation and integration to the arbitrary order (noninteger state). Thus, FC has been attracted a great deal of attention owing to its intrinsic advantages in modeling of natural phenomena involved with memory and hereditary properties. Moreover, FC has been utilized to define many physical models in which fractional differential and integral operators have been successfully used to describe their nature. However, to explain these physical phenomena in fractional language, authors have used several definitions. Among them are the well-known fractional derivative definitions used by Riemann-Liouville [16], Caputo [17] and Caputo–Fabrizio [18].

In fact, nonlocal differential and integral operators are better candidates for handling the chaotic behaviors of fractional derivatives, which are also classified based on their kernels. The Riemann-Liouville and Caputo derivatives possess nonlocal operators with singular kernels; however, the fractional derivative defined by Caputo and Fabrizio has a nonlocal operator with a nonsingular kernel.

Recently, the applications of fractional derivatives in physical models have been widely examined owing to their usefulness in many fields of physics such as viscoelasticity, transient heat diffusion, steady-state heat conduction, electrochemical double layer capacitors, dielectric polarization, DNA chain, electromagnetic waves, hybrid nanofluid, quantum mechanics, and quantum evolution of complex systems. Moreover, the exhibition of chaos in a fractional physical model and its suppression in such a model are two of the main problems that have been encountered. Chaotic attractors have also been reported in some physical models with fractional order such as the Liu system [19], the Van der Pol-Duffing circuit [20], a Volta’s model [21], and novel hyperchaotic circuits [22], [23]. Furthermore, the suppression of chaos in differential models involving fractional derivatives has received increasing attention [24], [25], [26], [27], [28].

In [29], Constantinescu et al. proposed a model for quasi-periodic plasma perturbations that consists of an integer-order system of ordinary differential equations with two nonlinear terms. This low dimensional integer-order model for quasi-periodic plasma perturbations explores the dynamical behaviors of the amplitude of magnetic field displacement and the plasma pressure gradient in tokamaks. In addition, Constantinescu et al. [30] studied existence of Hopf bifurcation in this model of quasi-periodic plasma perturbations and analyzed the fast-slow dynamics of this model. Moreover in [31], qualitative dynamical study in this integer-order model of quasi-periodic plasma perturbations like existence of Bogdanov-Takens bifurcation, pitchfork bifurcation, homoclinic bifurcation and chaotic states, was reported by Elsadany et al.

In this work, we explore dynamics of the quasi-periodic plasma perturbations model with fractional derivatives. We use the Caputo type fractional differential operator, which is widely used in real applications. Indeed, imposing nonlocal fractional differential operators to the quasi-periodic plasma perturbations model allows us to obtain more accuracy and adequacy of describing the natural phenomena, and to obtain greater degrees of freedom in this model. Consequently, the proposed fractional form of the quasi-periodic plasma perturbations model is better candidate for describing the expected complex dynamics since it is defined by integration. However, the existence of unpredictable or complex dynamics is not desirable in many practical situations. Therefore, erasing the unpredictable dynamics that may arise from the fractional-order quasi-periodic plasma perturbations model becomes a focal point of our interest. To the best of our knowledge, the results in this work are the first to report the complex dynamics and chaos suppression in the fractional-order quasi-periodic plasma perturbations model.

Here, new Routh-Hurwitz stability conditions in three dimensional fractional-order systems as the orders lie in the interval [0,2), are proved and applied to the proposed model. A condition for the existence and uniqueness of the solution of the quasi-periodic plasma perturbations model is obtained. Conditions for the approximating periodic solutions in this system are also discussed. Chaos in the proposed model is also found for fractional orders above and less than 1. Furthermore, chaotic behaviors in this model are suppressed to its steady states as the orders lie in the interval (0,2). Thus, our study helps to understand the complex dynamics arising from the quasi-periodic plasma perturbations model involving fractional derivatives based on Caputo nonlocal fractional operator which provides more appropriate and realistic description of the resulting complex dynamics and also our study helps to eliminate unpredictable dynamic behaviors of the proposed model.

Basic concepts of FC

The Caputo nonlocal fractional differential operator with singular kernel [17] is given as

$$D^q\varphi (\tau )={\int }_0^{\tau }{(\tau -l)}^{k-q-1}{\varphi }^{(k)}(l)dl/\mathrm{\Gamma }(k-q),$$ (1)

where and ${\varphi }^{(k)}$ refers to the kth-order derivative of $\varphi (l)$. Moreover, the stability of nonlinear systems involving fractional derivatives is summarized by the following results:

Assume that

$$D^q\mathrm{X}(t)=\mathrm{H}(\mathrm{X}(t)),$$ (2)

where $0<q<2,$$\mathrm{X}\in R^3$, and the vector function $\mathrm{H}$ is nonlinear. If ${\mathrm{X}}^{(e)}$ is an equilibrium point of (2) with the following eigenvalue equation:

$$\phi (\lambda )={\lambda }^3+s_1{\lambda }^2+s_2\lambda +s_3=0,$$ (3)

then the Matignon’s inequalities [32] are used to discuss local stability of ${\mathrm{X}}^{(e)}$ as follows

$$\left|arg({\lambda }_i)\right|>q\pi /2,i=1,2,3.$$ (4)

The corresponding region describing the local stability of ${\mathrm{X}}^{(e)}$ is depicted in Fig. 1. Also, the following fractional Routh–Hurwitz (FRH) criterion [33] is obtained for $q\in [0,2)$:

• (i)${\mathrm{X}}^{(e)}$ is locally asymptotically stable (LAS) for $q\in [0,2)$, if the discriminant of $\phi (\lambda )$ is positive in addition to $s_1>0,s_3>0$ and $s_1{s}_2-s_3>0.$
• (ii)${\mathrm{X}}^{(e)}$ is LAS for $q<\frac{2}{3}$ if the discriminant of $\phi (\lambda )$ is negative in addition to $s_1⩾0,s_2⩾0$ and $s_3>0.$
• (iii)${\mathrm{X}}^{(e)}$ is LAS for $q\in (0,1)$ if the discriminant of $\phi (\lambda )$ is negative in addition to $s_1>0,s_2>0$ and $s_1{s}_2-s_3=0.$

Fig. 1.

Stability region of linear fractional-order system as: (a) $q\in [0,1),$ (b) $q\in [1,2).$

Here, we also provide the following theorem.

Theorem 1 (Matouk’s). —

For the eigenvalue equation (3);

• (a)If $q\in [1,2),$ $s_3=s_1{s}_2$ and the discriminant of $\phi (\lambda )<0,$ then the Matignon’s inequalities (4) are not satisfied;
• (b)If $q\in [0,2)$ then $s_3>0$ is a necessary condition for ${\mathrm{X}}^{(e)}$ to be LAS.

Proof

To prove part (a), we recall that if discriminant of $\phi (\lambda )<0,$then Eq. (3) has the following eigenvalues

$${\lambda }_1={\lambda }_0,{\lambda }_{2,3}=p\pm \omega I,I=\sqrt{-1},{\lambda }_0,p,\omega \in R,\omega \ne 0.$$ (5)

So, Eq. (3) has the following coefficients

$$s_1=-2p-{\lambda }_0,s_2={\left|{\lambda }_2\right|}^2+2p{\lambda }_0,s_3=-{\lambda }_0{\left|{\lambda }_2\right|}^2.$$ (6)

Consequently, Eq. (3) has two pure imaginary roots if and only if $s_3=s_1{s}_2$, since the last condition implies that

$$(2p+{\lambda }_0)({\left|{\lambda }_2\right|}^2+2p{\lambda }_0)={\lambda }_0{\left|{\lambda }_2\right|}^2,$$ (7)

that is reduced to

$$p({\omega }^2+{({\lambda }_0+p)}^2)=0.$$ (8)

It is now clear that $p=0$ as $s_3=s_1{s}_2$ which means that the eigenvalues ${\lambda }_{2,3}$ lie in the unstable region (See Fig. 1b) of the linearized fractional order system as $q\in [1,2).$ □

To prove part (b), we firstly assume that the discriminant of $\phi (\lambda )<0,$ $q\in [0,2)$ then $s_3=-{\lambda }_0{\left|{\lambda }_2\right|}^2<0$ implies that ${\lambda }_0>0$ which also means that ${\lambda }_0$ lies in the unstable region of Fig. 1b. Secondly, we assume that the discriminant of $\phi (\lambda )>0,$ then $s_3=-{\lambda }_1{\lambda }_2{\lambda }_3<0,{\lambda }_i\in R,i=1,2,3$ implies that there exists at least one ${\lambda }_i>0$ which also implies that ${\lambda }_i$ lies in the unstable region of Fig. 1b. Also, the case $s_3=0$ is obviously belong to the unstable region. □

Theorem 2

(See [34]). Let system (2) be described as

$$D^q\mathrm{X}(t)=A\mathrm{X}(t)+B(\mathrm{X}(t)),$$ (9)

where $0<q<2,A\in R^{3\times 3}$, and $B$ is a nonlinear function such that

$$\underset{∥\mathrm{X}(t)∥\to 0}{lim}\frac{∥B(\mathrm{X}(t))∥}{∥\mathrm{X}(t)∥}=0,$$ (10)

then ${\mathrm{X}}^{(e)}=0$ is LAS if $\left|arg({\lambda }_i(A))\right|>q\pi /2,i=1,2,3,$ where $∥.∥$ is the $l_2-$norm.

The model

Here, we introduce the integer-order form of the model as follows:

$$\begin{array}{c}\frac{\mathit{dx}}{\mathit{dt}}=y(z-1)-\delta x,\\ \frac{\mathit{dy}}{\mathit{dt}}=x,\\ \frac{\mathit{dz}}{\mathit{dt}}=\nu (\mu -z-y^{2}z),\end{array}$$ (11)

where δ, μ and $\nu$ are all positive real numbers, with δ denoting the relaxation of the perturbation; $\mu$ the input normalized power; and $\nu$ the characteristic relation of the heat diffusion coefficients [29]. In fact imposing the Caputo fractional differential operator to system (11), provides a generalization of the existing classical differentiation to the arbitrary order (noninteger state). The fractional-order form of model (11) is given as

$$\begin{array}{c}{D}^{q}x(t)=y(t)(z(t)-1)-\delta x(t),\\ D^{q}y(t)=x(t),\\ D^{q}z(t)=\nu (\mu -z(t)-y^2(t)z(t)),\end{array}$$ (12)

where $q\in (0,2)$. So, higher degrees of freedom in the quasi-periodic plasma perturbations model (12) are obtained than the integer-order counter-parts. Moreover, the resulting long-term memory effect and hereditary properties of this operator are very useful to describe complicated natural dynamical phenomena. Thus, it is shown that the quasi-periodic plasma perturbations model (12) generalizes the original integer-order models in [29], [30] and helps to obtain more adequacy and realistic description of the resulting dynamical phenomena. The Model (12) has three equilibria, i.e., $S_1(0,0,\mu ),S_2(0,\sqrt{\mu -1},1)$, and $S_3(0,-\sqrt{\mu -1},1),$ for $\mu >1.$ Moreover, it has the unique equilibrium $S_1(0,0,\mu )$, where $\mu \in (0,1].$

Existence and uniqueness

According to the familiar existence and uniqueness procedure given in [22], [35], the following conditions are straightforwardly obtained.

Lemma 1

A solution of the model for quasi-periodic plasma perturbations (12) exists and is unique in the region $\mathrm{\Omega }\times (0,\tau ]$ with the initial conditions $(x(0),y(0),z(0))=(x_0,y_0,z_0)$ and $t\in (0,\tau ]$ if

$$0<\eta =\frac{{\tau }^q}{\mathrm{\Gamma }(1+q)}max\{1+\delta ,1+\gamma +2\nu {\gamma }^2,\nu +\gamma +\nu {\gamma }^2\}<1.$$ (13)

Stability of the quasi-periodic plasma perturbations model (12)

The Jacobian of the fractional model for quasi-periodic plasma perturbations (12), computed at $\overline{S}=({\overline{s}}_x,{\overline{s}}_y,{\overline{s}}_z)$, is described by

$$J(\overline{S})=\left(\begin{array}{ccc}-\delta & {\overline{s}}_z-1& {\overline{s}}_y\\ 1& 0& 0\\ 0& -2\nu {\overline{s}}_y{\overline{s}}_z& -\nu (1+{\overline{s}}_y^2)\end{array}\right).$$ (14)

Theorem 3

The equilibrium $S_1(0,0,\mu )$ of the fractional the model for quasi-periodic plasma perturbations (12) is (i) a saddle point if $\mu >1$ or (ii) LAS if ${\delta }^2⩾4(1-\mu ),$$\mu <1$, or ${\delta }^2<4(1-\mu ),$$\mu <1,$$q<\frac{2}{\pi }arctan\frac{\sqrt{4(1-\mu )-{\delta }^2}}{\delta }.$

Proof

The Jacobian (14) evaluated at $S_1(0,0,\mu )$ is given by

$$J(S_1(0,0,\mu ))=\left(\begin{array}{ccc}-\delta & \mu -1& 0\\ 1& 0& 0\\ 0& 0& -\nu \end{array}\right).$$

The Jacobian matrix $J(S_1(0,0,\mu ))$ has the eigenvalues ${\lambda }_1=-\nu <0,{\lambda }_{2,3}=\frac{-\delta \pm \sqrt{{\delta }^2+4(\mu -1)}}{2}.$ Therefore, if $\mu >1,$ then ${\lambda }_2>0$, which implies that $S_1(0,0,\mu )$ is a saddle point. Furthermore, if ${\delta }^2⩾4(1-\mu ),$$\mu <1,$ then ${\lambda }_i<0$ for all $i=1,2,3$, which implies that $S_1(0,0,\mu )$ is LAS. Moreover, if ${\delta }^2<4(1-\mu ),$$\mu <1,$ then $J(S_1)$ possesses two complex conjugate eigenvalues and the condition $q<\frac{2}{\pi }arctan\frac{\sqrt{4(1-\mu )-{\delta }^2}}{\delta }$ implies that $\left|arg({\lambda }_i)\right|>q\pi /2,i=2,3$, which means that $S_1(0,0,\mu )$ is LAS.

On the other hand, the Jacobian (14) evaluated at $S_{2,3}$ yields the same characteristic equation, i.e.,

$${\lambda }^3+(\mu \nu +\delta ){\lambda }^2+(\mu \nu \delta )\lambda +2\nu (\mu -1)=0.$$ (15)

Therefore, according to the FRH criterion, we obtain the following theorems which are easily to be proved by straightforward utilization of the classic FRH conditions (i)-(iii):

Theorem 4

If the discriminant of the polynomial given in Eq. (15) is positive, then $S_{2,3}$ are LAS for $0<q<2$ and $\delta >\sqrt{2}.$ However, if this discriminant is negative, then $S_{2,3}$ are LAS for $q<\frac{2}{3}$ and also LAS for $0<q<1$ when $\delta <\sqrt{2-\sqrt{8\delta \nu }},\mu ={\mu }_1$, or $\delta <\sqrt{2-\sqrt{8\delta \nu }},\mu ={\mu }_2,$ where ${\mu }_{1,2}=\frac{-{\delta }^2+2\pm \sqrt{{(2-{\delta }^2)}^2-8\delta \nu }}{2\delta \nu }.$

However, the results of applying the new FRH conditions given in Theorem 1 are summarized by the following lemma.

Lemma 2

If $q\in [1,2)$ and the discriminant of $\phi (\lambda )<0;$ then $S_1(0,0,\mu )$ is not LAS for $\mu ={\nu }^2+\delta \nu +1,$ and $S_{2,3}$ is not LAS for $\mu ={\mu }_1$ (or $\mu ={\mu }_2$). Moreover when $q\in [0,2)$; $S_1(0,0,\mu )$ is LAS only if $\mu <1,$ however $S_{2,3}$ are LAS only if $\mu >1.$

For the incommensurate case of the model (12), we have the following theorem that is proved in [36].

Theorem 5

Consider the fractional model for quasi-periodic plasma perturbations (12) with incommensurate orders $q_i\in \aleph ,0<q_i<1,i=1,2,3,$ where $q_i$ is the fractional order on the ith equation of system (12). Also, define the ratio $q_i=\frac{g_i}{d_i},d_i,g_i\in Z^{+},$ whose denominators have LCM = m, and $(d_i,g_i)=1.$ Hence, the equilibrium $S_k,k=1,2,3$ of the fractional model for quasi-periodic plasma perturbations (12) with incommensurate orders are LAS iff

$$\left|arg({\lambda }_i)\right|>\frac{\pi }{2m},$$

where ${\lambda }_{i,s}$ and $b_{\mathit{ij}}={\left(\frac{\partial {\mathrm{H}}_i}{\partial {\mathrm{Y}}_j}\right|}_{S_k}$must satisfy the following condition

$$\left|\begin{array}{ccc}{\lambda }^{m{q}_1}-b_{11}& -b_{12}& -b_{13}\\ -b_{21}& {\lambda }^{m{q}_2}-b_{22}& -b_{23}\\ -b_{31}& -b_{32}& {\lambda }^{m{q}_3}-b_{33}\end{array}\right|=0.$$

Conditions for the approximating periodic solution via Hopf bifurcation theory

In autonomous fractional-order system (AFOS), periodic solution cannot be analytically existed [37]. Only there are some asymptotically periodic signals satisfying the conditions of classical Hopf bifurcation theory, i.e. an approximation to the periodic solution around the steady state is expected as the AFQS, with order less than one, has negative real eigenvalues and a pair of complex conjugate eigenvalues ${\lambda }_{1,2}=u({\iota }_{\mathit{crh}})+Iw({\iota }_{\mathit{crh}}),I=\sqrt{-1},w\ne 0,$ where ${\iota }_{\mathit{crh}}$ is a critical value of the dynamical parameter, in addition to the existence of a function $\mathrm{\Xi }(\iota )$ such that $\mathrm{\Xi }({\iota }_{\mathit{crh}})=0$ and ${\left(\frac{d\mathrm{\Xi }(\iota )}{d\iota }\right|}_{\iota ={\iota }_{\mathit{crh}}}\ne 0.$

Asymptotically periodic signals near $S_1=(0,0,\mu )$

Obviously, the fractional parameter $q$ affects the stability of the quasi-periodic plasma perturbations model (12). So, we can use it as a dynamical parameter. Now, let $\mathrm{\Xi }(q)=\frac{q\pi }{2}-arctan(\frac{\sqrt{-{\delta }^2-4(\mu -1)}}{\delta }).$ Thus, $S_1=(0,0,\mu )$ changes its stability in the neighborhood of $q_{\mathit{crh}}=\frac{2}{\pi }arctan(\frac{\sqrt{4(1-\mu )-{\delta }^2}}{\delta }).$ Furthermore, the quantity ${\left(\frac{d\mathrm{\Xi }(q)}{\mathit{dq}}\right|}_{q=q_{\mathit{crh}}}$is not vanished. For $\mu =0.5,\nu =0.1,\delta =0.0001$, the fractional parameter has the critical value $q_{\mathit{crh}}=0.9999549838.$ So, asymptotically periodic signal is expected near $S_1=(0,0,\mu )$ for these parameter values. In Fig. 2a, we summarize these results.

Fig. 2.

Asymptotically periodic signal near $S_1=(0,0,\mu )$: (a) 2D plot using $\mu =0.5,\nu =0.1,\delta =0.0001$ and $q=0.9999549838;$ (b) 2D plot using $\mu =0.001,\nu =0.2,\delta =0.0003140024694$ and$q=0.9999.$

Moreover, the parameter $\delta$ can be selected as bifurcation parameter by setting $\mathrm{\Xi }(\delta )=-arctan(\frac{\sqrt{4(1-\mu )-{\delta }^2}}{\delta })+\frac{q\pi }{2}$. In this case, the critical bifurcation value ${\delta }_{\mathit{crh}}=\pm 2\frac{\sqrt{(1-\mu )(1+{tan}^2(\frac{q\pi }{2}))}}{1+{tan}^2(\frac{q\pi }{2})},$$0<q<1,0<\mu <1$ and ${\left(\frac{d\mathrm{\Xi }(\delta )}{d\delta }\right|}_{\delta ={\delta }_{\mathit{crh}}}$is not vanished since it equals $cot(\frac{q\pi }{2})/{\delta }_{\mathit{crh}},{\delta }_{\mathit{crh}}\ne 0.$ With the parameter selection $\mu =0.001,\nu =0.2,q=0.9999$, the critical value ${\delta }_{\mathit{crh}}$ becomes $0.0003140024694.$ So, asymptotically periodic signal is expected near $S_1=(0,0,\mu ).$ The indicated approximation to periodic signal is illustrated in Fig. 2b.

Asymptotically periodic signals near $S_{2,3}(0,\pm \sqrt{\mu -1},1)$

If the discriminant of the polynomial (15) is negative, then $S_{2,3}(0,\pm \sqrt{\mu -1},1)$ has a negative real root and a pair of complex conjugate roots. Then let $\mathrm{\Xi }(q)=\frac{q\pi }{2}-arctan(\frac{N}{L}),$ where $N\ne 0,L^2+N^2={\varpi }^3-\mu \nu \delta {\varpi }^2-2(\delta +\mu \nu )(\nu -\mu \nu )\varpi -4{(\mu \nu -\nu )}^2=0.$ The equilibrium points $S_{2,3}(0,\pm \sqrt{\mu -1},1)$ change their stability near the critical fractional parameter $q_{\mathit{crh}}=2{cos}^{-1}(\sqrt{\frac{L^2}{\varpi }})/\pi .$ Obviously, ${\left(\frac{d\mathrm{\Xi }(q)}{\mathit{dq}}\right|}_{q=q_{\mathit{crh}}}$is not vanished. For $\mu =1.2,\nu =0.2,\delta =0.2$, we get $q_{\mathit{crh}}=0.8703517205.$ Hence, periodic solutions are expected near $S_{2,3}(0,\pm \sqrt{\mu -1},1).$ The indicated approximation to periodic signals around $S_2$ and $S_3$, are depicted in Fig. 3a and b, respectively.

Remark 1

According to Proposition 3 of [30], Hopf bifurcation occurs in the quasi-periodic plasma perturbations model (12) near $S_{2,3}(0,\pm \sqrt{\mu -1},1)$ for $q=1,\delta \in (0,\sqrt{2}),\nu <\frac{{(2-{\delta }^2)}^2}{8\delta }$ and $\mu ={\mu }_1$ (or $\mu ={\mu }_2$).

Fig. 3.

2D plot of an asymptotically periodic signal near: (a) $S_2(0,\sqrt{\mu -1},1)$ using $\mu =1.2,\nu =0.2,\delta =0.2$ and $q=0.8703517205;$ (a) 2D plot $S_3(0,-\sqrt{\mu -1},1)$ using $\mu =1.2,\nu =0.2,\delta =0.2$ and$q=0.8703517205.$

Chaos in the fractional quasi-periodic plasma perturbations model

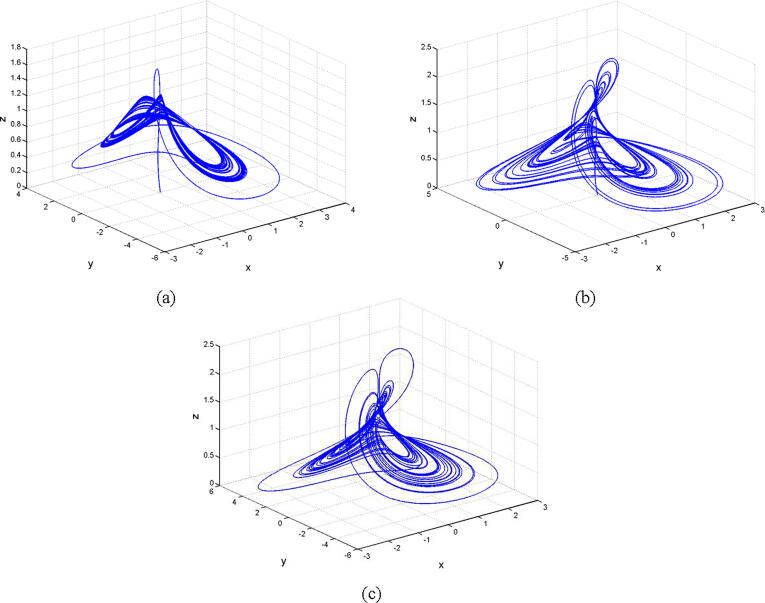
The fractional model for quasi-periodic plasma perturbations (12) is numerically integrated using $\mu =3.5,\nu =0.1$ and $\delta =0.5.$ Using the previous parameter values, the initial conditions $(0.1,0.1,0.1)$, the fractional parameters $q=1.1,q=1.0,q=0.99$ and $q=0.13,$ the system has a positive maximal Lyapunov exponent ${\mathrm{\Lambda }}_{max}=0.0172,0.0518,0.0739$ and $0.1320$ respectively, according to the algorithm given in [38]. The chaotic dynamics of system (12) are illustrated in Fig. 4. It can be seen that the lowest order in the commensurate fractional-order system for which chaos exists is approximately $3\times 0.13=0.39.$ Furthermore, we perform computations of the Lyapunov spectrum as the parameter (or the fractional order) are varied, as illustrated in Fig. 5, which also depicts the existence of a positive maximal Lyapunov exponent (MLE) that refers to the occurrence of a sensitive dependence on the initial conditions in the model.

Fig. 4.

Chaotic attractors appearing in the fractional model (12) using the parameter values $\mu =3.5,\nu =0.1,\delta =0.5$ and the following fractional order: (a) $q=1.1,$ (b) $q=1.0$ and (c)$q=0.99.$

Fig. 5.

Lyapunov spectrum of the fractional model (12) using $\nu =0.1$ and $\delta =0.5:$ (a) The Lyapunov exponents are functions of $\mu$ with $q=0.99.$ (b) The Lyapunov exponents are functions of $q$ with $\mu =3.5.$

Thus, it is shown that chaotic dynamics are found in the fractional quasi-periodic plasma perturbations model (12) for a wide scale of fractional orders $q\in (0,2)$ which confirm that the proposed model exhibits more rich complex dynamics comparing to the models reported in previous literatures such as Refs. [30], [31].

Achieving chaos control

Here, we will apply the stability results given by the FRH criterion and Theorems 2 to stabilize system (12) to its equilibrium points.

Stabilizing system (12) using the FRH criterion

We first consider the following controlled form of quasi-periodic plasma perturbations model (12):

$$\begin{array}{c}{D}^{q}x=y(z-1)-\delta x-k_1(x-{\overline{s}}_x),\\ D^{q}y=x-k_2(y-{\overline{s}}_y),\\ D^{q}z=\nu (\mu -z-y^{2}z)-k_3(z-{\overline{s}}_z),\end{array}$$ (16)

where $k_i\in R^{+},i=1,2,3.$ In the case of the point $({\overline{s}}_x,{\overline{s}}_y,{\overline{s}}_z)=S_1$, the characteristic polynomial of system (16) has the following coefficients:

$$s_1=\delta +\nu +\sum _{i=1}^3{k}_i,s_2=\nu (k_1+k_2)+\delta (k_2+k_3)+k_1{k}_2+k_2{k}_3+k_1{k}_3+1-\mu +\delta \nu ,s_3=\delta k_2(\nu +k_3)+\nu (k_1{k}_2+1-\mu )+k_3(1-\mu )+k_1{k}_2{k}_3.$$ (17)

However, the other equilibrium points $S_2$ and $S_3$ have the same coefficients of the eigenvalue equation of system (16). They are given as follows:

$$s_1=\delta +\mu \nu +\sum _{i=1}^3{k}_i,s_2=\mu \nu (k_1+k_2)+\delta (k_2+k_3)+k_1{k}_2+k_2{k}_3+k_1{k}_3+\delta \mu \nu ,s_3=\delta k_2(\mu \nu +k_3)+\nu (\mu k_1{k}_2-2+2\mu )+k_1{k}_2{k}_3.$$ (18)

For the parameter set $\mu =3.5,\nu =0.1,\delta =0.5$ and $k_1=3,k_2=1,k_3=10$ or $k_1=300,k_2=200,k_3=10,$ it is clear that the first FRH condition is satisfied for Eqs. (17), (18). Therefore, system (16) is controlled to its equilibria. The simulation results that verified the stabilization of system (16) to the points $S_1,S_2$, and $S_3$ are respectively illustrated in Fig. 6, Fig. 7, Fig. 8 for $q=1.1,1$, and $0.99.$

Fig. 6.

Trajectories of the controlled fractional model (16) approach to the equilibrium point $S_1(0,0,\mu )$ using $\mu =3.5,\nu =0.1,\delta =0.5$ and the following fractional order: (a) $q=1.1,$$k_1=300,k_2=200,k_3=10$; (b)$q=1.0,$$k_1=300,k_2=200,k_3=10$; and (c) $q=0.99,$$k_1=3,k_2=1,k_3=10.$

Fig. 7.

Trajectories of the controlled fractional model (16) approach to the equilibrium point $S_2(0,\sqrt{\mu -1},1)$ using $\mu =3.5,\nu =0.1,\delta =0.5$ and the following fractional order: (a) $q=1.1,$$k_1=300,k_2=200,k_3=10$; (b) $q=1.0,$$k_1=300,k_2=200,k_3=10$; and (c) $q=0.99,$$k_1=3,k_2=1,k_3=10.$

Fig. 8.

Trajectories of the controlled fractional model (16) approach to the equilibrium point $S_3(0,-\sqrt{\mu -1},1)$ using $\mu =3.5,\nu =0.1,\delta =0.5$and the following fractional order: (a) $q=1.1,$$k_1=300,k_2=200,k_3=10$; (b) $q=1.0,$$k_1=300,k_2=200,k_3=10$; and (c) $q=0.99,$$k_1=3,k_2=1,k_3=10.$

Stabilizing system (12) using the results of Theorem 2

A controlled form of the fractional model for quasi-periodic plasma perturbations (12) is represented as

$$D^q\mathrm{X}(t)=(A-\mathrm{K})\mathrm{X}(t)+B(\mathrm{X}(t))-U,$$ (19)

given that

$A=\left(\begin{array}{ccc}-\delta & -1& 0\\ 1& 0& 0\\ 0& 0& -\nu \end{array}\right),$ $\mathrm{K}=diag({\kappa }_{1}x-{\kappa }_1{\overline{s}}_x,{\kappa }_{2}y-{\kappa }_2{\overline{s}}_y,{\kappa }_{3}z-{\kappa }_3{\overline{s}}_z),{\kappa }_i\in R^{+},i=1,2,3,$ $U=\left(\begin{array}{c}0\\ 0\\ \mu \nu \end{array}\right).$

For the point $S_1(0,0,\mu )$, the condition $\left|arg({\lambda }_i(A-\mathrm{K}))\right|>q\pi /2,i=1,2,3,$ is always satisfied and the nonlinear function has the form $B(\mathrm{X}(t))=\left(\begin{array}{c}\mathit{yz}\\ 0\\ -\nu y^{2}z\end{array}\right).$ Hence, condition (10) is given by

$$\underset{∥\mathrm{X}(t)∥\to 0}{lim}\frac{∥B(\mathrm{X}(t))∥}{∥\mathrm{X}(t)∥}=\underset{∥\mathrm{X}(t)∥\to 0}{lim}\frac{\sqrt{y^2{z}^2+{\nu }^2{y}^4{z}^2}}{\sqrt{x^2+y^2+z^2}}⩽\underset{∥\mathrm{X}(t)∥\to 0}{lim}\frac{\sqrt{y^2(z^2+{\nu }^2{y}^2{z}^2)}}{\sqrt{y^2}}=\underset{∥\mathrm{X}(t)∥\to 0}{lim}\sqrt{z^2+{\nu }^2{y}^2{z}^2}=0.$$

Consequently, all the hypotheses of Theorem 2 are achieved, which implies that system (19) is controlled to$S_1(0,0,\mu ).$

To stabilize system (19) to the other equilibrium points $S_2(0,\sqrt{\mu -1},1)$ and $S_3(0,-\sqrt{\mu -1},1),$ we utilize the transformation ${\mathrm{X}}^{\prime }=\mathrm{X}-\overline{S}$, which transforms $\overline{S}$ to the origin. Hence, it is clear that all the conditions of Theorem 2 are also satisfied. Consequently, $(x-{\overline{s}}_x,y-{\overline{s}}_y,z-{\overline{s}}_z)$ is stabilized to the origin according to the postulates of Theorem 2.

Now, the controlled system (19) with orders $q=1.1,1$, and $0.99$ is numerically integrated using the selection $\mu =3.5,\nu =0.1,\delta =0.5,$ ${\kappa }_1=100,{\kappa }_2=30$ and ${\kappa }_3=30.$ The numerical results show that system (19) is controlled to $S_1,S_2$, and $S_3$, which are respectively depicted in Fig. 9, Fig. 10, Fig. 11.

Fig. 9.

Trajectories of the controlled fractional model (19) approach to the equilibrium point $S_1(0,0,\mu )$ using $\mu =3.5,\nu =0.1,\delta =0.5,{\kappa }_1=100,{\kappa }_2={\kappa }_3=30$ and the following fractional order: (a) $q=1.1,$ (b)$q=1.0$ and (c) $q=0.99$.

Fig. 10.

Trajectories of the controlled fractional model (19) approach to the equilibrium point $S_2(0,\sqrt{\mu -1},1)$ using $\mu =3.5,\nu =0.1,\delta =0.5,{\kappa }_1=100,{\kappa }_2={\kappa }_3=30$ and the following fractional order: (a) $q=1.1,$ (b) $q=1.0$ and (c) $q=0.99$.

Fig. 11.

Trajectories of the controlled fractional model (19) approach to the equilibrium point $S_3(0,-\sqrt{\mu -1},1)$ using $\mu =3.5,\nu =0.1,\delta =0.5,{\kappa }_1=100,{\kappa }_2={\kappa }_3=30$ and the following fractional order: (a) $q=1.1,$ (b) $q=1.0$ and (c) $q=0.99$.

Conclusion

A novel model for quasi-periodic plasma perturbations using nonlocal fractional differential operator with singular kernel has been proposed. A sufficient condition has been used to show that the solution of the proposed system exists and is unique in a specific region. Local stability of the system’s equilibria has been investigated with both commensurate and incommensurate orders. Conditions for the approximating periodic solution in this model via Hopf bifurcation theory have been obtained. Chaotic dynamics have been found in the commensurate system for a wide range of fractional orders. The Lyapunov exponents and Lyapunov spectrum of the model’s parameters and fractional order have also been calculated. Suppressing chaos in this system has been achieved via two different approaches.

The obtained results provide us with fundamental and useful information to further better understand the complex dynamics arising from the quasi-periodic plasma perturbations model and also help to erase its unpredictable dynamical behaviors. In addition, our study provides more appropriate and realistic description of the proposed model. Therefore, our results might be very useful for the physicists who work with tokamaks models.

Compliance with ethics requirements

This work does not contain any studies with human or animal subjects.

Declaration of Competing Interest

The authors have declared no conflict of interest.