Highlights
-
•
Two contrasting models are presented to understand and predict the spreading of COVID-19.
-
•
Estimation of turnaround (peak active cases) day is performed using a mathematical model for India, Italy and USA.
-
•
Trend and variability are extracted from the data for daily reported cases using DCT-based Fourier decomposition method.
-
•
Bi-modal Gaussian mixture model is fitted to the trend to predict the cases in near future.
-
•
End-dates for COVID-19 are predicted with 95% confidence interval in various parts of the world.
Keywords: COVID-19, Discrete cosine transform (DCT), Fourier decomposition method (FDM), Gaussian mixture model (GMM), Mathematical model, Susceptible-infected-recovered (SIR) model
Abstract
COVID-19 is caused by a novel coronavirus and has played havoc on many countries across the globe. A majority of the world population is now living in a restricted environment for more than a month with minimal economic activities, to prevent exposure to this highly infectious disease. Medical professionals are going through a stressful period while trying to save the larger population. In this paper, we develop two different models to capture the trend of a number of cases and also predict the cases in the days to come, so that appropriate preparations can be made to fight this disease. The first one is a mathematical model accounting for various parameters relating to the spread of the virus, while the second one is a non-parametric model based on the Fourier decomposition method (FDM), fitted on the available data. The study is performed for various countries, but detailed results are provided for the India, Italy, and United States of America (USA). The turnaround dates for the trend of infected cases are estimated. The end-dates are also predicted and are found to agree well with a very popular study based on the classic susceptible-infected-recovered (SIR) model. Worldwide, the total number of expected cases and deaths are 12.7 × 106 and 5.27 × 105, respectively, predicted with data as of 06-06-2020 and 95% confidence intervals. The proposed study produces promising results with the potential to serve as a good complement to existing methods for continuous predictive monitoring of the COVID-19 pandemic.
1. Introduction
COVID-19 is a viral disease quickly spreading its roots in various parts of the world. Its symptoms include fever, sore throat, coughing, and difficulty in breathing. The first few cases appeared in Wuhan, China, and then gradually, cases started coming up in many other countries as well. The entire world is facing an unforeseen emergency, and people have been caught unawares. This virus has infected millions of people globally. Many people have even lost their livelihoods and are struggling to fulfill their basic necessities in these difficult times. The current state of affairs requires immediate corrective measures with people across the world locked in their houses and living in fear of getting affected by this deadly virus if they step outside. The disease is highly contagious and can spread by coming in contact with an infected person or even by touching any common surfaces. It can survive over many surfaces for hours, and thus utmost caution needs to be adopted to avoid contracting the virus. In this regard, the World Health Organization (WHO) provided detailed information and advisories in its report on 02-04-2020 [1]. In addition to sincerely following the required precautions, the deployment of adequate medical facilities is also necessary to fight this pandemic.
The ever-increasing stress on health-care facilities and the resumption of economic activities can be managed more effectively by developing suitable models for understanding and predicting the spread of COVID-19. Prediction of turning point and duration of outbreaks in western countries is performed in Zhang et al. [2]. Regression analysis is performed in Ghosal et al. [3] to predict the number of deaths considering data from India. Authors in Tomar and Gupta [4] employ long short-term memory (LSTM) model for predicting the number of cases and analyze the effect of social isolation and lock-down. Forecasts relating to the spreading of COVID-19 in Italy, France, and China are presented in Fanelli and Piazza [5]. Prediction of infected cases in Italy is performed in Chintalapudi et al. [6] using an auto-regressive integrated moving average (ARIMA) model. A simplified SIR (susceptible-infected-recovered) model is applied in Zhong et al. [7] to study the outbreak of this disease in China. Identification of situational information from social media to help the authorities respond to epidemics is discussed using a case study in Li et al. [8]. A research conducted by Singapore University of Technology and Design (SUTD) [9] is using a data-driven SIR model characterized by regular updating of parameters, to predict the end of this pandemic in different parts of the world. The author in Batista [10] has implemented the SIR model for the estimation of the final size and other parameters of the COVID-19 epidemic across the globe.
This research area is still nascent, and hence it is difficult to rely on any single model for prediction. In this work, we design two contrasting models for capturing the daily variations in the number of cases. Herein, the first model is in the form of mathematical series with different parameters to account for various physical phenomena dictating the count of people getting infected by the virus. The model estimates the parameter values for three different countries, India, Italy, and United States of America (USA), and thereafter, the prediction is performed for the next 30 days to forecast the turnaround (peak active cases) day. On the other hand, the second model extracts the trend and variability from the available data using the Fourier decomposition method (FDM) based on the discrete cosine transform (DCT). The DCT works as an optimal method for many applications such as image de-noising, Fractal-based least mean squares (LMS) algorithm, image compression, and first-order Gauss-Markov random signals [11]. Prediction is performed using the Gaussian mixture model curve-fitting approach to predict the total number of cases and the end-dates (occurrence of 99% of the total expected cases) for the disease in various parts of the world.
The rest of the paper is organized as follows: Section 2 discusses the two models proposed in this work, defines various parameters associated with these models, and lays out the strategies for predicting the cases in the next few days. Results are presented in Section 3 for the three countries considered in this work with an end-date prediction for some other countries as well. Finally, the paper is concluded in Section 4.
2. Proposed methodology
2.1. Mathematical model
In this model, we signify the role of various parameters on the total number of active cases Yn nth day after the disease started spreading. The average number of people who came in contact with an infected person on a daily basis are denoted by Nc. Parameters α and γ represent the daily rate of testing and the daily death rate, respectively, i.e., α is the ratio of people getting tested and quarantined out of the total number of unidentified active cases on any given day, while γ is the ratio of people dying in a day out of the total number of active cases on that day. The number of new confirmed cases Xn reported on nth day, are computed as
| (1) |
where pi denotes the probability of an infected person causing infection to another person i days after he/she got infected. The virus is said to have an average life of days inside a human, and in the first few days, it multiplies in numbers before its degradation starts. Hence, we assume that for d days after catching the virus, pi remains unity and decays exponentially thereafter [12], i.e.,
| (2) |
where the rate of decay and d is assumed to vary between days, depending on the immunity levels or the treatment offered to the infected individual. The patient recovers after the virus has degraded substantially. Total number of active cases on nth day are obtained as
| (3) |
where the multiplicative factors and pi account for the number of deaths and recovery of the infected people, respectively. The value of Nc depends on the precautions being practiced by the people, such as social distancing, wearing of masks, washing hands on a regular basis, and staying in a quarantine environment after any suspected exposure to the virus. Government measures including the closing of shops, schools, offices, markets, restaurants, and travel restrictions or imposition of a complete lock-down also help in reducing Nc and thus contain the spread of this highly contagious disease. Further, as the value of α increases, more and more infected people are quarantined and hence cannot infect others, thereby reducing the number of new cases Xn. The total number of infected cases depends on all the parameters, as discussed above, with Nc and α being the most significant of these. On the basis of the most recent values of these parameters, as observed from the data available, the model can be used to predict the number of cases in the near future.
2.2. The Fourier decomposition method
The Fourier representation is a widely-used tool for the modeling and analysis of various physical phenomena. It decomposes a time-series in terms of sine and cosine basis functions. Here, the main concept is to decompose the COVID-19 time-series into a set of desired frequency bands using the Fourier decomposition method (FDM), and obtain various trends (low-pass components capturing the average behavior) and variabilities (high-pass components denoting the variations from the trend). These trends are then fitted with a mixture of Gaussian functions to predict the size of the pandemic. The FDM is an adaptive time-series and data analysis approach based on the zero-phase filtering [13]. It decomposes a time-series into a constant and a set of band-limited components termed as Fourier intrinsic band functions (FIBFs). The FIBFs are zero-mean, adaptive, and energy preserving functions.
The FDM can be practically implemented using (a) Fourier representations such as discrete Fourier transform, discrete sine transform, and discrete cosine transform (DCT); (b) Finite impulse response and infinite impulse response based zero-phase filtering. In this study, we have used the DCT based implementation of the FDM. Let c[n] be a time-series of a length N. The DCT type-2 of c[n] is defined as [14]
| (4) |
where for k ≠ 0 and for . The original time-series c[n] is recovered using the inverse DCT (IDCT) as
| (5) |
The DCT basis functions are a class of discrete polynomials [14] which form an orthogonal set. The time-series c[n] can be written as superposition of M FIBFs
| (6) |
where M < < N, and the values of are selected as per the application requirements. The trend τ[n] and variability v[n] can be computed from the time-series c[n] as
| (7) |
where and are uncorrelated. The trend and variability can also be written as and respectively, where the value of K is properly selected depending upon the desired time-scales of the trend and variability. The DCT based FDM can be efficiently implemented using the fast Fourier transform algorithm [15], [16].
From (7), one can easily show that as . Thus, it is interesting to observe that, if c[n] is the time series of COVID-19 cases per day, then total number of cases is same as the sum of estimated trend. Once the trend of data is estimated, it is fitted using the Gaussian mixture model (GMM) defined as
| (8) |
where parameters ai, μi and σi represent the amplitude, location and width, respectively, and L is the number of peaks to fit. All the parameters are computed using the MATLAB tool with 95% confidence bounds by minimizing the error . To measure how well g[n] fits the estimated trend τ[n], mean absolute error is obtained as
| (9) |
Finally, predictions are obtained by extrapolating the GMM (8) for time Q > N. Total number of cases is obtained by computing the area under the curve, i.e., summation of g[n] over the time range .
3. Results and discussion
3.1. Mathematical model
In this work, the data for the number of active cases (COVID-19) for India, Italy, and USA is taken from [17], last updated on 06-06-2020. The average value of γ is computed individually for each country. The values of Nc and α are updated as per change in the pattern of data owing to various precautions observed by the government and the residents of the nation, or occurrence of some sporadic events leading to a sudden spike in the spread of infections. The results for the three countries are as follows:
India: The first case in India appeared on 30-01-2020, but the number of cases started increasing rapidly after 01-03-2020. Hence, the proposed model is applied considering 01-03-2020 as day 1. The initial values for γ, Nc and α are empirically estimated as 0.0031, 1.59, and 0.5, respectively and . γ is estimated from the data regarding daily deaths, and the average value is then computed for the time period in consideration. The values for Nc and α are estimated in order to minimize the mean square error (MSE) between simulated Yi and actual value for the number of active cases i.e.,
| (10) |
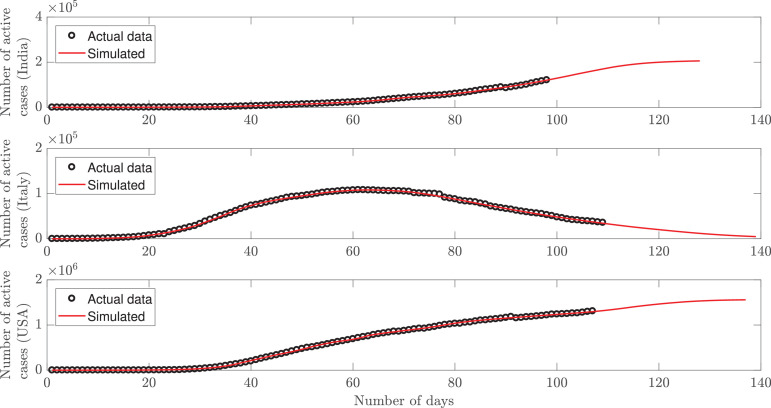
where the subscript i denotes the ith day, and n is the number of days considered. The initial values are carried until the MSE crosses a threshold e 0, and updated parameters are obtained to minimize the MSE again. In this work, we consider e 0 as 0.02. The number of active cases is depicted in Fig. 1 (top) as a function of number of days. The lock-down was imposed on 22-03-2020, and thereafter the slope of the plot has started reducing barring some sporadic occurrences on a few occasions. As per current statistics, the approximate values for Nc and α are 0.94 and 0.48, respectively. The model is used to predict the cases for the next 30 days, and it is observed that the plot indicates a turnaround (peak active cases) after 30 days from now, i.e., 07-07-2020. The less number of deaths in India than other countries is a result of early action of government, and probably a higher immunity of people than developed nations.
Fig. 1.
Mathematical model fitted to the number of active cases for India (top), Italy (middle) and USA (bottom).
Italy: The first case was identified on 29-01-2020, and the progression was not that rapid in the early days. However, the disease started spreading fast after 19-02-2020, which we consider as day 1. The parameter values for Italy are initialized as 0.0072, 2.49, and 0.5 for γ, Nc and α, respectively with . Fig. 1(middle) shows the active cases in the country. The lock-down orders were passed by the government on 09-03-2020, but the number of deaths has been more, owing to a lack of preparedness and lower immunity levels of the people. Moreover, after a sharp increase in the early days, the active cases have started declining since 21-04-2020 (turnaround date) as the medical staff and the government put up a consolidated fight with people adhering to the advisories circulated by global health organizations.
USA: It is a very big country with a population spread across large areas. In sparsely populated areas, it is thus easier to obey social distancing. Most of the cases have been reported from the densely populated areas of the country, with the first case being reported on 20-01-2020. The initial values are estimated as 0.0041, 1.75, and 0.5 for γ, Nc and α, respectively and . In our model, we consider 22-02-2020 as day one as the number of cases started increasing at a faster pace post this day. It is observed from Fig. 1(bottom) that after crossing 1,300,000 active cases as of today, the turnaround may occur in 28 days from now, i.e., 05-07-2020. No lock-down was imposed in the country; however, suitable restraining orders were observed by the various states, leading to a gradual decline in the slope of the curve for the active cases.
3.2. FDM-based model
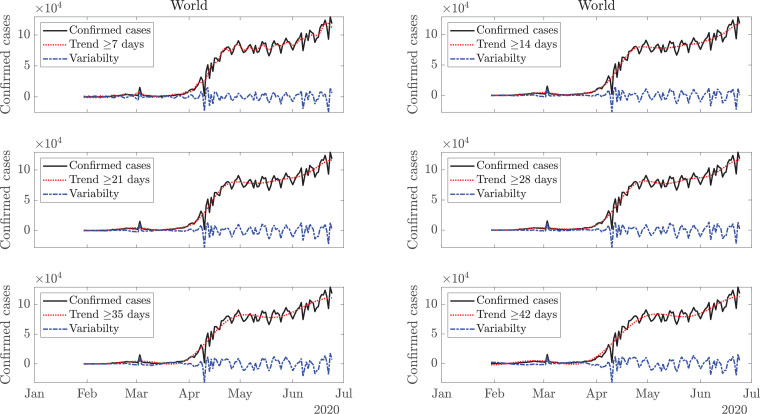
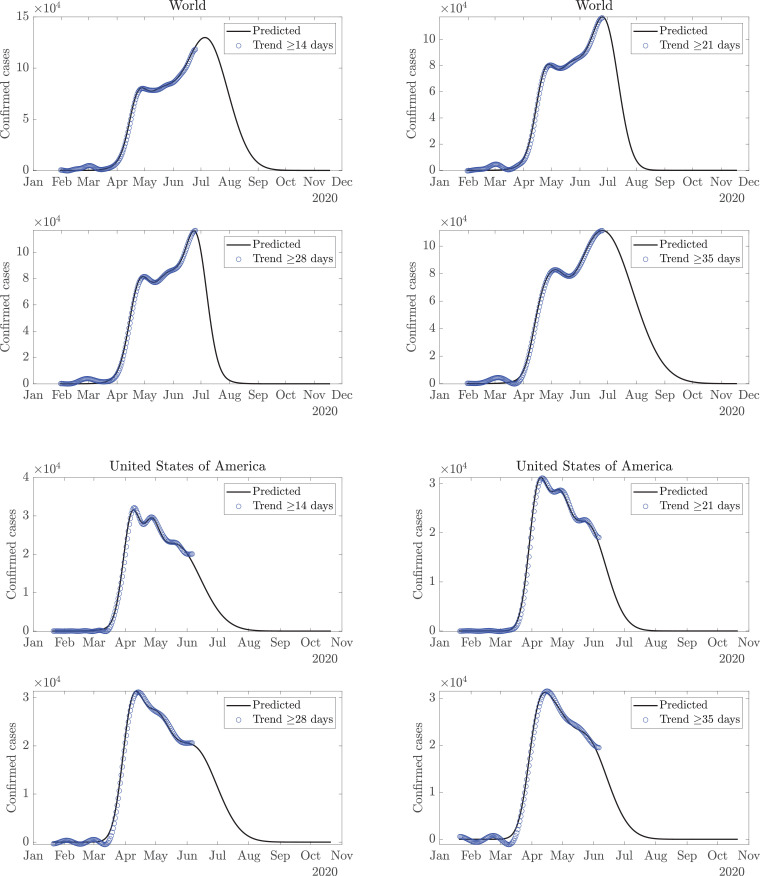
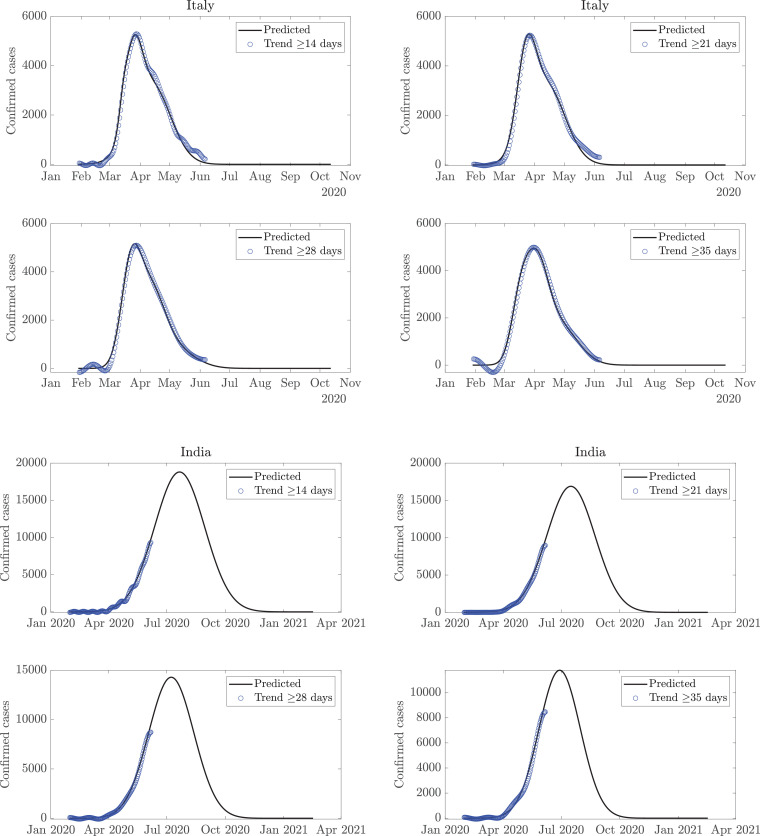
This model derives the trends and variabilities of COVID-19 data [18] for daily confirmed cases, using the FDM, as shown in Fig. 2 . Since the new confirmed cases are reported on a daily basis, therefore, sampling of the COVID-19 data is per day. Considering the normalized sampling frequency of data as the maximum frequency component present in the data is as per the Nyquist sampling criteria. For example, the low-pass signal with cutoff frequency is present in band which corresponds to 14 days or longer time-scale trend, and the remaining high-pass signal component in frequency band represents the corresponding variability. A single time-scale may not suffice in capturing the trend for all the countries. Moreover, it is evident from Fig. 2, that a trend with a time-scale of 35 days or more may not capture local maxima of smaller magnitude as it represents a long-term trend, while a shorter time-scale of 7 (or 14) days is more capable of capturing the local variations. However, one may argue whether the local variations should be captured in the trend or simply be referred to as variability. Also, the predictions for the future depend on the choice of time-scale, and it is difficult to ascertain a single time-scale, given the uncertain nature of the future trend. A time-scale of 14 days may turn out to be accurate for one country but rather inaccurate for another. Further, a given time-scale may be suited for current data and become unfit for future data. Therefore, trends are estimated on various time-scales (14 days or longer time-scale trend to 35 days or longer time-scale trend). They are extrapolated using GMM to obtain a forecast for the future. Fig. 3 depicts these trends and the future predictions for the world and USA, while the plots for Italy and India are presented in Fig. 4 . Considering multiple trends and corresponding predictions, averaging operation, excluding outliers, if any, is performed to obtain the final predictions. Total expected cases are obtained as a cumulative sum of the cases reported daily.
Fig. 2.
Plots of confirmed cases (or new cases) per day, various trends and variabilities. Trend and variability estimations in six time-scales from the COVID-19 data using the FDM with six frequency bands (FBs): (i) Trend ≥ 7 days with FB [0, 1/7], variability with FB (1/7, 0.5], (ii) Trend ≥ 14 days with FB [0, 1/14], variability with FB (1/14, 0.5], (iii) Trend ≥ 21 days with FB (0, 1/21], variability with FB (1/21, 0.5], (iv) Trend ≥ 28 days with FB [0, 1/28], variability with FB (1/28, 0.5], (v) Trend ≥ 35 days with FB [0, 1/35], variability with FB (1/35, 0.5], (vi) Trend ≥ 42 days with FB [0, 1/42], and variability with FB (1/42, 0.5].
Fig. 3.
Trend estimation from the COVID-19 data using the FDM; estimated trends are fitted with the Gaussian mixture model for the prediction of number of cases per day for World (top) and USA (bottom).
Fig. 4.
Trend estimation from the COVID-19 data using the FDM; estimated trends are fitted with the Gaussian mixture model for the prediction of number of cases per day for Italy (top) and India (bottom).
All the predictions are performed with 95% confidence intervals (CI). The parameter values for bi-modal GMM () and their CI estimated from the data are listed in Table 1 for the world, USA, Italy, and India. The parameters a 1 and a 2 indicate the peak values, while μ 1 and μ 2 mark the time of the peaks, with σ 1 and σ 2 referring to flatness (or sharpness) of these Gaussian curves. For example, the peak number of daily cases for Italy occur on 25-03-2020 (55th day after the outbreak on 29-01-2020). Similar dates for world, USA, and India are estimated as 25-06-2020, 26-04-2020, and 05-07-2020, respectively. Further, the trends estimated from data for daily deaths are also fitted using GMM, and corresponding predictions are obtained. Table 2 shows the GMM parameters and their CI estimated from this data. It is observed from this Table that the peak number of daily deaths for USA occurs on 04-05-2020. In order to measure the accuracy of proposed GMM model, we obtain the mean absolute error (MAE): (i) for daily new cases: World (MAE: 1842.5), USA (MAE: 731.00), Italy (MAE: 102.38), and India (MAE: 53.53), and (ii) for daily new deaths: World (MAE: 135.25), USA (MAE: 41.26), Italy (MAE: 15.51) and India (MAE: 2.13).
Table 1.
Parameters of the GMM (8) for confirmed cases (or new cases) per day with 95% confidence intervals (CI) for World, USA, Italy and India.
| Parameters | World | USA | Italy | India |
|---|---|---|---|---|
| L | 2 | 2 | 2 | 2 |
| a1 | 1.171e+05 | 2.207e+04 | 3310 | 468.9 |
| CI | (1.124e+05, 1.217e+05) | (1.733e+04, 2.682e+04) | (2914, 3706) | (128.4, 809.4) |
| μ1 | 153.8 | 82.45 | 55.51 | 126.9 |
| CI | (148.7, 158.8) | (81.7, 83.2) | (55.13, 55.89) | (125.8, 128) |
| σ1 | 52.41 | 16.28 | 13.33 | 2.796 |
| CI | (45.48, 59.34) | (14.18, 18.38) | (12.32, 14.35) | (0.476, 5.115) |
| a2 | 5.44e+04 | 2.45e+04 | 3200 | 1.537e+04 |
| CI | (4.863e+04, 6.018e+04) | (2.366e+04, 2.534e+04) | (3008, 3393) | (1.124e+04, 1.95e+04) |
| μ2 | 89.99 | 117.1 | 75.75 | 165.8 |
| CI | (89.38, 90.6) | (113.6, 120.7) | (73.57, 77.93) | (153.6, 178) |
| σ2 | 18.96 | 35.09 | 27.3 | 52.63 |
| CI | (17.4, 20.52) | (28.92, 41.26) | (25.84, 28.77) | (47.52, 57.74) |
Table 2.
Parameters of the GMM (8) for deaths per day with 95% confidence intervals for World, USA, Italy and India.
| Parameters | World | USA | Italy | India |
|---|---|---|---|---|
| L | 2 | 2 | 2 | 2 |
| a1 | 4766 | 1603 | 495.8 | 129 |
| CI | (3927, 5606) | (1479, 1728) | (442.3, 549.4) | (103.1, 154.8) |
| μ1 | 96.39 | 88.16 | 60.35 | 130.9 |
| CI | (95.48, 97.3) | (87.77, 88.54) | (59.87, 60.84) | (129.2, 132.7) |
| σ1 | 25.39 | 11.49 | 12.91 | 11.54 |
| CI | (24.09, 26.69) | (10.66, 12.32) | (11.79, 14.03) | (9.61, 13.48) |
| a2 | 4126 | 1571 | 433.4 | 129.8 |
| CI | (4026, 4226) | (1515, 1627) | (404.2, 462.5) | (119.9, 139.7) |
| μ2 | 143.4 | 110.9 | 80.56 | 116.7 |
| CI | (140.7, 146) | (109.4, 112.5) | (78.19, 82.92) | (113.1, 120.2) |
| σ2 | 42.75 | 29.93 | 29.41 | 32.82 |
| CI | (32.92, 52.58) | (28.39, 31.48) | (27.76, 31.06) | (30.52, 35.11) |
The end-date is defined as the date to reach 99% of the total expected cases. These dates are estimated from the predicted values for various countries and shown in Table 3 along-with the total number of cases currently and total cases expected till the end-date. Similar results obtained by SIR [9] are also indicated for comparison. The data source considered by SIR is different from the one considered in this work, and thus the values differ at some instants. The results reported in this work are more accurate in comparison to the earlier works [2], [5].
Table 3.
Prediction of the total expected cases and end-date (date to reach 99% of the total expected cases), SIR prediction [10] with data as of 06-06-2020, and proposed prediction with data as of 06-06-2020 [18] with 95% confidence intervals.
| S. No. | Country Name | Total cases as of 06-06-20 | Total expected cases (Proposed) | End-date (Proposed) | End-date (SIR) |
|---|---|---|---|---|---|
| 1 | USA | 1,857,872 | 2,370,992 | 12-07-2020 | 09-07-2020 |
| 2 | Spain | 240,978 | 249,754 | 28-05-2020 | 28-04-2020 |
| 3 | Italy | 234,531 | 239,260 | 09-06-2020 | 06-06-2020 |
| 4 | France | 149,495 | 159,308 | 03-06-2020 | 27-05-2020 |
| 5 | UK | 283,315 | 313,684 | 29-06-2020 | 04-07-2020 |
| 6 | Germany | 183,678 | 188,266 | 02-06-2020 | 22-05-2020 |
| 7 | Turkey | 168,340 | 180,449 | 23-06-2020 | 14-06-2020 |
| 8 | Russian Federation | 458,689 | 627,010 | 12-07-2020 | 17-07-2020 |
| 9 | Brazil | 614,941 | 225,536 | 02-09-2020 | 16-08-2020 |
| 10 | Canada | 94,070 | 107,100 | 13-07-2020 | 12-07-2020 |
| 11 | India | 236,657 | 1,083,000 | 14-09-2020 | 12-09-2020 |
| 12 | World | 6,663,304 | 12,702,528 | 23-09-2020 | 13-09-2020 |
4. Conclusion
In this paper, we have proposed two distinct methods for modeling the number of people getting infected with the novel coronavirus (COVID-19). Firstly, a mathematical model captures various factors critical in determining the spread of the virus, and appropriate values are estimated using the available data. The turnaround day for active cases is forecasted by predicting values for the next 30 days. The measures taken by the authorities to contain the infections are analyzed for three different countries, i.e., India, Italy, and USA. The second method develops a data-driven model to segregate the trend and variability from the data for daily cases of infection. The Gaussian mixture model is developed to obtain suitable predictions for the trend, which are used to ascertain the peak value and the corresponding date for the fresh cases reported in a single day. Further, the total number of cases, as well as the end-dates for this pandemic spread across various parts of the world, are estimated with 95% confidence intervals and are compared with a similar study performed earlier. This study is performed for academic and research purposes only, and the predictions for the future are based on the assumption that the current restrictive conditions would continue.
CRediT authorship contribution statement
Amit Singhal: Conceptualization, Methodology, Software, Validation, Writing - original draft, Writing - review & editing. Pushpendra Singh: Conceptualization, Methodology, Software, Validation, Writing - original draft, Writing - review & editing. Brejesh Lall: Supervision, Visualization, Validation, Writing - review & editing. Shiv Dutt Joshi: Supervision, Visualization, Validation, Writing - review & editing.
Declaration of Competing Interest
We declare that we have no conflict of inertest.
Acknowledgment
We would like to thank the editors and reviewers of this manuscript, who took out some precious time during these difficult times of COVID-19 pandemic, and provided valuable suggestions to improve the overall quality of the paper.
References
- 1.Coronavirus disease 2019 (COVID-19) situation report–73. World Health Organization. 2020 [Google Scholar]
- 2.Zhang X., Ma R., Wang L. Predicting turning point, duration and attack rate of COVID-19 outbreaks in major western countries. Chaos Solitons Fractals. 2020;135:109829. doi: 10.1016/j.chaos.2020.109829. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Ghosal S., Sengupta S., Majumder M., Sinha B. Prediction of the number of deaths in India due to SARS-CoV-2 at 5–6 weeks. Diabetes Metab Syndr. 2020;14:311–315. doi: 10.1016/j.dsx.2020.03.017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Tomar A., Gupta N. Prediction for the spread of COVID-19 in India and effectiveness of preventive measures. Sci Total Environ. 2020;728:138762. doi: 10.1016/j.scitotenv.2020.138762. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Fanelli D., Piazza F. Analysis and forecast of COVID-19 spreading in China, Italy and France. Chaos Solitons Fractals. 2020;134:109761. doi: 10.1016/j.chaos.2020.109761. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Chintalapudi N., Battineni G., Amenta F. COVID-19 disease outbreak forecasting of registered and recovered cases after sixty day lockdown in Italy: a data driven model approach. J Microbiol Immunol Infect. 2020;53(3):396–403. doi: 10.1016/j.jmii.2020.04.004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Zhong L., Mu L., Li J., Wang J., Yin Z., Liu D. Early prediction of the 2019 novel coronavirus outbreak in the mainland China based on simple mathematical model. IEEE Access. 2020;8:51761–51769. doi: 10.1109/ACCESS.2020.2979599. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Li L., Zhang Q., Wang X., Zhang J., Wang T., Gao T.-L. Characterizing the propagation of situational information in social media during COVID-19 epidemic: a case study on weibo. IEEE Trans Comput Soc Syst. 2020;7(2):556–562. [Google Scholar]
- 9.When will COVID-19 end? Data-driven prediction. https://ddi.sutd.edu.sg/when-will-covid-19-end/; Accessed: 04-05-2020.
- 10.Batista M.. Estimation of the final size of the COVID-19 epidemic. medRxiv preprint2020;01–11URL 10.1101/2020.02.16.20023606. [DOI]
- 11.Gupta A., Joshi S.D., Singh P. On the approximate discrete KLT of fractional Brownian motion and applications. J Frankl Inst. 2018;355:89899016. [Google Scholar]
- 12.Singhal A., Mallik R.K., Lall B. Performance analysis of amplitude modulation schemes for diffusion-based molecular communication. IEEE Trans Wireless Commun. 2015;14(10):5681–5691. [Google Scholar]
- 13.Singh P., Joshi S.D., Patney R.K., Saha K. The Fourier decomposition method for nonlinear and non-stationary time series analysis. Proc R Soc Lond A: Mathematical, Physical and Engineering Sciences. 2017;473:1–27. doi: 10.1098/rspa.2016.0871. [DOI] [PMC free article] [PubMed] [Google Scholar]; 20160871
- 14.Ahmed N., Natarajan T., Rao K.R. Discrete cosine transform. IEEE Trans Comput. 1974:90–93. [Google Scholar]
- 15.Britanak V., Yip P.C., Rao K.R. Fast Algorithms Integer Approx. 1 edition. Academic Press; 2006. Discrete cosine and sine transforms: general properties. ISBN-10: 0123736242, ISBN-13: 978-0123736246. [Google Scholar]
- 16.Singh P. Novel Fourier quadrature transforms and analytic signal representations for nonlinear and non-stationary time series analysis. Royal Society Open Science. 2018;5:1–26. doi: 10.1098/rsos.181131. [DOI] [PMC free article] [PubMed] [Google Scholar]; 181131
- 17.Novel Coronavirus (COVID-19) Cases Data. https://data.humdata.org/dataset/novel-coronavirus-2019-ncov-cases; Accessed: 06-06-2020.
- 18.WHO COVID-19 Dashboard. https://covid19.who.int/; Accessed: 06-06-2020.