Why Public Health Needs GIS: A Methodological Overview

Abstract

The short paper provides an overview on how geographic issues have become increasingly relevant to public health research and policy, particularly through the lens of geographic information systems (GIS). It covers six themes with an emphasis on methodological issues. (1) Our health-related behavior varies across geographic settings, so should public health policy. (2) Facilities (supply) and patients (demand) in a health care market interact with each other across geopolitical borders, and measures of health care accessibility need to capture that. (3) Our health outcome is the result of joint effects of individual attributes and neighborhood characteristics, and an adequate definition of neighborhood is critical for assessing neighborhood effect. (4) Disease rates in areas of small population are unreliable, and one effective way to mitigate the problem is to construct a larger, internally-homogenous and comparable area unit. (5) Defining a scientific geographic unit for health care market is critical for researchers, practitioners, and policy makers to evaluate health care delivery, and GIS enables us to define the unit (e.g., primary care service areas, hospital service areas, and cancer service areas) automatically, efficiently and optimally. (6) Aside from various optimization objectives around “efficiency”, it is as important to plan the location and allocation of health care resources toward maximum equality in health care access. Case studies are cited to illustrate each theme.

The seminal work of John Snow on the 1854 cholera outbreak in London is the best known example to illustrate the power of mapping and geographic approach in public health (see Shiode et al. 2015 for a recreation of the event by the modern GIS technology). Richardson et al. (2013) offers a recent perspective on how the advancement of geographic information science (GIScience) helps us understand the pattern, etiology, transmission, and treatment of diseases better. This short paper overviews how geography contributes to public health research and policy, particularly through the lens of geographic information systems (GIS). Given its page limit, the paper is not intended as a comprehensive review of this broad topic, rather focuses on methodological issues and more recent advancements. The purpose is simple: to facilitate the fusion of public health and GIS. For public health professionals, what are the values of GIS to further our understanding of health issues and help craft more effective public policy? For GIS practitioners, what areas of public health have been early beneficiaries and continue to benefit from a spatial perspective and GIS-enabled analytics?

Six themes are outlined in the following order: geographic heterogeneity, spatial accessibility, neighborhood effect, small population problem, health care market delineation, and planning toward equality. A section is devoted to each theme. Case studies are cited to illustrate each theme.

1. Modeling Geographic Heterogeneity in Health Behavior and Outcome

Goodchild (2004) highlights the importance of heterogeneous nature of geographic phenomena as the “Second Law of Geography.” This section uses several case studies to examine how geographic (spatial) heterogeneity is modeled and how such a perspective enriches scientific inquiry into public health issues. Spatial heterogeneity includes spatial stratified heterogeneity (SSH) and spatial local heterogeneity (SLH). The former emphasizes the heterogeneity between strata (regions), each of which is composed of a number of units, and the latter highlights the variability of traits, events, attributes and relationships across space in a spatial scale (Wang, Zhang & Fu, 2016). The following illustrates SSH first and then SLH.

There is considerable heterogeneity across geopolitical units in terms of culture, politics, policy and regulation, etc. In studying cancer screening behavior in the U.S., Mobley et al. (2012) run a model for one type of cancer for each of the 50 states with a focus on whether there is a significant disparity in cancer screening for African Americans and for Hispanics relative to whites. The results are then mapped to showcase the variability of presence/absence of the disparities across states. Among the findings, for colorectal cancer, African Americans in Michigan and Hispanics in New Jersey are significantly more likely than whites to utilize screening, while in other states the disparities are either opposite or not significant.

Public health also has a long tradition of examining the effect of urbanicity (i.e., degree of urbanization) on health behavior and outcome. Recent studies suggest two emerging consensuses: the rural-versus-urban dichotomous definition fails to capture variability across the full continuum of urbanicity (Hall et al. 2006), and spatial scale used in the measurement affects its reliability and validity (Cyril et al. 2013). Both can benefit a great deal from GIS. For example, McLafferty and Wang (2009) classify the zip code areas in Illinois into five categories of urbanicity such as the densely-populated City of Chicago, Chicago suburbs, other smaller metropolitan areas, large towns (with population 10–50k), and rural. The same multilevel logistic model on late-stage cancer risk of each cancer type is implemented for cancer patients in zip code areas grouped in each of the five urbanicity classifications, and the derived odd ratios for late stage are compared across these five categories. After controlling for individual attributes, zip-code-level socioeconomic characteristics and spatial access to health care, they find that late-stage cancer risks for four major types of cancer (breast, colorectal, lung, and prostate) are highest in the most highly urbanized area and decrease as urbanicity declines, with a small upturn in risk in the most isolated rural areas. Similarly, in a study on the association of built environments with individual physical inactivity and obesity in the U.S., Xu and Wang (2015) divide the data set into several subsets according to the urbanicity levels of counties where individuals reside, and apply a multilevel regression model in each subset. They use the Urban–Rural Classification Scheme for Counties prepared by the National Center for Health Statistics (NCHS, 2013), and also divide the counties into five categories based on urban population ratios (0–0.01 for completely rural, 0.01–0.50 for marginally urban, 0.50–0.90 for mostly urban, 0.90–0.99 for highly urban, and 0.99–1.00 for completely urban). The latter is achieved by overlaying counties and urban areas defined by the U.S. Census Bureau (2018). Since urban areas (including urbanized areas and urban clusters) are made of geographic units of fine scale such as census tracts and census block, a more accurate measure of urbanicity is attained. The study finds that the association between built environment and obesity vary across different urbanization levels. In short, separate models are run in areas of distinctive urbanicity in order to capture possible varying behavior and relationship across these areas. By extension, public policies cannot be one-size-fits-all and need to be geographically adaptable.

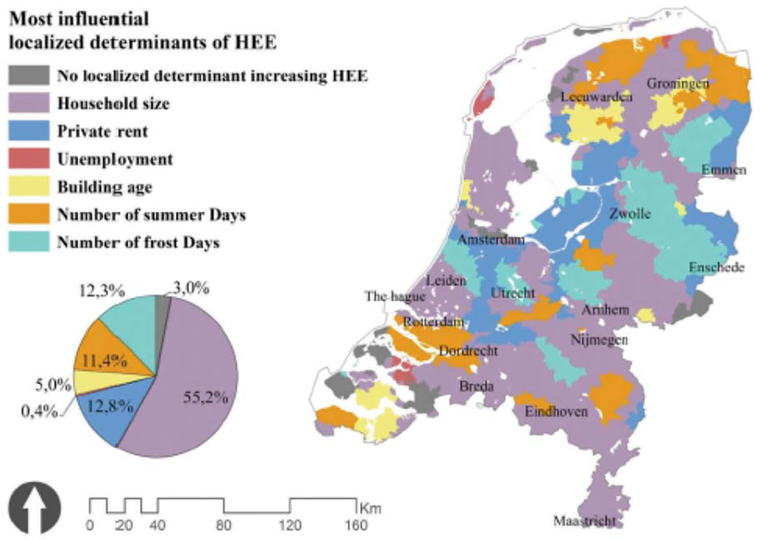
Now we turn to SLH. When geographic boundary for examining heterogeneity in relationship is not clearly defined as in the aforementioned cases, one can use the geographically-weighted regression (GWR) method to allow regression coefficients to vary across space and detect whether and how the effects are more significant in some areas than others. In more recent versions of GWR (Nakaya et al. 2009), the semi-parametric geographically weighted regression (SGWR) model detects whether the effect of an independent variable is global and thus a spatially homogenous determinant, or local and thus a spatially heterogeneous determinant. Using the SGWR model to explain the level of energy poverty in Netherland, Mashhoodi et al. (2019) identify two global determinants (% low-income households and % pensioners), six local determinants (household size, % unemployment, building age, % privately rented dwellings, number of summer days and number of frost days), and others insignificant. The results of all local determinants can be integrated in one map (Figure 1) to highlight which one exerts the most influence on where. The policy implication is obvious: national-level policies ought to focus on mitigation via the global determinants, and neighborhood-level funds need to respond to the most important local factor(s).

Figure 1.

Most influential local determinants of household energy expenditure (Source: Mashhoodi et al. 2019: 28)

In summary, human behavior varies across distinctive physical and social environments. Public health often examines such a variability across geographic settings such as geopolitical units, urbanicity and others. The spatial heterogeneity can be captured by running separate models in each setting, or modeled analytically by the GWR and more recently by the SGWR to detect whether the effect is global, local or insignificant. Therefore, public policy needs to be adjusted geographically and be applied only in effective areas.

2. Measuring Spatial Accessibility for Patients and Potential Crowdedness for Facilities

Uneven distributions of population and health care providers lead to geographic disparity in accessibility for patients and varying workload for staff in hospitals and clinics. The former leads to inequality in utilization of health care resources by people and subsequently their health outcomes; and the latter affects the stress level of health care professionals and quality of cares they deliver. Both contribute to health disparities across geographic areas and between population groups. Population and health care facilities represent the demand and supply sides of a health care system, and interact with each other across space. Recent advancements have been made to integrate the measures of spatial accessibility for patients and potential crowdedness for facilities into one framework in a GIS environment.

Among various measures of spatial accessibility, the two-step floating catchment area (2SFCA) method by Luo & Wang (2003) has been the most widely adopted as it accounts for both proximity to service providers and their availability. Wang (2012) reviews various refinements to the original 2SFCA method, and proposes the generalized 2SFCA method as a framework to synthesize all:

$$A_i={\mathrm{\Sigma }}_{j=1}^n[S_{j}f\left(d_{ij}\right)/{\mathrm{\Sigma }}_{k=1}^m\left(D_{k}f\right(d_{kj}\left)\right)]$$ (1)

where A_i is accessibility at demand (population or patients) location i, D_k is amount of demand at location k, S_j is the capacity of supply facility (e.g., number of doctors or hospital beds) at location j, d is the distance or travel time between them, and n and m are the total numbers of facility locations and population locations, respectively. Note that f(d) is a distance decay (e.g., exponential, power, and Gaussian) function that captures the patient-facility spatial interaction. When f(d) is a discrete variable such as binary (=1 if d ≤ d₀; and =0 if d > d₀ where d₀ is a constant that defines the catchment area size), the generalized 2SFCA regresses to the traditional 2SFCA. The method is convenient to implement in a GIS environment. Its result can be intuitively interpreted as the supply-demand ratio (e.g., doctors per person; or doctors per 1,000 people if A_i is inflated 1,000 times), and a larger value indicates better access (Wang, 2015: 95–101).

While the 2SFCA measures spatial accessibility of residents for a service, the newly developed inverted 2SFCA (or i2SFCA) method captures busyness for facilities (or scarcity of resource or intensity of competition for the service) (Wang, 2018). Denoted as C, it is formulated as

$$C_j={\mathrm{\Sigma }}_{i=1}^m[D_{i}f\left(d_{ij}\right)/{\mathrm{\Sigma }}_{l=1}^n\left(S_{l}f\right(d_{il}\left)\right)]$$ (2)

With all notations identical to Equation (1), Equation (2) is symmetric to Equation (1) by switching supply S and demand D, and therefore termed i2SFCA. Moreover, C_j is derived as the ratio of population served as projected by the Huff (1963) model versus the supply capacity at facility j, and thus the term may be interpreted as “projected or potential crowdedness” (e.g., patients served per bed in a hospital). A higher C_j value indicates a service facility being more crowded (saturated, stressed, or busy).

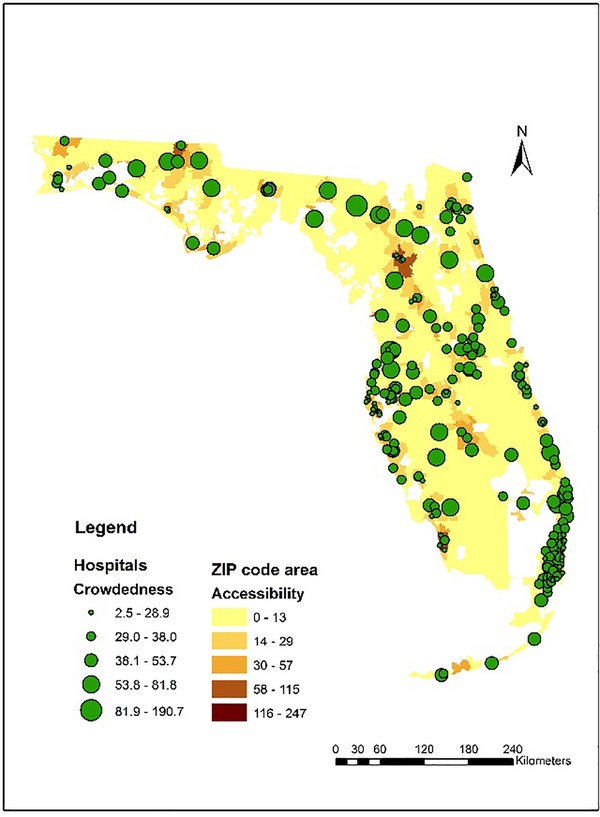
Based in a case study based on the 2011 all hospitalization data in Florida (Wang, 2018), Figure 2 shows the results of 2SFCA and i2SFCA on one map for comparison. Note that hospitals with higher values of crowdedness are general in areas with relatively lower accessibility. In other words, in areas where residents enjoy better accessibility for hospital care, those hospitals tend to experience less crowdedness.

Figure 2.

Hospital potential crowdedness vs. zip code area accessibility (Source: Wang 2018: 257)

In summary, residents-based accessibility and facility crowdedness are two sides of the same coin in examining the geographic variability of resource allocation. The two measures capture similar traits in surplus or scarcity of a resource in some areas, but have their distinctive emphases for different purposes. One can use 2SFCA to highlight the inequality of access for certain areas with disproportional concentration of particular demographic groups, and others use i2SFCA to gain a direct assessment of unbalance in resource allocation among service providers. The former identifies who and where need help to mitigate disparity, and the latter guides decision making and policy that targets facilities in order to achieve a fairer allocation of staff and resources.

3. From Area-based to Individualized Neighborhood Effects

Individual health behavior or outcome is usually a result of effects from both individual and neighborhood factors. As observations for individuals are nested within those of neighborhoods, researchers often use multilevel modeling (MLM) instead of the traditional ordinary least square (OLS) regression method for such an analysis. How can we define neighborhood that accurately captures the relevant geographic context, instead of relying on some predefined geopolitical or census area units? Kwan (2012) refers it to as the “uncertain geographic context problem (UGCoP).” Kwan (2018a) further attributes the uncertainty to the effect being highly person specific, temporally dependent, frame dependent, and selective mobility biased. When the contextual unit is ill defined, it either leads to an identified effect that is false positive, or no effect detected that is false negative. It is a challenge, once again, well suited for GIS to tackle.

When geocoding of individual-level data is limited to pre-defined area units, one needs to explore which level of neighborhood is most relevant and assess whether such an effect is supported by underlying behaviors. In a study on the associations between neighborhood built environments and individual odds of overweight and obesity in Utah, Xu et al. (2015) employ the measures of neighborhood variables at two levels. They found that distance to parks at the ZIP code area level and food environment (fast food ratio) at the county level are significant factors linked to risks of overweight and obesity. Based on the results, they speculate that individuals’ exercise levels are likely to be more responsive to parks nearby rather than those located distantly, whereas people normally drive to buy fast food beyond the zip code they live. The study suggests that the contextual variables need to be defined in a way that “reflects human mobility patterns pertaining to the specific trip purposes”, and “at a neighborhood size relevant to residents’ activity space” (Xu et al., 2015: 202).

Similarly, sociologists have increasingly recognized the importance of neighborhood effects on individuals and families. In a recent review of sociological work, Noah (2015) summarizes neighborhood effects in family studies via various mechanisms: family as a moderator or a mediator (e.g., negative effects of disadvantaged neighborhoods on children are moderated or mediated by parenting and family processes behaviors), neighborhood as a moderator or a mediator (e.g., negative impacts of family-level risk factors are magnified in socioeconomically disadvantaged neighborhoods, or positive family-level protective and harmful factors can disappear in disadvantaged neighborhood characteristics). While these hypotheses are important to establish the theoretical foundation of neighborhood effects, it remains a major challenge to define neighborhoods relevant to the processes. She recognizes the limitations of often-used residential neighborhood, and goes on to emphasize that neighborhoods need to be based on activity space of individuals. However, the methods of measuring activity space cited in her review (e.g., ellipse, kernel densities, shortest-path networks, and minimum convex hull) and others in sociology (e.g., “egohoods” as concentric circles around each block as proposed by Hipp and Boessen (2013)) remain primitive.

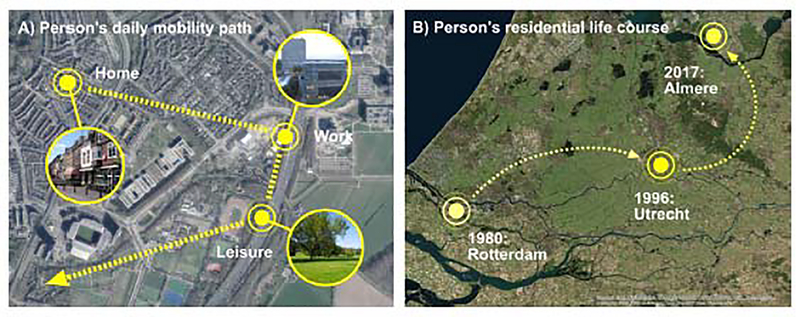
Following the long tradition of time geography, more recent studies use GIS to develop a more accurate measure of people’s exposures to and the health impact of environmental factors such as pollution, green space and other built environment factors by tracing their daily mobility. For example, Lu and Fang (2015) use a portable air pollutant sensor and a portable GPS unit on one person to measure personal exposure to air pollution and personal pollutant intake by tracing the individual’s space-time path over two days. A study based on mobile phone users in Belgium finds that when accounting for daily mobility, NO₂ exposure by mobile phone users needs to be significantly adjusted upward for low residence-based NO₂ exposure and downward for high residence-based NO₂ exposure (Dewulf et al. 2016). Kwan (2018b) uses the term “neighborhood effect averaging problem (NEAP)” to refer to the traditional approach of measuring neighborhood effect by one’s static residence while neglecting daily mobility. In a review article on environmental exposure in mental health, Helbich (2018) promotes dynamic exposure assessment on a person’s daily mobility path (e.g., home, work and leisure) and a person’s residential life course in order to capture the full effects of exposure duration, sequences and accumulation. While empirical studies from a residential life course perspective are few (e.g., Brazil and Clark, 2017; Veldman et al. 2017), there is a large body of work on improved exposure measures based on daily mobility. The latter has benefited from smartphone-based GPS tracking, modern GIS analytics, and environmental sensing.

In summary, individuals in one area vary a great deal in activity space or mobility trajectory due to their distinctive demographic and socioeconomic attributes. It is a natural evolution for researchers to move from area-based neighborhood effect to individualized exposure measure. Such a movement has been enabled by high-resolution spatial data and analytic power of GIS. Just like the importance of personalized medicine revolution in medical care, the “individualized neighborhood effect” approach will have a lasting impact on public health.

4. Constructing Geographic Areas for Health Data Dissemination and Analysis

Analysis and presentation of health data often suffers from the small population problem such as less reliable rate estimates, sensitivity to missing data and other data errors, and data suppression in sparsely populated areas. The problem is more evident in rates of rare diseases or by population subgroups. For example, on the State Cancer Profiles web site (statecancerprofiles.cancer.gov), one can query and map any cancer rates in a state at the county level for a 5-year period. However, regulations require that data with fewer than 16 counts or a population below 50,000 be suppressed to avoid unreliable rates and breach of confidentiality. This leads to missing data for many counties (sometimes the majority of counties) for rare cancers or particular age (racial-ethnic) groups. On the other hand, rate variations that might exist within large urban counties cannot be revealed. The example illustrates that health data in predefined administrative units have limited value to the public that desires a comprehensive overview of a region, or to researchers who are interested in patterns at finer geographic scales.

Several geographic strategies have been attempted to mitigate the problem. For instance, some spatial smoothing methods such as the floating catchment area method, kernel density estimation (Wang, 2015: 47–50), locally-weighted average (Shi, 2007) and adaptive spatial filtering (Tiwari and Rushton, 2004), all implemented in GIS, use a larger spatial window to compute average (and thus smoothed) disease rates of surrounding areas. But that is mainly for mapping. For data dissemination and analysis, this section focuses on the regionalization approach by constructing geographic areas that are homogenous, sufficiently large and comparable. Specifically, two GIS-automated methods are identified from the literature with desirable merits and briefly discussed here: regionalization with dynamically constrained agglomerative clustering and partitioning (REDCAP) method (Guo, 2008) and (2) mixed-level regionalization (MLR) (Mu et al., 2015).

The REDCAP method is composed of two steps. The first step constructs a hierarchy of spatially contiguous clusters. Two adjacent and most similar areas are grouped to form the first cluster; two adjacent and most similar clusters are grouped together to form a higher-level cluster; and so on until the whole study area is one cluster. A spatially contiguous tree is generated to fully represent the cluster hierarchy. The second step partitions the tree to generate two regions by removing the best edge that maximizes the total within-region homogeneity. The partitioning continues until a desired number of regions is reached. The method is later modified to accommodate additional constraints such as a minimum size in terms of region population and/or disease count (Wang et al. 2012). The MLR method decomposes areas of large population (to gain more spatial variability) and merges areas of small population (to mask privacy of data) in order to obtain regions of comparable population. For instance, for rural counties with small population, it is desirable to group counties to form regions of similar size; and for urban counties with large population, it is necessary to segment each into multiple regions also of similar size and each region is composed of lower-level census tracts. Therefore, resulting regions are made of areal units at multiple (mixed) levels. Another important property of MLR is to let users define the balance between how much spatial connectivity/compactness and how much attributive homogeneity to achieve in the derived regions.

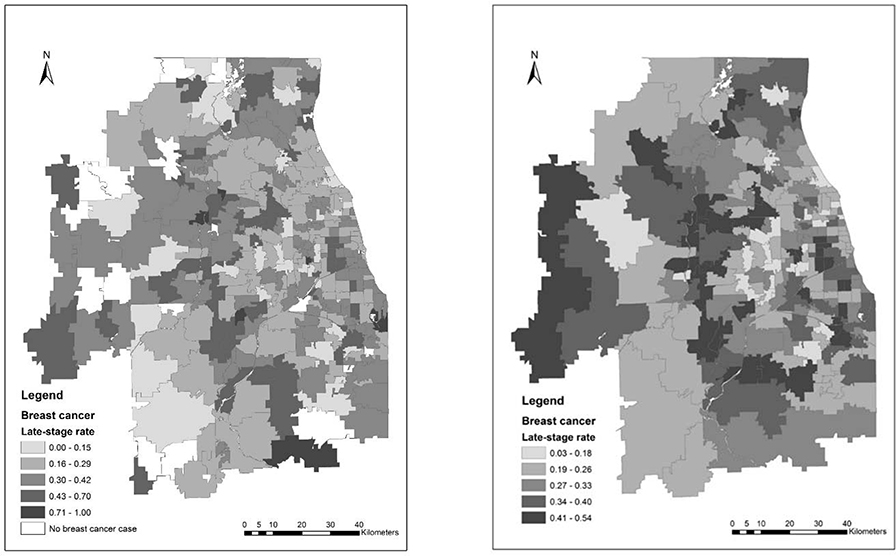
Figures 4a shows the late-stage breast cancer rates in Chicago region in 2000 across 317 ZIP code areas. As the rate in each area is calculated as its late-stage count divided by its total cases, the zip code areas have missing late-stage rates (in blank on the map) because of zero total case there. Among the zip code areas with valid late-stage rates, some have a late-stage rate of 0.0 and others with a rate of 1.0, which are unrealistic and unreliable. Figure 4b shows the rates across 195 REDCAP-derived areas. Since each constructed area has a minimum of 16 breast cancer incidents, all areas have valid late-stage rates within a reasonable range (0.03–0.54). Furthermore, the distribution of late-stage rates in the ZIP code areas is skewed to the left while the distribution in the constructed areas largely conforms to a normal distribution (Wang, 2015:207) (graphs not shown here due to limited space), which is assumed in many routine statistical analyses.

Figure 4.

Late-stage breast cancer rates in Chicago region in 2000: (a) ZIP code areas, (b) REDCAP-constructed areas (Source: Wang, 2015:206&210)

In short, GIS-automated regionalization methods enable us to construct geographic areas that are spatially contiguous and homogeneous in attributes. These areas are large enough to have health data disseminated and reliable rates calibrated. In the case of MLR, they are also comparable in size and compact in shape. As similar areas are merged, it mitigates the spatial autocorrelation problem commonly observed in data of geographic areas and simplifies subsequent analysis such as regressions. When the attributive homogeneity is defined as percentage of a disadvantaged group (e.g., racial-ethnic minority, population under poverty or with a language barrier), the derived areas represent different levels of concentrated disadvantages, and facilitate health disparity analysis between the haves and have-nots (Wang et al. 2019). The approach also frees us from relying on data often aggregated in administrative units. Instead one may generate a series of geographic areas and examine whether research results are sensitive to the use of these areas, commonly-referred to as “modifiable areal unit problem (MAUP)”.

5. Delineating Hospital Service Areas

Section 4 discusses the use of regionalization approach to define analysis areas for disease. This section introduces another theme on delineating geographic unit for researchers, practitioners, and policy makers to assess health care markets. The former is to derive regions that are homogeneous in socio-demographic structure, and here it is to delineate functional regions that are coherent in terms of connection. The Dartmouth Atlas Project (www.dartmouthatlas.org) piloted the work of deriving health care markets for inpatient care such as the Hospital Service Areas (HSAs) and Hospital Referral Regions (HRRs) and primary care such as the Primary Care Service Areas (PCSAs). These units capture local health care markets, and thus are more meaningful units than administrative or census units in evaluating resource allocation, service utilization, and health outcomes. They have been instrumental in informing health policy (U.S. Senate Committee on Finance, 2009; Newhouse and Garber 2013). This section reviews briefly how the Dartmouth HSAs/HRRs are defined, and introduces two new GIS-automated methods on the issue.

Based on the Medicare data, the Dartmouth HSAs/HRRs are defined through a three-step process: (1) assigning all acute care hospitals to the town/city where they are located, (2) assigning each ZIP code to the town/city containing the hospitals visited most often, and aggregating ZIP codes assigned to the same town/city to form a preliminary HSA, and (3) examining the geographic contiguity of all ZIP codes in a HSA, and assigning any enclave ZIP code(s) to its adjacent HSAs. Similarly, the larger HRRs are subsequently constructed from HSAs based on cardiovascular surgery and neurosurgery referral patterns (Cooper 1996).

The Dartmouth method is not automated, involves uncertainty or arbitrary choices, and lacks a theoretical foundation. Jia et al. (2017a) propose a refined Huff model, which estimates the probability (proportion) of patients in ZIP code i being discharged from hospital j (among other hospitals), Prob_ij, as

$${Prob}_{ij}=\left[S_j^{\sigma }{f(d}_{ij}\right)]/[{\mathrm{\Sigma }}_{k=1}^n{S}_k^{\sigma }{f(d}_{ik})]$$ (3)

where S_j is the size of hospital j (e.g., number of beds), σ is its associated elasticity parameter, d_ij (d_ik) is travel time from zip code i to hospital j (k) in minutes, and f(d_ij) is a generalized distance decay function (similar to Equations (1) and (2) in Section 2). In comparison to the classic Huff (1963) model, Equation (3) is more general by (1) adding an elasticity parameter σ associated with the facility size, and (2) taking a general distance decay function f in place of the specific power function. In Jia et al. (2017a), the parameter σ and function f(d_ij) are derived by regression analysis of all hospitalization data in Florida in 2011. The model is automated in a convenient toolkit (Wang, 2015:90–92).

With probability estimated from the toolkit, each ZIP code is assigned to the hospital with the greatest probability of discharging patients to it. Each cluster of ZIP codes assigned to the same hospital are merged into an initial HSA. These preliminary HSAs are then adjusted for ensuring spatial continuity and localization index (LI) higher than 0.50. LI refers to the fraction of patients visiting hospitals within a HSA out of all patients residing in the HSA, and is an important indicator to measure the quality of HSAs delineation. Similarly, HRRs are constructed from HSAs based on patient visit data for cardiovascular and neuro surgery (Jie et al. 2017b).

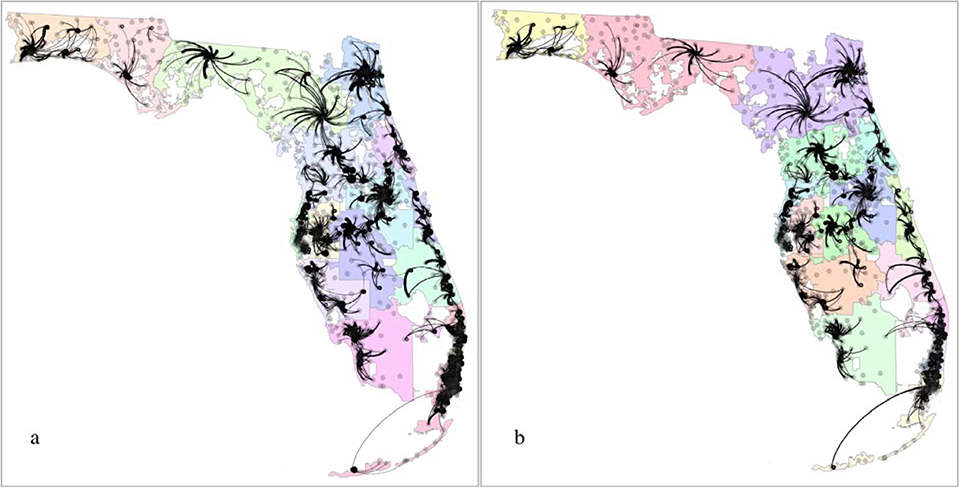
Most recently, Hu et al. (2018) uses a network optimization method to define HSAs and HRRs by maximizing patient-to-hospital flows within HSA/HRRs while minimizing flows between them. Specifically, it builds upon a community detection method, termed Louvain algorithm (Blondel et al., 2008), in the complex network science literature. At the beginning, the algorithm treats every node as a group (community), and then successively combines communities together to form larger communities. At each step, it chooses the best agglomeration measured in so-called modularity, until all nodes in the network are grouped into one large community or no improvements in the community configuration are observed. The case study uses the same data as Jia et al. (2017a, 2017b). In that context, ZIP codes become nodes, patient flows between them become edges, and detected communities are HSAs (HRRs). The method has several desirable properties. It is guided by an optimization objective to produce communities with the maximal modularity score, which leads to maximal intra-HSA flows and minimal inter-HSA flows. It is also an agglomerative hierarchical clustering (i.e., bottom-up) approach, and generates a series of HSAs, whose number corresponds to a user-defined scale. Therefore, it is scale flexible. Moreover, by examining the variation of modularity value in response to the number of HSAs, one can identify the global optimal modularity score, which may suggests the optimal configuration of HSAs. Figure 5a and 5b show such optimal HSAs and HRRs in the case study. Both flow maps appear to align well with the delineated geographic units.

Figure 5.

Network-based delineations of HSAs/HRRs in Florida: (a) HSAs with ≥200 inpatient discharge, and (b) HRRs with ≥50 inpatient discharge (Source: Hu et al., 2018: 250)

To recap, hospital service area (HSA) has increasingly been adopted as a basic geographic unit for health care market assessment, management and planning. Its delineation method needs to be scientifically sound, user friendly, and computationally efficient (thus adaptable for large scale such as nationwide markets). Recently-developed GIS methods, especially the network-optimization methods, show great promise to meet this challenge.

6. Spatial Optimization towards a Balance in Efficiency and Equality

Location–allocation analysis seeks the optimal placement of facilities for a desirable objective under certain constraints. Among the classic location-allocation problems, the p-median problem minimizes the weighted sum of distances between users and facilities, the location set covering problem (LSCP) minimizes the number of facilities needed to cover all demand, and the maximum covering location problem (MCLP) maximizes the demand covered within a desired distance or time threshold by locating a given number of facilities (Church, 1999). Most of these models emphasize efficiency, such as minimizing total travel, minimizing resources committed or maximizing population served. Only the minimax problem marginally addresses the issue of equity as it minimizes the travel for the most remote user. Social scientists have long argued the balance between the dual goals of efficiency and equality (e.g., Fried, 1975). The literature of location-allocation analysis is rich on efficiency but scarce on equality. Therefore, this section focuses more on modeling equality and possible integration of the two.

In health care, equality may be defined as equal access, utilization or outcomes among others, and most agree that equal access is the most appropriate principle from a public policy perspective (Oliver and Mossialos, 2004). Wang and Tang (2013) formulate the objective of minimal access inequality as minimizing the variance of accessibility scores defined by the 2SFCA in Section 2. Their case study examines the primary care access in Chicago with the demand defined as population in census tracts and the supply as physicians in ZIP codes. The planning problem is how to redistribute the same number of total physicians among ZIP code areas in order to achieve the minimal disparity in spatial accessibility across census tracts. The solution is illustrated as what adjustment (reduction or increase) in physicians needs to be made in each ZIP code area for an overall maximal equality, and thus highlights where potential surplus and shortage of the workforce exist. Tao et al. (2014) apply the same method to optimization of residential care facilities for seniors in Beijing. Wang et al. (2015) use a similar approach to simulating how the next round of designation of National Cancer Institute (NCI) Cancer Centers in the U.S. could guide the allocation of public resource toward maximal reduction in disparity of spatial accessibility of these high-quality hospitals.

In a recent study, Luo et al. (2017) propose a framework, termed “two-step optimization for spatial accessibility improvement (2SO4SAI)”, to integrate the dual objectives of efficiency and equality. Based on the case study of health care planning in a rural county in China, they adopt a sequential decision-making approach. Step 1 chooses where to site new hospitals by achieving an objective (or a compromised solution to multiple objectives) related to efficiency as outlined previously (i.e., p-median, LSCP, MCLP, minimax), where access is measured as proximity (travel distance) to the nearest facilities. Step 2 decides the capacities of sited facilities for minimal inequality in accessibility (thus the principle of equality), where access is measured by the 2SFCA that captures availability of hospital service. Both proximity and availability are two properties of access valued by residents (Luo et al., 2017:10). The design of 2SO4SAI in sequential decisions of site first and capacity second is supported by their field survey, and is echoed by others (e.g., Li et al. 2017). It is a valuable attempt of balancing the often competing goals of efficiency and equality.

Extensions to the 2SO4SAI framework can be made along several directions. Table 1 summarizes various configuration scenarios. Let’s stay with the decision sequence of site first and capacity second. Sites are derived by modeling accessibility as proximity, and capacities are solved by measuring accessibility by 2SFCA (denoted by 1 and 2 in Table 1 as they are sequential). Either goal (efficiency or equality, denoted by A and B in Table 1, not necessarily sequential) can be modeled by emphasizing one aspect of accessibility (proximity or availability). This leads to 4 ways of formulating the objective function (1A, 1B, 2A and 2B). Therefore, four sequential planning problems can be formulated: 1A-2A, 1A-2B, 1B-2A, and 1B-2B (as listed in Table 1). Note scenario 1A-2B is implemented in Luo et al. (2017), and three other scenarios remain to be explored.

Table 1.

Various Scenarios for a Sequential Location-Allocation Problem

		A. Efficiency		B. Equality
1. Proximity		1A: Efficiency goal with access measured by proximity		1B. Equality goal with access measured by proximity
2. Availability (2SFCA)		2A: Efficiency goal with access measured by availability		2B: Equality goal with access measured by availability
Sequential planning scenarios		1A-2A, 1A-2B (2SO4SAI), 1B-2A, 1B-2B

In summary, location-allocation problems have a wide range of applications in planning, industrial engineering, business management, logistics, and others. There is a large body of work from various disciplines on the problems that most focus on efficiency issues. This section calls for attention to modeling equality, which merits more work especially when it comes to planning for public health services. Analytical solutions to location-allocation problems are often computationally expensive or infeasible. Heuristic algorithms, coupled with modern GIS analytics, shows great promises in advancing the field (Lei et al., 2015).

7. Concluding comments

This paper provides a brief review on how GIS has increasingly been used in public health research. It covers six themes that I am most familiar with and have made some contributions to. Most cited case studies in this paper are based on my work (including collaborated work) funded by the U.S. National Institutes of Health over two decades. The overview has an emphasis on methodological issues. A brief recap on the six themes is as follows:

1. Our health-related behavior varies across geographic settings (e.g., areas of various urbanization levels, in different jurisdictions, with distinctive natural and built environments), so should public health policy. Researchers can run a model repeatedly in stratified subsets of data and identify the variability of results across those areas, or use analytical models such as SGWR to detect spatial non-stationarity.

2. The spatial interaction between facilities (supply) and patients (demand) in a health care market often conforms to the first law of geography (distance decay). The regularity is embedded in the popular 2SFCA and recently-developed i2SFCA methods, which measures the spatial accessibility of residents and potential crowdedness of facilities, respectively. Both help capture the uneven distribution of health care services.

3. In addition to individual attributes, neighborhood characteristics play an important role in affecting our health outcome. GIS helps define the most relevant neighborhood through their daily activity space or mobility trajectory over life course, and mitigate various sources of uncertainty in assessing neighborhood effect.

4. The small population problem prevents health data release in some areas or leads to unreliable disease rates in others. One effective way to mitigate the problem is to construct larger, internally-homogenous and comparable area unit by GIS-automated regionalization methods.

5. Defining a scientific geographic unit for health care market is critical for researchers, practitioners, and policy makers to evaluate health care delivery, and GIS enables us to define the units (e.g., primary care service areas, hospital service areas, and cancer service areas) automatically, efficiently and optimally.

6. Aside from various optimization objectives around “efficiency”, it is as important to plan the location and allocation of health care resources toward maximum equality or minimum disparity in health care access. This is an understudied area with important implications for public health policy and planning.

Due to constrained space and the author’s limited experiences, this short review does not represent an exhaustive list of important contributions of GIS to public health studies. Among the omissions, “edge effect” refers to less reliable results near the edge (border) of a study area if analysis involves spatial interaction beyond the confinement of the study site (e.g., the spatial accessibility measures in section 2 and the hospital service area delineation in section 5); “spatial uncertainty” in data and analysis arises due to measurement errors, generalization of spatial features, incomplete representation of factors in analysis, and other sources; and the rising participatory sensing data makes protection of “geoprivacy” an even more urgent issue in all stages of a health study (Kounadi and Resch, 2018). These issues and many others certainly merit an expanded review in the future.

To conclude, if there is anything certain in this world full of uncertainties, it is geographic complexity. In the context of public health, the complexity is manifested in the geographic variability of health behavior and outcome, spatial interaction of forces in health care market, dynamic nature of environmental and neighborhood effects, defining appropriate analysis units and health care submarket at multiple scales, and challenges for planning resources toward a balance in efficiency and equality. Geographic complexity is the reality, and the joint forces of public health professionals and GIS practitioners are best equipped to deal with it.

Figure 3.

Dynamic exposure assessments based on (A) person’s daily path (B) person’s residential trajectory (Source: Helbich, 2018: 132)