A modeling platform for the lymphatic system

Abstract

We present a physiologically-based pharmacokinetic modeling platform capable of simulating the biodistribution of different therapeutic agents, including cells, their interactions within the immune system, redistribution across lymphoid compartments, and infiltration into tumor tissues. This transport-based platform comprises a distinctive implementation of a tumor compartment with spatial heterogeneity which enables the modeling of tumors of different size, necrotic state, and agent infiltration capacity. We provide three validating and three exploratory examples that illustrate the capabilities of the proposed approach. The results show that the model can recapitulate immune cell balance across different compartments, respond to antigen stimulation, simulate immune vaccine effects, and immune cell infiltration to tumors. Based on the results, the model can be used to study problems pertinent to current immunotherapies and has the potential to assist medical techniques that rely on the transport of biological species.

1. Introduction

From a birds eye view, the lymphatic system (LS) provides the tracks along which the main players of the immune system move and communicate with the rest of the body. Unfortunately, these very same tracks are occasionally exploited by pathogens or cancer cells to disseminate and further spread the disease (Padera et al., 2016). For instance, melanoma, the most severe form of skin cancer (Owens, 2014), and breast cancer, the most common cancer in women affecting roughly 12% of the worldwide population (McGuire et al., 2015), predominantly propagate through the LS.

To facilitate the concepts developed in subsequent sections we briefly elaborate on the anatomy of the LS (Sherwood, 2015). The LS is composed of primary and secondary organs. The sites where the majority of leukocytes originate are in the primary organs, i.e., the thymus and the bone marrow. However, most of the action in terms of triggering and modulating an immune response takes place in the secondary organs. These comprise the tonsils, the spleen, the appendix, Peyer’s patches, and last but not least, the lymph nodes (LNs). A LN is essentially a filtration and a storage unit with an average diameter in humans of 5 to 10 mm. It houses different kinds of leukocytes that inspect the fluid that enters, called lymph, through the afferent lymphatic vessels, and that leaves through the efferent lymphatic vessels. Humans have on average 600 LNs distributed along the body. Their large numbers and their connectedness illustrate the importance that evolution has placed on being efficient at confronting a pathogen. But, as mentioned earlier, this same features are part of the reason why cancer is able to propagate to distant organs.

Hence, owing to the strong connection between the LS and cancer (Alitalo and Detmar, 2012), it is natural to inquire about efforts that have combined these two topics into a coherent mathematical framework. Some examples that explore the exchange of material between capillaries, lymph nodes (LNs), and lymphatics are (Heppell et al., 2013; Jafarnejad et al., 2015; Kojic et al., 2017). A summary of the relevant structures and transport mechanisms in the LS accompanied by a short discussion of models that derive from fluid flow equations such as the Navier-Stokes equations is given in (Margaris and Black, 2012). Nevertheless, even when some of the previously cited models are able to offer high resolution in the tissues under consideration, they tend to focus on specific portions of the LS and do not treat the body as a whole entity where complex cell interactions take place. In theory, one could simply enrich one of those models by adding sufficient structures to account for the missing entities. However, in the particular case of a whole-body model, high spatial resolution is typically not a critical aspect in answering the research questions of interest. Thus, scientists switched to an alternate modeling strategy that is more suitable to describe complex networks of organs where the focus is in the transport and interaction of biochemical species, rather than on the fine details of the fluid flow patterns. This is the physiologically-based pharmacokinetic modeling (PBPK) paradigm. We briefly discuss its key properties and review some relevant work done in conjunction with the LS.

Fundamentally, the PBPK approach consists of a network of organs or tissues connected via transport mechanisms in an anatomical fashion (Shah and Betts, 2012). The concept of PBPKs is not recent and can be traced back to the early 30s (Dominguez and Pomerene, 1934; Teorell, 1937a; 1937b). Moreover, despite the fact that more than 70 years have elapsed since its conception, we remark that PBPKs have remained relatively unchanged, consistently preserving the following three characteristics: (i) The conceptualization of organs or physiological structures as biochemical reactors where specific reactions take place, (ii) the incorporation of pharmacokinetic effects such as absorption, distribution, metabolism, and excretion of the drugs or species under consideration, and (iii) the use of mathematical expressions to relate rates of change and concentrations of the involved components within and throughout each of these compartments.

Representative PBPK examples related to the LS are given in (Boswell et al., 2011; Kletting et al., 2015; Offman et al., 2016; Peng et al., 2016; Tegenge and Mitkus, 2015). However, these models have at least one of the following limitations: The lymphatic organs are either absent or condensed into one or two compartments, cell-antigen interaction mechanisms are missing, or the parameters that drive the reactions are purely phenomenological constants.

This paper aims to resolve the aforementioned issues by proposing a modeling platform that incorporates the following elements: (i) A scalable network of LNs that can be adapted to different organisms, (ii) the possibility to include different cell populations and antigens that can interact, proliferate and perish according to a set of (potentially nonlinear) equations, and (iii) mechanisms that govern the exchange of material between compartments based on transport properties rather than phenomenological constants. Furthermore, a feature that we believe is not common in PBPKs is the addition of a heterogeneity character to a compartment. Concretely, the implementation of the tumor compartment offers the capability of fragmenting the domain into regions with individual properties such as vascular fraction and lymphatic fraction density. This functionality allows for a more realistic description of the tumor microenvironment.

In summary, the proposed paradigm, which we henceforth label L-PBPK, intends to alleviate the deficiencies of traditional approaches by providing a flexible modeling platform applicable but not limited to the LS, whose driving parameters are transport-based.

The remainder of the paper is organized as follows. The next section introduces the model and gives an overview of its functionality. Subsequently, we particularize the discussion towards the mouse model, illustrate how a network of LNs is created and discuss the underlying reaction and transport mechanisms. Then, we focus on a distinctive feature of our model, namely the tumor compartment and its connectivity with the rest of the components. We close that section stating some mathematical properties of the equations governing the L-PBPK. We illustrate the utility of the model by providing numerical results in the form of two sets of examples. The first one serves the purpose of validating the implementation, while the second explores some of its potential applications in transport phenomena. Finally, we summarize the results and make some concluding remarks.

2. Materials and methods

As discussed in the previous section, the biological question we intend to answer can be framed as a transport problem and amongst the multiple methodologies to describe it, we have chosen a PBPK approach. The foremost reason being its ability to simulate in a simple and scalable way the transport of materials (cells and antigens) between different organs belonging to a network. With the framework in place, what follows is the definition of the fundamental components of this model. Namely, what are the compartments and how are they connected? What kind of transport takes place between two compartments? What reactions occur at their interior? And lastly, how is the tumor compartment implemented? We address each question individually and discuss how each structure relates to the physiology.

2.1. Compartments and connectivity

The fundamental players in any PBPK model are the compartments and the cells or chemical species that reside within them. A generic compartment is a region in space and has properties such as volume (V), position, and vascular volumetric fraction (r_V). This last property is particularly relevant in transport since it represents the fraction of the volume that is occupied by functional (non-necrotic) vasculature. Furthermore, similar to the situation where an organ can be composed of several types of tissues, e.g., the layers of the stomach: mucosa, submucosa, muscularis and serosa (Wakefield et al., 1991), a compartment can be subdivided into different types of tissues, each with specific properties.

In the context of the L-PBPK, the main type of compartment represents an essential element of the LS, the LNs. In view that there are hundreds of LNs in organisms like a human, instead of attempting to account for the majority, we group them according to their anatomical location and call the ensemble a lymphoid compartment. As a concrete example, we consider a mouse model where a set of LNs follows the classification given in Shao et al. (2013). We cluster the LNs into compartments based on position and function, and generate the blocks depicted in Fig. 1. A list showing the LNs that belong to each group is given in Table S1.

Fig. 1.

Depiction of the fundamental structures of the L-PBPK. A: Graphical depiction of the grouping of LNs in the mouse model and the corresponding connectivity. An injection site located at the left hind footpad has been included to indicate the possibility of modeling the delivery of a biological agent at a specific location. B: Simplified diagram of the network of compartments in the mouse model.

Once the compartments are defined, the next step is to introduce the connectivity, i.e., specify for each compartment its set of neighboring compartments with whom it is allowed to interact. This defines a network that can be compactly represented as an array of numbers that we call the connectivity matrix. Physiologically, this network indicates which pairs of organs can directly exchange cells and antigens by means of blood and lymphatic vessels. In the mouse example, the connectivity is depicted in Fig. 1A by the thick green double-headed arrows that join two compartments. Lymphatics are not the sole route through which material can be transported. A connective tissue of paramount importance that perfuses all structures in our network is the blood compartment. Graphically, this type of connection is indicated by the double-headed red arrows in Fig. 1A. The connectivity matrix associated to Fig. 1A is given in Table S2, and a simplified diagram of the network is shown in Fig. 1B. Lastly, with regards to the addition of further lymphoid organs like the spleen or thymus, or for that matter any other organ, our implementation can easily handle such addition as long as the basic properties of the new organ are defined, and the corresponding connectivity is specified. The tumor compartment is treated separately and we defer its discussion to a later section. Now we proceed to address the question related to the transport between compartments.

2.2. Intercompartment transport

We assume a diffusive character as the fundamental mechanism utilized in the L-PBPK to exchange biological species between compartments. We remark that an stochastic approach could potentially be necessary in smaller length scales within the cellular and molecular level. That would be the case for example when considering local cell-to-cell interactions, or the delivery of nanoparticles to the tumor microenvironment (Dogra et al., 2019). However, even for such small dimensions, deterministic mathematical models have been successfully applied and verified using clinical data (Goel et al., 2019). Hence, we adopt a deterministic diffusion and interaction mechanism for our model. As pointed in (Margaris and Black, 2012), the assumption of a lymphatic laminar flow might be acceptable for lengthy vessels (such is the case we are considering), but breaks down for smaller conduits that also take into account the valves. For those instances, inertial effects are known to be significant and have to be included (Margaris and Black, 2012).

The model relies on parameters related to transport properties. These parameters are, in order of increasing estimation complexity: The partition coefficient (P), the transport length (ℓ), the transport coefficient (D), and the contact area between compartments ($\tilde{A}$).

The partition coefficient represents the affinity of a substance or cells to remain within a particular tissue or compartment (Kojic et al., 2015). Specifically, for a given biological species, e.g., CD8 cells, and two compartments, e.g., blood and a lymph node, we set the partition coefficient between these as the ratio of their corresponding equilibrium concentrations. Mathematically,

$$P_{\text{blood,lymph node}}=\frac{\text{Equilibrium concentration in blood}}{\text{Equilibrium concentration in lymph node}}.$$ (1)

The transport length encompasses different characteristic distances that a molecule or cell has to travel to reach a given tissue (Foster et al., 1991). For example, if a lymphocyte is to migrate into a LN through extravasation, the transport length would correspond to the thickness of the vessel that it has to cross. The transport coefficient aims to describe several interactions, one of them being the tendency of a species to move across a medium due to concentration gradients (Kitamura and Kinjo, 2018). Finally, the contact area is the effective transport area, i.e., the amount of area between two intersecting surfaces that is available for the exchange of material (Tolentino et al., 2008). The derivation of an expression that relates the contact area and the vascular fraction (r_V) is discussed in Derivation S1. Denoting the concentration of a biological species S in the ith compartment by [S]_i, and similarly for [S]_j, the expression that relates the aforementioned parameters is (see Chapter 17 in (Bird et al., 2002)) :

$$\text{Transport rate}=-D\cdot \tilde{A}\cdot \frac{[S{]}_j-[S{]}_i\cdot P}{\ell },$$ (2)

where the transport rate has units of amount of material per unit time. Note that between any two connecting compartments (or tissues), and for every biological species, there exists a unique set of transport parameters which could, potentially, vary in time. The following section discusses the type of reactions that take place within each compartment.

2.3. Compartment reactions

In the context of PBPKs, an accurate physical representation of a compartment is a biochemical reactor that exchanges mass with its surroundings. Hence, owing to the fact that one of the objectives of the L-PBPK is to model interactions between cell populations, we consider four elementary types of reactions. Proliferation, death, activation/conversion, and stimulation/inhibition of cells and antigens. To better understand each type, we provide a particular example which we explore in a later section.

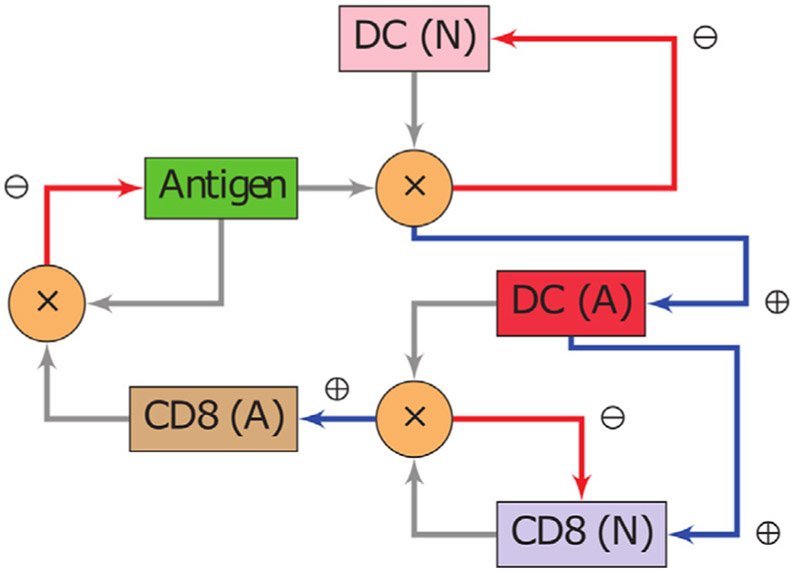
A population of naive DCs gets exposed to an antigen which causes the cells to mature and transition into an activated state DC^A. These cells in turn interact with naive CD8s, resulting in two outcomes. One is the conversion of CD8s into its activated form CD8^A, and the second is an increase in the proliferation rate of CD8s by means of stimulation. Finally, the antigen population is reduced (due to cytolytic proteins and induced apoptosis) after successive encounters with members of the pool of CD8^A. The conversion of cells from one state to another is regulated by means of transition functions introduced in Definition S5. A diagram summarizing the aforementioned interactions is shown in Fig. 2.

Fig. 2.

Interactions between cell populations and antigen. Depiction of an immunological response between an antigen, DCs and CD8s. The notation (N) indicates a naive population, whereas (A) represents an activated state. Whenever two arrows meet at a node marked with a ( × ), the product of the populations of the involved species is to be interpreted. The blue arrows (⊕) denote a positive impact (increase) in the cell population to which they point. Red arrows (⊖) indicate the opposite effect. Note that the system is closed and hence all cell populations and antigen affect each other.

The system of equations that describes the reactions illustrated in Fig. 2 is given in Definition S1. In general, for a given compartment, and for each biological species S, the expression

$$R_S(t)=\stackrel{\text{flat generation}}{\overbrace{g(t)}}-\stackrel{\text{death}}{\overbrace{d(t)}}\cdot S+\stackrel{\text{Conversion of species}}{\overbrace{C(S_1,\dots ,S_n,t)}}+\stackrel{\begin{array}{c}\hfill \text{Stimulation},\hfill \\ \hfill \text{proliferation},\hfill \\ \hfill \text{and nonlinear}\hfill \end{array}}{\overbrace{N(S_1,\dots ,S_n,t)}}$$ (3)

describes all possible reactions that S can experience. An extended version of Eq. (3) that provides further details is given in Eq. (12). Before closing this section we elaborate on a particular feature of our model that is approached in a nonstandard manner. Namely, the tumor compartment.

2.4. Tumor compartment

The canonical approach in PBPKs to simulate the presence of a tumor in an organism is to include a tumor compartment that typically shares the same attributes as the other compartments, the only difference being the value of the phenomenological constants that dictate the PK. Our approach, however, is different in that it takes into consideration the possibility of having tissue heterogeneity (Donahue et al., 2008), i.e., spatial variations in the physical and biological properties across a compartment. For instance, we can model necrotic regions where the perfusion of blood is heavily compromised (Please et al., 1998). This property is relevant in view that it is key in the context of cancer resistance (Dagogo-Jack and Shaw, 2017; Pascal et al., 2013; Brocato et al., 2014; Wang et al., 2016). A discussion of the implementation follows.

2.4.1. Implementation

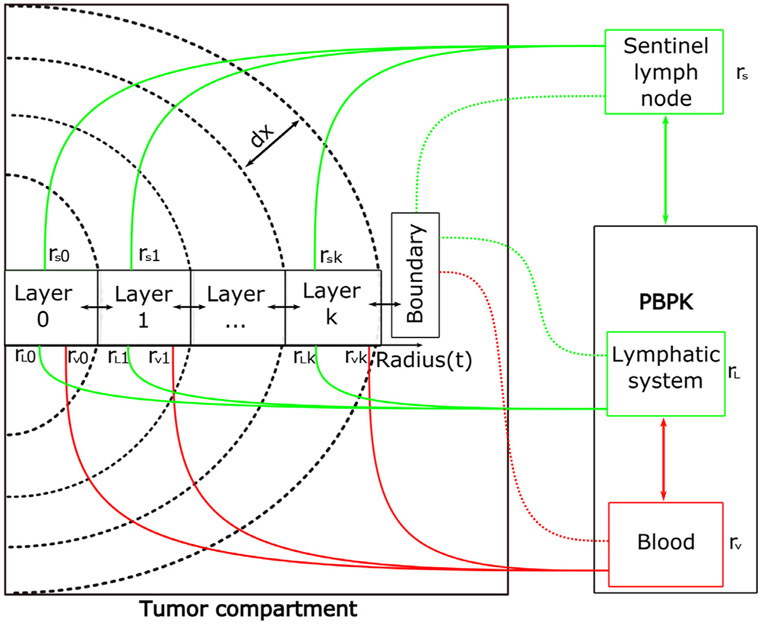
Assuming a spherical geometry, the tumor compartment is implemented as a collection of concentric shells or layers, each being a compartment with its independent set of attributes and transport properties. In particular, each layer has a separate vascular and lymphatic volume fraction that equates the degree of necrosis to the level of impairment of the vascular structures.

Another important characteristic is that the tumor layers can be connected to a LN which can potentially serve as a sentinel LN or a tertiary lymphoid structure(Carlson et al., 2002). The exchange of cells by means of lymph from such a LN to a given layer is regulated through a parameter which denotes the lymphatic volume fraction of the k-th layer of the tumor associated to the sentinel LN. A graphical representation of the defining characteristics of the tumor compartment is given in Fig. 3.

Fig. 3.

Internal structure of the tumor compartment. The tumor compartment is divided into layers, each of thickness dx which is itself a compartment with individual reaction and transport properties. To simulate tissue heterogeneity, parameters such as the vascular and lymphatic volumetric fraction, r_V and r_L, respectively, can be chosen in each layer. Moreover, the tumor object also allows the possibility of being connected to adjacent LNs to simulate the presence of sentinel LNs. The last layer designated as the boundary can also be separately manipulated to account for transport differences at the (well-perfused) tumor tissue interface.

In the next section we explain how the degree of vascularization in different tissue layers influences the local transport properties, thus conveying the idea of heterogeneity.

2.4.2. Heterogeneity and vascularization

Evidently, the more (functional) vessels are available to deliver material to a given tissue, the more efficient the transport should be. Hence, in order to modify the transport rate (see Eq. (2)), we need to find a mechanism that relates the degree of vascularization to one of the transport parameters introduced in Eq. (2). We relate the transport length to the vascular volumetric fraction of a given tumor layer. Following the derivation given in Derivation S2, the analysis shows that the transport length is inversely proportional to the square root of the vascular fraction. Hence, as the amount of available vasculature diminishes, the transport length increases, ultimately reducing the transport rate (see Eq. (2)). In a later section we illustrate the impact of different vascular fraction values across the layers of the tumor.

Summarizing, the L-PBPK represents a network of lymphoid organs and tumors connected through lymphatic and blood vessels that exchange biological species which experience a particular set of reactions.

In the next section we investigate some mathematical properties of the system of ordinary differential equations (ODEs) related to the L-PBPK model. For the sake of clarity we provide a condensed version of the analytical findings and move the discussion of the details to the supplemental material section.

2.5. Mathematical properties

In this section we briefly discuss the well-posedness and stability of the ODEs resulting from the application of Eqs. (2) and (3) to all compartments and biological species. This is relevant in view that an ODE may have a multiplicity of solutions, a unique solution, or no solution at all. An ODE exhibiting such behavior is included in Example S1.

In the next two subsections we summarize the analysis that is developed in Derivation S3 and Derivation S4. These results guarantee that the governing equations of the L-PBPK do not present the undesirable properties of Eq. (14) in Example S1.

2.5.1. Existence and uniqueness of a solution

Let x(t) represent the vector of populations of the various biological species in all the tissues under consideration. Then, one can find a matrix A, a nonlinear vector function H, and vectors g and d, of appropriate dimensions, such that the system of ODEs of the L-PBPK can be written as

$$\begin{gathered} \stackrel{.}{x}(t)=\stackrel{\text{transport}}{\overbrace{A\cdot x(t)}}+\stackrel{\begin{array}{c}\hfill \text{Stimulation},\hfill \\ \hfill \text{proliferation},\hfill \\ \hfill \text{and nonlinear}\hfill \end{array}}{\overbrace{H(x,t)}}-\stackrel{\text{cell death}}{\overbrace{d(t)\cdot x(t)}}+\stackrel{\text{cell generation}}{\overbrace{g(t)}}, \\ x(0)=x_0. \end{gathered}$$ (4)

The matrix A is related to the transport effects given in Eq. (2). The function H(x, t) encapsulates the conversion of cells, additional proliferation and stimulation effects, and nonlinear terms as shown in Eq. (3), d(t) represents the death rate, and g(t) the flat (independent of the concentration) proliferation rate. Assuming the involved functions do not exhibit nonphysical behaviors, e.g., they do not become unbounded, the existence and uniqueness of a solution to Eq. (4) follows directly from the Cauchy-Lipschitz result in the theory of ODEs (Braun and Golubitsky, 1983). We proceed to discuss the stability of the system.

2.5.2. Stability

We investigate the long term behavior of Eq. (4) Concretely, we give conditions under which the solution to Eq. (4) attains an equilibrium. The physiological relevance of this property is that after a transient perturbation, e.g., an infection that was successfully eradicated, the system should be able to regain homeostasis, i.e., the concentrations of the cell populations should return to normality.

The conditions for stability essentially translate to the following: (i) All compartments are connected either directly or indirectly, (ii) the nonlinear effects due to H(x, t) are insignificant after a certain period of time, and (iii) the death rate of every biological species is nonzero in at least one compartment. The first and third conditions are purely physiological. Naturally, under normal conditions, the blood perfuses all organs, hence connecting them, and most cell populations (at least the ones under consideration) eventually experience death. Nonlinearities, however, are ubiquitous in healthy and infectious states, thus making the second assumption harder to sustain. Nonetheless, if for instance the nonlinearities under consideration represent the conversion of cells from one population to another, then it is reasonable to assume that in the absence of immunological challenges, such effects should be nonexistent. With the aforementioned assumptions one can positively answer the stability question using the qualitative theory of ODEs (Nemytskii, 2015). We summarize our findings in the following statement. The L-PBPK system possesses a unique solution for a given initial condition. Moreover, regardless of the initial state, the lack of nonlinearities drives the system towards equilibrium. A detailed statement of this result is given in Theorem 3 in Derivation S4.

The next section validates our model by means of a series of numerical examples and provides evidence that supports the mathematical findings.

3. Results

We divide this section into two sets of examples. The first set is used to validate the implementation, while the second explores some applications. In the validation set we have chosen examples that satisfy two requirements. One is to serve as numerical evidence that corroborates the mathematical properties, and the second is to illustrate the capacity of the model to simulate physiological conditions and match experimental data reported in the literature. The examples used in the exploratory set, instead of replicating known conditions, serve to motivate potential future applications that are relevant to transport processes. For ease of reference we list all the biological species under consideration in the subsequent examples:

• Immature DCs

• Naive CD8s

• Activated DCs (DC^A)

• Activated CD8s (CD8^A)

• Antigen (Ag)

3.1. Validating examples

We provide three validating examples related to the mouse model. The reaction terms follow the mechanisms described in Fig. 2 and Definition S1. The lists of reaction coefficients and transport parameters are located in (Ruiz-Ramírez et al., 2019). A summary of the aforementioned parameters is given in Table S5, Table S6, Table S7, Table S8, Table S9, and Table S10.

The first example investigates the attainment of background concentrations of naive CD8s in different organs following a physiologically reasonable timescale. The second example models proliferation, death, and conversion of naive CD8s into its activated form. These events are either triggered or regulated by an antigen response. Lastly, the third example is concerned with transport kinetics in a tumor and a spleen compartment.

3.1.1. Homeostasis

This example serves the purpose of verifying the capacity of our model to attain equilibrium. This property is of paramount importance since it mimics the ability of an organism to autoregulate in the face of transient stimuli. Furthermore, it evinces the mathematical findings. Namely, that the system should tend towards equilibrium under the assumption of decaying or inexistent nonlinearities. To satisfy this requirement, we consider a scenario deprived of antigen. The fact that this condition leads to the absence of nonlinearities is justified in the next paragraph.

Owing to Fig. 2, the nonlinear terms introduced in Eq. (4) are directly linked to the interaction between the antigen and the populations of naive DCs (see also Definition S1). Hence, a lack of antigen implies that no such interactions will take place, and consequently that the function H(x, t) in Eq. (4) is zero. Thus, by Derivation S4, it follows that the L-PBPK should attain equilibrium. Since the idea of equilibrium typically involves a process occurring at infinity, we introduce the notion of a pseudo-equilibrium time (PET). Basically, it is defined as the time taken by a given species S in a given compartment to be within and remain at a certain percentage p of its equilibrium concentration. We denote this quantity by T_p(S). A formal definition is given in Definition S6.

To guarantee that the system starts from a nonequilibrium position, initially, all cell populations under consideration are depleted, i.e., the initial condition in Eq. (4) is x(0) = 0. Note that x = 0 is not an equilibrium solution due to the proliferation rate g(t) in Eq. (4), which is independent of the number of biological species. The aforementioned scenario is relevant, for instance, in the context of chemotherapy and radiation therapy, where the cytotoxic effect of these therapies not only depletes tumor cells but also normal host cells (Rebe and Ghiringhelli, 2015). Clinically, it has been observed that even after decimation the cell populations evolve towards equilibrium (Cox and Ang, 2009). This is consistent with the mathematical findings.

In order to specify the equilibrium concentrations in the model we employ the partition coefficient P introduced in Eq. (1). We remark that defining the partition coefficient as in Eq. (1) one can readily show (see Eq. (11)) that as the system approaches its limiting behavior, the exchange of biological species between compartments tends to zero.

The values for the background (equilibrium) concentrations of naive CD8s are given in Table S3 and derive from Druzd et al. (2017). Once the equilibrium concentrations are fixed, one still needs to define the rate at which the system progresses towards this state. This behavior is determined by the PET T₉₀. We set this quantity to 7 days since it is an average period of time for an initial adaptive immune response to become fully active (Janeway, 2005). The connection between the PET and the model parameters is through the generation and death rate of cells in the various compartments. These quantities can be simultaneously fitted using a variety of methods such as least squares.

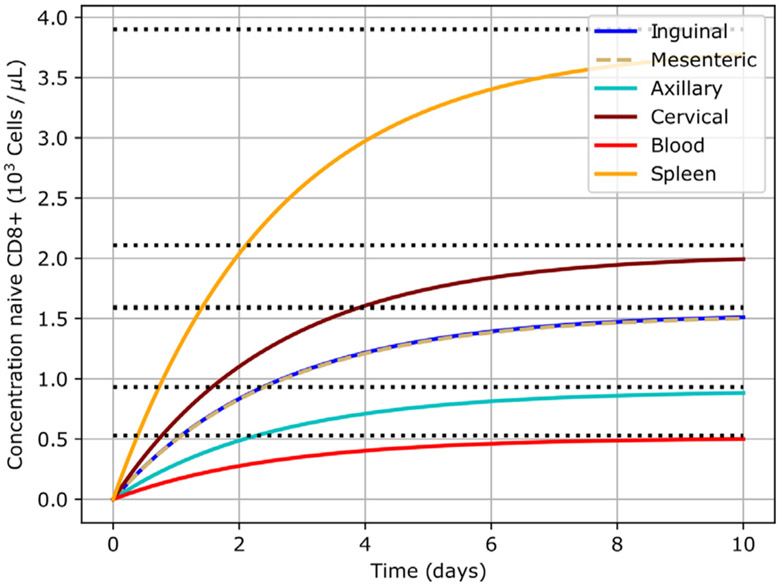
With the given data the temporal evolution of the concentrations can be computed and is summarized in Fig. 4. Note that the system approaches the equilibrium values given in Table S3. Moreover, at t = 7 days, all the concentrations are within 90% of their corresponding equilibrium, as expected. Hence, this example shows that indeed the system moves towards equilibrium in consistency with the analysis of Derivation S4, and that it does so in a reasonable time frame. In the next section we deliver an example of utmost importance for this paper in view that it illustrates an application of the L-PBPK to immunotherapies.

Fig. 4.

L-PBPK evolves towards equilibrium. The system starts from a fully depleted state (zero cells) and progressively approaches equilibrium. The equilibrium states in different compartments are represented by the black dotted lines.

3.2. Antigen driven immune response

In this example we study how the system responds to the presence of an antigen. In particular, we are interested in observing how the interaction of the cell populations under consideration leads to the mediation and eventual suppression of an infection. The interplay between cells is illustrated in Fig. 2.

The data we use to validate the model originates from two sources, (Lau et al., 1994) and Murali-Krishna et al. (1998). In Lau et al. (1994) an experimental murine model is considered. Therein, the authors inject intraperitoneally a strain of the lymphocytic choriomeningitis virus (LCMV) and study the evolution of its concentration in the spleen. Moreover, subsequent to the infection, they transfer LCMV-specific CD8^A to healthy mice and determine if those cells retain their memory phenotype and its protective qualities against LCMV. In Murali-Krishna et al. (1998) a similar model is considered but in contrast to Lau et al. (1994), total CD8s in spleen are quantified based on different viral epitopes. Hence, the LCMV model is relevant to the L-PBPK since it serves a testing platform for cell-antigen reactions.

As depicted in Fig. 2, we consider the conversion of immature DCs to mature DCs after being exposed to the antigen (LCMV). These cells in turn stimulate the proliferation of naive CD8s (Pozzi et al., 2005) and their conversion into CD8^A, whose task is to eliminate infected cells (antigen). Obviously, the mounting of an immune response is a gradual process which adapts to the presence of pathogens. Thus, in order to model the smooth evolution from a relaxed immune state to one active and vice versa, we use transition functions that trigger once a threshold concentration of antigen is attained. A precise definition of these functions is given in Definition S5.

An additional effect that is included in this example is the possibility to modulate the death rate of CD8^A. Two instances where such event is reported are Grayson et al. (2002) and Luu et al. (2006). In Grayson et al. (2002) it is shown that memory CD8s exhibit a more pronounced resilience to apoptosis in comparison to its naive counterparts, while in Luu et al. (2006) the authors develop an experimental model where CD8^A cells exhibit a delayed contraction in their population under a virulent infection. To model this effect we define a function that has a diminished death rate during infection, which smoothly transitions to its usual post-infection value. Such function is given in Eq. (5) and governs the behavior of the death rate of CD8^A ($d_{\text{CD8}}^{\mathrm{A}}$).

$$d_{\text{CD8}}^{\mathrm{A}}(t)=d_{\text{infection}}+\frac{(d_{\text{normal}}-d_{\text{infection}})\cdot \text{Switch}(t)}{1+e^{-k\cdot (t-t_0)}},$$ (5)

$$\text{Switch}(t)=\{\begin{array}{cc}0,\hfill & \text{Duringinfection},\hfill \\ 1,\hfill & \text{Post}-\text{infection}.\hfill \end{array}\phantom{\}}$$ (6)

The parameter d_infection indicates the death rate under an infectious state, while d_normal represents the death rate under healthy conditions. The function Switch(t) becomes active once the infection has been suppressed. Note that after an infection, $d_{\text{CD8}}^{\mathrm{A}}(t)$ tends to d_normal as time progresses. The steepness of the transition from d_infection to d_normal is controlled by k. Lastly, t₀ denotes the time at which the death rate is the average between d_infection and ^d_normal.

Note from Eq. 5 that the death rate of CD8^A for a time when there is an ongoing infection, the function Switch(t) is off (equal to zero since t < t_{post-infection}) and hence the death rate is constant and equal to d_infection. However, after the infection has been suppressed, Switch(t) becomes active (equal to one) and gradually the death rate returns to its normal value d_normal, which is chosen to be larger than d_infection. The post-infection time t_{post-infection} can be determined dynamically based on a threshold concentration of antigen.

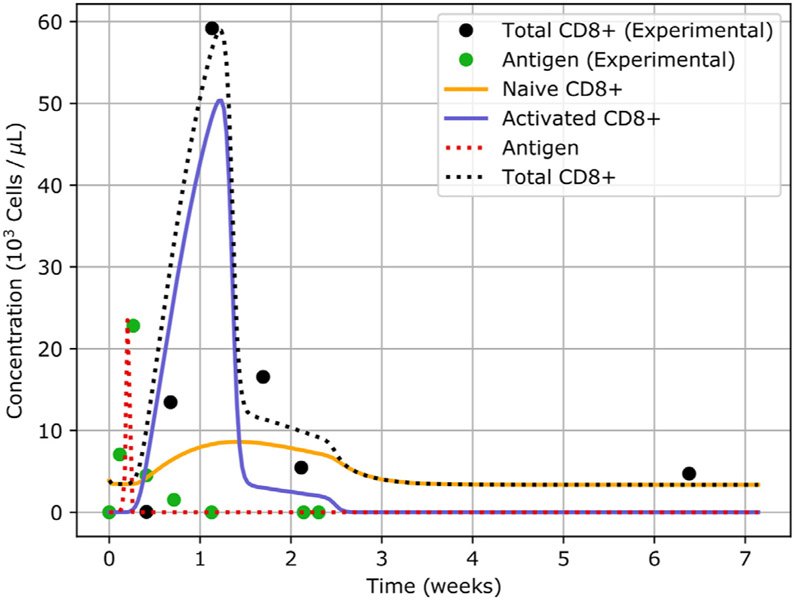
We use the equilibrium concentrations given in Table S3 and set an initial concentration of 5.4 antigen particles per microliter in the spleen. The results of the simulation after the fitting process is shown in Fig. 5. The tables of the parameters used in the simulation can be found in Ruiz-Ramírez et al. (2019).

Fig. 5.

Simulation of a CD8-meditated immune response. Plot of the concentration of different biological species in the spleen. The black dotted line denotes the total population of CD8s. The naive population of CD8s is depicted in orange, while the activated is shown in blue. The red dotted line indicates the concentration of antigen. The solid dots represent the experimental values.

We observe that the numerical results are in agreement with the reported experimental values. A summary of the events that take place in Fig. 5 follows. During the first day post-injection of the pathogen, the concentration of antigen exceeds the fixed threshold of 16 antigen particles per microliter and the transition function T₁ is activated (see Eq. (27)). This triggers an immune response. The population of CD8s starts to proliferate rapidly but their numbers remain fairly constant since most of the newly generated cells is being activated by antigen-presenting cells (APCs). Soon afterwards, the freshly generated CD8^A begin interacting with the pathogen until they drive the infection into eradication. However, even after the infection is under control, CD8s continue to proliferate until the immune response reaches its peak, roughly one week post-injection. Around this same time, the function Switch(t) in Eq. (5) becomes active, causing the death rate of CD8^A to gradually return to normality. Finally, once the transition functions revert to their original state, the system returns to homeostasis. The fact that CD8s continue to proliferate post-infection is by no means unexpected and has been documented. For instance, in van Stipdonk et al. (2001) it is shown that CD8s with short time exposures (t ≈ 2 h) to APCs exhibit a prolonged and steady proliferation even in the absence of further activation.

Before concluding this section we remark that other mathematical models have been used to describe the evolution of different subpopulations of CD8s facing an infection triggered by the LCMV. One such example that also uses the data given in Grayson et al. (2002) and Luu et al. (2006) is De Boer et al. (2001). Therein, the authors consider naive, activated, and memory cells interacting with the antigen. Though their model manages to mimic the changes in the experimental concentration of CD8s in the spleen, it has the limitation that the concentration of antigen through time is a predefined function rather than a variable. Moreover, it only considers one compartment. In summary, this example demonstrates the capacity of the L-PBPK to simulate an immune response and take into account modulating effects that influence the proliferation and death of cell populations as a function of external stimuli. In the next example we test one of the distinguishing features of the implementation. Namely, the tumor compartment.

3.2.1. Transport kinetics in tumor

The previous two examples showed that the L-PBPK is able to simulate conditions requiring the reequilibration of cell species and the mediation of an immune response triggered by an antigen. What yet remains to be verified is how a tumor model can be handled by our implementation. For that purpose we consider the setting described in Gattinoni et al. (2005), where B16 cells, a common mouse model for human melanoma (Overwijk and Restifo, 2000) and metastasis (Giavazzi and Decio, 2014), is the tumorigenic agent. A brief description of the experimental conditions follows. Mice bearing 10-day-old B16 tumors are exposed to CD8s at different differentiation stages ranging from naive to fully effector. The evolution of the tumors is then observed and changes in the population of CD8s in the spleen and tumor are quantified.

The data we use to inform our model is the fractional population of CD8^A in tumor and the concentration of CD8^A in the spleen reported in Overwijk and Restifo (20 00). We first discuss some properties pertaining the tumor compartment. The tumor compartment is connected to the rest of the PBPK as shown in Fig. 1 and is divided into 10 layers of tissue (see Fig. 3), each with a thickness of 0.26 mm. Two transport mechanisms are considered. One is the blood connectivity and the other is the material exchange between its internal layers. To test the effects of necrotic (dysfunctional) vasculature, we consider two scenarios. One where the interlayer diffusion is constant, and another where the intratumoral vascular fraction decreases towards the center. This last case is consistent with the physiology of solid tumors that grow above a certain critical radius (Soltani and Chen, 2011). The profile for the tumor vasculature fraction as a function of the radius is given in Figure S3. An important consequence of this variation is that, in view of the inverse relationship between the transport length and the vascular fraction (see Derivation S2)), the transport length changes across the different layers (see Figure S3). This in turn results in fluctuations of the transport rate (see Eq. (2)).

Combining the model parameters given in the previous example with the experimental data, we obtain the results illustrated in Fig. 6. We observe that the numerical simulations can reasonably approximate the cell kinetics in the spleen and the tumor. Furthermore, we note that our model is able to quantify a time difference of approximately 12 h between the peaks of CD8^A in the spleen and the tumor. This delay is due to the anatomical differences between compartments and the associated transport mechanisms.

Fig. 6.

Temporal evolution of the concentration of CD8^A in the spleen and the tumor. The black dashed curve corresponds to the case where the vasculature fraction is constant. The purple dashed curve also indicates the concentration of CD8^A in tumor, but employing the sigmoidal profile given in panel A of Figure S3 for the vascular fraction. The modifier ( × 30) is used to denote an amplification factor of 30, i.e., the concentration data was multiplied by 30. This is done to facilitate the comparison using similar scales. B: Concentration of CD8^A inside each layer of the tumor compartment for the case of a heterogeneous vascular fraction profile (see panel B of Figure S3).

Note that in order to compute the total concentration of CD8^A inside the tumor one has to consider the variation of properties in each layer. A precise definition of this computation is given in Definition S7.

Finally, we observe that when the vasculature fraction in the tumor follows a necrotic profile (see panel A in Figure S3), the peak of CD8^A in Fig. 6A differs by 27% with respect to the uniform vasculature fraction case. Clearly, this is due to the impaired transport in the necrotic regions of the tumor. This closes the set of validating examples and marks the transition to the set of examples that further substantiate the claim that the L-PBPK can be used to inform transport questions.

3.3. Exploratory examples

The remaining of this section is dedicated to the exploration of transport scenarios that further illustrate the potential applications of the L-PBPK. The first example considers two independent variables, the tumor size and the transport coefficient, and compares properties such as peak concentrations and rates of change of cells and antigen. The second example investigates the attachment of a sentinel LN to the tumor compartment and the resulting differences in transport. Lastly, in the third example, the hypothetical experiment of expanding the size an organism uniformly across all dimensions is probed. For the remainder of this section, unless otherwise stated, all CD8s are in its activated form.

3.3.1. Variations in tumor size and transport coefficients

For our first experiment we show how different transport properties and dimensions in a tumor can lead to immunological responses of various degrees of intensity. The setting is as follows. Under the conditions described in the last validating example (assuming a non-necrotic vasculature profile), we consider two tumor sizes. One with a radius R₁ = 0.25 mm, and the second 20 times larger with a radius R₂ = 5 mm. Additionally, we explore two transport coefficients D₁ and D₂ for the exchange of cells and antigen throughout the tumor tissue. The ratio r = D₂/D₁ is set to approximately 10³. The previous parameters generate four combinations: E₁ = (R₁, D₁), E₂ = (R₁, D₂), E₃ = (R₂, D₁). and E₄ = (R₂, D₂). To compare and contrast the various combinations we measure the parameters shown in Table 1.

Table 1.

Measured parameters to quantify the intensity of an immune response.

$C_{\max }^i(S)$	Peak concentration of species S in the i-th compartment
$t_{\max }^i(S)$	Elapsed time to reach $C_{\max }^i(S)$
AUCi(S)	Area under the curve describing the concentration of species S in the i-th compartment
${\stackrel{.}{C}}_{\max }^i(S)$	Maximum of the derivative of the concentration of species S in the i-th compartment

The results corresponding to the numerical simulations for a time horizon of j6 days are shown in Table 2.

Table 2.

Numerical results for the measured immunological parameters. The definition of the parameters is given in Table 1. The units for concentration are 10³ cells per μL and the time units are in days.

Property/ scenario	E1	E2	E3	E4
Radius (R)	0.25	0.25	5	5
Diffusion ratio (r)	1.00	103	1.00	103
$C_{\max }^{\text{Tumor}}$(Ag)	30.0	28.0	25.8	25.2
$C_{\max }^{\text{Blood}}$(CD8)	250.0	160.0	100.0	80.0
$C_{\max }^{\text{Tumor}}$(CD8)	26.7	156.7	105.5	86.2
$t_{\max }^{\text{Tumor}}$(CD8)	4.5	4.5	4.5	4.4
AUCTumor(Ag)	9.5	9.2	8.4	8.3
${\stackrel{.}{C}}_{\max }\text{Tumor}$(Ag)	109.3	104.0	93.5	90.8

First, note that there is a decreasing trend in the $C_{\max }^{\text{Blood}}$(CD8). This can be explained based on the fact that as the radius and the transport coefficient grow, transport tends to be faster due to a larger contact area and a proportional increase in the transport rate. Hence, it is reasonable to assume that the CD8s spend less time in the blood and instead migrate to other tissues. In order to evaluate the intensity of the immune response, the peak concentration of antigen in the tumor $C_{\max }^{\text{Tumor}}$(CD8) is measured. We observe that this parameter also exhibits a decreasing trend, suggesting that the increased transport allowed for a rapid mediation of the infection. Though the peak concentration of antigen was the smallest in E₄, one cannot decisively conclude that overall E₄ exhibited the least amount of total antigen throughout the simulation. This question is readily answered by quantifying the area under the curve of the concentration of antigen in the tumor AUC^Tumor (Ag). The data confirm that indeed the scenario with the least amount of antigen is E₄. To further contrast the variations amongst the immune responses we use as a measure of effectiveness to control an infection the maximum slope (rate of change) in the concentration function of antigen in the tumor. This quantity is denoted by ${\stackrel{.}{C}}_{\max }^{\text{Tumor}}$(Ag). The rationale is that an abrupt positive change during a period of time in the concentration of antigen strongly suggests that the infection was proliferating in an uncontrolled manner. As expected, the ${\stackrel{.}{C}}_{\max }^{\text{Tumor}}$(Ag) in E₄ is the smallest. Hence, we conclude that the immune response is least effective in E₁ and most effective in E₄.

Finally, we note that the peak concentration of CD8s in tumor $C_{\max }^{\text{Tumor}}$(CD8) increases from E₁ to E₂, but the opposite trend is observed from E₃ to E₄. The first effect is a direct consequence of the larger transport coefficient in E₂, which allows more CD8s to reach the tumor. However, the data suggests that there is a point where the transport becomes sufficiently efficient that the CD8s are able to neutralize the infection in the blood compartment at a high enough rate that the amount of CD8s reaching the tumor compartment in E₄ is noticeably smaller than in E₃. The idea of an efficient transport is partially supported by the slight decrease of $t_{\max }^{\text{Tumor}}$(CD8) in E₄ with respect to E₃. In conclusion, this examples illustrates two points. One is how variations in tumor size and transport coefficients can noticeably influence the course of an immune response. And second, how metrics dependent upon the concentration of cell species can facilitate the comparison of different immune scenarios. In the next example we continue exploring applications of the tumor compartment by analyzing the potential change in transport kinetics after attaching an adjacent LN to the tumor vasculature.

3.3.2. Sentinel lymph node

The second example in this section explores the question of how the transport of cells across a tumor is modified when assisted by a draining LN. This is the context of a sentinel LN. The motivation for this example stems from Baba et al. (2000), where a female patient exhibits inguinal LN metastasis from breast cancer. Though this type of dissemination is rare, it illustrates how a LN network can enable the delivery of antigen to distant sites.

The setting of this experiment is as follows. We assume that a tumor is located close to the left mammary gland and is connected to the blood compartment by means of severely impaired vessels (this is modeled by reducing the vasculature fraction). The tumor produces antigen which travels through all compartments and the organism reacts to it by generating CD8^A that mediate the infection. We consider four experiments divided into two sets. The first set consists of a tumor in the form of a cluster of cells (antigen) which proliferate at a given rate, whereas the second explores a tumor that exhibits twice the previous rate. Each set is composed of two experiments. The first experiment is used as a control. In this scenario the system evolves with the conditions derived from the last validating example. The second is analogous to the first except that the tumor compartment is also connected to the left axillary compartment (refer to Fig. 1 as a visualization aid). In each experiment we measure the time required for the antigen to exceed the threshold concentration of 10³ cells per microliter in the inguinal LN. If the threshold is not attained during the simulation, the reported time is infinity (∞).

We now address an aspect relevant to the experimental conditions. As exhibited in Figure S3, the vasculature fraction (VF) can influence the tumor transport kinetics by modifying the transport length between tissues. Hence, in an attempt to isolate the outcome of the additional connectivity from these effects, we choose the VF so that it minimizes its impact in the current example. Specifically, we find a critical value for the VF for which the antigen concentration levels do not manage to elicit an immune response (at least in the given time frame) due to the reduced speed at which the antigen can leave the tumor. We find that such value for the VF is 7.00 × 10⁻³. The precision of this bound can be determined by noting that when the VF is set to 7.11 × 10⁻³ a normal immune response is generated. Thus, we set the VF to the later value. A summary of the results is given in Table 3.

Table 3.

Antigen concentration in the inguinal LN. Elapsed time in days for the antigen concentration to reach the threshold value of 10³ cells per microliter in the inguinal LN compartment. The symbol ∞ indicates that the antigen concentration never exceeded the threshold value.

	Proliferation rate (R)	Proliferation rate (2R)
Control	3.17	1.6
Sentinel LN	∞	1.6

Interestingly, under the slow proliferation case (R), the additional connectivity conferred to the tumor by the sentinel LN actually negatively impacts the dissemination, i.e., the antigen concentration in the inguinal LN never exceeded the threshold concentration. This can be explained simply in terms of the additional number of CD8s that have access to the tumor, limiting its progression. This suggests that the CD8s were faster in mediating the infection than the antigen in reaching distant LNs.

In the setting of a tumor with a fast proliferation rate (2R) we note that there is not a significant difference between the control and the sentinel LN case. In this case we hypothesize that though there is an increase in transport of CD8s due to the addition of the sentinel LN, by doubling the proliferation rate, the immune response is not sufficiently strong to cope with the increased number of antigen, resulting in seemingly equal times. Moreover, with twice the proliferation rate, CD8s might spend more time in other compartments, delaying their arrival to the inguinal LN.

We remark that these results derive from very specific conditions and only serve as a means to explore a potential application. Redefining the whole family of immune parameters would certainly generate entirely different results. We close this section with one last example that investigates the hypothetical situation of comparing the changes in transport kinetics when increasing the dimensions of an organism in a uniform manner.

3.3.3. Effects of scaling in transport

For our final example we explore the effects of scaling the size of the compartments in the transport of cells. This experiment extends the validation example related to homeostasis by uniformly expanding all physical dimensions of the compartments by a constant multiplier M. The variable that we use to quantify the differences in transport is the PET (see Definition S6) of CD8s in the spleen. The action of amplifying the dimensions of a compartment results in two major changes. It extends the transport length ℓ between the lymphoid compartments (simply because they become more distant) by a factor of M, and expands the volume of each compartment by a factor of M³. Moreover, by modifying the dimensions of an organism one has to take into account the potential differences in the proliferation of cells within each compartment. In view of Eq. (4), we note that the flat generation rate g(t) is not multiplied by the concentration and therefore we also adjust this coefficient by a factor of M³.

An important observation is that, owing to Eq. (20), a modification of the proliferation rate g(t) redefines the equilibrium concentration (EC). Hence, when computing the PET it is always with respect to the EC determined by the given proliferation rate.

In order to test the effects of the expansion factor M. we consider the following experimental conditions. The system starts from an immunodepleted state (zero initial concentration) and is left to evolve towards equilibrium. Subsequently, the system is perturbed by delivering a certain amount of cells into one compartment (inguinal) and we measure the time elapsed between the peak concentration reached due to the perturbation and the attainment of 95% the EC in the spleen. We denote this quantity by T₉₅(CD8)_Spleen. Details on how the EC and the number of injected cells is computed as a function of M is given in Derivation S5. An example of the concentration profiles after perturbing the system is shown in Figure S4.

The results corresponding to various values of M are summarized in Fig. 7. We note that an exponential fit of the form T₉₅(M) = a · e^b·M with estimates $\widehat{a}$ = 4.21 and $\widehat{b}$ = 1.37 gives an accurate description of the model resulting in a determination coefficient R² ≈ 0.997. The exponential behavior of T₉₅(M) can be partially justified observing that the solution to a simplified version of the L-PBPK containing only a proliferation constant g and a death rate d in one compartment of volume V has a solution whose kinetics are governed by an equation of the form 1 − e^−d·t/V, where k is a constant. This equation readily shows that an increment in the volume slows the kinetics in an exponential fashion. Further details are given in Derivation S6.

Fig. 7.

PET of CD8s in the spleen as a function of the expansion factor. Plot of the PET T₉₅ (CD8)_Spleen as a function of the expansion factor M. The model is of the form T₉₅(M) = a · e^b·M with a coefficient of determination R² ≈ 0.997, $\widehat{a}$ = 4.2, $\widehat{b}$ = 1.37, and standard errors $s(\widehat{a})$ = 0.41, $s(\widehat{b})$ = 0.04.

In summary, though a uniform scaling of a small animal like a mouse cannot yield an anatomically consistent model of a larger animal like a human, one can draw the conclusion that size differences can in fact significantly impact the transport kinetics. This effect is observed in therapies that have specific effects in mouse models, but generate completely unexpected (and often undesirable) outcomes in other larger models. Hence, though size is not the only factor at play driving these differences, it does have a contribution. We close this manuscript by stating some concluding remarks.

4. Conclusion

In this work we have introduced a transport-based PBPK of relevance to the LS and in particular to cell immunotherapies, capable of simulating the transport of therapeutic agents across different compartments and tumors. The implementation incorporates different reaction mechanisms, some of them requiring the usage of nonlinear dynamical behaviors to describe cell intrinsic effects such as proliferation, death, and activation. These effects enabled the L-PBPK to simulate aspects inherent to pathogenic processes such as the delay in the triggering of an immune response and the reattainment of equilibrium. In addition, analytical properties of the model such as existence of a unique solution and stability were discussed and established.

Furthermore, six numerical examples were provided. The first three served two purposes. They produced computational evidence for the mathematical properties and demonstrated the ability of the L-PBPK to simulate experimental conditions of physiological significance. For instance, we showed that the system can recapitulate background concentrations and reach homeostasis in the face of perturbations. Additionally, we were able to successfully model complex interactions between diverse immunological agents in lymphoid and tumor compartments which appropriately described the onset, mediation, and eventual eradication of an infection. Lastly, owing to the distinctive implementation of the tumor compartment, the model proved to be applicable to investigate infiltration kinetics and cell exchange within a tumor. The subsequent three exploratory examples further evinced the potential usage of the L-PBPK to address transport research questions. This was done by probing the influence of tumor size, transport coefficients, and compartment dimensions in cell kinetics, and considering the effects of connecting a sentinel LN to a network composed of LNs and a tumor.

Finally, we remark that though the focus of the present paper was aimed towards cell immunotherapy, the current implementation is sufficiently flexible to allow the modeling of problems of an entirely different context but maintaining a transport character. For instance, modeling nanodelivery efficiency of pharmaceuticals as a function of material properties in the context of biological barriers, and the identification and subsequent mapping of transport routes of immunological character in different organisms. Evidently, both of these applications would contribute to the better understanding and design of cancer therapies and drug delivery strategies.