Toward Semi-autonomous Cryoablation of Kidney Tumors via Model-Independent Deformable Tissue Manipulation Technique

Abstract

We present a novel semi-autonomous clinician-inthe-loop strategy to perform the laparoscopic cryoablation of small kidney tumors. To this end, we introduce a model-independent bimanual tissue manipulation technique. In this method, instead of controlling the robot, which inserts and steers the needle in the deformable tissue (DT), the cryoprobe is introduced to the tissue after accurate manipulation of a target point on the DT to the desired predefined insertion location of the probe. This technique can potentially reduce the risk of kidney fracture, which occurs due to the incorrect insertion of the probe within the kidney. The main challenge of this technique, however, is the unknown deformation behavior of the tissue during its manipulation. To tackle this issue, we proposed a novel real-time deformation estimation method and a vision-based optimization framework, which do not require prior knowledge about the tissue deformation and the intrinsic/extrinsic parameters of the vision system. To evaluate the performance of the proposed method using the da Vinci Research Kit, we performed experiments on a deformable phantom and an ex vivo lamb kidney and evaluated our method using novel manipulability measures. Experiments demonstrated successful real-time estimation of the deformation behavior of these DTs while manipulating them to the desired insertion location(s).

INTRODUCTION

Autonomous and semi-autonomous surgical systems can improve accuracy, dexterity, and repeatability of surgical interventions, and consequently reduce surgical errors, tissue damage, and operating time.¹⁶ These systems have already been used in various interventions including bony tissues (e.g. orthopedic⁷ and neurosurgery¹⁰), where hard tissue (bone) simplifies the preplanning and operation of robots when compared to deformable tissues (DTs). A DT usually provides a dynamic environment, which may exhibit unknown behavior during the operation and, therefore, its preoperative and real-time intraoperative images may differ. Hence, autonomous DT interventions are more challenging than interventions involving hard tissues.

Needle insertion is a type of DT intervention, which is used for tissue sampling through biopsy or treatment of tumors via drug injection or ablation. Examples include venipuncture,⁶ cryoablation of renal tumors,⁸ and brachytherapy.^13,14 The main challenges of this procedure are associated with the accurate placement and/or steering of the needle on the surface and/or through the DT. Several important factors make this placement very difficult. These factors include: unknown tissue deformation and heterogeneity, potential movement of the desired target on the surface or inside of the DT—which may result in incorrect insertion location and orientation, avoiding tissue damage, and patient’s movement.^14,19

To overcome the difficulties of this procedure, researchers have implemented various autonomous or semi-autonomous control methods on robotic systems, which steer or insert the needle to the desired target.¹ Performance of these procedures is very dependent on the considered models for the needle-DT interaction. To this end, usually mechanical or computational (e.g. Finite Element (FE)) methods are used to accurately model and simulate the dynamics of the DT and predict either behavior of the needle in the tissue or movement of the target. Examples of needle-DT interaction models include various types of nonholonomic kinematics-based^15,19 and beam-theory-based^11,15 approaches. In addition, a range of control methods have been implemented for the above-mentioned models to steer the needle to the desired target.^13–15 The performance of these model-based control techniques, however, is often limited to and dependent on the accuracy of the selected needle-tissue interaction model.¹⁴ Further, although FE modelling approaches can be accurate, they cannot be efficiently implemented in real-time due to their long run-time caused by intensive computations.¹⁴

Laparoscopic cryoablation is a minimally invasive procedure for treatment of small peripheral kidney tumors in the range of 1–5 cm⁸. In this procedure, after creation of laparoscopic port sites and abdominal insufflation, a laparoscopic camera is inserted to view the area and help to adequately dissect kidney for better exposing the lesion. A laparoscopic ultrasound probe is then introduced to scan the entire kidney and define the exact diameter and location of the lesion. After localization of the tumor, target insertion location(s) on the kidney surface with appropriate insertion orientation(s) are determined. Of note, the number of these locations(i.e.utilizedcryoprobes)dependsonthesizeof the tumor.⁵ Then, a clinician accurately inserts cryoprobe(s) under direct vision of the camera and advances to an appropriate depth under guidance of ultrasound inside or in the boundary of the tumor. Finally, a double freeze-thaw technique is used to ablate the tumor under real-time ultrasound monitoring.^5,8

The success of this task is highly dependent on the clinician skill and requires great hand-eye coordination and multiple trials, compromising the patient’s safety. Further, due to (1)the deformable characteristics of the tissue, (2) patient’s movement, and (3) interaction between instruments and tissue, the probe(s) target location(s) and orientation(s) may vary significantly, which may result in kidney fracture during cryotreatment.⁵ Tremor and tiredness of the clinician’s hands during the relatively long ablation procedure (about 30 min⁸) may also impede the success of this surgery. To prevent these complications, it is essential to insert the probe into the kidney with appropriate angles and firmly maintain its location and orientation during the procedure.⁵

To address the limitations of the model-based needle insertion approaches and mentioned difficulties in the laparoscopic cryoablation of kidney tumors, an alternative novel intermediate approach can be semi-autonomous model-independent needle insertion using the tissue manipulation technique. In this procedure, a clinician collaborates with a robotic system to ensure safe and accurate needle insertion in the desired lesion inside the DT, while the robotic system is in charge of manipulatingthetissueforaccurateplacementoftheneedleon the surface of DT. This model-independent tissue manipulationtechniquedoesnotneedapriormodeland estimates the deformation behavior of DT in real-time.

OBJECTIVE AND CONTRIBUTION

In this paper, we present a novel model-independent clinician-in-the-loop strategy to perform the laparoscopic cryoablation of small peripheral kidney tumors via an uncalibrated vision-based bimanual tissue manipulation technique. In this clinical procedure, one (or multiple) cryoprobe(s) is (are) inserted under direct vision of the laparoscope to the pre-determined location(s) on the surface of kidney, while the tissue is safely manipulated using one or two laparoscopic forceps. A clinician then inserts the cryoprobe(s) into the kidney to an appropriate depth under the guidance of ultrasound.^5,8 To guarantee the patient’s safety and complete cryoablation of the tumor, the clinician should be careful about appropriate placement of the probe(s) (i.e. both position and orientation) to avoid kidney fracture during cryotreatment and increased bleeding.⁵

To perform this minimally invasive procedure via a semi-autonomous robotic procedure, in this paper, we implemented our optimization-based method and carried out a set of experiments with the da Vinci Research Kit (dVRK).¹² In the performed experiments, two manipulators of the dVRK autonomously collaborated to manipulate an unknown DT—to be cryoablated—in order to overlay one or two target points on the DT to their desired insertion locations. Then, the probe was manually introduced to the simulated soft tissue organ using another manipulator holding it. To ensure patient’s safety during manipulation of the DT, we also constrained movement of the robots and evaluated the performance of our method in this case as well.

The unique features of this study include: (1) the novel model-independent bimanual tissue manipulation technique does not depend on a prior DT model and does not require a calibrated vision system; (2) the method allows defining constraints in either image plane or Cartesian space to enhance patients’ safety during the needle insertion procedure; (3) the proposed bimanual tissue manipulation technique, as experimentally demonstrated, can simultaneously manipulate more than one insertion locations; (4) the extension of Yoshikawa’s manipulability measure and the area of the manipulability ellipse were used for the analysis of the manipulation of deformable tissues.

MATERIALS AND METHODS

Semi-autinomous Laparoscopic Cryoablation of Small Kidney Tumors

We propose the following procedure to facilitate the laparoscopic cryoablation of peripheral kidney tumors using a semi-autonomous vision-guided robotic system. After scanning the kidney using an ultrasound probe, a clinician first assigns and fixes a feasible desired orientation(s) and insertion location(s) for the robot(s) holding the needle(s) as well as the desired target location(s) on the kidney surface. Next, a modelindependent control method is utilized to autonomously and safely manipulate the organ using robotic manipulator(s) to overlay target location(s) on the kidney on the assigned location(s) in the workspace—without having prior knowledge about the deformation behavior and geometry of the kidney. Finally, a clinician carefully advances the probe(s) inside the DT under the guidance of ultrasound. Of note, during the insertion step, robot(s) maintain(s) the orientation and location of probes (Fig. 1). For the proposed method, the following assumptions have been made by the authors:

FIGURE 1.

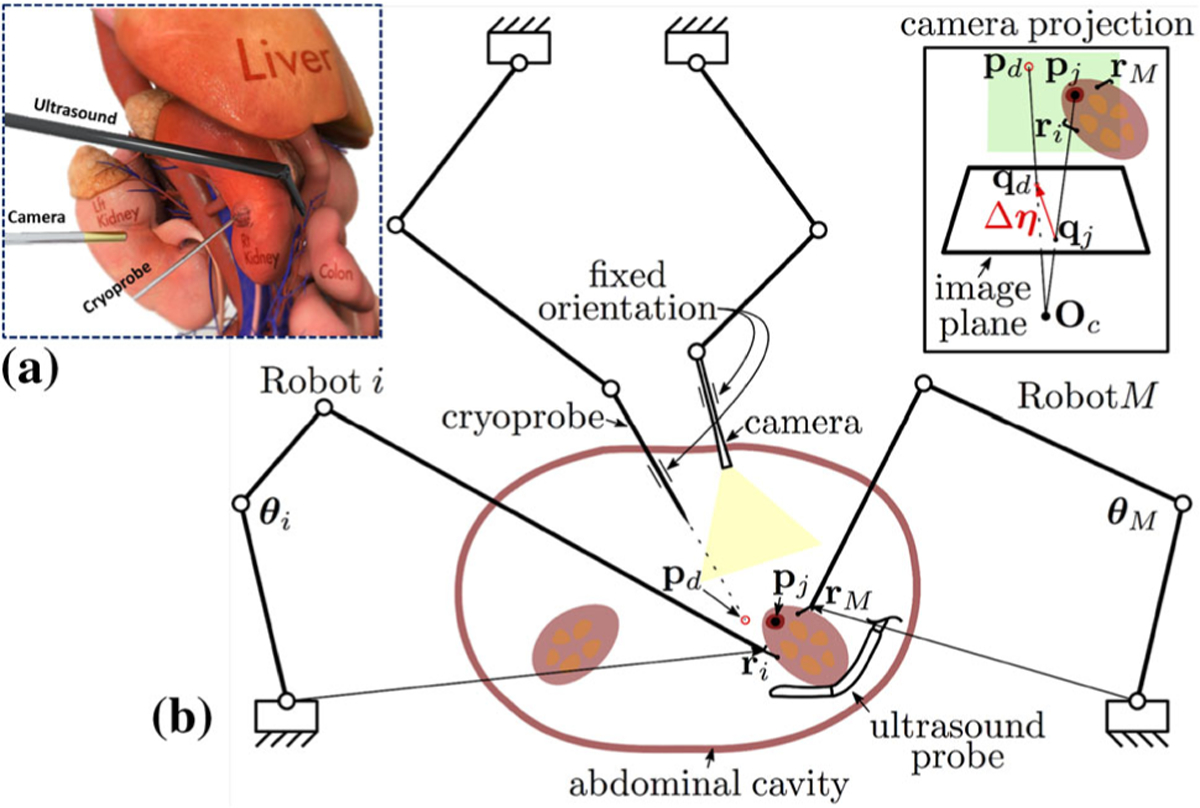
(a) Conceptual illustration of the current procedure for laparoscopic cryoablation of small peripheral kidney tumors; (b) Conceptual illustration of the semiautonomous laparoscopic cryoablation of small peripheral kidney tumors using the collaborative tissue manipulation technique. In this technique, Robots i – M autonomously and safely manipulate the organ to overlay target locations (p_j) on the kidney on the assigned insertion location(s) in the workspace (p_d)—without having prior knowledge about the deformation behavior and geometry of the kidney. Finally, the clinician carefully advances the cryoprobe with fixed orientation inside the DT under the guidance of ultrasound. The green rectangles in the camera projection view demonstrates the defined constraints in the task space of each robot, the red region illustrates the kidney tumor, and O_c denotes the camera optical center.

Assumption 1

The visual feedback is always available from a camera and we can measure the object’s deformation visually in real-time—although the location of the camera is not calibrated with respect to the robot(s) and this sensing can be noisy.

Assumption 2

The grasped location(s) of the DT have been chosen such that the probe(s) insertion location(s) can be indirectly manipulated.

In the following sections, the details of the proposed model-independent clinician-in-the-loop tissue manipulation technique are presented. These include the derivation of the equations for the robot(s) kinematics, deformation Jacobian of the DT, our model-independent control framework, and real-time estimation of the DT deformation Jacobian.

Robot(s) Kinematics

The configuration-dependent robot manipulator Jacobian $J_{r_i}\left({\theta }_i(t)\right)$ maps the actuation input velocities ${\dot{\theta }}_i(t)\in {ℝ}^{n_i}$ to the vector of end effector velocities in the Cartesian space ${\dot{r}}_i(t)\in {ℝ}^{m_i}\left(n_i\ge m_i\right)$. Now, considering M kinematically controlled robots, we can write:

$${\dot{r}}_i(t)=J_{r_i}\left({\theta }_i(t)\right){\dot{\theta }}_i(t)$$ (1)

where i ∈ {1;…;M}.

Considering (1), for an infinitesimal period Δt, the changes in the end effector position Δr_i(t) can be related to the joint angles changes Δθ_i(t) as:

$$\mathbf{\Delta }{r}_i(t)=J_{r_i}\left({\theta }_i(t)\right)\mathbf{\Delta }{\theta }_i(t)$$ (2)

The DT deformation Jacobian

Let’s consider a feature point $p_j(t)\in {ℝ}^3$ on the surface of the DT that represents the probe target location (in the Cartesian space) as shown in Fig. 1:

$$p_j(t)=\left[x_j(t)y_j(t)z_j(t)\right]$$ (3)

Further, let’s denote the corresponding image coordinates of the feature point p_j(t) in the image plane is $q_j(t)\in {ℝ}^2$:

$$q_j(t)=\left[{\mu }_j(t)v_j(t)\right]$$ (4)

Considering Assumption 2, if we can indirectly manipulate the desired target location(s) on the surface of the DT using the grasping point(s), then we are able to locally model the interactive DT deformation in the image plane. To this end, we can relate the changes in the end effector(s) position Δr(t) to the displacement of the feature point(s) in the Cartesian space Δp(t) as well as the image plane Δq(t) as the following:

$$\frac{\text{d}}{\text{d}t}q(t)=\underset{J_d(r(t))}{\underbrace{\frac{\partial q}{\partial p}(p(t))\frac{\partial p}{\partial r}(r(t))}}\frac{\text{d}}{\text{d}t}r(t)$$ (5)

where $\frac{\partial q}{\partial p}(p(t))$ defines the unknown projection model of the feature point and J_d(r(t)) is a $2N\times \sum _{i=1}^M{m}_i$ matrix. This matrix determines the deformation Jacobian matrix of an unknown DT relative to an uncalibrated vision system.

Substituting (1) in (5), we can relate the joint angle changes to the displacements of the feature point in the image plane:

$$\frac{\text{d}}{\text{d}t}q(t)=J_d(r(t))J_r(\theta (t))\frac{\text{d}}{\text{d}t}\theta (t)$$ (6)

where $J_r(\theta (t))\in {ℝ}^{\sum _{i=1}^M{m}_i\times \sum _{i=1}^M{n}_i}$ is a block diagonal matrix, whose blocks define the Jacobian of each robot $\left(J_{r_i}\left({\theta }_i(t)\right),i\in \left\{1,2,\dots ,M\right\}\right)$.

Therefore, for an infinitesimal time Δt, we can approximate (6) as:

$$\mathbf{\Delta }q(t)=J_d(r(t))J_r(\theta (t))\mathbf{\Delta }\theta (t)$$ (7)

Model-Independent Control Framework

Considering (7), one reasonable control strategy for indirect positioning of the desired target location(s) in the image plane (feature point q(t)) to the predefined location(s) of the cryoprobe(s) in the image plane q_d is to find appropriate incremental robot(s) joint angles Δθ(t) that moves the feature point(s) to its desired location(s) in the image plane.

In this regard, we define Δη(t) as the error between the current target location of the feature point(s) (i.e. q(t)) with respect to the desired insertion location(s) in the workspace (i.e. q_d):

$$\mathbf{\Delta }\eta (t)=q(t)-q_d$$ (8)

Considering (7) and (8), we can define the following optimization problem—subject to various constraints—to successfully correspond these locations:

$$\begin{array}{r}\hfill \underset{\mathbf{\Delta }\theta (t)}{\text{arg min}}\parallel J_d(r(t))J_r(\theta (t))\mathbf{\Delta }\theta (t)-\mathbf{\Delta }\eta (t){\parallel }_2^2\\ \hfill \text{s.t. }A(\text{t})\mathbf{\Delta }\theta (\text{t})\le b(\text{t}),\\ \hfill \mathbf{\Delta }\theta (\text{t})\le \mathbf{\Delta }{\theta }_{\text{max}},\\ \hfill \mathbf{\Delta }\theta (\text{t})\le \mathbf{\Delta }{\theta }_{\text{min}}.\end{array}$$ (9)

where matrix $A(t)\in {ℝ}^{h\times \sum _{i=1}^M{n}_i}$ and vector $b(t)\in {ℝ}^h$ define h linear inequality constraints. Of note, these constraints can easily be defined in the task space and (or) image plane using the appropriate Jacobian matrix.

Real-Time Estimation of the Deformation Jacobian

In this study, we assume there is no prior knowledge (or model) of the deformation behavior of the DT as well as the camera parameters. As such, matrix J_d(r(t)) in (9) is considered as an unknown matrix, which needs to be estimated in real-time during manipulation. In fact, Eq. (9) is a system of 2N linear equations with $2N\times \sum _{i=1}^M{m}_i,i\in \left\{1,2,\dots ,M\right\}$ unknowns, where the unknowns contain the information of the DT deformation matrix. Therefore, this equation is under-determined and does not uniquely determine all the components of J_d(r(t)). To solve this equation and estimate the deformation Jacobian matrix, we implement a recursive first-rank update rule, called Broyden method, which is used for solving under-determined nonlinear system of equations.⁴ It is proved that the estimated Jacobian by the Broyden method results in the smallest possible change in the Frobenius matrix norm with its last estimated value.²⁰ This important feature prevents jerky motions during implementation of our model-independent approach.

In the Broyden estimation method, in each time instant t, the estimated Jacobian matrix ${\widehat{J}}_d(t+\mathbf{\Delta }t)$ is calculated based on the Jacobian estimation ${\widehat{J}}_d(t)$, displacement of the robot(s) joint angles Δθ(t), and the resulted image change Δη(t) of the last step as the following:

$${\widehat{J}}_d(t+\mathbf{\Delta }t)={\widehat{J}}_d(t)+\Gamma \frac{\mathbf{\Delta }\eta (t)-{\widehat{J}}_d(t)J_r(t)\mathbf{\Delta }\theta (t)}{\left(J_r(t)\mathbf{\Delta }\theta (t)\right)J_r(t)\mathbf{\Delta }\theta (t)}\left(J_r(t)\mathbf{\Delta }\theta (t)\right)$$ (10)

where 0 ≤ Γ ≤ 1 is a constant parameter, controlling the rate of change of ${\widehat{J}}_d(t)$.

Of note, Eq. (10) also satisfies the following equation—called Secant condition, which guarantees the estimated Jacobian has theoretically similar behavior with the true deformation Jacobian of the DT²⁰:

$$\mathbf{\Delta }\eta (t)={\widehat{J}}_d(t+\mathbf{\Delta }t)J_r(t)\mathbf{\Delta }\theta (t)$$ (11)

Control Algorithm

Considering (9) and (10), we can summarize the proposed control algorithm for semi-autonomous target manipulation as the following: In each time instant (t + Δt), given the estimated deformation Jacobian matrix ${\widehat{J}}_d(t)$ and actuation control input calculated from (9) (i.e. Δθ(t)), the robot(s) are moved. Then, the corrected DT Jacobian ${\widehat{J}}_d(t+\mathbf{\Delta }t)$ is calculated using the actual displacement of the feature point q_j(t)—caused by Eq. (6) and the displacements of the end effector(s) in the image plane, which will result in reduced error compared to the time instant t. This algorithm iterates while a predefined error threshold e is satisfied (as shown in Algorithm 1).

Experimental Setup

We used the dVRK system to conduct all the validation experiments (Fig. 2). This system consists of mechanical parts from da Vinci Classic Surgical System donated by Intuitive Surgical Inc., and open source electronics and software (cisst/SAW libraries) developed by researchers at Johns Hopkins University.¹² This surgical robot has three Patient Side Manipulators (PSMs), one Endoscopic Camera Manipulator (ECM), and two Master Tool Manipulators (MTMs). In the following evaluation experiments, we used two PSMs holding the ProGrasp Forceps (Intuitive surgical, Inc., California, USA) for active manipulation of the DT, one PSM holding a Large Needle Driver (Intuitive surgical, Inc., California, USA) to manipulate an 18 Gauge needle (simulating the cryoprobe), and an endoscope mounted on the ECM for obtaining the image feedback (Fig. 2).

FIGURE 2.

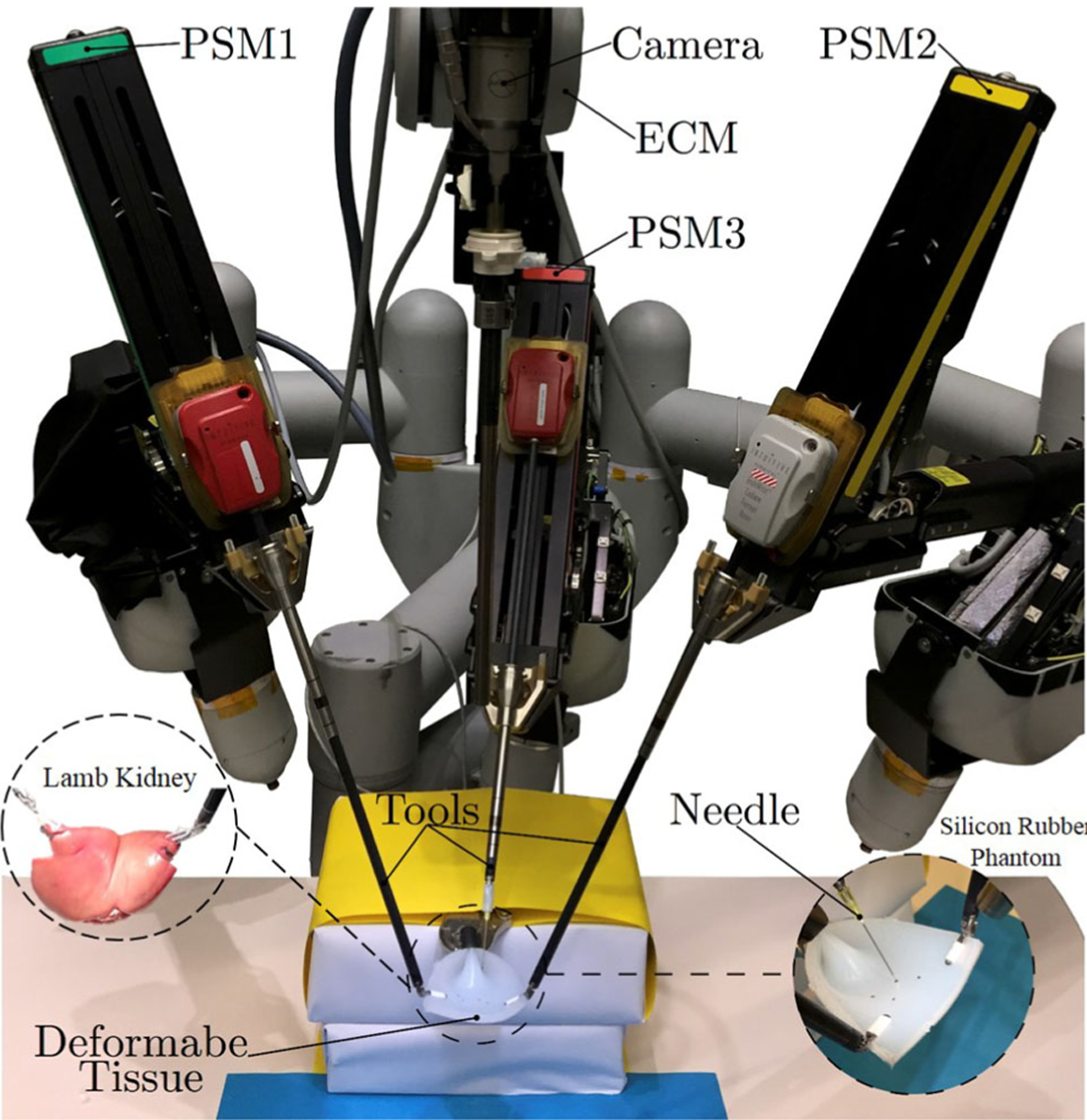
The setup used for the semi-autonomous laparoscopic cryoablation of small kidney tumors using the dVRK system on the considered deformable tissues.

For measuring the deformation of the DT (i.e., image displacements of the feature points), we implemented a visual tracker algorithm with the Optical Flow package of the OpenCV library,³ which uses Lucas-Kanade algorithm.² We developed our control algorithm using the cisst/SAW libraries in C++ and Matlab (MathWorks, Inc.) and used Matlab-ROS bridge¹⁷ to communicate between these environments in real-time.

The Deformable Phantoms

As shown in Fig. 2, for the experiments, we used a soft, tear-resistant silicon rubber phantom (Ecoflex 00–50, Smooth-On, Inc.). The dimension of the sample phantom used in the experiments was 100 mm × 70 mm × 10 mm. We also performed a validation experiment on an ex vivo lamb kidney. The 120 mm × 60 mm × 300 mm ex vivo phantom had 150 g weight (Fig. 2).

Experiments Procedure

In the following experiments, we first fixed the location of the camera to provide sufficient field of view during the experiment. We then used the ProGrasp Forceps and grasped the corners of the phantoms (Fig. 2). We assumed that before each experiment, the target location(s) on the DT (feature point(s) q_j), the desired cryoprobe(s) insertion location(s) (q_d), and the fixed orientation of the PSM holding the probe are well defined. In these experiments, the location of the vision system was arbitrarily chosen such that it could provide sufficient field of view during the procedure. The goal was to indirectly manipulate the target location(s) on the surface of DT to their desired insertion location(s) in the workspace—using two PSMs—without having prior knowledge about the tissue deformation model. Once the feature points coincided with the desired insertion points, the needle was inserted manually to the DT phantom using the third PSM. Of note, during insertion, the other PSMs held the tissue firmly in the desired location. In addition, in the following experiments, we mainly focused on the indirect autonomous manipulation tasks and assumed the needle insertion, using the third PSM, is only limited to a simple insertion motion by the clinician.

As mentioned in Assumption 1, the visual feedback provided by the vision system can be noisy. To mitigate this issue, we implemented the following first-order low-pass filter and used the filtered measurements in (9) and (10):

$${\stackrel{.}{x}}_f=-\Lambda \left(x_f-x\right)$$ (12)

where x and x_f represent the original and filtered signals, respectively. The diagonal matrix Λ = diag(λ₁; λ₂;…; λ_k) allows us to adjust the dissipative properties of the filtered signal. Further, to solve (9), we used the active-set algorithm⁹—i.e. the lsqlin function in MATLAB, which is used for solving constrained linear least-squares problems.

Performance Evaluation Measures

For each feature point on the DT, we can define a deformation Jacobian matrix. This matrix defines the relation between the movements of the end effectors Δr_i (as the input) and the resulted displacement of each feature point Δq_j (as the output). Notably, considering the number of robotic arms grasping the DT, we can have more degrees of freedom (DoF) than what we need for manipulation of the feature point(s) (i.e. a redundancy in the DoF).

To analyze the results of each experiment as well as the performance of the proposed model-independent method in estimating the phantom deformation Jacobian, we used various measures. We plotted the trajectory of the end effector(s) in the Cartesian space and the trajectory of the feature point(s) in the image plane. Further, the Euclidean distance between the desired insertion location(s) and the feature point location(s) was calculated at each time step and plotted to monitor the convergence of the proposed algorithm.

We also implemented the Yoshikawa’s manipulability measure w²¹:

$$w=\sqrt{\text{det}\left({\widehat{J}}_d{\widehat{J}}_d^T\right)}$$ (13)

where det(.) denotes determinant of a matrix. This quantitative measure is usually used for conventional redundant manipulators with rigid links and quantifies the difficulty of moving the robot end effector in a certain direction.²¹ With the same analogy, we extended the application of this measure as a criterion for indirect collaborative manipulation of deformable tissues. Of note, the difficulty of moving these points in a certain direction (i.e. small values) convey the deterioration of the manipulability in that direction and vice versa. This situation may happen due to inaccurate estimation of the deformation behavior or sudden change in the experimental conditions.

In addition, we utilized the singular value decomposition representation of the estimated Jacobian to calculate the manipulability ellipse. For conventional robots with rigid links, the volume and principal axes of this ellipse is used to determine the direction of end-effector movements with maximum and minimum manipulability.²¹ We used this ellipse as a graphical means to represent the manipulability of the feature point(s).

RESULTS

Constraint-Free Manipulation Experiment with Single Insertion Point

We first examined our indirect manipulation approach in a probe insertion task with one feature point (i.e. cryotreatment with one probe) and no constraints defined either in the image or joint space. For this type of experiments, we performed several preliminary experiments to obtain the optimal values of the following parameters: Γ = 0:7, Λ₁ = diag (2;2;2;2) for filtering the PSMs signals provided by the dVRK system, Λ₂ = diag(2;2) for the visual feedbacks of the image feature point provided by the ECM, and ε = 1 pixel as the error threshold. Further, for simplicity, we constrained movement of the end effector(s) to be in an X–Y plane relative to the PSM’s base frame. Therefore, considering (5) with a single insertion point in the image space and two grasping points with two PSMs, dimension of the deformation Jacobian matrix is ${\widehat{J}}_d\in {ℝ}^{2\times 4}$, which demonstrates a redundancy in the required DoF. For this experiment, we arbitrarily initialized the deformation Jacobian matrix with diagonal entries of all ones corresponding to each PSM. The computation time for each iteration was measured as 3 ms.

Of note, although in this paper, we are constraining the end effector movements to be planar, the presented method in (9) is a general procedure. Therefore, based on the physical constraints and objectives of the problem, this deformation matrix can be extended to a ${\widehat{J}}_d\in {ℝ}^{2N\times \sum _{i=1}^M{s}_i}$, where i ∈ {1;…;M} is the number of robots involved in the manipulation, and s ∈ {2N;…;6M} is the number of the overall controlled DoF of all robots in the Cartesian space.

We repeated this set of experiments three times with identical experimental conditions (i.e. initial experimental setup, grasping location, and target point(s)). As the representative of these similar trials, Fig. 3a shows the sequence of snapshots related to one of these experiments. As shown, the target point on the tissue reached the desired insertion point within 66 seconds. Figures 3b and 3c show how two PSMs successfully manipulated the single feature point to the desired location with the predefined error threshold (i.e. ε = 1 pixel). These demonstrate the corresponding trajectories of the end-effectors in the Cartesian space (in mm) as well as image space (in pixel). Also, Fig. 3d shows the Euclidean distance error between the target point and its desired location in each time instant. The other Jacobian-related measures were calculated in Figs. 3e, 3f, and 3g, i.e. manipulability ellipses and their corresponding areas as well as the Yoshikawa’s manipulability measure of the estimated Jacobian along the trajectory.

FIGURE 3.

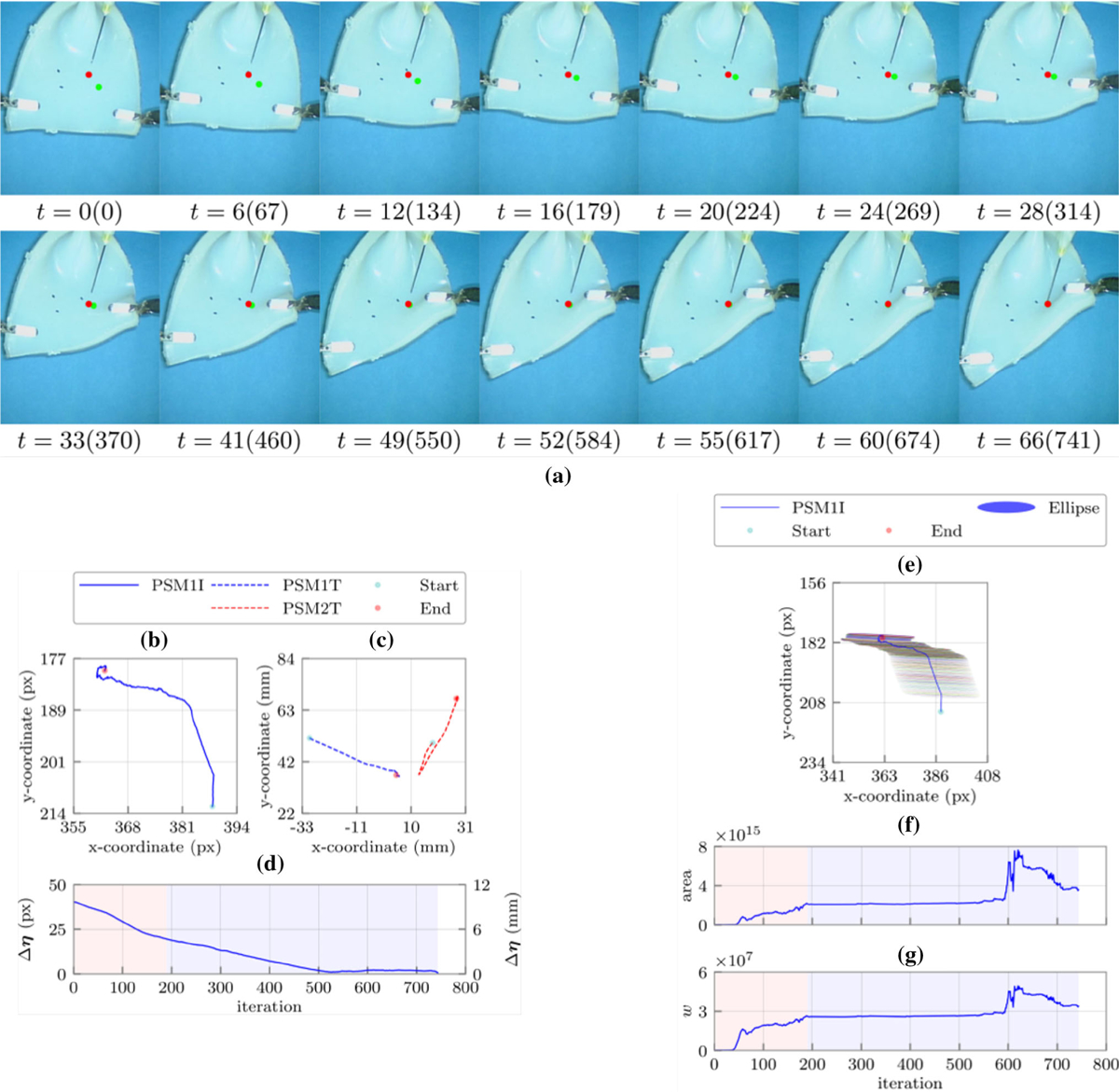
(a) Sequence of snapshots with their corresponding time in second and iteration number during the constraint-free manipulation experiment with single insertion point. The green and red points represent the target point on the tissue and the desired probe insertion locations in the workspace, respectively; (b) the feature point (target location) trajectory in the image plane; (c) the robots end effectors trajectories in the robot’s frame; (d) the Euclidean distance error between the target location and the desired needle insertion location; (e) the manipulability ellipses along the target location trajectory in the image plane; (f) the areas of the manipulability ellipses in each iteration, and (g) the Yoshikawa’s manipulability measure in each iteration. Shaded regions represent the learning and identification (red) as well as the converging (blue) phases, respectively.

Investigation of Figs. 3b, 3c, 3d, 3e, 3f, and 3g demonstrate that how the target point is indirectly manipulated to the desired location in two main phases. Each phase includes a few steps, which the number of these steps depends on the experimental conditions as well as the location of the target point(s). The first three steps of Figs. 3b, 3c, 3d, 3e, 3f, and 3g demonstrate the learning and identification phase of the proposed algorithm while the last two are the converging phase of the method. During the learning and identification phase, we see a continuous increase in the Yoshikawa’s manipulability measure, which demonstrate convergence of the estimated Jacobian to the actual value.

In the first step (iterations 0–27), the estimated deformation Jacobian is almost singular, since according to Figs. 3e, 3f, and 3g, the Yoshikawa’s manipulability measure is a small value. Similarly, calculated area of the manipulability ellipses in this period confirms this claim. Additionally, as we can see in Fig. 3d, the Euclidean distance error does not decrease very much (~ 2 pixel). The second (iterations 27–81) and third steps (iterations 81–190) demonstrate a fast decrease in the Euclidean distance error (~ 19 pixel), which means a good approximation of the deformation Jacobian in this period. This claim is also well understandable from a sharp increase in the Yoshikawa’s manipulability measure as well as the area of the ellipses demonstrated in Fig. 3f. The fourth step (iterations 190–540) shows a stable estimated Jacobian (Fig. 3d), which resulted in a decrease in the error (~ 12 pixel) with constant slope (Fig. 3d). In the last step, both manipulators collaborate to slowly move the target point to the desired location. Furthermore, Fig. 3 shows that the beginning of each step corresponds to a change in the feature point trajectory direction. A sharp change in the direction of the movement is also followed by a sharp change in the estimated Jacobian to usually increase the manipulability and overlay the target point on its desired location. For instance, in step 5, the observed pick in the Yoshikawa’s measure is due to the change in the configuration of the robots (Fig. 3a), which resulted in a better manipulability followed by a reduction in the Euclidean distance errors. It is worth noting that flat manipulability ellipses (Fig. 3e) demonstrate that indirect manipulation of the insertion point along one of the principal axis of the ellipses is much easier than the other one.

Constrained Manipulation Experiment with Two Insertion Points

In this experiment, we simulated a constrained cryotreatment scheme with two probes and two feature points on the DT. This additional constraint helps to avoid tissue damage by limiting undesirable tissue stretching during the manipulation task. In this regard, we constrained the movement of end-effectors in rectangular boxes defined in the Cartesian space (shown in Fig. 5). Of note, in this collaborative task movement of each robot affects the local deformation of both feature points. For this experiment, we considered both robots and the grasped DT as one system and defined one deformation Jacobian and one Euclidean error vector for both target points. A square Jacobin matrix ${\widehat{J}}_d\in {ℝ}^{4\times 4}$ is, therefore, created for this task. To formulate the constraints, considering (9) and the lsqlin function, we used the stack of the PSMs’ Jacobians $J_r(t)\in {ℝ}^{4\times 7}$, and defined matrix $A(\text{t})\in {ℝ}^{8\times 14}$ and vector $b(\text{t})\in {ℝ}^8$ as A(t) = [J_r(t) −J_r(t)]^T and b(t) = [b_max −r(t) r(t) −b_min]^T, where b_min and b_max define the boundaries of the two rectangular spaces (shown in Fig. 4) using 8 linear inequality constraints. Considering these constraints by solving the optimization problem in (9), we attempted to simultaneously move both target points to their desired locations.

FIGURE 5.

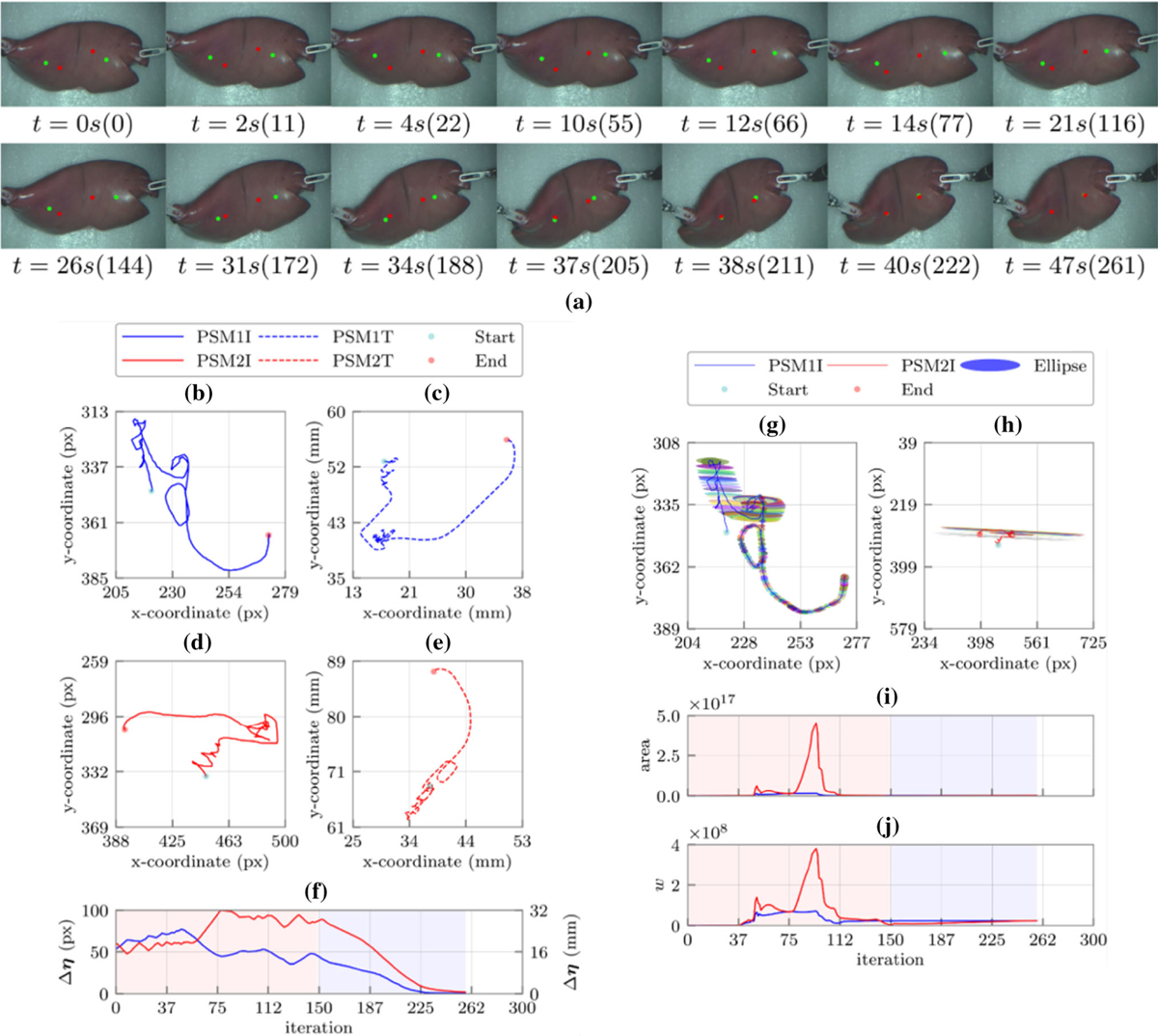
(a) Sequence of snapshots with their corresponding time in second and iteration number during the constraint-free manipulation experiment with an ex vivo lamb kidney with two insertion points. The green and red points represent the target points on the tissue and the desired probe insertion locations in the workspace, respectively; the left (b) and right (d) feature points (target locations) trajectories in the image plane, the left (c) and right (e) robots end effectors trajectories in the robot’s frame; (f) the Euclidean distance errors between the target locations and their corresponding desired cryoprobes insertion locations. The black dashed lines demonstrate the trajectories and error of the corresponding constraint free experiment; the manipulability ellipses along the left (g) and right (h) target locations trajectories in the image plane, (i) the areas of the manipulability ellipses for the left (blue) and right (red) target locations in each iteration, and (j) the Yoshikawa’s manipulability measure for the left (blue) and right (red) target locations in each iteration. Shaded regions represent the learning and identification (red) as well as the converging phases (blue), respectively.

FIGURE 4.

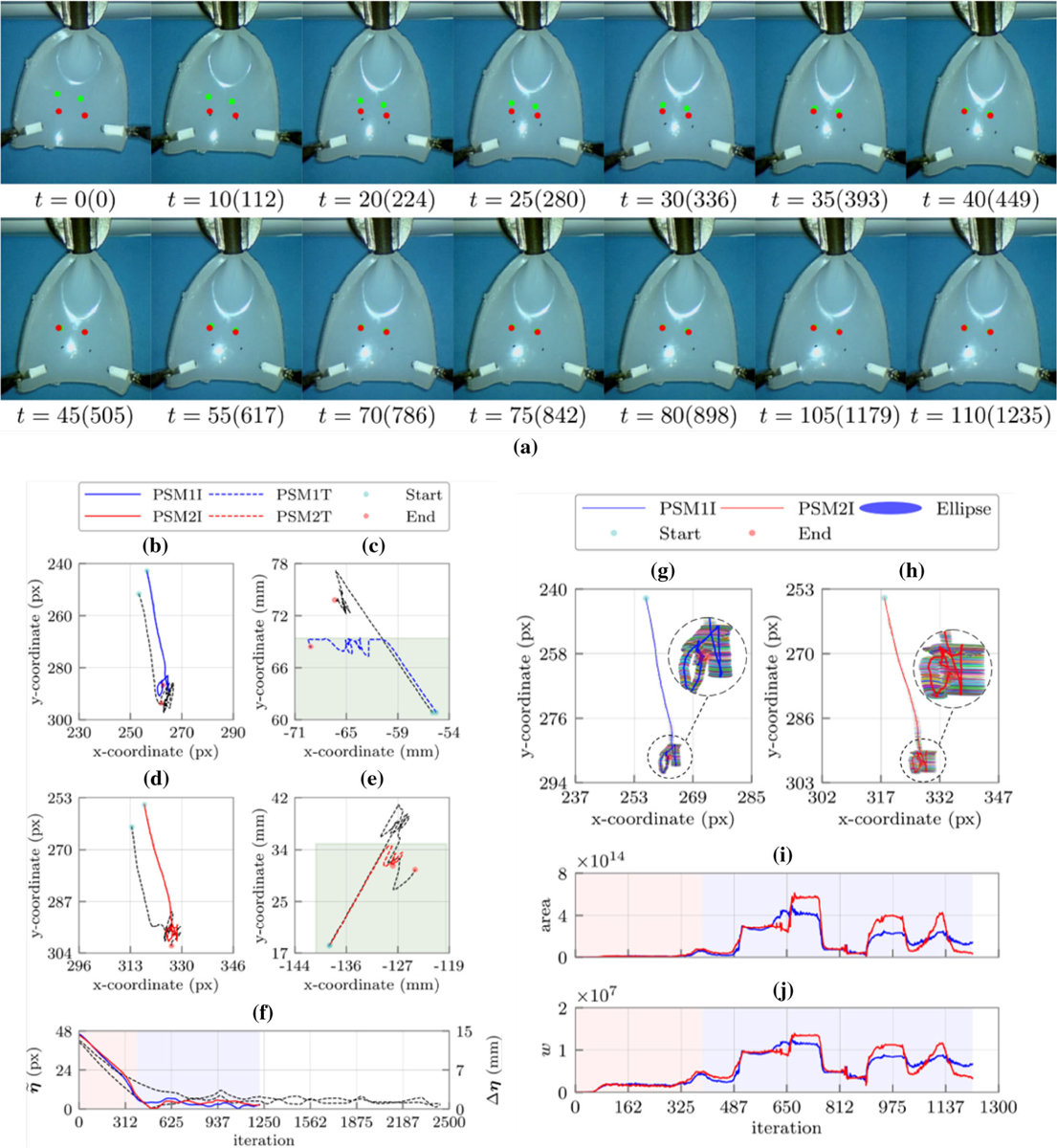
(a) Sequence of snapshots with their corresponding time in second and iteration number during the constrained manipulation experiment with two target points. The green and red points represent the target points on the tissue and the desired probe insertion locations in the workspace, respectively; the left (b) and right (d) feature points (target locations) trajectories in the image plane, the left (c) and right (e) robots end effectors trajectories in the robot’s frame; (f) the Euclidean distance errors between the target locations and their corresponding desired cryoprobes insertion locations. The black dashed lines demonstrate the trajectories and error of the corresponding constraint free experiment; the manipulability ellipses along the left (g) and right (h) target locations trajectories in the image plane, (i) the areas of the manipulability ellipses for the left (blue) and right (red) target locations in each iteration, and (j) the Yoshikawa’s manipulability measure for the left (blue) and right (red) target locations in each iteration. Shaded regions represent the defined constraints (green) learning and identification (red) as well as the converging phases (blue), respectively.

We repeated this set of experiments three times with identical experimental parameters and computational time as the previous experiment. The representative results are shown in Figs. 4a, 4b, 4c, 4d, 4e, and 4f. Further, Figs. 4c and 4e show the rectangular constraints regions in the Cartesian space. Investigation of these figures show that the learning and identification phase included 390 iterations, which can be divided to four steps. The first step, similar to the other experiments, was the singular step (iterations 0–45) followed by a sharp increase in the manipulability of the estimated Jacobian in the second step (iterations 46–95), which resulted in about 12 pixels decrease in the error. In steps three and four of this phase (iteration 96–390) the estimated Jacobians were very close to their actual value since the Euclidean distance significantly dropped (~ 35 pixel). Other iterations were related to the converging phase where the defined constraints in the Cartesian space caused sharp changes in the estimated Jacobians. According to Figs. 4b, 4c, 4d, 4e, 4f, 4g, 4h, 4i, and 4j, whenever the end effectors reached to the border of the constraint regions, a drastic change in the manipulability measures was observed. However, due to the accurate estimation of the Jacobian in the identification phase, the feature points converged to their desired locations. Similar to the previous experiment, flat manipulability ellipses (Figs. 4g and 4h) demonstrate that indirect manipulation of the insertion points along one of the principal axis of the ellipses is much easier than the other one.

Comparison between the constraint-free and constrained case showed the effect of the introduced constraints in the convergence time (Fig. 4f). As shown in Fig. 4f, the convergence time of the constrained case (i.e. 110 s) was almost half of the constraint-free case (~ 220 s). In fact, the introduced constraints served as virtual guides for the indirect manipulation and helped the algorithm converge faster to the desired locations.

Constraint-Free Manipulation Experiment on an Ex Vivo Lamb Kidney with Two Insertion Points

In this experiment, in order to simulate a cryotreatment scheme with two probes on a more realistic 3D phantom and to evaluate performance of our algorithm for real-time deformation estimation of a different unknown DT, we defined two feature points on a lamb kidney. We used identical experimental parameters to the previous section and constrained movement of the end effectors in the X–Y plane. As the representative of the performed trials, Figs. 5a, 5b, 5c, 5d, 5e, and 5f demonstrate the snapshots and resulted trajectories during the indirect manipulation of the two feature points. For this experiment, the target points overlayed on the insertion points in 47 s with identical computation time to previous experiments. Figure 5f shows how two PSMs successfully manipulated both target points to the desired locations satisfying the predefined error threshold (i.e. ε = 1 pixel). Figure 5g, 5h, 5i, and 5j show the manipulability measure defined in (13) and manipulability ellipses along the trajectory of each feature point as well as their corresponding area. Comparison of these figures with the results of the previous experiments demonstrates a different deformation behavior for the 3D kidney when compared to the 2D silicon rubber phantom. Nevertheless, similar to the previous experiments, we can identify the learning and identification (iterations 0–150) as well as the converging (151–261) phases for each feature point (Figs. 5b, 5c, 5d, 5e, 5f, 5g, 5h, 5i, and 5j).

For this ex vivo experiment, in contrast to other experiments, the Euclidean distance error during the first 50 iterations increases for both feature points. This increase is due to inaccurate initialization of the Jacobian matrix (i.e. singular step). After this step, the manipulability of the estimated Jacobian increases (iterations 51–75), resulting in a decreased Euclidean distance for the left feature point. From iterations 74–150, the estimated Jacobians for both feature points are very close to their actual values leading to a decrease in the Euclidean distance. Investigation of the feature points’ trajectories in this step demonstrates how the change in the estimated Jacobians has been reflected in the change in the movement of the feature points. After this step, both feature points traverse a smooth trajectory toward the desired points—due to the accurate estimation of the kidney’s deformation behavior (i.e. converging phase). Further, similar to the previous experiments, flat manipulability ellipses (Figs. 5g and 5h) can be justified.

DISCUSSION

We presented a novel vision-based semi-autonomous collaborative bimanual procedure for laparoscopic cryoablation of small peripheral kidney tumors using the dVRKsystem. Instead of directing the cryoprobe(s) tip(s) to the desired target location(s) on the soft tissue, we used this robotic system to manipulate the target location(s) on theDT tothe pre-defineddesired insertion location(s) of the probe(s). Our proposed tissue manipulation technique does not require any prior knowledge of tissue property and geometry and can estimate the tissue deformation model in real-time. To estimate the deformation behavior of the tissue, we implemented a firstrank update rule for solving under-determined nonlinear system of equations. We evaluated our method on a deformable silicon phantom and an ex vivo lamb kidney with unknown properties. Of note, the main focus of the performed experiments was on the tissue manipulation control strategy, while the insertion step assumed to be performed manually by a clinician under guidance of the ultrasound. As mentioned, the main step in cryotreatment of kidney tumorsisaccurateinsertion of the probes in the target locations on the kidney with an appropriate orientation. Further, maintaining this pose during the treatmentisessentialtoavoidkidneyfracture.Withthese goals, we designed three experiments to simulate three cryoprobe insertion situations.

In the performed experiments we used a fixed camera to measure the object’s deformation visually in real-time. This simplification was considered in order to mainly focus on the feasibility of the proposed technique for estimation of the change in the DT deformation behavior and subsequently model-independent DT manipulation. It is notable that the proposed method, in theory, can also estimate the change in the location of the camera.

The experimental results demonstrated that our proposed method can successfully estimate the unknown deformation properties of the DT in real-time and indirectly manipulate the tissue to overlay one or two target location(s) simultaneously on their desired predefined location(s) with the predefined error threshold of 1 pixel. These results also showed that the performance of the estimation method is robust against uncertainty in the initial value of the deformation Jacobian matrix. Furthermore, the capability of the proposed technique in a constrained manipulation was successfully tested. We showed that the defined constraints not only increase the success rate of the procedure in reducing the risk of false cryoablation and tissue damage, it also may reduce the time of the procedure, which makes the presented method clinically viable. Experiments on both 2D silicon phantom and 3D ex vivo kidney showed that the proposed technique can successfully estimate the deformation of DTs in real-time without prior knowledge of their geometry and physical properties. We extended the application of conventional manipulability measures (i.e. Yoshikawa’s manipulability measures and the area of the manipulability ellipses), and used them as means for evaluation of our vision-based method.

It is worth noting that in our clinician-in-the-loop approach, the robots only manipulate the tissue to overlay the target points on to the planned insertion points. Thus, the clinician has direct control on the insertion velocity of the probe, while having direct haptic feedback during insertion. Moreover, since the clinician uses ultrasound for monitoring the tumor boundary and assigning the trajectory of the probe, any potential motion of the tumor due to the tissue manipulation can be detected and subsequently compensated by assigning new target points on the surface.

Some of the limitations of the current work are as follows. Current implementation uses one camera (2D) view of the DT. The future work will include the extension of the algorithm for 3D deformable tissue manipulation. Laparoscope occlusion may also pose limitations to the performance of our vision-based algorithm. To address this issue, the future work may consider implementing and testing other real-time imaging modalities (e.g. a near-infrared fluorescent imaging system¹⁸). Excessive grasping force may damage the tissue while inadequate force may cause tissue slippage, which may result in a failure in our tissue manipulation technique. The effect of tissue grasping/slippage on the performance of the algorithm requires further investigation. We presented a preliminary ex vivo experiment demonstrating the feasibility of our method on a DT with similar geometry and properties of a human kidney. The transition to the clinical practice, however, will require comprehensive evaluation of the clinician/robot interaction to investigate the safety and the optimal workflow for the proposed method.