Enabling machine learning in X-ray-based procedures via realistic simulation of image formation

Abstract

Purpose

Machine learning-based approaches now outperform competing methods in most disciplines relevant to diagnostic radiology. Image-guided procedures, however, have not yet benefited substantially from the advent of deep learning, in particular because images for procedural guidance are not archived and thus unavailable for learning, and even if they were available, annotations would be a severe challenge due to the vast amounts of data. In silico simulation of X-ray images from 3D CT is an interesting alternative to using true clinical radiographs since labeling is comparably easy and potentially readily available.

Methods

We extend our framework for fast and realistic simulation of fluoroscopy from high-resolution CT, called DeepDRR, with tool modeling capabilities. The framework is publicly available, open source, and tightly integrated with the software platforms native to deep learning, i.e., Python, PyTorch, and PyCuda. DeepDRR relies on machine learning for material decomposition and scatter estimation in 3D and 2D, respectively, but uses analytic forward projection and noise injection to ensure acceptable computation times. On two X-ray image analysis tasks, namely (1) anatomical landmark detection and (2) segmentation and localization of robot end-effectors, we demonstrate that convolutional neural networks (ConvNets) trained on DeepDRRs generalize well to real data without re-training or domain adaptation. To this end, we use the exact same training protocol to train ConvNets on naïve and DeepDRRs and compare their performance on data of cadaveric specimens acquired using a clinical C-arm X-ray system.

Results

Our findings are consistent across both considered tasks. All ConvNets performed similarly well when evaluated on the respective synthetic testing set. However, when applied to real radiographs of cadaveric anatomy, ConvNets trained on DeepDRRs significantly outperformed ConvNets trained on naïve DRRs (p < 0.01).

Conclusion

Our findings for both tasks are positive and promising. Combined with complementary approaches, such as image style transfer, the proposed framework for fast and realistic simulation of fluoroscopy from CT contributes to promoting the implementation of machine learning in X-ray-guided procedures. This paradigm shift has the potential to revolutionize intra-operative image analysis to simplify surgical workflows.

Introduction

Clinical context

Machine learning-based approaches, and in particular deep convolutional neural networks (ConvNets), now define the state of the art across a variety of well-studied problems in computer vision, and more recently, medical imaging. It is not surprising that the most impressive improvements until now were achieved in the sub-discipline of medical image computing [16,29]. This field is dominated by diagnostic imaging tasks where traditionally:

1. All imaging data are archived,

2. Expert annotations that define potential learning targets are well established (e.g., for mammographic lesion detection [13] or brain lesion segmentation [20]) or can be approximated efficiently in a self-supervisory manner (e.g., using automatic tools that yield either imperfect [24] or sparse [17] signals), and

3. Comparably simple augmentation strategies, such as rigid and non-rigid displacements [21,23], ease the limited data problem.

One may be tempted to conclude from the above reasoning that diagnostic image analysis provides a comfortable environment for machine learning, but this is not generally the case. This is because, compared to general computer vision, datasets in diagnostic image analysis are still small considering the dimensionality of the data and variability of its presentation. However, in interventional imaging, and particularly in X-ray-guided procedures, the situation is even more complicated. First, while hundreds of X-ray images are acquired for procedural guidance [4], only very few radiographs are archived suggesting a severe lack of meaningful data. Second, learning targets are not well established or defined. Third, interventional images are acquired from multiple view points onto the anatomy, the exact poses of which cannot accurately be reproduced during surgery [9,33]. Finally, the overall variability in the data is further amplified by surgical changes in anatomy and the presence of tools. Overall, the archived data are heavily unstructured and exhibit enormous variation, which challenges meaningful augmentation. As a consequence, in order to enable machine learning for fluoroscopy-guided procedures the dataset curation and annotation problem must be addressed first. Successfully overcoming this hurdle seems challenging and is reflected in the observation that, despite clear opportunities, only very little work has considered learning in this context.

Contribution

In this manuscript, we describe a hybrid pipeline for fast, physics-based simulation of digitally reconstructed radiographs (DRRs) with corresponding annotations from labeled 3D CT volumes. We extend our DeepDRR framework introduced previously [34] with the capability of simulating tools made from arbitrary materials that may move relative to anatomy defined by the CT volume. The code will be integrated into our open-source repository¹ upon publication of this manuscript. Compared to ConvNets trained on naïve DRRs and not considering re-training or domain adaptation, ConvNets trained on DeepDRRs generalize better to unseen clinical data. We demonstrate this on two use cases: (1) viewpoint-invariant detection of anatomical landmark of the pelvis and (2) concurrent segmentation and localization of dexterous robotic end-effectors. In both scenarios, we train the same ConvNet on naïve DRRs and DeepDRRs, respectively, to reveal performance changes resulting solely from realistic modeling of image formation.

Related work

Physics-based simulation of image formation from volumetric data is at the core of the proposed methodology. Traditionally, realistic simulation is achieved using Monte Carlo (MC) simulation during which photons emitted in a specified imaging geometry are traced as they propagate through the medium [2]. Consequently, the distribution of materials within the volume to be imaged must be precisely known, since photon–tissue interaction is highly material dependent. The concept of MC simulation is often used for radiation treatment planning since MC simulation not only yields an image, but also provides highly accurate estimates of tissue dose deposited upon irradiation [27,28]. In addition, it has recently regained some attention for generating medical images in the context of virtual clinical trials [3]. These two examples suggest that MC simulation is capable of producing highly realistic results, but comes at the cost of long computation times that are prohibitive when trying to generate training datasets with hundreds–thousands of images. Our own experiments revealed that accelerated MC simulation [2] on an NVIDIA Titan Xp takes ≈ 4hours for a single X-ray image with 10¹⁰ photons. The medical physics community provides strategies for acceleration if prior knowledge on the problem exists. A well-studied example is variance reduction for scatter correction in cone-beam CT, since scatter is of low frequency [30]. Due to these limitations, the use of MC simulation of X-ray images to train machine learning algorithms is not a particularly tractable solution and has, to the best of our knowledge, only been explored by highly specialized groups for scatter estimation [19,38], a task for which no other approach is possible.

The general idea of boosting dataset size by simulating digital radiographs from volumetric CT is fairly obvious and not new, but the challenge is achieving scenarios in which results obtained on synthetic data generalize to clinical cases. Most of the previous works [1,14,15,32] use straightforward ray casting for image formation, which is very fast and allows for the generation of arbitrarily large datasets. Ray casting mimics mono-energetic X-ray sources passing through objects that consist of a single material, an assumption that undoubtedly is violated in clinical X-ray imaging. As a consequence, the synthetic images do not exhibit the characteristic artifacts encountered in practice, such as beam hardening and complex noise characteristics. This shortcoming raises questions regarding performance on real data, with several manuscripts limiting evaluation to synthetic images generated using the same tools [14,32,37] or reporting poor generalizability when applied to clinical data [34,42].

In addressing this problem, unpaired conditional image-to-image style transfer networks [43] constitute the largest competitor to realistic simulation. For digital radiography-based procedures, Zhang et al. show that ConvNets trained on naïvely generated DRRs can be applied to clinical data if the clinically acquired image is first processed with such ConvNet to explicitly mimic the appearance of DRRs [42]. This approach is currently studied across various disciplines [18,25,35] with convincing results; however, it is unclear how well this approach handles new target image styles as this may require a large amount of new target images to retrain the style transfer network.

Methodology

We describe a pipeline for realistic DRR generation from CT volumes that is implemented in Python, PyCUDA, and PyTorch to seamlessly integrate with the tools native to machine learning, and enables fast data generation due to its hybrid design that relies on analytic formulations of projection, attenuation, and noise injection while approximating statistic and heuristic processes via state-of-the-art ConvNets. The pipeline consists of four major modules: (1) decomposition of CT volumes into multiple materials using a deep segmentation ConvNet; (2) material and X-ray source spectrum-aware forward projection using GPU-parallelized ray casting; (3) neural network-based Rayleigh scatter estimation; and (4) quantum and electronic readout noise injection. A schematic overview of the pipeline is provided in Fig. 1 and explained in greater detail in the remainder of this section.

Fig. 1.

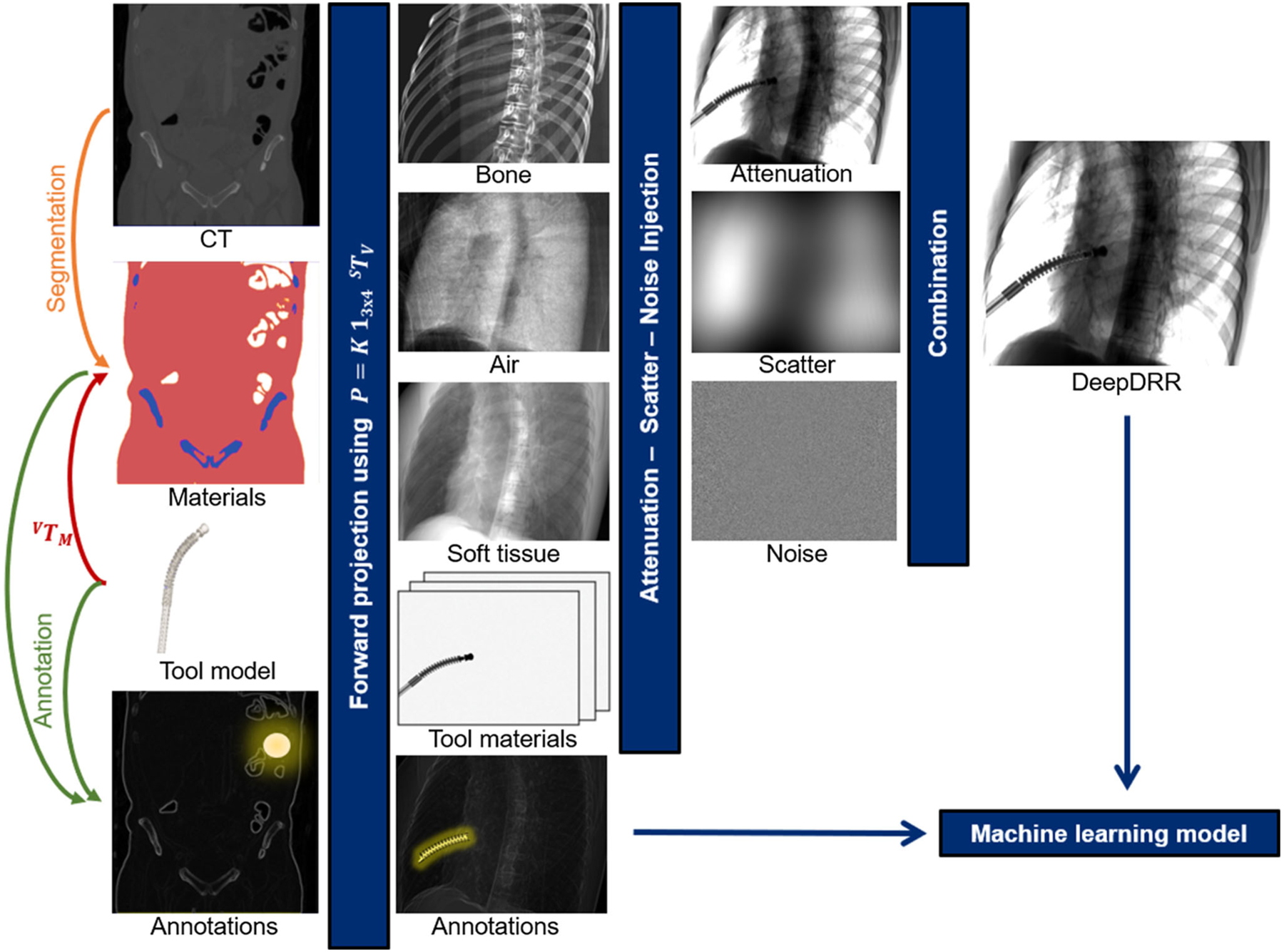
Schematic overview of our realistic simulation pipeline

Physics-based simulation pipeline: DeepDRR

Material decomposition and tool integration

X-ray absorption heavily depends on material properties and photon energy, giving rise to several physical effects such as beam hardening that must be modeled accurately. To this end, we need to derive the 3D distribution of materials from the grayscale CT volume. Traditionally, the task of material decomposition is accomplished by simple thresholding of the CT intensity values. This becomes possible since CT intensities, measured in Hounsfield units (HU), are related to the average linear attenuation coefficient of a particular material and can thus be used to define material characteristic HU ranges [26]. Thresholding works reasonably well for large HU discrepancies, e.g., separating air ([−1000] HU) and bone ([200, 3000] HU), but is prone to failure otherwise, particularly between soft tissue ([−150, 300] HU) and bone in the presence of low mineral density. This is problematic since, despite similar HU, and thus, average linear attenuation, the energy-resolved attenuation characteristic of bone is substantially different from soft tissue [11]. To overcome the limitations of thresholding-based material decomposition, we use a deep volumetric ConvNet adapted from [21] to automatically decompose air, soft tissue, and bone in CT volumes. The ConvNet is of encoder–decoder structure with skip-ahead connections to retain information of high spatial resolution while enabling large receptive fields. For the experiments described here, we use the ConvNet described in [34] that accepts patches with 128³ voxels with voxel sizes of 0.86 × 0.86 × 1.0 mm³ yielding a material map M(x) that assigns a candidate material to each 3D point x. The material decomposition ConvNet was trained (validated) on 10 (2) whole-body CT data from the NIH Cancer Imaging Archive [8] that were manually annotated using ITK Snap [39] using the multi-class Dice loss [21,31] as optimization target for prediction of M = 3 materials, i.e., air, soft tissue, and bone. The network achieved a mis-classification rate of (2.03 ± 3.63)%, a performance that is in agreement with previous studies using similar architectures [12,21,40]. During application, patches of 128³ voxels are fed-forward with stride of 64 since only labels for the central 64³ voxels are accepted. After application of the ConvNet to a CT volume of size N_x, N_y, N_z voxels, we have the material map $M\left(x\right)\in {\left\{0,1\right\}}^{N_x\times N_y\times N_z\times M}$ and corresponding material density $\rho \left(x\right)\in {ℝ}^{N_x\times N_y\times N_z}$.

In order to enable the integration of tools, a second volume is defined that fully contains the tool model, e.g., by voxelizing CAD surface models, yielding a map of materials M_M(x) with associated material densities ρ_M(x). The spatial relation of the tool to anatomy is defined by a rigid body transform ^VT_M. When the tool is positioned within anatomy as defined by the CT volume V, CT densities in the overlapping area must be omitted. However, this cannot be achieved by simply setting ρ(x) to zero at appropriate positions, since M_m, ρ_m can be of different resolutions than the CT volume ρ(x) and arbitrarily oriented relative to the CT coordinate system. Rather, we allocate a third volume M_O with densities ρ_O that is defined by

$$\begin{gathered} {\rho }_O(x)=\rho \left({}^{\text{V}}T{}_{\text{M}}x\right)\text{and }{M}_O(x) \\ =M\left({}^{\text{V}}T{}_{\text{M}}x\right)\forall \left(x\in {\rho }_M,{\rho }_M(x)>0\right). \end{gathered}$$ (1)

This will allow compensating for the excess contributions of the overlapping area in projection domain described as follows.

Primary computation via ray casting

Once material maps of the considered materials in CT {air, soft tissue, bone} and materials of tools, e.g., {Nitinol, steel}, are available, the contribution of each material to the total attenuation density at detector position u can be computed. We project in predetermined cone-beam geometry (pin-hole camera model) described by projection matrix $P\in {ℝ}^{3\times 4}$, that is defined by a rigid transformation ^XT_V that maps CT volume coordinates to the X-ray source coordinate frame followed by projection onto a detector described by intrinsic parameter matrix K:

$$P=K\left(1_{3}0\right){}^X{T}_V$$ (2)

Then, using the X-ray spectral density p₀(E), the total attenuation is obtained by ray-tracing as

$$\begin{gathered} p\left(u\right)=\int p\left(E,u\right)\text{d}E \\ =\int p_0\left(E\right)\text{exp}\left(-\sum _{m\in M}{\left(\frac{\mu }{\rho }\right)}_m\left(E\right)L\left(u,m,M,\rho \right)\right)\text{d}E \end{gathered}$$ (3)

$$=\int p_0\left(E\right)\text{exp}\left(-\sum _{m\in M}{\left(\frac{\mu }{\rho }\right)}_m\left(E\right)\int \delta \left(m,M\left(x\right)\right)\rho \left(x\right)\text{d}{l}_u\right)\text{d}E,$$ (4)

where δ (·, ·) is the Kronecker delta, l_u is the 3D ray connecting the source position and 3D location of detector pixel u determined by P, ${\left(\frac{\mu }{\rho }\right)}_m\left(E\right)$ is the material- and energy-dependent linear attenuation coefficient [11], and ρ(x) is the material density at position x that can either be derived from HU values or defined explicitly (e.g., for tools). For a single volume, Eq. 4 can be evaluated in a straightforward manner. For multiple volumes as considered here, however, it is beneficial to first compute the line integral L(u, m, M, ρ) of every volume and material first in order to merge the volumes of different sizes and resolutions in projection domain as discussed above. Then and using the total set of materials $\widehat{M}=\left\{M\cup M_M\right\}$ and line-integral images of every material $m\in \widehat{M}$, we compute the total contribution per material as

$$\begin{gathered} \tilde{L}\left(u,m\right)=\underset{\text{Adjustment}\text{for overlap}}{\underbrace{L\left(u,m,M,\rho \right)-L\left(u,m,M_0,{\rho }_0\right)}} \\ +\underset{\text{Tool}\text{contribution}}{\underbrace{L\left(u,m,M_M,{\rho }_M\right)}}. \end{gathered}$$ (5)

Then, Eq. 3 is evaluated using the overlap-adjusted line integrals

$$p\left(u\right)=\int p_0\left(E\right)\text{exp}\left(-{\sum _{m\in \widehat{M}}\left(\frac{\mu }{\rho }\right)}_m\left(E\right)\tilde{L}\left(u,m\right)\right)\text{d}E.$$ (6)

The projection domain image p(u) s then used as basis for scatter prediction.

Learning-based scatter estimation

Traditional scatter estimation relies on variance-reduced MC simulations [30], which requires a complete MC setup. In clinical applications, kernel-based methods are widely used due to their simplicity and have proven to work reasonably well since scatter is of low frequency. Recent approaches to scatter estimation via ConvNets outperform these methods [19] while retaining a low computational demand. In addition, they inherently integrate with deep learning software environments. Unfortunately, our task fundamentally differs from most previous scatter estimation scenarios: In clinical applications, we are interested in separating signal from scatter in an already acquired image. This is in contrast to our image synthesis pipeline that must only rely on clean, high-frequency data to estimate scatter. Considering the very low frequency nature of the scatter signal, kernel-based methods are well justified, as they basically perform low-pass filtering of the joint signal and thus result in a well-separated scatter signal. Solely relying on kernel-based methods in our case would impute that the scatter signal not only is of low frequency, but linearly depends on the frequency content of anatomy, as this corresponds to the information that is extracted via kernel-based low-pass filtering. The success of MC simulations from uncorrected 3D reconstructions [30] affirms that the above does not hold, rendering the direct utilization of kernel-based methods unsuitable in our application.

Nevertheless, the ten-layer ConvNet architecture as presented in [34] is heavily inspired by kernel-based methods but introduces modeling of a nonlinear relationship between the anatomy and scatter signal. The first six layers consist of 11 × 11 kernels arranged in multiple channels to extract basic image features, required for the generation of Rayleigh scatter estimates and the last four layers, with 31×31 kernels and a single channel, ensure smoothness. The network was trained on 330 images generated via MC simulation [2] from whole-body CT volumes, and then augmented by random rotations and reflections. As per [34], the trained scatter estimation network achieved a normalized mean squared error of 9.96%.

Noise injection

After adding scatter, p(u) expresses the energy deposited by a photon in detector pixel u. The number of photons is estimated as:

$$N\left(u\right)=\sum _E\frac{p\left(E,u\right)}{E}{N}_0,$$ (7)

to obtain the number of registered photons N(u) and perform realistic noise injection. In Eq. 7, N₀ (potentially location dependent N₀(u), e.g., due to bow-tie filters) is the emitted number of photons per pixel. Noise in X-ray images is a composite of multiple sources, mainly uncorrelated quantum noise due to photon statistics that becomes correlated due to pixel crosstalk, and correlated readout noise [41]. Due to beam hardening, the spectrum arriving at any detector pixel differs. This effect is most prominent at locations with highly attenuating objects in the beam path. To account for this fact in the Poisson noise model, we compute a mean photon energy for each pixel by $\overline{E}\left(u\right)$ and estimate quantum noise as $\frac{\overline{E}}{N_0}\left(p_{\text{Poisson}}\left(N\right)-N\right)$, where p_Poisson is the Poisson generating function. Since real flat panel detectors suffer from pixel crosstalk, we correlate the quantum noise of neighboring pixels by convolving the noise signal with a blurring kernel [41]. The second major noise component is electronic readout noise. While the magnitude of crosstalk-correlated quantum noise depends on the signal, i.e., the number of photons incident on the detector pixel, electronic noise is signal independent and can be modeled as additive Gaussian noise is correlated along the rows due to the sequential readout of current detectors [41]. After noise injection, we obtain a realistically simulated DRR that we refer to as DeepDRR.

Experimental setup, results, and discussion

Since the DeepDRR pipeline as such was previously evaluated in [34], here we focus on task-based evaluation of the proposed realistic simulation pipeline. To this end, we consider two applications in X-ray-guided surgery: Anatomical landmark detection and concurrent segmentation and localization of snake-like robots that will be described in greater detail in Sects. 3.1 and 3.2, respectively. For both applications, we train ConvNets on synthetic data and then investigate how well the learned models generalize to unseen clinical data without any re-training or domain adaptation. The synthetic data we train on will be generated (1) using DeepDRR the physics-driven approach described here, or (2) using the naïve approach to DRR generation:

$$p\left(u\right)=p_0\text{exp}\left(-\overline{\left(\frac{\mu }{\rho }\right)\left(E\right)}\sum _{m\in \widehat{M}}\tilde{L}\left(u,m\right)\right),$$ (8)

a special case of Eq. 6, where p₀ represents the total spectral density and $\overline{\left(\frac{\mu }{\rho }\right)\left(E\right)}$ is the mean linear attenuation coefficient averaged over all materials and energies. In other words, naïve DRR generation considers a mono-energetic source, objects made from a single material, and neglects image corruption, e.g., due to noise. In addition to these extremal cases, we perform an ablation study for the application of anatomical landmark detection to determine the contributions of ConvNet-based material decomposition and scatter estimation, respectively. For DeepDRR simulation, we used the spectrum of a tungsten anode operated at 120 kV with 4.3 mm aluminum filtration and assumed a high-dose acquisition with N₀ = 5 · 10⁵ photons per pixel. While our simulation yields intensity domain images, all ConvNets are trained on line-integral domain data, i.e., after logarithmic transform, to decrease the dynamic range. For images acquired with a real C-arm X-ray system, N₀ is not known, and therefore, approximated by the highest intensity value in that image. All real X-ray images of cadaveric specimens used in the experiments were acquired in the International Center of Orthopedic Advancement at Johns Hopkins Bayview Medical Center using a Siemens Cios Fusion C-arm X-ray system (Siemens Healthineers, Forchheim, Germany) equipped with a flat panel detector.

Anatomical landmark detection

Experimental setup

This experiment focuses on detecting anatomical landmarks of the pelvis in radiographs from arbitrary views [6]. In 20 CT scans of the pelvis (split 18-1-1 into training, validation, and testing), we annotate 23 anatomical landmarks (Fig. 2, last column contains all landmarks) and generate naïve and DeepDRRs with corresponding annotations on a spherical segment centered on the anterior–posterior pelvis covering 120° and 90° in RAO/LAO and CRAN/CAUD, respectively. A total of 20,000 DRRs were generated per method, i.e., 1000 per CT volume. Then, a sequential prediction framework [6,36] is trained and, upon convergence, used to predict the 23 anatomical landmarks in the respective testing set and in unseen, real X-ray images of cadaveric lower torso specimens. We trained the network using Adam over 30 epochs with a learning rate of 10⁻⁶. We then evaluate the ConvNet on the respective synthetic test set, where exact landmark locations are known, and on 78 real X-ray images of two cadaveric lower torso specimens. To establish reference anatomical landmark positions in real radiographs, we rely on metal beads (BBs) injected into the pelvis prior to CT and radiographic imaging. The BBs were annotated and matched semi-automatically, so that correspondences between BB locations in 3D CT and all X-rays were known. Using this information and for every X-ray image i, we recover projection matrices P_i that map 3D CT points onto the detector. Finally, we manually annotate the 23 target landmarks in the CT scans of both cadaveric specimens and project them via P_i to establish our X-ray image-domain reference for quantitative evaluation on real data. For synthetic data generation, we consider the following ablations:

Fig. 2.

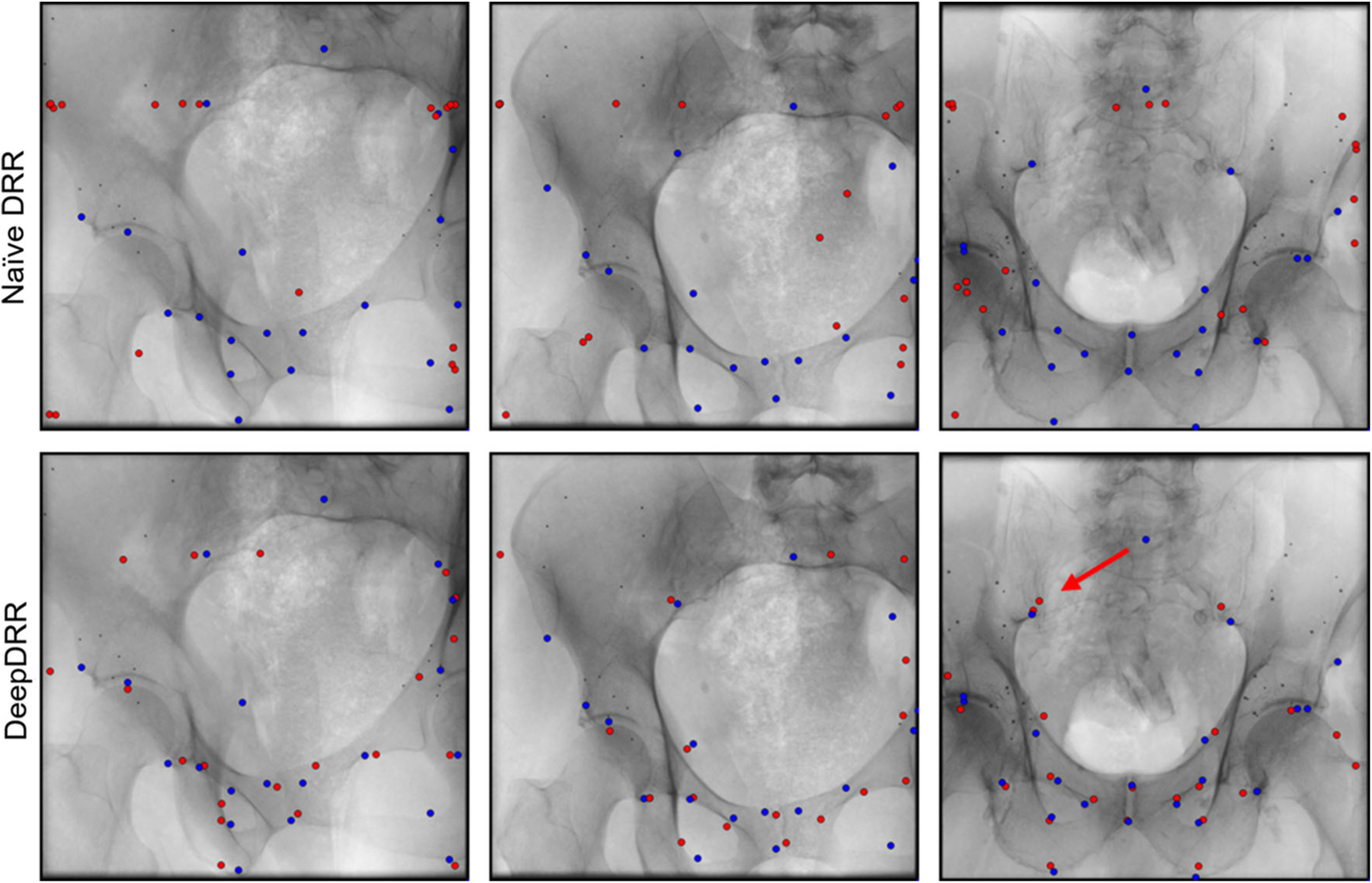
Anatomical landmark predictions on real X-ray images of cadaveric specimen. Reference landmark positions are shown in blue, while ConvNet predictions are shown in red. We highlight a representative outlier using a red arrow that connects a target landmark with the corresponding prediction

• Ablation 1 DRRs generated as per Eq. 8: Mono-energetic, single material, no noise, no scatter.

• Ablation 2 DRRs generated as per Eq. 6: Poly-chromatic, multi-material, noise injection, no scatter. Material decomposition via thresholding (air < −700 HU, soft tissue ∈ [−700, 250]HU, bone > 250 HU [26])

• Ablation 3 DRRs generated as per Eq. 6: Poly-chromatic, multi-material, noise injection, no scatter. Material decomposition via ConvNet (Sect. 2.1)

• Ablation 4 DRRs generated as per Eq. 6: Poly-chromatic, multi-material, noise injection, scatter. Material decomposition and scatter estimation via ConvNets (Sect. 2.1)

Results and discussion

The quantitative results of the ablation study are summarized in Table 1. In every ablation, ConvNets perform similarly well when applied to the respective synthetic test sets. However, when applied to real data we observe substantial improvements in landmark detection accuracy as the DRR simulation pipeline more accurately models X-ray image formation. From Table 1, it becomes apparent that the improvement is most notable when transitioning from Ablation 1 to Ablation 2, i.e., when considering the material dependence and energy dependence of photon attenuation. This is likely due to the fact that Ablation 2 introduces beam hardening, which increases bone to soft tissue contrast, substantially altering image appearance. Accuracy is further improved slightly as threshold-based material decomposition is replaced by the proposed ConvNet-based decomposition (Ablation 3). This improvement can partially be attributed to the capability of the ConvNet to use structural information to disambiguate soft tissue in the [−150, 300] HU interval and trabecular bone > 200 HU, thus yielding more realistic X-ray image appearance. However, we noticed that the poor performance in Ablation 2 is affected by catastrophic failure cases in 8 of the 78 real X-ray images. Omitting these from analysis would reduce this error to 27.3±27.0 mm. However, while the addition of scatter (Ablation 4, the full DeepDRR pipeline) further improves detection accuracy, this improvement is not significant. This observation is further discussed in Sect. 3.3. Our analysis suggests that, while learning-based material decomposition and scatter estimation can further improve detection accuracy, the significant boost in performance (p < 0.01) is to be attributed to poly-energetic and multi-material-based modeling of image formation, and is less sensitive to the method used for material decomposition. In light of the results of our ablation study, we limit all subsequent analysis to the two extreme cases Ablation 1 and Ablation 4, i.e., naïe DRRs and DeepDRRs, respectively. A qualitative analysis of landmark predictions versus true reference locations is presented in Fig. 2. For landmark prediction on real data, we observe both, compromised performance and a very high standard deviation that is partly due to outliers. Considering this decrease in performance, it is unclear whether directly interpreting the detected landmarks is clinically practical. However, the amount of outliers can, in principle, be reduced substantially by only considering landmarks that are detected with a certain belief [5,6], yielding landmark detection accuracy that is appropriate for initializing 2D/3D registration. While this approach proved feasible for the DeepDRR-based ConvNet, using a threshold above 20% would reduce the accepted detections in the naïve DRR-based ConvNet close to zero, impeding meaningful validation. It is worth mentioning that reference targets used for quantitative assessment are likely imperfect since (1) anatomical landmarks in 3D CT are defined manually, and (2) P_i are estimated from data. While this observation challenges the overall magnitude of error reported on real data, comparisons remain valid since both methods are affected in the same way.

Table 1.

Ablation results of anatomical landmark detection on synthetic and real data

	Ablation 1		Ablation 2
	Synthetic	Real	Synthetic	Real
Mean L2	6.70 ± 4.32	78.2 ± 26.5	6.09 ± 4.19	34.4 ± 41.9
	Ablation 3		Ablation 4
	Synthetic	Real	Synthetic	Real
Mean L2	6.60 ± 5.44	26.9 ± 15.1	6.35 ± 5.02	24.7 ± 21.3

All results are stated in mm on the detector. Ablation 4 corresponds to the full DeepDRR pipeline

Robotic end-effector localization

Experimental setup

This experiment builds upon our previous work on detecting continuous dexterous manipulators in radiographs [10]. An encoder–decoder-like architecture with skip connections is trained to concurrently segment and localize a snake-like robot end-effector in X-ray images. Localization in this context refers to predicting the location of two keypoints on the end-effector, namely the start and end point of its centerline. In the decoding stage, the final feature layer is shared across the segmentation and localization branch, and the final segmentation mask is backward concatenated to this shared feature to boost keypoint detection. The robot end-effector consists of body and base made from Nitinol, and a shaft and inserted drilling tool made from stainless steel. In our simulation, the shape of the snake-like body is controlled by adjusting the control points of a cubic spline that describes the snake’s centerline. Once a body shape is defined, the tool model is voxelized with high resolution to preserve details. We use a total of 5 CT volumes (4 training, 1 test) and, for each of the 10 femurs, manually define ^VT_M such that the robot is enclosed in bone. Then, fluoroscopic images are generated by randomly sampling the snake shape by adjusting the control point angles ∈ [−7.9°, 7.9°], and the C-arm pose relative to scene by adjusting the source-to-isocenter distance ∈ [400 mm, 500 mm], the source rotation (LAO/RAO ∈ [0°, 360°] and CRAN/CAUD ∈ [75°, 105°]), and translation along all three axes ∈ [−20, 20]mm. For every femur, 1000 configurations were sampled randomly and for each configuration a DeepDRR, a naïve DRR, and the corresponding segmentation mask and keypoint locations were generated. The ConvNet was then trained using Dice loss for the segmentation task and the standard L₂ loss for the localization task. Learning rate started at 10⁻³ and decayed by 10⁻¹ every 10 epochs. For quantitative evaluation on real data, we manually annotated 87 X-ray images of a dexterous robot [22] drilling in femoral bone specimens.

Results and discussion

The results are summarized in Table 2. ConvNets trained on naïve and DeepDRRs performed similarly well on their respective synthetic testing data. However, when considering cadaveric data from a real C-arm system, the ConvNet trained on DeepDRRs substantially outperformed the network trained on naïve DRRs in the segmentation task (p < 0.01) and, particularly, in the keypoint detection task (p ≪ 0.01). Representative results on synthetic and real data are shown in Figs. 3 and 4, respectively. While the naïve DRR ConvNet performed comparably on some real images (cf. Fig. 4, bottom row), it was prone to over-segmentation reducing the overall Dice score (cf. Fig. 4, middle row). In addition, we observed that, when applied to real data, the network would often detect the same landmark twice giving rise to the large L₂ error for this task (cf. Fig. 4, top row). The cadaveric dataset contains scenarios not observed during training, e.g., the end-effector being fully in air before insertion into femoral bone, causing deteriorated performance which is reflected in the high standard deviation for both, ConvNets trained on naïve and DeepDRRs.

Table 2.

Segmentation and localization accuracy in %-dice and in mm, respectively

	Naïve DRR		DeepDRR
	Synthetic	Real	Synthetic	Real
Segmentation
Mean dice	99.3 ± 0.3	88.7 ± 7.7	99.6 ± 0.1	91.5 ± 6.3
Median dice	99.3	91.7	99.6	93.8
Localization
Mean L2	0.43 ± 0.36	26 ± 19	0.37 ± 0.35	2.5 ± 1.0
Median L2	0.37	32	0.31	2.8

Fig. 3.

Representative results of concurrent segmentation and keypoint detection [10] on synthetic X-ray images generated by the same method the ConvNets were trained on. Segmentations are shown in green, keypoints as red heatmaps, and magnifications of the region of interest are shown in the top right corner of each image, delimited by an orange border

Fig. 4.

Representative results of concurrent segmentation and keypoint detection [10] on real X-ray images of cadaveric anatomy of ConvNets trained on naïe DRRs and DeepDRRs, respectively. We also show the input X-ray image after logarithm transform and reference annotations is obtained manually. Segmentation results are shown as green overlay, while keypoint predictions are shown as red heatmaps. Magnifications of a region of interest around the snake end-effector are provided in the top right corner of every image, marked-off by an orange border

Challenges and limitations

While DeepDRR-based ConvNets significantly outperformed their counterpart trained on naïve DRRs in all studied cases, we observed compromised performance on real data compared to the synthetic testing data. This degradation results from multiple factors: (1) The reference annotations for evaluation on real data are obtained using semi-automatic techniques, suggesting that the targets used for quantitative assessment may not be the true targets. While this shortcoming slightly compromises synthetic–real comparisons, they do not affect comparisons of real data performance between naïve- and DeepDRR-based ConvNets since for such comparison the above error is systematic. (2) The images provided by the clinical C-arm X-ray system are not, in fact, raw images but are pre-processed by a vendor-specific, proprietary filtering pipeline (including but not limited to noise reduction and scatter correction) that can substantially alter image characteristics. As a consequence, the DeepDRR framework cannot accurately mimic image formation since part of the process is unknown. (3) DRRs are generated from 3D CT volumes that exhibit finite resolution. This shortcoming is emphasized during DRR generation due to magnification in cone-beam geometry and detectors with very high spatial resolution down to $<0.2\frac{\text{mm}}{\text{px}}$. An interesting next step would be to investigate whether super-resolution strategies, as they have become popular in MRI [7], could mitigate this problem. It is worth mentioning that the proposed DeepDRR pipeline could be formulated as an end-to-end neural network, since forward projection can be easily incorporated as a layer [37]. This is appealing, since it would allow incorporation of all ConvNet-based processing, e.g., for 3D segmentation and super-resolution, or 2D pre-processing, and enable end-to-end training of these networks by maximizing the resulting DRRs’ similarity with real X-ray images of the target application via adversarial training.

It is interesting to see that the degradation observed here occurs to a similar extent in the most similar work to ours that uses unpaired image-to-image style transfer to convert real X-ray images to a DRR-like counterpart [42]. On the example of anatomical landmark detection, where we now have a solid basis for evaluation, we plan on investigating how the approaches compare and whether combining both strategies can yield real data performance that is on a par with the performance on synthetic data. Doing so will require us to collect a sufficiently large database of clinical pelvic X-ray images, ideally acquired without tools in the image. While these images would not need to be annotated for style transfer, the dataset must still be representative with respect to anatomy and views thereof for style transfer to succeed. Since intra-operative X-rays are not commonly archived in pelvis surgery, curating this database requires a prospective study design which we will implement in future work.

Currently, simulation using DeepDRR is limited to flat panel detectors. Supporting image intensifiers is possible but would require adjustment of noise model and incorporation of distortions that occur in this detector technology.

In contrast to MC simulation where the rendering time is dependent on the number of photons injected, simulation using DeepDRR requires the same computation time irrespective of the required imaging parameters. It is worth mentioning, however, that material decomposition using the 3D ConvNet is comparably slow and is performed before every rendering. For practical application of the DeepDRR pipeline, this suggests that a large set of projections should be defined first and then submitted for rendering to reduce the per-image computation time. As an example, for 1000 images with 620 × 480 px, the simulation per image took 0.56s on an Nvidia Quadro P6000.

Conclusion

We proposed a fast and realistic framework for simulating intra-operative X-ray images with corresponding annotations from 3D CT volumes. The framework supports modeling of tools or surgical implants and is publicly available and open source. We evaluated our framework on two complementary tasks in X-ray-guided interventions, namely detecting anatomical landmark on the pelvis and segmenting and localizing robotic end-effectors during drilling in the femur. ConvNets trained on DeepDRRs, generated with our physics-based framework, significantly outperformed networks trained on naïve DRRs on real X-ray images, suggesting that realistic generation of X-ray image formation is a practicable way to establishing machine learning in fluoroscopic image analysis. While our results are promising, in future work we will investigate strategies to further improve the real data performance of ConvNets trained on synthetic data, e.g., via image style transfer for domain adaptation. Once introduced into clinical practice, learning-based algorithms that analyze intra-operative images to automatically extract semantic or contextual information, e.g., by measuring objects of interest, have the potential to radically improve the state-of-care by simplifying surgical workflows.