Disentangling the complexity of low complexity proteins

Abstract

There are multiple definitions for low complexity regions (LCRs) in protein sequences, with all of them broadly considering LCRs as regions with fewer amino acid types compared to an average composition. Following this view, LCRs can also be defined as regions showing composition bias. In this critical review, we focus on the definition of sequence complexity of LCRs and their connection with structure. We present statistics and methodological approaches that measure low complexity (LC) and related sequence properties. Composition bias is often associated with LC and disorder, but repeats, while compositionally biased, might also induce ordered structures. We illustrate this dichotomy, and more generally the overlaps between different properties related to LCRs, using examples. We argue that statistical measures alone cannot capture all structural aspects of LCRs and recommend the combined usage of a variety of predictive tools and measurements. While the methodologies available to study LCRs are already very advanced, we foresee that a more comprehensive annotation of sequences in the databases will enable the improvement of predictions and a better understanding of the evolution and the connection between structure and function of LCRs. This will require the use of standards for the generation and exchange of data describing all aspects of LCRs.

Short abstract

There are multiple definitions for low complexity regions (LCRs) in protein sequences. In this critical review, we focus on the definition of sequence complexity of LCRs and their connection with structure. We present statistics and methodological approaches that measure low complexity (LC) and related sequence properties. Composition bias is often associated with LC and disorder, but repeats, while compositionally biased, might also induce ordered structures. We illustrate this dichotomy, plus overlaps between different properties related to LCRs, using examples.

Introduction

The traditional notion that protein sequences fold into a structure that dictates their function, while generally correct, is being increasingly challenged by the discovery of many proteins with complex biological roles despite a lack of permanent secondary or tertiary structure [1, 2]. Many of these proteins contain low complexity regions (LCRs), where the frequency distribution of amino acids deviates from the common amino acid usage. Residues in LCRs have been estimated to represent 20% and 8% of all known sequences of eukaryotes and non-eukaryotes, respectively [3]. The functional importance of LCRs and their involvement in disease has also been extensively discussed—e.g. [4–7]. Overcoming early reluctance to consider these regions for biological studies, mainly due to their unknown properties and ‘annoying’ statistical features, there is an intensification of research on LCRs—e.g. [8–10], reminiscent of the paradigm shift that brought non-coding RNAs to the forefront of genomics research in the recent past.

In the definition of LCRs, multiple concepts related to sequence composition, periodicity and structure have been used (Table 1). Regarding amino acid composition, while there is a general notion that LCRs in proteins should have an excess of one or a few types of amino acid residues, there is no consensus about which metrics are the most appropriate. Additionally, the concept of LCR is intermingled with the concept of sequence repeats. Repeats are inevitably associated with LCRs, since shorter repeats result in regions with lower amino acid diversity. An extreme case of minimal complexity is represented by tracts of a single repeated residue, known as homorepeats.

Table 1.

Overview of complexity terms and their definitions

Term	Definition	References
Definition based on amino acid composition
LCR	Regions with a skewed amino acid composition	[27, 79–85]
Compositionally biased region		[27, 79–81, 86–88]
X-rich region	Region with a high proportion of a specific amino acid, where X is the abundant residue	—
Definition based on amino acid periodicity
Repeat motif	Reiteration of residues: (...)n	—
Homorepeat (polyX)	Consecutive runs of a single residue: (X)n	[39]
Direpeat	Consecutive runs of two ordered different residues: (XY)n	—
Tandem repeat	Pattern of residues which are directly adjacent to each other: (XYZ…)n	[14]
Cryptic repeat	Scrambled arrangements of repetitive motifs	[28]
Imperfect repeat	Regions in which the repeat units are not the same	[89]
Definition based on structure
Intrinsically disordered protein	Protein that lacks a fixed or ordered 3D-structure	[90]
Coiled coil	Structural motif characterized by a seven-residue sequence repeat in which alpha-helices are coiled together to form an extended rope-like structure: (a-b-c-d-e-f-g)n	[91, 92]
(Charged) single alpha-helix	A segment forming stable monomeric alpha-helix in aqueous solution, typically rich in Arg/Lys/Glu forming an alternating pattern of short runs of oppositely charged residues	[93]
Protein flexibility	Ability of a protein to fold into multiple stable 3D-structures	[94]
Amyloid fibrils	Stable insoluble protein assemblies composed predominantly of β-sheet structures in a cross-β conformation	[95]

Regarding protein structure, LCRs mostly have a disordered conformation. Factors such as the sequence context (features present in the flanking regions) and the molecular context of the protein (e.g. interacting proteins, cell tissue or state when it is expressed) can influence their structural state. This landscape is complemented by emerging concepts such as intrinsic disorder and protein phase separation, formalized in the literature (see e.g. [11–13]).

The many shades of complexity

To illustrate the overlap between the three levels described above (i.e. amino acid composition, periodicity and structure), we use a 2D diagram where we can compare proteins (or regions) of various degrees of complexity from intermediate to unbiased (‘normal’) sequences according to their compositional bias and repetitiveness (Figure 1). This diagram applies ideally to sequence regions with lengths in the range of 10 to 50 residues, for the sake of simplicity (considering that long structural repeats have a length of about 50 residues [14] and fragments of less than 10 residues would suffer from low-count statistical effects). Suppose that we compute for such region two simplified measurements of complexity: one reflecting variability of amino acid usage (compositional bias) and the other indicating periodicity. For example, AEEAEAAEEA and a perfect direpeat like AEAEAEAEAE have the same amino acid composition (50% A and 50% E) but different periodicities.

Figure 1.

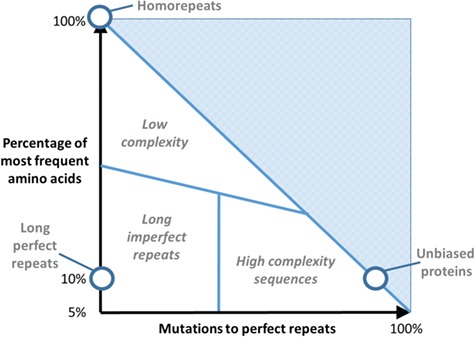
The LC diagram: sequence complexity composition versus periodicity. The diagram illustrates where several types of sequences would be placed in relation to two measures related to sequence complexity.

As a simplified measurement of amino acid variation, we can take the percentage of the most frequent amino acid in the region (see [15] for another measure of repeat perfection). For example, given the 10-amino acid sequence ACDEFEGEIE, the most abundant amino acid is E, at 40%. To measure repetitiveness, we could calculate how distant this sequence is from a sequence with perfect repeats. A simple measure for that distance is how many residues we need to mutate to convert the query sequence to a perfect repeat. The simplest instance of a repeat is the homorepeat; any sequence with n% for the most frequent amino acid can be converted to a homorepeat by changing the other residues to the most frequent residue, i.e. 100% − n%. For our example sequence, ACDEFEGEFE, we would have to change 6 residues to E, 60%, to have 10 E residues. This sets the upper limit to this value. But if a less trivial repeat can be found using fewer mutations, this second value will be necessarily lower. In this case, we can change ACDEFEGEFE to FEFEFEFEFE with only 40% of changes.

Using these metrics, we can conceptually position in the diagram (Figure 1) the examples of regions of variable degrees of complexity (y-axis) and repetition (x-axis). All perfect repeats are placed at x = 0, and homorepeats have y = 100%. Direpeats have y = 50%, AABAAB repeats have y = 66%, ABCABC repeats have y = 33% and so forth.

Proteins without repeats are placed in the trivial diagonal, with a y value for the most frequent amino acid and x = 100% − y. A protein composition with all 20 amino acids equally abundant sets 5% as the lower limit for y. Rather, most proteins will have unbiased compositions where the most abundant amino acid forms around 10% of the sequence (e.g. aspartate 10.7% or glutamate 9.9% in [16]).

Then, unbiased proteins, far from repeats and with the expected amino acid variation, will populate the bottom-right corner of the diagram. We can imagine intermediate situations, which can be constructed by adding mutations from regions with perfect repeats. In this manuscript, we will discuss the hypothesis that there is a border between LCRs influenced by periodicity (i.e. repetitiveness), so that given two LCRs with the same amino acid composition, the one with more repetitiveness might be prone to form a structure, whereas the other one would have a stronger tendency to be disordered. This would give a slant to the low complexity (LC) border (line separating the `Low complexity’ area, Figure 1). Not all repeats are LCRs, but LCRs tend to be close to short repeat sequences, since groups of short repeats have necessarily a limited number of amino acids, and thus can be considered a LC unit. In other words, LC can only be compositionally biased, while compositional bias can be of low or high complexity.

In order to explore how the different measurements of complexity and repetition relate to this graphical representation in reality, we will take a few proteins with LCRs, repeats of various types and a range of structures, measure their complexity using available methods and locate these regions in the model graph. Note that parts of these proteins will have an expected composition, which will populate the point of unbiased proteins, where most globular proteins reside. This will constitute a contrast to which we can compare their LCRs.

Detection of low complexity sequences

We collected a set of 21 protein sequences to illustrate the phenomena involved in LCRs (Table 2). This dataset is a collection of examples of what is commonly defined as a compositionally biased protein. It includes enzymes (serine tRNA ligase, P34945—UniProt accession number), transcription factors (transcriptional repressor CTCF, P49711), membrane channels (outer membrane protein TolC, P02930), transporters (autotransporter adhesin SadA, Q8ZL64), structural proteins (collagen alpha-1 chain, P02452), proteins that respond to changes of physical states (glycine-rich antifreeze protein, Q38PT6), typical disordered proteins (cellular tumor antigen p53, P04637) and proteins related to diseases (huntingtin, P42858). With this selection, we aim at relating the concept of compositional bias in proteins to a variety of cellular processes, compartments and structural states. We note that associating function to LCRs is not our goal here; rather, the functional variety in the set of proteins chosen to highlight the diversity of biological situations where LC plays a relevant role.

Table 2.

Illustrative set of proteins with LCRs, ordered by the length of the protein

AC	ID	Description	Length (aa)	Organism
Q38PT6	Q38PT6_9HEXA	6.5 kDa glycine-rich antifreeze protein	103	Hypogastrura harveyi
P35226	BMI1_HUMAN	Polycomb complex protein BMI-1	326	Homo sapiens
P20226	TBP_HUMAN	TATA-box-binding protein	339	H. sapiens
P04637	P53_HUMAN	Cellular tumor antigen p53	393	H. sapiens
P32583	SRP40_YEAST	Suppressor protein SRP40	406	Saccharomyces cerevisiae
P34945	SYS_THET2	Serine-tRNA ligase	421	Thermus thermophilus
P0C2W0	YADA2_YEREN	Adhesin YadA	422	Yersinia enterocolitica
P02930	TOLC_ECOLI	Outer membrane protein TolC	493	Escherichia coli (s. K12)
P35637	FUS_HUMAN	RNA-binding protein	526	H. sapiens
P49711	CTCF_HUMAN	Transcriptional repressor CTCF	727	H. sapiens
P15502	ELN_HUMAN	Elastin	786	H. sapiens
P42566	EPS15_HUMAN	Epidermal growth factor receptor substrate 15	896	H. sapiens
Q9BVN2	RUSC1_HUMAN	RUN and SH3 domain-containing protein 1	902	H. sapiens
P10275	ANDR_HUMAN	Androgen receptor	920	H. sapiens
Q8WVM7	STAG1_HUMAN	Cohesin subunit SA-1	1258	H. sapiens
Q9NZW4	DSPP_HUMAN	DSPP	1301	H. sapiens
Q8ZL64	SADA_SALTY	Autotransporter adhesin SadA	1461	Salmonella typhimurium
P02452	CO1A1_HUMAN	Collagen alpha-1(I) chain	1464	H. sapiens
A3M3H0	ATA_ACIBT	Adhesin Ata autotransporter	1873	Acinetobacter baumannii
P24928	RPB1_HUMAN	DNA-directed RNA polymerase II subunit RPB1	1970	H. sapiens
P42858	HD_HUMAN	Huntingtin	3142	H. sapiens

In the following sections, a series of methods that are widely used to detect LC in protein sequences are introduced and applied to the dataset of the selected 21 proteins. The methods are presented in chronological order, to facilitate the understanding of the historical context within which each method was developed. In each section, we discuss the features and possible functions of detected LCRs, to illustrate the current knowledge on those regions and directions to obtain further insights about them. Related structural aspects and methods that take them into account are discussed after this part.

We provide a list of 100 proteins from the human genome annotated as per their amino acid type bias for further studies (Suppl. File S1). This collection of proteins with compositionally biased regions (CBRs) should remain stable for the foreseeable future and can form the basis for additional research toward the deeper understanding of the structure and function of LC proteins.

SEG (1993): detection of LCRs

SEG was the first algorithm developed to specifically detect LCRs within protein sequences [17], as masking of LCRs has been found to improve the detection of homology (e.g. [18]). This method is based on the concept of local complexity of a subsequence defined for a window of length L. Such subsequences can be represented in the form of a state complexity vector, where each position represents the number of amino acid occurrences in that window. For any state complexity vector, its compositional complexity and probability of occurrence of the particular complexity state can be computed. Based on these values any subsequence can be classified as a low or high complexity subsequence. Here we applied SEG to the collected set of proteins (Table 2) to characterize their LCRs and putative function based on their sequence homology with other non-related proteins. As proposed in [19], we used the SEG algorithm with intermediary parameters (these are window length W = 15, trigger complexity k₁ = 1.9 and extension complexity k₂ = 2.5).

We found that 12 proteins from the dataset contain a total of 46 LCRs, with the longest having 760 residues (dentin sialophosphoprotein, DSPP) (Suppl. Table S1). Moreover, both elastin and Collagen alpha-1(I) chain have 11 LCRs each. On average, the 12 LCR-containing proteins have 3.8 LCRs with an average length of 67 residues.

Similarity between LCRs in different proteins can be used to propose hypotheses about the function of the similar proteins. However, many caveats apply, i.e. in the case of LC sequences, matching hits do not guarantee evolutionary relationship even with statistically significant scores. We illustrate this with one of our example proteins: DSPP, which contains the longest LCR of all the examples. We used the NCBI BLAST search engine with default options to find other proteins with similar LCRs.

DSPP (UniProt:Q9NZW4) is cleaved into two chains: dentin phosphophoryn (DPP; amino acids 16-462) and dentin sialoprotein (DSP; amino acids 463-1301). A very long LCR was detected in DSP covering most of the sequence (amino acids 511-1270). DSP is an extracellular matrix protein synthesized by odontoblasts. It is highly acidic, and the phosphorylated protein possesses a strong affinity for calcium ions. Therefore, DSP in the extracellular matrix can promote hydroxyapatite nucleation and can regulate the size of the growing crystal [20–22]. Apart from its calcium binding property, DSP can initiate signaling functions from the extracellular matrix [23–26]. We found a high degree of similarity of the DSP fragment of DSPP to two hypothetical proteins, BCR41DRAFT_427036 (NCBI Reference Sequence AC: XP_021875136.1) from Lobosporangium transversale (a fungus) and JF76_17750 (GenBank AC: KJY54264) from Lactobacillus kullabergensis (a bacterium). Both are highly acidic sequences, rich in serine and aspartic acid. The bacterial protein possesses three MucBP domains, which are characteristic for peptidoglycan binding proteins; the presence of these domains suggests a function outside of the cell, probably in adhesion.

CAST (2000): detection of CBRs

A next logical step following the detection of LCRs with SEG is to focus on CBRs. While the usage of the terms LCR and CBR has been interchangeable in many contexts (Table 1), as they overlap significantly, the use of one term or the other depends on the focus of the method used for their detection, i.e. sequence variability or amino acid composition, respectively. Indeed, the terms LCR and CBR are somehow imprinted by the fields of computer science and biology, respectively.

CAST was developed based on the idea that CBRs are enriched in at least one amino acid type [27]. In brief, CAST detects (and scores) CBRs using comparisons of a query sequence against a database of 20 degenerate homopolymeric sequences based on each of the 20 amino acid types. Overlapping CBRs of different type (residue) may be detected in the same sequence tract.

Here we applied the CAST algorithm to our dataset with default parameters (BLOSUM62 substitution matrix and a detection threshold value of 40). All 21 proteins from the dataset were detected to contain at least one CBR, with 54 CBRs in total (mean, 2.6; median, 2; SD, 1.5 CBRs/sequence; Table 3 and Suppl. Table S1). The number of CBRs per protein vary between 1 (n = 7 proteins) and 5 (n = 3 proteins). CBRs vary considerably in length, with the shortest one being just 10 residues long (a P-rich region in the androgen receptor) and the longest being an S-rich region extending over 1436 residues covering almost the entirety of the autotransporter adhesin SadA. It is worth mentioning that in our dataset CAST did not detect half of the possible CBR types, namely CBRs enriched in R, C, H, I, L, M, F, W, Y and V residues. Some of these CBR types are indeed rare in the overall sequence database (Table 3).

Table 3.

CBRs detected by CAST. A single protein sequence may contain one or more CBRs of the same or even different residue types. The last two columns refer to UniProt/Swiss-Prot entries (release 2014_05) as retrieved from LCR-eXXXplorer

CBR type	No. CBRs	No. CBRP	CBRPs, %	No. CBRPs in UniProt	CBRPs in UniProt, %
A	4	4	19.0	19465	19.5
D	1	1	4.8	5293	5.3
E	8	7	33.3	25438	25.5
G	7	5	23.8	8771	8.8
K	2	1	4.8	14936	15.0
N	2	2	9.5	5428	5.4
P	9	8	38.1	12000	12.0
Q	5	5	23.8	9149	9.2
S	14	13	61.9	25081	25.1
T	2	2	9.5	4216	4.2
R	0	0	0	3768	3.8
C	0	0	0	1083	1.1
H	0	0	0	2584	2.6
I	0	0	0	2178	2.2
L	0	0	0	2422	2.4
M	0	0	0	766	0.8
F	0	0	0	756	0.8
W	0	0	0	274	0.3
Y	0	0	0	562	0.6
V	0	0	0	1487	1.5

CBRP, CBR protein.

Our analysis stresses the fact that composition bias is related to LC (as discussed in the complexity diagram) but is more widely spread and commonly found in many proteins. Along these lines, of the 54 CBRs detected in this dataset using CAST, only 12 instances correspond to sequences with high sequence complexity values (k₂ > 2.5), illustrating that the majority of CBRs in this dataset are also LCRs. Interestingly, these 12 CBRs with high complexity values correspond to relatively long regions (often spanning along hundreds of residues) and, nevertheless, dominated by serine-rich tracts (9 out of 12).

Importantly, CAST offers the possibility to explore another dimension of LCRs, which is the residue type characterizing each region. In addition, when plotting the CAST score normalized by the sequence length for each detected CBR against the Shannon entropy (Figure 2), we observe a correlation sorted in a triangle with many points crowding the bottom-right corner (high entropy and low normalized CAST score), which is reminiscent of the LC diagram (Figure 1).

Figure 2.

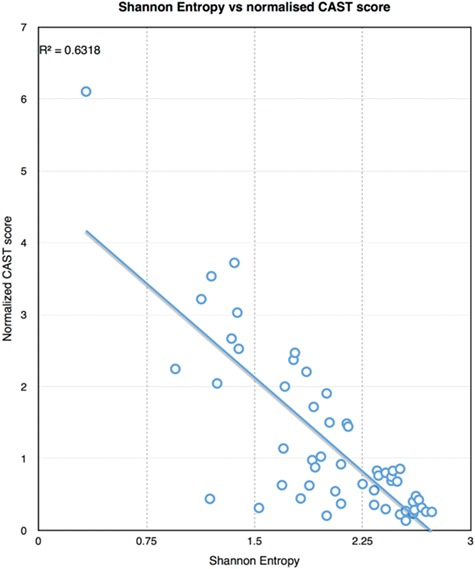
Shannon entropy value for each detected CBR against the CAST score normalized by the sequence length.

SIMPLE (2002): detection of tandem and cryptic repeats

The tool SIMPLE was first developed in 1986 to quantify the amount of simple sequences in DNA [28]. A version for proteins was developed in 2002 [29]. The original aim of SIMPLE was to identify genomic sequences with a propensity to undergo replication slippage and to quantify the concept of cryptic simplicity, which corresponds to one or more short sequence motifs within a sequence region, above a baseline, random concentration. The 2002 implementation extends this original concept to detect comparably cryptic sequences at the amino acid sequence level.

To provide a rich overview of the repeat landscape of the 21 proteins in our dataset, we analyzed them using an updated version of the SIMPLE tool [30]. Significant repeat motifs of length 1 to 10 were identified at a per-analysis probability cutoff of 0.99 (aggregate cutoff probability 0.9) by awarding a score of 1 for the selected length and 0 for all other lengths. Analyses were carried out using an 11-residue moving window. Sixteen of the sequences analyzed using the SIMPLE method contained significant repeat motifs to some degree (Table 4 and Suppl. Table S1).

Table 4.

Numbers and major classes of repeats identified by SIMPLE analysis

ID	No. repeats identified	Characteristic repeat(s) (frequency)
Q38PT6_9HEXA	23	G (19)
TBP_HUMAN	336	Q (41)
P53_HUMAN	11	AP (6)
SRP40_YEAST	794	S (168)
FUS_HUMAN	175	G (60)
CTCF_HUMAN	1	EP (1)
ELN_HUMAN	350	A (30), GV (28)
EPS15_HUMAN	11	DPF (6)
RUSC1_HUMAN	6	PP (3)
ANDR_HUMAN	351	Q (25), G (23)
DSPP_HUMAN	3082	S (459)
SADA_SALTY	3	NTT (2)
CO1A1_HUMAN	113	GP (17)
ATA_ACIBT	21	NTK, TKTEL (3)
RPB1_HUMAN	948	SP (96)
HD_HUMAN	211	P (27)

SIMPLE analysis provides two types of motif information: motif identity and motif hit frequency information—defined as the frequency with which a given motif is detected as being significantly repeated within a given sequence. As examples, three of the proteins in the test set (huntingtin, TATA-binding protein and androgen receptor) contained significantly repeated motifs of all possible Qn motifs (from n = 1 to n = 10), characteristic of a simple polyQ repeat. However, the most prominently repetitive protein in the set was dentin, which, as described before, contained numerous highly repeated motifs with serine as the primary repeated amino acid.

Examining the list of motifs detected in the most repetitive proteins in the dataset reveals many similar or closely related motifs. To portray these relationships, the motifs can be represented graphically. As an example, Figure 3 shows a motif graph for Collagen alpha-1(I) chain. The representation links different motifs identified in the sequence with their sequence overlap. The example in Figure 3 shows a closely knit set of motifs linked to the submotifs PGP and GPP alongside others linked to PGA. Some motifs in this example (and in other sets) are less connected than others—the extreme example in P02452 being PAG, which, although related to others by circular permutation, does not overlap with them.

Figure 3.

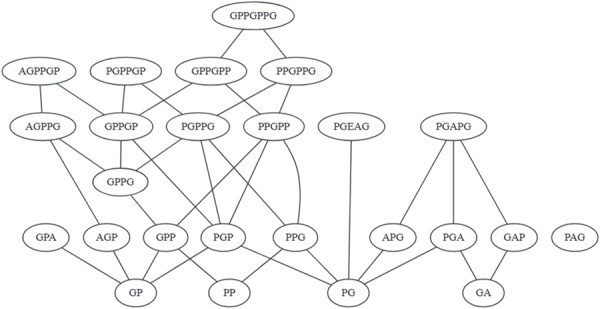
Motif graph based on SIMPLE analysis of CO1A1_HUMAN.

Correlation between low complexity and disorder

LC and compositionally biased sequences often overlap with protein disorder [31]. However, their precise relation largely depends on the applied methods used for their quantification. Here the IUPred method was used to characterize protein disorder and to calculate the overlap with the various features determined with the methods SEG, CAST and SIMPLE described earlier. IUPred captures the basic biophysical properties of ordered and disordered sequences by relying on an energy estimation scheme. According to this, sequences composed of amino acids that cannot form enough favorable intrachain interactions would be disordered and can be recognized from the amino acid sequence by their less favorable estimated energies [32].

All the 21 sequences in our dataset contained at least one disordered segment, and nearly 45% of residues were predicted as disordered (see details in Suppl. Table S1). This was lower compared to the average residues predicted by CAST, but higher than those predicted by SEG (15%). Table 5 and Figure 4 describe the overlap between the various methods. The matrix of overlaps is non-symmetrical (Table 5(A)), as the overlap is computed on the percentage of residues with a given feature. For example, 81% of SEG LC residues are predicted to be in disordered regions by IUPred. However, only 27% of residues predicted to be disordered by IUPred are found in a SEG detected region. Overall, there is a fairly good agreement between the methods that detect LC and the disordered regions detected by IUPred. Between the methods that detect LC, the largest agreement (relative to random overlap) was observed in the case of SEG and SIMPLE, likely because both produce relatively conservative predictions (Table 5(B)). Interestingly, by this metrics, the overlap between IUPred and the LC methods was not much lower as the overlap between CAST and the other methods.

Table 5.

(A) Fraction of residues predicted by one method (columns) that are predicted by another method (rows). (B) Enrichment ratio of overlapping residues between two methods compared to random overlap

A				% residues predicted by
% residues predicted by		IUPred	SEG	CAST	SIMPLE
	Total	44.89	15.04	50.16	18.51
	IUPred	100.00	27.07	78.66	32.03
	SEG	80.78	100.00	98.41	90.32
	CAST	70.40	29.51	100.00	35.27
	SIMPLE	77.69	73.42	95.89	100.00
B				Enrichment of overlap
Enrichment of overlap		IUPred	SEG	CAST	SIMPLE
	IUPred	1.00	1.80	1.57	1.73
	SEG	1.80	1.00	1.96	4.88
	CAST	1.57	1.96	1.00	1.91
	SIMPLE	1.73	4.88	1.91	1.00

Figure 4.

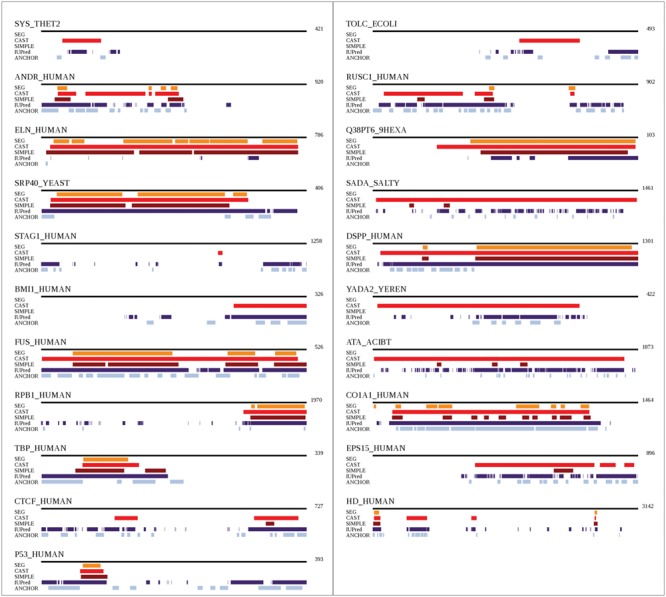
Comparison of positions detected to be of LC in the 21 proteins of our dataset. Methods SEG (in orange), CAST (in red), SIMPLE (in brown) and IUPred (in purple) were used. ANCHOR (in light blue), which includes structural aspects, is also compared.

The low complexity diagram: a proof of principle

The LC diagram described before (Figure 1) allows us to situate and compare protein sequences in a framework that reflects two simple properties that are intimately associated to LC: compositional bias and repeats. These two features are measured by computing the abundance of the most frequent amino acid in the tract and by the fraction of residues that needs to be mutated to have a perfectly repeated tract.

We calculated the properties that define the two axes of the LC diagram for a dataset of globular monomeric proteins (globular) and a dataset of disordered proteins (IUP) [33] and for fragments of our own protein dataset (Table 2) determined to be of LC by the SEG, CAST, and SIMPLE methods (with a minimum length of 10 residues; Figure 5). To place them in the LC diagram, the percentage of the most common amino acid in each sequence was determined as a function of the percentage of the mutations to form perfect repeats. The latter quantity was calculated in a brute force way by considering all potential fragments of the sequence of lengths between 1 and 30. From these fragments, an artificial sequence of perfect repeats was generated by iterating these elements to be long enough to cover the original sequence region. At least three repeats were required; therefore, only fragments no longer than a third of the sequence were considered. The minimum number of mutations between the original and these artificial sequences was calculated and normalized by the sequence length. This approach cannot consider insertions and deletions. Thus, the x values calculated represent an estimate, and the real values (if different) can only be closer to zero.

Figure 5.

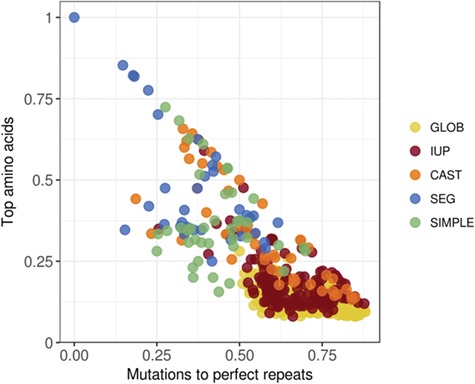
LC diagram for various sequence datasets. The percentage of the top amino acid as a function of the percentage of mutations to perfect repeats calculated for a dataset of globular (GLOB), disordered (IUP) sequences as well as fragments of our protein dataset with LC character according to the SEG, CAST and SIMPLE methods.

The regions from globular proteins are distributed as a compact cloud (yellow points) that edges on the point described as globular in Figure 1 (bottom-right corner; Figure 5). An inferior limit around 10% of top amino acid agrees with the estimation published in 1966 [16]. The globular cloud overlaps with the disorder cloud (red points) outside the immediate vicinity of ‘regular’ proteins and extends into the realm of LC (orange, blue and green points). The separation between the globular cloud and the LC cloud described by SEG is very strong: the clouds touch each other but they do not overlap. Disordered regions overlap with both globular proteins and LCRs, as expected.

The disorder cloud overlaps with the globular cloud but does not touch the extreme, indicating that a globular sequence can transition to disorder both by gaining a biased sequence but also via slight repetitions. In this respect, however, it is interesting to note that the disorder cloud overlaps very little with the repeat cloud, confirming that long perfect repeats are predicted to confer order. This is a structural aspect that we address in the next section.

Structural properties of LCRs

The experimental determination of protein structure is much more challenging for LCRs than for globular and fibrous proteins [34], and only few cases have been studied experimentally. This is due to various reasons that we will explain in this section.

To guide our tour from the sequence to the structural aspects of LCRs, we will continue our strategy to illustrate LC with the set of 21 examples, taking into consideration the previously obtained information for these sequences. There are prediction tools specialized for the study of the structural properties of proteins, which we will apply to the selected proteins with LCR. It should be noted that for many of them there is experimentally known 3D structure covering parts of the sequence, but these generally do not overlap with LCRs. For example, the recently solved structure of huntingtin [35] does not resolve the N-terminal 90 amino acids, which contains a CBR including the polyQ whose expansion causes Huntington’s disease, and the 2622-2660 fragment, both of which practically overlap to the regions identified as LCRs in our SEG analysis (Suppl. Table S1).

Analysis of the structural properties of low complexity sequences

The structural properties of LCRs can be predicted with several bioinformatics methods. To classify the incidence of different phenomena in the dataset, we used FELLS, a predictor that aggregates sequence and structural propensity predictions in a single view [36]; this includes secondary structure, LCR, disorder and aggregation predictions displayed along sequence positions. We focused on four predictions: LCRs (SEG), disorder (ESpritz-NMR), aggregation propensity (Pasta 2.0 [37]) and secondary structure (FESS). We classified each protein in the dataset as belonging to one category (LC, disordered, aggregating and structured) if more than the 30% of its sequence is predicted to be in that state. The results are shown in a Venn diagram (Figure 6). In our dataset, focused on LCRs, only one protein falls outside the LCR and/or disorder categories. This is huntingtin, the longest of the 21 proteins (3142 amino acids) known to harbor homorepeats, alpha-solenoid repeats and globular domains [35, 38].

Figure 6.

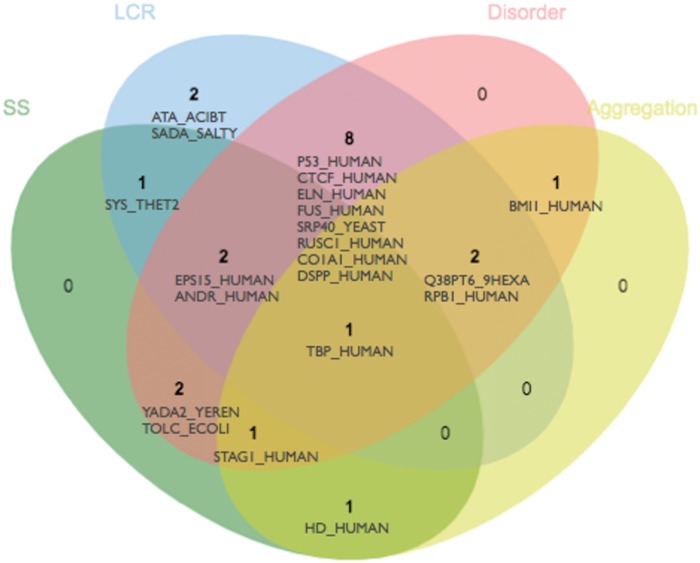
Structural features of LC proteins. Venn diagram representing the FELLS prediction of dataset proteins, in four categories: secondary structure (SS), LCRs, disorder and aggregation. Each protein is assigned to a category if more than 30% of the residues in its sequence are predicted in that state.

In agreement with the sequence analyses presented before, we observe a large overlap between LCR and disorder (13 of 21 proteins), including proteins such as the Glycine-rich antifreeze protein (Q38PT6_9HEXA), dentin (DSPP_HUMAN) and human RNA binding protein FUS (FUS_HUMAN).

Regarding aggregation, while three of the six proteins classified as aggregating are also in the LCR category (TBP_HUMAN, RPB1_HUMAN and Q38PT6_9HEXA), we need to look at the sequence level. For example, for both TBP_HUMAN and RPB1_HUMAN the regions with aggregation propensity do not overlap with the LCRs. Even in FUS, a largely disordered protein with generally low sequence complexity, its few regions presenting aggregation propensity are localized in the small ordered part of the protein. A possible explanation of this is that LCRs and aggregation prone regions have different amino acid frequencies. Hydrophobic residues inducing aggregation are probably less abundant in LCRs. This was the case in our dataset (see Table 3 for CBRs).

Therefore, our small dataset supports the previous association between LCR and disorder but not to aggregation propensity. However, TBP leads to another turn in our story, by bringing another player relating LCR, structure and aggregation: homorepeats. TBP’s LCR is a large stretch of consecutive glutamines (positions 55–95), which is interestingly predicted both in helical conformation and as a disordered region. These contradictory predictions are most probably due to the lack of detailed understanding of the conformational preferences adopted by homorepeats. In the next section, we discuss the challenges posed by homorepeat structure prediction and determination, and the strategies that have been proposed for their study.

Deciphering the structural basis of homorepeat function

Homorepeats are an extreme case of LC, and in this respect, they can help us to illustrate the origin of the difficulties in relating sequence and structure in LCRs. In homorepeats, the presence of multiple copies of a single amino acid in a protein region confers very specific physicochemical properties to the hosting protein and enables it to perform specialized biological tasks (see, for example, [39]). Despite their relevance, the connection between amino acid sequence, 3D structure and biological function in homorepeats remains poorly understood due to the challenges they pose to structural biology.

Homorepeats and short repeats are found in disordered regions, a property that typically precludes their crystallization. In the case of polyQ, there are, however, examples that have been crystallized in the presence of fusion proteins [40, 41] or specific antibodies [42, 43]. These studies yield contradictory results regarding the secondary structural preferences of polyQ tracts. This observed structural variability most likely originates from the inherent conformational plasticity of the homorepeat regions, which cannot be captured in crystallographic studies. Nuclear magnetic resonance (NMR), a high resolution structural technique in solution, seems more adapted to study homorepeats. However, the similarity of the nuclear resonance frequencies within homorepeats has hampered these studies. Some pioneering NMR studies of polyQ homorepeats in huntingtin [44, 45], and the androgen receptor [46] have shown these studies are possible. These examples show that the N-terminal flanking region of the polyQ adopts an α-helical conformation that extends toward the homorepeat. In the absence of this structured flanking region, polyQ adopts a random coil conformation [46, 47].

Homorepeats are frequent in our LCR-focused set of 21 proteins (Suppl. Table S1). Using a relatively lax cutoff of four residues of the same type in a window of six (which was identified as already inducing structural effects for polyQ [48]), only TOLC_ECOLI has no homorepeat region (as detected with dAPE [49]), hinting at the large overlap of LCRs with homorepeats. While there is a variety of homorepeat types, we can observe preferences in particular sequences, like polyS in SRP40_YEAST, DSPP_HUMAN and RPB1_HUMAN, polyP in CO1A1_HUMAN or polyG in FUS_HUMAN. Elastin has many polyA and polyG tracts, since these residues participate in motifs discussed above that surround and support functional lysines and prolines. PolyQ is present once in TBP_HUMAN (followed by polyA), EPS15_HUMAN, HD_HUMAN, and three times in ANDR_HUMAN. All overlap the predicted regions by CAST (which identifies the Q-rich region) and IUPred (indicating disorder). While there was no overlap with FELLS (PASTA 2.0) indicating aggregation, the aggregation propensity regions predicted by ArchCandy ([50]; Suppl. Table S1) do overlap with the three regions (in TBP, HD and ANDR) that are involved in polyQ repeat expansions causing disease [51]. This result suggests that ArchCandy detects aggregation of the type involved in CAG/CAA triplet expansions. The ArchCandy analysis of our dataset identifies aggregation regions in a subset of the proteins identified by PASTA 2.0, suggesting that distinct methods for detection of aggregation have different sensitivity depending on the sequence.

Analysis of repeating patterns of charged regions/residues

As discussed above, repetition within LCRs can result in structure and function. Another type of repetition that can occur within LCRs, beyond homorepeats, are those with alternating blocks of oppositely charged residues. To our knowledge, the only such motif that has been characterized in detail is the Charged single alpha-helix (CSAH), also often referred to simply as single alpha-helix (SAH). In these regions, generally three to four negatively charged residues are followed by three to four positively charged ones, although only few of such repeats are perfect. The structure of these segments is an alpha-helix that is stable in water as a monomer. CSAH segments can act as rigid linkers, rulers or lever arms in various proteins [52–54] and may also behave as constant force springs [55]. CSAHs are very rare in protein sequences and, in a number of cases, are adjacent to coiled coil segments. One of the most well-characterized segments is found in myosin 6, where it forms the extended lever arm [52]. There are currently three methods for detecting CSAHs in protein sequences, Waggawagga [56], FT_CHARGE and SCAN4CSAH, which are generally used together for consensus predictions [57]. Of these, FT_CHARGE identifies repeating charge patterns of any frequency, not just those characteristic of CSAHs.

We applied the FT_CHARGE method [57] allowing all repeat frequencies to our dataset of 21 proteins (Suppl. Table S1). In agreement with their known low frequency, we only found CSAHs in two of the 21 proteins: a short region in huntingtin (HD_HUMAN, residues 2633–2664), and a 120 amino acid segment in the human transcriptional repressor CTCF (CTCF_HUMAN, residues 557–673). The first 20 residues of the CTCF region largely match the 11th, atypical Zinc-finger motif of the protein as annotated in UniProt (positions 555–577). The structural information available for this protein suggests that its C-terminal part is intrinsically unstructured [58]. However, this is typically found for CSAHs because, due to their highly charged nature, they are almost always predicted to be intrinsically disordered for most of their length [59]. However, CSAHs can adopt a stable conformation as monomers (e.g. [52]).

The notion that several structural motifs formed by LCRs are predicted to be intrinsically disordered is often found in the literature [60–63]. Most notably, there are many segments that are predicted to form alpha-helical coiled coils and also to be intrinsically disordered. In the case of coiled coils this can be justified on the basis that coiled coil forming regions are generally viewed as disordered in their monomeric state and they adopt helical conformation upon dimerization/multimerization [64]. Collagen triple-helical motifs are another example of similar behavior, providing a case of folding upon binding/multimerization [65]. In the next section, we study the overlaps of these structural predictions to LCRs.

Overlap of structural predictions and LCRs

Our previous analyses suggest that LCRs tend to lie in regions without much structure. However, there are LCRs with repetitions that seem to provide structure, even multiple structures influenced by interactions with protein partners. To illustrate the overlaps of different structural predictions and LCRs, we use again our protein dataset. Overlaps of predictions were computed in three steps. First, we applied IUPred [32], VSL2B [66], ncoils [67], Paircoil2 [68] and hmmsearch [69] using Collagen.hmm (Pfam family PF01391), all with default parameters. Then, using in-house scripts, we computed (i) the consensus of the two disorder predicting methods, IUPred and VSL2B (only regions with a minimum of 30 residues predicted by both methods were considered), and (ii) the consensus of the coiled coil predicting methods, ncoils and Paircoil2 (only regions with a minimum of 21 residues predicted by both methods were considered). Finally, we computed the number of residues predicted to be disordered, located in coiled coil regions or in polyproline II-like helices (PPLLH; according to their similarity to collagen evaluated with hmmsearch). No residue was predicted to be both in a PPLLH and in a coiled coil: such overlap is unrealistic because of the incompatible structural preferences of amino acids (both Gly and Pro, abundant in PPLLH, are very rare in alpha-helical regions). PPLLH and coiled coils were predicted for two and four proteins, respectively (Table 6). Full overlap to disorder was found for the PPLLH predicted for Q38PT6_9HEXA (glycine-rich antifreeze protein) and partially for the coiled coils in EPS15_HUMAN (epidermal growth factor receptor substrate 15) and ATA_ACIBT (adhesin autotransporter).

Table 6.

Number of residues predicted to be in different structural states

ID	Disordered	Only disordered	Disordered + cc	Disordered + polyproline II-like helices	cc	Only cc	Polyproline II-like helices	Only polyproline II-like helices
Q38PT6_9HEXA	0	0	0	0	0	0	48	48
SYS_THET2	0	0	0	0	63	63	0	0
EPS15_HUMAN	287	228	59	0	161	102	0	0
STAG1_HUMAN	202	202	0	0	31	31	0	0
CO1A1_HUMAN	1168	390	0	778	0	0	778	0
ATA_ACIBT	546	450	96	0	96	0	0	0

While these overlaps might reflect reality in terms of dynamic rearrangements of the segments, the general wisdom could be that the more specific prediction should usually be considered, meaning that coiled coil and collagen predictions have prevalence over disorder predictions. In this respect, disorder detection is regarded as a method to recognize non-globular sequences that might either form fibrillar structures or be disordered in their functional form, depending, among others, on their repetitiveness.

Our knowledge about the sequence/structure relationship for disordered proteins is certainly less advanced compared to globular proteins, perhaps precluding initiatives on protein design. This can be extended to disordered LCRs that represent a huge challenge for structural biology. Some studies have engineered LC proteins to decipher the role of specific amino acid types or sequence patterning with biological function. For instance, the effect on the overall structure of the charge distribution within isolated disordered chains [70] and when tethered to globular domains [71] have been addressed from a theoretical perspective. Moreover, in the recent years, liquid–liquid phase separation (LLPS) has emerged as a general phenomenon that is involved in fundamental biological processes [72]. It has been demonstrated that many LCRs experience LLPS under specific experimental conditions. This demixing phenomenon depends on the balance of intramolecular, intermolecular, protein–solvent and solvent–solvent interaction strengths [73]. Despite the growing interest in LLPS, the relationship between amino acid composition and patterning within the chain is poorly understood, and it is the matter of an intense research including the design of synthetic LC sequences with enhanced or reduced demixing properties [74, 75]. In general, LCRs inducing phase separation can be classified as polar with a strong compositional bias for serine, glycine, asparagine and glutamine. The remaining amino acids are variable, although low fractions of regularly spaced charged and/or aromatic amino acids are observed [73]. The relevance of aromatic residues has been demonstrated in FUS protein where the replacement of tyrosines by phenylalanines, serines or leucines reduces or impedes the phase separation capacity of the protein [76, 77].

Multimerization: a final variable adding complexity to the study of LCRs

As discussed above, structural variability and folding upon binding are properties that can characterize some LCRs. Thus, the structural behavior of LCRs is context dependent. The interactions of LCRs with additional copies of either the same molecule (homomultimers) or other proteins/(macro)molecules (heteromeric complexes) is a key factor and largely influences the ability of the sequence to adopt a specific structure or interchange between conformations. Current methods are typically able to predict either the structure of the ‘isolated’ molecule or the propensity to form specific structures, which typically stem from the underlying repeated sequence. The limitation of such methods is that they usually predict homomultimeric structures, because it is impractical to consider the sequence information of all possible interaction partners. However, there are efforts to identify interaction motifs that might fold upon partner interaction (e.g. ANCHOR [78]). Indeed, application of this method to our protein dataset indicates some cases where this property applies (Figure 4), and while there is a general overlap of folding propensity overlapping LCRs, there are also examples of striking complementarity (e.g. DSPP_HUMAN).

Conclusions

In this critical review, we have focused on the description of several features of LCRs by using computational methods. We chose a set of 21 proteins with a variety of functions and types of LCRs to test these methods and their overlapping predictions. At the strict level of sequence, LC is related to composition bias and repeats. At the level of structure, there is a direct, yet not fully understood, relation to disorder, aggregation and flexibility. While some connections have been established previously, we demonstrate the difficulty of defining general rules connecting sequence features and structural properties.

We hypothesize that the problem lies in the strong non-linearities of the connections between the sequence/structure relationships in LC sequences. Some stem from the fact that variables used to measure sequence order cannot capture all the effects of amino acid combinations at the structural level, which for example depend crucially on the amino acid side chains. The second reason for this non-linearity is the flexibility of disordered regions and their possibilities to adopt ordered structures in the context of flanking sequences or interacting molecules, which complicates any standalone predictions.

We have tried a pragmatic approach with two sides. On the one hand, a diagram of sequence properties that allows one to explore the overlaps in three variables (repeat perfection, composition bias and LC; Figure 1), which complements our intellectual discussion on these variables with actual distributions of real protein fragments (Figure 5). Along this exemplary path, we have chosen a small dataset to submit it to a variety of analyses and illustrate their potential overlaps.

The structural aspects were discussed separately, yet in conjunction with the above. The main conclusion from this latter section in light of sequence analysis is that LC manifests itself in apparently opposite effects: while disorder and flexibility seem to be common features of LCRs, repetition/periodicity in sequence at multiple levels can induce structure. Back to the LC diagram (Figure 1), this is reflected in two situations: between disordered and globular and between disordered to flexible. In evolutionary terms, this might imply that a disordered (LC) sequence can ‘escape’ disorder by either gaining a richer (higher complexity) composition maintaining aperiodicity (lower y for a given x), or by attaining a highly periodic structure (lower x for a given y).

We have demonstrated the intricacies of analyzing LC in protein sequences: even methods that are supposed to study the same properties (LC, sequence bias or aggregation) might not share similar assumptions. Our recommendation for researchers investigating a particular protein is to use several of these methods together. It must be noted that since sequence context might be influencing the structure adopted by a LCR, there is an additional advantage in having these multiple outputs. For instance, one could discover that a predicted disordered region is proximal to features involved in protein interaction (a repeat or a coiled coil region) or to an aggregation prone region that is also disordered and probably exposed. In this respect, joint bioinformatics research and development efforts to make the outputs of these methods compatible and consistent are highly desirable. We expect that ongoing efforts to annotate LC related features in as many protein sequences and structures as possible will eventually lead to the detection of additional features, or combinations thereof, and to a more specific classification of LCRs. This should allow accurate associations of LCRs with protein modifications, motifs, dynamic behaviors and interactors, thus gaining the ability to predict function for large parts of protein sequences that currently remain a mystery.

Pablo Mier is a postdoctoral researcher interested in the development of Web tools and databases related to protein evolution and low-complexity regions. He works in the Faculty of Biology at Johannes Gutenberg University Mainz.

Lisanna Paladin is a PhD student of Biomedical Sciences Department at University of Padova. Her research focuses on tools and databases development for the description of non-globular proteins structure and function.

Stella Tamana is a PhD candidate at the Department of Biological Sciences, University of Cyprus, where she studies bioinformatics. She is interested in the study of compositionally biased regions in protein sequences, the elucidation of their structural and functional properties and their handling in automated comparative genomics pipelines.

Sophia Petrosian was a final-year student at the Biological Computation and Process Laboratory, Thessalonica, Greece.

Borbála Hajdu-Soltész is a PhD student at the Eötvös Loránd University, Budapest, Hungary. She is a computational biologist interested in protein disorder and questions such as how do disorder properties contribute to cancer development. In keywords, her work is related to disordered proteins, cancer genome databases, somatic mutations in cancer, protein–protein interactions and short linear motifs.

Annika Urbanek is a postdoctoral researcher at the Centre de Biochimie Structurale in Montpellier (France) where she is developing tools to study highly disordered proteins with low-complexity regions experimentally.

Aleksandra Gruca is an assistant professor in the Institute of Informatics at the Silesian University of Technology in Gliwice, Poland. She is a member of the Board of the Polish Bioinformatics Society. Her research interests are focused on application of data mining and machine learning methods for automated functional interpretation of high-throughput biological experiments.

Dariusz Plewczynski is a professor at University of Warsaw in Center of New Technologies (Warsaw, Poland) and the head of Laboratory of Functional and Structural Genomics. His main expertise covers computational genomics, biostatistics and bioinformatics.

Marcin Grynberg is an assistant professor in the Department of Biophysics at The Institute of Biochemistry and Biophysics PAS, Warsaw, Poland. His main focus is on the protein world, especially on rare sequences, like low complexity regions. He is also working in the field of microbial proteomic analyses.

Pau Bernadó is a researcher at the Centre de Biochimie Structurale in Montpellier (France). His group is interested in establishing connections between the structure and function of highly disordered proteins and low complexity regions.

Zoltán Gáspári is an associate professor at the Faculty of Information Technology and Bionics at Pázmány Péter Catholic University, Budapest, Hungary. His group investigates the role of internal dynamics in protein function using computational and experimental approaches and their combination.

Christos A. Ouzounis is the Director of Research at Centre for Research & Technology Hellas (Thessalonica, Greece), where he directs the Biological Computation and Process Laboratory of the Chemical Process & Energy Resources Institute. His interests revolve around genome structure, function and evolution, biological sequence comparison and synthetic biology. Some of his best known contributions include the discovery of genomic context methods and the definition of the last universal common ancestor.

Vasilis J. Promponas is an assistant professor at the Department of Biological Sciences, University of Cyprus, heading the Bioinformatics Research Laboratory. He is interested in theoretical and practical aspects of sequence comparison and in developing methods for predicting features of protein structure and function from amino acid sequences. In particular, he studies different phenomena related to non-globular proteins and, recently, focuses on conserved eukaryotic processes, including nucleocytoplasmic transport and macroautophagy.

Andrey V. Kajava is the Director of Research at CNRS, Montpellier. His group (`Structural Bioinformatics and Molecular Modelling’) uses computational methods to understand the principles of protein structure and biomolecular interactions.

John M. Hancock is the Communities and Services Coordinator at ELIXIR. He has worked on repetitive sequences in DNA and proteins and led the development of SIMPLE method for over 30 years.

Silvio C. E. Tosatto is a full professor at the Department of Biomedical Sciences, University of Padua. His group develops tools and databases for the study of non-globular proteins in biomedicine and biotechnology.

Zsuzsanna Dosztanyi is a senior research scientist working as a group leader at the Biochemistry Department of the Eötvös Loránd University, Budapest. She is interested in understanding the structural and functional properties of intrinsically disordered proteins and their involvement in various diseases.

Miguel A. Andrade-Navarro is a professor of Faculty of Biology, at the Johannes Gutenberg University of Mainz. His group is interested in exploring gene function using computational techniques including algorithms and databases.

Key Points

• LC can only be compositionally biased, while compositional bias can be of low or high complexity.

• Repetition within LCRs can result in structure and function.

• Statistical measures alone cannot capture all structural aspects of LCRs.

• Factors such as the sequence context and the molecular context of the protein can influence the structural state of LCRs.

Funding

COST Association (Cost Action BM1405); European Union (the Marie Skłodowska-Curie grant agreement no. 778247 to S.C.E.T.); European Research Council (project chemREPEAT 648030 to P.B.); Hungarian Academy of Sciences (Lendület grant LP2014-18 to Z.D. and `János Bolyai Research Scholarship’ Program to Z.G.); National Research, Development and Innovation Office (NN124363 to Z.G.); Institute of Informatics (BK-213/RAU2/2018 to A.G.).