Spontaneous and field-induced crystallographic reorientation of metal electrodeposits at battery anodes

Metals use a chemotaxis-like process to overcome diffusion limitations and prevent dendritic electrodeposition in batteries.

Abstract

The propensity of metal anodes of contemporary interest (e.g., Li, Al, Na, and Zn) to form non-planar, dendritic morphologies during battery charging is a fundamental barrier to achievement of full reversibility. We experimentally investigate the origins of dendritic electrodeposition of Zn, Cu, and Li in a three-electrode electrochemical cell bounded at one end by a rotating disc electrode. We find that the classical picture of ion depletion–induced growth of dendrites is valid in dilute electrolytes but is essentially irrelevant in the concentrated (≥1 M) electrolytes typically used in rechargeable batteries. Using Zn as an example, we find that ion depletion at the mass transport limit may be overcome by spontaneous reorientation of Zn crystallites from orientations parallel to the electrode surface to dominantly homeotropic orientations, which appear to facilitate contact with cations outside the depletion layer. This chemotaxis-like process causes obvious texturing and increases the porosity of metal electrodeposits.

INTRODUCTION

Morphological evolution during formation of a crystalline, solid phase from a liquid solution is of scientific and practical interest in fields ranging from protein drug formulation, particle science, to metallurgy. Depending upon the conditions at which the phase transformation occurs, it is possible to interrogate both equilibrium and nonequilibrium phenomena associated with solid-phase nucleation and growth. Here, we are specifically interested in a subset of these problems centered around electrodeposition of metals, particles, and polymers, where the solidification transition is electrochemically driven (1–3). Our interest is motivated by the critical role electrodeposition has played as a scalable manufacturing process for creating well-defined, conformal coatings on conductive substrates (4). It is also driven by the important role that controlled electrodeposition of metals is thought to play in achieving high levels of reversibility in rechargeable batteries that use metal anodes (5, 6). We underscore that this interest spans cells that deliberately use metals as the anode for achieving greater storage per unit mass/volume or in which the metal anode is formed spontaneously on a too quickly charged insertion electrode [e.g., the graphite anode used in emergent fast-charge, lithium-ion battery technology (7)].

It is known that successful application of electrodeposition to create conformal coatings in any of these application contexts requires fast transport of charged species (e.g., ions, particles, and polymers) in an electrolyte medium and stable redox reactions and transport at the electrolyte/electrode interface at which the deposition occurs. The propensity of metals to violate these requirements and to deposit on planar substrates in rough, nonplanar morphologies has been actively studied since the discovery of electroplating in the 1800s (8). It has been shown that multiple factors, including temperature (9), transport properties of the electrolyte (10–12), substrate chemistry/geometry (5, 13), and their interplay, could either exacerbate or mitigate this propensity. The problem has reemerged as a priority research direction in recent years because of the role rough, dendritic electrodeposition of metals plays in premature failure and short-circuiting of high-capacity metallic battery anodes (14, 15). Classical transport theory predicts that the growth and proliferation of these dendrites are the result of a combination of morphological and hydrodynamic instabilities, which lead to complex interfacial transport behaviors, including formation of an ion-depleted extended space charge layer (ESCL) near any ion-selective interphase in an electrolyte and to the nucleation and rapid growth of diffusion-limited, classical tree-like structures termed dendrites (2, 16, 17). Dendritic electrodeposition is fundamentally unsafe in the battery context because once formed at a battery anode, dendrites may grow aggressively to fill the interelectrode space, short-circuiting the battery (18). The current contribution therefore focuses on the physicochemical processes that drive these instabilities in metal electrodeposition under conditions relevant in batteries.

A large body of work already exists, which shows that, consistent with classical transport theory, conformal electrodeposition of many metals (e.g., Zn, Cu, Sn, and Ag) at planar electrodes can only be sustained at current densities below a diffusion-limited critical value $i_L=\frac{4F{C}_{0}D}{L}$ and/or at voltages below the predicted threshold V < V_cr ≈ 8 RT/F for the onset of hydrodynamic instability termed electroconvection (19, 20). Here, C₀ is the salt concentration in the electrolyte, RT/F = kT/e is the thermal voltage, D is the diffusivity, and L is the interelectrode spacing. Electrodeposition under conditions outside these bounds has likewise been reported to produce nonplanar, classically dendritic (tree-like) morphologies (21–25). We note, nonetheless, that the vast majority of these reports focus on dilute electrolytes (e.g., C₀ < 0.1 M) with supporting salts (2, 26, 27). The concentrations of the electrochemically active salt are well below typical electrolyte concentrations used in battery cells (e.g., C₀ ≥ 1 M). In contrast, electrodeposition of many of the most promising metal anodes (e.g., Li, Na, and Al) is typically studied in moderately salty electrolytes (e.g., C₀ ≥ 1 M) and broadly found to exhibit the following nonclassical attributes: (i) formation of low-density mossy- or wire/whisker-like nonplanar electrodeposition morphologies, as opposed to classical tree-like dendrites; (ii) a transition from planar to nonplanar electrodeposit structure under far milder conditions (e.g., i << i_L and V << V_cr) than predicted by classical theory; and (iii) poor reversibility of the formed metallic deposits (5, 28–31).

Here, we report on the electrodeposition of metals in dilute (e.g., 0.05 M) and moderately concentrated (e.g., 2.5 M) electrolytes and find that transport plays fundamentally different roles. Specifically, we find that metals do not form classical dendritic electrodeposits under electrolyte conditions typically used in electrochemical cells. Instead, we observe that the transition from planar to nonplanar electrodeposition morphologies in metals is associated with the formation of highly porous, mossy structures driven by a chemotaxis-like anisotropic growth of the metal electrodeposits structures. The resultant morphologies are analogous to those attributed in the literature to metal electrodeposition regulated by a heterogeneous solid electrolyte interphase (SEI) layer (15, 32). In addition, we report that even moderate amounts of normal flow generated by rotating the electrode is sufficient to eliminate formation of nonplanar electrodeposition at metallic electrodes and to produce highly reversible electrodeposit growth, under aggressive deposition conditions.

Electrochemically driven solidification reactions of metals involve two dominant steps—transport of the metal ions to an electrode, which serves as a source of electrons, and reduction of the metal ions at the electrode to produce the metal (33). The interplay between physical and chemical kinetics associated with the two steps has been investigated for more than 100 years in the context of metal plating. It is known that the relative rate of transport of the metal ions to the rate at which they are reduced at the interface determines the size, morphology, and potentially even the shape of metal electrodeposits. In dilute electrolytes, the rate of ion transport in the electrolyte can be quantified using the Nernst-Planck (N-P) equation in terms of the cation flux density, $N_{+}=-D_{+}\frac{\mathrm{\partial }{C}_{+}}{\mathrm{\partial }\mathit{x}}-\frac{z_{+}F}{\mathrm{RT}}{D}_{+}{C}_{+}\nabla \mathrm{\Phi }+C_{+}\mathbf{v}$ . The rate of the surface reduction reaction may likewise be quantified by the exchange current density, i_o. Here, C₊ is the cation concentration in the electrolyte, D₊ is the diffusivity, z₊ is the valence number of the cationic species, ∇Φ is the potential gradient, and v is the flow velocity.

In the kinetic rate–limited regime, the rate of ion transport in the electrolyte is fast enough to provide ions to replenish the ones depleted by the surface reaction; the rate at which the solid electrodeposit forms and grows on the electrode then depends only on the rate at which electrons can be transported to reduce arriving ions. In closed electrochemical systems, such as batteries, convection is normally assumed to be unimportant, and the surface reaction kinetics are much faster than the rate of ion transport to the electrode; the electrodeposition rate is therefore said to be transport limited. At a certain deposition current, i_L, the rate of ion depletion at the electrode surface becomes larger than the rate of transport of fresh ions to the electrode, leading to the formation of a highly insulating ion depletion (extended space charge) zone at the electrode surface. Classical transport theory predicts that, in a dilute electrolyte, the thickness of this depletion layer, ${\mathrm{\delta }}_{\text{ESCL}}=1.31 L\times {(\frac{\mathit{VF}}{\mathit{RT}}\times \frac{{\mathrm{\lambda }}_D}{L})}^{\frac{2}{3}}$, increases with the applied voltage V and decreases with the electrolyte salt concentration, through the reciprocal relationship between the Debye screening length, λ_D,and the square root of the salt concentration (34). This means that, beyond a critical voltage V_cr ≈ 8 RT/F, the current density ceases to depend on V, and a plot of i versus V displays a plateau at i = i_L. For V >> V_cr, both experiments and theory show that the electric field exerts a body force on charged fluid in the ESCL, which drives unstable convective fluid motions via an instability termed electroconvection. The resultant electroconvection flux augments the diffusion and migration terms in the N-P equation, leading to a new regime, termed overlimiting conductance, in the i-V curve. Metal deposition is destabilized by electroconvection because the instability produces a nonuniform flux of ions to the electrode surface. Electrochemical reduction of ions in regions of high convective flux (i.e., “hot-spots”) produces rapid growth of nonplanar, fractal-like dendritic electrodeposit morphologies (35–37), as illustrated in Fig. 1A.

Fig. 1. Illustration showing proposed differences between electrodeposition morphology and ion concentration in dilute and concentrated electrolytes.

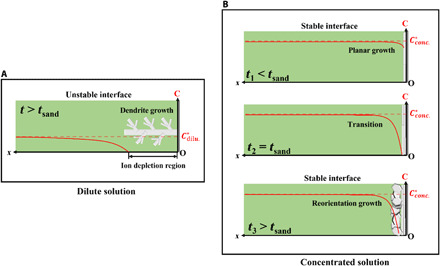
(A) Dendritic growth during metal deposition in dilute electrolyte solutions in the overlimiting ion transport regime. (B) Crystallographic reorientation and growth during metal electrodeposition in concentrated electrolyte solutions above the classical diffusion limit.

The large difference in electrolyte salt concentrations used in literature studies (C₀ < 0.1 M) of Zn, Cu, and Ag electrodeposition, which have largely validated these classical effects, in comparison to those used in battery studies (C₀ ≥ 1 M), is problematic for fundamental and practical reasons. Fundamentally, at high salt concentrations, both the chemical potential gradient and the ion transport coefficients are subject to many-body, nonpairwise additive interactions, which produce complex ion concentration dependences—invalidating the simple N-P expression for the cation flux density (38). In addition, at the much smaller λ_D values associated with the high salt content, the ESCL may become smaller than the diffusion boundary layer thickness (${\mathrm{\delta }}_{\mathit{DL}}=\frac{C_{+}\times \mathit{nF}\times D}{i_L})$, meaning that ion transport through a stagnant fluid film at the electrode may dominate the interfacial dynamics of cations at the electrode. A straightforward approach for evaluating this possibility is the use a rotating disc electrode (RDE) to generate a well-defined three-dimensional (3D) hydrodynamic flow field (v = v_r(r, y)e_r + v_y(y)e_y + v_θ(r)e_θ), where v_r(r, y) = 0.51ω^3/2ν^−1/2ry, v_y(y) = − 0.51ω^3/2ν^−1/2y², and v_θ(r) = rω, near the electrode surface (i.e., y → 0) (33). The normal (y −) component augments the transport of ions to the electrode surface, which makes it possible to precisely manipulate the diffusion boundary layer thickness, ${\mathrm{\delta }}_{\mathit{DL},\mathrm{\omega }}=1.61{\mathrm{\omega }}^{-1/2}{D}^{1/3}{\left(\frac{{\mathrm{\mu }}_s}{\mathrm{\rho }}\right)}^{1/6}$, by varying the angular rotation rate, ω, of the electrode. Here, D is the ionic diffusivity, μ_s is the viscosity of the electrolyte solvent, and ρ is the electrolyte mass density.

RESULTS

To study the role of electrolyte salt concentration on electrodeposition, we first investigated electrodeposition of Zn in aqueous ZnSO₄ electrolytes with three salt concentrations: 0.05, 0.5, and 2.5 M. The 2.5 M ZnSO₄ aqueous solution, as a typical mild pH electrolyte, is a promising next-generation Zn battery electrolyte featuring multiple favorable properties (39–41). The rationale for choosing Zn for the study is straightforward. First, Zn electrodeposition can be performed in aqueous electrolytes where complications associated with the formation of a SEI can be avoided. Zn therefore provides a platform to deconvolute the high salt concentration and SEI formation processes that are typical of electrodeposition studies for metals such as Li and Na. Zn metal is also promising in its own right as an energy-dense rechargeable battery anode and is under active research for this purpose (42–45). As acknowledged in previous literature (5, 46), regulating Zn deposition morphology appears crucial because Zn can more easily cause battery short circuits owing to its Young’s modulus that is one order of magnitude higher than Li (108 versus 5 GPa).

The red curves in Fig. 2 (A to C) report the current-potential (i-V) curves measured using linear potential sweep voltammetry in aqueous electrolytes with low, intermediate, and high ZnSO₄ concentrations. In each of the three cases, a critical overpotential exists, above which the i-V curve deviates from the linear relation as established in the initial, below-limiting ohmic region. The ohmic behavior observed at small potentials indicates that mass transport is sufficiently fast to replenish the ion consumption by the reaction so that the electrolyte conductivity remains unchanged (20, 47, 48). As the current density approaches a critical value, i.e., the limiting current, the curve slope decreases, which is indicative of the reduced conductivity caused by ion depletion. The observed limiting current densities are 300, 50, and 5 mA/cm² in 2.5, 0.5, and 0.05 M electrolytes, respectively. Our observations are consistent with the linear relationship between i_L and the electrolyte salt concentration. As the overpotential further increases, an overlimiting region is observable, again consistent with expectations based on the classical theory outlined in the introduction. This increase in slope is thought to reflect the initiation of additional mechanism(s) (e.g., electroconvection) that enhance the mass transport and thereby helps to overcome the diffusion limit.

Fig. 2. Electrochemical measurements of Zn electrodeposition.

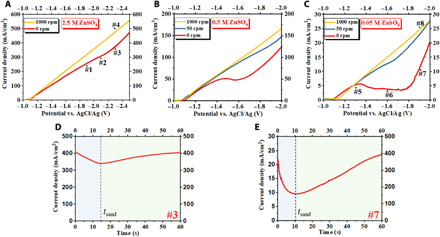
Current-voltage (i-V) curves of Zn electrodeposition on a glassy carbon electrode at a scan rate of 5 mV/s in (A) 2.5 M, (B) 0.5 M, and (C) 0.05 M ZnSO₄ (aq) electrolytes. Time-dependent current measured in constant-voltage, chronoamperometric Zn electrodeposition in the overlimiting transport regime: (D) 2.5 M and (E) 0.05 M ZnSO₄ (aq) electrolyte. For the results in (D), the potential was held at −2.3 V, and in (E) at −1.9 V versus (AgCl/Ag).

The results described by the red curves should be compared with the curves in yellow and blue plotted in Fig. 2 (A to C), which show the i-V responses under similar conditions but measured with electrode rotation. With the normal flow–assisted mass transport in the RDE, the limiting and overlimiting regions of the i-V curve are noticeably absent at the higher rotation rate; instead, an ohmic region showing a linear i-V relation holds throughout the entire sweep. It confirms that the changes of the i-V curve slope observed in the cases without normal flow, including the decrease and the increase, are attributable to mass transport in the liquid electrolyte bulk. Comparing Fig. 2 (A to C), we therefore conclude that, in both the dilute and concentrated electrolytes, mass transport–governed limiting and overlimiting behaviors play an important role in ion transport in the electrolyte bulk and would therefore be expected to influence electrodeposition of Zn.

To understand the mechanisms leading to the transition from limiting to overlimiting ion transport, in concentrated and dilute ZnSO₄ [aqueous (aq)] electrolytes, we characterized the microstructure of Zn electrodeposits obtained from chronoamperometry, i.e., constant-potential deposition for a certain period of time. Potentials that correspond to below-limiting, limiting, and overlimiting conditions as evidenced in Fig. 2 (A and C) were used in the study. We also monitored the time-dependent currents in the chronoamperometric deposition experiments. For applied potential corresponding to an overlimiting region, the current density profile exhibits a negative slope before the current minimum is reached at the Sand’s time (Fig. 2, D and E), implying that the concentration of metal cations falls to zero in a fluid layer near the electrode surface (49). Sand’s time can be calculated using the formula $t_{\text{sand}}=\mathrm{\pi }D\frac{{(\mathit{zCF})}^2}{4{(i(1-t_{+}))}^2}$, where t₊ is the cation transference number. The estimated Sand’s times for the 2.5 and the 0.05 M electrolytes are thus determined to be 11.2 and 8.5 s, respectively. We note further that both estimates are of comparable order of magnitude to the experimentally observed values. Subsequently, the current density increases after the Sand’s time, indicative of the initiation of additional mass transport mechanism(s). These observations from chronoamperometric electrodeposition are in good agreement with the linear sweep results discussed earlier.

The main results of the study are presented in Figs. 3 and 4. They show the morphological evolution of Zn under different conditions revealed by scanning electron microscopy (SEM). The numbers on the left side of the images indicate the deposition potentials and rotation rate as labeled in Fig. 2 [A (#1 to #4) and C (#5 to #8)] at which the measurements were performed. The rather clear but unexpected observation is that whereas classical, tree-like and highly branched dendrites are observed in the dilute electrolyte under mass transfer–controlled conditions (Fig. 4, C to F), the Zn deposited from concentrated electrolytes under these conditions exhibits a morphology that is obviously nondendritic. Instead, the Zn deposits as vertically aligned platelets with diameter, Φ, in the range 10 to 20 μm. Note that the areal deposition capacity used for the measurements is around 6 mAh/cm² (estimated using the current density and deposition time), which is beyond the usual areal capacity, i.e., <2 mAh/cm², used in Zn battery studies using mild pH electrolytes (50–52). The morphology formed in the overlimiting region can be compared with the Zn morphology formed in the below-limiting regime (Fig. 3, A and B) or under the influence of normal flow (Fig. 3, G and H) in the RDE, where the plates are observed to be clearly aligned in the plane of the electrode. The vertical alignment of Zn electrodeposits, as opposed to dendritic growth, has to our knowledge not been reported previously.

Fig. 3. SEM images showing morphological evolution of Zn electrodeposits in a concentrated, 2.5 M ZnSO₄ (aq) electrolyte at different potentials.

Values of (A and B) −1.9 V, (C and D) −2.1 V, and (E and F) −2.3 V without rotation and (G and H) −2.3 V with 1000 rpm rotation. Deposition time, 60 s.

Fig. 4. SEM images showing morphological evolution of Zn electrodeposits in a dilute, 0.05 M ZnSO₄ (aq) electrolyte at different potentials.

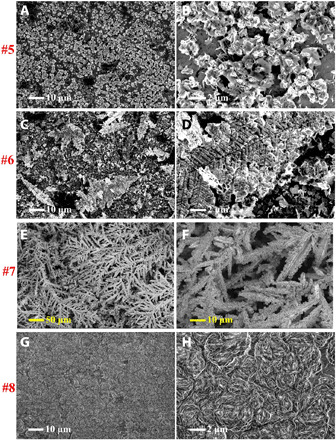
Values of (A and B) −1.3 V, (C and D) −1.6 V, and (E and F) −1.9 V without rotation and (G and H) −1.9 V with 1000 rpm rotation. Deposition time, 60 s.

The ease with which rotation switches the plate alignment from vertical to horizontal, the correlation of the onset of Zn platelet alignment with transported-limited deposition, and the absence of classical dendritic growth in the concentrated electrolytes under transport-limited conditions lead us to hypothesize that the plate-like Zn electrodeposits may undergo a reorientation transition to maximize access to the supply of ions just outside the depletion zone. As a first test of this hypothesis, we performed optical microscopy to visualize the morphology at a larger scale (fig. S1). The results show that the Zn morphology formed in dilute electrolyte is highly heterogeneous, featuring aggressively extending dendrites. In contrast, the Zn deposition morphology in concentrated electrolyte is homogeneous at the optical scale.

The observation that Zn tends to form plate-like deposits in concentrated electrolytes is consistent with previous postmortem analysis of Zn battery anodes (5). Because of the anisotropy of the hexagonal close-packed (HCP) zinc crystal, Zn preferentially exposes the basal plane, i.e., (002), which has the highest atomic packing density, to minimize its surface free energy. In other words, the plane normal of the plate-like Zn electrodeposits is parallel to the [002] direction of Zn crystal. On the basis of this connection between the microstructure and the crystal structure of Zn, the reorientation process from horizontal alignment in the below-limiting regime to vertical alignment in the overlimiting regime changes the texturing behavior of the deposits and therefore can be quantified using x-ray diffraction (XRD; see Fig. 5). The texturing behavior is characterized by the peak intensity ratio between (002)_Zn and (101)_Zn, as can be discerned in the line scan plot (Fig. 5A) and the 2D scan plot (Fig. 5, C to F). A greater I₀₀₂:I₁₀₁ means the deposit is more (002)-textured, i.e., more (002) planes are parallel to the substrate. As shown in Fig. 5B, the I₀₀₂:I₁₀₁ decreases from 5.2 to 0.6 as the overpotential increases. Under the influence of flow-assisted mass transport, the Zn deposits exhibits a strong (002) texturing, as indicated by the I₀₀₂:I₁₀₁ as high as 25. These XRD analyses statistically confirmed the reorientation growth induced by mass transport limit.

Fig. 5. X-ray analysis of the crystallographic evolution of Zn during electrodeposition in a concentrated, 2.5 M ZnSO₄ (aq) electrolyte with and without normal flow.

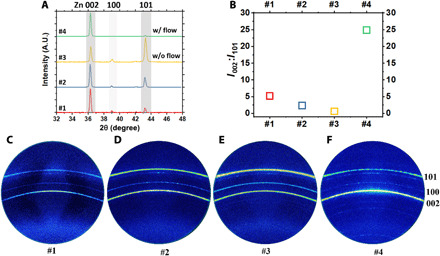
(A) XRD line scan patterns for the Zn electrodeposits. A.U., arbitrary units. (B) Peak intensity ratio of the Zn 002:101 deduced from the line scans in (A). 2D XRD patterns of Zn electrodeposited at (C) −1.9 V, (D) −2.1 V, and (E) −2.3 V without rotation and (F) −2.3 V with 1000 rpm rotation.

To determine the consequence of our observation on reversibility of a Zn electrode, we evaluated the plating/stripping efficiency of the Zn electrodeposits. The reoriented Zn plates formed in the overlimiting regime exhibit Coulombic efficiencies of 80 to 90% at different areal deposition capacities (see blue points in Fig. 6A), which are similar to the reported Zn plating/stripping efficiencies in battery anodes reported in the literature (5, 46). These values are significantly higher than the Coulombic efficiencies of 15 to 65% achieved by the classical dendrites formed in dilute electrolytes (fig. S2). As shown by the red points in Fig. 6 (A and B), the compact, planar Zn deposits formed under the influence of normal flow have a close to unity (~99.6%) reversibility. These results indicate that the electrodeposition morphologies are strongly influenced by salt concentration, normal flow, and deposition conditions, and that the electrodeposit morphology directly determines the plating/stripping reversibility of a metal.

Fig. 6. Electrochemical reversibility of Zn electrodeposits measured in a 2.5 M ZnSO₄ (aq) electrolyte.

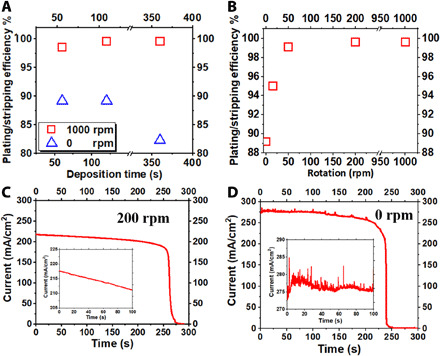
(A) Coulombic efficiency for Zn plating/stripping with and without rotation. (B) Coulombic efficiency for Zn plating/stripping at different RDE rotation rates. Time-dependent evolution of the current density during stripping of Zn deposited (C) with and (D) without normal flow.

Clues to interpreting the difference in reversibility between the nonplanar, reoriented Zn and the planar Zn can be discerned from Fig. 6 (C and D). As illustrated in the scheme (fig. S3), on a planar, compact Zn electrode, the stripping reaction evenly occurs at the interface between the metal and the liquid electrolyte; in contrast, the stripping of a porous, nonplanar Zn can proceed inside the structure, leading to the mechanical disconnection/reconnection of metal deposits (forming “dead” metal). This is evidenced in the results by the spiky current profile in the inset to Fig. 6D (28). These observations have obvious implications for battery anode design. Specifically, they show that although the porous Zn deposits formed by reorientation growth, as opposed to dendritic growth, are homogeneous over the electrode surface, they offer a plating/stripping efficiency that is far too low to meet the requirements of viable battery system (i.e., >99%). For stationary batteries, our results suggest that an obvious strategy to curb the reorientation growth is to introduce artificially generated normal flow to reorient the Zn plates. For portable batteries, an interphasial coating on the substrate that can epitaxially promote the planar, (002)-textured Zn growth has been suggested as an approach for crystallographic regulation of the deposition process (5).

DISCUSSION

An intriguing and fundamentally important question is—what mechanism(s) leads to the distinction between the overlimiting Zn morphologies in the dilute and the concentrated electrolytes? As the length scales of the Zn electrodeposited microstructures extending from the electrode surface into the electrolyte are quite different in the two cases (e.g., Φ_plate ≈ 10 to 20 μm, for reorientation growth in 2.5 M electrolyte versus a primary dendrite arm length L_arm > 200 μm for the nonplanar growth in a 0.05 M electrolyte), we hypothesize that these morphologically expressed length scales are a reflection of underlying transport length scales in the electrolyte, e.g., diffusion layer thickness δ_DL and/or ESCL thickness δ_ECSL, which control electrochemical access of the growing electrodeposit structures to Zn²⁺ ions in solution.

We calculated δ_ESCL and δ_DL for the three ZnSO₄(aq) electrolyte compositions used in the study: δ_ESCL(2.5M) ≈ 1.6 μm, δ_DL(2.5M) = 41 μm; δ_ESCL(0.5 M) ≈ 3.5 μm, δ_DL(0.5 M) = 71 μm; δ_ECSL (0.05 M) ≈ 5.6 μm, δ_DL(0.05 M) = 256 μm. It is noticeable that δ_DL is consistently closer to the average size of the Zn structures observed in the SEM images [e.g., Φ_plate (2.5 M) is of the same order of magnitude, i.e., 10¹ μm, as δ_DL(2.5 M) and δ_DL(0.05 M) and the characteristic length of primary dendrite arms is of the same order of magnitude, i.e., 10² μm]. This suggests that the Zn electrodeposit growth is constrained to the diffusion layer thickness and that the Zn deposits grow to the point where mass transport limitations in the liquid electrolyte are just overcome, as illustrated in Fig. 1 (A and B). In addition to the characteristic lengths, the specific geometries of the electrodeposits can be understood based on this analysis. Plates are 2D structures that extend not only toward the bulk electrolyte but also sideways; in contrast, dendrites show 1D characteristics, by extending primarily toward the bulk electrolyte (Fig. 1, A and B). In a dilute electrolyte, as the diffusion layer is thickened, the electrodeposits appear to adopt the more efficient growth mode, i.e., the latter 1D dendritic pattern, to overcome the mass transport limitation.

The increase in magnitude of δ_ESCL with increasing ion concentration nonetheless offers an alternative explanation. Specifically, previous literature reports indicate that the electroosmotic slip velocity at the edge of ESCL generated by electroconvective flow may also produce a nonuniform ion flux to the electrode, driving preferential growth at dendrite tips (53, 54). Related works show that the electroconvective flow can be readily attenuated by imposition of a convective cross flow (35, 55). We measured the average diameter Φ of the Zn platelets obtained after a fixed deposition time of 60 s (see Fig. 3) as a function of overpotential V to determine whether the classical δ_ECSL ~ V^2/3 scaling relation holds. The results reported in fig. S4 show that Φ_plate increases more strongly than V^2/3 and that the relationship is nearly linear. The N-P equation predicts a linear relation between the cation flux N₊ and the overpotential. For a fixed deposition time and surface area, this would lead to the trivial result Φ_plate ∝ V, as a larger electrodeposition amount is accumulated in the sheets over a fixed deposition time. Thus, we conclude that δ_DL is the dominant length scale that determines the size of the Zn plates.

We next studied how variations in the diffusion layer thickness influence the average size of the deposits. It is known that a convective flow produced by rotating the electrode in its plane at an angular speed ω produces a diffusion layer thickness ${\mathrm{\delta }}_{\text{DL}}=1.61D^{\frac{1}{3}}{\mathrm{\omega }}^{-\frac{1}{2}}{\mathrm{\upsilon }}^{\frac{1}{6}}$, which can be systematically altered through control of ω (33). Here, υ is taken as the kinematic viscosity of the electrolyte solvent, and we estimate δ_DL under the influence of normal flow in the RDE as follows: δ_DL(2.5 M,1000 rpm) = 10.5 μm; δ_DL(0.05 M,1000 rpm) = 13.3 μm. In both cases, the estimated δ_DL is smaller than the length scale of the microstructure observed in the overlimiting region without flow, implying that both the reorientation growth observed in a concentrated electrolyte and the dendritic growth in a dilute electrolyte can be suppressed in the 1000 rpm case, which is precisely what we observe.

Considering that the analysis above does not involve the specific chemistry of Zn, e.g., its crystal structure, we anticipate that analogous phenomena should be observable for other metals. To examine this, we performed a comparative study of Cu electrodeposition in dilute (0.05 M) and concentrated (1 M) aqueous CuSO₄ electrolytes. The selection of Cu deposition from CuSO₄ (aq) is mainly based on the following considerations: (i) both Zn and Cu do not form a passivating SEI like Li does (28, 56) that introduces additional complexity in ion transport, and (ii) Zn and Cu have a hexagonal and a cubic crystal symmetry, respectively. Therefore, a comparison between them can rule out the possibility that the observed phenomenon, i.e., the suppression of dendritic growth in battery concentration electrolyte, is specific to hexagonal metals, e.g., Zn. The results are reported in figs. S5 and S6, and their interpretation is straightforward—in 1 M CuSO₄, tree-like Cu dendrites are not observed in the overlimiting regime; instead, similar to the Zn case, Cu deposits in high-porosity morphologies that again, like Zn, appear macroscopically homogeneous, suggesting that the deposition interface is stable. In contrast, the Cu deposits formed under overlimiting conditions in the dilute 0.05 M CuSO₄ (aq) electrolyte exhibit obvious heterogeneous, dendritic morphology (figs. S7 and S8).

As a final question, it would be of broad interest to determine the relevance of our observations to other metals, including cubic Li, Na, K, Al, and hexagonal Mg. We note that these metals also form SEIs in liquid media, which is commonly thought to play a decisive role in their electrodeposition morphology. A preliminary assessment of Li electrodeposition in 1 M LiPF₆ in carbonate-based electrolyte is provided in figs. S9 and S10. Consistent with the results of Zn and Cu, no branched, tree-like dendritic structures are discernible in the moderately concentrated, 1 M electrolyte. Instead, highly porous, moss-like structures are formed, and the degree of porosity develops, as the deposition condition moves from the below-limiting regime to the overlimiting regime. Further exploration of the concept in the context of the electrodeposition of reactive metals that form SEI could be made with specific attention being paid to the potential influence of SEI on ion transport from the bulk electrolyte toward the deposition interface.

MATERIALS AND METHODS

Materials

Zn foil (99.9%) (0.25 mm), ZnSO₄·7H₂O, and battery-grade 1 M LiPF₆ dissolved in ethylene carbonate/dimethyl carbonate were purchased from Sigma-Aldrich. Li metal foil (750 μm) and CuSO₄·7H₂O were bought from Alfa Aesar. Cu foil was bought from MTI. Deionized water was obtained with a Milli-Q water purification system. The resistivity of the deionized water is 18.2 megohm·cm at room temperature.

Preparation of electrolytes

Zn electrolytes: ZnSO₄·7H₂O was dissolved into the deionized water to prepare the ZnSO₄ electrolytes for Zn electrodeposition. Cu electrolytes: CuSO₄·5H₂O was dissolved into the deionized water to prepare the CuSO₄ electrolyte for Cu electrodeposition. Li electrolyte was used as received from Sigma-Aldrich (commercial battery-grade 1 M LiPF₆ in ethylene carbonate/dimethyl carbonate, 1:1). All electrolytes were rested overnight before use.

Electrodeposition

The electrodeposition experiments in the present study were performed using a three-electrode system, including a working electrode made of glassy carbon, a counter electrode made of metal foils (Zn foil, Cu foil, or Li foil), and a reference electrode (AgCl/Ag for Zn and Cu deposition and Li foil for Li deposition). The substrate used for metal electrodeposition (i.e., the working electrode) is a glassy carbon electrode provided by with a mirror polish finish achieved by submicrometer alumina powder. Both the glassy carbon electrode and the RDE system were purchased from Pine Research. During the electroplating/stripping process, no bubbling is observable near the working electrode, which is attributable to the sluggish kinetics of the H₂ evolution reaction in this system. After electrodeposition, the obtained deposits on the working electrode were washed by deionized water for three times before materials characterization. In the washing protocol, the deionized water was slowly pipetted onto the electrode surface. For Li deposition, the apparatus was moved into Ar-filled glovebox to protect Li and the electrolyte against oxidants and moisture. The Li electrodeposits were washed using pure dimethyl carbonate to prepare them for characterization by SEM. All Li samples were transferred into the microscope under Ar gas protection.

Characterization of materials

Field-emission SEM was carried out on the Zeiss Gemini 500 Scanning Electron Microscope. Linear sweep voltammetry and chronoamperometry were performed using a CH 600E electrochemical workstation. 2D XRD was performed on the Bruker D8 General Area Detector Diffraction System with a Cu Kα x-ray source.

Coulombic efficiency measurement

Chronoamperometric plating/stripping of metals was conducted on glassy carbon electrode using three-electrode configuration. The metal plating/stripping $\text{Coulombic efficiency} (\text{CE})=\frac{\text{stripping capacity}}{\text{plating capacity on the substrate}}\times 100\%$, which quantifies the reversibility of the metal anode. For example, CE = 100% means that all the plated Zn on the substrate can be stripped, while CE = 80% means that 80% of plated Zn can be stripped and 20% Zn is electrochemically inactive.

SUPPLEMENTARY MATERIALS

Supplementary material for this article is available at http://advances.sciencemag.org/cgi/content/full/6/25/eabb1122/DC1