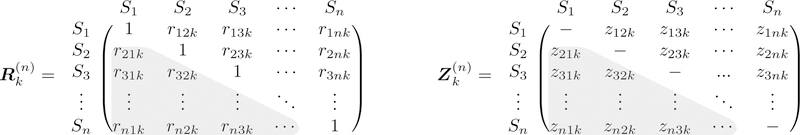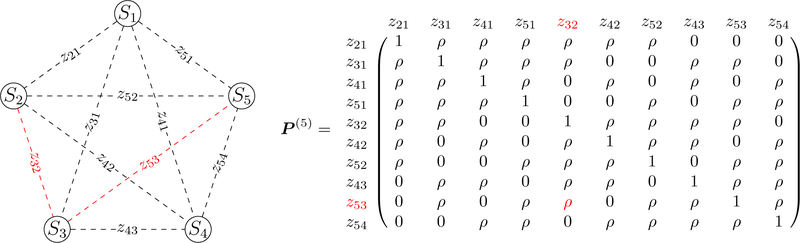Untangling the Relatedness among Correlations, Part III: Inter-Subject Correlation Analysis through Bayesian Multilevel Modeling for Naturalistic Scanning

Abstract

While inter-subject correlation (ISC) analysis is a powerful tool for naturalistic scanning data, drawing appropriate statistical inferences is difficult due to the daunting task of accounting for the intricate relatedness in data structure as well as handling the multiple testing issue. Although the linear mixed-effects (LME) modeling approach (Chen et al., 2017a) is capable of capturing the relatedness in the data and incorporating explanatory variables, there are a few challenging issues: 1) it is difficult to assign accurate degrees of freedom for each testing statistic, 2) multiple testing correction is potentially over-penalizing due to model inefficiency, and 3) thresholding necessitates arbitrary dichotomous decisions. Here we propose a Bayesian multilevel (BML) framework for ISC data analysis that integrates all regions of interest into one model. By loosely constraining the regions through a weakly informative prior, BML dissolves multiplicity through conservatively pooling the effect of each region toward the center and improves collective fitting and overall model performance. In addition to potentially achieving a higher inference efficiency, BML improves spatial specificity and easily allows the investigator to adopt a philosophy of full results reporting. A dataset of naturalistic scanning is utilized to illustrate the modeling approach with 268 parcels and to showcase the modeling capability, flexibility and advantages in results reporting. The associated program will be available as part of the AFNI suite for general use.

Introduction

Naturalistic scanning provides a window into shared brain responses at the population level under scenarios such as watching movies or listening to speech (Hasson et al., 2004, 2008). With minimal manipulation and dynamically evolving context, the naturalistic paradigm is closer to real-life experiences and more engaging than typical task-related experiments, and less vulnerable to confounds such as head motion and physiological artifacts than resting-state acquisitions. Under a context closer to the natural environment, neural responses are more reproducible and reliable than traditional simple repetitive stimuli (Hasson et al., 2010) due to the involvement of extensive cognitive processing (such as working memory, judgment, reasoning, social cognition, etc.). Its adoption has been steadily growing in investigating various aspects of brain function such as music imagery (Zhang et al., 2017), early childhood development (Moraczewski et al., 2018), personality traits (Finn et al., 2018) and mental illnesses and disorders (Salmi et al., 2013, Guo et al., 2015).

For typical task-related designs, the focus is usually on identifying regions activated by an explicit task or condition. In contrast, the interest for naturalistic scanning often hinges on the synchronization or similarity between any pair of subjects. For example, one major analytical approach is to calculate the inter-subject correlation (ISC) or the Pearson correlation between the EPI time series at the same voxel or region of the two subjects. In the end, the main issue is to summarize the results at the population level because of the complex relatedness among the subject pairs.

Various methods including both parametric and nonparametric approaches have been developed over the years to handle the complex relatedness in ISC analysis (Bartels and Zeki, 2004; Hasson et al., 2008a; Wilson et al., 2008; Abrams et al., 2013; Kauppi et al., 2014; Schmälzle et al., 2013; Cantlon and Li, 2013; Schmälzle et al., 2015). For example, a popular but problematic approach is to first calculate the ISC value between a voxel’s BOLD time course of a subject and the average of that voxel’s BOLD time course among all other subjects (Kauppi et al., 2010; Honey et al., 2012; Schmälzle et al., 2013; Schmälzle et al., 2015), and then perform the typical group analysis (e.g., Student’s t-test) under the false assumption that all the ISC values are independent across subjects. Recently, we examined the validity of those methods, and proposed more rigorous approaches (Chen et al., 2016; Chen et al., 2017a), among which the most flexible one in terms of analytical capability is linear mixed-effects (LME) modeling with a crossed random-effects structure (Chen et al., 2017a).

Preamble

We summarize briefly the background, notations, framework, and structure of the ISC group analysis that were introduced in our previous work (Chen et al., 2016, Chen et al., 2017a), since some shared concepts apply to the model formulation introduced here. Throughout this article, italic letters in lower case (e.g., α) stand for scalars; lowercase, boldfaced italic letters (a) and upper (X) cases for column vectors and matrices, respectively. With one group of n > 2 subjects S₁, S₂, …., S_n and m spatial units (voxels or regions), the total number of unique ISC values per spatial unit is $N=\frac{1}{2}n(n-1)$. For the kth spatial unit (k = 1, 2, …, m), the ISC values {r_ijk} correspond to N subject pairs, and they form a symmetric (r_ijk = r_jik, i, j = 1, 2, …, n) n × n positive semi-definite matrix ${\mathit{R}}_k^{\left(n\right)}$ with diagonals r_iik = 1 (Fig. 1, left). Their Fisher transformed version ${\mathit{Z}}_k^{\left(n\right)}$ (Fig. 1, right) through z = arctanh(r) is usually adopted during analysis so that methods assuming Gaussian distribution may be utilized, as Fisher z-values are more likely to be Gaussian-distributed than raw Pearson correlation coefficients. Because ${\mathit{R}}_k^{\left(n\right)}$ and ${\mathit{Z}}_k^{\left(n\right)}$ are both symmetric in (i, j), inferences at the population level can be made through the N elements in the lower triangular part (i > j, shaded gray in Fig. 1).

Figure 1:

Inter-subject correlation (ISC) matrix ${\mathit{R}}_k^{\left(n\right)}$ among the n subjects for the kth spatial unit and its Fisher-transformed counterpart ${\mathit{Z}}_k^{\left(n\right)}$. Due to the symmetry, only half of the off-diagonal elements (shaded in gray) are usually considered during ISC analysis.

The general interest of ISC analysis at the population level is the statistical inference about the population effect for each spatial unit. However, a complex issue to manage is that each ISC matrix element is correlated with some of others (Chen et al., 2017a). Suppose that $z_{i_1{j}_{1}k}$ and $z_{i_2{j}_{2}k}$ are two z-values that are associated with the ISC values of the kth spatial unit, $r_{i_1{j}_{1}k}$ and $r_{i_2{j}_{2}k}$, of two subject pairs. When any pair of two elements in the ISC matrix, $z_{i_1{j}_{1}k}$ and $z_{i_2{j}_{2}k}$, involve four separate subjects (i.e., i₁ ≠ i₂ and j₁ ≠ j₂), we assume that the two elements are unrelated; that is, their correlation is 0. We denote the correlation between any two elements, $z_{i_1{j}_{1}k}$ and $z_{i_2{j}_{2}k}$, that pivot around a common subject (e.g., i₁ = i₂ or j₁ = j₂) as ρ, with the assumption that the relatedness ρ remains the same across all subjects¹. In other words, ρ characterizes the inter-relatedness of $z_{i_1{j}_{1}k}$ and $z_{i_1{j}_{2}k}$ among the three subjects among which the two subject pairs share a common subject. To consider the group-wide set of ISCs, we further define ${\mathit{z}}_k=vec\left(\right\{z_{ijk},i>j\left\}\right)$ to be the vector of length N whose elements are the column-stacking of the lower triangular part of the matrix Z⁽ⁿ⁾ in Fig. 1. That is, z is the half-vectorization of ${\mathit{Z}}_k^{\left(n\right)}$ excluding the main (or principal) diagonal:${\mathit{z}}_k=vech\left({\mathit{Z}}_k^{\left(n\right)}\right)\backslash diag\left({\mathit{Z}}_k^{\left(n\right)}\right)$. The variance-covariance matrix of z_k can be expressed as the N × N matrix,

$${\mathrm{\Sigma }}^{\left(n\right)}={\mu }^2{\mathit{P}}^{\left(n\right)},$$ (1)

where µ² is the variance of z_ijk, i > j, and P ⁽ⁿ⁾ is the correlation matrix that is composed of 1 (diagonals), ρ and 0. An example of P ⁽⁵⁾ is shown in Fig. 2. It has been analytically shown (Chen et al., 2016) that −1/[2(m − 2)] ≤ ρ ≤ 0.5 (when m > 3), and because of the presence of correlations among some elements of ${\mathit{Z}}_k^{\left(n\right)}$, it becomes crucial to capture this correlation structure P ⁽ⁿ⁾ in any modeling framework.

Figure 2:

ISC with n = 5 subjects. Left: pictorial representation of 5 × 5 subject pairs. Right: The complex relatedness among the off-diagonal elements in ${\mathit{Z}}_k^{\left(n\right)}$ is illustrated with the correlation matrix P ⁽⁵⁾ for n = 5 subjects, in which ρ represents the correlation when two elements (e.g., z32 and z53, colored in red) are associated with a common subject (e.g., S3). Without loss of generality, the third index k in z_ijk for brain location is dropped here for clarity.

The situation with two groups can be similarly formulated (Chen et al., 2016; Chen et al., 2017a). Previously both nonparametric and parametric methods have been proposed to handle ISC analysis at the population level. Here we briefly summarize those methods, and lay out the background and motivations for our current work.

ISC analysis with conventional approaches

Early pioneering work with naturalistic stimuli was conducted either within each subject when the natural stimulus was repeated several times (Hasson et al., 2008b) or through ISC for each subject pair separately without summarization at the group level (Hasson et al., 2004), in which case the ISC results were typically verified through seed-based correlation analysis (Hasson et al., 2004; Hasson et al., 2008b; Schmälzle et al., 2013). Later on, some investigators simply ran one-sample (Bartels and Zeki, 2004; Hasson et al., 2008a; Wilson et al., 2008; Abrams et al., 2013; Kauppi et al., 2014), two-sample (Schmälzle et al., 2013; Cantlon and Li, 2013) or paired (Abrams et al., 2013; Schmälzle et al., 2015) t-tests on Fisher-tranformed z-values {z_ijk, i > j} of correlation coefficients, while it was generally acknowledged that the N elements {z_ijk, i > j} were not independent, as illustrated in the correlation structure of P⁽ⁿ⁾ in (1), thereby violating the independence assumption in the Student’s t-test and leading to the inflated degrees of freedom for the t-distribution as well as the underestimated standard error for the ISC estimate. The approach was mainly justified based on the observation that the null results generated by shifting each pair of time series by random steps roughly fitted to a t(N − 1)-distribution curve (Wilson et al., 2008).

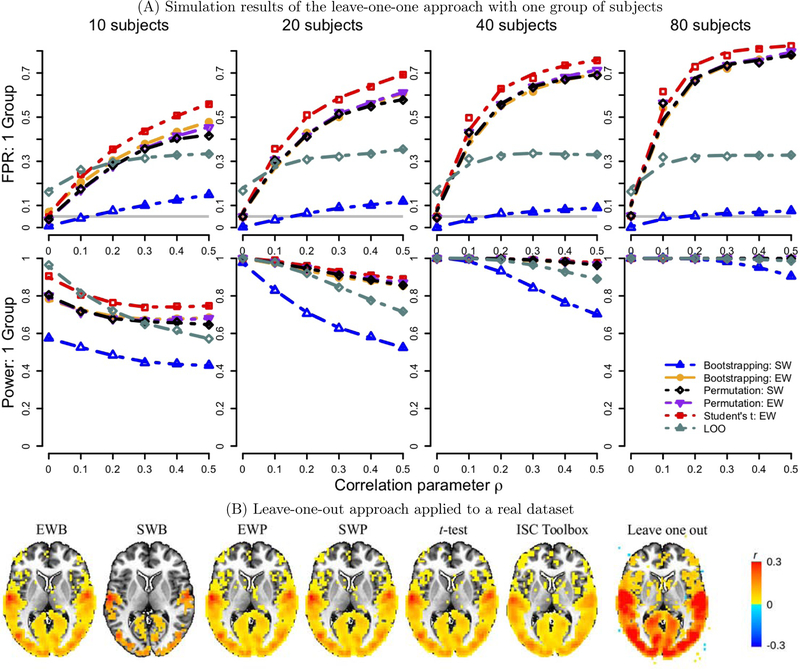
Previous studies have also proposed nonparametric methods. For example, one popular approach with one group of subjects is to construct a null distribution for the whole brain by randomizing the time series across voxels and time points (e.g., circularly shifting each subject’s time series by a random lag so that they were no longer aligned in time across the subjects), as implemented into an analytical package ISC toolbox in Matlab (Kauppi et al., 2014; https://www.nitrc.org/projects/isc-toolbox/). Alternatively, phase randomization of EPI time series has also been adopted to construct a sampling distribution (e.g., Lerner et al., 2011). However, a recent study has shown that all of these methods lead to largely inflated false positive rate (FPR) (Chen et al., 2016). One variation of these ISC analytical approaches is called leave-one-out: first calculate the ISC value between a voxel’s BOLD time course in one subject and the average of that voxel’s BOLD time course in the remaining subjects (Honey et al., 2012; Schmälzle et al., 2013; Schmälzle et al., 2015); then, perform Student’s t-test at the group level. The step of averaging time series across subjects, as smoothing process, adds more complexity besides the issue of relatedness in the ISC data. As a result, the ISC estimates get substantially inflated without proper adjustment at the group level and the FPR controllability remains problematic (Fig. 5 in Appendix A).

Figure 5:

Comparisons of the leave-one-out (LOO) approach with other nonparametric methods explored in Chen et al. (2016). The subfigures shown here are copied from Figures 2 and 3 in Chen et al. (2016) with the LOO results added.(A) The simulations were performed in the same fashion with one group of 10, 20, 40 and 80 subjects as in our previous work with nonparametric methods (Chen et al., 2016). The LOO approach (dark green) showed unsatisfactory controllability on false positive rate at the nominal level of 0.05 (horizontal gray line) compared to subject-wise bootstrapping (dot-dashed blue line). (B) When applied to the same experiment dataset in Chen et al. (2016), poor false positive control was also evident; in addition, the ISC estimates were substantially inflated. The acronyms are inherited from Chen et al. (2016): SW (subject-wise) EW (element-wise), EWB (element-wise bootstrapping), SWB (subject-wise bootstrapping), EWP (element-wise permutations) and SWP (subject-wise permutations).

A new set of nonparametric approaches, based on subject-wise resampling at the population level, has been proposed recently (Chen et al., 2016). In addition to satisfying exchangeability and independence assumptions and accounting for the correlation structure in P⁽ⁿ⁾, it was shown that proper FPR controllability under the conventional null hypothesis significance testing (NHST) can be achieved with subject-wise bootstrapping for ISC analysis with one group and with subject-wise permutation testing for the ISC comparison between two groups.

However, nonparametric methods are limited in terms of modeling flexibility. For instance, they have difficulty in incorporating explanatory variables; in addition, they are deficient, unwieldy and unconducive to data structure characterization and model comparisons. To counter these limitations, a linear mixed-effects (LME) modeling approach has been adopted (Chen et al., 2017a) with the benefit that the LME platform offers wider adaptability, more powerful interpretations, and greater quality control capability than nonparametric methods. Specifically, the LME model with crossed random effects is applied with a data-doubling step that further conveniently tracks the subject index in easy implementations.

ISC analysis with univariate linear mixed-effects modeling

Our previous work (Chen et al., 2017a), as implemented in the AFNI (Cox, 1996) program 3dISC, adopts a linear-effects model by decomposing an ISC effect z_ijk into multilevel components associated with subjects i and j at the kth voxel (k = 1, 2, …, m),

$$z_{ijk}={\tilde{b}}_{0k}+{\tilde{\xi }}_{ik}+{\tilde{\xi }}_{jk}+{\widetilde{ϵ}}_{ijk},\hspace{0.17em}\hspace{0.17em}i,j=1,2,\hspace{0.17em}\mathrm{..},n\hspace{0.17em}(i>n),$$ (2)

where ${\tilde{b}}_{0k}$ is the fixed effect (an unknown constant) under LME, representing the population ISC effect at the kth voxel or region; ${\tilde{\xi }}_{ik}$ and ${\tilde{\xi }}_{jk}$ are additive and independent random effects attributable to subjects i and j, respectively, that are deviations from the population ISC effect ${\tilde{b}}_{0k}$; and ${\widetilde{ϵ}}_{ijk}$ is the residual or error term for each subject pair (i, j). Due to the symmetry of the data in ${\mathit{Z}}_k^{\left(n\right)}$, only half of the elements excluding the diagonals (either the lower or upper triangular part) are utilized in the model (2), and thus the index inequality of i > j is placed for the input data. As a special LME model, the formulation (2) can actually be conceptualized as a two-way random-effects ANOVA with the two subject-specific terms serving as random-effects factors. The two random effects ${\tilde{\xi }}_{ik}$ and ${\tilde{\xi }}_{jk}$ form a stratified or crossed structure with a factorial (or combinatorial) layout among the levels (or indices) i and j of the two subject-specific factors.

One important aspect of the LME framework, which nonparametric methods lack, is that the interrelationships among the ISC values, as characterized in the correlation matrix P⁽ⁿ⁾, can be quantitatively captured. With the assumption of independent Gaussian distributions, ${\tilde{\xi }}_{ik}$, ${\tilde{\xi }}_{jk}\stackrel{iid}{~}\mathcal{N}(0,\hspace{0.17em}{\tilde{\lambda }}_k^2)$ and ${\widetilde{ϵ}}_{jk}\stackrel{iid}{~}\mathcal{N}(0,\hspace{0.17em}{\tilde{\sigma }}_k^2)$, the model (2) can be solved under LME. A big advantage of the LME model (2) over the nonparametric methods is the capability of characterizing as well as maintaining the integrity of the data structure. For example, the correlation ρ, as captured in P⁽ⁿ⁾ of (1), between any two ISC effects that pivot around a common subject is related to intraclass correlation (ICC) and can be expressed as (Chen et al., 2017a),

$$0\le \rho =\frac{{\tilde{\lambda }}_k^2}{2{\tilde{\lambda }}_k^2+{\tilde{\sigma }}_k^2}\le \mathrm{0.5.}$$ (3)

The LME model (2) can be easily extended to scenarios where the investigator would like to incorporate one or more subject-specific explanatory variables, either categorical (e.g., sex) or quantitative (e.g., age). For example, a model with one explanatory variable x can be formulated as,

$$z_{ijk}={\tilde{b}}_{0k}+{\tilde{b}}_{1k}{x}_i+{\tilde{b}}_{2k}{x}_j+{\tilde{\xi }}_{ik}+{\tilde{\xi }}_{jk}+{\widetilde{ϵ}}_{ijk},\hspace{1em}i>j,$$ (4)

where x_i and x_j are the x values for subjects i and j, respectively. Their corresponding effects ${\tilde{b}}_{1k}$ and ${\tilde{b}}_{2k}$ are presumably equal, but in the practical implementation of subject-specific effects through two separate components, the two fixed effects of ${\tilde{b}}_{1k}$ and ${\tilde{b}}_{2k}$ that are associated with the explanatory variable x would also have to be estimated separately through data duplication. The situation with more than one explanatory variable would be similar, and this modeling strategy has been applied at the whole-brain voxel level to a few studies (e.g., Moraczewski et al., 2018; Finn et al., 2018).

Nevertheless, the LME framework faces a few challenges. First, input data has to be duplicated in currently available implementations. Even though the random effects, ${\tilde{\xi }}_{ik}$ and ${\tilde{\xi }}_{jk}$, are assumed to follow the same Gaussian distribution $\mathcal{N}(0,{\tilde{\lambda }}^2)$, they would have to be treated as two separate components in practice through implementations (e.g, function lmer in the R package lme4 ). Furthermore, due to the fact that only half of the off-diagonal elements in ${\mathit{Z}}_k^{\left(n\right)}$ are utilized as input, ${\tilde{\xi }}_{ik}$ and ${\tilde{\xi }}_{jk}$ are generally not evenly arranged among all the subject pairs, leading to unequal estimation of the two components. On the one hand, ${\tilde{\xi }}_{ik}$ and ${\tilde{\xi }}_{jk}$ are basically cycled through those random effects from the n subjects, ${\tilde{\xi }}_{1k},{\tilde{\xi }}_{2k},\hspace{0.17em}\dots \hspace{0.17em},{\tilde{\xi }}_{nk}$, and the order of ${\tilde{\xi }}_{ik}$ and ${\tilde{\xi }}_{jk}$ can be rearranged without any impact on the model formulation. On the other hand, balance cannot be achieved under all scenarios. For example, when n is odd, a balance between the two factors can be achieved through the following: if the difference between i and j is odd, switch their order (i.e., z_ij effectively changes to z_ji); otherwise, no change is made. However, when n is even, balance cannot be reached but can be approximated with the first index alternatively one more (or less) than the second one². Nevertheless, even if balance can be established between the two sets of indices (i.e., n is odd), simulations indicate unsatisfying FPR control for the population effect. Because of this limitation, a data doubling strategy (i.e., i ≠ j) was used with both the lower (i > j) and upper (i < j) triangular parts of ${\mathit{Z}}_k^{\left(n\right)}$ as input to achieve the balance and proper FPR control (Chen et al., 2017a). As a result, in practice two copies of the variance ${\tilde{\lambda }}_k^2$ are estimated in (2) and (4) with the currently available implementation in the R package lme4, and inferences have to be properly adjusted to compensate for the inflated standard error (Chen et al., 2017a).

The second challenge is multiplicity. The LME model is analyzed through a massively univariate approach in which the same model is applied as many times as the number of voxels and with the presumption that all the voxels or regions are isolated and unrelated. Therefore, just as the typical neuroimaging data analysis with the massively univariate approach has to correct for multiple testing, so does such an ISC analysis face the issue of multiple testing, and has to be followed by an extra step: paying the price of multiplicity for the false assumption that no common information exists among voxels or regions. One approach is to control the overall FPR at the cluster level by leveraging the spatial extent among the neighboring voxels (“clustering”). Currently, permutation-based correction approaches through the integration of statistical evidence and spatial extent (e.g., Smith and Nichols, 2009) would be impractical due to the prohibitively high computation cost. On the other hand, cluster-based methods are purely based on leveraging spatial extent (e.g., Monte Carlo simulations, random field theory), thus it remains challenging to estimate the spatial correlation due to the difficulty in separating the pure noise from the signal. Specifically, cluster-size thresholds are determined based on the intrinsic smoothness of the data, which is estimated using the model residuals. However, it is not clear how to implement this method for naturalistic scanning with ISC-based methods, since there is no explicit (i.e., forward) model of the task, and therefore no residuals from which to estimate smoothness. Specific correction methods aside, the penalty is usually severe so that smaller brain regions may fail to survive the correction, in addition to other disadvantages of the massively univariate approach (Chen et al., 2019a; Chen et al., 2019b).

There are a few other limitations with the LME approach. For example, it remains difficult or even impossible to assign accurate degrees of freedom for each testing statistic under LME. In addition, the typical correction methods for multiple testing through spatial extent tend to dichotomize the statistical evidence and result in spatial clusters that are not necessarily aligned with anatomical structures in the brain, leading to interpretation ambiguities about spatial specificity. Lastly, correction for multiplicity tends to be over-penalizing (Chen et al., 2019a), and dichotomous decisions under NHST through thresholding are controversial in general (McShane et al., 2017; Amrhein and Greenland, 2017) and equally problematic in neuroimaging as well (Chen et al., 2019a). For instance, the popular practice of only reporting “statistically significant” results in neuroimaging not only wastes data information, but also distorts the full results as well as perpetuates the reproducibility crisis because of the fact that the difference between a “significant” result and a “non-significant” one is not necessarily significant (Cox et al., 1977).

To address those limitations, here we propose a Bayesian multilevel (BML) framework that integrates all the spatial elements (i.e., regions of interest) into one model. Such a framework has been applied to typical task-related FMRI experiments (Chen et al., 2019a; Xiao et al., 2019) as well as matrix-based data analysis (Chen et al., 2019b; Yin et al., 2019). We use dataset of naturalistic viewing to illustrate the modeling approach and to showcase the modeling capability, flexibility and advantages in reporting results. This paper is a sequel (i.e., Part III) to our previous work of Part I (Chen et al., 2016) and Part II (Chen et al., 2017a).

Structure of the work

In light of the aforementioned backdrop, we believe that the univariate LME approach can be further improved, because its current formulation ignores the common information shared across the brain. Here we propose a more integrative and efficient approach through Bayesian multilevel (BML) modeling that could be used to confirm, complement or replace the LME method. As a first step, we adopt an LME strategy by incorporating ROIs as crossed random effects relative to each subject pair. Then we translate the LME model to a Bayesian platform, resolving two issues: input data doubling and multiple testing. Those ROIs can be either determined independently from the current data at hand, or selected through various methods such as previous studies, an anatomical/functional atlas or parcellation. The proposed BML approach improves inference efficiency by dissolving multiple testing through a multilevel model that more accurately accounts for data structure as well as shared information.

The paper is structured as follows. In the next section, we first extend the region-wise LME model (2) to another LME by pivoting the ROIs as random effects, and then convert the extended LME to a full BML. The BML framework does not make statistical inferences for each region in isolation, but rather weights and borrows information based on the precision information across the full set of regions, striking a balance between local and global information; in a nutshell, the crucial feature here is that the ROIs, instead of being treated as isolated and unrelated with the univariate approaches, are associated with each other through a Gaussian distribution under BML. As a practical exemplar, we apply the modeling approach to an ISC dataset with 68 subjects at 268 ROIs. In the Discussion section, we elaborate the advantages and limitations of BML modeling for ISC data analysis.

Theory: ISC analysis through Bayesian multilevel modeling

Herein Roman and Greek letters, respectively, differentiate fixed and random effects in the conventional statistics context such as ANOVA and LME on the righthand side of a model equation. Although the terms of “fixed” and “random” effects are non-Bayesian, we expect most readers to be familiar with the conventional terminology. For instance, a fixed-effects parameter under ANOVA and LME is treated as constant (e.g, population mean), and a random-effect parameter as variable because it differs from one entity (e.g., subject, ROI) to another. The conventional distinction of fixed- vs. random-effects is replaced by one that separates the modeling decision (a parameter as varying or non-varying) under the Bayesian framework from the inference decision (e.g., prior choices or partial pooling) (Gelman, 2005).

Bayesian modeling based on three-way random-effects ANOVA

We start with with the simple LME model (2), without the complication of explanatory variables, for ISC analysis at m ROIs instead of whole brain voxel-wise modeling. With the Gaussian assumptions for ${\tilde{\xi }}_{ik}$, ${\tilde{\xi }}_{jk}$, and ${\widetilde{ϵ}}_{ijk}$, the m univariate LME models in (2) can be solved independently, but for the sake of model comparisons, the m separate LMEs can be merged into one by pooling the residual variances across the m ROIs with the ROI index k incorporated into the conventional LME formulation (2),

$$z_{ijk}=b_k+{\tilde{\xi }}_{ik}+{\tilde{\xi }}_{jk}+{\widetilde{ϵ}}_{ijk},\hspace{1em}i,j=1,2,\hspace{0.17em}\dots \hspace{0.17em},n\hspace{0.17em}(i\ne j),k=1,2,\hspace{0.17em}\dots \hspace{0.17em},m.$$ (5)

The essential difference between the two approaches, (2) and (5), lies in the assumption about the residuals. Under (2) each ROI is assumed to have its own residual distribution ${\widetilde{ϵ}}_{ijk}\stackrel{iid}{~}\mathcal{N}(0,\hspace{0.17em}{\tilde{\sigma }}_k^2)$, k = 1, 2, .., m; in contrast, all the regions share the same residual distribution ${\widetilde{ϵ}}_{ijk}\stackrel{iid}{~}\mathcal{N}(0,\hspace{0.17em}{\tilde{\sigma }}^2)$ under (5). The two approaches usually render similar inferences unless the sampling variances are dramatically different across the m ROIs. To compare different models through leave-one-out information criteria³ (LOOIC) (Vehtari et al., 2017), we can solve the LME (5) in a Bayesian fashion,

$$z_{ijk}|b_k,{\tilde{\xi }}_{ik},{\tilde{\xi }}_{jk}~\mathcal{N}(b_k+{\tilde{\xi }}_{ik}+{\tilde{\xi }}_{jk},{\tilde{\sigma }}^2),{\tilde{\xi }}_{ik},{\tilde{\xi }}_{jk}~\mathcal{N}(0,\hspace{0.17em}\hspace{0.17em}{\tilde{\lambda }}^2),\hspace{0.17em}\hspace{0.17em}{\widetilde{ϵ}}_{ijk}\mathcal{N}(0,\hspace{0.17em}\hspace{0.17em}{\tilde{\sigma }}^2),\hspace{0.17em}i,j=1,2,\hspace{0.17em}\dots \hspace{0.17em},n\hspace{0.17em}k=1,2,\hspace{0.17em}\dots \hspace{0.17em},m,$$ (6)

where b_k are assigned with a noninformative prior (i.e., uniform distribution) so that no information is shared among the ROIs, leading to virtually identical inferences as the LME (5). In fact, all the three LME models, (2), (5), or (6), share the same feature of no pooling: the information at one ROI reveals nothing about any other ROIs. Therefore, these three LME models all face the same multiplicity issue and may potentially lead to overfitting.

To improve model fitting and achieve higher efficiency, we first adopt a three-way random-effects ANOVA or LME by adding ROIs as random effects, and formulate the following platform,

$$\text{LME}0:z_{ijk}=a_0+{\xi }_i+{\xi }_j+{\pi }_{0k}+{ϵ}_{ijk},\hspace{0.17em}i,j=1,2,\hspace{0.17em}\dots \hspace{0.17em},n\hspace{0.17em}(i\ne j),\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}k=1,2,\hspace{0.17em}\dots \hspace{0.17em},m,$$ (7)

where a₀ represents the population ISC effect across all ROIs and all subjects; ξ_i and ξ_j code the random effect of the ith and jth subject, respectively, and both share the same iid Gaussian distribution $\mathcal{N}(0,\hspace{0.17em}{\tilde{\lambda }}^2)$ embodies the random effect at the kth ROI, and is assumed to be iid with $\mathcal{N}(0,\hspace{0.17em}{\tilde{\tau }}^2)$; and ϵ_ij is the residual term that follows $\mathcal{N}(0,\hspace{0.17em}{\tilde{\sigma }}^2)$.

One essential feature of the extended LME model (7) lies in information sharing or partial pooling among the ROIs. Just as we typically assume a Gaussian distribution for cross-subject variability in linear models, so too we make a Gaussian assumption for the cross-region variability π_0k in (7), playing the role of global calibration. In contrast, with the conventional approach of no pooling, one implicitly assumes a uniform distribution of variabilities across voxels or regions in the brain, and it is this assumption that leads to the multiplicity issue, as shown in the no-pooling model (2), (5), or (6).

Under the extended LME model (7), the correlation between two subject pairs, (i₁, j) and (i₂, j) (i₁ ≠ i₂), that share a common subject S_j can be derived as,

$$\begin{gathered} \text{LME}0:{\rho }_s=corr(z_{i_{1}jk},z_{i_{2}jk})=\frac{cov(a_0+{\xi }_{i_1}+{\xi }_j+{\pi }_{0k}+{ϵ}_{i_{1}jk},a_0+{\xi }_{i_2}+{\xi }_j+{\pi }_{0k}+{ϵ}_{i_{2}jk})}{\sqrt{var(b+{\xi }_{i_1}+{\xi }_j+{\pi }_{0k}+{ϵ}_{ijk})var(b+{\xi }_{i_2}+{\xi }_j+{\pi }_{0k}+{ϵ}_{ijk})}} \\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{0.17em}=\frac{{\text{λ}}^2+{\tau }^2}{2{\text{λ}}^2+{\tau }^2+{\sigma }^2},\hspace{0.17em}{i}_1,i_2=1,2,\hspace{0.17em}\mathrm{..},n\hspace{0.17em}(i_1\ne i_2,i_1\ne j,i_2\ne j),\hspace{0.17em}k=1,2\dots \hspace{0.17em},m. \end{gathered}$$ (8)

Similarly, the correlation of the same subject pairs between two ROIs, k₁ and k₂, can be derived as,

$$\begin{gathered} \text{LME}0:{\rho }_r=corr(z_{ij{k}_1},z_{ij{k}_2})=\frac{cov(a_0+{\xi }_i+{\xi }_j+{\pi }_{k_1}+{ϵ}_{ij{k}_1},a_0+{\xi }_i+{\xi }_j+{\pi }_{k_2}+{ϵ}_{ij{k}_2})}{\sqrt{var(b+{\xi }_i+{\xi }_j+{\xi }_{k_1}+{ϵ}_{ij{k}_1})var(b+{\xi }_i+{\xi }_j+{\xi }_{k_2}+{ϵ}_{ij{k}_2})}} \\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{0.17em}=\frac{{\text{2λ}}^2}{2{\text{λ}}^2+{\tau }^2+{\sigma }^2},\hspace{0.17em}{j}_1,j_2=1,2,\hspace{0.17em}\mathrm{..},n\hspace{0.17em}(i\ne j),\hspace{0.17em}{k}_1,k_2=1,2,\hspace{0.17em}\dots \hspace{0.17em},m\hspace{0.17em}\hspace{0.17em}(k_1\ne k_2). \end{gathered}$$ (9)

Due to the incorporation of ROI effects into the extended LME model (7), a slightly different formulation (8) at the group level for the correlation between two subject pairs that share a common subject exists from the interrelationship (3) at the individual subject level. Because of this difference, the upper bound of 0.5 in (3) does not hold for ρ_s in (8) and is replaced by 1, which is reached when both cross-subject and residual variances λ² and σ² are 0.

In addition to the challenge of input data redundancy discussed in the Introduction, now we have a different hurdle in place of multiplicity. Under this new LME framework (7), we need to refocus on the effects of interest. The overall ISC effect a₀ across all ROIs is usually not our focus; instead, it is the ISC effect at each ROI,

$$b_{0k}=a_0+{\pi }_{0k},\hspace{0.17em}\hspace{0.17em}k=1,2,,\hspace{0.17em}\dots ,m,$$ (10)

that is typically of research interest. However, the LME formulation (7) cannot offer a solution in making inferences regarding the ROI effects b_0k: to estimate b_0k, the LME (7) would become over-parameterized or overfitting.

To proceed, a shift of modeling framework is needed here. We adopt a Bayesian approach that extends the LME model (2) from our previous work using LME modeling for voxelwise ISC analysis (Chen et al., 2017a) and utilizing region-based group analysis for neuroimaging data (Chen et al., 2019a) as well as the BML approach for matrix-based analysis (Chen et al., 2019b),

$$\begin{gathered} \text{BML}0:z_{ijk}|{\xi }_i,{\xi }_j,{\pi }_{0k}~\mathcal{N}(a_0+{\xi }_i+{\xi }_j+{\pi }_{0k},{\sigma }^2),\hspace{0.17em}\hspace{0.17em}{\xi }_i,{\xi }_j~\mathcal{N}(0,\hspace{0.17em}{\text{λ}}^2),\hspace{0.17em}{\pi }_{0k}~\mathcal{N}(0,\hspace{0.17em}{\tau }^2), \\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{0.17em}\hspace{0.17em}{ϵ}_{ijk}~\mathcal{N}(0,\hspace{0.17em}{\sigma }^2),\hspace{0.17em}i,j=1,2,\hspace{0.17em}\dots ,n\hspace{0.17em}(i>j),\hspace{0.17em}\hspace{0.17em}k=1,2,\hspace{0.17em}\dots ,m. \end{gathered}$$ (11)

In fact, the effect decomposition of z_ijk under the BML framework (11) is basically the same as its LME counterpart (7). The different model expression here is formulated to accentuate the paradigm shift and to emphasize the fact that the responses z_ijk under BML are conditional on the parameters and priors. One crucial aspect of this paradigm shift is that the distinction between fixed- vs. random-effects in conventional statistics is fundamentally dissolved under the Bayesian framework (Chen et al., 2019c), enabling a new approach to making statistical inferences. For example, the component π_0k associated with the kth region is considered a random effect under the LME model (7); thus, we would be able to estimate the cross-region variance τ ², but nothing about the effect estimate at that region. In contrast, the BML model (11) can directly make inferences at each region as elaborated below.

Both of the aforementioned challenges under the LME model (2) can be resolved now under the BML framework (11). First, only half of the off-diagonal elements (e.g., the lower triangular part) in Z⁽ⁿ⁾ are required as input under BML through a numerical implementation of multi-membership modeling scheme⁴ (Bürkner, 2018). Second, with a prior (e.g., noninformative uniform distribution) for a₀, the posterior distribution for each ROI can be obtained through the formulation (10). In addition, the ISC effect that is attributable to each subject can be similarly derived through the corresponding posterior distribution with

$$s_i=\frac{1}{2}{a}_0+{\xi }_i,\hspace{0.17em}\hspace{0.17em}i=1,2,\hspace{0.17em}\dots ,n.$$ (12)

The factor of $\frac{1}{2}$ in the subject-specific effect formula for s_i in (12) reflects the fact that the effect of each subject pair is evenly shared between the two associated subjects. The subject-specific effects s_i can be utilized to assess the contribution or importance of a subject relative to all other subjects, which might provide some auxiliary information for further association with, for example, subject-level effects such as sex, disease, age or behavioral data.

Recently we applied the BML modeling approach to matrix-based analyses (Chen et al., 2019b) when the input data are either functional (e.g. inter-region correlation) or structural (e.g., white matter properties among gray matter regions) attribute matrix from each subject. In that case, the intricacy lies in the interrelationships among the brain region pairs while the summarization or generalization hinges upon the subjects, and three basic entity-level components are specified in the corresponding BML model: subject and the two regions that are associated with each region pair. In contrast, ISC analyses deal with the interrelationships among subject pairs while at the same time the summarization or generalization is made across subjects; the regions under BML are pooled together among each other through the shrinkage effect of the Gaussian distribution (Chen et al., 2019a; Chen et al., 2019c). In fact, the theoretical aspects of BML application for ISC analyses can largely be borrowed from our previous work for matrix-based analysis (MBA; Chen et al., 2019b) by swapping the entities between subject and region. Therefore, here we only present the modeling framework directly related to the ISC context. Refer to our previous work (Chen et al., 2019a; Chen et al., 2019c) for the coverage of common issues such as partial pooling, prior selection, model validation and multiplicity handling.

Further extensions of BML for ISC analyses

The LME0 model in (7) can be expanded by including two types of random-effects interaction components - one component is the subject-pair-specific term (i.e., the interaction between two subjects), and the other component is the interaction between a region and a subject:

$$\begin{gathered} \text{LEM}1:z_{ijk}=a_0+{\xi }_i+{\xi }_j+{\eta }_{ij}+{\zeta }_{ik}+{\zeta }_{jk}+{\pi }_{0k}+{ϵ}_{ijk},\hspace{1em}i,j=1,2,\hspace{0.17em}\dots ,n\hspace{0.17em}(i\ne j),k=1,2,\hspace{0.17em}\dots ,m, \\ \hspace{0.17em}\hspace{0.17em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}{\xi }_i,{\xi }_j\stackrel{iid}{~}\mathcal{N}(0,\hspace{0.17em}{\text{λ}}^2),\hspace{0.17em}\hspace{0.17em}{\eta }_{ij}~\mathcal{N}(0,\hspace{0.17em}{\mu }^2),\hspace{0.17em}{\zeta }_{ik},{\zeta }_{jk}~\mathcal{N}(0,\hspace{0.17em}{\nu }^2),\hspace{0.17em}\hspace{0.17em}{\pi }_k\stackrel{iid}{~}\mathcal{N}(0,\hspace{0.17em}{\tau }^2),\hspace{0.17em}\hspace{0.17em}{ϵ}_{ijk}~\mathcal{N}(0,\hspace{0.17em}{\sigma }^2), \end{gathered}$$ (13)

where η_ij is the effect of the subject pair that is associated with subjects i and j (i.e., the interaction effect between two subjects i and j) relative to the overall effect a₀ and the two subject effects, ξ_i and ξ_j, while ζ_ik and ζ_jk are the interaction effects between subject i and region k as well as the interaction between subject j and region k, respectively. We note that the subject-pair-specific effect η_ij captures the unique global (i.e., brain-wide) effect of each subject pair in addition to the overall population effect a₀ and the common effects from the two involved subjects, ξ_i and ξ_j; the same subtlety applies to the subject-region interactions ζ_ik and ζ_jk. The two ICC measures in (8) and (9) can be correspondingly updated to,

$$\text{LEM}1:{\rho }_s=\frac{{\text{λ}}^2+{\nu }^2+{\tau }^2}{2{\text{λ}}^2+{\mu }^2+2{\nu }^2+{\tau }^2+{\sigma }^2},\hspace{1em}{\rho }_r=\frac{{\text{2λ}}^2+{\mu }^2}{2{\text{λ}}^2+{\mu }^2+2{\nu }^2+{\tau }^2+{\sigma }^2}.$$ (14)

We further consider two types of BML extension based on the primary model BML0 in (11). The first type involves all potential interaction effects, in parallel with the three LME expansions from LME0. Specifically, we incorporate the interaction effect between the two subjects of each subject pair as well as the interaction effect between each region and each subject:

$$\begin{gathered} \text{BML}1:z_{ijk}|a_0,{\xi }_i,{\xi }_j,{\eta }_{ij},{\zeta }_{ik},{\zeta }_{jk},{\pi }_{0k}~\mathcal{N}(a_0+{\xi }_i+{\xi }_j+{\eta }_{ij}+{\zeta }_{ik}+{\zeta }_{jk}+{\pi }_{0k},{\sigma }^2), \\ \hspace{0.17em}\hspace{0.17em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}{\xi }_i,{\xi }_j\stackrel{iid}{~}\mathcal{N}(0,\hspace{0.17em}{\text{λ}}^2),\hspace{0.17em}\hspace{0.17em}{\eta }_{ij}\stackrel{iid}{~}\mathcal{N}(0,\hspace{0.17em}{\mu }^2),\hspace{0.17em}{\zeta }_{ik},{\zeta }_{jk}\stackrel{iid}{~}\mathcal{N}(0,\hspace{0.17em}{\nu }^2),\hspace{0.17em}\hspace{0.17em}{\pi }_k\stackrel{iid}{~}\mathcal{N}(0,\hspace{0.17em}{\tau }^2), \\ \hspace{0.17em}\hspace{0.17em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}i,j=1,2,\hspace{0.17em}\dots ,n\hspace{0.17em}(i>j),\hspace{0.17em}k=1,2,\hspace{0.17em}\dots ,m, \end{gathered}$$ (15)

where η_ij is the subject-pair-specific effect or the interaction between subjects i and j, while ζ_ik is the interaction effect between subject i and region k and ζ_jk, between subject j and region k. The two interaction effects, ζ_ik and ζ_jk, are considered as two members, i and j, of a multi-membership cluster. Under these three extended BML models, the region- and subject-specific effects can be similarly reassembled through (10) and (12), respectively.

Another type of model extension is to investigate the effect associated with a subject-level (e.g., sex, disease, genotype, age, behavioral measure) explanatory variable. With one explanatory variable x, we may have,

$$\begin{gathered} \text{BML}{0}^{*}:z_{ijk}|a_0,a_1,x_i,x_j,{\xi }_i,{\xi }_j,{\pi }_{0k},{\pi }_{1k}~\mathcal{N}(a_0+a_1(x_i+x_j)+{\xi }_i+{\xi }_j+{\pi }_{0k}+{\pi }_{1k}(x_i+x_j){\sigma }^2), \\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{0.17em}\hspace{0.17em}{\xi }_i,{\xi }_j\stackrel{iid}{~}\mathcal{N}(0,\hspace{0.17em}{\lambda }^2),{\left({\pi }_{0k},{\pi }_{1k}\right)}^T\hspace{0.17em}\stackrel{iid}{~}\mathcal{N}(0,\hspace{0.17em}\mathit{\tau }),\hspace{0.17em}\hspace{0.17em}i,j=1,2,\hspace{0.17em}\dots ,n\hspace{0.17em}(i>j),\hspace{0.17em}\hspace{0.17em}k=1,2,\hspace{0.17em}\dots ,m, \end{gathered}$$ (16)

$$\begin{gathered} \text{BML}{1}^{*}:z_{ijk}|a_0,a_1,x_i,x_j,{\xi }_i,{\xi }_j,{\pi }_{0k},{\pi }_{1k}~\mathcal{N}(a_0+a_1(x_i+x_j)+{\xi }_i+{\xi }_j+{\eta }_{ij}+{\pi }_{0k}+{\pi }_{1k}(x_i+x_j){\sigma }^2), \\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{0.17em}\hspace{0.17em}{\xi }_i,{\xi }_j\stackrel{iid}{~}\mathcal{N}(0,{\lambda }^2),{\eta }_{ij}\stackrel{iid}{~}\mathcal{N}(0,{\mu }^2),{\left({\pi }_{0k},{\pi }_{1k}\right)}^T\hspace{0.17em}\stackrel{iid}{~}\mathcal{N}(0,\hspace{0.17em}\mathit{\tau }),\hspace{0.17em}\hspace{0.17em}i,j=1,2,\hspace{0.17em}\dots ,n\hspace{0.17em}(i>j),\hspace{0.17em}\hspace{0.17em}k=1,2,\hspace{0.17em}\dots ,m, \end{gathered}$$ (17)

where τ is a 2 × 2 variance-covariance matrices. For example, a between-subject factor with l levels (e.g., l = 2 for males vs females, or patients vs controls) can be incorporated into the BML model with l − 1 dummy-coded variables. On the other hand within-subject or repeated-measures factors could be naturally modeled under BML through the hierarchical structure; however, we recommend that one directly take each contrast (e.g., condition A vs B) as input data z_ijk as a practical approach to save computational time.

Six aspects are noteworthy about the two extended models, BML0* and BML1*. First, multi-membership modeling allows us to utilize only half of the off-diagonals in the ISC matrix from each subject as input, as indicated by the index relationship i > j. Second, the effect associated with the covariate x at the population level, a₁, and at the region level, π_1k, is shared by all subjects (including subject pairs), thus a simplified notation for a derived covariate $x_{ij}^{*}=x_i+x_j$ for each subject pair can be adopted for easier implementation, in contrast to the LME counterpart in which two separate effects have to be included in the model. Third, the inclusion of any subject-level explanatory variable in the model is intended to account for cross-subject variation in the data, thereby precluding the justification for incorporating the subject-region interaction effects, ζ_ij and ζ_jk, as shown BML1 (15). In light of this consideration, we do not consider any extended models, in the presence of any subject-specific covariate, that correspond to BML1 (15). Four, cases with more than one explanatory variable can be similarly formulated as in the BML0* and BML1*. Five, under BML0* or BML1*, the region- and subject-specific effects can be similarly reassembled through (10) and (12), respectively; in addition, the region-specific effect for the covariate x can be derived through,

$$b_{1k}=a_1+{\pi }_{1k},\hspace{0.17em}k=1,2,\hspace{0.17em}\mathrm{..},m.$$ (18)

Lastly, model complexity under BML is usually not a concern from a theoretical and numerical perspective except for computation cost. Even though there have been some technical debates about the model selection between the maximum complexity (Bar et al., 2013) and a parsimonious one (Bates et al., 2018), a Bayesian model balance tends to be less likely to have a convergence problem due to the regularization of priors.

To recapitulate our modeling strategy here about ISC analyses, we first untangle each subject-pair-specific effect into the additive effects of the two involved subjects through a multi-membership structure, maintaining the relatedness as embodied in the correlation matrix P ⁽ⁿ⁾. Because of this untangling step, we can obtain the relative contribution, s_i in (12), from each subject even though the input data (ISC values) are the jointed contributions from subject pairs, not individual subjects. In addition, the cross-region effects (and sometimes subject-region interaction effects) are included in the BML models to account for cross-region variability. The main difference between univariate LME (Chen et al., 2017a) and BML lies in the assumption about the brain regions: the effects (e.g., π_0k and π_1k in (17)) are assigned with a Gaussian prior under BML while they are assumed to have a noninformative flat prior under the corresponding LME model. In other words, the effect at each region is estimated independently from other regions under univariate LME, thus there is no information shared across regions. In contrast, the effects across regions are shared, regularized and partially pooled through the Gaussian assumption under BML for the effects across regions; the Gaussian assumption about cross-region variability shares the same rationale as the cross-subject Gaussian distribution under the conventional framework (e.g., GLM). On the one hand, partial pooling drags the region effects from both ends toward the center, resulting in conservative effect estimates relative to univariate LME. On the other hand, partial pooling through an integrative model sidesteps the multiplicity issue (Chen et al., 2019c). In the same vein, partial pooling has been previously applied to resting-state data in improving predictability of a subject’s seed-based correlation with the average of the other subjects in the group (Shou et al., 2014).

Implementations of BML for ISC analyses

As no analytical solution is available for BML models in general, we draw samples from the posterior distributions via Markov chain Monte Carlo (MCMC) simulations with the algorithms implemented in Stan, a publicly available probabilistic programming language and a math library in C++ (Stan Development Team, 2019). The present implementations are executed with the R package brms that is is based on Stan, and multi-membership modeling is directly available in brms (Bürkner, 2017; Bürkner, 2018).

For typical BML models, the priors for cross-region and cross-subject effects as well as their interactions have been laid out in the previous section. We typically adopt an improper flat (noninformative uniform) distribution for population parameters (e.g., a₀ and a₁ in BML0* (16) and BML1* (17)). As for hyperpriors, we follow the general recommendations in Stan (Stan Development Team, 2019). Specifically, for the scaling parameters at the region and subject level, the standard deviations for the cross-region and cross-subject effects, ξ_i, ξ_j, and π_k as well as their interactions, we adopt a weakly informative prior such as a Student’s half-t(3, 0, 1) or half-Gaussian ${\mathcal{N}}_{+}(0,1)$ (restricting to the positive values of the respective distribution). For covariance structure (e.g., τ in BML0* (16) and BML1* (17)), the LKJ correlation prior⁵ is used with the shape parameter taking the value of 1 (i.e., jointly uniform over all correlation matrices of the respective dimension) (Gelman et al., 2017). Lastly, the standard deviation σ for the residuals is assigned using a half-Cauchy prior with a scale parameter depending on the standard deviation of z_ijk. To summarize, besides the Bayesian framework under which hyperpriors provide a computational convenience through numerical regularization, the major difference between BML and its univariate GLM counterpart is the application of the Gaussian prior in the BML models that plays the pivotal role of pooling and sharing the information among the brain regions. It is this partial pooling that effectively takes advantage of the effect similarities among the ROIs and achieves higher modeling efficiency (Chen et al., 2019c).

Bayesian inferences are usually expressed in the whole posterior distribution of each effect of interest. For practical considerations in results reporting, point estimates from these distributions such as mean and median are typically used to show the effect centrality, while quantile-based (e.g., 90%, 95%) intervals also provide a condensed summary of the posterior distribution. A typical workflow to obtain the posterior distribution is the following. Multiple (e.g., 4) Markov chains are usually run in parallel with each of them going through a predetermined number (e.g., 2000) of iterations, half of which are thrown away as warm-up (or “burn-in”) iterations while the rest are used as random draws from which posterior distributions are derived. To gauge the consistency of an ensemble of Markov chains, the split $\widehat{R}$ statistic (Gelman et al., 2014) is provided as a potential scale reduction factor on split chains and as a diagnostic parameter to assist the analyst in assessing the quality of the chains. In practice $\widehat{R}<1.1$ is considered acceptable. Another useful statistic, effective sample size (ESS), measures the number of independent draws from the posterior distribution that would be expected to produce the same amount of information of the posterior distribution as is calculated from the dependent draws obtained by the MCMC algorithm. We suggest a minimum ESS of 200 for deriving the quantile intervals for the posterior distribution.

BML applied to ISC data

To demonstrate the modeling capability and performances of BML, we used a dataset from the Child Mind Institute Healthy Brain Network (CMI-HBN), a publicly available naturalistic scanning dataset (Alexander et al. 2017). Briefly, the dataset consisted of a community-based sample of generally healthy children and adolescents who were scanned while resting as well as watching two different videos. Rich phenotypic data are also available for each individual. We focus here on data acquired during “The Present,” an animated short about a boy who receives a puppy as a gift. The video has a social theme and is emotionally evocative, which led us to hypothesize that it would evince individual differences along a phenotypic spectrum related to social functioning. Data used here come from the CMI-HBN data releases 1 and 2, which represented all of the available data in January 2018 when we began the project.

Functional MR images were acquired with the following EPI scan parameters: B0 = 3 T, flip angle = 31°, TR = 800 msec, TE = 30 msec, 60 slices, voxel size = 2.4 mm isotropic, multiband factor = 6, 250 volumes with a total scanning time of 3:20 min:sec. Other details, including parameters for anatomical scans as well as full protocols for MRI and phenotypic data, can be found in the data descriptor (Alexander et al. 2017) and at the following URL: http://fcon_1000.projects.nitrc.org/indi/cmi_healthy_brain_network/

Data were preprocessed as follows. First, we used Freesurfer (Fischl, 2012) to extract subject-specific ventricle and white-matter masks using each subject’s anatomical image. Next, we used the afni_proc.py program in AFNI to perform the following preprocessing steps on the functional images: despiking, head motion correction, affine alignment with anatomy, nonlinear alignment to a standard template, and smoothing with an isotropic FWHM of 5 mm. Confounding effects during preprocessing included: the first three principal components of the ventricles, local white matter regressors generated from fast ANATICOR (Jo et al, 2010), each subject’s 6 motion time series, their derivatives and linear polynomials for slow drifts. Censoring of time points was performed whenever the per-time-point motion (Euclidean norm of the motion derivatives) was 0.3 mm or more or when more than 10% of the brain voxels were outliers. Censored time points were set to zero rather than removed altogether (this is the conventional way to do censoring, but especially important for inter-subject correlation analyses, to preserve the temporal structure across participants). Because this is a pediatric sample, we used a recently developed pediatric template brain as the standard template (“Haskins template”; Molfese et al., in prep).

Our primary phenotypic measure of interest was the Social Responsiveness Scale-2, abbreviated here as SRS (Constantino and Gruber, 2012). This parent-report scale measures the presence and severity of social impairment using items such as “seems much more fidgety in social situations than when alone”, “takes things too literally and doesn’t get the real meaning of a conversation”, and “avoids eye contact or has unusual eye contact”. There are 65 total items and each is rated on a Likert scale from 0–3; higher scores indicate poorer social functioning.

We selected a subset of subjects for analysis based on the following criteria: (1) a usable T1-weighed anatomical image (for registration purposes), (2) the functional movie-watching run of interest (“The Present”), with at least 85% (213/250) volumes remaining after censoring of head motion and outliers, (3) valid demographic information including age and sex; and (4) a valid SRS score. There were 68 subjects that met these criteria (age range = 6–17 years, mean ± standard deviation = 10.8 ± 3.1 years; 30 females). SRS scores followed a right-skewed distribution with range = 3–140, median (mean) = 43.5 (53.3), and median absolute deviation (standard deviation) = 17 (33.6). In this subset, there was negligible correlation between age and SRS (r = 0.046) or between head motion (as measured by mean frame-wise displacement) and SRS (r = −0.064). There was a moderate negative correlation between age and head motion (r = −0.25). Males and females did not differ much in age (males 10.35 ± 2.95 years, females 11.3 ± 3.19 years). However, SRS scores were moderately higher among males than females (males 58.26 ± 35.26, females 47.07 ± 30.88).

Owing to the computational intractability of conducting BML at the voxel-wise level, we defined ROIs using a preexisting functional brain parcellation (Shen et al., 2013), which contains 268 regions covering the whole brain (cortex, subcortex and cerebellum). It was originally defined in MNI space and nonlinearly warped to Haskins template space using 3dQwarp in AFNI for purposes of this study. Region-wise time courses for each subject were calculated by averaging the signal of all the voxels in each region at each time point. Thus, the final dataset that entered into the ISC calculation consisted of 268 regions × 250 time-points × 68 subjects. To demonstrate that the method is robust to the choice of ROIs and spatial resolution of the parcellation, we also conducted the same analysis using a coarser, anatomically defined parcellation containing 107 nodes that is included as part of the Haskins template space (Molfese et al., in prep).

The ISC data of Fisher-transformed z-values from the n = 68 subjects at m = 268 ROIs were analyzed with three models: BML0* (16) and BML1* (17), and the region-wise LME model that corresponds to BML1*. Three explanatory variables (SRS, Age, and Sex), plus their two- and three-way interactions, yield a total of eight effects of interest at each ROI: overall ISC (intercept), main effects (SRS, Age, Sex), two-way interactions (SRS:Age, SRS:Sex, Age:Sex), and three-way interaction (SRS:Age:Sex). The ROI dataset was analyzed with the three models using the R package brms. Runtime for BML was three weeks on a Linux system of Fedora 25 with AMD Opteron 6376 at 1.4 GHz; in contrast, the runtime of the same model with the coarser parcellation of 107 ROIs was five days.

To compare the two BML models, we assessed their point-wise out-of-sample prediction accuracy through the LOOIC. As the LOOIC for the BML1* model (with subject pair specific effects) relative to BML0* (without subject pair specific effects) is −56406.34 ± 474.65, the higher predictive accuracy of BML1* is shown by its substantially lower LOOIC than BML0*. We thereafter focus our results discussion on BML1*.

The summary of the BML1* parameter estimates is shown in Table 1. One noteworthy aspect is that the interaction effect η_ij of subject pairs was substantial with a standard deviation λ = 0.091 (with a 95% quantile interval of [0.090, 0.092], Table 1), and such an interaction was stronger than the additive effects of individual subjects ξ_i or ξ_j with a standard deviation µ = 0.079 (with a 95% quantile interval of [0.076, 0.084], Table 1). In other words, cross-subject-pairs effects η_ij account for a little more ISC variability than cross-subjects effects ξ_i and ξ_j. These results justify our adoption of the extended BML1* model (17) that contains the cross-subject-pairs effects η_ij instead of BML0* (16) without the effect η_ij. This result is also interesting from a scientific perspective, as it suggests that the interaction between a given subject pair is more important for determining ISC levels than either of the two subjects on their own. In other words, it is generally not the case that an individual subject tends to have high (or low) ISC values across the board (i.e., with all potential pairs); rather, it is the specific subject pair that explains more variability in observed ISC effects.

Table 1:

Summary results from the ISC dataset fitted with an extended version of BML1* in (17) and its LME counterpart. The column headers Estimate, SD, QI, and ESS are short for effect estimate, standard deviation, quantile interval, effective sample size, respectively. LME1* shares the same effect components as BML1*, and shows virtually the same effect estimate for the population mean b₀ and the standard deviations for those effect components despite: (1) the two modeling frameworks were solved through two different numerical schemes (REML for LME and MCMC for BML); and 2) in practice the input data for LME1 had to be duplicated to maintain the balance between the two crossed random-effects components associated with each subject pair. In addition, the nearly identical parameter estimates between the two models indicate that the use of priors under BML had a negligible effect. However, the LME framework cannot provide uncertainty measures for those variances, as indicated by the dashes in the table. $\widehat{R}$ is the split statistic of a convergence indicator for the Markov chains. All $\widehat{R}$ values under BML1* were less than 1.1, indicating that all the four MCMC chains converged well. The effective sample sizes (ESSs) for the population- and region-level effects were large enough to warrant quantile accuracy in summarizing the posterior distributions for region-specific effects. The correlations among the eight cross-region effects π_·k under BML are not shown in the table because their inferences are not available under LME.

Term	BML1*					LME1*
	Estimate	SD	95% QI	ESS	$\widehat{R}$	Estimate	SD
population-level effects
a0: Intercept	0.057	0.064	[0.045, 0.069]	104	1.04	0.057	0.063
a1: SRS	−1.27e-4	8.35e-5	[−2.86e-4, 3.99e-5]	492	1.00	−1.31e-4	5.54e-5
a2: Age	−1.12e-3	8.78e-4	[−2.78e-3, 5.80e-4]	377	1.00	−1.14e-3	6.06e-4
a3: Sex	−3.54e-3	5.38e-3	[−1.39e-2, 7.37e-3]	349	1.01	−3.70e-3	3.76e-3
a4: Age:Sex	7.85e-4	3.23e-4	[1.51e-4, 1.42e-3]	317	1.01	7.54e-4	2.44e-4
a5: SRS:Sex	9.22e-6	3.07e-5	[−5.12e-5, 7.04e-5]	244	1.01	9.45e-6	2.21e-5
a6: Age:SRS	5.53e-6	5.35e-6	[−4.56e-6, 1.64e-5]	295	1.00	5.68e-6	3.81e-6
a7: Sex:Age:SRS	1.54e-6	6.30e-6	[−1.06e-5, 1.42e-5]	257	1.01	1.75e-6	4.56e-6
cross-subjects effects (levels: 68)
λ: standard deviation for ξi, ξj	0.079	0.060	[0.076, 0.084]	561	1.01	0.079	-
cross-subject-pairs effects (levels: 2278)
µ: SD for ηij	0.091	0.058	[0.090, 0.092]	395	1.01	0.091	-
cross-ROIs effects (levels: 268)
τ0: SD for Intercept π0k	0.106	0.060	[0.102, 0.111]	66	1.06	0.106	-
τ1: SD for SRS π1k	1.19e-4	6.14e-6	[1.08e-4, 1.31e-4]	563	1.01	1.23e-4	-
τ2: SD for Age π2k	1.40e-3	7.0e-5	[1.27e-3, 1.54e-3]	705	1.01	1.44e-3	-
τ3: SD for Sex π3k	8.0e-3	4.0e-4	[7.22e-3, 8.80e-3]	948	1.00	8.22e-3	-
τ4: SD for Age:Sex π4k	1.27e-3	7.54e-5	[1.13e-3, 1.43e-3]	1442	1.00	1.36e-3	-
τ5: SD for SRS:Sex π5k	1.05e-4	6.50e-6	[9.29e-5, 1.18e-4]	1468	1.00	1.14e-4	-
τ6: SD for Age:SRS π6k	2.03e-5	1.20e-6	[1.79e-5, 2.27e-5]	1130	1.00	2.22e-5	-
τ7: SD for Sex:Age:SRS π7k	1.48e-5	1.62e-6	[1.16e-5, 1.79e-5]	1274	1.00	1.96e-5	-
residuals
σ: SD for residuals	0.160	0.058	[ 0.160, 0.160]	3097	1.00	0.160	-

The results comparison between BML and LME is quite revealing. Despite the injection of priors and hyperpriors, the two modeling frameworks produced virtually identical estimates for the population parameters and variances for cross-subjects, cross-subject-pairs and cross-regions effects (Table 1), validating the adoption of the BML approach. However, the differential treatment of model parameters under LME and BML results in a crucial difference. Under LME we can estimate the population effects and their uncertainties (e.g., a₀, a₁, …, a₇); we can only obtain the standard errors (e.g., λ, µ, τ ‘s) for the random-effects variables. In other words we cannot make inferences at the region level (e.g., effects of τ ‘s at each region) under LME. In contrast, under BML we can directly assess these effects through (10) and (18) with Bayesian simulations.

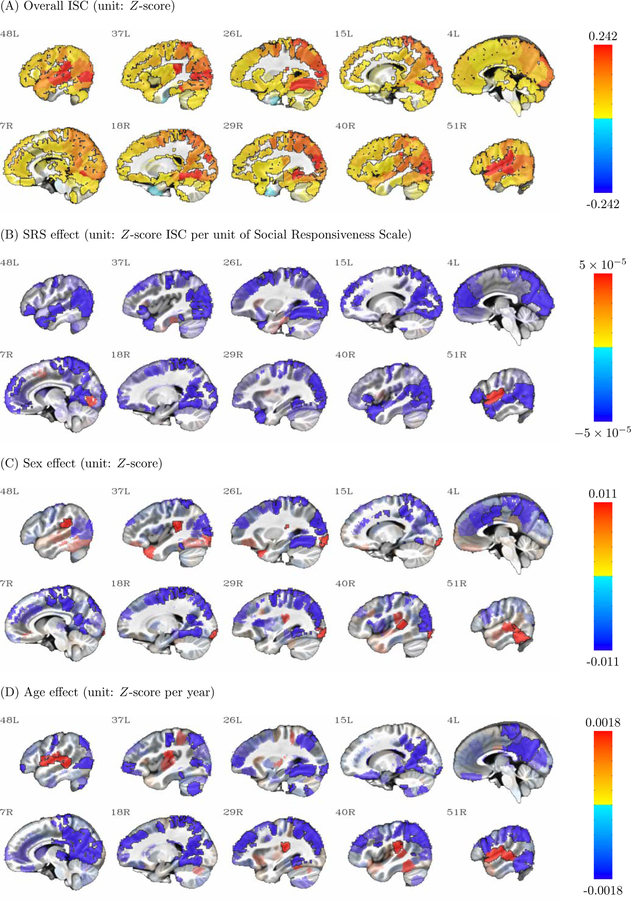
The eight effects of interest under BML1* can be shown with their respective posterior distributions. However, with 268 ROIs, it is more practical to summarize the results with the mean, standard error and 90% and 95% quantile intervals at each ROI. To demonstrate the results, here we illustrate the four main effects at the 268 parcels in the brain (Fig. 3): overall ISC, SRS, Sex, and Age. These effects can be interpreted in light of what is known from previous naturalistic scanning studies and the demographic and behavioral covariates of interest.

Figure 3:

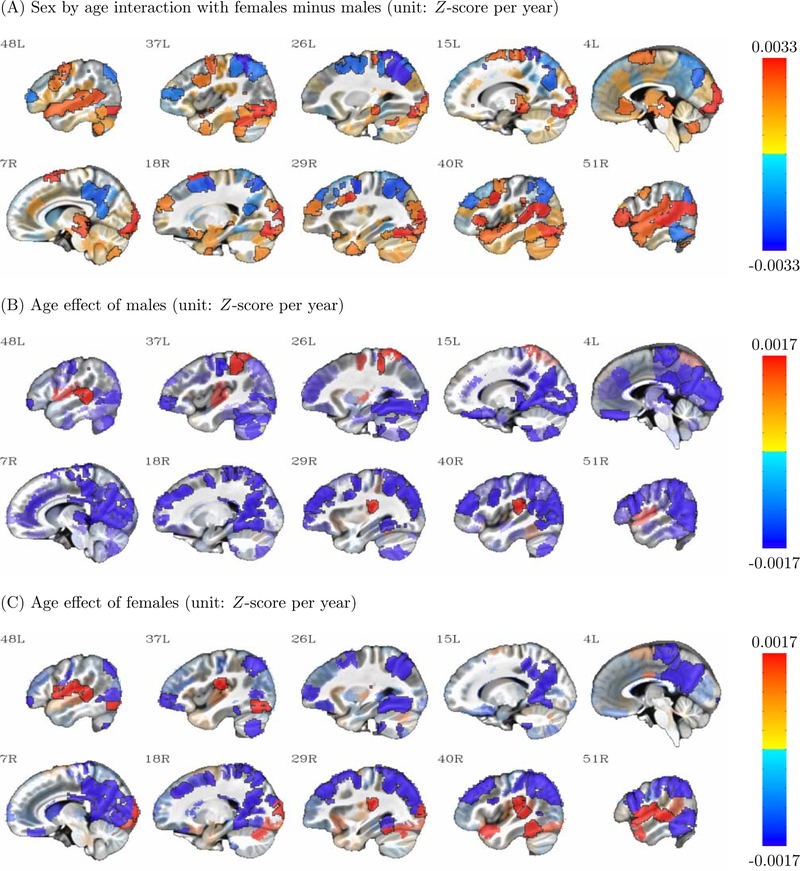
Four effects (overall ISC, SRS, Sex, and Age) derived from BML are shown here for the 268 parcels in sagittal view with slice numbers indicating the relative left-right location. Warm (or cold) colors show positive (or negative) effects, with the colorbar range set to the 95% quantile of the respective effect; effect opacity is determined by the posterior density: opaque regions outlined in black are beyond 90% quantile tail (strong evidence), with transparency increasing toward the median (weak evidence). Note that the sex effect is shown as females minus males, meaning that in panel (C), blue regions show higher ISC in males while red regions show higher ISC in females.

First, much of the brain shows a substantial overall ISC effect (Fig. 3A). While this effect is particularly strong in primary visual and auditory cortex, there is evidence for synchrony in higher-order regions of association cortex as well. This is consistent with a large body of literature using naturalistic scanning to show that by exposing subjects to the same time-locked, complex, engaging stimulus, much of the brain becomes synchronized across subjects (Hasson et al., 2010).

Atop this general synchrony, our method revealed that subject-level covariates of interest affect the strength of ISC. In the case of Social Responsiveness Scale (SRS), most of these effects are negative (Fig. 3B), meaning that ISC is relatively stronger among children with low SRS scores than those with higher SRS scores. This is the expected direction given that lower SRS scores reflect better social function; in other words, children with good social skills are more synchronized while viewing a socially and emotionally evocative film as compared to children with more autistic traits and tendencies, corroborating previous reports (Hasson et al., 2009; Salmi et al., 2013; Byrge et al., 2015). There was substantial evidence for an effect in this direction in anterior and posterior regions along the midline as well as in temporal cortex, many of which are known to be involved in processing social information.

In the case of Sex (Fig. 3C), we observed higher ISC among males as compared to females in many posterior and central midline regions, as well as some visual association areas. In contrast, we observed higher ISC among females in the temporo-parietal junction and an inferior temporal region partially encompassing the fusiform gyrus.

In the case of Age (Fig. 3D), we observed that ISC generally declines with age, such that many regions (especially those in posterior midline and visual association regions) are more synchronized in younger children relative to older ones. One possible explanation for this is that idiosyncratic (i.e., subject-specific) responses emerge with age, leading to an increase in variance (and decrease in cross-subject synchrony) as children get older. Another potential explanation of these effects might be the choice of stimulus itself: the animated film may have been more engaging for younger subjects than older ones, who require more sophisticated content to fully capture their attention; future studies should explore the effect of stimulus on ISC values through development. The exception was a handful of regions along the superior temporal lobe, in which ISC increased with age. This may in part reflect language processes that are developed and refined as children mature, leading to more consistent responses among older subjects in these areas.

Beyond main effects, the BML framework also allows us to examine interactions among the covariates. For example, as shown for the Sex:Age interaction (Fig. 4A) and the Age effect in each sex (Fig. 4B, C), a region in the inferior temporal lobe encompassing the fusiform gyrus seems to increase its ISC with age among females (Fig. 4C), while among males there is almost no evidence for such an age effect (Fig. 4B). Additionally, in some of the regions along the superior temporal lobe and insula, the increase in ISC with Age seems to be driven largely by females, which may reflect differing developmental trajectories in language and affect between the sexes.

Figure 4:

Interaction effects between sex and age derived from BML are shown here for the 268 parcels in sagittal view with slice numbers indicating the relative left-right location. Warm (or cold) colors show positive (or negative) effects, with the colorbar range set to the 95% quantile of the respective effect; effect opacity is determined by the posterior density: opaque regions outlined in black are beyond 90% quantile tail (strong evidence), with transparency increasing toward the median (weak evidence). Note that the sex effect is shown as females minus males, meaning that in panel (1), blue regions show higher age effect in males while red regions show higher age effect in females.

One aspect in which ROI-based BML excels is the completeness and transparency in results reporting: if the number of ROIs is not overwhelming (e.g., less than 100), the summarized results for every ROI can be completely presented in a tabular form or in full distributions of posterior density (Chen et al., 2019a). It is worth emphasizing that Bayesian inferences focus less on the point estimate of an effect and its associated quantile interval, but more on the whole posterior density that offers more detailed information about the effect uncertainty. Unlike the whole brain analysis in which the results are typically reported as the tips of icebergs above the water, posterior density reveals the extent of uncertainty regardless of strength of statistical evidence. In addition, one does not have to stick to a single harsh thresholding when deciding a criterion on the ROIs for discussion; for instance, even if an ROI lies outside of, but close to, the 95% quantile interval, it can still be reported and discussed as long as all the details are revealed. Such flexibility and transparency, as illustrated in Figures 3 and 4, are difficult to navigate or maneuver through the conventional cluster-based thresholding at the whole-brain level.

Discussion

Here, we introduce an extension to the LME platform, namely Bayesian multilevel modeling (BML), for jointly estimating inter-subject correlation during naturalistic scanning in a series of predefined regions. The advantages of this BML approach over previous approaches include: dissolution of multiplicity, ability to incorporate covariates, modeling efficiency, spatial specificity in outcome interpretation, results reporting and visualization.

ROI-based ISC analysis through BML as an extension of LME

The advantage of multilevel modeling lies in its capability of stratifying the data in a hierarchical or multilevel layout so that complex dependency or correlation structures can be properly accounted for coherently within a single modeling platform. Specifically applicable in the ISC context is a crossed or factorial layout across three crisscross layers, two sets of subject pairs and the list of ROIs. Even though the LME approach can quantitatively characterize the ISC effect of each subject pair as the combined effect of the respective subjects, the decomposition remains coarse. For instance, an LME model can accommodate neither the uniqueness of each subject pair nor that of each subject-ROI interaction, due to the LME system being potentially underdetermined from the overwhelming number of parameters. These limitations evince one motivation for our current work with BML as an extension to our previous work of LME modeling for ISC data analysis. That is, the idiosyncratic effect of each subject pair as well as that of each subject-ROI interaction can be modeled under BML since non-identifiability would be dissolved under BML because a Bayesian model can be identified as long as the posterior distribution is proper.

The multiple testing issue is a fundamental aspect of the massively univariate approach widely adopted in neuroimaging, and it produces several challenges, including artificial dichotomization of the results, inflated errors of incorrect sign and incorrect magnitude, vulnerability to data manipulations, suboptimal predictive accuracy, and lack of model validation (Chen et al., 2019c). To address these limitations, we have adopted the use of a single, integrative BML model that shares information across regions. Instead of fighting multiplicity through leveraging the relatedness only among the neighboring voxels, the hierarchical structure of BML implements just one model that calibrates the information globally shared across all regions; in addition to avoiding the need for an unrelated, corrective test, the BML approach leads to better control of errors of incorrect sign and incorrect magnitude; to improved modeling efficiency; to a reduction in the susceptibility to fishing expeditions; to inherent validation of each model; and to complete results reporting.

One controversial aspect of Bayesian modeling in popular discussions is selection of priors, since Bayesian methods are frequently deemed “subjective” due to this feature. It should be noted first that all statistical models are subjective in the sense of idealizing or approximating reality – consider analogous assumptions of model linearity or Gaussianity of residuals in other modeling frameworks. The Gaussian priors adopted here for cross-subject and cross-region effects under BML are based on two considerations: one aspect is convention and pragmatism (many features in practice tend to be approximately single-peaked and drop-off into relatively thin tails), and the other is the fact that, per maximum entropy principle, the Gaussian distribution is the most conservative choice if the data have a finite variance. More importantly, the Gaussian priors only stipulate the distribution shape, and its specific parameters (e.g., variance) are actually determined a posteriori through the model conditioning on the data (Chen et al., 2019a; Chen et al., 2019c). In fact, the impact of our prior choices for ISC analysis under BML is negligible as demonstrated in Table 1. Lastly, the validity of prior choices and model specifications (including LME and BML) can be assessed through validation tools under the Bayesian framework – if a prior is ill-suited to the model and negatively affects results, this step will alert the researcher.

Applying the general BML modeling strategy (Chen et al., 2019a) to the ISC context, we formulate the BML data generation mechanism for each dataset on a set of ROIs by extending the univariate LME framework. Our adoption of BML, as illustrated with the demonstrative data analysis, indicates that BML holds some promise for ROI-based ISC data analysis. By incorporating the effects from both subject pairs and region pairs, we can formulate a BML model that accounts for both inter-subject and inter-region relationships, potentially extending the BML-based ISC and matrix-based analysis (Chen et al., 2019b) further to broader situations such as inter-subject functional correlation (Simony et al., 2016) and representational similarity analysis (Cai et al., 2019). In general, the BML approach offers several advantages over traditional voxel-wise approaches:

1. Two multiplicity issues with whole brain voxel-wise ISC analysis form another background for our work here. Just as with conventional whole-brain GLM-based analyses, ISC analysis through univariate LME would still face the multiplicity issue in the sense that the same model is applied as many times as the number of voxels. Therefore, correction for FWE would still have to be executed as an extra step. The popular approach of leveraging between cluster size and statistical strength has been widely adopted to control the overall FWE, but the penalty is usually too severe as the information shared across brain regions is not effectively considered in modeling (Chen et al., 2019a; Chen et al., 2019c). Another difficulty with the whole brain analysis is the sidedness issue in statistical testing. For a symmetric statistical distribution, one-sided testing for one direction (e.g., positive) would be justified if prior information is available regarding the sign of the effect for a particular brain region. When no prior information is available for all regions in the brain, one cannot simply perform two separate one-sided tests in place of one two-sided test, and such a double-sidedness practice, although popularly practiced in neuroimaging, warrants a Bonferroni correction because the two directions are independent with each other. However, simultaneously testing both tails in tandem for whole brain analysis without correction for sidedness is widely used without clear justification, and this forms a source of multiplicity issue that needs proper accounting.

   Instead of separately correcting for multiple testing, BML incorporates multiple testing as part of the model by assigning a prior Gaussian distribution among the ROIs. In doing so, multiple testing is handled under the scaffold of the multilevel data structure by conservatively shrinking the original effect toward the center with the reasonable assumption that the effects among brain regions are usually similar and largely center within a finite range. In other words, instead of leveraging cluster size or statistical strength, BML leverages the commonality among ROIs through effective regularization, simultaneously achieving meaningful spatial specificity and detection efficiency. Even though the conventional correction for FWE in neuroimaging is considered desirable in controlling overblown FWE, it is not necessarily efficient nor practically meaningful to fight the strawman of absolutely zero effect anywhere in the brain. More importantly, arbitrary thresholding, regardless of the extent of rigor, artificially dichotomizes the data, resulting in an undesirable situation: reporting only the results that pass thresholding unavoidably ignores the ones that may not differ much from the former.

   In addition, BML offers a flexible approach to dealing with double sidedness at the ROI level. When prior information about the directionality of an effect is available on some, but not all, regions (e.g., from previous studies), with the massively univariate approach for the whole brain one may face the issue of performing two one-tailed t-tests at the same time in a blindfold fashion. In contrast, the ROI-based BML approach disentangles the complexity since the posterior inference for each ROI can be made separately.

2. No duplication for input data is needed under BML. To keep a balanced data structure and to maintain proper overall FPR controllability under the current LME implementations, we have to duplicate the input data with both the lower and upper triangular components of the ISC correlation matrix due to the fact those two sets of subject effects are parameterized as two separate parameter sets. In contrast, input data duplication under BML is unnecessary thanks to an implementation technique similar to the multi-membership modeling strategy available in the R package brms (Bürkner, 2017), halving the input data and the number of parameters for subject effects under BML, as opposed to LME.

3. BML may achieve higher spatial specificity through efficient modeling. A statistically identified cluster through the conventional whole brain analysis is not necessarily anatomically or functionally meaningful. In other words, a statistically identified cluster is not always aligned well with a brain region for diverse reasons such as “bleeding” effect due to contiguity among regions, and suboptimal alignment to the template space, as well as spatial blurring. In fact, investigators usually tabulate the location of the “peak” (i.e., maximum effect magnitude or statistic value) voxel for a cluster even though the cluster may only partially cover an anatomical region or overlap multiple brain regions or subregions. In contrast, under BML, the regions are utilized as prior spatial information, and the statistical inference for each region under BML is assessed by its effect strength relative to its peers, not by its spatial extent, providing an alternative to the conventional whole brain analysis with more accurate spatial specificity.

4. BML may potentially alleviate the arbitrariness of data space selection. Under the conventional framework, if the data space changes because of an evolving research focus (e.g., from whole brain to gray matter, a large network or a list of regions), the impact due to the different domain for multiple testing correction can be substantial, leading to the vulnerability to the issue of “the garden of forking paths”, “data snooping” or p-hacking. In contrast, the region-based ISC analysis under the Bayesian framework is more adaptive to the situation of region selection due to the adaptivity of the Gaussian priors. In other words, the amount of regularization is derived from the data through partial pooling that embodies the similarity assumption of effects among the brain regions. Such adaptivity of the Gaussian prior is supported by our ongoing analyses of a task-related dataset but with different numbers of regions of interest (e.g., 30, 300, and 1000), resulting in consistent inferences.

5. Full results reporting is possible for all ROIs under BML. The conventional NHST focuses on the point estimate of an effect supported with statistical evidence in the form of a p-value. In the same vein, typically the results from the whole brain analysis are displayed with sharp-thresholded maps or tables that only show the surviving clusters with peak statistic- or p-values. In contrast, as the focus under the Bayesian framework is on the posterior distribution, not the point estimate, of an effect, the totality of BML results can be summarized as shown in Figures 3 and 4. Such totality is more advantageous than the typical practice in which the effect estimates are usually not reported in the whole brain analysis (Chen et al., 2017b). In other words, BML modeling at the ROI level directly allows the investigator to present the effect estimate. More importantly, BML substantiates the reporting advantage not only because of modeling at the ROI level, but also due to the fact that the uncertainty associated with each effect estimate can be demonstrated in a much richer fashion.

   To some extent, the ROI-based BML approach can alleviate the arbitrariness of thresholding using the current FPR correction practices. Even though BML allows the investigator to present the whole results for all regions, for example, in a table format, we do recognize that the investigator may prefer to focus the discussion on some regions with strong statistical evidence. Nevertheless, the decision can hinge on the statistical evidence from the current data, combined with prior information from previous studies. For example, one may still choose the 95% quantile interval as an equivalent benchmark to the conventional p-value of 0.05 when reporting the BML results. However, those effects with, say, 90% quantile intervals can still be utilized with a careful and transparent description, which can be used as a reference for future studies to validate or refute; or, such effects can be reported if they have been shown in previous studies. Moreover, rather than a cherry-picking approach on reporting and discussing statistically significant clusters in whole brain analysis⁶, we recommend a principled approach in results reporting in which the ROI-based results be reported in totality with a summary as shown in Figures 3 and 4 and be discussed through transparency and soft, instead of sharp, thresholding. We believe that such a highlighting and soft thresholding strategy is more healthy and wastes less information for a study that goes through a strenuous pipeline of experimental design, data collection, and analysis.

• 5)Inferences at the level of individual subjects are possible. As BML partitions the effect at the subject-pair level as the summation of multiple additive effects including the two involved subjects, the effect from each individual subject can be teased apart, revealing the contribution at the subject level as shown in formula (12), even though the input data for ISC analysis are at subject-pair level. Such effects at the subject level could be beneficial as auxiliary information in exploring, for example, outlying subjects or association with behavior data.

One crucial aspect of Bayesian modeling is model validation. In fact, a full Bayesian workflow includes several steps, such as prior predictive checks, model sensitivity analysis and posterior predictive checks (Gelman et al., 2014). Here we have demonstrated only the leave-one-out information criterion for model comparison and cross validation between BML and its LME counterpart in Table 1, but the other steps can play important roles in properly capturing the data structure and in guaranteeing robust inferences. For example, data can be simulated from prior distributions and fitted with the proposed model, and numerical behaviors of Markov chains for the posterior distributions can be checked (Chen et al., 2019a). Furthermore, simulation-based calibration can be utilized to assess whether estimated posterior parameters follow the same distribution as the true model parameters adopted to generate simulated data. Building, comparing, tuning and improving models is a daunting task with a sophisticated BML model due to the high computational cost. In the presence of the huge number of parameters involved in the BML model for the current experiment dataset, it is impractical to fully and systematically explore the full spectrum of the whole Bayesian workflow here, but we plan to continue these additional validation steps in our future work.

Limitations of ROI-based BML and future directions

The performance of BML requires more testing to assess and validate its consistency and replicability under different scenarios and when applied to multiple datasets. For example, would the inference be consistent when the number of regions varies in real data analysis? The linearity of effect decomposition under BML is a strong assumption, and, as in all linear models, it is an approximation. In addition, other limitations of the ROI-based BML exist as follows.

1. ROI data extraction involves averaging among voxels within the region. As a spatial smoothing or low-pass filtering process, averaging condenses, reduces or dilutes the information among the voxels within the region to one number, and loses any finer spatial structure within the ROI. In addition, the variability of extracted values across subjects and across ROIs could be different from the variability at the voxel level. The issue might be alleviated through approaches such as the principal component of each region, hyperalignment algorithm (Haxby et al, 2011) or shared response modeling (Chen et al., 2015).

2. ROI-based analysis is conditional on the availability and quality of the ROI definition. One challenge facing ROI definition is the inconsistency in the literature due to the inaccuracies across different coordinate/template systems and publication bias. In addition, some extent of arbitrariness is embedded in ROI definition; for example, a uniform adoption of a fixed radius may not work well due to the heterogeneity of brain region sizes. When not all regions or subregions currently can be accurately defined, or when no prior information is available to choose a region in the first place, the ROI-based approach may miss any potential regions if they are not included in the model.

3. The exchangeability requirement of BML assumes that no differential information is available across the ROIs in the model. Under some circumstances ROIs can be expected to share differential information among some subgroups, especially when they are anatomically contiguous or more functionally related than the other ROIs (e.g., homologous regions in opposite hemisphere); more exploration is needed to incorporate such a hierarchical structure. On the other hand, exchangeability, as an epistemological – neither physical nor ontological – assumption, provides a convenient approximation of a prior distribution by a mixture iid distributions (de Finetti’s theorem) (Gelman et al., 2014). Such an approximation, similar to suboptimal assumptions such as linearity in most models, does leave room for further improvement. Ignoring such hierarchical structure in the data, if substantially present, may lead to underestimated variability and inflated inferences. Nevertheless, Bayesian inferences build on posterior distributions without invoking the degrees of freedom, and the violation of exchangeability usually leads to negligible effect on the final shape of posterior distributions except for the precise sequence in which the posterior draws occur (McElreath, 2016). Furthermore, the performance of BML can be effectively examined against the conventional approaches through posterior predictive checks and cross validations (Chen et al., 2019a). In the future we will continue to explore the possibility of accounting for such a hierarchical correlation structure.

4. BML computation can be time-consuming or even prohibitive in cases. For example, the number of parameters grows quadratically with the number of subjects. In addition, the number of regions and explanatory variables increases linearly the number of parameters. Due to model complexity and limited experience, no simple dependence of computational cost is currently available on the number of subjects or regions. Currently parallelization can only be performed across chains. However, the improvement in numerical schemes are currently under fast development, and the use of graphical processing units and within-chain parallelization may be implemented in the near future (Stan Development Team, 2019), substantially improving the usability of BML for ISC analysis.

5. The BML performance requires more validation and assessment for its consistency and replicability from various perspectives and when applied to different data. For example, partial pooling under BML may not always be effective. On one hand, partial pooling acts as a compromise between the two forces: one force drags all regions toward the center, and the other toward each individual region. Pooling through a weighted average of these two extremes is particularly effective when the across-region variance is at roughly the same order of magnitude as the within-region variance (sum of cross-subject variance and residual variance). However, when one variance is substantially overwhelmed by the other (e.g., by an order of magnitude), then there is no compromising and information sharing is essentially reduced to one of the two degenerative cases: either “no pooling” (relatively huge within-region variability) or “complete pooling” (relatively negligible within-region variability). Under these scenarios, partial pooling is ineffective, and larger sample sizes would be most likely required.

Conclusion

Inter-subject correlation (ISC) captures the extent of the simultaneous synchronization at a brain region among a group of subjects who experience the same naturalistic setting such as movie watching or music listening. Extending our previous work of linear mixed-effects (LME) modeling, we adopt here an ROI-based Bayesian multilevel (BML) approach to decomposing each ISC effect into multiple additive effects. In addition to dissolving the multiplicity issue and achieving higher inference efficiency, the BML approach allows for full results reporting that pales in comparison with the prevalent adoption of dichotomous decision making under NHST, increasing transparency and reproducibility.