A method to visualize a complete sensitivity analysis for loss to follow-up in clinical trials

Abstract

Loss to follow-up occurs in randomized controlled trials. Missing data methods, including multiple imputation (MI), can be used but often rely upon untestable assumptions. Sensitivity analysis can quantify violations of these assumptions. Since an adequate sensitivity analysis requires evaluation of multiple scenarios, presenting this information in an easily interpretable manner is challenging.

We propose to graphically represent a thorough sensitivity analysis displaying all possible outcomes for loss to follow-up in randomized controlled trial data relating a completely observed binary exposure to a binary outcome. We describe plausible results under different missingness mechanisms using data from the EAGeR Trial (n = 1228) on low-dose aspirin versus placebo on pregnancy and live birth, in which 140 participants had early withdrawal. For the effect of aspirin on live birth, sensitivity analysis risk ratios (RR) for all potential outcome scenarios ranged from 0.88 to 1.34, applicable to any possible missingness mechanism. MI produced RR = 1.10; 95% confidence interval: (0.98, 1.22). RRs from individual imputations ranged from 1.04 to 1.16, the range of results that could have been observed if data were missing at random. Under this mechanism, the conclusions about the efficacy of low-dose aspirin could have been sensitive to the missing outcome data. Rather than limiting sensitivity analysis for loss to follow-up to a few scenarios that can be presented tabularly, results of a complete sensitivity analysis can be presented in a single plot, which should be implemented in all studies with missing outcome data to convey certainty or uncertainty, confidence or caution.

Highlights

• •Loss to follow-up can cause selection bias in randomized controlled trials.
• •Sensitivity analysis is often limited to a few scenarios presented tabularly.
• •A complete sensitivity analysis is demonstrated for binary exposure and outcomes.
• •All possible and probable outcomes can be graphically displayed in a single plot.

1. Introduction

Loss to follow-up occurs in nearly every longitudinal epidemiologic study [1,2], including randomized controlled trials. While it can be a source of selection bias [3], its impact is rarely quantified. Numerous techniques, commonly complete-case analysis and, increasingly, multiple imputation, can be used to produce unbiased estimates accounting for missing data, including loss to follow-up. Implicit to all missing data techniques are assumptions about the underlying missing data and the manner or mechanism by which it came to be unobserved.

The impact of loss to follow-up on estimation depends on both the degree of loss to follow-up and its independence with respect to measured or unmeasured variables that arise from certain causal structures [[4], [5], [6], [7], [8]]. Missing data is generally described in the literature as resulting from one of three missingness mechanisms, missing completely at random (MCAR), missing at random (MAR) and missing not at random (MNAR). Detailed discussion of these mechanisms has been provided extensively in existing literature [1,7,9,10] but briefly, data could be missing because loss to follow-up is independent of all other measured or unmeasured variables (MCAR), or the missingness could be dependent on observed (MAR) and/or unobserved (MNAR) variables. Violations of these assumptions can lead to bias and unfortunately, some assumptions cannot be empirically tested. Since missing data methods rely upon untestable assumptions about the missing data mechanism, sensitivity analyses are necessary to quantify the potential impact of violations of these assumptions [9]. Despite a robust literature on missing data methods [[11], [12], [13], [14], [15], [16], [17]], and specifically, existing work on loss to follow-up and selection [[18], [19], [20]], randomized controlled trials under-utilize sensitivity analysis in assessing the potential impact of loss to follow-up.

A complete sensitivity analysis consists of quantifying all potential realizations of outcomes for the unobserved outcome data. Given this potential large volume of results, researchers often limit their sensitivity analysis to a few scenarios that can be presented tabularly. Existing sensitivity analysis to account for loss to follow-up and selection [[18], [19], [20]] have focused on bounding potential bias, but this neither provides an intuitive understanding of all possible results, nor insight into likely trial findings had all of the outcome data been observed.

We propose conducting the complete sensitivity analysis for loss to follow-up and employing a graphical representation to visualize possible and probable trial findings, had all of the outcome data been observed. We do this by identifying and mapping three components of the graphical representation: 1) point estimates from complete-case and MI based on the observed data, 2) all combinations of potential outcomes for the unobserved outcome data bounded by the extremes of what could have been observed, and 3) what is likely to have been observed under assumptions about the mechanism behind the missing outcomes. Estimation based on the observed data (component 1) is not a sensitivity analysis but acts as the anchor and reference for components 2 and 3. This sensitivity analysis and resulting plot are limited to the relation of a binary exposure to a binary outcome, in which one variable (most often exposure or treatment assignment for a randomized controlled trial) is completely observed.

As motivation for a sensitivity analysis, we introduce the Effects of Aspirin in Gestation and Reproduction (EAGeR) trial on the effectiveness of low-dose aspirin on improvement of pregnancy and live birth rates that was impacted by withdrawals. We apply this sensitivity analysis to the EAGeR trial data to demonstrate the interpretation of the sensitivity plots, and discuss the necessity and implications of applying this sensitivity analysis to other trials with missing binary outcome data.

1.1. Example: The EAGeR trial

The Effects of Aspirin in Gestation and Reproduction (EAGeR) trial [21], a placebo-controlled randomized trial of 81 mg low dose aspirin (LDA) focused on the effects on pregnancy and live birth among women with a history of pregnancy loss. The trial block randomized 1228 women by site and two eligibility strata (Original: 1 documented pregnancy loss less than 20wks gestation in the prior 12 months, Expanded: 1 or 2 documented pregnancy losses at any gestational age or timing). The withdrawal rate in the trial was 11.4% (140/1228), 12.7% (78/615) in the low-dose aspirin arm, and 10.1% (62/613) in the placebo arm (eTable 1). A complete-case, intent-to-treat analysis of the 1088 women with complete follow-up yields relative risks (RR) and 95% confidence intervals (CI) of 1.10 (0.99, 1.23) and 1.09 (1.02, 1.18) for live birth and positive pregnancy test (PPT), respectively, overall (Table 1). Multiple imputation using M = 500 datasets results in nearly identical estimates for both live birth and PPT (Table 1). The imputation model only consisted of treatment randomization (low-dose aspirin = 1, placebo = 0) for both PPT and live birth outcomes. Due to borderline significant findings, the 140 withdrawals have the potential to impact trial interpretation and conclusions, making it an ideal setting to investigate the impact of loss to follow-up. The Institutional Review Board at each study site and data coordinating center approved the trial protocol and obtained approvals. All participants provided written informed consent prior to enrolling.

Table 1.

Relative risks and 95% confidence intervals for live birth and positive pregnancy test (PPT) in the EAGeR trial, overall and by eligibility stratum (original and expanded) using complete case analysis, multiple imputation, and for bounding missing outcome data scenarios.

Outcome	Overall	Live birth	Expanded	Overall	PPT	Expanded
Eligibility stratum		Original			Original
Complete case	1.10 (0.99, 1.23)	1.17 (1.00, 1.36)	1.04 (0.90, 1.22)	1.09 (1.02, 1.18)	1.16 (1.05, 1.29)	1.04 (0.94, 1.15)
Multiple imputation	1.10 (0.98, 1.22)	1.17 (1.00, 1.36)	1.04 (0.89, 1.21)	1.09 (1.01, 1.18)	1.15 (1.04, 1.28)	1.04 (0.94, 1.16)
Poor outcomes regardless of the exposure	1.07 (0.95, 1.20)	1.12 (0.96, 1.32)	1.02 (0.87, 1.20)	1.07 (0.98, 1.16)	1.13 (1.00, 1.27)	1.02 (0.90, 1.14)
Positive outcome regardless of the exposure	1.10 (1.01, 1.21)	1.17 (1.02, 1.33)	1.05 (0.92, 1.19)	1.09 (1.02, 1.16)	1.15 (1.05, 1.26)	1.04 (0.95, 1.14)
Positive outcome in the placebo and poor outcome in the treatment assignment and vice versa	0.88 (0.79, 0.98)	0.96 (0.83, 1.12)	0.81 (0.70, 0.94)	0.93 (0.86, 1.00)	1.01 (0.91, 1.12)	0.87 (0.78, 0.96)
Positive outcome in the treatment and poor outcome in the placebo assignment	1.34 (1.21, 1.49)	1.36 (1.17, 1.58)	1.32 (1.14, 1.53)	1.25 (1.16, 1.35)	1.29 (1.16, 1.43)	1.22 (1.10, 1.35)

2. Methods

Three graphical components are used to represent the sensitivity analysis presented here. In the first component, point estimates are calculated using complete-case analysis and multiple imputation, used as a reference for the sensitivity analysis. In the second component, all combinations of potential outcomes for the unobserved outcome data are estimated. The last component includes a smaller range of results under a priori assumptions of MCAR or MAR for unobserved data scenarios.

2.1. First component

Complete-case analysis [10], the most commonly employed and easiest method of handling missing data, provides a fitting starting point for a sensitivity analysis. Records with any missing data (here, the outcome) are not utilized. This analysis provides an unbiased estimate when data are MCAR. However, complete-case analysis may suffer from inefficiency and bias under MAR and MNAR [1,5,7,9,10]. Specifically, in a randomized controlled trial, missing outcome data could be MAR or MNAR if there was differential loss to follow-up by exposure (MAR) and/or outcome status (MNAR). If, for example in EAGeR, there was differential loss to follow-up by live birth status, then the missingness mechanism would be MNAR. Only if not and there was differential loss-to follow-up by aspirin treatment, then the missingness mechanism would be MAR. MCAR could be realized if exposure were blinded, there were no side effects of treatment that were related to study withdrawal, participants who experienced an undesired outcome did not differentially withdraw, and withdrawal was independent of one or more unbalanced covariates (measured or unmeasured). Of these criteria, side effects and undesired outcome related to withdrawal may be the most difficult to achieve in trial practice, though they are indeed trial specific, dependent upon trial treatment and the desirability of a positive outcome, respectively. Missing outcome data could also be MAR or MNAR by a measured or unmeasured covariate that by chance happened to be unbalanced between treatment strata (MAR if observed, MNAR if unobserved). Although there are some causal structures in which complete-case analysis can be used to provide unbiased estimates for data that are MAR [5], assuming MAR over MNAR is an untestable assumption. In our study in which data are missing if the outcome is unobserved, if this missingness is dependent upon the outcome, the mechanism is MNAR [5]. Unless the mechanism is known to be MCAR then sensitivity analysis is needed.

Another common method for handling missing data is multiple imputation, which is more principled than complete-case analysis in that missingness is directly addressed, rather than ignored. An extensive literature exists for multiple imputation; briefly, the method models the relation between the observed and missing data and imputes values from those models, forming multiple, complete datasets. Each imputed dataset is analyzed, and the resulting point estimates are combined to produce a single unbiased estimate (given the data are MCAR or MAR [15]) and a standard error that is appropriate for the modeled data used in place of the unobserved data. Since all observations are utilized, multiple imputation can be more efficient than complete-case analysis. To impute missing data, multiple imputation requires building a model from observed data that characterizes the relation between variables and carries with it assumptions (often multivariate normality) regarding the relation of the missing data and the observed data, which in theory could lead to bias. However, multiple imputation has been shown to be fairly robust to model misspecification [22].

2.2. Second component

Given point estimates from complete-case analysis and multiple imputation, the next step is to map the space of all potential results that could have been observed had the outcome data been complete. This space is constructed by attributing every combination of potential outcomes for the missing data beginning with the bounding scenarios. For a clinical trial with loss to follow-up, these bounds are created by assigning all individuals with missing outcome to: 1) poor outcomes regardless of the exposure; 2) positive outcomes regardless of the exposure; 3) positive outcomes in the placebo and poor outcomes in the treatment assignment and vice versa, 4) positive outcomes in the treatment and poor outcomes in the placebo assignment.

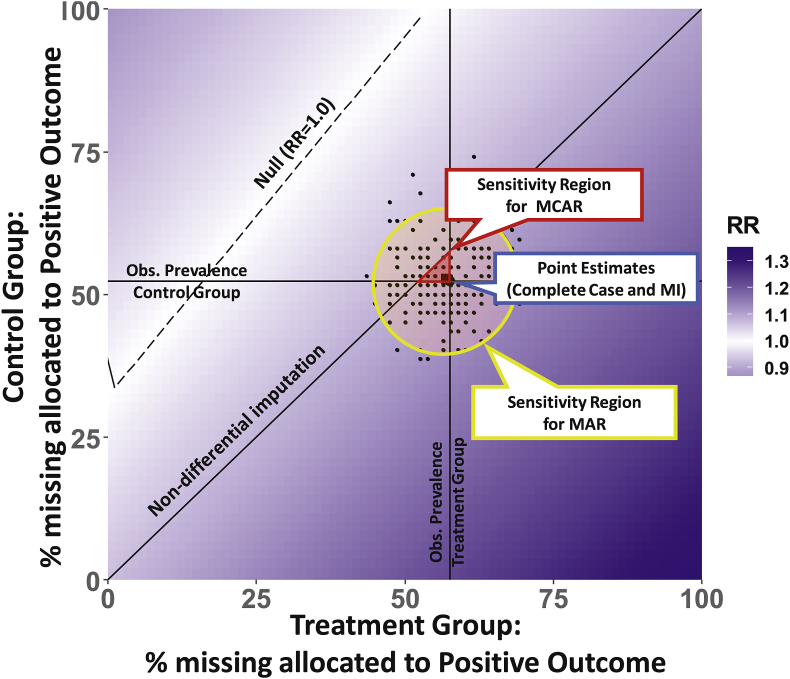
These four scenarios correspond to the corners of the sensitivity plot in Fig. 1. The axes of Fig. 1 are the percent of the missing in the treatment and control group assigned to a positive outcome, such that the figure origin (0,0) corresponds to scenario 1, (100,100) corresponds to scenario 2, and the points (0,100) and (100,0) correspond to scenarios 3 and 4, respectively. Since the four estimates form the bounds of the potential analysis results, any potential realization of missing outcome data will lie in the space of Fig. 1, regardless of the missingness mechanism.

Fig. 1.

Plot of sensitivity analysis of the relative risk for the relation between a binary exposure and a binary outcome with missingness in the outcome. The dotted line (white region) depicts the percent of missing allocated positive outcome in each group for the overall trial results to be null (relative risk, RR = 1.0); increasing darker gradation reflects further departures from the null. The full plot encompasses any potential mechanism, including MNAR.

2.3. Third component

Within these bounds of all possible complete data scenarios, we can identify and compare subsets of scenarios within Fig. 1, which we define a priori, that are more plausible given the observed data and/or prior knowledge.

A reasonable scenario would be that missing data could be in alignment with the null hypothesis. This corresponds to the 45° diagonal in Fig. 1 (labeled non-differential imputation), in which the percent of missing with a positive outcome is non-differential by treatment group. This null scenario is not tied to any missingness mechanism and leaves any existing relation in the observed data unchanged, so does not necessarily correspond to a null estimate for the trial overall.

Other plausible scenarios rely on the same assumption of MCAR or MAR necessary for the complete-case and multiple imputation estimators, respectively. Reasonable under MCAR would be that the missing data could mirror observed data, in which the positive outcome prevalence in the missing data would equal the observed prevalence within treatment groups. In this scenario, missing outcomes would be imputed in the observed proportions, corresponding to the vertical and horizontal lines of Fig. 1, which intersect at the point estimate for complete-case analysis. Finally, reasonable under MAR would be the modeled multiple imputation datasets, represented in Fig. 1 by the cloud of points. Multiple imputation is a technique for handling missing data where the relations and variability within the observed data are imposed by filling in the unobserved data to form multiple complete datasets. Rather than marginalizing results across potential scenarios (as is done for a multiple imputation point estimate), we consider the individual estimates in the context of all possible potential outcomes for the missing outcome data. Each point in Fig. 1 constitutes a random draw from a conditional distribution that captures differential relations between the observed data and the imputed outcome. Banding these estimates by a 95% elliptical confidence region produces a distinct sensitivity region for MAR. This MAR region in Fig. 1 is generated assuming the default bivariate t-distribution within the “stat_ellipse” function in R.

Interpretation of results within and between each component provides insight into the sensitivity of the results from a given dataset. To further aid interpretation, other key plot features can be added such as a line depicting percent of missing allocated positive outcome in each group for the overall trial results to be null. This is represented in Fig. 1, as the dashed line, which depicts a trial relative risk of 1.0 for the estimator of interest. If p-values from hypothesis testing are of interest, a boundary line of significance can additionally be added. These components comprise a thorough sensitivity analysis for loss to follow-up that is easy to interpret graphically and can convey main analysis reliability.

3. Example revisited: Sensitivity analysis in the EAGeR trial

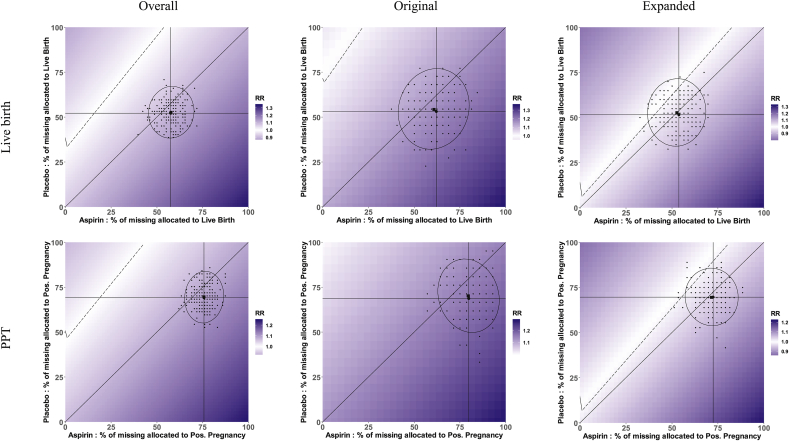
Given point estimates from complete-case analysis and multiple imputation (first component), conducting the sensitivity analysis as outlined follows with constructing complete datasets under each of the four bounding scenarios (second component) and all possibilities contained within. For women lost to follow-up in EAGeR, these bounds are constructed by consecutively imputing 1) no live births 2) all live births 3) all live births in placebo arm and none in LDA arm 4) all live births in LDA arm and none in placebo arm. These relative risk bounds are listed in Table 1 and correspond to the corners of the plots in Fig. 2, in which the x- and y-axes are the percentages of the missing outcomes assigned a positive outcome (live birth or PPT) in the LDA and placebo arms, respectively. Bounds are similarly constructed for the pregnancy sensitivity analysis (Table 1). The plots in Fig. 2 contain trial relative risks that include all possible combinations of outcomes for the 140 individuals with unobserved outcome data. Notably, the dotted line in the white region reflects the missing outcome scenarios for the overall trial results to be null (RR = 1.0), with increasing darker gradation reflecting further departures from the null.

Fig. 2.

Sensitivity plots of relative risks for a randomized controlled trial accounting for all possible missing outcome (live birth and positive pregnancy test (PPT)) scenarios. Percent of missing allocated to positive outcome within the aspirin and placebo treatment arms is displayed on the x- and y-axis, respectively. Trial results are displayed overall (first column) and stratified by two block randomized eligibility strata (original – second column, and expanded – third column). The dotted line (white region) depicts the percent of missing allocated positive outcome in each group for the overall trial results to be null (relative risk, RR = 1.0); increasing darker gradation reflects further departures from the null. The full plot encompasses any potential mechanism, including MNAR.

Within the boundaries of possible scenarios are features corresponding to more likely scenarios (third component). The 45° diagonals in Fig. 2 correspond to all scenarios of no treatment effect of LDA on live birth and pregnancy among the missing observations. The vertical and horizontal lines in Fig. 2 correspond to the observed rate of live birth and pregnancy in the LDA and placebo arms, respectively. Intuitively, these two lines intersect at the point estimate for complete-case analysis. Under a MCAR mechanism, the triangular region formed by these two lines and the main diagonal uses the point estimate under the MCAR assumption as the strongest potential effect in the missing data, and only considers alternatives towards a non-differential effect of treatment among the missing outcome data.

Also for the third component, we plot the 500 individual datasets from multiple imputation as points in Fig. 2, with the ellipse forming a defined region that captures 95% of the imputed datasets. We consider this a reasonable region under a MAR mechanism (as with the multiple imputation point estimate) for sensitivity to missing live birth and pregnancy. Code for implementation is provided in the supplementary material.

Interpretation of the resulting plots in Fig. 2 is now largely intuitive. The plots display the bounds for the potential for sensitivity due to missing outcomes, with shading variability corresponding to relative risk sensitivity. Within the Original stratum of Fig. 2, it is easy to see that results for live birth are more sensitive than for pregnancy displayed by the stronger difference in gradation. The plots for the Original stratum also show that there is no scenario whereby missing outcomes could lead to a null or harmful point estimate for pregnancy, as the null line is absent from the plot. However, a null point estimate is possible for live birth, depicted by the presence of the null line. We use the triangular and the elliptical regions to refine our interpretation from what is possible to what is more reasonable. These respective regions represent MCAR and MAR mechanism assumptions, whereas the full plot encompasses any potential mechanism, including MNAR. The sizes of these regions relative to one another and the full plot show the potential for sensitivity of point estimates under MCAR relative to MAR, and each relative to any potential mechanism. This will largely depend on the groupwise prevalence of missingness, meaning that larger magnitudes of sensitivity are possible with increasing missing outcome prevalence.

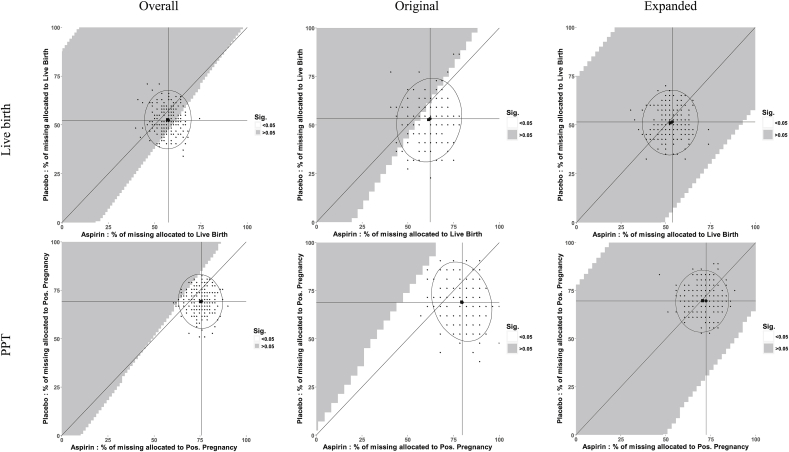
For live birth and positive pregnancy test Overall, Fig. 2 shows that the complete-case result and the entire triangular region are of similar shading, meaning that when using the point estimate under an MCAR assumption as the strongest potential effect in the missing data, and only considering alternatives towards a null effect of treatment in the missing data, point estimates would likely have not meaningfully changed had all of the data been observed. Further, Fig. 3, a “tipping-point” plot [23], shows that the complete-case result and the entire triangular region are non-significant for live birth and significant for positive pregnancy test, indicating that under this same scenario upper bounded by the MCAR point estimate, significance would not have changed and no tipping-point exists for live birth or positive pregnancy test overall had all of the data been observed. However, about 40% and 80% of the 500 imputations for live birth and positive pregnancy test, respectively, lie in the significant region in Fig. 3. When a decision point is considered, this implies that under MAR, the conclusions about the efficacy of LDA could have been sensitive to the missing data and warrant further investigation.

Fig. 3.

Sensitivity plots of significance for a randomized controlled trial accounting for all possible missing outcome (live birth and positive pregnancy test (PPT)) scenarios. Percent of missing allocated to positive outcome within the aspirin and placebo treatment arms is displayed on the x- and y-axis, respectively. Trial results are displayed overall (first column) and stratified by two block randomized eligibility strata (original – second column, and expanded – third column). The full plot encompasses any potential mechanism, including MNAR.

4. Limitations

To understand the potential effects of missing outcome data on study results, we performed a sensitivity analysis in which all missing data realizations were calculated, highlighting likely possibilities based on reasonable missing data mechanisms, and presented our results in an easily interpretable plot instead of in multiple tables. In context of the EAGeR findings, use of this methodology enabled us to determine the sensitivity of estimates to withdrawal and display this information completely in a single Figure (Fig. 2) rather than using a subset of results and multiple tables. However, this sensitivity analysis and plot are limited to binary exposure and outcome data. While we applied this methodology to randomized controlled trial data for which the exposure data are complete, this methodology has been used in more complex settings such time-to-event data [24], and could potentially be extended to the setting of observational data in which exposure data are incomplete.

Since we do not typically know with certainty the data missingness mechanism or the underlying causal structure, it is important to consider a variety of missing data mechanisms and principled methods that account for missing data. Here we utilized multiple imputation for MAR scenarios because complete datasets are modeled and formed as part of the standard procedure, and it can be easily performed on a variety of statistically computing software platforms. Alternative methods exist, such as maximum likelihood and inverse probability weighting, that could also be used to generate point estimates and the sensitivity analysis. With respect to missing data, these methods are unbiased under different assumptions and researchers should choose the method or methods best suited to their particular data. Each of these cited methods depend on the untestable assumption that the value of the outcome does not affect its probability of being observed (assuming MAR vs. MNAR) and that there are no unmeasured common causes of the outcome and missingness. Since missing data techniques do not address the other potential sources of bias that may exist, such as confounding or model misspecification, sensitivity analysis interpretation should not be extended to the relation of interest besides with respect to the missing data.

5. Conclusions

While principled estimation techniques such as multiple imputation are important, they only tell a portion of the story. The sensitivity analysis demonstrated herein displays all possible trial results had all the missing outcome data been observed (applicable for any missingness mechanism), as well as likely results if the missing data mechanism can be assumed to be MCAR or MAR. It is accordingly an important tool in conveying certainty or uncertainty, confidence or caution in results with missing data. The plots demonstrated here provide a context and vehicle for intuitive interpretation of a broader assessment of a result's sensitivity to missing data and should be implemented in other studies with missing outcome data, as well as in other areas of study, to allow researchers to understand how results could have changed had all outcome data been observed.

Funding

This work was supported by the Intramural Research Program of the Eunice Kennedy Shriver National Institute of Child Health and Human Development, National Institutes of Health, Bethesda, Maryland [contract numbers HHSN267200603423, HHSN267200603424, HHSN267200603426].

Disclaimer

The views expressed in this manuscript are the authors’ own and not an official position of the institution or funder.

Clinical trial registration

#NCT00467363 (ClinicalTrials.gov).

Appendix A. Supplementary data

The following are the Supplementary data to this article: