Protein Diffusion on Charged Biopolymers: DNA versus Microtubule

Abstract

Protein diffusion in lower-dimensional spaces is used for various cellular functions. For example, sliding on DNA is essential for proteins searching for their target sites, and protein diffusion on microtubules is important for proper cell division and neuronal development. On the one hand, these linear diffusion processes are mediated by long-range electrostatic interactions between positively charged proteins and negatively charged biopolymers and have similar characteristic diffusion coefficients. On the other hand, DNA and microtubules have different structural properties. Here, using computational approaches, we studied the mechanism of protein diffusion along DNA and microtubules by exploring the diffusion of both protein types on both biopolymers. We found that DNA-binding and microtubule-binding proteins can diffuse on each other’s substrates; however, the adopted diffusion mechanism depends on the molecular properties of the diffusing proteins and the biopolymers. On the protein side, only DNA-binding proteins can perform rotation-coupled diffusion along DNA, with this being due to their higher net charge and its spatial organization at the DNA recognition helix. By contrast, the lower net charge on microtubule-binding proteins enables them to diffuse more quickly than DNA-binding proteins on both biopolymers. On the biopolymer side, microtubules possess intrinsically disordered, negatively charged C-terminal tails that interact with microtubule-binding proteins, thus supporting their diffusion. Thus, although both DNA-binding and microtubule-binding proteins can diffuse on the negatively charged biopolymers, the unique molecular features of the biopolymers and of their natural substrates are essential for function.

Significance

Several cellular functions are governed by linear diffusion of proteins on biopolymers. For example, diffusion is essential for DNA scanning while proteins search for their cognate site or protein localization to specific microtubule regions. Because both DNA and microtubule are negatively charged and the corresponding measured diffusion coefficients are similar, it is tempting to classify these two types of diffusion as sharing similar driving forces. Here, we investigate what is needed for a protein to linearly diffuse on a charged biopolymer and what distinguishes diffusion on DNA from diffusion on a microtubule. Quantifying the diffusion mechanisms may not only shed light on their molecular determinants but also formulate principles for manipulating protein diffusion in a low-dimensional space.

Introduction

Diffusion is a common transport mechanism in the cell, particularly when it takes place in lower-dimensionality spaces, such as proteins diffusing along one-dimensional (1D) biological polymers or on two-dimensional surfaces. Examples for 1D diffusion are the dynamics of proteins along DNA or along microtubules (MTs), whereas two-dimensional diffusion describes the motion of proteins along membranes. These diffusion processes are essential for proper cellular function. Although each diffusion mechanism potentially has unique characteristics, they share some common features, such as the role of long-range electrostatic forces in mediating diffusion.

MTs, which are an essential component of the eukaryotic cytoskeleton, provide mechanical support to the cell and serve as “highways” for intracellular trafficking. In addition to the well-known ATPase-mediated unidirectional active transport of cargo by motor proteins from the kinesin and dynein superfamilies (1, 2, 3), many MT-binding proteins (MBPs) diffuse along the MT lattice to reach various target sites (4). For instance, EB1 (5), the Dam1 complex (6), XMAP215 (7), kinesin 13 (mitotic centromere-associated kinesin) (8), and the Ndc80 complex (9) use diffusion to reach the plus end of MTs, where they are involved in tight regulation of MT length, which is crucial for cell division and neuronal development. By contrast, both PRC1 (5) (which cross-links two antiparallel MTs to form spindle midzones at anaphase (10)) and the intrinsically disordered protein Tau (11) (which increases the stability of neuronal MTs) diffuse along the MT lattice, although they do not need to reach a specific end. Interestingly, some motor proteins combine diffusional and directed motility to diffuse in a biased manner along the MT lattice (12, 13, 14, 15) or to sidestep across MT protofilaments (16,17), which may provide them with a mechanism to overcome roadblocks on a crowded MT lattice.

Protein diffusion along DNA constitutes another important example of protein diffusion along charged biopolymers. DNA-binding proteins (DBPs) perform various biological tasks, such as controlling transcription and repairing damaged DNA, all of which involve scanning the DNA by linear diffusion before specific recognition at the functional site. Theoretical and experimental perspectives have attributed the remarkable efficiency and specificity of protein-DNA recognition to the 1D diffusion of proteins on DNA (18, 19, 20). Furthermore, diffusion along DNA has been observed experimentally for various DBPs, such as RNA polymerase (21), the lac repressor (22), p53 (23, 24, 25), and Egr-1 (26,27) transcription factors, and for mismatch repair complexes (28), and its mechanisms have been further quantified by theoretical and computational studies (29, 30, 31, 32, 33, 34, 35, 36, 37, 38, 39, 40, 41).

Protein diffusion along DNA and MTs share many similarities. First, the diffusion coefficients for DBPs and MBPs are similar and span four orders of magnitude from 0.001 to 1 μm²/s (Fig. 1). Interestingly, the diffusion of proteins on membranes, another charged biological surface, has been reported for several systems (42, 43, 44, 45), and diffusion coefficients were found to be in the range of 0.4–2.5 μm²/s, which is the same order of magnitude as for DBPs and MBPs.

Figure 1.

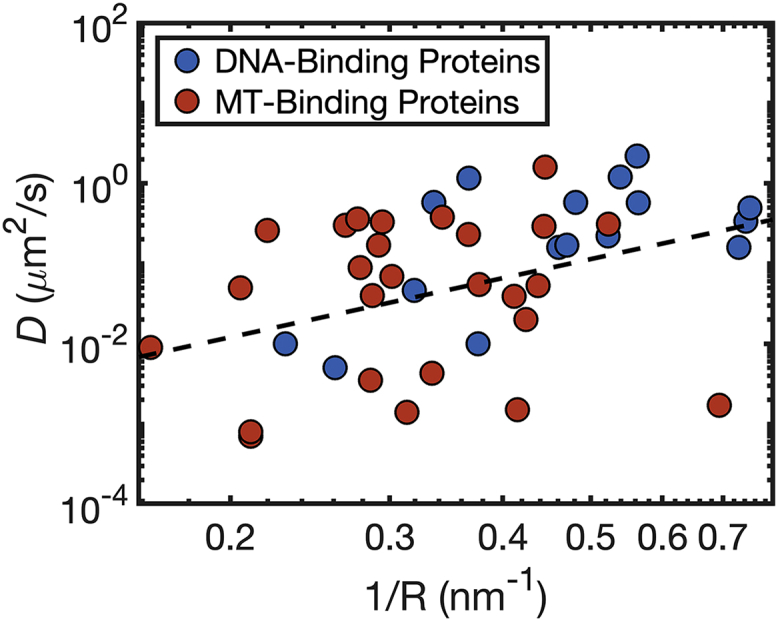
A survey of experimentally measured protein diffusion coefficients on DNA and MT molecules. The diffusion coefficients, D, of 16 DNA-binding proteins (DBPs; blue circles) and 26 MT-binding proteins (MBPs; red circles) are shown as a function of the reciprocal radius (R) of each protein. The diffusion coefficients of both types of proteins span approximately four orders of magnitude and depend linearly on 1/R, consistently with the Stokes-Einstein diffusion relation (D = K_BT/6πηR), as indicated by the dashed black line, which is the best linear fit to all the data points in this figure (slope = 2.4, R = 0.41). The protein radius, R, was estimated from the protein chain length (73) because the three-dimensional structures of many of these proteins have not been resolved. The full data set is summarized in Table S1. To see this figure in color, go online.

The similarity between DBP-DNA and MBP-MT interactions is also reflected in their corresponding binding affinities. The affinity of MBPs and DBPs to their respective polymers covers approximately three orders of magnitude, with dissociation constants ranging from the micromolar to low nanomolar ranges (5,27,46, 47, 48, 49). The affinity of DBPs may depend on whether they bind to a nonspecific or specific DNA sequence (27), whereas the affinity of MBPs may depend not only on the binding site but also on the nucleotide state of the MT (49) or nucleotide state of the MBP itself (for motor proteins) (47).

The similar range of diffusion coefficients for protein diffusion on MTs and on DNA can be attributed to the similarity of their driving forces because the two processes share similar electrostatic characteristics: the surface of both MT and DNA are negatively charged, and their corresponding diffusing proteins are positively charged. Moreover, because of their long-range nature, electrostatic interactions were suggested to play a central role in the mechanism of various diffusion processes along periodic substrates (39,50, 51, 52). Particularly, the role of electrostatic forces in the protein diffusion emerges from computational and experimental studies, illustrating for both DNA (39,53) and MTs (5,11) the sensitivity of their diffusion coefficient to salt concentration.

Although the surfaces of both MTs and DNA are negatively charged, the similar protein diffusion coefficient values are somewhat surprising given the structural differences between the two polymers. First, MTs are much larger than DNA: the diameter of MTs is ∼25 nm, which is an order of magnitude larger than the ∼2-nm-wide DNA. In addition, DNA and MT differ in their periodicity, which affects the elementary step size of diffusion along their main axis. The step size relevant for diffusion along DNA is on the order of a single basepair, i.e., ∼0.5 nm, whereas the step size for diffusion along MTs is on the order of a tubulin monomer or dimer, i.e., 4–8 nm (54,55). Moreover, the double helix of DNA is characterized by two grooves that do not exist in MTs. On the other hand, MTs are decorated with intrinsically disordered, negatively charged C-terminal tails that are known to regulate the interactions of MTs with several partner proteins (56, 57, 58, 59, 60). Hence, it is possible that these structural differences will be reflected in the diffusion mechanisms of proteins on DNA and MTs.

Although there have been extensive independent studies of each biopolymer and its binding proteins, no direct comparison has been made between the diffusion of proteins on DNA and MTs despite the potential of such a comparison to elucidate the unique features of MTs, DNA, and their binding proteins. In this study, we explored the difference between the two linear diffusion processes by asking whether DBPs can diffuse on MTs or whether MBPs can diffuse on DNA in a similar fashion to the diffusion performed on their functional biopolymer substrates. Specifically, we applied coarse-grained (CG) molecular dynamics (MD) simulations complemented by bioinformatic analysis to directly compare the molecular details of protein diffusion on DNA and MTs. For this purpose, we chose three DBPs (Skn1, SAP1, and the engrailed homeodomain (HD)) and three MBPs (EB1, PRC1, and Tau) and studied their diffusion on both DNA and MTs. We found that MBPs diffuse faster than DBPs on both DNA and MTs, mainly because MBPs are less positively charged than DBPs. In addition, we demonstrated that the major groove of the DNA and the disordered tubulin tails on MTs are key regulators of protein diffusion on charged biological polymers. These observations were complemented by a bioinformatic analysis, which supports the generalizability of our conclusions.

Methods

CG-MD simulations

The dynamics of protein diffusion along MTs and DNA was studied using CG-MD simulations that enable the investigation of long timescale processes that are challenging for high-resolution models. Each residue was represented by a single bead at the position of its Cα-atom. The DNA was modeled with three beads per nucleotide, representing the phosphate, sugar, and base (61).

The force field applied in our simulations used a native-topology-based model that includes a Lennard-Jones potential to reward native contacts and a repulsive potential to penalize non-native contacts (62, 63, 64). Electrostatic interactions between charged residues (the bead representing the DNA phosphate groups that bear a negative charge in our model) were modeled using the Debye-Hückel potential (65). The explicit form of the force field is the following:

$$V\left(\Gamma ,{\Gamma }_0\right)=\sum _{bonds}{K}_{bonds}\left(b_{ij}-b_{ij}^0\right)+\sum _{angles}{K}_{angles}\left({\theta }_{ijk}-{\theta }_{ijk}^0\right)+\sum _{dihedrals}{K}_{dihedrals}\left(\left[1-\cos \left({\phi }_{ijkl}-{\phi }_{ijkl}^0\right)\right]+\frac{1}{2}\left[1-\text{cos}\left(3\left({\phi }_{ijkl}-{\phi }_{ijkl}^0\right)\right)\right]\right)+\sum _{i\ne j}{K}_{contacts}\left[5{\left(\frac{A_{ij}}{r_{ij}}\right)}^{12}-6{\left(\frac{A_{ij}}{r_{ij}}\right)}^{10}\right]+\sum _{i\ne j}{K}_{repulsions}{\left(\frac{C_{ij}}{r_{ij}}\right)}^{12}+\sum _{i\ne j}{K}_{electrostatics}B\left(\kappa \right)q_i{q}_j\frac{e^{-\kappa r}}{{\text{ε}}_{\text{r}}{r}_{ij}},$$

where K_bonds = 100 kcal mol⁻¹ Å⁻²; K_angles = 20 kcal mol⁻¹; and K_dihedrals, K_contacts, and K_repulsion are each valued at 1 kcal mol⁻¹. The term b_ij is the distance (in angstroms) between bonded beads i-j, θ_ijk is the angle (in radians) between sequentially bonded beads i-j-k, φ_ijkl is the dihedral angle (in radians) between sequentially bonded backbone beads i-j-k-l, and r_ij is the distance (in angstroms) between beads i-j in a given conformation along the trajectory. A_ij is the distance (in angstroms) between beads i-j that are in contact with each other in the experimentally determined structure. The parameters denoted with the superscript 0 (x⁰) represent the minima of the various potential energy terms that were assigned according to the atomic coordinates of the structures. C_ij is the sum of radii for any two beads not forming a native contact; the repulsion radius of the backbone bead is 2.0 Å. The last term in the force field is the Debye-Hückel potential, where K_{electrostatics} = 332 kcal Å mol⁻¹ e⁻², q_i/j is the sign of the charged residue, ε_r is the dielectric constant, κ is the screening factor, B(κ) is the salt-dependent coefficient, and r_ij is the distance (in angstroms) between charged residues i and j. We note that, because of the CG representation of the systems, the effective salt concentration may correspond to a value higher (by a factor of ∼3) than for an atomistic representation. More details regarding the Debye-Hückel potential can be found in (65).

To reduce computational time, electrostatic interactions between the diffusing proteins and the charged residues of both α- and β-tubulins located at the interior of the MTs were eliminated. This elimination did not affect the properties of the MT surface, which is the side relevant to the diffusion process because the distance between the MT lumen and surface is ∼40 Å.

The beads of the structured part of the MT (referred to herein as the “MT body”) were kept fixed in our simulations, whereas the MT tails were flexible. Avoiding internal flexibility for the folded domains of the MT body is a reasonable assumption given the rigidity of MT structures. This approach also avoids deformation of the MT slice used in our summations. Furthermore, the internal dynamics of the tubulin monomers is not expected to contribute to diffusion on MT. The flexibility of the disordered MT tails was controlled by their bonds and dihedral angles.

The dynamics of protein diffusion along MTs and DNA was simulated using the Langevin equation. The simulation temperature was set to 0.4 (reduced units), which is lower than the folding temperatures of EB1, PRC1, SAP1, HD, and Skn1. The Tau protein is intrinsically disordered and was simulated at the same temperature for consistency. The dielectric constant was 70, and the salt concentration was 0.02 M unless stated otherwise.

Diffusion on DNA

The DNA and diffusing protein were confined in a box of dimensions 300 × 300 × 300 Å, and the longitudinal direction of the DNA was aligned along the z axis. We performed 10 simulations consisting of 10⁷ MD steps. The DNA was modeled as a linear double-stranded B-DNA molecule with a length of 100 basepairs. The diffusing DBPs were HD (66) (Protein Data Bank, PDB: 1hdd), SAP1 (67) (PDB: 1bc8), and Skn1 (68) (PDB: 1skn).

Diffusion on MTs

To study the diffusion of proteins along MTs, we constructed an MT lattice consisting of four protofilaments, each consisting of three heterodimeric tubulin molecules (i.e., the lattice included 6 × 4 monomeric tubulin proteins). The coordinates of the MT lattice were based on the structure of a single isoform neuronal human MT (PDB: 5JCO) (69). The disordered tails (residues 438–451 of α-tubulin and 427–450 of β-tubulin) were added as linear chains to the C-terminal of each tubulin monomer. A more realistic conformation of the tails was obtained by the simulations. We chose to study MT-bearing tails of isoform α1A and β3, which comprise 14 and 24 residues, respectively. The sequences of the tubulin tails were DSVEGEGEEEGEEY for α-tubulin (isoform α1A, net charge of −8) and DATAEEEGEMYEDDEEESEAQGPK for β-tubulin (isoform β3, net charge of −11). The diffusing MBPs were domains of EB1 (70) (PDB: 1pa7), PRC1 (71) (PDB: 5kmg), and Tau (72) (PDB: 6cvj). The MT and diffusing proteins were confined in a box of dimensions 350 × 400 × 330 Å, and the longitudinal direction of the MT was aligned along the y axis. Because the scale of diffusion length along an MT lattice is longer than that along a DNA molecule, we performed 50 simulations consisting of 2 × 10⁷ essential MD steps to achieve sufficient sampling. Trajectory frames were saved every 1000 steps. Periodic boundary conditions were not used in our model.

Calculation of diffusion coefficients

The trajectories from the CG simulations were analyzed using in-house scripts. The mean-square displacements of the proteins’ centers of mass (COMs) were calculated using the equation as follows:

$$MSD\left(\tau \right)=\sum _{i=t_0}^{t-\tau }\frac{{\left(r_{i+\tau }-r_i\right)}^2}{t-\tau }=2dD\tau ,$$

where r is the position of the protein COM, t is the number of time steps measured, and τ is the measurement window ranging from t₀ to t. The slope of the mean-square displacement is 2dD, where d is the dimensionality of diffusion and D is the diffusion coefficient, which was calculated between time frames 1500 and 3000 for diffusion on MTs because shorter timescales do not capture the slow diffusion process. For diffusion along DNA, D was calculated between time frames 1 and 200. We calculated diffusion along MT protofilaments or the DNA axis; hence, d = 1 in all the calculations used in this study.

Calculation of rotation-translation coupling

The angle of rotation between the diffusing protein and the DNA was calculated by the following:

$$\theta ={\tan }^{-1}\left(\frac{y}{x}\right),$$

where y and x are the corresponding coordinates of the protein COM around the DNA that was aligned along the z axis.

Data set of DBPs and MBPs with experimentally measured diffusion coefficients

The diffusion data for DBPs and MBPs were collected from experimental studies (see Table S1 and references therein). Because many proteins in our data set do not have a resolved three-dimensional structure, we estimated the radius of gyration of each protein using Flory’s scaling law: R_g = a × N^ν, where a = 0.3 nm (73), N is the length of the protein, and ν = 0.34. Scaling of ν = 0.34 is expected for a polymer chain in a poor solvent and was confirmed for proteins by fitting >10,000 structures of folded proteins from the PDB (73) to the Flory expression above.

Data set of DBPs and MBPs with resolved structures

To perform structural analyses of DBPs and MBPs, we analyzed data sets of proteins with resolved structures, using a data set of proteins that form dimeric complexes as a control. The data sets of DBPs and of the control proteins were based on lists (74, 75, 76) that were further refined (34) such that 118 DBPs and 121 control proteins were included in the respective data sets. The list of MBPs was curated as follows: first, we searched the PDB for the Gene Ontology molecular function of “microtubule binding,” for which we found 1007 protein chain entries. Only nontubulin structures with resolution <5 Å were retained, and the list was sorted in order of decreasing resolution. Next, we performed pairwise sequence alignment between all proteins in the list using the BioPython pairwise alignment module (77). Percent identity between two sequences was defined by dividing the number of matches by the length of the shorter sequence. Using the identity data, we kept the top structure (with the highest resolution) and eliminated chains with >70% sequence identity. This procedure was repeated with the second chain in the list and so on until the list was exhausted. The resulting set contained 78 MBPs (the full list of DBPs, MBPs, and dimers is in Table S2). All the proteins in the DBP, MBP, and dimeric protein data sets were analyzed for their charge densities and dipole moments (using the Protein Dipole Moment Server (78)).

Results and Discussion

Proteins diffuse on DNA and MT with similar rates

To compare diffusion of proteins on DNA and on MTs, we first curated a data set containing experimentally studied DBPs and MBPs having known coefficients for diffusion on their respective biopolymer substrates. In Fig. 1, the diffusion coefficients, D, for a data set of 26 MBPs and 16 DBPs (see Table S1) are plotted vs. 1/R, where R is the radius of the diffusing protein, estimated using Flory’s scaling law for a polymer in a poor solvent (see Methods). The values of D for both DBPs and MBPs span approximately four orders of magnitude, between 0.001 and 1 μm²/s. The dashed line in Fig. 1 is a liner fit of all the data points. The dashed line follows the Stokes-Einstein equation, which states D = K_BT/6πηR, where K_B is the Boltzmann constant, T is the temperature, η is viscosity, and R is the radius of the diffusing molecule. Energetic ruggedness for diffusion may contribute to deviation from a linear fit plot. The characteristic barrier for the energetic ruggedness of diffusion depends on the individual interactions of each DBP with DNA or each MBP with MT.

Electrostatic properties of diffusing proteins

Having observed that DBPs and MBPs diffuse at similar rates on DNA and MTs, respectively, we sought to compare their molecular mechanisms of diffusion on each substrate. For that purpose, we applied CG-MD simulations, which have previously been used to determine the molecular mechanism of protein diffusion on DNA (34,39,51, 52, 53) within protein-protein interfaces (50) and on MTs (54). In this study, we focused on three MBPs (PRC1, EB1, and Tau) and three DBPs (SAP1, HD, and Skn1), whose diffusion mechanisms were previously studied computationally (34,39) and experimentally (5,11).

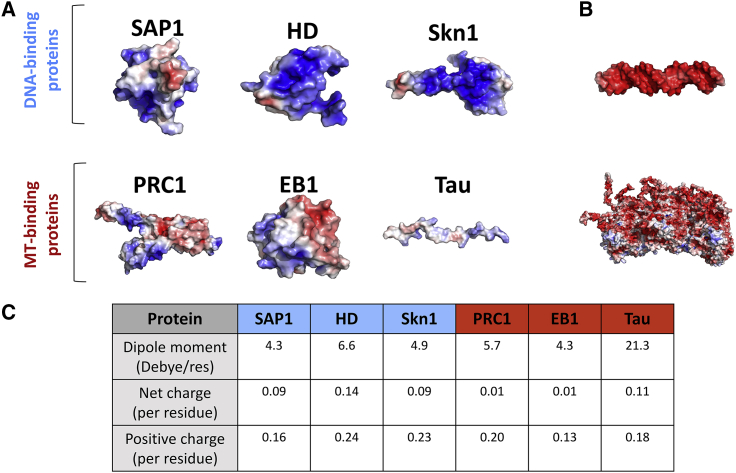
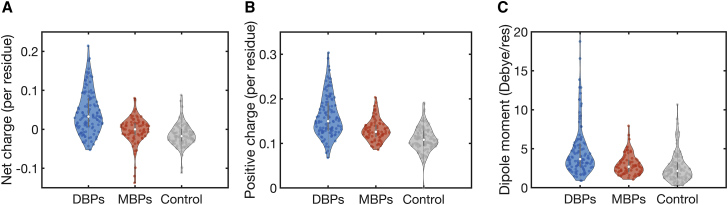
The selected DBPs and MBPs have positively charged electrostatic surfaces (Fig. 2 A, blue patches; (79)) and similar dipole moment values (Fig. 2 C; (78)). However, the charge density of the DBPs is higher than the charge density of the MBPs (Fig. 2 C), as illustrated also by the darker shades of blue in the surface electrostatic map (Fig. 2 A). The higher content of positively charged residues in DBPs may lead to different diffusion mechanisms for DBPs and MBPs, as discussed below.

Figure 2.

Electrostatic properties of the simulated DBPs and MBPs. (A) Shown are cartoon representations of the three DBPs (SAP1, homeodomain (HD), and Skn1) and three MBPs (PRC1, EB1, and Tau) selected for the diffusion study. The electrostatic potential (79) is mapped on the surface of these proteins, with the positive and negative potential illustrated in blue and red, respectively. Both DBPs and MBPs have a large patch of positive potential, yet this is more pronounced for DBPs than for MBPs. (B). Electrostatic potentials for a DNA (upper representation) and an MT (lower representation) are shown, illustrating their negative electrostatic potential. (C). An electrostatic analysis of the six studied proteins is shown, highlighting their dipole moment, total net charge, and number of positive charges per residue. Although the dipole moment is similar for globular DBPs and MBPs, the DBPs have a higher net charge than the MBPs. Fig. 7 presents a similar analysis for 351 proteins. To see this figure in color, go online.

Electrostatic interactions dominate protein diffusion on DNA and MTs

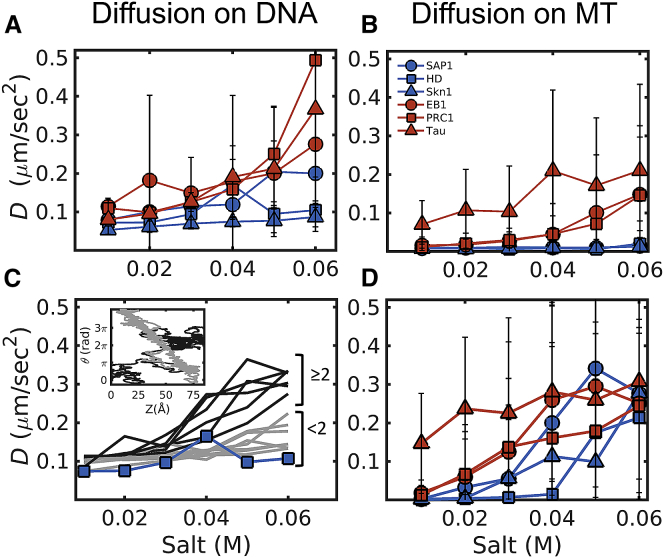
To decipher the molecular determinants of protein diffusion, we studied the diffusion of the six selected DBPs and MBPs on both DNA and MTs to determine whether DBPs are likely to diffuse on MTs and MBPs are likely to diffuse on DNA simply because of the similarity in their electrostatic properties. The simulations revealed that all six proteins are attracted electrostatically to both DNA and MTs. Furthermore, the linear dependence of their mean-square displacement with time suggests that they diffuse along the main axis of the biopolymer (i.e., DNA or MTs). Fig. 3 shows the diffusion coefficients of these proteins on DNA (Fig. 3 A) and MTs (Fig. 3 B) for different salt concentrations (DBPs are shown in blue and MBPs in red). First, we note that the diffusion coefficients of the three DBPs on DNA and of the three MBPs on MTs have similar values, consistent with the experimental survey presented in Fig. 1. Specifically, the value of D for an HD diffusing on DNA (27) is ∼2-fold higher than the value of D for EB1 and PRC1 on MTs, as was measured experimentally (5). Furthermore, MBPs diffuse faster than DBPs on both DNA and MTs. For all studied proteins, increasing salt concentration leads to an increase in the diffusion coefficient. However, MBPs diffuse faster than DBPs at any given salt concentration, and the increase in diffusion coefficient for MBPs is more pronounced than the increase for DBPs on all substrates, namely DNA (Fig. 3 A), MTs (Fig. 3 B), and MTs lacking disordered C-terminal tails (Fig. 3 D). However, although MBPs diffuse faster than DBPs on tail-less MTs at low salt concentration (<0.03 M), this difference diminishes at higher salt concentrations. The contribution of tubulin C-terminal tails to the mechanism of protein diffusion on MTs will be discussed below.

Figure 3.

Properties of protein diffusion on DNA and MTs. (A and B) The diffusion coefficients, D, are given as a function of the salt concentration for the three selected DBPs (blue) and three selected MBPs (red) on DNA (A) and on MTs (B). The error bars represent the SD obtained from averaging the independent simulations (see Methods for details). D increases with the salt concentration for the diffusion of both types of proteins on both DNA and MTs. In addition, MBPs diffuse faster than DBPs on both DNA and MTs. (C) This is the same as (A) but for the mutants of DBP HD. Each line represents an HD mutant, in which three positive residues were replaced with three negative residues. The gray lines show mutants with <2 mutations in the recognition helix, and the black lines show mutants with ≥2 mutations in the recognition helix (residues 40–56 of HD). Inset: the coupling between the rotation (θ) around and translation (Z) along the DNA is shown for one HD mutant with <2 mutations in the recognition helix (gray) and one mutant with ≥2 mutations in the recognition helix (black). All the mutants have a positive charge per residue of 0.19 and a net charge per residue of 0.01. (D) This is the same as (B) but for the diffusion on MTs lacking C-terminal tails. Note that at low salt concentrations, MBPs (red) diffuse faster than DBPs (blue) and that this difference diminishes at higher salt concentrations. To see this figure in color, go online.

One possible explanation for the faster diffusion of MBPs compared with DBPs is the observation that the charge density of the MBPs is lower than the charge density of the DBPs (Fig. 2). To test this possibility, we created 12 mutants of the DBP HD characterized by different combinations of three positive-to-negative residue substitutions, leading in all cases to a charge density similar to that of MBPs (positive charge per residue = 0.19 and net charge per residue = 0.01). We found that, although all the mutants tested had higher D than wild-type HD when diffusing on DNA (Fig. 3 C, mutants shown in gray and black; wild-type shown in blue), mutants with at least two mutated residues at the DNA recognition helix (Fig. 3 C, black lines) had higher D than the rest of the mutants at any given salt concentration (Fig. 3 C, gray lines). Moreover, mutating at least two positive residues at the DNA recognition helix led to loss of the characteristic rotation-translation-coupled diffusion along double-stranded DNA (Fig. 3 C, inset). Hence, we conclude that charge density alone does not fully explain the differences in D between MBPs and DBPs. The spatial organization of the charges within the structure of the diffusing protein is also important, as tested here for mutations in or out of the recognition helix of HD.

Furthermore, we tested whether there is a minimal number of positively charged residues at the recognition helix required to enable sliding of HD. For that purpose, we created an additional series of HD mutants in which the amount of positively charged residues at the recognition helix was varied and the rest of the residues of HD were neutralized: one mutant in which all six charged residues of the recognition helix remained charged, six mutants in which five residues remained charged, and 15 mutants in which four residues remained charged, considering all possible charge positions. We found that neutralizing two or more positive charges in any position of the recognition helix leads to the loss of the characteristic rotation-translation-coupled diffusion. Therefore, it appears that at least for the case of HD, a minimum of five positive charges at the recognition helix is sufficient, yet required, to slide along DNA in a rotation-translation coupled manner.

Diffusion of charged proteins along DNA or along MTs

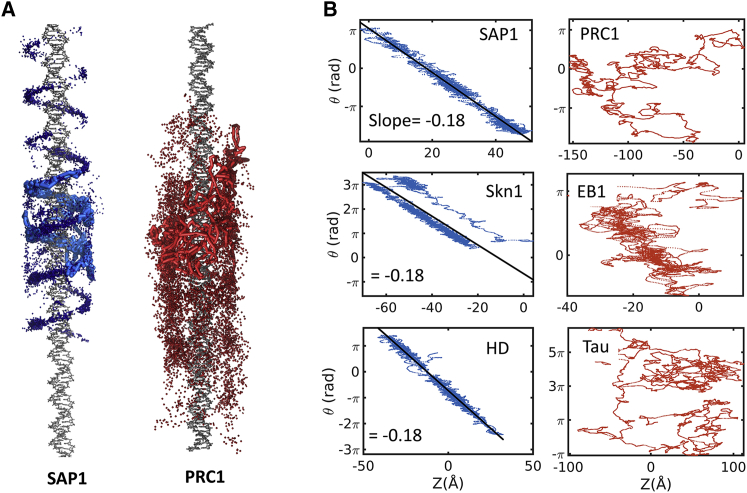
To better understand the difference between MBPs and DBPs diffusing on DNA and MTs, we quantified the effect of the unique structural properties of DNA and MTs on diffusion. Fig. 4 A shows a projection of the COM of the DBP SAP1 (blue) and MBP PRC1 (red) as they diffuse on DNA, as simulated by CG-MD. Although SAP1 follows the DNA major groove, PRC1 does not. In a more quantitative analysis, Fig. 4 B shows the rotation angle between the diffusing proteins and the DNA as a function of translocation distance along the DNA axis (z). Whereas there is no clear relationship between rotation angle and translocation distance for any of the three MBPs (shown in red), the three DBPs demonstrate coupling between rotation and translocation along the DNA axis, as reflected by the slope of 2π/34 = 0.18, which is characteristic of rotation-translation-coupled diffusion along double-stranded DNA. This indicates that all three DBPs diffuse along the DNA major groove, whereas the MBPs do not. Diffusion along the major DNA groove together with higher positive charge content can explain why DBPs diffuse more slowly than MBPs on DNA.

Figure 4.

Structural properties of protein diffusion along DNA. (A) Shown is the projection of the location of the COM of the DBP SAP1 (blue) and the MBP PRC1 (red) during diffusion on DNA. Five trajectories are projected, and one of them is shown as a continuous thick line, demonstrating that SAP1 follows the DNA major groove and PRC1 does not. (B) Coupling between rotation and translation when diffusing along the DNA is examined by plotting the rotation angle (θ) versus the distance the protein traversed along the DNA axis (Z). The coupling between rotation and translation manifests as a straight-line relationship between θ and Z with a slope of 2π/34 = 0.18, illustrating that DBPs diffuse helically on DNA (left column, blue); however, MBPs (right column, red) show no such coupling. To see this figure in color, go online.

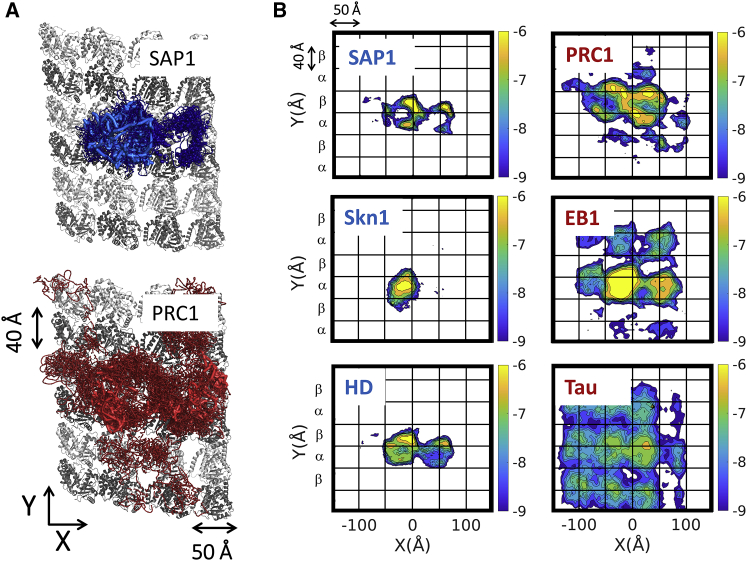
To complement this comparison, the diffusion of DBPs and MBPs was studied on an MT to examine why MBPs diffuse faster than DBPs on MTs, which do not have a major groove. Projections of the trajectories of the six studied proteins on an MT are shown in Fig. 5. Fig. 5 A shows that, whereas the DBP SAP1 is restricted to specific locations on the MT lattice, the MBP PRC1 samples a larger area of the MT lattice in the same accumulated simulation time. The heatmaps of the probability of finding the proteins at different locations on an MT lattice for all six proteins (Fig. 5 B) show that MBPs sample a larger fraction of the MT lattice than DBPs and that sidesteps across MT protofilaments, as discussed in detail elsewhere (54), also take place. It is possible that DBPs diffuse more slowly than MBPs on MTs and demonstrate a more restricted motion on MTs because they are more positively charged (Fig. 2).

Figure 5.

Structural properties of protein diffusion along MTs. (A) Shown is the projection of the location of the COM of the DBP SAP1 (blue) and MBP PRC1 (red) during diffusion on an MT lattice. 10 trajectories are projected on a slice of an MT lattice used in the CG simulations, and one trajectory is highlighted as a continuous thick line for each protein, demonstrating that PRC1 covers a larger fraction of the MT lattice than SAP1. (B) Shown are heatmaps of the probability of finding the diffusing protein at different locations on an MT lattice. The regions that are highly populated across the simulation time are colored yellow, and regions that are poorly populated are blue (see color bar on the right). The probability intensities are on a log scale and calculated for the COM of the diffusing proteins. DBPs sample a limited area of the MT lattice (left panels), whereas MBPs sample a larger fraction (right panels). The heatmaps shown here are from simulations at a salt concentration of 0.02 M. The grid lines reflect the lattice of α- and β-tubulins. To see this figure in color, go online.

MT tails modulate the diffusion of DBPs and MBPs on MTs

Although DNA and MTs are both very negatively charged (Fig. 2 B), they differ in that MTs are composed of two structural elements that are negatively charged: the globular parts of tubulin (MT body) and its C-terminal disordered tail (MT tail). A DBP or an MBP can, in principle, interact with both negatively charged elements, either in alternating or concomitant fashion. It is expected that DBP-MT interactions will be stronger than MBP-MT interactions even though the MT is not a natural substrate of DBPs simply because the DBPs have a greater net charge than MBPs.

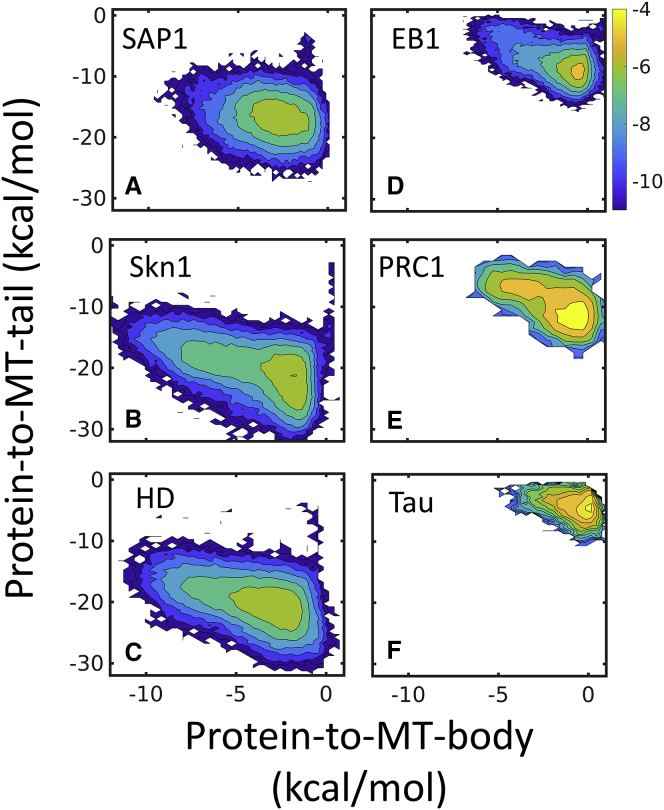
To further explore the diffusion of DBPs and MBPs on MT, we followed the interactions of each protein with the two structural components of the MT. Heatmaps of the electrostatic interaction energies of the six studied proteins with MT body and MT tails are shown in Fig. 6. For all MBPs, the interaction energy between the protein and the MT body is >−5 kcal/mol, and the interaction energy between the protein and the MT tails is >−10 kcal/mol. The interaction of DBPs with the MT body and MT tails is ∼2- to 3-fold stronger compared with the interaction of MBPs with these MT elements. Interestingly, although the DBP-to-MT-body interaction is ∼2-fold stronger than the corresponding interaction for MBPs, the DBP-to-MT-tails interaction is ∼3-fold stronger than the MBP-to-MT-tail interaction. The larger difference found in the strength of each protein’s interaction with MT tails may indicate that whereas the MT body can interact with the diffusing proteins at a limited and defined interface, several disordered tubulin tails can interact with the protein simultaneously, resulting in a greater difference in interaction energy between DBPs and MBPs interacting with MT tails compared with MT bodies. Thus, the tubulin C-terminal tails, rather than the bodies, appear to be the more dominant contributor to the slow diffusion of DBPs on MTs. In addition, when we removed the C-terminal tails from the MTs, the difference in diffusion coefficients between the MBPs and DBPs at high salt concentrations diminished (Fig. 3 D).

Figure 6.

MT tails modulate the diffusion of DBPs and MBPs on MTs. The interactions of the DBPs or MBPs with the MT tails are shown in (A)–(C) and (D)–(F), respectively. Heatmaps of the interaction energy between the proteins and MT lattice, examined with respect to the MT tails (y axis) and MT body (x axis), show that DBPs interact more strongly than MBPs with MTs. The interaction energy between DBPs and the MT body is ∼2-fold higher than that for MBPs, and the interaction energy between the DBPs and the MT tails is ∼3-fold higher than that for MBPs. The analyzed trajectories were sampled at a salt concentration of 0.02 M. To see this figure in color, go online.

Bioinformatic analysis of the electrostatic properties of DBPs and MBPs

Our results thus far suggest that for a protein to diffuse on a negatively charged biological polymer, be it DNA or an MT, the protein must have a combination of positively and negatively charged residues and, at least for the proteins used in this study, also a dipole moment. In addition, it appears that DBPs are more positively charged than MBPs and that the diffusion of DBPs and MBPs on DNA and MTs can be regulated by the unique structural features of each substrate (the major groove of DNA and the disordered C-terminal tails of tubulin). To test whether our observations can be generalized, we analyzed the electrostatic properties of 118 DBPs, 78 MBPs, and 121 dimers that served as a control set (see Methods for details on curation of the data sets). Indeed, the total charge density of DBPs (Fig. 7 A, blue) is higher than that of MBPs (Fig. 7 A, red) and the control set (Fig. 7 A, gray). In addition, the fraction of positively charged residues is greater in DBPs than in MBPs and the control set (Fig. 7 B). Similarly, DBPs have a larger dipole moment than MBPs and the control set. Hence, we conclude that our observations, namely that proteins that diffuse on DNA or MTs are more positively charged than proteins that do not and that DBPs have a larger dipole moment than MBPs, are general properties of DBPs and MBPs.

Figure 7.

Electrostatic properties of DBPs and MBPs in large data sets. For 118 DBPs, 78 MBPs, and 121 homo- and heterodimeric proteins (control), the Protein Dipole Moment Server (78) was used to calculate the following: (A) net charge per residue, (B) positive charge per residue, and (C) dipole moment per residue. The mean dipole moments, the mean net charge, and the mean number of positive charges per residue are higher for the DBPs than for the MBPs. The mean number of positive charges is higher for MBPs compared with the control proteins. To see this figure in color, go online.

Conclusions

Protein diffusion on charged biopolymers, such as DNA and MTs, enables efficient scanning of DNA while proteins search for their cognate site and the localization of proteins to specific MT regions to perform their function, respectively. Because both DNA and MTs are negatively charged and proteins diffuse on the surfaces of DNA and MTs at similar rates, it is tempting to classify these two types of diffusion as sharing many similarities. However, a direct comparison between the two was lacking. Here, we addressed this question by quantifying the diffusion mechanisms of DBPs and MBPs on both their natural and unnatural substrates.

Using CG-MD modeling, we found that MBPs diffuse faster than DBPs on both DNA and MTs. The faster diffusion of MBPs was attributed to their lower net charge compared with DBPs. The lower charge density of MBPs compared with DBPs was confirmed by bioinformatic analysis of a larger data set of experimentally classified MBPs and DBPs. Although many positively charged proteins can diffuse on DNA, as demonstrated in this study, DBPs are unique in the sense that they can diffuse helically along the major groove, which may enable them to probe the DNA sequence and subsequently to bind specifically to their target sites. The ability of DBPs to slide along DNA while situated at the major groove is related to both electrostatic and structural complementarities. Reducing the electrostatic strength by increasing the salt concentration may shift diffusion on DNA from rotation-coupled translation along the major groove (also called sliding) to diffusion that lacks this coupling and is across major grooves (also called hopping). Mutating DBPs to reduce their charge density may result in diffusion via hopping, but this will strongly depend on the location of the mutations. Accordingly, charge density is not the only parameter that governs the ability of DBPs to slide by rotation-coupled diffusion or that distinguishes between DBPs and MBPs. We note that several DBPs have been found to diffuse on DNA in a nonhelical fashion (i.e., hopping) (80,81).

MBPs, which have a lower charge density than DBPs, mostly perform hopping diffusion along DNA. The diffusion of MBPs along the MT is supported by the negatively charged disordered tails, which may compensate for the lower charge density of the MBPs and therefore increase their affinity to the MT. The interactions of MBPs with the tubulin tails can also explain why the experimentally observed diffusion rates of MBPs on MTs and of DBPs on DNA are similar, although MBPs have a lower charge density than DBPs. The observation that tubulin tails regulate protein diffusion on MTs is consistent with the regulatory role tubulin tails play in the interactions of several MBPs with MTs (56, 57, 58, 59, 60).

Although DBPs and MBPs are expected to usually diffuse on their natural substrates, in some cases they may encounter non-natural substrates. Proper cell division in eukaryotes requires recognition of the centromere by the DNA segregation machinery, connection between chromosomal DNA and spindle MTs, and force generation to move DNA to daughter cells (82). Therefore, during cell division, the MTs and DNA are in close proximity. Nonfunctional diffusion of DBPs on MTs and of MBPs on DNA may interfere with the functional interactions of DBPs and MBPs with their natural substrates. Hence, we speculate that the unique structural properties of MBPs, DBPs, MT, and DNA have co-evolved to assure proper cell division and to minimize the interference between the two types of proteins and their corresponding charged biopolymers.

Author Contributions

L.S.B. and Y.L. designed the research and wrote the manuscript. L.S.B. performed the research and analyzed the data.

Editor: Anatoly Kolomeisky.