Microtubule Simulations Provide Insight into the Molecular Mechanism Underlying Dynamic Instability

Abstract

The dynamic instability of microtubules (MTs), which refers to their ability to switch between polymerization and depolymerization states, is crucial for their function. It has been proposed that the growing MT ends are protected by a “GTP cap” that consists of GTP-bound tubulin dimers. When the speed of GTP hydrolysis is faster than dimer recruitment, the loss of this GTP cap will lead the MT to undergo rapid disassembly. However, the underlying atomistic mechanistic details of the dynamic instability remains unclear. In this study, we have performed long-time atomistic molecular dynamics simulations (1 μs for each system) for MT patches as well as a short segment of a closed MT in both GTP- and GDP-bound states. Our results confirmed that MTs in the GDP state generally have weaker lateral interactions between neighboring protofilaments (PFs) and less cooperative outward bending conformational change, where the difference between bending angles of neighboring PFs tends to be larger compared with GTP ones. As a result, when the GDP state tubulin dimer is exposed at the growing MT end, these factors will be more likely to cause the MT to undergo rapid disassembly. We also compared simulation results between the special MT seam region and the remaining material and found that the lateral interactions between MT PFs at the seam region were comparatively much weaker. This finding is consistent with the experimental suggestion that the seam region tends to separate during the disassembly process of an MT.

Significance

Our study aims to understand the effects of different nucleotide states on the conformational dynamics of microtubules (MTs) at the free-growing plus end. We have carried out large-scale simulations for both small MT patches and fully closed MT segments in different nucleotide states. We show that the lateral interactions between neighboring protofilaments are significantly weakened for GDP state MT. Our simulations also strongly suggest the seam region to be a weak point of the MT lattice. In summary, we propose a model in which the lateral contacts of GDP state MT will gradually weaken from the seam region to nearby homogeneous lateral interfaces. This leads to the outward bending of the protofilaments and eventually the complete disassembly of the MT.

Introduction

Microtubules (MTs), one of the three major components of a cytoskeleton, are widely involved in cellular processes, such as intracellular transport, chromosomal separation during cell division, and maintaining cell structure (1). MTs are long hollow cylinder structures formed by laterally combined protofilaments (PFs), with each PF consisting of repeating αβ tubulin heterodimers (2,3). The dynamic instability of MTs, first described by Mitchison and Kirschner in 1984 (4), refers to their ability to quickly switch between polymerization and depolymerization states. This unique feature enables MTs to be reorganized rapidly depending on environmental variations (5). The growing or shrinkage of MTs can also push or pull objects attached to their ends. Thus, the dynamic instability of MTs is intrinsically linked to their cellular function.

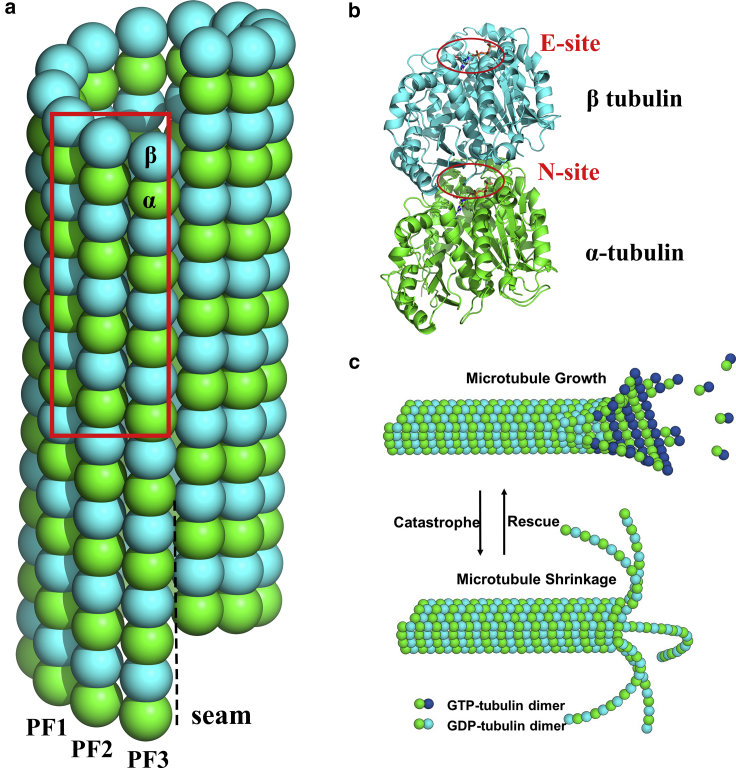
The dynamic instability of MTs is known to be regulated by the hydrolysis of GTP to guanosine diphosphate (GDP), which is bound to the αβ tubulin heterodimers (6,7). As the basic building block of MTs, the αβ tubulin dimer has two nucleotide binding sites, one located at the β and the other at the α subunit (8,9). The α subunit binding site, known as the nonexchangeable nucleotide binding site, can only bind to GTP. In contrast, because the β subunit binding site is able to bind to either GTP or GDP, it is referred to as the exchangeable nucleotide binding site (E-site), as noted in Fig. 1 b. During MT assembly, only the αβ tubulin heterodimers with GTP bound at the E-site can be recruited at the growing end. The GTP is then hydrolyzed to GDP in the MT lattice (10). Thus, the MT consists principally of αβ tubulin dimers in the GDP state, whereas in the GTP state, the growing end contains newly recruited αβ tubulin dimers, forming a “GTP cap” (11,12). In the in vitro state, the size of the GTP cap has been estimated to be as small as only one layer of GTP-bound tubulin dimers (13,14). However, in the in vivo state, the size has been measured to be ∼750 tubulin subunits on average (15). Studies using a nonhydrolyzable GTP analog, guanylyl-(α, β)-methylene-diphosphonate (GMPCPP), have shown that tubulin dimers binding GMCPP at the E-site can polymerize to MT at a rate similar to GTP-tubulin dimers (16). However, the depolymerization rate of MT in the GMPCPP state is much slower compared with MT in the GDP state. This outcome means that the presence of GMPCPP almost completely suppresses the dynamic stability of MT. Thus, it is commonly accepted that the growing MT ends are protected by the GTP cap, which is due to the lagging of GTP hydrolysis behind the newly recruited GTP-tubulin dimers. When the speed of GTP hydrolysis becomes faster than the binding of new GTP-tubulin dimers, the loss of the GTP cap will expose the GDP-tubulin at the MT end and lead to rapid disassembly of the MT (6,10,12,17, 18, 19), as shown in Fig. 1 c.

Figure 1.

(a) Schematic view of the MT structure. Each tubulin domain contains around 440 residues, which is represented by one bead. The three PFs included in the red rectangle consist of our first MT patch simulation system, whereas all the 13 PFs with a length of 16 tubulin domains are included in our closed MT segment simulation system. (b) Shown is a cartoon representation of the αβ tubulin heterodimer, which serves as the basic building block of the MT. The nonexchangeable nucleotide binding site (N-site), located at the intradimer interface, can only bind GTP molecules. In contrast, the E-site, exposed at the top of β tubulin domain, can bind either GTP or GDP molecules. (c) Illustration of MT dynamic instability is shown. MT can switch between the growth state and shrinkage state, depending on the presence of GTP cap. To see this figure in color, go online.

Two canonical models exist to explain how MT dynamics are regulated by different nucleotide states. According to the “allosteric model,” the free tubulin dimers adopt different conformations in solution, depending on the binding nucleotide. GTP-tubulin dimers exist in straight conformations that are compatible to be recruited and integrated into the straight MT lattice, whereas GDP-tubulin dimers show curved structures. The increased curvature of MT PFs caused by GTP hydrolysis is thus the driving force of MT disassembly. This model is supported by experimental observations of less curved tubulin oligomers bound with the nonhydrolyzable GTP analog, GMPCPP, which is obtained from MT disassembly at low temperatures (20, 21, 22). Alternatively, the so-called “lattice model” posits that free tubulin dimers will adopt curved conformations in solution for both GTP and GDP states. The curved-to-straight conformational change of GTP-tubulin dimers occurs after integration into the MT wall, driven by the lattice contacts formed with neighboring tubulin dimers (23, 24, 25). This model was originally supported by the crystal structures of γ-tubulin and bacterial tubulins (FtsZ and BtuA/B) (26, 27, 28, 29, 30), which showed curved conformations independent of their nucleotide-bound states. Solution x-ray scattering results and the structures of free αβ-tubulin dimers solved in different nucleotide states also did not reveal any significant structural differences, thus favoring the lattice model (24,31, 32, 33, 34, 35). In addition, computer simulations of tubulin dimers, as well as PFs in both the GTP- and GDP-bound states, have confirmed that they adopt an intrinsic bent conformation (36, 37, 38). More recently, a combination of the two limiting models was proposed (39), in which GTP binding is thought to induce the increased flexibility of tubulin dimers, thereby lowering the free energy barrier of the transition between the curved and straight conformations, which in turn facilitates the recruitment of GTP-tubulin dimers to the MT growing end. This phenomenon is indirectly supported by mutation experiments of residues distal to the nucleotide binding site, which can reduce the MT “catastrophe” by increasing the propensity of tubulin dimers to be in straight conformation (40,41).

Whether referring to the experimentally more favored lattice model or the combined model, lattice interactions typically play a key role in regulating MT dynamics, especially the lateral contacts formed between neighboring tubulin dimers (42, 43, 44). As such, it is important to investigate how different nucleotide states affect these lattice contacts, as well as their impact on altering MT dynamics. Comparing the cryo-electron microscopy (cryo-EM) structures of MT in GMPCPP, GTPγS, and GDP states has indicated that the posthydrolysis states undergo lattice compaction while also distorting the α:H8 helix; this outcome suggests that GTP hydrolysis generates a conformational strain that is stored in the MT lattice (45,46). The lateral contacts in all three states are reported to be very similar, dominated by the interaction of the M-loop (S7-H9 loop) on one side and sandwiched by the H2-S3 loop and the H1-S2 loop on the other side. Molecular dynamics (MD) simulations have also been widely used to study the effects of nucleotide states to MT systems from the scale of tubulin dimers to MT lattice patches (36, 37, 38, 39,47, 48, 49, 50, 51, 52, 53, 54, 55, 56, 57, 58, 59, 60). For example, all atomic simulations by Grafmüller et al. (48) have suggested that both the lateral and longitudinal contacts in the GDP MT lattice are weakened and more likely to disassemble when exposed at the growing end. Additionally, tubulin octamer simulations conducted by Manandhar et al. (57) indicate that the GTP cap can increase the flexibility of the octamers, contributing to the formation of contacts within and between PFs, thereby stabilizing the MT lattice.

In this work, we have addressed the effects of different nucleotide states on the conformational dynamics of MTs at the free-growing plus end using atomistic simulations. Based on the recently elucidated high-resolution cryo-EM structure of MTs by Zhang et al. (46), we performed extensive large-scale solvent atomistic simulations of both MT patches containing three lateral combined PFs as well as closed MT segments in different nucleotide states, as illustrated in Fig. 1 a. Detailed comparisons have revealed that lateral interactions between neighboring PFs will be significantly weakened for GDP state MTs in cases where the neighboring interactions are not as complete as those found in the lattice. The intrinsic bending of GDP MT PFs will also become less cooperative, coupled with the loss of lateral contacts. This makes GDP state MTs more likely to disassemble. In addition, the seam region represents a weak point in the closed MT segment in the GDP state, in which the interdomain interactions are much weaker because of further distance in comparison to MT in the GTP state. As such, the seam region may serve as the starting point for MT disassembling, which is consistent with experimental results (61, 62, 63).

Methods

Details of MD simulations

Two different system types were studied using atomistic MD simulations: 1) MT patches containing three laterally aligned PFs with homogeneous lateral interactions with each other. Each of the PFs featured a length of four αβ tubulin dimers. The MT patches were simulated in GTP, GDP, and GDP + Pi bound states with a simulation length of 1 μs; and 2) closed MT segments containing 13 PFs. The length of each PF was extended to eight αβ tubulin dimers to better study conformational changes in the closed tubule. The segments were simulated in GTP- and GDP-bound states over a simulation time of 200 ns.

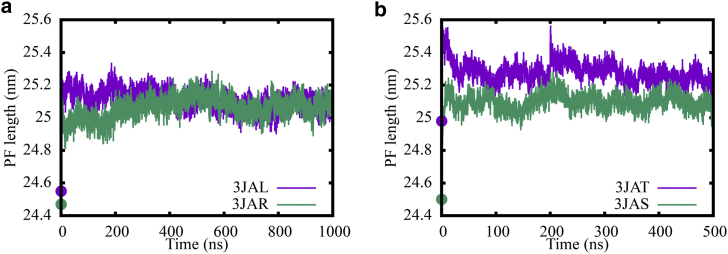
Two cryo-EM structures (Protein Data Bank, PDB: 3JAL (GMPCPP state) and PDB: 3JAR (GDP state)) were used to construct initial structures of the MD simulations (46). The nonhydrolyzable GTP analog GMPCPP in the structure of 3JAL was converted to GTP molecules by replacing the carbon atom between the α- and β-phosphate with an oxygen atom. The MT configuration in the GDP + Pi state was modeled by inserting an additional phosphate group near the β-phosphate of the GDP molecule. Mg²⁺ ions were also in included in the GDP and GDP + Pi state simulations. The atomic coordinates of the GTP and GDP + Pi molecules, as well as the Mg²⁺ ions, were then optimized by a series of energy minimizations with the positional restraint of tubulin domains gradually removed. The 3 × 2 lattice patches (three PFs with two tubulin dimers in length) contained in the original cryo-EM structures were extended longitudinally and laterally through superimposing the β/α tubulin dimers at different locations. For example, the bottom β/α tubulin dimer of one object was superposed on the top β/α tubulin dimer of another object to obtain the coordinates of the stacked dimers. Similarly, the PFs were to be duplicated laterally to form closed tubule structures. In the work by Zhang et al. (46), they also reported two similar cryo-EM structures (PDB: 3JAT (GMPCPP state) and PDB: 3JAS (GDP state)) which forms 14-PF MT lattice instead of the most common 13-PF architecture. We also performed 500 ns atomistic MD simulations for 3-PF MT patches constructed from these two structures following the same process described above. They were served as complementary MD simulation results.

All MD simulations were performed using the Gromacs 2016 suite of MD software (64) with the Charmm27 force field (65) with CMAP corrections (66). The initial protein structures were placed in rectangle boxes with a buffer distance of at least 0.15 nm. The systems were then solvated using Charmm-modified TIP3P water (67) and 150 mM NaCl, which served as counterions to neutralize the system. Because significant PF bending was observed during preliminary simulations of the MT patches, the simulation boxes of the MT patch simulations were further extended by 5 nm along the y axis (the direction in which bending occurred) to prevent potential interactions between periodic images of protein molecules. The resulting solvated MT patch systems contained ∼1.1 M total atoms each, and the closed tubule systems contained ∼8.7 M total atoms each.

Each MD simulation system was equilibrated through the steepest descent energy minimization, followed by 100 ps MD simulation in the constant NVT ensemble and 100 ps MD simulation in the constant NPT ensemble with the protein-heavy atom position restrained to fully relax the solvent molecules. The production runs were then continued in the constant NPT ensemble at 310 K and 1 atm using the velocity rescaling thermostat (68) and isotropic Parrinello-Rahman pressure coupling algorithm (69). The length of covalent bonds involving hydrogen atoms were constrained using the LINCS algorithm, allowing an integration time step of 2 fs. The Lennard-Jones interactions were cut off at 1.2 nm with a switching function ranging from 1.0 to 1.2 nm, whereas the short-range electrostatic cutoff was set at 1.2 nm. The long-range electrostatic interactions were computed using the particle-mesh Ewald method (70) with a 0.16 nm grid spacing.

Based on the goal of simulating the free-growing plus end of the MT, positional restraints were applied to the tubulin domains at the bottom of each PF to prevent any large conformational changes at the end, which would be interacting with other tubulin domains in a real MT lattice. This positional restraint also prevented the MT PFs from rotating during our simulations. VMD (71) and PyMol (72) were used for the visualization of simulation trajectories. Gromacs native analysis tools, combined with our homemade scripts, were employed for trajectory analysis.

Measurement of PF bending

PF bending angles were computed to quantify all bending conformational changes for the MT PFs during the simulation process. In our simulations, positional restraints were applied to the tubulin domains at the bottom of each PF. Because outward bending accumulated along the PF from bottom to the free-growing plus end, the orientation of the β/α tubulin dimer at the very top end indicated the bending direction of the entire PF. The vector v between the center of mass of the β and α tubulin domain was used to represent the orientation of the tubulin dimer, whereas v₀, which was estimated from the initial straight PF conformation, was set to be the reference direction. The angle between v and v₀ was computed to be the PF bending angle. The bending angles of intermediate tubulin dimers were also computed using a similar approach.

The PF outward bending observed in our simulations was not exactly along the direction perpendicular to the MT wall. Thus, to measure the deviation of PF bending from the perpendicular direction, which shows the twisting of tubulin dimers during the outward bending conformational change, we also calculated the tangential component of the PF bending angle, noted as the ϕ angle. We built a reference coordinate system, in which the z axis was along the vector between the center of mass of the β and α tubulin domain in the initial straight PF conformation (same as v₀ shown above). The x axis, perpendicular to the MT wall, was defined using the cross product of the z axis and the vector along the center of mass of the two α tubulin domains at the bottom of neighboring PFs. The ϕ angle of the PF bending was then computed as the angle between the projection of v on the xy plane and the x axis.

Heterogeneous elastic network model

We parameterized a heterogeneous elastic network model (HENM) for each simulation system to understand the effective interaction strength between tubulin domains. Each tubulin domain was represented by one coarse-grained (CG) bead positioned at its center of mass. The fluctuation-matching method inherent in the HENM method (73) was used to obtain the heterogeneous collection of effective force constants of elastic bonds formed between two CG sites, i and j, within a distance cutoff range. This method minimizes the mean-square distance fluctuation Δx_ij² observed in typical atomistic MD simulations as estimated from normal mode analysis of the HENM CG model. Starting from a simple ENM with equal force constants for all the elastic bonds, each force constant k_ij is updated using the following equation until convergence is achieved:

$$\frac{1}{k_{ij}^{n+1}}=\frac{1}{k_{ij}^n}-c\left(\Delta x_{ij,CG}^2-\Delta x_{ij,AA}^2\right)$$

Here, c represents the scaling factor during the iteration, chosen to be 0.5 in this study.

Results and Discussion

Simulation of 3-PF MT patches

In most of the MT wall, neighboring PFs display homogeneous lateral interactions, in which β tubulin interacts with β tubulin, and α tubulin interacts with α tubulin. To compare the dynamics of this homogeneous lateral interface in the presence of different nucleotide states, we first constructed small MT patches containing three PFs laterally aligned to each other as depicted in the red rectangle in Fig. 1 a, with each PF having a length of four αβ tubulin dimers. To study the conformational change at the growing MT plus end, we applied positional restraints to the tubulin domains at the bottom of each PF to mimic their interactions with the MT lattice. We then performed 1 μs plain MD simulations for the MT patches in GTP, GDP, and the GDP + Pi state. The initial structures of the three states were chosen from the cryo-EM structures PDB: 3JAL (GTP), PDB: 3JAR (GDP), and PDB: 3JAR (GDP + Pi, by inserting one Pi group near the GDP). The last 500 ns of the trajectories were used for subsequent analysis. As a complementary set of results, we also performed 500 ns MD simulations for the MT patches starting from two similar cryo-EM structures, PDB: 3JAT (GTP) and PDB: 3JAS (GDP), which forms a 14-PF MT lattice. As before, the latter half of the trajectories were used for analysis.

We inspected the convergence of our simulation trajectories by monitoring the time evolution of several quantities, such as root mean-square deviation, the PF bending angle, and the tubulin domain distance at the plus end. As shown in Figs. S1 and S3, all of these measured quantities converged reasonably quickly to equilibrium values and are quite stable during most of the simulations. Thus, our subsequent analyses were based on equilibrated sampling by using the latter half of the trajectories. Fig. S2, a–c shows the snapshot views of the E-site of the central PFs from the three 1 μs simulation trajectories. This reveals that our simulations are maintaining the protein-nucleotide interactions in a reasonable way.

Comparison of initial structures

In our 3-PF MT patch simulations, we have used two sets of initial structures as detailed in Methods. 3JAL/3JAR are EB3-bound MT structures forming a 13-PF lattice. It is reported that EB3 could potentially promote GTP hydrolysis in an MT, making the initial structure 3JAL potentially more similar to a posthydrolysis state rather than a GTP state. 3JAL is also more compact, with a dimer rise of 81.7 Å (46). As a comparison, 3JAT/3JAS are EB3-free structures that form a 14-PF lattice, which is not commonly presented in cells. To this end, Fig. 2 shows the evolutions of PF lengths of the middle PF in both sets of simulations, as computed by adding up the dimer rises of the βα tubulin dimers. It is shown that the PF lengths are converging to 25.1 nm in all the simulations, a clear difference from their initial PF length differences. The convergence of the GTP-bound PF lengths for both 3JAL and 3JAT indicates that the compaction induced by EB3 has been removed through the equilibration process, and a biologically relevant 13-PF MT can be constructed.

Figure 2.

Evolution of PF lengths in lattice patch simulations starting from different initial structures: (a) EB3-bound, 13-PF starting structures 3JAL (GTP) and 3JAR (GDP) and (b) kinesin-bound, 14-PF starting structures 3JAT (GTP) and 3JAR (GDP). The initial lengths, before any equilibration, are labeled by large dots at t = 0. To see this figure in color, go online.

The bending of GDP state MT PFs are less cooperative

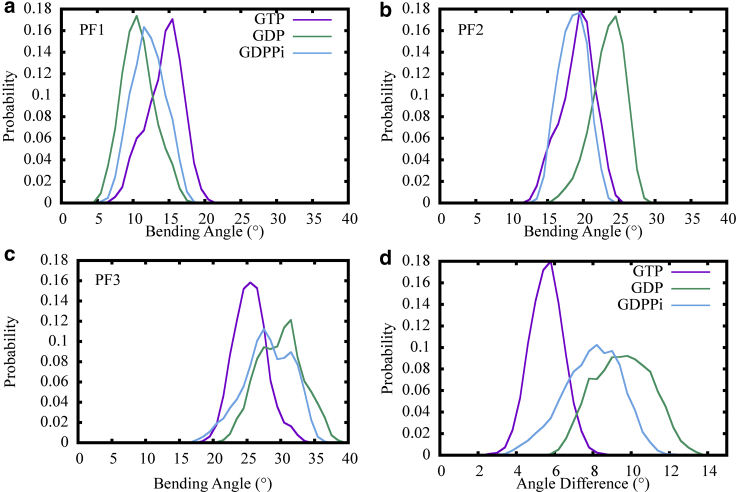
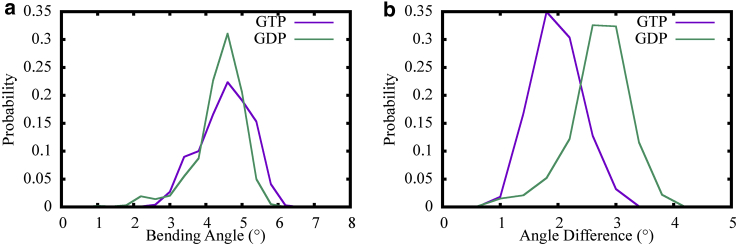
The most obvious conformational change observed in all three simulations was the bending of the MT PFs, which we attribute to the fact that the lateral interactions are not sufficiently strong to hold the PFs in a straight conformation (in contrast to the initial cryo-EM structure of the full tubule). An example of the PF outward bending during the simulation is shown in Fig. S2 d. Only the PF in the middle of the 3-PF MT patch is shown for clarity. To measure the extent of PF bending, we used the vectors connecting the center of mass (COM) of the topmost β and α tubulin domain for each PF. The bending angles were then computed between the vectors during the simulation and the initial state (i.e., the straight PFs; see Methods for details). Fig. 3, a–c provides a comparison of bending angle distributions for all three PFs in three different nucleotide states. Note that the GTP state displayed slightly larger bending angles for PF1, whereas the GTP state exhibited the smallest bending angles for PF3. Conversely, the GDP state presented the exact opposite trend, whereas the GDP + Pi state was between the two. A reasonable interpretation from this distribution is that the bending between neighboring PFs tends to be more cooperative for the MT patch in the GTP state, resulting in a smaller difference between neighboring PF bending angles. Fig. 3 d plots the distribution of bending angle differences between neighboring PFs for all three nucleotide states, which again shows a clear trend that the differences were largest for PFs in the GDP state, followed by GDP + Pi state and then GTP state. When an MT PF is isolated, it has been shown to display an intrinsically curved conformation, with the extent of bending fairly similar for GDP- and GTP-bound filaments (37). Thus, the observed difference between bending angles for our 3-PF patch simulations is the likely result of the presence of lateral interactions, suggesting different lateral interaction strengths in our simulations between different nucleotide states.

Figure 3.

(a–c) Comparison of bending angle distributions of the MT PFs in the GTP (purple), GDP (green), and GDP + Pi (cyan) states. (d) The probability distributions of bending angle differences between neighboring PFs in three different nucleotide states are given. To see this figure in color, go online.

It is also obvious that the bending angle distributions are quite different for the three PFs in the same simulation. This asymmetric PF bending shown here should originate from the rise of tubulin domains between neighboring PFs. As shown in Fig. 1 a, PF3 is located at the right part of the MT patch when viewing from the outside of the MT wall, and the tubulin domains are slightly lower compared with other two PFs. Thus, PF3 will have a larger bending motion with the tubulin domain at the bottom of each PF restrained during our MT patch simulation.

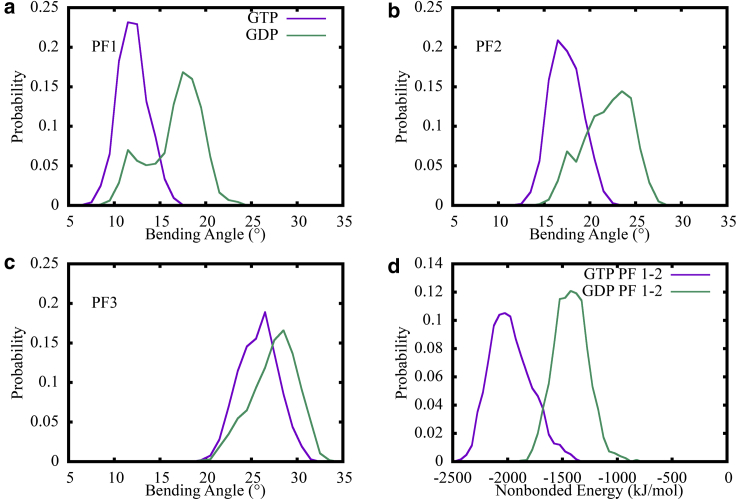
The bending angle distributions were also computed from the 500 ns MT patch simulations using two alternative initial structures, as shown in Fig. 6, a–c. Importantly, the GDP state MT patch exhibited larger bending angles for all the three PFs. The bending angle differences between neighboring PFs were not as large as that in Fig. 3 d. This difference is likely due to the data in Fig. 3 being drawn from 500 ns of simulation following 500 ns of equilibration, whereas the data in Fig. 6 is drawn from the latter half of 500 total ns of simulation time. This can also be noticed by observing the wider distribution of the GDP states, indicating conformational change as the structure relaxed. The similar trends between the two different sets of simulations indicate that the less cooperative bending motion of GDP state PFs compared with the GTP state is likely to be universal. This also demonstrates the reproducibility of our simulations due to the differences between the two starting structures, as described in Comparison of Initial Structures above.

Figure 6.

The bending angle distributions computed from 500 ns MT patch simulations using alternative initial structures PDB: 3JAT (GTP) and PDB: 3JAS (GDP). (a–c) Comparison of bending angle distributions of the MT PFs in the GTP (purple) and GDP (green) states is shown. (d) The distribution of nonbonded interaction energy between lateral interacting αβ tubulin dimers at the top of MT PFs in GTP (purple) and GDP (green) states is shown. To see this figure in color, go online.

The PF bending angle computed using the tubulin dimer at the top of each PF represents the overall bending motion of the PF. It is also helpful to inspect the bending of other intermediate tubulin dimers in the PF. We thus computed the intermediate bending angle from the third αβ tubulin dimers numbering from the PF bottom. As shown in Fig. S4, the comparison between different nucleotide states shows the same pattern as Fig. 3, whereas the intermediate bending angles are generally smaller, and the bending angle differences, shown in Fig. S4 d, are also not as large as the overall PF bending angle differences. This implies an accumulation of bending conformational change along the PF when lateral contact is not intact, as is the case for PFs on the edges of the MT patch in our simulations.

We also noticed that the PF bending is not strictly along the direction perpendicular to the MT wall in the 3-PF MT patch simulation. To measure this twisting motion of tubulin dimer when it undergoes outward bending, we calculated the tangential component of the bending angle (see Methods for details), denoted as the ϕ angle. This is computed for the middle PFs only as we need to define the x axis of the reference coordinate system using two neighboring PFs. The distributions of ϕ angles from simulations of different nucleotide states are shown in Fig. 4. The twisting motion of GDP state tubulin dimers are larger compared to the GTP state, which should also contribute to their less cooperative bending motion. Unexpectedly, the twisting motion of GDP + Pi is shown to be the largest. This may be caused by the relatively strong interactions between PF1 and PF2 in the GDP + Pi simulation, as will be shown in the next section. In recent work by Fedorov et al. (60), bending and twisting was also observed in a simulation of laterally aligned PFs. We found that the overall PF bending and twisting directions (outward bending and right twisting when viewing from inside the MT wall) observed in our simulations match with their results, although the measured quantities of bending and twisting angles are not directly comparable in the two studies because of the slightly different methods to compute these angles (we consider the full dimer, while the bending measure in (60) is relative to isolated domains).

Figure 4.

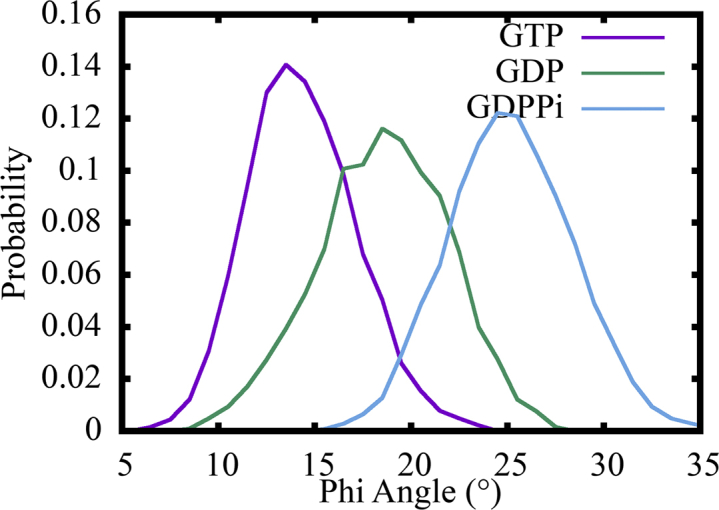
Distributions of the tangential component of PF bending angle for GTP (purple), GDP (green), and GDP + Pi (cyan) state simulations. The middle PF of the MT patch is used for calculation in each case. To see this figure in color, go online.

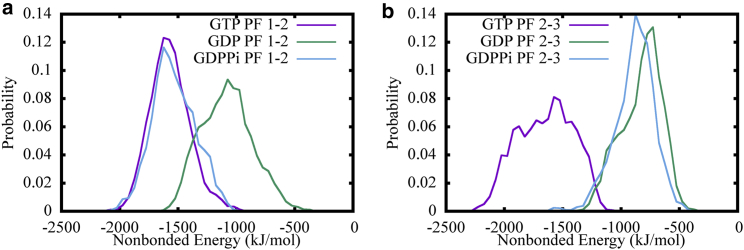
GDP state MT PFs show weaker lateral interaction strength

Based on our observations of the varying bending angles, we then quantified the lateral interaction strength between neighboring MT PFs in our three patch simulations. Note that we chose to maintain the αβ tubulin dimers at the top of each PF as they represent the growing plus end of MT. Subsequently, using atomistic MD trajectories, we computed the nonbonded interaction energy (van der Waals and electrostatic interaction energy) between the lateral interacting tubulin dimers to estimate the lateral interaction strength. Fig. 5 shows the distribution of lateral interaction strength between PF 1–2 and PF 2–3. For both of the two lateral interacting tubulin dimers, the GDP state exhibited significantly higher interaction energy—and thus weaker interaction strength—compared with the MT patches in the GTP state. However, it is interesting to note that the interaction strength of the GDP + Pi state was similar to the GTP state for lateral interactions between PF 1–2, whereas it was similar to the GDP state for PF 2–3. This finding indicates that the lateral interactions for the GDP + Pi state can actually switch between a stronger interaction state (resembling GTP) and a weaker interaction state (resembling GDP). As a result, the overall lateral interaction strength of the GDP + Pi state is between that of GTP and GDP. The nonbonded interaction energy distributions for the 1–2 interacting PFs computed from the complementary 500 ns simulations (starting from the 14-PF structures as discussed in Methods) are also shown in Fig. 6 d, with a matching trend. This signifies the universality of these results, as discussed in the bending analysis and the length analysis below.

Figure 5.

Distributions of nonbonded interaction energy between lateral interacting αβ tubulin dimers at the top of MT PFs in GTP (purple), GDP (green), and GDP + Pi (cyan). The interaction strengths between PF1 and PF2 are shown in (a), while PF2 and PF3 are shown in (b). To see this figure in color, go online.

To develop a more thorough understanding of the interaction strength between tubulin domains in our MT patch simulation, we also parameterized a simple HENM (73) that included all the tubulin domains. Each tubulin domain is represented by one CG bead in the HENM. The fluctuation matching method inherent in HENM was used to quantify the interaction strength between connecting beads by minimizing their distance fluctuations, which can be evaluated from atomistic MD trajectories and the HENM model. Accordingly, the obtained force constants of the HENM effective harmonic bonds should represent the interaction strength between corresponding tubulin domains. Selected HENM interaction strengths are listed in Table 1. As one can see, with the exception of the ββ lateral interaction between PF 1–2, all other tubulin domain lateral interactions follow the same trend—namely, that the GTP state exhibits the strongest interaction, the GDP state the weakest, and the GDP + Pi state falling between those two. The equilibrium distance between CG beads in our HENM model represents the averaged COM distance between tubulin domains. Our findings indicate that the GDP state displayed a significantly larger lateral domain distance compared with the GTP state. Using the β tubulin domain between PF 1–2 as an example, the average domain distance was found to be 5.3 nm for the GTP state compared with 5.7 nm for the GDP state. We also computed the averaged effective force constants between the laterally interacting tubulin domains in the top halves of neighboring PFs, which better represents the interaction strength between neighboring PFs. The averaged force constant is 1.57 kcal/(mol·Å²) for the GTP state simulation and 0.84 kcal/(mol·Å²) for the GDP state. This again shows the weaker lateral interaction between MT PFs in the GDP state.

Table 1.

The Interaction Force Constants for HENM Effective Harmonic Bonds Formed between Lateral Interacting Tubulin Domains at the Top of the MT PFs

	ββ PF1-PF2	αα PF1-PF2	ββ PF2-PF3	αα PF2-PF3
GTP	1.0	2.4	0.7	2.6
GDPPi	1.3	1.4	0.4	1.5
GDP	0.1	1.0	0.4	0.7

Those values were fitted using a simple one-site-per-domain HENM model to reproduce the mean-square distance fluctuations observed in our atomistic simulations. The units of force constants are in kcal/(mol·Å²).

Recently, Hemmat et al. (59) presented a multiscale model of the tubulin-tubulin lateral interaction. They concluded that the potential energy of tubulin lateral interaction is not significantly different for the three nucleotide states (GTP, GDP, and GMPCPP), which appears to be contradictory to the results of our study. However, it should be noted that the potential mean force (PMF) shown in their study (Fig. 4 A) is obtained from atomistic simulations of two laterally aligned tubulin heterodimers only. By comparison, our simulations include three laterally aligned PFs, each containing four tubulin heterodimers in the longitudinal direction. Thus, we argue that the difference should mainly originate from the different model systems used. The results coming from the simulation of two heterodimers may not be as pertinent to the larger PF and full tubule systems as studied in this work. Additionally, the global minimum of their reported GDP state PMF does exhibit slightly larger equilibrium distance (1.3 Å longer) and weaker interaction energy (1 k_BT, or 0.6 kcal/mol weaker) compared with the GTP state.

A portion of the lateral contacts are lost in a GDP state simulation

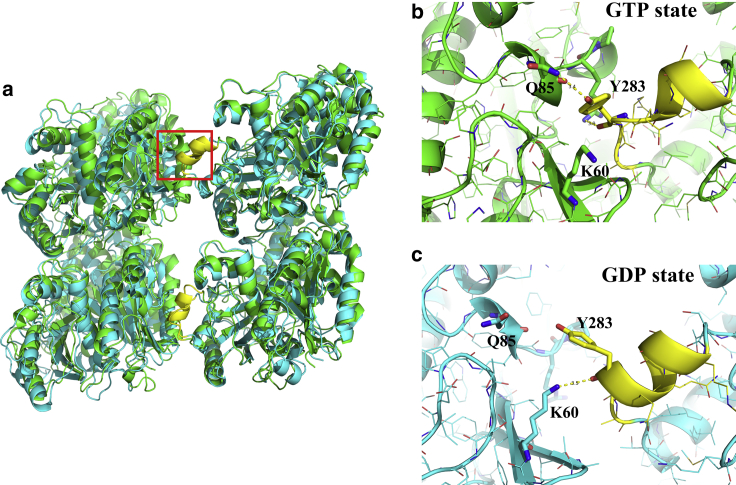
To elucidate the nature of weaker lateral interaction in our GDP state simulation, we examined the detailed structure of the lateral interface. Fig. 7 illustrates the superimposition of tubulin dimers along the lateral interface in both the GTP and GDP states. Note that the right portion of the tubulin dimers serves to align the structure. The M-loop, which is crucial for lateral contact, is highlighted in yellow; a magnified view is provided in Fig. 7, b and c. From a structural comparison, it is clear that the left tubulin dimer in the GDP state shows a slight vertical shift, resulting in a larger interdomain distance. Correspondingly, the position of contacting residues at the lateral interface also changed. In our GTP simulation, residue Y283 in the M-loop was found to be sandwiched between the H1-S2 and H2-S3 loops of the left tubulin domain, thereby creating close contact with key residues (K60, Q85, R88, and P89, shown as “sticks”) on the two loops. In the GDP simulation, however, although residue Y283 still had some contact with those residues, the M-loop was found to be floating outside the pocket formed by the H1-S2 and H2-S3 loops. Behind this, we also determined that the residue interactions between H3 of the left tubulin domain and H10 of the right domain were also lost because of the increased domain distance, which is not shown here.

Figure 7.

(a) Superimposition of the lateral interacting αβ tubulin dimers at the top of neighboring MT PFs for the GTP (green) and GDP (cyan) states. The M-loop, which is crucial for lateral interactions, is shown in yellow. (b and c) Shown is a magnified view of the lateral interactions formed between the M-loop and the other side for GTP (b) and GDP (c) states. Key residues K60, Q85, R88, P89, and Y283 are shown using “sticks” representation in PyMol. To see this figure in color, go online.

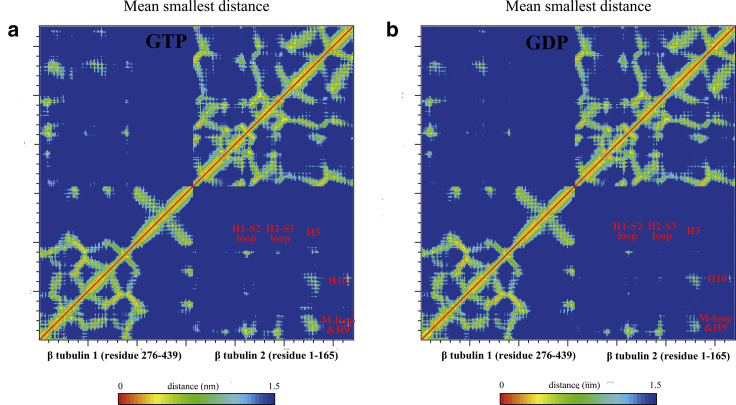
Table 2 lists the average number of lateral contacting residue pairs computed from atomistic MD trajectories using a cutoff of 1.2 nm. The data shown here match well our findings that the GTP state has the largest number of contacting residue pairs, followed by GDP + Pi and then the GDP state. The averaged contact maps between neighboring β tubulin domains, plotted in Fig. 8, also show the loss of lateral contacts in the GDP state simulation at regions near the M-loop, helix 9, and helix 10.

Table 2.

Average Number of Contacting Residues between Lateral Interacting αβ Tubulin Dimers for All the Three Different Nucleotide States

	GTP	GDPPi	GDP
PF1-PF2	76 ± 3	68 ± 4	56 ± 7
PF2-PF3	74 ± 6	45 ± 6	41 ± 5

Residue pairs within the cutoff of 1.2 nm are considered to be interacting with each other.

Figure 8.

Residue contact map between lateral interacting β tubulin domains at the top of MT PF1 and PF2 calculated from (a) GTP state and (b) GDP state MT patch simulations, showing the loss of lateral contacts in GDP state simulation. To see this figure in color, go online.

Simulation of fully closed MT segments

To better understand the dynamic instability in the real MT structure, we also performed much larger atomistic simulations of whole MT segments containing all the 13 PFs needed to form closed tubular structures (Fig. 1 a, all the tubulin domains plotted). Each PF in the segment has a length of eight αβ tubulin dimers. Similar to the prior simulations, we also applied positional restraint to the tubulin domains at the bottom to mimic the growing MT plus end. A total of 200 ns for each atomistic simulation were performed for MT segments in both the GTP- and GDP-bound states, with the final 100 ns trajectories utilized for further analysis.

It should be noted that the 200 ns simulation time here is the current state of the art method for such a large atomistic system with more than 8 million atoms. We performed convergence analysis on our trajectories, shown in Fig. S5, to make sure we are using the most equilibrated sampling part of the trajectories for analysis.

MT PFs in the GDP state exhibit somewhat larger bending angle differences between neighboring PFs

We first determined the bending angles of the MT PFs used in our tubule simulations. Fig. 9 a shows the averaged bending angle distributions for all 13 PFs in the entire tubule structure. Note that the PFs for both GTP and GDP states exhibit similar averaged bending angles. Fig. 9 b shows the difference between neighboring PF bending angles at the nonseam interface. The bending angle differences for the GDP state PFs were found to be somewhat larger than the corresponding GTP state PFs, which is consistent with our finding that the bending of MT PFs in the GDP state tends to be less cooperative compared to the GTP state. We also observed, however, that the bending angles for all our tubule simulations were also much smaller compared with those of MT patches—despite the fact that the PFs were twice as long as those utilized in our prior MT patch simulations. This outcome can be attributed to better preserved lateral contacts in the closed tubule simulations in both the GTP and GDP state.

Figure 9.

(a) The average bending angle distributions of all the 13 PFs in closed MT segment simulations for the GTP (purple) and GDP (green) states. (b) Shown is the probability distribution of bending angle difference between neighboring PFs at the nonseam interface for the GTP (purple) and GDP (green) states. To see this figure in color, go online.

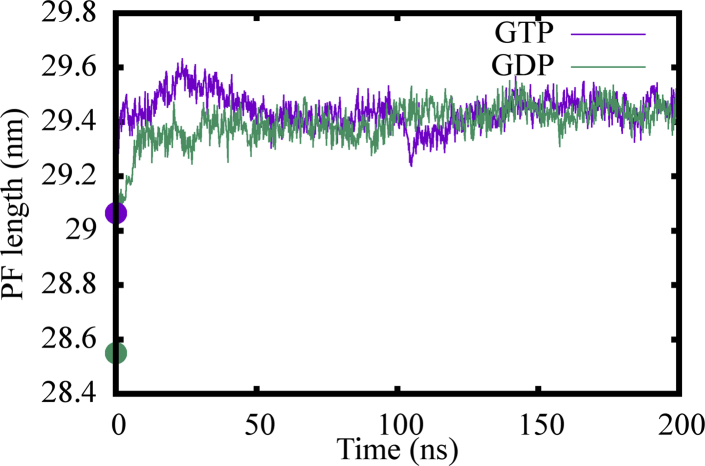
MTs in the GDP state display more significant PF elongation

We also examined the length of the MT PFs during our simulation studies. It was found that the PF length increases for both GTP and GDP simulations, which we referred to as PF elongation. Fig. 10 shows the length of the upper half of the first PF at the left side of the seam for both the GTP and GDP states. Compared with their starting lengths obtained in experimental studies, which are represented by the spherical dots, both PFs exhibited elongation during our simulations. Although the equilibrium PF lengths were almost the same for both nucleotide states, the GDP state PFs exhibited much larger elongations in comparison to those in the GTP state. We note that in the cryo-EM structure, the GDP state MTs display a more compact lattice structure compared to their GTP state counterparts. It is proposed from those experiments that GTP hydrolysis during MT assembly generates a conformational strain that is stored in this more compact lattice structure. Because our simulation studies are able to mimic the free MT plus end, the larger elongation we observed for the GDP state PFs should be related to the release of stored conformational strain.

Figure 10.

Length variations in the upper half of PF1 during a 200 ns simulation involving a closed MT segment simulation for both the GTP (purple) and GDP (green) states. The initial length measured in cryo-EM structures are labeled by spheres located at t = 0. To see this figure in color, go online.

We also compared the length of the upper and lower halves of the same PF during a GDP state simulation. Interestingly, we found that the upper half typically displayed larger elongation compared with the lower part. Moreover, because of the fact that the bottom tubulin domains were positionally restrained in our simulations to mimic the lattice interactions, the lower half of the PFs resembled those in the lattice structure, whereas the upper half resembled the exposed growing plus end. Our observation that the upper half PF displayed larger elongation indicates that the GDP state PFs only become elongated when they were exposed at the growing end because of the loss of the GTP cap. The GDP state PF elongation observed for the terminal tubulin subunits, presumably caused by the release of stored conformational strain in the MT lattice, may be the first step of MT disassembly.

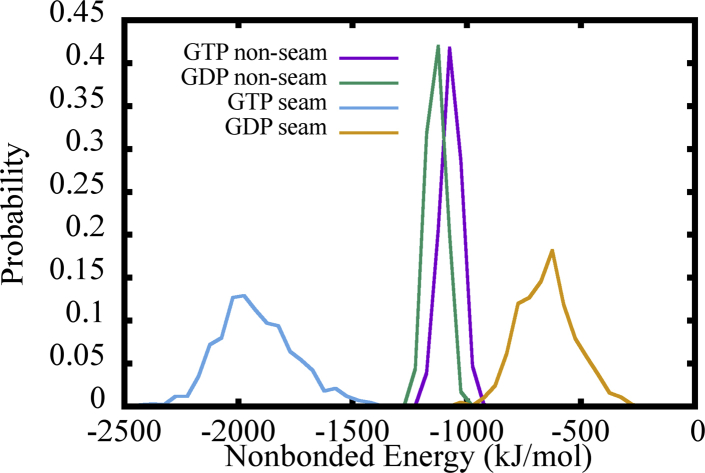
MTs in the GDP state displayed much weaker lateral interactions at the seam region

We also quantified the lateral interaction strength between PFs in our tubule simulations by the αβ tubulin dimers at the top of each PF. Our findings indicated that the homogeneous lateral interaction at the nonseam regions were similar for both the GTP and GDP states. In contrast, the heterogeneous lateral interaction strength at the seam region was significantly weaker for the GDP state MT, as shown in Fig. 11. We note that the interaction energy distributions of closed MT segments shown here are somewhat different from those of the 3-PF patch simulations. The differences can be attributed to the different conformations sampled in the two simulations. The PFs here in the MT segment simulations are locked in a nearly straight conformation as lateral interactions from both neighboring sides are well preserved, whereas the PFs in the MT patch simulations show significant bending motions. We then parameterized the simple one-bead-per-domain HENM for all of our whole tubule simulations. The resulting effective force constant and equilibrium distance data between the top tubulin domains at the seam interface are provided in Table 3. As indicated, the effective interaction strength of the GTP state was about one order of magnitude larger than that of the GDP state at the seam region; moreover, the tubulin domains were also much closer to each other in the GTP simulation.

Figure 11.

The distribution of nonbonded interaction energy between lateral interacting αβ tubulin dimers at the top of the MT PFs. The distributions are distinguished by different nucleotide states (GTP or GDP) as well as according to the type of lateral interface (seam or non-seam). To see this figure in color, go online.

Table 3.

Comparison of the Interaction Effective Force Constants and Equilibrium Distances of HENM Elastic Bonds Formed between Lateral Interacting Tubulin Domains at the Top of the MT Seam Interface

	GTP		GDP
	k (kcal/(mol·Å2))	d0 (nm)	k (kcal/(mol·Å2))	d0 (nm)
αβ seam	1.6	5.3	0.2	5.9
βα seam	3.7	5.2	0.6	5.5

These values were fitted using a simple one-site-per-domain HENM model to reproduce the mean-square distance fluctuations observed in our atomistic simulations. The units of force constants are in kcal/(mol·Å²).

There may be a concern that the local structures around the seam region in the initial closed MT segment structure is not accurate enough because the cryo-EM PDB structure we used to construct the closed MT segment was from symmetrized cryo-EM reconstruction. As a result, the local features of the seam interface and homogeneous non-seam interface may be averaged out to some degree during this process. However, these are the best initial structures one can start from to study the lateral interactions in the seam interface. We also emphasize the very large difference of lateral interaction strength between the GTP and GDP state, as shown in Table 3. This should be a result of larger domain motions, as we will see in the following section. As a result, these concerns do not affect our major conclusion here.

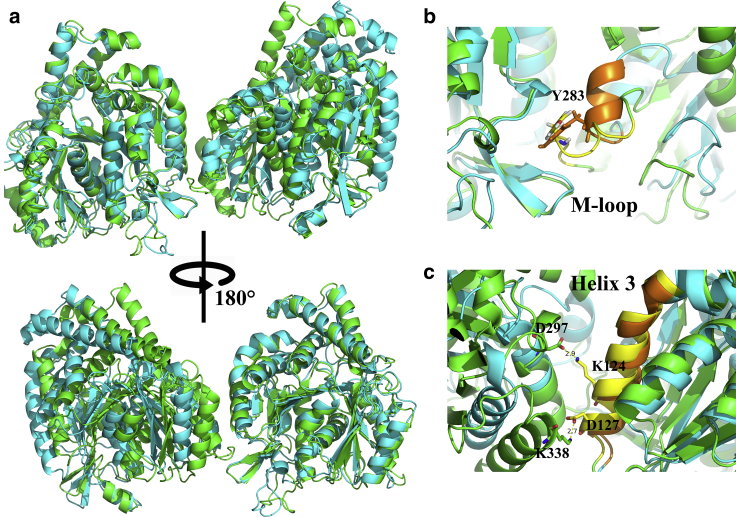
GDP state tubulin domain at the seam region shows outward rotation

Structural details for the lateral interacting αβ tubulin domains at the α|β seam interface are provided in Fig. 12, wherein the structures of both the GTP and GDP states are superposed by aligning the α tubulin subunit (Fig. 12 a). Note that the β tubulin domain in the GDP state exhibits significant rotation toward the outside of the MT wall compared with the GTP state. As a result, the β tubulin domain becomes more distant to the α tubulin at the other side of the seam interface in the GDP state simulation. The interactions between the M-loop of the β tubulin domain with the corresponding sandwich structure are shown in Fig. 12 b. For the GDP state, although the side chain of Y283 still points to the pocket formed by the H1-S2 and H2-S3 loops on the other side, the M-loop floats out of the sandwich structure because of the larger distance between the two tubulin domains. We also investigated interactions between the helix 3 in α tubulin with helix 9 and helix 10 in the β tubulin, as plotted in Fig. 12 c. Key interacting residue pairs (K127-D297 and D124-K338) are labeled for the GTP state structure. Note that, by contrast, analogous interactions are completely absent in the GDP state. When examining the seam region more broadly, we observed that the two PFs along the seam tended to splay apart during the GDP state simulation; this drift eventually weakened the lateral interactions and expanded the interdomain distances.

Figure 12.

(a) Superimposition of lateral interacting tubulin domains at the α|β seam interface. The top figure shows the view from inside the MT lattice, whereas the bottom figure shows the view from outside the MT wall. The tubulin domains are colored in green for the GTP state and cyan for the GDP state. (b) Detailed structures around the M-loop lateral interacting interface are shown. The M-loop of the β tubulin domain is shaded yellow for the GTP state and orange for the GDP state, with the key residue Y283 shown as sticks for both states. (c) Shown are detailed structures around the lateral interacting interface between helix 3 in the α tubulin domain and the other side. Note that the structures in this panel are viewed from the outside of the MT wall, as in the bottom figure of (a). The helix 3 structure is shaded yellow for the GTP state and orange for the GDP state. Key interaction residue pairs found in the GTP state (but absent in the GDP state) are shown as sticks. To see this figure in color, go online.

Conclusions

In this work, we carried out atomistic MD simulations of both 3-PF MT patches and closed MT segments in different nucleotide states. For the MT patch simulations, we showed that the GDP state PFs exhibited much weaker lateral interactions between each other, which resulted in less cooperative bending conformational change and the partial loss of favorable lateral contacts presented in the experimental cryo-EM structure. In contrast, the homogeneous lateral interactions of the nonseam region remained similar throughout our full tubule segment simulations. It should be noted of course that lateral interactions for the PFs at the edges were incomplete in our patch simulation. Therefore, these findings indicate that the GDP state MT PFs should be able to maintain strong lateral interactions when both sides of the lateral contacts are intact, as is the case in the full tubule lattice structure. GDP state MT PFs undergo outward bending and lose key residue interactions in the lateral interface once the lateral contacts have become weakened.

Importantly, the results of our fully closed MT segment simulations strongly suggest that a critical region is the seam region, for which the GTP and GDP state simulations revealed significant differences in interaction strength and interdomain distance. We also note that the observed similar homogeneous lateral interactions between the GDP and GTP states may be impacted by the limitations of the full tubule segment simulation study—notably, the limited system size and MD sampling.

In summary, our results indicate that the GDP state PFs are generally less stable compared with their GTP state analogs. This observation is supported by the fact that the former are more likely to disassemble once the MT growing plus end is exposed when the GTP cap is lost because of faster GTP hydrolysis. Our results also suggest that when GDP state tubulin domains are exposed at the growing MT end, the release of stored conformational strain will initially lead to the elongation of MT PFs and the subsequent weakening of lateral contact in the seam region. At that point, the lateral contacts will gradually weaken at nearby homogeneous lateral interfaces and cause the outward bending of the PFs, which eventually results in the complete disassembly of the MT. In contrast, the conformation of the growing end GTP cap is more structurally favorable and will not undergo large PF elongations; additionally, the lateral contacts at the seam region are also more stable, thus preventing MT disassembly.

While providing key physical insight into the molecular origins of the dynamic instability of MT, our results also provide a starting point for eventually deriving a “bottom-up” CG model for these important systems, which will allow us to study their cooperative dynamics in greater detail over larger length and timescales as well as more complex scenarios, such as the interaction with MT-associated proteins such as Tau. These and other avenues of study will be explored in future research.

Author Contributions

D.T. and G.A.V. designed the research. D.T. performed the research. D.T. and G.A.V. analyzed the research and wrote the article.

Editor: David Sept.