Abstract
Cell migration is orchestrated by a complicated mechanochemical system. However, few cell migration models take into account the coupling between the biochemical network and mechanical factors. Here, we construct a mechanochemical cell migration model to study the cell tension effect on cell migration. Our model incorporates the interactions between Rac-GTP, Rac-GDP, F-actin, myosin, and cell tension, and it is very convenient in capturing the change of cell shape by taking the phase field approach. This model captures the characteristic features of cell polarization, cell shape change, and cell migration modes. It shows that cell tension inhibits migration ability monotonically when cells are applied with persistent external stimuli. On the other hand, if random internal noise is significant, the regulation of cell tension exerts a nonmonotonic effect on cell migration. Because the increase of cell tension hinders the formation of multiple protrusions, migration ability could be maximized at intermediate cell tension under random internal noise. These model predictions are consistent with our single-cell experiments and other experimental results.
Significance
Cell migration plays a vital role in many biological processes such as tumor metastasis. It is a complicated process regulated by dynamic coupling between the biochemical network and mechanical forces. Nonetheless, few cell migration models take both factors into account. Here, we construct a mechanochemical cell migration model to study how cell migration is regulated by cell tension. Our model predicts that cell tension not only inhibits cell movement under persistent external stimuli but also promotes cell migration under random internal noise when cell tension is low. Optimized cell tension could, therefore, maximize the ability to migrate under random internal noise. We further confirmed that these model predictions are consistent with our single-cell experiments and other published experimental results.
Introduction
Cell migration plays a vital role in many biological processes, including tumor metastasis, embryonic morphogenesis, tissue repair, and regeneration. One of the key features of migration in most eukaryotic cells is the combined effect of actin filament polymerization against cell membranes and the action of molecular motors to retract the back of the cell. The polymerization of F-actin leads to the reorganization of the cytoskeleton and subsequently the formation of lamellipodia. This process of cytoskeletal rearrangement is regulated by a number of chemical factors, notably the Rho family GTPases (1). The active Rho GTPase positively enhances the activity of cytoskeleton effector proteins through integrated signaling pathways, resulting in a myriad of processes such as actomyosin movement (2). Another aspect taken into account is cell membrane tension, which provides feedback to inhibit the propulsion of actin filaments (3, 4, 5, 6, 7). Membrane tension has been widely assumed to equilibrate across the cell in milliseconds and acts as a globe inhibitor to cell polarization (6), although some recent studies also indicate that long-range propagation of membrane tension could be suppressed in cells by the flow resistance from cytoskeleton-bound transmembrane proteins (8). In addition, membrane bending rigidity is also relevant, especially for cell collisions with an obstacle or other cells.
Cell migration is regulated by dynamic coupling between the biochemical network and mechanical forces. Cytoskeletal rearrangements and the mechanical forces, i.e., cell tension, are not only downstream outputs of biochemical cascades but also provide feedback on biochemical signaling networks (9,10) to allow cells to make cellular decisions. The cross talk between the biochemical network and mechanical forces exists on different spatial scales (11). At the subcellular scale, both the signaling events (12,13) and the patterned activity of actomyosin lead to protrusive or contractile dynamics of the cortical cytoskeleton, which generate forces that eventually incorporate whole-cell behaviors like cell shape changes and migrations (14), whereas at the cellular scale, polymerized F-actin contributes to part of cell membrane tension, and vice versa, the increase of tension stalls actin assembly by mechanical means (15,16).
However, despite numerous mathematical models on cell migration, few of them take into account the coupling between biochemical signals and mechanical factors. Many one-dimensional models have been developed to capture specific aspects of cell migration (17, 18, 19), e.g., the thickness and flow profile of lamellipodium (17). In two-dimensional models, different models are used for different types of cells. Lee et al. introduced graded radial extension to explain the steady motion of fish keratocytes (20). This model considers a sharp interface of the cell membrane, which assumes the extension of the front and retraction of the rear of keratocytes occurring perpendicularly to the cell edge (21). Another approach developed for modeling the chemotactic behavior of social amoeba and human neutrophils was the level set method, which has the advantage of describing featureless interfaces without tension or other physical properties (22). For diffusive interface models, a popular one was the phase field model, which can combine actin flows with physical forces and was applied to a wide range of cell types to investigate migration mechanisms (23, 24, 25). The phase field model was also used to study multiple cell motion behaviors such as membrane fusion (26) and cell delamination (27). Although the precise mechanisms for the cytoskeletal mechanics remain unknown, some attempts have been made to reveal this aspect. Lim et al. provide a summary of continuum-based models of the mechanical stiffness of cells (28). There are also reviews for cell mechanics, such as the cytoskeleton (29, 30, 31), actin protrusion (32), or cell signaling and cell migration (33).
In our previous work (3), we established a mechanochemical model of cell polarization and performed single-cell experiments to show that the elevation of tension inhibits the polarization tendency and enhances the persistence of polarity. Cell polarization precedes cell migration. Here, we extend this mechanochemical model to study cell migration via tunable cell tension. Our cell migration model integrates the interactions between Rac-GTP, Rac-GDP, F-actin, myosin, and cell tension, and it is based on the phase field model, which is therefore very convenient to explain cell shape change. We show that our mechanochemical cell migration model captures two typical cell morphological patterns and yields three migration modes with high to low migration capability under random internal noise and a persistent movement mode under external stimuli. When cell tension is lower, cell shape deformation is more significant, and cell migration capability is higher. Our model predicts that cell tension inhibits protrusion and therefore stalls cell movement under persistent external stimuli. It also shows that elevated cell tension could prompt cell migration because directional migration can be hindered by the formation of multiple protrusions under random internal noise when cell tension is low. Therefore, migration ability could be maximized at intermediate cell tension under random internal noise. We further confirm that these model predictions are consistent with our single-cell experiments and other experimental results.
Materials and Methods
Mechanochemical migration model
A cell is considered as a round disk Ω0 with the radius R = 5 μm, which is close to the actual cell size and imbedded into a larger 2D computational domain Ω with a size of 40 × 40 μm. The choices of all parameters are listed in Table S1. The diffusion coefficients of Rac-GTP (Du) and Rac-GDP (Dv) are set according to experimental results. Some parameters (i.e., the basal conversion rate b, maximum activation rate c3, dephosphorylation rate r, dissociation constants Ki (i = 1, 2, 3), etc.) are based on published studies. We estimate the values of all other parameters, including the maximum activation or inhibition rate ci (i = 1, 2, 4, 5) and equilibrium constants in the Hill function Ki (i = 4, 5). The degradation rate of F-actin is estimated based on our previous work (3). We also perform a sensitivity analysis for estimated parameter values, and the results indicate that the change in the maximum concentration of F-actin is less than 5% for the majority of estimated parameter values because the parameter values varied by 30%, suggesting that our model is insensitive to parameter values (Fig. S3).
Our model includes protein interactions between four species, namely polarity marker proteins in active form Rac-GTP (u) and inactive Rac-GDP (v), polymerized F-actin (f), and motor protein myosin (m). Notably, the wave pinning (WP) model provides a minimal reaction-diffusion system with bistable kinetics to pin the waves into a stable polar distribution by expressing protein interactions within a modeling framework (34). Therefore, we extend the WP model to describe interchange between Rac-GTP on the cell membrane and Rac-GDP is in the cytosol, as well as their interaction with F-actin and myosin in the cytosol. Because molecules move more freely in the cytoplasm than on membrane, the ordering between diffusion coefficients Du, Dv, Dm, and Df is Du < Df ≈ Dm ≪ Dv. The basal conversion rate from Rac-GDP to Rac-GTP is denoted as b, and inversely, Rac-GTP dephosphorylating to Rac-GDP is with the rate of r. The total number of Rac-GTP and Rac-GDP molecules is conserved. Self-activation of Rac-GTP and the positive feedback from F-actin are described by the nonlinear Hill functions and , with c1 and c2 representing the maximum self-activation rate, whereas K1 and K2 represent microscopic dissociation constants. The positive feedback from F-actin to Rac-GTP has also been proposed to exert a gradient-amplifying effect. This hypothesis has been confirmed in multiple experiments (9,35,36). However, the negative feedback from F-actin to Rho GTPase (such as Rac-GTP) was also incorporated into the WP model (37,38), and a variety of patterns from static polarization to actin wave formation can be observed as the feedback strength increases. It remains to be clarified whether the two different feedbacks coexist or happen at different timescales or different cell types. Likewise, the mutual inhibitions between F-actin and myosin are expressed by the form of and , with c4 and c5 being the corresponding maximum self-production rates, whereas K4 and K5 denote the equilibrium constants. Meanwhile, the degradation rates of F-actin and myosin are denoted as df and dm, respectively.
For simplification, cell tension (denoted as mt) in our two-dimensional (2D) model is still regarded as a global inhibition factor consisting of cortical tension and bilayer membrane. In a unit length of membrane, cortical tension is proportional to the total amount of polymerized F-actin, whereas membrane tension is determined by the cell shape. Hence, the total tension can be derived as mt(f) = σL, where σ represents the initial line membrane tension and L represents the cell perimeter. F-actin polymerization is activated by Rac-GTP as , where c3 is the maximum regulation rate and K3 is again the dissociation constant. In addition, this process is also downregulated by cell tension, i.e., proportional to , where KF is a scaling factor for nondimensionalization.
Based on the descriptions above, the dynamics of the model system are expressed by the following equations.
| (1) |
| (2) |
| (3) |
| (4) |
Considering Ω0 constantly changes its shape because of deformation from various forces, we use the phase field model to track the cell interface by introducing an order parameter ϕ to distinguish Rac-GTP (u) on ∂Ω0 from Rac-GDP (v), F-actin (f), and myosin (m) in Ω0.
| (5) |
where (x0, y0) is the initial position of the cell. Thus, two phases (ϕ(x, y) = 1 and ϕ(x, y) = 0) are naturally distinguished via this order parameter. The cell membrane is described by a narrow transition layer between the interior of the cell (ϕ(x, y) = 1) and the exterior of a cell (ϕ(x, y) = 0) with a width of ε. The position of the cell membrane is approximated by B(ϕ) = 3ϕ2(1 − ϕ)2, which vanishes outside the narrow interface. By coupling the order parameter, Eqs. 1, 2, 3, and 4 can be rearranged as follows.
| (6) |
| (7) |
| (8) |
| (9) |
where mt(f, ϕ) = σ because the cell perimeter L is approximated as dxdy in the diffusive interface.
The shape of the cell membrane is determined by interactions of various forces, such as the tension force from cell tension mt(f, ϕ), which converts from area density to line density (24) and yields
and the pressure from volume conservation constraints, which is defined as
where M is the penalty coefficient and A0 is the prescribed area. The displacement of the cell membrane is due to protrusion force from polymerized F-actin and contraction force from myosin
where α and β are the protrusive and contractive coefficients, respectively. Note that I(⋅) is an indicator function assuming protrusion exists only if the concentration of F-actin exceeds the critical value fc because actin filaments form part of the cytoskeleton first, and then the excessive polymerized actin induces protrusion. For simulations, we presume fc = 0.8fmax, where fmax represents the maximum concentration of F-actin under the steady state. Also, adhesiveness from the attachment or detachment from the substrate can be viewed as friction, which is defined as Ffriction = −τV, where τ is the friction coefficient and V is the velocity of membrane motility on a normal direction. Meanwhile, we assume the motion of the cell membrane is overdamped and thus satisfies force balance criteria, meaning Ftension + Farea + Fpropel + Ffriction = 0. Because the evolution of phase field ϕ follows ∂tϕ = −V × ∇ϕ, we obtain the final equation
| (10) |
As expressed in Eq. 10, the friction force is balanced by active forces, and the movement of membrane results in cell motility. Note that we neglect the momentum transfers from F-actin to the substrate and the area constraint because the perimeter of the cell is not preserved from experiments.
The stimulus is applied to Eqs. 6 and 7 to fluctuate the rate of transformation from Rac-GDP to Rac-GTP. In simulations, the stimulus is expressed as ksv, and ks is spatially dependent. The details of the incorporation of persistent external stimulus and random internal noise into model system are provided in the Supporting Materials and Methods.
The global graded stimulus ks is
| (11) |
where ksamp means the amplitude of the stimulus and D(t) is the time-dependent maximal radius of cells as cells change morphology and move during simulations. In the beginning, D(0) = 2R which is the diameter of cells at the initial shape. We also define the random internal noise as local stimuli,
| (12) |
where R0 is a normally distributed random number. Both global graded stimuli and local stimuli are persistent in simulations.
We choose the periodic boundary condition and apply the semi-implicit Fourier-spectral method for the spatial discretization to solve Eqs. 6, 7, 8, 9, and 10. The initial conditions affect the spatial profile of Rac-GTP. If the initial concentrations of Rac-GTP and Rac-GDP are too low, their distributions are unlikely to break symmetry; therefore, the cell remains nonpolarized regardless of the strength of the stimulus, let alone cell deformation and motility. Homogeneous initial conditions of u = 2 μm2, v = 6 μm2, f = 0, and m = 2 μm2 are provided.
Cell lines and cell culture
The human breast cancer cell lines, MCF-7 and MDA-MB-231, were purchased from American Type Culture Collection (ATCC, Manassas, VA). MDA-MB-231 cells were stably transfected with plasmids coding for the 3-phosphoinositide-specific Akt-PH domain fused with CFP and plasmids coding for Rac1 fused with YFP using FuGENE HD transfection reagents (Promega, Madison, WI). MCF-7 cells and MDA-MB-231 cells were cultured in Dulbecco’s Modified Eagle’s Medium (DMEM) supplemented with 10% fetal bovine serum, 100 μg/mL penicillin, and 100 μg/mL streptomycin at 37°C in a 5% CO2 atmosphere mixed with 95% air. MCF-7 cells were stained with anti-CD44-PE (BD Pharmingen, San Jose, CA), and anti-CD24-Alexa Fluor 488 (BioLegend, San Diego, CA) antibodies for sorting with a flow cytometer (BD FACS Aria II; BD Biosciences, San Jose, CA). The CD44+/CD24− phenotype was regarded as cancer stem cells (CSCs), whose proportion was ∼1.6% (39); the other three phenotypes, CD44+/CD24+,CD44−/CD24+, and CD44−/CD24−, represented the non-stem cancer cells (NSCCs) (40,41). CSCs sorted from MCF-7 cells were cultured in DMEM/F12 (1:1 mixture of DMEM and Ham’s F-12 medium) with 20 ng/mL basic fibroblast growth factor, 10 ng/mL epidermal growth factor, B27 serum-free supplement, and N-2 supplement to inhibit the differentiation of CSCs (39). The phenotype of CSCs was maintained for at least 1 month.
Imaging and image processing
Before loading cells, the culture dish was incubated with Geltrex (120–180 μg/mL; Gibco, Gaithersburg, MD) at 37°C for an hour. MCF-7 cells cultured in the 24-well plate were stained with 1 μg/mL of Hoechst 33342 for 20 min at 37°C and rinsed with phosphate-buffered saline. Subsequently, they were stained with 333 μg/mL of Golgi-Tracker Red (Molecular Probes, Eugene, OR) at 4°C for 30 min, rinsed with ice-cold medium, and incubated in fresh medium for 30 min at 37°C. Then, the cells were loaded into confocal culture dishes to measure the movements of spontaneous polarization. Time-lapse imaging was performed on a Zeiss inverted microscope (Axio Observer.Z1 (SP); Carl Zeiss, Oberkochen, Germany) every 5 min for at least 1 h. The objective was 20× with a numerical aperture of 0.5 in air. The detection channels included bright field, DAPI (4',6-diamidino-2-phenylindole), and mCherry using an X-cite lamp (Excelitas, Waltham, MA).
MDA-MB-231 cells were harvested by trypsinization and then seeded in the six-well glass-bottom cell culture plates coated with Geltrex at the density of 1700 cells/cm2 in DMEM supplemented with 1% fetal bovine serum medium (isotonic medium). The samples were incubated at 37°C for 12 h. The medium was replaced by fresh isotonic (ISO) medium; hypotonic medium HYPO or HYPO+ (corresponding to a 3:1 or 1:1 mixture of isotonic medium and double distilled water, respectively), which increased cell tension (42); or medium containing deoxycholate (Sigma-Aldrich, St. Louis, MO) DC or DC+ at a concentration of 200 or 400 μM, respectively, which decreased cell tension (42). After 2 h, the plates were mounted in the motorized stage of a Nikon Eclipse Ti-E wide-field fluorescence microscope (Nikon, Tokyo, Japna) to record cell deformation and migration. The objective was 20× with a numerical aperture of 0.75 in air, and the intermediate magnification was 1.5×. The detection channels included bright field, YFP, and CFP. 30 regions of interest in each well were selected, and images were recorded every 6 min for at least 2 h. Then fresh isotonic medium, water, or deoxycholate was added into the plates to adjust the cell tension. After 2 h, 30 new regions of interest in each well were selected, and images were recorded every 6 min for another 2 h. Quantifications of cell deformation, velocity, and motion direction were carried out using MATLAB (The MathWorks, Natick, MA).
RESULTS
The mechanochemical cell migration model captures characteristic features of cell polarization
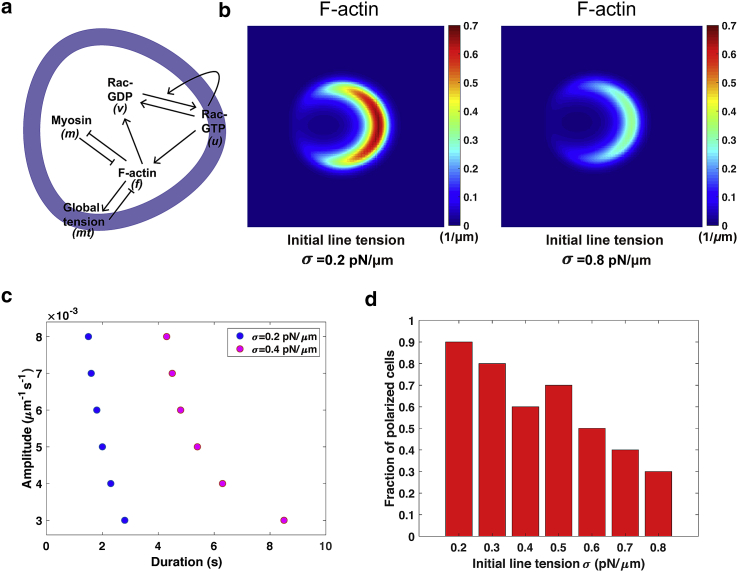
We confirm that the new, to our knowledge, cell migration model preserves the same characteristic features of cell polarization as our previous cell polarization model (3). First, the simulations display F-actin filaments congregating at one side of the polarized cell at a steady state in response to a gradient external stimulus, and the maximum concentration of F-actin decreases from 0.7 μm−1 to around 0.3 μm−1 as cell tension increases from 0.2 to 0.8 pN/μm (Fig. 1 b). Second, cells polarize only when the amplitude or duration of the external stimulus is above a certain threshold, and these thresholds increase at higher cell tension; e.g., the threshold of the duration at fixed amplitudes triples when cell tension is doubled (Fig. 1 c). Third, cells with lower tension have a higher tendency to polarize (Fig. 1 d), consistent with the experimental results that membrane tension serves as a global inhibitor of cell polarization (6). Note that cell polarity is assessed when the steady-state spatial profile of F-actin is formed (i.e., Fig. 1 b) under the persistent external stimulus.
Figure 1.
Characterization of the cell polarization occurring before migration in the mechanochemical cell migration model. (a) The schematic diagram of the regulatory network in the model of cell migration is given. Cell tension (mt) globally inhibits (denoted by —|) the formation of F-actin (f) in the cell. However, F-actin polymerization increases (black solid arrow →) the cortical part of cell tension and meanwhile activates the membrane-bound Rac-GTP (u) (light blue). Rac-GTP is also activated by stimulation and itself. In addition, Rac-GTP on the membrane and Rac-GDP (v) in the cytosol interconvert. Myosin (m) attached to the actin bundles is mutually antagonized with F-actin. (b) The steady-state spatial profiles of F-actin in a polarized cell with initial line tension σ = 0.2 and 0.8 pN/μm, respectively, are shown. To respond to a gradient external stimulus, F-actin accumulates at the cell front in the cytoplasm. As σ rises to 0.8 pN/μm, the maximum concentration of F-actin decreases. (c) The threshold of the amplitude of stimuli as a function of the duration of stimuli for inducing cell polarity at different values of initial line tension is shown. (d) The fraction of polarized cells under various values of σ is shown. Each bar counts the results from repetitive simulations under the sample size N = 20. To see this figure in color, go online.
The deformation of the cell membrane under different cell tension
Polarized cells are capable of protruding outward and form lamellipodia toward the directions in which F-actin has polarized distributions. As a consequence, the cell membrane is deformed. Just like cell polarization, the deformation of the cell membrane should be strongly influenced by cell tension. The maximum concentration of F-actin is significantly low in cells with larger tension (Fig. 1 b), and the probability of cell polarization drops at higher cell tension.
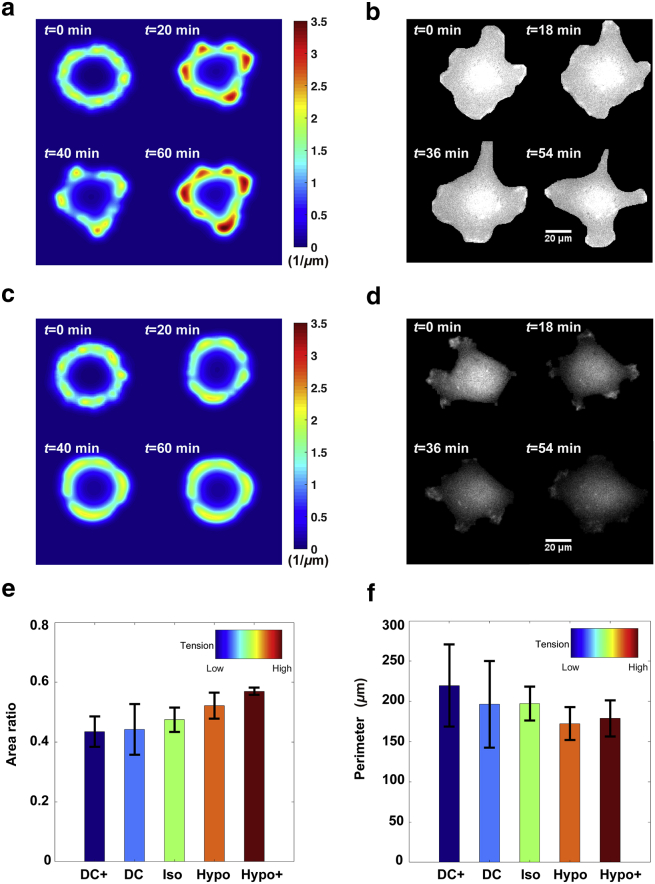
Stochasticity (or noise) at the molecular level has been observed extensively to affect cellular plasticity in living systems (43). Our cell migration model demonstrates cell membrane deformation due to random internal noise, i.e., the varying conversion rate from Rac-GDP to Rac-GTP, the same as the local stimulus defined in Eq. 12 with R0 as an N(0, 1) Gaussian distribution random variable. The model displays two typical types of morphological patterns when the initial line tension is attuned as 0.005 and 0.015 pN/μm accordingly (Fig. 2, a and c; Videos S1 and S2). Initially, the cell is round, with an even distribution of F-actin. In one type, F-actin starts to form several clusters because of a slight change in positive feedback from Rac-GTP, and the cytoskeleton is slightly changed (Fig. 2 a, t = 20 min). Finally, F-actin clusters spread in a larger area as the maximum concentration increases, and the cell membrane has distinct protrusions (Fig. 2 a, t = 60 min). Depending on the random stimuli, cells present different morphologies. In the other type of pattern, F-actin remains at low concentrations and is distributed more homogeneously, meaning the cell is unpolarized (Fig. 2 c), and the cells have a stable shape. Moreover, the tendency of the two types of patterns varies at different cell tension. The first has a greater tendency to be observed at low cell tension because the cell membrane is more flexible.
Figure 2.
Comparison of cell deformation under random internal noise in silico and in vitro. (a) The cell membrane is manifestly deformed under low cell tension of σ = 0.005 pN/μm. The color bar on the right represents the concentration of F-actin. (b) MDA-MB-231 cells are more flexible in the hypertonic condition in vitro. The higher fluorescence intensity of CFP-Akt indicates a higher concentration of PI3K, which is an upper stream kinase of Rac-GTP. Scale bars, 20 μm. (c) Cells lack dominant protrusions under a large tension of 0.015 pN/μm. Likewise, the color bar shows the concentration of F-actin. (d) MDA-MB-231 cells are more rigid in the hypo-condition in vitro. Scale bars, 20 μm. For better comparison of (b) and (d), after removing the background outside the cell, the images are shown on the same grayscale. (e) Area ratio of cells with different cell tensions is shown. The area ratio is defined as the ratio of cell area to the area of an equal-perimeter circle. In the experiment, it reaches above 0.4 at the lowest tension (DC+ media), meaning cells attain the maximum deformation ability. The value increases to around 0.55 at the highest tension (Hypo+ media), showing cells are the least deformable. Error bar indicates standard errors. The sample number is n = 277 in DC+ media, n = 283 in DC media, 3290 samples in iso media, 486 samples in hypo media, and 459 samples in hypo+ media. (f) Cell perimeters with different cell tensions are shown. Error bar indicates standard errors. To see this figure in color, go online.
Meanwhile, we used two indices—namely the maximum perimeter, which is calculated as the maximal cell perimeter during 60-min simulations, and area ratio, which is defined as the ratio of cell area/the area of an equal-perimeter circle (which means the deformability for cells to stay away from a round shape)—to measure deformation in both low and high cell tension. Because volume constraint is one of our model assumptions, the cell with a larger deformable shape also has a larger maximum perimeter. In simulations, the maximum perimeter reaches 35.5 ± 1.4 μm for cells with low tension (five simulations) and 31.5 ± 0.1 μm with high tension (five simulations). The area ratio reaches 0.79 ± 0.06 for cells with low tension and 0.99 ± 0.01 with high tension.
We test these predictions of our model by imaging on MDA-MB-231 cells in hypertonic and hypotonic conditions in vitro, i.e., low and high cell tension, respectively. These cells express CFP-Akt, and Akt is a widely used readout of PI3K (44), which activates Rac-GTP inducing F-actin polymerization. The cells under lower tension show a higher fluorescence intensity of CFP-Akt (Fig. 2, b and d), indicating higher activity of F-actin polymerization. Notably, only PI3K molecules accumulating in the “hot spots” at the cell periphery, not those accumulating on the nuclear membrane in the middle of the cell (Fig. 2, b and d), can activate Rac-GTP and are related to the F-action polymerization (44). Moreover, we calculated the area ratio and the maximum cell perimeter to measure cell deformation ability. The result shows that the maximum and minimum deformation ability were attained at the lowest tension using DC+ media and highest tension using Hypo+ media (Fig. 2, e and f), respectively, consistent with the trend observed in the simulation.
Both the results in silico and in vitro reveal that cell tension could be a shape regulator under the condition of random internal noise and from a qualitative point of view. Furthermore, our numerical results shed light on further explorations and pose a number of questions that require more detailed and quantitative analysis, such as how to measure cell migration ability, the relationship between speed of migration and cell tension, and so on.
Various migration modes
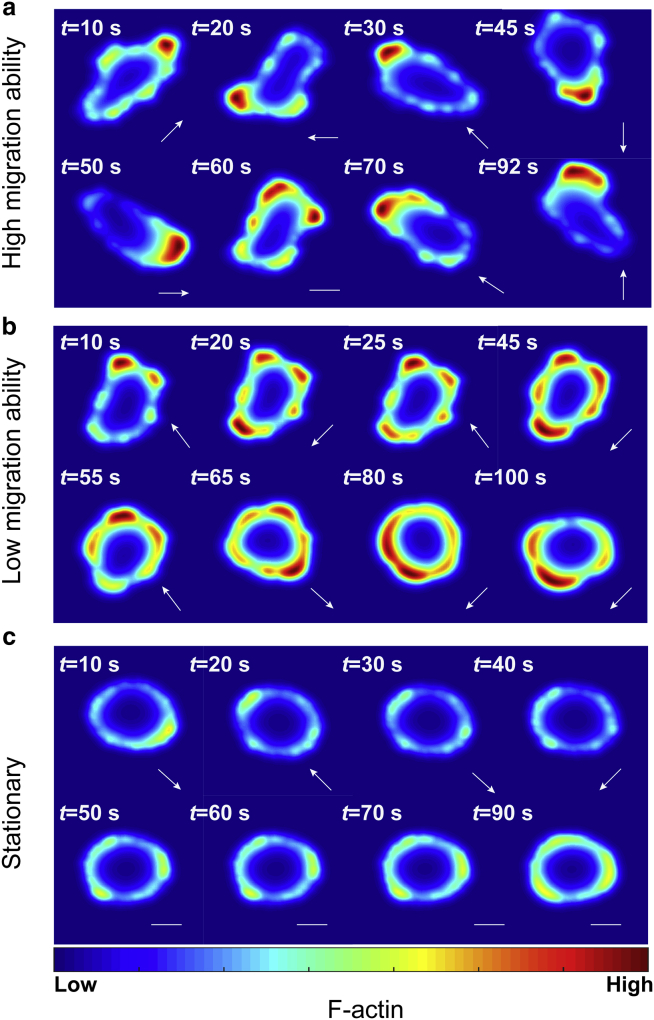
Cell migration displays a variety of patterns, depending on the strength and spatiotemporal distribution of stimuli as well as cell tension. Under random stimuli, our cell migration model generates three modes of cell migration. The distinctions of these migrating modes are based on the mean value of the instant speed, which is numerically computed as the difference of cell centroids at each time step. The speed of the high migration mode is greater than 0.3 μm/s, the speed of the low migration mode is between 0.1 and 0.3 μm/s, and the speed of the stationary mode is less than 0.1 μm/s (Fig. S1 a). The threshold speeds to distinguish these three migrating modes are obtained via k-means clustering, and they are in line with the measurements for sperm cell motility in hypertonic, isotonic, and hypotonic media (42). Notably, this is a universal phenomenon at different cell tensions (initial line tension) by adjusting suitable protrusive coefficients.
The high migration ability pattern is the most common migrating behavior (8 out of 10 simulations at low tension of 0.2 pN/μm) induced by random internal noise (Fig. 3 a). Because of the nonuniformity of noise, the conversion rate from Rac-GDP to Rac-GTP is increased in some areas of the cell while inhibited in others. The amplification of this effect results in a polarized distribution of F-actin before the formation of protrusions. The cells then move along the main direction on which the dominant protrusion exists. This dominant protrusion disappears and reappears in different directions. As a result, the direction of migration of cells varies randomly accordingly.
Figure 3.
Three cell migration modes generated by the cell migration model. (a) The representative time series of the high migration mode emerges because of the translocation of polarity patterns when σ is also chosen as 0.2 pN/μm. The white bar stands for the tendency of staying at rest state. (b) The representative time series of the low migration ability mode as the parameter of initial line tension σ is attuned as 0.2 pN/μm. The white arrow at the bottom right corner indicates the instant direction for cell movement. (c) Stationary migration mode occurs when σ increases to 0.8 pN/μm. Cells tend to maintain a regular morphology with a low concentration of F-actin and have either a stable movement or a stable morphology. To see this figure in color, go online.
Cells also show low migration ability patterns, with ∼20% probability at low tension of 0.2 pN/μm in the simulations (Fig. 3 b). An interesting feature of this pattern is that the polarized distribution of F-actin occurring on opposite sides of the cell appears and vanishes periodically. Therefore, under the influence of oscillatory polarized distributions, cells migrate in a periodic pattern because the protrusive force is proportional to the concentration of F-actin. Oscillation of movement may be interrupted because cells are capable of repolarizing and producing protrusions along with other directions. When other protrusions are in a dominant position, the equilibrium of the oscillatory pattern is broken, and the cell moves toward a new direction (Fig. 3 b).
Stationary patterns are generated when cell tension is 0.8 pN/μm (7 out of 10 simulations). Because high tension increases the threshold of polarization, compared with cells in low tension, the maximum concentration of F-actin is strongly inhibited, although polarized distribution of F-actin could still sometimes occur in some parts of the membrane because of the nonhomogeneity of random noise and because the cell membrane does not show noticeable deformations (Fig. 3 c).
The arrows for directions are calculated according to the concentration of F-actin because protrusive force is solely associated with the concentration of F-actin in our model. Note that there are multiple polarity areas under random internal noise; cells tend to move in the direction in which the polarity area has the highest concentration of F-actin. These simulated patterns are consistent with the observed movements of spontaneous polarized MDA-MB-231 cells without any external gradient stimuli (Videos S3, S4, and S5).
High cell tension inhibits movement under persistent external stimuli
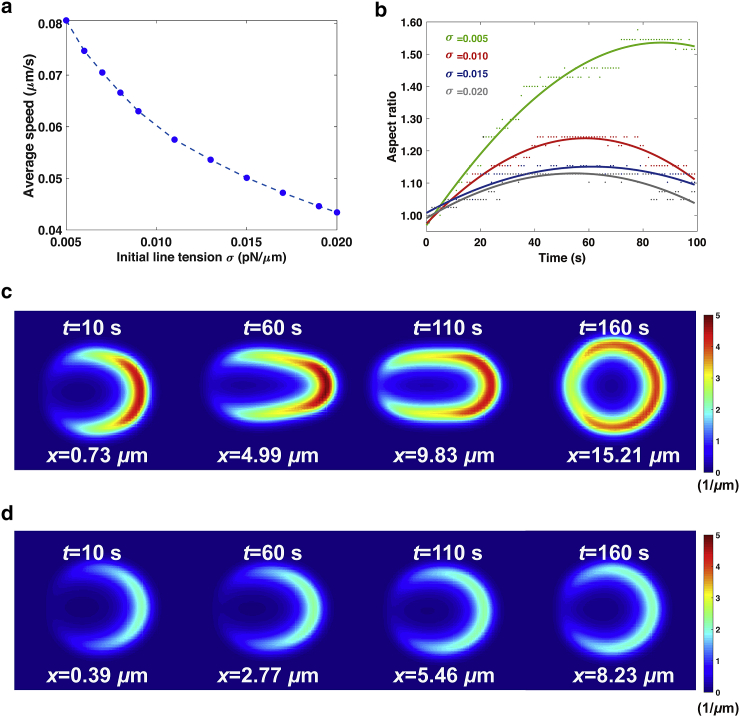
Our models also show other migration patterns, such as the persistent pattern due to the presence of external stimuli (Fig. S2 c). As can be seen in Fig. 4, c and d, given external stimuli in a fixed direction, the cells are stretched and move in the direction of the external stimuli.
Figure 4.
Cell migration ability under persistent external stimuli. (a) The average speed as a function of different initial line tension is shown. The average speed is determined by the ratio between the distance traveled and the total simulation time. (b) Reduction in the aspect ratio of cells to four representative values of initial line tension is shown. The aspect ratio measures the ratio between the maximum/minimum radius of cells, depending on the time of movement. Dots in green, red, blue, and gray mean the sample points collected via simulations, whereas the corresponding sinusoidal smoothing curves have an average coefficient of determination R2 = 0.8855. (c) Cell migration ability and spatial profile of F-actin in low tension is shown. σ is at the value of 0.005 pN/μm, and the color bar indicates the concentration of F-actin. (d) The cell barely changes shape, with the maximum concentration of F-actin falling significantly, at a high cell tension of 0.02 pN/μm. To see this figure in color, go online.
Cell tension is found to serve as an inhibitor for the movement, as the average speed decreases by almost half, from 0.08 μm/s at 0.005 pN/μm to 0.044 μm/s at 0.02 pN/μm (Fig. 4 a). This is for the following reasons. First, cells tend to remain unpolarized under higher cell tension (Fig. 1 d). Second, the polarized cells lose the propensity of changing their shape to be elongated under higher cell tension (Fig. 4, b and c). However, based on our simulations, elongated cells with a large aspect ratio move faster (Fig. S2 a). As shown in Fig. S2 a, the average speed is linearly dependent on the aspect ratio with a goodness of fit up to 0.95. This strong correlation is reasonable. As shown in the simulation, cells polarize in response to external spatial cues; newly polymerized F-actin leads to rearrangement of cytoskeleton structure, and the cells elongate along the polarization direction and are poised for movement. They then migrate through the collective efforts of protrusion and retraction (Videos S6 and S7). Last but not least, the persistent time of cell movement decreases under higher cell tension (Fig. S2 b). Polarized cells can only retain shape with a high aspect ratio and keep moving in a certain duration, which is denoted as the persistent time. Once cells deform and crawl, the cumulative concentration of F-actin accumulates because of the positive feedback of Rac-GTP. Furthermore, the cell perimeter notably increases as cell extends. These two factors coordinately elevate cell tension inhibiting the polymerization of F-actin. As a result, the maximum concentration of F-actin gradually decreases and eventually redistributes evenly around the cell, and the cell ends migration with a reduced aspect ratio. Because cells with lower cell tension are more likely to deform in shape (Fig. 3), it takes a much longer time for a cell with lower cell tension to return its shape to initial round disk (Fig. 4 b, σ = 0.005 pN/μm).
Our simulation result shows that in the circumstance of persistent external stimuli, cell migration ability is restricted under high tension as movement is merely driven by a solo lamellipodium. This finding is consistent with the published result showing elevated membrane tension binds actin assembly, resulting in a larger leading edge and defective chemotaxis (45).
Migration ability maximizes at intermediate cell tension under random internal noise
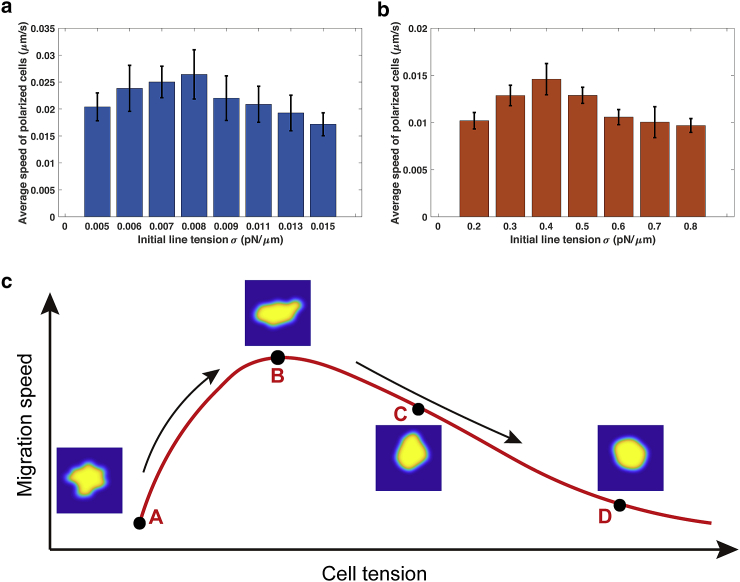
In comparison to external stimuli with protrusion-driven migration directly toward the stimulus source, the cells are capable of generating multiple lamellipodia (or filopodia) spontaneously under the regulation of random internal noise, which is more frequently observed in vitro. Surprisingly, our cell migration model shows a nonmonotonic relationship of average speed and cell tension within the range of [0.005–0.015 pN/μm].
As shown in the simulation, when cell tension is low, cells are easy to polarize and more likely to generate multiple protrusions under small perturbations from internal noise. These lamellipodia on random directions offset the momentum in the movement on principle direction. With the increase of cell tension, certain protrusions caused by small perturbations are reduced as tension stabilizes polarity, and therefore, cells are more streamlined. Cells with a streamlined body have a higher migration ability. Cells thus achieve a fast average speed. Nonetheless, if cell tension continues to increase, the stiffness of the membrane prohibits F-actin polymerization (Fig. 5 a). In our simulations, we calculate the average speed over the entire simulation period and also take an average of all samples. A similar trend is observed when initial line tension is within the range of [0.2–0.8 pN/μm] (MCF-7 cells). The optimized average speed is around σ = 0.4 pN/μm (Fig. 5 b).
Figure 5.
Nonmonotonic relationship between the migration speed and cell tension under random internal noise. (a) The average speed of polarized cells as a function of initial line tension σ within the range of [0.005–0.015 pN/μm] is shown. Error bars represent the standard errors of the average speed under sample size N = 20. (b) The average speed of polarized cells as a function of initial line tension σ within the range of [0.2–0.8 pN/μm] is shown. Because only a fraction of the cells are polarized (Fig. 1d), the data for the average speed is recorded only from those polarized cells. Error bars represent standard errors. (c) A hypothetical curve regarding migration speed and cell tension is given. The black arrows indicate the tendency of migration speed. Points A–D are four representative phases of the tension regulation. Point A is the initial cell shape, and B–D stand for different cell morphologies under different cell tensions. To see this figure in color, go online.
We summarize the bell curve for the speed of cell migration and the tension in the simulation (Fig. 5 c). These simulated results are consistent with previously published experimental results. Batchelder et al. used a simple model of the Caenorhabditis elegans sperm cell to quantify the relation between membrane tension and cell migration speed. Surprisingly, they find that a reduction in membrane tension is correlated with a decrease in the cell displacement speed, whereas an increase in membrane tension enhances motility (42). Similar results are seen in human neutrophils (5). Similarly, cell movement is impeded by multiple lamellipodia in moving keratocytes (6) and protruding fibroblasts (46). From the observations of both cases, cells are more streamlined under a relatively high cell tension. It is hypothesized that membrane tension will lead to a coalescence of protrusions and thus enhance motility, and a nonmonotone curve between tension and migration speed is also expected (15,42). More systematic tests of the simulation results remain to be carried out in future studies.
DISCUSSION
Cell migration is orchestrated by a complicated mechanochemical system. This includes F-actin polymerization and morphological transition through the combined effects from various forces such as protrusive force, retraction, cell tension, and adhesion. Here, protrusive force and retraction are correlated with the activities of polarity marker proteins Rac-GTPase and protein motor myosin, respectively. Cell tension consists of cortical tension and membrane tension. In response to external stimuli and/or random internal noise, polarity proteins accumulate on certain cell edges under positive feedback to form polarized distributions. The cytoskeleton is rearranged to deform the cell’s shape under the inhibition from cell tension. Cells move with the synergy of protrusions such as lamellipodia and retraction. Different migration modes emerge depending on the cell type, extracellular matrix (ECM), and stimuli. It is difficult to model all the phenomena of cell migration. Our models focus on the coupling between cell tension and biochemical factors including Rac-GTPase, F-actin, and myosin. In our work, tension is proportional to the total concentration of polymerized F-actin. On the other hand, it is also used as a long-range inhibitor to deactivate F-actin activities. We describe mechanical properties via a phase field model and use reaction-diffusion equations to express biochemical processes. Our model has successfully demonstrated how cell tension influences cell polarization and movement. In simulations, our models recapitulate common features of polarization (Fig. 1). Based on our models, cells utilize one particular parameter initial line tension, in addition to the chemical systems, to regulate cell morphological changes through competitions of protrusions (Fig. 2).
Cell tension is determined by both the stiffness of membrane and polymerization of actin filaments. The rigidity of the membrane depends on molecular structure and varies from cell to cell. In our model, the stiffness of the membrane can be altered by attuning initial line tension . Different values of σ can represent various cell types; e.g., we select σ = 0.2 pN/μm and σ = 0.8 pN/μm to stand for cancer stem cells and non-stem cancer cells in the MCF-7 cell line. In the meantime, σ = 0.005 pN/μm is selected to represent MDA-MB-231 cells in the hypertonic condition and σ = 0.015 pN/μm for those cells in the hypotonic condition. Notably, after taking into the cortical tension into consideration, within the range of [0.005–0.015 pN/μm], the effective cell tension σ′ is around 10–25 pN/μm, and σ′ soars to around 70–140 pN/μm when the parameter of initial line tension is taken as [0.2–0.8 pN/μm] based on the calculation of mt(f, ϕ) in Eq. 8, which is compatible with the measurement findings for other cell types (15). We may adjust one parameter, the protrusive coefficient, to ensure membrane deformation under different initial line tension σ. Because the deformity of the cell membrane depends on the strength of protrusive force, which is proportional to the concentration of F-actin, the synthesis of F-actin is inhibited by cell tension.
Our model produces representative migration modes. When there is only random internal noise, a highly motile mode is the most common at low cell tension, whereas cells prefer to be stationary at high tension (Fig. 3). Given external stimuli without random internal noise, cells exhibit a persistent motion. These results are consistent with the experimental results. We further investigate how tension affects cell movement. It is confirmed that cell tension inhibits the formation of protrusion; hence, the cell with only one protrusion under a strong external stimulus shows reduced migration ability because cell tension is high (Fig. 4, a, c, and d). Interestingly, when internal random noise dominates and cells form multiple protrusions, we discover a biphasic nonmonotonic effect of tension regulation on cell migration ability, i.e., cells achieve the maximum migration ability at intermediate tension. This finding is consistent with a previously proposed hypothesis (15).
Our proposed model provides a minimal system that cell tension regulates migration ability. This model assumes the uniformity of cell tension over the cell membrane. It will be interesting to further investigate the effect of the localized cell tension on the mechanical signaling in future studies. Meanwhile, our model neglects the influence from the ECM on movement. The ECM activates signal transduction in cells, and when the cell membrane deforms, the contact area between membrane and substrate is also changing. Besides, increasing contacts between cells and the extracellular matrix could increase the stiffness and viscosity of the actin cytoskeleton (47). Hence, a more comprehensive model can be constructed to describe how ECM, mechanical, and biochemical signals interact with each other (48). With this mode, more migration modes such as directed cell migration under topographic ECM gradients (49) and oscillation patterns (50) could be investigated. Also, our model considers myosin as a passive player for cell migration. Other studies report that in response to membrane tension changes, cells actively regulate cortical myosin contraction to balance external forces (51). Others study tissue dynamics with cell tension directly on GTPase, with the mechanochemical waves reorienting to a back-to-front and front-to-back propagating pattern in a migrating tissue (52,53). Some work suggests that plasma membrane tension could inhibit F-actin polymerization through membrane-bound protein FBP17, whereas conversely, FBP17 exerts negative feedback on actin filament polymerization (54). As for the characteristics to measure migration ability, we only focus on the instant and average speed in the model. It will be interesting to use other characteristics such as cell turning to measure migration ability in the future.
Acknowledgments
We thank Yihan Lin lab for providing the transfected cell lines used in this study.
This work was supported by the National Natural Science Foundation of China (11622102, 11861130351, 11434001, 31670852).
Editor: Ruth Baker.
Footnotes
Supporting Material can be found online at https://doi.org/10.1016/j.bpj.2020.04.030.
Contributor Information
Feng Liu, Email: liufeng-phy@pku.edu.cn.
Lei Zhang, Email: zhangl@math.pku.edu.cn.
Supporting Citations
References (55,56) appear in the Supporting Material.
Author Contributions
K.T., F.L., L.Z., and W.W. designed the research. F.L. and L.Z. supervised the reserach. K.T., J.W., and X.K. perform the research. F.L., L.Z., K.T., and J.W. wrote the article.
Supporting Material
References
- 1.Lee S.H., Dominguez R. Regulation of actin cytoskeleton dynamics in cells. Mol. Cells. 2010;29:311–325. doi: 10.1007/s10059-010-0053-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Ridley A.J., Hall A. The small GTP-binding protein rho regulates the assembly of focal adhesions and actin stress fibers in response to growth factors. Cell. 1992;70:389–399. doi: 10.1016/0092-8674(92)90163-7. [DOI] [PubMed] [Google Scholar]
- 3.Wang W., Tao K., Liu F. Exploring the inhibitory effect of membrane tension on cell polarization. PLoS Comput. Biol. 2017;13:e1005354. doi: 10.1371/journal.pcbi.1005354. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Diz-Muñoz A., Fletcher D.A., Weiner O.D. Use the force: membrane tension as an organizer of cell shape and motility. Trends Cell Biol. 2013;23:47–53. doi: 10.1016/j.tcb.2012.09.006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Houk A.R., Jilkine A., Weiner O.D. Membrane tension maintains cell polarity by confining signals to the leading edge during neutrophil migration. Cell. 2012;148:175–188. doi: 10.1016/j.cell.2011.10.050. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Lieber A.D., Yehudai-Resheff S., Keren K. Membrane tension in rapidly moving cells is determined by cytoskeletal forces. Curr. Biol. 2013;23:1409–1417. doi: 10.1016/j.cub.2013.05.063. [DOI] [PubMed] [Google Scholar]
- 7.Gauthier N.C., Masters T.A., Sheetz M.P. Mechanical feedback between membrane tension and dynamics. Trends Cell Biol. 2012;22:527–535. doi: 10.1016/j.tcb.2012.07.005. [DOI] [PubMed] [Google Scholar]
- 8.Shi Z., Graber Z.T., Cohen A.E. Cell membranes resist flow. Cell. 2018;175:1769–1779.e13. doi: 10.1016/j.cell.2018.09.054. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Wang F., Herzmark P., Bourne H.R. Lipid products of PI(3)Ks maintain persistent cell polarity and directed motility in neutrophils. Nat. Cell Biol. 2002;4:513–518. doi: 10.1038/ncb810. [DOI] [PubMed] [Google Scholar]
- 10.Weiner O.D., Marganski W.A., Kirschner M.W. An actin-based wave generator organizes cell motility. PLoS Biol. 2007;5:e221. doi: 10.1371/journal.pbio.0050221. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Lewis O.L., Guy R.D., Allard J.F. Actin-myosin spatial patterns from a simplified isotropic viscoelastic model. Biophys. J. 2014;107:863–870. doi: 10.1016/j.bpj.2014.06.041. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Xiong D., Xiao S., Wu M. Frequency and amplitude control of cortical oscillations by phosphoinositide waves. Nat. Chem. Biol. 2016;12:159–166. doi: 10.1038/nchembio.2000. [DOI] [PubMed] [Google Scholar]
- 13.Bhalla U.S., Iyengar R. Emergent properties of networks of biological signaling pathways. Science. 1999;283:381–387. doi: 10.1126/science.283.5400.381. [DOI] [PubMed] [Google Scholar]
- 14.Lecuit T., Lenne P.F., Munro E. Force generation, transmission, and integration during cell and tissue morphogenesis. Annu. Rev. Cell Dev. Biol. 2011;27:157–184. doi: 10.1146/annurev-cellbio-100109-104027. [DOI] [PubMed] [Google Scholar]
- 15.Sens P., Plastino J. Membrane tension and cytoskeleton organization in cell motility. J. Phys. Condens. Matter. 2015;27:273103. doi: 10.1088/0953-8984/27/27/273103. [DOI] [PubMed] [Google Scholar]
- 16.Fletcher D.A., Mullins R.D. Cell mechanics and the cytoskeleton. Nature. 2010;463:485–492. doi: 10.1038/nature08908. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Kruse K., Joanny J.F., Prost J. Contractility and retrograde flow in lamellipodium motion. Phys. Biol. 2006;3:130–137. doi: 10.1088/1478-3975/3/2/005. [DOI] [PubMed] [Google Scholar]
- 18.Carlsson A.E. Mechanisms of cell propulsion by active stresses. New J. Phys. 2011;13:073009. doi: 10.1088/1367-2630/13/7/073009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Recho P., Putelat T., Truskinovsky L. Contraction-driven cell motility. Phys. Rev. Lett. 2013;111:108102. doi: 10.1103/PhysRevLett.111.108102. [DOI] [PubMed] [Google Scholar]
- 20.Lee J., Ishihara A., Jacobson K. Principles of locomotion for simple-shaped cells. Nature. 1993;362:167–171. doi: 10.1038/362167a0. [DOI] [PubMed] [Google Scholar]
- 21.Ziebert F., Aranson I.S. Computational approaches to substrate-based cell motility. npj Comput. Mater. 2016;2:16019. [Google Scholar]
- 22.Shi C., Huang C.H., Iglesias P.A. Interaction of motility, directional sensing, and polarity modules recreates the behaviors of chemotaxing cells. PLoS Comput. Biol. 2013;9:e1003122. doi: 10.1371/journal.pcbi.1003122. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Shao D., Levine H., Rappel W.J. Coupling actin flow, adhesion, and morphology in a computational cell motility model. Proc. Natl. Acad. Sci. USA. 2012;109:6851–6856. doi: 10.1073/pnas.1203252109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Shao D., Rappel W.J., Levine H. Computational model for cell morphodynamics. Phys. Rev. Lett. 2010;105:108104. doi: 10.1103/PhysRevLett.105.108104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Ziebert F., Swaminathan S., Aranson I.S. Model for self-polarization and motility of keratocyte fragments. J. R. Soc. Interface. 2012;9:1084–1092. doi: 10.1098/rsif.2011.0433. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Han Y., Xu Z., Zhang L. Pathways connecting two opposed bilayers with a fusion pore: a molecularly-informed phase field approach. Soft Matter. 2020;16:366–374. doi: 10.1039/c9sm01983a. [DOI] [PubMed] [Google Scholar]
- 27.An Y., Xue G., Yan Y. Apical constriction is driven by a pulsatile apical myosin network in delaminating Drosophila neuroblasts. Development. 2017;144:2153–2164. doi: 10.1242/dev.150763. [DOI] [PubMed] [Google Scholar]
- 28.Lim C.T., Zhou E.H., Quek S.T. Mechanical models for living cells--a review. J. Biomech. 2006;39:195–216. doi: 10.1016/j.jbiomech.2004.12.008. [DOI] [PubMed] [Google Scholar]
- 29.Banerjee N., Park J. Modeling and simulation of biopolymer networks: classification of the cytoskeleton models according to multiple scales. Korean J. Chem. Eng. 2015;32:1207–1217. [Google Scholar]
- 30.Yamaoka H., Matsushita S., Adachi T. Multiscale modeling and mechanics of filamentous actin cytoskeleton. Biomech. Model. Mechanobiol. 2012;11:291–302. doi: 10.1007/s10237-011-0317-z. [DOI] [PubMed] [Google Scholar]
- 31.Broedersz C.P., MacKintosh F.C. Modeling semiflexible polymer networks. Rev. Mod. Phys. 2014;86:995. [Google Scholar]
- 32.Mogilner A. On the edge: modeling protrusion. Curr. Opin. Cell Biol. 2006;18:32–39. doi: 10.1016/j.ceb.2005.11.001. [DOI] [PubMed] [Google Scholar]
- 33.Holmes W.R., Edelstein-Keshet L. A comparison of computational models for eukaryotic cell shape and motility. PLoS Comput. Biol. 2012;8:e1002793. doi: 10.1371/journal.pcbi.1002793. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Mori Y., Jilkine A., Edelstein-Keshet L. Wave-pinning and cell polarity from a bistable reaction-diffusion system. Biophys. J. 2008;94:3684–3697. doi: 10.1529/biophysj.107.120824. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Wang F. The signaling mechanisms underlying cell polarity and chemotaxis. Cold Spring Harb. Perspect. Biol. 2009;1:a002980. doi: 10.1101/cshperspect.a002980. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Sasaki A.T., Chun C., Firtel R.A. Localized Ras signaling at the leading edge regulates PI3K, cell polarity, and directional cell movement. J. Cell Biol. 2004;167:505–518. doi: 10.1083/jcb.200406177. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Holmes W.R., Carlsson A.E., Edelstein-Keshet L. Regimes of wave type patterning driven by refractory actin feedback: transition from static polarization to dynamic wave behaviour. Phys. Biol. 2012;9:046005. doi: 10.1088/1478-3975/9/4/046005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Mata M.A., Dutot M., Holmes W.R. A model for intracellular actin waves explored by nonlinear local perturbation analysis. J. Theor. Biol. 2013;334:149–161. doi: 10.1016/j.jtbi.2013.06.020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Yang G., Quan Y., Wang Y. Dynamic equilibrium between cancer stem cells and non-stem cancer cells in human SW620 and MCF-7 cancer cell populations. Br. J. Cancer. 2012;106:1512–1519. doi: 10.1038/bjc.2012.126. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Ponti D., Costa A., Daidone M.G. Isolation and in vitro propagation of tumorigenic breast cancer cells with stem/progenitor cell properties. Cancer Res. 2005;65:5506–5511. doi: 10.1158/0008-5472.CAN-05-0626. [DOI] [PubMed] [Google Scholar]
- 41.Sheridan C., Kishimoto H., Nakshatri H. CD44+/CD24- breast cancer cells exhibit enhanced invasive properties: an early step necessary for metastasis. Breast Cancer Res. 2006;8:R59. doi: 10.1186/bcr1610. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Batchelder E.L., Hollopeter G., Plastino J. Membrane tension regulates motility by controlling lamellipodium organization. Proc. Natl. Acad. Sci. USA. 2011;108:11429–11434. doi: 10.1073/pnas.1010481108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Nie Q., Qiao L., Zhao W. Noise control and utility: from regulatory network to spatial patterning. Sci. China Math. 2020;63:425–440. [Google Scholar]
- 44.Park J., Holmes W.R., Levchenko A. Mechanochemical feedback underlies coexistence of qualitatively distinct cell polarity patterns within diverse cell populations. Proc. Natl. Acad. Sci. USA. 2017;114:E5750–E5759. doi: 10.1073/pnas.1700054114. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Diz-Muñoz A., Thurley K., Weiner O.D. Membrane tension acts through PLD2 and mTORC2 to limit actin network assembly during neutrophil migration. PLoS Biol. 2016;14:e1002474. doi: 10.1371/journal.pbio.1002474. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Raucher D., Sheetz M.P. Cell spreading and lamellipodial extension rate is regulated by membrane tension. J. Cell Biol. 2000;148:127–136. doi: 10.1083/jcb.148.1.127. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Wang N., Ingber D.E. Control of cytoskeletal mechanics by extracellular matrix, cell shape, and mechanical tension. Biophys. J. 1994;66:2181–2189. doi: 10.1016/S0006-3495(94)81014-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Holmes W.R., Park J., Edelstein-Keshet L. A mathematical model coupling polarity signaling to cell adhesion explains diverse cell migration patterns. PLoS Comput. Biol. 2017;13:e1005524. doi: 10.1371/journal.pcbi.1005524. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Park J., Kim D.H., Levchenko A. Topotaxis: a new mechanism of directed cell migration in topographic ECM gradients. Biophys. J. 2018;114:1257–1263. doi: 10.1016/j.bpj.2017.11.3813. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Peyret G., Mueller R., Ladoux B. Sustained oscillations of epithelial cell sheets. Biophys. J. 2019;117:464–478. doi: 10.1016/j.bpj.2019.06.013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.He L., Tao J., Sun S.X. Role of membrane-tension gated Ca2+ flux in cell mechanosensation. J. Cell Sci. 2018;131:jcs208470. doi: 10.1242/jcs.208470. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Bui J., Conway D.E., Weinberg S.H. Mechanochemical coupling and junctional forces during collective cell migration. Biophys. J. 2019;117:170–183. doi: 10.1016/j.bpj.2019.05.020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Zmurchok C., Bhaskar D., Edelstein-Keshet L. Coupling mechanical tension and GTPase signaling to generate cell and tissue dynamics. Phys. Biol. 2018;15:046004. doi: 10.1088/1478-3975/aab1c0. [DOI] [PubMed] [Google Scholar]
- 54.Tsujita K., Takenawa T., Itoh T. Feedback regulation between plasma membrane tension and membrane-bending proteins organizes cell polarity during leading edge formation. Nat. Cell Biol. 2015;17:749–758. doi: 10.1038/ncb3162. [DOI] [PubMed] [Google Scholar]
- 55.Postma M., Bosgraaf L., Van Haastert P.J. Chemotaxis: signalling modules join hands at front and tail. EMBO Rep. 2004;5:35–40. doi: 10.1038/sj.embor.7400051. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 56.Dawes A.T., Edelstein-Keshet L. Phosphoinositides and Rho proteins spatially regulate actin polymerization to initiate and maintain directed movement in a one-dimensional model of a motile cell. Biophys. J. 2007;92:744–768. doi: 10.1529/biophysj.106.090514. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.