Abstract
Amyloid aggregates are found in many neurodegenerative diseases, including Huntington’s, Alzheimer’s, and prion diseases. The precise role of the aggregates in disease progression has been difficult to elucidate because of the diversity of aggregated states they can adopt. Here, we study the formation of fibrils and oligomers by exon 1 of huntingtin protein. We show that the oligomer states are consistent with polymer micelles that are limited in size by the stretching entropy of the polyglutamine region. The model shows how the sequences flanking the amyloid core modulate aggregation behavior. The N17 region promotes aggregation through weakly attractive interactions, whereas the C38 tail opposes aggregation via steric repulsion. We also show that the energetics of cross-β stacking by polyglutamine would produce fibrils with many alignment defects, but minor perturbations from the flanking sequences are sufficient to reduce the defects to the level observed in experiment. We conclude with a discussion of the implications of this model for other amyloid-forming molecules.
Significance
Numerous diseases are caused by the aggregation of proteins into amyloids. The similarities between aggregates formed by widely varying proteins raises a question as to the extent that sequence details are important for driving assembly into pathological states. An interesting test case is huntingtin, the aggregating protein in Huntington’s disease, which has a remarkably low-complexity sequence featuring a polyglutamine core. This work models huntingtin as a triblock copolymer and shows that the aggregation behavior follows directly from generic polymer properties with only minor perturbations from the sequence.
Introduction
Protein aggregates are implicated as the causative factor in numerous diseases, including neurodegenerative diseases such as Alzheimer’s and Huntington’s (1,2). The most conspicuous of these assemblies are insoluble fibrils consisting of molecules stacked in a cross-β motif. However, the predominant evidence is that disease progression is actually driven by smaller, soluble oligomers (3). These states are more difficult to study than fibrils because they tend to be transient and heterogeneous. In most cases, it is believed that the oligomers are metastable with respect to the fibril but favored kinetically because of the fact that they lack the large nucleation barrier associated with fibril formation (4, 5, 6, 7, 8, 9, 10). Confounding the issue is the fact that in vitro conditions inevitably differ from those in vivo, raising the question of whether the oligomers observed in the lab are the same as those occurring naturally. This question would be more readily answered with an understanding of the nature and stability of the various states.
The common features of amyloid diseases give rise to another question. To what extent are aggregation and toxicity dependent on the specific sequence and structural states of the proteins? An interesting case study for this question is exon 1 of huntingtin protein, which contains a polyglutamine (polyQ) core flanked by short, unstructured sequences at the N- and C-terminal ends. The aggregation behavior is driven by the polyQ core, with increasing polyQ lengths correlating with earlier disease onset (11,12). However, the terminal sequences modulate the aggregation propensity, with the N-terminus promoting aggregation and the C-terminus promoting higher solubility (13). The behavior of the latter sequence is not surprising because the C-terminal fragment is composed primarily of proline residues. However, the aggregation-promoting property of the N-terminus is more difficult to understand because this segment has a high solubility in isolation (R. Pappu, personal communication).
Huntingtin (Htt) shows qualitatively similar aggregation behavior to other amyloid proteins with distinct fibril and oligomer states. The low sequence complexity of huntingtin suggests that these states are not due to sequence-specific interactions but arise more generally from the polymer nature of the molecule. Here, we show that the stability of these states can be modeled by treating huntingtin as a triblock copolymer.
For a simple polymer, we expect two limiting behaviors: either the swollen random walk of a polymer in good solvent or the collapsed state typical of a polymer in poor solvent. Recent experiments and simulations have shown that monomeric huntingtin adopts conformations consistent with the poor solvent case (14,15). Accordingly, we allow the collapsed globules in our model to coalesce further to form copolymer micelles, which we associate with the oligomer state. To account for the fibril state, we add a second form of intermolecular interactions in which the backbones and side chains pack more efficiently at the cost of conformational entropy. Surprisingly, experiments have shown that huntingtin fibrils are highly ordered despite the discrete translational symmetry of the polyQ core (16). We show that this alignment specificity arises naturally from the energetics of the binding ensemble, and it is further assisted by the N- and C-terminal regions.
Methods
Monomer and oligomer are modeled as collapsed globule
To construct our free energy for Htt, we take the reference state to be a well-solvated Flory coil. In this state, contacts between amino acids are negligible, and the random-walk entropy is maximized. This state is purely hypothetical because experiments and simulation have shown that Htt adopts configurations consistent with a polymer in poor solvent (15,17, 18, 19). This means that favorable interactions between amino acids are sufficient to pay the entropy cost to collapse the random coil into a globule. These same interactions can also drive the condensation of Htt molecules into oligomers. Because monomer collapse and oligomer formation are driven by the same desolvation reaction, we describe them both by the free energy
| (1) |
where the terms represent the amino acid contact energy, the change in conformational entropy, and the contribution from the C38 tail. N is the size of oligomer in monomer units and Q/N are the number of amino acids in the polyQ and N-terminal (if present) regions. The contact energy has a bulk and surface term
| (2) |
Simulations have shown that the collapsed globule contains both the polyQ region and the N-terminal region (14,17). Therefore, the bulk term is proportional to the total length of these regions L = , where = 17 for molecules containing the N-terminal segment and = 0 for molecules without the tail. For the burial energy, we take a weighted average for the desolvation of glutamine and N17 amino acids.
| (3) |
The bulk term, LNεG, overcounts the driving force for collapse because residues at the surface of the globule are incompletely desolvated. This is corrected by the surface term AγεG(NL)2/3. Simple geometrical considerations give a value Aγ = −2.4 for the constant (see Appendix).
The entropic contribution to the free energy takes the form
| (4) |
The two terms account for polymer stretching in the oligomer state and the compression of the coils in the collapsed monomer state, respectively. In practice, only one of these terms is significant at any time, which allows for the additive approximation in Eq. 4.
The stretching term provides a repulsive energy that arrests oligomer growth. This term arises in polymer micelles because the molecules must extend from the surface to fill the interior of the aggregate when its radius grows longer than the radius of gyration of a random-walk polymer (20). This stretching energy will arrest oligomer growth as long as one end of the molecule remains solvated at the surface of the oligomer. In the full-length exon 1, this role will be filled by the C38 region. For constructs lacking C38, surface pinning is likely due to the two lysine residues placed at the C-terminus (13). It is also possible that the N17 and polyQ regions demix in the oligomer core. Without surface pinning of the C-terminus, this demixing would result in an inverted structure, with the more soluble N17 at the surface and polyQ in the interior.
To compute the stretching term, we note that each monomer in the oligomer has a stretching energy of kBTR2/, where R is the oligomer radius (calculated in the Appendix) and Rg = is the radius of gyration for a monomer. Here, we have taken the Flory exponent to be ν = 1/2 because the excluded-volume swelling of the polymer will be screened by excluded-volume interactions with neighboring molecules. The total stretching energy for the whole oligomer is then
| (5) |
which simplifies to the first term in Eq. 4.
In the monomer state, the molecules face the opposite problem, in which the entropic loss is due to compression of the random coil. For a polymer under confinement, the free energy change can be estimated by the blob model (21). In this model, the polymer can be subdivided into statistically independent segments that are each small enough that the effects of confinement are not felt. Confinement effects arise at the interface between these statistical blobs, where it exerts a perturbation on the order of kBT. Therefore the free energy of confinement is ∼L/, where g is the number of statistically independent segments per blob and is the Kuhn length. The number of segments per blob can be found by requiring that the segment density per blob g/(agν)3 is equal to the density of the entire system, L/V, where V is the confinement volume. Therefore, g3ν − 1 = V/a3L. In this case, we are interested in a collapsed globule in which the confinement volume is equal to the total volume of the chain V = La3. This gives g = 1. Therefore, the compression free energy is just kBT times the number of Kuhn lengths. To estimate this, we note that the persistence length of polyQ is ∼1.3 nm (22) and that the Kuhn length is twice the persistence length (23). Therefore, the statistical correlation along a polymer extends over 2.6 nm/0.3 nm 8.7 amino acids, where we have taken 0.3 nm as the contour length per amino acid.
The final contribution to the globule free energy comes from the C-terminal tail. This region has the sequence P11-QLPQPPPQAQPLLPQPQ-P10. Given the limited flexibility of proline and the propensity to form polyproline helices, this tail will be more rigid, although largely disordered (24). We assume that the tails interact primarily by excluded-volume interactions. Because of the nonuniform flexibility of the tails, it is difficult to apply the blob model to compute the confinement effect due to neighboring tails. Still, inspection of the sequence suggests that 1–3 blobs per tail is reasonable. In fact, our results are insensitive to values in this range. Here, we report results for fC38 = 2 kBT.
The fibril state is a cross-β core with disordered tails
Htt fibrils consist of a cross-β core that spans the polyQ region but does not include N17 or C38 (16,24). Evidence suggests that the β-sheet core is most likely antiparallel, as shown in Fig. 1 (25), although parallel cores may also occur (26). The specifics of parallel or antiparallel do not enter our model because the parameters give the average interaction experienced by each sequence block.
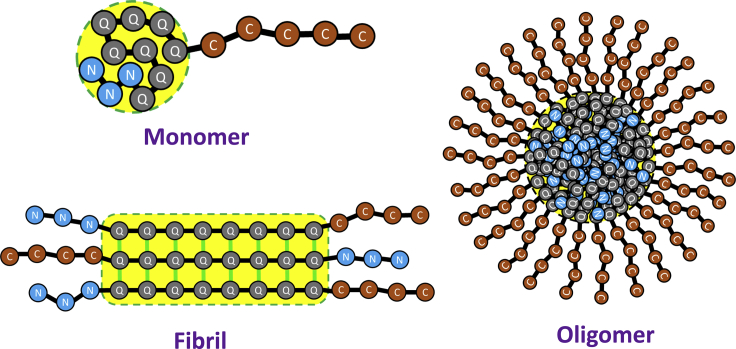
Figure 1.
Cartoon representation of the three states of Htt. In the monomer state, the peptide collapses into a globule containing both polyQ and N-terminal regions. The oligomer state is a micelle-like assembly of a few thousand monomers with a spherical core containing the polyQ and N-terminal regions. The fibril state is a cross-β amyloid core of polyQ flanked by disordered tails on both sides. To see this figure in color, go online.
We write the fibril free energy as a β-sheet term that scales linearly with the length of the polyQ core, modified by perturbations from the terminal segments.
| (6) |
Here, εβ is the free energy gain to move one glutamine residue from the solvated random coil state into the cross-β core. The second term accounts for the interaction between C-terminal segments, which we expect to be the same as in the globule state. Finally, fN17 accounts for the interaction of N17 tails. These segments are soluble, but not purely repulsive like the proline-rich C38 (16). To account for the possibility of sequence-specific interactions between N17 tails, we obtain this parameter by fitting.
Critical concentrations are computed from the change in free energy
Our next task is to compute the concentration dependence of fibril and oligomer formation. At low concentration, the attractive interactions cannot overcome the translational entropy cost of condensing the molecules. At higher concentrations, equilibrium is established when the monomer pool is depleted to the point where the translational entropy cost balances the attractive free energy. In the micellization literature, this point is called the critical micelle concentration. This terminology has been adopted to define a critical oligomer concentration and critical fibril concentration in amyloid systems (27,28). These critical concentrations should not be confused with the critical point of a phase transition and are more similar to the saturation concentration at an arbitrary point along the coexistence (binodal) line. However, the finite size of oligomers results in a more gradual transition than the sharp solubility limit of a macroscopic phase transition (28). This introduces some ambiguity in the definition of the critical concentration, although in practice, the transition is sufficiently sharp that this is not experimentally significant.
Following (28), we start by writing down the equilibrium constant for N-fold oligomerization.
| (7) |
where
| (8) |
where C0 is a reference concentration. We identify the critical concentration for oligomerization as the point at which there is an equal amount of protein in the monomer and oligomer states C1 = NCN, which can be combined with Eq. 7 to yield a relationship between the critical concentration and the free energy of the oligomer state
| (9) |
Equation 9 requires the size of the oligomer, N, which we obtain by minimizing Eq. 8
| (10) |
The formation of fibrils can also be associated with a critical concentration. However, unlike the soft transition seen in oligomers, the critical concentration for fibril formation is very sharp (28), analogous to the solubility limit in a phase transition. The critical concentration for fibril formation is (28)
| (11) |
where
| (12) |
is the free energy for transferring a molecule from the monomer state to the fibril state.
Fibril alignment defects incur a free energy penalty
Atomic resolution models of amyloid fibrils show striking order in the alignment of molecules (29). However, it is not known whether this order is generally present or whether it is an artifact of structural methods that are limited to systems that possess such order. PolyQ aggregates represent an extreme test of the alignment tendency of amyloids because of the discrete translational symmetry they possess.
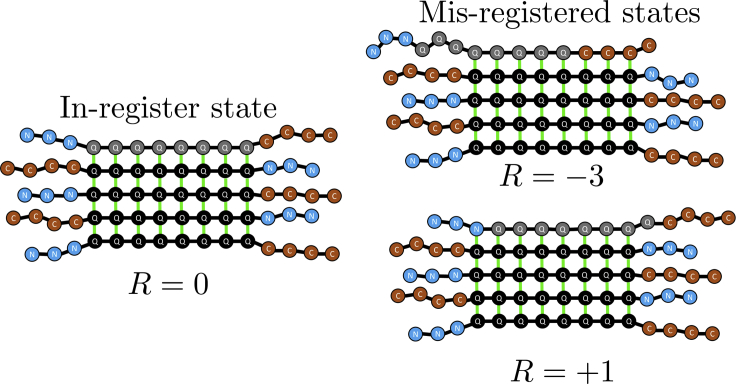
Here, we introduce an equilibrium model to compute the frequency of alignment defects in polyQ fibrils. Following previous work (30), we quantify the alignment using the registry variable R, which can take the values where is the number of glutamine residues in each molecule. The value R = 0 denotes the in-register state, positive values of R indicate that the incoming molecule is shifted toward its C-terminus, and negative values of R indicate a shift toward the N-terminus (see Fig. 2).
Figure 2.
Cartoon representation of the in-register state and misregistered states. The registry variable, R, defines the alignment of an incoming molecule with the existing fibril. R = 0 indicates perfect alignment of the polyQ region, whereas negative and positive values indicate N-terminal and C-terminal shifts, respectively. To see this figure in color, go online.
For misaligned states with R < 0, there will be H-bonds between glutamines of the existing fibril and amino acids in C38 of the incoming molecule. Conversely, if R > 0, there will be H-bonds between glutamines of the existing fibril and N17 of the incoming molecule.
We compute the probability for a given alignment by
| (13) |
where the denominator is the partition function for the alignment states and εM is equal to εNQ or εCQ to account for interaction between the polyQ core and the N- or C-terminal tail of misaligned molecules. The misalignment energy is not symmetric because we assume that residues lying outside the β-core are too disordered to have a significant interaction energy.
Results
PolyQ desolvation competes with polymer entropy
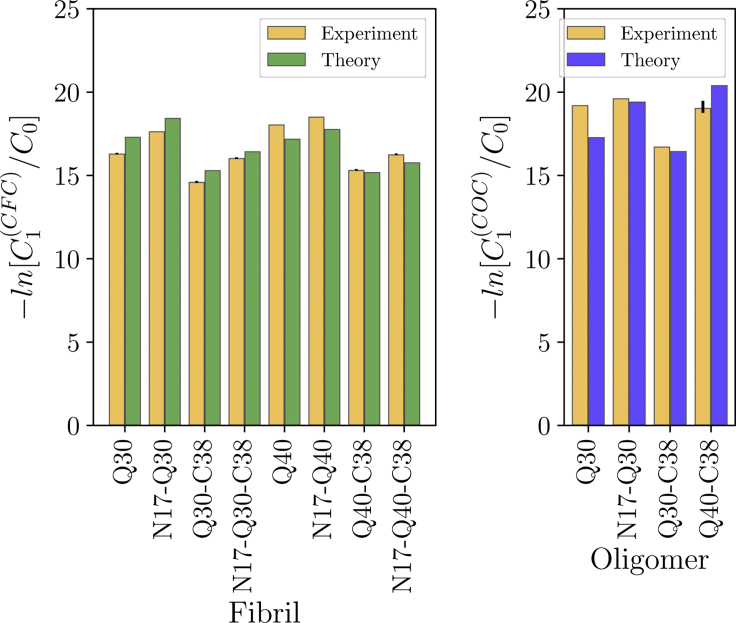
To obtain values for the energies appearing in the model, we fitted the calculated critical concentration to the experiments of Crick et al. (13) and Posey et al. (31). There are four free parameters: εQ, εN, εβ, and fN17. To fix the reference concentration, we adopt a lattice approximation in which the lattice constant is set by the size of a water molecule C0 = 55.5 M. Other choices for the reference concentration would result in a constant shift to the free energy that would not affect the results in a meaningful way. The measured and fitted free energy are compared in Fig. 3. The agreement is good with discrepancies ranging from 0.1 to 1.9 kBT.
Figure 3.
Comparison between the theoretical model and experimentally measured critical concentrations. The model captures the effects of N17 and increasing polyQ length in promoting aggregation and the effect of C38 in inhibiting it. To see this figure in color, go online.
The parameter values, shown in Table 1, help to clarify the driving forces for aggregation. The free energy of β-sheet formation is almost 1 kBT per amino acid, which is stronger than the ∼0.5 kBT found for Aβ and other amyloid-forming molecules (28,32). This is likely due to fact that polyQ is a homopolymer in which all amino acids contribute equally, whereas other molecules have sequence heterogeneity as well as portions of the molecule in hairpins and disordered fragments that do not contribute to the stability. Interestingly, we find that the free energy of glutamine burial in the oligomer state, εQ, is even stronger than that of β-sheet formation. This reflects the fact that Htt is one of the few molecules in which the oligomer state has a lower critical concentration than the fibril state (13,15). However, it should also be noted that the entropic penalty for elongating the peptide into a β-strand is included in εβ, whereas the conformational entropy contributions to globule formation are separately calculated in Eq. 4.
Table 1.
Parameters Obtained by Model Fitting
| Parameter | Value (kBT) |
|---|---|
| εQ | −2.05 |
| εN | −1.04 |
| εβ | −0.91 |
| fN17 | −11.70 |
The model allows us to understand several features of the aggregation behavior. From our results, the oligomer sizes are in the range of 3300–4900 monomers. Using a density of 1.3 g/cm3, we estimate an oligomer diameter range of 30–50 nm, consistent with the 10–50 nm spheres measured by electron microscopy (13,31).
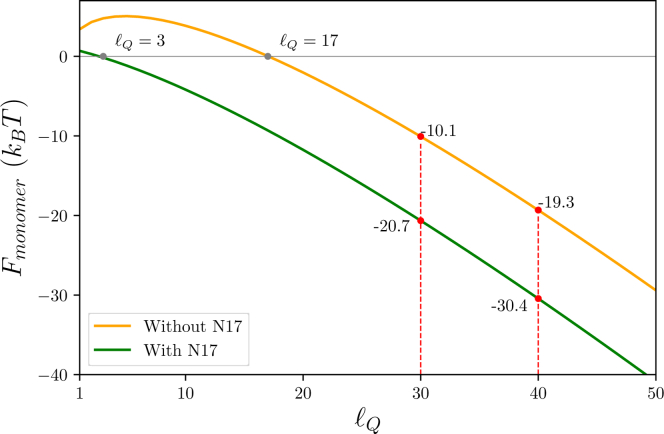
Fig. 4 shows the free energy of monomer collapse as a function of the polyQ length. In the absence of the N17 tail our model predicts that the free energy is zero for = 17, meaning that peptides with fewer glutamines will be found primarily in the expanded state, whereas longer polyQ regions will favor the collapsed state. In the presence of N17, the crossover point is at = 3. Although this is fewer glutamine residues than molecules without N17, the total peptide length is longer (20 vs. 17 amino acids), reflecting the fact that it takes more N17 residues to achieve the same desolvation energy of the glutamines.
Figure 4.
Predicted free energy of monomer collapse for peptides with and without the N-terminal tail as a function of . The results show that peptides with fewer glutamines will prefer the expanded state, whereas longer glutamine peptides will favor the collapsed states. The presence of the N17 tail contributes to the collapse free energy, but less strongly than glutamine residues. To see this figure in color, go online.
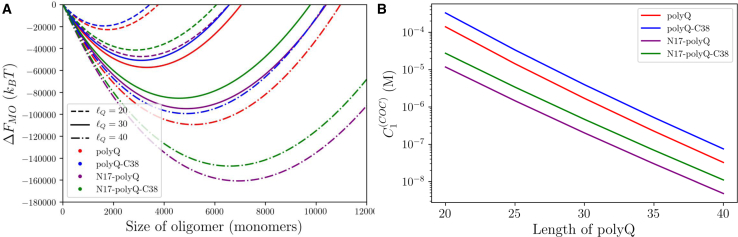
Fig. 5 shows the oligomer free energy as a function of polyQ length in the presence and absence of the flanking regions. Increasing the peptide length, either by adding glutamines or N17 residues, results in larger oligomers because the longer molecules can more easily stretch to fill the interior of the oligomer. However, the C38 region adds a repulsive energy that favors smaller oligomers.
Figure 5.
(A) Predicted free energy of oligomer formation for = 20, 30, and 40 in the presence and absence of N- and C-terminal tails. Increasing the length of the polyQ region or adding the N17 tail results in larger oligomers because the extra length more easily stretches to fill the oligomer core. However, adding the C38 tail adds a repulsive energy that favors smaller oligomers. (B) Changing the polyQ length has an exponential effect on the critical concentration for oligomer formation. The critical concentration drops by more than a factor of 103 upon changing the from 20 to 40. To see this figure in color, go online.
Although the polyQ length has a roughly linear effect on the oligomer size, it has a much more dramatic effect on the critical concentration. Fig. 5 B shows that the critical concentration scales exponentially with the polyQ length. When both flanking sequences are present, the critical concentration varies from 11 nM for = 40 to 27,000 nM for = 20. Although this calculation does not account for important cellular factors like crowding, it is easy to speculate that this 103 factor could make a difference in the presence of toxic oligomers when the polyQ length increases above the threshold associated with disease.
Flanking sequences prevent large alignment errors
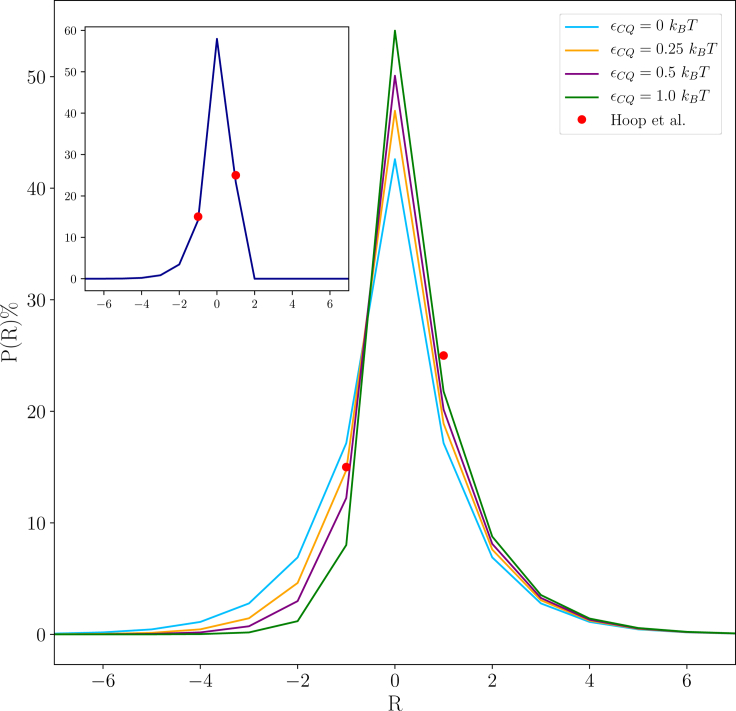
The parameter εQ, obtained by fitting the fibril solubilities, can also be used to compute the frequency of registry errors in polyQ fibrils. NMR experiments have shown that single amino acids shifts occur at frequency of 25% (R = +1) and 15% (R = −1), with larger shifts occurring below the detection limit (16). In comparison, a simple version of our model that does not account for the N- and C-terminal tails (Eq. 13 with εNQ = εCQ = 0) yields registry errors of 17% for R = ±1 and 7% for R = ±2 (blue line, Fig. 6). From this, we make two observations. First, even the weak penalty for registry shifts is sufficient to prevent registry errors for most molecules. Second, the presence of the N- and C-terminal tails have the dual effect of suppressing shifts of |R| > 1 and breaking the symmetry between the shift directions. An inspection of the sequence readily suggests mechanisms by which this may occur. The C-terminus of the polyQ region is connected to a stretch of 28 prolines. Prolines will be poorly tolerated in the cross-β core because of their lack of a backbone H-bond donor and their inability to adopt the extended β-sheet conformation. To account for this, we add a free energy penalty for negative registry shifts. Fig. 6 shows that εCQ-values between 0.25 and 1.0 kBT have the expected effect of shifting the alignment distribution closer to the experimental observation. However, they also raise the probability of R = +2 shifts near the 10% level that are experimentally observable. This discrepancy is easily resolved by an inspection of the N-terminal tail, which has a sequence MATLEKLMKAFESLKSF, with the serine and phenylalanine incorporated in the cross-β core (16). This means that positive registry shifts would move the lysine into the cross-β core. Although the long side chain could presumably allow for partial solvation of the charge for an R = +1 shift, larger registry shifts would require a total desolvation of the charge, thereby incurring a large free energy penalty. If we exclude registry shifts larger than R = +1, the predicted distribution of registries is in nearly perfect agreement with experiment (Fig. 6, inset).
Figure 6.
Probabilities of misaligned molecules within an Htt fibril as a function of the alignment registry R and εCQ (for εβ = −0.91 kBT). The inset shows alignment probabilities for εCQ = 0.5 kBT, with an additional constraint preventing states with R > 1 because this would lead to the burial of the lysine charge. To see this figure in color, go online.
Discussion
The micelle-like oligomers described by our theory contrast with the highly ordered β-barrel oligomers that have been reported for other amyloid-forming molecules (33,34). It is difficult to imagine a low-complexity sequence like huntingtin adopting such an ordered state. But, it is worth asking whether the micellar structure of huntingtin might also be formed by other molecules. Supporting this view is the fact that the A11 antibody, which specifically recognizes amyloid oligomers, was developed by forcing Aβ to form a micelle-like structure (35). In addition, hydrophobicity correlates strongly with aggregation propensity (36,37), suggesting that most amyloid-forming molecules will contain a stretch of hydrophobic amino acids sufficiently long to form a polymer micelle. This implies that the amyloid phase diagram often contains both ordered and disordered oligomers in addition to the fibril state. The ordered oligomer could be added to our model with a free energy of the form of Eq. 9. Notably, because of the smaller size of ordered oligomers (on the order of 4–20 molecules, compared with 103 for disordered oligomers), the ordered species will show a softer, power-law-concentration-dependent onset compared to the steep, phase-transition-like onset seen with large oligomers and fibrils (28).
Our model also provides insights into the mechanism of fibril formation. Specifically, there is the question of whether the highly ordered fibrils reported from NMR or x-ray studies are typical or an artifact of structural methods that work best with ordered systems. Our results show that even for a homopolymer, the binding energy is sufficient to align almost half of the molecules. Also, consistent with previous work, only minor perturbations from a uniform sequence are necessary to generate highly ordered fibrils (30). In the equilibrium analysis employed in this work, the fraction of alignment defects is independent of peptide length. However, the kinetic search over alignments scales exponentially with the peptide length, meaning longer peptides will be more easily trapped in nonequilibrium states under conditions of rapid aggregation (28,30).
In conclusion, we have shown that the block copolymer model is able to explain many features of oligomer and fibril formation in huntingtin. These findings may also have broader implications for other amyloid-forming systems.
Acknowledgments
This work was supported by National Institutes of Health grant R01GM107487.
Editor: Rohit Pappu.
Appendix: Calculation of Surface Constant
The bulk energy term of Eq. 1 accounts for the desolvation of every amino acid in the globule. However, amino acids on the surface of the globule will only be partially desolvated. To estimate the surface correction to the desolvation energy, we assume that amino acids on the surface only get half the desolvation energy. This gives
where Nsurface is the number of amino acids on the surface of the globule.
To calculate the Nsurface, we relate the radius of the globule to the number of molecules
where a3 is the volume of an amino acid. The number of residues on the surface is
| (14) |
The surface term is therefore
| (15) |
| (16) |
Author Contributions
T.T.M.P. and J.D.S. designed the research, analyzed the data, and wrote the article. T.T.M.P. conducted the research.
References
- 1.Ross C.A., Poirier M.A. Protein aggregation and neurodegenerative disease. Nat. Med. 2004;10(Suppl):S10–S17. doi: 10.1038/nm1066. [DOI] [PubMed] [Google Scholar]
- 2.Aguzzi A., O’Connor T. Protein aggregation diseases: pathogenicity and therapeutic perspectives. Nat. Rev. Drug Discov. 2010;9:237–248. doi: 10.1038/nrd3050. [DOI] [PubMed] [Google Scholar]
- 3.Kim Y.E., Hosp F., Hartl F.U. Soluble oligomers of polyQ-expanded huntingtin target a multiplicity of key cellular factors. Mol. Cell. 2016;63:951–964. doi: 10.1016/j.molcel.2016.07.022. [DOI] [PubMed] [Google Scholar]
- 4.Zhang L., Schmit J.D. Theory of amyloid fibril nucleation from folded proteins. Isr. J. Chem. 2017;57:738–749. doi: 10.1002/ijch.201600079. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Zhang L., Schmit J.D. Pseudo-one-dimensional nucleation in dilute polymer solutions. Phys. Rev. E. 2016;93:060401. doi: 10.1103/PhysRevE.93.060401. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Miti T., Mulaj M., Muschol M. Stable, metastable, and kinetically trapped amyloid aggregate phases. Biomacromolecules. 2015;16:326–335. doi: 10.1021/bm501521r. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Knowles T.P., White D.A., Weitz D.A. Observation of spatial propagation of amyloid assembly from single nuclei. Proc. Natl. Acad. Sci. USA. 2011;108:14746–14751. doi: 10.1073/pnas.1105555108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Auer S., Ricchiuto P., Kashchiev D. Two-step nucleation of amyloid fibrils: omnipresent or not? J. Mol. Biol. 2012;422:723–730. doi: 10.1016/j.jmb.2012.06.022. [DOI] [PubMed] [Google Scholar]
- 9.Auer S., Dobson C.M., Vendruscolo M. Characterization of the nucleation barriers for protein aggregation and amyloid formation. HFSP J. 2007;1:137–146. doi: 10.2976/1.2760023. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Auer S., Dobson C.M., Maritan A. Self-templated nucleation in peptide and protein aggregation. Phys. Rev. Lett. 2008;101:258101. doi: 10.1103/PhysRevLett.101.258101. [DOI] [PubMed] [Google Scholar]
- 11.Langbehn D.R., Hayden M.R., Paulsen J.S., and the PREDICT-HD Investigators of the Huntington Study Group CAG-repeat length and the age of onset in Huntington disease (HD): a review and validation study of statistical approaches. Am. J. Med. Genet. B. Neuropsychiatr. Genet. 2010;153B:397–408. doi: 10.1002/ajmg.b.30992. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Walker F.O. Huntington’s disease. Lancet. 2007;369:218–228. doi: 10.1016/S0140-6736(07)60111-1. [DOI] [PubMed] [Google Scholar]
- 13.Crick S.L., Ruff K.M., Pappu R.V. Unmasking the roles of N- and C-terminal flanking sequences from exon 1 of huntingtin as modulators of polyglutamine aggregation. Proc. Natl. Acad. Sci. USA. 2013;110:20075–20080. doi: 10.1073/pnas.1320626110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Warner J.B., IV, Ruff K.M., Lashuel H.A. Monomeric huntingtin exon 1 has similar overall structural features for wild-type and pathological polyglutamine lengths. J. Am. Chem. Soc. 2017;139:14456–14469. doi: 10.1021/jacs.7b06659. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Crick S.L., Jayaraman M., Pappu R.V. Fluorescence correlation spectroscopy shows that monomeric polyglutamine molecules form collapsed structures in aqueous solutions. Proc. Natl. Acad. Sci. USA. 2006;103:16764–16769. doi: 10.1073/pnas.0608175103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Hoop C.L., Lin H.K., van der Wel P.C. Polyglutamine amyloid core boundaries and flanking domain dynamics in huntingtin fragment fibrils determined by solid-state nuclear magnetic resonance. Biochemistry. 2014;53:6653–6666. doi: 10.1021/bi501010q. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Newcombe E.A., Ruff K.M., Hatters D.M. Tadpole-like conformations of huntingtin exon 1 are characterized by conformational heterogeneity that persists regardless of polyglutamine length. J. Mol. Biol. 2018;430:1442–1458. doi: 10.1016/j.jmb.2018.03.031. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Vitalis A., Wang X., Pappu R.V. Quantitative characterization of intrinsic disorder in polyglutamine: insights from analysis based on polymer theories. Biophys. J. 2007;93:1923–1937. doi: 10.1529/biophysj.107.110080. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Ruff K.M., Harmon T.S., Pappu R.V. CAMELOT: A machine learning approach for coarse-grained simulations of aggregation of block-copolymeric protein sequences. J. Chem. Phys. 2015;143:243123. doi: 10.1063/1.4935066. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Leibler L., Orland H., Wheeler J.C. Theory of critical micelle concentration for solutions of block copolymers. J. Chem. Phys. 1983;79:3550–3557. [Google Scholar]
- 21.Hoseinpoor S.M., Nikoofard N., Zahedifar M. Accuracy limits of the blob model for a flexible polymer confined inside a cylindrical nano-channel. J. Stat. Phys. 2016;163:593–603. [Google Scholar]
- 22.Singh V.R., Lapidus L.J. The intrinsic stiffness of polyglutamine peptides. J. Phys. Chem. B. 2008;112:13172–13176. doi: 10.1021/jp805636p. [DOI] [PubMed] [Google Scholar]
- 23.Rubinstein M., Colby R.H. Volume 23. Oxford University Press; New York: 2003. Polymer Physics. [Google Scholar]
- 24.Chen M., Wolynes P.G. Aggregation landscapes of Huntingtin exon 1 protein fragments and the critical repeat length for the onset of Huntington’s disease. Proc. Natl. Acad. Sci. USA. 2017;114:4406–4411. doi: 10.1073/pnas.1702237114. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Punihaole D., Workman R.J., Asher S.A. Polyglutamine fibrils: new insights into antiparallel β-sheet conformational preference and side chain structure. J. Phys. Chem. B. 2016;120:3012–3026. doi: 10.1021/acs.jpcb.5b11380. [DOI] [PubMed] [Google Scholar]
- 26.Hoffner G., Djian P. Monomeric, oligomeric and polymeric proteins in huntington disease and other diseases of polyglutamine expansion. Brain Sci. 2014;4:91–122. doi: 10.3390/brainsci4010091. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Lee C.F. Self-assembly of protein amyloids: a competition between amorphous and ordered aggregation. Phys. Rev. E Stat. Nonlin. Soft Matter Phys. 2009;80:031922. doi: 10.1103/PhysRevE.80.031922. [DOI] [PubMed] [Google Scholar]
- 28.Schmit J.D., Ghosh K., Dill K. What drives amyloid molecules to assemble into oligomers and fibrils? Biophys. J. 2011;100:450–458. doi: 10.1016/j.bpj.2010.11.041. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Tycko R. Amyloid polymorphism: structural basis and neurobiological relevance. Neuron. 2015;86:632–645. doi: 10.1016/j.neuron.2015.03.017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Huang C., Ghanati E., Schmit J.D. Theory of sequence effects in amyloid aggregation. J. Phys. Chem. B. 2018;122:5567–5578. doi: 10.1021/acs.jpcb.7b11830. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Posey A.E., Ruff K.M., Pappu R.V. Profilin reduces aggregation and phase separation of huntingtin N-terminal fragments by preferentially binding to soluble monomers and oligomers. J. Biol. Chem. 2018;293:3734–3746. doi: 10.1074/jbc.RA117.000357. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Baldwin A.J., Knowles T.P., Dobson C.M. Metastability of native proteins and the phenomenon of amyloid formation. J. Am. Chem. Soc. 2011;133:14160–14163. doi: 10.1021/ja2017703. [DOI] [PubMed] [Google Scholar]
- 33.Laganowsky A., Liu C., Eisenberg D. Atomic view of a toxic amyloid small oligomer. Science. 2012;335:1228–1231. doi: 10.1126/science.1213151. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Serra-Batiste M., Ninot-Pedrosa M., Carulla N. Aβ42 assembles into specific β-barrel pore-forming oligomers in membrane-mimicking environments. Proc. Natl. Acad. Sci. USA. 2016;113:10866–10871. doi: 10.1073/pnas.1605104113. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Kayed R., Head E., Glabe C.G. Common structure of soluble amyloid oligomers implies common mechanism of pathogenesis. Science. 2003;300:486–489. doi: 10.1126/science.1079469. [DOI] [PubMed] [Google Scholar]
- 36.Chiti F., Stefani M., Dobson C.M. Rationalization of the effects of mutations on peptide and protein aggregation rates. Nature. 2003;424:805–808. doi: 10.1038/nature01891. [DOI] [PubMed] [Google Scholar]
- 37.Yagi S., Akanuma S., Yamagishi A. Addition of negatively charged residues can reverse the decrease in the solubility of an acidic protein caused by an artificially introduced non-polar surface patch. Biochim. Biophys. Acta. 2014;1844:553–560. doi: 10.1016/j.bbapap.2013.12.011. [DOI] [PubMed] [Google Scholar]