Abstract
Intrinsically disordered proteins are proteins whose native functional states represent ensembles of highly diverse conformations. Such ensembles are a challenge for quantitative structure comparisons because their conformational diversity precludes optimal superimposition of the atomic coordinates necessary for deriving common similarity measures such as the root mean-square deviation of these coordinates. Here, we introduce superimposition-free metrics that are based on computing matrices of the Cα-Cα distance distributions within ensembles and comparing these matrices between ensembles. Differences between two matrices yield information on the similarity between specific regions of the polypeptide, whereas the global structural similarity is captured by the root mean-square difference between the medians of the Cα-Cα distance distributions of two ensembles. Together, our metrics enable rigorous investigations of structure-function relationships in conformational ensembles of intrinsically disordered proteins derived using experimental restraints or by molecular simulations and for proteins containing both structured and disordered regions.
Significance
Important biological insight is obtained from comparing the high-resolution structures of proteins. Such comparisons commonly involve superimposing two protein structures and computing the residual root mean-square deviation of the atomic positions. This approach cannot be applied to intrinsically disordered proteins (IDPs) because IDPs do not adopt well-defined three-dimensional structures; rather, their native functional state is defined by ensembles of heterogeneous conformations that cannot be meaningfully superimposed. We report, to our knowledge, new measures that quantify the local and global similarity between different conformational ensembles by evaluating differences between the distributions of residue-residue distances and their statistical significance. Applying these measures to IDP ensembles and to a protein containing both structured and intrinsically disordered domains provides deeper insights into how structural features relate to function.
Introduction
Comparing the high-resolution structures of proteins is critical for understanding their function and evolutionary history (1,2). Structural comparisons rely on quantitative similarity measures. The most common measure is the root mean-square deviation (RMSD) of the atomic positions between two structures, which is minimized upon rigid-body superimposition of these structures (3,4). But, the RMSD is often not very informative because it averages out differences across regions of the structures with varying similarity levels. Therefore, superimposition-independent measures relying on inter-residue distances have been proposed that are, moreover, invariant under reflection, unlike the superimposition-based RMSD (5). Distance-based metrics have been used to compare well-defined protein structures (4, 5, 6), simulated or experimentally restrained conformational ensembles (7, 8, 9, 10), or unfolded states of proteins (11, 12, 13).
Similar to the unfolded state, intrinsically disordered proteins (IDPs) and intrinsically disordered regions (IDRs) must be described as ensembles of heterogeneous, rapidly interconverting conformations. Characterizing and comparing such ensembles is therefore particularly challenging. By employing restraints primarily obtained by nuclear magnetic resonance (NMR) and small-angle x-ray scattering (SAXS), conformational ensembles have been characterized for many functionally important IDPs, such as α-synuclein (14), Sic1 (15), p27Kip1 (16), and tau (17), and these are made accessible in the Protein Ensemble Database (PED) (18). Owing to their high conformational variability, however, adequately characterizing an IDP or IDR ensemble from a limited amount of experimental data is an inherently underdetermined problem (19). A given disordered protein may therefore be modeled as multiple, seemingly equivalent ensembles, representing alternative fits to the experimental data (18). Although these alternative ensembles may carry functionally relevant structural information (20,21), their critical analysis and comparative evaluation are particularly challenging and have so far not been attempted for two main reasons. First, their extreme conformational heterogeneity makes it difficult to evaluate the degree of global similarity between two ensembles by any measure, let alone by RMSD-based metrics. Second, the function of disordered proteins is often mediated by short, sequentially contiguous binding motifs (22,23) adopting locally relevant conformations. The latter are interconnected through more structurally variable linkers (24) that determine the relative overall configuration of these important motifs. Therefore, the similarity of the IDP and IDR ensembles must be evaluated at both the local and global levels in a statistically meaningful approach.
To address these issues, we developed superimposition-independent measures for evaluating the local and global similarity between two ensembles. The local similarity between specific regions of the polypeptide is evaluated from the differences between the distance distributions of individual residue pairs and their statistical significance. The global similarity is captured by the RMSD-like quantity representing the root mean-square difference between the medians of the inter-residue distance distributions of the two ensembles (ens_dRMS). We show that our superimposition-free structural similarity measures are effective in describing both global and local differences between conformational ensembles of IDPs and IDRs derived using experimental restraints or by molecular simulations and that they also conveniently quantify the structural similarity of proteins containing both structured and disordered regions.
Materials and Methods
Data sets of protein conformational ensembles
Conformational ensembles of IDPs and IDRs
Data on conformational ensembles of the fully disordered K18 segment of human tau protein (130 residues) and the measles virus (MeV) N-tail protein (132 residues (17)) were downloaded from the PED (18), which currently stores such data for 16 different protein systems or fragments thereof, comprising more than 50 ensembles of 24 fully or partially disordered protein regions. For both tau-K18 and the MeV N-tail, five ensembles comprising 199 conformations were retrieved. These ensembles were generated by combining conformational sampling with an ensemble selection based on NMR data from residual dipolar coupling and chemical shift analyses (17,25). Random pool ensembles for the two systems (comprising 100 ensembles of 200 conformers each) were obtained from the authors (M. Blackledge, personal communication). These random pools were generated as previously described (25).
Conformational ensembles generated using molecular dynamics simulations with different force fields
Five distinct ensembles of the intrinsically disordered 24-residue serine-arginine (SR)-rich peptide (residues 22–45 of SR-rich splicing factor 1) were generated using microsecond-timescale replica exchange molecular dynamics (MD) simulations (26) with GROMACS 4.5.4 (27) using CHARMM (28) (CHARMM22∗ (29) and CHARMM36 (30)) and AMBER (31) (99sb∗-ildn (29) and 03w (32)) force fields, and also with CAMPARI using the ABSINTH implicit solvent model (33). Here, using simulation parameters identical to those previously described (31), with GROMACS 2016.3 and the CHARMM22∗ force field with CHARMM-modified TIP3P water, three independent, high-temperature (600 K), 0.2-μs-long MD simulations were used to generate a model for the random coil ensemble of the same system, denoted as the “High-T” ensemble.
Conformational ensembles of the human prion protein
Three distinct conformational ensembles of truncated human prion protein (huPrP; full length: 231 amino acids (aa)) determined by NMR were downloaded from the Protein Data Bank (PDB) (34). These were two huPrP (90–226) structures, PDB: 2LSB (35) and PDB: 5L6R (36), and one huPrP (90–231), PDB:5YJ5 (37).
Distance-based metrics for comparing conformational ensembles
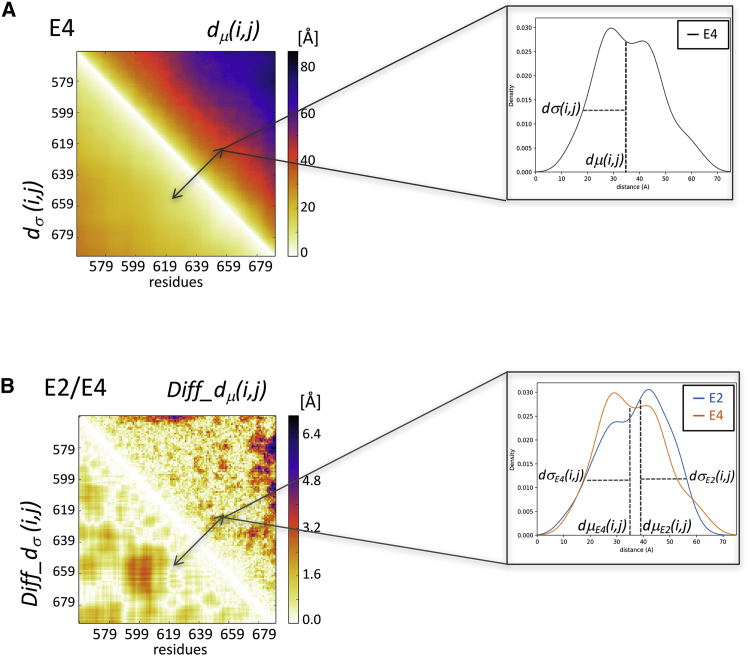
To compare the two conformational ensembles A and B, we use metrics based on the Cα-Cα distances within individual conformers in the ensembles. Because IDRs of proteins display very diverse conformations, Cα-Cα distances of a given pair of residues i,j of the polypeptide follow a distribution of values across conformers. This distribution differs between residue pairs and may therefore provide useful information on the variation of the spatial proximity of specific regions along the polypeptide. To derive this information, two matrices are computed for each of the two ensembles (Figs. 1 and 2 A). One is a matrix whose elements represent the median of the Cα-Cα distance distributions dμ(i,j) for equivalent residue pairs i,j in the conformations belonging to the same ensemble. The other matrix contains the strandard deviations dσ(i,j) of the corresponding distributions.
Figure 1.
Composite heatmaps representing the dμ(i,j) and dσ(i,j) and Diff_dμ(i,j) and Diff_dσ(i,j) matrices. (A) Upper left: shown is a heatmap in which the upper triangle displays the median of the inter-residue distance distributions dμ(i,j) (computed between Cα atoms) for equivalent residue pairs i,j in the conformations of one ensemble (E4 of the MeV N-tail domain). The lower triangle displays the SDs dσ(i,j) of the corresponding distributions. Upper right: shown is an example of the distribution contributing to one element of the dμ(i,j) and dσ(i,j) composite heatmap. (B) Lower left: a heatmap is shown in which the upper triangle depicts the Diff_dμ(i,j) matrix, whose elements are the absolute differences of the medians of the Cα-Cα distance distributions between two ensembles (E2 and E4 of the MeV N-tail domain); the lower triangles displays the absolute differences between the corresponding SDs of Diff_dσ(i,j). Lower right: an example is shown of two distance distributions contributing to one element of the Diff_dμ(i,j) and Diff_dσ(i,j) composite heatmap.
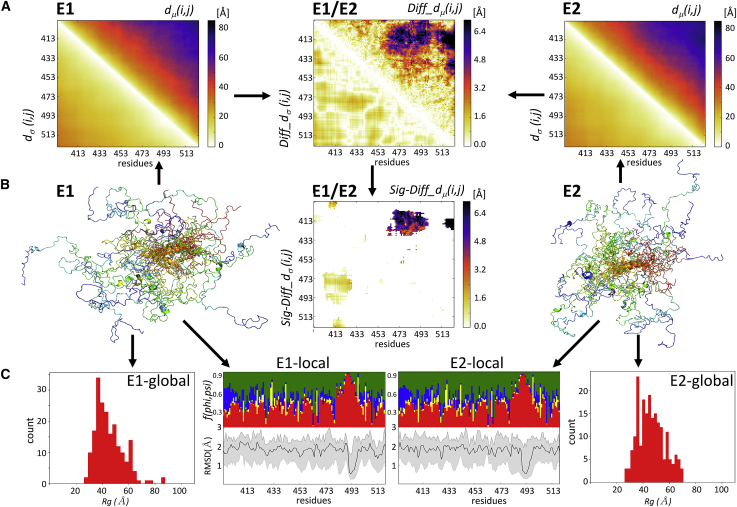
Figure 2.
The ensemble-comparison approach: an overview. (A) Three heatmaps are displayed. Two represent a composite matrix for each of the ensembles E1 and E2 that are being compared. The upper triangle of each map displays the medians of the inter-residue distance distributions dμ(i,j). The lower triangle displays the SDs dσ(i,j) of the corresponding distributions. The third heatmap depicts the composite difference matrix (E1 and E2) between the two ensembles; its upper triangle depicts the Diff_dμ(i,j) matrix whose elements are the absolute differences between the dμ(i,j) distributions in the two ensembles; its lower triangles represents the absolute differences between the corresponding SDs of Diff_dσ(i,j) (see Materials and Methods for details). The inter-residue distances and differences thereof are given in angstroms. (B) A heatmap is given, highlighting only Sig_Diff_dμ(i,j) for the E1-E2 pair, i.e., elements of the Diff_dμ(i,j) matrix representing statistically significant differences between the corresponding d(i,j) distributions (p < 0.05) (upper triangle) and the corresponding Diff_dσ(i,j)-values (lower triangle). The highlighted differences concern d(i,j) distance distributions between a segment spanning residues 473–493 and the N-terminal region (residues 405–420) of the polypeptide. Flanking this map are cartoon models depicting the backbones of individual conformations of the E1 (left) and E2 (right) ensembles. The conformations are color coded from blue (N-terminus) to red (C-terminus) and are superimposed onto the equivalent helical segment (orange ribbon) in both ensembles. (C) Shown are the graphs of the local flexibility properties and conformational preferences of the E1-E2 ensembles (E1 local and E2 local). Shown are the lower graph plots of the medians and 95 percentile confidence interval of the local backbone RMSD distributions for conformations of the E1 and E2 ensembles. The upper graph shows the fraction of the conformations in each ensemble, adopting backbone (ϕ,ψ)-values mapped onto the corresponding four regions of the Ramachandran map (Fig. S10; red: α-helix; yellow: left-handed helix; blue: β-strand; and green: polyproline I and II) (17). The RMSD-values are computed as described in Materials and Methods. The local plots are flanked by bar graphs showing the Rg distributions of conformations in each ensemble (E1 global and E2 global) that indicate that the E2 ensemble is somewhat more compact than E1.
For each pair of conformational ensembles A and B, we then compute a difference matrix (Fig. 1, bottom, and Fig. 2 A, center) in which the i,j elements above the diagonal represent the absolute values of the difference between the median distances between residues i,j:
| (1) |
whereas the i,j elements below the diagonal contain the absolute differences between the corresponding SDs:
| (2) |
Because the difference matrix evaluates differences of i,j distance distributions, it is important to assess the statistical significance of these differences (Fig. 2 B, center). This is done using the nonparametric Mann-Whitney-Wilcoxon test so that the resulting difference matrix displays Diff_dμ(i,j)- and Diff_dσ(i,j)-values only for statistically different d(i,j) distributions (p < 0.05).
The difference matrices of Eq. 1 deal with differences between median values of distances, which themselves may span a wide range of sizes (from 3 to 20 Å). The same Diff_dμ(i,j)-value of, say, 5 Å amounts to a more drastic distance variation for a median distance of 10 Å than for that of 50 Å. To account for this bias, we also compute normalized difference matrices:
| (3) |
To provide a single global measure of the differences between the two conformational ensembles A and B, we computed the ens_dRMS, defined as the following:
| (4) |
where dμA(i,j) and dμB(i,j) are the medians of the distance distributions of i,j residue pairs in ensembles A and B, respectively, and n equals the number of i,j pairs. The ens_dRMS is computed over all i,j pairs of the conformations in the two ensembles to enable comparison between different ensembles of the same polypeptide.
In addition to these distance-based metrics, we compute the radius of gyration, Rg, of the conformations in the ensemble, using only Cα atom coordinates. We use it as a global measure of the ensemble dimensions (Fig. 2 C).
Using the median of the Cα-Cα distance distributions instead of their averages as the basis for our ensemble-comparison metrics has the advantage of representing a more robust measure. A significant fraction of these distances is not normally distributed; their average value may therefore be more readily affected by a few outlier values than the distribution median. Clearly, however, difference matrices computed using the two measures are closely related, and our approach could readily accommodate either measure. Indeed, difference matrices were obtained for pairs of experimentally derived ensembles using the median and the root mean-square average d(i,j)-value (or the average d(i,j)-value) (see Supporting Materials and Methods, Section S1.1), respectively, to display virtually identical patterns. Nevertheless, the Diff_dμ(i,j) matrix exhibits more prominent features than the difference matrix based on the root mean-square average d(i,j)-value in line with the more robust nature of the median, as illustrated in Fig. S1, A and B. Global measures based on d(i,j) averages computed for the 10 pairs of experimentally characterized human tau-K18 IDP and IDR ensembles are also highly correlated (Pearson’s r = 0.87 or 0.89) with the ens_dRMS-values.
We also note that measuring the differences in the distances between the backbone atoms (here, Cα-Cα distance) in IDP ensembles is a reasonable first step. In these ensembles, including those generated by MD simulations, side chains remain highly flexible. They sample, on average, a much wider range of orientations than in globular proteins, and hence, their interactions are weaker in general. In support of this view, we find that considering Cβ-Cβ distance distributions instead of those between Cα-atoms yields indistinguishable results, as illustrated in Fig. S2, A and B. When dealing with proteins containing structured regions or when formation of more long-lived contacts with side chains is of interest, our backbone-centric approach would need to be refined to quantify differences in contacts between both the side chains and backbone atoms.
Relation to other metrics for comparing ensembles
Metrics for quantifying global differences between ensembles
The ens_dRMS of Eq. 4 is related to, but distinct from, several other intuitive or published metrics that quantify the global difference between two conformational ensembles.
One obvious metric is the difference between the average Rg-values of the conformations in each of the two ensembles that are being compared. Another example is the difference between the inter-residue distance-based versions of the ensemble “structural radius” originally defined using position-dependent RMSD (38). The latter is expressed as the root mean-square average pairwise RMSD between all pairs of conformations in a given ensemble and captures the structural diversity of the ensemble.
Using the five experimentally characterized IDP and IDR ensembles of the human tau-K18 and MeV N-tail proteins of our data set (representing 10 pairwise comparisons for each system), respectively, we evaluated the relationships between these two metrics and the ens_dRMS of Eq. 4. The difference between average Rg-values of two ensembles was computed as the following: Diff_ensRg = |<Rg(A)> − <Rg(B)>|, where < and > indicate ensemble averages and A and B are different ensembles. The derivation of the distance-based version of the “structural radius” for each ensemble, dRstruct, is provided in the Supporting Materials and Methods. The difference between the dRstruct-values of two ensembles was computed as the following: Diff_dRstruct = |dRstruct(A) − dRstruct(B)|.
This analysis revealed a moderately high correlation between the ens_dRMS- and Diff_ensRg-values (Pearson’s r = 0.69) computed for the same pairs of ensembles but a very low correlation of ens_dRMS with Diff_dRstruct (Fig. S3, A and B). The low correlation with Diff_dRstruct was mainly due to the very low correlation between these two quantities for the 10 pairs of the MeV N-tail ensembles caused by the more compact nature of one of the ensembles (Fig. S3D; Table S1). These results confirm that the ens_dRMS is indeed a distinct measure from metrics such as Diff_ensRg and Diff_dRstruct. The ens_dRMS directly computes averages over the difference in median distances of individual residue pairs in conformations from different ensembles. The other two metrics first compute averages over distances within conformations within the same ensemble (Rg) or over the difference in distances between conformations, again within the same ensemble (dRstruct). Both metrics then use these ensemble averages to quantify the between-ensemble differences. Interestingly, we find that Diff_ensRg and Diff_dRstruct are only moderately correlated with one another (Pearson’s r = 0.53), indicating in turn that even these seemingly related measures quantify the distinct average global features of the conformational ensembles (Fig. S3 C).
Metrics based on the Kullback-Leibler divergence of two distributions
Our distance-dependent metrics evaluate quantities that capture differences between the distance distributions of two ensembles, but do not evaluate the differences between the distributions themselves. A classical measure of the difference between two distributions is the Kullback-Leibler divergence (KLD) (39).
Several studies have illustrated the effectiveness of KLD-based metrics in comparing conformational ensembles of globular proteins generated by molecular simulations and modeled using experimental restraints (8,40,41). These studies analyzed distributions of different structural parameters (e.g., pairwise global RMSD-values between conformations or backbone and side chain dihedral angles) and preprocessed the underlying conformational ensembles in different ways. They also clearly indicate that extracting statistically significant values from such KLD-based metrics requires a large sample size and is computationally intensive. Given the small size of the experimentally restrained IDP data sets analyzed here, estimating the statistical significance of KLD-based metrics, which measure differences between the underlying d(i,j) distributions, remains challenging. This makes it difficult to compare such metrics with our distance-dependent local (Diff_dμ(i,j) and Diff_dσ(i,j)) and global (ens_dRMS) metrics.
We nevertheless performed a rough comparison of the symmetrized form of the KLD between two distance distributions (symKLD_d(i,j)) and our Diff_dμ(i,j) metric for the 10 pairs of the tau-K18 IDP ensembles of our data set (see Supporting Materials and Methods, Section S2.3 for details). The results showed moderate correlation coefficients (Pearson’s r = 0.42–0.51) between the two metrics for pairs of ensembles exhibiting significantly different d(i,j) distributions, but a negligible correlation for ensemble pairs displaying no significantly different d(i,j) distributions (evaluated by the Mann-Whitney-Wilcoxon test) (Fig. S4). Interestingly, however, a much higher correlation (Pearson’s r = 0.8) was obtained between the two global metrics, ens_dRMS- and ensKLD-values (the ensemble-averaged symKLD_d(i,j)-values) between two ensembles computed for the 10 pairs of tau-K18 ensembles (Table S2).
Taken together, these results suggest that symKLD_d(i,j) and Diff_dμ(i,j) capture the differences between distinct aspects of the individual d(i,j) distributions (or differ because of the small sample size) and these differences are averaged out when the global metrics are compared, hence suggesting that our simple global metric, ens_dRMS, captures the differences between the underlying d(i,j) distributions of two ensembles rather well. Clearly such comparisons need to be repeated using a careful formulation of KLD-based metrics that depend on inter-residue distances as well as larger data sets. Furthermore, such metrics may themselves be a useful addition to the toolbox of methods, enabling the analysis of a more complete range of properties of IDP ensembles than the metrics proposed here.
Measuring local backbone flexibility and conformational biases within ensembles
To evaluate possible biases of individual ensembles toward specific local backbone conformations (α-helix, left-handed helix, extended β-strand, etc.) as well as the extent of local backbone flexibility, we carry out superimpositions of backbone atoms for overlapping five-residue segments along the polypeptide chain for pairs of conformations within a given ensemble (Fig. 2 C, center). The average and the 95 percentile confidence interval of the classical backbone RMSD-values computed across all k,l pairs of conformations are computed for each segment and assigned to the first residue of the segment, representing the residue number n along the polypeptide serving as the segment anchor:
| (5) |
where P is the total number of k,l pairs of conformations in the ensemble.
These local backbone comparisons are complemented with an analysis of the frequencies of backbone (ϕ,ψ) torsion angle values, mapped onto regions of the Ramachandran map corresponding to the four common secondary structure motifs: α-helix, β-strand, polyproline, and left-handed α-helix (see Fig. S10; (17)).
Code availability
The code is available from https://github.com/lazartomi/ens-dRMS.
Results and Discussion
Comparing conformational ensembles of IDPs
We propose a general approach for comparing conformational ensembles that combines several complementary metrics (Fig. 2). At its core are novel, to our knowledge, distance-based metrics quantifying the global and local similarity between two conformational ensembles by comparing distributions of inter-residue distances.
Essential components of the distance-based metrics are two matrices for each of the ensembles E1 and E2 to be compared (E1 and E2 heatmaps Fig. 2 A). One contains the medians of the inter-residue distance distributions dμ(i,j) (computed between Cα atoms) for equivalent residue pairs i,j in conformations of the ensemble (top right half of the heatmaps). The second contains the SDs dσ(i,j) of the corresponding distributions (bottom left half of the heatmaps). For a given pair of ensembles, two difference matrices are computed (E1 and E2, Fig. 2 A): the Diff_dμ(i,j), matrix containing the absolute differences between the medians of inter-residue distance distributions of the two ensembles (top right half of the heatmaps), and the matrix containing the absolute differences between the corresponding SDs, Diff_dσ(i,j) (bottom left half of the heatmaps). Because the Diff_dμ(i,j) matrix evaluates differences between distributions, the statistical significance of these differences is evaluated, and the resulting difference matrices list only the values for the significantly different d(i,j) distributions (p < 0.05) (E1 and E2 in Fig. 2 B; for further details, see Materials and Methods), named Sig-Diff_dμ(i,j) and Sig-Diff_dσ(i,j).
To obtain a single global measure of the differences between the two conformational ensembles E1 and E2, we compute the RMSD between the median distance elements dμ(i,j) of the conformations in the two ensembles, denoted as ens_dRMS (see Materials and Methods).
The distance-based metrics are complemented with several classical measures applied to individual ensembles (Fig. 2 C and Materials and Methods). The local backbone variability within one ensemble is quantified by the distributions of the average backbone RMSD-values of five-residue segments along the polypeptide computed over pairs of conformations in each ensemble. Local conformational preferences within a given ensemble are evaluated by the frequencies of backbone (ϕ,ψ) torsion angles of individual residues mapped onto the regions of the Ramachandran map corresponding to secondary structure motifs (see Materials and Methods). We see, for example, that the region near residue 490 of the polypeptide in the analyzed ensembles displays low backbone variability and adopts a helical conformation in both E1 and E2 ensembles (E1 local and E2 local, Fig. 2 C) but that the same region adopts different spatial positions relative to the N-terminus of the polypeptide in the two ensembles (residues 400–430) (E1 and E2 heatmaps, Fig. 2 B).
Global conformational parameters of individual ensembles are also quantified from the distribution of the radius of gyration (Rg) of conformations within an ensemble, with examples presented below.
Application to conformational ensembles of specific protein systems
To illustrate the potential of our approach, we apply it to experimentally characterized IDR ensembles of the two proteins. One is the N-tail region (132 residues) of the MeV nucleoprotein, which includes a short transient α-helix that mediates the interaction with the C-terminal X domain of the MeV phosphoprotein (42,43), which is important for the replication of the viral genome. The second is the K18 segment (130 residues) of human tau protein, a microtubule-associated protein, which binds microtubules via four imperfect microtubule-binding repeats (R1–R4) located within the K18 segment (44,45) and promotes microtubule polymerization and stability (see Fig. S5 for the sequences of these domains). For each of these proteins, five ensembles comprising 199 conformations were retrieved from the PED database (see Materials and Methods). These ensembles represent distinct modeling solutions derived by sampling random coil conformations, denoted here as “random pool,” followed by ensemble selection based on the fit to NMR data (residual dipolar coupling and chemical shift data) as described in references (17) and (25).
The ens_dRMS-values for the 10 pairs of conformational ensembles of the tau-K18 and MeV N-tail segments (Table 1) span a very similar small range: 1.47–2.15 Å (tau-K18) and 1.48–2.90 Å (MeV N-tail), suggesting a substantial average structural similarity between the conformations of the five ensembles of each protein. This similarity was also reflected by indistinguishable Rg distributions of the conformations in the corresponding ensembles.
Table 1.
ens_dRMS-Value for Pairs of Ensembles of the tau-K18 and MeV N-Tail IDR
| tau-K18 |
MeV N-tail |
||||||||
|---|---|---|---|---|---|---|---|---|---|
| ens_dRMS | E2 (Å) | E3 (Å) | E4 (Å) | E5 (Å) | ens_dRMS | E2 (Å) | E3 (Å) | E4 (Å) | E5 (Å) |
| E1 | 1.91 | 1.72 | 1.83 | 1.98 | E1 | 2.83 | 2.90 | 2.43 | 1.62 |
| E2 | – | 2.15 | 1.84 | 1.93 | E2 | – | 1.74 | 1.48 | 2.10 |
| E3 | – | – | 1.47 | 2.06 | E3 | – | – | 1.82 | 2.14 |
| E4 | – | – | – | 2.04 | E4 | – | – | – | 1.75 |
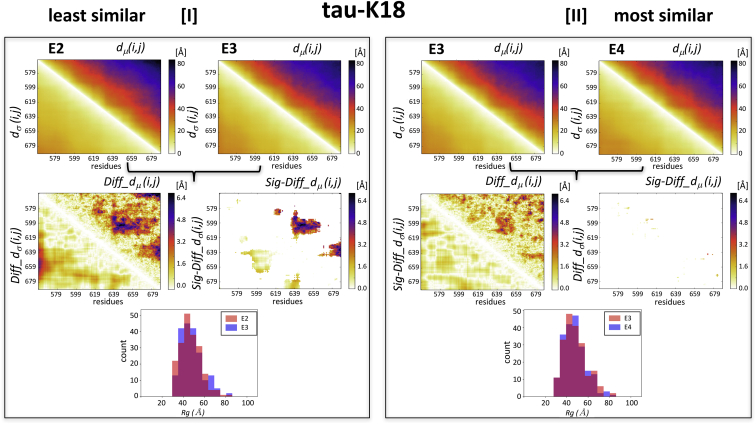
To evaluate how conformational properties between ensembles differ, we examine pairs of ensembles in each protein system featuring the largest and smallest ens_dRMS-values in Table 1. For each of these pairs, we examined the dμ(i,j) matrices as well as the difference matrices Diff_dμ(i,j) and Diff_dσ(i,j). Results show that the Diff_dμ(i,j) matrix for the least similar E2-E3 pair of tau-K18 (ens_dRMS = 2.15 Å) features four regions with the largest Diff_dμ(i,j)-values (>4.8 Å) (Fig. 3 I). Only three of these regions (residues 578–582 and 619–622, 585–600 and 630–660, and 620–640 and 660–680) represent statistically significant differences of the distance distributions between segments at medium separation (30–40 residues) along the polypeptide. In contrast, the Diff_dμ(i,j) matrix of the most similar E3-E4 pair of tau-K18 (ens_dRMS = 1.47 Å) features only very small regions with Diff_dμ(i,j)-values >4.8 Å (Fig. 3 II), none of which represent statistically significant differences between the underlying distance distributions, indicating that the E3 and E4 ensembles are indistinguishable at this level of the analysis. This was the only pair of tau-K18 ensembles with indistinguishable distance distributions. All the remaining pairs (including E2 and E3) display varying patterns of significant differences but only between residues positioned at medium to large separation (20–70 residues) along the polypeptide (Fig. S6).
Figure 3.
Comparisons of experimentally characterized tau-K18 IDR ensembles. Illustrated are the similarities between the E2-E3 and E3-E4 pairs of tau-K18 ensembles, displaying the largest (2.15 Å) and smallest (1.47 Å) ens_dRMS-values in Table 1, respectively. (I) Top: shown are the heatmaps of dμ(i,j) and dσ(i,j) matrices for the individual E2 and E3 ensembles. Middle left: shown are the heatmaps of the Diff_dμ(i,j) and Diff_dσ(i,j) computed for the E2-E3 pairs, featuring four regions with the largest differences (>4.8 Å). Middle right: shown are the heatmaps depicting only the statistically significant elements of these maps (Sig-Diff_dμ(i,j) and Sig-Diff_dσ(i,j)). These elements span three regions (residues 578–582 and 619–622, 585–600 and 630–660, and 620–640 and 660–680), representing distances between segments with medium range separation (30–40 residues) along the polypeptide. Bottom: shown is a histogram of the distributions of the gyration radii (Rg) of E2 and E3, which were found to be statistically indistinguishable (p = 0.3). (II) Results for E3-E4 pair are displayed. The top, middle, and bottom panels display the same quantities as in (I), computed for this most similar pair. The Diff_dμ(i,j) and Diff_dσ(i,j) matrices computed for this pair highlight similar differences to those of the E2-E3 pair, but these differences are not statistically significant, resulting in the virtually empty Sig-Diff_dμ(i,j) and Sig-Diff_dσ(i,j) heatmap. The Rg distributions of the E3-E4 pair (bottom plot) are likewise statistically indistinguishable (p = 0.9).
Essentially, the same observations were made for the five ensembles of the N-tail region of MeV nucleoprotein (Figs. S7 and S8), although among the 5 N-tail ensembles, members of two pairs (E2 and E4 and E1 and E5) were statistically indistinguishable.
These results suggest that the five experimentally derived conformational ensembles of the two IDP and IDR domains closely adopt similar local structures but display significant differences in their nonlocal structures, i.e., how short segments located at medium to large separations along the polypeptide are positioned relative to each other. Considering that the NMR data used to model the ensembles provide only local-structure restraints (17), the observed differences in the nonlocal structure likely represent the random “noise” of the IDP and IDR ensemble solutions, which is not functionally relevant, and they contribute little to the average global conformational properties. This is a reasonable assumption considering that the function of IDPs and IDRs tends to be mediated by short recognition motifs that are interspersed between longer flexible linker regions adopting highly variable conformations (24), as will be further discussed below.
Experimentally derived versus random-pool ensembles
To further characterize the experimentally derived and apparently very similar ensembles, it is important to evaluate how they differ from the ensembles of random coil conformations (random pools) from which they were selected based on the NMR data. To this end, we combined all the conformations from the five tau-K18 and MeV N-tail ensembles (199 conformers × 5 ensembles per protein), respectively, and compared them with those of the random pools of each protein (100 ensembles × 200 conformers) generated by the authors of the ensembles (17).
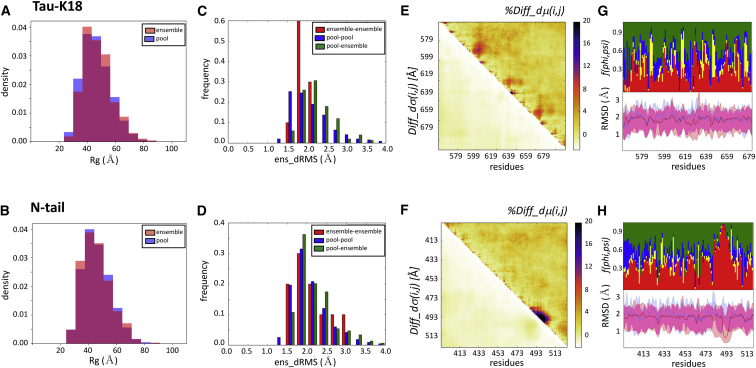
The results show that the experimental ensembles of the tau-K18 and MeV N-tail proteins display similar average conformational parameters to those of their random-pool versions. The two types of ensembles feature somewhat distinct Rg distributions for tau-K18 (p = 0.08; Fig. 4 A) but indistinguishable distributions in the case of the MeV N-tail (p = 0.4; Fig. 4 B). The differences in the ens_dRMS distributions between the experimental and random-pool ensembles (Fig. 4, C and D) are more noticeable (although not statistically significant (p = ∼0.4) because of the small sample size: there are only five experimental ensembles for each system). Those of the experimental ensembles span a narrower range (1.5–2.2 Å for the tau-K18 and 1.5–2.9 Å for the MeV N-tail) than their random-pool counterparts (1.0–3.0 and 1.0–3.4 Å, respectively), with a somewhat wider range for the experimental MeV N-tail than the tau-K18 ensembles. On the other hand, pairs of conformations from both types of ensembles (experimental versus random pool) follow distinct distributions of ens_dRMS-values from those of pool-pool pairs (p = 2.8e−13 and 2.5e−3 for tau-K18 and MeV N-tail, respectively). These distributions display a small shift toward higher values (Fig. 4, C and D), indicating that the conformations in the experimental ensembles tend to differ more from random-pool conformations than random-pool conformations among each other.
Figure 4.
Experimental ensembles compared with their random-pool versions. The conformations of all five tau-K18 and MeV N-tail ensembles were combined and compared with those of the random-pool ensembles of each protein, respectively (25). (A and B) Shown are the histograms of the Rg distributions of the experimentally restrained versus the random-pool ensembles for the tau-K18 and MeV N-tail IDR domains, respectively. The tau-K18 ensembles are somewhat more compact than their random-pool version (p = 0.008), whereas both types of ensembles are indistinguishable for the MeV N-tail (p = 0.36). (C and D) Shown are the histograms of the pairwise ens_dRMS (in Angstroms)-values for the conformations of the experimentally restrained tau-K18 and MeV N-tail ensembles (red bars), random-pool versions of the corresponding proteins (blue bars), and pairs comprising members of both types of ensembles (green bars), respectively. (E and F) Shown are the heatmaps of the statistically significant portions of the normalized version of the difference matrix and the corresponding SD differences for the tau-K18 and MeV N-tail IDR domains versus their random-pool versions, respectively. The normalized version of the difference matrix %Diff_dμ(i,j) is defined as the percent difference between the dμ(i,j)-values from the two types of ensembles (see Materials and Methods). (G and H) Shown are twin graphs highlighting the regions of the IDRs with different backbone flexibility and local-structure preferences in conformations of the experimental and random-pool ensembles. Bottom graph: given are the medians and 95% confidence interval of the local backbone RMSD distributions for conformations of the merged pool (blue) and experimental (pink) ensembles of the tau-K18 (G) and MeV N-tail (H) ensembles, respectively, with the overlapping portions of the plots appearing in purple. Top graph: fractions of the conformations are given with specific (ϕ,ψ) preferences (see the legend of Fig. S10 for details).
Taken together, these observations suggest that the two experimental IDP ensembles analyzed here represent conformationally biased subsets of the random-pool ensemble, with the extent of bias depending on the protein system and the quality of the experimental data. It is therefore difficult to define an ens_dRMS threshold that reliably distinguishes experimental ensembles from their random-pool versions.
To evaluate the nature of the conformational bias introduced by experimental restraints and their functional relevance, we examine differences in more local conformational parameters between the experimental and random-pool ensembles. Merging the conformations of all five experimental tau-K18 ensembles (5 × 199 conformations) and those of the 100 random-pool ensembles (100 × 200 conformations) together, we compute the distance-based difference matrices between these two sets of ensembles. Fig. 4 E plots the normalized version of the Diff_dμ(i,j) matrix and the differences in the corresponding SDs (see the legend of Fig. 4 and Materials and Methods for details). Interestingly, the most prominent differences are observed not between more distant regions of the tau-K18 but along the diagonal of the matrix, along which three regions spanning residues 580–604, 615–632, and 647–665 display significantly nonrandom local conformational preferences. These regions correspond to the structurally constrained microtubule-binding motifs of tau repeats (44,45), suggesting that the differences captured by comparing experimentally restrained and random ensembles are functionally relevant. By the same logic, the significant differences in the relative positions of more distant segments often observed between the experimental ensembles are probably not functionally relevant, as already suggested above.
Local conformational preferences are likewise observed in the experimental versus random-pool difference plots of the MeV N-tail domain (Fig. 4 F). They concern a contiguous segment (residues 487–507) along the diagonal, which is α-helical in the MeV N-tail ensembles but a random coil in the pools. Because this helix is critical in mediating the interaction of the MeV nucleoprotein N-tail with the X domain of phosphoprotein (42,43), the strong signal around this motif confirms the important discriminatory power of comparing the two types of ensembles. The specific local-structure preferences of the tau-K18 and MeV N-tail IDP domains are confirmed by the plots of per-residue RMSD distributions and backbone (ϕ,ψ) values (Fig. 4, G and H).
Comparing flexible peptide ensembles generated by MD with different force fields
MD simulations are the technique of choice for modeling the dynamic properties of proteins (46) and should be a valuable tool for modeling the highly dynamic conformational states of IDPs and IDRs. For IDPs of small enough size, one may indeed expect de novo MD simulations to generate realistic models of conformational ensembles without experimental restraints, provided appropriate force fields are used and conformational space is sufficiently sampled (47).
This was the rationale of an earlier study of Rauscher et al. (26), in which microsecond-timescale MD simulations were run using eight different force fields and solvent model combinations to generate conformational ensembles for the intrinsically disordered 24-residue SR-rich peptide (residues 22–45 of SR-rich splicing factor 1). These ensembles were then evaluated for their consistency with NMR chemical shifts, scalar couplings, and hydrodynamic radius derived from SAXS data, measured for the same system. This comparison allowed the authors to identify the force fields that produced ensembles that were in agreement with the experimental data (26).
Here, we illustrate how our ensemble-comparison measures may be used to obtain useful insights into the differences between ensembles of the SR-rich peptide generated using five different force fields, as described in reference (26). Furthermore, we evaluate how these ensembles differ from a “random” ensemble generated by MD simulations of the same system at a high temperature (600 K) using the CHARMM22∗ force field with the CHARMM-modified TIP3P water model, denoted as the “High-T” ensemble (see Materials and Methods for details).
An analysis of the Rg and ens_dRMS-values of the different ensembles (Fig. S9; Table 2) confirms earlier findings (26) that the Amber-99sb∗-ildn and CHARMM36 force fields produce the most compact ensembles. These ensembles are shown here to differ most from the High-T ensemble, as witnessed by the larger corresponding ens_dRMS-values. Ensembles produced by the Amber-03w, ABSINTH, and CHARMM22∗ force fields feature similar Rg distributions to those of the High-T ensemble and the smallest ens_dRMS-values relative to that ensemble.
Table 2.
ens_dRMS-Values for Pairs of Ensembles of the SR-Rich Peptide Derived Using MD Simulations with Five Different Force Fields and Additionally One at High-T
| ens_dRMS | 99sb (Å) | ABSINTH (Å) | c22 (Å) | c36 (Å) | High-T (Å) |
|---|---|---|---|---|---|
| 03w | 6.91 | 1.76 | 1.78 | 5.74 | 1.80 |
| 99sb | – | 8.13 | 5.51 | 2.26 | 7.47 |
| Absinth | – | – | 2.83 | 6.72 | 1.37 |
| c22 | – | – | – | 4.32 | 2.07 |
| c36 | – | – | – | – | 6.09 |
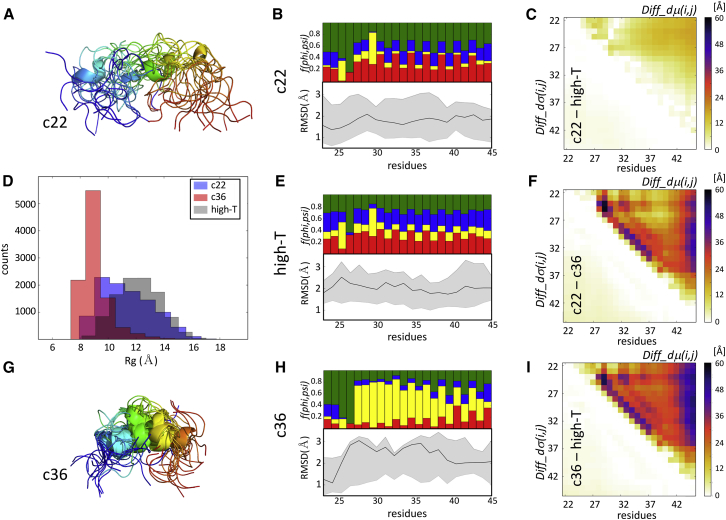
Fig. 5 illustrates the detailed results for two ensembles: those produced with the CHARMM22∗ and CHARMM36 force fields, reported as featuring the best fit and a poor fit to the experimental data in the original study, respectively (26). The small normalized Diff_dμ(i,j)-values (≤10%) between the CHARMM22∗ and High-T ensembles (Fig. 5 C) confirm the close structural similarity between the two ensembles, also reflected by their similar wider Rg distributions (Fig. 5 D).
Figure 5.
Comparing ensembles of an intrinsically disordered peptide generated using molecular simulations. Shown is a pictorial summary of the comparative analysis of two ensembles generated using de novo molecular dynamics (MD) simulations for the 24-residue serine-arginine (SR)-rich peptide (residues 22–45 of SR-rich splicing factor 1). These ensembles were generated with the CHARMM22∗ and CHARMM36 force fields, previously reported as featuring the best fit and a poor fit to the experimental data in the original study, respectively (26). (A) Shown is a cartoon representation of the superimposed first 15 conformations from the SR-rich peptide ensemble generated using the CHARMM22∗ force field, which is color coded from blue (N-terminus) to red (C-terminus). (B) Given are twin plots highlighting the regions of the peptide with different backbone flexibility and local-structure preferences in conformations of the CHARMM22∗ ensemble. Bottom graph: medians and 95 percentile confidence interval of the local backbone RMSD distributions for conformations of the ensemble are given. Top graph: fractions of the conformations are given with specific (ϕ,ψ) torsion angle preferences (see the legend of Fig. 1C for details). (C) Shown is a heatmap displaying the statistically significant portions of the Diff_dμ(i,j) and Diff_dσ(i,j) matrices computed between the CHARMM22∗ ensemble and an ensemble generated by the high-temperature MD simulations (High-T) using the same force field. This map shows only small differences, indicating a rather high degree of conformational similarity between the CHARMM22∗ ensemble and its High-T counterpart. (D) Shown is a histogram of the Rg distributions of the ensembles generated using the CHARMM22∗, CHARMM36, and denatured (High-T) ensembles, respectively, illustrating the higher compactness of the CHARMM36 ensemble relative to the other two versions. (E) Shown are twin plots that are analogous to those in (B) computed for the High-T ensemble. (F) Shown is a heatmap displaying the statistically significant portions of the Diff_dμ(i,j) and Diff_dσ(i,j) matrices computed between the CHARMM22∗ and CHARMM36 ensembles. (G) A cartoon representation is given of the superimposed first 15 conformations from the SR-rich peptide ensemble generated using the CHARMM36 force field, which is color coded as in (A). (H) Shown are twin plots highlighting the regions of the peptide with different backbone flexibility and local-structure preferences in conformations of the CHARMM36 ensemble. (I) Shown is a heatmap displaying the statistically significant portions of the Diff_dμ(i,j) and Diff_dσ(i,j) matrices computed between the CHARMM36 and High-T ensembles.
Significantly larger normalized Diff_dμ(i,j)-values, reaching up to 60%, are observed when comparing the CHARMM36 ensemble with both the CHARMM22∗ version and the High-T ensemble (Fig. 5, F and I). The largest differences occur between the C-terminus and residues 22–36 of the peptide and more locally in the segment spanning residues 24–34. The latter segment is highly enriched in the left-handed helix conformations in the CHARMM36 ensemble, as clearly visible on the per-residue secondary structure frequency plot (Fig. 5, B, E, and H). As a result, this ensemble is also more compact (<Rg> = 9 Å) than the other two ensembles (Fig. 5 D). Considering the poor fit of the CHARMM36 ensemble to the experimental data, the formation of this helical structure was deemed an artifact of the CHARMM36 force field in the original study.
Thus, when ensembles are modeled de novo, e.g., in the absence of experimental restraints, situations may arise in which statistically significant differences between an ensemble and its random counterpart have no physical or functional relevance but merely reflect biases introduced by the modeling procedure.
Comparing conformational ensembles of partially disordered proteins
The PDB contains many examples of proteins that feature a mix of structured domains and IDRs. These are mainly smaller proteins whose structures are determined by NMR and represented as conformational ensembles often spanning both the structured and disordered domains. Comparing such ensembles is challenging. It often involves structural superimpositions of the structured domains, which are then used to derive positional backbone and side chain fluctuations for the superimposed residues, whereas the IDRs are usually described only qualitatively.
Here, we show that our ensemble-comparison protocol enables a quantitative description of such systems, which provides deeper insights into the structure-function relationship than analyses based on classical RMSD-values. As an example, we use huPrP, which is considered the causative agent of diverse prion diseases in humans, such as Creutzfeldt-Jakob disease, kuru, and fatal insomnia (48). huPrP can undergo an autocatalytic, self-templated structural rearrangement to an infectious, transmissible scrapie state that causes propagation of the disease (49). The protein features an intrinsically disordered N-terminal domain (1–125) and a folded, α-helical C-terminal domain (126–226) (35). We analyze three NMR ensembles of huPrP with 20 conformers each downloaded from the PDB. Two are of a construct of huPrP (90–226) (PDB: 2LSB (35) and PDB: 5L6R (36)) containing the folded domain and the adjoining 35 residues of the disordered domain, and one is for a somewhat different construct of huPrP (91–231) (PDB: 5YJ5 (37)).
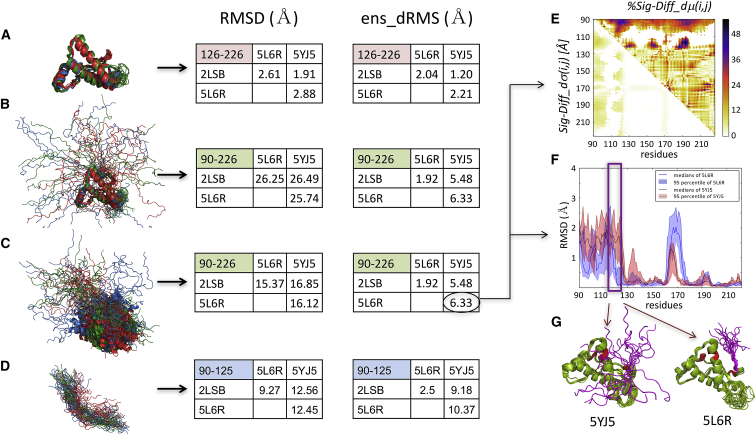
Fig. 6 summarizes the main results for the huPrP system. It lists the average pairwise backbone RMSD-values (Fig. 6, RMSD tables) corresponding to four different structural superimpositions of the conformations from the three considered ensembles. Relatively low RMSD-values (1.9–2.9 Å), implying clear structural similarity, are only obtained when superimposing the C-terminal structured domain (residues 126–226; Fig. 6 A) and evaluating the corresponding backbone deviations. On the other hand, rather large RMSD-values indicative of low structural similarity are achieved for the full huPrP fragment (90–226) after superimposing its backbone (∼16 Å) (Fig. 6 C) or only the backbone of the structured domain (∼26 Å) (Fig. 6 B). However, somewhat lower RMSD-values (9–13 Å) obtained comparing only the N-terminal IDR segment (90–125) (Fig. 6 D) reflect some structural similarity for this segment, which is completely blurred by large variations of its orientation relative to the structured domain when considering the full huPrP fragment (Fig. 6, B and C).
Figure 6.
Comparing ensembles of truncated huPrP comprising both a structured and an IDR. The results are displayed for the superimposed backbone structures of the three NMR ensembles with 20 conformations each. Given are two structures of huPrP (90–226) (PDB: 2LSB and PDB: 5L6R) and one of huPrP (91–231) (PDB: 5YJ5). Also displayed are the tables listing the corresponding ens_dRMS and average classical RMSD-values (in Angstroms). (A and D) Superimpositions and analysis were performed considering only the C-terminal-structured huPrP domain (residues 126–226) (A) or only the N-terminal IDR segment (residues 90–125) (D), respectively. (B) Shown is the analysis of huPrP (90–226 and 91–231) after superimposing the structured domain. (C) Shown is the analysis of huPrP (90–226 and 91–231) after superimposing the entire polypeptide (see the main text for details). (E) Shown are the Diff_dμ(i,j) and Diff_dσ(i,j) heatmaps of the two huPrP NMR ensembles displaying the largest ens_dRMS difference (PDB: 5YJ5 and PDB: 5LR6), depicting prominent differences involving the disordered segments (90–125). (F) Given are the medians and 95% confidence intervals of the local backbone RMSD distributions for conformations of the same two ensembles, highlighting the local differences in backbone flexibility of the 10-residue segment immediately preceding the structured domain. (G) Shown are cartoon models of the two huPrP ensembles highlighting the different conformations of the 10-residue IDR segment relative to the C-terminal-structured domain. (F and G) The 115–125 segment of the IDR domain features more diverse conformations in PDB: 5YJ5 than in the PDB: 5L6R structure, whereas the turn segment of the structured domain (residues 160–170) adopts more diverse conformations in PDB: 5L6R.
In contrast, structural similarities between the three huPrP ensembles can be clearly concluded from the superimposition-free ens_dRMS measure, even when comparing only the IDR segment (Fig. 6, ens_dRMS tables). The ens_dRMS and RMSD-values are comparable for the structured domain (Fig. 6 A), confirming that the distance-based measure is effective in quantitatively describing similarity of folded proteins (5). Moreover, this measure is clearly superior to the RMSD when evaluating the similarity of the full huPrP fragment (90–226) because it features low values (Fig. 6, B and C), indicating very close structural similarity, which is not recognized by the RMSD-based analysis. Importantly, the ens_dRMS measure also detects a clear structural relatedness of the IDR segments, particularly in the PDB: 5L6R and PDB: 2LSB PDB entries (ens_dRMS: ∼2.5 Å), which may explain why this particular pair features a significantly smaller ens_dRMS (∼1.9 Å) than the remaining two pairs (∼6 Å) for the full PrP fragment.
The small ens_dRMS-values between the PDB: 5L6R - PDB: 2LSB pair likely result from a bias toward similar conformational ensembles in the corresponding NMR structures because these structures were determined by some of the same authors (35,36). On the other hand, the larger ens_dRMS-values for the other two pairs of huPrP ensembles (∼9–10 Å for the IDR (Fig. 6 D) and ∼5–6 Å for the full huPrP fragment (Fig. 6, B and C)) likely reflect the different conformational properties of the huPrP PDB: 5YJ5 (37), to which the two other ensembles are compared.
Indeed, for the PDB: 5YJ5 - PDB: 5L6R pair with the largest ens_dRMS (6.3 Å), the ensembles of the full huPrP fragments display distinct patterns of local backbone fluctuations notably in the C-terminus of the IDR domain (residues 115–125) (Fig. 6 F). This 10-residue segment, which immediately precedes the structured domain of huPrP, stands out as displaying large differences in median distances (40–50%) relative to three specific regions of the structured domain in the vicinity of residues 130, 155, and 190 (Fig. 6 E). These various features are illustrated in the molecular models of Fig. 6 G. It is noteworthy that this 10-residue huPrP segment overlaps with the palindromic sequence (AGAAAAGA) thought to be critical for the transition to the scrapie form (50) and was reported to be buried in PrP fibrils (51).
Conclusions
This study presented a novel, to our knowledge, approach for evaluating the global and local similarity of conformational ensembles of the same protein employing metrics that forego superimposition of the atomic coordinates and, instead, compare the distributions of inter-residue distances. These metrics are based on quantities that capture the differences between the distributions of residue-residue distances and their statistical significance. Computing these quantities is inexpensive, and the results can be readily interpreted by researchers with basic knowledge in molecular modeling. Furthermore, we showed that our global similarity metric, the ens_dRMS, is distinct from other inter-residue distance-dependent global similarity metrics that evaluate the radius of gyration (Rg) or the so-called “structural radius” (Rstruct) (38), reformulated here using inter-residue distances. The latter metrics first average intramolecular distances of individual conformations or compare individual conformations within ensembles, whereas the ens_dRMS directly averages differences between medians of individual inter-residue distance distributions across different ensembles.
The power of our simple approach was illustrated in comparative analyses of multiple ensembles of three different systems: those of the MeV N-tail and tau-K18 IDR segments modeled using restraints derived from NMR experiments, ensembles of the intrinsically disordered SR-rich peptide generated by MD simulations, and NMR conformational ensembles of the huPrP, a protein containing a structured and an intrinsically disordered domain.
Comparison of the inter-residue distance distributions within the experimentally derived MeV N-tail and tau-K18 IDR ensembles and between these ensembles and the random-pool versions from which they were selected readily identified previously reported regions with enhanced preferences for specific local conformational features. These regions adopted a similar pattern of inter-residue distance distributions in all the experimentally derived ensembles of both systems. However, this pattern differed significantly from that adopted by the same regions of the polypeptide in the corresponding random-pool ensembles. It was particularly satisfying to verify that these very regions are functionally relevant. For tau-K18, they comprise the microtubule-binding motifs, whereas for the MeV N-tail, it corresponds to the helical region mediating the interaction with the X domain of MeV phosphoprotein.
This notwithstanding, the experimental ensembles were not necessarily less conformationally diverse than their random-pool versions in terms of distance distributions between more remote regions of the polypeptide. The two types of ensembles also displayed similar global compactness as measured by the corresponding gyration radii (Rg) distributions, suggesting in turn that nonlocal conformational features of the experimental ensembles that are not subjected to the restraints provided by the NMR data conserve a “noisy,” random-pool-like character. This could potentially be remedied by the inclusion of the SAXS data in the ensemble calculation (52,53).
Our superimposition-free structural similarity measures were likewise effective in detecting the conformational biases in ensembles of the intrinsically disordered, 24-residue, SR-rich peptide generated by room-temperature MD simulations using different force fields and water models. One of these ensembles was previously reported as featuring a left-handed helix conformation that was incompatible with the experimental data available for this system (26). Our approach singled out this particular ensemble as the most globally compact and locally structurally constrained that differed significantly from the ensembles derived using other force fields or from the ensemble generated by a high-temperature MD simulation (Fig. 5).
Lastly, applying our ensemble-comparison protocol to three NMR ensembles of huPrP comprising both structured and IDRs provided a highly informative description of this system. In stark contrast to the RMSD-based comparisons, the superimposition-free ens_dRMS metric revealed sizable structural similarities between the NMR ensembles of the huPrP (90–226) fragment that includes the C-terminal segment (∼35 aa) of the disordered PrP domain. The ens_dRMS also detected a particularly close structural relatedness between both the full-length (90–226) and IDR portions (90–125) in two of the huPrP structures, which, as we subsequently verified, were determined by some of the same authors. Also quite remarkably, in the third huPrP structure, our analysis discovered significant differences in the median distances between the IDR segment around residues 115–125 and residues of the adjoining structured domain, which we could attribute to the substantial differences of the local backbone flexibility and orientation of the 10-residue disordered segment in the huPrP structures (Fig. 6, E–G). It was gratifying to find that this very segment is believed to be critical for the transition of huPrP to the disease-associated, scrapie form.
Our distance-based structural similarity measures should be very useful for evaluating the global and local similarity between conformational ensembles of the same or closely related IDPs and IDRs or proteins with both structured and disordered regions. By quantifying the structural relatedness of these flexible systems, a task that classical RMSD-based analyses strain to accomplish, a deeper insight is provided into how their structural features relate to function.
Author Contributions
S.J.W., P.T., and T.L. designed the study. W.V. contributed to the study design. T.L. carried out the analysis. S.J.W., P.T., and M.G., supervised the analysis. S.R. contributed computed SR-rich splicing factor 1 conformational ensembles. S.J.W., P.T., and T.L. wrote the manuscript.
Acknowledgments
We acknowledge the supercomputer resources provided by Compute Canada to S.R. for the MD simulations.
This work was supported by the Odysseus grant G.0029.12 from Research Foundation Flanders; grants K124670, K125340 and K131702 from the National Research Development and Innovation Office of Hungary; and the Spearhead grant SRP51 from Vrije Universiteit Brussel, Brussels, Belgium. S.R. is supported by an Natural Sciences and Engineering Research Council of Canada Discovery Grant.
Editor: Rohit Pappu.
Footnotes
Supporting Material can be found online at https://doi.org/10.1016/j.bpj.2020.05.015.
Contributor Information
Shoshana J. Wodak, Email: shoshana.wodak@gmail.com.
Peter Tompa, Email: peter.tompa@vub.be.
Supporting Material
References
- 1.Redfern O.C., Dessailly B., Orengo C.A. Exploring the structure and function paradigm. Curr. Opin. Struct. Biol. 2008;18:394–402. doi: 10.1016/j.sbi.2008.05.007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Worth C.L., Gong S., Blundell T.L. Structural and functional constraints in the evolution of protein families. Nat. Rev. Mol. Cell Biol. 2009;10:709–720. doi: 10.1038/nrm2762. [DOI] [PubMed] [Google Scholar]
- 3.Maiorov V.N., Crippen G.M. Significance of root-mean-square deviation in comparing three-dimensional structures of globular proteins. J. Mol. Biol. 1994;235:625–634. doi: 10.1006/jmbi.1994.1017. [DOI] [PubMed] [Google Scholar]
- 4.Kufareva I., Abagyan R. Methods of protein structure comparison. Methods Mol. Biol. 2012;857:231–257. doi: 10.1007/978-1-61779-588-6_10. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Cohen F.E., Sternberg M.J. On the prediction of protein structure: the significance of the root-mean-square deviation. J. Mol. Biol. 1980;138:321–333. doi: 10.1016/0022-2836(80)90289-2. [DOI] [PubMed] [Google Scholar]
- 6.Holm L., Sander C. Protein structure comparison by alignment of distance matrices. J. Mol. Biol. 1993;233:123–138. doi: 10.1006/jmbi.1993.1489. [DOI] [PubMed] [Google Scholar]
- 7.Klepeis J.L., Lindorff-Larsen K., Shaw D.E. Long-timescale molecular dynamics simulations of protein structure and function. Curr. Opin. Struct. Biol. 2009;19:120–127. doi: 10.1016/j.sbi.2009.03.004. [DOI] [PubMed] [Google Scholar]
- 8.Tiberti M., Papaleo E., Lindorff-Larsen K. ENCORE: software for quantitative ensemble comparison. PLoS Comput. Biol. 2015;11:e1004415. doi: 10.1371/journal.pcbi.1004415. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.De Simone A., Richter B., Vendruscolo M. Toward an accurate determination of free energy landscapes in solution states of proteins. J. Am. Chem. Soc. 2009;131:3810–3811. doi: 10.1021/ja8087295. [DOI] [PubMed] [Google Scholar]
- 10.Yang S., Salmon L., Al-Hashimi H.M. Measuring similarity between dynamic ensembles of biomolecules. Nat. Methods. 2014;11:552–554. doi: 10.1038/nmeth.2921. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Kazmirski S.L., Li A., Daggett V. Analysis methods for comparison of multiple molecular dynamics trajectories: applications to protein unfolding pathways and denatured ensembles. J. Mol. Biol. 1999;290:283–304. doi: 10.1006/jmbi.1999.2843. [DOI] [PubMed] [Google Scholar]
- 12.Zagrovic B., Snow C.D., Pande V.S. Native-like mean structure in the unfolded ensemble of small proteins. J. Mol. Biol. 2002;323:153–164. doi: 10.1016/s0022-2836(02)00888-4. [DOI] [PubMed] [Google Scholar]
- 13.Zagrovic B., Pande V.S. How does averaging affect protein structure comparison on the ensemble level? Biophys. J. 2004;87:2240–2246. doi: 10.1529/biophysj.104.042184. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Allison J.R., Rivers R.C., Dobson C.M. A relationship between the transient structure in the monomeric state and the aggregation propensities of α-synuclein and β-synuclein. Biochemistry. 2014;53:7170–7183. doi: 10.1021/bi5009326. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Mittag T., Marsh J., Forman-Kay J.D. Structure/function implications in a dynamic complex of the intrinsically disordered Sic1 with the Cdc4 subunit of an SCF ubiquitin ligase. Structure. 2010;18:494–506. doi: 10.1016/j.str.2010.01.020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Sivakolundu S.G., Bashford D., Kriwacki R.W. Disordered p27Kip1 exhibits intrinsic structure resembling the Cdk2/cyclin A-bound conformation. J. Mol. Biol. 2005;353:1118–1128. doi: 10.1016/j.jmb.2005.08.074. [DOI] [PubMed] [Google Scholar]
- 17.Ozenne V., Schneider R., Blackledge M. Mapping the potential energy landscape of intrinsically disordered proteins at amino acid resolution. J. Am. Chem. Soc. 2012;134:15138–15148. doi: 10.1021/ja306905s. [DOI] [PubMed] [Google Scholar]
- 18.Varadi M., Kosol S., Tompa P. pE-DB: a database of structural ensembles of intrinsically disordered and of unfolded proteins. Nucleic Acids Res. 2014;42:D326–D335. doi: 10.1093/nar/gkt960. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Fisher C.K., Stultz C.M. Constructing ensembles for intrinsically disordered proteins. Curr. Opin. Struct. Biol. 2011;21:426–431. doi: 10.1016/j.sbi.2011.04.001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Tompa P. Unstructural biology coming of age. Curr. Opin. Struct. Biol. 2011;21:419–425. doi: 10.1016/j.sbi.2011.03.012. [DOI] [PubMed] [Google Scholar]
- 21.Tompa P., Varadi M. Predicting the predictive power of IDP ensembles. Structure. 2014;22:177–178. doi: 10.1016/j.str.2014.01.003. [DOI] [PubMed] [Google Scholar]
- 22.Diella F., Haslam N., Gibson T.J. Understanding eukaryotic linear motifs and their role in cell signaling and regulation. Front. Biosci. 2008;13:6580–6603. doi: 10.2741/3175. [DOI] [PubMed] [Google Scholar]
- 23.Tompa P., Davey N.E., Babu M.M. A million peptide motifs for the molecular biologist. Mol. Cell. 2014;55:161–169. doi: 10.1016/j.molcel.2014.05.032. [DOI] [PubMed] [Google Scholar]
- 24.Tompa P. The interplay between structure and function in intrinsically unstructured proteins. FEBS Lett. 2005;579:3346–3354. doi: 10.1016/j.febslet.2005.03.072. [DOI] [PubMed] [Google Scholar]
- 25.Ozenne V., Bauer F., Blackledge M. Flexible-meccano: a tool for the generation of explicit ensemble descriptions of intrinsically disordered proteins and their associated experimental observables. Bioinformatics. 2012;28:1463–1470. doi: 10.1093/bioinformatics/bts172. [DOI] [PubMed] [Google Scholar]
- 26.Rauscher S., Gapsys V., Grubmüller H. Structural ensembles of intrinsically disordered proteins depend strongly on force field: a comparison to experiment. J. Chem. Theory Comput. 2015;11:5513–5524. doi: 10.1021/acs.jctc.5b00736. [DOI] [PubMed] [Google Scholar]
- 27.Pronk S., Páll S., Lindahl E. GROMACS 4.5: a high-throughput and highly parallel open source molecular simulation toolkit. Bioinformatics. 2013;29:845–854. doi: 10.1093/bioinformatics/btt055. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Brooks B.R., Brooks C.L., III, Karplus M. CHARMM: the biomolecular simulation program. J. Comput. Chem. 2009;30:1545–1614. doi: 10.1002/jcc.21287. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Piana S., Lindorff-Larsen K., Shaw D.E. How robust are protein folding simulations with respect to force field parameterization? Biophys. J. 2011;100:L47–L49. doi: 10.1016/j.bpj.2011.03.051. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Best R.B., Zhu X., Mackerell A.D., Jr. Optimization of the additive CHARMM all-atom protein force field targeting improved sampling of the backbone φ, ψ and side-chain χ(1) and χ(2) dihedral angles. J. Chem. Theory Comput. 2012;8:3257–3273. doi: 10.1021/ct300400x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Case D.A., Cheatham T.E., III, Woods R.J. The Amber biomolecular simulation programs. J. Comput. Chem. 2005;26:1668–1688. doi: 10.1002/jcc.20290. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Best R.B., Mittal J. Protein simulations with an optimized water model: cooperative helix formation and temperature-induced unfolded state collapse. J. Phys. Chem. B. 2010;114:14916–14923. doi: 10.1021/jp108618d. [DOI] [PubMed] [Google Scholar]
- 33.Vitalis A., Pappu R.V. ABSINTH: a new continuum solvation model for simulations of polypeptides in aqueous solutions. J. Comput. Chem. 2009;30:673–699. doi: 10.1002/jcc.21005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.wwPDB consortium Protein Data Bank: the single global archive for 3D macromolecular structure data. Nucleic Acids Res. 2019;47:D520–D528. doi: 10.1093/nar/gky949. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Zahn R., Liu A., Wüthrich K. NMR solution structure of the human prion protein. Proc. Natl. Acad. Sci. USA. 2000;97:145–150. doi: 10.1073/pnas.97.1.145. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Kovač V., Zupančič B., Čurin Šerbec V. Truncated prion protein PrP226∗ - a structural view on its role in amyloid disease. Biochem. Biophys. Res. Commun. 2017;484:45–50. doi: 10.1016/j.bbrc.2017.01.078. [DOI] [PubMed] [Google Scholar]
- 37.Zheng Z., Zhang M., Lin D. Structural basis for the complete resistance of the human prion protein mutant G127V to prion disease. Sci. Rep. 2018;8:13211. doi: 10.1038/s41598-018-31394-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Kuzmanic A., Zagrovic B. Determination of ensemble-average pairwise root mean-square deviation from experimental B-factors. Biophys. J. 2010;98:861–871. doi: 10.1016/j.bpj.2009.11.011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Kullback S.L., Leibler R.A. On information and sufficiency. Ann. Math. Stat. 1951;22:79–86. [Google Scholar]
- 40.Cukier R.I. Dihedral angle entropy measures for intrinsically disordered proteins. J. Phys. Chem. B. 2015;119:3621–3634. doi: 10.1021/jp5102412. [DOI] [PubMed] [Google Scholar]
- 41.McClendon C.L., Hua L., Jacobson M.P. Comparing conformational ensembles using the kullback-leibler divergence expansion. J. Chem. Theory Comput. 2012;8:2115–2126. doi: 10.1021/ct300008d. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Shu Y., Habchi J., Longhi S. Plasticity in structural and functional interactions between the phosphoprotein and nucleoprotein of measles virus. J. Biol. Chem. 2012;287:11951–11967. doi: 10.1074/jbc.M111.333088. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Blocquel D., Habchi J., Longhi S. Interaction between the C-terminal domains of measles virus nucleoprotein and phosphoprotein: a tight complex implying one binding site. Protein. Sci. 2012;21:1577–1585. doi: 10.1002/pro.2138. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Mukrasch M.D., Markwick P., Blackledge M. Highly populated turn conformations in natively unfolded tau protein identified from residual dipolar couplings and molecular simulation. J. Am. Chem. Soc. 2007;129:5235–5243. doi: 10.1021/ja0690159. [DOI] [PubMed] [Google Scholar]
- 45.Mukrasch M.D., Biernat J., Zweckstetter M. Sites of tau important for aggregation populate beta-structure and bind to microtubules and polyanions. J. Biol. Chem. 2005;280:24978–24986. doi: 10.1074/jbc.M501565200. [DOI] [PubMed] [Google Scholar]
- 46.Perilla J.R., Goh B.C., Schulten K. Molecular dynamics simulations of large macromolecular complexes. Curr. Opin. Struct. Biol. 2015;31:64–74. doi: 10.1016/j.sbi.2015.03.007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Henriques J., Cragnell C., Skepö M. Molecular dynamics simulations of intrinsically disordered proteins: force field evaluation and comparison with experiment. J. Chem. Theory Comput. 2015;11:3420–3431. doi: 10.1021/ct501178z. [DOI] [PubMed] [Google Scholar]
- 48.Prusiner S.B. Prions. Proc. Natl. Acad. Sci. USA. 1998;95:13363–13383. doi: 10.1073/pnas.95.23.13363. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Singh J., Udgaonkar J.B. Molecular mechanism of the misfolding and oligomerization of the prion protein: current understanding and its implications. Biochemistry. 2015;54:4431–4442. doi: 10.1021/acs.biochem.5b00605. [DOI] [PubMed] [Google Scholar]
- 50.Baumann F., Tolnay M., Aguzzi A. Lethal recessive myelin toxicity of prion protein lacking its central domain. EMBO J. 2007;26:538–547. doi: 10.1038/sj.emboj.7601510. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Peretz D., Williamson R.A., Burton D.R. A conformational transition at the N terminus of the prion protein features in formation of the scrapie isoform. J. Mol. Biol. 1997;273:614–622. doi: 10.1006/jmbi.1997.1328. [DOI] [PubMed] [Google Scholar]
- 52.Bernadó P., Mylonas E., Svergun D.I. Structural characterization of flexible proteins using small-angle X-ray scattering. J. Am. Chem. Soc. 2007;129:5656–5664. doi: 10.1021/ja069124n. [DOI] [PubMed] [Google Scholar]
- 53.Bernadó P., Svergun D.I. Structural analysis of intrinsically disordered proteins by small-angle X-ray scattering. Mol. Biosyst. 2012;8:151–167. doi: 10.1039/c1mb05275f. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.