Optimized quantification of spin relaxation times in the hybrid state

Abstract

Purpose

The optimization and analysis of spin ensemble trajectories in the hybrid state—a state in which the direction of the magnetization adiabatically follows the steady state while the magnitude remains in a transient state.

Methods

Numerical optimizations were performed to find spin ensemble trajectories that minimize the Cramér-Rao bound for T₁-encoding, T₂-encoding, and their weighted sum, respectively, followed by a comparison between the Cramér-Rao bounds obtained with our optimized spin-trajectories, Look-Locker sequences, and multi-spin-echo methods. Finally, we experimentally tested our optimized spin trajectories with in vivo scans of the human brain.

Results

After a nonrecurring inversion segment on the southern half of the Bloch sphere, all optimized spin trajectories pursue repetitive loops on the northern hemisphere in which the beginning of the first and the end of the last loop deviate from the others. The numerical results obtained in this work align well with intuitive insights gleaned directly from the governing equation. Our results suggest that hybrid-state sequences outperform traditional methods. Moreover, hybrid-state sequences that balance T₁- and T₂-encoding still result in near optimal signal-to-noise efficiency for each relaxation time. Thus, the second parameter can be encoded at virtually no extra cost.

Conclusions

We provided new insights into the optimal encoding processes of spin relaxation times in order to guide the design of robust and efficient pulse sequences. We found that joint acquisitions of T₁ and T₂ in the hybrid state are substantially more efficient than sequential encoding techniques.

1 |. INTRODUCTION

The dynamics of large spin-1/2 ensembles in a magnetic field are commonly described by the Bloch equations, which capture the macroscopic effects of spin-lattice and spin-spin interactions with the characteristic time constants T₁ and T₂, respectively. Robust and rapid quantification of these parameters may lead to more objective diagnoses, improved longitudinal studies, and simplify computer aided diagnosis. The large dynamic range of inversion-recovery experiments makes them a natural choice for quantitative T₁ mapping. Similarly, a series of spin-echo experiments with varying echo times probe a wide dynamic range for estimating T₂. Both methods effectively strive to trace exponential relaxation curves following a single perturbation from thermal equilibrium—without being affected by the other relaxation time. However, T₁ and T₂ can also—and arguably more efficiently—be estimated by measuring magnetization in various steady-state conditions,^2–5 or even in more complex conditions that depart from the steady state.^6–8 Magnetic Resonance Fingerprinting (MRF),⁸ e.g., opened a door for flexible parameter mapping and initiated various research efforts to increase the signal-to-noise ratio (SNR) efficiency of quantitative MRI. However, the large number of design options for MRF pulse sequences has limited the optimization of MRF experiments to heuristic approaches.^1,8–12 Furthermore, the lack of an intuitive understanding of the spin dynamics in MRF, and the over-simplified nature of the Bloch models employed in typical MRF implementations, creates a risk of introducing biases in the estimated relaxation times.¹¹ We have recently analyzed the biases introduced by inhomogeneities of the RF-excitation field $\left(B_1^{+}\right)$ and the main magnetic field (B₀), including intra-voxel dephasing, which is also known as inhomogeneous broadening.¹³ It is known that this sensitivity to inhomogeneities originates from the magnetization component orthogonal to the steady-state magnetization.¹⁴ Therefore, we derived an upper bound for variations of the flip angle and the phase increment of the RF-pulses that forces the direction of the magnetization to adiabatically follow the steady state. We found that this adiabaticity condition is considerably less stringent than the condition that ensures adiabaticity of the magnetization’s magnitude (cf. Ref. 13 for details). Flip angle variations in between these bounds result in a so-called hybrid state, which combines the steady state’s robustness—by virtue of the direction’s adiabaticity—with the efficiency of the transient state—by virtue of the magnitude’s diabaticity, i.e. non-adiabaticy.¹³

The adiabaticity of the magnetization’s direction effectively decouples the Bloch equations when formulated in spherical coordinates. The angular dimension can be described by the well-established steady-state equations,^15,16 whereas the entire spin dynamics is trapped in the radial dimension, i.e., in the magnitude of the magnetization. Section 2.1 recaps and visualizes the hybrid-state equation of spin motion, which is the decoupled Bloch equation along the radial dimension, and highlights that the polar angle is the effective force that drives these dynamics. Thereafter, we provide an in-depth analysis of hybrid-state sequences and discuss how relaxation times can be encoded efficiently with this approach. By comparing hybrid-state sequences that were optimized to encode either T₁ or T₂ alone against those that resulted from joint optimizations, we show that the second parameter can be measured at virtually no extra cost.

2 |. METHODS

2.1 |. Hybrid-state spin dynamics

We start by describing the spin dynamics in spherical coordinates,¹⁶ which are here defined by x = r sin ϑ cos φ, y = r sin ϑ sin φ and z = r cos ϑ, where r is the radius, ϑ the polar angle or the angle between the magnetization and the z-axis and φ the azimuth or the angle between the x-axis and the projection of the magnetization onto the x-y-plane. For practicability, we use the limits −1 ≤ r ≤ 1, 0 ≤ ϑ ≤ π/2, and 0 ≤ φ < 2π to uniquely identify the polar coordinates. Recapitulating Ref. 13, the entire spin dynamics in hybrid state is captured by the radius r of the magnetization, i.e., its magnitude combined with a sign, which is controlled only by the polar angle ϑ:

$$\dot{r}(t)=-\left(\frac{{\cos }^2\vartheta (t)}{{\text{T}}_1}+\frac{{\sin }^2\vartheta (t)}{{\text{T}}_2}\right)r(t)+\frac{\cos \vartheta (t)}{{\text{T}}_1}$$ (1)

Here, $\dot{r}(t)$ denotes the partial derivative of r with respect to time.

The flip angle and the phase of the radio frequency (RF) pulses, as well as the repetition time T_R have only an indirect and joint effect on the spin dynamics:

$$\tan \vartheta =\frac{\tan \frac{\alpha }{2}}{\sin \frac{\varphi }{2}},$$ (2)

where ϕ =ω_zT_R describes the phase accumulated during one repetition time T_R and α denotes the flip angle. This equation reduces to ϑ = α/2 for ϕ = π, which we define as the on-resonance condition. In practice, ϕ = π is assigned to the on-resonant spin isochromat by the common phase increment of π in consecutive RF pulses. Note that Equation (2) is equivalent to Equation (3) described by Schmitt et al¹⁷ (given a different definition of ϕ), as well as to Equation (5) in Ref. 13. Further, Equation (1) generalizes the transient-state behavior described by Schmitt et al^6,17 to variable ϑ (cf. Equation (6) in Ref. 6 and the supporting information of Ref. 13).

In order to provide some intuition for the hybrid-state spin dynamics, we visualize its governing differential equation (Equation (1)) in Figure 1A. One can identify the so-called steady-state ellipse,^15–20 which separates areas of the Bloch sphere in which the magnetization grows (red) or shrinks (blue). The absolute value of the derivative of Equation (1) with respect to T₁ is in the upper limit twice as high on the southern hemisphere as it is on the northern hemisphere (note the asymmetric color bar in Figure 1B), which indicates that T₁ can be encoded faster on the southern hemisphere. A second benefit of inversion recovery experiments becomes evident when comparing the derivative with respect to T₁ (Figure 1B) to the one with respect to T₂ (Figure 1C). One changes sign between the hemispheres while the other does not. Thus, encoding data on the southern and northern hemisphere minimizes the correlation between the derivatives, which should yield a superior SNR in the estimated relaxation times by virtue of a lower Cramér-Rao bound^21,22 (cf. Equations (3)–(5)).

FIGURE 1.

Equation (1) describes the spin dynamics and is visualized in (A). The white area indicates the steady-state ellipse which separates the area in which the magnetization grows (red) and shrinks (blue). This particular sub-figure is valid for the ratio T₁∕T₂ = 781 ms∕65 ms ≈ 12, which are values reported for brain white matter.¹ The derivatives of Equation (1) with respect to T₁ and T₂ are depicted in (B) and (C), respectively. These plots are normalized by the respective relaxation times and are, therefore, valid for any combination of T₁ and T₂

When considering T₁ only, Figure 1B suggests that there is a benefit in keeping the magnetization close to the z-axis on the southern hemisphere, and close to the origin on the northern hemisphere, since the absolute value of the derivative is largest in those areas. The derivative with respect to T₂, on the other hand, reaches its maximum far away from the z-axis (Figure 1C). This suggests that spin trajectories with large r may be desirable in order to probe these areas.

2.2 |. Numerical optimizations

In order to verify this intuitive understanding, and to glean some insights on how to best probe the important areas of the Bloch sphere, we numerically optimize spin ensemble trajectories for a maximal SNR per unit time. To this end, the Cramér-Rao bound^21,22 is used to provide a universal limit for the noise variance of the estimated parameters. Given an unbiased estimator, i.e., the fitting algorithm used to calculate the proton density (M₀), T₁, and T₂, the noise variance of these parameters is at least as big as the corresponding Cramér-Rao lower bound. This very general and established metric has been utilized for optimizing MR parameter mapping experiments in Refs. ^23–25 among others, and for MRF in particular in Ref. 26.

Assuming balanced gradient moments and small intravoxel dephasing, the hybrid state allows us to approximate a voxel’s signal at the echo time T_E = T_R∕2 by a single isochromat,¹³ similar to balanced steady-state sequences.²⁷ With s(t) = M₀r(t) sin ϑ(t), where M₀ captures the complex valued proton density incl. coil sensitivity effects, we can calculate a discretized signal vector $\mathbf{s}\in {ℂ}^{1\times N_t}$ from Equations (1) and (2). This vector describes the observed signal at N_t time points, and is used to calculate the Fisher information matrix $\mathbf{F}\in {ℂ}^{3\times 3}$ whose entries are ${\mathbf{F}}_{i,j}={\mathbf{b}}_i^H{\mathbf{b}}_j/{\sigma }^2$, where the vectors b_i describe the derivatives of the signal evolution with respect to all model parameters

$${\mathbf{b}}_1=d\mathbf{s}/\text{d}{M}_0,{\mathbf{b}}_2=d\mathbf{s}/{\text{dT}}_1,{\mathbf{b}}_3=d\mathbf{s}/{\text{dT}}_2,$$ (3)

and the superscript H denotes the complex conjugate transposed. By normalizing with M₀, the input variance σ², the duration of the experiment T_exp = N_tT_R, the repetition time T_R, and the squared relaxation time, we can define the relative Cramér-Rao bounds to be

$$rCRB\left({\text{T}}_1\right)=M_0^2\frac{{\left({\mathbf{F}}^{-1}\right)}_{2,2}}{{\sigma }^2{\text{T}}_1^2}\frac{T_{\text{exp}}}{T_R}$$ (4)

$$rCRB\left({\text{T}}_2\right)=M_0^2\frac{{\left({\mathbf{F}}^{-1}\right)}_{3,3}}{{\sigma }^2{\text{T}}_2^2}\frac{T_{\text{exp}}}{T_R}.$$ (5)

The normalization by $M_0^2$ cancels out the M₀ scaling factor in the input signal, as does the σ² with the variance in the definition of the Fisher information matrix. The normalization by the squared relaxation time is performed in order to best reflect the T_1,2-to-noise ratio (defined as $T_{1,2}/{\sigma }_{T_{1,2}}$), and the normalization with T_exp∕T_R makes the rCRB invariant to the number of measurements so that it describes the noise efficiency per unit time. In absolute numbers, the noise in the resulting parameter estimations is given by

$${\sigma }_{T_{1,2}}\ge \frac{\sigma \cdot T_{1,2}}{M_0}\sqrt{rCRB\left(T_{1,2}\right)\frac{T_R}{T_{\text{exp}}}}.$$ (6)

Note that the simulations published in Ref. 13 indicate that the actual noise in the estimated parameters is close to this bound. Without loss of generality, we assume M₀ = 1 for all theoretical considerations.

Given that ϑ is the effective drive of the spin dynamics,¹³ we optimized ϑ directly and picked the sequence parameter (α, T_R, ϕ) retrospectively (cf. Equation (2)). Equation (1) is an uncoupled first order differential equation and can be solved for different boundary conditions.¹³ Here, we focus on inversion-recovery balanced hybrid-state free precession (IR-bHSFP) sequences, i.e., hybrid-state sequences that depart from thermal equilibrium by the application of an inversion pulse, which is accounted for by the boundary condition r(0) = −1.

We used a Broyden-Fletcher-Goldfarb-Shanno (BFGS) algorithm²⁸ with rCRB(T₁), rCRB(T₂) and rCRB(T₁) + rCRB(T₂) as objective functions. The numerical optimization was based on (nT_R) with the repetition time of T_R = 4.5 ms and with n ∈ {1, 2, …, N_t}. The derivatives in Equation (3) were calculated analytically, as was the gradient of the objective function with respect to each (nT_R).

Since the rCRB intrinsically compares a fingerprint to its neighborhood in the parameter space, only a single set of relaxation times was used for the optimization. In particular, we used the relaxation times T₁ = 781 ms and T₂ = 65 ms, which correspond to values reported for white matter¹ at 3T. All optimizations were initialized with the pattern provided in Ref. 11.

We performed the above optimizations of IR-bHSFP sequence that exploit the full quadrant of the Bloch sphere (0 ≤ ϑ ≤ π/2), and repeated the same optimizations with 0 ≤ ϑ ≤ π/4 in order to limit the flip angle to α ≤ π/2, ensuring consistent slice profiles by virtue of the linearity in the small tip-angle approximation,²⁹ and aiding compliance with safety considerations by avoiding high power large flip-angle pulses. For comparison, we also performed unconstrained optimizations of Look-Locker³⁰ and multi-spin-echo experiments.

2.3 |. In vivo experiments

An asymptomatic volunteer’s brain was imaged following written informed consent, and according to a protocol approved by our institutional review board. Measurements were performed with the IR-bHSFP sequences that minimize rCRB(T₁), rCRB(T₂) and rCRB(T₁) + rCRB(T₂), limited to 0 ≤ ϑ ≤ π/4. All experiments were performed on a 3T Prisma scanner (Siemens, Erlangen, Germany). The 44 head elements of the manufacturer’s 64 channel head/neck coil were used for signal reception. At the beginning of the sequence, a secant inversion pulse³¹ with a duration of 10.24ms was applied, followed by a spoiler gradient. The other RF-pulses were implemented as slice-selective sinc pulses with a time-bandwidth product of two and a duration of 1 ms.

Spatial encoding was performed with a radial trajectory and a golden angle increment.³² The spatial resolution of the maps is 1 mm × 1 mm × 3 mm at a FOV of 256 mm × 256 mm × 3 mm. The readout dwell time was set to 2.4 μs and an oversampling factor of 2 was applied. The total scan time of each sequence was approximately 3.8 s. In order to allow for a noise-analysis, we repeated the scan with each of the three sequences 49 times, separated by a 10 s pause in order to allow the magnetization to relax to thermal equilibrium. The k-space trajectory of consecutive scans were rotated by the tiny golden angle³³ φ_tGA ≈ 32.04°.

The raw data were compressed to eight virtual receive coils via SVD compression.³⁴ Thereafter, image reconstruction was performed with the low rank alternating direction method of multipliers^35,36 (ADMM) approach proposed in Ref. 37. A rank 6 subspace was estimated from a coarse dictionary³⁸ that was computed with Equations (1) and (2) and covered the range of T₁ values between 300 ms and 6 s and T₂ values in the range of 10 ms and 3 s, both in logarithmic steps of 10%. The data consistency step of the ADMM algorithm was performed with 20 conjugate gradient steps.

In the second step, the relaxation times were estimated with a nonlinear least-squared fit directly on the data in this low-rank sub-space. The fitting algorithm accounts for the slice profile and finite pulse duration³⁹ by approximating the profile by 12 isochromats, evenly distributed over the range with signal larger than 0.5% of the maximum value. For each of these isochromats, we calculated ϑ(t) with Bloch- simulations and retrospectively discretized this function to steps of 50 μs. This pre-calculated ϑ(t) was then plugged into the hybrid-state simulation based on Equation (1). Further, we correct for B₀ and B₁ based on separate scans with a double-echo SPGR and a turboFLASH⁴⁰ sequence, respectively. In order to prevent nonlinear effects from complicating the noise assessment, only a single ADMM iteration was performed and no spatial regularization was applied.

3 |. RESULTS

3.1 |. Spin dynamics on the Bloch sphere

Figure 2 depicts the hybrid-state spin ensemble trajectories and the corresponding driving functions ϑ(t) that were numerically optimized for T₁ and/or T₂ encoding. Some features are shared by all patterns, while others differ depending on the figure of merit. In the paragraphs that follow, the common features are described first, followed by the optimization-specific features.

FIGURE 2.

The spin dynamics in inversion recovery balanced hybrid-state free precession (IR-bHSFP) sequences are depicted on Bloch-spheres (A, D, G, J, M, and P). The polar angle patterns are shown in (B, E, H, K, N, and Q), with the color scale providing a reference for the trajectories on the Bloch-sphere. The absolute value of the magnetization (with a negative sign indicating the southern hemisphere) and its normalized derivatives with respect to the relaxation times are the foundation of the relative Cramér-Rao bound and are shown in (C, F, I, L, O, and R). The optimizations depicted in the left-hand column are limited to 0 ≤ ϑ ≤ π/2, while the right-hand column shows the same optimizations with the limit 0 ≤ ϑ ≤ π/4

All patterns are comparatively smooth, which is not explicitly enforced by the optimization. They start with a nonrecurring inversion segment on the southern hemisphere, followed by repetitive loops on the northern hemisphere. The beginning of the first loop differs slightly from that of the other loops, which can be explained by the initial conditions of the loop. At the time when the magnetization crosses the origin (turquoise segments in Figure 2), the derivatives with respect to the relaxation times are comparatively large. Furthermore, the derivative with respect to T₂ has not yet changed its sign. These two properties make this segment a valuable asset to help minimize the correlation between the derivatives with respect to the two relaxation times. As a consequence, the optimized trajectories have a comparatively large polar angle in this segment. In contrast, the subsequent loops start with a segment in which the magnetization recovers along the z-axis, reflecting small and correlated derivatives.

Another common feature of all trajectories is that the polar angle decreases rapidly when the shrinking magnetization reaches the steady-state ellipse (magnifications in Figure 2A, D, G, J, M, P). The arrival at the steady-state ellipse (blue ellipse in Figure 2) also concludes the last loop in the T₂-specific and in the jointly optimized patterns so that they take advantage of the T₂-dominated shrinkage of the magnetization (D, G, M, P). By contrast, the T₁-specific trajectories (A, J) conclude by maximizing r and dr∕dT₁ and then briefly bringing the prepared magnetization close to the equator in order to maximize the signal.

Taking a closer look at the T₁-optimized hybrid-state pattern, we observe that the spin trajectory stays close to the z-axis on the southern hemisphere and close to the origin on the northern hemisphere (Figure 2A), which is exactly the behavior we expect from the intuitive understanding of the derivatives (Section 2.1). In fact, the numerical optimization suggests that it is beneficial to forgo any signal at the beginning of the sequence (dark blue segment) in favor of an information-rich signal thereafter. Comparing the unconstrained optimization (0 ≤ ϑ ≤ π/2) with the constrained one (0 ≤ ϑ ≤ π/4), we find that the spin trajectory remains virtually unaffected on the southern hemisphere (Figure 2J–L). On the northern hemisphere, however, the unconstrained pattern exploits the maximum polar angle of π/2 to quickly kill the magnetization and create a sort of saturation- recovery loop. When the polar angle is constrained, on the other hand, the magnetization shrinks more slowly and, consequently, fewer loops can be performed in the same amount of time.

When a hybrid-state sequence is optimized purely for T₂ encoding without constraining the polar angle, the magnetization first decays along the equator (Figure 2D), which is in agreement with the intuitive understanding described in Section 2.1. As r approaches zero, its derivatives with respect to the relaxation times become small as well and the spins follow a trajectory along the z-axis (bright blue segment). Thereafter, the spins follow large loops that probe the spin dynamics far from the z-axis where the derivative d²|r|∕(dtdT₂) is large (cf. Figure 1C). Surprisingly, the optimization does not result in further segments with ϑ = π/2. Instead, the trajectory traverses this value only briefly as the magnetization approaches the origin, before dropping to ϑ = 0. Limiting the polar angle to 0 ≤ ϑ ≤ π/4 distorts the spin trajectory and the maximum value ϑ = π/4 is exploited during several segments (M, N).

After the inversion pulse, the trajectory of the combined optimization oscillates between large and small ϑ-values. The corresponding derivatives of the magnetization have peaks that are shifted with respect to one another (Figure 2G–I). The size of the loops lies in between the ones of the T₁- and T₂-optimized trajectories. When the polar angle is limited to 0 ≤ ϑ ≤ π/4, the spin trajectory is distorted in a similar way as for the T₂-optimized case.

The hybrid-state equation of spin motion (Equation (1)) can be written in a dimensionless form (Equation S1 in the supporting information), which highlights the fact that only the ratios T_exp∕T₂ and T₁∕T₂ of the involved time constants affect the hybrid-state spin trajectories. Varying T_exp∕T₂ in the joint optimization results in different trade-offs between the inversion phase and the repetitive loops (see Supporting Information Figure S1). Short sequences (T_exp ≈ T₂) require a T₂-optimized inversion phase similar to Figure 2M since the temporal constraints allow only for small, T₁-dominated loops. Increasing the sequence duration allows for larger loops so that the optimized inversion phase increasingly trades T₂ for T₁ encoding (cf. Figure 2P). Long sequences (T_exp ≫ T₂) use a T₁-optimized inversion-recovery segment (cf. Figure 2J) followed by a combination of large loops, which predominantly encode T₂, and smaller loops, which provide additional T₁ encoding (Supporting Information Figure S1). In this limit, the shape of the loops changes little when varying T_exp and—considering the non-convexity of the optimization landscape—we can cautiously conclude that a combination of these two loops is superior to other loops, given the particular set of relaxation times.

Supporting Information Figure S2 analyzes the effect of T₁∕T₂ variations on the spin ensemble trajectory and demonstrates that the optimized loop size decreases as the ratio between T₁ and T₂ increases. Large T₁ values limit how much the magnetization can grow within a given time. Therefore, the optimized ϑ-pattern spends most of the time for this recovery and the resulting loop size is small. One can further observe that the optimization of rCRB(T₁) + rCRB(T₂) results in different trade-offs between T₁ and T₂ encoding at different T₁∕T₂ ratios (Figure S2C). At intermediate ratios, the algorithm slightly favors the T₁-encoding, which is reflected both in the Cramér-Rao bound and in the corresponding spin ensemble trajectory, as evident by the inversion-recovery segment. Both at small and large ratios, the individual Cramér-Rao bounds are similar.

3.2 |. The Cramér-Rao bound

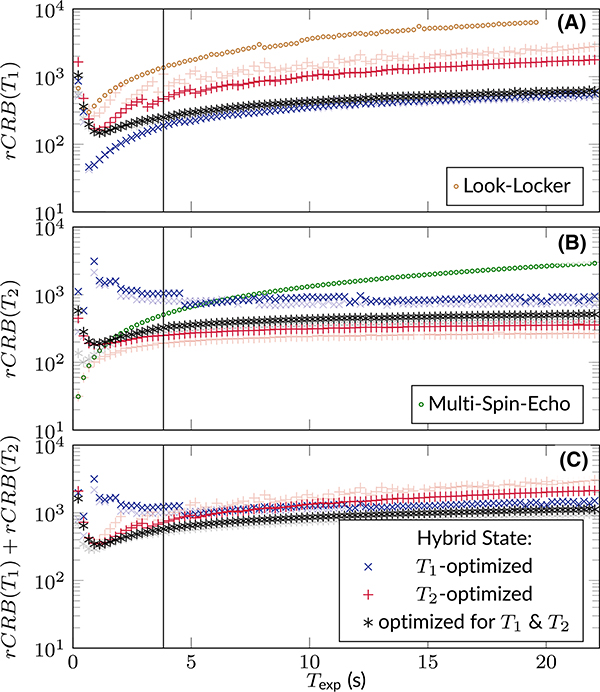
This section analyzes the SNR-efficiency of different optimized spin ensemble trajectories. Examining rCRB(T₁), we can observe that the purely T₁-optimized trajectories shine most at short experiment durations T_exp (Figure 3A).As the duration increases, the advantage of the T₁-optimized trajectories over the joint optimizations starts to vanish. At T_exp = 3.8 s, which is used for the in vivo experiments, we expect only a minor advantage of the T₁-optimized sequence in comparison to the joint optimization. In contrast, the T₂-optimized sequence shows a poor T₁-encoding power. Furthermore, we can see that the limit ϑ ≤ π/4 compared to ϑ ≤ π/2 has only minor effects on the T₁ and joint optimizations (light colored vs. dark colored marks in Figure 3). For comparison, we also show the Cramér-Rao bound of an optimized Look-Locker sequence³⁰ in which we also allowed the flip angle to vary over time. One can observe a substantially worse performance compared to the hybrid state, even if one is interested only in T₁.

FIGURE 3.

The depicted relative Cramér-Rao bounds are defined by Equations (4) and (5) and can be understood as a lower bound of the squared inverse SNR efficiency per unit time. They result from numerical optimization for rCRB(T₁), rCRB(T₂), and rCRB(T₁) + rCRB(T₂), while limiting the polar angle to 0 ≤ ϑ ≤ π/2 (lightly colored markers) and 0 ≤ ϑ ≤ π/4 (dark colored markers), respectively

Examining rCRB(T₂), we also find the difference of the purely T₂-optimized and the jointly optimized sequences to be rather small (Figure 3B), especially when limiting the polar angle to π/4. The T₁-optimized patterns, on the other hand, show a poor T₂-encoding. For comparison, we also depict the Cramér-Rao bound of a multi-spin-echo sequence. For short experiments, this sequence has the same rCRB(T₂) as the hybrid-state sequence that was optimized for T₂ without constraining ϑ. In fact, in this limit, both optimizations result in the same sequences (not shown here). For long experiments, however, the performance of the multi spin-echo sequence does degrade and the more general hybrid state allows for more efficient sequence design.

Overall, we can observe that the rCRB has a minimum at T_exp ≈ T₁. For longer T_exp, the Cramér-Rao bound asymptotically approaches a constant value, which corresponds to the standard averaging property $SNR\propto \sqrt{T_{\exp }}$ of Gaussian noise. This is in line with the optimized spin trajectories in the limit of long T_exp, where a change in T_exp results in negligible changes in the shapes of the loops, instead merely adding averages over the same loop.

So far, the Cramér-Rao bound was analyzed only at the specific T₁ = 781 ms and T₂ = 65 ms that were used for the optimization. Figure 4 shows the performance of sequences optimized for these particular relaxation times over the range of T₁ and T₂ values commonly found in biological tissue. We found that optimizing for a single set of relaxation times does not merely result in good performance in the proximity of this set of parameters (visualized by the red dot), but over a large area in the T₁-T₂-space. In fact, the lowest Cramér-Rao bound is located at relaxation times different from those used during the optimization.

FIGURE 4.

The performance of IR-bHSFP sequences optimized with 0 ≤ ϑ ≤ π/4 (Figure 2J–R) is illustrated through plots of the relative Cramér-Rao bounds, which provide a lower bound for the noise in the estimated relaxation times. All patterns were optimized for T₁ = 781 ms and T₂ = 65 ms, as indicated by the red square, and were tested for the entire parameter space in a sample MRF dictionary. Note the logarithmic scale in all three dimensions

3.3 |. Correlation coefficients

In order to relate the Cramér-Rao bound analysis in Figure 4 to the matching procedures commonly used in MRF, we calculated the correlation coefficient β between the dictionary atoms. Figure 5 depicts the correlation between the fingerprint corresponding T₁ = 781 ms and T₂ = 65 ms (red square) and the other fingerprints in the dictionary. These results are in good agreement with the rCRB plots shown in Figure 4. Optimizing for a single relaxation time results in a comparably narrow peak of high correlation coefficients in the optimized dimension and a broad peak along the other dimension. The broadest peak is observed along T₂ in the T₁-optimized sequence, which is in agreement with the Cramér-Rao bound analysis (Figure 4). The joint optimization results in narrow peaks along both dimensions and confirms that adding a second relaxation time to the optimization has a very small penalty on the original relaxation time.

FIGURE 5.

The performance of IR-bHSFP optimized with 0 ≤ ϑ ≤ π/4 (Figure 2J–R) is illustrated through plots of the correlation of the fingerprint using the optimization parameters T₁ = 781 ms and T₂ = 65 ms (red square) with the rest of the parameter space

Figure 6 shows maximum intensity projections of the full correlation matrix among all fingerprints in the dictionary. These projections can be understood as the worst case correlations for a single parameter under consideration of all values of the other parameter. The generally larger rCRB(T₂) compared to rCRB(T₁) (cf. Figure 4) is reflected by the correlation coefficients. These findings confirm that the joint optimization results in encoding power that is comparable to respective specialized sequences. Further, the least precise encoding is along T₂ when using the T₁-optimized sequence, as already found in the Cramér-Rao bound analysis.

FIGURE 6.

The performance of IR-bHSFP optimized with 0 ≤ ϑ ≤ π/4 (Figure 2J–R) is depicted through plots of the correlation coefficient. The correlation matrix was calculated for the entire parameter space. Thereafter, a maximum intensity projection was performed along the T₂ (A-D) and the T₁-dimension (E-H), respectively. The result can be understood as the worst case correlations for a single parameter under consideration of all values of the other parameter. The red lines indicates the set of parameters used for optimizing the patterns

3.4 |. In vivo experiments

Figure 7 depicts quantitative in vivo maps acquired with the patterns shown in Figure 2K, N, Q. The total scan time of each experiment was 3.8 s. Systematic deviations can be noted in the measured relaxation times between the three sequences. This becomes even more evident when averaging the relaxation times over 49 experiments (Figure 8). Compared to literature (Table 1), we can observe a mild under-estimation of T₁, and T₂-values that are less than half of the relaxation times of ex vivo mouse samples, measured with an extensive protocol that does not have the time-, hardware-, and safety-related limitations we have for in vivo imaging. This underestimation is slightly less pronounced when using the T₂-optimized sequence.

FIGURE 7.

The in vivo data were acquired with the excitation patterns depicted in Figure 2K, N, and Q with the limit 0 ≤ ϑ ≤ π/4. The parameter maps have an in-plane resolution of 1 mm and were acquired in 3.8 s. Note the logarithmic scale of the T₁ and T₂ color maps

FIGURE 8.

The parameter maps are the average of 49 measurements like the one shown in Figure 7, each acquired in 3.8 s with a 10 s pause in between. Note the logarithmic scale of the T₁ and T₂ color maps. The red rectangles indicate the regions of interest used for calculating the values in Table 1

TABLE 1.

The relaxation times are the mean values depicted in Figure 8 and the standard deviation (cf. Figure 9) of the 49 experiments, both averaged over respective region of interest. Therefore, the standard deviation does not reflect biological variations over the region of interest and is dominated by thermal noise

	White matter		Gray matter		CSF
	T1 (ms)	T2 (ms)	T1 (ms)	T2 (ms)	T1 (ms)	T2 (ms)
T1-optimized	961 ± 59	29.9 ± 5.5	1789 ± 48	43.7 ± 4.0	4494 ± 378	1421 ± 782
T2-optimized	1100 ± 75	33.7 ± 2.8	1738 ± 60	48.6 ± 2.5	4256 ± 223	1642 ± 969
optimized for T1 & T2	963 ± 59	29.4 ± 3.2	1672 ± 55	43.0 ± 3.1	4354± 215	1079 ± 647
Ref. 41	1084 ± 45	69 ± 3	1820 ± 114	99 ± 7

Figure 9 verifies the noise properties predicted by the Cramér-Rao bound (Figure 4). As anticipated, the purely T₁-optimized pattern has superior noise performance in T₁, most notably in gray matter. This agrees with Figure 4A, which reveals a lower Cramér-Rao bound for longer relaxation times, as typically found for gray matter in comparison to white matter. The predicted poor T₂-encoding of the T₁-optimized sequence is also reflected in a low ${\text{T}}_2/{\sigma }_{T_2}$, especially in white matter (Figure 9D). We find a higher ${\text{T}}_2/{\sigma }_{T_2}$ in gray matter, which is also in good agreement with the Cramér-Rao bound (Figure 4D). As predicted, the purely T₂-optimized and the jointly optimized sequences have very similar noise performance, with a slightly higher ${\text{T}}_1/{\sigma }_{T_1}$ in the jointly optimized sequence (Figure 9B vs. C) and a slightly higher ${\text{T}}_2/{\sigma }_{T_2}$ in the T₂-optimized sequence (Figure 9E vs. F).

FIGURE 9.

In order to verify the theoretically derived noise properties, we depict the mean relaxation times divided by the standard deviation over the 49 consecutive experiments. This metric provides an analog to the signal-to-noise ratio. The upper limit of this metric is directly proportional to the square root of the inverse rCRB(T_1,2)

4 |. DISCUSSION

Steady-state free precession sequences¹⁵ are known for their superior signal-to-noise efficiency. However, in first approximation, they only allow for a T₁∕T₂ contrast, limiting their clinical versatility. In the context of quantitative MRI, it has been suggested to disentangle T₁ and T₂ information with a second measurement using an SPGR sequence,⁴ or by exploiting deviations from this first order approximation.⁴² The latter approach requires deviating from the on-resonance condition (ϕ = π) and driving the magnetization into the stop band (i.e., the banding artifact). In the stop band, the spin-echo-like nature of the bSSFP sequence breaks down,²⁷ which introduces a sensitivity to the Larmor frequency distribution and can result in systematic errors in the presence of multiple spectral peaks.^43,44 Driving the magnetization’s magnitude into a transient state, on the other hand, enables efficient encoding of T₁ and T₂ on resonance.^6,13 When the direction of the magnetization is maintained in a steady state, the spin-echo-like nature of the bSSFP sequence is preserved, and the signal response becomes comparatively robust to the frequency distribution.¹³

The hybrid state constitutes a large sequence design space, and the main purpose of this paper is to shed some light on the optimal encoding of spin relaxation times in this space. The adiabatic behavior of the magnetization’s direction traps the spin dynamics in a single dimension. This reduces the equation of spin motion to a single, uncoupled first order differential equation (Equation (1)), which may be conveniently visualized (Figure 1). Insights gleaned from an intuitive understanding of the governing equation were found to align well with numerical optimizations (Figure 2). Numerically searching for the optimal spin trajectories is a non-convex problem, so we can only speculate about the optimality of our results. However, the notable correspondence to the intuitive understanding of the governing differential equation, together with the number of reproducible features in the optimized trajectories, gives us confidence that the obtained numerical results are closely related to the truly optimal trajectories.

The Cramér-Rao bound was used as figure of merit since it provides a universal lower bound for the noise transfer from a time series to the estimated parameters. It also provides the flexibility to tailor the acquisition to, e.g., encode T₁ while accounting for correlations in T₂-space. Within the limits of this analysis—most notably our neglect of the incomplete spatial encoding and the non-convexity of the optimization problems—we showed that the hybrid state has superior SNR properties compared to traditional methods, namely Look-Locker for T₁-encoding and multi-spin-echo sequences for T₂-encoding. Moreover, we found that the joint optimizations have nearly the same performance in encoding each relaxation time compared to hybrid-state sequences that are specialized to encode a single parameter. Thus, the second relaxation time can be measured at virtually no extra cost.

The rCRB has a minimum around T_exp ≈ T₁. For a 2D multi-slice experiment, this suggests that one should use this optimal value and interleave multiple acquisitions of each slice. However, such short T_exp requires the repetition of power-consuming slice-selective inversion pulses that could exceed the overall SAR limit. Therefore, we used T_exp ≈ 3.8 s as a compromise that allows for single-inversion imaging of a single slice with 1mm in-plane resolution.

Here, we optimized the sequences only for a single set of relaxation times, which correspond to values typical for white matter. However, we found that the resulting optimized sequences perform well over a large range of relaxation times. To extend this property further, one could optimize for the sum of the Cramér-Rao bounds at different relaxation times. Another option could be to minimize the maximum Cramér-Rao bound of multiple parameters and multiple parameter values. However, the non-linearity of such norms might impair the convergence of the optimization.

Our least-constrained optimizations used the limits −1 ≤ r(t) ≤ 1 and 0 ≤ ϑ(t) ≤ π/2. This unusual definition of spherical coordinates was chosen to deliberately prohibit magnetization from revisiting the southern hemisphere after passing through the origin. This allows us to implement the RF-pulses without major violations of the small tip-angle approximation. However, we demonstrated the benefits of the southern hemisphere and for long experiments as might be required, e.g., for 3D imaging, it might be desirable to revisit the southern hemisphere. This could be achieved by simply changing the limits to 0 ≤ r(t) ≤ 1 and 0 ≤ ϑ(t) ≤ π. However, this would change the optimization landscape, and the convergence behavior might be impaired. Alternatively, one could use anti-periodic boundary conditions, as demonstrated in Ref. 13.

The primary purpose of the present work was to analyze the noise properties of hybrid-state sequences when quantifying relaxation times. Even though we correct for B₀ and $B_1^{+}$ inhomogeneities, as well as the slice profile and the finite duration of the RF-pulses, we found substantial systematic errors in the relaxation times measured in vivo (Figures 7 and 8), whereas, in previous work, we demonstrated good agreement between hybrid-state and gold standard measurements in a phantom.¹³ It is known that the Bloch equation applies well to uniform liquids, but is an over-simplification of signal acquired in biological tissue as it neglects diffusion-mediated dephasing and magnetization transfer effects, among others.^41,45–49 Since the hybrid-state model was derived from the standard Bloch equation, it inherits this oversimplification, and we believe this to be the predominant cause for the systematic deviations from literature values.

Simultaneously avoiding diffusion-mediated dephasing and magnetization transfer is a key challenge for in vivo relaxometry. The decay of the transverse magnetization occurs on two distinct scales.⁴⁸ At the molecular level, the intrinsic T₂-relaxation originates from molecular rotations with a correlation time on the order of nanoseconds.^50,51 The cellular scale, present in biological tissues, provides a different relaxation mechanism, where spins diffuse through susceptibility-induced magnetic fields varying on the scale of ∼1-10 μm, causing temporal field fluctuations with a correlation time of ∼1-100 ms, depending on the tissue composition.^45–48 This loss of coherence can be partially undone by applying refocusing pulses. Since the timing of standard MR pulse sequences is exactly in this range, the overall T₂-relaxation crucially depends on the specifics of the sequence. Thus, measuring the intrinsic, molecular T₂ in vivo requires employing refocusing pulses with echo-spacing shorter than the corresponding correlation time. Depending on the tissue, standard CPMG⁵² and bSSFP sequences,^15,27 as well as balanced hybrid-state sequences¹³ approximate this requirement well. Therefore, we believe diffusion-mediated dephasing to be negligible in the hybrid-state. However, the repeated refocusing in any of those sequences requires a high duty cycle of the RF-pulses. In biological tissue, this saturates the magnetization of protons bound in macro-molecules, which are found in myelin, cell membranes, etc.^53,54 Therefore, apart from some very time-consuming methods,^41,49 most standard methods for measuring relaxation times are corrupted by cross-relaxation between the macro-molecular and the free water pool. We attribute the systematic errors observed here (Figure 8) to this effect, similar to Ref. 55. Note that the hybrid state model can be extended to include magnetization transfer,⁵⁶ and our preliminary data indicate that such a model describes the spin dynamics in good agreement with literature.

5 |. CONCLUSION

The goal of this paper was to provide insights into optimized encoding of spin relaxation times in order to guide the design of robust and efficient pulse sequences. We reviewed how the Bloch equation can be simplified under the hybrid-state adiabaticity condition and demonstrated the intuition that can be gained from this simplification. Further, we showed that numerical optimizations of hybrid-state sequences reproducibly converge to spin trajectories that align well with intuitive understanding. We analyzed the SNR efficiency of the optimized hybrid-state sequences, demonstrated superior efficiency in comparison to traditional methods, and highlighted the good agreement between theoretical Cramér-Rao bounds and experimentally-observed noise properties. Future work will translate the insights gained in this work to hybrid-state models that include more complex phenomena, such as magnetization transfer, which we consider central for fast and reproducible quantification of tissue properties.

Supplementary Material

Supplementary Figures 1 and 2

FIGURE S1 The influence of the duration the experiment T_exp on the spin ensemble trajectory is analyzed at the example of the joint optimization for T₁ and T₂. Note that essentially T_exp∕T₂ is varied by keeping T₂ = 65 ms fixed. In order to run the animation, please use a PDF-viewer capable of Java-Script, such as the Adobe Acrobat Reader

FIGURE S2 The influence of T₁ on the spin ensemble trajectory is analyzed at the example of the joint optimization for T₁ and T₂. Note that essentially T₁/T₂ is varied by keeping T₂ = 65 ms fixed. In order to run the animation, please use a PDF-viewer capable of Java-Script, such as the Adobe