Determinants of Photolyase’s DNA Repair Mechanism in Mesophiles and Extremophiles

Abstract

Light-driven DNA repair by extremophilic photolyases is of tremendous importance for understanding the early development of life on Earth. The mechanism for flavin adenine dinucleotide repair of DNA lesions is the subject of debate and has been studied mainly in mesophilic species. In particular, the role of adenine in the repair process is poorly understood. Using molecular docking, molecular dynamics simulations, electronic structure calculations, and electron tunneling pathways analysis, we examined adenine’s role in DNA repair in four photolyases that thrive at different temperatures. Our results indicate that the contribution of adenine to the electronic coupling between the flavin and the cyclobutane pyrimidine dimer lesion to be repaired is significant in three (one mesophilic and two extremophilic) of the four enzymes studied. Our analysis suggests that thermophilic and hyperthermophilic photolyases have evolved structurally to preserve the functional position (and thus the catalytic function) of adenine at their high temperatures of operation. Water molecules can compete with adenine in establishing the strongest coupling pathway for the electron transfer repair process, but the adenine contribution remains substantial. The present study also reconciles prior seemingly contradictory conclusions on the role of adenine in mesophile electron transfer repair reactions, showing how adenine-mediated superexchange is conformationally gated.

Graphical Abstract

INTRODUCTION

Early life on Earth developed before the advent of oxygen-evolving plants,¹ encountering extremes of temperature and intense ultraviolet (UV) irradiation. UV irradiation causes photochemical damage to adjacent pyrimidine bases in DNA, forming a cyclobutane pyrimidine dimer (CPD) moiety. This damage can induce mutagenesis and finally lead to cell death.² Photolyases repair UV-induced lesions in DNA using photoinduced electron transfer (ET). Understanding the DNA-repairing ET mechanism of mesophiles and extremophiles may help to shed light on the early evolution of life on Earth. Furthermore, the photoinduced ET function of DNA photolyases makes their structure of great interest in the context of protein engineering and design.^3,4

The repair mechanism of DNA photolyases has been studied extensively.^5–12 DNA repair by photolyase is initiated when an antenna chromophore (Figure 1) absorbs near UV/blue light and transfers its excitation energy to flavin adenine dinucleotide (FADH⁻).¹³ In the photolyase–DNA complex, the pyrimidine dimer flips out of the DNA backbone and comes into van der Waals contact with the excited FADH⁻, which is accessible to DNA through a gap in the protein helical domain.^14–18 The excited FADH⁻ can then donate an electron to the CPD (forward ET), which leads to its cleavage.^{14,17,19–21} After DNA repair, back ET restores the negative charge of the FADH cofactor.²²

Figure 1.

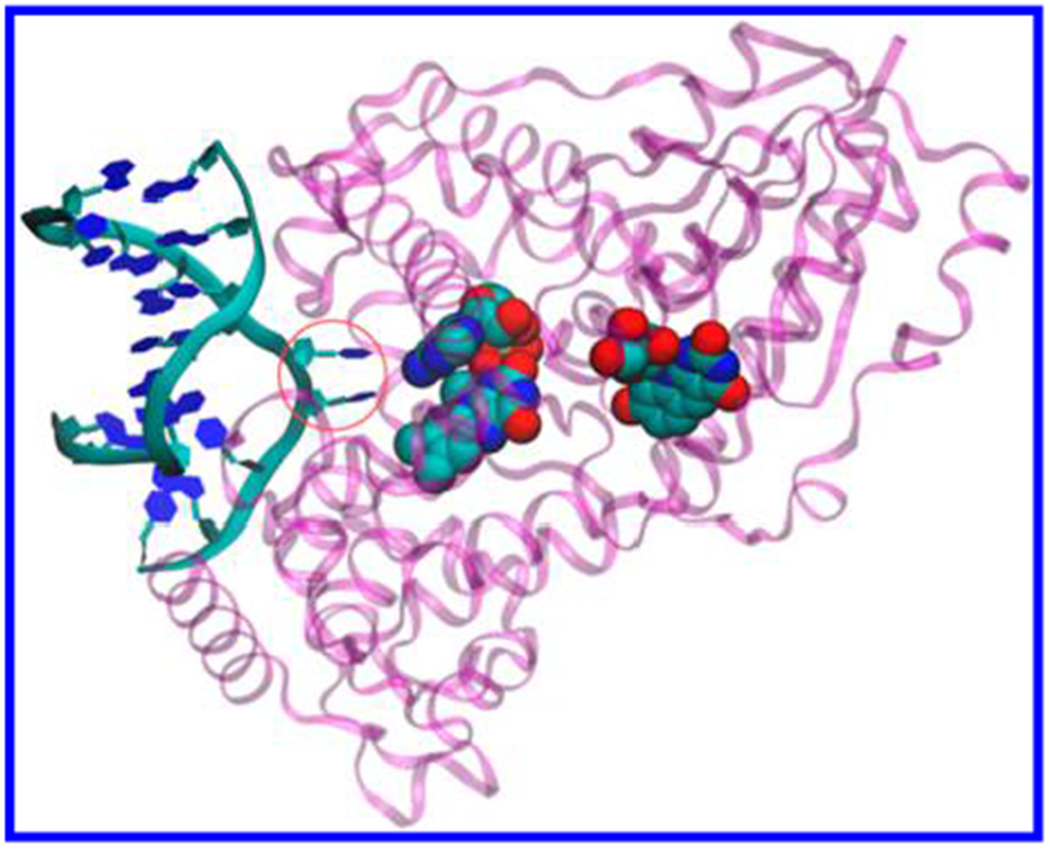
DNA photolyase from A. nidulans (purple) complexed with repaired DNA analog (left) (crystal structure from the PDB file 1TEZ²⁰). ET from the excited FADH⁻ cofactor (CPK representation, center) splits the two thymines in CPD (circled blue hexagons). The 5-deazaflavin antenna cofactor is also shown (CPK representation, right).

The detailed mechanism of the critical forward ET step in the enzyme–CPD complex is poorly understood. Depending on the adenine orientation relative to the flavin and CPD, the electron can tunnel from the flavin donor to the CPD acceptor without the assistance of virtual electronic states localized on the adenine moiety.²³ A previous theoretical study²⁴ identified a shortest tunneling pathway that starts from the terminal methyl group of the flavin and ends on the thymine at the 3′ side of CPD. Portions of the protein cannot enter the gap between the FADH cofactor and the CPD (confirmed by inspection of the molecular dynamics trajectories produced in this study), while water molecules can assist the tunneling process. We refer to the ET repair reaction without adenine mediation as direct ET; the direct mechanism includes through-space and water-mediated tunneling.

The “U” shape of FADH⁻ in DNA photolyases (Figure 2) can allow the adenine to come into proximity with CPD, thus enabling adenine-mediated electron superexchange²⁵ or hopping from flavin to adenine to CPD.²⁴ The electron hopping mechanism was excluded in earlier studies.^25–27 Experiments by MacFarlane and Stanley,⁸ as well as later experiments by Kao et al.,²⁷ found no ET from the flavin to adenine in the absence of DNA substrate, thus ruling out the hopping mechanism. A recent theoretical study by Lee et al.²⁴ supports the possible coexistence of charge hopping and tunneling (either mediated by adenine or not). Wang et al. recently suggested a proton-coupled ET mechanism that proceeds via a water wire.²⁸

Figure 2.

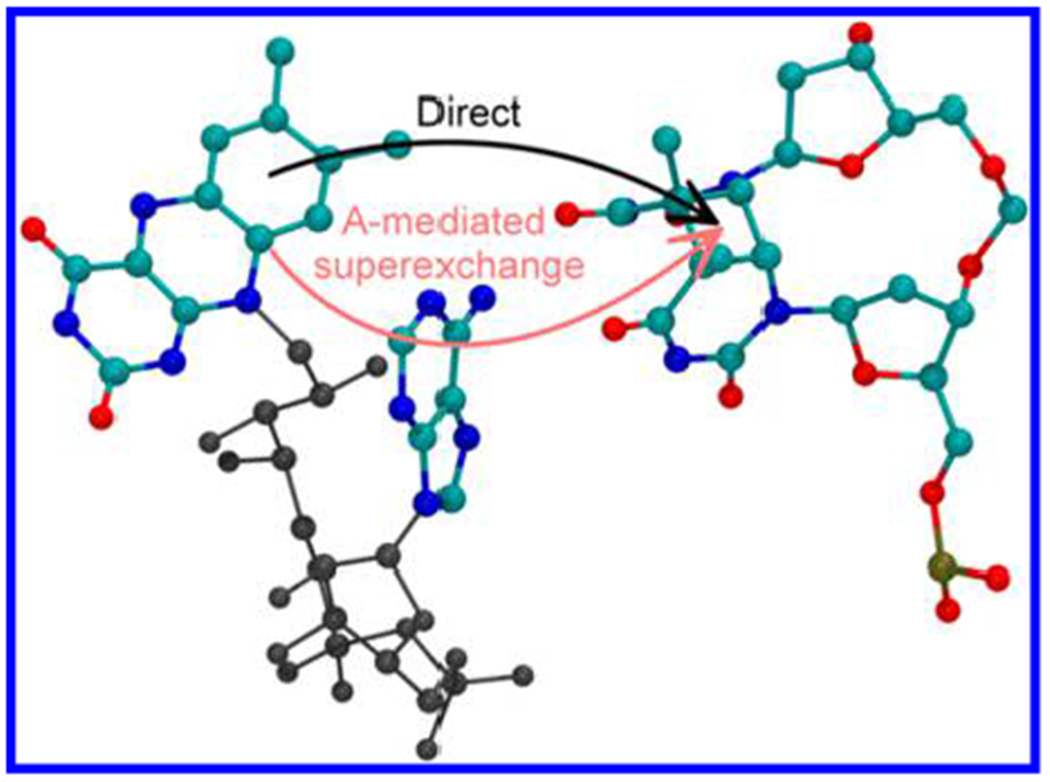
Geometry of FADH⁻ and CPD in E. coli photolyase (from ref 25). The arrows indicate two possible mechanisms for forward ET: direct (not adenine-mediated, in black) ET from flavin to CPD, which includes through-space tunneling and water-mediated tunneling (surrounding water molecules are not shown) and adenine-mediated superexchange (red).

Studies of the forward ET in photolyases provide evidence of both direct ET and adenine-mediated superexchange. Stuchebrukhov et al., in their computational analysis, found that the forward ET rate was sensitive to the presence of adenine and to its distance from CPD.^25,26 Their theoretical finding was corroborated by recent experiments of Liu et al. using ultrafast absorption spectroscopy.^29,30 The experiments were interpreted in the context of non-adiabatic ET theory, ruling out two-step hopping through the adenine and supporting a superexchange mechanism.³⁰ In fact, it was argued that, if hopping were feasible, the first ET step from flavin to adenine could occur in the absence of the DNA substrate, but Kim et al.,¹³ MacFarlane and Stanley,⁸ and Liu et al.^29,30 did not find rapid decay of the FADH⁻ excited state (caused by ET to the adenine) when the DNA substrate was absent.³⁰ However, the change in local environment that is produced by the DNA presence may influence, both geometrically and energetically, a potential ET step from the flavin to the adenine. Furthermore, recent experiments, using photolyases with adenine-modified FAD,³¹ support the possible occurrence of two-step hopping, but a radical anion intermediate of the modified adenine was not observed. Electronic structure calculations by Weber et al. found that the protein environment surrounding the FADH anion favors strong electronic overlap between the flavin radical and the adenine moiety³² (and therefore a large electronic coupling between them³³). The crystal structure of a DNA lesion bound to photolyase after in situ repair shows that the adenine bridges the flavin and CPD with two H bonds, thus supporting adenine-mediated superexchange.²⁰

The theoretical and experimental studies mentioned above support a one-step tunneling mechanism for ET rather than hopping, but these studies do not quantify the relative importance of direct ET vs adenine-mediated superexchange. Theoretical analysis by Prytkova et al.²³ found that the lowest electronic excited state of FADH⁻ is localized on the side of the flavin farthest from adenine and closest to CPD (“proximal side”), suggesting a role for direct ET.

The recent theoretical study of Lee et al.²⁴ identified eight possible pathways for ET from the excited FADH⁻ to CPD. Two of these pathways involve sequential electron hopping through adenine. The other six ET paths involve tunneling, and start from the two lowest-lying singlet excited states of FADH⁻, which originate in localized ππ* excitations of the flavin. The computations²⁴ did not distinguish between direct and adenine-mediated ET pathways.

Here, we focused on the mechanisms of electron tunneling from flavin’s excited electronic states to CPD. We used quantum chemistry calculations, molecular dynamics (MD) simulations, and electron tunneling pathway analysis to assess the role of adenine as a superexchange mediator in four photolyases from mesophiles and extremophiles. We found that adenine conformational flexibility can cause the charge transfer repair reaction to occur either by direct ET or by adenine-mediated superexchange, and we explored how the balance of the two ET mechanisms varies among proteins that operate at different temperatures.

MATERIALS AND METHODS

Enzymes Studied.

We studied two mesophilic (Anacystis nidulans³⁴ and Escherichia coli¹⁵), one thermophilic (Thermus thermophilus),¹⁹ and one hyperthermophilic (Sulfolobus tokodaii)³⁵ photolyases (Table 1). The structure of S. tokodaii photolyase is more similar to that of A. nidulans photolyase (sequence similarity of about 35%) than to the structures of E. coli (32%) or T. thermophilus (28%) photolyases. However, all four proteins have large structural homology in the FADH⁻ binding domain.

Table 1.

Summary of Photolyases Studied

organism	optimal growth temperature (°C)	simulation temperature (°C)	classification
A. nidulans (PDB: 1QNF34)	unknowna	20b	mesophile
E. coli (PDB: 1DNP15)	37	20 and 37	mesophile
T. thermophilus (PDB: 1IQR19)	~60	60	thermophile
S. tokodaii (PDB: 2E0I35)	80	80	hyperthermophile

^aThe A. nidulans crystal structure in the 1QNF file was obtained for the PCC 6301 strain of S. elongatus. Recently, an optimal growth temperature of 33 °C was reported for the PCC 7942 strain of this bacterium.³⁶

^bCrystallization temperature.

Molecular Docking.

We used the structure of E. coli photolyase¹⁵ in a complex with the CPD moiety from ref 25. For A. nidulans, T. thermophilus, and S. tokodaii photolyases, we docked the CPD to photolyase using the Autodock Vina program.³⁷

The docking was preceded by thermal equilibration of the separated enzyme and CPD. Since the crystallization temperatures do not match the bacterial physiological growth temperatures (at which the photolyases operate), classical MD simulations were used to equilibrate the DNA photolyases at their physiological temperatures (we carried out 10⁵ energy minimization steps, followed by 50 ps of equilibration at constant temperature, 200 ps of equilibration at constant temperature and pressure, and 2.5 ns of MD simulation). The CPD moiety was equilibrated at the physiological temperatures of the different photolyases using a similar protocol (see Supporting Information (SI)). Five structure snapshots separated by 0.5 ns were taken from the final MD trajectory of each protein and the CPD moiety at the pertinent temperature. The two molecular components were then docked, producing 25 conformations for each complex. The initial conformations of the T. thermophilus and A. nidulans complexes for the ET study were selected, from the 25 conformations available for each of them, as the docked structures that were most consistent with structural information on protein–DNA complexes obtained in previous crystallographic studies of these two enzymes.^19,20 By exploiting the homology of different photolyases in their active domains^15,19,35 (this homology is strictly related to the highly conserved CPD recognition mechanism in DNA photolyases^20,25), we selected the docked structure of the FADH⁻–CPD complex in S. tokodaii that has the minimum geometric difference from the active domain structure of A. nidulans photolyase (PDB: 1QNF³⁴). The initial structures chosen for the four photolyases are shown in Figure 3.

Figure 3.

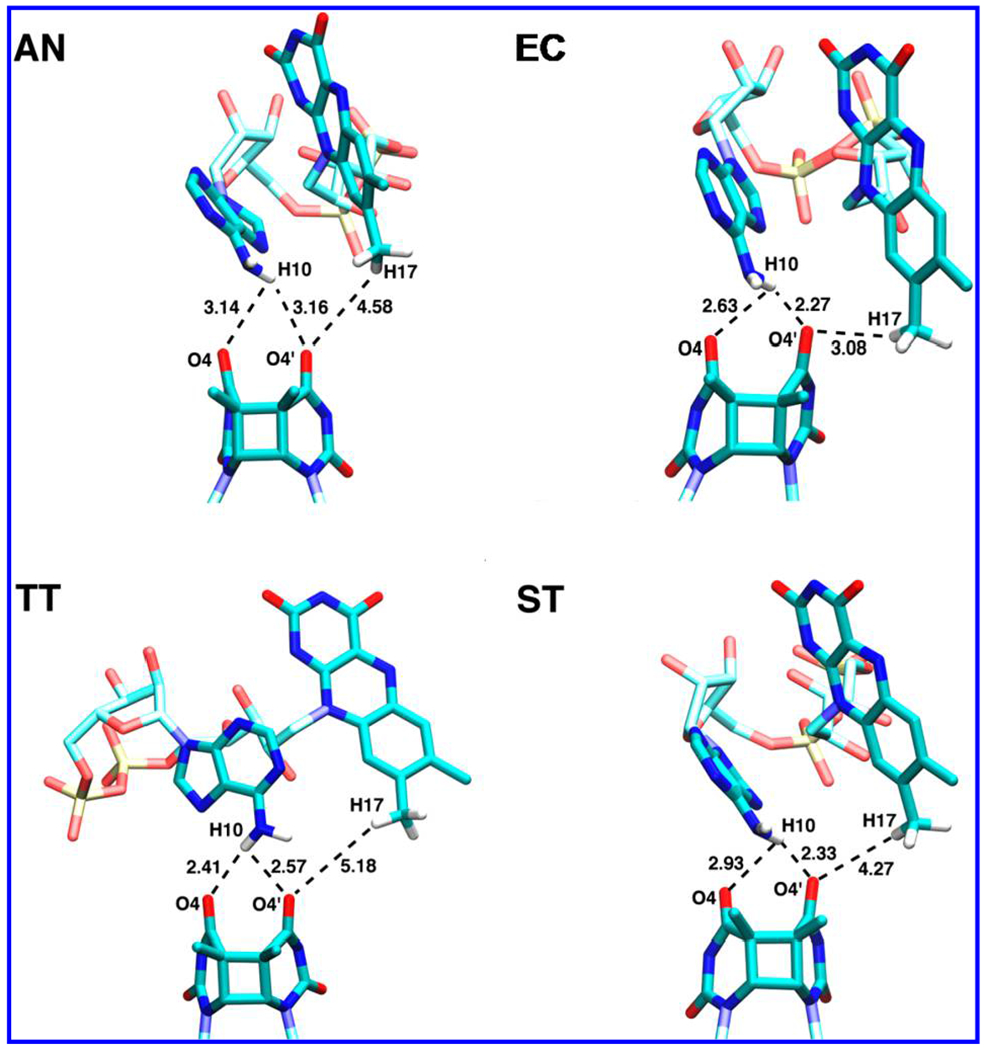
Docked FADH⁻–CPD conformations used in the ET study: the structures of the photolyase–CPD complex in E. coli (EC) from ref 25, and the crystal structures produced by our docking protocol for A. nidulans (AN), T. thermophilus (TT), and S. tokodaii (ST). Only the hydrogen atoms at the FADH⁻–CPD interface are shown in this picture.

MD Simulations.

The Amber12 software package³⁸ and AMBER force fields (ff12SB) were used to describe the interactions. Parametrizations for CPD and FADH⁻ were taken from a modified version³⁹ of the force field developed by Antony et al.²⁵ The overall system was charge neutralized with Na⁺ ions⁴⁰ and solvated in a box of TIP3P water extending 10.0 Å on each side of the complex.⁴¹ The SETTLE algorithm⁴² was used to constrain the hydrogen atom positions relative to the heavy atoms. The particle mesh Ewald method⁴³ was used to calculate the electrostatic interactions in the system. A Langevin thermostat and piston^44,45 were used to control the temperature and pressure (see SI). Trajectories of 60 ns each were produced for the four systems using the NAMD software package.⁴⁶ A total of 10 000 conformations were extracted from the last 50 ns of the MD for ET analysis. The ET pathway analysis was performed over time ranges of different length (25 and 50 ns) to test the robustness of the results with respect to the simulation time.

Tunneling Pathways Analysis.

The pathway model^47–50 identifies through-bond and through-space interactions that mediate tunneling between the donor (D) and acceptor (A).^51,52 The D–A pathway-mediated coupling (H_DA) is approximated as

$$H_{\text{DA}}\text{∝}\prod _i{\epsilon }_{\text{C}}(i)\prod _j{\epsilon }_{\text{H}}(j)\prod _k{\epsilon }_{\text{S}}(k)$$ (1)

In eq 1, i, j, and k denote the through-covalent bond, through-hydrogen bond, and through-space steps between D and A. ε_C, ε_H and ε_S are the decay factors for the corresponding superexchange steps:⁵³

$$\begin{gathered} {\epsilon }_{\text{C}}=0.6 \\ {\epsilon }_{\text{H}}={{\epsilon }_{\text{C}}}^2{\text{e}}^{-{\beta }_{\text{S}}(R_{\text{H}}-2.8)} \\ {\epsilon }_{\text{S}}={\epsilon }_{\text{C}}{\text{e}}^{-{\beta }_{\text{S}}(R_{\text{S}}-1.4)} \end{gathered}$$ (2)

where R_H (R_S) is the length in angstroms of the H-bond (through-space) step and β_S = 1.1 Å⁻¹.^53,54 The strongest electron tunneling pathway is produced by the combination of steps that maximizes the product in eq 1.

We used the VMD⁵⁵ pathways plugin⁵³ to identify and to visualize the strongest ET pathways from FADH⁻ to CPD. For each photolyase–DNA complex, pathway analysis was used on all selected MD snapshots to compute the fraction of strongest coupling pathways that contain adenine atoms. This fraction is a measure of adenine’s role in mediating D-to-A superexchange.

Electron Donor and Acceptor.

We carried out density functional theory (DFT) calculations on the pruned flavin (Figure 4) to describe the donor charge distribution in the pathway model, rather than to assume a uniform charge distribution. This enables improved assessment of adenine’s role as a superexchange mediator. Two facts allow us to limit the DFT analysis to the pruned flavin moiety (without including the adenine in the excited electronic state analysis): (i) We are treating electron tunneling from the excited flavin donor, so we can disregard the charge-transfer excited states that correspond to ET from flavin to the adenine moiety, which were considered to study the hopping mechanism in ref 24. (ii) D-to-A tunneling proceeds from excited electronic states that are localized with the flavin.²⁴ The excitations were identified and characterized using the NWChem⁵⁶ and Gaussian⁵⁷ software packages, using time-dependent DFT (TDDFT) at different levels of computational accuracy (basis set: cc-pVTZ;⁵⁸ exchange-correlation functionals: PBE0,⁵⁹ M06-2X,⁶⁰ CAM-B3LYP,⁶¹ and B3LYP⁶² in conjunction with the Casida-Salahub’00 asymptotic correction⁶³). These flavin excitations consist essentially of an electron transition from the Kohn–Sham highest occupied molecular orbital (HOMO) of FADH⁻ to its lowest unoccupied molecular orbital (LUMO) or to the LUMO+1 (see next section).

Figure 4.

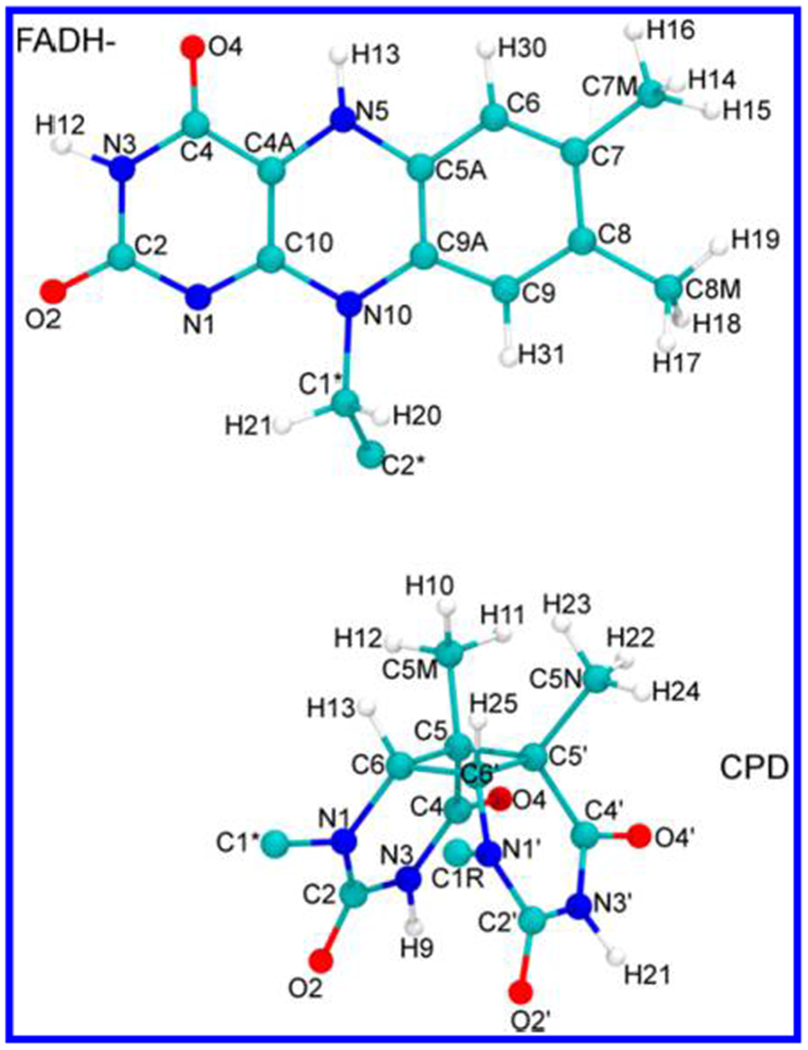
Pruned flavin (above) and CPD (below) used for DFT and TDDFT calculations. The dangling C2* atom in FADH⁻, and the C1*, C1R atoms in CPD, were replaced with hydrogen atoms. The molecular geometries were optimized at the B3LYP/6-31g* level before carrying out the single-point electronic structure calculations described in the text.

For each of the two flavin excited electronic states considered (that is, in the single-particle approximation, for the LUMO and the LUMO +1), we computed the strongest coupling pathways starting from all atoms with non-zero amplitude of the pertinent molecular orbital. The pathways were weighed by the contributions of the starting and ending atoms to the molecular orbital, which were calculated using the Mulliken population analysis.⁶⁴ The wave function ψ (either the LUMO or the LUMO+1) is expanded in a non-orthogonal set of normalized basis functions {χ_i}:

$$\psi =\sum _{i=1}^N{c}_i{\chi }_i$$ (3)

The integrated electron density associated with ψ is

$$\parallel \psi \parallel \equiv {\int |\psi (\mathbf{r})|}^{2}d\mathbf{r}=\sum _p{\mathit{\mu }}_p^{\text{D}}$$ (4)

where

$${\mathit{\mu }}_p^{\text{D}}\equiv {\left[{\int |\psi (\mathbf{r})|}^{2}d\mathbf{r}\right]}_p=\sum _{i\in p}\sum _{j=1}^N{c}_i{c}_j{S}_{ij}$$ (5)

is a measure of the fraction of ∥ψ∥ on atom p. S_ij is the overlap of χ_i and χ_j. In the sum, p indicates the set of electron basis functions localized on the given atom. ${\mu }_p^{\text{D}}$ is an atomic electron-localization factor,⁶⁵ identified with the Mulliken electron population of atom p when the molecular orbital ψ is occupied by the excited electron charge.

The singly occupied molecular orbital (SOMO) of the anionic CPD was used in the pathway analysis to describe the distribution of transferred charge on the acceptor. The SOMO was calculated at the M06-2X/cc-pVTZ level of theory, and was similarly partitioned among the CPD atoms, thus generating a further atomic weighting factor ${\mu }_q^{\text{A}}$ for the ET pathways terminating on atom q of the acceptor. An ET pathway connecting atom p of D to atom q of A is therefore weighted by the factor ${\mu }_p^{\text{D}}{\mu }_q^{\text{A}}$.

The LUMO and LUMO+1 of the flavin, as well as the SOMO of the CPD moiety, depend weakly on the nuclear geometry,⁶⁶ and this dependence is neglected.

Role of Adenine in Forward ET.

The ET pathways were used in the following protocol to assess the contributions of the direct ET mechanism and the adenine-mediated superexchange to the forward ET:

1. For each MD snapshot, the pathways plugin⁵³ was used to identify the strongest coupling pathway linking each D–A atom pair (p, q).

2. For each (p, q) pair, a Python program was used to calculate the fraction $f_{pq}^{\text{DA}}$ of system snapshots with adenine atoms in the strongest pathway.

3. The average fraction f of strongest ET pathways that include adenine (that is, our measure of adenine-mediated superexchange contribution to forward ET) was calculated as⁶⁷

$$f=\sum _{p,q}{\mathit{\mu }}_p^{\text{D}}{\mathit{\mu }}_q^{\text{A}}{f}_{pq}^{\mathrm{DA}}$$ (6)

This fraction f ranges between 0 and 1. Zero corresponds to direct ET. One corresponds to the opposite limit in which $f_{pq}^{\text{DA}}=1$ for any p,q. That is, when f = 1, at least one adenine atom is included in all of the strongest ET pathways connecting each D–A atomic pair in the different snapshots (entirely adenine-mediated tunneling). Adenine-mediated superexchange is at play in a given structural snapshot even if adenine atoms are involved in only a fraction of the strongest ET pathways between D–A atomic pairs. However, f is less than one in this case. In addition, there can be structure snapshots where adenine is not involved in the strongest ET pathway but participates in a pathway of very similar strength (multiple tunneling pathways and their possible interferences were not considered in this analysis). Thus, a value of f that is an appreciable fraction of unity indicates an important superexchange mediation role for adenine in repair ET.

RESULTS AND DISCUSSION

Flavin and CPD Electronic States.

Our TDDFT analysis (Table 2) finds that the two lowest-lying singlet excited electronic states of flavin, S1 and S2, correspond approximately to electron transitions from the HOMO to the LUMO and to the LUMO+1, respectively. Only calculations that use the CAM-B3LYP exchange-correlation functional describe the S2 state as arising from an electron excitation to the LUMO+2. This result arises from the interchange of the LUMO+1 and LUMO+2 that can be ascribed⁶⁸ to the incompleteness of the basis set and the small energy difference (less than 0.1 eV) between the two molecular orbitals. B3LYP and PBE0 functionals underestimate the S2 excitation energy compared to the observed absorption maximum of FADH^– in DNA photolyase at 3.5 eV.⁶⁹ The two other functionals, with a larger Hartree–Fock exchange component, produce an excitation energy for S2 that is only slightly larger than the experimental value. Overall, the computed S1 and S2 state energies are in agreement with the experimental values, which correspond approximately to wavelengths of 425 and 360 nm, respectively.^69,70 In fact, considering the averages of the excitation energy values from the different functionals as our best estimates and using confidence intervals of 95%, we find the excitation wavelengths (413 ± 12) nm and (364 ± 11) nm for S1 and S2, respectively. Previous experimental and theoretical studies (see ref 24 and references therein, as well as ref 70) describe the S1 excitation energy as lying between the computed PBE0 and M06-2X values, while only the latter functional produces the observed order of magnitude for the small oscillator strength associated with this excitation. Overall, the M06-2X density functional showed the best agreement with the experiment on the properties of the S1 and S2 states, and was thus used to calculate the LUMO and LUMO+1 of the flavin (Figure 5), as well as the SOMO of CPD.

Table 2.

Vertical Excitation Energy (ΔE) and Oscillator Strength (OS) of S1 and S2 Flavin States, from TDDFT Calculations with the Indicated Density Functionals^71a

	S1		S2
TDDFT method	ΔE	OS	ΔE	OS
B3LYP + ‘00	2.79	10−4	3.15	0.123
	444		394
PBE0	2.89	2 × 10−4	3.26	0.132
	429		380
M06-2X	3.17	10−3	3.62	0.168
	391		342
CAM-B3LYP	3.20	2 × 10−4	3.63	0.166
	387		342
experimental wavelength69,70 (nm)	~425		~360

^aFor each method, the excitation energies are given first, in eV units, with the corresponding wavelengths, in nm, below.

Figure 5.

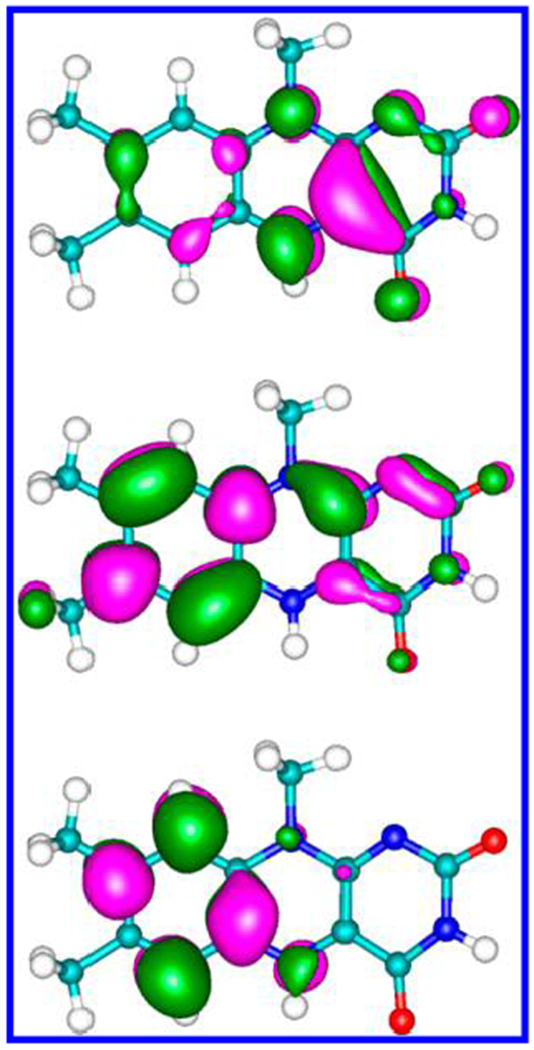
HOMO (top), LUMO (middle), and LUMO+1 (bottom) of the flavin, calculated using DFT with the M06-2X density functional and the cc-pVTZ basis set.

The charge distributions of the LUMO and LUMO+1 on the flavin atoms are reported in detail in SI, Table S1 (which also contains the atomic decomposition of the SOMO of CPD) and shown in Figure 5 (cf. Figures 4 and 5). The C7 and C9A atoms make the largest contributions to the LUMO, in agreement with the results of Prytkova et al.²³ that found significant electronic localization on the proximal side of flavin, especially on C6, C7, C9 and C9A. Our results for CPD are consistent with the SOMO localization on the C2═O2, C4═O4 carbonyl groups reported by Antony et al.²⁵ However, Table S1 shows that many other flavin and CPD atoms need to be included in the analysis to describe the role of adenine in the forward ET. In fact, D and A atoms with small electron-localization factors can be linked by efficient coupling pathways. In our pathways analysis, we included all possible D–A atom pairs.

Tunneling Mediated by Adenine.

By substituting the localization factors of Table S1 and the $f_{\mathit{pq}}^{\mathit{DA}}$ values calculated from the MD simulations in eq 6, we computed the average fraction f of adenine-mediated strongest ET pathways for each photolyase species (Table 3).

Table 3.

f Values, in Percentage Form, for A. nidulans (AN), E. coli (EC), T. thermophilus (TT), and S. tokodaii (ST) Photolyases at the Listed Temperatures (in K), with the Flavin Initially in the S1 or S2 State

	species, temperature
	AN, 293	EC, 293	EC, 310	TT, 333	ST, 353
	from 25 ns of MD production run
f (S1)	32%	28%	3%	33%	36%
f (S2)	30%	23%	2%	32%	34%
	from 50 ns of MD production run
f (S1)	33%	26%	5%	30%	31%
f (S2)	31%	21%	3%	28%	29%

There is a significant adenine-mediated superexchange contribution to the ET repair reaction when CPD is complexed with the photolyases in A. nidulans (mesophile) and in the two extremophiles (T. thermophilus and S. tokodaii) at their physiological temperatures. In contrast, the predominant ET mechanism in the E. coli photolyase at its physiological temperature (37 °C) is direct ET, with only about 3% of the strongest ET pathways mediated by adenine. When E. coli photolyase is simulated at the same temperature as the A. nidulans photolyase (20 °C), the contribution of the superexchange mechanism to the forward ET also becomes important in the E. coli species. This change is ascribed to a more nearly locked adenine orientation between flavin and CPD at lower temperatures (see below).

Effects of Conformation, Temperature, and Water on the Adenine-Mediated ET.

The MD trajectory explains the tunneling mediation role of adenine in E. coli photolyase as a function of temperature. In this enzyme, at 310 K, the adenine portion of FADH⁻ frequently exhibits a “tilted” geometry with respect to CPD (Figure 6). At 293 K, adenine rarely exhibits this tilted conformation, remaining largely in a conformation proximal to the DNA lesion that supports superexchange. Our MD simulations of the four photolyase species indicate that adenine can fluctuate between the tilted and proximal conformations, but the population of the tilted conformation is significantly higher in the mesophilic photolyase of E. coli than in the photolyases of the other three species studied at their respective physiological temperatures.

Figure 6.

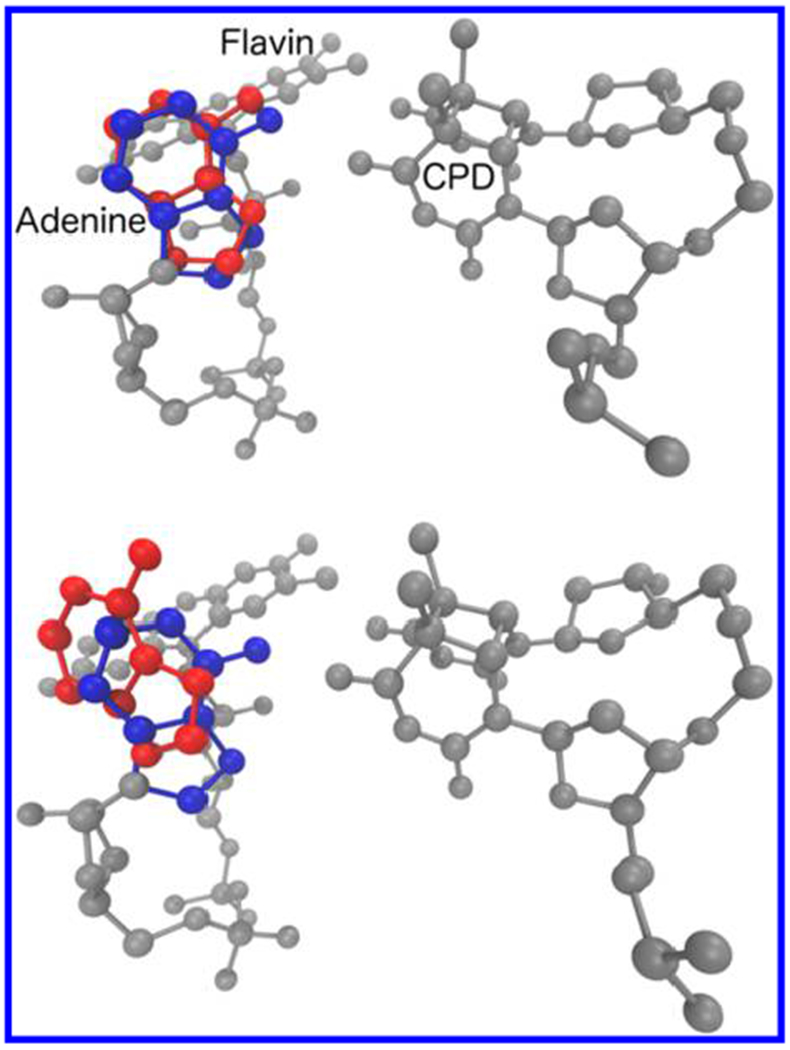
Tilted conformation of E. coli adenine (red) at 310 K (bottom) and 293 K (top) compared to the typical proximal conformation (blue) seen in the other DNA photolyases.

Adenine flipping between two geometries in the simulations helps to explain the origins of the debate in the literature regarding the role of adenine in the CPD repair. For example, Prytkova et al.²³ found that direct ET dominates the ET repair reaction in E. coli photolyase, which was ascribed to a geometry of the enzyme that is similar to the average geometry obtained in our MD simulation at 310 K. The looser architecture of the flavin and CPD when the adenine is tilted is expected to reduce the D–A electronic coupling and to increase its sensitivity to geometry, in agreement with the small value of the coherence parameter^72–74 reported in ref 23. A different average position of the adenine with respect to the flavin and CPD may have led to the opposite conclusion, namely that adenine mediates forward ET, in the theoretical study by Antony et al.²⁵ The tilted adenine that we found at 310 K (that is, 10 K above the temperature used in ref 25) may explain the reduced ET-mediation role of adenine at this temperature, and this result motivates future MD studies to assess the population of this geometry that arises at longer times. Reducing the temperature to 20 °C locks the complex in a conformational subspace that favors adenine-mediated tunneling. We conclude that, in E. coli DNA photolyase, adenine-mediated superexchange is conformationally gated, with an occurrence that depends on temperature.

The f values computed for the A. nidulans mesophile and for the two extremophiles indicate an important role for adenine in mediating ET from the photoexcited flavin to the CPD lesion (in agreement with recent experimental findings on mesophiles^12,30). We also found that water can cause appreciable fluctuations in the value of f on a nanosecond time scale (see SI section 4), but the occurrence, or lack thereof, of significant adenine mediation of the forward ET is only species and temperature dependent. That is, irrespective of the presence of water, in E. coli photolyase at 37 °C adenine makes a small contribution to the ET mediation, while in the same enzyme at 20 °C, and in the other photolyases studied, adenine significantly contributes to mediate the ET (cf. the upper panel of Table 3 and SI, Table S3). The decrease in f due to water mediation of the forward ET (see SI, section S4) is overestimated by considering only the strongest ET pathway, since ET pathways through adenine and water may have similar donor–acceptor couplings (see SI, Figure S2). Future theoretical studies using multi-pathway analysis will help to quantify the water effects on the extent of adenine’s ET mediation with higher accuracy. While the increase in temperature seems to cause adenine displacement and consequent loss of its role as a tunneling bridge in the case of E. coli, we found a significant adenine role in both extremophiles, despite their significantly higher temperatures of operation. We found an appreciable correlation of the f value with the bacterium growth temperature for the first 25 ns of the MD production run. However, the dependence of f on the species at room temperature is of a size comparable to the f increase with enzyme temperature. Furthermore, the correlation between f and the enzyme temperature is erased by thermal fluctuations over 50 ns of MD simulation (lower panel in Table 3). The adenine contribution to the strongest ET pathway shows a more evident correlation with the bacterial growth temperature if the effect of water on the electron tunneling by superexchange is excluded (SI, Table S3). This finding (taken with the possible coexistence of through-adenine and through-water ET pathways of similar strength) suggests that a correlation may be found in future theoretical investigations by considering multiple electron tunneling pathways and extending the analysis to examine a wider set of photolyase species.

The recent finding of an optimal growth temperature of 33 °C for the PCC 7942 strain of S. elongatus³⁶ suggests that a similar optimal temperature might be found for the PCC 6301 strain. In this event, it would be useful to study (theoretically and experimentally) whether DNA photolyase from A. nidulans above 30 °C experiences a loss of superexchange contribution to the forward ET that is similar to the loss found for the E. coli photolyase.

The significant extent of functional ET by superexchange through adenine in the extremophiles (and its structural implications, as derived from our MD analysis) is consistent with Klinman’s perspective on functional ET in thermophiles,⁷⁵ namely that conformational changes enabled at typical thermophile temperatures allow enzymes to attain a closely packed, rigid, and catalytically efficient active site, at the expense of increased flexibility in other parts of the protein.

CONCLUSIONS

We have combined molecular docking, classical MD simulations, electronic-structure analysis, and pathway analysis to quantify the importance of adenine for mediating electron tunneling from the excited photolyase FADH⁻ to the DNA CPD lesion to be repaired. Our study extends prior theoretical analysis of DNA photolyases to thermophiles and hyperthermophiles, with the aim of understanding photolyase repair mechanisms of relevance to the early stages of life on Earth. The results reported in Table 3 (taken with the relationship, found in this study, between the adenine-mediated repair mechanism and the structure of the FADH–CPD complex) suggest that the early evolution of DNA photolyases favored those species with a sufficiently rigid active domain structure to support adenine-mediated ET, while mesophiles with looser assemblies of the enzyme active domain could appear at a later stage of the photolyase evolutionary history. Therefore, adenine mediation is also expected to influence the efficiency of the biologically important forward ET. This expectation may be tested in future calculations of the coupling between FADH⁻ and CPD (aiming to find out whether the direct ET mechanism or the adenine-mediated superexchange mechanism leads to faster repair by ET), as well as through theoretical or experimental adenine-mutation studies.

Our results explain the extent of direct ET (through space or water mediated) vs through-adenine superexchange in the forward ET reaction from the flavin to the DNA lesion. Either mechanism can prevail, depending on thermal access to the corresponding photolyase conformations. Our MD simulations indicate the possible occurrence of two adenine geometries that produce the two different tunneling mechanisms, thus providing a consistent explanation of the divergent conclusions on adenine mediation role in previous studies.^23,25 The population of the two adenine conformations is expected to be enzyme and temperature dependent. At 293 K, we found a somewhat higher adenine-mediated superexchange contribution to the forward ET for A. nidulans compared to E. coli photolyase. Since the temperatures at which these two enzymes function are expected to differ by a few degrees, it will be useful to investigate the role of adenine in the A. nidulans DNA photolyase above 30 °C. This investigation could show whether the ET mediation roles of adenine in A. nidulans and in E. coli. photolyases decrease at similar temperatures, or if there is a temperature range where adenine’s role is significantly different in the two mesophile enzymes (species-dependent adenine role).

Our simulations and f-value analysis indicate that adenine is positioned stably between flavin and CPD in extremophile photolyases. In the E. coli mesophile photolyase, adenine tends to flip out of the region between the flavin and CPD at the enzyme operation temperature of 37 °C (see SI, Figure S3). For photolyase from A. nidulans mesophile, adenine is predominantly located between the flavin and CPD. However, this enzyme might have a working temperature above 30 °C, similar to the case of the PCC 7942 strain of this bacterium,³⁶ with possible effects on the stability of adenine’s position between the flavin and CPD. Simulations of A. nidulans DNA photolyase at temperatures above 30 °C (as well as experimental assessment of the bacterial growth temperature), and of extremophilic DNA photolyases at temperatures different from the optimal growth temperatures, would allow us to establish whether the DNA photolyases of thermophiles and hyperthermophiles, compared to those in mesophiles, maintain the adenine in positions that support superexchange ET over wider temperature ranges.