Statistical properties of cerebral CT perfusion imaging systems. Part II. Deconvolution-based systems

Abstract

Purpose:

The purpose of this work was to develop a theoretical framework to pinpoint the quantitative relationship between input parameters of deconvolution-based cerebral computed tomography perfusion (CTP) imaging systems and statistical properties of the output perfusion maps.

Methods:

Deconvolution-based CTP systems assume that the arterial input function, tissue enhancement curve, and flow-scaled residue function k(t) are related to each other through a convolution model, and thus by reversing the convolution operation, k(t) and the associated perfusion parameters can be estimated. The theoretical analysis started by deriving analytical formulas for the expected value and autocovariance of the residue function estimated using the singular value decomposition-based deconvolution method. Next, it analyzed statistical properties of the “max” and “arg max” operators, based on which the signal and noise properties of cerebral blood flow (CBF) and time-to-max (t_max) are quantitatively related to the statistical model of the estimated residue function [k*(t)] and system parameters. To validate the theory, CTP images of a digital head phantom were simulated, from which signal and noise of each perfusion parameter were measured and compared with values calculated using the theoretical model. In addition, an in vivo canine experiment was performed to validate the noise model of cerebral blood volume (CBV).

Results:

For the numerical study, the relative root mean squared error between the measured and theoretically calculated value is ≤0.21% for the autocovariance matrix of k*(t), and is ≤0.13% for the expected form of k*(t). A Bland–Altman analysis demonstrated no significant difference between measured and theoretical values for the mean or noise of each perfusion parameter. For the animal study, the theoretical CBV noise fell within the 25th and 75th percentiles of the experimental values. To provide an example of the theory’s utility, an expansion of the CBV noise formula was performed to unveil the dominant role of the baseline image noise in deconvolution-based CBV. Correspondingly, data of the three canine subjects used in the Part I paper were retrospectively processed to confirm that preferentially partitioning dose to the baseline frames benefits both nondeconvolution- and deconvolution-based CBV maps.

Conclusions:

Quantitative relationships between the statistical properties of deconvolution-based CTP maps, source image acquisition and reconstruction parameters, contrast injection protocol, and deconvolution parameters are established.

1. INTRODUCTION

In a separate Part I paper, the signal and noise properties of cerebral blood volume (CBV) generated from nondeconvolution-based computed tomography perfusion (CTP) systems were analyzed.¹ In this Part II paper, the focus will be switched to the signal and noise properties of deconvolution-based systems. These systems are based on a tracer kinetic model that quantitatively relates tissue enhancement curve with the so-called flow-scaled residue function and arterial input function (AIF) through a convolution operation.² The flow-scaled residue function is modeled as a function of tissue perfusion parameters such as CBV. In principle, by reversing the convolution process, namely deconvolving AIF from the tissue enhancement curve, the flow-scaled residue function and the associated perfusion parameters can be estimated. Although the convolution model may be overly simplified compared with the actual microcirculation processes within brain tissues, it often provides physiologically reasonable results under a broad range of conditions encountered in practice. For example, unlike the nondeconvolution (i.e., slope) method that requires a rapid rise of the contrast uptake curve in order to satisfy the “no venous outflow” assumption,^3,4 the deconvolution method is not as sensitive to the contrast enhancement rate and thus is more robust against possible variations in patients’ cardiac outputs. Due to this and many other advantages,^4,5 deconvolution-based perfusion analysis has been incorporated into the majority of commercial CTP postprocessing platforms and employed at many clinical institutions.^6–8

Despite its popularity, deconvolution has not yet gained universal acceptance as a reliable perfusion analysis method due to substantial variability in its implementation methods that leads to significant differences in the measured values of CTP parameters.^3,4 A common approach to solve the deconvolution problem is to perform singular value decomposition (SVD) of a convolution matrix constructed from the AIF.^4,9–13 As reviewed later in Section 3.A, SVD enables the pseudo-inverse of the convolution matrix, namely the deconvolution matrix, to be estimated algebraically. It was found that the SVD-based deconvolution method can be sensitive to noise and bias in the measured CTP source images and may produce overly oscillatory residue functions that are physiologically improbable.^4,5 Therefore, SVD-based deconvolution usually incorporates additional regularizer(s) such that the derived residue function must be positive and smooth. Owing to differences in the strength and model of the regularizer across different software platforms, substantial variations in the image quality and quantification accuracy were reported in literature.⁵ Besides the variation in regularizer, different ways to construct the convolution matrix or parameterize the contrast enhancement curves have led to other deconvolution methods such as parametric deconvolution and block-circulant SVD.^16–18 As shown in a large-scale comparison study, there is marked variability in the estimated “penumbra” and infarction core among various deconvolution implementation methods.¹³ In another study, the threshold value of tissue perfusion parameter that optimally distinguishes penumbra from benign oligemia in acute stroke patients demonstrated a strong dependence on the deconvolution method.¹⁹ Unless all clinical institutions are mandated to use the same perfusion postprocessing software, this variability impose a major challenge to the standardization of CT perfusion imaging techniques recommended in the Acute Stroke Imaging Research Roadmap.²⁰

To address this challenge, knowledge needs to be gained about deconvolution-based CTP imaging systems, particularly about the signal and noise properties of each perfusion parameter and their quantitative relationship with system components. With a clearer understanding of the relationship, input parameters in these systems can be tuned more synergetically and efficiently, so that biases, uncertainties, and other nonidealities that contribute to intersystem variability can be minimized. This rationale has been widely employed in streamlining other CT applications such as noncontrast head CT (NCCT), where a solid understanding about the quantitative relationship between NCCT image quality and CT system parameters has facilitated the optimization of the NCCT protocol for a given CT scanner, and a thorough understanding about the physical origin of image artifacts has facilitated the development of the corresponding correction methods. These approaches have greatly reduced the variation of NCCT image quality across vendors and scanner models.

To advance knowledge about deconvolution-based CTP systems, a series of research efforts have been made in the previous works. Through a canine study, Nabavi et al. observed that the uncertainty (noise) of cerebral blood flow (CBF) is strongly dependent on the tissue type, as it increased from 17 ml/min/100 g for white matter to 30 ml/min/100 g for gray matter.²¹ In a retrospective study, Murase et al. demonstrated that bias exists in deconvolution-derived CBF maps and the bias is strongly dependent on the x-ray tube current (mA): a lower mA led to a higher bias.²² In another study, van der Schaaf et al. found significant overestimation of CBV and CBF when a thicker source image slice thickness was used, as a thicker slice corresponds to severe partial volume effect (PVE).²³ These experimental studies suggested that the signal and noise properties of a deconvolution-based CTP system depend on the system parameters and scan subject. However, unlike for NCCT and other CT applications, a unified theoretical framework was not available for deconvolution-based CTP system to explain the physical origins and mathematical principles behinds these experimental findings. The absence of such a theory may be attributed to the deconvolution operator and a “max” (maximal value) operator used in CBF calculation: both of these operators seem to be uncommon in linear imaging systems theory compared with other operators such as multiplication and summation.

This article describes how to model these operators so that linear systems theory can be extended to embrace deconvolution-based CTP systems. Some of the theoretical developments such as the signal and noise models of the residue function and the CBV map were previously reported in a conference proceeding paper.²⁴ This Part II paper presents statistical models of additional perfusion parameters such as CBF and time-to-max, and reports in vivo animal results to validate these models. In addition, this work demonstrates how the theoretical framework can be used to answer the following question: what are the quantitative relationships between the signal and noise properties of the parametric perfusion maps, CT acquisition and reconstruction parameters, contrast injection protocol, and the deconvolution method?

2. BRIEF REVIEW OF DECONVOLUTION-BASED CTP SYSTEMS

To facilitate the presentation of the proposed theoretical model, a brief review of deconvolution-based CTP systems is provided in this section. In addition, some mathematical symbols and variables used in this work are summarized in Table I.

TABLE I.

Glossary of symbols

VOI	Volume of interest in the brain tissue
Ca	Contrast concentration at the arterial inlet of a VOI
Cv	Contrast concentration at the venous outlet of the VOI
Ctis	Contrast concentration in the brain tissue
$m_{\text{voi}}^{\text{c}}\left(t\right)$	Mass of contrast in the VOI at time t
$m_{\text{in}}^{\text{c}}\left(t\right)$	Mass of contrast passing though arterial inlet by t
$m_{\text{out}}^{\text{c}}\left(t\right)$	Mass of contrast drained though venous outlet by t
F	Volume of blood passing through the VOI per unit time
$V_{\text{voi }}^{\text{tis }}$	Volume of brain tissue in the VOI
ρ	Mass density of brain tissue
H	Ratio between arterial and capillary hematocrits
h(t)	Probability density function of blood transit time
r(t)	Residue function
k(t)	Flow-scaled residue function
x	Spatial location in the brain
xa	Spatial location of a major feeding artery
$\mathcal{I}\left(x,t\right)$	True pixel value of CTP source image
I(x,t)	Pixel value of the measured source image
Ib(x)	Pixel value of the measured baseline image
I′ (x, t)	Baseline-corrected image: I′ (x, t) = I(x, t) − Ib(x)
c	Measured tissue enhancement curve, vectorized
$\overline{c}$	Expected form of c
c0	Truth of the tissue enhancement curve
biasc	$\overline{c}-c_0$
A	Arterial enhancement convolution matrix
σ1	The largest singular value of A
λ	Weight of regularizer used in deconvolution
λrel	Relative weighting factor: λ = λrelσ1
k*	Estimated flow-scaled residue function
C	Autocovariance matrix of a temporal curve
N	Total number of postbaseline time frames
Nb	Total number of baseline time frames
${\sigma }_0^2$	Noise variance of CTP source images
${\sigma }_{\text{b}}^2$	Noise variance of the baseline image
max	Peak value of a dynamic curve
tmax	Time to peak of the residue function
⊤	Transpose of a matrix or vector
Δt	Time interval between two consecutive source frames
E	The identity matrix
J	The all-one matrix

2.A. Physiological model

Unlike the Doppler ultrasound or other imaging modalities, conventional CT imaging does not directly provide blood flow information. Instead, it requires the injection of an iodinated contrast bolus into the blood circulation system to help “probe” the flow property. In the ideal case, the injected contrast creates a Dirac delta function-like pulse in the dynamic attenuation curve; by measuring the dynamic curve, blood flow information can be estimated based on certain models. The indicator-dilution theory² is such a model: it states that, when an impulse of contrast bolus enters a volume of interest (VOI) in the brain tissue via an arterial inlet, it may follow any of the capillaries inside the VOI to reach the venous outlet. The probability of spending a time of t for the contrast bolus to travel through the VOI can be described by a statistical distribution function h(t). The mean transit time (MTT) for the contrast bolus to travel though the VOI is given by

$$\text{MTT}\triangleq {\int }_0^{\infty }\tau h\left(\tau \right)\text{d}\tau ,$$ (1)

where t = 0 is usually defined at the time point at which the contrast bolus first arrives at the arterial inlet, and thus h(t) = 0 when t < 0.

In reality, the temporal profile of the contrast bolus is wider than an ideal Dirac delta function. In this case, the contrast concentration at the venous outlet (C_v) of a VOI is given by convolving the temporal profile of the contrast bolus with h(t), namely

$$C_{\text{v}}(t)=C_{\text{a}}\left(t\right)⊛h\left(t\right).$$ (2)

In Eq. (2), C_a(t) denotes the contrast concentration curve measured at the arterial inlet and is used as a surrogate for the true temporal profile of the contrast bolus.

Although the contrast concentrations of the arterial inlet and the venous outlet may be different at certain time points, the blood flow rate F, defined as the volume of blood moving through a given VOI per unit time, can be assumed to be constant during the time period of measurement in the absence of blood–brain barrier breakage and bolus dispersion. Based on the principle of mass conservation, the accumulated mass of contrast agent in the VOI at t is given by

$$\begin{gathered} m_{\text{voi}}^{\text{c}}\left(t\right)=m_{\text{in}}^{\text{c}}\left(t\right)-m_{\text{out}}^{\text{c}}\left(t\right) \\ =F{\int }_0^t{C}_{\text{a}}\left(\tau \right)\text{d}\tau -F{\int }_0^t{C}_{\text{v}}\left(\tau \right)\text{d}\tau \\ =F{\int }_0^t{C}_{\text{a}}\left(\tau \right)⊛\left[\delta \left(\tau \right)-h\left(\tau \right)\right]\text{d}\tau . \end{gathered}$$ (3)

Note that the physiological model in Eq. (3) assumes the blood–brain barrier is intact and there is no bolus dispersion. Through integration by parts and based on the general properties of convolution, it can be proven that⁵

$$m_{\text{voi}}^{\text{c}}\left(t\right)=F\cdot C_{\text{a}}\left(t\right)⊛r\left(t\right),$$ (4)

where r(t) is commonly referred to as the residue function. It is related to h(t) by

$$r(t)=\{\begin{array}{ll}1-{\int }_{t_0}^{t}h\left(\tau \right)\text{d}\tau \hfill & t\ge t_0;\hfill \\ 0\hfill & t<t_0,\hfill \end{array}$$ (5)

where t₀ denotes a possible delay time between contrast arrival at the feeding artery and at the tissue VOI. The so-called CBF is defined as the volume of blood moving through a unit mass of brain per unit time, usually with the units of ml of blood per minute per 100 g of brain tissue (ml/min/100 g). It is given by normalizing F with the mass of brain tissue in the VOI:

$$\text{CBF}\triangleq \frac{F}{m_{\text{voi}}^{\text{tis}}}=\frac{F}{\rho V_{\text{voi}}^{\text{tis}}}.$$ (6)

By combining Eqs. (4) and (6), the following relationship can be derived:

$$\begin{gathered} C_{\text{tis}}\left(t\right)\triangleq \frac{m_{\text{voi}}^{\text{c}}\left(t\right)}{V_{\text{voi}}^{\text{tis}}} \\ =\rho \cdot \text{CBF}\cdot C_{\text{a}}\left(t\right)⊛r\left(t\right), \end{gathered}$$ (7)

where C_tis denotes contrast concentration in the tissue VOI. In practice, the right-hand side of Eq. (7) is often divided by a correction factor H that is the ratio between the arterial and capillary hematocrits^8,25,26:

$$C_{\text{tis}}\left(t\right)=\frac{\rho }{H}\cdot \text{CBF}\cdot C_{\text{a}}\left(t\right)⊛r\left(t\right).$$ (8)

Equation (8) describes the quantitative relationship between CBF, contrast concentration curves of tissue and artery, and the residue function.

2.B. Deconvolution-based perfusion measurement method

Based on the physiological model in Eq. (8), perfusion parameters can be estimated from the contrast concentration curves C_a(t) and C_tis(t). In CT imaging, the concentration of iodine be obtained from the CT number based on the following linear relationships:

$$C_{\text{tis}}\left(x,t\right)=\alpha \left[\mathcal{I}\left(x,t\right)-{\mathcal{I}}_b\left(x\right)\right]=\alpha \mathcal{I}\prime \left(x,t\right),$$ (9)

and

$$C_{\text{a}}\left(t\right)=\alpha \left[\mathcal{I}\left(x_{\text{a}},t\right)-{\mathcal{I}}_{\text{b}}\left(x_{\text{a}}\right)\right]=\alpha {\mathcal{I}}_{\text{a}}^{\prime }\left(t\right),$$ (10)

where $\mathcal{I}\left(x,t\right)$ denotes the true CT number at a spatial location x and time point t, x_a denotes the spatial location of the feeding artery, ${\mathcal{I}}_{\text{b}}\left(x\right)$ denotes the true baseline (unenhanced) image, $\mathcal{I}\prime$ denotes the true enhancement in CT number (relative to the baseline), and α is a scaling factor that converts the HU enhancement into the iodine concentration.

By putting the C_a(t) and C_tis(t) formulas in Eqs. (9) and (10) to the convolution model in Eq. (8), α on the two sides of the equation are canceled, leading to the following form:

$$\mathcal{I}\prime \left(x,t\right)=\frac{\rho }{H}\text{CBF}\left(x\right){\mathcal{I}}_{\text{a}}^{\prime }\left(t\right)⊛r\left(x,t\right).$$ (11)

In practice, CBF, r, and ρ are often combined to form the so-called flow-scaled residue function:

$$k\left(x,t\right)\triangleq \frac{\rho }{H}\text{CBF}\left(x\right)r\left(x,t\right).$$ (12)

Correspondingly, Eq. (11) can be written as

$$\mathcal{I}\prime \left(x,t\right)={\mathcal{I}}_{\text{a}}^{\prime }\left(t\right)⊛k\left(x,t\right).$$ (13)

In principle, a deconvolution of $\mathcal{I}\prime \left(x,t\right)$ and ${\mathcal{I}}_{\text{a}}^{\prime }\left(t\right)$ along the temporal dimension can generate k((x,t), from which CBF is given by

$$\text{CBF}\left(x\right)=\frac{H}{\rho }\text{max}\left[k\left(x,t\right)\right].$$ (14)

In reality, the right-hand side of Eq. (14) is often multiplied by 60 × 100 to convert the CBF’s units from [ml/s/g] to [ml/min/100 g].

From the flow-scaled residue function, other perfusion parameters can also be measured. For example, MTT is related to k(x,t) by⁵

$$\text{MTT}\left(x\right)=\frac{1}{\text{max}\left[k\left(x,t\right)\right]}{\int }_0^{\infty }k\left(x,t\right)\text{d}t.$$ (15)

Based on the central volume theorem of CBF = CBV/MTT, it can be proven that CBV is related to k by

$$\begin{gathered} \text{CBV}\left(x\right)=\text{CBF}\left(x\right)\cdot \text{MTT}\left(x\right) \\ =\frac{H}{\rho }{\int }_0^{\infty }k\left(x,t\right)\text{d}t. \end{gathered}$$ (16)

In practice, the right-hand side of Eq. (16) is often multiplied by 100 to convert the units of CBV from [ml/g] to [ml/100 g].

The other commonly used perfusion parameter is the time-to-maximum (t_max) of the flow-scaled residue function, namely

$$t_{\text{max}}\left(x\right)\triangleq \underset{t}{\text{arg}\text{max}}\left[k\left(x,t\right)\right].$$ (17)

In summary, as long the true tissue enhancement curve and the true arterial enhancement curve are available, perfusion parameters such as CBF, MTT, CBV, and t_max can be calculated. In clinical practice, however, a CTP examination only provides a single observation (sample) of $\mathcal{I}\prime \left(x,t\right)$; this observation, denoted as I′(x, t), may deviate from $\mathcal{I}\prime \left(x,t\right)$ as

$$\begin{gathered} I\prime \left(x,t\right)=\overline{I}\prime \left(x,t\right)+\Delta I\prime \left(x,t\right) \\ =\mathcal{I}\prime \left(x,t\right)+\left[\overline{I}\prime \left(x,t\right)-\mathcal{I}\prime \left(x,t\right)\right]+\Delta I\prime \left(x,t\right) \\ =\mathcal{I}\prime \left(x,t\right)+\text{bias}\left[I\prime \left(x,t\right)\right]+\Delta I\prime \left(x,t\right), \end{gathered}$$ (18)

where $\overline{I}\prime$ the expected value of the measured I′; bias(I′) and ΔI′ denote deterministic deviation and stochastic deviation, respectively, of I′ from $\mathcal{I}\prime$. To name a few mechanisms that can contribute to bias(I′): spatial blurring, temporal sampling, PVE, bolus dispersion and delay, etc.

During a clinical workflow, the deconvolution process and the calculation of individual perfusion parameters have to use I′ since the true $\mathcal{I}\prime$ is generally unavailable. The following section concerns the consequence of using I′ to replace $\mathcal{I}\prime$, particularly the corresponding impact on the statistical properties of perfusion maps.

3. STATISTICAL MODEL OF DECONVOLUTION-BASED CTP SYSTEMS

3.A. Flow-scaled residue function

Since CT images are digitized along both the spatial and temporal directions, the analog convolution in Eq. (13) can be discretized as follows:

$$\mathcal{I}\prime (i)=\Delta t\sum _{j=1}^N{\mathcal{I}}_{\text{a}}^{\prime }\left(j\right)k\left(i-j+1\right),$$ (19)

where Δt is the temporal sampling interval of CTP source images. In the remainder of this section, the spatial position x was omitted. However, the theoretical derivations are applicable to an arbitrary x location in the brain parenchyma.

Note that the summation operation in Eq. (19) should exclude the baseline frames since they contribute nothing but zero-mean noise. Therefore, j = 1 refers to the first postbaseline time frame, and N in Eq. (19) denotes the total number of nonbaseline time frames.

The digitized convolution operation in Eq. (19) can be expressed using the following matrix–vector notation as

$$c_0=A_0{k}_0,$$ (20)

where

$$c_0\triangleq {\left[\mathcal{I}\prime \left(1\right),\mathcal{I}\prime \left(2\right),\dots ,\mathcal{I}\prime \left(N\right)\right]}^{\top }$$ (21)

is a N × 1 vector representing the true tissue enhancement curve, k₀ is a N × 1 vector representing the true flow-scaled residue function, and A₀ is given by the following N × N matrix:

$$A_0\triangleq \Delta t\left[\begin{array}{cccc}{\mathcal{I}}_{\text{a}}^{\prime }\left(1\right)& 0& \cdots & 0\\ {\mathcal{I}}_{\text{a}}^{\prime }\left(2\right)& {\mathcal{I}}_{\text{a}}^{\prime }\left(1\right)& \cdots & 0\\ ⋮& ⋮& \ddots & ⋮\\ {\mathcal{I}}_{\text{a}}^{\prime }\left(N\right)& {\mathcal{I}}_{\text{a}}^{\prime }\left(N-1\right)& \cdots & {\mathcal{I}}_{\text{a}}^{\prime }\left(1\right)\end{array}\right].$$ (22)

In principle, the true flow-scaled residue function is given by

$$k_0=A_0^{-1}{c}_0.$$ (23)

Since A₀ is unavailable in the clinical practice, it is replaced by a A matrix constructed by replacing ${\mathcal{I}}_{\text{a}}^{\prime }$ in A₀ by the measured $I_{\text{a}}^{\prime }$. Similar to Eq. (18), A may contain both deterministic and stochastic deviations from A₀:

$$A=A_0+bia{s}_A+\Delta A$$ (24)

$$=\overline{A}+\Delta A,$$ (25)

where bias_A is a lower-triangular matrix built from the bias of measured $I_{\text{a}}^{\prime }\left(t\right)$ relative to ${\mathcal{I}}_{\text{a}}^{\prime }\left(t\right)$. The bias may be induced by PVE, spatial blurring, spatial/temporal sampling, etc. ΔA in Eq. (25) is also lower-triangular matrix constructed from the stochastic noise of $I_{\text{a}}^{\prime }\left(t\right)$. $\overline{A}=A_0+bia{s}_A$ is the expected value of A.

Similarly, c₀ is unavailable in reality and has to be replaced by c≜[I′(1), I′(2), …, I′(N)]^⊤. c is related to c₀ by

$$c=c_0+bia{s}_c+\Delta c$$ (26)

$$=\overline{c}+\Delta c.$$ (27)

The actual deconvolution operates on c and A, and we refer the flow-scaled residue function estimated from c and A as k* to distinguish it from k₀ in Eq. (23). To get k*, matrix A can be inverted by performing its SVD:

$$A=U\Sigma V^{\top },$$ (28)

where Σ is a diagonal matrix containing the singular values of A, U and V are two orthogonal matrices containing the left- and right-singular vectors of A. With the factorization of A in Eq. (28), k* can be estimated using

$$\begin{gathered} k^{*}=A^{†}c \\ =V{\Sigma }^{†}{U}^{\top }c \\ =\sum _{i=1}^R\frac{u_i^{\top }c}{{\sigma }_i}{v}_i, \end{gathered}$$ (29)

where A^† denotes the pseudoinverse of A, σ_i denotes the ith singular value of A (ranked from the largest to the smallested), and R denotes the rank of A.

In practice, a residue function estimated based on the SVD method in Eq. (29) is usually overly oscillatory due to noise and bias in A and c. Therefore, further regularization is needed to obtain a physiological reasonable k*. One of most popular regularization methods is to use the following the Tikhonov weighting factor to suppress the contribution of smaller singular values to A^†:

$$f_{\lambda ,i}=\frac{{\sigma }_i^2}{{\lambda }^2+{\sigma }_i^2},$$ (30)

where λ is related to the largest singular value (σ₁) of matrix A and a dimensionless regularization parameter λ_rel by

$$\lambda ={\lambda }_{\text{rel}}{\sigma }_1.$$ (31)

Using the weighting factor in Eq. (30), a regularized solution of k* is given by

$$k^{*}=\sum _{i=1}^R{f}_{\lambda ,i}\frac{u_i^{\top }c}{{\sigma }_i}{v}_i.$$ (32)

For this Tikhonov regularization method, its solution of k* is identical to that of the following regularized least squares problem (Appendix I):

$$k^{*}=\underset{k\in {ℝ}^N}{\text{arg}\text{min}}\Vert Ak-c{\Vert }_2^2+{\lambda }^2\Vert k{\Vert }_2^2,$$ (33)

The Tikhonov method falls into a more general category of regularization strategy:

$$k^{*}=\underset{k\in {ℝ}^N}{\text{arg}\text{min}}\Vert Ak-c{\Vert }_2^2+{\lambda }^2\Vert \Psi k{\Vert }_2^2.$$ (34)

Here matrix Ψ could be an identity matrix (for Tikhonov method), a gradient matrix, or another operation to incorporate a priori knowledge of the residue function. By negating the partial derivative of the objective function in Eq. (34) with respect to k, the following closed-form solution for k* can be derived:

$$k^{*}={\left(A^{\top }A+{\lambda }^2{\Psi }^{\top }\Psi \right)}^{-1}{A}^{\top }c.$$ (35)

As shown in Appendix II, the expected value of this estimator can be approximated by

$$\begin{gathered} \overline{k^{*}}\approx {\left({\overline{A}}^{\top }\overline{A}+{\lambda }^2{\Psi }^{\top }\Psi \right)}^{-1}{\overline{A}}^{\top }\overline{c} \\ ={\overline{B}}^{\top }\overline{c}, \end{gathered}$$ (36)

where

$$\overline{B}\triangleq \overline{A}{\left({\overline{A}}^{\top }\overline{A}+{\lambda }^2{\Psi }^{\top }\Psi \right)}^{-1}$$ (37)

$$=\left(A_0+{\mathbf{\text{bias}}}_A\right){\left[{\left(A_0+bia{s}_A\right)}^{\top }\left(A_0+bia{s}_A\right)+{\lambda }^2{\Psi }^{\top }\Psi \right]}^{-1}$$ (38)

A comparison between Eqs. (36) and (23) shows that the difference between $\overline{k^{*}}$ and the true flow-scaled residue function k₀ is

$$\overline{k^{*}}-k_0\approx {\overline{B}}^{\top }\overline{c}-A_0^{-1}{c}_0$$ (39)

$$={\overline{B}}^{\top }\left(c_0+bia{s}_c\right)-A_0^{-1}{c}_0$$ (40)

Similarly, Appendix III shows that the autocovariance matrix of k* is given by

$$C_{k^{*}}\approx {\overline{B}}^{\top }{C}_c\overline{B},$$ (41)

where C_c is the autocovariance matrix of the measured tissue enhancement curve c. Note that both C_k* and C_c are defined along the temporal dimension instead of the spatial dimension.

As shown in Appendix IV, C_c is related to the noise variance of the baseline images $\left({\sigma }_{\text{b}}^2\right)$ and the noise variance of nonbaseline source images $\left({\sigma }_0^2\right)$ by

$$C_c={\sigma }_0^{2}E+{\sigma }_{\text{b}}^{2}J,$$ (42)

where E denotes the N × N identity matrix, J denotes the N × N all-ones matrix. If a temporal filter g(t) is applied to the baseline-corrected source images, Eq. (42) becomes

$$C_c=g\left({\sigma }_0^{2}E+{\sigma }_{\text{b}}^{2}J\right)g^{\top }.$$ (43)

As a brief summary of Section 3.A, both the signal and noise properties of the estimated flow-scaled residue function can be quantitatively connected to the signal and noise properties of the CTP source images and other processing parameters such as λ.

3.B. Cerebral blood volume

Based on Eq. (16), the estimated CBV (CBV*) is related to k* by

$$\begin{gathered} {\text{CBV}}^{*}=\Delta t\frac{H}{\rho }\sum _{i=1}^N{k}^{*}\left(t_i\right) \\ =\Delta t\frac{H}{\rho }{J}_{1\times N}{k}^{*}. \end{gathered}$$ (44)

Correspondingly, the expected value of CBV* is directly related to that of k* by

$$\overline{{\text{CBV}}^{*}}=\Delta t\frac{H}{\rho }{J}_{1\times N}\overline{k^{*}}.$$ (45)

The noise variance of CBV* is given by

$$\begin{gathered} {\sigma }_{{\text{cbv}}^{*}}^2=\langle {\left(\Delta {\text{CBV}}^{*}\right)}^2\rangle \\ =\langle {\left(\frac{H\Delta t}{\rho }\right)}^2{J}_{1\times N}{\Delta }_{k^{*}}{\Delta }_{k^{*}}^{\top }{J}_{N\times 1}\rangle \\ ={\left(\frac{H\Delta t}{\rho }\right)}^2{J}_{1\times N}{C}_{k^{*}}{J}_{N\times 1}, \end{gathered}$$ (46)

where 〈·〉 is the expected value operator. As shown in Eq. (46), ${\sigma }_{{\text{cbv}}^{*}}^2$ is related to all elements (both diagonal and nondiagonal) of C_k*. ${\sigma }_{{\text{cbv}}^{*}}^2$ is independent of $\overline{k^{*}}$ and thus independent of $\overline{c}$ and the tissue type.

3.C. Cerebral blood flow

According to Eq. (14), CBF can be estimated from the maximal value of k*. The probability density function of obtaining an arbitrary value of x as the maximal value of k* is²⁷

$$P_{\text{max}\left(k^{*}\right)}\left(x\right)=\sum _{j=1}^N{\int }_{-\infty }^x{\int }_{-\infty }^x{\text{mP}}_{k^{*}}\left(k_j\right)\prod _{i\ne j}\text{d}{x}_i,$$ (47)

where the integration is (N − 1)-dimensional, i is an integer ∈ [1, N], and k_j is an N × 1 vector whose i element is related to the integration variables x_i by

$$k_j[i]\triangleq \{\begin{array}{ll}x\hfill & \text{ if }i=j;\hfill \\ x_i\hfill & \text{ if }i\ne j.\hfill \end{array}$$ (48)

In Eq. (47), mP_k* denotes the multivariate probability density function of k*. Except at ultra-low dose levels, mP_k* usually can be approximated by the multivariate normal distribution as

$${\text{mP}}_{k^{*}}\left(k_j\right)=\frac{\text{exp}\left[-\frac{1}{2}{\left(k_j-\overline{k^{*}}\right)}^{\top }{C}_{k^{*}}^{-1}\left(k_j-\overline{k^{*}}\right)\right]}{\sqrt{{(2\pi )}^N\left|C_k\right|}}.$$ (49)

Based on the probability density function of max(k*) given in Eq. (47), the first and second moments of max(k*) can be obtained as

$$\overline{\text{max}\left(k^{*}\right)}={\int }_{-\infty }^{\infty }x{\text{P}}_{\text{max}\left(k^{*}\right)}\left(x\right)\text{d}x,$$ (50)

and

$$\overline{{\left[\text{max}\left(k^{*}\right)\right]}^2}={\int }_{-\infty }^{\infty }{x}^2{\text{P}}_{\text{max}\left(k^{*}\right)}\left(x\right)\text{d}x.$$ (51)

Since the estimated CBF is linearly related to max(k*) as

$${\text{CBF}}^{*}=\frac{H}{\rho }\text{max}\left(k^{*}\right),$$ (52)

its expected value and noise variance are given by

$$\overline{{\text{CBF}}^{*}}=\frac{H}{\rho }\overline{\text{max}\left(k^{*}\right)},$$ (53)

and

$${\sigma }_{{\text{cbf}}^{*}}^2=\frac{H^2}{{\rho }^2}\left(\overline{{\left[\text{max}\left(k^{*}\right)\right]}^2}-{\left[\overline{\text{max}\left(k^{*}\right)}\right]}^2\right).$$ (54)

As P_max(k*) depends on ${\text{mP}}_{k^{*}}$ in Eq. (49), and mP_k* depends on ${\text{mP}}_{k^{*}}$ that is related to $\overline{k^{*}}$ as shown in Eq. (36), the noise variance of CBF in Eq. (54) depends on tissue type. This is different from the noise model of CBV shown in Eq. (46), which is independent of the tissue type.

3.D. Time-to-maximum (t_max)

Assuming k* reaches its peak at the j^th time frame, the corresponding probability mass function (PMF) is given by

$$\text{PMF}\left(j\right)={\int }_{-\infty }^{+\infty }\text{d}x{\int }_{-\infty }^x\cdots {\int }_{-\infty }^x\text{m}{\text{P}}_{k^{*}}\left(k_j\right)\prod _{i\ne j}\text{d}{x}_i,$$ (55)

where k_j is defined in Eq. (48).

The estimated time-to-maximum $t_{\text{max}}^{*}$ (units: seconds) and the index of the postbaseline time frame (j) is related by

$$t_{\text{max}}^{*}=\left(j-1\right)\Delta t.$$ (56)

The expected value and noise variance of $t_{\text{max}}^{*}$ are given by

$$\overline{t_{\text{max}}^{*}}=(\overline{j}-1)\Delta t,$$ (57)

and

$${\sigma }_{t_{\text{max}}^{*}}^2={\left(\Delta t\right)}^2\left[\overline{j^2}-{\left(j\right)}^2\right],$$ (58)

where $\overline{j}$ and $\overline{j^2}$ are the first and second moments of j that can be calculated using the PMF in Eq. (55). Similar to CBF, the signal and noise of $t_{\text{max}}^{*}$ are dependent on both the signal and the noise of the tissue enhancement curve.

3.E. Summary of the theoretical model

As a brief summary of the theoretical model:

1. The signal of the estimated flow-scaled residue function depends on $\overline{A}$, $\overline{c}$, regularization method (Ψ) and its strength λ. It is independent of source image noise level;

2. Three mechanisms can introduce bias to the estimated flow-scaled residue function (and eventually biases of individual perfusion parameters): bias in the measured arterial enhancement curve (via term bias_A), bias in the measured tissue enhancement curve (via term bias_c, and regularizer used in deconvolution (via term λ²Ψ^⊤Ψ);

3. The fundamental origin of noise in the estimated flow-scaled residue function and perfusion maps is the noise in the source image. As shown in Eqs. (41)–(43), if the noise in the baseline and nonbaseline source images goes to zero, C_k* becomes an all-zero matrix, which eliminates uncertainties in the measured k* and thus removes noise of individual perfusion parameters;

4. The noise of k* also depends on the arterial enhancement curve (via term $\overline{A}$), regularizer (Ψ) and its strength (λ). It is independent of $\overline{c}$ and thus independent of the tissue type;

5. The signal of the estimated CBV map is dependent on tissue type and is independent of source image noise. In contrast, the noise of CBV is independent of tissue type;

6. For the estimated CBF and t_max, both of their signal and noise depend on the tissue type and source image noise level;

7. A comparison between the all-one matrix J and the identity matrix I in Eq. (43) suggests that the contributions of the baseline noise ${\sigma }_{\text{b}}^2$ and the nonbaseline source image noise ${\sigma }_0^2$ to the perfusion maps are not the same. This point will be revisited later in Section 6.

The following section describes numerical simulation methods to validate the theoretical model. The major advantage of numerical simulations is the availability of absolute ground truth for A₀, c₀, k₀, and individual perfusion parameters. In vivo animal experiments were also performed to supplement the numerical simulations and demonstrate an example application of the theoretical model.

4. NUMERICAL AND EXPERIMENTAL METHODS

4.A. Numerical validation study

The numerical validation study used the same digital CTP phantom as the one in the Part I paper.¹ Descriptions of this digital phantom can be found in the Part I paper. The simulated CTP image acquisition used the following parameters: N_b = 4, N = 21, and Δt = 2 s. For each time point, the true dynamic attenuation profile of this digital phantom was forward-projected along 1000 view angles uniformly distributed over an angular span of 360 degrees. Poisson noise was added to the simulated prelog projection data, and the filtered backprojection (FBP) reconstruction was used to generate noisy CTP source images. The filtering kernel used in FBP was adjusted until the noise power spectrum of the reconstructed source images match that of experimental CTP sources acquired using a physical head phantom, a clinical MDCT scanner (GE Discovery CT750 HD), and a clinical CTP protocol. The simulation process was repeated 510 times, generating an ensemble of noisy CTP source images. Fig. 1 shows an example artery and tissue attenuation curves measured from the simulated CT images of the digital phantom. The measured I_a(t) is biased toward lower magnitudes compared with the ground truth curve ${\mathcal{I}}_{\text{a}}\left(t\right)$ due to spatial blurring and PVE. However, the stochastic deviation of I_a(t) from ${\overline{I}}_{\text{a}}\left(t\right)$ is negligible due to the high vessel signal-to-noise ratio (SNR). In comparison, I(t) of each tissue is dominated by noise. However, its ensemble average, $\overline{I}\left(t\right)$, is almost identical to the truth since the tissue territory has a much larger volume and thus less sensitive to spatial blurring and PVE compared with the blood vessels.

FIG. 1.

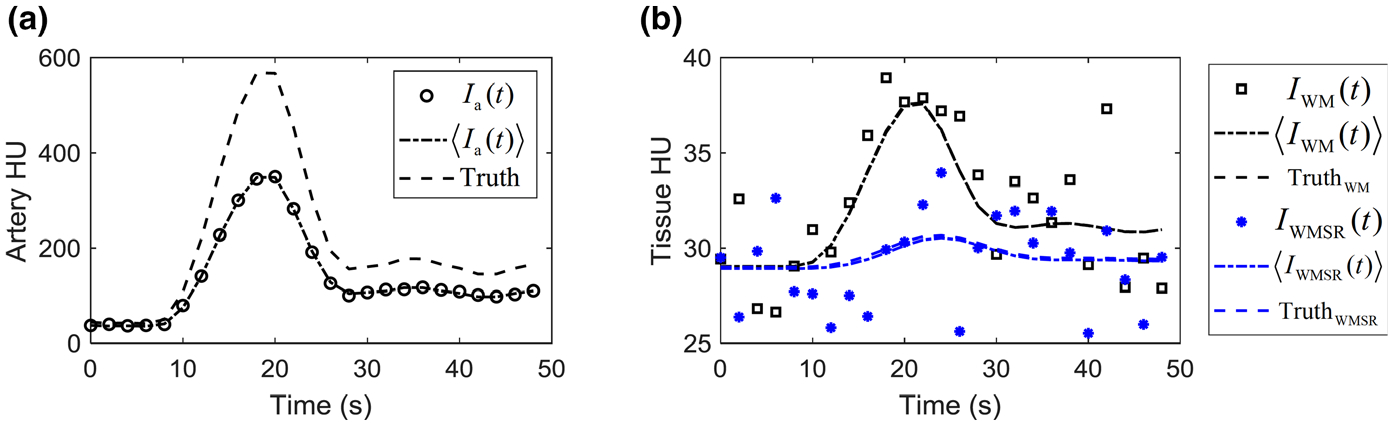
Artery (a) and tissue (b) enhancement curves of the digital phantom. The ground truth curves [${\mathcal{I}}_{\text{a}}\left(t\right)$ and $\mathcal{I}\left(t\right)$] were shown as dashed lines. The expected CT signal (〈I_a(t)〉 and 〈I(t)〉) are shown as dash-dotted lines, and a single set of their noisy realizations is also included. WM: white matter; WMSR: white matter with severely reduced blood flow.

For each source image dataset in the ensemble, a baseline image was calculated by taking the average of the first 4 time frames. The other 21 frames was subtracted by this baseline image, and I_a(t) was extracted from the anterior cerebral artery of the phantom and used to construct matrix A. An SVD-based deconvolution with the Tikhonov regularizer described in Eqs. (30)–(32) was used to estimate k*(x, t). The regularizer strength λ_rel was adjusted from 0 to 1.5 to study the impact of λ on the signal and noise of perfusion parameters. From k*(x, t), CBV*(x), CBF*(x), and $t_{\text{max}}^{*}\left(x\right)$ were calculated. This process was repeated for all datasets in the source image ensemble, allowing the mean and noise standard deviation of each perfusion parameter to be measured. Since the theoretical models shows that the signal and noise of perfusion parameters are closely related to $\overline{k^{*}}$ and C_k*, the following measurements were also performed using the simulated data ensemble:

$$\overline{k^{*}}=\frac{1}{M}\sum _{i=1}^M{k}_i^{*}$$ (59)

and

$$C_{k^{*}}=\frac{1}{M-1}\sum _{i=1}^M\left(k_i^{*}-\overline{k^{*}}\right){\left(k_i^{*}-\overline{k^{*}}\right)}^{\top },$$ (60)

where M denotes the total number of k* samples.

The measured values were compared with those calculated using the theory in Section 3. The agreement between the measured and calculated values was quantified using the relative root mean squared error (rRMSE) and the Bland–Altman method.

4.B. In vivo animal study

The theoretical model was also validated using an in vivo canine experiment conducted under the approval of the Institutional Animal Care and Use Committee (IACUC) of University of Wisconsin-Madison. Unlike the numerical validation study, the expected form of the tissue enhancement curve, namely $\overline{c}$, is not available for the in vivo study. Therefore, the animal study cannot be used to validate the signal models of CBF, CBV, and t_max. In addition, the animal study cannot be used to validate the noise models of CBF and t_max that require knowledge of $\overline{c}$. However, it can be used to validate the CBV noise model in Eq. (46) that is independent of $\overline{c}$. For the animal study, ensemble statistics-based noise measurement is not feasible, therefore experimental measurement of noise variance has to use the region-of-interest (ROI)-based approach. Since all pixels in an ROI share the same arterial enhancement curve, A is not a source of uncertainty for the ROI-based noise variance results, and thus it can be considered equivalent to $\overline{A}$ for the purpose of theoretical noise calculation. Using A and Eq. (41), C_k* was theoretically calculated for a given λ, and then ${\sigma }_{{\text{cbv}}^{*}}^2$, was theoretically calculated using Eq. (46).

The animal experiment used an adult beagle with an acute ischemic infarction built in the left hemisphere. After an intravenous injection of 15 ml Isovue 370 and 10 ml saline at a rate of 3 ml/s, CTP source images were acquired using a 64-slice CT scanner (Discovery CT750 HD, GE Healthcare) with the following protocol: kV = 80, tube current = 200 mA, sequential axial scan mode, beam collimation = 64 × 0.625 mm, time/gantry rotation = 0.5 s, scan field of view = “head,” total acquisition time T = 48 s, Δt = 2 s, display field of view = 6 cm, “Standard” reconstruction kernel, reconstruction slice thickness = 5 mm, and reconstruction matrix size = 256 × 156 × 8. After extracting the AIF, a two-dimensional pillbox filter with a radius of 0.7 mm was applied to the source images to reduce image noise. To facilitate the noise measurement, each time frame was double scanned, generating two sets of source images that can be subtracted to remove anatomical structure (Fig. 2). A scaling factor of $1/\sqrt{2}$ was multiplied to the subtraction result to account for the doubling of noise variance associated with image subtraction. ${\sigma }_0^2$ was measured at each nonbaseline time, and the measured values were averaged.

FIG. 2.

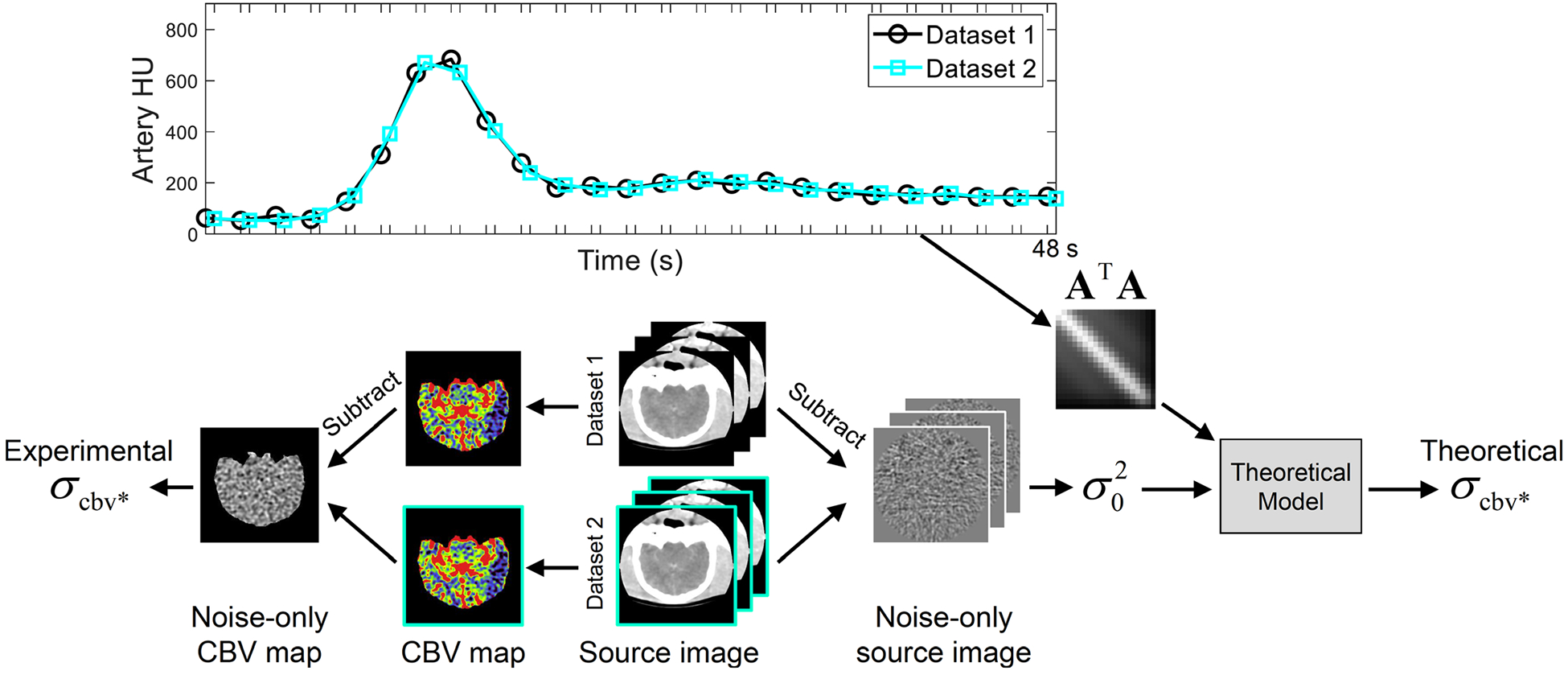
Workflow for the canine subject-based validation study. The top figure illustrates the time sequence of canine computed tomography perfusion source image acquisition: each frame in Dataset 1 was accompanied by an extra scan, providing a Dataset 2 to facilitate noise measurements. Based on the arterial attenuation curve shown in the top figure, matrix A^⊤A was constructed and fed to the theoretical model to calculate ${\sigma }_{{\text{cbv}}^{*}}^2$. Meanwhile, the two source image datasets produced two sets of CBV maps, from which ${\sigma }_{{\text{cbv}}^{*}}^2$ was experimentally measured.

For each set of CTP source images, SVD-based deconvolution with the Tikhonov regularizer was performed to estimate k*(x, t) for each pixel location x in the brain parenchyma, and then CBV*(x) were calculated, using Eq. (44). The two source image datasets generated two sets of CBV images, which were subtracted to remove anatomical structure and facilitate noise measurement. A scaling factor of $1/\sqrt{2}$ was multiplied to the subtraction result before CBV noise variance was measured. For a given λ, the measured ${\sigma }_{{\text{cbv}}^{*}}^2$ was compared with the value theoretically calculated using Eq. (41) and matrix A.

In addition to this canine study, image data of another three canine subjects used in the Part I paper¹ were retrospectively processed by the deconvolution-based processing method to demonstrate an example application of the theoretical model, which is on the prediction of the benefit of baseline noise reduction to deconvolution results. Data acquisition methods for these three canine studies can be found in the Part I paper. The example applications are reported in Section 6.

5. RESULTS

5.A. Numerical validation study: flow-scaled residue function

Figures 3–6 compare autocovariance matrices of k* generated from numerical simulations and theoretical calculations. All C_k* results have the same units of [s⁻¹]. To demonstrate the robustness of the theoretical model, comparisons were performed at different source image noise levels, λ values, and tissue types. In Fig. 3, the simplified C_k* model shown in Eq. (41) and a more complete model shown in Appendix II [Eq. (A20)] were compared. The comparison was conducted under two different input conditions: results in the top row of Fig. 3 used σ₀ = 1 HU and λ_rel = 0:5, Using C_k* from repeated simulations as a reference, the rRMSE of the complete and the simplified theoretical model are 0.001% and 0.002%, respectively. Results in the bottom row of Fig. 3 used σ₀ = 5 HU and λ_rel = 0.1, and the rRMSE of the complete and the simplified theoretical model are both 0.210%. With this level of accuracy, theoretical results reported in the remainder of the paper were calculated using the simplified model.

FIG. 3.

Comparisons of C_k* of gray matter generated from repeated simulations and theoretical calculation using Eq. (41) (simplified model) or Eq. (A20) (relatively complete model). For the top row: σ₀ = 1 HU, λ_rel = 0.5; for the bottom row: σ₀ = 5 HU, λ_rel = 0.1.

FIG. 6.

Comparisons of measured (top row) and theoretically calculated (bottom row) C_k* for three types of brain tissue with different perfusion properties. σ₀ and λ_rel were fixed at 4 HU and 0.4, respectively.

The theoretical model can be used to obtain a better understanding of noise properties of the residue function. For example, Fig. 4 shows the dependence of C_k* on source image noise standard deviation σ₀: As indicated by the color bars in this figure, the magnitude of C_k* is proportional to ${\sigma }_0^2$, but the shape of C_k* is independent of ${\sigma }_0^2$ for a given λ. This behavior is predicted in Eqs. (41) and (42). rRMSEs of the theoretical C_k* in the three columns in Fig. 4 are 0.001%, 0.003%, and 0.051%, respectively.

FIG. 4.

Comparisons of measured (top row) and theoretically calculated (bottom row) C_k* of white matter in the digital phantom. The Tikhonov regularization strength (λ_rel) was fixed at 0.2. Three source image noise levels (σ₀) were used. Note that the color bars of the three columns are not matched: C_k* in the last column have significantly higher magnitudes.

Figure 5 shows the dependence of C_k* on $\lambda ={\lambda }_{\text{rel}}{\sigma }_1^{\text{A}}$. As indicated by the color bars, the magnitude of C_k* decreased with increasing λ_rel, but the noise magnitude reduction was accompanied by stronger noise covariance along the temporal direction. rRMSEs of the theoretical C_k* in the three columns in Fig. 4 are 0.009%, 0.003%, and 0.003%, respectively.

FIG. 5.

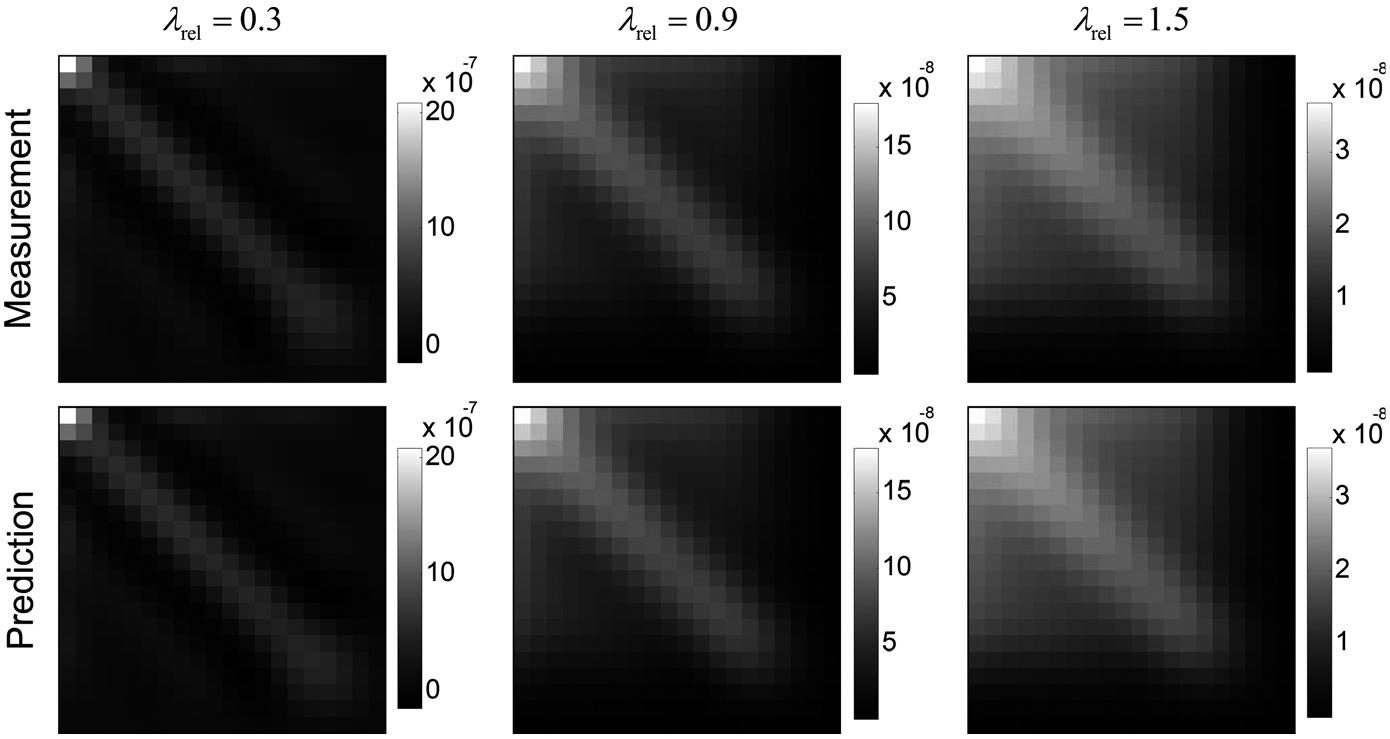
Comparisons of measured (top row) and theoretically calculated (bottom row) C_k* of white matter in the digital phantom. The source image noise level (σ₀) was fixed at 3 HU. Three levels of Tikhonov regularization strength were used.

As indicated by the theoretical model in Eq. (41), C_k* is independent of tissue enhancement curve and perfusion properties. This point is validated in Fig. 6, which shows the measured and theoretically calculated C_k* for three types of brain tissue that have different perfusion properties.

The theoretically calculated and measured $\overline{k^{*}}$ curves were compared in Fig. 7. rRMSEs of the theoretical curves were smaller than 0.130%. For a given σ₀ value, flattening of $\overline{k^{*}}$ became more severe with increasing λ, indicating stronger signal correlation along the temporal dimension. Compared with the truth (k₀) shown in Fig. 7(a), a flatter $\overline{k^{*}}$ curve corresponds to a lower peak value, which may corresponds to a lower CBF value. Meanwhile, the position of the peak along the temporal direction did not demonstrate any shift with changing λ, suggesting that the expected value of estimated t_max is less sensitive to regularization strength compared to CBF.

FIG. 7.

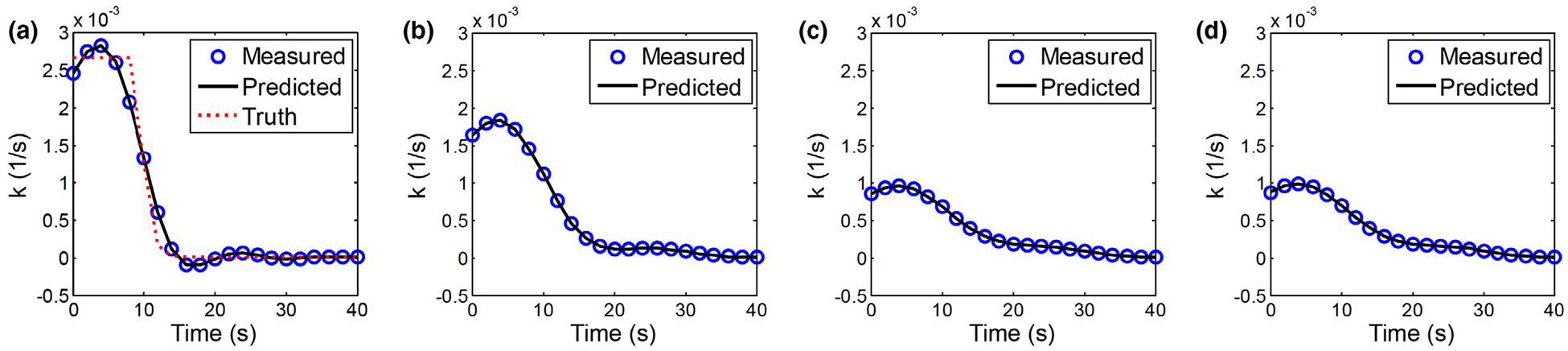
Comparison of measured and theoretically calculated $\overline{k^{*}}$ for gray matter with reduced blood flow in the digital phantom. The following input parameters were used: (a) σ₀ = 1 HU, λ_rel = 0.1; (b) σ₀ = 1 HU, λ_rel = 0.5; (c) σ₀ = 1 HU, λ_rel = 1.0; (d) σ₀ = 10 HU, λ_rel = 1.0.

In addition to the k dependence, Figs. 7(c)–7(d) showed that as long as λ is fixed, $\overline{k^{*}}$ is independent of the source image noise level σ₀. This is consistent with the theoretical model in Eq. (36).

5.B. Numerical validation study: perfusion parameters

Figure 8 compares the measured and theoretically calculated $\overline{{\text{CBV}}^{*}}$ (a), $\overline{{\text{CBF}}^{*}}$ (b), and $\overline{t_{\text{max}}^{*}}$ (c) of gray matter at different regularization strength levels. The theoretical values are consistent with the simulation results: as shown by the Bland–Altman plots, the difference between the measured and theoretically calculated $\overline{{\text{CBV}}^{*}}$ are within ±0.03 ml/100 g. For CBF and t_max, the differences are within ±1.5 ml/min/100 g and [0.03,0.21] s, respectively, which are significantly smaller than the corresponding mean values. The theoretical model accurately predicted the dependence of the signal value of each perfusion parameter on $\overline{{\text{CBV}}^{*}}$ decreased almost linearly with increasing λ_rel (R² of a linear fit is 0.998); $\overline{{\text{CBF}}^{*}}$ also decreased with increasing λ_rel, and their relationship can be empirically modeled as a power law of $\overline{\text{CBF}}\propto {\left({\lambda }_{\text{rel}}\right)}^{-0.9}$. $\overline{t_{\text{max}}^{*}}$ reached its minimum at λ_rel = 0.4 then increased slightly with larger λ_rel. However, the relative change of $\overline{t_{\text{max}}^{*}}$ over different λ_rel values was less than 0.5 s.

FIG. 8.

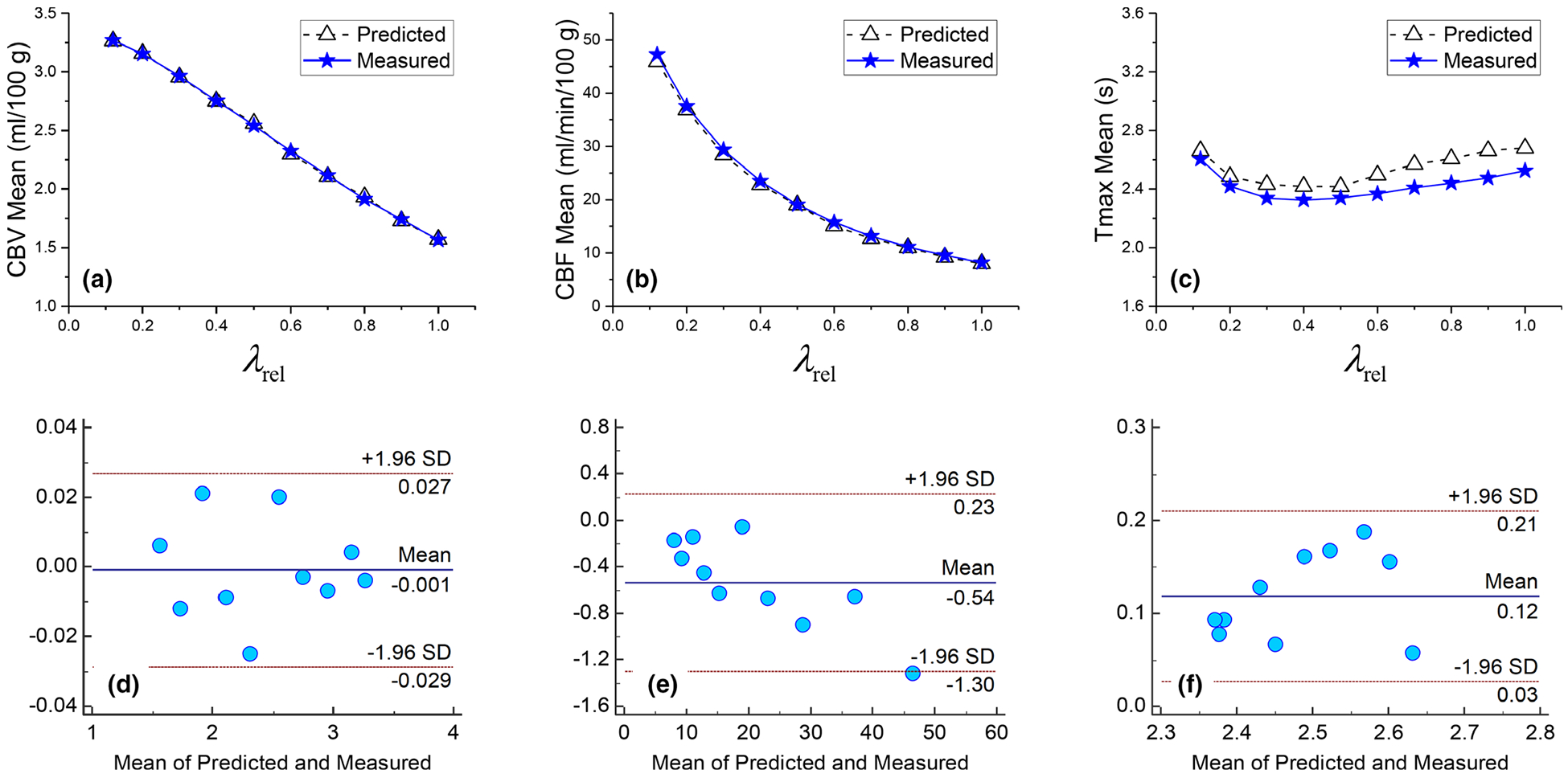
Comparison of measured and theoretically calculated $\overline{{\text{CBV}}^{*}}$ (a), $\overline{{\text{CBF}}^{*}}$ (b), and $\overline{t_{\text{max}}^{*}}$ (c) for gray matter in the digital phantom. The corresponding Bland–Altman plots are shown in (d), (e), and (f), respectively. The ground truth values of cerebral blood volume, cerebral blood flow, and tmax are 3.3 ml/100 g, 53 ml/min/100 g, and 0 s, respectively. SD: standard deviation.

Figure 9 shows the measured and theoretically calculated noise standard deviations of perfusion parameters of gray matter. The theoretical values matched those measured from repeated simulations: as shown by the Bland–Altman plots, the difference between the measured and predicted σ_cbv* values are within ±0.015 ml/100 g. For CBF and t_max, the differences are within ±0.2 ml/min/100 g and ±0.18 s, respectively, which are insignificant differences. The theoretical model shows that σ_cbv* decreased almost linearly with increasing λ_rel (R² of linear fit is 0.991); σ_cbf* decreased with increasing λ_rel, and the trend can be empirically modeled as a power law of σ_cbf* ∝ (λ_rel)^−1.0; ${\sigma }_{t_{\text{max}}^{*}}$ reached a minimum at λ^rel = 0.4 then increased slightly with larger λ_rel. Overall speaking, the dependence of ${\sigma }_{t_{\text{max}}^{*}}$ on λ_rel is not as strong as in the case of CBVor CBF.

FIG. 9.

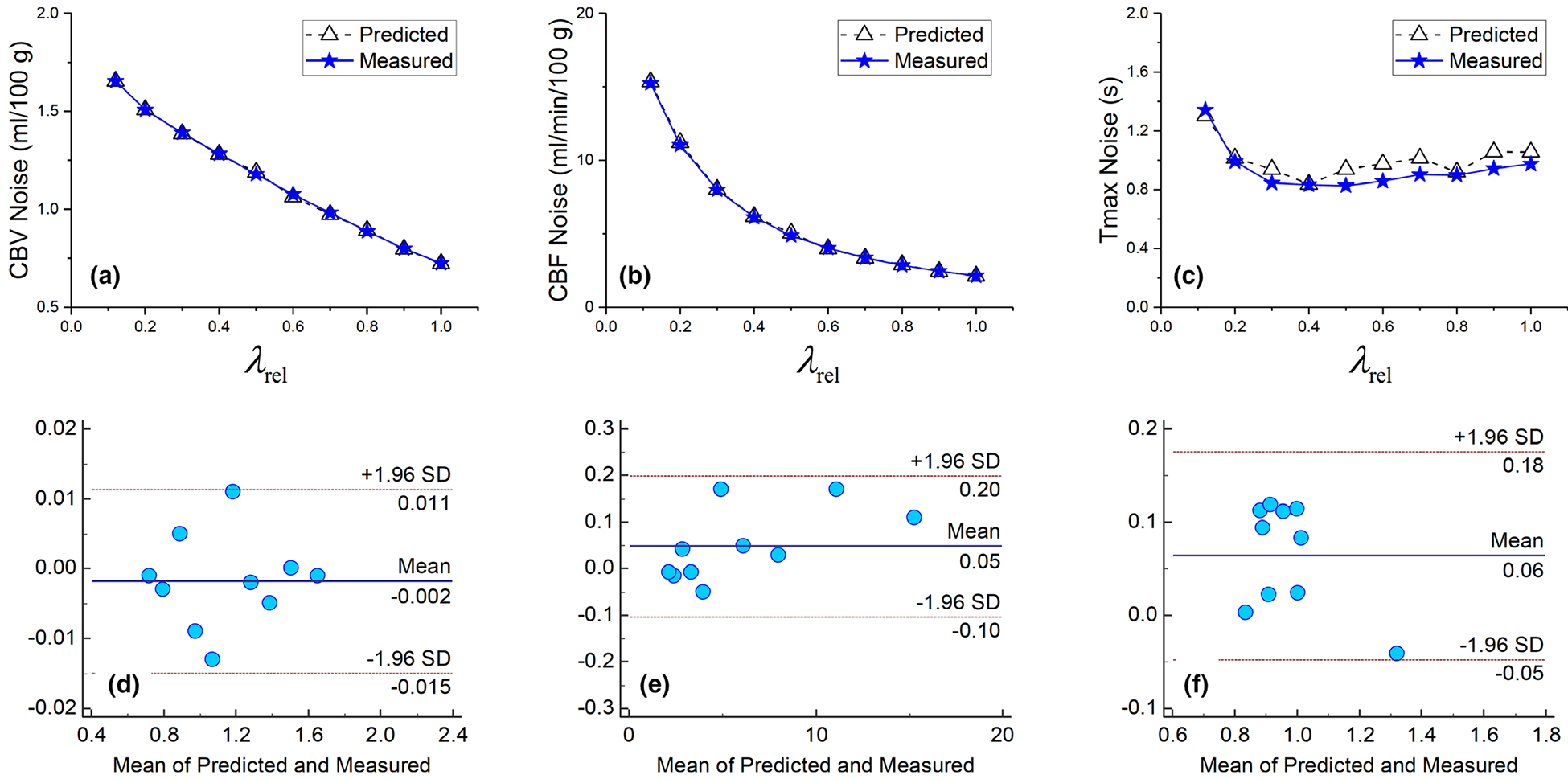
Comparison of measured and theoretically calculated σ_cbv* (a), σ_cbf* (b), and ${\sigma }_{t_{\text{max}}^{*}}$ (c) for gray matter in the digital phantom. The corresponding Bland–Altman plots are shown in (d), (e), and (f), respectively in the second row.

5.C. Animal validation study

As shown in Fig. 10, the theoretical values of ${\sigma }_{{\text{cbv}}^{*}}^2$ calculated using the workflow shown in Fig. 2 are consistent with the experimental values: at all of the λ_rel levels evaluated, the theoretical ${\sigma }_{{\text{cbv}}^{*}}^2$ fell within the 25th and 75th percentiles of the experimental ${\sigma }_{{\text{cbv}}^{*}}^2$. The trend of the ${\sigma }_{{\text{cbv}}^{*}}^2-{\lambda }_{\text{rel}}$ curve is consistent with results of the numerical study shown in Fig. 9(a).

FIG. 10.

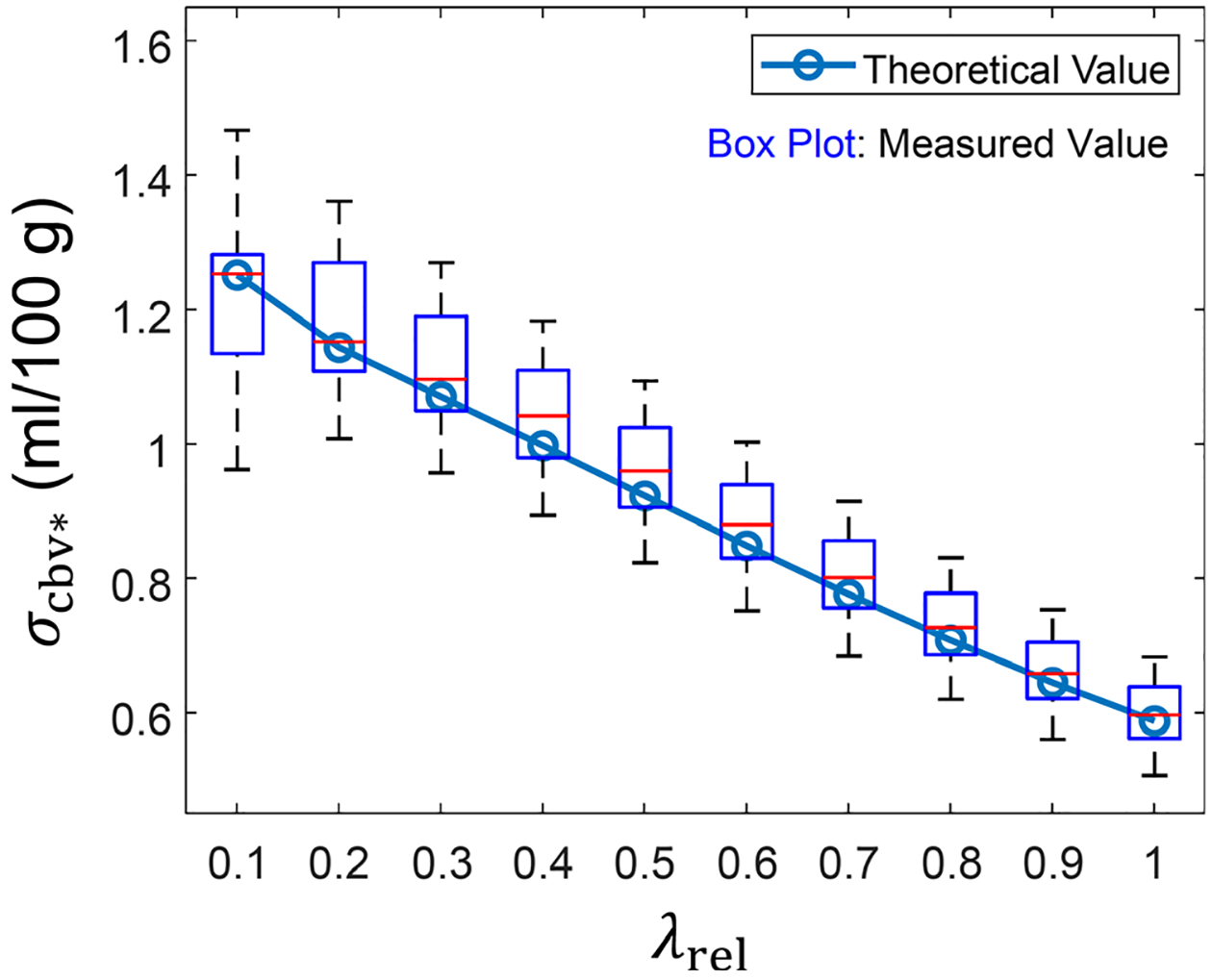
Experimental and theoretical σ_cbv* values of the canine subject described in Section 2.

6. EXAMPLE APPLICATION OF THE THEORETICAL MODEL: IMPACT OF BASELINE NOISE IN DECONVOLUTION-BASED SYSTEMS

As shown by the theoretical model in Eqs. (41), (42) and (46), the noise variance of the measured CBV map is related to baseline noise variance $\left({\sigma }_{\text{b}}^2\right)$ and nonbaseline source image noise variance ${\sigma }_0^2$ by

$$\begin{gathered} {\sigma }_{{\text{cbv}}^{*}}^2\approx {\left(\frac{H\Delta t}{\rho }\right)}^2{J}_{1\times N}{\overline{B}}^{\top }{C}_{\text{c}}\overline{B}{J}_{N\times 1} \\ ={\left(\frac{H\Delta t}{\rho }\right)}^2\left[{\sigma }_0^2{J}_{1\times N}{\overline{B}}^{\top }\overline{B}{J}_{N\times 1}+{\sigma }_{\text{b}}^2{J}_{1\times N}{\overline{B}}^{\top }J\overline{B}{J}_{N\times 1}\right] \\ ={\left(\frac{H\Delta t}{\rho }\right)}^2\left[{\sigma }_0^2\sum _{i=1}^N\sum _{j=1}^N\sum _{k=1}^N{B}_{ki}{B}_{kj}+{\sigma }_b^2{\left(\sum _{i=1}^N\sum _{j=1}^N{B}_{ij}\right)}^2\right] \end{gathered}$$ (61)

Since the N³ summation terms in (Σ_i Σ_j Σ_k B_kiB_kj)is only is only a small subset of the N⁴ summation terms in (Σ_i Σ_j B_ij)², the weight on ${\sigma }_{\text{b}}^2$ should be much larger than the weight on ${\sigma }_0^2$. Reducing the baseline noise, therefore, should be very effective in reducing the noise of deconvolution-derived CBV map.

Motivated by this theoretical analysis, we retrospectively analyzed CTP data of the three canine subjects used in the Part I paper.¹ For each subject, a CTP acquisition was performed using an x-ray tube current (mA) modulation scheme optimized for nondeconvolution-based CBV imaging, so that ${\sigma }_{\text{b}}^2$ is only 5% of ${\sigma }_0^2$. Each subject also underwent another CTP scan with a constant mA; the radiation dose of the two scans was matched. As shown in Fig. 11 and Table II, despite the fact that the mA modulation scheme was optimized for the nondeconvolution-based systems, it still led to effective noise reductions in the deconvolution-based CBV maps because of the reason stated in the previous paragraph. The specific percentage of noise reduction depends on matrix A and thus varies across the three subjects.

FIG. 11.

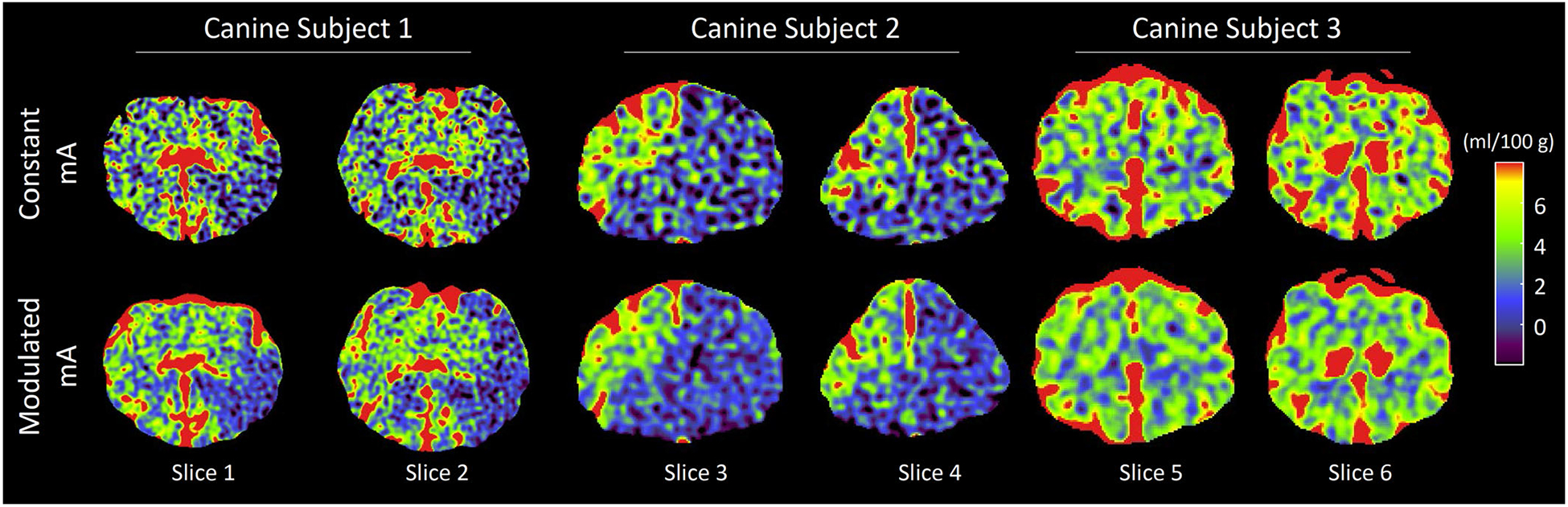
Cerebral blood volume (CBV) maps of the three in vivo canine subjects used in the Part I paper.¹ CTDI_vol of the computed tomography perfusion (CTP) exam with modulated mA was matched to that of the constant mA CTP exam. The singular value decomposition-based deconvolution method with a Tikhonov regularization strength of λ_rel =0.5 was used to generate these CBV maps.

TABLE II.

Comparison of experimental and theoretical σ_cbv* of the three canine subjects used in the Part I paper.¹ The values after the ± sign are standard deviation of data measured at 8 slice locations. The units of σ_cbv* are (ml/100 g).

	Experimental			Theoretical
Canine Subject Number	σcbv* (constant mA)	σcbv* (modulated mA)	% noise reduction	σcbv* (constant mA)	σcbv* (modulated mA)	% noise reduction
1	2.17 ± 0.12	1.32 ± 0.12	39% ± 7%	2.18	1.35	38%
2	2.24 ± 0.35	1.60 ± 0.18	29% ± 13%	2.24	1.64	27%
3	1.99 ± 0.14	1.33 ± 0.06	33% ± 6%	1.94	1.32	32%

Using the AIF of each subject previous measured for the Part I paper, matrix A was constructed and used to calculate σ_cbv* for each dose delivery method and subject. As shown in Table II, the theoretically calculated σ_cbv* and noise reduction percentage (by using modulated mA) are consistent with the experimental values, which again proved the validity of the CBV noise model.

7. DISCUSSION

The major findings of the theoretical model have been summarized in Section 3.E and thus are not repeated in this section. Here we would like to emphasize the major assumptions used in the theoretical derivations, so that a user of the theory is aware of the conditions under which the model remains valid. First and foremost, the theory assumes the indicator-dilution theory and other components of the the physiological model in Section 2.A to be valid. If there is a blood–brain barrier breakage or strong bolus dispersion, the convolution model may no longer be strictly valid, and the associated CTP signal and noise model may need to be modified. Second, the signal and noise models of k* presented in Eqs. (36) and (41) assume that the deconvolution operation was implemented using SVD with Tikhonov or other regularizers that allow the deconvolution to be formulated as a quadratic optimization problem. Third, the derivation of C_c in Appendix IV assumes that for a given spatial location, CT noise is uncorrelated and stationary along the temporal direction before a temporal filter is applied. As shown in the Part I paper,¹ the “temporally white noise” assumption is often valid for the native source images acquired from modern CT scanners with negligible detector lag; the temporally stationary noise assumption could be slightly violated by the temporal variation of the iodine concentration in the brain.

In addition to the presented example, the theoretical models can be potentially used to facilitate the understanding of the quantitative relationship between CTP imaging performance and system parameters and conditions such as the temporal sampling interval (Δt), CT reconstruction kernel, deconvolution regularizer, contrast injection protocol, and PVE. Taking PVE as an example, it often creates bias in the measured AIF and matrix $\overline{A}$, which impacts the signal and noise of the flow-scaled residue function and individual perfusion parameters. Using the theoretical model, the transfer of the PVE-induced bias through the CTP imaging chain and its specific impact to each perfusion parameter can be quantitatively analyzed.

Although the theoretical models were derived based on the conventional delay-sensitive deconvolution method, it can be directly extended to the delay-insensitive block-circulant deconvolution method. The major difference between these two deconvolution methods points to how matrices A₀ is defined: in the block-circulant method, matrix A₀ in Eq. (20) is augmented as follows:⁵

$$A_0^{\prime }=\left[\begin{array}{cc}{A}_0& A_0^{\text{circ}}\\ A_0^{\text{circ}}& A_0\end{array}\right],$$ (62)

where $A_0^{\text{circ}}$ is an N × N matrix defined as

$$A_0^{\text{circ}}\triangleq \Delta t\left[\begin{array}{cccc}0& {\mathcal{I}}_{\text{a}}^{\prime }\left(N\right)& \cdots & {\mathcal{I}}_{\text{a}}^{\prime }\left(2\right)\\ 0& 0& \cdots & {\mathcal{I}}_{\text{a}}^{\prime }\left(3\right)\\ ⋮& ⋮& \ddots & ⋮\\ 0& 0& \cdots & 0\end{array}\right].$$ (63)

Since the matrix size of $A_0^{\prime }$ is 2N × 2N instead of N × N, the vector c₀ in the convolution model in Eq. (20) needs to be padded with N zeros to meet the dimensionality requirement for matrix multiplication. Similarly, the size of k₀ needs to be expanded from N × 1 to 2N × 1. Despite these modifications in the matrix definition and dimensionality, the theoretical models are still applicable to the block-circulant deconvolution method since the derivation in Section 3 did not rely on the specific value of N and the contents of A₀ and c₀. One potential future work is to theoretically compare the statistical signal estimation efficiency of the delay-sensitive and delay-insensitive deconvolution methods for a given set of CTP system inputs under the following two conditions: (a) tracer delay is present; (b) tracer delay is absent.

8. CONCLUSIONS

A theoretical analysis was performed to disentangle the relationship between statistical properties of parametric perfusion maps, CTP source images, and deconvolution method. A set of theoretical models were established to pinpoint how each component of the CTP imaging system quantitatively impacts the precision and accuracy of parametric perfusion maps. These models can be potentially used to provide the needed scientific guidance for the development, optimization, and standardization of deconvolution-based CTP systems.

APPENDIX I. REGULARIZED LEAST SQUARES SOLUTION OF k*

The solution of k* in Eq. (33) is given by taking the derivative of the objective function with respect to k, then setting the result to 0 at k = k*. The solution is given by

$$k^{*}={\left(A^{\top }A+{\lambda }^{2}E\right)}^{-1}{A}^{\top }c.$$ (A1)

Using the SVD of A in Eq. (28), A^⊤A can be decomposed into

$$\begin{gathered} A^{\top }A={\left(U\Sigma V^{\top }\right)}^{\top }U\Sigma V^{\top } \\ =V\Sigma U^{\top }U\Sigma V^{\top } \\ =V{\Sigma }^2{V}^{\top }, \end{gathered}$$ (A2)

where Σ² is a diagonal matrix with its i^th diagonal element being ${\sigma }_i^2$ (square of the i^th singular value of A). Correspondingly, term (A^⊤A + λ²E) in Eq. (A1) can be written as

$$A^{\top }A+{\lambda }^{2}E=V{\Sigma }^2{V}^{\top }+V\left({\lambda }^{2}E\right)V^{\top }=V\mathbf{\Sigma }\prime V^{\top },$$ (A3)

where Σ′ = Σ² + λ²E is a diagonal matrix with its i^th diagonal element being ${\sigma }_i^2+{\lambda }^2$. Based on Eq. (A3), the least squares solution of k* in Eq. (A1) can be expressed as

$$\begin{gathered} k^{*}={\left(V\Sigma \prime V^{\top }\right)}^{-1}{A}^{\top }c \\ =V\mathbf{\Sigma }{\prime }^{{}^{-1}}{V}^{-1}\left(V\mathbf{\Sigma }{U}^{\top }\right)c \\ =V\left(\Sigma {\prime }^{-1}\Sigma \right)U^{\top }c \\ =\sum _{i=1}^R\frac{{\sigma }_i}{{\sigma }_i^2+{\lambda }^2}{u}_i^{\top }c{v}_i \\ =\sum _{i=1}^R{f}_{\lambda ,i}\frac{u_i^{\top }c}{{\sigma }_i}{v}_i, \end{gathered}$$ (A4)

where $f_{\lambda ,i}={\sigma }_i^2/\left({\sigma }_i^2+{\lambda }^2\right)$. As shown in Eq. (A4), solving the least squares problem in Eq. (33) leads to the same solution of k* as performing an SVD-based deconvolution with the Tikhonov regularization described in Eqs. (30)–(32).

APPENDIX II. SIGNAL MODEL OF k*

Based on Eq. (35), k* is related to A and c as

$$\left(A^{\top }A+{\lambda }^2{\Psi }^{\top }\Psi \right)k^{*}=A^{\top }c.$$ (A5)

By substituting A with $\left(\overline{A}+\Delta A\right)$ and c with $\left(\overline{c}+\Delta c\right)$ and applying the expected value operator 〈·〉 on both sides of the equation, Eq. (A5) becomes

$$\langle \left[{\left(\overline{A}+{\Delta }_A\right)}^{\top }\left(\overline{A}+{\Delta }_A\right)+{\lambda }^2{\Psi }^{\top }\Psi \right]k^{*}\rangle$$ (A6)

$$\begin{gathered} =\langle {\left(\overline{A}+{\Delta }_A\right)}^{\top }\left(\overline{c}+{\Delta }_c\right)\rangle \\ =\langle \left({\overline{A}}^{\top }\overline{c}+{\Delta }_A^{\top }\overline{c}+{\overline{A}}^{\top }{\Delta }_c+{\Delta }_A^{\top }{\Delta }_c\right)\rangle \\ =\langle {\overline{A}}^{\top }\overline{c}\rangle +\langle {\Delta }_A^{\top }{\Delta }_c)\rangle \end{gathered}$$ (A7)

$$\approx {\overline{A}}^{\top }\overline{c}.$$ (A8)

From (A7) to (A8), we ignored $\langle {\Delta }_A^{\top }{\Delta }_c)\rangle$ since the covariance between arterial and tissue enhancement curves is usually negligible except for tissue in close proximity of x_a.

The formula in (A6) can be expanded as

$$\begin{gathered} \langle \left[{\left(\overline{A}+{\mathbf{\Delta }}_A\right)}^{\top }\left(\overline{A}+{\Delta }_A\right)+{\lambda }^2{\Psi }^{\top }\Psi \right]k^{*}\rangle \\ ={\overline{A}}^{\top }\overline{A}\langle k^{*}\rangle +\langle {\overline{A}}^{\top }{\Delta }_A{k}^{*}\rangle +\langle {\Delta }_A^{\top }\overline{A}{k}^{*}\rangle \\ +\langle {\Delta }_A^{\top }{\Delta }_A{k}^{*}\rangle +{\lambda }^2{\Psi }^{\top }\Psi \langle k^{*}\rangle \end{gathered}$$ (A9)

Since the SNR of each point on the arterial enhancement curve is usually very high, an element in term ${\overline{A}}^{\top }\overline{A}\langle k^{*}\rangle$ can be considered much higher than the corresponding element in $\langle {\overline{A}}^{\top }{\Delta }_A{k}^{*}\rangle$. Similarly, $\langle {\Delta }_A{}^{\top }\overline{A}{k}^{*}\rangle$ and 〈Δ_A^⊤Δ_Ak*〉 in (A9) can also be considered insignificant compared with ${\overline{A}}^{\top }\overline{A}\langle k^{*}\rangle$. Therefore, the left-hand side of Eq. (A6) can be approximated by

$$\begin{gathered} \langle \left[{\left(\overline{A}+{\Delta }_A\right)}^{\top }\left(\overline{A}+{\Delta }_A\right)+{\lambda }^2{\Psi }^{\top }\Psi \right]k^{*}\rangle \\ \approx {\overline{A}}^{\top }\overline{A}\langle k^{*}\rangle +{\lambda }^2{\Psi }^{\top }\Psi \langle k^{*}\rangle . \end{gathered}$$ (A10)

A combination of Eqs. (A8) and (A10) gives

$$\left({\overline{A}}^{\top }\overline{A}+{\lambda }^2{\Psi }^{\top }\Psi \right)\langle k^{*}\rangle \approx {\overline{A}}^{\top }\overline{c},$$ (A11)

or equivalently,

$$\langle k^{*}\rangle \approx {\left({\overline{A}}^{\top }\overline{A}+{\lambda }^2{\Psi }^{\top }\Psi \right)}^{-1}{\overline{A}}^{\top }\overline{c},$$ (A12)

APPENDIX III. NOISE MODEL OF k*

The solution of k* in Eq. (34) is given by taking the derivative of the objective function with respect to k, then setting the result to 0 at k = k*, namely

$$0=A^{\top }A{k}^{*}-A^{\top }c+{\lambda }^2{\Psi }^{\top }\Psi k^{*}$$ (A13)

By substituting c with $\overline{c}+{\Delta }_c$ and substituting A with $\overline{A}+{\mathbf{\Delta }}_A$ Eq. (A13) becomes:

$$\begin{gathered} 0=\left({\overline{A}}^{\top }+{\Delta }_A^{\top }\right)\left(\overline{A}+{\Delta }_A\right)k^{*}-\left({\overline{A}}^{\top }+{\Delta }_A^{\top }\right)\left(\overline{c}+{\Delta }_c\right)+{\lambda }^2{\Psi }^{\top }\Psi k^{*} \\ \approx \left({\overline{A}}^{\top }\overline{A}+{\overline{A}}^{\top }{\Delta }_A+{\Delta }_A^{\top }\overline{A}\right)k^{*}-{\overline{A}}^{\top }\overline{c}-{\overline{A}}^{\top }{\Delta }_c-{\Delta }_A^{\top }\overline{c}+{\lambda }^2{\Psi }^{\top }\Psi k^{*}, \end{gathered}$$ (A14)

where second-order error terms such as ${\Delta }_A^{\top }{\Delta }_A{k}^{*}$ and ${\Delta }_A^{\top }{\Delta }_c$ are ignored. By decomposing k* into $\overline{k^{*}}+{\Delta }_{k^{*}}$, Eq. (A14) becomes

$$\begin{gathered} 0\approx \left({\overline{A}}^{\top }\overline{A}+{\overline{A}}^{\top }{\Delta }_A+{\Delta }_A^{\top }\overline{A}+{\lambda }^2{\Psi }^{\top }\Psi \right)\left(\overline{k^{*}}+{\Delta }_{k^{*}}\right)-{\overline{A}}^{\top }\overline{c}-{\overline{A}}^{\top }{\Delta }_c-{\Delta }_A^{\top }\overline{c} \\ \approx \left[\left({\overline{A}}^{\top }\overline{A}+{\lambda }^2{\Psi }^{\top }\Psi \right)\overline{k^{*}}-{\overline{A}}^{\top }\overline{c}\right]+\left({\overline{A}}^{\top }{\Delta }_A+{\Delta }_A^{\top }\overline{A}\right)\overline{k^{*}}+\left({\overline{A}}^{\top }\overline{A}+{\lambda }^2{\Psi }^{\top }\Psi \right){\mathbf{\Delta }}_{k^{*}}-{\overline{A}}^{\top }{\Delta }_c-{\Delta }_A^{\top }\overline{\text{c}}. \end{gathered}$$ (A15)

Again, second-order error terms ${\overline{A}}^{\top }{\Delta }_A{\Delta }_{k^{*}}$ and ${\Delta }_A^{\top }\overline{A}{\Delta }_{k^{*}}$ are ignored. Based on Eq. (A11), $\left[\left({\overline{A}}^{\top }\overline{A}+{\lambda }^2{\Psi }^{\top }\Psi \right)\overline{k^{*}}-{\overline{A}}^{\top }\overline{c}\right]\approx 0$. Therefore, Eq. (A15) can be further simplified to

$$0\approx \left({\overline{A}}^{\top }{\Delta }_A+{\Delta }_A^{\top }\overline{A}\right)\overline{k^{*}}+\left({\overline{A}}^{\top }\overline{A}+{\lambda }^2{\Psi }^{\top }\Psi \right){\mathbf{\Delta }}_{k^{*}}-{\overline{A}}^{\top }{\Delta }_c-{\Delta }_A^{\top }\overline{c},$$ (A16)

From Eq. (A16), term Δ_k* can be isolated as

$${\Delta }_{k^{*}}\approx {\left({\overline{A}}^{\top }\overline{A}+{\lambda }^2{\Psi }^{\top }\Psi \right)}^{-1}\left({\overline{A}}^{\top }{\Delta }_c+{\Delta }_A^{\top }\overline{c}-{\overline{A}}^{\top }{\Delta }_A\overline{k^{*}}-{\Delta }_A^{\top }\overline{A}\overline{k^{*}}\right).$$ (A17)

Based on the expression of Δ_k* in Eq. (A17), the autocovariance matrix of k* is given as

$$\begin{gathered} C_{k^{*}}=\langle {\Delta }_{k^{*}}{\Delta }_{k^{*}}{}^{\top }\rangle \\ \text{}\approx {\left({\overline{A}}^{\top }\overline{A}+{\lambda }^2{\Psi }^{\top }\Psi \right)}^{-1} \end{gathered}$$ (A18)

$$\begin{gathered} \times \langle \left({\overline{A}}^{\top }{\Delta }_c+{\Delta }_A^{\top }\overline{\text{c}}-{\overline{A}}^{\top }{\Delta }_A\overline{k}-{\Delta }_A^{\top }\overline{A}\overline{k}\right){\left({\overline{A}}^{\top }{\Delta }_c+{\Delta }_A^{\top }\overline{\text{c}}-{\overline{A}}^{\top }{\Delta }_A\overline{k}-{\Delta }_A^{\top }\overline{A}\overline{k}\right)}^{\top }\rangle \\ \times {\left[{\left({\overline{A}}^{\top }\overline{A}+{\lambda }^2{\Psi }^{\top }\Psi \right)}^{-1}\right]}^{\top } \end{gathered}$$ (A19)

$$={\left({\overline{A}}^{\top }\overline{A}+{\lambda }^2{\Psi }^{\top }\Psi \right)}^{-1}\langle \left({\Delta }_1+{\Delta }_2-{\Delta }_3-{\Delta }_4\right){\left({\Delta }_1+{\Delta }_2-{\Delta }_3-{\Delta }_4\right)}^{\top }\rangle {\left({\overline{A}}^{\top }\overline{A}+{\lambda }^2{\Psi }^{\top }\Psi \right)}^{-1},$$ (A20)

where

$${\Delta }_1\triangleq {\overline{A}}^{\top }{\Delta }_c,{\Delta }_2\triangleq {\Delta }_A^{\top }\overline{c},{\Delta }_3\triangleq {\overline{A}}^{\top }{\Delta }_A\overline{k},{\Delta }_4\triangleq {\Delta }_A^{\top }\overline{A}\overline{k}.$$ (A21)

Essentially, Δ₁ is the noise of c filtered by the signal of the arterial enhancement curve; Δ₂ is noise of the arterial enhancement curve filtered by the signal of c. As shown in the Part I paper,¹ the noise variances of the arterial and tissue enhancement curves are usually on the same order of magnitude, but the nonzero elements in A is usually an order of magnitude higher than element in c. Therefore, 〈Δ₂Δ₂^⊤〉can be considered insignificant when compared to 〈Δ₁Δ₁^⊤〉. Using similar arguments, 〈Δ₃Δ₃^⊤〉 and 〈Δ₄Δ₄^⊤〉 can also be considered insignificant compared with 〈Δ₁Δ₁^⊤〉.

In addition, if the covariance between tissue and arterial enhancement curves can be ignored, the covariance terms in Eq. (A20) such as such as 〈Δ₁Δ₂^⊤〉 and 〈Δ₁Δ₃^⊤〉can be neglected. As a result, the formula of C_k* can be simplified to

$$\begin{gathered} C_{k^{*}}\approx {\left({\overline{A}}^{\top }\overline{A}+{\lambda }^2{\Psi }^{\top }\Psi \right)}^{-1}\langle {\Delta }_1{\Delta }_1{}^{\top }\rangle {\left({\overline{A}}^{\top }\overline{A}+{\lambda }^2{\Psi }^{\top }\Psi \right)}^{-1} \\ ={\left({\overline{A}}^{\top }\overline{A}+{\lambda }^2{\Psi }^{\top }\Psi \right)}^{-1}{\overline{A}}^{\top }\langle {\Delta }_c{\Delta }_c^{\top }\rangle \overline{A}{\left({\overline{A}}^{\top }\overline{A}+{\lambda }^2{\Psi }^{\top }\Psi \right)}^{-1} \\ ={\left({\overline{A}}^{\top }\overline{A}+{\lambda }^2{\Psi }^{\top }\Psi \right)}^{-1}{\overline{A}}^{\top }{C}_c\overline{A}{\left({\overline{A}}^{\top }\overline{A}+{\lambda }^2{\Psi }^{\top }\Psi \right)}^{-1}. \end{gathered}$$ (A22)

The covariance model in Eq. (A22) is referred to as the simplified model, while the one in Eq. (A20) is referred to as the complex (or more complete) model.

APPENDIX IV. AUTOCOVARIANCE OF THE BASELINE-CORRECTED TISSUE ENHANCEMENT CURVE

With the baseline correction, the tissue enhancement curve for a given spatial location can be written as the following vectorized form

$$c=\left[\begin{array}{c}I(1)\\ I(2)\\ ⋮\\ I(N)\end{array}\right]-\left[\begin{array}{c}{I}_{\text{b}}\\ I_{\text{b}}\\ ⋮\\ I_{\text{b}}\end{array}\right]=I-I_{\text{b}}{J}_{N\times 1},$$ (A23)

where I(1) denotes the first postbaseline time frame, and J_N×1 denotes an N × 1 all-one vector. Eq. (A23) can be decomposed into

$$\begin{gathered} c=\left(\overline{I}+{\mathbf{\Delta }}_I\right)-\left({\overline{I}}_{\text{b}}+{\mathbf{\Delta }}_{I_{\text{b}}}\right)J_{N\times 1} \\ =\left(\overline{I}-{\overline{I}}_{\text{b}}{J}_{N\times 1}\right)+\left({\Delta }_I-{\mathbf{\Delta }}_{I_{\text{b}}}{J}_{N\times 1}\right) \\ =\overline{c}+{\Delta }_c, \end{gathered}$$ (A24)

where ${\Delta }_c={\Delta }_I-{\Delta }_{I_{\text{b}}}{J}_{N\times 1}$ denotes the stochastic deviation of c from expected form $\overline{c}$. The autocovariance matrix of c is given by

$$C_c=\langle {\Delta }_c{\Delta }_c^{\top }\rangle$$ (A25)

$$\begin{gathered} =\langle {\Delta }_I{\Delta }_I^{\top }\rangle +\langle {\left({\Delta }_{I_{\text{b}}}\right)}^2\rangle J_{N\times N}-\langle {\Delta }_{I_{\text{b}}}{\mathbf{\Delta }}_{\mathbf{\text{I}}}{J}_{1\times N}\rangle -\langle {\Delta }_{I_{\text{b}}}{J}_{N\times 1}{\Delta }_I{}^{\top }\rangle , \\ =C_I+{\sigma }_{\text{b}}^2{J}_{N\times N}-\text{matri}{\text{x}}_3-\text{matri}{\text{x}}_4, \end{gathered}$$ (A26)

where C_I = 〈Δ_IΔ_I^⊤〉 denotes the autocovariance matrix of the nonbaseline source images, ${\sigma }_{\text{b}}^2=\langle {\left({\Delta }_{I_{\text{b}}}\right)}^2\rangle$ denotes the noise variance of the baseline image. Since the covariance between baseline and nonbaseline frames is usually negligible, matrix₃ and matrix₄ in Eq. (A26) can be ignored, and C_I can be approximated by

$$C_c\approx C_I+{\sigma }_{\text{b}}^2{J}_{N\times N}.$$ (A27)

As shown in the Part I paper,¹ prior to applying any temporal filter, the original source image noise can be considered white along the temporal direction with a relatively uniform variance of σ₀, and thus C_I can be approximated by

$$C_I\approx {\sigma }_0^2{E}_{N\times N}.$$ (A28)

Accordingly, Eq. (A27) becomes

$$C_c={\sigma }_0^2{E}_{N\times N}+{\sigma }_{\text{b}}^2{J}_{N\times N}.$$ (A29)

Further, if the baseline and nonbaseline frames were acquired with the same exposure level, ${\sigma }_{\text{b}}^2={\sigma }_0^2/N_{\text{b}}$, where N_b is the total number of baseline frames. In this special case,

$$C_c={\sigma }_0^2\left(E_{N\times N}+\frac{1}{N_{\text{b}}}{J}_{N\times N}\right).$$ (A30)